Fat Tail in the Phytoplankton Movement Patterns and Swimming Behavior: New Insights into the Prey-Predator Interactions
Abstract
1. Introduction
2. Preminaries
3. Materials and Methods
3.1. Phytoplankton Movement Data Series Description
3.2. Calculation of Movement Pattern and Parameter Estimation
3.3. Goodness of Fit
4. Results
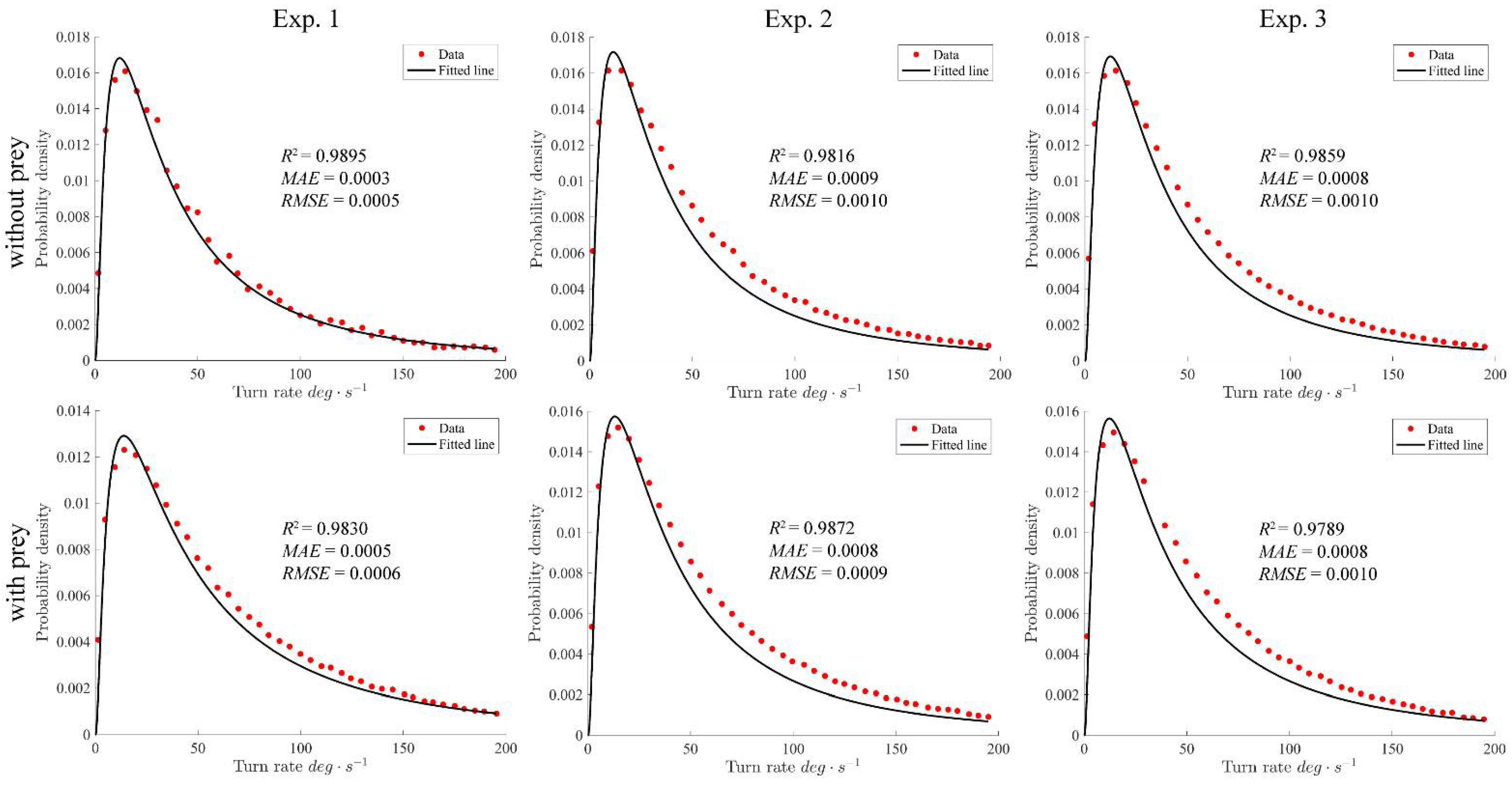
4.1. Turning Rates
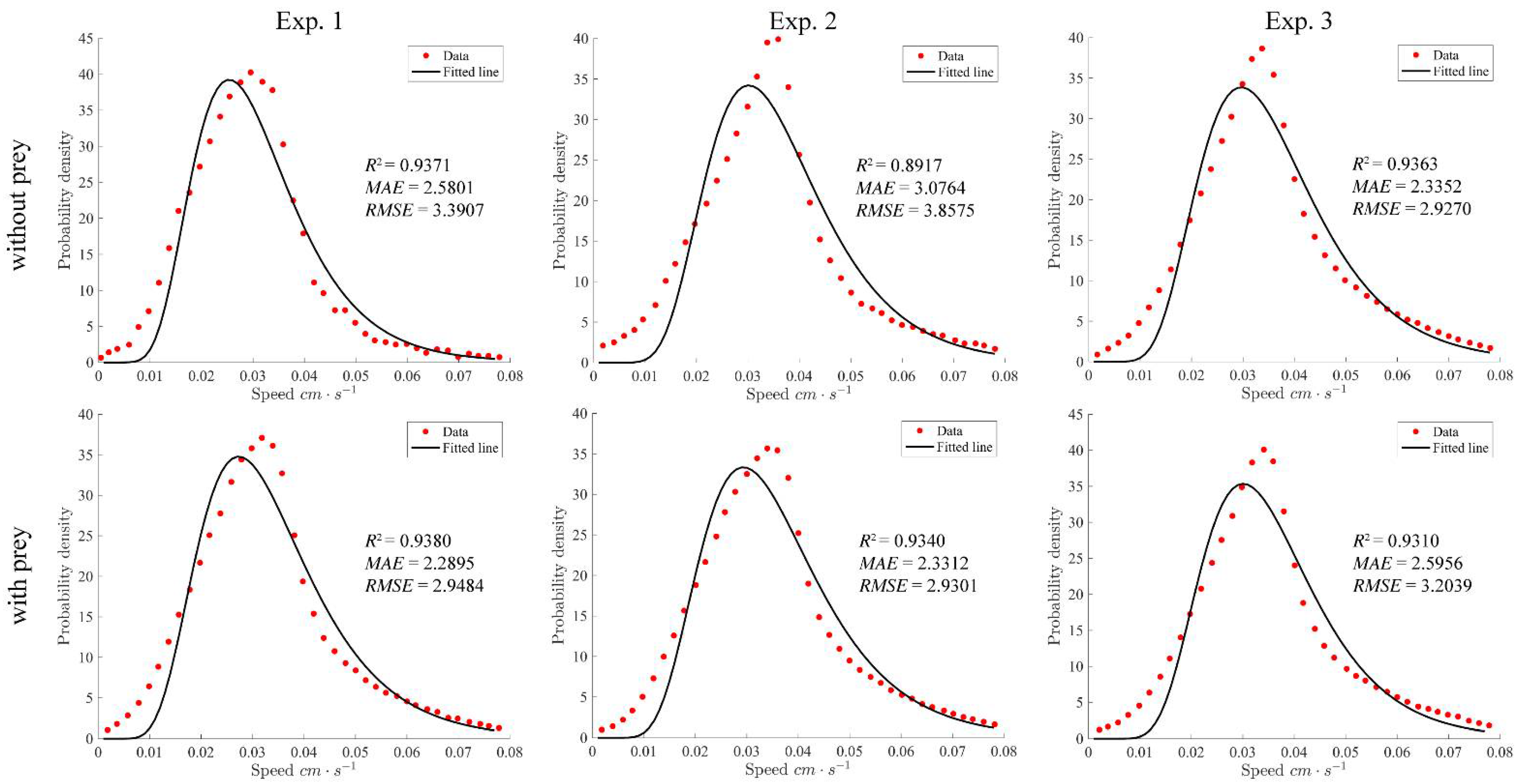
4.2. Swimming Speed
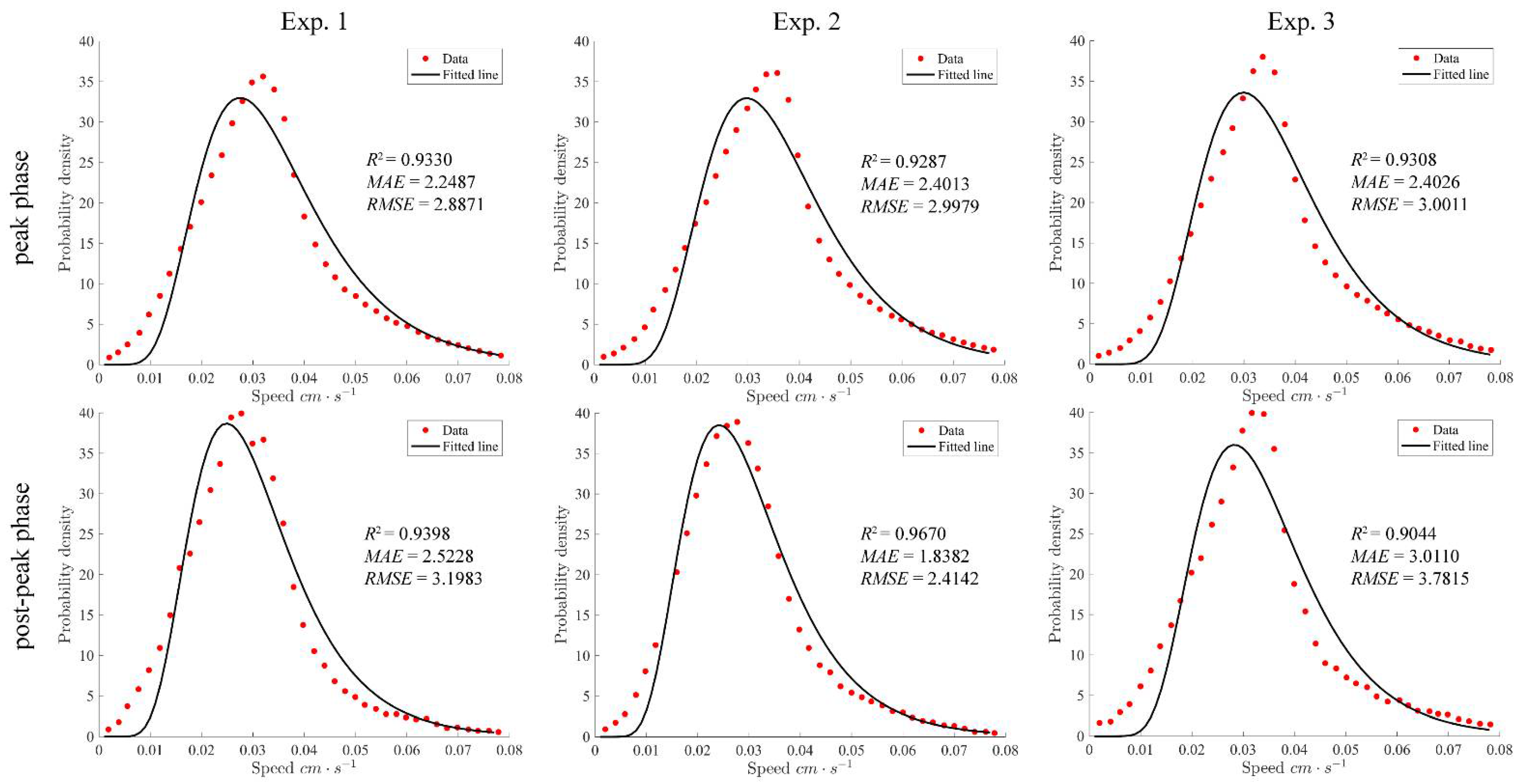
4.3. Swimming Speeds during the Peak and Post-Peak Phases
4.4. Run Lengths
4.5. Path Curvature
5. Discussion
5.1. The Known Knowns
5.2. The Known Unknowns
5.3. The Unknown Unknowns
5.4. Fractal and Fractional Characteristics of Movement Patterns of Phytoplankton
5.5. Prospect
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Fractal Analysis of Time Series of Phytoplankton Movement Patterns
Appendix A.1. Long-Range Dependence (LRD) of Phytoplankton Movement Patterns
Appendix A.2. Fractal Dimension and Local Self-Similarity of Phytoplankton Movement Patterns
Appendix A.3. Fractal Mechanism of Phytoplankton Movement Patterns
References
- Hays, G.C.; Richardson, A.J.; Robinson, C. Climate change and marine plankton. Trends Ecol. Evol. 2005, 20, 337–344. [Google Scholar] [CrossRef] [PubMed]
- Levandowsky, M.; Klafter, J.; White, B. Swimming behavior and chemosensory responses in the protistan microzooplankton as a function of the hydrodynamic regime. Bull. Mar. Sci. 1988, 43, 758–763. [Google Scholar]
- Menden-Deuer, S. Inherent high correlation of individual motility enhances population dispersal in a heterotrophic, planktonic protist. PLoS Comput. Biol. 2010, 6, e1000942. [Google Scholar] [CrossRef] [PubMed]
- Visser, A.W. Lagrangian modelling of plankton motion: From deceptively simple random walks to Fokker-Planck and back again. J. Mar. Syst. 2008, 70, 287–299. [Google Scholar] [CrossRef]
- Menden-Deuer, S.; Grunbaum, D. Individual foraging behaviors and population distributions of a planktonic predator aggregating to phytoplankton thin layers. Limnol. Oceanogr. 2006, 51, 109–116. [Google Scholar] [CrossRef]
- Bartumeus, F.; Peters, F.; Pueyo, S.; Marrasé, C.; Catalan, J. Helical Lévy walks: Adjusting searching statistics to resource availability in microzooplankton. Proc. Natl. Acad. Sci. USA 2003, 100, 12771–12775. [Google Scholar] [CrossRef]
- Xiao, X.; He, J.; Yu, Y.; Cazelles, B.; Li, M.; Jiang, Q.; Xu, C. Teleconnection between phytoplankton dynamics in north temperate lakes and global climatic oscillation by time-frequency analysis. Water Res. 2019, 154, 267–276. [Google Scholar] [CrossRef]
- Xiao, X.; He, J.; Huang, H.; Miller, T.R.; Christakos, G.; Reichwaldt, E.S.; Ghadouani, A.; Lin, S.; Xu, X.; Shi, J. A novel single-parameter approach for forecasting algal blooms. Water Res. 2017, 108, 222–231. [Google Scholar] [CrossRef]
- Xiao, X.; Agusti, S.; Pan, Y.; Yu, Y.; Li, K.; Wu, J.; Duarte, C.M. Warming amplifies the frequency of Harmful Algal Blooms with eutrophication in Chinese coastal waters. Environ. Sci. Technol. 2019, 53, 13031–13041. [Google Scholar] [CrossRef]
- Xu, C.; Ge, Z.; Li, C.; Wan, F.; Xiao, X. Inhibition of harmful algae Phaeocystis globosa and Prorocentrum donghaiense by extracts of coastal invasive plant Spartina alterniflora. Sci. Total Environ. 2019, 696, 133930. [Google Scholar] [CrossRef]
- Xiao, X.; Li, C.; Huang, H.; Lee, Y.P. Inhibition effect of natural flavonoids on red tide alga Phaeocystis globosa and its quantitative structure-activity relationship. Environ. Sci. Pollut. Res. 2019, 26, 23763–23776. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Janowitz, G.S.; Kamykowski, D. Influence of environmental nutrient conditions on Gymnodinium breve (Dinophyceae) population dynamics: A numerical study. Mar. Ecol. Prog. Ser. 2001, 213, 13–37. [Google Scholar] [CrossRef]
- Kim, H.; Spivack, A.J.; Menden-Deuer, S. pH alters the swimming behaviors of the raphidophyte Heterosigma akashiwo: Implications for bloom formation in an acidified ocean. Harmful Algae 2013, 26, 1–11. [Google Scholar] [CrossRef]
- Harvey, E.L.; Menden-Deuer, S. Avoidance, movement, and mortality: The interactions between a protistan grazer and Heterosigma akashiwo, a harmful algal bloom species. Limnol. Oceanogr. 2011, 56, 371–378. [Google Scholar] [CrossRef]
- Sengupta, A.; Carrara, F.; Stocker, R. Phytoplankton can actively diversify their migration strategy in response to turbulent cues. Nature 2017, 543, 7646. [Google Scholar] [CrossRef]
- Carrara, F.; Sengupta, A.; Behrendt, L.; Vardi, A.; Stocker, R. Bistability in oxidative stress response determines the migration behavior of phytoplankton in turbulence. Proc. Natl. Acad. Sci. USA 2021, 118. [Google Scholar] [CrossRef] [PubMed]
- An, X.; Li, X.; Gong, C. Research progress on ecological characteristics of Oxyrrhis marina. J. Shanghai Ocean Univ. 2013, 22, 364–369. [Google Scholar]
- Krishnamurthy, D.; Li, H.; Du Rey, F.B.; Cambournac, P.; Larson, A.G.; Li, E.; Prakash, M. Scale-free vertical tracking microscopy. Nat. Methods 2020, 17, 1040–1051. [Google Scholar] [CrossRef]
- Lohmann, A.C.; Evangelista, D.; Waldrop, L.D.; Mah, C.L.; Hedrick, T.L. Covering Ground: Movement Patterns and Random Walk Behavior in Aquilonastra anomala Sea Stars. Biol. Bull. 2016, 231, 130–141. [Google Scholar] [CrossRef]
- Seuront, L.; Duponchel, A.C.; Chapperon, C. Heavy-tailed distributions in the intermittent motion behaviour of the intertidal gastropod Littorina littorea. Phys. A Stat. Mech. Its Appl. 2007, 385, 573–582. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.; Murphy, E.; Prince, P.; Stanley, H.E. Lévy flight search patterns of wandering albatrosses. Nature 1996, 381, 413. [Google Scholar] [CrossRef]
- Michalec, F.G.; Ka, S.; Holzner, M.; Souissi, S.; Ianora, A.; Hwang, J.S. Changes in the swimming behavior of Pseudodiaptomus annandalei (Copepoda, Calanoida) adults exposed to the diatom toxin 2-trans, 4-trans decadienal. Harmful Algae 2013, 30, 56–64. [Google Scholar] [CrossRef]
- Huo, H.; He, R.; Zhang, R.; Yuan, J. Swimming Escherichia coli Cells Explore the Environment by Lévy Walk. Appl. Environ. Microbiol. 2021, 87. [Google Scholar] [CrossRef]
- Dannemann, T.; Boyer, D.; Miramontes, O. Lévy flight movements prevent extinctions and maximize population abundances in fragile Lotka–Volterra systems. Proc. Natl. Acad. Sci. USA 2018, 115, 3794–3799. [Google Scholar] [CrossRef] [PubMed]
- Ghanbari, B.; Günerhan, H.; Srivastava, H.M. An application of the Atangana-Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos Solitons Fractals 2020, 138, 109910. [Google Scholar] [CrossRef]
- Ghanbari, B.; Djilali, S. Mathematical analysis of a fractional-order predator-prey model with prey social behavior and infection developed in predator population. Chaos Solitons Fractals 2020, 138, 109960. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, R.; Cattani, C.; Samet, B. Chaotic behaviour of fractional predator-prey dynamical system. Chaos Solitons Fractals 2020, 135, 109811. [Google Scholar] [CrossRef]
- Yavuz, M.; Sene, N. Stability Analysis and Numerical Computation of the Fractional Predator–Prey Model with the Harvesting Rate. Fractal Fract. 2020, 4, 35. [Google Scholar] [CrossRef]
- Owolabi, K.M. Dynamical behaviour of fractional-order predator-prey system of Holling-type. Discret. Contin. Dyn. Syst. S 2020, 13, 823–834. [Google Scholar] [CrossRef]
- Bonyah, E.; Atangana, A.; Elsadany, A.A. A fractional model for predator-prey with omnivore. Chaos Interdiscip. J. Nonlinear Sci. 2019, 29, 013136. [Google Scholar] [CrossRef]
- Yu, S.; Li, C.; Xu, C.; Effiong, K.; Xiao, X. Understanding the inhibitory mechanism of antialgal allelochemical flavonoids from genetic variations: Photosynthesis, toxin synthesis and nutrient utility. Ecotoxicol. Environ. Saf. 2019, 177, 18–24. [Google Scholar] [CrossRef] [PubMed]
- Wu, Y.; Wang, F.; Xiao, X.; Liu, J.; Wu, C.; Chen, H.; Kerr, P.; Shurin, J. Seasonal changes in phosphorus competition and allelopathy of a benthic microbial assembly facilitate prevention of cyanobacterial blooms. Environ. Microbiol. 2017, 19, 2483–2494. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Xiao, X.; Lin, F.; Grossart, H.-P.; Nie, Z.; Sun, L.; Xu, C.; Shi, J. Continuous-release beads of natural allelochemicals for the long-term control of cyanobacterial growth: Preparation, release dynamics and inhibitory effects. Water Res. 2016, 95, 113–123. [Google Scholar] [CrossRef]
- Huang, H.; Xiao, X.; Ghadouani, A.; Wu, J.; Nie, Z.; Peng, C.; Xu, X.; Shi, J. Effects of Natural Flavonoids on Photosynthetic Activity and Cell Integrity in Microcystis aeruginosa. Toxins 2015, 7, 66–80. [Google Scholar] [CrossRef] [PubMed]
- Xiao, X.; Huang, H.M.; Ge, Z.W.; Rounge, T.B.; Shi, J.Y.; Xu, X.H.; Li, R.; Chen, Y. A pair of chiral flavonolignans as novel anti-cyanobacterial allelochemicals derived from barley straw (Hordeum vulgare): Characterization and comparison of their anti-cyanobacterial activities. Environ. Microbiol. 2014, 16, 1238–1251. [Google Scholar] [CrossRef]
- Blanc-Mathieu, R.; Krasovec, M.; Hebrard, M.; Yau, S.; Desgranges, E.; Martin, J.; Schackwitz, W.; Kuo, A.; Salin, G.; Donnadieu, C.; et al. Population genomics of picophytoplankton unveils novel chromosome hypervariability. Sci. Adv. 2017, 3, e1700239. [Google Scholar] [CrossRef]
- Guo, R.; Liang, Y.; Xin, Y.; Wang, L.; Cao, C.; Xie, R.; Zhang, C.; Tian, J.; Zhang, Y. Insight into the pico-and nano-phytoplankton communities in the deepest biosphere, the Mariana Trench. Front. Microbiol. 2018, 9, 2289. [Google Scholar] [CrossRef]
- Khan, S.; Arakawa, O.; Onoue, Y. Neurotoxins in a toxic red tide of Heterosigma akashiwo (Raphidophyceae) in Kagoshima Bay, Japan. Aquac. Res. 1997, 28, 9–14. [Google Scholar] [CrossRef]
- Hansen, F.C.; Witte, H.J.; Passarge, J. Grazing in the heterotrophic dinoflagellate Oxyrrhis marina: Size selectivity and preference for calcified Emiliania huxleyi cells. J. Aquat. Microb. Ecol. 1996, 10, 307–313. [Google Scholar] [CrossRef]
- Berg, H.C.; Brown, D.A. Chemotaxis in Escherichia coli analysed by Three-dimensional Tracking. Nat. Cell Biol. 1972, 239, 500–504. [Google Scholar] [CrossRef]
- He, J.; Chen, Y.; Wu, J.; Stow, D.; Christakos, G. Space-Time Chlorophyll-a Retrieval in Optically Complex Waters that Accounts for Remote Sensing and Modeling Uncertainties and Improves Remote Estimation Accuracy. Water Res. 2020, 171, 1–17. [Google Scholar] [CrossRef]
- Samorodnitsky, G.; Taqqu, M.S. Stable Non-Gaussian Random Processes: Stochastic Models with Infinite Variance; Chapman and Hall: New York, NY, USA, 1994. [Google Scholar]
- Adler, R.J.; Feldman, R.E.; Taqqu, M.S. (Eds.) A Practical Guide to Heavy Tails: Statistical Techniques and Applications; Birkhäuser: Boston, MA, USA, 1998. [Google Scholar]
- Li, M. Fractal time series—A tutorial review. Math. Probl. Eng. 2010, 2010, 157264. [Google Scholar] [CrossRef]
- Fontugne, R.; Abry, P.; Fukuda, K.; Veitch, D.; Cho, K.; Borgnat, P.; Wendt, H. Scaling in internet traffic: A 14 year and 3 day longitudinal study, with multiscale analyses and random projections. IEEE/ACM Trans. Netw. 2017, 25, 2152–2165. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; van Ness, J.W. Fractional Brownian motions, fractional noises and applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Mandelbrot, B.B. Gaussian Self-Affinity and Fractals; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Mandelbrot, B.B. Fast fractional Gaussian noise generator. Water Resour. Res. 1971, 7, 543–553. [Google Scholar] [CrossRef]
- Li, M. Record length requirement of long-range dependent teletraffic. Physics A 2017, 472, 164–187. [Google Scholar] [CrossRef]
- Davies, S.; Hall, P. Fractal analysis of surface roughness by using spatial data. J. R. Stat. Soc. Ser. B 1999, 61, 3–37. [Google Scholar] [CrossRef]
- Li, M. Generation of teletraffic of generalized Cauchy type. Phys. Scr. 2010, 81, 025007. [Google Scholar] [CrossRef]
- Li, M.; Sun, X.; Xiao, X. Revisiting fractional Gaussian noise. Physics A 2019, 514, 56–62. [Google Scholar] [CrossRef]
- Li, M. Multi-fractional generalized Cauchy process and its application to teletraffic. Physics A 2020, 550, 123982. [Google Scholar] [CrossRef]



| Parameter | |||||
|---|---|---|---|---|---|
| + Prey Cells | + Cell-Free Filtrate 3 | + Prey Cells | + Cell-Free Filtrate | ||
| turning rate | before | 3.6743 | 3.6600 ± 0.0060 | 1.0883 | 1.0862 ± 0.0233 |
| after | 3.9522 | 3.7450 ± 0.0094 | 1.1505 | 1.0978 ± 0.0261 | |
| swimming speed | before | −3.5349 | −3.3756 ± 0.0071 | 0.3738 | 0.3666 ± 0.0061 |
| after | −3.4491 | −3.3825 ± 0.0035 | 0.3896 | 0.3662 ± 0.0189 | |
| peak speed | peak | −3.4297 | −3.3722 ± 0.0002 | 0.4050 | 0.3748 ± 0.0060 |
| post-peak | −3.5459 | −3.4982 ± 0.0949 | 0.3851 | 0.3812 ± 0.0209 | |
| run length | before | −4.0249 | −3.9421 ± 0.0082 | 0.6347 | 0.5847 ± 0.0075 |
| after | −4.0531 | −3.9862 ± 0.0297 | 0.5585 | 0.5576 ± 0.0075 | |
| path curvature | before | 3.5458 | 3.6899 ± 0.0271 | 1.2895 | 1.5173 ± 0.0303 |
| after | 3.7050 | 3.7333 ± 0.0176 | 1.3763 | 1.5295 ± 0.0060 | |
| Parameter | |||||
|---|---|---|---|---|---|
| + Prey Cells | + Cell-Free Filtrate 1 | + Prey Cells | + Cell-Free Filtrate | ||
| turning rate | before | 71.2775 | 70.1197 ± 1.3512 | 11,527.8962 | 11,115.1684 ± 1236.9613 |
| after | 100.8914 | 77.3377 ± 2.9383 | 28,065.6870 | 14,057.3602 ± 2208.8363 | |
| swimming speed | before | 0.03127 | 0.03658 ± 0.00018 | 0.00015 | 0.00019 ± 0.00000 |
| after | 0.03428 | 0.03632 ± 0.00013 | 0.00019 | 0.00019 ± 0.00002 | |
| peak speed | peak | 0.03517 | 0.03681 ± 0.00007 | 0.00022 | 0.00020 ± 0.00001 |
| post-peak | 0.03106 | 0.03260 ± 0.00283 | 0.00015 | 0.00017 ± 0.00001 | |
| run length | before | 0.02185 | 0.02303 ± 0.00029 | 0.00024 | 0.00022 ± 0.00001 |
| after | 0.02030 | 0.02170 ± 0.00055 | 0.00015 | 0.00017 ± 0.00000 | |
| path curvature | before | 79.6141 | 126.7970 ± 9.2541 | 27,089.9745 | 146,528.6200 ± 35,998.8028 |
| after | 104.8132 | 134.7220 ± 3.6178 | 62,047.0017 | 170,352.2146 ± 12,615.5869 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, X.; Xu, C.; Yu, Y.; He, J.; Li, M.; Cattani, C. Fat Tail in the Phytoplankton Movement Patterns and Swimming Behavior: New Insights into the Prey-Predator Interactions. Fractal Fract. 2021, 5, 49. https://doi.org/10.3390/fractalfract5020049
Xiao X, Xu C, Yu Y, He J, Li M, Cattani C. Fat Tail in the Phytoplankton Movement Patterns and Swimming Behavior: New Insights into the Prey-Predator Interactions. Fractal and Fractional. 2021; 5(2):49. https://doi.org/10.3390/fractalfract5020049
Chicago/Turabian StyleXiao, Xi, Caicai Xu, Yan Yu, Junyu He, Ming Li, and Carlo Cattani. 2021. "Fat Tail in the Phytoplankton Movement Patterns and Swimming Behavior: New Insights into the Prey-Predator Interactions" Fractal and Fractional 5, no. 2: 49. https://doi.org/10.3390/fractalfract5020049
APA StyleXiao, X., Xu, C., Yu, Y., He, J., Li, M., & Cattani, C. (2021). Fat Tail in the Phytoplankton Movement Patterns and Swimming Behavior: New Insights into the Prey-Predator Interactions. Fractal and Fractional, 5(2), 49. https://doi.org/10.3390/fractalfract5020049








