Elastic Rough Surface Contact and the Root Mean Square Slope of Measured Surfaces over Multiple Scales
Abstract
1. Introduction
2. Methods
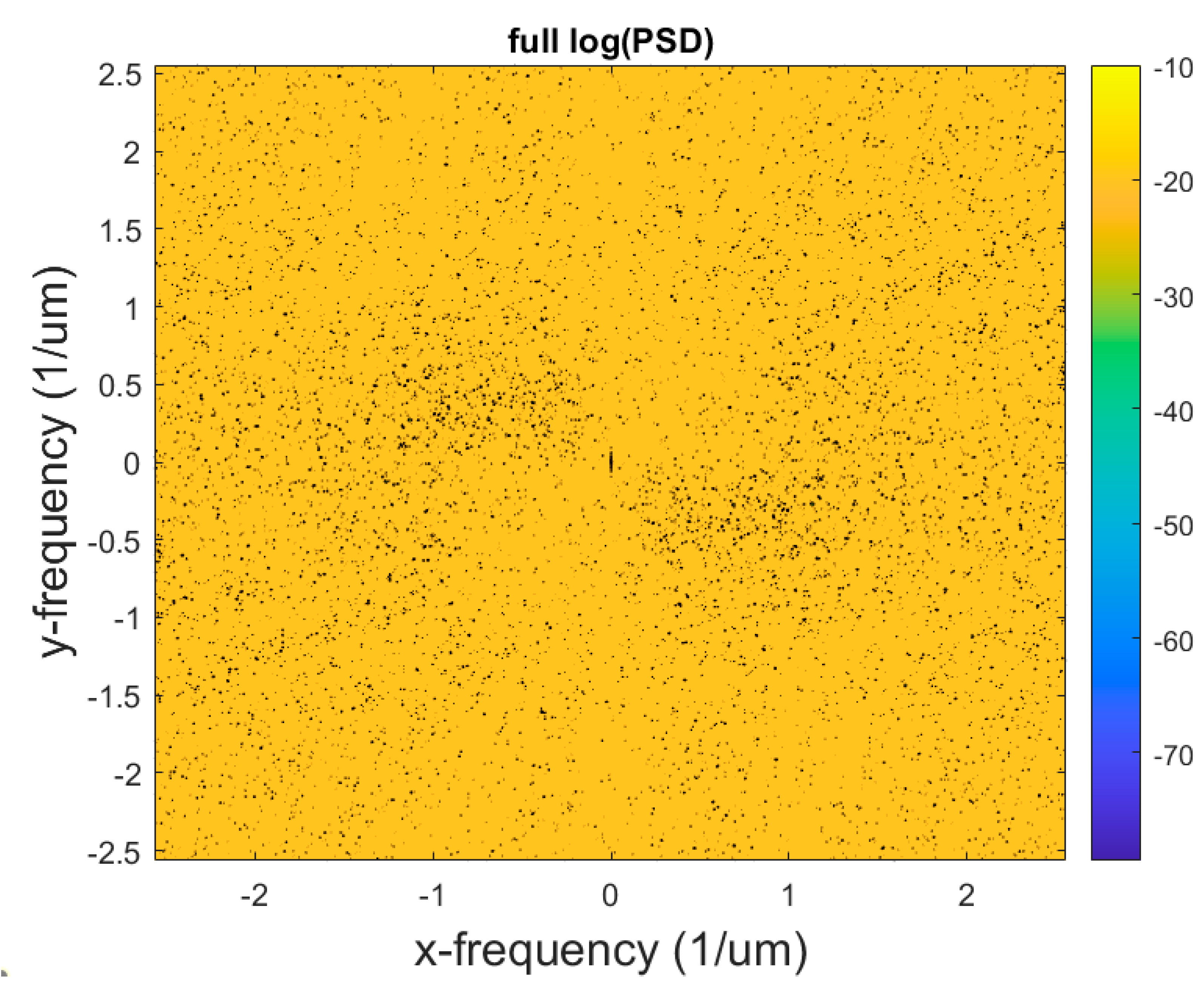
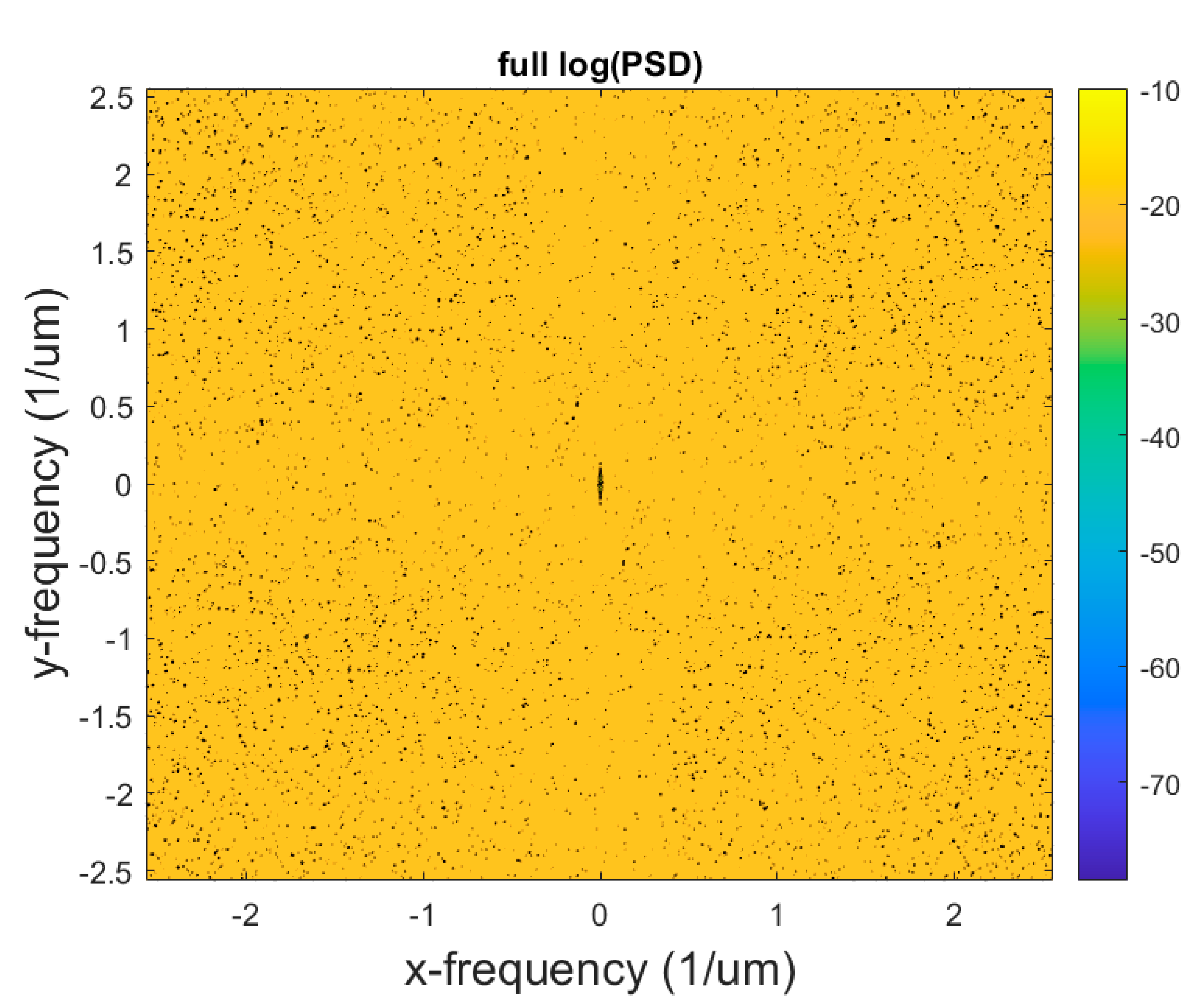
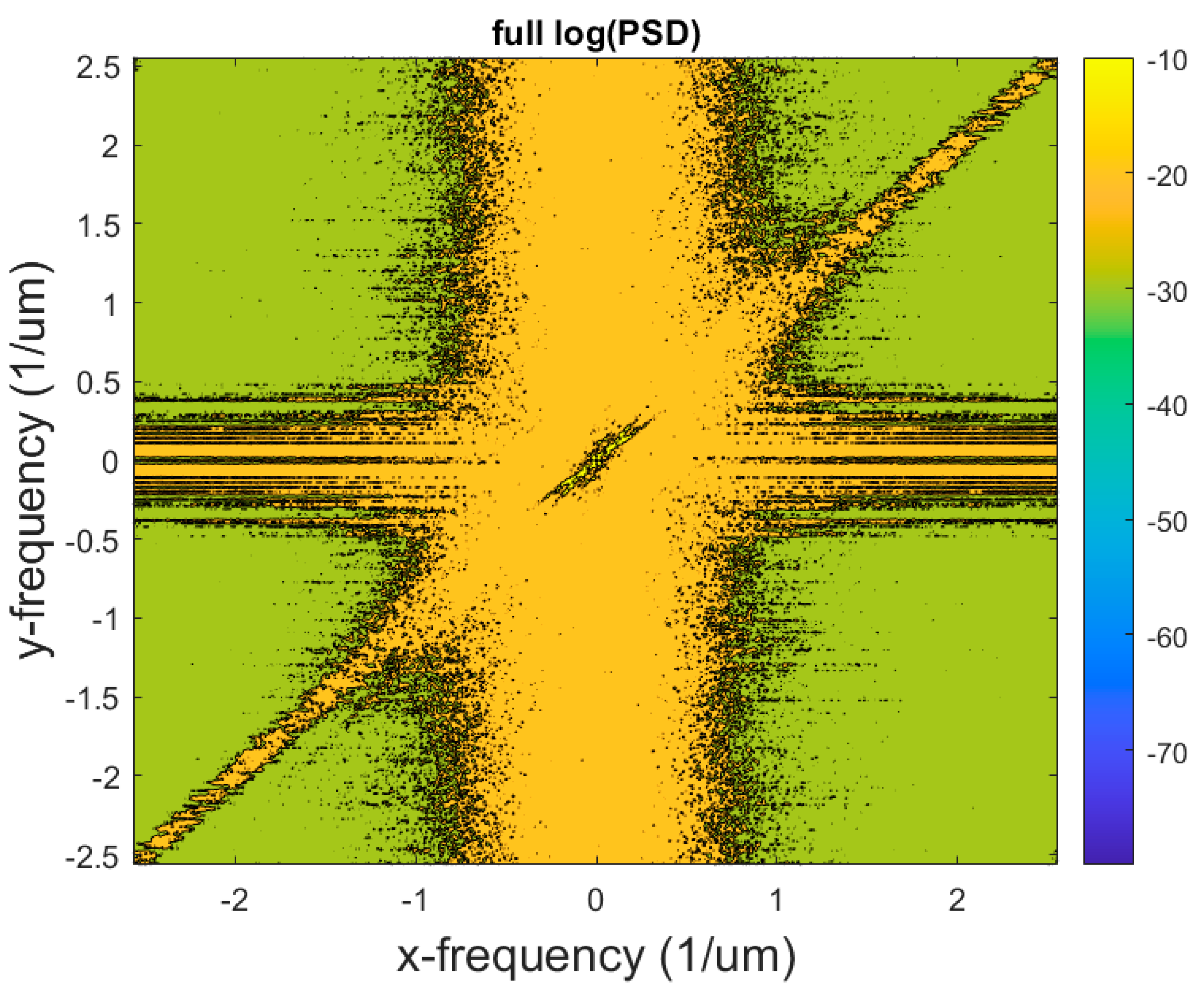
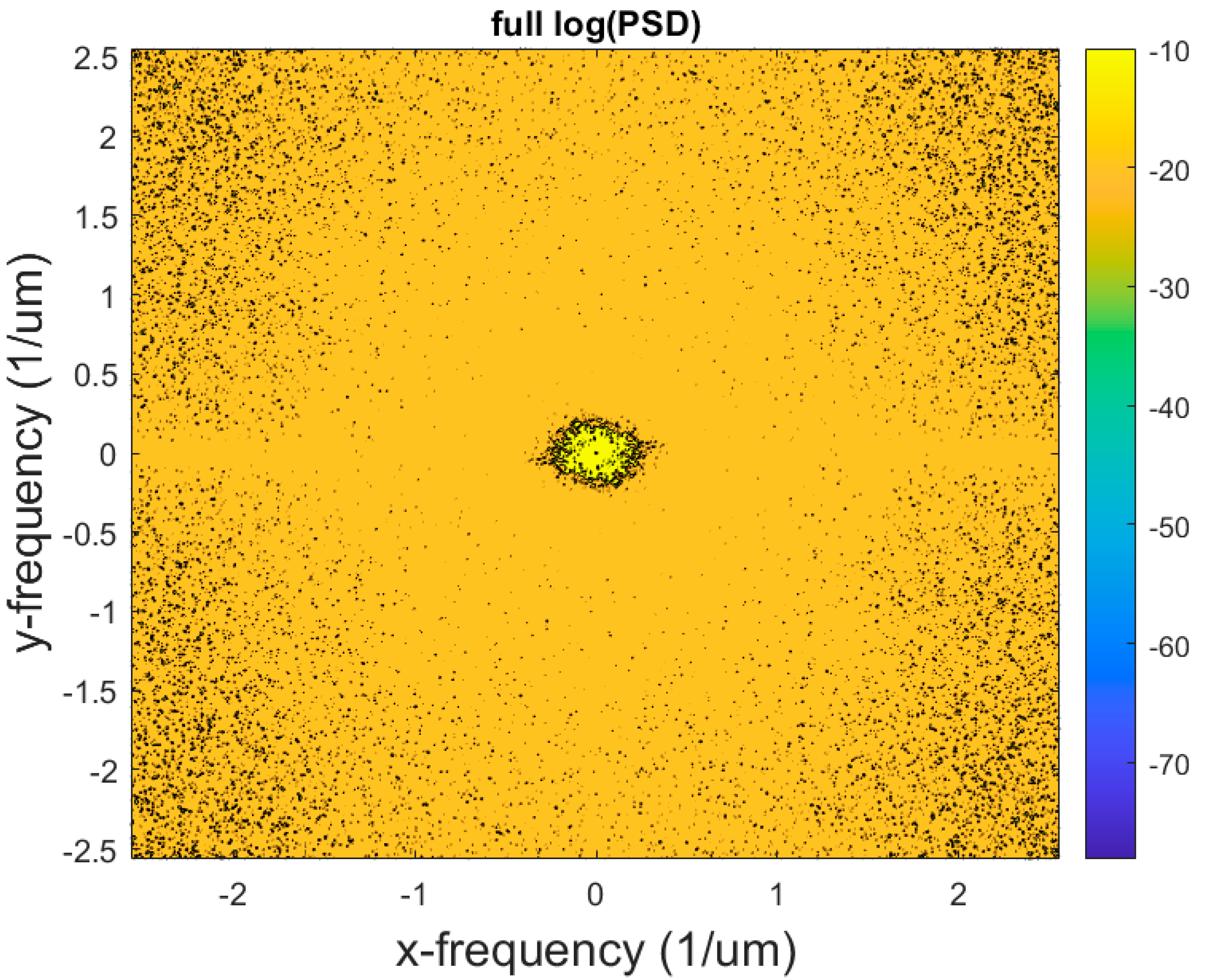
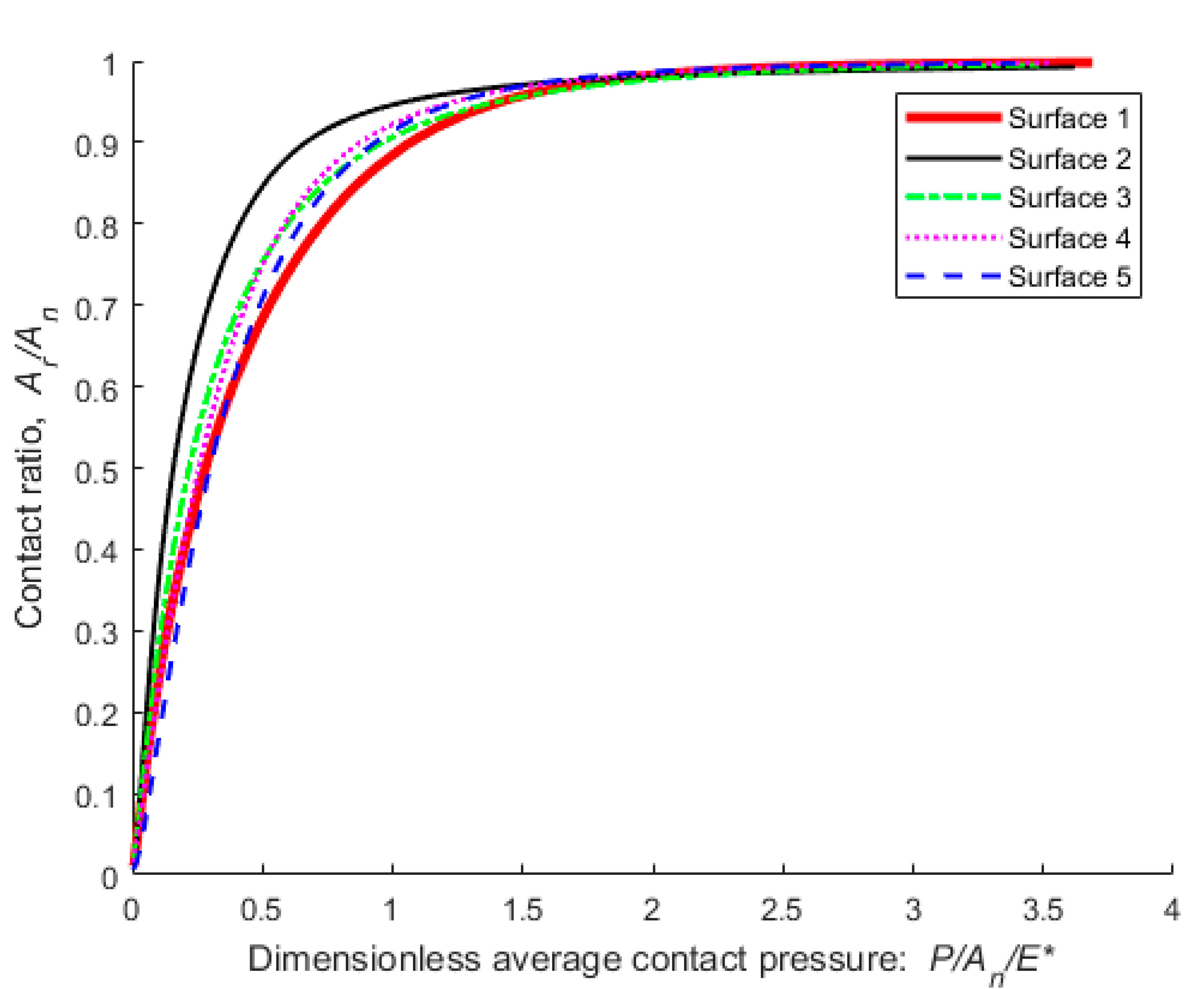
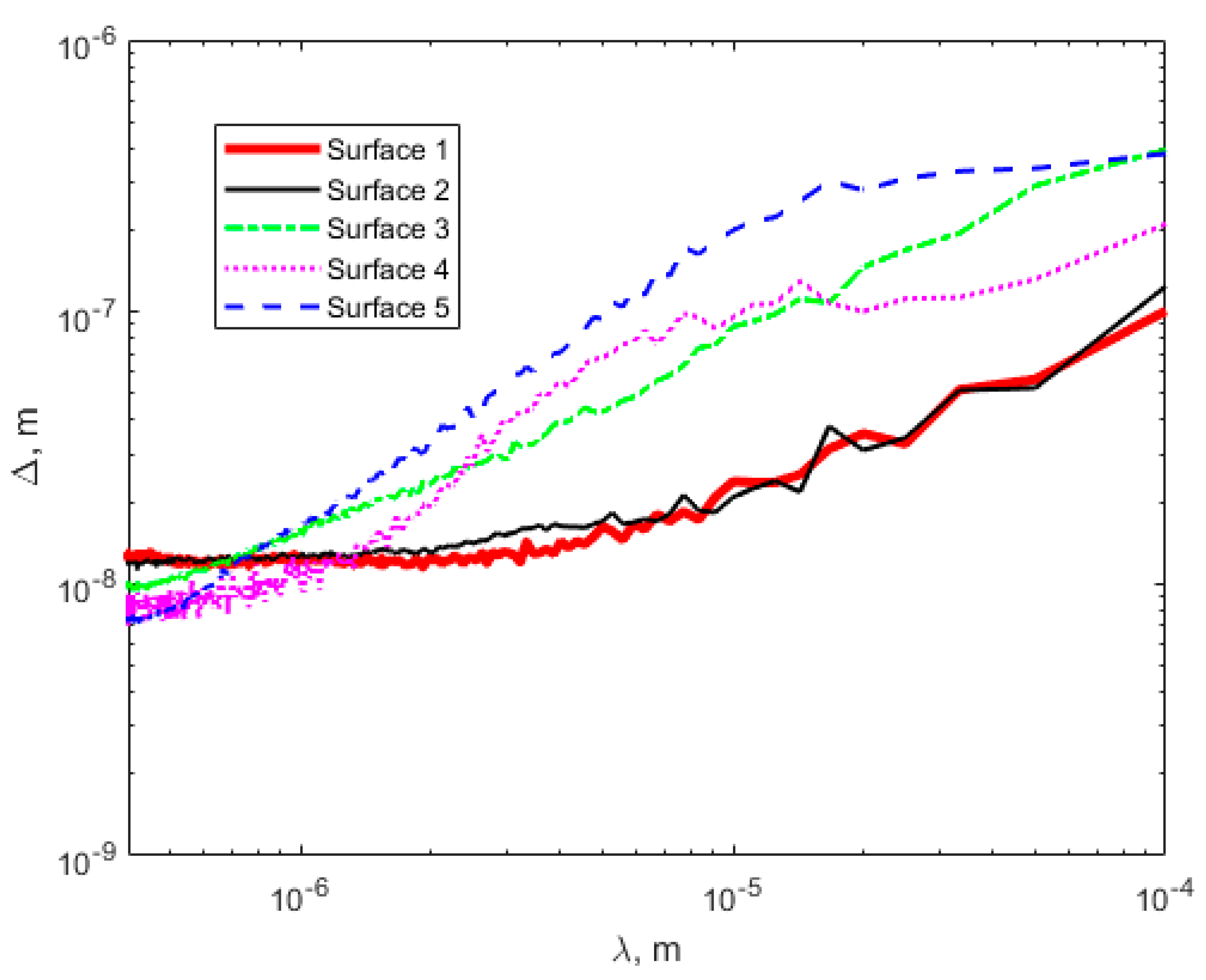
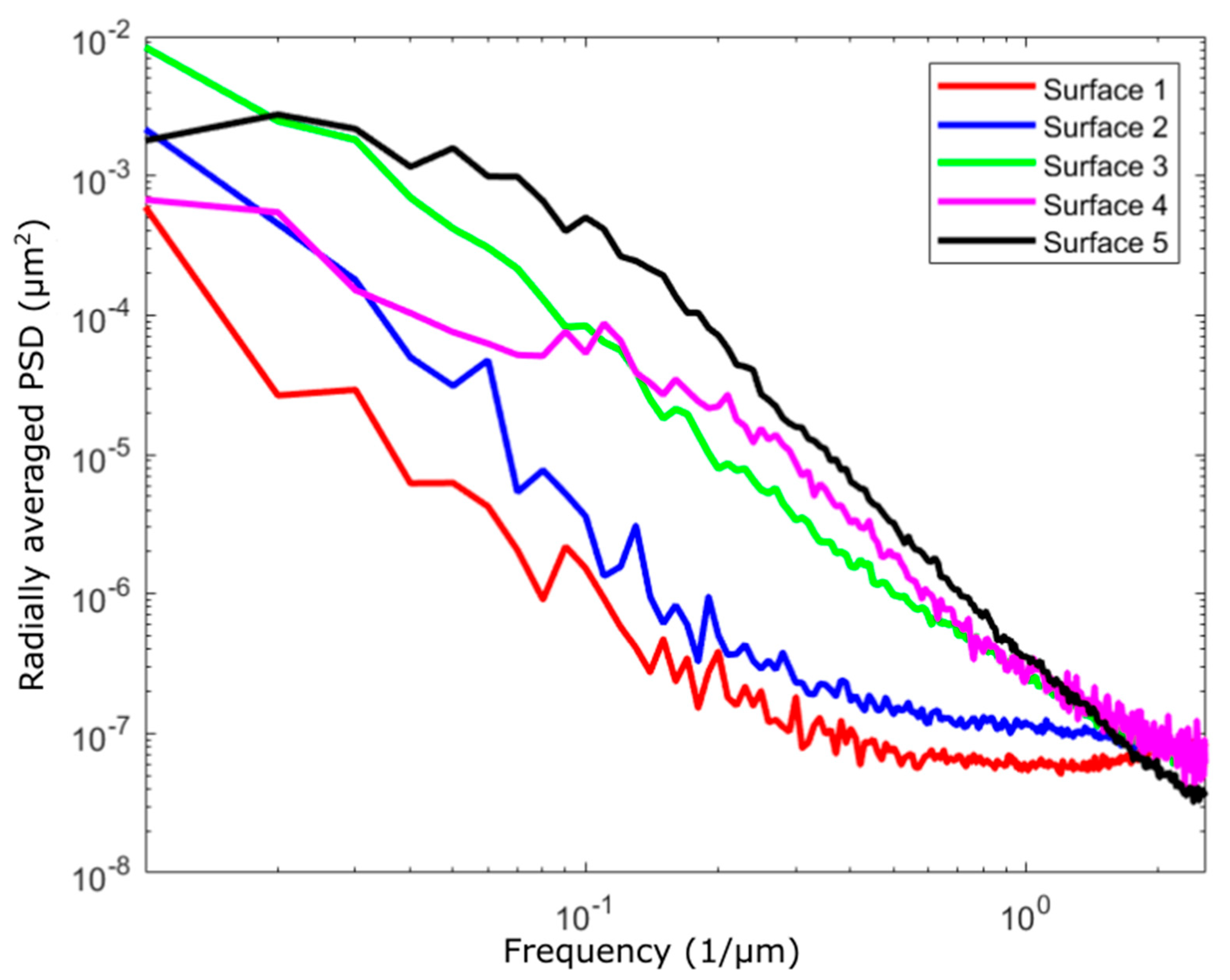
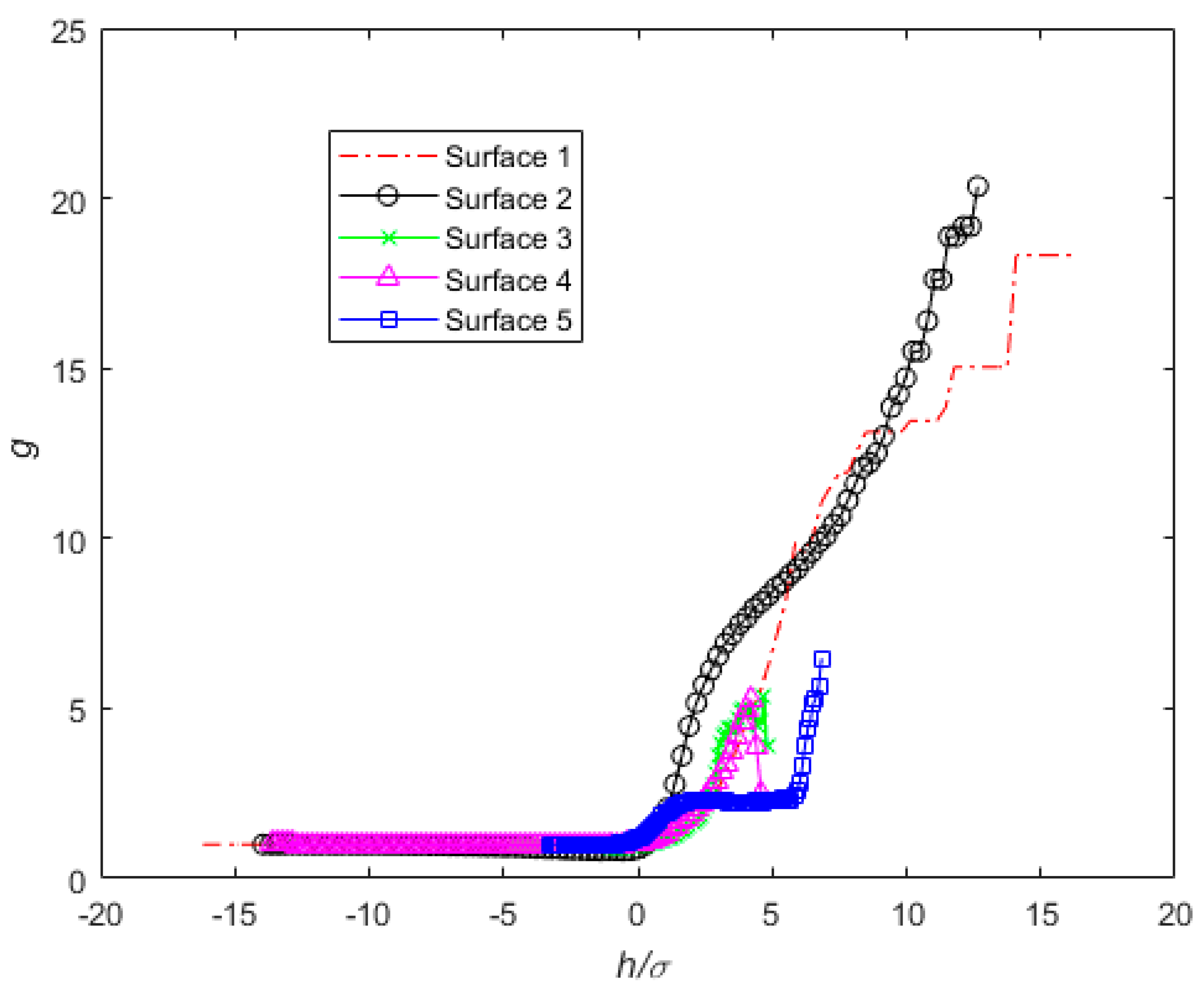
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

References
- Kligerman, Y.; Etsion, I.; Brizmer, V.; Kadin, Y. Friction and contact between rough surfaces based on elastic-plastic sphere and rigid flat interaction. In Analysis and Simulation of Contact Problems; Springer: Berlin/Heidelberg, Germany, 2006; pp. 223–229. [Google Scholar]
- Lee, C.-H.; Polycarpou, A.A. Static friction experiments and verification of an improved elastic-plastic model including roughness effects. J. Tribol. 2007, 129, 754–760. [Google Scholar]
- Cohen, D.; Kligerman, Y.; Etsion, I. A model for contact and static friction of nominally flat rough surfaces under full stick contact condition. J. Tribol. 2008, 130, 031401. [Google Scholar]
- Cohen, D.; Kligerman, Y.; Etsion, I. The effect of surface roughness on static friction and junction growth of an elastic-plastic spherical contact. J. Tribol. 2009, 131, 021404. [Google Scholar]
- Chen, W.W.; Wang, Q.J. A numerical static friction model for spherical contacts of rough surfaces, influence of load, material, and roughness. J. Tribol. 2009, 131, 021402. [Google Scholar]
- Lee, C.-H.; Eriten, M.; Polycarpou, A.A. Application of elastic-plastic static friction models to rough surfaces with asymmetric asperity distribution. J. Tribol. 2010, 132, 031602. [Google Scholar]
- Li, L.; Etsion, I.; Talke, F. Contact area and static friction of rough surfaces with high plasticity index. J. Tribol. 2010, 132. [Google Scholar] [CrossRef]
- Menezes, P.L.; Kailas, S.V.; Lovell, M.R. Role of surface texture, roughness, and hardness on friction during unidirectional sliding. Tribol. Lett. 2011, 41, 1–15. [Google Scholar]
- Patil, D.B.; Eriten, M. Effects of interfacial strength and roughness on the static friction coefficient. Tribol. Lett. 2014, 56, 355–374. [Google Scholar]
- Wang, X.; Xu, Y.; Jackson, R.L. Elastic–Plastic sinusoidal waviness contact under combined normal and tangential loading. Tribol. Lett. 2017, 65, 45. [Google Scholar]
- Wang, X.; Xu, Y.; Jackson, R.L. Theoretical and finite element analysis of static friction between multi-scale rough surfaces. Tribol. Lett. 2018, 66, 146. [Google Scholar]
- Wang, X.; An, B.; Xu, Y.; Jackson, R.L. The effect of resolution on the deterministic finite element elastic-plastic rough surface contact under combined normal and tangential loading. Tribol. Int. 2020, 144, 106141. [Google Scholar]
- Ciavarella, M.; Murolo, G.; Demelio, G.; Barber, J.R. Elastic contact stiffness and contact resistance for the Weierstrass profile. J. Mech. Phys. Solids 2004, 52, 1247–1265. [Google Scholar]
- Greenwood, J.A. Constriction Resistance and the Real Area of Contact. Br. J. Appl. Phys. 1966, 17, 1621–1632. [Google Scholar]
- Kogut, L.; Komvopoulos, K. Electrical contact resistance theory for conductive rough surfaces. J. Appl. Phys. 2003, 94, 3153. [Google Scholar]
- Wilson, W.E.; Angadi, S.V.; Jackson, R.L. Electrical Contact Resistance Considering Multi-Scale Roughness. In Proceedings of the IEEE Holm Conference on Electrical Contacts, Orlando, FL, USA, 27–29 October 2008. [Google Scholar]
- Wilson, W.E.; Angadi, S.V.; Jackson, R.L. Surface Separation and Contact Resistance Considering Sinusoidal Elastic-Plastic Multi-Scale Rough Surface Contact. Wear 2010, 268, 190–201. [Google Scholar]
- Barber, J. Incremental stiffness and electrical contact conductance in the contact of rough finite bodies. Phys. Rev. E 2013, 87, 013203. [Google Scholar]
- Kogut, L.; Etsion, I. Electrical conductivity and friction force estimation in compliant electrical connectors. Tribol. Trans. 2000, 43, 816–822. [Google Scholar]
- Jackson, R.L.; Crandall, E.R.; Bozack, M.J. Rough surface electrical contact resistance considering scale dependent properties and quantum effects. J. Appl. Phys. 2015, 117, 195101. [Google Scholar]
- Greenwood, J.A.; Williamson, J.B.P. Contact of Nominally Flat Surfaces. Proc. R. Soc. Lond. A 1966, 295, 300–319. [Google Scholar]
- Jackson, R.L.; Malucci, R.D.; Angadi, S.; Polchow, J.R. A Simplified Model of Multiscale Electrical Contact Resistance and Comparison to Existing Closed Form Models. In Proceedings of the 55th IEEE Holm Conference on Electrical Contacts, Vancouver, BC, Canada, 14–16 September 2009; pp. 28–35. [Google Scholar]
- Malucci, R.D. Multi-spot model showing the effects of nano-spot sizes. In Proceedings of the IEEE Holm Conference on Electrical Contacts, Chicago, IL, USA, 26–28 September 2005; pp. 291–297. [Google Scholar]
- Bush, A.W.; Gibson, R.D.; Thomas, T.R. The elastic contact of a rough surface. Wear 1975, 35, 87–111. [Google Scholar] [CrossRef]
- Persson, B.N.J. Elastoplastic contact between randomly rough surfaces. Phys. Rev. Lett. 2001, 87, 116101. [Google Scholar]
- Carbone, G. A slightly corrected Greenwood and Williamson model predicts asymptotic linearity between contact area and load. J. Mech. Phys. Solids 2009, 57, 1093–1102. [Google Scholar] [CrossRef]
- Manners, W.; Greenwood, J.J.W. Some observations on Persson’s diffusion theory of elastic contact. Wear 2006, 261, 600–610. [Google Scholar]
- Xu, Y.; Jackson, R.; Marghitu, D.B. Structures. Statistical model of nearly complete elastic rough surface contact. Int. J. Solids Struct. 2014, 51, 1075–1088. [Google Scholar]
- Ciavarella, M. Rough contacts near full contact with a very simple asperity model. Tribol. Int. 2016, 93, 464–469. [Google Scholar]
- Archard, J.F. Elastic Deformation and the Laws of Friction. Proc. R. Soc. Lond. A 1957, 243, 190–205. [Google Scholar]
- Müser, M.H.; Dapp, W.B.; Bugnicourt, R.; Sainsot, P.; Lesaffre, N.; Lubrecht, T.A.; Persson, B.N.; Harris, K.; Bennett, A.; Schulze, K. Meeting the contact-mechanics challenge. Tribol. Lett. 2017, 65, 1–18. [Google Scholar]
- McGhee, A.J.; Pitenis, A.A.; Bennett, A.I.; Harris, K.L.; Schulze, K.D.; Urueña, J.M.; Ifju, P.G.; Angelini, T.E.; Müser, M.H.; Sawyer, W.G. Contact and deformation of randomly rough surfaces with varying root-mean-square gradient. Tribol. Lett. 2017, 65, 1–7. [Google Scholar]
- Campaná, C.; Müser, M.H. Contact mechanics of real vs. randomly rough surfaces: A Green’s function molecular dynamics study. EPL 2007, 77, 38005. [Google Scholar]
- Putignano, C.; Afferrante, L.; Carbone, G.; Demelio, G. The influence of the statistical properties of self-affine surfaces in elastic contacts: A numerical investigation. J. Mech. Phys. Solids 2012, 60, 973–982. [Google Scholar] [CrossRef]
- Yastrebov, V.A.; Anciaux, G.; Molinari, J.-F. The role of the roughness spectral breadth in elastic contact of rough surfaces. J. Mech. Phys. Solids 2017, 107, 469–493. [Google Scholar]
- Whitehouse, D.J.; Archard, J.F. The Properties of Random Surfaces of Significance in their Contact. Proc. R. Soc. Lond. A 1970, 316, 97–121. [Google Scholar]
- McCool, J.I. Relating Profile Instrument Measurements to the Functional Performance of Rough Surfaces. ASME J. Tribol. 1987, 109, 264–270. [Google Scholar]
- Sayles, R.S.; Thomas, T.R. Surface Topography as a nonstationary Random Process. Nature 1978, 271, 431–434. [Google Scholar]
- Zhang, X.; Jackson, R.L. An analysis of the multiscale structure of surfaces with various finishes. Tribol. Trans. 2017, 60, 121–134. [Google Scholar]
- Zhang, X.; Xu, Y.; Jackson, R.L. An analysis of generated fractal and measured rough surfaces in regards to their multi-scale structure and fractal dimension. Tribol. Int. 2017, 105, 94–101. [Google Scholar]
- Green, I. Exact Spectral Moments and Differentiability of the Weierstrass-Mandelbrot Fractal Function. J. Tribol. 2019, 142. [Google Scholar] [CrossRef]
- Gujrati, A.; Khanal, S.R.; Pastewka, L.; Jacobs, T.D.B. Combining TEM, AFM, and Profilometry for Quantitative Topography Characterization Across All Scales. ACS Appl. Mater. Interfaces 2018, 10, 29169–29178. [Google Scholar] [CrossRef]
- Gujrati, A.; Sanner, A.; Khanal, S.R.; Moldovan, N.; Zeng, H.; Pastewka, L.; Jacobs, T.D.B. Comprehensive topography characterization of polycrystalline diamond coatings. Surf. Topogr. Metrol. Prop. 2021, 9, 014003. [Google Scholar]
- Whitehouse, D. Fractal or fiction. Wear 2001, 249, 345–353. [Google Scholar]
- Candela, T.; Renard, F.; Bouchon, M.; Brouste, A.; Marsan, D.; Schmittbuhl, J.; Voisin, C. Characterization of Fault Roughness at Various Scales: Implications of Three-Dimensional High Resolution Topography Measurements. Pure Appl. Geophys. 2009, 166, 1817–1851. [Google Scholar]
- Pavelescu, D.; Tudor, A. On the Roughness Fractal Character, the Tribological Parameters and the Error Factors. Proc. Rom. Acad. 2004, 5, 1–6. [Google Scholar]
- Morag, Y.; Etsion, I. Resolving the contradiction of asperities plastic to elastic mode transition in current contact models of fractal rough surfaces. Wear 2007, 262, 624–629. [Google Scholar]
- Ciavarella, M.; Delfine, V.; Demelio, G. A “re-vitalized” Greenwood and Williamson model of elastic contact between fractal surfaces. J. Mech. Phys. Solids 2006, 54, 2569–2591. [Google Scholar] [CrossRef]
- Jackson, R.L.; Green, I. On the Modeling of Elastic Contact between Rough Surfaces. Tribol. Trans. 2011, 54, 300–314. [Google Scholar] [CrossRef]
- Xu, Y.; Jackson, R.L. Boundary element method (BEM) applied to the rough surface contact vs. BEM in computational mechanics. Friction 2019, 7, 359–371. [Google Scholar] [CrossRef]
- Xu, Y.; Jackson, R.L. Statistical models of nearly complete elastic rough surface contact-comparison with numerical solutions. Tribol. Int. 2017, 105, 274–291. [Google Scholar] [CrossRef]
- Vakis, A.I.; Yastrebov, V.A.; Scheibert, J.; Nicola, L.; Dini, D.; Minfray, C.; Almqvist, A.; Paggi, M.; Lee, S.; Limbert, G.; et al. Modeling and simulation in tribology across scales: An overview. Tribol. Int. 2018, 125, 169–199. [Google Scholar] [CrossRef]
- Jackson, R.L. An Analytical Solution to an Archard-type Fractal Rough Surface Contact Model. Trib. Trans. 2010, 53, 543–553. [Google Scholar]

| Parameter | Surface 1 | Surface 2 | Surface 3 |
|---|---|---|---|
| σ (µm) | 0.4057 | 0.6513 | 15.01 |
| mo (10−12/m2) | 0.1646 | 0.4242 | 225.3 |
| m2 | 0.0286 | 0.1143 | 8.03 |
| m4 (1012/m−2) | 0.01904 | 0.07683 | 3.560 |
| Bmax | 0.019 | 0.0283 | 0.1958 |
| Parameter | Surface 1 | Surface 2 | Surface 3 | Surface 4 | Surface 5 |
|---|---|---|---|---|---|
| σ (µm) | 0.2282 | 0.2293 | 0.5241 | 0.4133 | 0.7838 |
| mo (10−12/m2) | 0.05207 | 0.05257 | 0.2748 | 0.1708 | 0.6144 |
| m2 | 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
| m4 (1012/m−2) | 79.41 | 76.88 | 61.72 | 65.14 | 2.584 |
| α | 4.135 | 4.042 | 16.96 | 11.12 | 1.588 |
| Bave | 0.0158 | 0.0158 | 0.0165 | 0.0136 | 0.0168 |
| Bmax | 0.0329 | 0.0307 | 0.0257 | 0.0237 | 0.0224 |
| 1.000 | 1.000 | 1.000 | 1.000 | 1.000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jackson, R.L.; Xu, Y.; Saha, S.; Schulze, K.D. Elastic Rough Surface Contact and the Root Mean Square Slope of Measured Surfaces over Multiple Scales. Fractal Fract. 2021, 5, 44. https://doi.org/10.3390/fractalfract5020044
Jackson RL, Xu Y, Saha S, Schulze KD. Elastic Rough Surface Contact and the Root Mean Square Slope of Measured Surfaces over Multiple Scales. Fractal and Fractional. 2021; 5(2):44. https://doi.org/10.3390/fractalfract5020044
Chicago/Turabian StyleJackson, Robert L., Yang Xu, Swarna Saha, and Kyle D. Schulze. 2021. "Elastic Rough Surface Contact and the Root Mean Square Slope of Measured Surfaces over Multiple Scales" Fractal and Fractional 5, no. 2: 44. https://doi.org/10.3390/fractalfract5020044
APA StyleJackson, R. L., Xu, Y., Saha, S., & Schulze, K. D. (2021). Elastic Rough Surface Contact and the Root Mean Square Slope of Measured Surfaces over Multiple Scales. Fractal and Fractional, 5(2), 44. https://doi.org/10.3390/fractalfract5020044







