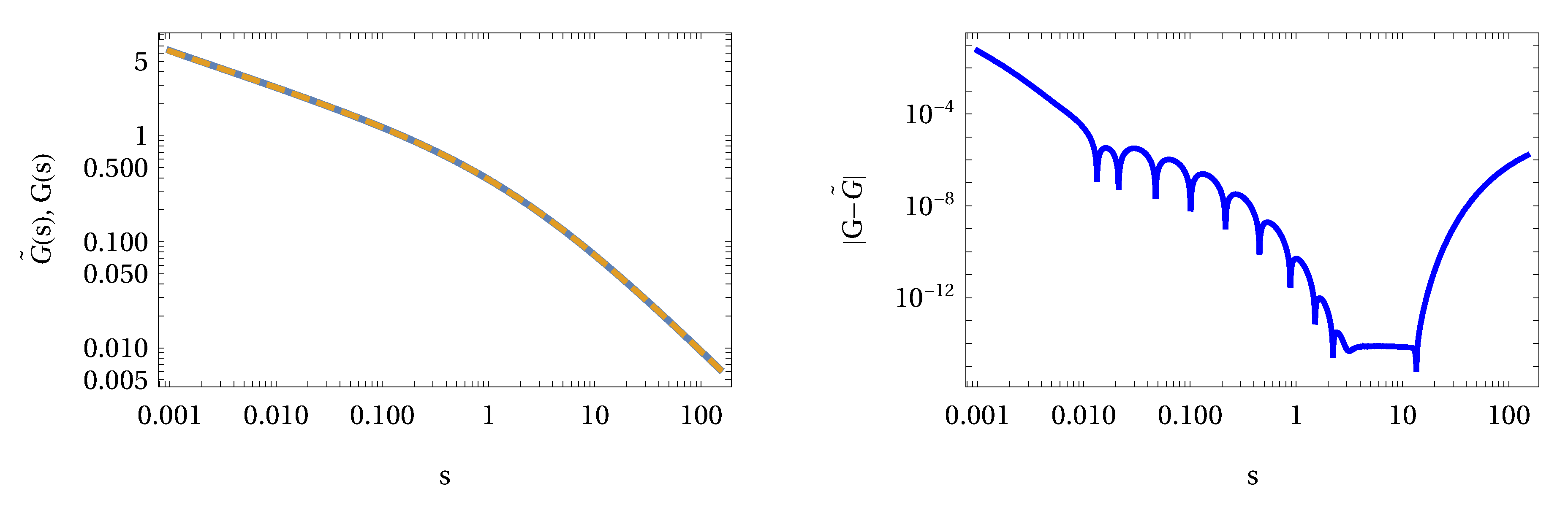
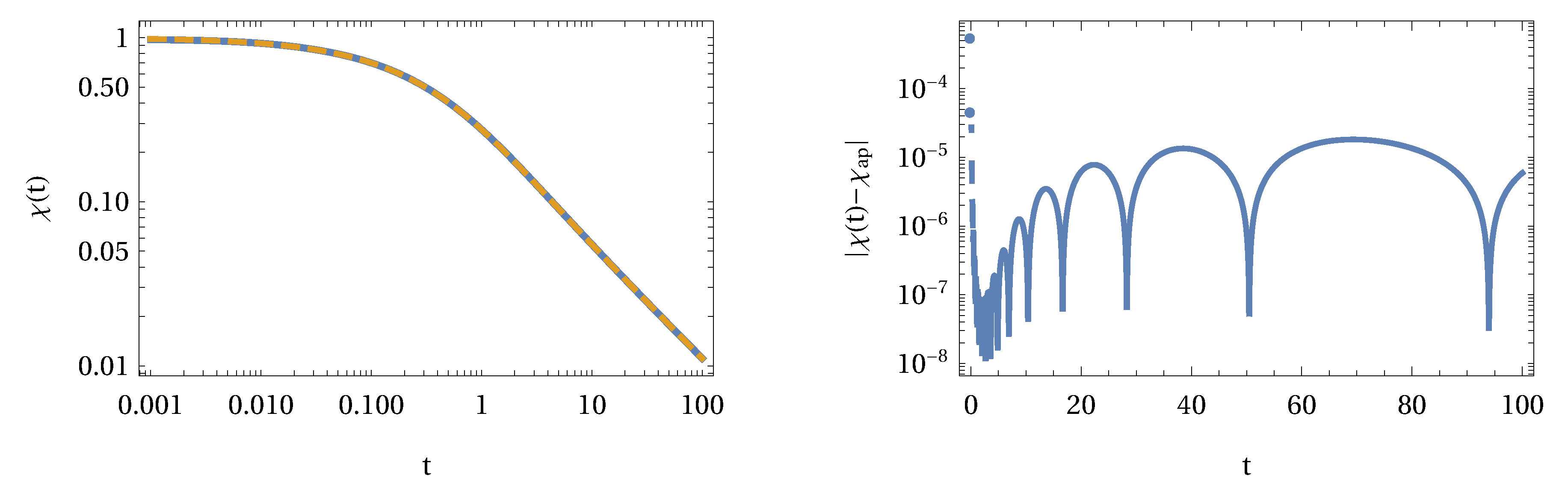
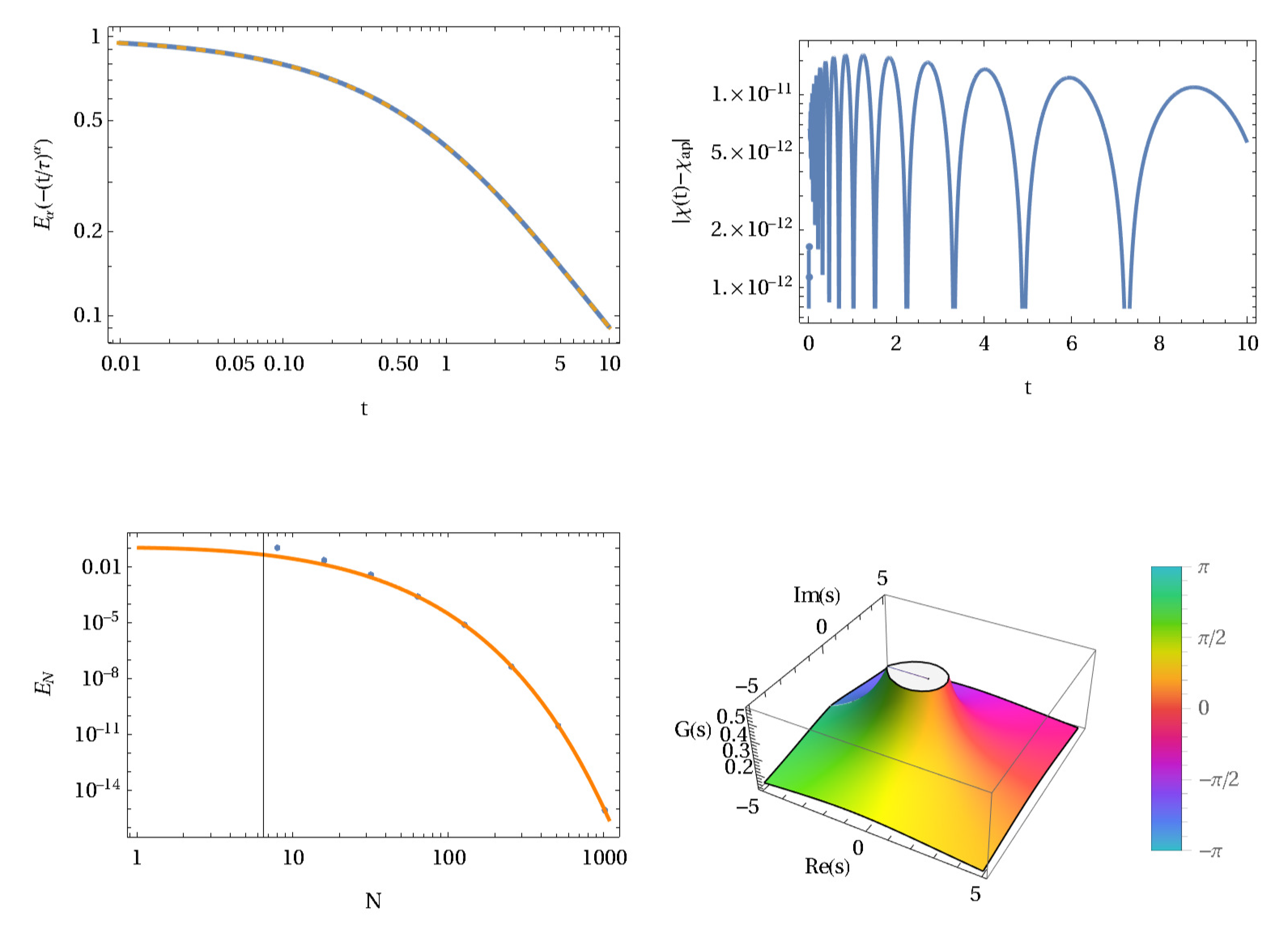
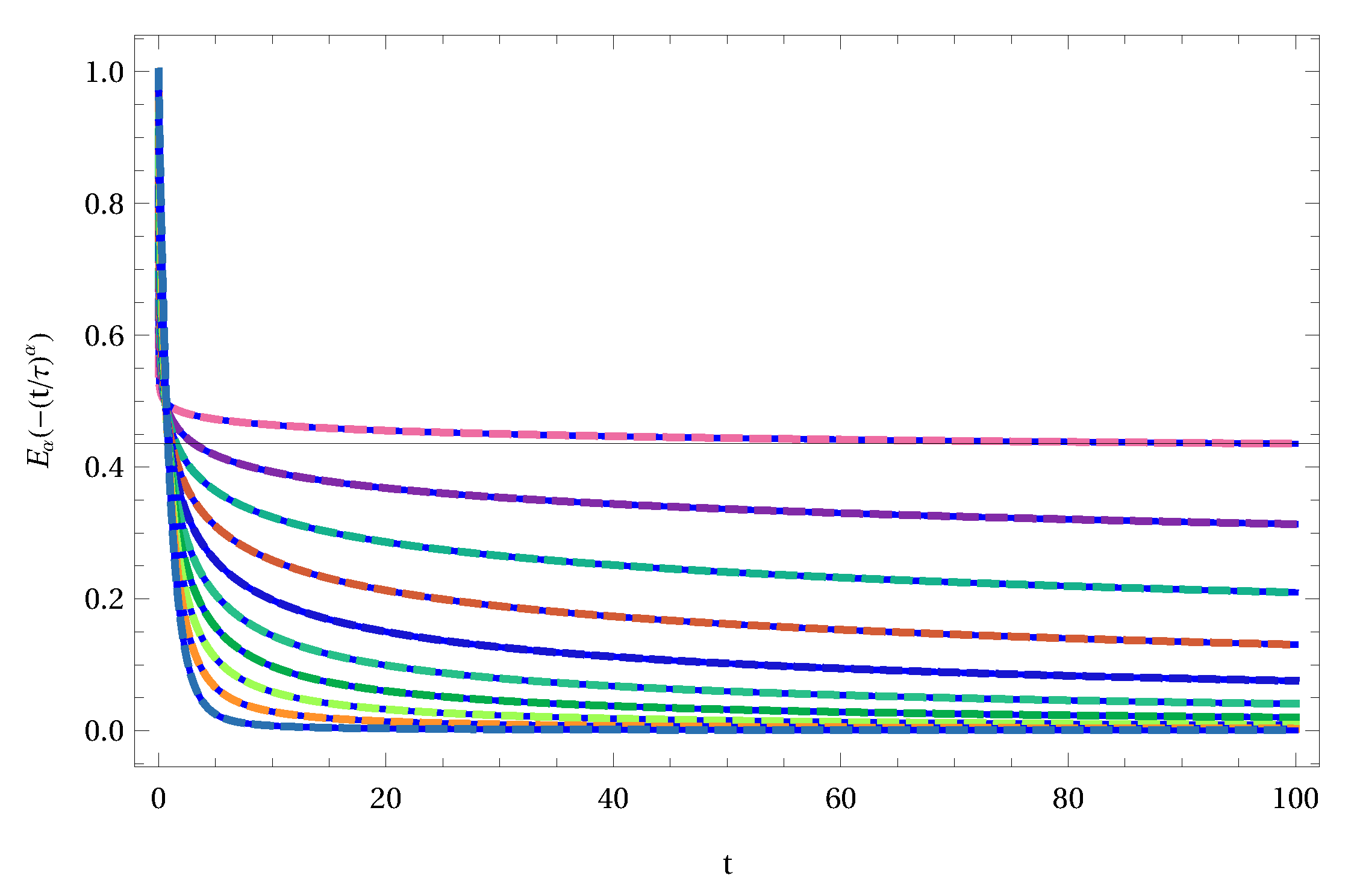
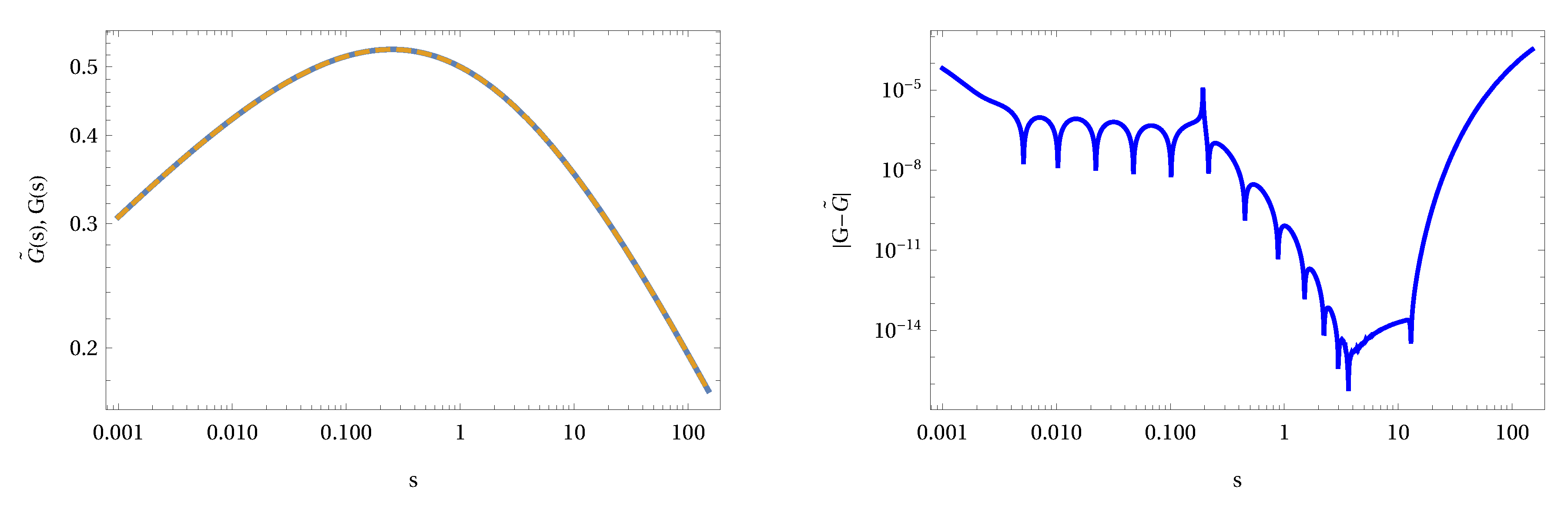
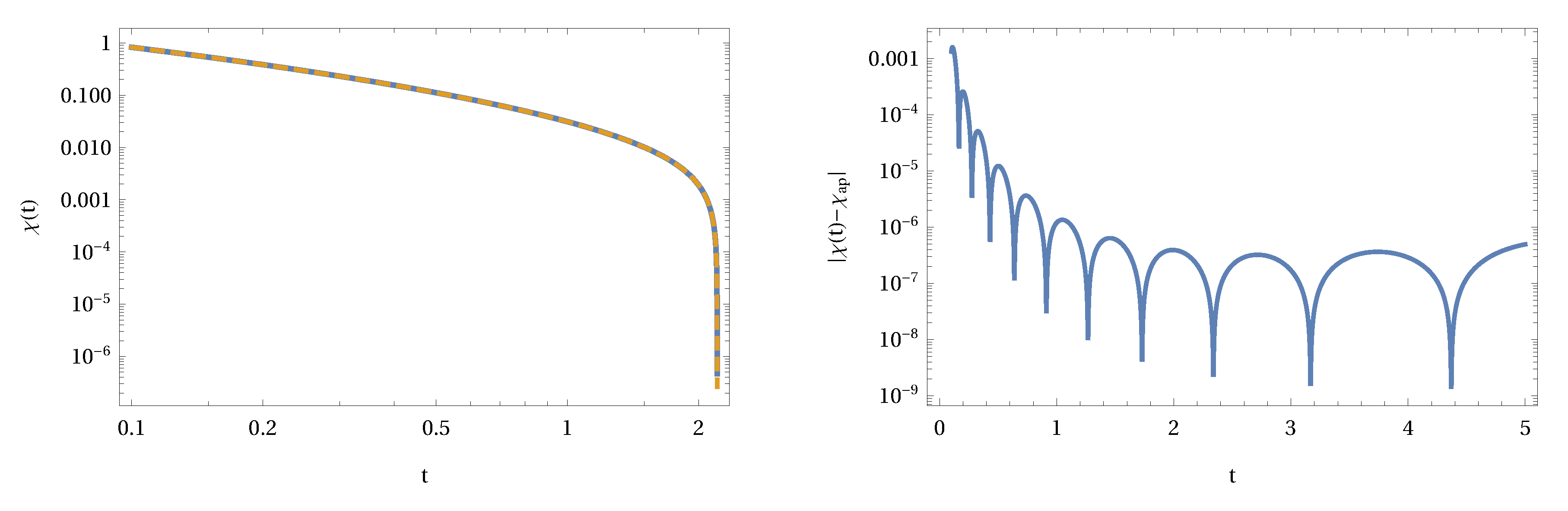
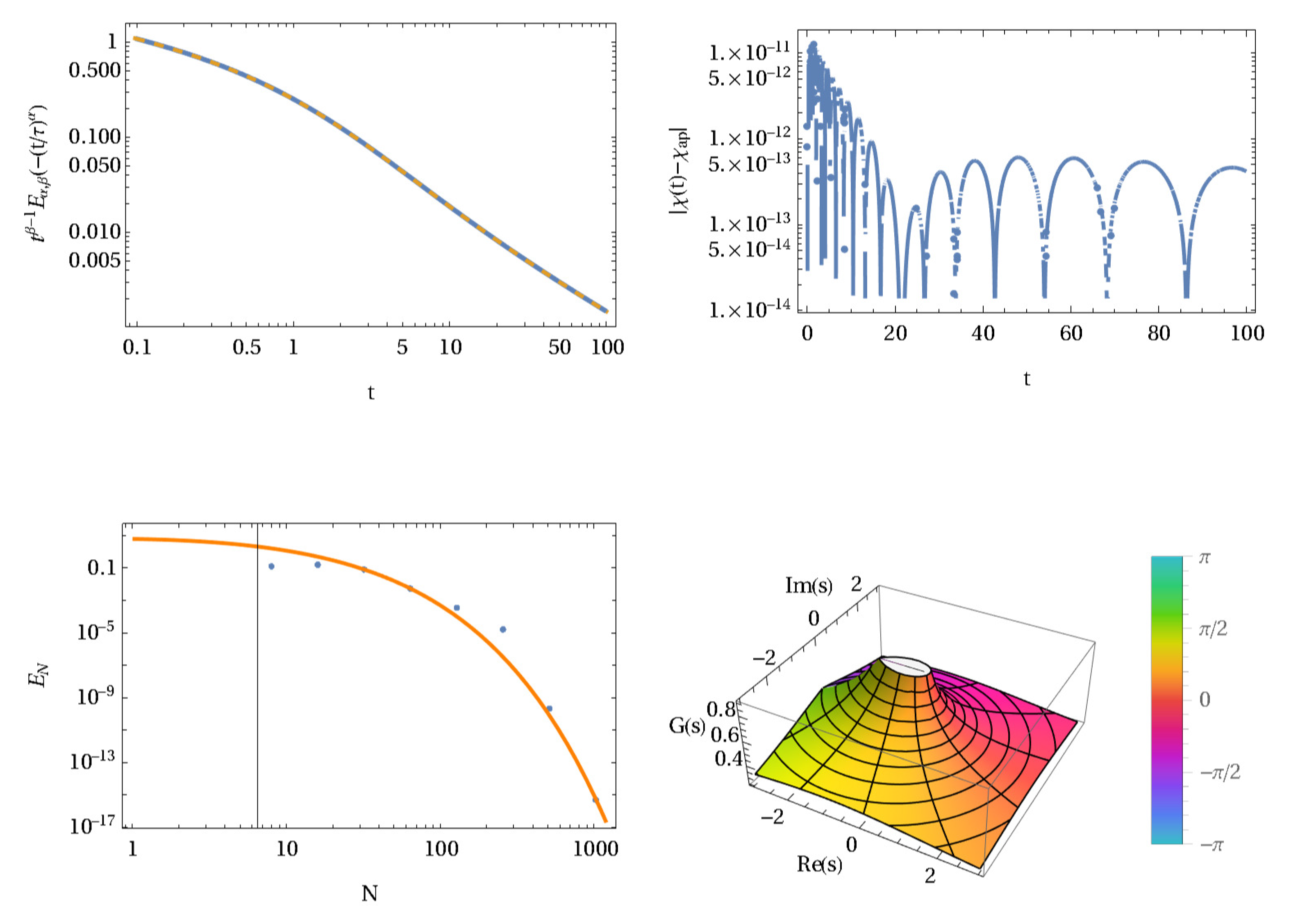
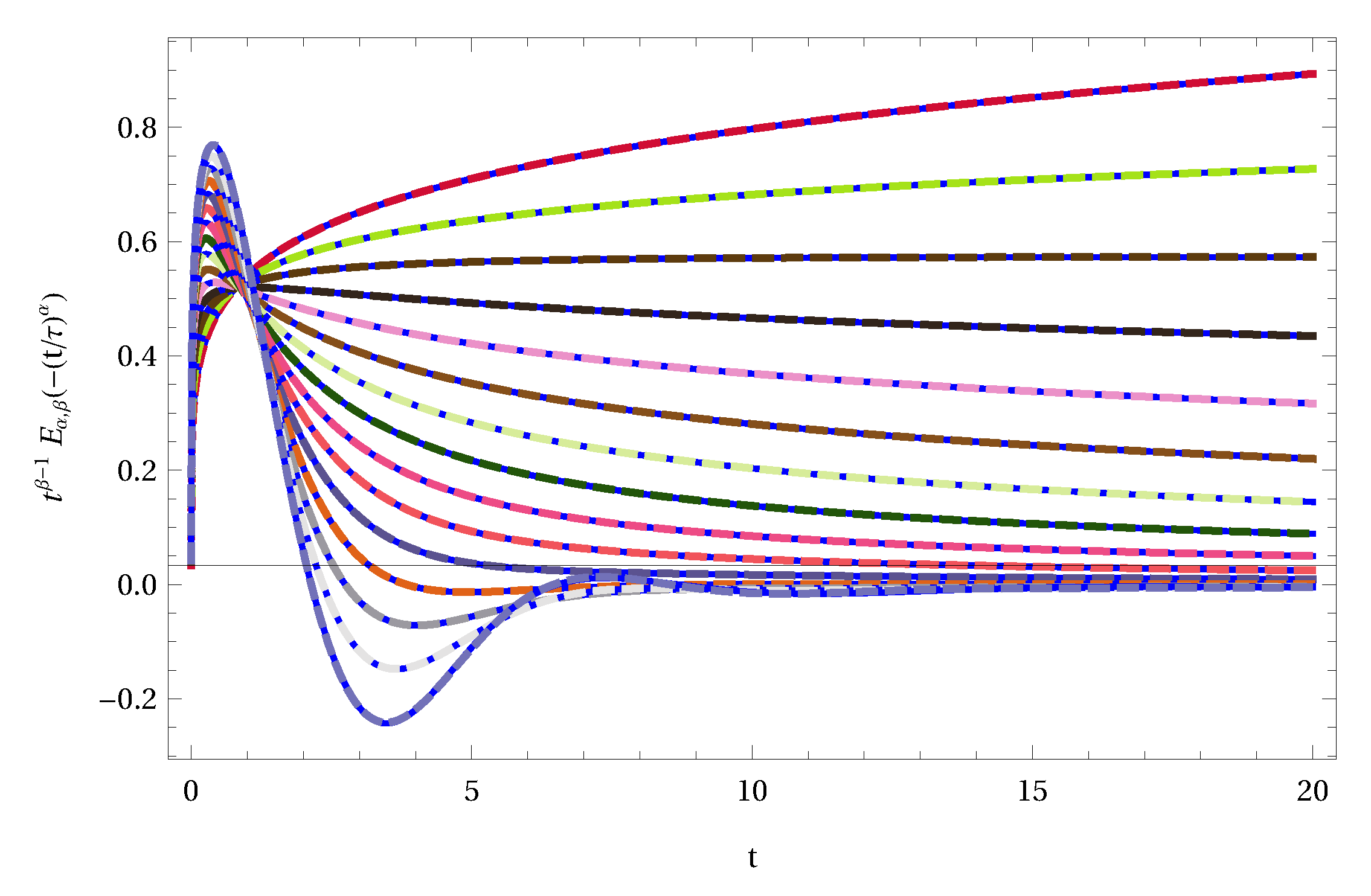
1. Introduction
In the present paper, we present three methods for carrying out the numerical inversion of the Laplace transform [
1]. The methods are all based on Sinc approximations of rational expressions via Thiele’s continued fraction approximation (STh) [
2], indefinite integral approximations based on a Sinc basis [
3], and indefinite integral approximations based on a Sinc-Gaussian (SG) basis [
4]. The three methods avoid Bromwich contours requiring a special parameter adaptation on each time step [
5,
6,
7,
8,
9]. The motivation behind avoiding Bromwich contours is to represent numerically generalized functions and provide a practical method for computing inverse Laplace transforms. Among the generalized functions, we aim at Mittag-Leffler (ML) functions, and especially Prabhakar functions among them. ML functions are frequently used in fractional calculus [
10,
11,
12,
13,
14]. For an overview and detailed discussion of theoretical properties and applications of the Mittag-Leffler functions, see the recent book by Gorenflo et al. [
14] and Kilbas [
15]. Mittag-Leffler a Swedish mathematician introduced this function at the beginning of the last century [
16] to generalize the exponential function by a parameter
:
Three years later, Wiman [
17] extended the one-parameter function to a two-parameter function also defined as an infinite series using gamma functions
to replace the factorial in its definition:
In 1971, the Indian mathematician Prabhakar [
18] proposed another generalization to three parameters, i.e.,
Comparing these series definitions of higher parameter ML functions, it is obvious that all of them are generalizations of the exponential and, thus, include the exponential function as a limiting case. There are many other ML functions in use with larger numbers of parameters especially in fractional calculus; for a detailed discussion of these types of functions, see Reference [
15]. We shall restrict our examinations of the numerical representation to the above three variants because, currently, they are the most frequently used in fractional calculus. However, the higher-order ones can be included in our approach in a straightforward way if needed. One common property of the ML functions as stated above is the Laplace representation
as a transfer function instead of the infinite series. The series representation is not an efficient option for numerical computations because the convergence of the series is sometimes restricted to
, the sequence of the terms in the series do not decrease monotonically [
19], and the numerical evaluation of the
function is usually limited to a restricted magnitude of the argument if single or double precision is used in computations. For this reason, we use the Laplace route to avoid such kinds of convergence limiting problems.
That is, if
denotes the interval
, we obtain accurate approximations to
f defined on
by
where
G the transfer function is given on
. The Laplace transform
is defined by
The Laplace transform occurs frequently in the applications of mathematics, physics, engineering and is a major tool today in fractional analysis [
13,
20], especially in the representation of special functions. We will use this technique to numerically represent functions, like the ML functions needed in practical applications of relaxation processes. However, one of the major problems of the Laplace transform is and especially its inverse, contrary to Fourier transform, is that there is no universal method of inverting the Laplace transform. In applications, such as fractional calculus,
G is frequently known on
, and the use of the Bromwich inversion formula [
21]
is, therefore, not analytically feasible in many cases. Recently, the Bromwich inversion formula was used in connection with Talbot’s idea to replace the Bromwich contour
by a simplified contour in
[
5,
6,
7,
8]. However, it turned out that a special tuning of the parameters in the parametric representation of the contour is needed to achieve trust-able results. The lack of universal methods for inverting the Laplace transforms stems from the fact that the space of functions
f for which
exists is simply speaking too big. We immediately restrict this space by assuming that
, which implies that
. In applications, it is generally possible to achieve this criterion via elementary manipulations [
22]. An excellent summary of other methods for inverting the Laplace transform is contained in Reference [
23]. Furthermore, the methods summarized in Reference [
23] are tested on several functions. While the tests in Reference [
23] are interesting, the criteria of testing do not restrict the space of functions; thus, it is possible to write down test functions for which any one of the methods does extremely well, while all of the others fail miserably. A variety of other methods are discussed in Reference [
20] and references in Reference [
22].
The connection between the Laplace transform
and the function
is easily recognized if we recap the physical background in dielectric relaxation processes. Let us assume for simplicity of the discussion that the orientation polarization
is related to the alignment of dipoles in the electric field, whereby the permanent dipoles are rigidly connected to the geometry of the molecule. Thus, the time for complete development of
is coupled to the rotational mobility of the molecules. This, in turn, is a variable that is closely related to the viscosity
of the substance. The simplest approach to describe a temporal law for
is incorporated in the idea that, after switching on an electric field,
for
, the change
depends linearly on
, which is known as Debye relaxation of dielectrics [
24], resulting in the celebrated relaxation equation
The solution of the initial value problem (
7) is given by the exponential function
with
the relaxation time. More interestingly, the Laplace representation of this relation which, in terms of a standard relaxation function
, reads
or
Delivering immediately the time dependent solution
using the inverse Laplace transform. A canonical fractionalization of the standard relaxation Equation (
7) in terms of
result to
using the initial condition
; here,
represents the Riemann-Liouville fractional derivative. Since Equation (
10) is a linear equation, we can get the Laplace transform of this equation including the initial condition
as
Inversion of the transfer function by involving a Mellin transform results to the time dependent solution
[
25], where
is the one parameter ML function
defined in classical terms as an infinite series by Equation (
1). The comparison with the exponential function
reveals that
is in fact a generalization of the exponential function using the fractional parameter
restricted to
.
Another type of fractional relaxation equation which changes the initial decay of the process by an additional fractional exponent
is given by the following two-parameter equation
Applying the same procedure as before, we get the transfer function representation as
After inverting the Laplace transform by using the Mellin transform [
12,
25,
26], we gain the two-parameter ML function
Again, the comparison with
and
reveals that
is a generalization of the exponential function. We could continue in this way by adding additional parameters to get generalized rational expressions in Laplace space resulting in generalized functions of the exponential. We will get back to this idea in a moment. However, Prabhakar followed another route which is based on the following Laplace representation of a function (see. Kilbas et al. [
15]) using multiplications instead of additions in the parameter set
, and
as follows:
delivering a three parameter generalization of the exponential function as
with
where
is the Pochhammer symbol, and
denotes the Euler gamma function. Note that Prabhakar’s function is an entire function of order
and type
[
14]. The above Prabhakar model can be reduced to a Riemann-Liouville fractional integral equation of relaxation type [
27]. In this framework of Laplace transforms, we can introduce generalized transfer functions
in the Laplace space incorporating many parameters combined in different ways.
Such an approach was proposed in the field of electronic filter design, such as low-pass, high-pass, and bandpass filters, including the construction of a rational function that satisfies the desired specifications for cutoff frequencies, pass-band gain, transition bandwidth, and stop-band attenuation. Recently, these rational approximations were extended to fractal filters improving the design methodology in some direction. Following Podlubny [
28], a fractional-order control system can be described by a fractional differential equation of the form:
or by an equivalent continuous transfer function
The use of the continuous transfer function is today the standard approach to design filters. The transfer function uses fractional exponents
and
to represent the fractional orders of the differential equations. The problem with this approach is that only in rare cases a direct inversion of the Laplace representation to the time domain is possible. One way to solve this problem was originally proposed by Roy; that is the transfer function
with fractional exponents can be replaced by a rational approximation
using natural number exponents [
29]. Such kind of rational approximation
can be generated by a Sinc point based Thiele algorithm (STh) [
2,
30]. Thiele’s algorithm converts a rational expression to a continued fraction representation which is related to a rational expression possessing exponents of natural numbers. Such kind of approximation will change of course the representation of the rational character of the transfer function but allows us to use a fraction with integer orders if we need to invert the Laplace transformation. The benefit here is that, for rational functions with integer powers, a well-known method by Heaviside exists, also called the partial fraction method, to invert a Laplace transform to a sum of exponential functions. This is in short how the method of numerical approximation of all the different transfer functions mentioned above can be transformed to the time domain with sufficient accuracy.
From a practical point of view of the STh approach, we gain a numerical representation of the function but miss the analytic properties if we are not able to compute the inverse Laplace transform analytically. In some cases, an analytic representation is possible via Mellin-Barns integrals delivering special function included in the class of Fox-H functions [
11,
13,
15,
26]. For our numerical computations, however, this is not a disadvantage if we are aware that the numerical results belong to this larger class of special functions which are representable by Mellin-Barns integrals. Given the ML function, we know that these functions belong to this class of Fox-H functions. The gain of the numerical inversion of the Laplace transform, however, is that, at least for practical work, we have access to the determining parameters of the function.
The paper is organized as follows:
Section 2 introduces, in short, the methodology of Sinc methods.
Section 3 discusses some applications and error estimations.
Section 4 summarizes the work and gives some perspectives for additional work.
2. Sinc Methods of Approximation
This section discusses the used methods of approximation for the two sets of basis functions. First, the approximation of functions is introduced defining the terms and notion. The second part deals with approximations of indefinite integrals. Based on these definitions, we introduce the approximation of inverse Laplace transform in the next step. We use the properties of Sinc functions allowing a stable and accurate approximation based on Sinc points [
31]. The following subsections introduce the basic ideas and concepts. For a detailed representation, we refer to References [
30,
32,
33].
In their paper, Schmeisser and Stenger proved that it is beneficial to use in Sinc approximations a Gaussian multiplier [
4]. The idea of using a Gauss multiplier in connection with Sinc approximations is a subject discussed in literature from an application point of view by Qian [
34]. The group around Qian observed that a Gauss multiplier improves under some conditions the convergence of an approximation [
35]. Schmeisser and Stenger verified this observation on a theoretical basis and proved an error formula possessing exponential convergence [
4]. A similar approach was used by Butzer and Stens [
36] to improve the convergence in a Sinc approximation in connection with the Whittaker-Kotelnikov-Shannon sampling theorem. The general multiplier used by Butzer and Stens is here replaced by a Gaussian. We note that the used multiplier function used by Butzer and Stens in the limit
is the same as the Gaussian for
. It turned out that the approximation is useful not only to represent functions but can be also applied to integrals and integral equations, as well as to derivatives.
It is a well-known fact that numerical Laplace transform and especially its inversion is much more difficult than numerical integration. It turns out that numerical inverse Laplace transform based on Bromwich’s integral is influenced by several factors, like the choice of nodes, the method of integration used, the algorithmic representation, and the structure of the contour to mention only a few. In applications, it is sometimes required that a certain accuracy is achieved over a definite or semi-infinite interval, and specifically at the boundaries. It would be beneficial if the method is easy to implement, and the number of computing steps is minimized. In addition, from the mathematical point of view, we may gain some insights if an ad hoc estimation of the error is possible. Such a set of requirements is, in most of the cases, not available; either one of the properties is missing, or the whole set of requirements cannot be satisfied by a specific method. We will discuss a new method that was mentioned in a basic form in an application to initial value problems [
1]. Our new method uses the basic idea of collocating indefinite integrals in connection with the fundamental theorem of calculus. This allows us to approximate a basic relation using either a Sinc basis or a Sinc-Gaussian (SG) basis. Both approaches will be discussed and used in examples.
To put our results in perspective, we briefly discuss the basics of approximations using a Sinc-Gaussian basis, indefinite integrals, convolution integrals, and the inverse Laplace transform.
2.1. Sinc Basis
To start with, we first introduce some definitions and theorems allowing us to specify the space of functions, domains, and arcs for a Sinc approximation.
Definition 1. Domain and Conditions.
Let be a simply connected domain in the complex plane and having a boundary . Let a and b denote two distinct points of and ϕ denote a conformal map of onto , where , such that and . Let denote the inverse conformal map, and let Γ be an arc defined by . Given ϕ, ψ, and a positive number h, let us set , to be the Sinc points, let us also define .
Note the Sinc points are an optimal choice of approximation points in the sense of Lebesgue measures for Sinc approximations [
37].
Definition 2. Function Space.
Let , and let the domains and be given as in Definition 1. If is a number such that , and, if the function ϕ provides a conformal map of onto , then . Let α and β denote positive numbers, and let denote the family of functions , for which there exists a positive constant such that, for all ,Now, let the positive numbers α and β belong to , and let denote the family of all functions , such that and are finite numbers, where and , and such that where These definitions directly allow the formulation of an algorithm for a Sinc approximation. Let
denote the set of all integers. Select positive integers
N and
so that
. The step length is determined by
where
,
, and
d are real parameters. In addition, assume there is a conformal map
and its inverse
such that we can define Sinc points
,
[
38]. The following relations define the basis of a Sinc approximation:
The sifted Sinc is derived from relation (
23) by translating the argument by integer steps of length
h and applying the conformal map to the independent variable.
where
represents the Sinc function and
is the Sinc-Gaussian. The first type of approximation results to the representation
using the basis set of orthogonal functions
where
is a conformal map. As discussed by Schmeisser and Stenger [
4], a Sinc approximation of a function
f can be given in connection with a Gaussian multiplier in the following representation:
with
c a constant, and
denoting a conformal map. This type of approximation allows to represent a function
on an arc
with an exponential decaying accuracy [
4]. As demonstrated in Reference [
4], the approximation works effective for analytic functions. The definition of the Sinc-Gaussian basis by
allows us to write the approximation in a compact form as
The two approximations allow us to formulate the following theorem for Sinc approximations.
Theorem 1. Let for , , and d as in Definition 2, take M = [β N/α], where [x] denotes the greatest integer in x, and then set . If , and, if , then there exists a positive quantity, such thatusing as basis functions (see (31)). Here, and are constants independent of N. The proof of this theorem is given for the pure Sinc case in References [
4,
30] discusses the SG case. Note the choice
is close to optimal for an approximation in the space
in the sense that the error bound in Theorem 1 cannot be appreciably improved regardless of the basis [
38]. It is also optimal in the sense of the Lebesgue measure achieving an optimal value less than Chebyshev approximations [
37].
Here,
are the discrete points based on Sinc points
. Note that the discrete shifting allows us to cover the approximation interval
in a dense way, while the conformal map is used to map the interval of approximation from an infinite range of values to a finite one. Using the Sinc basis, we can represent the basis functions as a piecewise-defined function
by
and
or
, where
. This form of the Sinc basis is chosen as to satisfy the interpolation at the boundaries. The basis functions defined in (
31) suffice for purposes of uniform-norm approximation over
.
This notation allows us to define a row vector
of basis functions
with
defined as in (
31). For a given vector
, we now introduce the dot product as an approximation of the function
by
Based on this notation, we will introduce in the next few subsections the different integrals we need [
32].
2.2. Indefinite Integral Approximation
In this section, we pose the question of how to approximate indefinite integrals on a sub-domain of
. The approximation will use our basis system introduced in
Section 2.1. We will introduce two different approximations using Sinc and Sinc-Gaussian basis. It turns out that, for both basis systems, we can get an approximation converging exponentially. Specifically, we are interested in indefinite integrals of the two types
If the function
f is approximated by one of the approximations given in
Section 2.1, we write, for
,
Scaling the variable
and collocating the expression with respect to
t, we end up with the representation
The collocation of the variable
delivers an integral
, which will be our target in the next steps.
Note that, with
, the integral simplifies to the expression
. The discrete approximation of the integral
, thus, becomes
and delivers the approximation of
via
For the discrete approximation, we need to know the value of
to be able to find the approximation of the indefinite representation
The matrix
can be written as
reducing the problem to the structure of a Toeplitz matrix if the indefinite integral has some finite values. To get the values of the integrals, we divide the integration domain into two parts
The two integrals deliver the following:
and
with
, and
; thus,
. A similar procedure can be applied to the integral
. The difference is a transposition of the matrix
in the representation of approximation. The following Theorem summarizes the results.
Theorem 2. Indefinite Integrals
If ϕ denotes a one-to-one transformation of the interval onto the real line , let h denote a fixed positive number, and let the Sinc points be defined on by , , where denotes the inverse function of the conformal map ϕ. Let M and N be positive integers, set , and, for a given function f defined on , define the vector , and a diagonal matrix by . Let be the vector of basis functions, and let be a square Töplitz matrix of order m having , as its entry, ,Define square matrices and bywhere the superscript “T” denotes the transpose. Then, the indefinite integrals (34) and (35) are approximated byThe error of this approximation was estimated for the pure Sinc case in Reference [30] aswhere and are constants independent of N. Note the matrices
and
have eigenvalues with
, which guaranties the convergence of the solution. A proof for the pure Sinc case for the matrix
was recently given by Han and Xu [
39].
If we use the properties of the matrices defined above, we know that
where
is a
matrix filled with 1’s, and
is antisymmetric. The elements of the diagonal matrix
are all positive according to their definition. If we assume that
is diagonalizable, then, for each eigenvalue
, there exists a complex valued eigenvector
. Since the eigenvalues of
are the same as
, we can write
equivalent to
The real part of this expression delivers
and the second term vanishes because the matrix
is anti-symmetric; thus, since
and
, we have
If we assume that the norm is defined on the vector space, we can use the Rayleigh quotient of a matrix
H given by
to bound the eigenvalues
. According to References [
40,
41], there exist a minimal and maximal eigenvalue defined by
The relations were examined numerically by computing the eigenvalues of the Hermitian matrix
with
the conjugate transpose of
. The results for different size
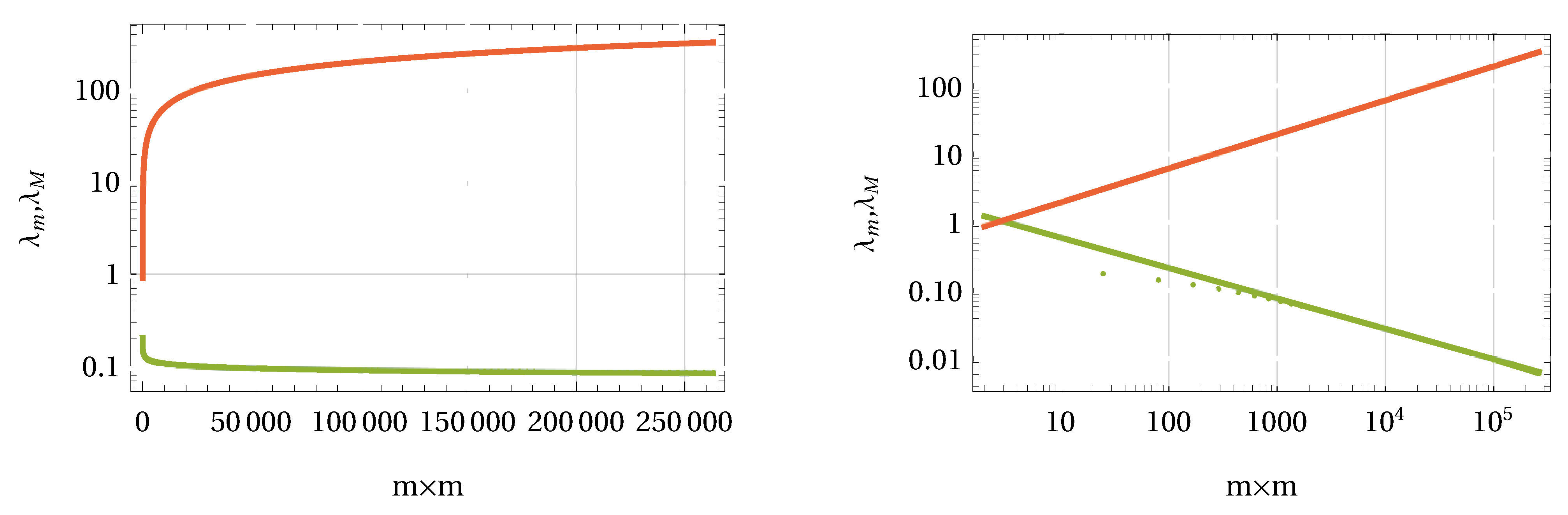
matrices are shown in
Figure 1. The left panel in
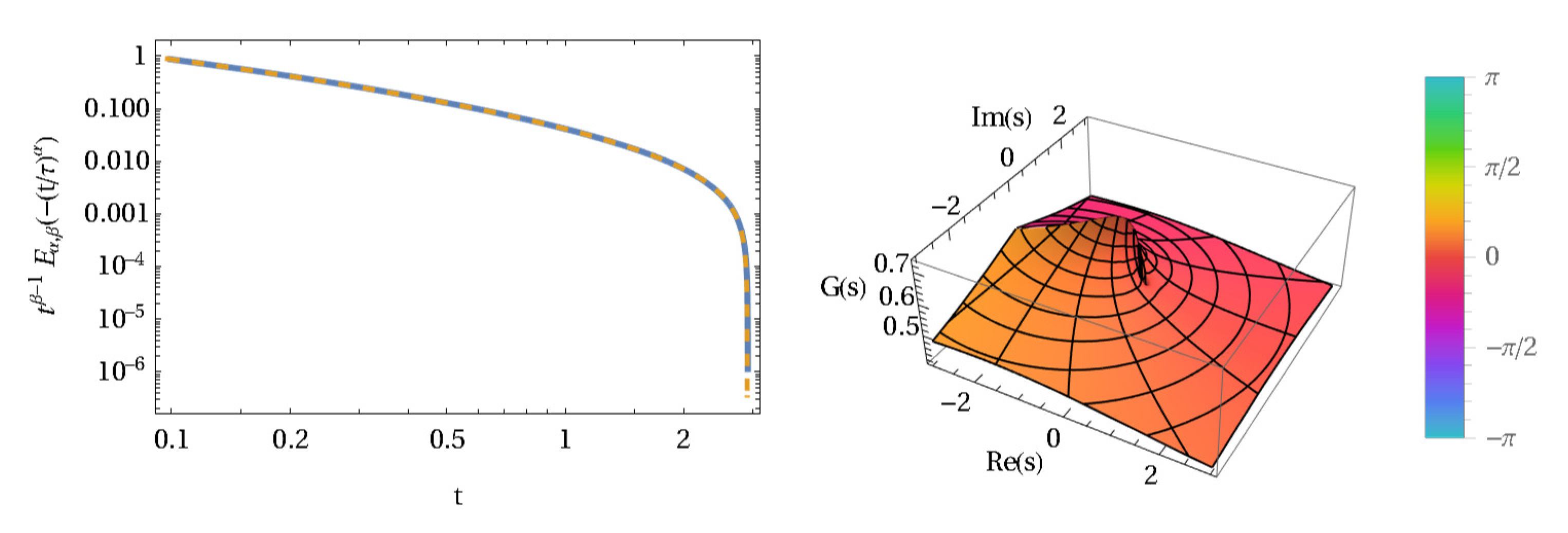
Figure 1 is related to the pure Sinc basis, while the right panel represents results for the Sinc-Gaussian basis. It is obvious that, for the Sinc-Gaussian, the limits are symmetric to
. In all cases, the relation between
and the size
of
H follows a power law
. The value for
for the upper limit
is estimated to be nearly
. For the lower limit
, the exponents are different. In the Sinc-Gaussian case, we find
, while the pure Sinc case shows a much smaller value of
. However, in both cases, the lower limit is a positive decaying function that is always greater than zero. Only in the limit
is the value zero reached. This, in turn, tells us, based on Grenander and Szegö theory [
42], that the eigenvalues of
are strictly positive for finite matrix sizes.
2.3. Convolution Integrals
Indefinite convolution integrals can also be effectively collocated via Sinc methods [
38]. This section discusses the core procedure of this paper, for collocating the convolution integrals and for obtaining explicit approximations of the functions
p and
q defined by
where
. In presenting these convolution results, we shall assume that
, unless otherwise indicated. Note also that being able to collocate
p and
q enables us to collocate definite convolutions, like
.
Before we start to present the collocation of the Equations (
68) and (
69), we mention that there is a special approach to evaluate the convolution integrals by using a Laplace transform. Lubich [
43] introduced this way of calculation by the following idea
for which the inner integral solves the initial value problem
with
. We assume that the Laplace transform
with
E any subset of
such that
, exists for all
.
In the notation introduced above, we get that
and
are accurate approximations, at least for
g in a certain space [
32]. The procedure to calculate the convolution integrals is now as follows. The collocated integral
and
, upon diagonalization of
and
in the form
with
as the eigenvalues arranged in a diagonal matrix for each of the matrices
and
. Then, the Laplace transform (
71), introduced by Stenger, delivers the square matrices
and
defined via the equations
We can get the approximation of (
72) and (
73) by
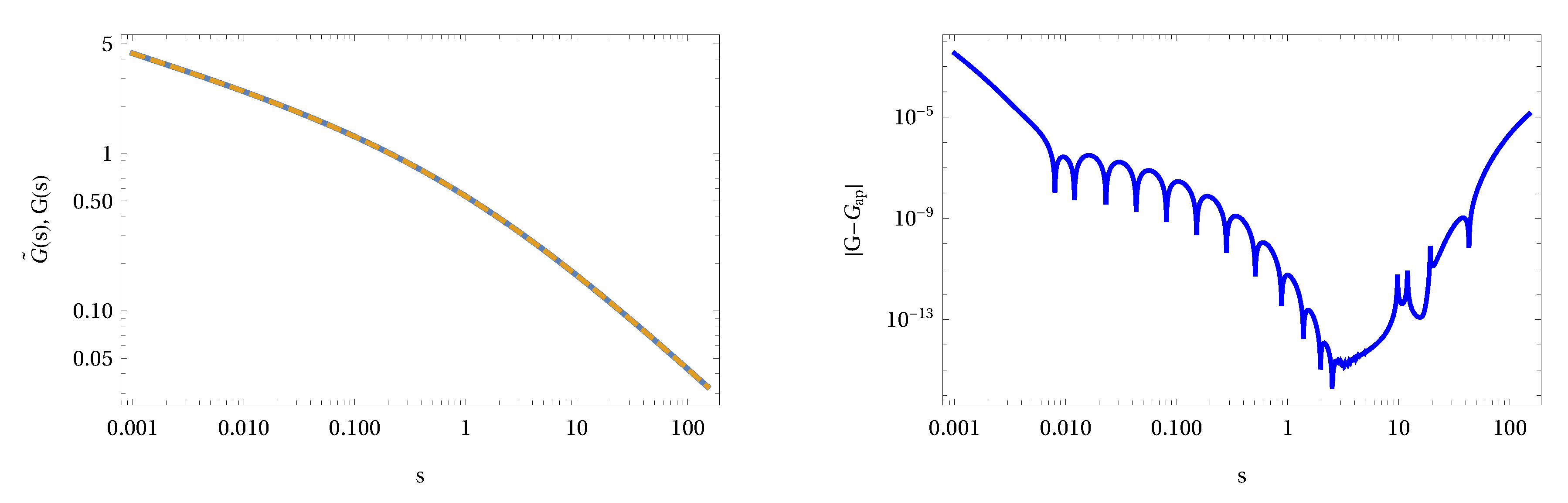
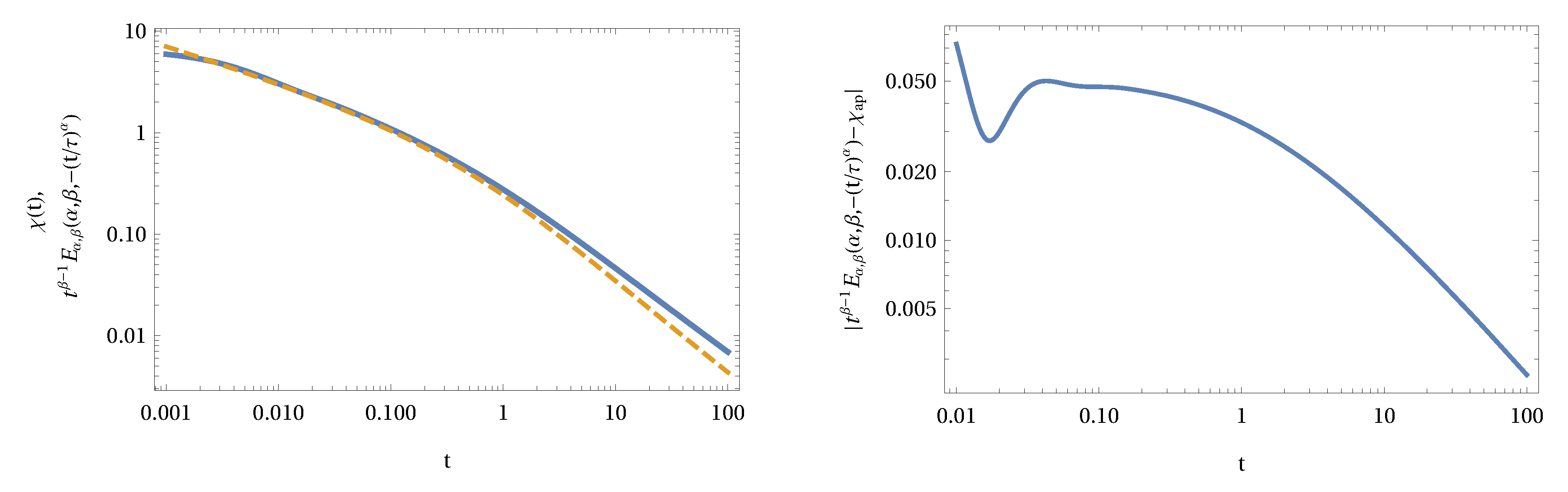
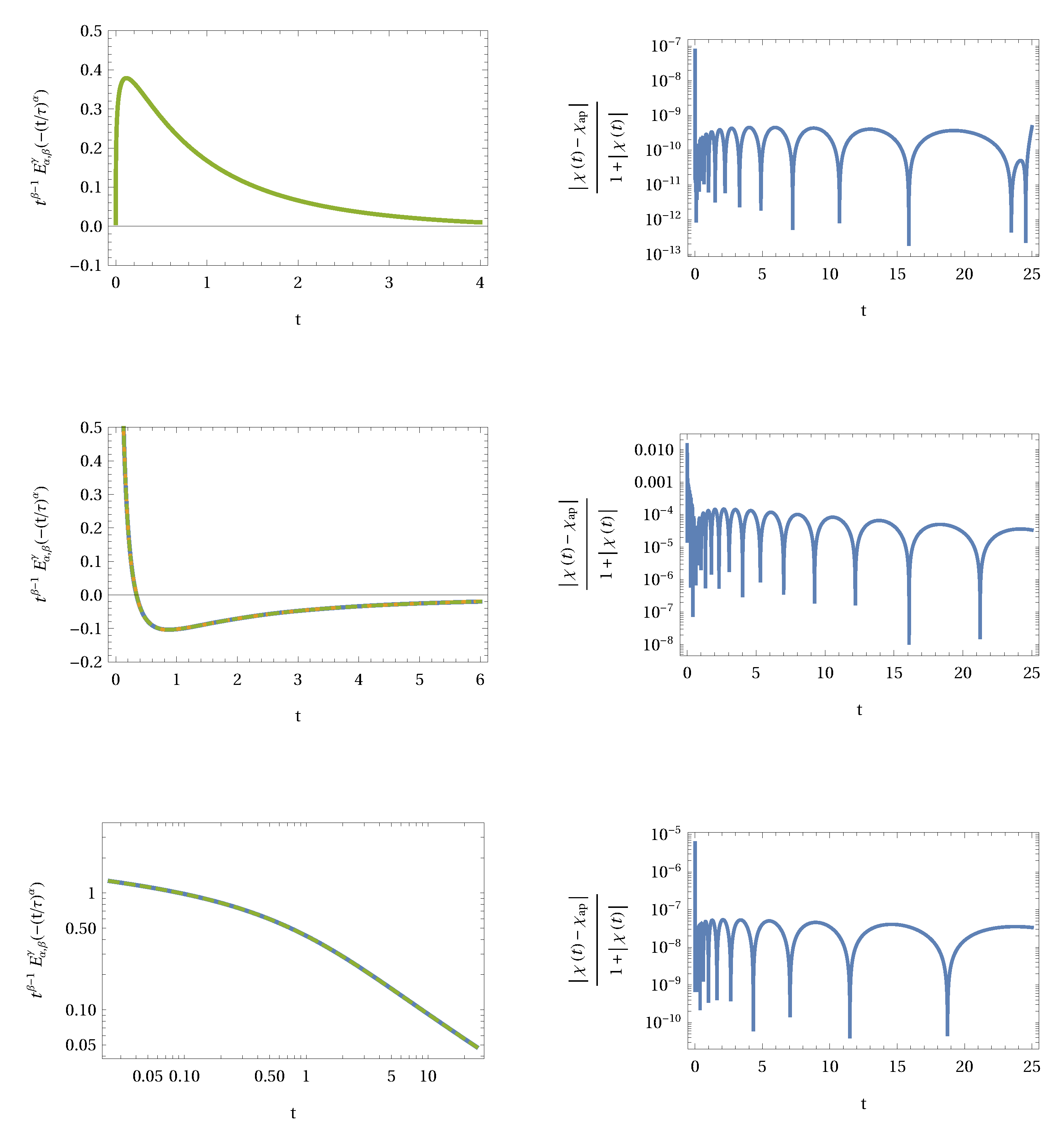
These two formulas deliver a finite approximation of the convolution integrals
p and
q. The convergence of the method is exponential as was proved in Reference [
38].
2.4. Inverse Laplace Transform
The inversion formula for Laplace transform inversion was originally discovered by Stenger in Reference [
32]. This exact formula presented here is only the third known exact formula for inverting the Laplace transform, the other two being due to Post [
44] and Bromwich [
21], although we believe that practical implementation of the Post formula has never been achieved, while the evaluation of the vertical line formula of Bromwich is both far more difficult and less accurate than our method, which follows.
Let the Laplace transform
be defined as in (
71). If
denotes the indefinite integral operator defined on
, then the exact inversion formula is
where 1 denotes the function that is identically 1 on
. Hence, with
, with
,
, we can proceed as follows to compute the values
of
f:
Assume that matrix X and vector have already been computed from ; then, compute the column vector , where 1 is a vector of ones:
All operations of this evaluation take a trivial amount of time, except for the last matrix-vector evaluation. However, the size of these matrices is nearly always much smaller than the size of the DFT matrices for solving similar problems via FFT.
Then, we have the approximation
, which we can combine, if necessary, with our interpolation Formula (
33) to get a continuous approximation of
f on
.