Using Fractal Calculus to Solve Fractal Navier–Stokes Equations, and Simulation of Laminar Static Mixing in COMSOL Multiphysics
Abstract
1. Introduction
1.1. Fractal Calculus
1.2. Static Mixers
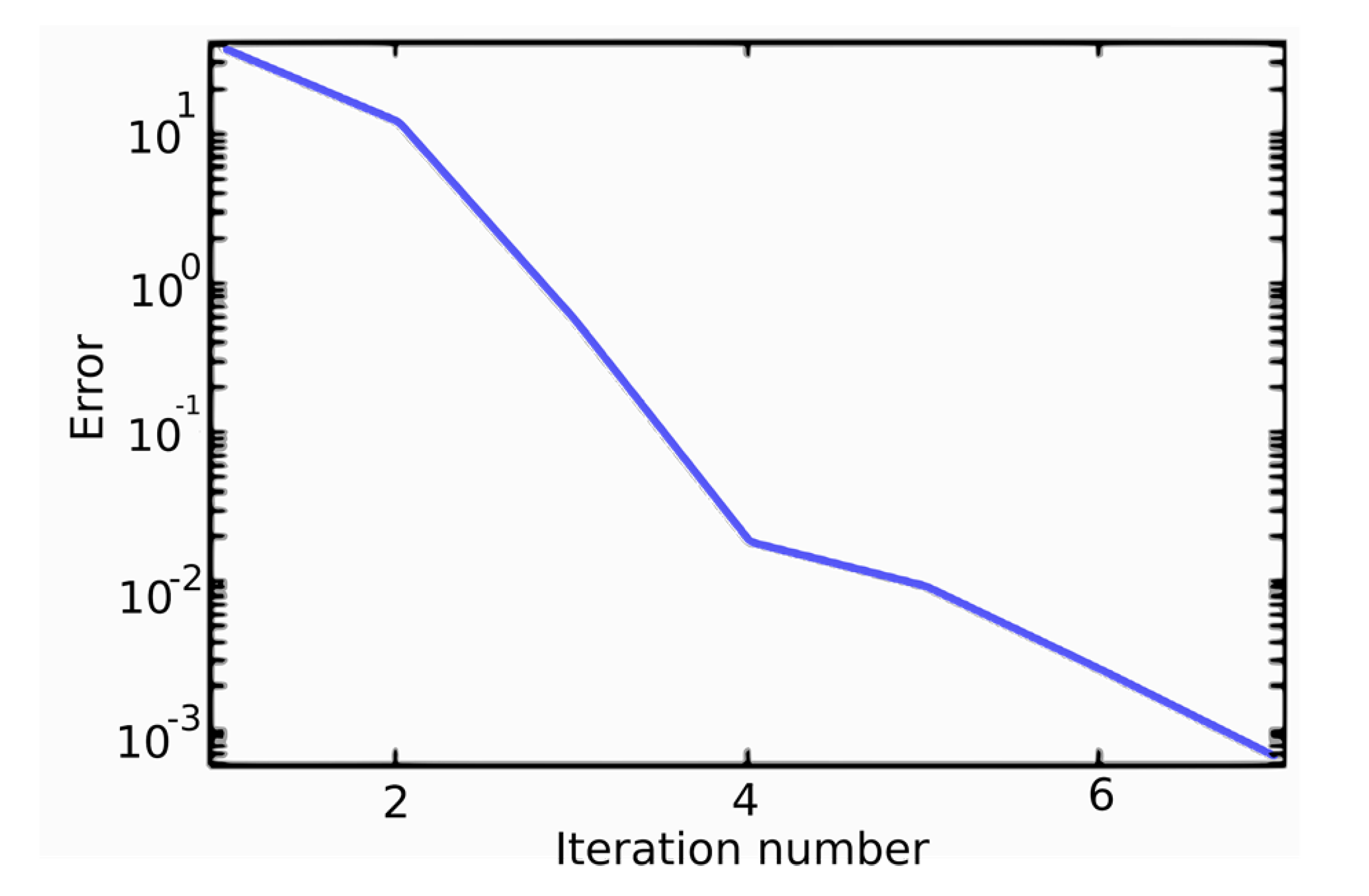
2. Main Results
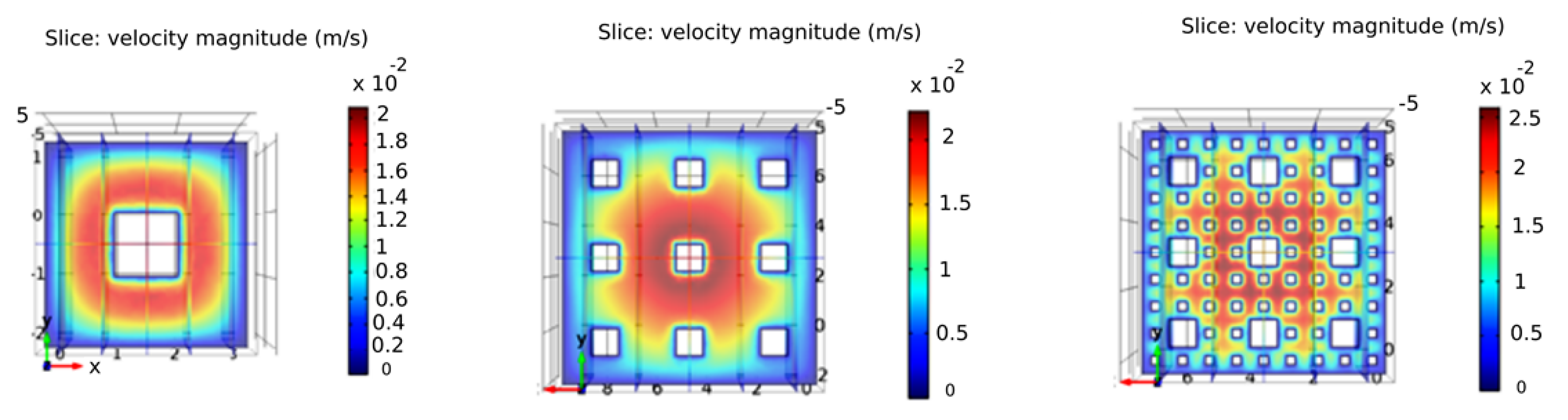
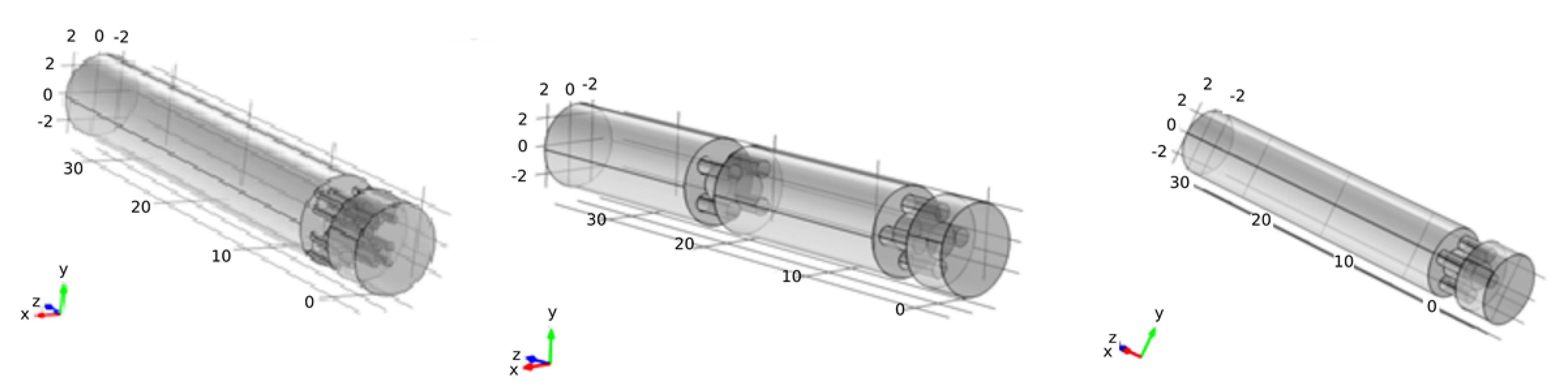
3. To Model Diluting the Fluid with Fractal Mixing Patterns
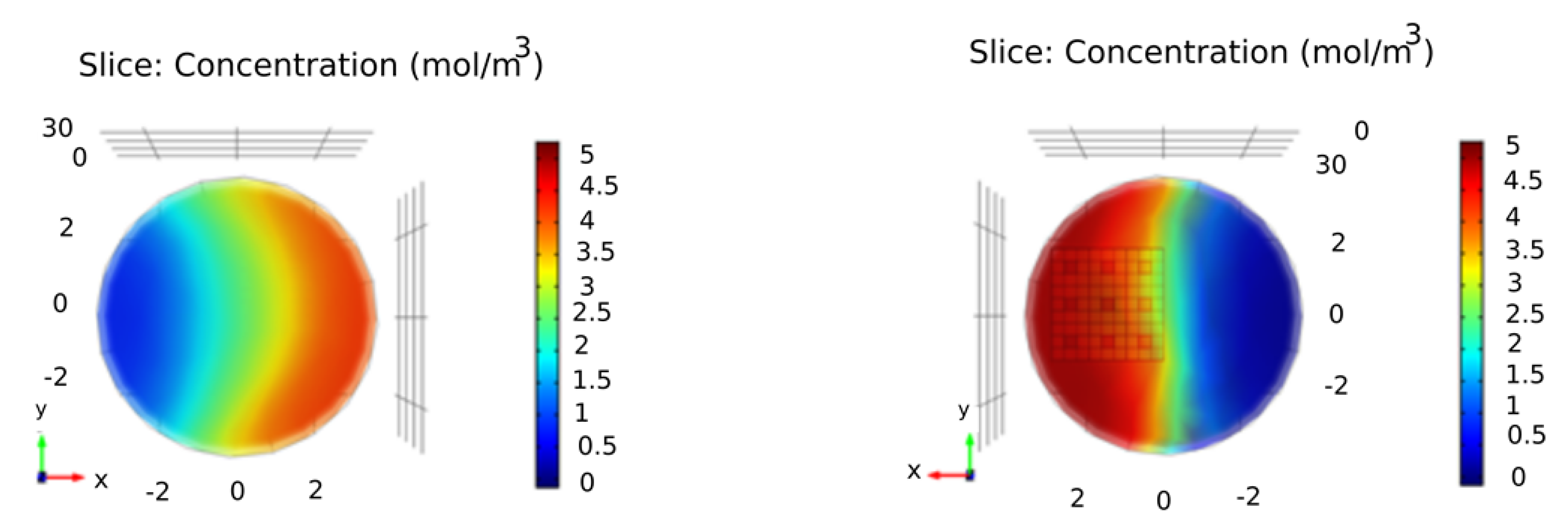
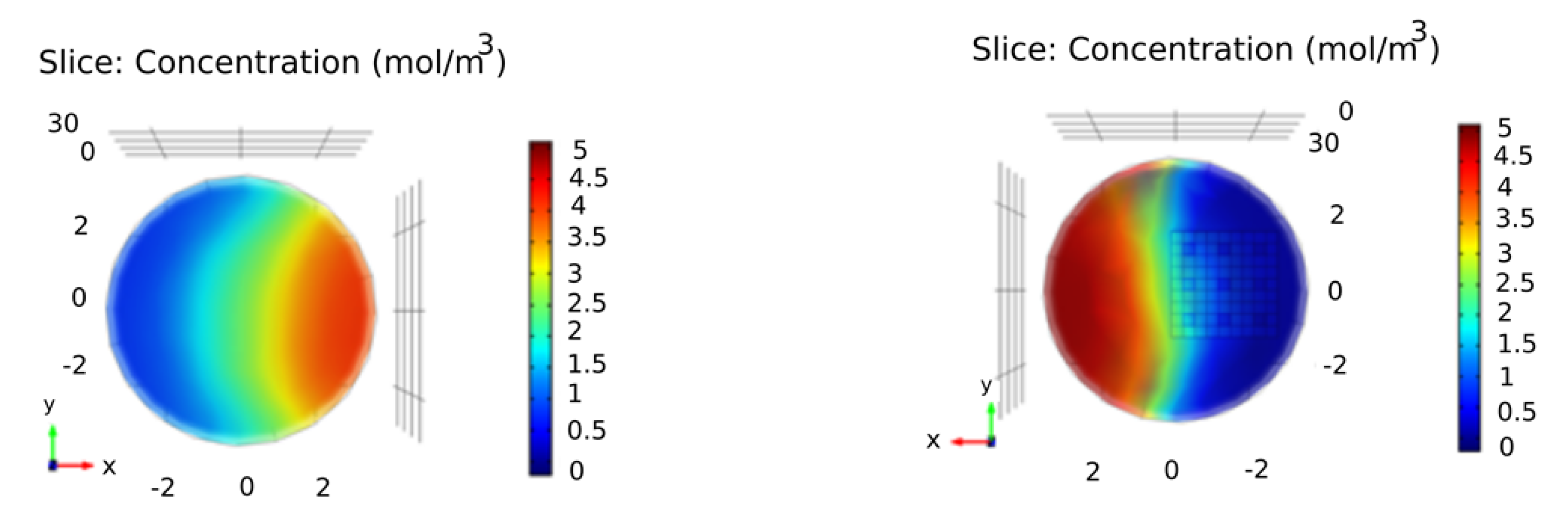
4. Results and Discussion
5. Conclusions
- The fractal mixing simulation showed that if the fluid passes through the fractal pattern, it leads to a smaller CoV than it passes through its sides.
- Using the second and third iterations instead of the first iteration of a fractal pattern does not necessarily lead to better quality in mixing of the two fluids.
- Using more than one fractal pattern in the path can decrease CoV to a smaller value. Of course, the shorter distance between the two fractal patterns, the better efficiency will be.
- Simulation results in mixing two fluids by Sierpinski carpet patterns and the square barrier showed somewhat smaller CoV than the patterns of the Sierpinski triangle and the circular fractal patterns.
- We can continue the studies by studying the gas–liquid fluids phase and gas–gas fluids phase, while the study area will be extended from laminar flow to turbulent flow.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CoV | Coefficient of Variation |
| FEM | Finite Element Method |
References
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications, 2nd ed.; Wiley: New York, NY, USA, 2007. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1977. [Google Scholar]
- Lazopoulos, K.A.; Lazopoulos, A.K. On fractional bending of beams. Arch. Appl. Mech. 2016, 86, 1133–1145. [Google Scholar] [CrossRef]
- Sumelka, W. On fractional non-local bodies with variable length scale. Mech. Res. Commun. 2017, 86, 5–10. [Google Scholar] [CrossRef]
- Drapaca, C.S.; Sivaloganathan, S. A fractional model of continuum mechanics. J. Elast. 2012, 107, 105–123. [Google Scholar] [CrossRef]
- Zingales, M.; Failla, G. The finite element method for fractional non-local thermal energy transfer in non-homogeneous rigid conductors. Commun. Nonlinear Sci. Numer. Simul. 2015, 29, 116–127. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real-line I: Formulation. Fractals 2009, 17, 53–148. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line II: Conjugacy with ordinary calculus. Fractals 2011, 19, 271–290. [Google Scholar] [CrossRef]
- Gangal, A.D.; Parvate, A.; Satin, S. Caclulus on fractal curves in rn. Fractals 2011, 19, 15–27. [Google Scholar]
- Gangal, A.D.; Satin, S. Langevin equation on fractal curves. Fractals 2016, 24, 1650028. [Google Scholar]
- Gangal, A.D.; Satin, S.; Parvate, A. Fokker-planck equation on fractal curves. Chaos Solitons Fractals 2013, 5, 30–35. [Google Scholar]
- Golmankhaneh, A.K.; Fernandez, A. Fractal Calculus of Functions on Cantor Tartan Spaces. Fractal Fract. 2018, 2, 30. [Google Scholar] [CrossRef]
- Balankin, A.S.; Golmankhaneh, A.K. Sub- and super-diffusion on cantor sets: Beyond the paradox. Phys. Lett. A 2018, 382, 960–967. [Google Scholar]
- Golmankhaneh, A.K.; Baleanu, D. Non-local Integrals and Derivatives on Fractal Sets with Applications. Open Phys. 2016, 14, 542–548. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Baleanu, D. Calculus on Fractals. In Fractional Dynamics; De Gruyter Open: Basel, Switzerland, 2015; pp. 307–332. [Google Scholar]
- Jafari, F.K.; Asgari, M.S.; Pishkoo, A. Fractal calculus for fractal materials. Fractal Fract. 2019, 3, 8. [Google Scholar] [CrossRef]
- Delfan, N.; Pishkoo, A.; Azhini, M.; Darus, M. Using fractal calculus to express electric potential and electric field in terms of staircase and characteristic functions. Eur. J. Pure Appl. Math. 2020, 13, 19–32. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Golmankhaneh, A.K.; Baleanu, D. About Maxwell’s equations on fractal subsets of R3. Open Phys. 2013, 11, 863–867. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Golmankhaneh, A.K.; Baleanu, D. About Schrödinger Equation on Fractals Curves Imbedding in R3. Int. J. Theor. Phys. 2015, 54, 1275–1282. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K. On the Fractal Langevin Equation. Fractal Fract. 2019, 3, 11. [Google Scholar] [CrossRef]
- Fernandez, A.; Golmankhaneh, A.K. Random variables and stable distributions on fractal cantor sets. Fractal Fract. 2019, 3, 31. [Google Scholar]
- Cattani, C.; Golmankhaneh, A.K. Fractal logistic equation. Fractal Fract. 2019, 3, 41. [Google Scholar]
- Fractal-Mixing. Available online: http://www.arifractal.com/technologies-applications/fractal-mixing (accessed on 5 February 2021).
- Baldyga, J.; Bourne, J.R.; Dubuis, B.; Etchells, A.W.; Gholap, R.V.; Zimmermann, B. Jet reactor scale-up for mixing controlled reactions. Chem. Eng. Res. Des. 1995, 73, 497. [Google Scholar]
- Fournier, M.C.; Falk, L.; Villermaux, J. A new parallel competing reaction system for assessing micro-mixing efficiency—Experimental approach. Chem. Eng. Sci. 1996, 51, 5053–5064. [Google Scholar] [CrossRef]
- Sutherland, W.S. Improvement in Apparatus for Preparing Gaseous Fuel. UK Patent 1784, 1874. [Google Scholar]
- Les Consommateurs de Petrole. Dispositif pour le mélangede deux ou plusieurs fluides. French Patent 735,033, 1931.
- Bakker, M.J. Dispositif pour préparer du béton ou unematière analogue. French Patent 959,155, 1949. [Google Scholar]
- Lynn, R.S. Turbulator. U.S. Patent 2,852,042, 1958. [Google Scholar]
- Stearns, R.F. Method and Apparatus for Continuous Flow Mixing. U.S. Patent 2,645,463, 1953. [Google Scholar]
- Tollar, J.E. Interfacial Surface Generator. U.S. Patent 3,239,197, 1966. [Google Scholar]
- Static Mixing: Advanced Mixing Technology. Available online: https://www.fluitec.ch/download.php?f=3fe420f8be822be48f8d6fe85fdfb79f (accessed on 5 February 2021).
- Veasey, T.M. Plate Type Fluid Mixer. U.S. Patent 3,382,534, 1968. [Google Scholar]
- Thakur, R.K.; Vial, C.; Nigam, K.D.P.; Nauman, E.B.; Djelveh, G. Static mixers in the process industries—A review. Trans. IChemE 2003, 81, 787–826. [Google Scholar] [CrossRef]
- Baker, J.R. Motionless mixers stir up new uses. Chem. Eng. Prog. 1991, 87, 32–38. [Google Scholar]
- Myers, K.J.; Bakker, A.; Ryan, D. Avoid agitation by selecting static mixers. Chem. Eng. Prog. 1997, 93, 28–38. [Google Scholar]
- Yang, X.-J.; Baleanu, D.; Tenreiro Machado, J.A. Systems of Navier–Stokes Equations on Cantor Sets. Math. Probl. Eng. 2013, 2013, 769724. [Google Scholar]
- Otarod, S.; Otarod, D. Analytical Solution For Navier–Stokes Equations In Two Dimensions For Laminar Incompressible Flow. arXiv 2006, arXiv:physics/0609186v1. [Google Scholar]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; McGraw-Hill Education: New York, NY, USA, 2015. [Google Scholar]
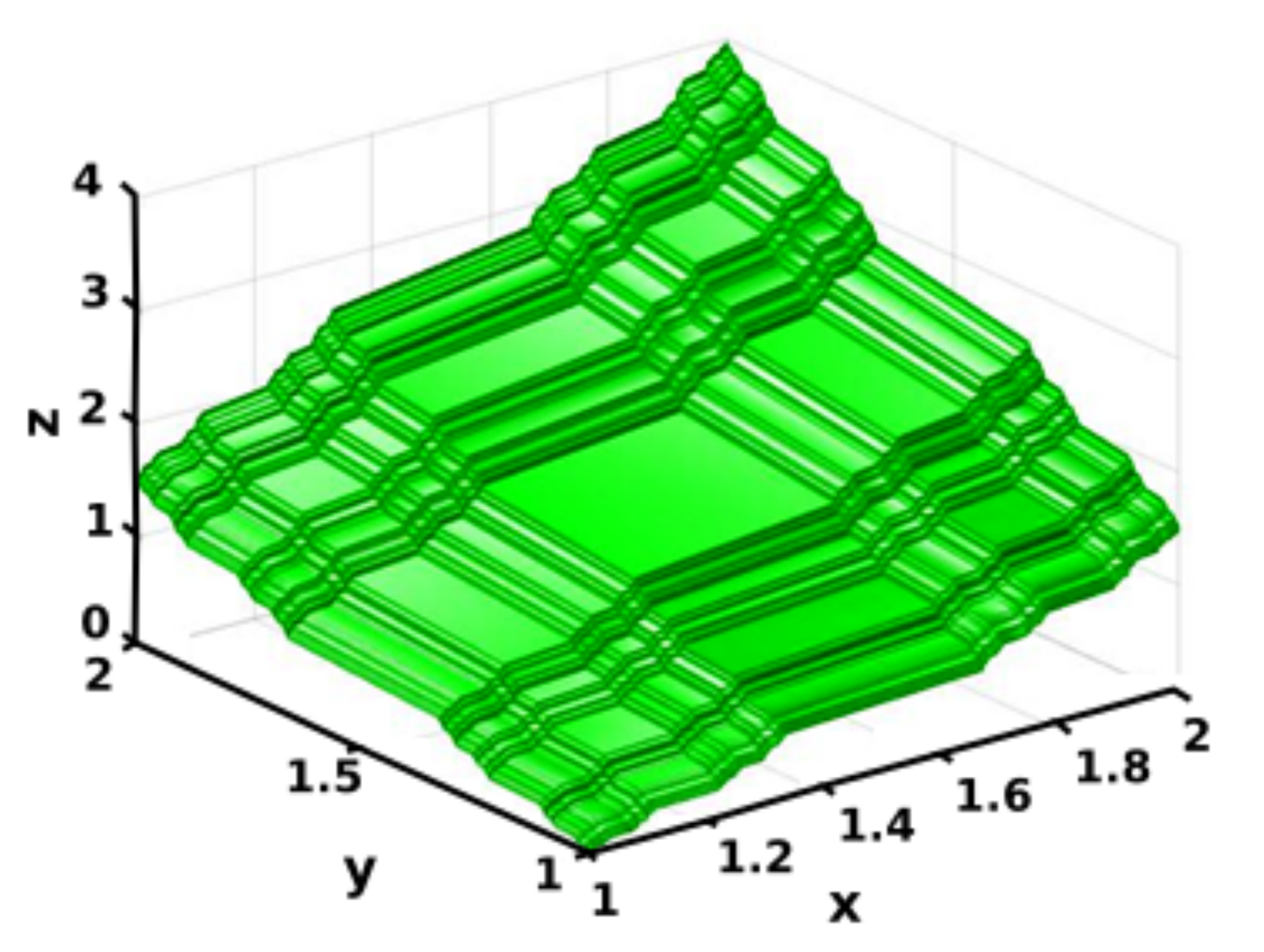
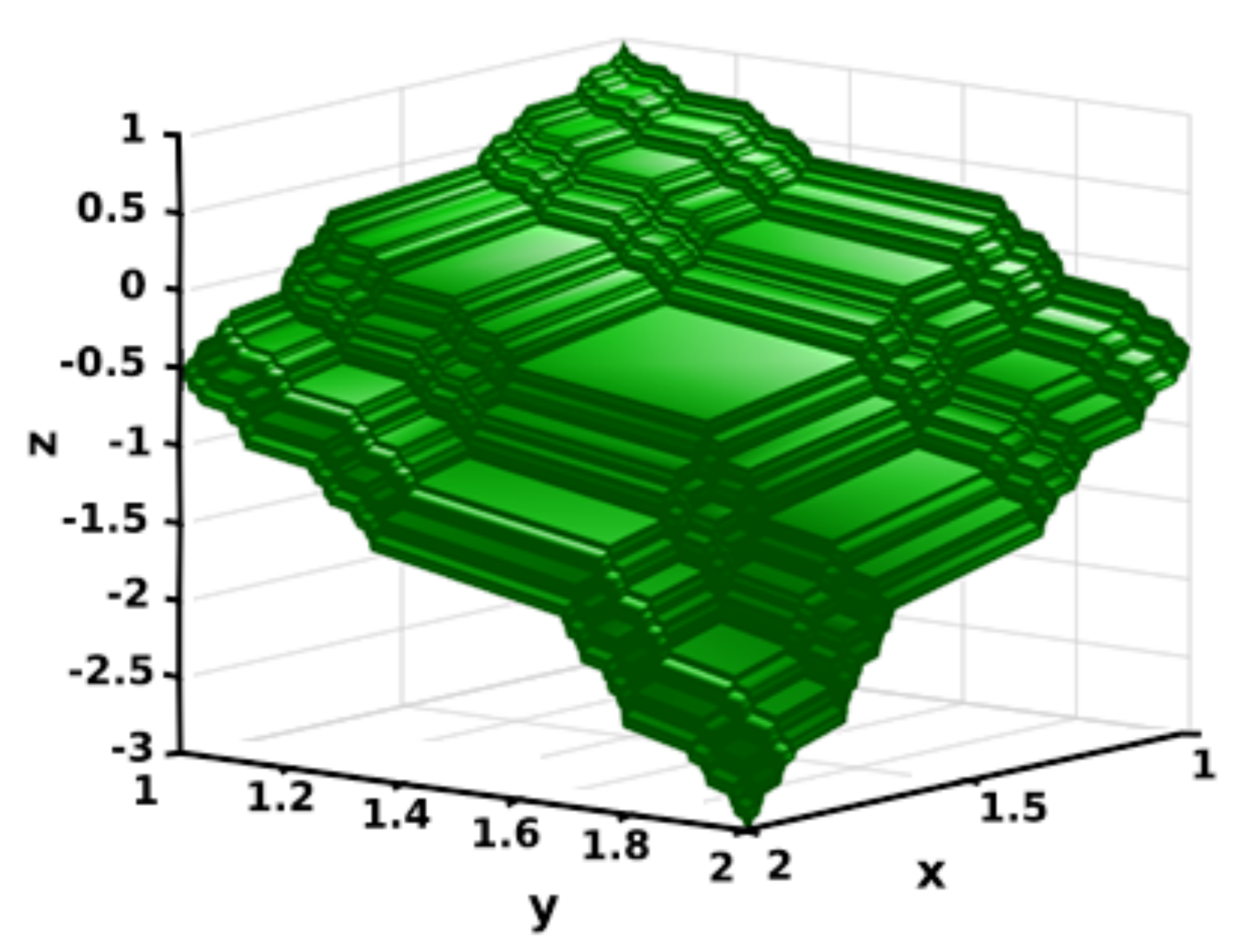
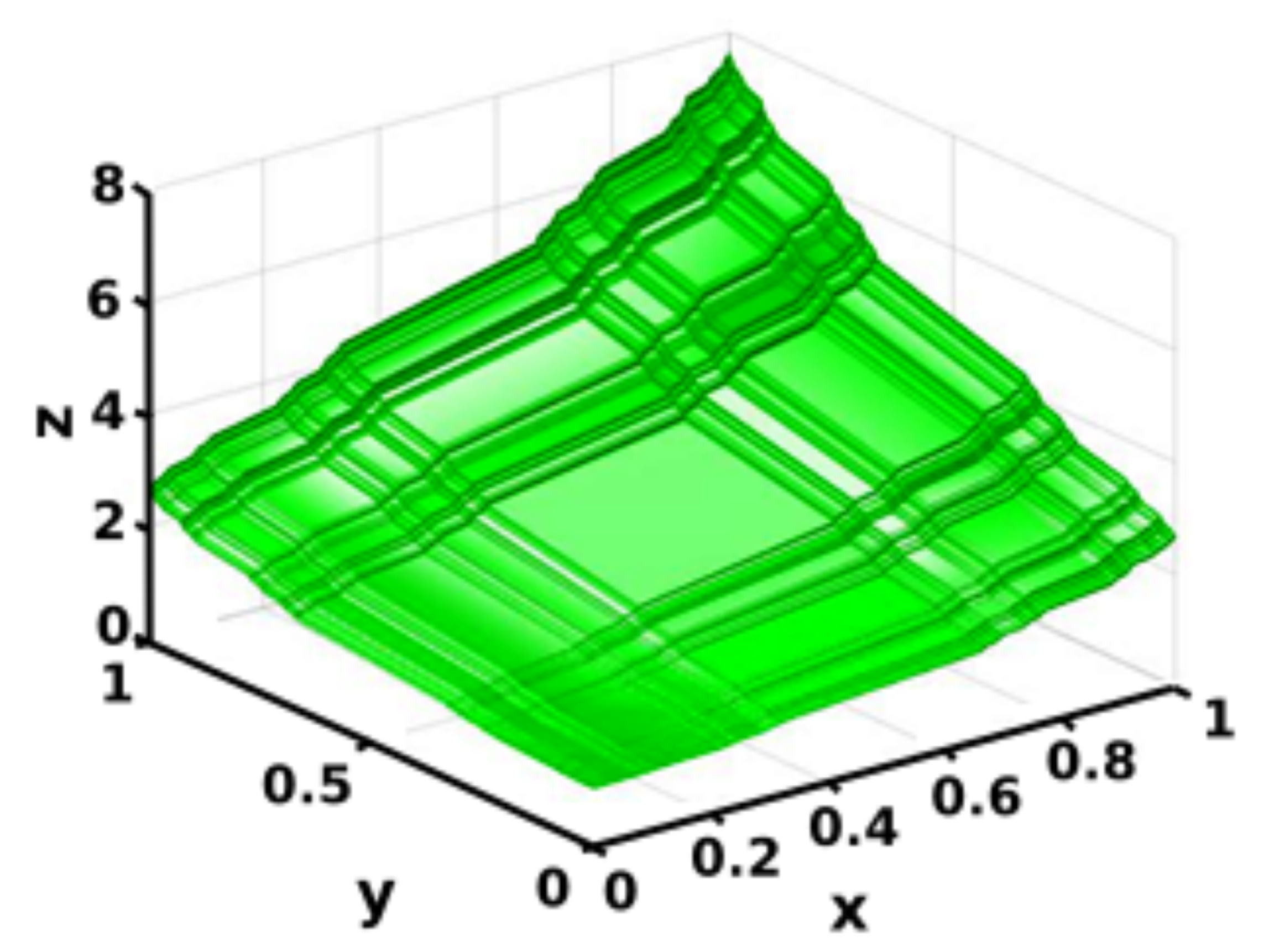
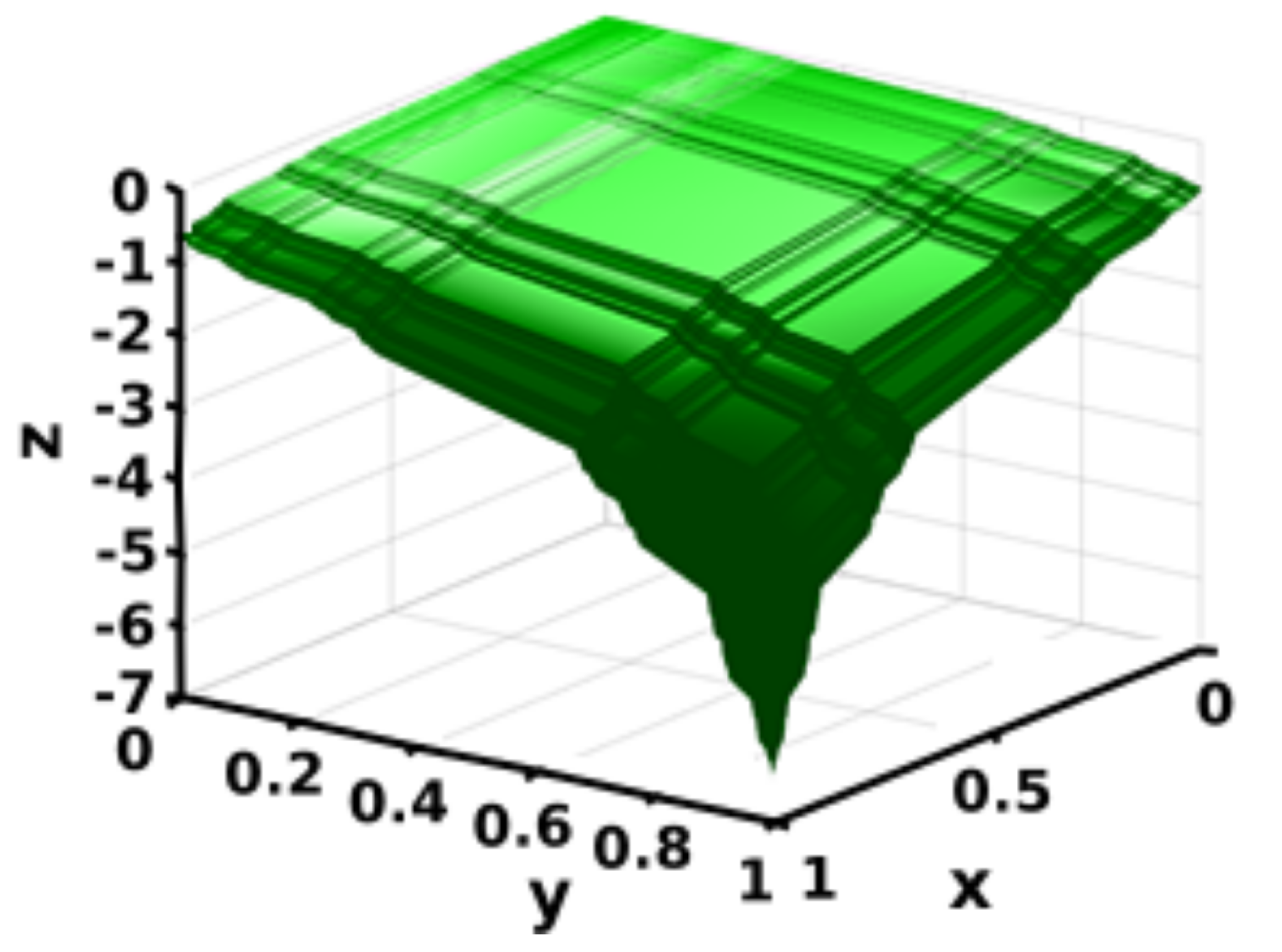

| Geometry | Position-Fluid Moves | Iteration Number | Average Concentration (mol/m) | Standard Deviation | CoV |
|---|---|---|---|---|---|
 | center-inside | 0 | 2.3737 | 0.0103 | 0.004 |
 | center-inside | 1 | 2.5447 | 1.4684 | 0.57 |
 | center-outside | 1 | 2.5423 | 1.5468 | 0.60 |
 | left-outside | 1 | 2.7951 | 1.2634 | 0.45 |
 | left-right-outside | 0 | 2.5819 | 0.9720 | 0.37 |
 | 2left-right-outside | 1 | 2.6781 | 0.9815 | 0.36 |
 | 2left-right-outside | 0 | 2.8165 | 0.7936 | 0.28 |
 | center-outside | 3 | 2.4421 | 1.5908 | 0.65 |
 | left-outside | 3 | 2.6013 | 1.3515 | 0.51 |
| Geometry | Position-Fluid Moves | Iteration Number | Average Concentration (mol/m) | Standard Deviation | CoV |
|---|---|---|---|---|---|
 | right-outside | 1 | 2.4645 | 1.4082 | 0.57 |
 | center-outside | 2 | 2.4144 | 1.4952 | 0.61 |
 | center-outside | 2 | 2.4199 | 1.5225 | 0.62 |
 | center-outside | 3 | 2.4532 | 1.4953 | 0.55 |
 | left-outside | 1 | 2.5447 | 1.4684 | 0.57 |
 | center-outside | 1 | 2.5802 | 1.5240 | 0.59 |
 | right-outside | 1 | 2.5817 | 1.4226 | 0.55 |
 | left-outside | 0 | 2.6297 | 1.3808 | 0.52 |
 | right-outside | 0 | 2.6497 | 1.3242 | 0.49 |
| Geometry | Position-Fluid Moves | Iteration Number | Average Concentration (mol/m) | Standard Deviation | CoV |
|---|---|---|---|---|---|
 | left-outside | 0 | 2.7011 | 1.1828 | 0.43 |
 | center-inside | 1 | 2.8975 | 1.2115 | 0.41 |
 | center-inside-rotated | 2 | 2.8208 | 1.2538 | 0.51 |
 | center-inside | 2 | 2.6588 | 1.5469 | 0.58 |
 | two-center-inside | 2 | 2.8538 | 0.9486 | 0.33 |
 | two-center-outside | 2 | 2.4532 | 1.4953 | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pishkoo, A.; Darus, M. Using Fractal Calculus to Solve Fractal Navier–Stokes Equations, and Simulation of Laminar Static Mixing in COMSOL Multiphysics. Fractal Fract. 2021, 5, 16. https://doi.org/10.3390/fractalfract5010016
Pishkoo A, Darus M. Using Fractal Calculus to Solve Fractal Navier–Stokes Equations, and Simulation of Laminar Static Mixing in COMSOL Multiphysics. Fractal and Fractional. 2021; 5(1):16. https://doi.org/10.3390/fractalfract5010016
Chicago/Turabian StylePishkoo, Amir, and Maslina Darus. 2021. "Using Fractal Calculus to Solve Fractal Navier–Stokes Equations, and Simulation of Laminar Static Mixing in COMSOL Multiphysics" Fractal and Fractional 5, no. 1: 16. https://doi.org/10.3390/fractalfract5010016
APA StylePishkoo, A., & Darus, M. (2021). Using Fractal Calculus to Solve Fractal Navier–Stokes Equations, and Simulation of Laminar Static Mixing in COMSOL Multiphysics. Fractal and Fractional, 5(1), 16. https://doi.org/10.3390/fractalfract5010016





