Cole-Impedance Model Representations of Right-Side Segmental Arm, Leg, and Full-Body Bioimpedances of Healthy Adults: Comparison of Fractional-Order
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Participants
2.2. Dual-Energy X-ray Absorption Measurements
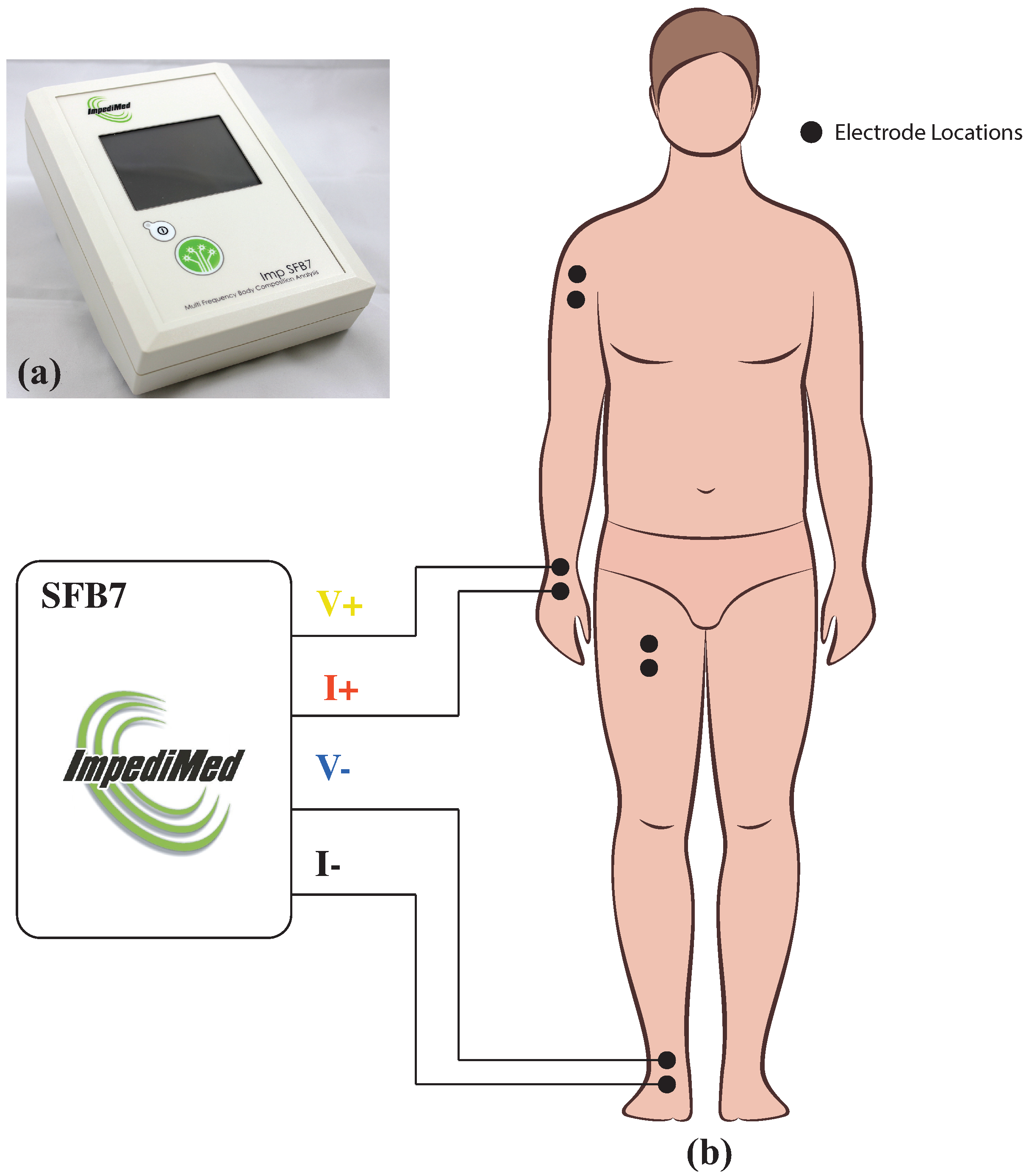
2.3. Electrical Impedance Measurements
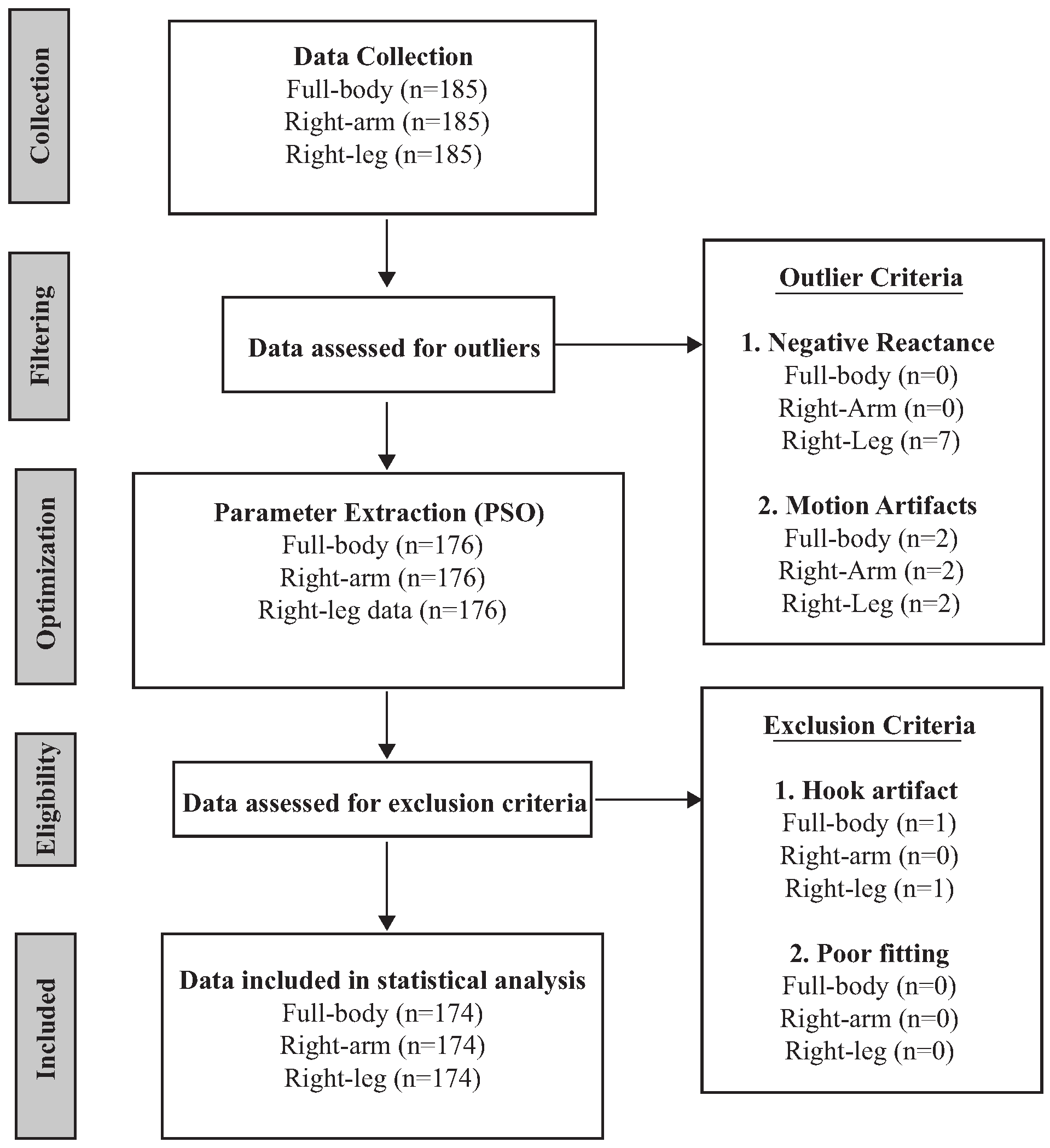
2.4. Outlier Identification/Removal
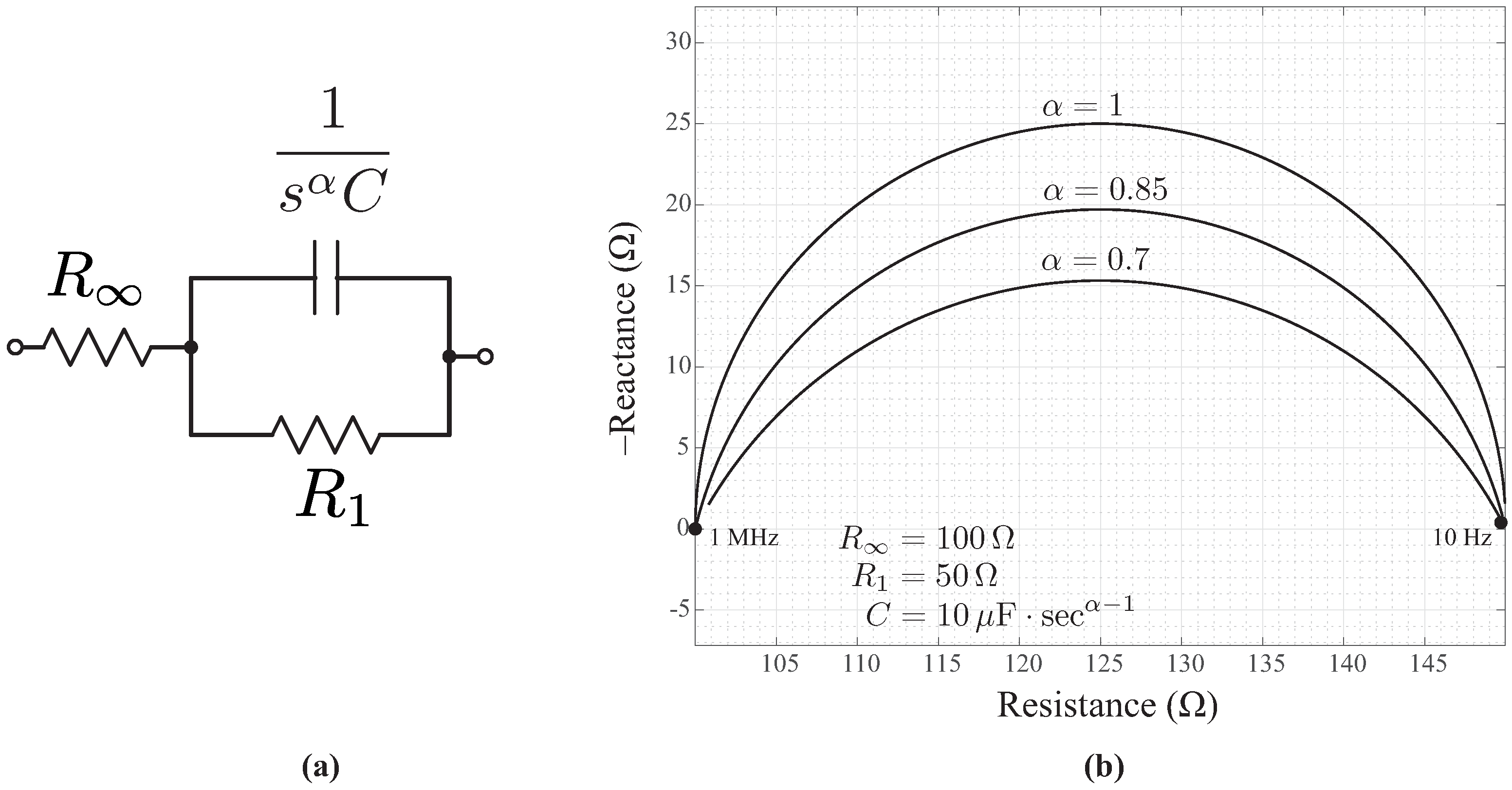
2.5. Cole-Impedance Model Parameter Identification
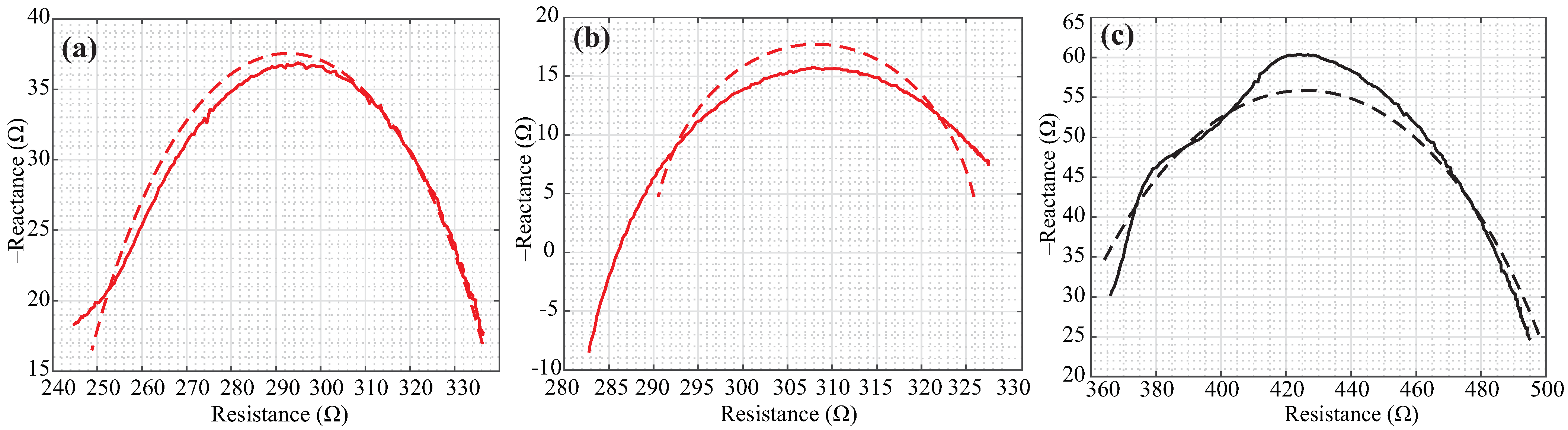
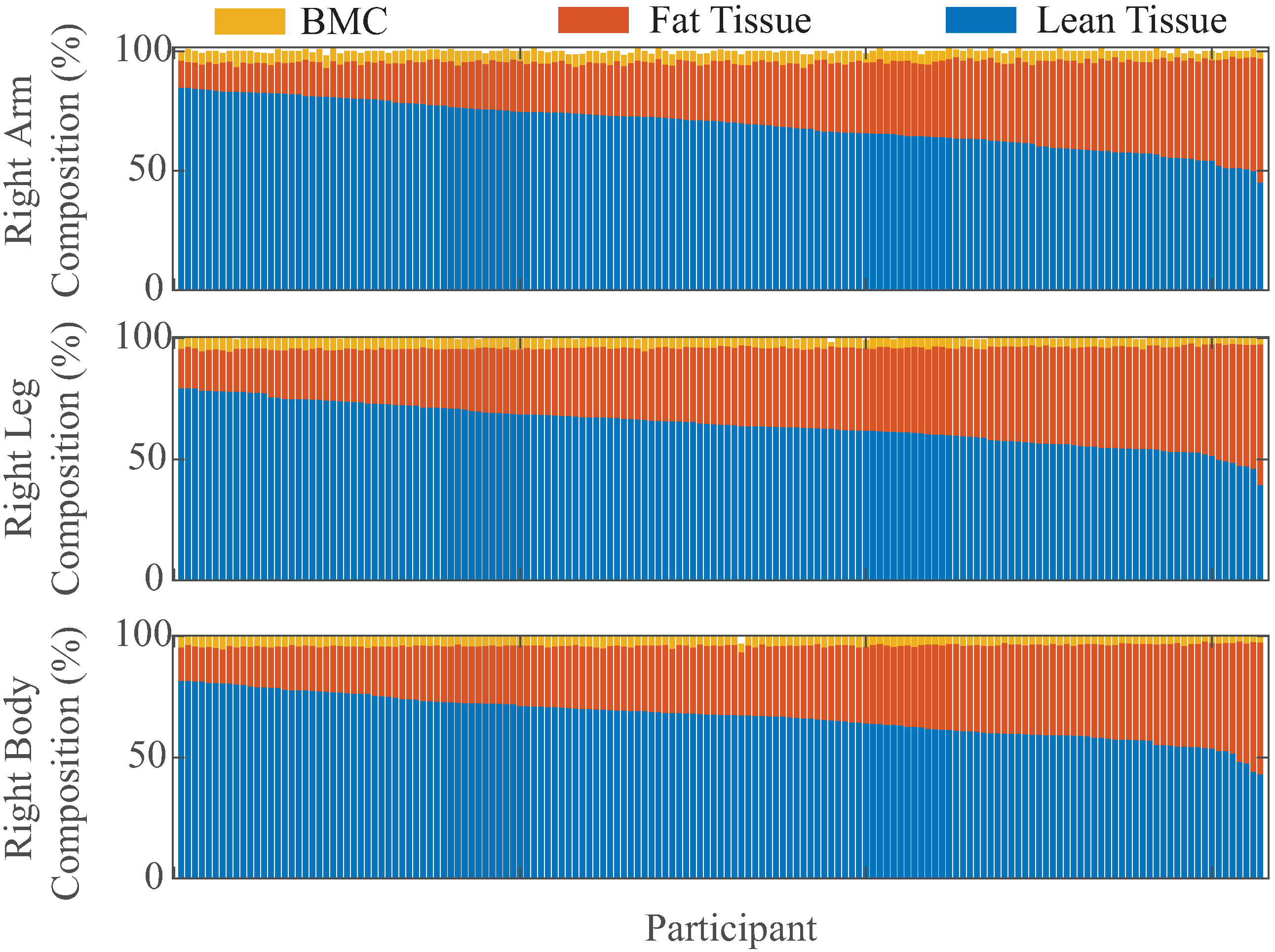
3. Results
3.1. Statistical Testing: Friedman Test
3.2. Statistical Testing: Spearman Correlation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cole, K. Permeability and impermeability of cell membranes for ions. Cold Spring Harbor Symp. Quant. Biol. 1940, 8, 110–122. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Fu, B. Fatigue-induced cole electrical impedance model changes of biceps tissue bioimpedance. Fractal Fract. 2018, 2, 27. [Google Scholar] [CrossRef]
- Fu, B.; Freeborn, T. Cole-impedance parameters representing biceps tissue bioimpednace in healthy adults and their alterations following eccentric exercise. J. Adv. Res. 2020, 25, 285–293. [Google Scholar] [CrossRef] [PubMed]
- Sanchez, B.; Li, J.; Geisbush, T.; Bardia, R.; Rutkove, S. Impedance alterations in healthy and diseased mice during electrically induced muscle contraction. IEEE Trans. Biomed. Eng. 2016, 63, 1602–1612. [Google Scholar] [CrossRef]
- Al-Surkhi, O.; Naser, R. Detection of cell morphological changes of ischemic rabbit liver tissue using bioimepdance spectroscopy. IEEE Trans. Nanobiosci. 2018, 17, 402–408. [Google Scholar] [CrossRef]
- Parramon, D.; Erill, I.; Guimer, A.; Ivorra, A.; Munoz, A.; Sola, A.; Fondevila, C.; Garcia-Valdecasas, J.; Villa, R. In vivo detection of liver steatosis in rats based on impedance spectroscopy. Physiol. Meas. 2007, 28, 813–828. [Google Scholar] [CrossRef]
- Taji, B.; Chan, A.; Shirmohammadi, S. Effect of Pressure on Skin-Electrode Impedance in Wearable Biomedical Measurement Devices. IEEE Trans. Instrumen. Meas. 2018, 67, 1900–1912. [Google Scholar] [CrossRef]
- Bai, X.; Hou, J.; Wang, L.; Wang, M.; Wang, X.; Wu, C.; Yu, L.; Yang, J.; Leng, Y.; Sun, Y. Electrical impedance analysis of pork tissues during storage. Food Meas. 2018, 12, 164–172. [Google Scholar] [CrossRef]
- Ribeiro, D.; Abrantes, J. Application of electrochemical impedance spectroscopy (EIS) to monitor the corrosion of reinforced concrete: A new approach. Constr. Build. Mater. 2016, 111, 98–104. [Google Scholar] [CrossRef]
- Westerhoff, U.; Kurbach, K.; Lienesch, F.; Kurrat, M. Analysis of Lithium-Ion Battery Models Based on Electrochemical Impedance Spectroscopy. Energy Technol. 2016, 4, 1620–1630. [Google Scholar] [CrossRef]
- Ionescu, C.; Tenreiro Machado, J.; De Keyser, R. Modeling of the Lung Impedance Using a Fractional-Order Ladder Network With Constant Phase Elements. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Podlubny, I. Fractional Differential Equations; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Freeborn, T.J. A survey of fractional-order circuit models for biology and biomedicine. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 416–424. [Google Scholar] [CrossRef]
- Ionescu, C.; Lopes, A.; Copot, D.; Machado, J.T.; Bates, J. The role of fractional calculus in modeling biological phenomena: A review. Commun. Nonlinear Sci. Numer. Simul. 2017, 51, 141–159. [Google Scholar] [CrossRef]
- Shantanu, D. Functional Fractional Calculus for System Identification and Controls; Springer: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Davis, H.T. The Theory of Linear Operators; Principia Press: Grand Rapids, MI, USA, 1936. [Google Scholar]
- Ross, B. Fractional Calculus. Math. Mag. 1977, 50, 115–122. [Google Scholar] [CrossRef]
- Westerlund, S.; Ekstam, L. Capacitor theory. IEEE Trans. Dielectr. Elec. Insul. 1994, 1, 586–839. [Google Scholar] [CrossRef]
- Rigaud, B.; Hamzaoui, L.; Frikha, M.R.; Chauveau, N.; Morucci, J.P. In vitro tissue characterization and modelling using electrical impedance measurements in the 100 Hz–10 MHz frequency range. Physiol. Meas. 1995, 16, A15–A28. [Google Scholar] [CrossRef]
- Esco, M.R.; Fedewa, M.V.; Freeborn, T.J.; Moon, J.R.; Wingo, J.E.; Cicone, Z.; Holmes, C.J.; Hornikel, B.; Welborn, B. Agreement between supine and standing bioimpedance spectroscopy devices and dual-energy X-ray absorptiometry for body composition determination. Clin. Physiol. Funct. Imaging 2019, 39, 355–361. [Google Scholar] [CrossRef]
- Pietrobelli, A.; Formica, C.; Wang, Z.; Heymsfield, S. Dual-energy X-ray absorptiometry body composition model: Review of physical concepts. Am. J. Physiol. Endocrinol. Metab. 1996, 271, E941–E951. [Google Scholar] [CrossRef]
- Pateyjohns, I.; Brinkworth, G.; Buckley, J.; Boakes, M.; Clifton, P. Comparison of three bioelectrical impedance methods with DXA in overweight and obese men. Obesity 2006, 14, 2064–2070. [Google Scholar] [CrossRef]
- Vine, S.; Painter, P.; Kuskowski, M.; Earthman, C. Bioimpedance spectroscopy for the estimation of fat-free mass in end-stage renal disease. e-SPEN Eur. J. Clin. Nutr. Metab. 2011, 6, e1–e6. [Google Scholar] [CrossRef]
- Freeborn, T.J.; Milligan, A.; Esco, M.R. Evaluation of ImpediMed SFB7 BIS device for low-impedance measurements. Measurement 2018, 129, 20–30. [Google Scholar] [CrossRef]
- Grimnes, S.; Martinsen, O. Journal of Physics D: Applied Physics Sources of error in tetrapolar impedance measurements on biomaterials and other ionic conductors. J. Phys. D Appl. Phys. 2006, 20, 9–14. [Google Scholar]
- Aliau-Bonet, C.; Pallas-Areny, R. On the Effect of Body Capacitance to Ground in Tetrapolar Bioimpedance Measurements. IEEE Trans. Biomed. Eng. 2012, 59, 3405–3411. [Google Scholar] [CrossRef] [PubMed]
- Yousri, D.; AbdelAty, A.; Said, L.; AboBakr, A.; Radwan, A. Biological inspired optimization algorithms for cole-impedance parameters identification. Int. J. Electron. Commun. 2017, 78, 79–89. [Google Scholar] [CrossRef]
- Naranjo-Hernandez, D.; Reina-Tosina, J.; Roa, L.; Barbarov-Rostan, G.; Areste-Fosalba, N.; Lara-Ruiz, A.; Cejudo-Ramos, P.; Ortega-Ruiz, F. Smart bioimpedance spectroscopy device for body composition estimation. Sensors 2020, 20, 70. [Google Scholar] [CrossRef]
- Fu, B.; Freeborn, T. Estimating localized bio-impedance with measures from multiple redundant electrode configurations. In Proceedings of the 2018 40th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Honolulu, HI, USA, 17–21 July 2018; pp. 4351–4354. [Google Scholar]
- Janssen, I.; Hymsfield, S.; Baumgartner, R.; Ross, R. Estimation of skeletal muscle mass by bioelectrical impedance analysis. J. Appl. Physiol. 2000, 89, 465–471. [Google Scholar] [CrossRef]
- Kyle, U.; Bosaeus, I.; De Lorenzo, A.; Deurenberg, P.; Elia, M.; Gomez, J.; Heitmann, B.; Kent-Smith, L.; Melchior, J.; Pirlich, M.; et al. Bioelectrical impedance analysis—Part i: Review of principles and methods. Clin. Nutr. 2004, 23, 1226–1243. [Google Scholar] [CrossRef]
- Arnold, W.; Taylor, R.; Li, J.; Nagy, J.; Sanchez, B.; Rutkove, S. Electrical impedance myography detects age-related muscle change in mice. PLoS ONE 2017, 12, e0185614. [Google Scholar] [CrossRef]
- Nagy, J.; Kapur, K.; Taylor, R.; Sanchez, B.; Rutkove, S. Electrical impedance myography as a biomarker of myostatin inhibition with ActRIIB-mFc: A study in wild-type mice. Future Sci. OA 2018, 4, FSO308. [Google Scholar] [CrossRef]
- Clark-Matott, J.; Nagy, J.; Sanchez, B.; Taylor, R.; Riveros, D.; Abraham, N.; Simon, D.; Rutkove, S. Altered muscle electrical tissue properties in a mouse model of premature aging. Muscle Nerve 2019, 60, 801–810. [Google Scholar] [CrossRef]
- Sanchez, B.; Bragos, R.; Rutkove, S. Differentiation of the intracellular structure of slow- versus fast-twitch muscle fibers through evaluation of the dielectric properties of tissue. Phys. Med. Biol. 2014, 59, 2369–2380. [Google Scholar] [CrossRef] [PubMed]
- Sato, H.; Nakamura, T.; Kusuhara, T.; Kenichi, K.; Kuniyasu, K.; Kawashima, T.; Hanayama, K. Effectiveness of impedance parameters for muscle quality evaluation in healthy men. J. Physiol. Sci. 2020, 70, 53. [Google Scholar] [CrossRef] [PubMed]
- McAdams, E.; Jossinet, J. Problems in equivalent circuit modelling of the electrical properties of biological tissues. Bioelectrochem. Bioenerg. 1996, 40, 147–152. [Google Scholar] [CrossRef]
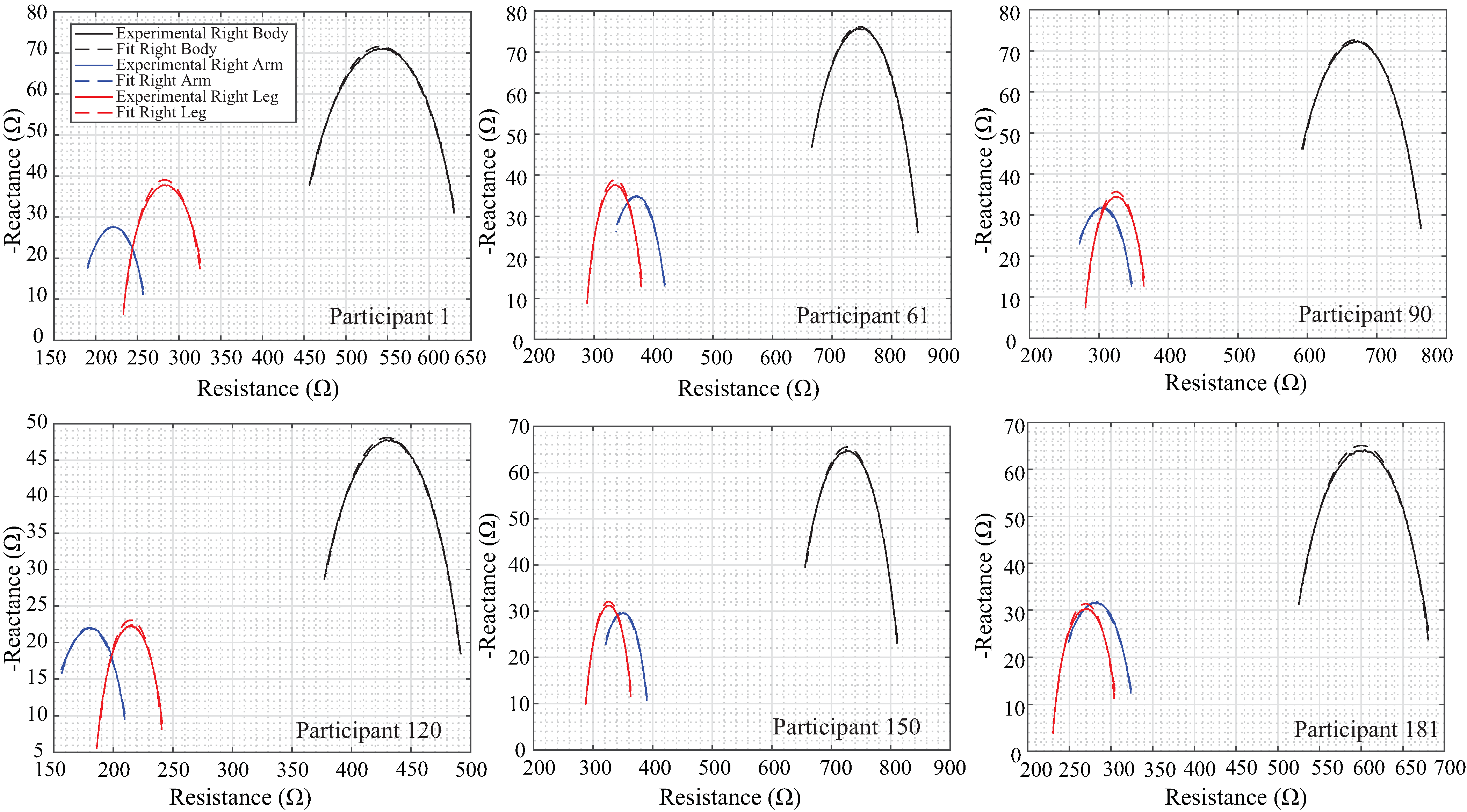
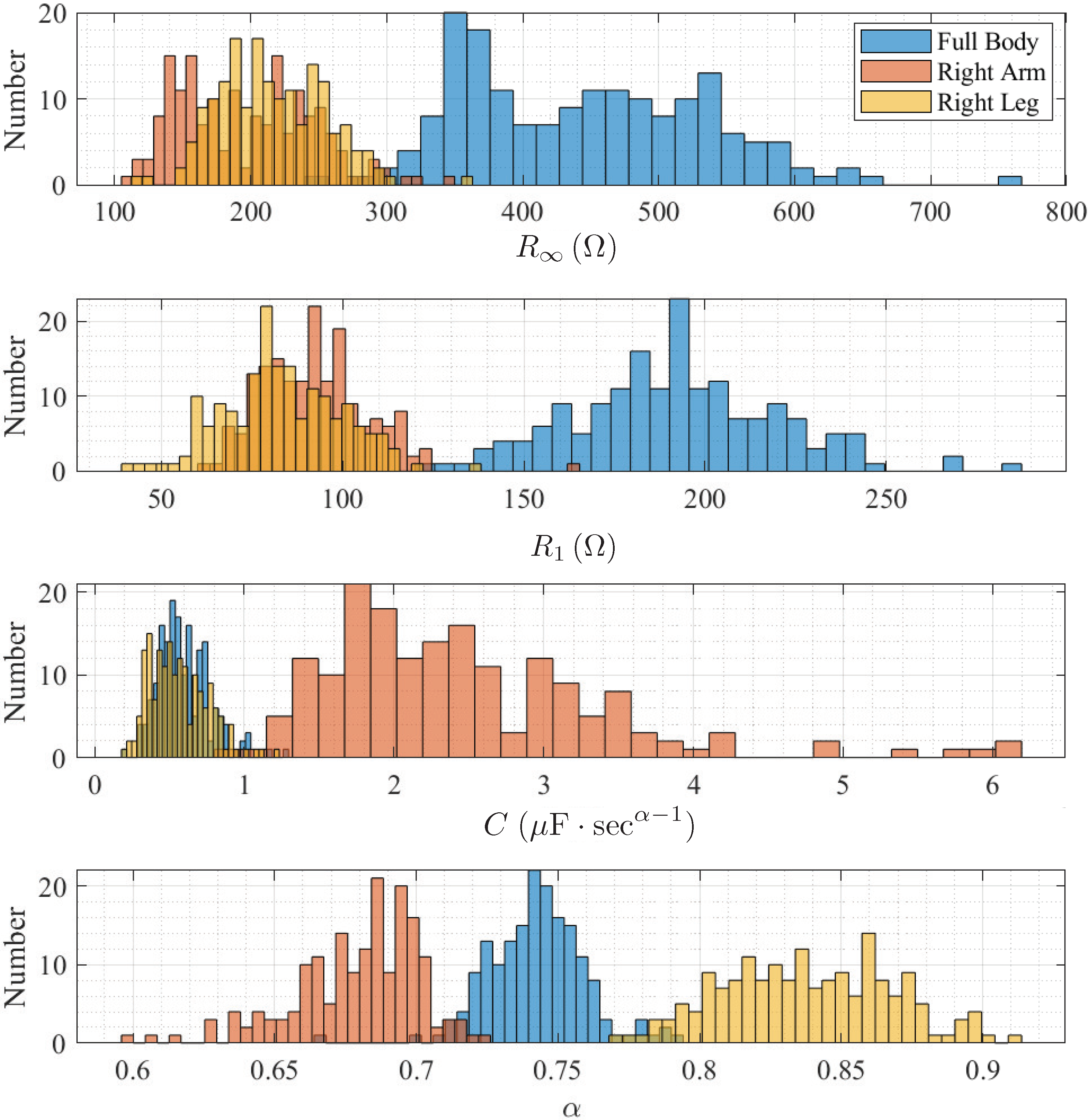

| Body Segment | () | () | C | |
|---|---|---|---|---|
| Right-side Full Body | ||||
| Right Arm | ||||
| Right Leg |
| Total Tissue (kg) | Lean Tissue (kg) | Fat Tissue (kg) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Full-Body | Arm | Leg | Full-Body | Arm | Leg | Full-Body | Arm | Leg | |
| () | |||||||||
| − | − | − | |||||||
| p | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | − | − | − |
| () | |||||||||
| − | − | ||||||||
| p | <0.001 | <0.001 | <0.001 | − | <0.001 | − | <0.001 | ||
| C () | |||||||||
| − | |||||||||
| p | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | <0.001 | − |
| − | − | − | − | ||||||
| p | <0.001 | − | <0.001 | <0.001 | − | <0.001 | − | <0.001 | − |
| Authors | Sample Population | Muscle Location | Frequency Band | Fractional-Order () |
|---|---|---|---|---|
| Rigaud et al. [19] | Sheep | Gemellus (Ex Vivo) | kHz–720 kHz | Longitudinal: Traverse: |
| Arnold et al. [32] | Mice | Gastrocnemius (Surface) | 1 kHz–10 MHz | Longitudinal (Young): Traverse (Young): Longitudinal (Aged): Traverse (Aged): |
| Nagy et al. [33] | Mice | Gastrocnemius (Surface) | 1 kHz–10 MHz | Longitudinal: – Traverse: – |
| Clark-Matott et al. [34] | Mice | Gastrocnemius Ex Vivo | 1 kHz–10 MHz | Longitudinal: – Traverse: – |
| Sanchez, Bragos, & Rutkove [35] | Rat | Gastrocnemius (Ex Vivo) Soleus (Ex Vivo) | 1 kHz–1 MHz 1 kHz–1 MHz | Longitudinal: Traverse: Longitudinal: Traverse: |
| Freeborn & Fu [2] | Healthy Adults | Biceps (Surface) | 10 kHz–100 kHz | Pre Exercise: – Post Exercise: – |
| Fu & Freeborn [3] | Healthy Adults | Biceps (Surface) | 10 kHz–100 kHz | Exercised: – Unexercised: – |
| Sato et al. [36] | Healthy Men (Surface) | Lower Extremities | 5 kHz–250 kHz | |
| This work | Healthy Adults | Right-Body, Segmental Arm/Leg | 3 kHz–200 | Right-Body: 0.687–0.769 Right Arm: 0.606–0.725 Right Leg: 0.778–0.971 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Freeborn, T.J.; Critcher, S. Cole-Impedance Model Representations of Right-Side Segmental Arm, Leg, and Full-Body Bioimpedances of Healthy Adults: Comparison of Fractional-Order. Fractal Fract. 2021, 5, 13. https://doi.org/10.3390/fractalfract5010013
Freeborn TJ, Critcher S. Cole-Impedance Model Representations of Right-Side Segmental Arm, Leg, and Full-Body Bioimpedances of Healthy Adults: Comparison of Fractional-Order. Fractal and Fractional. 2021; 5(1):13. https://doi.org/10.3390/fractalfract5010013
Chicago/Turabian StyleFreeborn, Todd J., and Shelby Critcher. 2021. "Cole-Impedance Model Representations of Right-Side Segmental Arm, Leg, and Full-Body Bioimpedances of Healthy Adults: Comparison of Fractional-Order" Fractal and Fractional 5, no. 1: 13. https://doi.org/10.3390/fractalfract5010013
APA StyleFreeborn, T. J., & Critcher, S. (2021). Cole-Impedance Model Representations of Right-Side Segmental Arm, Leg, and Full-Body Bioimpedances of Healthy Adults: Comparison of Fractional-Order. Fractal and Fractional, 5(1), 13. https://doi.org/10.3390/fractalfract5010013







