Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees
Abstract
1. Introduction
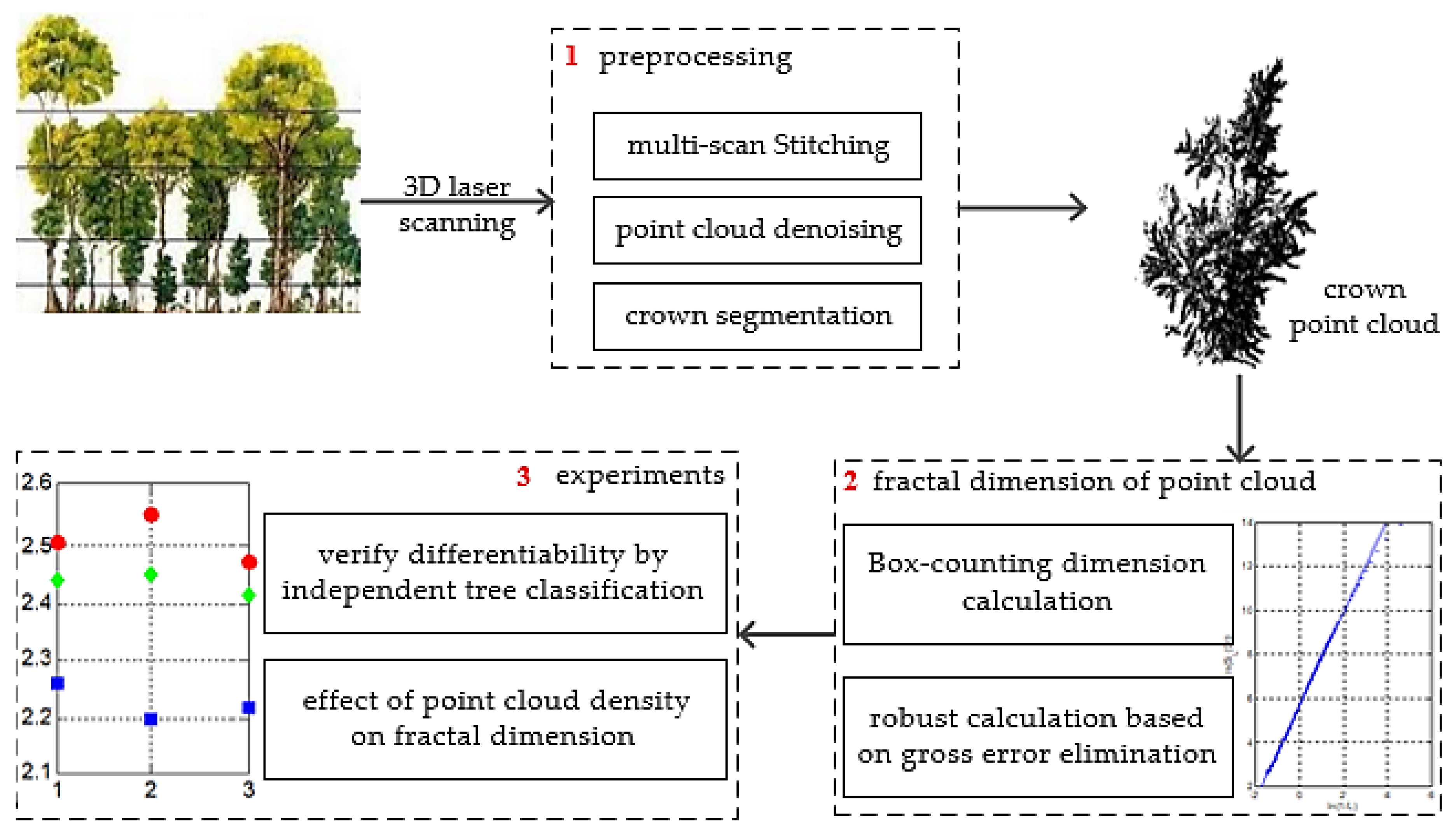
2. Materials and Methods
2.1. Independent Tree Point Cloud Acquisition and Preprocessing
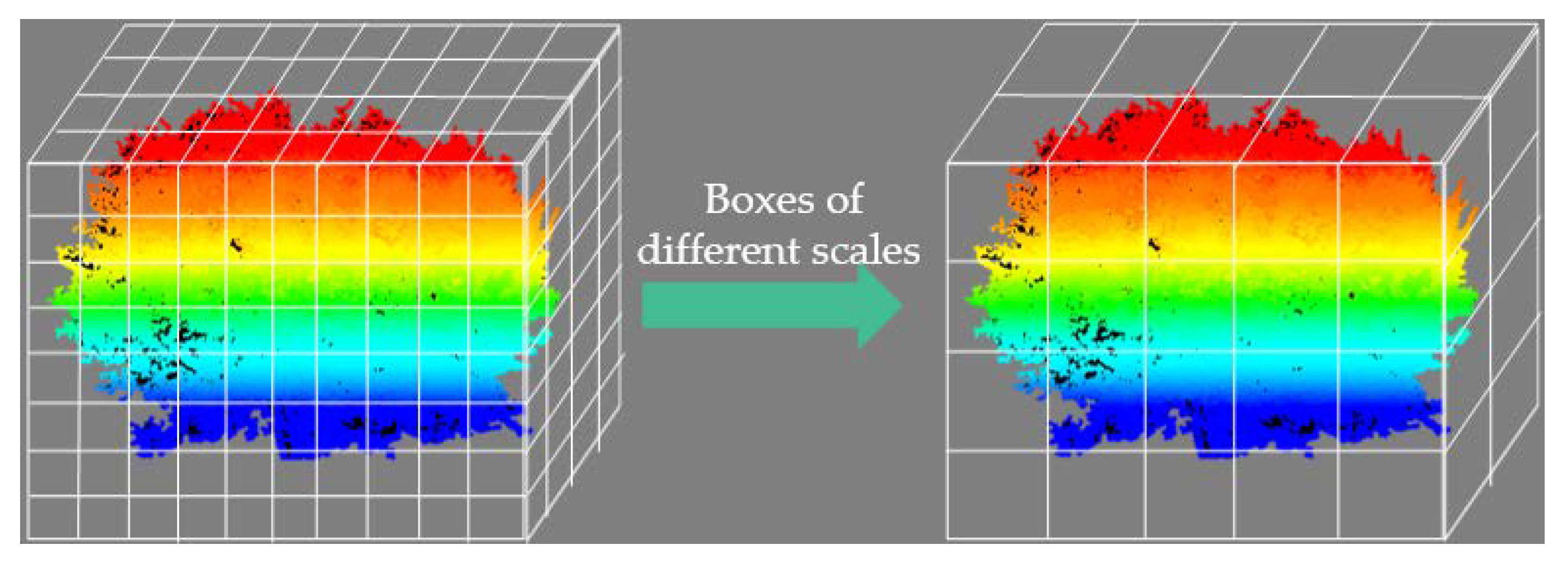
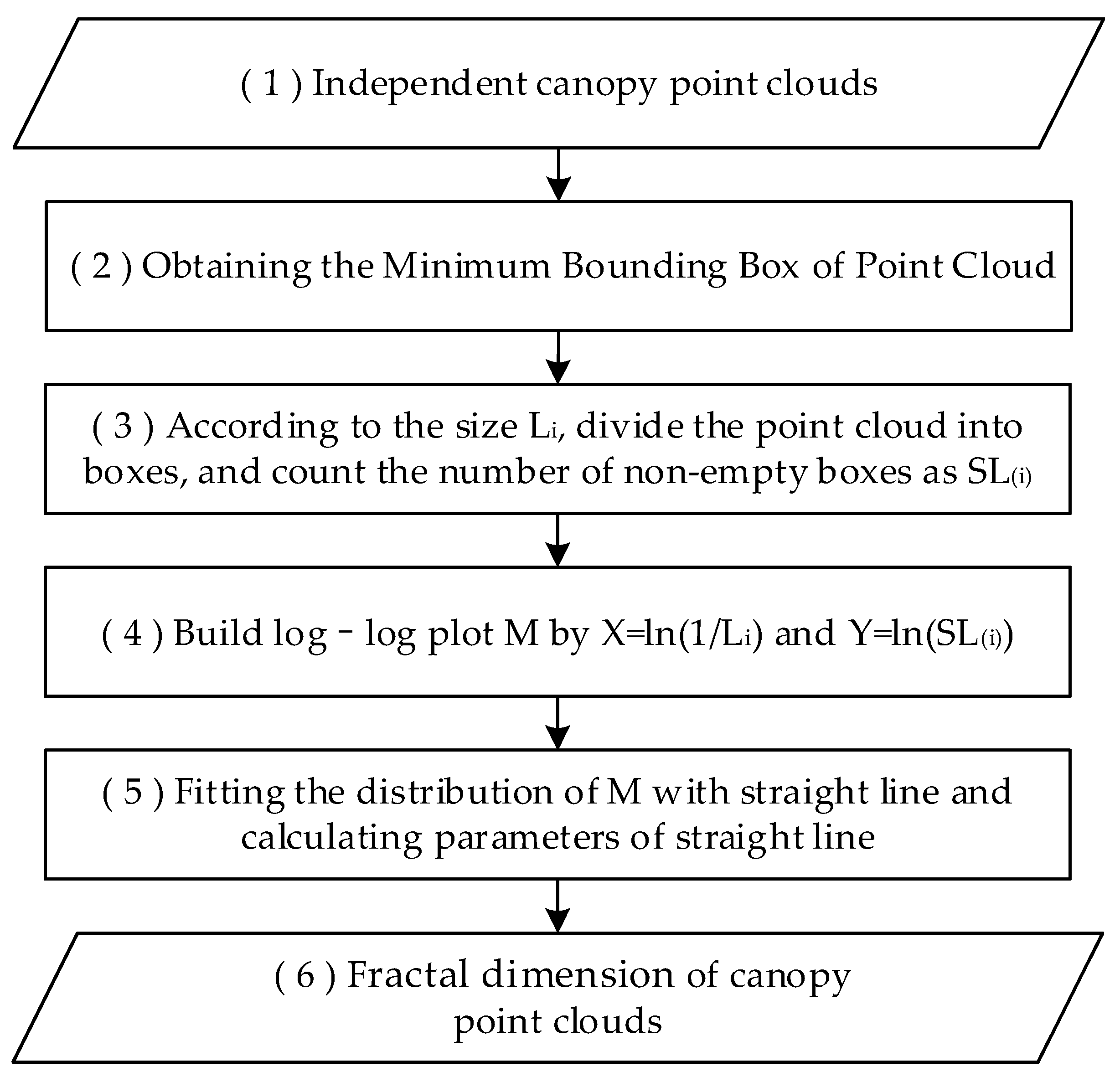
2.2. Box-Counting of Terrestrial Point Clouds
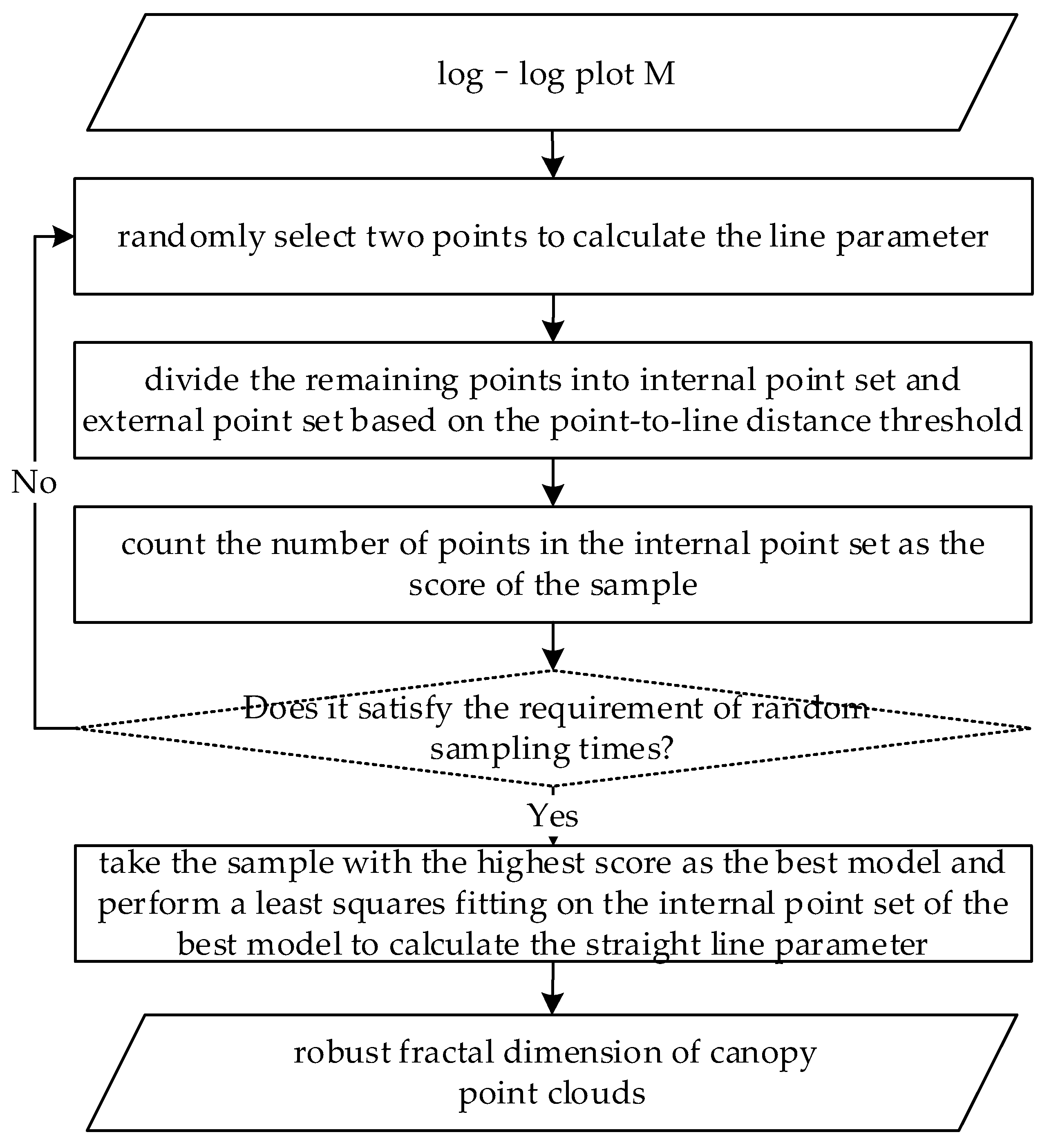
2.3. Box-Counting Dimension Fitting Based on RANSAC Gross Error Elimination
- Data in the point set of the log-log plot only conform to linear models;
- There is no same point in the point set of the log-log plot. Each point in the point set corresponded to a spatial partition, and side length of the box in each partition was different (the side length would be monotonically increasing from initial side length as the iterative spatial partition proceeds). Accordingly, the abscissa of every point in the point set of the log-log plot was different, and parameters of the straight line could be fitted from any two points in the point set;
- The spatial extent of the terrestrial point clouds of an individual tree was limited, so the number of points in the point set of the log-log plot would not be excessively large.
2.4. Evaluating Indicator
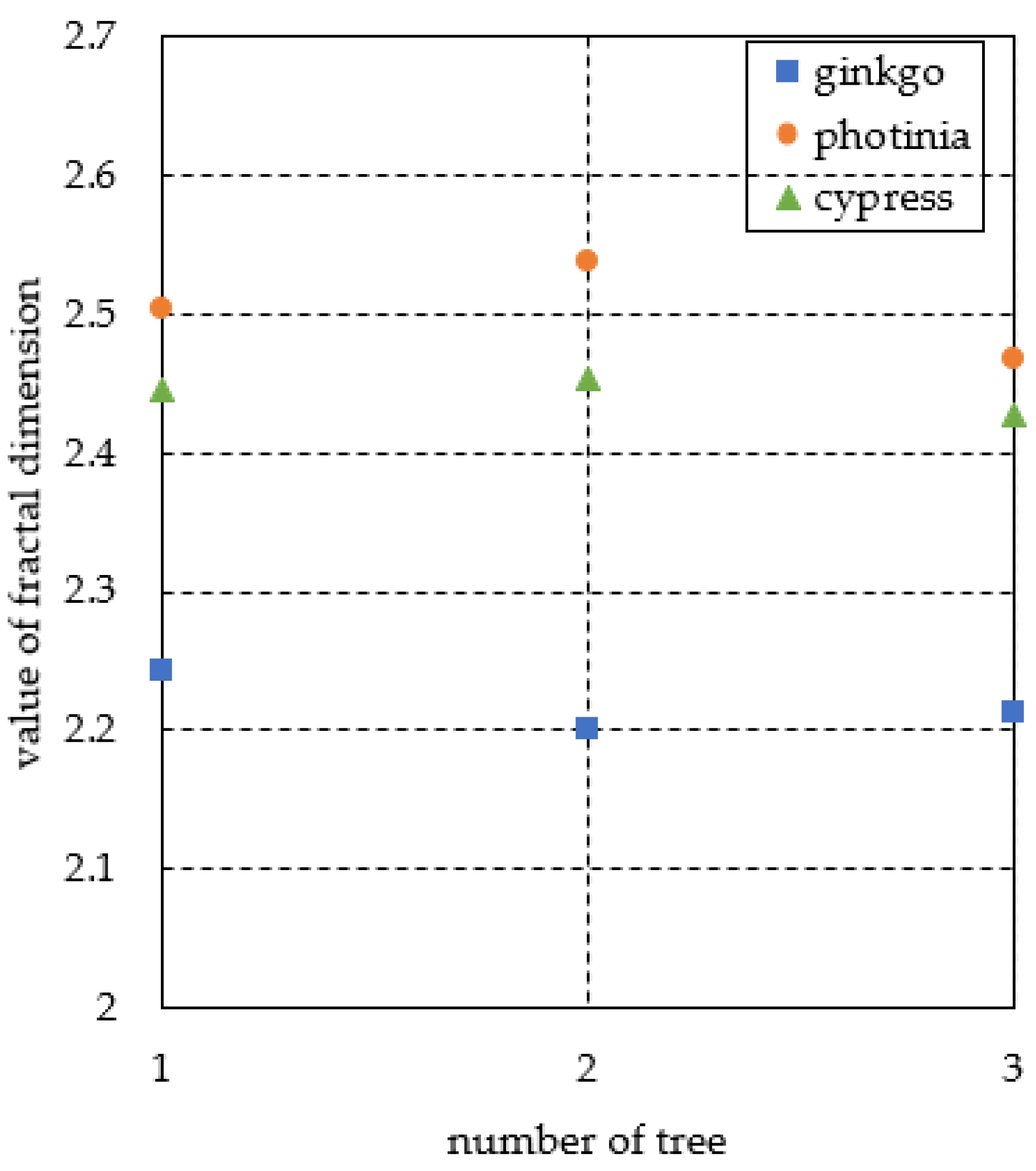
3. Results
3.1. Fractal Dimension of Three Ginkgo Trees
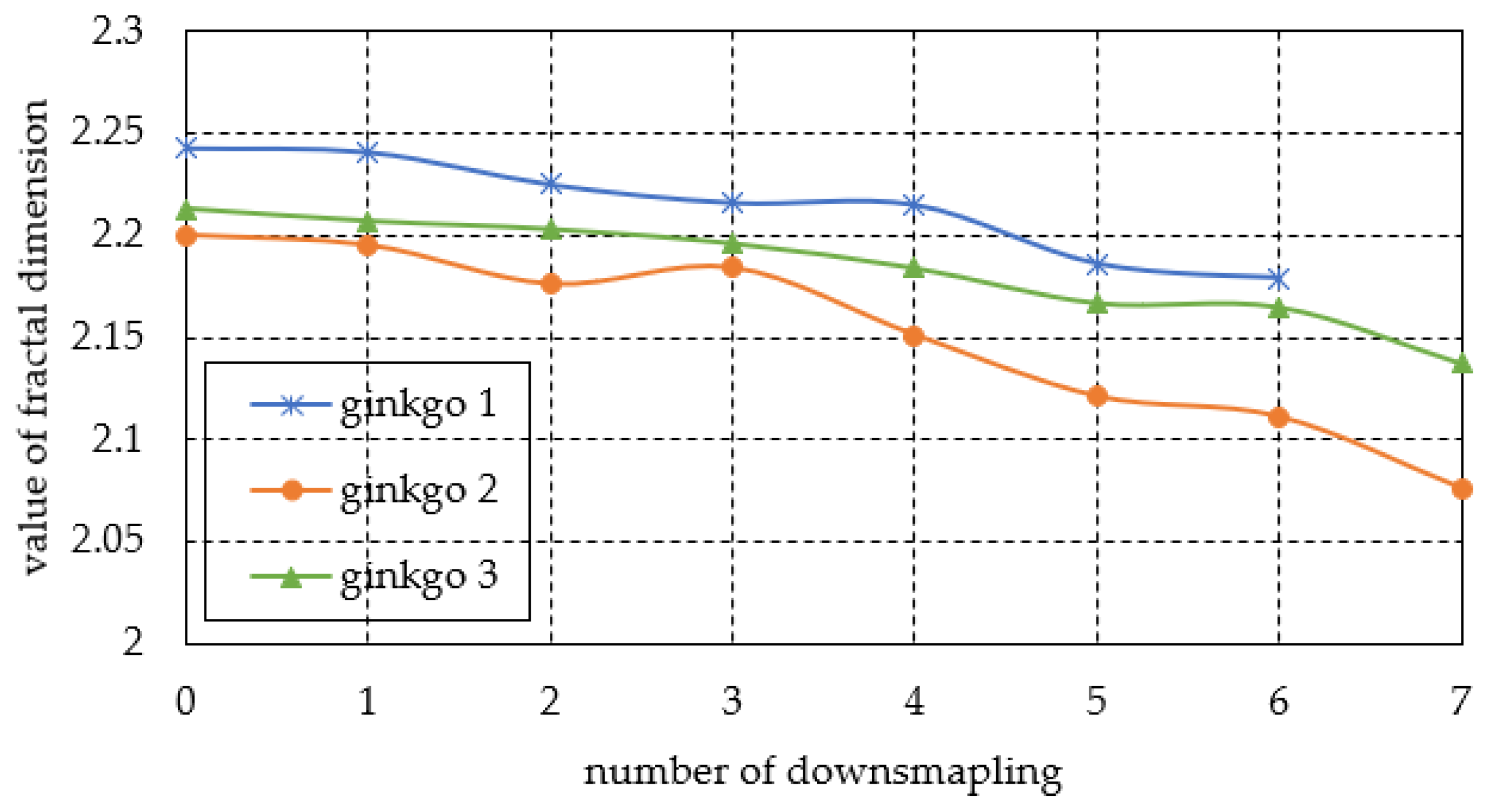
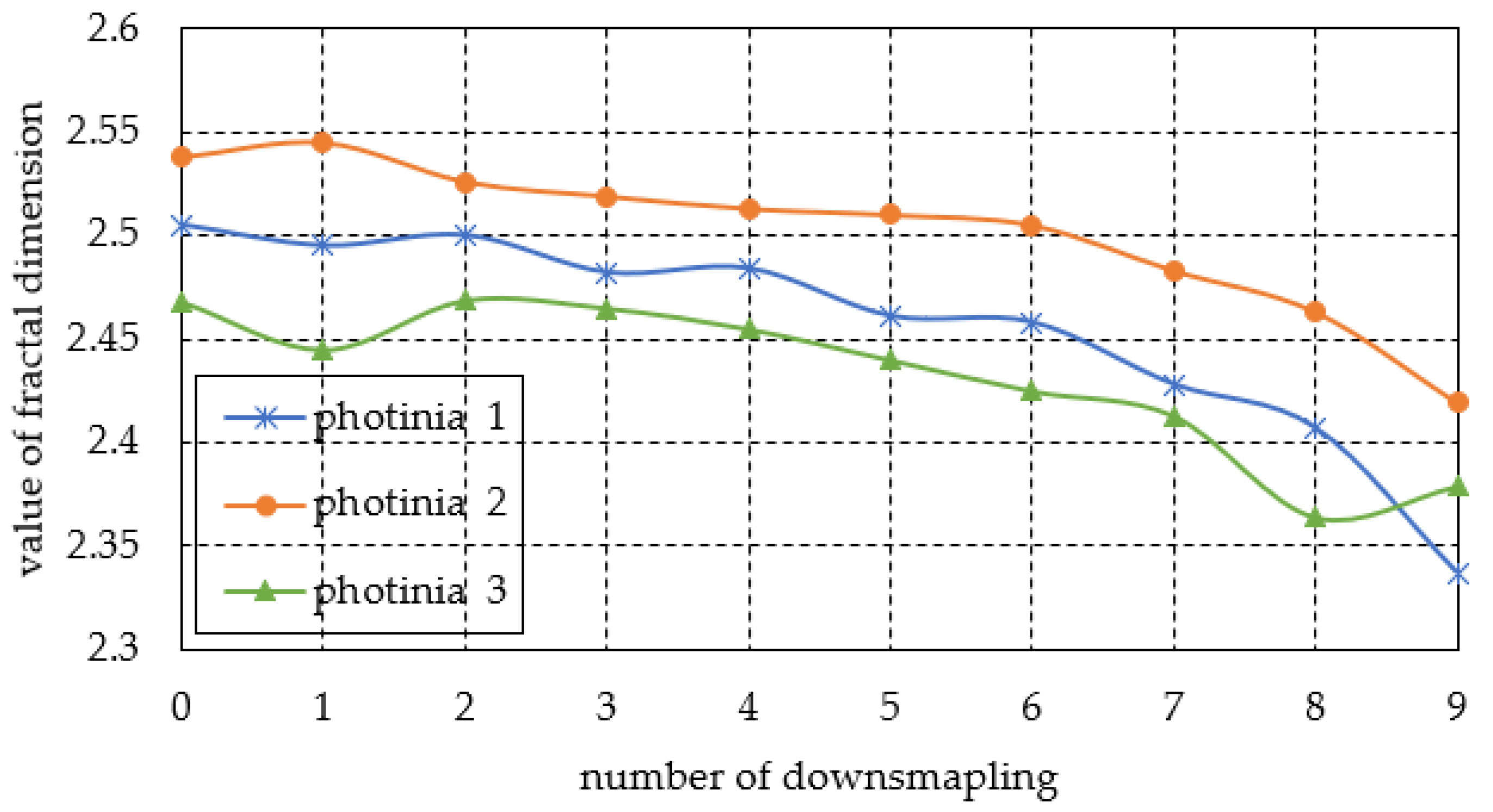
3.2. Effect of Point Cloud Density on Fractal Dimension
3.2.1. The Experimental Results of the Ginkgo Trees
3.2.2. The Experimental Results of the Photinia Trees
4. Discussion and Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Lesica, P.; Allendorf, F.W. Ecological genetics and the restoration of plant communities: Mix or match? Restor. Ecol. 1999, 7, 42–50. [Google Scholar] [CrossRef]
- Walter, J.; Jentsch, A.; Beierkuhnlein, C.; Kreyling, J. Ecological stress memory and cross stress tolerance in plants in the face of climate extremes. Environ. Exp. Bot. 2013, 94, 3–8. [Google Scholar] [CrossRef]
- Savage, J.A.; Clearwater, M.J.; Haines, D.F.; Klein, T.; Mencuccini, M.; Sevanto, S.; Turgeon, R.; Zhang, C. Allocation, stress tolerance and carbon transport in plants: How does phloem physiology affect plant ecology? Plant Cell Environ. 2016, 39, 709–725. [Google Scholar] [CrossRef] [PubMed]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Ferreira, M.P.; Wagner, F.H.; Aragão, L.E.; Shimabukuro, Y.E.; de Souza Filho, C.R. Tree species classification in tropical forests using visible to shortwave infrared WorldView-3 images and texture analysis. ISPRS J. Photogramm. Remote Sens. 2019, 149, 119–131. [Google Scholar] [CrossRef]
- Cardoso, D.; Särkinen, T.; Alexander, S.; Amorim, A.M.; Bittrich, V.; Celis, M.; Daly, D.C.; Fiaschi, P.; Funk, V.A.; Giacomin, L.L.; et al. Amazon plant diversity revealed by a taxonomically verified species list. Proc. Natl. Acad. Sci. USA 2017, 114, 10695–10700. [Google Scholar] [CrossRef]
- Raczko, E.; Zagajewski, B. Comparison of support vector machine, random forest and neural network classifiers for tree species classification on airborne hyperspectral APEX images. Eur. J. Remote Sens. 2017, 50, 144–154. [Google Scholar] [CrossRef]
- Ballanti, L.; Blesius, L.; Hines, E.; Kruse, B. Tree species classification using hyperspectral imagery: A comparison of two classifiers. Remote Sens. 2016, 8, 445. [Google Scholar] [CrossRef]
- Li, F.; Wang, R.; Paulussen, J.; Liu, X. Comprehensive concept planning of urban greening based on ecological principles: A case study in Beijing, China. Landsc. Urban Plan. 2005, 72, 325–336. [Google Scholar] [CrossRef]
- Lovell, S.T.; Taylor, J.R. Supplying urban ecosystem services through multifunctional green infrastructure in the United States. Landsc. Ecol. 2013, 28, 1447–1463. [Google Scholar] [CrossRef]
- Yang, J.; McBride, J.; Zhou, J.; Sun, Z. The urban forest in Beijing and its role in air pollution reduction. Urban For. Urban Green. 2005, 3, 65–78. [Google Scholar] [CrossRef]
- Parsa, V.A.; Salehi, E.; Yavari, A.R.; van Bodegom, P.M. Analyzing temporal changes in urban forest structure and the effect on air quality improvement. Sustain. Cities Soc. 2019, 48, 101548. [Google Scholar] [CrossRef]
- Wu, S.G.; Bao, F.S.; Xu, E.Y.; Wang, Y.-X.; Chang, Y.-F.; Xiang, Q.-L. A leaf recognition algorithm for plant classification using probabilistic neural network. In Proceedings of the 2007 IEEE International Symposium on Signal Processing and Information Technology, Giza, Egypt, 15–18 December 2007; pp. 11–16. [Google Scholar]
- Guyer, D.; Miles, G.; Gaultney, L.; Schreiber, M. Application of machine vision to shape analysis in leaf and plant identification. Trans. ASAE USA 1993. [Google Scholar]
- Abbasi, S.; Mokhtarian, F.; Kittler, J. Reliable classification of chrysanthemum leaves through curvature scale space. In Proceedings of the International Conference on Scale-Space Theories in Computer Vision; Springer: Berlin/Heidelberg, Germany, 1997; pp. 284–295. [Google Scholar]
- Mokhtarian, F.; Abbasi, S. Matching shapes with self-intersections: Application to leaf classification. IEEE Trans. Image Process. 2004, 13, 653–661. [Google Scholar] [CrossRef]
- Fu, X.; Lu, H.; Luo, M.; Cao, W.; Yu, X. Preliminary Study on Automatical Plant Classification by Use of Computer. Chin. J. Ecol. 1994, 2, 69–71. [Google Scholar]
- Qi, H.; Shou, T.; Jin, S. Computer Aided Plant Recognition Model Based on Leaf Characteristics. J. Zhejiang AF Univ. 2003, 20, 281–284. [Google Scholar]
- Wang, Z.; Chi, Z.; Feng, D. Shape based leaf image retrieval. IEE Proc. Vis. Image Signal Process. 2003, 150, 34–43. [Google Scholar] [CrossRef]
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar remote sensing for ecosystem studies: Lidar, an emerging remote sensing technology that directly measures the three-dimensional distribution of plant canopies, can accurately estimate vegetation structural attributes and should be of particular interest to forest, landscape, and global ecologists. BioScience 2002, 52, 19–30. [Google Scholar]
- Chen, Q.; Qi, C. Lidar remote sensing of vegetation biomass. Remote Sens. Nat. Resour. 2013, 399, 399–420. [Google Scholar]
- Castillo, M.; Rivard, B.; Sánchez-Azofeifa, A.; Calvo-Alvarado, J.; Dubayah, R. LIDAR remote sensing for secondary Tropical Dry Forest identification. Remote Sens. Environ. 2012, 121, 132–143. [Google Scholar] [CrossRef]
- Zhao, K.; García, M.; Liu, S.; Guo, Q.; Chen, G.; Zhang, X.; Zhou, Y.; Meng, X. Terrestrial lidar remote sensing of forests: Maximum likelihood estimates of canopy profile, leaf area index, and leaf angle distribution. Agric. For. Meteorol. 2015, 209, 100–113. [Google Scholar] [CrossRef]
- Cabo, C.; Ordóñez, C.; López-Sánchez, C.A.; Armesto, J. Automatic dendrometry: Tree detection, tree height and diameter estimation using terrestrial laser scanning. Int. J. Appl. Earth Obs. Geoinf. 2018, 69, 164–174. [Google Scholar] [CrossRef]
- Newnham, G.; Armston, J.; Muir, J.; Goodwin, N.; Tindall, D.; Culvenor, D.; Püschel, P.; Nyström, M.; Johansen, K. Evaluation of Terrestrial Laser Scanners for Measuring Vegetation Structure; CSIRO: Canberra, Australia, 2012. [Google Scholar]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; de Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for terrestrial laser scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Li, L.; Liu, C. A new approach for estimating living vegetation volume based on terrestrial point cloud data. PLoS ONE 2019, 14, e0221734. [Google Scholar] [CrossRef] [PubMed]
- Côté, J.-F.; Fournier, R.A.; Frazer, G.W.; Niemann, K.O. A fine-scale architectural model of trees to enhance LiDAR-derived measurements of forest canopy structure. Agric. For. Meteorol. 2012, 166, 72–85. [Google Scholar] [CrossRef]
- Zhao, Y.; Hu, Q.; Li, H.; Wang, S.; Ai, M. Evaluating carbon sequestration and PM2. 5 removal of urban street trees using mobile laser scanning data. Remote Sens. 2018, 10, 1759. [Google Scholar] [CrossRef]
- Cipolletti, M.P.; Delrieux, C.A.; Perillo, G.M.; Piccolo, M.C. Border extrapolation using fractal attributes in remote sensing images. Comput. Geosci. 2014, 62, 25–34. [Google Scholar] [CrossRef]
- Kolwankar, K.M.; Gangal, A.D. Definition of fractal measures arising from fractional calculus. arXiv 1998, arXiv:chao-dyn/9811015. [Google Scholar]
- Ge, M.; Lin, Q. Realizing the box-counting method for calculating fractal dimension of urban form based on remote sensing image. Geo Spat. Inf. Sci. 2009, 12, 265–270. [Google Scholar] [CrossRef]
- Lindenmayer, A. Mathematical models for cellular interactions in development II. Simple and branching filaments with two-sided inputs. J. Theor. Biol. 1968, 18, 300–315. [Google Scholar] [CrossRef]
- Prusinkiewicz, P.; Lindenmayer, A. The Algorithmic Beauty of Plants; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Leitner, D.; Klepsch, S.; Knieß, A.; Schnepf, A. The algorithmic beauty of plant roots–an L-system model for dynamic root growth simulation. Math. Comput. Model. Dyn. Syst. 2010, 16, 575–587. [Google Scholar] [CrossRef]
- Manabe, Y.; Kawata, S.; Usami, H. A PSE for a plant factory using L-system. In Proceedings of the 2012 7th International Conference on Computing and Convergence Technology (ICCCT), Seoul, Korea, 3–5 December 2012; pp. 1455–1459. [Google Scholar]
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. In Intuitionistic Fuzzy Sets; Springer: Berlin/Heidelberg, Germany, 1999; pp. 1–137. [Google Scholar]
- Wu, Q.; Zhang, H.; Chen, Y.; Liu, M. Others Study on visual simulation technology of Cunninghamia lanceolata morphological characters. For. Res. Beijing 2010, 23, 59–64. [Google Scholar]
- Demko, S.; Hodges, L.; Naylor, B. Construction of fractal objects with iterated function systems. In Proceedings of the 12th Annual Conference on Computer Graphics and Interactive Techniques, San Francisco, CA, USA, 22–26 July 1985; pp. 271–278. [Google Scholar]
- Wang, X.; Lin, L. Particle System Model for Tree Simulation and Its Implementation. J. South China Norm. Univ. Sci. Ed. 2003, 3, 49. [Google Scholar]
- Zheng, S.; Lv, Y. Fractal Dimension of Point Clouds for Tree Crowns and Its Algorithm Realization. Value Eng. 2014, 1, 190–191. [Google Scholar]
- Coops, N.C.; Morsdorf, F.; Schaepman, M.E.; Zimmermann, N.E. Characterization of an alpine tree line using airborne LiDAR data and physiological modeling. Glob. Change Biol. 2013, 19, 3808–3821. [Google Scholar] [CrossRef]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. High-resolution mapping of aboveground shrub biomass in Arctic tundra using airborne lidar and imagery. Remote Sens. Environ. 2016, 184, 361–373. [Google Scholar] [CrossRef]
- Greaves, H.E.; Vierling, L.A.; Eitel, J.U.; Boelman, N.T.; Magney, T.S.; Prager, C.M.; Griffin, K.L. Estimating aboveground biomass and leaf area of low-stature Arctic shrubs with terrestrial LiDAR. Remote Sens. Environ. 2015, 164, 26–35. [Google Scholar] [CrossRef]
- Kankare, V.; Holopainen, M.; Vastaranta, M.; Puttonen, E.; Yu, X.; Hyyppä, J.; Vaaja, M.; Hyyppä, H.; Alho, P. Individual tree biomass estimation using terrestrial laser scanning. ISPRS J. Photogramm. Remote Sens. 2013, 75, 64–75. [Google Scholar] [CrossRef]
- Rusinkiewicz, S.; Levoy, M. Efficient variants of the ICP algorithm. In Proceedings of the Third International Conference on 3-D Digital Imaging and Modeling, Quebec City, QC, Canada, 28 May–1 June 2001; pp. 145–152. [Google Scholar]
- Ai, T.; Zhang, R.; Zhou, H.; Pei, J. Box-counting methods to directly estimate the fractal dimension of a rock surface. Appl. Surf. Sci. 2014, 314, 610–621. [Google Scholar] [CrossRef]
- Perret, J.; Prasher, S.; Kacimov, A. Mass fractal dimension of soil macropores using computed tomography: From the box-counting to the cube-counting algorithm. Eur. J. Soil Sci. 2003, 54, 569–579. [Google Scholar] [CrossRef]
- Yang, Z.; Li, Y. The Box-counting Dimension of Spatial Patterns of Population Distribution of Lilium regale. In Proceedings of the 2018 7th International Conference on Energy and Environmental Protection (ICEEP 2018), Shenzhen, China, 14–15 July 2018. [Google Scholar]
- Palanivel, D.A.; Natarajan, S.; Gopalakrishnan, S.; Jennane, R. Trabecular Bone Texture Characterization Using Regularization Dimension and Box-counting Dimension. In Proceedings of the TENCON 2019-2019 IEEE Region 10 Conference (TENCON), Kochi, India, 17–20 October 2019; pp. 1047–1052. [Google Scholar]
- Fernández-Martínez, M.; Guirao, J.L.G.; Sánchez-Granero, M.Á.; Segovia, J.E.T. Fractal Dimension for Fractal Structures: With Applications to Finance; Springer: Berlin/Heidelberg, Germany, 2019; Volume 19. [Google Scholar]
- Falconer, K. Fractal Geometry: Mathematical Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Sohn, G.; Jing, L. Individual tree species classification using structure features from high density airborne lidar data. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium, Honolulu, HI, USA, 25–30 July 2010; pp. 2099–2102. [Google Scholar]
- Heinzel, J.; Koch, B. Exploring full-waveform LiDAR parameters for tree species classification. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 152–160. [Google Scholar] [CrossRef]
- Richter, R.; Reu, B.; Wirth, C.; Doktor, D.; Vohland, M. The use of airborne hyperspectral data for tree species classification in a species-rich Central European forest area. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 464–474. [Google Scholar] [CrossRef]
- Shen, X.; Cao, L. Tree-species classification in subtropical forests using airborne hyperspectral and LiDAR data. Remote Sens. 2017, 9, 1180. [Google Scholar] [CrossRef]
- Zou, X.; Cheng, M.; Wang, C.; Xia, Y.; Li, J. Tree classification in complex forest point clouds based on deep learning. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2360–2364. [Google Scholar] [CrossRef]
- Erins, G.; Lorencs, A.; Mednieks, I.; Sinica-Sinavskis, J. Tree species classification in mixed Baltic forest. In Proceedings of the 2011 3rd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Lisbon, Portugal, 6–9 June 2011; pp. 1–4. [Google Scholar]
- Li, J.; Hu, B.; Noland, T.L. Classification of tree species based on structural features derived from high density LiDAR data. Agric. For. Meteorol. 2013, 171, 104–114. [Google Scholar] [CrossRef]
- El Sheikh, A.M.F.; El Sherif, A.H.; Hussien, W.I. Construction of point cloud by slice-adaptive thresholding of computer tomography (CT) images at the human knee joint. In Proceedings of the 2011 IEEE 3rd International Conference on Communication Software and Networks, Xian, China, 27–29 May 2011; pp. 610–614. [Google Scholar]

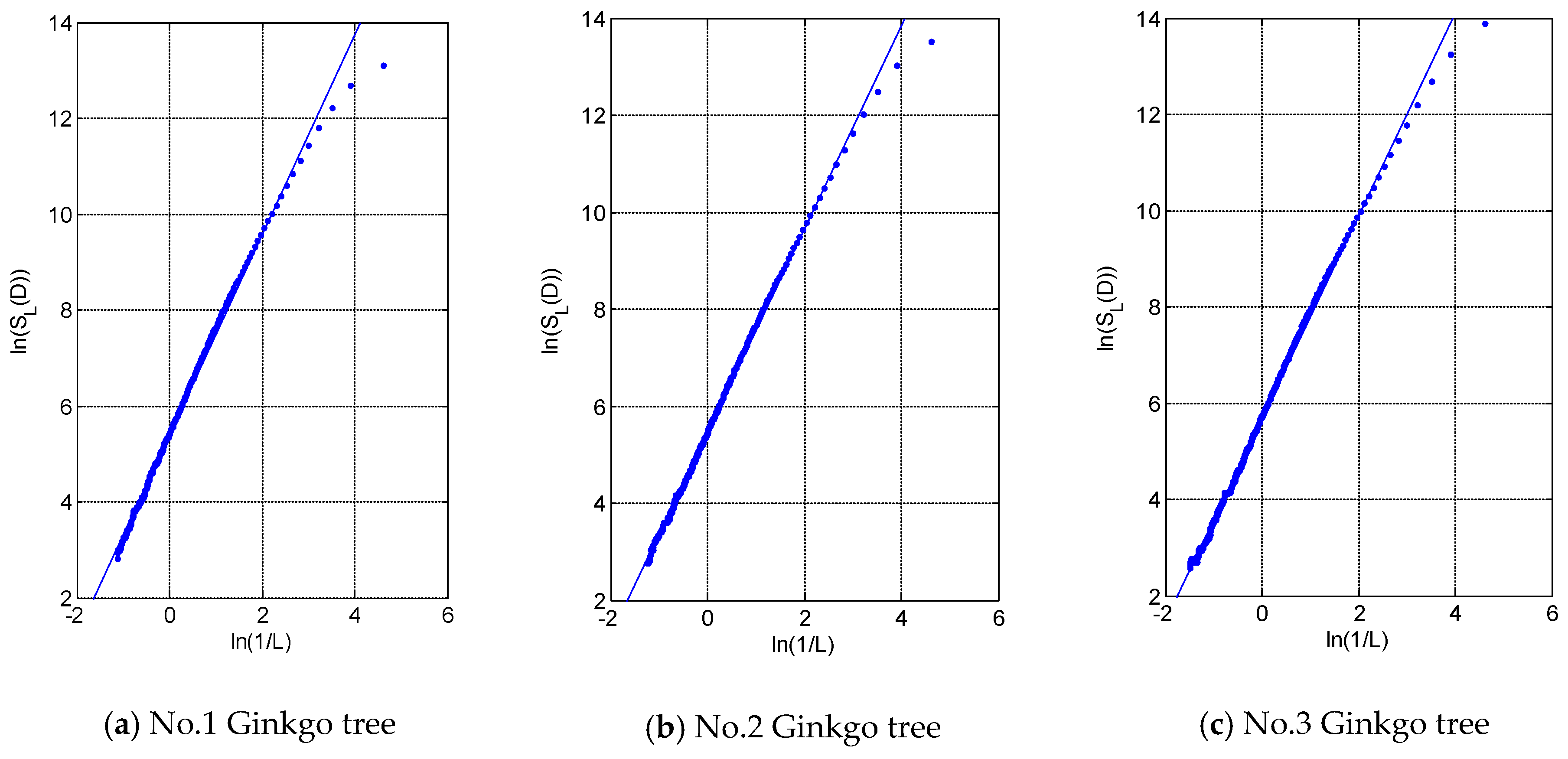

| Category | The Serial Number of Ginkgo Trees | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| The number of points in point clouds | 522865 | 888394 | 1209585 |
| The number of points in the double logarithmic plot | 309 | 346 | 445 |
| The slope of the fitted straight line | 2.093 | 2.091 | 2.106 |
| The intercept of the fitted straight line | 5.392 | 5.466 | 5.690 |
| RMSE of the slope | 0.0093 | 0.0064 | 0.0058 |
| RMSE of the intercept | 0.0091 | 0.0064 | 0.0064 |
| RMSE of the unit weight | 0.1586 | 0.1152 | 0.1208 |
| Category | The Serial Number of Ginkgo Trees | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| The number of points in point clouds | 522865 | 888394 | 1209585 |
| The number of points in the double logarithmic plot | 309 | 346 | 445 |
| The distance threshold of RANSAC | 0.01 | 0.01 | 0.01 |
| The used data ratio of RANSAC | 0.540 | 0.462 | 0.375 |
| The slope of the fitted straight line | 2.246 | 2.208 | 2.211 |
| The intercept of the fitted straight line | 5.448 | 5.497 | 5.761 |
| RMSE of the slope | 0.0016 | 0.0017 | 0.0013 |
| RMSE of the intercept | 0.0011 | 0.0011 | 0.0012 |
| RMSE of the unit weight | 0.0134 | 0.0140 | 0.0137 |
| Number | Number of Point Clouds | Ginkgo 1 | Ginkgo 2 | Ginkgo 3 | |||
|---|---|---|---|---|---|---|---|
| Slope | RMSE of Unit Weight | Slope | RMSE of Unit Weight | Slope | RMSE of Unit Weight | ||
| 0 | 1209585 | - | - | 2.200 | 0.0166 | 2.213 | 0.0205 |
| 1 | 522865 | 2.243 | 0.0124 | 2.195 | 0.0162 | 2.207 | 0.0205 |
| 2 | 261432 | 2.241 | 0.0126 | 2.176 | 0.0175 | 2.203 | 0.0200 |
| 3 | 130716 | 2.225 | 0.0144 | 2.184 | 0.0163 | 2.196 | 0.0192 |
| 4 | 65358 | 2.216 | 0.0145 | 2.151 | 0.0180 | 2.184 | 0.0201 |
| 5 | 32679 | 2.215 | 0.0130 | 2.121 | 0.0181 | 2.167 | 0.0200 |
| 6 | 16339 | 2.186 | 0.0148 | 2.111 | 0.0172 | 2.165 | 0.0214 |
| 7 | 8169 | 2.179 | 0.0174 | 2.076 | 0.0183 | 2.13765 | 0.0222 |
| Number | Number of Point Clouds | Photinia 1 | Photinia 2 | Photinia 3 | |||
|---|---|---|---|---|---|---|---|
| Slope | RMSE of Unit Weight | Slope | RMSE of Unit Weight | Slope | RMSE of Unit Weight | ||
| 0 | 2816299 | 2.505 | 0.0161 | 2.538 | 0.0126 | 2.468 | 0.0196 |
| 1 | 1408149 | 2.495 | 0.0164 | 2.545 | 0.0126 | 2.445 | 0.0186 |
| 2 | 704074 | 2.500 | 0.0157 | 2.526 | 0.0129 | 2.469 | 0.0173 |
| 3 | 352037 | 2.482 | 0.0168 | 2.519 | 0.0135 | 2.465 | 0.0167 |
| 4 | 176018 | 2.484 | 0.0157 | 2.513 | 0.0121 | 2.455 | 0.0164 |
| 5 | 88009 | 2.461 | 0.0171 | 2.510 | 0.0113 | 2.440 | 0.01703 |
| 6 | 44004 | 2.458 | 0.0187 | 2.505 | 0.0147 | 2.425 | 0.0159 |
| 7 | 22002 | 2.428 | 0.0204 | 2.483 | 0.0141 | 2.413 | 0.0171 |
| 8 | 11001 | 2.407 | 0.0207 | 2.463 | 0.0171 | 2.364 | 0.0154 |
| 9 | 5500 | 2.337 | 0.0227 | 2.419 | 0.0187 | 2.379 | 0.0174 |
| Category | Ginkgo Trees | Photinia Trees | Cypress Trees | ||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 1 | 2 | 3 | 1 | 2 | 3 | |
| NofPC | 522865 | 888394 | 1209585 | 2816299 | 2822194 | 2989034 | 3947350 | 3163402 | 5840268 |
| NofLP | 309 | 346 | 445 | 203 | 178 | 179 | 217 | 170 | 301 |
| DTofR | 0.009 | 0.012 | 0.015 | 0.011 | 0.008 | 0.012 | 0.01 | 0.01 | 0.011 |
| URofR | 0.508 | 0.511 | 0.521 | 0.502 | 0.505 | 0.519 | 0.520 | 0.517 | 0.518 |
| FD | 2.243 | 2.200 | 2.213 | 2.505 | 2.538 | 2.468 | 2.446 | 2.453 | 2.428 |
| RMSE | 0.0015 | 0.0019 | 0.0018 | 0.0025 | 0.0021 | 0.0027 | 0.0022 | 0.0026 | 0.0019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Hu, Q.; Wu, H.; Su, J.; Zhao, P. Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees. Fractal Fract. 2021, 5, 14. https://doi.org/10.3390/fractalfract5010014
Zhang J, Hu Q, Wu H, Su J, Zhao P. Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees. Fractal and Fractional. 2021; 5(1):14. https://doi.org/10.3390/fractalfract5010014
Chicago/Turabian StyleZhang, Ju, Qingwu Hu, Hongyu Wu, Junying Su, and Pengcheng Zhao. 2021. "Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees" Fractal and Fractional 5, no. 1: 14. https://doi.org/10.3390/fractalfract5010014
APA StyleZhang, J., Hu, Q., Wu, H., Su, J., & Zhao, P. (2021). Application of Fractal Dimension of Terrestrial Laser Point Cloud in Classification of Independent Trees. Fractal and Fractional, 5(1), 14. https://doi.org/10.3390/fractalfract5010014






