Abstract
Robust stability is a major concern for real-world control applications. Realization of optimal robust stability requires a stabilization scheme, which ensures that the control system is stable and presents robust performance for a predefined range of system perturbations. This study presented an optimal robust stabilization approach for closed-loop fractional order proportional integral derivative (FOPID) control systems with interval parametric uncertainty and uncertain time delay. This stabilization approach, which is carried out in a v-plane, relies on the placement of the minimum angle system pole to a predefined target angle within the stability region of the first Riemann sheet. For this purpose, tuning of FOPID controller coefficients was performed to minimize a root angle error that is defined as the squared difference of minimum angle root of interval characteristic polynomials and the desired target angle within the stability region of the v-plane. To solve this optimization problem, a particle swarm optimization (PSO) algorithm was implemented. Findings of the study reveal that tuning of the target angle can also be used to improve the robust control performance of interval uncertain FOPID control systems. Illustrative examples demonstrated the effectiveness of the proposed v-domain, optimal, robust stabilization of FOPID control systems.
1. Introduction
Since fractional order system modeling provides more realistic mathematical modeling of real systems, fields of control theory have been extended toward fractional order system modeling and fractional order controller design. Particularly, fractional order systems have paved the way for improved frequency-domain modeling and controller designs. Numerous works have illustrated enhancement of control performance, which is possible by the use of fractional calculus: these research studies have reported robust performance improvements of fractional order controllers in case of parametric perturbations [1,2,3,4,5,6]. Several works have also revealed that fractional order control can enhance the disturbance rejection performance of closed-loop control systems [7,8,9,10]. One of the underlying basic reasons for such performance improvements is the fact that fractional orders of controller functions provide more tuning options that enable one to achieve more restricted frequency-domain design objectives.
System stability is the main concern in control system design, and it is a fundamental stage of control system design efforts. For this reason, stabilization of fractional order control systems has been addressed in several perspectives: stabilization of the systems according to system pole placements [11,12,13,14,15,16,17], closed-loop system stabilization based on stability boundary locus (SBL) analyses [18,19], stabilization based on value set analysis and zero exclusion principle [20,21]. The linear matrix inequalities (LMIs) method has been widely used for the stability checking of fractional order systems [22,23,24]. Graphical stabilization methods have been proposed for robust stabilization of interval plant functions [25] and time-delay system models [26]. Tuning of FOPID controllers for fractional order uncertain systems was shown by using a robust D-stability method [27].
Due to parametric uncertainty of real systems and limitations of mathematical modeling to represent real-world systems, the robust stabilization problem of interval systems becomes one of the essential topics of practical control system design. Ensuring system stability for the interval uncertainty ranges of mathematical models improves the real-world performance of the designed control systems and is an important outcome of robust controller design methodologies. As is well-known, the stability region for integer order systems is the left half-side of the complex s-plane, hence stability analysis based on the checking of system pole placements in the complex s-plane was referred to as the left half-plane (LHP) stability analysis. Previously, stabilization based on the placement of system poles was carried out by residing all roots of interval characteristic polynomials into the stability region of the first Riemann sheet [12,13,14,16,17]. In these works, stability checking for fractional order characteristic polynomials was facilitated by applying a polynomial order expansion approach that is employed by conformal mapping. Thus, fractional order characteristic polynomials are transformed to the expanded order integer order polynomials in the v-plane. However, this transformation maps the LHP stability region in the s-plane into the region with an angle range of within the first Riemann sheet of the v-plane [11,12,15,28,29,30]. This conformal mapping preserves the argument and magnitude relations of system poles, and thus it allows the implications of the edge theorem for the robust stability analysis of interval uncertain fractional order systems and consideration of edge and vertex polynomials in stability checking within the complex v-plane [15]. An application of the edge theorem was shown for the robust stability analysis of fractional order interval systems [14,15]. Later, the edge theorem was discussed for the general interval uncertainty cases, and the necessary and sufficient conditions to check system stability were proposed in [31]. Kharitonov-theorem-based approaches were also utilized for the robust stability checking of fractional order systems [32,33]. Principal characteristic equations and stability relation between the s-plane and v-plane were discussed in [30].
Even though simulation results indicate a satisfactory control performance, the real-world control systems should be designed robust against a certain level of system perturbations and parameter fluctuations. Therefore, robust stability analysis and robust system design have a major significance in the practical fractional order control system design process.
The so-called “fractal robustness” has become a central motivation for studies that have addressed fractional order control system design [34,35,36,37,38,39,40,41]. Fractional order dynamics has been widely harnessed to utilize iso-damping property in robust controller design processes [36,37,38,39,40,41]. The optimal fractional order systems have been designed [42,43,44]. A group of works has proposed graphical approaches for the robust stabilization of interval fractional order systems [25,26,27]. Stabilization of fractional order controllers based on minimum angle characteristic root placement within the first Riemann sheet of the v-plane has been shown [16,17,45]. Optimal FOPID controller design has been demonstrated in the v-plane [46,47]. Effects of pole placements on a fractional order proportional integral (FOPI) controller performance were discussed in [48]. The main advantage of this approach is that the placement of the minimum argument root of an interval characteristic polynomial set can be easily carried out to guarantee the robust stability of interval control systems for a predefined uncertainty range of system parameters, and the uncertainty ranges can be given as a design specification to be achieved. Utilization of these advantages for robust FOPID control system design was our main motivation in the current study. Due to complications in analytically deriving a general rule to govern the placement of system poles, we implemented a meta-heuristic optimization method and developed a computer-aided design scheme, which can perform the placement of the minimum angle system pole of a given interval uncertain FOPID control system model to a target angle within the stability region. In addition to the robust stabilization of the interval uncertain system by optimally tuning FOPID controller coefficients, the target angle specification allows the adjustment of the control performance of resulting robust stable FOPID control systems. This property can be useful to improve the control performance besides the robustness of the designed FOPID control system.
In the literature, several heuristic optimization methods, for example, evolutionary methods [42] and particle swarm methods [43,44], have been applied for the tuning of fractional order controllers. The main advantage of heuristic optimization methods comes from the fact that their implications on real-world problems are relatively straightforward, and they can provide satisfactory solutions in the case of complicated optimization problems. For the stabilization of fractional order systems in the v-domain, Alagoz demonstrated that the brute force search could deal with the stabilization of nominal closed-loop control systems according to a minimum angle target root specification in the Riemann sheet [17]. Afterward, Tufenkci et al. implemented a genetic algorithm to stabilize fractional order PID control systems for one-pole fractional order nominal plant models and demonstrated the effectiveness of the v-domain design approach for FOPID controller stabilization [45]. These results became a motivation for extending this approach to the optimal robust stabilization of interval uncertain control systems in the v-domain by using a metaheuristic optimization method. Accordingly, the present study illustrated a design framework that employs computational intelligence for optimal robust stabilization of FOPID control system design in the v-domain. Authors referred to this approach as v-domain design because design efforts were conducted in the v-plane after applying the conformal mapping to fractional order transfer functions. It can be an alternative to well-known design domains (e.g., time domain, frequency domain and s-domain) when designing fractional order systems.
Essentially, the current study presented a methodology for the optimal robust stabilization of interval uncertain closed-loop FOPID control systems according to the minimum angle system pole placement strategy in the v-plane. For this purpose, the problem of robust stabilization of an interval uncertain fractional order plant function was considered. For a solution to this problem, the purposed approach aimed to stabilize a set of sampled characteristic polynomials of parametric uncertain FOPID control systems that are defined by an interval uncertainty box of the plant parameters. The five design coefficients of the FOPID controller were tuned by the particle swarm optimization (PSO) algorithm in order to ensure robust stability of the system by considering the minimum angle root of all characteristic polynomials that were uniformly sampled from the interval uncertainty box. To guarantee robust stability of the uncertain system, the PSO algorithm places the minimum angle characteristic root of whole interval systems on a target angle line within the stability region. Furthermore, we observed that the robust control performance of the designed FOPID control systems for a given parameter uncertainty range specification can be improved by changing the target angle line specification. This promises an advantage of tuning the control performance of the FOPID control systems by tuning a single design parameter, namely the target angle, and provides optimal robust stabilization of the interval uncertain control systems.
2. Theoretical Background and Preliminaries
2.1. Stability Analysis of Fractional Order Systems According to Minimum Angle Root Placement
Nominal fractional order transfer functions are written in the form of
where the denominator polynomial coefficients and numerator polynomial coefficients are real numbers [28,29]. The fractional orders are denoted by , () and , () [21]. The characteristic polynomial of this function class is expressed as
In order to calculate roots of fractional order characteristic polynomials, mapping is commonly used [12,13,29]. Thus, stability analysis of fractional order models is carried out by examining the root locus of expanded degree integer order characteristic polynomials within the first Riemann sheet [11,12,13,14,16,29]. By applying the transformation to Equation (2), one obtains expanded degree integer order characteristic polynomials in the v-plane as follows:
Roots of the expanded degree integer order characteristic polynomials are calculated, and only the roots that lie in the first Riemann sheet are evaluated for stability analysis [11,12,13,14,16,29]. The rest of the roots, which are not in the first Riemann sheet, are assumed not to be meaningful for system stability. The first Riemann sheet is a portion of the complex plane that is confined within an argument range of [11,29]. The first Riemann sheet splits into two sections that are stable and unstable root regions by the stability line with the angle of . Since the first Riemann sheet is symmetrical with respect to the real axis in the complex plane, one can perform stability analysis in the positive angle side of the first Riemann sheet that is in the angle range of . As a consequence, a fractional order system model is said to be stable when all characteristic roots lie in the range of . Figure 1 depicts the stability region in the v-plane.
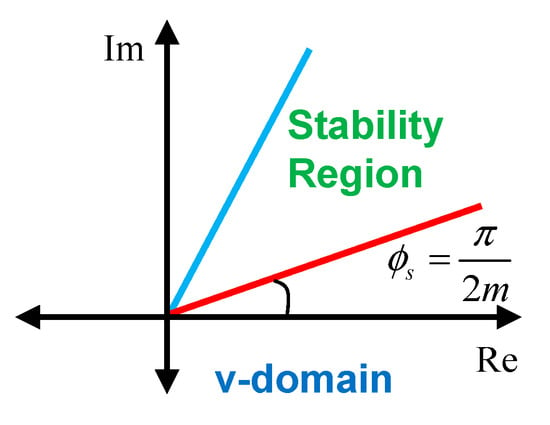
Figure 1.
The stability regions under mapping [11,14,17].
To perform stability analysis, the root set of expanded degree integer order characteristic polynomials is written as [14,16]
The expanded degree integer order characteristic polynomials are said to be robust stable polynomials if the minimum argument condition given by is satisfied [13,17,29]. This analysis can be extended to interval uncertain fractional order system models. Interval uncertainty of the characteristic polynomials is expressed by [14,15,16]
where the interval uncertainty of gain coefficients and interval uncertainty of fractional orders are defined by the parameter ranges of and , respectively. These uncertainty ranges of parameters define an n-dimensional interval uncertainty box within the parameter space of the system model, and it is represented by a hyperrectangle that is expressed by the Cartesian product of intervals [14,15],
A point of hyperrectangle is expressed by a design parameter vector, which is defined in the parameter space as
Each vector represents a possible characteristic polynomial of an interval uncertain system and if all polynomials from hyperrectangle are stable, the interval system is said to be robustly stable. In other words, when is satisfied for all roots of the polynomials of hyperrectangle that are written by
the interval uncertain system is robustly stable [13,15,17].
2.2. Brief Introduction of PSO Algorithms
Meta-heuristic optimization methods have an important milestone in computational intelligence practice because of their three prominent advantages: (i) they can be easily implemented to solve complicated optimization problems, (ii) the random search nature of these methods presents a potential of a new solution at each run of algorithms, and (iii) they can be easily applied for the optimization of simulation models or even real systems in offline or online manners. For these reasons, meta-heuristic methods have become popular optimization tools for computer-aided solutions to complex engineering problems.
Due to difficulties in obtaining an analytical solution of fractional calculus, meta-heuristic optimization methods have been widely preferred for optimization problems of fractional order system design [17,42,43,44]. The PSO algorithm could find satisfactory solutions for the parameter tuning problems of fractional order systems [42,43,44]. The effectiveness of the PSO algorithm in the tuning of control systems mainly originates from the fact that the search space of control systems generally has smoothly changing characteristics that are suitable for the traveling of particles for the search of an optimal point.
The PSO algorithm is an essential swarm-based search algorithm, which can imitate the collective intelligence in animal swarms. The algorithm of PSO benefits from the collective behavior of search agents, namely particles. The particles can move under the effects of interactions with other particles and form a global coherence for the search of a particle swarm [49,50]. Interactions and coherence at particle motions result in a swarm intelligence that can be similar to collective motions of animal swarms in their natural environments. To resemble natural swarm intelligence in the search of an optimal solution, the PSO algorithm presumes that particles move collectively in a multidimensional search space of an optimization problem. Coherence and interactions among the particles of PSO form dynamics in swarm motion, which tends to gather particles to minima of search spaces. Thus, the positions of particles in the search space represent a candidate solution for the PSO algorithm.
The motion of a particle is expressed by particle positions and the particle velocity parameters. The PSO models coherent particle motions by the following formulation [49,50,51].
where is the personal best position, and is the global best position. Parameters and are personal learning coefficients of and global learning coefficient of , respectively. These parameters are used to adjust the strength of local and global interactions among particles. Parameters and are pseudo-random numbers. These random parameters enable particles to have a stochastic nature in their motions and allow finding new solutions in the case of subsequent running of the algorithm [49,50,51]. The parameter is the weight coefficient for particle inertias. It is used to decrease the inertia of particles during the optimization process, and a damping rate is used to update the weight coefficient at each iteration as [29]. While particles are moving in the search space, the local best position and the global best position are updated at each iteration according to particle scores. These scores are provided by a predefined objective function. The objective function of the optimization evaluates particle positions and decides whether or not to be a valuable point for the solution for an optimization problem [49,50,51].
3. Methodology for Robust Stabilization of FOPID Control System
Adjusting places of minimum argument roots within the stability region was demonstrated in [17,45]. Optimal FOPI and FOPID controller tuning in the v-domain was illustrated in [46,47,48]. The current study extended this approach to solve the optimal robust stabilization problem of FOPID control systems. Especially, it extended the works in [17] and [45] to stabilization of interval uncertain FOPID control systems, and it demonstrates the effectiveness of the v-domain stabilization approach for optimal stabilization of uncertain FOPID control systems with interval coefficients and interval time-delay uncertainty. Figure 2 illustrates a general block diagram of closed-loop FOPID control systems. The FOPID controller is commonly expressed in the form of
where denotes the transfer function of the FOPID controller. The nominal plant function is assumed to be a time-delay, one-pole fractional order plant, which is commonly written in a general form as
where the parameter stands for the time delay parameter of the plant, and the parameter is the fractional order of plant function. The parametric interval uncertainty model of this plant function can be expressed in the form of
where interval uncertainty of the system is defined with parameter alteration ranges of ,, and . These interval ranges define a four-dimensional interval uncertainty box, that is, a hyperrectangle in the parameter space of the plant model. Here, each point of hyperrectangle is expressed by a parameter vector that stands for an uncertain model of the interval plant function.
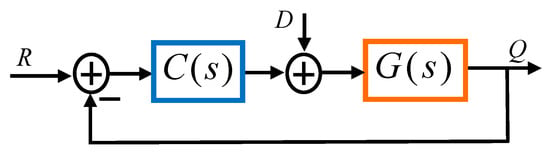
Figure 2.
Block diagram of the closed-loop FOPID control system.
The transfer function of this interval system can be written as
To obtain a constant coefficient polynomial, the term is substituted with the first order Padé approximation, which is written by
where the relation between coefficients and time delay parameter is . The characteristic polynomial of the closed-loop control system is the denominator polynomial of the transfer function , and it can be expressed for this interval system model as
One applies mapping and obtains the expanded degree integer order characteristic polynomials as
Based on Equation (8), the characteristic root set of the interval system can be written by considering FOPID controller coefficients
To achieve placement of the minimum angle root of all polynomials in near to a target minimum angle root position, the angle error is defined as
where is the target angle for minimum angle root placement inside the stability region of the first Riemann sheet [17,45]. The term refers to the minimum angle of roots in the set . The squared angle error (SAE) is expressed as
The optimization problem that minimizes the SAE is written by
Specifying the minimum target angle in the range of ensures the placement of the minimum angle root within the stability region of the v-plane, and thus stabilizes the resulting FOPID control system according to a target angle . The can be configured to obtain improved robust control performance. This optimization problem is solved by using the PSO method according to the flow chart in Figure 3, and the results are discussed in the following section.
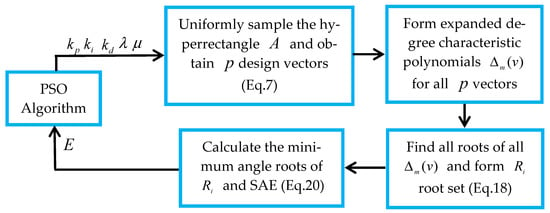
Figure 3.
The block diagram describes the implication of the particle swarm optimization (PSO) algorithm for optimal robust stabilization. SAE: squared angle error.
4. Illustrative Design Examples
This section presents illustrative examples to demonstrate the robust stabilization of FOPID control system models. For the initial PSO configuration, the search ranges of FOPID controller coefficients were set to , , , and . The population size of particles was configured to 30 particles. The personal learning coefficient () was set to 2.0, and the global learning coefficient () was set to 2.0. The inertia weight () and damping rate () were 1 and 0.99, respectively [50,51]. The iteration number of PSO is limited to 200. To perform time-domain simulations of control systems, step() function of the FOTF toolbox was used in MATLAB [52]. Figure 4 depicts a design process that includes optimization, simulation and validation stages.
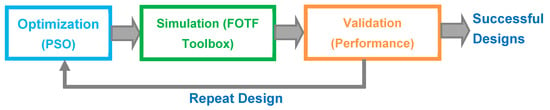
Figure 4.
Relations between optimization, simulation and validation processes.
Example 1.
Suppose that one tries to figure out a stabilizing FOPID controller for an interval uncertain plant function with an interval delay,
We used mapping, and the target angle for the stabilization was set to within the first Riemann sheet.
The characteristic polynomial of the interval system was expressed as
In the case of mapping, the expanded degree integer order characteristic polynomial with interval uncertainty is written by
For 200 iterations of the optimization process, a decrease of the minimum angle error is shown in Figure 5. The figure clearly demonstrates that the PSO algorithm can significantly decrease SAE during the optimization process. This result confirms that the problem can be solved by the PSO algorithm.
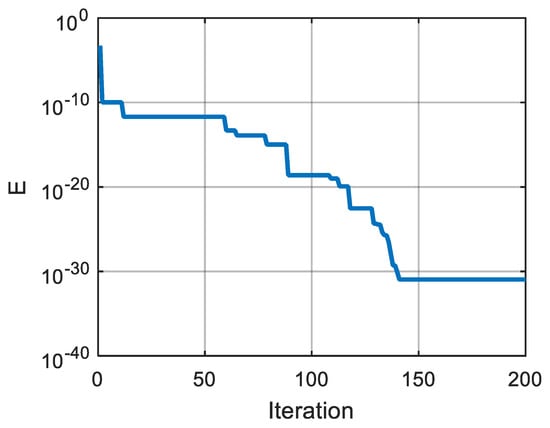
Figure 5.
Change of minimum angle error during 200 iterations.
After completion of optimization, the PSO algorithm yielded the design parameters , , , and for the stabilizing FOPID controller. The SAE is almost zero (at the level of ). Figure 6 shows placements of all roots of sampled characteristic polynomials from the interval uncertainty box, where the characteristic roots are indicated by red asterisks and dots. The figure confirms that the minimum argument root of the interval system was placed on the target angle that is indicated by the green line within the stability region. To illustrate the stabilization of a conventional controller, a PI controller was also optimally stabilized by using the proposed method. The PSO algorithm yielded the design parameters and for the stabilizing PI controller. It is useful to demonstrate step responses of the stabilized control systems to validate robust system stability in transient analysis. Figure 7 shows step responses of the stabilizing FOPID and PI controllers for the nominal plant function that was formed by the parameter values from the mid-points of uncertainty intervals.
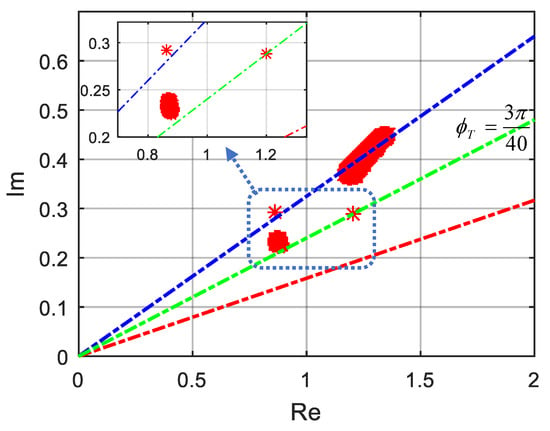
Figure 6.
Minimum angle root placement in the Riemann sheet for the FOPID control system.
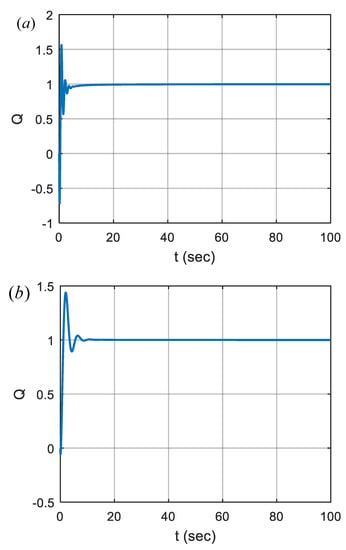
Figure 7.
Step response of the stabilized FOPID control system for nominal plant function ; (a) FOPID controller and (b) PI controller.
To evaluate unit step performances of systems at boundaries of interval parameters, Figure 8 shows step responses of the FOPID and the PI controllers for the stabilization of 16 plant functions that were sampled from vertices of the uncertainty box. These plant functions are listed in Table 1 by considering all possible combinations of interval boundaries. These functions express vertices of the interval uncertainty box, which are the most probable to cause instability of the system. The figure shows that responses of both FOPID and PI control systems for all vertex plant functions are stable, and this indicates that the controllers can control the interval uncertain plants even if plant parameters change to the boundaries of uncertainty intervals. The high overshoot responses in the figure are mainly related to higher magnitude minimum angle roots of the interval system. The settling of FOPDI control systems is faster than the settling of PI control systems for the control of 16 plant functions because most responses of the PI control system have prolonging ripples. This is an indication of improved robust stabilization of the FOPID controller compared to the PI controller.
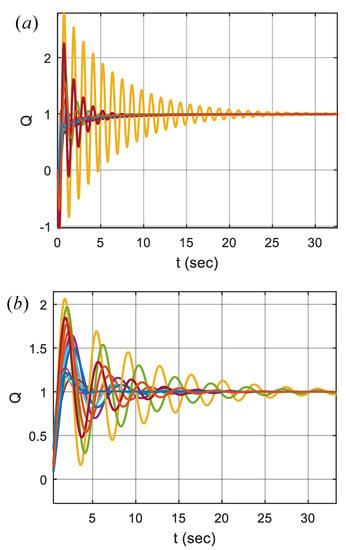
Figure 8.
Step responses of 16 vertex plant functions; (a) FOPID controller and (b) PI controller.

Table 1.
16 plant functions that form vertices of the interval uncertainty box.
Table 2 lists the mean squared error (MSE) performance of these plants for step response (MSE performance for step response is calculated by ).

Table 2.
Mean squared error (MSE) values of step responses for the FOPID control of 16 plant functions and the nominal plant function .
Example 2.
Suppose that one tries to figure out stabilizing FOPID control coefficients for an interval uncertain plant function with an interval delay,
for several target angle specifications {,,}.
The characteristic polynomial of the system was expressed as
In the case of mapping, the expanded degree integer order characteristic polynomials can be written by
To observe the effect of target angle configuration, PSO optimization was performed for three different target angle specifications within the stability region of the v-plane. These are (for a placement close to the stability boundary by taking ), (for a placement in the middle of the stability region by taking ) and (for a placement close to the upper bound of the first Riemann sheet by taking ). Specification of the target angle can be performed by using the formula , where is a partitioning factor of the stability region by a target angle line. For 200 iterations of the optimization process, decreases in SAEs for each target angle specifications are shown in Figure 9. The figures clearly show that the PSO algorithm can significantly decrease SAE during the optimization process. Table 3 shows the stabilizing FOPD controller designs that were obtained after the completion of the PSO algorithm.
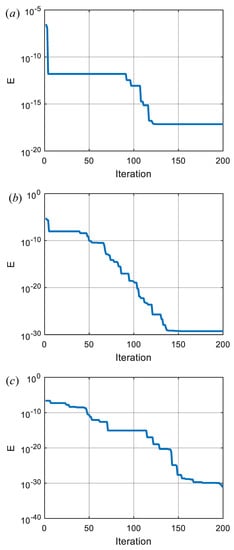
Figure 9.
Changes of SAEs (a) for , (b) for and (c) for .

Table 3.
Stabilizing FOPID controller designs that are obtained for , and .
Figure 10a–c show the placements of all roots of characteristic polynomials from the interval uncertainty box (characteristic roots are indicated by red asterisks and dots). The figures reveal that the minimum argument root of the interval system was placed on the specified target angles and all FOPID designs can optimally stabilize the system by placing the minimum angle root on the target angles.
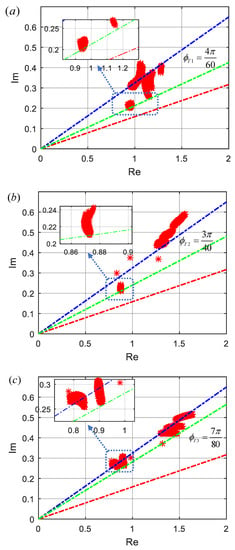
Figure 10.
Minimum angle root placement in the first Riemann sheet (a) for , (b) for and (c) for .
Figure 11 shows step responses of the stabilizing FOPID controller designs for a nominal plant function from the uncertainty box. This function is formed by the mid-points of the uncertainty intervals as
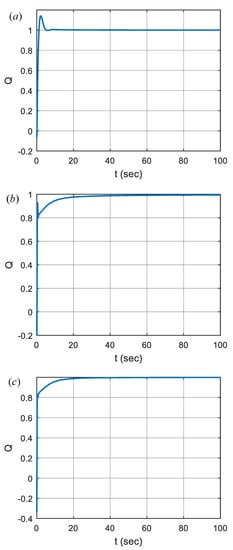
Figure 11.
Step responses of stabilized FOPID control systems for target angle specifications (a) for , (b) for and (c) for .
Figure 12 shows the step responses of 16 vertex functions of the uncertainty box. For the target angle specification , step performances of the control system for the vertex functions are more similar than the results of other target angle specifications. This indicates that the FOPID controller for is more robust than other FOPID designs due to less variability among step responses that were obtained for the vertex plant functions. Therefore, we observed in this example that the control performance of can be more robust than other target angle specifications against parametric perturbation of the plant function. The FOPID controller design for can be more suitable for real control applications.
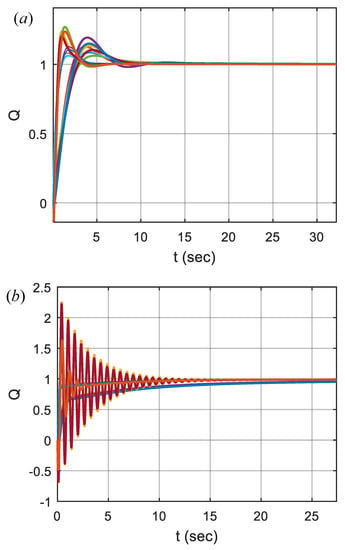
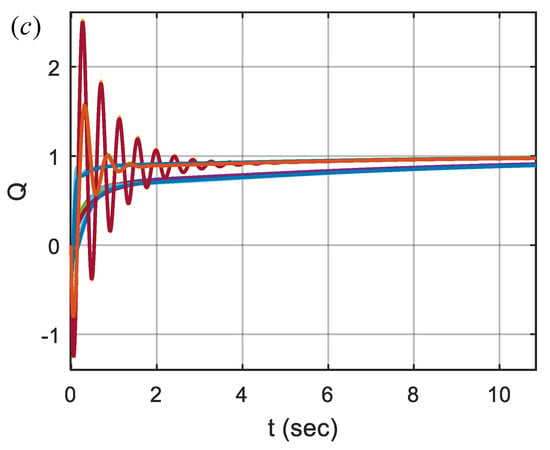
Figure 12.
Step responses of 16 vertex plant functions for target angle specifications (a) for , (b) for and (c) for .
In Figure 12b,c, the variability of control performance is higher between vertices of the interval box, and it indicates more deterioration of the control performance while parameters are changing inside the interval box. The step response MSE performances in Table 4 and Table 5 validate these effects.

Table 4.
MSE values of step responses for nominal plant functions and 7 plant functions ( to ).

Table 5.
MSE values of step responses for the other 8 plant functions ( to ).
In order to evaluate disturbance rejection performances of the robust stabilized FOPID control system designs for the target angle specifications , and , step disturbance responses of the systems are shown in Figure 13. In these control systems, a set-point prefilter function was used to overcome overshoots, and it improves settling to the step input before applying the additive step disturbance to the input of the plant function. The figure indicates satisfactory disturbance rejection performances of the optimally stabilized robust FOPID controllers in this example.
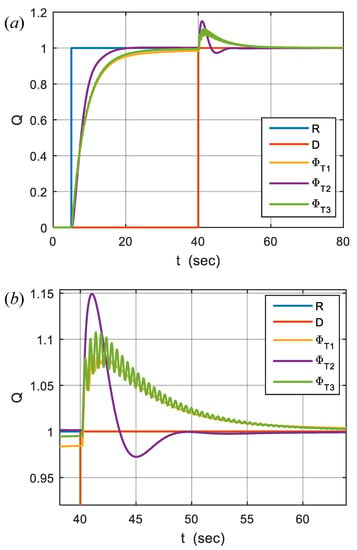
Figure 13.
Step disturbance responses of FOPID controller designs for the target angle specifications , and ; (a) a full view from simulation and (b) a close view of disturbance responses.
In these example designs, convergence rates of the PSO algorithm were measured by considering the decrease in error () per iteration until the convergence of the algorithm and the convergence rates were calculated at levels of error/iteration. However, the computation time can take four to five hours for a standard PC (hardware configuration is I5-3230M 2.60 GHz, 4GB RAM) because it requires the computation of minimum angle roots for all sampled systems ( vectors) from the uncertainty box of the interval plant functions (, , ,) for each particle of PSO as shown in the pseudo code in Appendix A. Searching the minimum angle root for each sample model of the uncertainty box significantly increases the computational load in the optimization task. Since classical PSO is a low-complexity search algorithm, it is preferable to reduce the overall computational load of the optimization task.
5. Conclusions
This study demonstrated an optimal robust stabilization scheme for FOPID control systems. This method is based on the placement of the minimum angle system pole over a stabilization line in the v-domain. To this end, the robust stabilization problem was introduced as an optimization problem that aims to place the minimum angle root of interval characteristic polynomials on a target angle line that was specified within the stability region of the first Riemann sheet. This study extended stabilization efforts to the optimal robust stabilization of interval uncertain closed-loop FOPID control systems with an interval time delay. It implemented PSO for computational intelligence. Some remarks of the study can be summarized as follows:
- This study demonstrated a v-domain design scheme that is straightforward for optimal robust stabilization of fractional order control systems and the development of computer-aided-design tools.
- The PSO algorithm can find optimal FOPID controller coefficients that lead to minimum angle roots of interval systems placed on the desired angle line within the stability region of the first Riemann sheet. Thus, the proposed approach can ensure the stability of FOPID control systems in uncertainty ranges of plant parameters. The angle of this line is configured by a target angle specification.
- Target angle specifications can improve the robust control performance of FOPID control systems. We observed that the target angle specifications could be utilized to reduce the sensitivity of the time response performances of control systems to the variation of plant parameters within the uncertainty ranges. Thus, the method can achieve optimal stabilization of FOPID control system designs.
- The proposed stabilization scheme may have implications for variable time-delay systems such as the control and robust stabilization problems of the networked control systems.
In summary, this research work addressed optimal robustly stabilizing FOPID controller design for variable time-delay, interval uncertain fractional order plant functions. A straightforward computer-aided design solution for this type of control problems is not frequent in the literature. In future works, the presented v-domain design methodology can be applied to other fractional order model types, and the associated optimization problems can be solved by other search algorithms.
Author Contributions
Conceptualization, S.T. and B.B.A.; methodology, S.T., B.B.A. and B.S.; software, S.T.; validation, B.S. and B.B.A.; formal analysis, B.S. and R.M.; investigation, B.S. and R.M.; writing—original draft preparation, B.B.A. and S.T.; writing—review and editing, B.S. and R.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Pseudo code for the employment of the PSO algorithm in this optimization problem:
Receive controller parameters (kd,kp,ki,λµ) as a candidate particle from the PSO algorithm.
% This part uniformly samples the hyperrectangle A and calculates minimum angle roots of p sample designs and stores them.
For a0 = ao_min:a0_step:a0_max
For b0 = b0_min:b0_step:b0_max
For b1=b1_min:b1_step:b1_max
For L = L_min:L_step:L_max
Form p design vectors (Equation (7)) that sample the hyperrectangle A.
Form expanded degree integer order characteristic polynomials by using Equation (17).
Calculate roots of the expanded degree integer order characteristic polynomial.
Find minimum argument roots among the roots with positive angle values and store them.
End
End
End
End
% This part selects the minimum argument root of the whole hyperrectangle A and calculates SAE error accordingly.
Find the minimum angle value among the stored minimum angle roots.
Calculate squared angle error (SAE) of the minimum angle value according to Equation (20).
Return SAE to the PSO algorithm for the next evaluation.
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Vinagre, M.B.; Chen, Y.Q.; Petras, I. Two direct Tustin discretization methods for fractional-order differentiator/integrator. J. Frankl. Inst. 2003, 340, 349–362. [Google Scholar] [CrossRef]
- Oustaloup, A. La Dérivation non Entière; Hermes: Paris, France, 1995. [Google Scholar]
- Oustaloup, A.; Mathieu, B.; Lanusse, P. The CRONE control of resonant plants: Application to a flexible transmission. Eur. J. Control 1995, 1, 113–121. [Google Scholar] [CrossRef]
- Xue, D.; Chen, Y.Q. A Comparative Introduction of Four Fractional Order Controllers. In Proceedings of the 4th World Congress on Intelligent Control and Automation, Shanghai, China, 10–14 June 2002; pp. 3228–3235. [Google Scholar]
- Chen, Y.Q.; Bhaskaran, T.; Xue, D. Practical tuning rule development for fractional order proportional and integral controllers. J. Comput. Nonlinear Dyn. 2008, 3, 214031–214038. [Google Scholar] [CrossRef]
- Deniz, F.N.; Keles, C.; Alagoz, B.B.; Tan, N. Design of fractional-order PI controllers for disturbance rejection using RDR measure. In Proceedings of the International Conference on Fractional Differentiation and Its Applications, Catania, Italy, 23–25 June 2014. [Google Scholar]
- Alagoz, B.B.; Deniz, F.N.; Keles, C.; Tan, N. Disturbance rejection performance analyses of closed loop control systems by reference to disturbance ratio. ISA Trans. 2015, 55, 63–71. [Google Scholar] [CrossRef] [PubMed]
- Ates, A.; Alagoz, B.B.; Yeroglu, C.; Yuan, J.J.; Chen, Y.Q. Disturbance rejection FOPID control of rotor by multi-objective BB-BC optimization algorithm. In Proceedings of the ASME/IEEE International Conference on Mechatronic and Embedded Systems and Applications, Cleveland, OH, USA, 6–9 August 2017. [Google Scholar]
- Li, M.; Li, D.; Wang, J.; Zhao, C. Active disturbance rejection control for fractional-order system. ISA Trans. 2013, 52, 365–374. [Google Scholar] [CrossRef] [PubMed]
- Matignon, D. Stability results on fractional differential equations to control processing. In Proceedings of the Computational Engineering in Systems and Application Multiconference, Lille, France, 9–12 July 1996; pp. 963–968. [Google Scholar]
- Radwan, A.G.; Soliman, A.M.; Elwakil, A.S.; Sedeek, A. On the stability of linear systems with fractional-order elements. Chaos Solitons Fractals 2009, 40, 2317–2328. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Ahn, H.S.; Podlubny, I. Robust stability check of fractional order linear time invariant systems with interval uncertainties. Signal Process. 2006, 86, 2611–2618. [Google Scholar] [CrossRef]
- Senol, B.; Ates, A.; Alagoz, B.B.; Yeroglu, C. A numerical investigation for robust stability of fractional-order uncertain systems. ISA Trans. 2014, 53, 189–198. [Google Scholar] [CrossRef] [PubMed]
- Alagoz, B.B. A Note on Robust Stability Analysis of Fractional Order Interval Systems by Minimum Argument Vertex and Edge Polynomials. IEEE/CAA J. Autom. Sin. 2016, 3, 411–421. [Google Scholar]
- Alagoz, B.B.; Yeroglu, C.; Senol, B.; Ates, A. Probabilistic robust stabilization of fractional order systems with interval uncertainty. ISA Trans. 2015, 5, 101–110. [Google Scholar] [CrossRef]
- Alagoz, B.B. Fractional order linear time invariant system stabilization by brute-force search. Trans. Inst. Meas. Control 2018, 40, 1447–1456. [Google Scholar] [CrossRef]
- Hamamci, S.E. An algorithm for stabilization of fractional-order time delay systems using fractional-order PID controllers. IEEE Trans. Autom. Control 2007, 52, 1964–1969. [Google Scholar] [CrossRef]
- Tan, N.; Kaya, I.; Yeroglu, C.; Atherton, D.P. Computation of stabilizing PI and PID controllers using the stability boundary locus. Energy Convers. Manag. 2006, 47, 3045–3058. [Google Scholar] [CrossRef]
- Tan, N.; Ozguven, O.F.; Ozyetkin, M.M. Robust stability analysis of fractional order interval polynomials. ISA Trans. 2009, 48, 166–172. [Google Scholar] [CrossRef]
- Senol, B.; Yeroglu, C. Robust stability analysis of fractional order uncertain polynomials. In Proceedings of the 5th IFAC Workshop on Fractional Differentiation and Its Applications, Nanjing, China, 14–17 May 2012. [Google Scholar]
- Ahn, H.S.; Chen, Y.Q. Necessary and sufficient condition of fractional-order interval linear systems. Automatica 2008, 44, 2985–2988. [Google Scholar] [CrossRef]
- Lu, J.G.; Chen, Y.Q. Robust stability and stabilization of fractional-order interval systems with the fractional order α: The 0 <α <1 case. IEEE Trans. Automat. Control 2010, 55, 152–158. [Google Scholar]
- Farges, C.; Sabatier, J.; Moze, M. Fractional order polytopic systems: Robust stability and stabilization. Adv. Differ. Equ. 2011, 35, 1–10. [Google Scholar] [CrossRef]
- Gao, Z. Robust stabilization criterion of fractional-order controllers for interval fractional-order plants. Automatica 2015, 61, 9–17. [Google Scholar] [CrossRef]
- Gao, Z. Robust stability criterion for fractional-order systems with interval uncertain coefficients and a time-delay. Isa Trans. 2015, 58, 76–84. [Google Scholar] [CrossRef]
- Zheng, S.; Tang, X.; Song, B. Graphical tuning method of FOPID controllers for fractional order uncertain system achieving robust D-stability. Int. J. Robust Nonlin 2015, 26, 1112–1142. [Google Scholar] [CrossRef]
- Chen, Y.Q.; Petras, I.; Xue, D. Fractional Order Control—A Tutorial. In Proceedings of the American Control Conference, St. Louis, MO, USA, 10–12 June 2009; pp. 1397–1411. [Google Scholar]
- Petras, I. Stability of Fractional-order systems with rational orders: A Survey. Fract. Calc. Appl. Anal. 2009, 12, 269–298. [Google Scholar]
- Alagoz, B.B. Hurwitz Stability Analysis of Fractional Order LTI Systems According to Principal Characteristic Equations. ISA Trans. 2017, 70, 7–15. [Google Scholar] [CrossRef] [PubMed]
- Zheng, S. Robust stability of fractional order system with general interval uncertainties. Syst. Control Lett. 2017, 99, 1–8. [Google Scholar] [CrossRef]
- Moornani, K.A.; Haeri, M. Robust stability testing function and Kharitonov-like theorem for fractional order interval systems. IET Control Theory Appl. 2010, 4, 2097–2108. [Google Scholar] [CrossRef]
- Petras, I.; Chen, Y.Q.; Vinagre, B.M. A robust stability test procedure for a class of uncertain LTI fractional order systems. In Proceedings of the International Carpathian Control Conference ICCC’ 2002, Malenovice, Czech Republic, 27–30 May 2002. [Google Scholar]
- Dastjerdi, A.A.; Vinagre, B.M.; Chen, Y.Q.; Hosseinnia, H. Fractional Order PID controllers; A survey in the Frequency Domain. J. Latex Cl. Files 2015, 14, 1–19. [Google Scholar]
- Monje, C.A.; Vinagre, B.M.; Feliu, V.; Chen, Y.Q. Tuning and auto-tuning of fractional order controllers for industry applications. Control Eng. Pract. 2008, 16, 798–812. [Google Scholar] [CrossRef]
- Beschi, M.; Padula, F.; Visioli, A. The generalized iso-damping approach for robust fractional PID controllers design. Int. J. Control 2017, 90, 1157–1164. [Google Scholar] [CrossRef]
- Wang, C.; Jin, Y.; Chen, Y.Q. Auto-tuning of FOPI and FO[PI] controllers with iso-damping property. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 7309–7314. [Google Scholar]
- Sabatier, J.; Lanusse, P.; Melchior, P.; Oustaloup, A. Fractional Order Differentiation and Robust Control Design. In CRONE, H-infinity and Motion Control; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Farokhi, F.; Sandberg, H. A Robust Control-Design Method Using Bode’s Ideal Transfer Function. In Proceedings of the 19th Mediterranean Conference on Control and Automation, Corfu, Greece, 20–23 June 2011; pp. 712–717. [Google Scholar]
- Barbosa, R.S.; Machado, J.A.T.; Ferreira, I.M. Tuning of PID controllers based on bodes ideal transfer function. Nonlinear Dyn. 2004, 38, 305–321. [Google Scholar] [CrossRef]
- Azarmi, R.; Tavakoli-Kakhki, M.; Sedigh, A.K.; Fatehi, A. Robust fractional order PI controller tuning based on bode’s ideal transfer function. IFAC-Pap. 2016, 49, 158–163. [Google Scholar] [CrossRef]
- Biswas, A.; Das, S.; Abraham, A.; Dasgupta, S. Design of fractional-order PIλDμ controllers with an improved differential evolution. Eng. Appl. Artif. Intell. 2009, 22, 343–350. [Google Scholar] [CrossRef]
- Zamani, M.; Karimi-Ghartemani, M.; Sadati, N.; Parniani, M. Design of a fractional order PID controller for an AVR using particle swarm optimization. Control Eng. Pract. 2009, 17, 1380–1387. [Google Scholar] [CrossRef]
- Zhe, G.; Liao, X. Rational approximation for fractional-order system by particle swarm optimization. Nonlinear Dyn. 2012, 67, 1387–1395. [Google Scholar]
- Tufenkci, S.; Senol, B.; Alagoz, B.B. Stabilization of Fractional Order PID Controllers for Time-Delay Fractional Order Plants by Using Genetic Algorithm. In Proceedings of the International Artificial Intelligence and Data Processing Symposium (IDAP), Malatya, Turkey, 28–30 September 2018; pp. 1–4. [Google Scholar]
- Tufenkci, S.; Senol, B.; Alagoz, B.B. Disturbance Rejection Fractional Order PID Controller Design in v-domain by Particle Swarm Optimization. In Proceedings of the International Artificial Intelligence and Data Processing Symposium (IDAP), Malatya, Turkey, 21–22 September 2019; pp. 1–6. [Google Scholar]
- Tufenkci, S.; Senol, B.; Alagoz, B.B.; Matusu, R. Disturbance rejection FOPID controller design in v-domain. J. Adv. Res. 2020, 25, 171–180. [Google Scholar] [CrossRef] [PubMed]
- Tufenkci, S.; Senol, B.; Alagoz, B.B. Fractional order PI control design in v-domain according to minimum angle pole placement method and investigation of robust control performance. EJOSAT 2019, 17, 9–19. [Google Scholar]
- Valle, Y.D.; Venayagamoorthy, G.K.; Mohagheghi, S.; Mejia, J.C.H. Particle swarm optimization: Basic concepts, variants and applications in power systems. IEEE Trans. Evol. Comput. 2008, 2, 171–195. [Google Scholar] [CrossRef]
- Ozlem, I.; Alagoz, B.B. Discretization of fractional order transfer functions by weighted multi-objective particle swarm optimization method. In Proceedings of the 2017 International Artificial Intelligence and Data Processing Symposium, Malatya, Turkey, 16–17 September 2017; pp. 1–4. [Google Scholar]
- Mostapha, K.H. Particle Swarm Optimization in Matlab. Available online: http://yarpiz.com/ (accessed on 1 September 2017).
- Dingyu, X. Fractional-Order Control Systems: Fundamentals and Numerical Implementations; Walter de Gruyter: Berlin, Germany; Boston, MA, USA, 2017. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).