Numerical Simulation of the Fractal-Fractional Ebola Virus
Abstract
:1. Introduction, Historical Background and Motivation
- (i)
- By coming into contact with a person who has died of the Ebola virus disease or in contact with the body fluids of a sick person;
- (ii)
- Through direct contact with humans, body fluids, animal tissues and blood.
2. Numerical Scheme for Fractal-Fractional Ebola Virus Via the Power Law Kernel
3. Numerical Scheme for the Fractal-Fractional Ebola Virus Involving the Exponential Decay Kernel
4. Numerical Scheme for the Fractal-Fractional Ebola Virus With the Generalized Mittag-Lefller Kernel
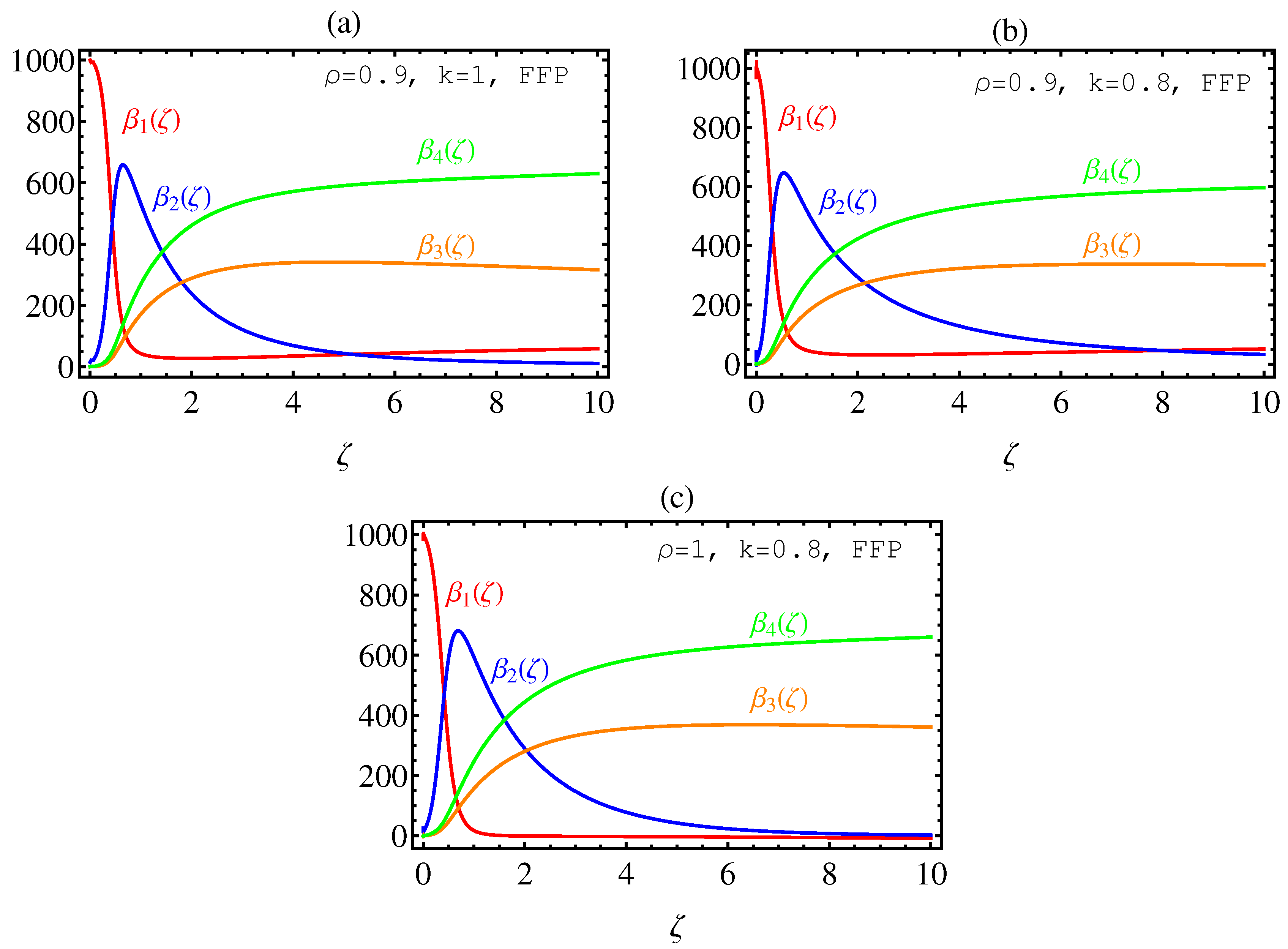
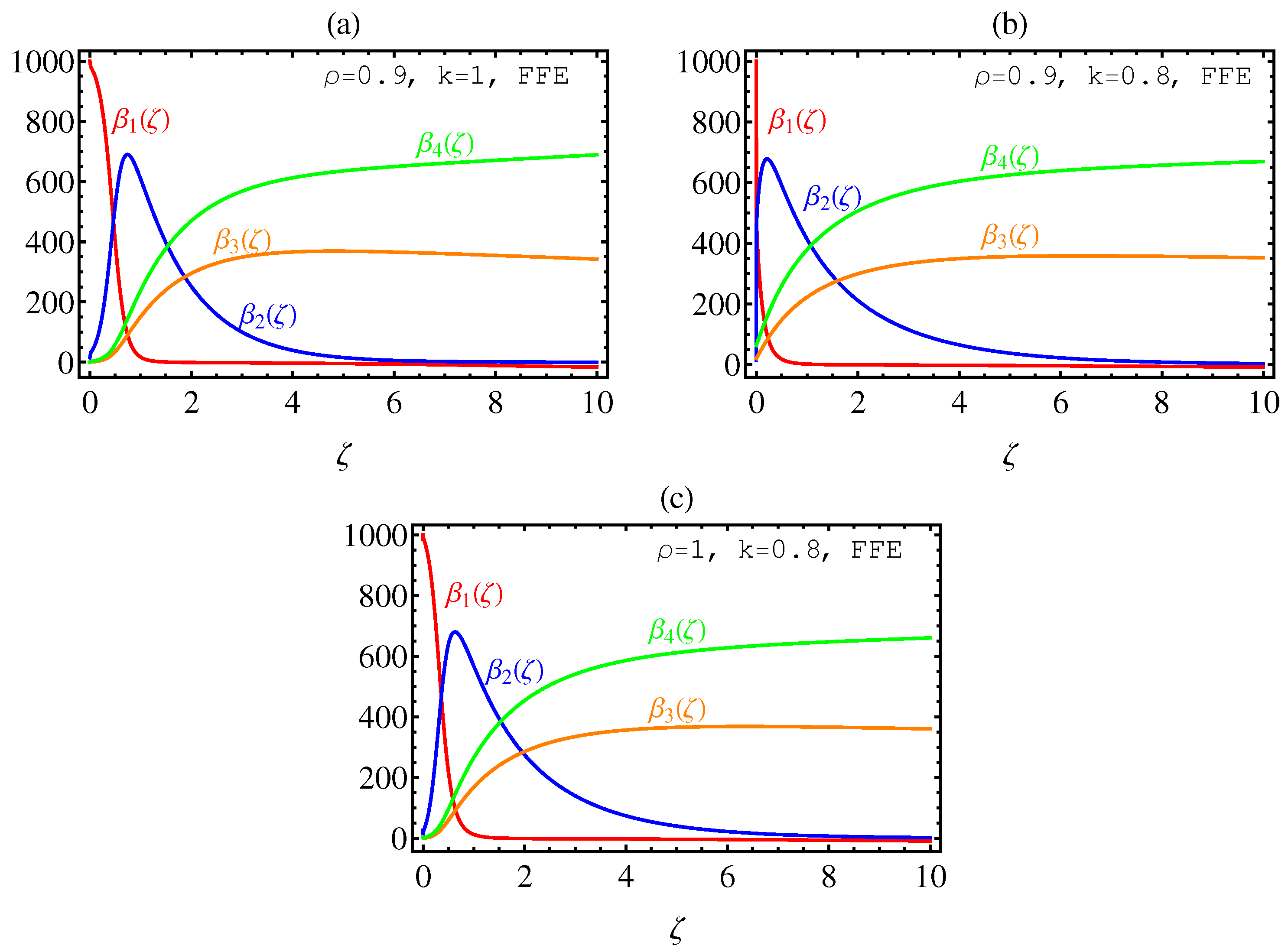
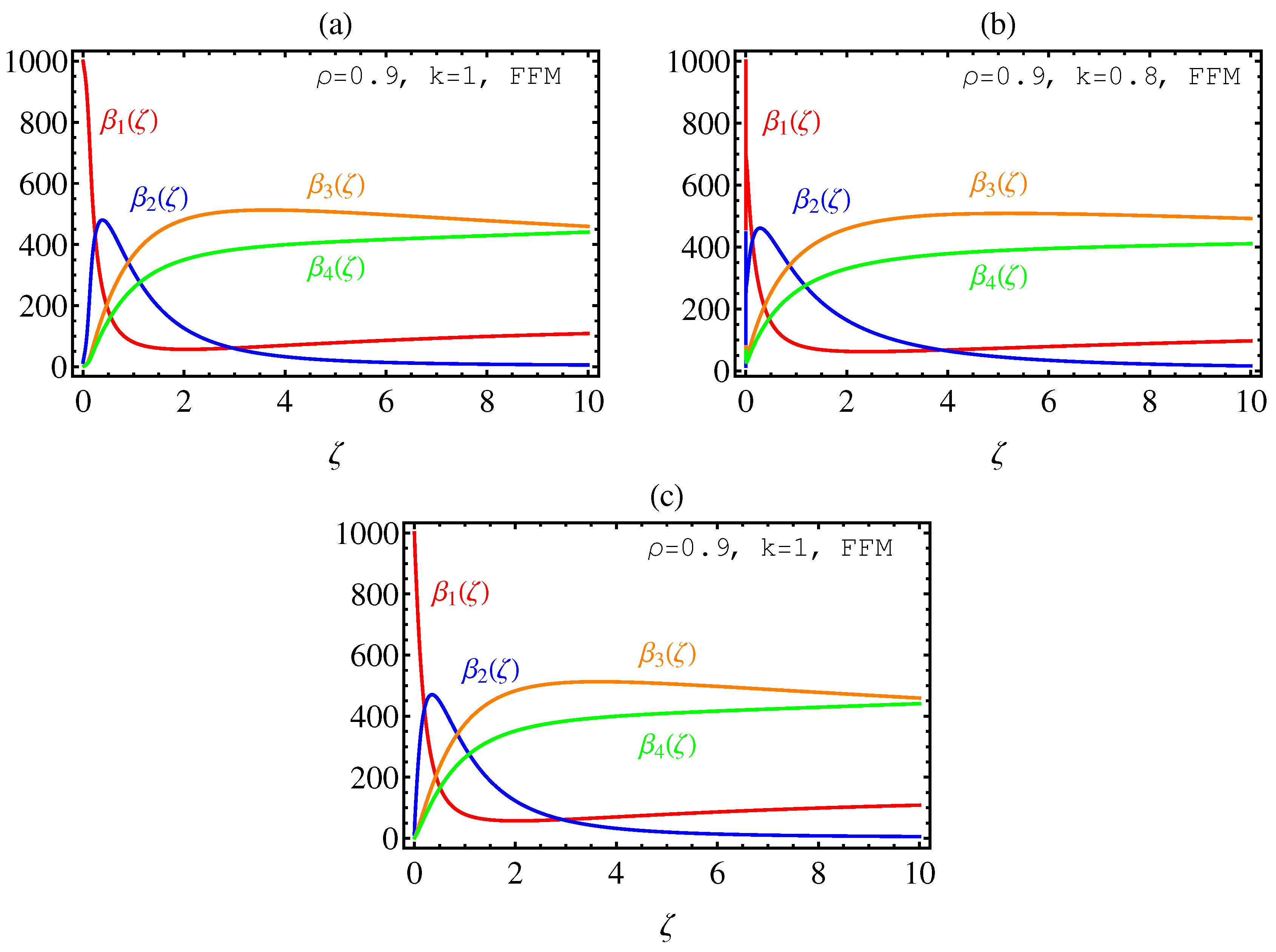
5. Numerical Results and Graphical Illustrations
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rachah, A.; Torres, D.F.M. Mathematical modelling, simulation, and optimal control of the 2014 Ebola outbreak in West Africa. Discret. Dyn. Nat. Soc. 2015, 3, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Area, I.; Ndairou, F.; Nieto, J.J.; Silva, C.J. Ebola model and optimal control with vaccination constraints. J. Ind. Manag. Optim. 2018, 14, 427–446. [Google Scholar] [CrossRef] [Green Version]
- Mazandu, G.K.; Nembaware, V.; Thomford, N.E.; Bope, C.; Ly, O.; Chimusa, E.; Wonkam, A. A potential roadmap to overcome the current eastern DRC Ebola virus disease outbreak: From a computational perspective. Sci. Afr. 2020, 7, e00282. [Google Scholar] [CrossRef]
- Abdo, M.S.; Shah, K.; Wahash, H.A.; Panchal, S.K. On a comprehensive model of the novel Coronavirus (COVID-19) under Mittag-Leffler derivative. Chaos Solitons Fractals 2020, 135, 109867. [Google Scholar] [CrossRef] [PubMed]
- Ndairou, F.; Area, I.; Nieto, J.J.; Torres, D.F.M. Mathematical modeling of COVID-19 transmission dynamics with a case study of Wuhan. Chaos Solitons Fractals 2020, 135, 109846. [Google Scholar] [CrossRef] [PubMed]
- Postnikov, E.B. Estimation of COVID-19 dynamics “on a back-of-envelope”: Does the simplest SIR model provide quantitative parameters and predictions? Chaos Solitons Fractals 2020, 135, 109841. [Google Scholar] [CrossRef] [PubMed]
- Baseler, L.; Chertow, D.S.; Johnson, K.M.; Feldmann, H.; Morens, D.M. The pathogenesis of Ebola virus disease. Annu. Rev. Pathol. Mech. Dis. 2017, 12, 387–418. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, H.M.; Dubey, R.S.; Jain, M. A study of the fractional-order mathematical model of diabetes and its resulting complications. Math. Methods Appl. Sci. 2019, 42, 4570–4583. [Google Scholar] [CrossRef]
- Ghanbari, B.; Günerhan, H.; Srivastava, H.M. An application of the Atangana-Baleanu fractional derivative in mathematical biology: A three-species predator-prey model. Chaos Solitons Fractals 2020, 138, 1–15. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Günerhan, H. Analytical and approximate solutions of fractional-order susceptible-infected-recovered epidemic model of childhood disease. Math. Methods Appl. Sci. 2019, 42, 935–941. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Shah, F.A.; Irfan, M. Generalized wavelet quasilinearization method for solving population growth model of fractional order. Math. Methods Appl. Sci. 2020, 43, 8753–8762. [Google Scholar] [CrossRef]
- Liao, S.-J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Saad, K.M.; Al-Shareef, E.H.F.; Mohamed, M.S.; Yang, X.-J. Optimal q-homotopy analysis method for time-space fractional gas dynamics equation. Eur. Phys. J. Plus 2017, 132, 23. [Google Scholar] [CrossRef]
- Saad, K.M. A reliable analytical algorithm for spacetime fractional cubic isothermal autocatalytic chemical system. Pramana 2018, 91, 51. [Google Scholar] [CrossRef]
- Saad, K.M.; Al-Shareef, E.H.F.; Alomari, A.K.; Baleanu, D.; Gómez-Aguilar, J.F. On exact solutions for time-fractional Korteweg-de Vries and Korteweg-de Vries-Burgers equations using homotopy analysis transform method. Chinese J. Phys. 2020, 63, 149–162. [Google Scholar] [CrossRef]
- He, J.-H. Variational iteration method-a kind of nonlinear analytical technique: Some examples. Int. J. Nonlinear Mech. 1999, 34, 708–799. [Google Scholar] [CrossRef]
- Saad, K.M. and Al-Sharif, E.H. Analytical study for time and time-space fractional Burgers equation. Adv. Differ. Equa. 2017, 2017, 300. [Google Scholar] [CrossRef] [Green Version]
- Shi, X.-C.; Huang, L.-L.; Zeng, Y. Fast Adomian decomposition method for the Cauchy problem of the time-fractional reaction diffusion equation. Adv. Mech. Engrg. 2016, 8, 1–5. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Al-Sharif, E.H.F. A new analysis of the time-fractional and space-time fractional-order Nagumo equation. J. Inform. Math. Sci. 2018, 10, 545–561. [Google Scholar]
- Bueno-Orovio, A.; Kay, D.; Burrage, K. Fourier spectral methods for fractional-in-space reaction-diffusion equations. BIT Numer. Math. 2014, 54, 937–954. [Google Scholar] [CrossRef]
- Takeuchi, Y.; Yoshimoto, Y.; Suda, R. Second order accuracy finite difference methods for space-fractional partial di?erential equations. J. Comput. Appl. Math. 2017, 320, 101–119. [Google Scholar] [CrossRef]
- Çeneciz, Y.; Keskin, Y.; Kurnaz, A. The solution of the Bagley-Torvik equation with the generalized Taylor collocation method. J. Franklin Inst. 2010, 347, 452–466. [Google Scholar] [CrossRef]
- Khader, M.M.; Saad, K.M. A numerical approach for solving the fractional Fisher equation using Chebyshev spectral collocation method. Chaos Solitons Fractals 2018, 110, 169–177. [Google Scholar] [CrossRef]
- Saad, K.M. New fractional derivative with non-singular kernel for deriving Legendre spectral collocation method. Alex. Eng. J. 2020, 59, 1909–1917. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; North-Holland Mathematical Studies; Elsevier (North-Holland) Science Publishers: Amsterdam, The Netherlands; London, UK; New York, NY, USA, 2006. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications, Mathematics in Science and Engineering; Academic Press: New York, NY, USA; London, UK; Sydney, Australia; Tokyo, Japan; Toronto, ON, Canada, 1999. [Google Scholar]
- Srivastava, H.M. Fractional-order derivatives and integrals: Introductory overview and recent developments. Kyungpook Math. J. 2020, 60, 73–116. [Google Scholar]
- Srivastava, H.M. Operators of basic (or q-) calculus and fractional q-calculus and their applications in geometric function theory of complex analysis. Iran. J. Sci. Technol. Trans. A: Sci. 2020, 44, 327–344. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Khader, M.M. An efficient spectral collocation method for the dynamic simulation of the fractional epidemiological model of the Ebola virus. Chaos Solitons Fractals 2020, 140, 110174. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M.; Gómez-Aguilar, J.F.; Almadiy, A.A. Some new mathematical models of the fractional-order system of human immune against IAV infection. Math. Biosci. Eng. 2020, 17, 4942–4969. [Google Scholar] [CrossRef]
- Singh, H.; Srivastava, H.M. Numerical Simulation for Fractional-Order Bloch Equation Arising in Nuclear Magnetic Resonance by Using the Jacobi Polynomials. Appl. Sci. 2020, 10, 2850. [Google Scholar] [CrossRef] [Green Version]
- Caputo, M. Linear models of dissipation whose Q is almost frequency independent. II Geophys. J. R. Astron. Soc. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new defnition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 73–85. [Google Scholar]
- Atangana, A. Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system. Chaos Solitons Fractals 2017, 102, 396–406. [Google Scholar] [CrossRef]
- Li, Z.-F.; Liu, Z.-N.; Khan, M.A. Fractional investigation of bank data with fractal-fractional Caputo derivative. Chaos Solitons Fractals 2020, 131, 109528. [Google Scholar] [CrossRef]
- Gómez-Aguilar, J.F.; Atangana, A. New chaotic attractors: Application of fractal-fractional differentiation and integration. Math. Methods Appl. Sci. 2020. [Google Scholar] [CrossRef]
- Atangana, A.; Khan, M.A. Fatmawati, Modeling and analysis of competition model of bank data with fractal fractional Caputo-Fabrizio operator. Alex. Engrg. J. 2020, 59, 1985–1998. [Google Scholar] [CrossRef]
- Wang, W.-T.; Khan, M.A. Analysis and numerical simulation of fractional model of bank data with fractal-fractional Atangana-Baleanu derivative. J. Comput. Appl. Math. 2020, 369, 112646. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Saad, K.M. New approximate solution of the time-fractional Nagumo equation involving fractional integrals without singular kernel. Appl. Math. Inform. Sci. 2020, 14, 1–8. [Google Scholar]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres-Iglesias, A. On a fractional order Ebola epidemic model. Adv. Differ. Equa. 2015, 2015, 1–8. [Google Scholar] [CrossRef] [Green Version]
- Bonyah, E.; Badu, K.; Asiedu-Addo, S.K. Optimal control application to an Ebola model. Asian Pac. J. Trop. Biomed. 2016, 6, 283–289. [Google Scholar] [CrossRef] [Green Version]
- Koca, I. Modelling the spread of Ebola virus with Atangana-Baleanu fractional operators. Eur. Phys. J. Plus 2018, 133, 100. [Google Scholar] [CrossRef]
- Rachah, A.; Torres, D.F.M. Predicting and controlling the Ebola infection. Math. Methods Appl. Sci. 2017, 40, 6155–6164. [Google Scholar] [CrossRef] [Green Version]
- Saad, K.M.; Gómez-Aguilar, J.F.; Almadiy, A.A. A fractional numerical study on a chronic hepatitis C virus infection model with immune response. Chaos Solitons Fractals 2020, 139, 110062. [Google Scholar] [CrossRef]
- Amundsen, S.B. Historical analysis of the Ebola virus: Prospective implications for primary care nursing today. Clin. Excell. Nurse Pract. 1998, 2, 343–351. [Google Scholar] [PubMed]


| Symbol | Definition |
|---|---|
| The susceptible population | |
| The infected population | |
| The recovery population | |
| The population died in the region | |
| N | The total population in the region |
| The rate of infection with the disease | |
| The rate of susceptibility | |
| The rate of natural death | |
| The rate of death from the disease | |
| The rate of recovery from the disease |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Srivastava, H.M.; Saad, K.M. Numerical Simulation of the Fractal-Fractional Ebola Virus. Fractal Fract. 2020, 4, 49. https://doi.org/10.3390/fractalfract4040049
Srivastava HM, Saad KM. Numerical Simulation of the Fractal-Fractional Ebola Virus. Fractal and Fractional. 2020; 4(4):49. https://doi.org/10.3390/fractalfract4040049
Chicago/Turabian StyleSrivastava, H. M., and Khaled M. Saad. 2020. "Numerical Simulation of the Fractal-Fractional Ebola Virus" Fractal and Fractional 4, no. 4: 49. https://doi.org/10.3390/fractalfract4040049
APA StyleSrivastava, H. M., & Saad, K. M. (2020). Numerical Simulation of the Fractal-Fractional Ebola Virus. Fractal and Fractional, 4(4), 49. https://doi.org/10.3390/fractalfract4040049






