Design of Cascaded and Shifted Fractional-Order Lead Compensators for Plants with Monotonically Increasing Lags

Abstract

This paper concerns cascaded, shifted, fractional-order, lead compensators made by the serial connection of two stages introducing their respective phase leads in shifted adjacent frequency ranges. Adding up leads in these intervals gives a flat phase in a wide frequency range. Moreover, the simple elements of the cascade can be easily realized by rational transfer functions. On this basis, a method is proposed in order to design a robust controller for a class of benchmark plants that are difficult to compensate due to monotonically increasing lags. The simulation experiments show the efficiency, performance and robustness of the approach.

1. Introduction

Fractional calculus is an old field of science that, based on the initial idea of generalizing derivatives with integer order to derivatives with non-integer order, has given rise to many results in the pure field of mathematics [1,2,3,4]. However, today the field has tremendously grown and has many and various applications in science and engineering [5,6,7,8], such that even modeling, analysis, and control of complex systems requiring a multi-disciplinary approach [9,10] can be approached by fractional calculus tools [11,12,13].

In the specific field of automatic control, it is now more than two decades since the influential book [14] reported that the $95\%$ of the control loops worldwide were of Proportional-Integral-Derivative (PID) type. Today, the technological trends and the increasing demand of better tuning make it clear that the PID controllers are still a subject of intensive research. Hence, following the boost to innovation in the late twentieth century, the fractional-order controllers (FOCs) are also proposed for industrial applications [15,16,17,18,19,20,21,22].

The first attempt to classify the FOCs used in process applications mentioned four types [23]: the TID controller [24], the CRONE controller [25,26], the $P{I}^{\lambda }{D}^{\mu }$ controller [27], and the fractional lead-lag compensator [28]. All share the same idea of using irrational compensators ensuring flat phase in Bode plots. Namely, if the phase derivative with respect to the frequency is zero (or nearly zero), then robustness to gain variations and iso-damping behavior of the step response is achieved. Hence, ensuring flat phase property is a main reason justifying the interest for FOCs.

In the years following the publication of [23], a great effort has been made to develop efficient FOC tuning procedures in both the frequency and time domain. A noticeable, present-day research direction in tuning approaches opts for optimization techniques with constraints that are expressed by time-domain specifications (rise time, settling time, percentage overshoot, error indices, etc.) or by frequency-domain specifications (phase/gain margin, crossover frequency, bandwidth, sensitivity magnitudes, etc.). For example, the tuning of a fractional-order PID (FPID) controlling a first-order plus delay-time process is converted into an optimization problem [17,29]. In other cases, the tuning is based on parameter searching in a multidimensional space [30]. In addition, as regards the time-domain optimization approaches, many authors employed evolutionary algorithms for tuning FPID controllers. For example, they applied Particular Swarm Optimization (PSO) or Genetic Algorithms to minimize the Integral Time Absolute Error (ITAE) [31,32] or a combination of the ITAE and the Integral Square Error (ISE) [33] or the integral absolute error (IAE) [34] or a combination of the integral gain and closed-loop system bandwidth [35]. Additionally, a combination of differential evolution and PSO was proposed to design and realize FOC based on time-domain performance specifications [36].

Clearly, the drawback of all the optimization-based tuning procedures is that they should be repeated for any specific model that one takes into account. However, in practice, control engineers need easy-to-apply, efficient tuning rules. For this reason, some attempts generalized the Ziegler and Nychols rules to FPID tuning [37,38]. New formulas also extended the Symmetrical Optimum approach [14] to tune the fractional-order PI (FPI), also named PI${}^{\alpha }$ controller, in positions control of a class of electromechanical systems [39]. To overcome the difficulties, the research on FPIDs developed empirical tuning rules and some auto-tuning approaches [17,39,40,41,42,43,44,45,46,47,48]. Whatever tuning approach is chosen, the practical implementation of FPID is a critical issue. Namely, the fractional-order transfer functions (TFs) of the FOC frequently require to be approximated by high-order rational TFs.

On the basis of the above considerations, this paper considers the Cascaded, Shifted, Fractional-order, LEad Compensators (CS-FLECs), a new class of compensators enjoying the following characteristics:

(A)

The CS-FLECs are multistage compensators, in which each stage is in its turn a fractional-order lead compensator (FLEC). Each FLEC stage is frequency-scaled with respect to the previous one, so that it provides phase lead values with a nearly flat phase on an adjacent interval. When compared with a cascade of identical FLECs that are superposed on the same frequency interval, a CS-FLEC exhibits a nearly flat phase in a much larger frequency interval. This is a direct result of the serial structure of the shifted stages.

(B)

To implement a CS-FLEC, each stage needs a rational TF approximation. As the paper shows, a second-order TF provides a satisfactory approximation in the frequency interval of each stage of the cascade. The values of the coefficients in each second-order TF ensure low sensitivity in both analogue and digital realizations.

(C)

The paper shows how to apply CS-FLEC structures to compensate a class of plants that are notoriously difficult to control [49,50]. The approach is especially suited for plants that are characterized by monotonically increasing lags. The fundamental ideas underlying the design pattern are simple and refer to formulas based on the properties of the CS-FLEC. The paper also brings out the limits of the CS-FLEC in controlling the chosen benchmarks.

The organization of the paper is the following. Section 2 introduces the CS-FLEC controller and illustrates its properties. Section 3 provides a new and easy method for implementing rational, low-order TF of these controllers. Section 4 describes the procedure to design a CS-FLEC. Section 5 presents and discusses two case-studies that show how CS-FLECs control classes of processes, reported as benchmarks by the technical literature. Section 6 provides the conclusions.

2. Cascaded, Shifted, Fractional-Order Lead Compensator

This section describes the CS-FLEC that is composed by two elements, indicated by $H_1\left(s\right)$ and $H_2\left(s\right)$, which are defined in shifted, partially overlapping, intervals of the frequency axis.

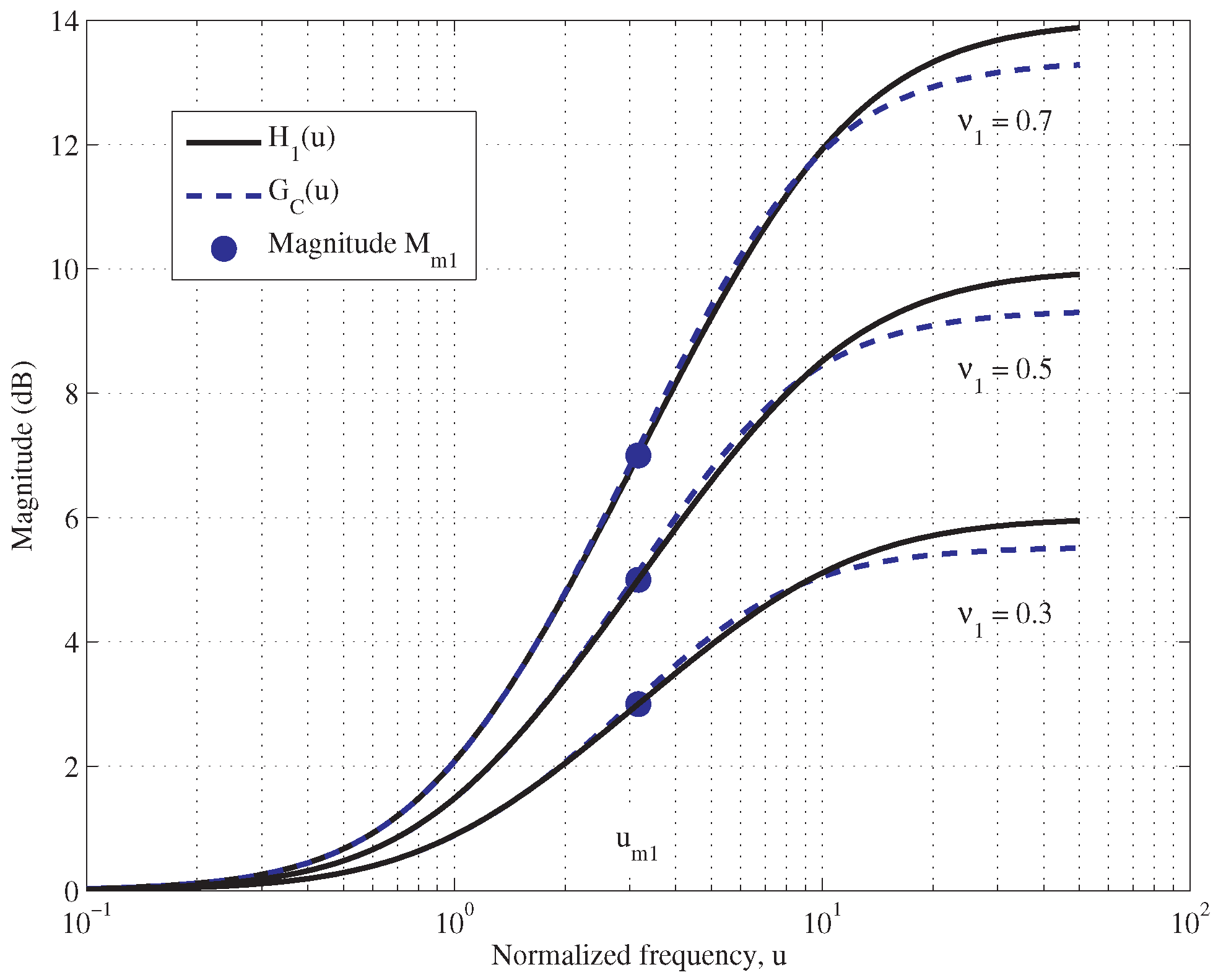
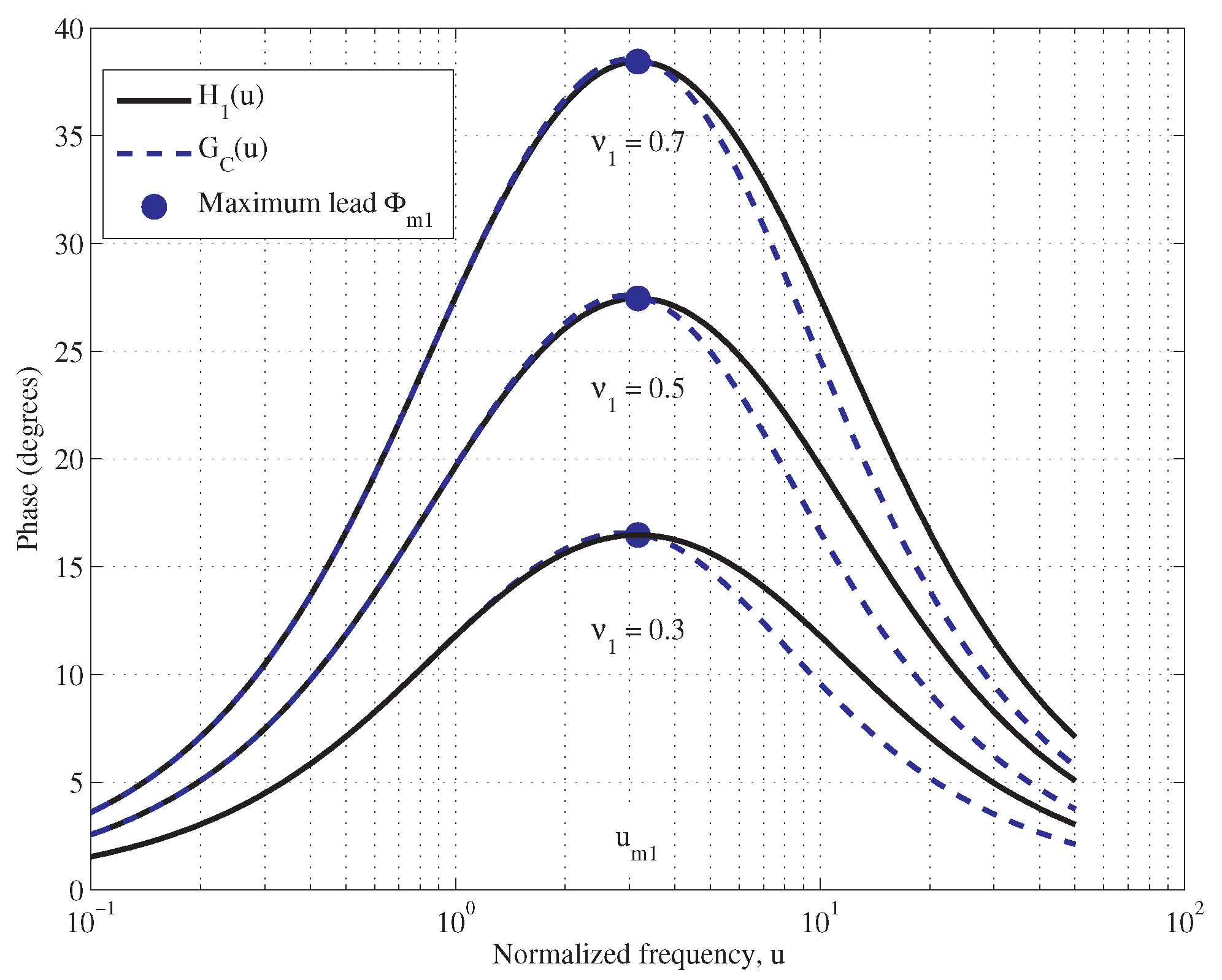
2.1. The First Compensator Stage

The basic element of the proposed CS-FLEC is the first compensator, that is described as

$$H_1\left(s\right)={\left(\frac{1+\tau s}{1+\tau \mathsf{\Delta }s}\right)}^{{\nu }_1},$$

(1)

with $0<{\nu }_1<1$ and $0<\Delta <1$ when considering a fractional-order lead compensator (FLEC) [40]. The symbols $\tau$ and ${\nu }_1$ represent the time constant and the fractional order, respectively. Now, put $s=j\omega$ to recall the frequency key features of a FLEC. It is well known that the maximum phase lead ${\phi }_{m1}$ of $H_1\left(s\right)$ is obtained at the geometric mean of $1/\tau$ and $1/(\tau \Delta )$ [27,51]:

$${\omega }_{m1}=\frac{1}{\tau {\Delta }^{0.5}}.$$

(2)

In this frequency, the magnitude, say $M_{m1}=\left|H_1\left(j{\omega }_{m1}\right)\right|$, and the phase, ${\phi }_{m1}=\angle H_1\left(j{\omega }_{m1}\right)$, are:

$$M_{m1}={(\Delta )}^{-0.5{\nu }_1},$$

(3)

$${\phi }_{m1}={\nu }_1\left[arctan\left(\frac{1}{\sqrt{\Delta }}\right)-arctan\left(\sqrt{\Delta }\right)\right]={\nu }_{1}arctan\left(\frac{1-\Delta }{2\sqrt{\Delta }}\right).$$

(4)

Figure 1 and Figure 2 show, in solid lines, the magnitude and phase plots of the normalized frequency response of the compensator $H_1\left(ju\right)$, where $u=\tau \omega$ is a normalized frequency, for ${\nu }_1=0.3,0.5,0.7$, and $\Delta =0.1$. The circles represent the pairs $({\omega }_{m1},M_{m1})$ and $({\omega }_{m1},{\phi }_{m1})$ corresponding to the assigned values of ${\nu }_1$.

Higher values of ${\nu }_1$ provide higher phase leads while the lower ones lead to a flatter behavior of the phase plots.

By Equation (4), the maximum phase lead ${\phi }_{m1}$ depends on ${\nu }_1$ and $\Delta$, whose values dictate the amount of the introduced phase lead. For integer-order compensators (${\nu }_1=1$), many authors usually consider values of $\Delta$ in the range between $0.05$ and $0.3$ [52], in particular $\Delta \ge 0.1$. Subsequently, with $\Delta =0.1$, the Equation (4) gives ${\phi }_{m1}\approx {\nu }_1{55}^{\circ }$. Accordingly, integer-order compensators consisting of a series of two stages with the same zero-pole pair provide greater phase leads. In this conventional structures, the serial stages have equal characteristics and, at each frequency, provide equal contributions to the resulting phase lead.

2.2. The Second Compensator Stage

The proposed structure differs from the conventional one. A CS-FLEC, indeed, is a cascade of two FLECs with the same Bode plots, but the position on the $\omega$-axis of the second stage is shifted with respect to the first one. The shifting amount is established to make the phase of each FLEC element dominate on its nearly flat phase frequency interval. The resulting lead network, i.e., the CS-FLEC, has a relatively low order and enjoys the flat phase property in a large frequency band. In details, once the parameters of $H_1\left(s\right)$ have been chosen, the second FLEC, say $H_2\left(s\right)$, is obtained by using ${\nu }_2$ in place of ${\nu }_1$ and by scaling $H_1\left(s\right)$ with the substitution $s\to \Delta s$, where $\Delta$ is used as scaling factor:

$$H_2\left(s\right)={\left(\frac{1+\tau \Delta s}{1+\tau {\Delta }^{2}s}\right)}^{{\nu }_2}.$$

(5)

In this way, the frequencies delimiting the flatness interval of the CS-FLEC can be fixed in terms of the features of the two stages in the series. Namely, it is easy to show that $H_2\left(s\right)$ gives its maximum phase lead ${\phi }_{m2}$ at the frequency

$${\omega }_{m2}=\frac{1}{\tau {\Delta }^{1.5}}$$

(6)

and

$$M_{m2}=\left|H_2\left(j{\omega }_{m2}\right)\right|={(\Delta )}^{-0.5{\nu }_2}$$

(7)

$${\phi }_{m2}=\angle H_2\left(j{\omega }_{m2}\right)={\nu }_{2}arctan\left(\frac{1-\Delta }{2\sqrt{\Delta }}\right).$$

(8)

Moreover, comparing Equations (3), (4), (7), and (8), and using ${\nu }_2={\nu }_1$ yields: $M_{m2}=M_{m1}$, ${\phi }_{m2}={\phi }_{m1}$ and, for any frequency $\omega$, $H_1(j\omega \Delta )=H_2\left(j\omega \right)$. Figure 3 and Figure 4 show the magnitude and phase plots for the analogue compensators $H_1$ and $H_2$ (see dashed and dash-dotted lines, respectively). For clarity reasons, these figures only use the values ${\nu }_2={\nu }_1=0.3,0.5,0.7$. The curves assume $\Delta =0.1$ and they are drawn in terms of the nondimensional frequency $u=\tau \omega$, so that $u_{m1}=\frac{1}{{\Delta }^{0.5}}$ and $u_{m2}=\frac{1}{{\Delta }^{1.5}}$ correspond to the maximum leads the two stages respectively provide.

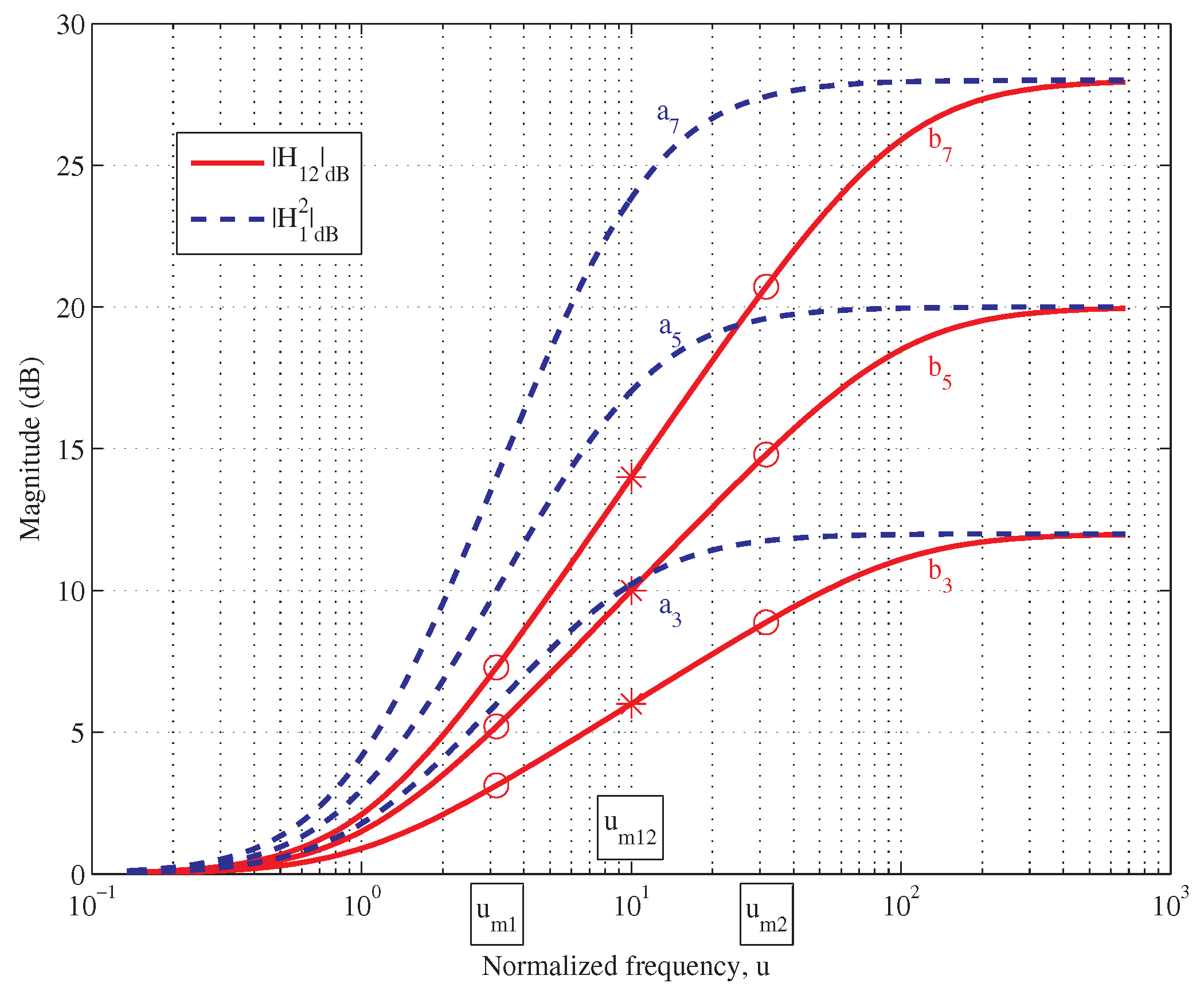
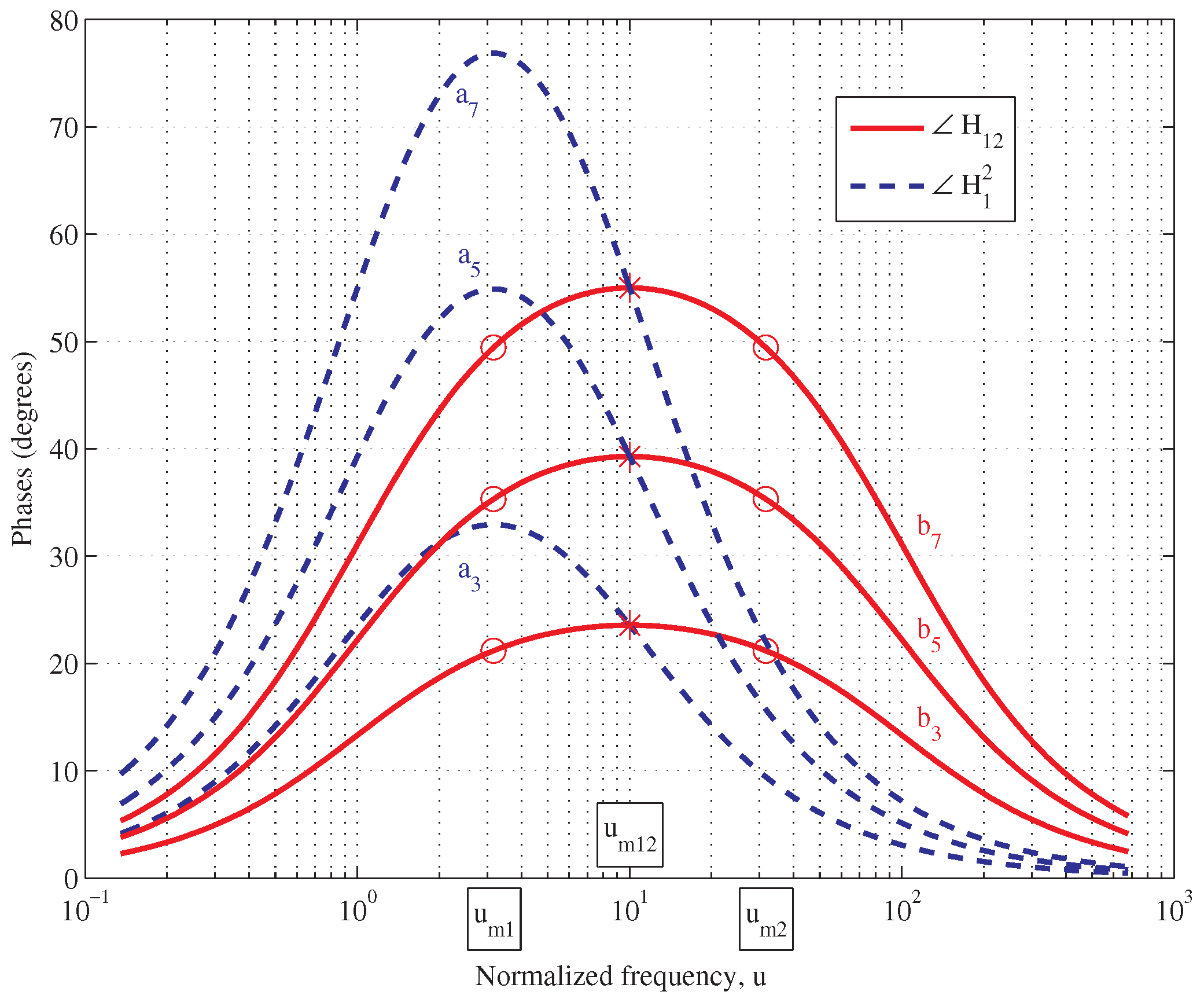
2.3. The Serial Compensator

With the chosen parameters and $\nu ={\nu }_1={\nu }_2$, the series connection of the two compensators is equivalent to a single unit:

$$H_{12}\left(s\right)=H_1\left(s\right)H_2\left(s\right)={\left(\frac{1+\tau s}{1+\tau {\Delta }^{2}s}\right)}^{\nu }.$$

(9)

By using $u=\tau \omega$, it follows

$$H_{12}\left(ju\right)=H_1\left(ju\right)H_2\left(ju\right)={\left(\frac{1+ju}{1+ju{\Delta }^2}\right)}^{\nu }$$

(10)

and, by Equations (2) and (9), the maximum phase lead ${\phi }_{m12}$ is obtained at the geometric mean of the new break-away frequencies:

$${\omega }_{m12}=\frac{1}{\tau \Delta }.$$

(11)

At $u_{m12}=\frac{1}{\Delta }$, the magnitude is

$$M_{m12}=\left|H_{12}\left(j{u}_{m12}\right)\right|={(\Delta )}^{-\nu }$$

(12)

and the maximum phase lead is

$${\phi }_{m12}=\angle H_{12}\left(j{u}_{m12}\right)=\nu arctan\left(\frac{1-{\Delta }^2}{2\Delta }\right).$$

(13)

The frequencies $u_{m1}=\frac{1}{{\Delta }^{0.5}}$ and $u_{m2}=\frac{1}{{\Delta }^{1.5}}$ define the interval $(u_{m1},u_{m2})$, where the phase is nearly flat (see Figure 4) and where the magnitude characteristic of $H_{12}\left(j\omega \right)$ follows a nearly straight pattern (solid lines in Figure 3). Beyond this range, the magnitude plot tends to a horizontal line and the CS-FLEC provides the maximum magnitude for each value of $\nu$.

Figure 5 and Figure 6 compare the Bode diagrams of the CS-FLEC specified by $H_{12}\left(j\omega \right)$ with the Bode diagrams of the conventional series of two identical FLECs, specified by ${\left[H_1\left(j\omega \right)\right]}^2$. The cases with $\nu =\{0.3,0.5,0.7\}$ and $\Delta =0.1$ are considered. Compensators $H_{12}$ and $H_1^2$ provide the same high-frequency gain, even if the magnitude of the former increases more gradually than the magnitude of the latter. Finally, by Equations (4) and (13), the maximum phase lead given by $H_1^2$ is $2{\phi }_{m1}\approx \nu {110}^{\circ }$ that is greater than ${\phi }_{m12}=\nu {79}^{\circ }$, which is provided by $H_{12}$. However, the phase characteristics of $H_{12}$ are flatter than those of $H_1^2$. Moreover, the slopes of the plots of $\angle H_{12}\left(ju\right)$ and $\angle H_1^2\left(ju\right)$, evaluated on the right (or left) of $u_{m12}$ and $u_{m1}$, respectively, are measures of the flatness of the phase. Because the decreasing of $\angle H_1^2\left(ju\right)$ around $u_{m1}$ is more rapid than the falling of $\angle H_{12}\left(ju\right)$ around $u_{m12}$, the latter plot is flatter than the former one.

3. Realization

Because the CS-FLEC is an irrational function, its implementation needs a rational integer-order TF approximation. Literature shows many frequency domain approaches to approximate irrational operators and functions, starting with early contributions like [53,54,55]. The most referred methods are the Oustaloup recursive approximation (ORA) [56] and the modified Oustaloup technique [57]. They employ popular formulas to alternate zeros and poles of the rational transfer function in the frequency interval of practical interest, but they often determine approximations of very high order. Methods that are based on continued fraction expansions (CFE), interpolation, and curve-fitting methods are also important [58,59], and even the Matsuda approach, which is one of the best known, combines CFE and a fitting technique [55]. Moreover, CFE-based methods are preferred to those using power series expansions, because better convergence properties imply less coefficients to obtain a good approximation [58]. A good review of the basic approaches and techniques was given by [60].

In recent years, researchers proposed several other techniques, among which one may consider [61,62,63,64,65,66,67]. Namely, it was pointed out that fractional-order lead compensators found difficult application in industry, because it is difficult to obtain the desired functions with the commercially available electronic components, such that special methods that are based on operational amplifiers and field programmable analog arrays should be used [61]. In [63], the authors design two fractional-order lead-lag compensators to control a benchmark refrigeration system (the PID2018 benchmark challenge) such that a more aggressive response is obtained. In this case, approximation is simply performed via the Matlab command fitmagfrd from the Robust Control Toolbox. Other peculiar techniques could take advantage from orthonormal rational basis functions, which can be used to improve fitting and approximation of frequency response, as shown in [64]. Some other authors proposed curve fitting techniques (with built-in Matlab functions) that use frequency response data of fractional-order operators to improve the ORA, the modified ORA, or the Matsuda approximation [65]. A Scilab Based Toolbox is also available for fractional-order operators, transfer functions, filters, and controllers [66]. Finally, the recent work presented in [67] implements fractional-order lead/lag compensators using Operational Transconductance Amplifiers as active blocks. To this aim, the authors consider a Padé approximation proposed in [68] and obtain the same form of realization for the two types of fractional transfer functions, which allows them to use the same active core and to electronically tune the characteristics of the compensators. Contributions for the discretization and digital implementation of fractional functions are many and beyond the scope of this paper.

Here, each stage of the CS-FLEC is approximated by a second-order rational TF, which gives sufficient accuracy in the frequency range of interest. Note that a low-order implementation is advantageous, because the changes of the coefficients due to passive component tolerances (analogue implementation) or to the limitations of microprocessor words and the quantization effects (digital implementation) are quite contained [69,70], such that a low sensitivity to parameter variations is obtained.

The realization method leads to the following expression of the approximated FLEC (see Appendix A)

$${\left(\frac{1+\tau s}{1+\tau \Delta s}\right)}^{\nu }\approx G_C\left(s\right)=\frac{{\sum }_{k=0}^2{B}_{2-k}{s}^k}{{\sum }_{k=0}^2{A}_{2-k}{s}^k},$$

(14)

with

$$A_{2-k}=\sum _{i=0}^2{a}_{2-i}{L}_{ki}^C,B_{2-k}=\sum _{i=0}^2{b}_{2-i}{L}_{ki}^C,$$

(15)

where $b_2=a_0=(1-\nu )(2-\nu )$, $b_1=a_1=2(2-\nu )(2+\nu )$, $b_0=a_2=(1+\nu )(2+\nu )$ [71] and

$$L_{ki}^C=\sum _{j={\mu }_1}^{{\mu }_2}\left(\genfrac{}{}{0pt}{}{i}{j}\right)\left(\genfrac{}{}{0pt}{}{2-i}{k-j}\right){\Delta }^{k-j}{\tau }^{k}k=0,1,2,$$

(16)

where ${\mu }_1=max\{0,k+i-2\}$, ${\mu }_2=min\{i,k\}$.

Figure 1 and Figure 2 show in dashed lines magnitude and phase plots of a second-order realization $G_C\left(s\right)$ of the FLEC. The approximation accuracy is satisfactory in the frequency range of interest for the single (irrational) stage FLEC. The plots in Figure 1 and Figure 2 show that both the magnitude and the phase practically coincide with the plots representing the irrational FLEC in the frequency interval $u\in ({10}^{-1},u_{m1})$, which is important for compensation. Instead, for $u>u_{m1}$, the approximation gets worse. On the other hand, for practical purpose, it can be easily verified that higher-order, rational TFs do not significantly improve the approximation in the frequency range where a nearly flat phase is achieved.

Now, consider the rational TFs indicated by $G_{CH1}\left(s\right)$ and $G_{CH2}\left(s\right)$, respectively representing the second-order realizations of $H_1\left(s\right)$ and $H_2\left(s\right)$. Subsequently, the cascade $G_{CH12}\left(s\right)=G_{CH1}\left(s\right)·G_{CH2}\left(s\right)$ provides a fourth-order realization of $H_{12}\left(s\right)$.

4. The Design Method

To achieve robustness to gain variations, the phase margin $PM$ must be nearly constant in a frequency interval around the gain crossover frequency of the compensated system, ${\overline{\omega }}_{gc}$. That is, the tangent line to the curve of the phase angle of the open-loop TF should have a small slope in a given range around ${\overline{\omega }}_{gc}$. Even if this curve is not completely flat, the robustness can be ensured if $PM$ is greater than an established minimum value for a wide frequency spread around ${\overline{\omega }}_{gc}$. The width of the range is also important to guarantee robustness.

Hence, let $H_{OL}\left(s\right)=H\left(s\right)G_p\left(s\right)$ be the open-loop TF, including the controller $H\left(s\right)=K_c{H}_{12}\left(s\right)=K_c{H}_1\left(s\right)H_2\left(s\right)$ and the plant $G_p\left(s\right)$. To introduce the design method, the following essential facts clarify the objectives, specify the assumptions, and provide some advice.

a.

The features of the CS-FLEC are suitable for controlling plants with phase lags which are monotonic increasing with the frequency $\omega$. Afterwards, putting ${\phi }_p\left(\omega \right)=\angle G_p\left(j\omega \right)$, the phase margin $P{M}_p$ of the plant at its gain crossover frequency ${\omega }_{pgc}$, $P{M}_p=\pi +{\phi }_p\left({\omega }_{pgc}\right)$, is often negative.

b.

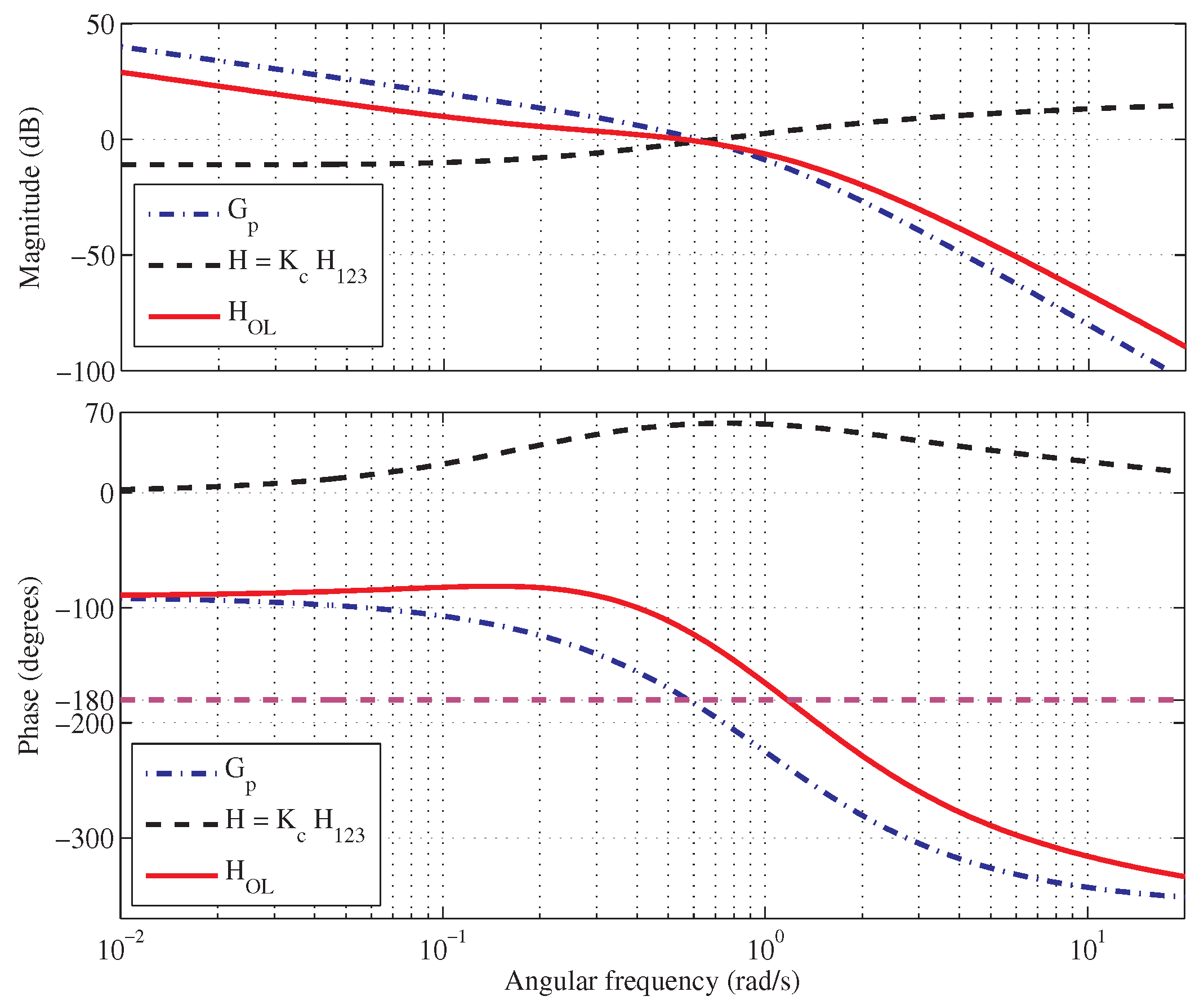
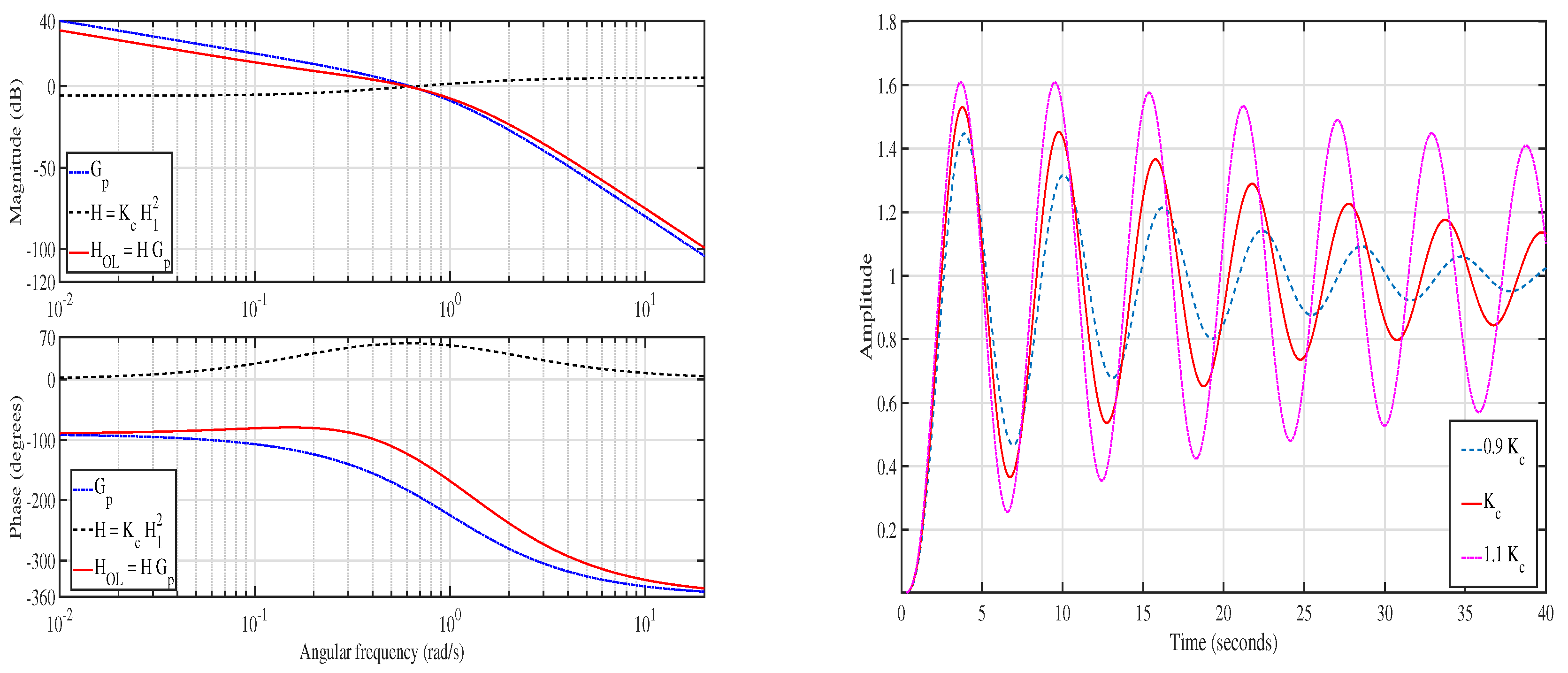
The compensator will introduce a phase lead compensating the lag of the plant so as to obtain the flattest possible phase trend in the range surrounding ${\overline{\omega }}_{gc}$, i.e., the gain crossover frequency of $H_{OL}\left(j\omega \right)$. However, the CS-FLEC shifts ${\overline{\omega }}_{gc}$ to the right of ${\omega }_{pgc}$. Accordingly, if $\angle G_p\left(j\omega \right)$ and $|G_p\left(j\omega \right)|$ decrease sharply beyond ${\omega }_{pgc}$, $H\left(j\omega \right)$ cannot introduce leads balancing the greater lags (see the plant phase diagrams in Figure 7 and Figure 8). For this reason, the value of gain $K_c$ must be properly adjusted to make ${\overline{\omega }}_{gc}\approx {\omega }_{pgc}$ or even ${\overline{\omega }}_{gc}<{\omega }_{pgc}$ if these frequencies are not too far from each other.

c.

To satisfy the previous requirements, $H_{12}\left(s\right)=K_c{H}_1\left(s\right)H_2\left(s\right)$ is chosen by composing $H_1\left(s\right)$ and $H_2\left(s\right)$, having phase plots in shifted frequency ranges. More precisely

$$H_1\left(s\right)={\left(\frac{1+\tau s}{1+\tau \Delta s}\right)}^{{\nu }_1}\mathrm{and}{H}_2\left(s\right)={\left(\frac{1+\tau \Delta s}{1+\tau {\Delta }^{2}s}\right)}^{{\nu }_2},$$

(17)

where ${\nu }_1>{\nu }_2$ and $\Delta$ is the scaling factor. The strategy is that $H_1\left(s\right)$ introduces the larger lead amount, while $H_2\left(s\right)$ improves the flatness. It holds $\Delta =0.1$.

d.

The compensated system must show an adequate phase margin (e.g., $PM\ge {55}^{\circ }$) with a phase decay rate beyond ${\overline{\omega }}_{gc}$ that is less than that of the corresponding plant. Finally, ${\overline{\omega }}_{gc}$ from $H_{OL}\left(j\omega \right)$ must be ${\overline{\omega }}_{gc}\approx {\omega }_{pgc}$, without excessively reducing the system bandwidth.

e.

Let ${\phi }_{OL}\left(\omega \right)=\angle H_{OL}\left(j\omega \right)$ and define the slope $sl\left(\omega \right)=\left|\frac{d{\phi }_{OL}\left(\omega \right)}{dlog\left(\omega \right)}\right|$. Afterwards, to improve the robustness to gain variations in a frequency range around ${\overline{\omega }}_{gc}$, the slope $sl\left({\overline{\omega }}_{gc}\right)$ must decrease as much as possible. Since the value of $sl\left({\overline{\omega }}_{gc}\right)$ estimates the robustness to gain variations, some approaches are proposed for evaluating this parameter [43]. In the present case, simple calculations give (see Appendix B)

$$\begin{array}{c}sl\left({\overline{\omega }}_{gc}\right)=\left|{\left.\frac{d{\phi }_p\left(\omega \right)}{d\omega }\right|}_{{\overline{\omega }}_{gc}}+\frac{{\nu }_1\tau }{1+{\left({\overline{\omega }}_{gc}\tau \right)}^2}-\frac{({\nu }_1-{\nu }_2)\tau \Delta }{1+{({\overline{\omega }}_{gc}\tau \Delta )}^2}-\frac{{\nu }_2\tau {\Delta }^2}{1+{\left({\overline{\omega }}_{gc}\tau {\Delta }^2\right)}^2}\right|{\overline{\omega }}_{gc}2.30.\hfill \end{array}$$

(18)

It can be verified that ${\nu }_1$, ${\nu }_2$, and $\tau$ make $sl\left({\overline{\omega }}_{gc}\right)<s{l}_p\left({\omega }_{pgc}\right)$, where $s{l}_p\left({\omega }_{pgc}\right)=\left|{\left.\frac{d{\phi }_p\left(\omega \right)}{d\omega }\right|}_{{\omega }_{pgc}}\right|$ provides the plant slope.

To sum up, the parameters of the compensator to be determined are $\tau$, ${\nu }_1$, ${\nu }_2$, and $K_c$, while ${\omega }_{pgc}$ and $\Delta$ are known from the start. The procedure to set the parameters is specified, as follows.

I.

By Equation (2), the time constant $\tau$ can be easily determined in terms of ${\omega }_{m1}$, the frequency where ${\phi }_{m1}$ occurs. However, due to the lead contribution of $H_2\left(s\right)$, the controller $H\left(s\right)$ reaches the maximum phase lead at frequency ${\omega }_{m12}>{\omega }_{m1}$. Hence, to put ${\omega }_{m12}\approx {\omega }_{pgc}$, ${\omega }_{m1}$ is chosen, so that ${\omega }_{m1}\approx h{\omega }_{pgc}$ with $0.5\le h\le 0.9$. The parameter h can be determined by few successive attempts. A first one can be $h=1$.

II.

To set ${\nu }_1$ and ${\nu }_2$, the phase margin specification $PM$ on $H_{OL}\left(s\right)$ is considered. Hence, since ${\overline{\omega }}_{gc}\approx {\omega }_{pgc}$ and ${\omega }_{pgc}\approx {\omega }_{m1}$, the following approximate relation can be used:

$$PM=P{M}_p+\angle H_1\left(j{\omega }_{m1}\right)+\angle H_2\left(j{\omega }_{m1}\right)=P{M}_p+{\nu }_1{55}^{\circ }+{\nu }_2{16}^{\circ }$$

(19)

where $\angle H_1\left(j{\omega }_{m1}\right)\approx {\nu }_1{55}^{\circ }$ by Equation (4) and $\angle H_2\left(j{\omega }_{m1}\right)\approx {\nu }_2{16}^{\circ }$ is computed by Equation (5). Note that, if the plant shows a phase lag rapidly increasing with the frequency, $P{M}_p$ can be negative. Moreover, it is suitable to choose ${\nu }_1>{\nu }_2$, otherwise large values for ${\nu }_2$ would increase the magnitude of $H_2\left(j\omega \right)$, that shifts the crossover of $H_{OL}\left(j\omega \right)$ too far beyond ${\omega }_{pgc}$. A rule of thumb, which is tested by numerical experiments, indicates ${\nu }_1\approx 3{\nu }_2$. Moreover, Equation (19) shows that values of ${\nu }_2\in (0.3,0.5)$ allow to compensate $P{M}_p<0$ in order to obtain $PM\ge {55}^{\circ }$ and achieve a right compromise between robustness and dynamic response.

III.

$K_c$ is set, so that $K_c\le \frac{1}{|H_{12}\left(j{\omega }_{pgc}\right)|}$. The gain crossover frequency ${\overline{\omega }}_{gc}$, indeed, can also assume values that are less than ${\omega }_{pgc}$. This choice is convenient if a greater phase margin is required and if $sl\left({\overline{\omega }}_{gc}\right)$ decreases. However, ${\overline{\omega }}_{gc}$ must be quite close (to the left) to ${\omega }_{pgc}$.

IV.

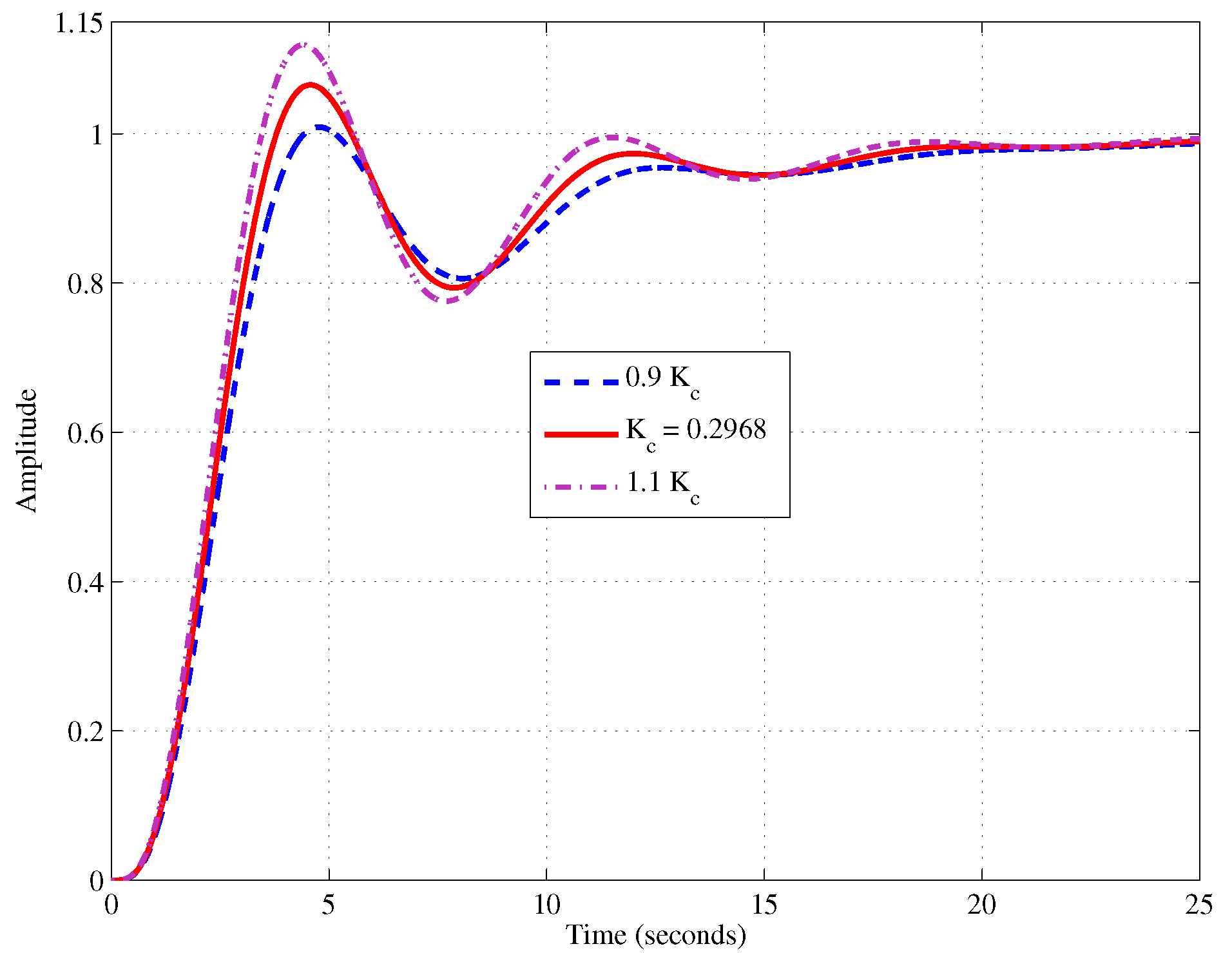
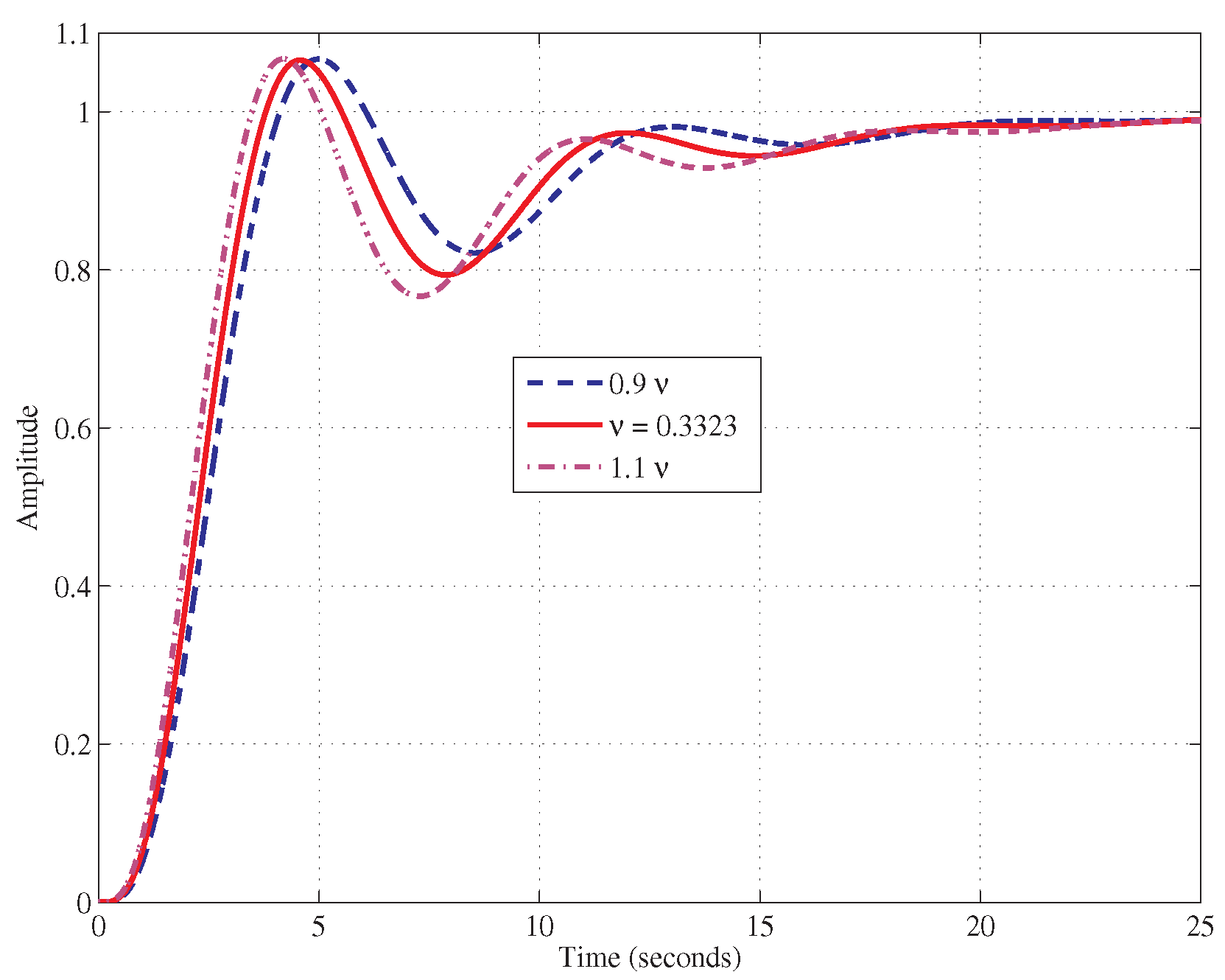
The performance is verified. If specifications are not met, then the procedure must be repeated by going back to step I. (or III.), decreasing ${\omega }_{m1}$ (or $K_c$), then changing $\tau$ and so on.

Note that the design pattern refers to the irrational TF $H\left(s\right)=K_c{H}_{12}\left(s\right)$. Usually, the step response characterizes the system performance in terms of rise time $\left(t_r\right)$, maximum overshoot $\left(o_m\right)$, and settling time $t_s$ (if necessary). To establish a total reliance on computer simulation, $H_{12}\left(s\right)$ is replaced by its rational approximation $G_{CH12}\left(s\right)$ according to the approach presented in Section 3, thus providing a rational approximation $G_{CH}\left(s\right)$ for $H\left(s\right)$.

Finally, for comparison purpose, one can design a cascade of two identical FLECs, namely ${\left[H_1\left(j\omega \right)\right]}^2$, where $H_1$ is specified by Equation (1). In this case, the maximum phase lead is $2{\phi }_{m1}$ at ${\omega }_{m1}$. By using the same values of ${\omega }_{pgc}$, $P{M}_p$, and $\Delta$, a procedure that is similar to that for the CS-FLEC can be followed. At step I, by putting ${\omega }_{m1}\approx h{\omega }_{pgc}$ with $0.5\le h\le 0.9$ (e.g., $h=1$) and using Equation (2), the time constant $\tau$ is determined in terms of ${\omega }_{m1}$ and $\Delta$. At step II, the relation $PM=P{M}_p+{\nu }_1{110}^{\circ }$ provides ${\nu }_1$. At step III, $K_c$ is set so that $K_c\le \frac{1}{|H_1^2\left(j{\omega }_{pgc}\right)|}$. At step IV, performance is verified.

5. Two Illustrative Benchmark Examples

The design approach is illustrated by two meaningful and demonstrative benchmarks taken from the literature.

5.1. First Example

Consider the plant model

$$G_{p1}\left(s\right)=\frac{1}{s{(1+s)}^3}$$

(20)

that is a benchmark proposed by [50]. In Figure 7, the Bode diagrams give ${\omega }_{pgc}=0.62\mathrm{rad}/\mathrm{s}$ with $\angle G_{p1}\left(j{\omega }_{pgc}\right)=-{185}^{\circ }$ then $P{M}_p=-5^{\circ }$ and $s{l}_p\left({\omega }_{pgc}\right)=3.09$.

The design method is applied with $\Delta =0.1$. The specifications are a phase margin $PM\ge {55}^{\circ }$ to ensure stability, despite plant gain and parameter variations. The overshoot in the unit step response of the closed-loop system should not be much higher than $20\%$.

One choice of the CS-FLEC parameter set comes from a first iteration of the design method and is as follows:

–

Step I: ${\omega }_{m1}={\omega }_{pgc}\Rightarrow \tau =5.13$ s

–

Step II: $PM={55}^{\circ }\Rightarrow {\nu }_2=0.33$ and ${\nu }_1=0.99$

–

Step III: $K_c=1/\left|H_{12}\left(j{\omega }_{pgc}\right)\right|=0.31$

–

Step IV: the obtained phase margin is $54.6^{\circ }$ in ${\overline{\omega }}_{gc}=0.62$ rad/s. The slope of the phase plot is $sl\left({\overline{\omega }}_{gc}\right)=2.90$. The step response shows a $9.40\%$ overshoot and settling time of $17.80$ s.

These results could be satisfactory, however a second iteration gives:

–

Step I: ${\omega }_{m1}={\omega }_{pgc}\Rightarrow \tau =5.13$ s

–

Step II: $PM={55}^{\circ }\Rightarrow {\nu }_2=0.33$ and ${\nu }_1=0.99$

–

Step III: $K_c=0.95/\left|H_{12}\left(j{\omega }_{pgc}\right)\right|=0.30$

–

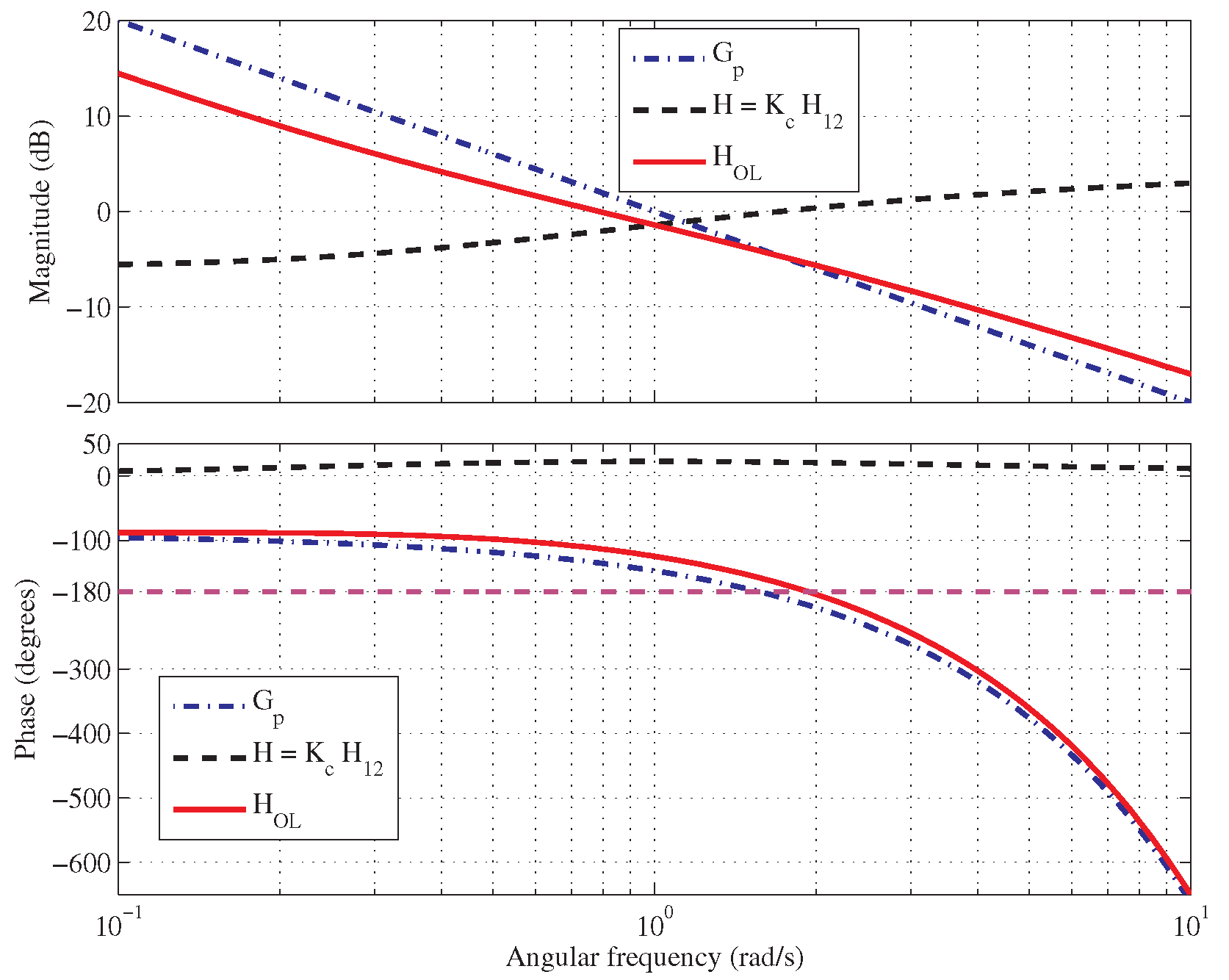
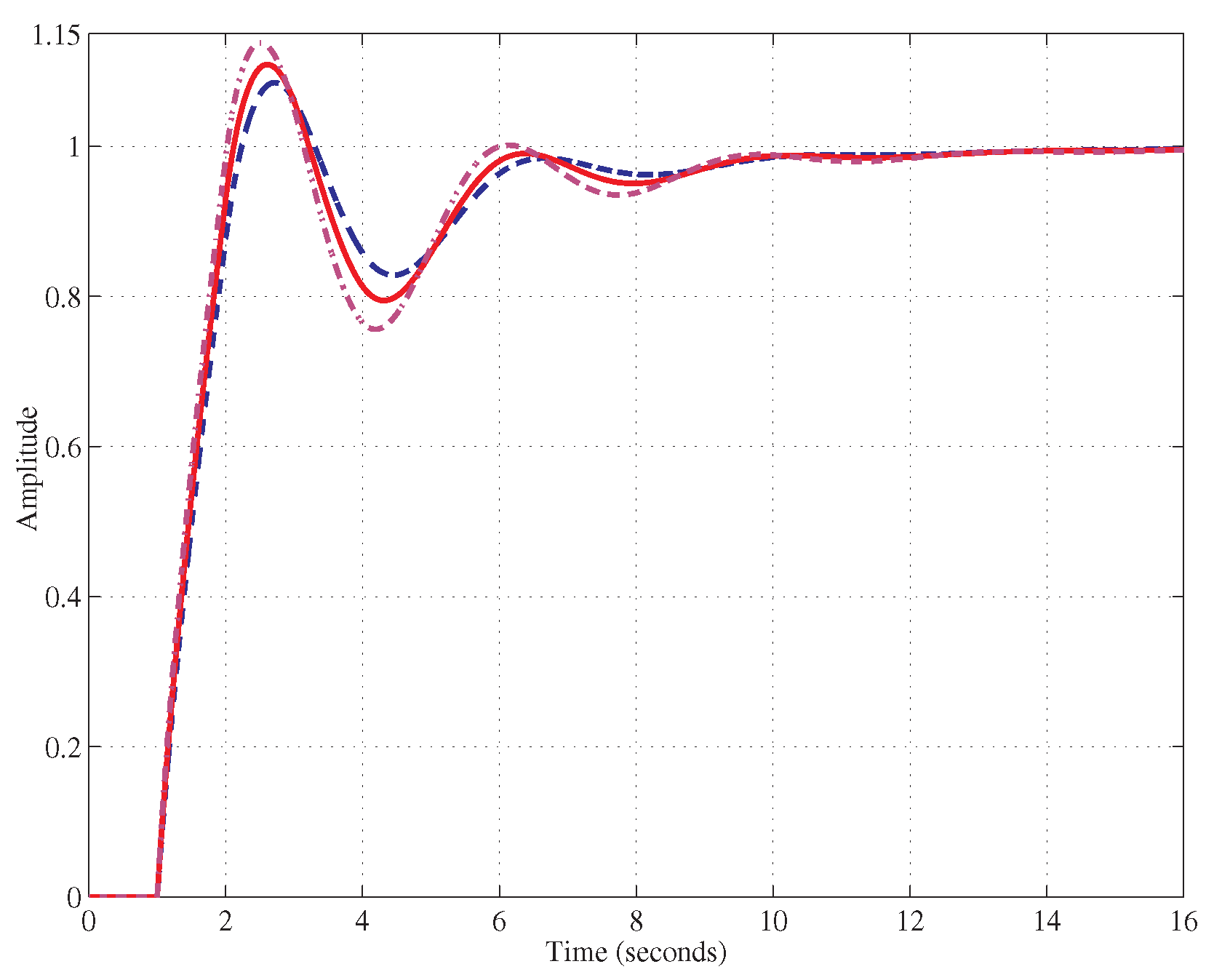
Step IV: the obtained phase margin is $58.9^{\circ }$ in ${\overline{\omega }}_{gc}=0.58$ rad/s. Moreover, $sl\left({\overline{\omega }}_{gc}\right)=2.75$, which is a good improvement. The step response shows a $6.55\%$ overshoot and settling time of $18.50$ s.

The controller $K_c{H}_1\left(s\right)H_2\left(s\right)$ is realized, as follows:

$$G_{CH}\left(s\right)=5.97\frac{(s+5.29)(s+2.21)(s+0.36)(s+0.20)}{(s+8.90)(s+2.67)(s+1.94)(s+0.35)}.$$

Table 1. Characteristics of the step response with parameter variations: $t_r$, $t_s$ (expressed in seconds), $o_m$ (in % values). Changing parameters: ${\overline{K}}_c$, ${\overline{\tau }}_p$, $\overline{\nu }$. Design values: ${\tau }_p=1$, $\nu =0.33$, $K_c=0.30$ (first example); $D=1$, $\nu =0.12$, $K_c=0.51$ (second example).

	${\overline{\mathit{K}}}_{\mathit{c}}$	${\overline{\mathit{\tau }}}_{\mathit{p}}$	$\overline{\mathit{\nu }}$	${\mathit{t}}_{\mathit{r}}$	${\mathit{o}}_{\mathit{m}}$	${\mathit{t}}_{\mathit{s}}$
First example	0.9 $K_c$	${\tau }_p$	$\nu$	2.46	0.90	21.47
	$K_c$	${\tau }_p$	$\nu$	2.19	6.55	18.50
	1.1 $K_c$	${\tau }_p$	$\nu$	2.00	11.90	17.34
	$K_c$	0.9 ${\tau }_p$	$\nu$	2.04	4.46	21.30
	$K_c$	1.1 ${\tau }_p$	$\nu$	2.34	8.64	19.29
	$K_c$	${\tau }_p$	0.9 $\nu$	2.38	6.68	19.01
	$K_c$	${\tau }_p$	1.1 $\nu$	2.01	6.70	21.90
Second example	0.9 $K_c$	–	$\nu$	1.03	2.16	10.30
	$K_c$	–	$\nu$	0.89	10.89	9.40
	1.1 $K_c$	–	$\nu$	0.78	19.71	9.03
	$K_c$	–	0.9 $\nu$	0.95	8.47	9.56
	$K_c$	–	1.1 $\nu$	0.82	13.76	11.47

reports the performance indexes when $K_c$ or the plant time constant ${\tau }_p$ or the fractional order $\nu ={\nu }_2$ change by a $\pm 10\%$ amount with respect to their nominal values $K_c=0.30$, ${\tau }_p=1$ s, and $\nu =0.33$. $\Delta$ and $\tau$ take the values assigned by the design. See Figure 9, Figure 10 and Figure 11 for the responses. Note that, here, the rise time $t_r$ is required for the response to rise from $0.1$ to $0.9$ of the steady-state value. The settling time $t_s$ is defined for a $\pm 5\%$ requirement. In all cases, $t_r$ is contained and $o_m$ stays below $12\%$ and it does not change in a significant way. The settling time has satisfactory values. All of the responses show undershoots that increase with $\nu$.

To validate an auto-tuning technique, the authors of [43] proposed simulation results referred to the process (20) controlled by a FPID tuned by an iso-damping approach. The specifications were the desired “tangent frequency” ${\omega }_c=0.4$ rad/s and the “tangent phase margin” at ${\omega }_c$, i.e., ${\mathsf{\Phi }}_m={45}^{\circ }$. Subsequently, the Bode plots in [43] showed a flat phase curve near ${\omega }_c$ (at the peak of the phase plot). Hence, the step responses remained nearly constant with respect to the gain variation, thus showing robustness. The overshoot was roughly $35\%$. The design approach proposed here gives ${\overline{\omega }}_{gc}=0.58$ rad/s with a phase margin of $58.9^{\circ }$. Moreover, limited changes of the step responses occur due to the gain (or other parametric) variations and the overshoots are below $12\%$ (see Figure 9, Figure 10 and Figure 11 and Table 1).

Finally, the control variable and the unit step disturbance rejection are illustrated in Figure 12 and Figure 13 for variations of $K_c$. The results obtained in case ${\tau }_p$ or $\nu$ change do not affect the performance in a substantially different way. Figure 12 shows that high initial values of the control variable are obtained. However, the amplitude of the manipulated variable is usually subject to limitations deliberately placed on actuators for accounting the limited power available to the control system and avoiding damages to the process [72].

The design of two identical FLECs gives the following results:

–

Step I: ${\omega }_{m1}={\omega }_{pgc}\Rightarrow \tau =5.13$ s

–

Step II: $PM={55}^{\circ }\Rightarrow {\nu }_1=0.55$

–

Step III: $K_c=0.95/\left|H_1^2\left(j{\omega }_{pgc}\right)\right|=0.51$

–

Step IV: the obtained phase margin is $56.9^{\circ }$ in ${\overline{\omega }}_{gc}=0.60$ rad/s.

The controller $K_c{H}_1^2\left(s\right)$ is realized, as follows:

$$G_{CH}\left(s\right)=10.585\frac{{(s+0.461)}^2{(s+0.2113)}^2}{{(s+1.1)}^2{(s+0.288)}^2}.$$

Figure 14 shows the frequency response. Although the specification on phase margin is met and the crossover is kept the same, the phase diagram is not as flat as with a CS-FLEC. Namely, the slope in the crossover is $sl\left({\overline{\omega }}_{gc}\right)=3.05$, which is only a bit lower than before compensation. Moreover, as shown by the same Figure 14, the step response shows a $53.05\%$ overshoot, sustained oscillations, a long settling time. Finally, variations with the gain are much more significant than with a CS-FLEC: with a 10% gain reduction, the overshoot is 44.7%, while with a 10% gain increase, the overshoot is 60.9%. All of these considerations explain why the CS-FLEC is preferable to a conventional cascade of identical FLECs.

5.2. Second Example

Whenever it does not compromise the clarity, the same symbols are used as the notations of the first case-study. Consider a plant that consists of an integrator with a time delay D:

$$G_{p2}\left(s\right)=\frac{e^{-Ds}}{s}$$

(21)

that is another common reference model. This case-study has also been considered by [49]. Moreover, time-delays are important in modeling many physical devices, such as large-scale flexible structures or electric networks [73]. For this reason, the results shown here were obtained by simulating (21) without approximating the dead-time element.

For instance, if $D=1$ s, Figure 8 shows the Bode diagrams of $G_{p2}$ with ${\omega }_{pgc}=1$ rad/s, $\angle G_{p2}\left(j{\omega }_{pgc}\right)=-{147}^{\circ }$ then $P{M}_p={33}^{\circ }$ and $s{l}_p\left({\omega }_{pgc}\right)=2.30$. After few iterations of the step-wise algorithm, the proposed design pattern, with $\Delta =0.1$ and with the specification $PM\ge {55}^{\circ }$, gives: ${\omega }_{m1}=0.8{\omega }_{pgc}\Rightarrow \tau =3.95$ s; ${\nu }_1=0.37$ and ${\nu }_2=0.12$; $K_c=0.85/\left|H_{12}\left(j{\omega }_{pgc}\right)\right|=0.51$; a phase margin of $66.8^{\circ }$ in ${\overline{\omega }}_{gc}=0.79$ rad/s. Moreover, $sl\left({\overline{\omega }}_{gc}\right)=1.75$. The controller is realized by

$$G_{CH}\left(s\right)=1.47\frac{(s+7.94)(s+3.02)(s+0.67)(s+0.28)}{(s+9.62)(s+3.24)(s+1.20)(s+0.35)}.$$

Figure 8 shows the frequency response of the compensated system and Figure 15 illustrates the step response, whose characteristics are presented in Table 1. The step response shows a $10.89\%$ overshoot and settling time of $9.40$ s with the designed parameters. However, $10\%$ variations of the gain $K_c$ induce $o_m\le 20\%$ and $t_s\le 11$ s. If $\nu$ changes, $o_m\le 14\%$ and $t_s\le 12$ s. Similar considerations to the first case hold for the control variable and the disturbance rejection.

Note that some rules can be established to guide the controller design.

(a)

The initial choice in the design procedure, ${\omega }_{m1}={\omega }_{pgc}$ and $K_c=1/\left|H_{12}\left(j{\omega }_{pgc}\right)\right|$, is sufficient for small delays $D\le 0.6$.

(b)

The positions ${\omega }_{m1}={\omega }_{pgc}$ and $K_c=0.85/\left|H_{12}\left(j{\omega }_{pgc}\right)\right|$ are applied to delays $0.7\le D\le 0.9$.

(c)

The design choice ${\omega }_{m1}=0.8{\omega }_{pgc}$ and $K_c=0.85/\left|H_{12}\left(j{\omega }_{pgc}\right)\right|$ can be used to satisfy the specifications and obtain good performance for delays $1\le D\le 1.2$ (see

Table 2. Characteristics of the step response for $1.1\le D\le 1.2$ with parameter variations: $t_r$, $t_s$ (expressed in seconds), $o_m$ (in % values). Changing parameters: ${\overline{K}}_c$, $\overline{\nu }$.

	${\overline{\mathit{K}}}_{\mathit{c}}$	$\overline{\mathit{\nu }}$	${\mathit{t}}_{\mathit{r}}$	${\mathit{o}}_{\mathit{m}}$	${\mathit{t}}_{\mathit{s}}$
	0.9 $K_c$	$\nu$	1.01	3.01	12.95
$D=1.1$	$K_c$	$\nu$	0.87	12.65	12.65
$\tau =3.95,\nu =0.16$	1.1 $K_c$	$\nu$	0.76	22.38	12.58
$K_c=0.45$	$K_c$	0.9 $\nu$	0.96	8.87	10.15
	$K_c$	1.1 $\nu$	0.78	17.24	12.50
	0.9 $K_c$	$\nu$	1.00	4.04	14.12
$D=1.2$	$K_c$	$\nu$	0.85	14.54	13.32
$\tau =3.95,\nu =0.19$	1.1 $K_c$	$\nu$	0.73	25.12	16.29
$K_c=0.40$	$K_c$	0.9 $\nu$	0.96	9.05	13.60
	$K_c$	1.1 $\nu$	0.74	21.23	16.06

).

(d)

The relations ${\omega }_{m1}=0.8{\omega }_{pgc}$ and $K_c=0.8/\left|H_{12}\left(j{\omega }_{pgc}\right)\right|$ are used for delays $1.3\le D\le 1.5$ that are more difficult to compensate.

Subsequently, these rules may help the control engineer and set the limits of application of the proposed controllers.

6. Conclusions

The introduced CS-FLEC are new types of two-stages fractional-order controllers, whose phase diagrams are nearly flat in large frequency intervals of the Bode plots. Each stage of the cascade can be implemented as a second-order TF, which approximates irrational FLEC elements with sufficient accuracy. Because it is composed by a series of independent stages, a CS-FLEC is approximated by cascade of rational low-order TFs with limited coefficients sensitivity to parameter variations. Different alternatives in choosing the number of stages and their free parameters make these new controllers flexible and suitable for also solving difficult control problems. The potentiality of the CS-FLEC has been tested for controlling two plants that often are assumed as benchmark to verify the design proposals. The introduced design method follows an intuitive, practical pattern based on the developed formulas. Namely, the main strategy consists in compensating the rapidly and monotonically increasing phase lag by the lead introduced by the CS-FLEC in the same frequency range. The two examples show that the CS-FLEC allows for a desired set-point response and the stability robustness to gain and parameter variations. Finally, the study of the second benchmark identifies the interval values of the dead-time D, where the CS-FLEC can be used to satisfy strict specifications.