Dynamic Analysis of the Viscoelastic Pipeline Conveying Fluid with an Improved Variable Fractional Order Model Based on Shifted Legendre Polynomials
Abstract
1. Introduction
2. Mathematical Model
2.1. Mathematical Preliminaries
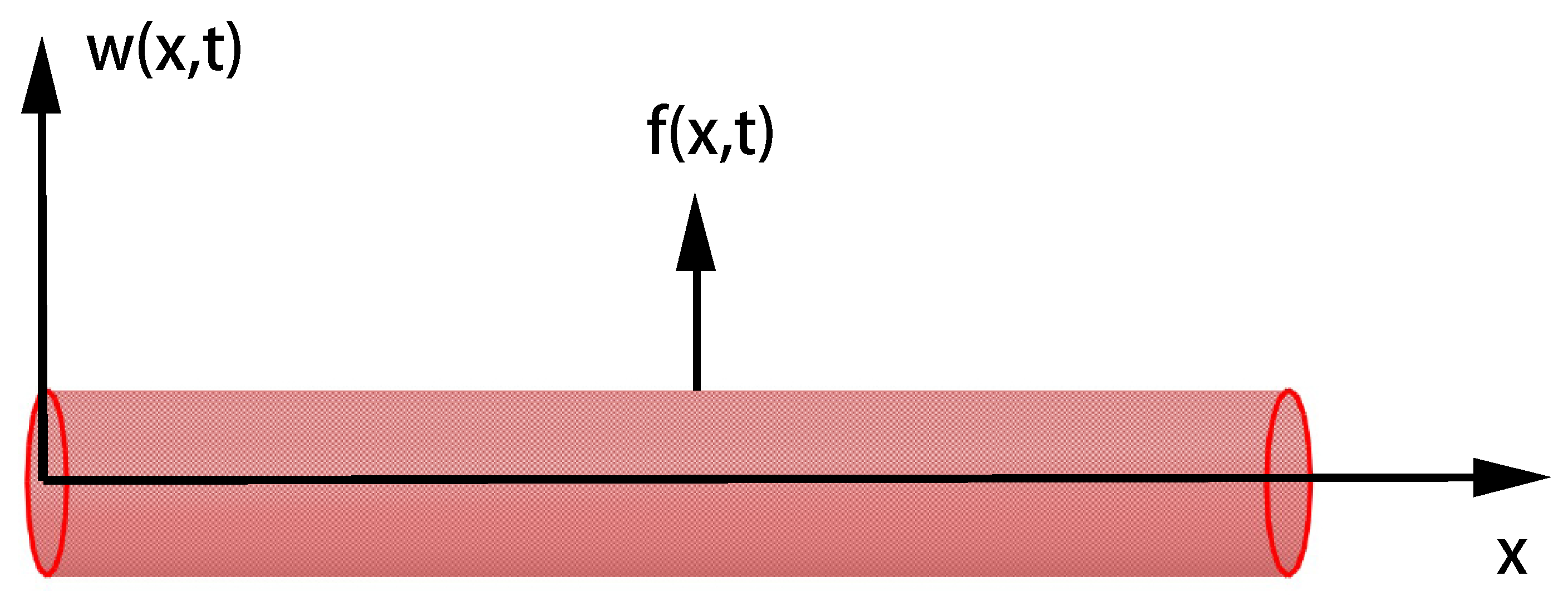
2.2. Motion Equation of Viscoelastic Pipeline Conveying Fluid
3. Numerical Study
3.1. Shifted Legendre Polynomials
3.2. Function Approximation
3.3. Differential Operator Matrix
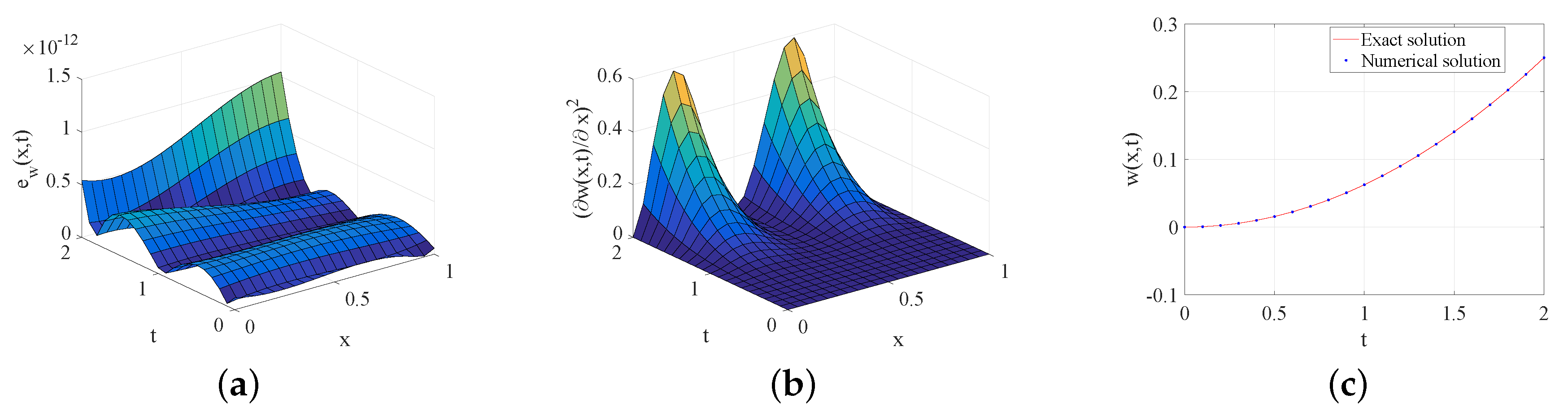
3.4. Numerical Example
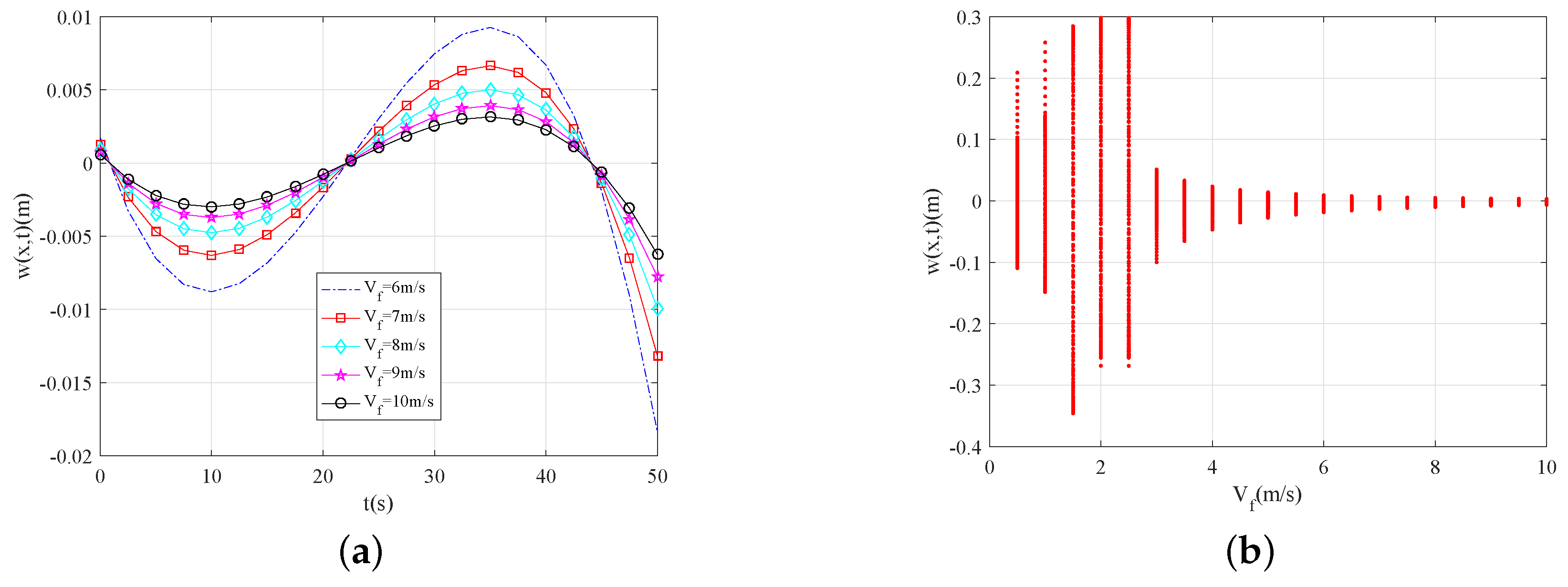
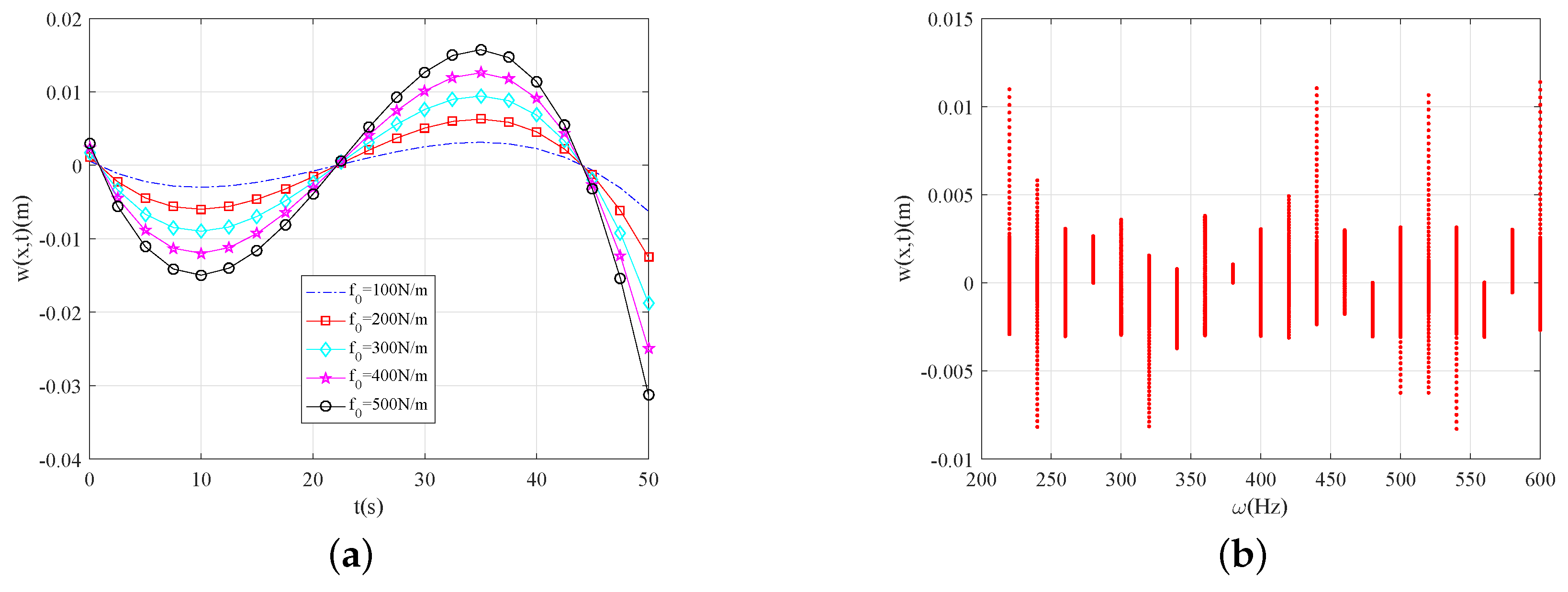
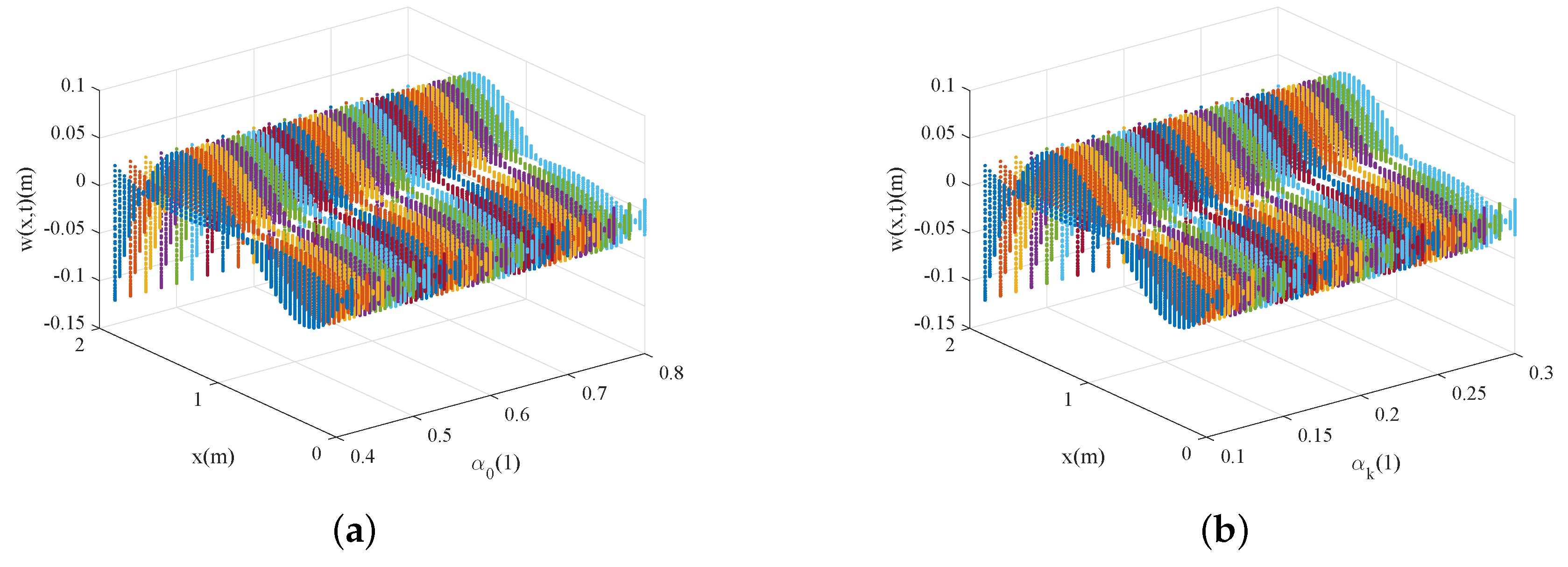
4. Numerical Results and Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Peng, G.; Xiong, Y.M.; Liu, L.M.; Gao, Y.; Wang, M.H.; Zhang, Z. 3D nonlinear dynamics of inclined pipe conveying fluid supported at both ends. J. Sound Vib. 2019, 449, 405–426. [Google Scholar] [CrossRef]
- Chang, G.H.; Sadeghi, Y.M. Flow-induced oscillations of a cantilevered pipe conveying fluid with base excitation. J. Sound Vib. 2014, 333, 4265–4280. [Google Scholar] [CrossRef]
- He, F.; Dai, H.L.; Huang, Z.H.; Wang, L. Nonlinear dynamics of a fluid-conveying pipe under the combinedaction of cross-flow and top-end excitations. Appl. Ocean Res. 2017, 62, 199–209. [Google Scholar] [CrossRef]
- Rahmati, M.; Mirdamadi, H.R.; Goli, S. Divergence instability of pipes conveying fluid with uncertain flow velocity. Physica A 2018, 491, 650–665. [Google Scholar] [CrossRef]
- Zhang, Y.F.; Yao, M.H.; Zhang, W.; Wen, B.C. Dynamical modeling and multi-pulse chaotic dynamics of cantilevered pipe conveying pulsating fluid in parametric resonance. Aerosp. Sci. Technol. 2017, 68, 441–453. [Google Scholar] [CrossRef]
- Zhang, Y.L.; Chen, L.Q. External and internal resonances of the pipe conveying fluid in the supercritical regime. J. Sound Vib. 2013, 332, 2318–2337. [Google Scholar] [CrossRef]
- Wang, L.; Liu, Z.Y.; Abdelkefi, A.; Wang, Y.K.; Dai, H.L. Nonlinear dynamics of cantilevered pipes conveying fluid: Towards a further understanding of the effect of loose constraints. Int. J. Non-Linear Mech. 2017, 95, 19–29. [Google Scholar] [CrossRef]
- Tang, Y.; Zhen, Y.X.; Fang, B. Nonlinear vibration analysis of a fractional dynamic model for the viscoelastic pipe conveying fluid. Appl. Math. Model. 2018, 56, 123–136. [Google Scholar] [CrossRef]
- Mitsotakis, D.; Dutykh, D.; Li, Q.; Peach, E. On some model equations for pulsatile flow in viscoelastic vessels. Wave Motion 2019, 90, 139–151. [Google Scholar] [CrossRef]
- Yano, D.; Ishikawa, S.; Tanaka, K.; Kijimoto, S. Vibration analysis of viscoelastic damping material attached to a cylindrical pipe by added mass and added damping. J. Sound Vib. 2019, 454, 14–31. [Google Scholar] [CrossRef]
- Husain, S.A.; Anderssen, R.S. Modelling the relaxation modulus of linear viscoelasticity using Kohlrausch functions. J. Non-Newton. Fluid Mech. 2005, 125, 159–170. [Google Scholar] [CrossRef]
- Yan, W.; Ying, J.; Chen, W.Q. The behavior of angle-ply laminated cylindrical shells with viscoelastic interfaces in cylindrical bending. Compos. Struct. 2007, 78, 551–559. [Google Scholar] [CrossRef]
- Machiraju, C.; Phan, A.V.; Pearsall, A.W.; Madanagopal, S. Viscoelastic studies of human subscapularis tendon: Relaxation test and a Wiechert model. Comput. Methods Programs Biomed. 2006, 83, 29–33. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Zhao, J.Z.; Li, Y.M. A wellbore creep model based on the fractional viscoelastic constitutive equation. Pet. Explor. Dev. 2017, 44, 1038–1044. [Google Scholar] [CrossRef]
- Long, J.M.; Xiao, R.; Chen, W. Fractional viscoelastic models with non-singular kernels. Mech. Mater. 2018, 127, 55–64. [Google Scholar] [CrossRef]
- Mokhtari, M.; Permoon, M.R.; Haddadpour, H. Aeroelastic analysis of sandwich cylinder with fractional viscoelastic core described by Zener model. J. Fluids Struct. 2019, 85, 1–16. [Google Scholar] [CrossRef]
- Yu, Y.; Perdikaris, P.; Karniadakis, G.E. Fractional modeling of viscoelasticity in 3D cerebral arteries and aneurysms. J. Comput. Phys. 2016, 323, 219–242. [Google Scholar] [CrossRef]
- Meng, R.F.; Yin, D.; Drapaca, C.S. A variable order fractional constitutive model of the viscoelastic behavior of polymers. Int. J. Non-Linear Mech. 2019, 113, 171–177. [Google Scholar] [CrossRef]
- Meng, R.F.; Yin, D.; Drapaca, C.S. Variable-order fractional description of compression deformation of amorphous glassy polymers. Comput. Mech. 2019, 64, 163–171. [Google Scholar] [CrossRef]
- Sene, N.; Fall, A.N. Homotopy perturbation ρ-Laplace transform method and its application to the fractional diffusion equation and the fractional diffusion–reaction equation. Fractal Fract. 2019, 3, 14. [Google Scholar] [CrossRef]
- Baleanu, D.; Jassim, H.K.; Qurashi, M.A. Solving Helmholtz equation with local fractional derivative operators. Fractal Fract. 2019, 3, 43. [Google Scholar] [CrossRef]
- Malmir, I. A new fractional integration operational matrix of Chebyshev wavelets in fractional delay systems. Fractal Fract. 2019, 3, 46. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, L.Q.; Li, B.F.; Sun, Y.N. Numerical solution for the variable order linear cable equation with Bernstein polynomials. Appl. Math. Comput. 2014, 238, 329–341. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, L.Q.; Li, X.; Sun, Y.N. Numerical solution for the variable order time fractional diffusion equation with Bernstein polynomials. Comput. Model. Eng. Sci. 2014, 97, 81–100. [Google Scholar]
- Chen, Y.M.; Wei, Y.Q.; Liu, D.Y.; Yu, H. Numerical solution for a class of nonlinear variable order fractional differential equations with Legendre wavelets. Appl. Math. Lett. 2015, 46, 83–88. [Google Scholar] [CrossRef]
- Chen, Y.M.; Liu, L.Q.; Liu, D.Y.; Boutat, D. Numerical study of a class of variable order nonlinear fractional differential equation in terms of Bernstein polynomials. Ain Shams Eng. J. 2018, 9, 1235–1241. [Google Scholar] [CrossRef]

| Physical Quantity | Symbol | Value | Dimension |
|---|---|---|---|
| External radius | D | ||
| Internal radius | d | ||
| Length | H | 2 | |
| Area moment of inertia | I | ||
| Constitutive model parameter | E | 600 | |
| Constitutive model parameter | 1 | ||
| Density of viscoelastic pipeline | |||
| Density of internal fluid | |||
| Mass per unit length of viscoelastic pipeline | |||
| Mass per unit length of internal fluid | |||
| Tensional force | 500 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Chen, Y. Dynamic Analysis of the Viscoelastic Pipeline Conveying Fluid with an Improved Variable Fractional Order Model Based on Shifted Legendre Polynomials. Fractal Fract. 2019, 3, 52. https://doi.org/10.3390/fractalfract3040052
Wang Y, Chen Y. Dynamic Analysis of the Viscoelastic Pipeline Conveying Fluid with an Improved Variable Fractional Order Model Based on Shifted Legendre Polynomials. Fractal and Fractional. 2019; 3(4):52. https://doi.org/10.3390/fractalfract3040052
Chicago/Turabian StyleWang, Yuanhui, and Yiming Chen. 2019. "Dynamic Analysis of the Viscoelastic Pipeline Conveying Fluid with an Improved Variable Fractional Order Model Based on Shifted Legendre Polynomials" Fractal and Fractional 3, no. 4: 52. https://doi.org/10.3390/fractalfract3040052
APA StyleWang, Y., & Chen, Y. (2019). Dynamic Analysis of the Viscoelastic Pipeline Conveying Fluid with an Improved Variable Fractional Order Model Based on Shifted Legendre Polynomials. Fractal and Fractional, 3(4), 52. https://doi.org/10.3390/fractalfract3040052




