The Unexpected Fractal Signatures in Fibonacci Chains
Abstract
:1. Introduction
2. The Fractal Signature of the Fibonacci Chain in Fourier Space
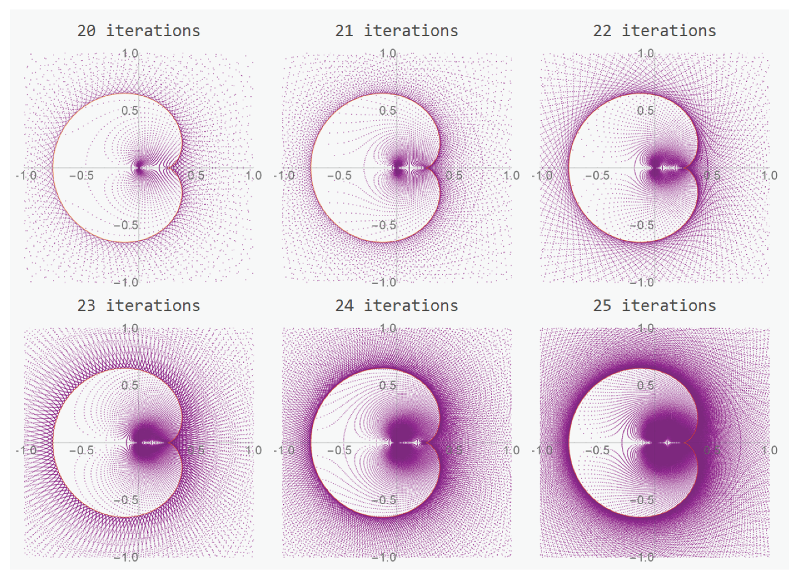
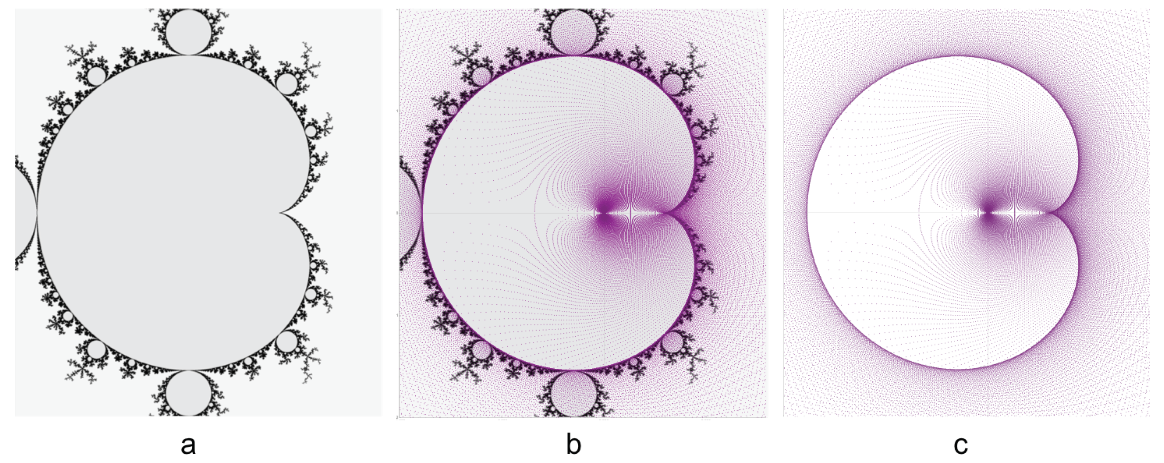
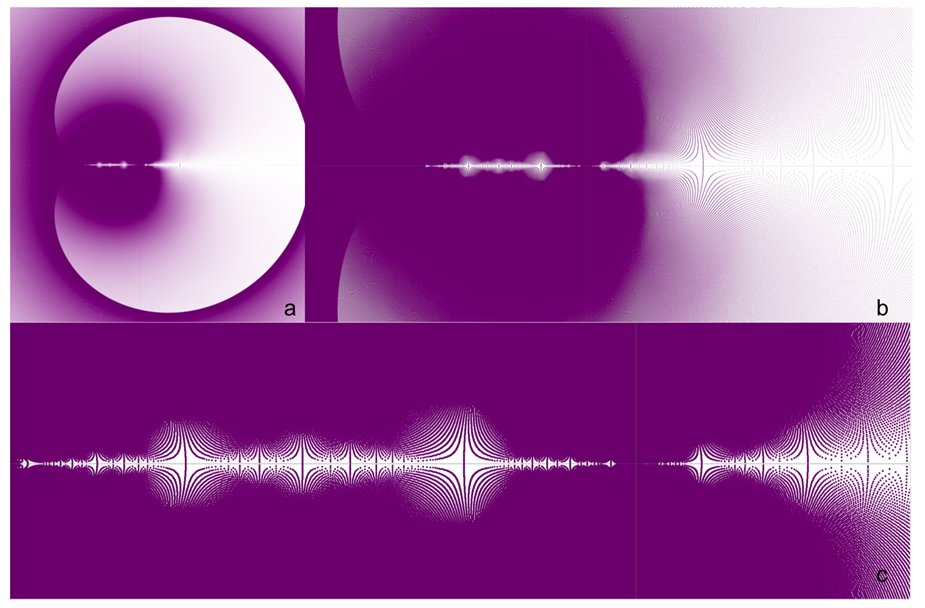
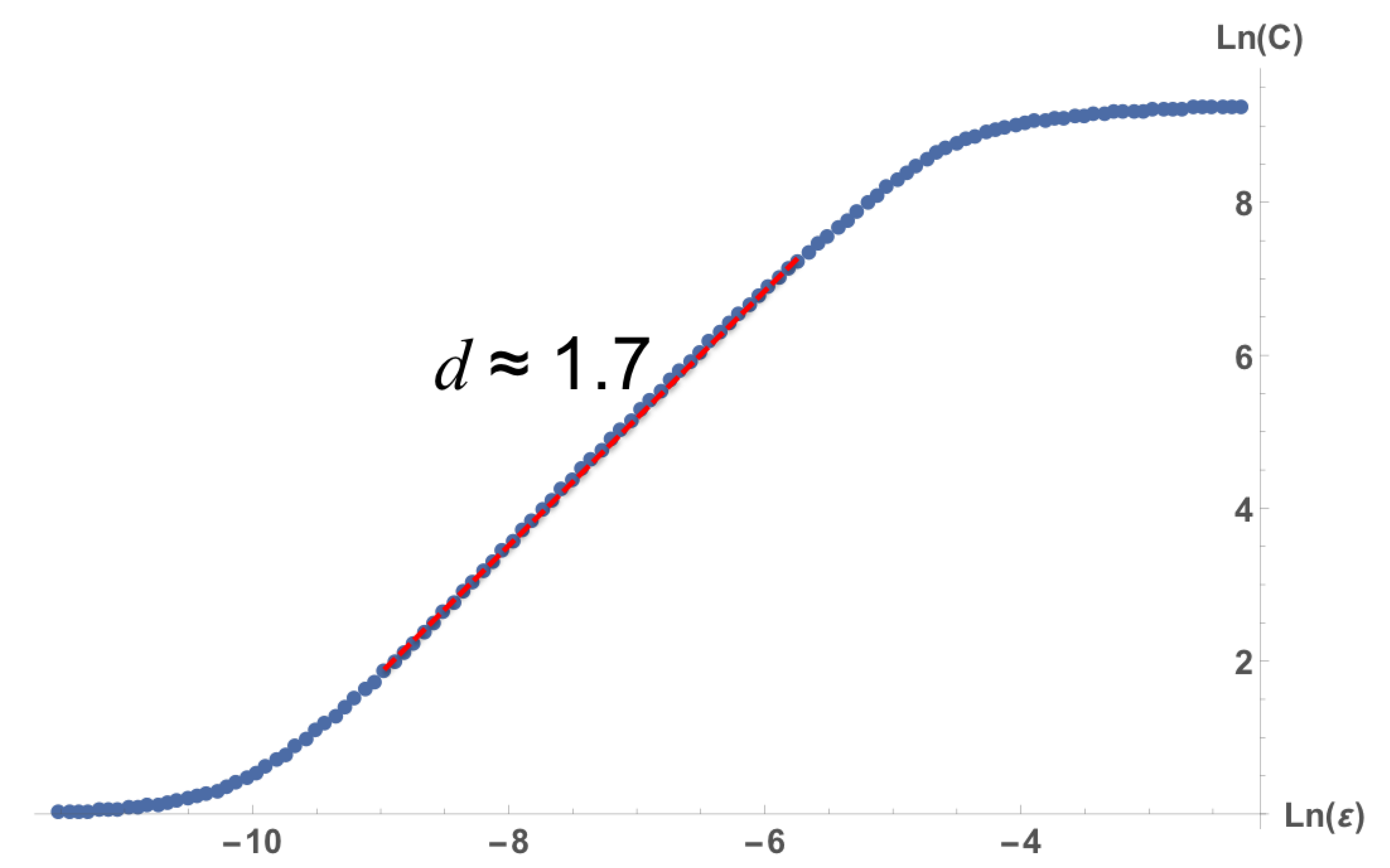
2.1. Fractal Dimension
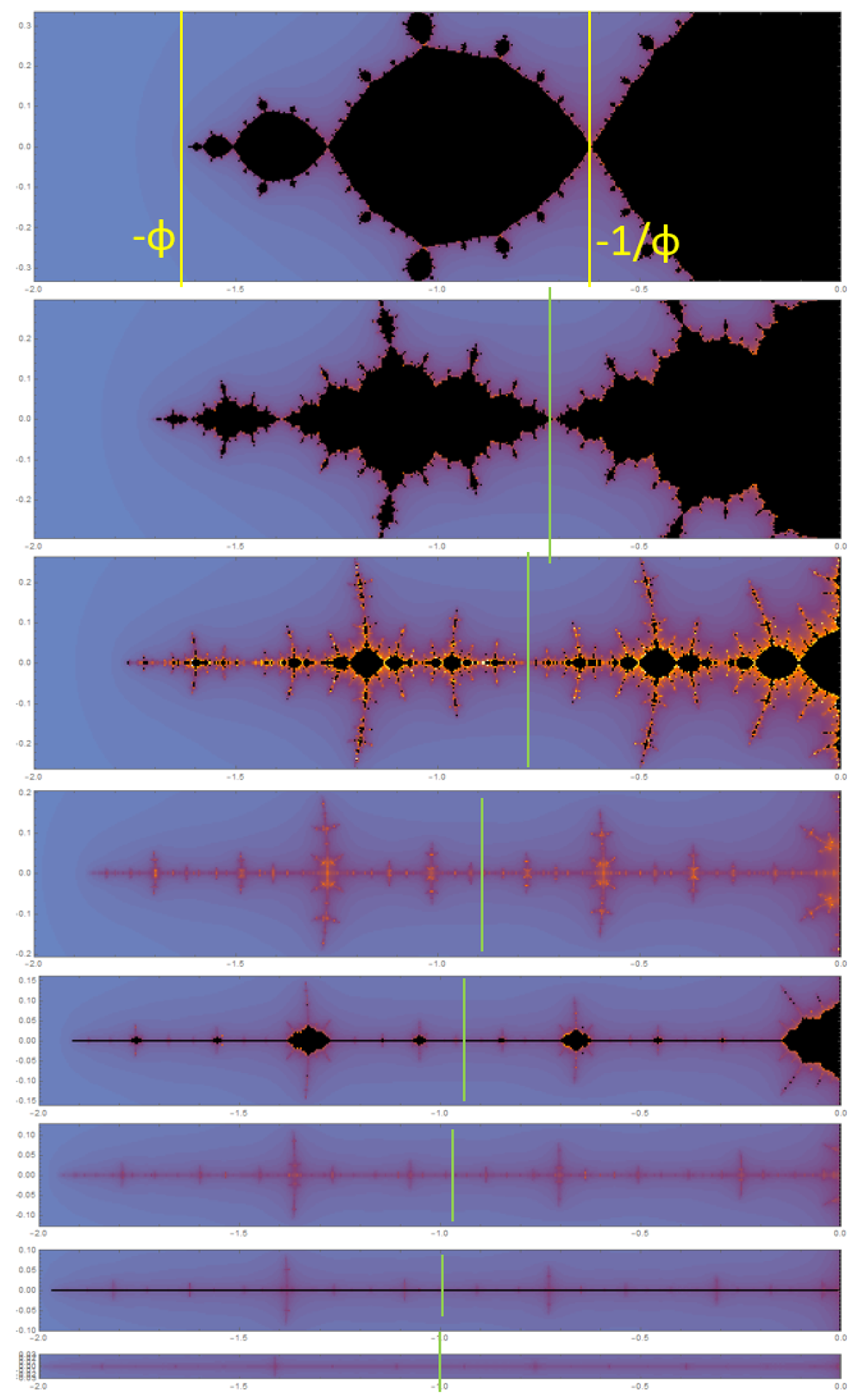
2.2. Universality Near the Real Line
2.3. Self Similarity
3. The Variations of the Fibonacci Chain in Fourier Space
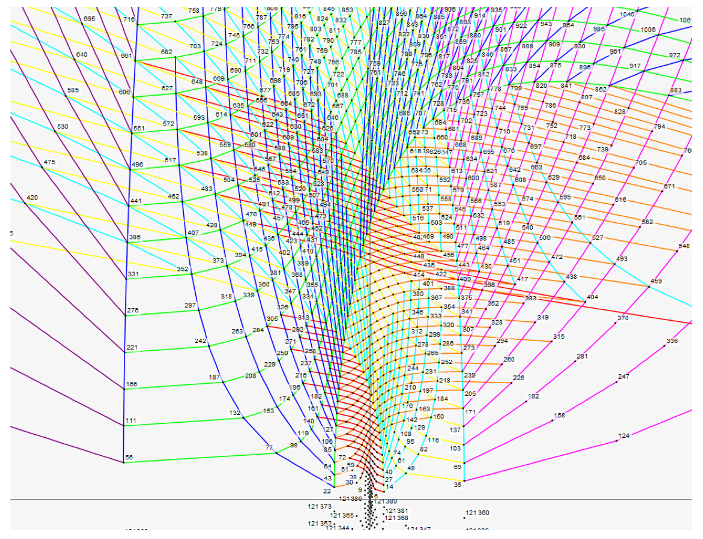
3.1. Variations by Cyclic Permutations
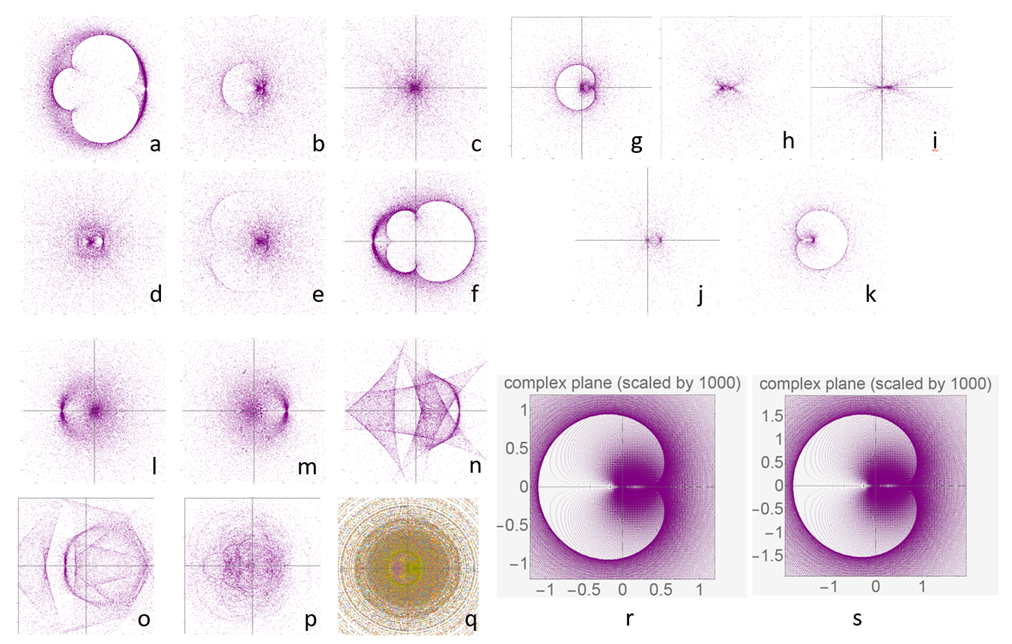
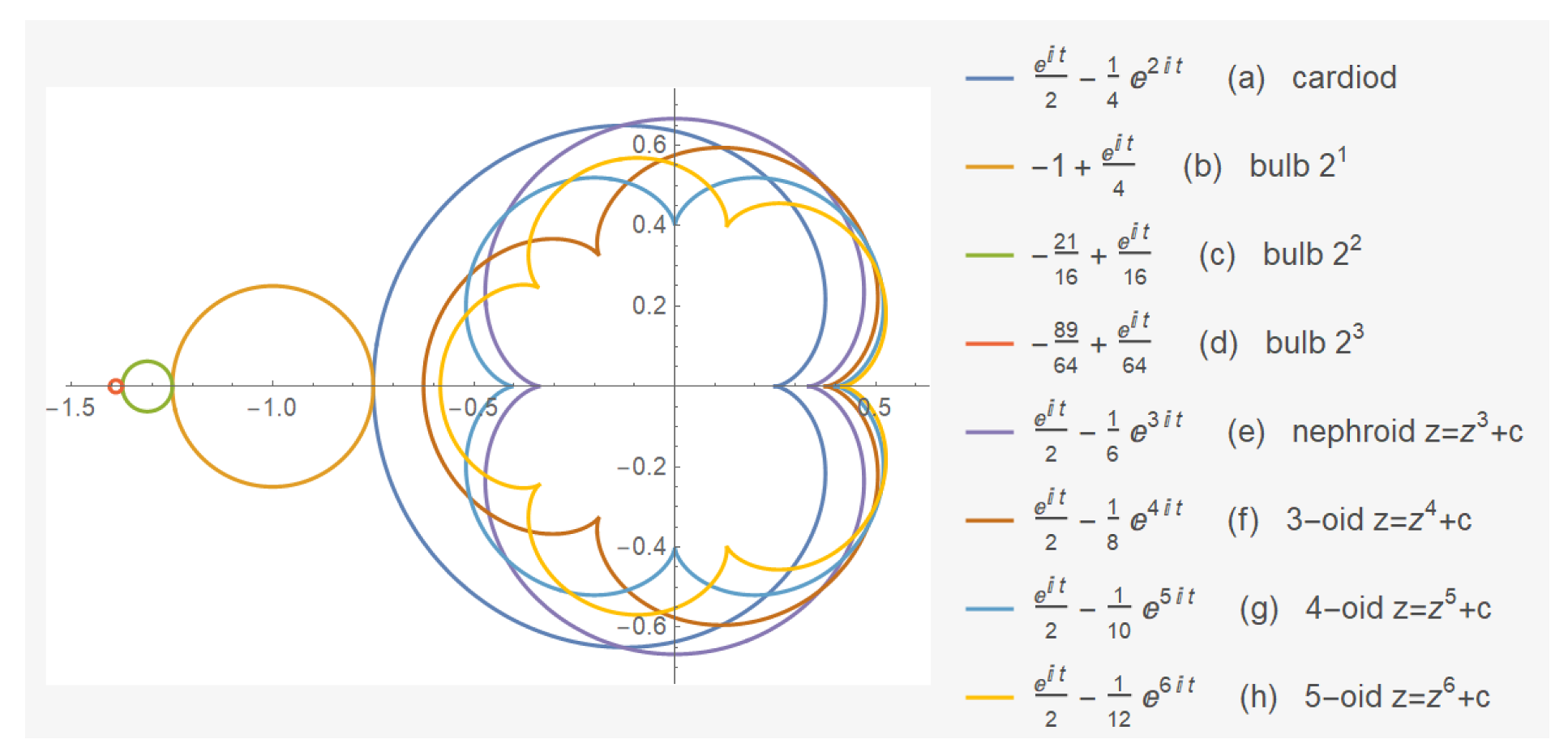
3.2. Variations and the Generalized Mandelbrot Set
4. Summary
Author Contributions
Funding
Conflicts of Interest
References
- Shechtman, D.; Blech, I.; Gratias, D.; Cahn, J.W. Metallic phase with long-range orientational order and no translational symmetry. Phys. Rev. Lett. 1984, 53, 1951. [Google Scholar] [CrossRef]
- Strichartz, R.S. Differential Equations on Fractals; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Grimm, U.; Schreiber, M. Energy spectra and eigenstates of quasiperiodic tight-binding hamiltonians. arXiv 2002, arXiv:cond-mat/0212140. [Google Scholar]
- Repetowicz, P.; Grimm, U.; Schreiber, M. Exact eigenstates of tight-binding hamiltonians on the penrose tiling. arXiv 1998, arXiv:cond-mat/9805321. [Google Scholar] [CrossRef]
- Macé, N.; Jagannathan, A.; Piéchon, F. Fractal dimensions of the wavefunctions and local spectral measures on the fibonacci chain. arXiv 2016, arXiv:1601.00532. [Google Scholar]
- Luck, J.M.; Godreche, C.; Janner, A.; Janssen, T. The nature of the atomic surfaces of quasiperiodic self-similar structures. J. Phys. A 1993, 26, 1951. [Google Scholar] [CrossRef]
- Baake, M.; Grimm, U. Aperiodic Order. In Encyclopedia of Mathematics and its Applications; Vol. 1: A Mathematical Invitation; Cambraidge University Press: Cambraidge, UK, 2013. [Google Scholar]
- Ramachandrarao, P.; Sina, A.; Sanyal, D. On the fractal nature of Penrose tiling. Curr. Sci. 2000, 79, 364–367. [Google Scholar]
- Yudin, V.; Karygina, Y. Fractal images of quasicrystals as an example of Penrose lattice. Crystallogr. Rep. 2001, 46, 922–926. [Google Scholar] [CrossRef]
- Fang, F.; Irwin, K. An icosahedral quasicrystal as a golden modification of the icosagrid and its connection to the e8 lattice. arXiv 2015, arXiv:1511.07786. [Google Scholar] [CrossRef]
- Levine, D.; Steinhardt, P.J. Quasicrystals. I. definition and structure. Phys. Rev. B 1986, 34, 596. [Google Scholar] [CrossRef] [PubMed]
- Douady, A.; Hubbard, J.H.; Lavaurs, P. Etude Dynamique des Polynômes Complexes; Université de Paris-Sud, Dép. de Mathématique: Orsay, France, 1984. [Google Scholar]
- Devaney, R.L. The Fractal Geometry of the Mandelbrot Set. II. How to Count and How to Add. Available online: http://math.bu.edu/DYSYS/FRACGEOM2/FRACGEOM2.html (accessed on 1 August 2019).
- Strogatz, S.H. Nonlinear Dynamics and Chaos with Applications to Physics, Biology, Chemistry, and Engineering; Perseus Books: New York, NY, USA, 1994. [Google Scholar]
- Bazley, T.S. Index to Geometric Chuck; Waterlow and Sons: London, UK, 1875. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, F.; Aschheim, R.; Irwin, K. The Unexpected Fractal Signatures in Fibonacci Chains. Fractal Fract. 2019, 3, 49. https://doi.org/10.3390/fractalfract3040049
Fang F, Aschheim R, Irwin K. The Unexpected Fractal Signatures in Fibonacci Chains. Fractal and Fractional. 2019; 3(4):49. https://doi.org/10.3390/fractalfract3040049
Chicago/Turabian StyleFang, Fang, Raymond Aschheim, and Klee Irwin. 2019. "The Unexpected Fractal Signatures in Fibonacci Chains" Fractal and Fractional 3, no. 4: 49. https://doi.org/10.3390/fractalfract3040049
APA StyleFang, F., Aschheim, R., & Irwin, K. (2019). The Unexpected Fractal Signatures in Fibonacci Chains. Fractal and Fractional, 3(4), 49. https://doi.org/10.3390/fractalfract3040049




