Tempered Fractional Equations for Quantum Transport in Mesoscopic One-Dimensional Systems with Fractal Disorder

Abstract

New aspects of electron transport in quantum wires with Lévy-type disorder are described. We study the weak scattering and the incoherent sequential tunneling in one-dimensional quantum systems characterized by a tempered Lévy stable distribution of spacing between scatterers or tunneling barriers. The generalized Dorokhov–Mello–Pereyra–Kumar equation contains the tempered fractional derivative on wire length. The solution describes the evolution from the anomalous conductance distribution to the Dorokhov function for a long wire. For sequential tunneling, average values and relative fluctuations of conductance and resistance are calculated for different parameters of spatial distributions. A tempered Lévy stable distribution of spacing between barriers leads to a transition in conductance scaling.

1. Introduction

Several experiments and numerical simulations have shown that disorder in mesoscopic systems can be of a fractal (self-similar) type [1,2,3,4,5,6]. In [3], fractal disorder is observed in optical material, in which light waves perform a random walk characterized by path length distributions of power law type $p\left(s\right)\propto s^{-1-\alpha }$ if $s\to \infty$, where $0<\alpha <2$. This random walk is known as Lévy flights, and the system has been called “Lévy glass”. Studies [4,5] report on the scaling behavior of diameter modulations in SiC quantum wires grown via a self-organization process. The probability distribution function of displacements of diameter fluctuation has been shown to have heavy tails of the Lévy type [4].

There is a series of theoretical studies devoted to electron and wave transport in quantum wires with Lévy-type disorder [7,8,9,10,11,12,13]. Beenakker et al. [7] calculated moments of conductance for the incoherent sequential tunneling through disordered fractal wire. They showed that the average transmission is proportional to $L^{-\alpha }lnL$ ($0<\alpha <1$). Falceto and Gopar [8] studied weak scattering in quantum wires with Lévy-type disorder and modified the solution of the Dorokhov–Mello–Pereyra–Kumar (DMPK) equation by changing the number of scatterers according to the corresponding fractal distribution. They have shown that the conductance distribution for fractal wire is also universal in the sense that it is fully determined by the Lévy index $\alpha$ and the average quantity 〈ln G〉. Fernández-Marín et al. [10] derived the statistics of electromagnetic transmission through a one-dimensional (1D) photonic heterostructure whose random layer thicknesses follow a long-tailed Lévy-type distribution. Amanatidis et al. [11] investigated the conductance through a 1D disordered system where the envelope of electron wavefunction decays spatially according to the stretched exponential law.

Here, using tempered fractional calculus and tempered fractional stable statistics, we consider two regimes of quantum transport (weak scattering and incoherent sequential tunneling) in one-dimensional mesoscopic systems (quantum wires) characterized by the tempered Lévy stable distribution of spacing between scatterers. These wires are homogeneous at a large scale and fractal at an intermediate scale.

2. Tempered Fractional Stable Distributions

For the description of the problem under consideration, the “tempered” generalization of the fractional stable statistics is introduced below for a particular case. Fractional stable distributions (FSDs) appeared in [14] as limit laws for the continous-time random walk (CTRW) [15]. The class of FSDs was studied in work [16]. FSDs can be expressed in terms of the Lévy stable densities [16], and we use this representation to introduce the one-sided tempered FSD. The tempered stable distributions were introduced in [17] (see also [18]). Koponen [17] considered smoothly (exponentially) truncated Lévy flights [19] and provided a convenient analytic representation of limit distributions for a walker coordinate. The process shows a slow convergence to a Gaussian one. In [20,21], using inverse tempered stable laws, authors provided probabilistic interpretation of transition from the dispersive transport regime to the normal diffusion-drift in disordered semiconductors.

The simplest (one-dimensional decoupled) version of the CTRW model [15] assumes that different jump lengths $R_j$, as well as waiting times $T_j$ between two successive jumps, are random variables independent of each other and among themselves. To model super- or sub-diffusion, it is usually supposed that distributions of jump lengths and waiting times have the following asymptotic behavior:

$$\mathrm{P}\{R>r\}\propto r^{-\alpha },\alpha >0,r\to \infty ;\mathrm{P}\{T>t\}\propto t^{-\beta },\beta >0,t\to \infty .$$

The case $\alpha >2$ and $\beta >1$ corresponds to normal diffusion at the diffusion limit ($t\to \infty$, $\left|x\right|\to \infty$). All other values of $\alpha$ and $\beta$ lead to anomalous diffusion with characteristic exponents $\alpha ,\beta$.

The main asymptotic term of the probability density function $p(x,t)$ obeys the fractional diffusion equation (see, e.g., [22,23]):

$${}_0{\mathsf{D}}_t^{\beta }p(x,t)=C{\mathsf{L}}^{(\alpha ,\theta )}p(x,t)+\frac{t^{-\beta }}{\mathsf{\Gamma }(1-\beta )}\delta \left(x\right),0<\alpha \le 2,0<\beta \le 1.$$

(1)

Here,

$${}_0{\mathsf{D}}_t^{\beta }p(x,t)=\frac{1}{\mathsf{\Gamma }(1-\beta )}\frac{\partial }{\partial t}\underset{0}{\overset{t}{\int }}\frac{p(x,\tau )d\tau }{{(t-\tau )}^{\beta }}$$

is the Riemann–Liouville fractional derivative and ${\mathsf{L}}^{(\alpha ,\theta )}$ is the Feller fractional differential operator. In case of symmetrical walking, $\theta =0$ and $\mathsf{L}(\alpha ,0)={({\partial }^2/\partial x^2)}^{\alpha /2}\equiv {|\partial /\partial x|}^{\alpha }$ (see for details [24]).

This partial differential equation of fractional orders has the self-similar fundamental solution

$$p(x,t)={\left(C{t}^{\beta }\right)}^{-1/\alpha }q\left(x{\left(C{t}^{\beta }\right)}^{-1/\alpha };\alpha ,\beta ,\theta \right),$$

where the function

$$q(x;\alpha ,\beta ,\theta )={\int }_0^{\infty }{g}^{(\alpha ,\theta )}\left(x{\tau }^{\beta /\alpha }\right)g^{(\beta ,1)}\left(\tau \right){\tau }^{\beta /\alpha }d\tau$$

(2)

is expressed through the Lévy stable densities $g^{(\alpha ,\theta )}\left(x\right)$. Densities (2) belong to the class of fractional stable densities [16]. The Lévy stable densities are defined by their characteristic functions,

$${\tilde{g}}^{(\alpha ,\theta )}\left(k\right)=\underset{-\infty }{\overset{\infty }{\int }}{e}^{-ikx}{g}^{(\alpha ,\theta )}\left(x\right)dx=exp\left\{-{\left|k\right|}^{\alpha }exp[-i(\pi /2)\theta \alpha \mathrm{sign}k]\right\}.$$

Here, $\theta \in [-{\theta }_{\alpha },{\theta }_{\alpha }]$ is a skewness parameter, where ${\theta }_{\alpha }=\min \{1,2/\alpha -1\}$. The width of the anomalous diffusion packet $\Delta \left(t\right)\propto t^{\beta /\alpha }$. When $\beta /\alpha <1/2$, a subdiffusive regime takes place, when $\beta /\alpha >1/2$ superdiffusion is observed. Applications of fractional stable laws to problems of anomalous kinetics in solids can be found in book [25].

The important case for this study is the one-sided solutions for $\alpha \in (0,1]$ and $\beta \in (0,1]$. Instead of function (2), we will use the function of two variables

$$q^{(\alpha ,\beta )}(x,t)=t^{-\beta /\alpha }{\int }_0^{\infty }{g}_{+}^{\left(\alpha \right)}\left(x{(\tau /t)}^{\beta /\alpha }\right)g_{+}^{\left(\beta \right)}\left(\tau \right){\tau }^{\beta /\alpha }d\tau ,$$

(3)

which is convenient for further generalization.

This pdf satisfies the following fractional diffusion equation containing Riemann–Liouville derivatives:

$${}_0{\mathsf{D}}_t^{\beta }[q^{(\alpha ,\beta )}(x,t)-\delta \left(x\right)]={}_0{\mathsf{D}}_x^{\alpha }{q}^{(\alpha ,\beta )}(x,t),0<\alpha \le 1,0<\beta \le 1.$$

(4)

Function (3) can be written with the use of the inverse stable subordinator,

$$q^{(\alpha ,\beta )}(x,t)={\int }_0^{\infty }{\tau }^{-1/\alpha }{g}_{+}^{\left(\alpha \right)}\left(x{\tau }^{-1/\alpha }\right)h^{\left(\beta \right)}(\tau ,t)d\tau ,$$

(5)

where function

$$h^{\left(\beta \right)}(\tau ,t)={\beta }^{-1}t{\tau }^{-1-1/\beta }{g}^{(\beta ,1)}\left(t{\tau }^{-1/\beta }\right)$$

is the inverse one-sided stable density with the following Laplace transform:

$${\tilde{h}}^{\left(\beta \right)}(\tau ,s)=s^{\beta -1}{e}^{-\tau s^{\beta }}.$$

Using the representation (5), it is easy to introduce the tempered generalization of FSD using the tempered Lévy stable subordinator [26]:

$$g^{(\alpha ,\mu )}(x,\tau )=e^{-\mu x}{\tau }^{-1/\alpha }{g}_{+}^{\left(\alpha \right)}(x{\tau }^{-1/\alpha })e^{\tau {\mu }^{\alpha }},$$

with the Laplace transform

$${\tilde{g}}^{(\alpha ,\mu )}(u,\tau )=e^{-\tau \left[{(u+\mu )}^{\alpha }-{\mu }^{\alpha }\right]}.$$

(6)

Let us define tempered fractional stable density as follows:

$$q_{\mu ,\nu }^{(\alpha ,\beta )}\left(x,t\right)={\int }_0^{\infty }{e}^{-\mu x}{\tau }^{-1/\alpha }{g}_{+}^{\left(\alpha \right)}(x{\tau }^{-1/\alpha })e^{\tau {\mu }^{\beta }}{h}^{(\beta ,\nu )}(\tau ,t)d\tau ,$$

(7)

where the inverse tempered stable subordinator [27,28,29] is used. It can be defined via its Laplace transform [27,28]:

$${\tilde{h}}^{(\beta ,\nu )}(\tau ,s)=\frac{{(s+\nu )}^{\beta }-{\nu }^{\beta }}{s}{e}^{-\tau \left[{(s+\nu )}^{\beta }-{\nu }^{\beta }\right]}.$$

(8)

From expressions (6)–(8), the double Laplace transform of the one-sided tempered fractional stable density can be derived:

$${\tilde{q}}_{\mu ,\nu }^{(\alpha ,\beta )}\left(u,s\right)=\frac{{(s+\nu )}^{\beta }-{\nu }^{\beta }}{s\left[{(u+\mu )}^{\alpha }-{\mu }^{\alpha }+{(s+\nu )}^{\beta }-{\nu }^{\beta }\right]}.$$

(9)

The tempered fractional stable density satisfies the following equation:

$${}_0{\mathsf{D}}_t^{\beta ,\nu }\left[q_{\mu ,\nu }^{(\alpha ,\beta )}\left(x,t\right)-\delta \left(x\right)\right]=C{}_0{\mathsf{D}}_x^{\alpha ,\mu }{q}_{\mu ,\nu }^{(\alpha ,\beta )}\left(x,t\right),0<\alpha \le 1,0<\beta \le 1,$$

(10)

with the tempered fractional derivative [26]

$${}_0{\mathsf{D}}_t^{\beta ,\nu }p(x,t)=e^{-\nu t}{}_0{\mathsf{D}}_t^{\beta }{e}^{\nu t}p(x,t)-{\nu }^{\beta }p(x,t).$$

Tempered fractional stable laws describe the distribution of a walker for CTRW with smoothly truncated power law distributions of jump lengths and waiting times [27,30]:

$$\mathrm{P}\{R>r\}\propto r^{-\alpha }{e}^{-\mu r},\mathrm{P}\{T>t\}\propto t^{-\beta }{e}^{-\nu t}.$$

3. Weak Scattering in Mesoscopic Fractal Wires

Disorder plays an important role in mesoscopic systems. Quantum interference effects and randomly distributed impurities lead to localization phenomena and fluctuations in the conductance for different samples. One of the approaches to describe coherent quantum transport and localization in disordered wires is the transfer matrix theory (see review [31]). In this approach, the transport is considered as a quantum scattering problem, and the conductance is related to the transmission matrix t by the Landauer formula. In [32,33], an equation known as the DMPK equation was derived for the joint probability distribution of the transmission eigenvalues. Considering strongly disordered systems, Muttalib and Klauder [34] proposed the generalized DMPK equation to describe the electron transport. These equations of the Fokker–Planck type have been derived on the assumption of a Poissonian ensemble of scatterers. Here, we consider the tempered fractional Poisson distribution of scatterers along wire and generalize the transport equation.

The standard DMPK-equation for the evolution of the eigenvalue distribution function $P\left(\right\{\lambda \},L)$ in the ensemble of long ($L\gg l$) wires with increasing length L has the following form:

$$l\frac{\partial P}{\partial L}={\mathsf{\Lambda }}_{\mathrm{DMPK}}P,$$

where,

$${\mathsf{\Lambda }}_{\mathrm{DMPK}}P=\frac{2}{bN+2-b}\sum _{j=1}^N\frac{\partial }{\partial {\lambda }_j}\left[{\lambda }_j(1+{\lambda }_j)J\left(\lambda \right)\frac{\partial }{\partial {\lambda }_j}\frac{P}{J\left(\lambda \right)}\right]$$

is the DMPK operator, ${\lambda }_j$ are eigenvalues of quantum-mechanical transfer matrix t, N is the number of transverse modes in the wire, and $P\left(\right\{\lambda \},L)$ is the N-dimensional probability distribution function of random vector $({\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_N)$. The integer parameter b equals 1 in a zero magnetic field and 2 in a time-reversal-symmetry-breaking magnetic field. In the case of zero field and strong spin–orbit scattering, $b=4$. The Jacobian $J={\prod }_{i<j}{|{\lambda }_j-{\lambda }_i|}^b$ corresponds to the transformation from the transfer matrix space to the eigenvalue space. The DMPK equation can be derived by computing the change in the scattering matrix S when the length of the wire is increased from L to $L+\delta L$, under the condition that the mean free path l exceeds the wavelength $\lambda$. Another essential assumption is the isotropy assumption of the statistical equivalence of scattering from one channel to another. It is correct when the length of the wire is much greater than the width, and time for transverse diffusion can be neglected.

For wire with a tempered Lévy-type disorder, according to the limit theorem, the length of the wire corresponding to the large number $m\gg 1$ of scatterers is distributed according to the tempered Lévy stable law (see, e.g., [26]). In the limit of weak scattering ($m^{1/\alpha }l\to \infty$), we have

$$\underset{m^{1/\alpha }l\to \infty }{lim}\underset{0}{\overset{L}{\int }}\left[P(\left\{\lambda \right\},L)-P(\left\{\lambda \right\},\xi )\right]\frac{1}{l{m}^{1/\alpha }}{g}^{(\alpha ,\gamma )}\left(\frac{L-\xi }{l{m}^{1/\alpha }}\right)d\xi =\frac{m}{N}{\langle \mathrm{tr}{\lambda }^{\prime }\rangle }_1{\mathsf{\Lambda }}_{\mathrm{DMPK}}P(\left\{\lambda \right\},L).$$

Here, $g^{(\alpha ,\gamma )}\left(x\right)$ is the one-sided tempered Lévy stable density with exponent $0<\alpha <1$ coinciding with the fractal dimension of distributed scatterers in the wire. The Laplace transform of the tempered stable density is

$${\tilde{g}}^{(\alpha ,\gamma )}\left(s\right)=exp[{\gamma }^{\alpha }-{(s+\gamma )}^{\alpha }].$$

The scale ${\gamma }^{-1}$ is the parameter defining homogenization of the spatial distribution of scatterers.

Taking into account the initial condition $P\left(\right\{\lambda \},L\to 0)=\delta \left(\lambda \right)$ and introducing notation $K={\langle \mathrm{tr}{\lambda }^{\prime }\rangle }_1/N$, we arrive at the generalized DMPK equation for quantum wire with quasi-fractal disorder,

$$l^{\alpha }{\mathrm{D}}_L^{\alpha ,\gamma }\left[P\left(\right\{\lambda \},L)-\delta \left(\lambda \right)\right]=K{\mathsf{\Lambda }}_{\mathrm{DMPK}}P(\left\{\lambda \right\},L),$$

(11)

where

$${}_0{\mathsf{D}}_L^{\alpha ,\gamma }P(\left\{\lambda \right\},L)=e^{-\gamma L}{}_0{\mathsf{D}}_L^{\alpha }{e}^{\gamma L}P(\left\{\lambda \right\},L)-{\gamma }^{\alpha }P(\left\{\lambda \right\},L)$$

is the tempered fractional derivative [26]. The Laplace transformation on length leads to the equation

$$\left[{(s+\gamma )}^{\alpha }-{\gamma }^{\alpha }\right]\left[P(\left\{\lambda \right\},s)-\frac{\delta \left(\lambda \right)}{s}\right]=l^{-\alpha }K{\mathsf{\Lambda }}_{\mathrm{DMPK}}\tilde{P}(\left\{\lambda \right\},L).$$

Interpreting the process described by Equation (11) as a subordinated process, one can represent the solution as the following integral

$$P(\left\{\lambda \right\},L)=\underset{0}{\overset{\infty }{\int }}{P}_1\left(\left\{\lambda \right\},\frac{\xi }{l^{\alpha }}\right)h(\xi ,L)d\xi ,$$

(12)

where $h(\xi ,L)$ is the inverse density to the tempered stable pdf (tempered subordinator) [27] with the following Laplace transform (see Equation (8)): $\tilde{h}(\xi ,s)=s^{-1}{\left[\right(s+\gamma )}^{\alpha }-{\gamma }^{\alpha }]e^{-\xi \left[{(s+\gamma )}^{\alpha }-{\gamma }^{\alpha }\right]}.$ Function $P_1(\left\{\lambda \right\},\xi )$ represents the solution of the standard DMPK equation, where $\xi$ is associated with the dimensionless length $L/l$. It can be found, e.g., in [35]. For $L\gg {\gamma }^{-1}$, the standard DMPK approach can be used. 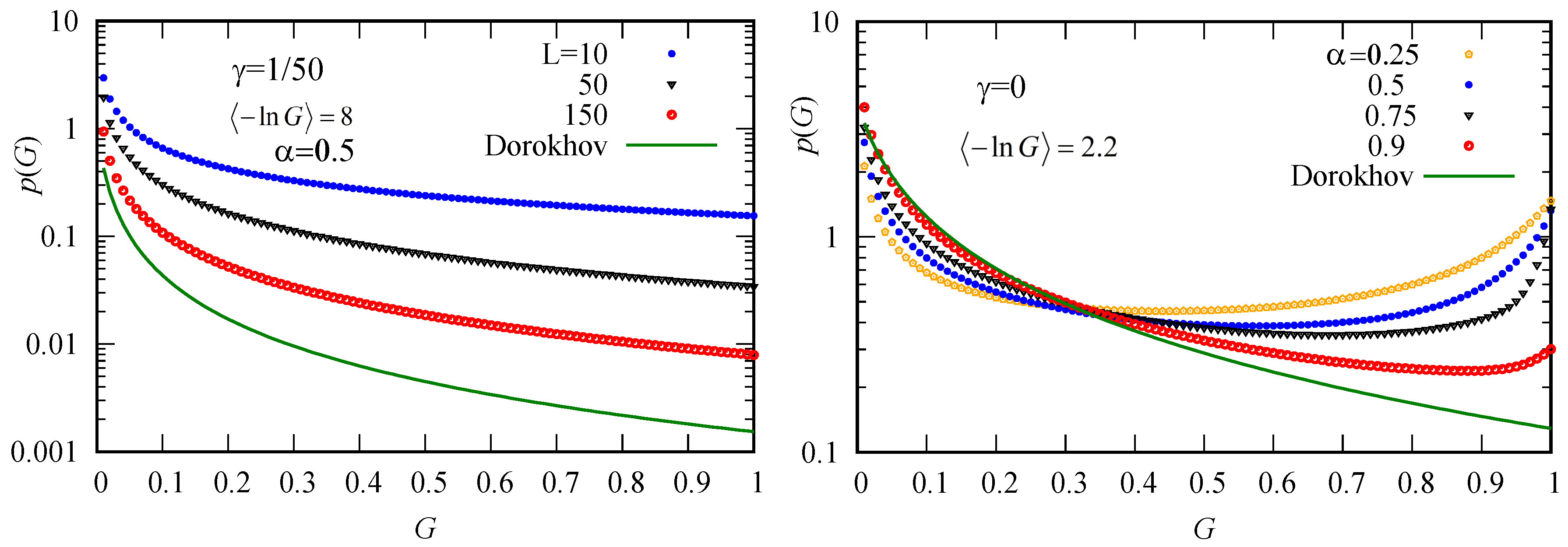Solution (12) describes evolution from the anomalous conductance distribution to the Dorokhov function for a long wire (Figure 1).

In regular quantum wires, $\langle -lnG\rangle$ scales linearly with length $\xi$. For quasi-fractal wires from (12), we obtain

$$\widetilde{〈-lnG〉}=\underset{0}{\overset{\infty }{\int }}\xi \tilde{g}(\xi ,s)d\xi =\frac{l^{-\alpha }}{s\left[{(s+\gamma )}^{\alpha }-{\gamma }^{\alpha }\right]}.$$

Inverting this Laplace transform, we arrive at the following expression:

$$〈-lnG〉=l^{-\alpha }\underset{0}{\overset{L}{\int }}d\lambda {\lambda }^{\alpha -1}{E}_{\alpha ,\alpha }\left({\gamma }^{\alpha }{\lambda }^{\alpha }\right)exp(-\gamma \lambda ).$$

Here, $E_{\alpha ,\alpha }\left(x\right)$ is the two-parameter Mittag–Leffler function [36]. The scaling of $〈-lnG〉$ for intermediate lengths is of the form

$$〈-lnG〉\approx \frac{1}{\mathsf{\Gamma }(1+\alpha )}\frac{L^{\alpha }}{l^{\alpha }},l\ll L\ll {\gamma }^{-1}.$$

(13)

For very long wires, we observe the normal scaling

$$〈-lnG〉\approx \frac{{\left(\gamma l\right)}^{1-\alpha }}{\alpha }\frac{L}{l},l\ll {\gamma }^{-1}\ll L.$$

(14)

Plots of $\langle -lnG\rangle$ vs. $L/l$ for different values of $\alpha$ and $\gamma$ are shown in Figure 2. They demonstrate crossover from power law ($\propto L^{\alpha }$) to linear behavior ($\propto L$). As follows from (13) and (14), this crossover should be observed near value $L_{\mathrm{cr}}={\gamma }^{-1}{[\alpha /\mathsf{\Gamma }(1+\alpha )]}^{1/(1-\alpha )}$.

For the intermediate length (fractality domain), when $l\ll L\ll {\gamma }^{-1}$, the tempered subordinator can be replaced by the stable one, and relation (12) for conductance distribution takes the form

$$p_{\alpha }(G,L)\sim \frac{L}{l\alpha }\underset{0}{\overset{\infty }{\int }}{p}_1(G,\tau )g_{+}\left(\frac{L}{l}{\tau }^{-1/\alpha };\alpha \right){\tau }^{-1-1/\alpha }d\tau ,l\ll L\ll {\gamma }^{-1}.$$

(15)

The latter formula coincides with the expression obtained in [8]. They use the standard DMPK equation, modifying the solution by changing the number of scatterers according to the fractal distribution. Change of the integration variable leads to the Monte Carlo algorithm for the calculation of $p_{\alpha }(G,L)$:

$$p_{\alpha }(G,L)=\underset{0}{\overset{\infty }{\int }}{p}_1\left(G,{(L/ly)}^{\alpha }\right)g_{+}\left(y;\alpha \right)dy=〈p_1\left(G,\frac{L^{\alpha }}{l^{\alpha }{S}_{\alpha }^{\alpha }}\right)〉,$$

(16)

where $S_{\alpha }$ is the stable random variable.

For a regular distribution of scatterers, the relative fluctuations of their number in the wire decay to zero when $L\to \infty$. Parameter $s=L/l$ represents the number of scatterers in the long wire, and it is the unique parameter of the universal conductance distribution. In the fractal case, the relative fluctuations tend to a non-zero value, and the behavior depends on $\alpha$. Falceto and Gopar [8] use $\xi =\langle -lnG\rangle$ as the second (scale) parameter. It is related to l by expression (13). So ${(L/l)}^{\alpha }$ in Formula (16) can be replaced by $\langle -lnG\rangle \mathsf{\Gamma }(1+\alpha )$. For $\alpha <1$, the conductance distributions have meaningful values in all regions $(0,1)$ and can have two peaks [8].

4. Incoherent Sequential Tunneling Through Wire with Lévy-Type Disorder

Beenakker et al. [7] considered the one-dimensional chain of tunnel barriers where distances between neighboring barriers are distributed according to an asymptotical power law. Considered barriers were characterized by identical transmission probabilities $\mathsf{\Gamma }\ll 1$ and resistance $\rho =h/e^{2}N\mathsf{\Gamma }$, where N is the number of transverse modes. The authors [7] considered the case $N\mathsf{\Gamma }\ll 1$, which means that $\rho \ll h/e^2$, so that the Coulomb blockade of single-electron tunneling can be neglected. Beenakker et al. [7] considered the asymptotical (L → ∞) behavior of negative moments of resistance $\langle R{\left(L\right)}^{-k}\rangle$, where $k=1,2,3,\dots$, which correspond to positive moments of the conductance $G=1/R$. Here, we generalize this model using tempered stable distribution of distances between barriers, and similar distribution for barrier resistances.

Let us consider a wire of length L. The wire resistance is the sum of resistances of individual barriers. The number of tunneling barriers is random and determined by the distribution of distance between neighboring barriers and the wire length. In addition, the individual resistances themselves may be random. The total resistance can be considered as a coordinate of a CTRW process where length L plays the role of time. All resistances are positive, and the process is one-sided. Let us assume the tempered power law distribution of distances between tunneling barriers with parameters $\alpha$ and $\mu$. In addition, we imply the similar distribution of resistances with parameters $\beta$ and $\nu$. According to Section 2, the distribution of wire resistance can be presented in the form of the tempered fractional stable density. Furthermore, we put $l=1$, ${\rho }_{\beta }=1$:

$$w_R(r;L,\beta ,\alpha )\sim q_{\nu ,\mu }^{(\beta ,\alpha )}\left(r,L\right),L\gg l.$$

(17)

The corresponding Laplace transform on r and L has the form (see Equation (9) in Section 2)

$${\tilde{w}}_R(u;s,\beta ,\alpha )\sim {\tilde{q}}_{\nu ,\mu }^{(\beta ,\alpha )}\left(u,s\right)=\frac{{(s+\mu )}^{\alpha }-{\mu }^{\alpha }}{s\left[{(u+\nu )}^{\beta }-{\nu }^{\beta }+{(s+\mu )}^{\alpha }-{\mu }^{\alpha }\right]}.$$

Finding first and second derivatives of this function on u at point $u=0$, we find two first moments of the random resistance,

$$\widetilde{\langle R\rangle }\left(s\right)=\frac{\beta {\nu }^{\beta -1}}{s\left[{(s+\mu )}^{\alpha }-{\mu }^{\alpha }\right]},\widetilde{\langle R^2\rangle }\left(s\right)=\frac{\beta (1-\beta ){\nu }^{\beta -2}}{s\left[{(s+\mu )}^{\alpha }-{\mu }^{\alpha }\right]}+\frac{2{\beta }^2{\nu }^{2\beta -2}}{s{\left[{(s+\mu )}^{\alpha }-{\mu }^{\alpha }\right]}^2}.$$

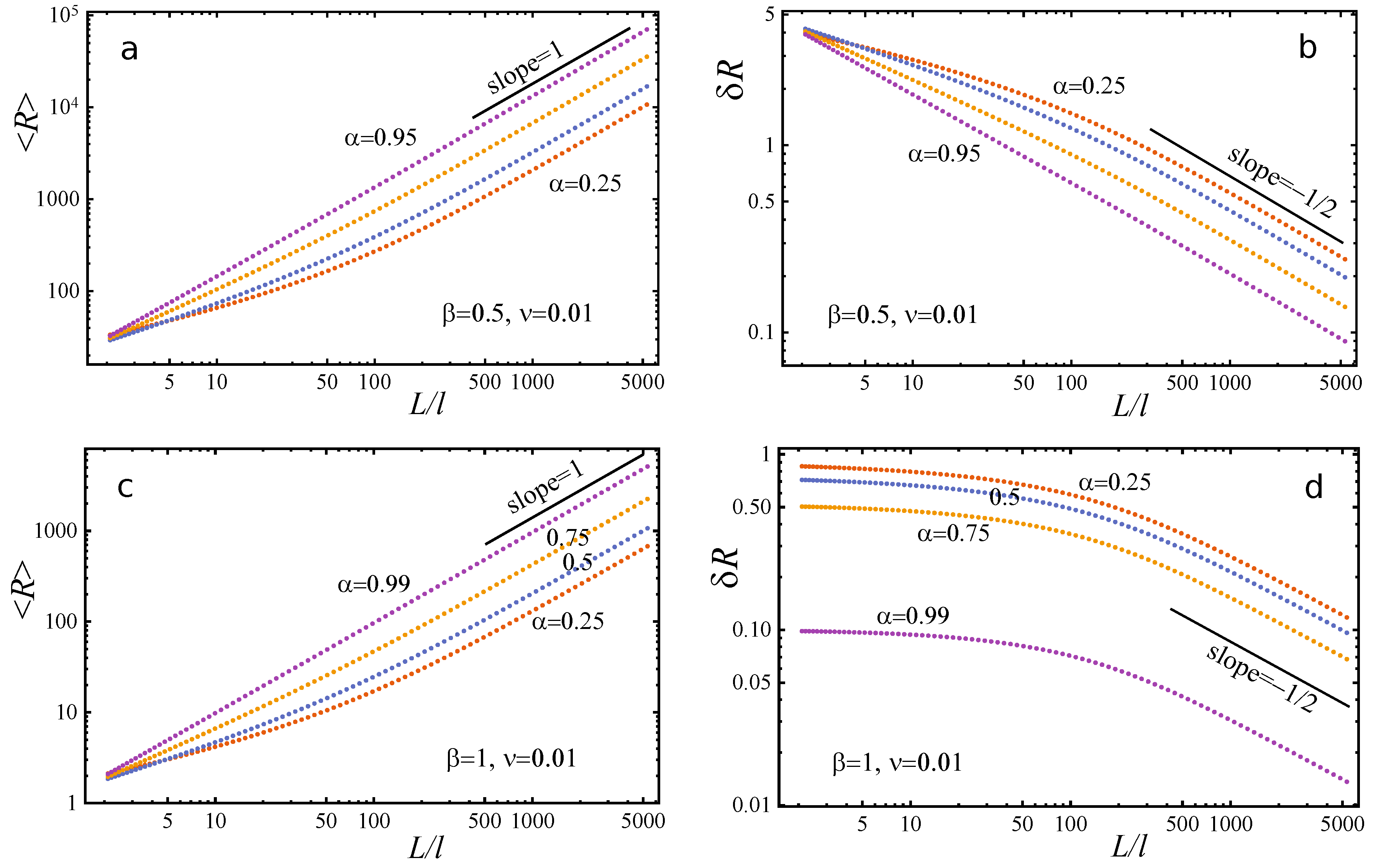
Using the Gaver method of numerical Laplace transform inversion [37], we find dependence of average resistance $\langle R\rangle$ and relative fluctuations $\delta R=(\langle R^2\rangle -{\langle R\rangle }^2)/\langle R\rangle$ on wire length for several values of $\alpha$ and $\beta$ (See Figure 3). Dependencies of $\langle R\rangle$ and $\delta R$ on L demonstrate crossover between two scaling behaviors. This crossover disappears when $\alpha \to 1$.

For the case of a non-truncated power law distribution of individual barrier resistance, when $0<\beta <1$, all moments of the total resistance diverge. Below, we pass to the distribution of wire conductance. The asymptotic distribution of the resistance R of a long quantum wire with length L presents the pdf of a one-sided fractal random walk, which is expressed through the fractional stable density [16],

$$w_R(r;L,\beta ,\alpha )\sim \frac{1}{{\rho }_{\beta }}{\left(\frac{L}{l}\right)}^{-\alpha /\beta }{q}^{(\beta ,\alpha )}\left(\frac{r}{{\rho }_{\beta }}{\left(\frac{L}{l}\right)}^{-\alpha /\beta }\right),L\gg l.$$

(18)

This function satisfies the equation

$${}_0{\mathsf{D}}_L^{\alpha }[w_R-\delta \left(r\right)]=\frac{{\rho }_{\beta }^{\beta }}{l^{\alpha }}{}_0{\mathsf{D}}_r^{\beta }{w}_R,0<\alpha \le 1,0<\beta \le 1.$$

(19)

The conductance $G=1/R$ is distributed according to

$$w_G(y;L,\beta ,\alpha )\sim \frac{1}{{\rho }_{\beta }{y}^2}{\left(\frac{L}{l}\right)}^{-\alpha /\beta }{q}^{(\beta ,\alpha )}\left(\frac{1}{{\rho }_{\beta }y}{\left(\frac{L}{l}\right)}^{-\alpha /\beta }\right),L\gg l.$$

(20)

Using the Mellin transform of the fractional stable density [38], we found the expression for the conductance moments:

$$\langle G^k\rangle \sim \frac{\mathsf{\Gamma }(1+k/\beta )\mathsf{\Gamma }(1-k/\beta )}{\mathsf{\Gamma }(1+k)\mathsf{\Gamma }(1-\alpha k/\beta )}{\rho }_{\beta }^{-k}{\left(\frac{L}{l}\right)}^{-\alpha k/\beta }.$$

This formula is inapplicable when $\beta$ and k are equal to 1 simultaneously. For this case, result are presented in [9],

$$〈G\left(L\right)〉\propto {\rho }^{-1}{(L/l)}^{-\alpha }lnL,\delta G\left(L\right)\propto {(L/l)}^{-\alpha /2}/lnL$$

In the case of a regular spatial distribution of barriers ($\alpha =1$),

$$\langle G\rangle \sim \mathsf{\Gamma }(1+1/\beta ){\rho }_{\beta }^{-1}{\left(\frac{L}{l}\right)}^{-1/\beta },\langle G^2\rangle \sim \frac{\mathsf{\Gamma }(1+2/\beta )}{2}{\rho }_{\beta }^{-2}{\left(\frac{L}{l}\right)}^{-2/\beta }.$$

Relative fluctuations do not depend on $\alpha$ and tend to a constant positive value for large L in the case of $\beta <1$:

$$\delta G=\frac{\sqrt{\mathrm{Var}G}}{\langle G\rangle }\sim \sqrt{\frac{\mathsf{\Gamma }(1+2/\beta )}{2{\left[\mathsf{\Gamma }(1+1/\beta )\right]}^2}-1},L\gg l.$$

Figure 4 demonstrates the agreement of analytical results with numerical Monte Carlo calculations.

Results for resistance distribution (17) and conductance distribution (20) are generalizations of the solutions presented in [7,9]. New results correspond to the case of truncated power law distribution of distances between tunneling barriers and random barrier resistances $R_i$. It should be noted, however, that in the case of wide distribution of $R_i$, the Coulomb blockade can play a sufficient role. The latter effect was neglected here.

Tempered fractional stable law and corresponding tempered fractional equation introduced in Section 2 allowed us to simplify sufficiently consideration of the problem. New distributions expressed via two tempered stable laws with different parameters can describe not only the transition from one mode of anomalous diffusion to normal diffusive transport, but also more complex evolution with several transitions.

5. Concluding Remarks

Electron transport in quasi-fractal one-dimensional mesoscopic systems (quantum wires) is studied. These systems are characterized by a tempered Lévy stable distribution of spacing between scatterers or tunneling barriers. Wires are homogeneous at a large scale and fractal at an intermediate scale. Regimes of weak scattering and sequential incoherent tunneling in such quasi-fractal wires are described. For description, “tempered” generalization of the fractional stable statistics is introduced. Corresponding densities satisfy the equation with tempered fractional derivatives. For the weak scattering, we generalized the DMPK equation for the distribution of eigenvalues of the transmission matrix. The corresponding solutions expressed via the tempered Lévy stable laws describe evolution from the anomalous conductance distribution for a relatively short wire to the Dorokhov function for a long wire. For the sequential tunneling through quasi-fractal wires containing barriers with widely distributed resistances, average values and relative fluctuations are calculated for resistance and conductance that demonstrate crossover between different scaling behaviors.