Novel Fractional Models Compatible with Real World Problems
Abstract
:1. Introduction
2. Preliminaries
3. Main Results
3.1. The Fractional Vertical Motion of a Falling Body Problem in a Resistant Medium
3.1.1. The Vertical Motion of a Falling Body Problem in a Resistant Medium with Liouville–Caputo Fractional Conformable Derivative
3.1.2. Vertical Motion of Falling Body Problem in a Resistant Medium with Liouville–Caputo Fractional Derivative
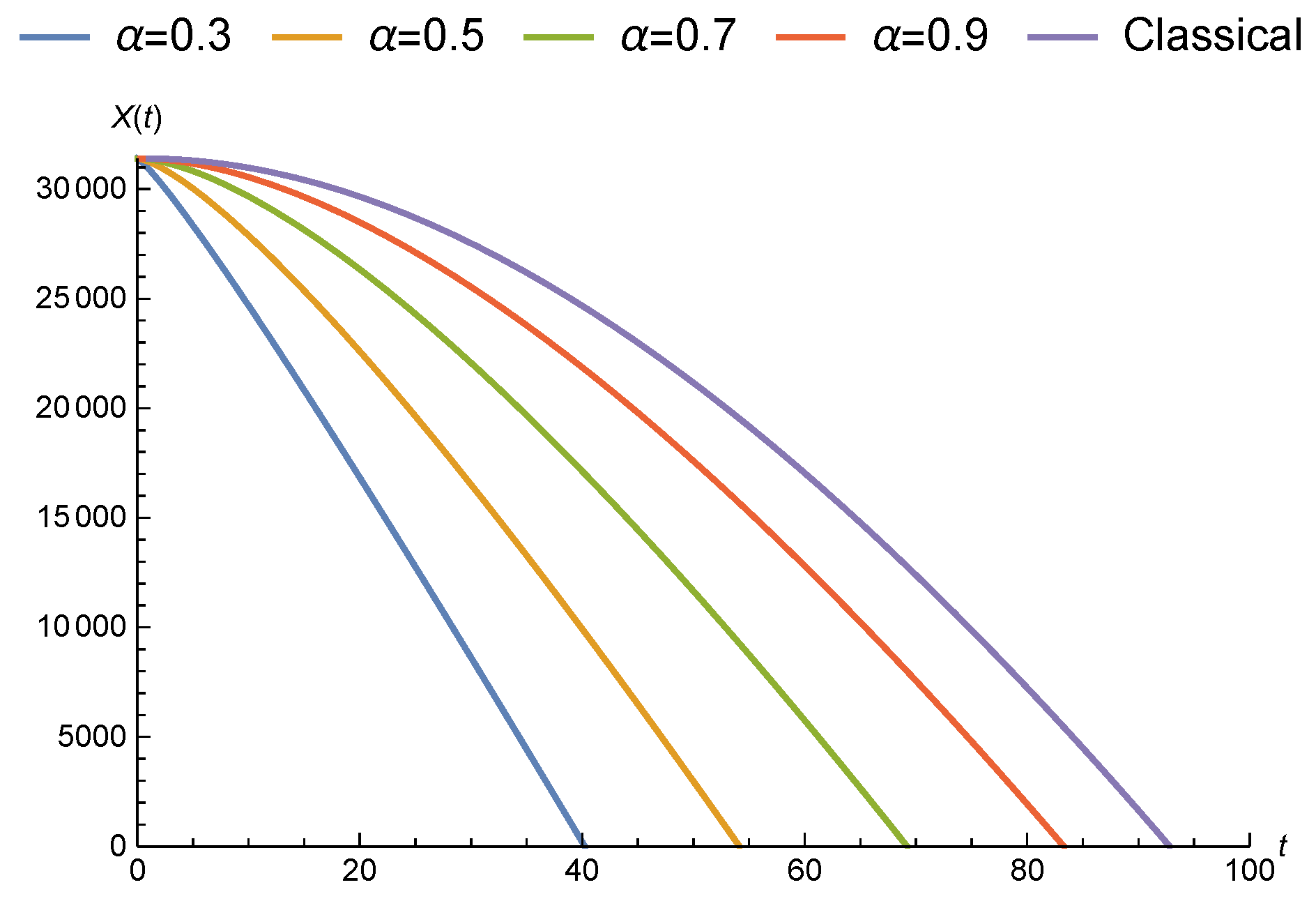
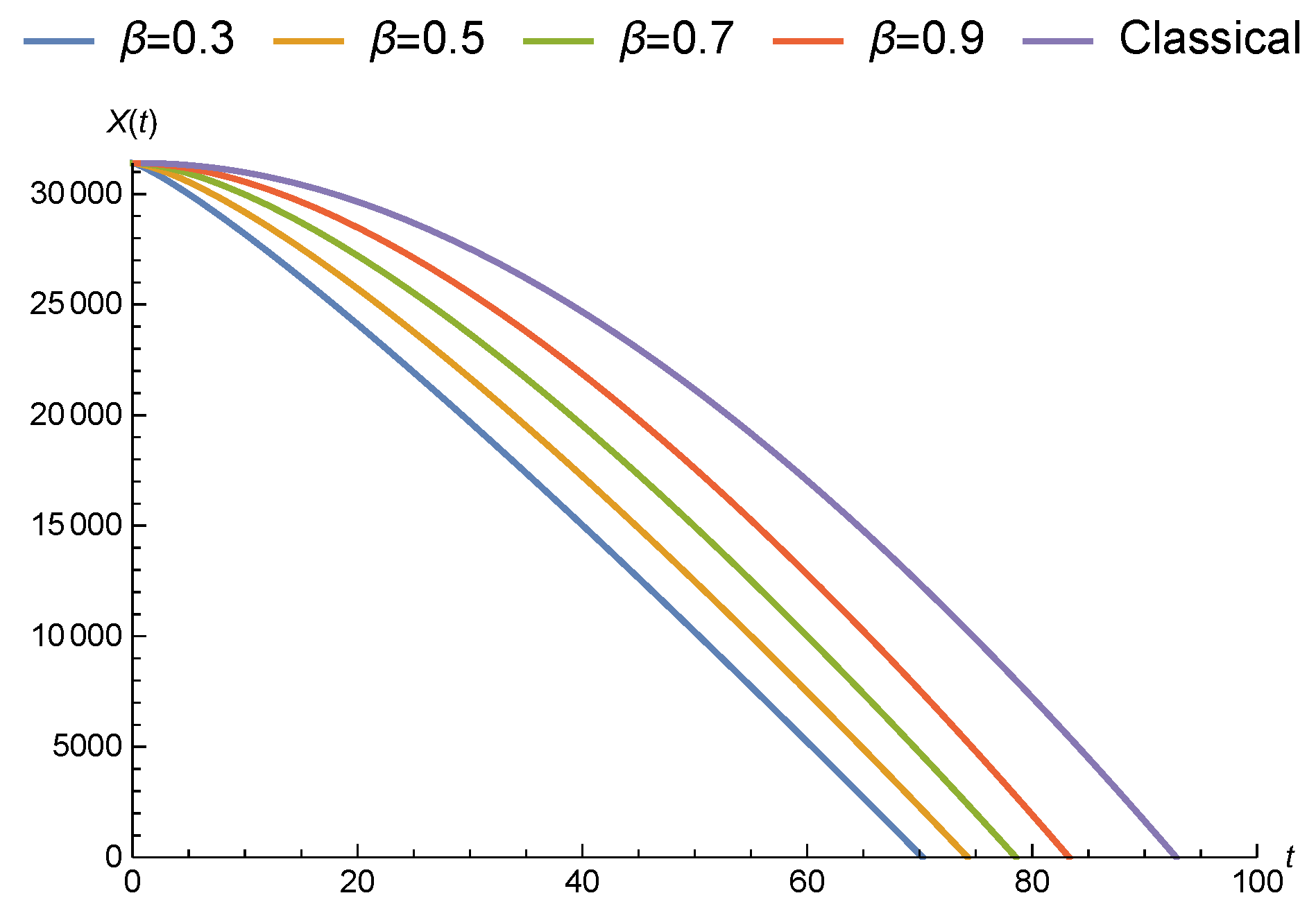
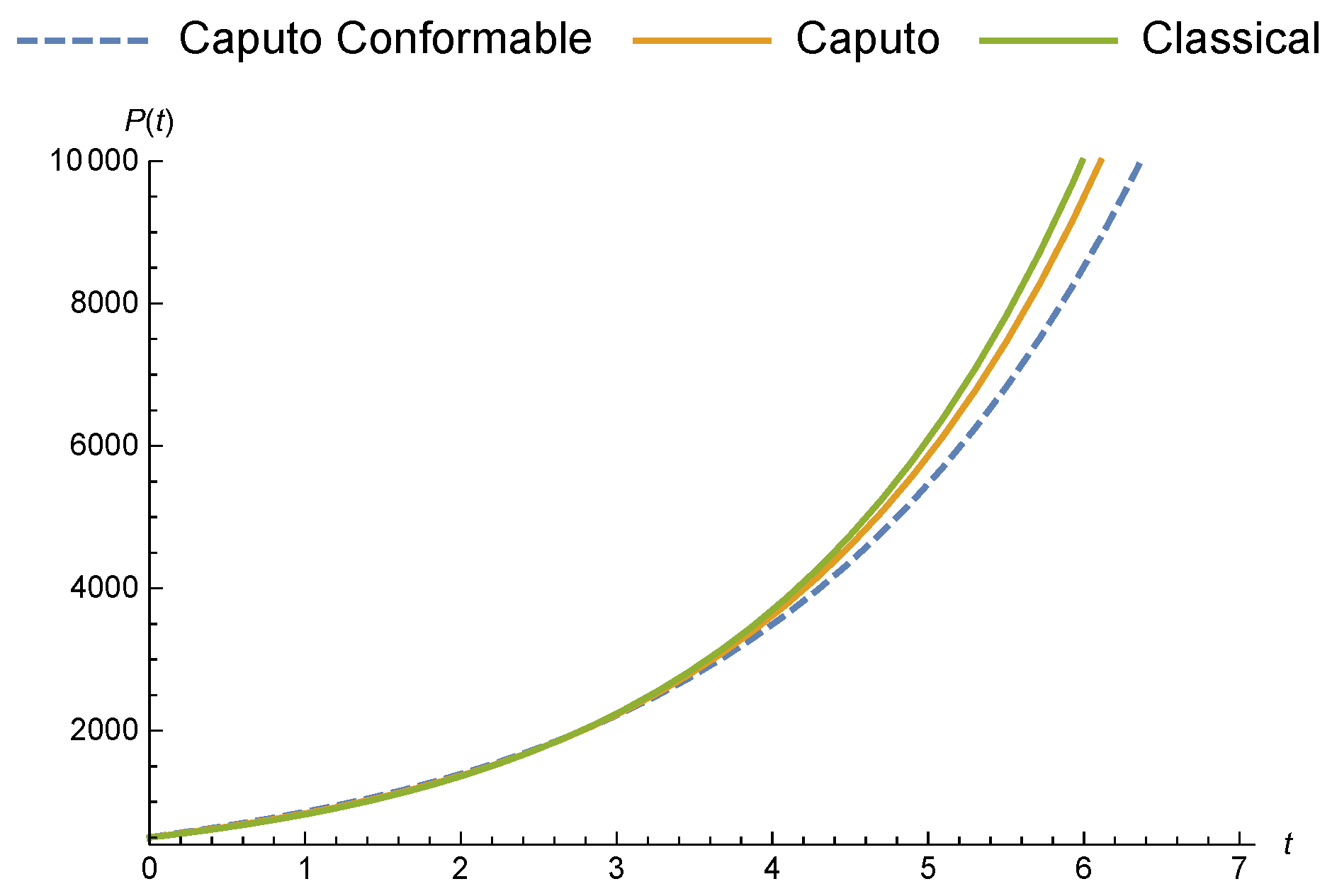
3.2. Fractional Malthusian Growth Model
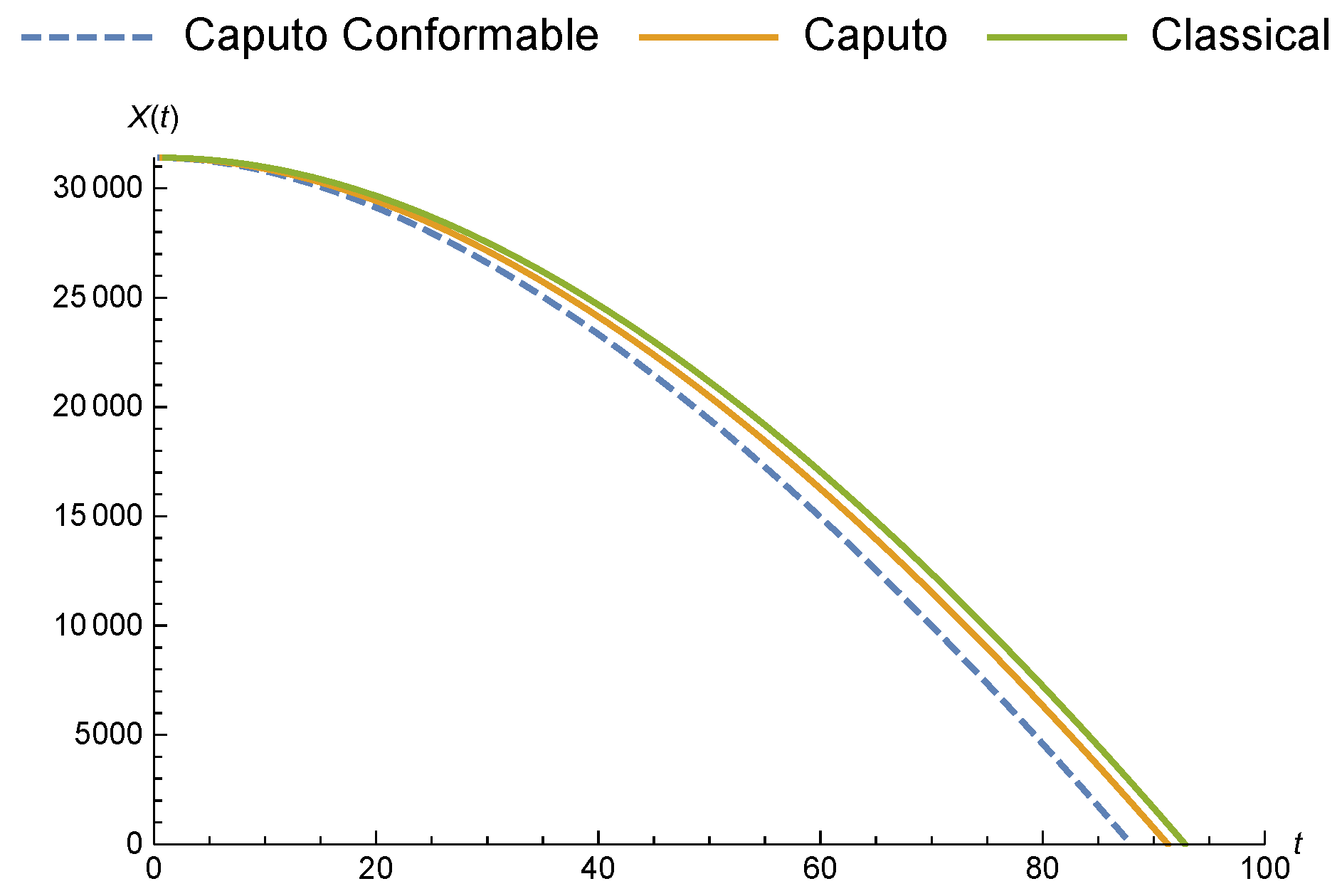
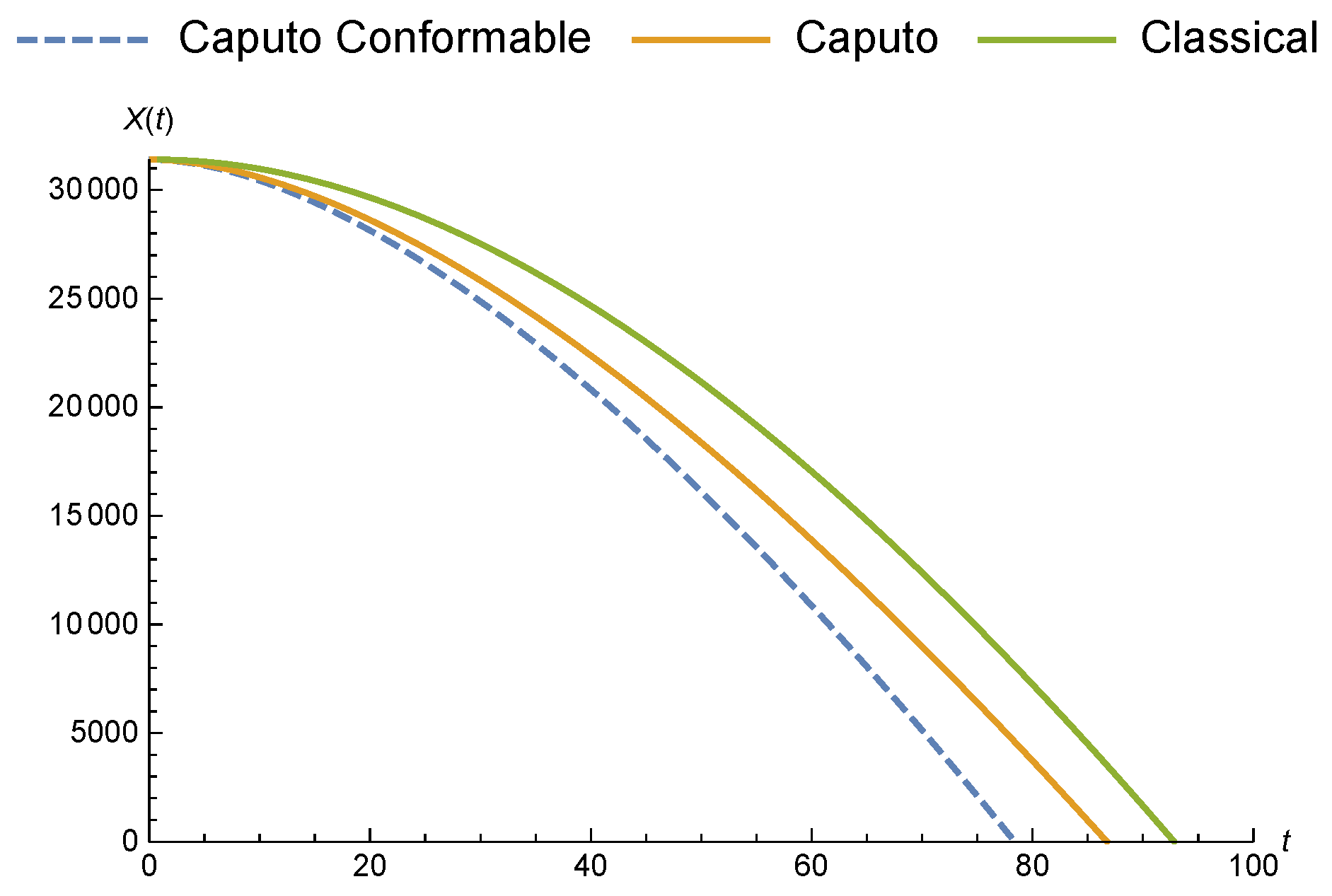
3.2.1. Malthusian Growth Model with Liouville–Caputo Fractional Conformable Derivative
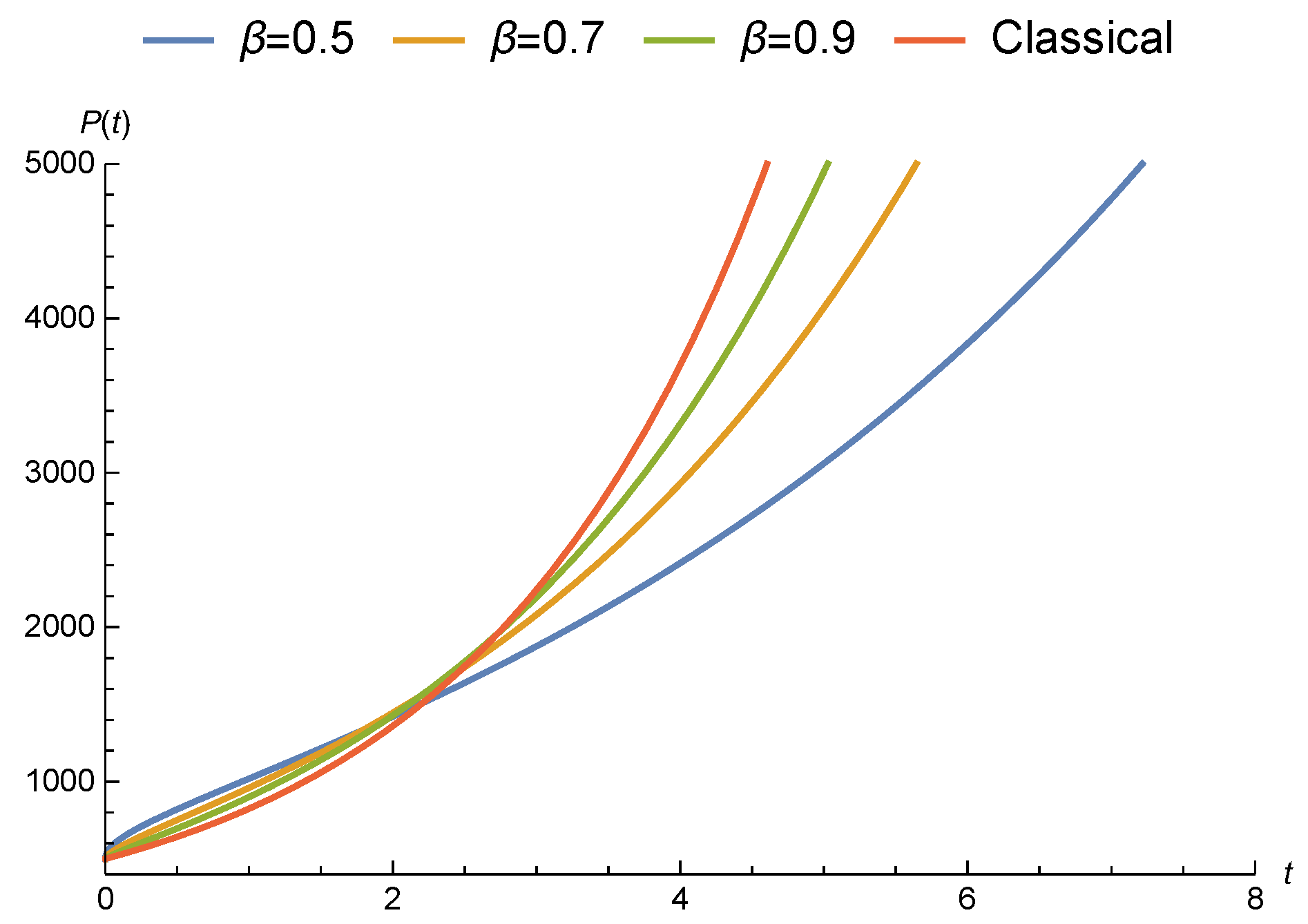
3.2.2. Malthusian Growth Model with Liouville–Caputo Fractional Derivative
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jarad, F.; Uğurlu, E.; Abdeljawad, T.; Baleanu, D. On a new class of fractional operators. Adv. Differ. Equ. 2017, 2017, 247. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Gómez-Aguilar, J.F.; Taneco-Hernandez, M.A. Analytical solutions of electrical circuits described by fractional conformable derivatives in Liouville–Caputo sense. AEU Int. J. Electron. Commun. 2018, 85, 108–117. [Google Scholar] [CrossRef]
- Almeida, R. What is the best fractional derivative to fit data? arXiv, 2017; arXiv:1704.00609. [Google Scholar]
- Ebaid, A.; Masaedeh, B.; El-Zahar, E. A new fractional model for the falling body problem. Chin. Phys. Lett. 2017, 34, 020201. [Google Scholar] [CrossRef]
- Bas, E.; Ozarslan, R. Real world applications of fractional models by Atangana–Baleanu fractional derivative. Chaos Solitons Fractals 2018, 116, 121–125. [Google Scholar] [CrossRef]
- Bas, E.; Acay, B.; Ozarslan, R. Fractional models with singular and non-singular kernels for energy efficient buildings. Chaos 2019, 29, 023110. [Google Scholar] [CrossRef] [PubMed]
- Bas, E.; Ozarslan, R.; Baleanu, D.; Ercan, A. Comparative simulations for solutions of fractional Sturm–Liouville problems with non-singular operators. Adv. Differ. Equ. 2018, 2018, 350. [Google Scholar] [CrossRef]
- Bas, E. The Inverse Nodal problem for the fractional diffusion equation. Acta Sci. Technol. 2015, 37, 2. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New fractional derivatives with non-local and nonsingular kernel: Theory and application to heat transfer model. Therm. Sci. 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Anatoly, A.K. Hadamard-type fractional calculus. J. Korean Math. Soc. 2001, 38, 1191–1204. [Google Scholar]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Abdeljawad, T. On conformable fractional calculus. J. Comput. Appl. Math. 2015, 279, 57–66. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D.; Alsaedi, A. Analysis of time-fractional Hunter–Saxton equation: A model of neumatic liquid crystal. Open Phys. 2016, 14, 145–149. [Google Scholar] [CrossRef]
- Khalil, R.; Al Horani, M.; Yousef, A.; Sababheh, M. A new definition of fractional derivative. J. Comput. Appl. Math. 2014, 264, 65–70. [Google Scholar] [CrossRef]
- Anderson, D.R.; Ulness, D.J. Properties of the Katugampola fractional derivative with potential application in quantum mechanics. J. Math. Phys. 2015, 56, 063502. [Google Scholar] [CrossRef]
- Abdeljawad, T.; Al-Mdallal, Q.M.; Jarad, F. Fractional logistic models in the frame of fractional operators generated by conformable derivatives. Chaos Solitons Fractals 2019, 119, 94–101. [Google Scholar] [CrossRef]
- Abdeljawad, T. Fractional operators with boundary points dependent kernels and integration by parts. Discrete Contin. Dyn. Syst. Ser. S 2019, 1098–1107. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. Generalized fractional derivatives and Laplace transform. Discrete Contin. Dyn. Syst. Ser. S 2019, 1775–1786. [Google Scholar] [CrossRef]
- Jarad, F.; Abdeljawad, T. Variational principles in the frame of certain generalized fractional derivatives. Discrete Contin. Dyn. Syst. Ser. S 2019, 574–582. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Garcia, J.R.; Calderon, M.G.; Ortiz, J.M.; Baleanu, D.; de Santiago, C.S.V. Motion of a particle in a resisting medium using fractional calculus approach. Proc. Rom. Acad. A 2013, 14, 42–47. [Google Scholar]
- Almeida, R.; Bastos, N.R.; Monteiro, M.T.T. Modeling some real phenomena by fractional differential equations. Math. Methods Appl. Sci. 2016, 39, 4846–4855. [Google Scholar] [CrossRef]
- Baskonus, H.M.; Bulut, H. Regarding on the prototype solutions for the nonlinear fractional-order biological population model. AIP Conf. Proc. 2016, 1738, 290004. [Google Scholar]
- Yavuz, M.; Ozdemir, N.; Baskonus, H.M. Solutions of partial differential equations using the fractional operator involving Mittag-Leffler kernel. Eur. Phys. J. Plus 2018, 133, 215. [Google Scholar] [CrossRef]
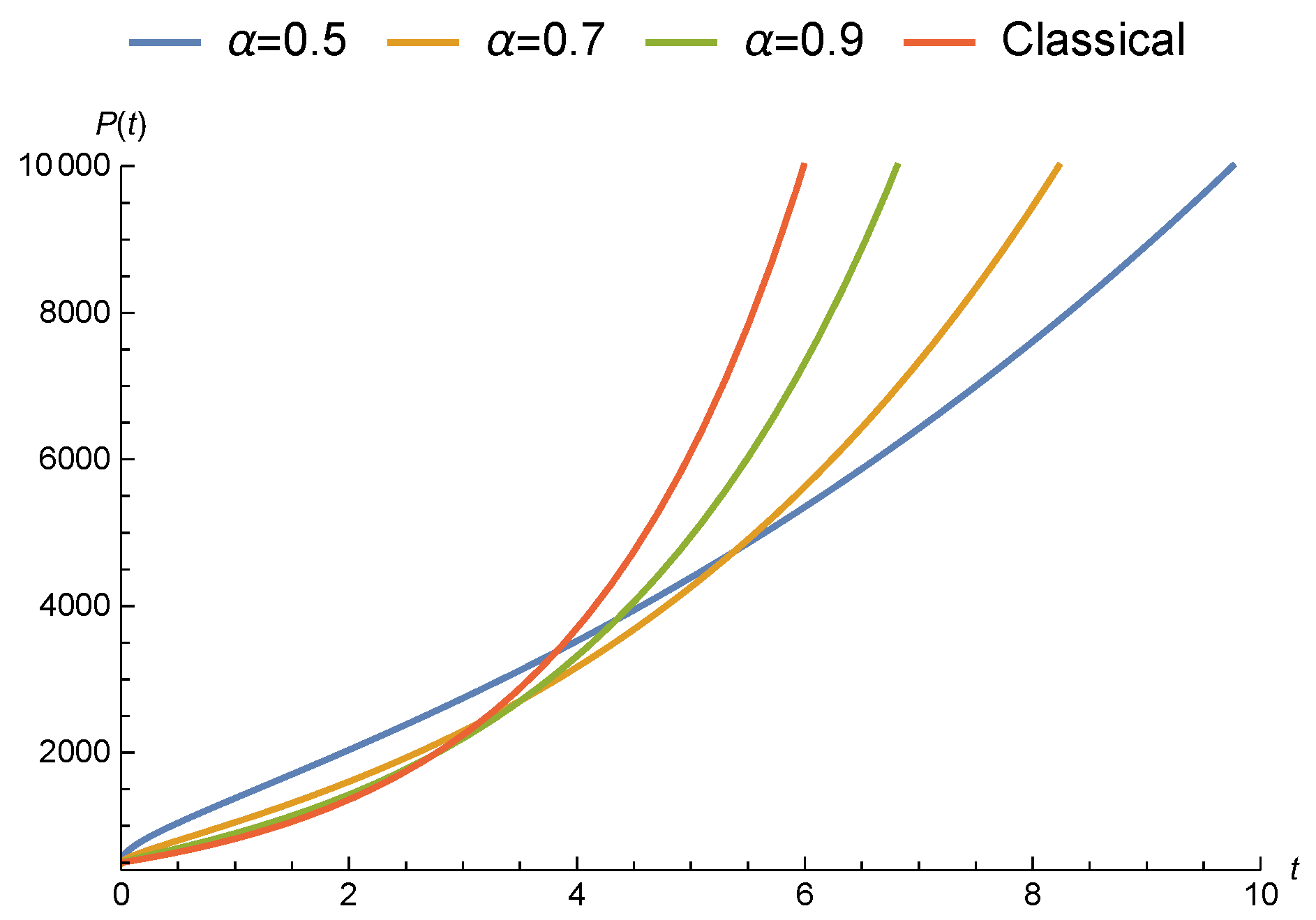

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozarslan, R.; Ercan, A.; Bas, E. Novel Fractional Models Compatible with Real World Problems. Fractal Fract. 2019, 3, 15. https://doi.org/10.3390/fractalfract3020015
Ozarslan R, Ercan A, Bas E. Novel Fractional Models Compatible with Real World Problems. Fractal and Fractional. 2019; 3(2):15. https://doi.org/10.3390/fractalfract3020015
Chicago/Turabian StyleOzarslan, Ramazan, Ahu Ercan, and Erdal Bas. 2019. "Novel Fractional Models Compatible with Real World Problems" Fractal and Fractional 3, no. 2: 15. https://doi.org/10.3390/fractalfract3020015
APA StyleOzarslan, R., Ercan, A., & Bas, E. (2019). Novel Fractional Models Compatible with Real World Problems. Fractal and Fractional, 3(2), 15. https://doi.org/10.3390/fractalfract3020015




