Fractal Calculus of Functions on Cantor Tartan Spaces

Abstract

In this manuscript, integrals and derivatives of functions on Cantor tartan spaces are defined. The generalisation of standard calculus, which is called $F^{\eta }$-calculus, is utilised to obtain definitions of the integral and derivative of functions on Cantor tartan spaces of different dimensions. Differential equations involving the new derivatives are solved. Illustrative examples are presented to check the details.

1. Introduction

Fractal shapes and objects are frequently seen in nature, e.g., clouds, mountains, coastlines, the human body, and so on. The geometry of fractals has been studied a great deal, e.g., see [1,2,3,4]. Analysis of fractals has been established using various different methods—such as fractional calculus, probability theory, measure theory, fractional spaces, and time scale theory—by many researchers and has found many applications [5,6,7,8,9,10,11,12,13,14,15].

Fractional calculus, which involves derivatives with arbitrary orders, has been applied to processes with fractal structures [16,17,18]. Fractional derivatives have non-locality properties, which makes them suitable to model processes with memory effects in statistical mechanics, and provide mathematical models for non-conservative systems in classical mechanics [19,20,21,22,23,24,25,26].

Anomalous diffusion processes have been modelled using fractals, where the concepts of fractal invariance and equivalence can be used to formulate fractional quantum mechanics [27]. These models behave differently from fractional models for anomalous diffusion, due to the locality of the fractal models [28,29,30,31]. This also covers sub-diffusion and super-diffusion, in view of different random walks [32,33].

Fractal geometry has also been used in antenna design: specifically, the idea of space-filling curves is useful in designing miniaturised antenna elements, because it enables long wires to be fitted into a small volume [34,35].

Laminar flow of a fractal fluid in a cylindrical tube has been studied using homogeneous flow in a fractional-dimensional space [36,37]. On the Cantor cubes, Maxwell’s equations were obtained using fractal vector calculus and used to build a model of fractal continuum electrodynamics; as an application, the electric field due to Cantor dust was obtained [38].

Recently, an algorithmic model called $F^{\eta }$-calculus was suggested and applied to model some physical processes [39,40,41,42]. The advantage of this model is that it can be used in contexts where the usual calculus cannot be applied, e.g., for functions with fractal support that are not differentiable or integrable in the usual sense.

This manuscript is structured as follows. In Section 2, we set up the notation and terminology of $F^{\eta }$-calculus on fractals embedded in ${\Re }^2$ and verify some basic properties of this new $F^{\eta }$-calculus. In Section 3, we study some example functions on the Cantor tartan using these suggested definitions. In Section 4, we consider the diffusion equation on the Cantor tartan, as another example. Section 5 is devoted to the conclusion.

2. Terminology and Notations

In this section, we review and define the basic tools we need in our work.

Fractals are sets with self-similar properties such that their fractal dimension exceeds their topological dimension. We shall consider calculus on the Cantor tartan, a space $\mathbb{F}$, which is established by first taking the Cartesian product F of a Cantor set and a continuous interval and then taking the union of two orthogonal copies of this F. In other words:

$$\begin{array}{c}\mathbb{F}=F_1\cup F_2\subset {[0,1]}^2,\\ F_1=C\times [0,1],F_2=[0,1]\times C,\end{array}$$

where $C\subset [0,1]$ is a Cantor set of some fractal dimension less than one [2]. We can consider intersections of the Cantor tartan $\mathbb{F}$ with a box $I=[a_1,a_2]\times [b_1,b_2],a_1,a_2,b_1,b_2\in \Re$. The sketches in Figure 1 show finite iterations (approximations to fractal space) of the Cantor tartan with different dimensions.

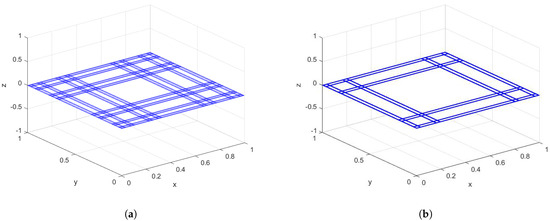
Figure 1. Variants of the Cantor tartan with different dimensions are plotted. (a) Cantor tartan with dimension 1.63; (b) Cantor tartan with dimension 1.43.

Definition 1

(Flag functions and subdivisions). The flag function for the Cantor tartan $\mathbb{F}=F_1\cup F_2\subset {\Re }^2$ and the box $I=[a_1,a_2]\times [b_1,b_2]$, which is denoted by $\Psi (\mathbb{F},I)$, is defined as follows:

$$\Psi (\mathbb{F},I)=\left\{\begin{array}{c}1,if\mathbb{F}\cap I\ne \varnothing ,\hfill \\ 0,otherwise.\hfill \end{array}\right.$$

(1)

A subdivision of the box $I=[a_1,a_2]\times [b_1,b_2]$ is a set of the following form:

$${\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}=\{a_1=x_0,x_1,x_2,\dots ,x_n=a_2\}\times \{b_1=y_0,y_1,y_2,\dots ,y_m=b_2\},$$

(2)

where × denotes the Cartesian product.

Definition 2

(Mass functions). For a Cantor tartan space $\mathbb{F}$ and a subdivision ${\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}$ as above and for any $\eta ,ϵ$ between zero and one, we define:

$${\sigma }^{\eta ,ϵ}\left(\mathbb{F},{\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}\right)=\sum _{j=1}^m\sum _{i=1}^n\Gamma (\eta +1)\Gamma (ϵ+1){(x_i-x_{i-1})}^{\eta }{(y_j-y_{j-1})}^{ϵ}\Psi (\mathbb{F},[x_{i-1},x_i]\times [y_{j-1},y_j]).$$

(3)

For a Cantor tartan space $\mathbb{F}$ and box $I=[a_1,a_2]\times [b_1,b_2]$ as above, and for any $\eta ,ϵ$ between zero and one, the mass function ${\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)$ is defined as:

$${\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)=\underset{\delta \to 0}{lim}\left[\underset{{\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}:|\mathbb{P}|\le \delta }{inf}{\sigma }^{\eta ,ϵ}\left(\mathbb{F},{\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}\right)\right],$$

(4)

where $|\mathbb{P}|$ is defined as:

$$|\mathbb{P}|=\underset{1\le i\le n,1\le j\le m}{max}(x_i-x_{i-1})\times (y_j-y_{j-1}).$$

(5)

Lemma 1.

For a Cantor tartan space $\mathbb{F}$ and fixed $\eta ,ϵ\in (0,1)$ as above, the mass function ${\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)$ is continuous and monotonically increasing in each of the four real variables $a_1$, $a_2$, $b_1$, $b_2$.

Proof. 

This is similar to the one-dimensional case, which was proven in [39] (Theorem 7) and [39] (Lemma 6), respectively. □

Lemma 2.

For a Cantor tartan space $\mathbb{F}$ and fixed $\eta ,ϵ\in (0,1)$ as above, the mass function ${\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)$ is zero for any $a_1,a_2,b_1,b_2$ such that $\mathbb{F}$ does not intersect $(a_1,a_2)\times (b_1,b_2)$.

Proof. 

If $\mathbb{F}$ does not intersect $I=[a_1,a_2]\times [b_1,b_2]$, then the flag function $\Psi (\mathbb{F},[x_{i-1},x_i]\times [y_{j-1},y_j])$ is zero for all $i,j$, so we are done.

Therefore, we assume that $\mathbb{F}$ intersects the boundary of I. Fix $\nu >0$; we aim to find a subdivision $\mathbb{P}={\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}$ such that ${\sigma }^{\eta ,ϵ}\left(\mathbb{F},\mathbb{P}\right)<\nu$. In order to do this, we choose $\mathbb{P}$ such that, in the notation of (2), we have:

$$\begin{array}{cc}\hfill {(x_1-x_0)}^{\eta }{(y_j-y_{j-1})}^{ϵ}& <\frac{\nu }{m\Gamma (\eta +1)\Gamma (ϵ+1)},\hfill \\ \hfill {(x_n-x_{n-1})}^{\eta }{(y_j-y_{j-1})}^{ϵ}& <\frac{\nu }{m\Gamma (\eta +1)\Gamma (\nu +1)},\hfill \\ \hfill {(x_i-x_{i-1})}^{\eta }{(y_1-y_0)}^{ϵ}& <\frac{\nu }{n\Gamma (\eta +1)\Gamma (ϵ+1)},\hfill \\ \hfill {(x_i-x_{i-1})}^{\eta }{(y_m-y_{m-1})}^{ϵ}& <\frac{\nu }{n\Gamma (\eta +1)\Gamma (ϵ+1)},\hfill \end{array}$$

for all i and j. Thus, by the definition (3), we have ${\sigma }^{\eta ,ϵ}\left(\mathbb{F},\mathbb{P}\right)<\nu$. Since $ϵ>0$ was arbitrary, this is enough to prove ${\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)=0$ as required. □

Definition 3

(Integral staircase functions). The integral staircase function $S_{\mathbb{F}}^{\eta ,ϵ}(x,y)$ for the Cantor tartan $\mathbb{F}$ is defined by:

$$S_{\mathbb{F}}^{\eta ,ϵ}(x,y)=\left\{\begin{array}{c}{\gamma }^{\eta ,ϵ}(\mathbb{F},a_0,b_0,x,y),ifx\ge a_0,y\ge b_0;\hfill \\ -{\gamma }^{\eta ,ϵ}(\mathbb{F},a_0,b_0,x,y),otherwise,\hfill \end{array}\right.$$

(6)

where $a_0,c_0$ are real numbers chosen according to convenience (e.g., often we might choose $a_0=c_0=0$). The integral staircase functions for different Cantor tartan spaces with different dimensions are plotted in Figure 2.

Figure 2. The staircase functions corresponding to the Cantor tartan with different dimensions are presented. (a) For the Cantor tartan with dimension 1.63; (b) for the Cantor tartan with dimension 1.43.

Corollary 1.

For a Cantor tartan space $\mathbb{F}$ and fixed $\eta ,ϵ\in (0,1)$ as above, the integral staircase function $S_{\mathbb{F}}^{\eta ,ϵ}(x,y)$ is continuous and monotonically increasing in each of the two real variables x, y.

Proof. 

This follows directly from Lemma 1 and the definition of the integral staircase function. □

Definition 4

(γ2-dimension). The ${\gamma }_2$-dimension of $\mathbb{F}\cap ([a_1,a_2]\times [b_1,b_2])$ is given by:

$$\begin{array}{ccc}\hfill {dim}_{{\gamma }_2}(\mathbb{F}\cap ([a_1,a_2]\times [b_1,b_2]))& =& inf\{max\{\eta ,ϵ\}:{\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)=0\}\hfill \\ & =& sup\{max\{\eta ,ϵ\}:{\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)=\infty \}.\hfill \end{array}$$

(7)

Lemma 3.

The Hausdorff dimension is finer than the ${\gamma }_2$-dimension.

Proof. 

Here, we must prove that ${dim}_H(\mathbb{F})\le {dim}_{{\gamma }_2}(\mathbb{F})$ for any Cantor tartan $\mathbb{F}$ as above.

We use the notation $H_{\delta }^{\gamma }(\mathbb{F})$ for the coarse grained Hausdorff measure and $H^{\gamma }(\mathbb{F})$ for the Hausdorff measure. For any subdivision ${\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}$ with $|\mathbb{P}|\le \delta$, we have:

$${\sigma }^{\eta ,ϵ}[\mathbb{F},\mathbb{P}]\ge \Gamma (\eta +1)\Gamma (ϵ+1)H_{\delta }^{\gamma }(\mathbb{F}\cap [a_1,a_2]\times [b_1,b_2]).$$

(8)

Therefore, taking limits as $\delta \to 0$, we obtain:

$${\gamma }^{\eta ,ϵ}(\mathbb{F},a_1,a_2,b_1,b_2)\ge \Gamma (\eta +1)\Gamma (ϵ+1)H_{\delta }^{\gamma }(\mathbb{F}\cap [a_1,a_2]\times [b_1,b_2]).$$

(9)

This leads to:

$$di{m}_H(\mathbb{F}\cap [a_1,a_2]\times [b_1,b_2])\le di{m}_{{\gamma }_2}(\mathbb{F}\cap [a_1,a_1]\times [b_1,b_2]),$$

(10)

as required. Note that for compact sets, equality holds in (10). □

It can be verified [39] that the ${\gamma }_2$-dimension equates to the Hausdorff dimension for standard fractals, namely:

$${dim}_H(\mathbb{F})=max\{{dim}_H(F_1),{dim}_H(F_2)\}=1+{dim}_H(C),$$

where ${dim}_H$ is the Hausdorff dimension.

Definition 5

(F^η,ϵ-integration). Let $h(x,y)$ be a bounded function on $\mathbb{F}$; then we define:

$$\begin{array}{ccc}\hfill \mathbb{M}[h,\mathbb{F},I]& =& \underset{(x,y)\in \mathbb{F}\cap I}{sup}h(x,y),\mathrm{if}\mathbb{F}\cap I\ne \varnothing .\hfill \\ & =& 0,otherwise,\hfill \end{array}$$

(11)

and similarly:

$$\begin{array}{ccc}\hfill \mathbb{K}[h,\mathbb{F},I]& =& \underset{(x,y)\in \mathbb{F}\cap I}{inf}h(x,y),\mathrm{if}\mathbb{F}\cap I\ne \varnothing .\hfill \\ & =& 0,otherwise,\hfill \end{array}$$

(12)

Now, the upper ${\mathbb{U}}^{\eta ,ϵ}$-sum and lower ${\mathbb{L}}^{\eta ,ϵ}$-sum for the function $h(x,y)$ over the subdivision $\mathbb{P}$ are given as follows:

$$\begin{array}{cc}\hfill {\mathbb{U}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}]& =\sum _{j=1}^m\sum _{i=1}^n\mathbb{M}[h,\mathbb{F},[x_{i-1},x_i]\times [y_{j-1},y_j]]\left(S_{\mathbb{F}}^{\eta ,ϵ}(x_i,y_j)-S_{\mathbb{F}}^{\eta ,ϵ}(x_{i-1},y_{j-1})\right),\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill {\mathbb{L}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}]& =\sum _{j=1}^m\sum _{i=1}^n\mathbb{K}[h,\mathbb{F},[x_{i-1},x_i]\times [y_{j-1},y_j]]\left(S_{\mathbb{F}}^{\eta ,ϵ}(x_i,y_j)-S_{\mathbb{F}}^{\eta ,ϵ}(x_{i-1},y_{j-1})\right).\hfill \end{array}$$

(14)

The function $h(x,y)$ is called $F^{\eta ,ϵ}$-integrable on the Cantor tartan $\mathbb{F}$ if the two expressions:

$$\underline{{\int }_{(a_1,a_2)}^{(b_1,b_2)}}h(x,y)d_F^{\eta }x{d}_F^{ϵ}y=\underset{{\mathbb{P}}_{[a_1,a_2]\times [b_1,b_1]}}{sup}{\mathbb{L}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}]$$

(15)

and:

$$\overline{{\int }_{(a_1,a_2)}^{(b_1,b_2)}}h(x,y)d_F^{\eta }x{d}_F^{ϵ}y=\underset{{\mathbb{P}}_{[a_1,a_2]\times [b_1,b_2]}}{inf}{\mathbb{L}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}]$$

(16)

are equal. In this case, the $F^{\eta ,ϵ}$-integral is denoted by:

$${\int }_{(a_1,a_2)}^{(b_1,b_2)}h(x,y)d_F^{\eta }x{d}_F^{ϵ}y.$$

Lemma 4.

For a Cantor tartan space $\mathbb{F}$ and fixed $\eta ,ϵ\in (0,1)$ as above and for any two subdivisions $\mathbb{P}$ and $\mathbb{Q}$ of the same box $I=[a_1,a_2]\times [b_1,b_2]$, we have:

$${\mathbb{U}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}]\ge {\mathbb{L}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{Q}].$$

This confirms that the definition of the $F^{\eta }$-integral makes sense.

Proof. 

It suffices to show that taking refinements of subdivisions will always decrease ${\mathbb{U}}^{\eta ,ϵ}$ and increase ${\mathbb{L}}^{\eta ,ϵ}$. To see why, note that the subdivision $\mathbb{P}\cup \mathbb{Q}$ is a refinement of both $\mathbb{P}$ and $\mathbb{Q}$, and so, it suffices to show:

$${\mathbb{U}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}]\ge {\mathbb{U}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}\cup \mathbb{Q}]\ge {\mathbb{L}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}\cup \mathbb{Q}]\ge {\mathbb{L}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{Q}].$$

Thus, we let ${\mathbb{P}}^{\prime }$ be a refinement of the general subdivision $\mathbb{P}$, and we aim to prove that:

$${\mathbb{U}}^{\eta ,ϵ}[h,\mathbb{F},{\mathbb{P}}^{\prime }]\le {\mathbb{U}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}]\mathrm{and}{\mathbb{L}}^{\eta ,ϵ}[g,\mathbb{F},{\mathbb{P}}^{\prime }]\ge {\mathbb{L}}^{\eta ,ϵ}[h,\mathbb{F},\mathbb{P}].$$

Without loss of generality, we suppose that:

$$\begin{array}{cc}\hfill \mathbb{P}& =\{a_1=x_0,x_1,x_2,\cdots ,x_n=a_2\}\times \{b_1=y_0,y_1,y_2,\cdots ,y_m=b_2\},\hfill \\ \hfill {\mathbb{P}}^{\prime }& =\{x_0,\cdots ,x_{i-1},x_i,\cdots ,x_n\}\times \{y_0,\cdots ,y_m\}.\hfill \end{array}$$

Thus, we are replacing, for each j, the box $[x_{i-1},x_i]\times [y_{j-1},y_j]$ by the pair of boxes $[x_{i-1},x_i]\times [y_{j-1},y_j]$ and $[x_{i-1},x_i]\times [y_{j-1},y_j]$. We can now use the argument of [39] (Lemma 34) a total of m times, summing up the inequalities to yield our desired result. □

Definition 6

(F^η-differentiation). A point $(x,y)$ is called a point of change of a function $h(x,y)$ if it is not constant over any open set $[a_1,a_2]\times [b_1,b_2]$ containing $(x,y)$. The set of all points of change of $h(x,y)$ is indicated by $Sch(h)$. The set $Sch(S_{\mathbb{F}}^{\eta ,ϵ}(x,y))$ is called ζ-perfect if $S_{\mathbb{F}}^{\eta ,ϵ}(x,y)$ is finite for all $(x,y)\in \Re$.

If $\mathbb{F}$ is a ζ-perfect set, then we define the $F^{\eta }$-partial derivative of $h(x,y)$ with respect to x as:

$${}^x{D}_{\mathbb{F}}^{\eta }h(x,y)=\left\{\begin{array}{c}\mathbb{F}\text{-}\underset{(x^{\prime },y)\to (x,y)}{lim}\frac{h(x^{\prime },y)-h(x,y)}{S_{\mathbb{F}}^{\eta ,ϵ}(x^{\prime },y)-S_{\mathbb{F}}^{\eta ,ϵ}(x,y)},if(x,y)\in \mathbb{F},\hfill \\ 0,otherwise,\hfill \end{array}\right.$$

(17)

if the limit exists, where $\mathbb{F}\text{-}lim$ is defined as the limit taken within the set $\mathbb{F}$, as seen in [39].

Similarly, we define the $F^{ϵ}$-partial derivative of $h(x,y)$ with respect to y as:

$${}^y{D}_{\mathbb{F}}^{ϵ}h(x,y)=\left\{\begin{array}{c}\mathbb{F}\text{-}\underset{(x,y^{\prime })\to (x,y)}{lim}\frac{h(x,y^{\prime })-h(x,y)}{S_{\mathbb{F}}^{\eta ,ϵ}(x,y^{\prime })-S_{\mathbb{F}}^{\eta ,ϵ}(x,y)},if(x,y)\in \mathbb{F},\hfill \\ 0,otherwise,\hfill \end{array}\right.$$

(18)

if the limit exists.

Example 1.

For a Cantor tartan space $\mathbb{F}$ and fixed $\eta ,ϵ\in (0,1)$ as above, the $F^{\eta }$-partial derivative and the $F^{ϵ}$-partial derivative of the integral staircase function $S_{\mathbb{F}}^{\eta ,ϵ}(x,y)$ are both equal to the characteristic function ${\chi }_{\mathbb{F}}(x,y)$ of the space $\mathbb{F}$.

3. Example Functions with Cantor Tartan Support

The task is now to apply definitions to examples. In this section, we give some examples to show more details.

Example 2.

Let us consider the following function, supported on the Cantor tartan with different fractal dimensions:

$$f(x,y)=sin(x{\chi }_F^{\eta }(x))sin(y{\chi }_F^{ϵ}(y)),(x,y)\in \mathbb{F},$$

(19)

where ${\chi }_F^{\eta },{\chi }_F^{ϵ}$ are characteristic functions for the fractal sets $F_1,F_2$ whose union is $\mathbb{F}$ [40,43] (the indices η and ϵ denote the dimension of the respective Cantor sets used to form the sets $F_1$ and $F_2$). Graphs of the function $f(x,y)$ are shown in Figure 3.

Figure 3. We plot the graph of the function $sin({\chi }_F^{\eta }x)sin({\chi }_F^{ϵ}y)$ with different Cantor tartan supports. (a) On the Cantor tartan with dimension 1.63; (b) on the Cantor tartan with dimension 1.43.

The fractal integral of $f(x,y)$ on the Cantor tartan $\mathbb{F}\subset [0,1]\times [0,1]$ is as follows:

$$\begin{array}{cc}g(x,y){|}_{(x=y=1)}\hfill & ={\int }_0^x{\int }_0^{y}sin({\chi }_F^{\eta }x)sin({\chi }_F^{ϵ}y)d_F^{\eta }{x}^{\prime }{d}_F^{ϵ}{y}^{\prime }{|}_{(x=y=1)}\hfill \\ & ={\int }_0^1\Gamma (ϵ+1)cos\left(\frac{S_F^{ϵ}(y^{\prime })}{\Gamma (ϵ+1)}\right)sin({\chi }_F^{\eta }x){|}_0^1{d}_F^{\eta }{x}^{\prime }\hfill \\ & ={\int }_0^1[\Gamma (ϵ+1)cos\left(\frac{S_F^{ϵ}(1)}{\Gamma (ϵ+1)}\right)sin({\chi }_F^{\eta }x)\hfill \\ & -\Gamma (ϵ+1)cos\left(\frac{S_F^{ϵ}(0)}{\Gamma (ϵ+1)}\right)sin({\chi }_F^{\eta }x)]d_F^{\eta }{x}^{\prime }\hfill \\ & =\Gamma (ϵ+1)\Gamma (\eta +1)\left(cos(1)cos\left(\frac{S_F^{ϵ}(x^{\prime })}{\Gamma (\eta +1)}\right)-cos\left(\frac{S_F^{ϵ}(x^{\prime })}{\Gamma (\eta +1)}\right)\right){|}_0^1\hfill \\ & =\Gamma (ϵ+1)\Gamma (\eta +1){(cos(1)-1)}^2\hfill \end{array}$$

(20)

since here $S_F^{\eta }(1)=\Gamma (1+\eta ),S_F^{ϵ}(1)=\Gamma (1+ϵ),S_F^{\eta }(0)=S_F^{ϵ}(0)=0$ [39]. We note the following special cases as examples:

$$g(x,y){|}_{(x=y=1)}=\left\{\begin{array}{cc}0.170,\hfill & \eta =ϵ=0.63(Cantortartanofdimension1.63)\hfill \\ 0.165,\hfill & \eta =ϵ=0.43(Cantortartanofdimension1.43)\hfill \end{array}\right.$$

(21)

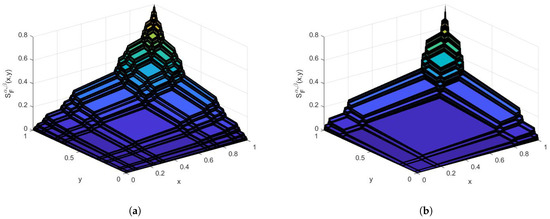
In Figure 4, we sketch the function $g(x,y)$, which is called the fractal integral of $f(x,y)$.

Figure 4. The fractal integral of $sin(x{\chi }_F^{\eta }(x))sin(y{\chi }_F^{ϵ}(y))$ on the Cantor tartan of different dimensions is sketched. (a) On the Cantor tartan with dimension 1.63; (b) on the Cantor tartan with dimension 1.43.

Example 3.

Consider a function with Cantor tartan support as follows:

$$f(x,y)=sin(x{\chi }_F^{\eta }(x)+y{\chi }_F^{ϵ}(y)),(x,y)\in \mathbb{F}$$

(22)

We present in Figure 5 the graph of Equation (22). The fractal integral of Equation (22) is as follows:

$$\begin{array}{cc}\hfill g(x,y){|}_{(x=y=1)}& ={\int }_0^x{\int }_0^{y}sin({\chi }_F^{\eta }x+{\chi }_F^{ϵ}y)d_F^{\eta }{x}^{\prime }{d}_F^{ϵ}{y}^{\prime }{|}_{(x=y=1)}\hfill \\ & ={\int }_0^1-\Gamma (ϵ+1)cos\left({\chi }_F^{\eta }x+\frac{S_F^{ϵ}(y)}{\Gamma (ϵ+1)}\right){|}_0^1{d}_F^{\eta }{x}^{\prime }\hfill \\ & ={\int }_0^1[-\Gamma (ϵ+1)cos({\chi }_F^{\eta }x+1)+\Gamma (ϵ+1)cos({\chi }_F^{\eta }x)]d_F^{\eta }{x}^{\prime }\hfill \\ & =-\Gamma (\eta +1)\Gamma (ϵ+1)sin\left(\frac{S_F^{\eta }(x^{\prime })}{\Gamma (\eta +1)}+1\right)\hfill \\ & +\Gamma (\eta +1)\Gamma (ϵ+1)sin\left(\frac{S_F^{\eta }(x^{\prime })}{\Gamma (\eta +1)}\right){|}_0^1\hfill \\ & =\Gamma (\eta +1)\Gamma (ϵ+1)[2sin(1)-sin(2)]\hfill \end{array}$$

(23)

since $S_F^{\eta }(1)=\Gamma (1+\eta ),S_F^{ϵ}(1)=\Gamma (1+ϵ),S_F^{\eta }(0)=S_F^{ϵ}(0)=0$ [39]. We note the following special cases as examples:

$$g(x,y){|}_{(x=y=1)}=\left\{\begin{array}{cc}0.622,\hfill & \eta =ϵ=0.63(Cantortartanofdimension1.63)\hfill \\ 0.607,\hfill & \eta =ϵ=0.43(Cantortartanofdimension1.43)\hfill \end{array}\right.$$

(24)

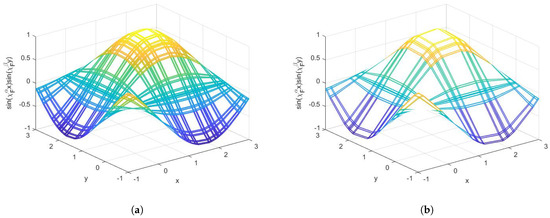
Figure 5. We plot the graph of the function $sin(x{\chi }_F^{\eta }(x)+y{\chi }_F^{ϵ}(y))$ with different Cantor tartan supports. (a) On the Cantor tartan with dimension 1.63; (b) on the Cantor tartan with dimension 1.43.

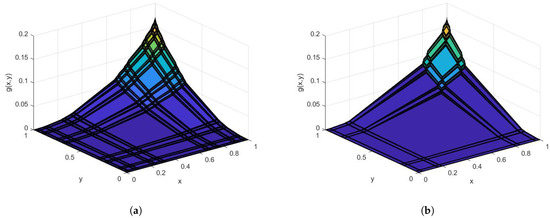
In Figure 6, we plot the fractal integral of $sin(x{\chi }_F^{\eta }(x)+y{\chi }_F^{ϵ}(y))$ supported on Cantor tartan spaces with different dimensions.

Figure 6. The fractal integral of $sin({\chi }_F^{\eta }x+{\chi }_F^{ϵ}y)$ on the Cantor tartan of different dimensions is shown. (a) On the Cantor tartan with dimension 1.63; (b) on the Cantor tartan with dimension 1.43.

Example 4.

Consider a function on a Cantor tartan space as follows:

$$f(x,y)=S_F^{\eta }{(x)}^2+S_F^{ϵ}{(y)}^2.$$

(25)

The fractal partial derivatives of $f(x,y)$ with respect to x and y are:

$${}^x{D}_F^{\eta }f(x,y)=2S_F^{\eta }(x),{}^y{D}_F^{\eta }f(x,y)=2S_F^{\eta }(y).$$

(26)

In Figure 7, we plot Equation (25) and also its partial derivative ${}^x{D}_F^{\eta }f(x,y)$.

Figure 7. Graphs of the function $S_F^{\eta }{(x)}^2+S_F^{ϵ}{(y)}^2$ and its derivative ${}^x{D}_F^{\eta }f(x,y)$ on the Cantor tartan with dimension 1.63. (a) Graph of the function; (b) graph of the derivative.

Remark 1.

One can obtain standard results by choosing $\eta =1,$ $ϵ=1$, to get $\mathbb{F}=[0,1]\times [0,1]$, which leads to $S_F^{\eta }(x)=x,S_F^{ϵ}(y)=y$.

4. Anomalous Diffusion on the Fractal Cantor Tartan

As an example application of the ideas in Section 2, we consider the diffusion equation on the Cantor tartan as the following:

$${}_0^C{\mathcal{D}}_t^{\beta }u(x,y,t)=\mathbf{K}\left({{(}^x{D}_F^{\eta })}^{2}u(x,y,t)+{{(}^y{D}_F^{\eta })}^{2}u(x,y,t)\right),$$

(27)

for $(x,y)\in \mathbb{F}$ and $t\in F$. Here, ${}_0^C{\mathcal{D}}_t^{\beta }$ is the left-sided Caputo-like fractional derivative of order $\beta$ on a fractal set F (see [43]); the fractal derivatives on the right-hand side of (27) are as defined in Section 2; and $\mathbf{K}$ is the diffusion coefficient. We also impose the following initial and boundary conditions:

$$u(x,y,t)=0,(x,y)\in \partial \mathbb{F},t>0,$$

(28)

$$u(x,y,0)=sin(x\pi )sin(y\pi ),(x,y)\in \mathbb{F}\cup \partial \mathbb{F}.$$

(29)

The solution of the differential Equation (27), using the conjugacy of $F^{\eta }$-calculus and standard calculus as described in [39,40], will be [31]:

$$u(x,y,t)=sin(S_F^{\eta }(x)\pi )sin(S_F^{\eta }(y)\pi )E_{F,\beta }^{\eta }\left(-2{(S_F^{\eta }(t))}^{ϵ}\right),\mathbf{K}=\frac{1}{\pi },$$

(30)

where $E_{F,\beta }^{\eta }(.)$ is the generalised Mittag–Leffler function on a Cantor set [43].

If we consider a random walk on a fractal Cantor tartan set, the probability distribution will be described by Equation (27). Thus, the analysis presented here will be useful in modelling different random walks on fractal sets [44,45]. Future research in the field of random walks on fractal sets may be able to proceed along such lines as these.

5. Conclusions

In this work, we define the local derivative and integral on the Cantor tartan. The standard calculus cannot be applied to integrate and differentiate functions on fractals of this form. Therefore, we need a new type of calculus to calculate the physical properties and describe phenomena on fractals. As a result, the $F^{\eta }$-calculus on the Cantor tartan of fractal dimension $1<\zeta <2$ is given. Furthermore, we recall the standard calculus results, which show that the suggested definitions are the natural generalisation of standard calculus. Three illustrative examples were investigated, and the corresponding graphs of the functions were drawn.