Fractal Calculus of Functions on Cantor Tartan Spaces
Abstract
1. Introduction
2. Terminology and Notations
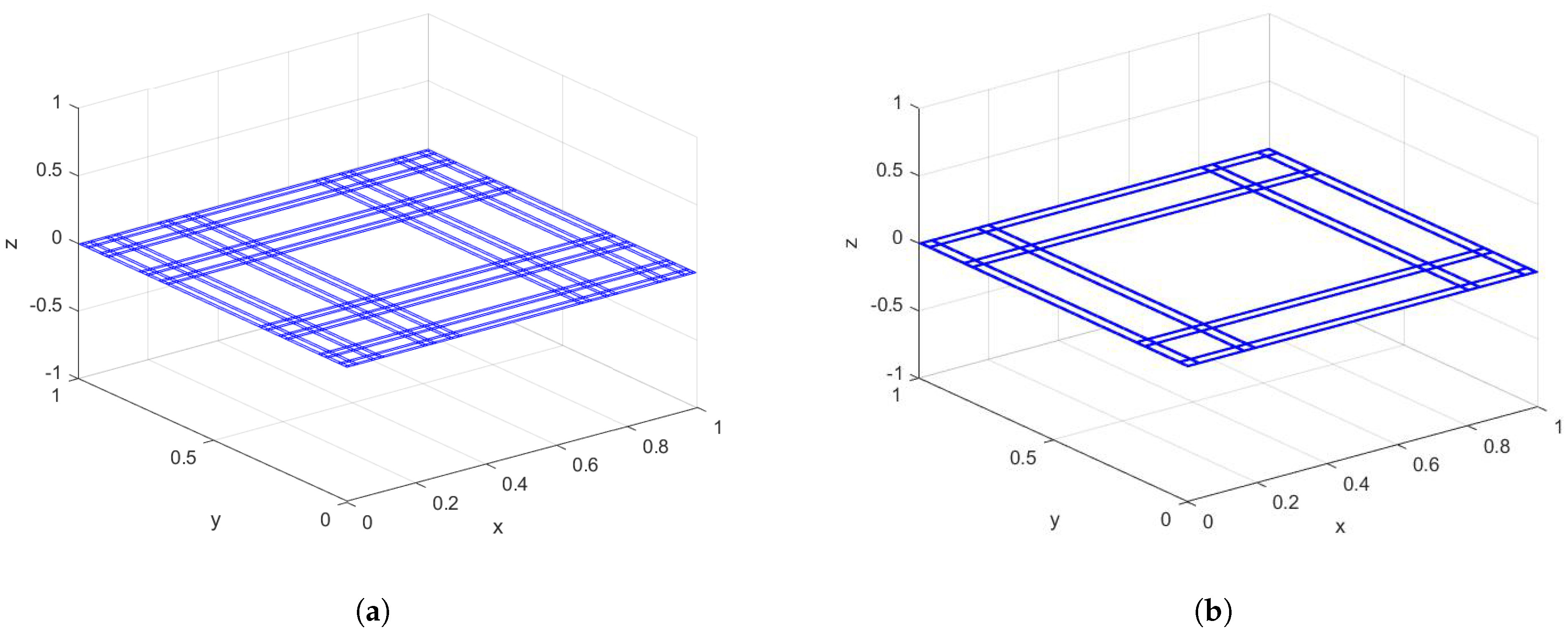
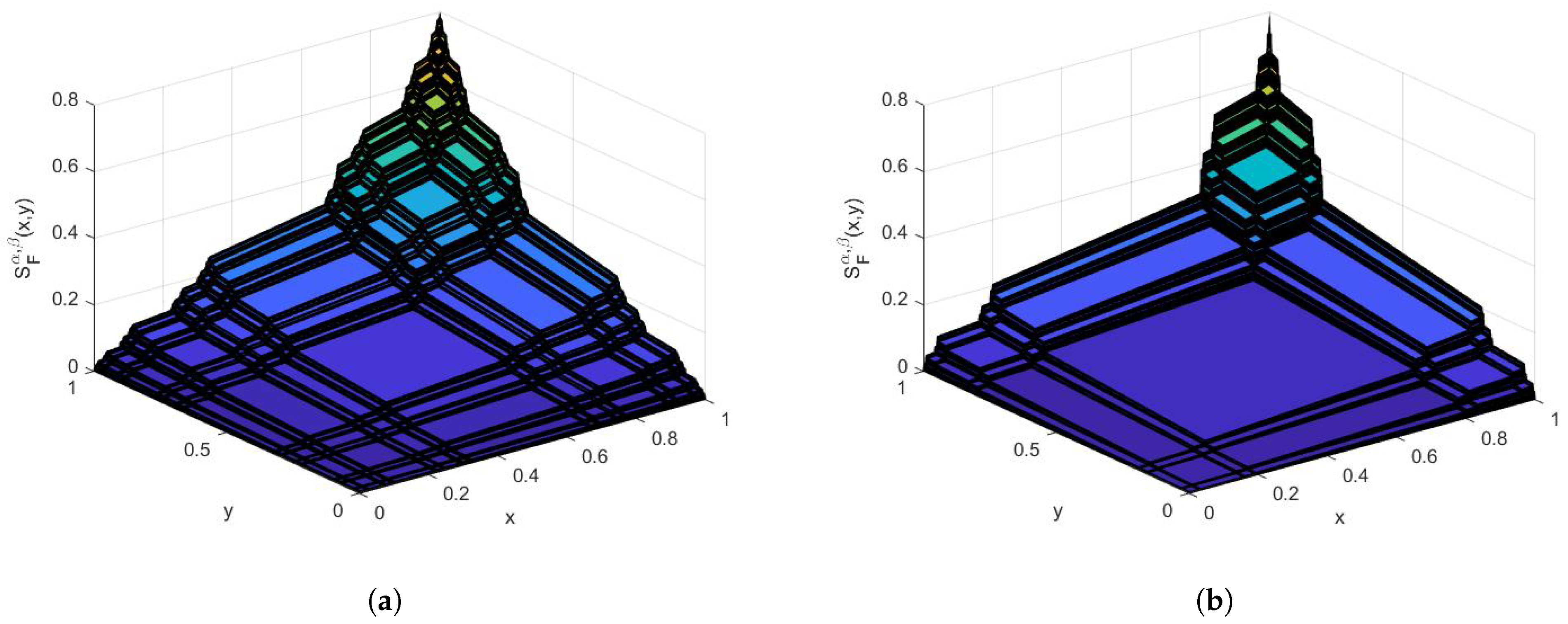
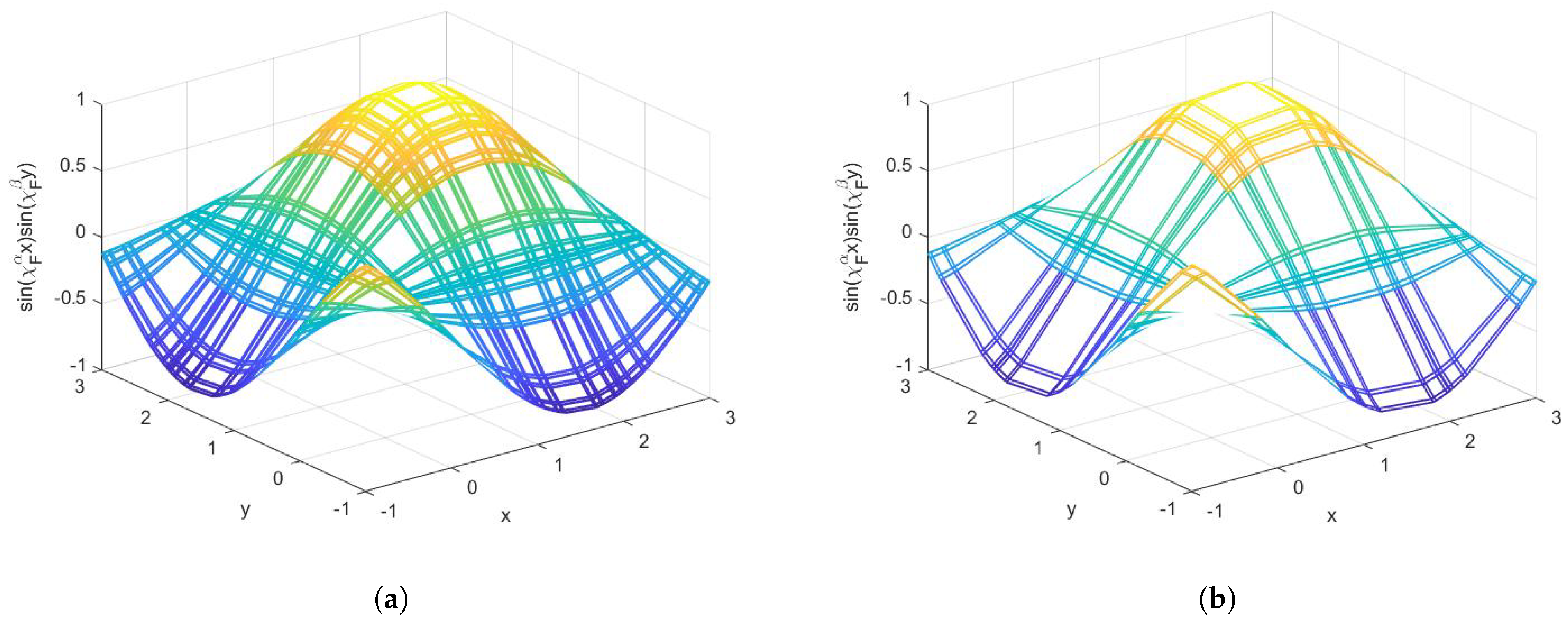
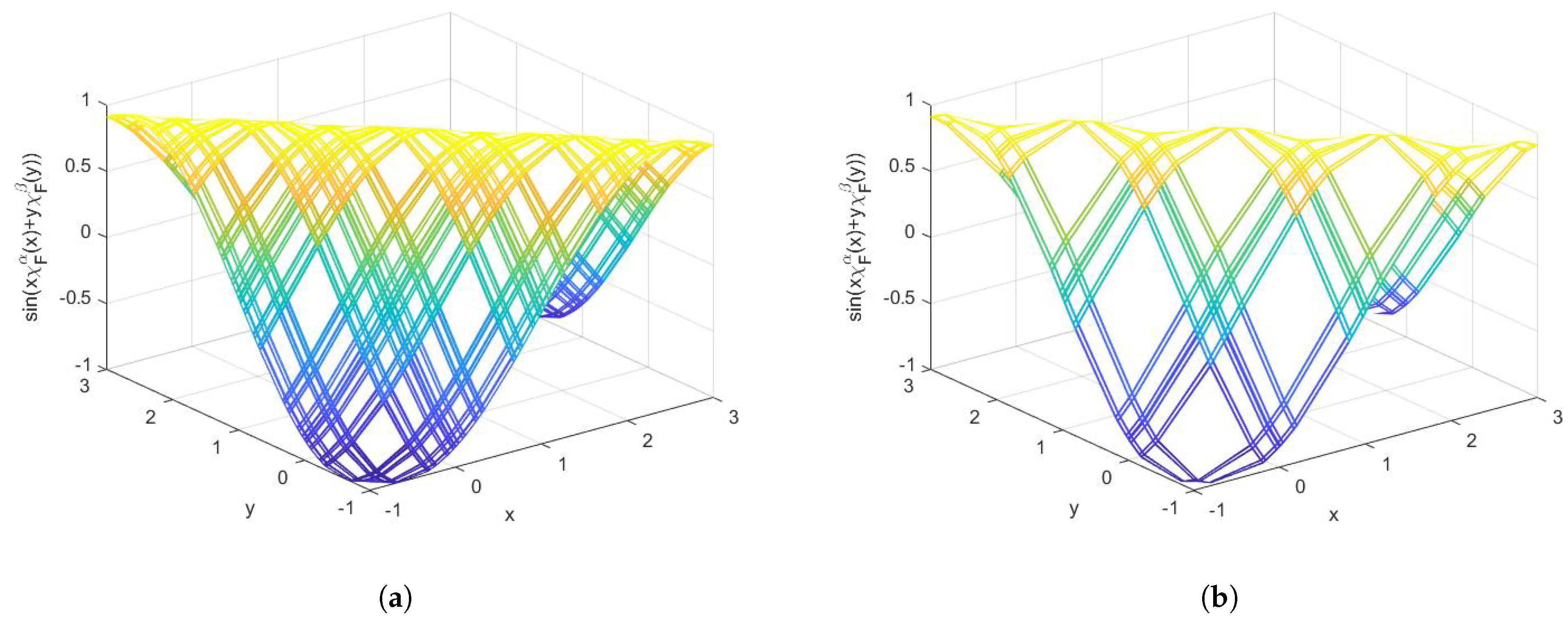
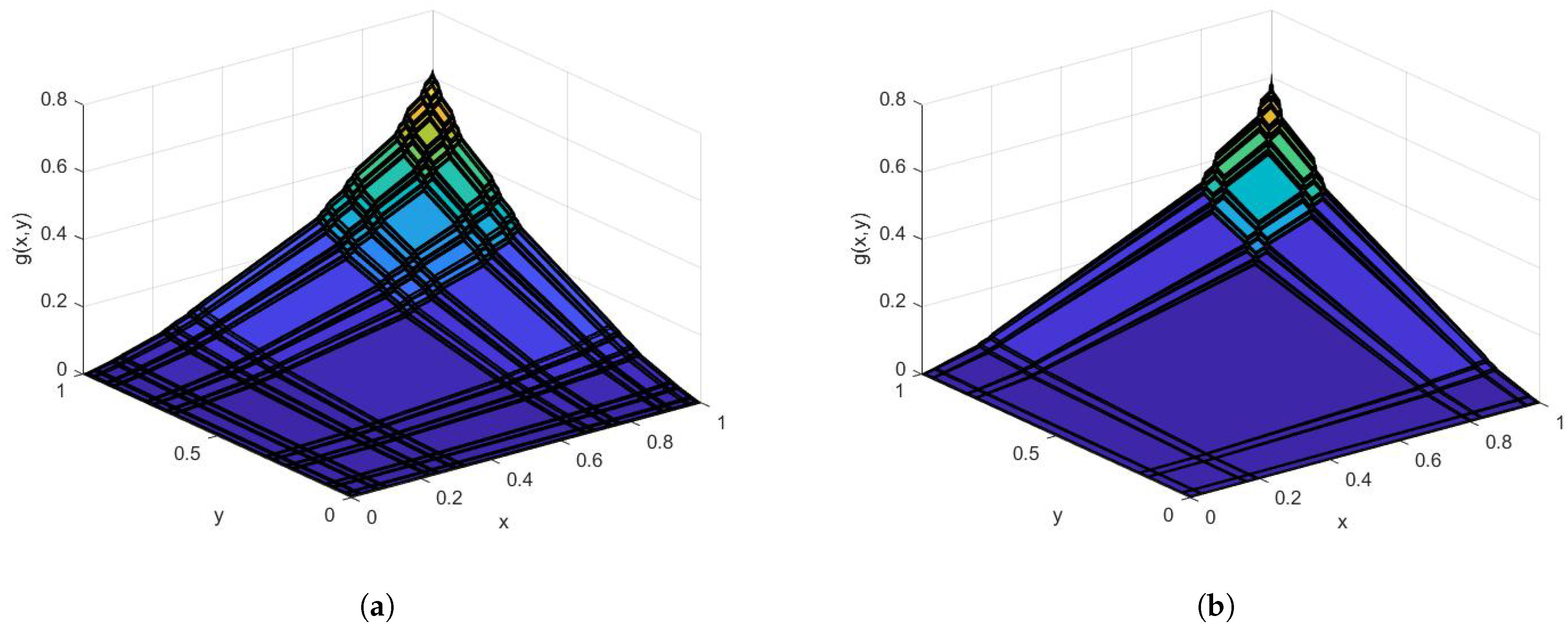
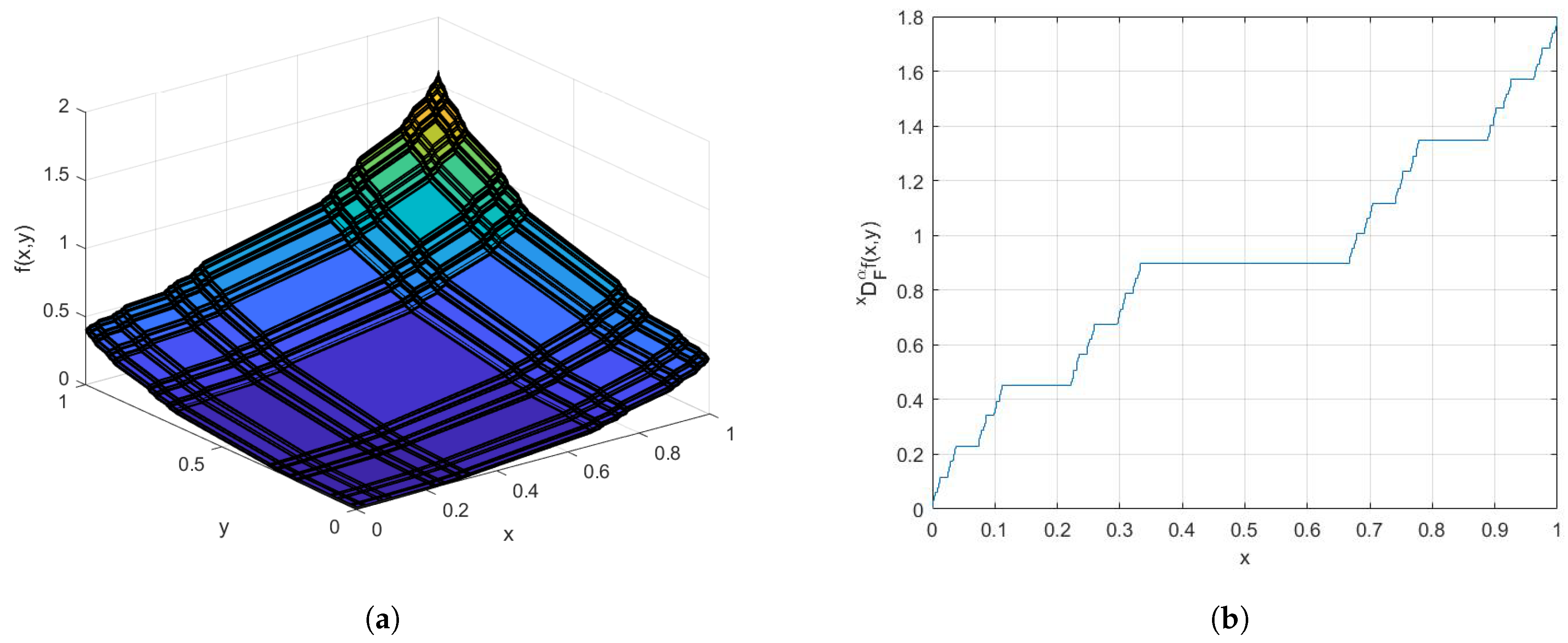
3. Example Functions with Cantor Tartan Support
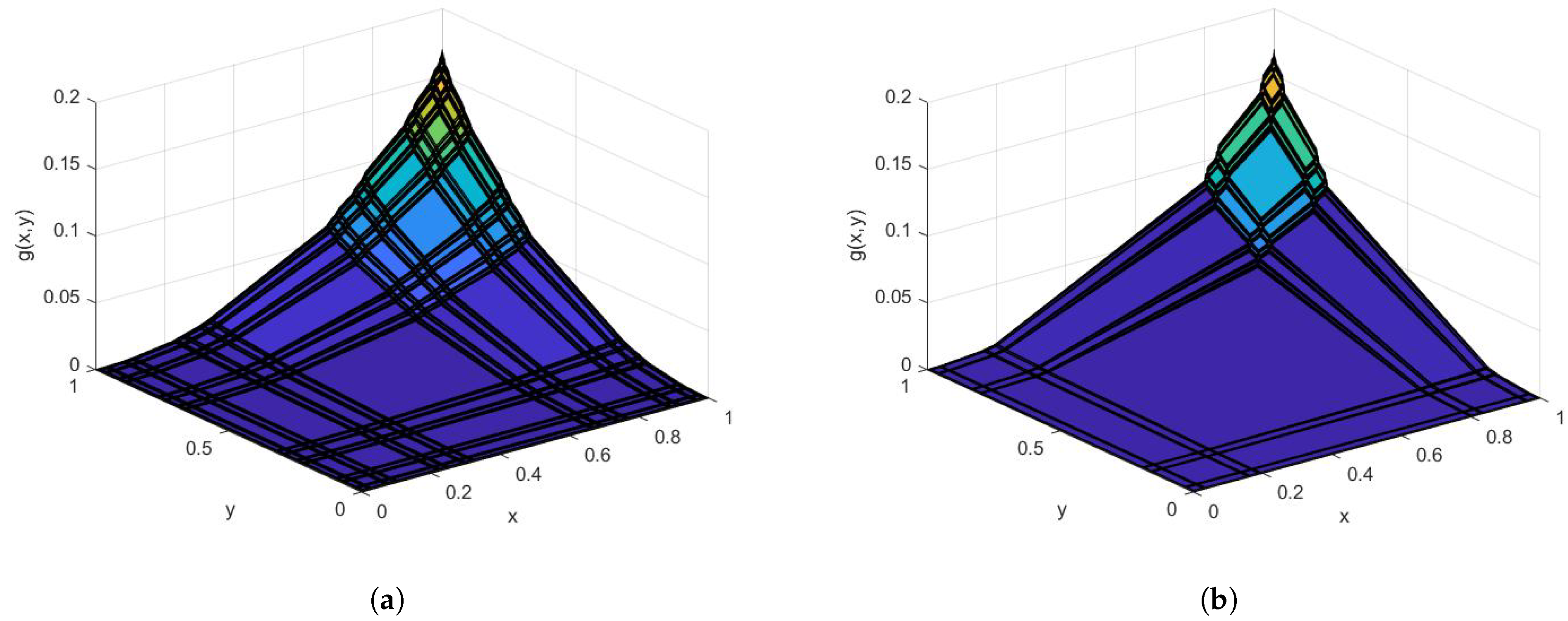
4. Anomalous Diffusion on the Fractal Cantor Tartan
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mandelbrot, B.B. The Fractal Geometry of Nature; W. H. Freeman and Company: New York, NY, USA, 1982. [Google Scholar]
- Falconer, K. Techniques in Fractal Geometry; John Wiley & Sons: Hoboken, NJ, USA, 1997. [Google Scholar]
- Cattani, C.; Pierro, G. On the fractal geometry of DNA by the binary image analysis. Bull. Math. Biol. 2013, 75, 1544–1570. [Google Scholar] [CrossRef] [PubMed]
- Heydari, M.H.; Hooshmandasl, M.R.; Maalek Ghaini, F.M.; Cattani, C. Wavelets method for the time fractional diffusion-wave equation. Phys. Lett. A 2015, 379, 71–76. [Google Scholar] [CrossRef]
- Freiberg, U.; Zahle, M. Harmonic calculus on fractals-a measure geometric approach I. Potential Anal. 2002, 16, 265–277. [Google Scholar] [CrossRef]
- Barlow, M.T.; Perkins, E.A. Brownian motion on the Sierpinski gasket, Probab. Theory Relat. Fields 1988, 79, 543–623. [Google Scholar] [CrossRef]
- Metzler, R.; Klafter, J. Boundary value problems for fractional diffusion equations. Phys. A Stat. Mech. Appl. 2000, 278, 107–125. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Bohner, M. Basic calculus on time scales and some of its applications. Results Math. 1999, 35, 3–22. [Google Scholar] [CrossRef]
- Agarwal, R.P.; Mahmoud, R.R.; Saker, S.H.; Tunc, C. New generalizations of Németh–Mohapatra type inequalities on time scales. Acta Math. Hung. 2017, 152, 383–403. [Google Scholar] [CrossRef]
- Kigami, J. Analysis on Fractals. Volume 143 of Cambridge Tracts in Mathematics; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Bohner, M.; Peterson, A. Dynamic Equations on Time Scales: An Introduction with Applications; Birkhäuser: Boston, MA, USA, 2001. [Google Scholar]
- Naqvi, Q.A.; Fiaz, M.A. Electromagnetic behavior of a planar interface of non-integer dimensional spaces. J. Electromagn. Waves Appl. 2017, 31, 625–1637. [Google Scholar] [CrossRef]
- Strichartz, R.S. Differential Equations on Fractals: A Tutorial; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Tarasov, V.E. Fractional Dynamics: Applications of Fractional Calculus to Dynamics of Particles, Fields and Media; Springer: New York, NY, USA, 2011. [Google Scholar]
- Brossard, J.; Carmona, R. Can one hear the dimension of fractal? Commun. Math. Phys. 1986, 104, 103–122. [Google Scholar] [CrossRef]
- Tatom, F.B. The relationship between fractional calculus and fractals. Fractals 1995, 3, 217–229. [Google Scholar] [CrossRef]
- Nigmatullin, R.R.; Zhang, W.; Gubaidullin, I. Accurate relationships between fractals and fractional integrals: New approaches and evaluations. Fract. Calc. Appl. Anal. 2017, 20, 1263–1280. [Google Scholar] [CrossRef]
- Butera, S.; Paola, M.D. A physically based connection between fractional calculus and fractal geometry. Ann. Phys. 2014, 350, 146–158. [Google Scholar] [CrossRef]
- Herrmann, R. Fractional Calculus: An Introduction for Physicists; World Scientific: London, UK, 2014. [Google Scholar]
- Hilfer, R. (Ed.) Applications of Fractional Calculus in Physics; World Scientific: London, UK, 2000. [Google Scholar]
- Nigmatullin, R.R.; Evdokimov, Y.K. The concept of fractal experiments: New possibilities in quantitative description of quasi-reproducible measurements. Chaos Soliton Fract. 2016, 9, 319–328. [Google Scholar] [CrossRef]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers Vol. 1 Background and Theory; Application Springer: Berlin, Germany, 2013; Volume 2. [Google Scholar]
- Wu, G.C.; Baleanu, D.; Xie, H.P.; Chen, F.L. Chaos synchronization of fractional chaotic maps based on stability results. Phys. A Stat. Mech. Appl. 2016, 460, 374–383. [Google Scholar] [CrossRef]
- Magin, R.L. Fractional Calculus in Bioengineering; Begell House Publisher, Inc.: Connecticut, CT, USA, 2006. [Google Scholar]
- Malinowska, A.B.; Torres, D.F.M. Introduction to the Fractional Calculus of Variations; Imperial College Press: London, UK, 2012. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Chen, W. Time-space fabric underlying anomalous diffusion. Chaos Solitons Fract. 2006, 28, 923–929. [Google Scholar] [CrossRef]
- Chen, W.; Sun, H.G.; Zhang, X.; Koroak, D. Anomalous diffusion modeling by fractal and fractional derivatives. Comp. Math. Appl. 2010, 59, 1754–1758. [Google Scholar] [CrossRef]
- Arkhincheev, V.E.; Baskin, E.M. Anomalous diffusion and drift in a comb model of percolation clusters. Sov. Phys. JETP 1991, 73, 161–300. [Google Scholar]
- Sandev, T.; Iomin, A.; Kantz, H. Fractional diffusion on a fractal grid comb. Phys. Rev. E 2015, 91, 032108. [Google Scholar] [CrossRef] [PubMed]
- Çetinkaya, A.; Kıymaz, O. The solution of the time-fractional diffusion equation by the generalized differential transform method. Math. Comput. Model. 2013, 57, 2349–2354. [Google Scholar] [CrossRef]
- Kameke, A.V.; Huhn, F.; Fernández-García, G.; Muñuzuri, V.; Pérez-Muñuzuri, A.P. Propagation of a chemical wave front in a quasi-two-dimensional superdiffusive flow. Phys. Rev. E 2010, 81, 066211. [Google Scholar] [CrossRef] [PubMed]
- Telcs, A. The Art of Random Walks; Springer: New York, NY, USA, 2006. [Google Scholar]
- Gianvittorio, J.P.; Rahmat-Samii, Y. Fractal antennas: A novel antenna miniaturization technique and applications. IEEE Antennas Propag. 2002, 44, 20–36. [Google Scholar] [CrossRef]
- Cohen, N. Fractal Antenna Applications in Wireless Telecommunications. In Proceedings of the Electronics Industries Forum of New England, Boston, MA, USA, 6–8 May 1997. [Google Scholar]
- Balankin, A.S.; Mena, B.; Susarrey, O.; Samayoa, D. Steady laminar flow of fractal fluids. Phys. Lett. A 2017, 381, 623–628. [Google Scholar] [CrossRef]
- Butera, S.; Di Paola, M. A physical approach to the connection between fractal geometry and fractional calculus. In Proceedings of the 2014 International Conference on Fractional Differentiation and Its Applications, ICFDA 2014, Catania, Italy, 23–25 June 2014; p. 6967378. [Google Scholar] [CrossRef]
- Balankin, A.S.; Mena, B.; Patino, J.; Morales, D. Electromagnetic fields in fractal continua. Phys. Lett. A 2013, 377, 783–788. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line I: Formulation. Fractals 2009, 17, 53–81. [Google Scholar] [CrossRef]
- Parvate, A.; Gangal, A.D. Calculus on fractal subsets of real line II: Conjugacy with ordinary calculus. Fractals 2011, 19, 271–290. [Google Scholar] [CrossRef]
- Seema, S.; Gangal, A.D. Langevin Equation on Fractal Curves. Fractals 2016, 24, 1650028. [Google Scholar]
- Golmankhaneh, A.K.; Fernandez, A.; Golmankhaneh, A.K.; Baleanu, D. Diffusion on middle-ξ Cantor sets. Entropy 2018, 20, 504. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Baleanu, D. Non-local Integrals and Derivatives on Fractal Sets with Applications. Open Phys. 2016, 14, 542–548. [Google Scholar] [CrossRef]
- Golmankhaneh, A.K.; Balankin, A.S. Sub-and super-diffusion on Cantor sets: Beyond the paradox. Phys. Lett. A 2018, 382, 960–967. [Google Scholar] [CrossRef]
- Balankina, A.S.; Golmankhaneh, A.K.; Patiño-Ortiza, J.; Patiño-Ortiz, M. Noteworthy fractal features and transport properties of Cantor tartans. Phys. Lett. A 2018, 382, 1534–1539. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Golmankhaneh, A.K.; Fernandez, A. Fractal Calculus of Functions on Cantor Tartan Spaces. Fractal Fract. 2018, 2, 30. https://doi.org/10.3390/fractalfract2040030
Golmankhaneh AK, Fernandez A. Fractal Calculus of Functions on Cantor Tartan Spaces. Fractal and Fractional. 2018; 2(4):30. https://doi.org/10.3390/fractalfract2040030
Chicago/Turabian StyleGolmankhaneh, Alireza Khalili, and Arran Fernandez. 2018. "Fractal Calculus of Functions on Cantor Tartan Spaces" Fractal and Fractional 2, no. 4: 30. https://doi.org/10.3390/fractalfract2040030
APA StyleGolmankhaneh, A. K., & Fernandez, A. (2018). Fractal Calculus of Functions on Cantor Tartan Spaces. Fractal and Fractional, 2(4), 30. https://doi.org/10.3390/fractalfract2040030





