Fatigue-Induced Cole Electrical Impedance Model Changes of Biceps Tissue Bioimpedance

Abstract

Bioimpedance, or the electrical impedance of biological tissues, describes the passive electrical properties of these materials. To simplify bioimpedance datasets, fractional-order equivalent circuit presentations are often used, with the Cole-impedance model being one of the most widely used fractional-order circuits for this purpose. In this work, bioimpedance measurements from 10 kHz to 100 kHz were collected from participants biceps tissues immediately prior and immediately post completion of a fatiguing exercise protocol. The Cole-impedance parameters that best fit these datasets were determined using numerical optimization procedures, with relative errors of within approximately $\pm 0.5\%$ and $\pm 2\%$ for the simulated resistance and reactance compared to the experimental data. Comparison between the pre and post fatigue Cole-impedance parameters shows that the $R_{\infty }$, $R_1$, and $f_p$ components exhibited statistically significant mean differences as a result of the fatigue induced changes in the study participants.

1. Introduction

Bioimpedance, or the electrical impedance of biological tissues, describes the passive electrical properties of these materials. The aim of collecting these measurements is to provide details regarding the electrochemical structures and processes within a tissue or material under study [1]. These measurements are being used in a wide range of applications including: As a method to monitor hydration during hemodialysis [2], to detect changes resulting from muscle injury [3], assessing lympoedema [4], and to assess neuromuscular disorders [5]. There is also a small set of studies that have investigated the bioimpedance of skeletal muscle for changes that result from fatigue [6,7,8].

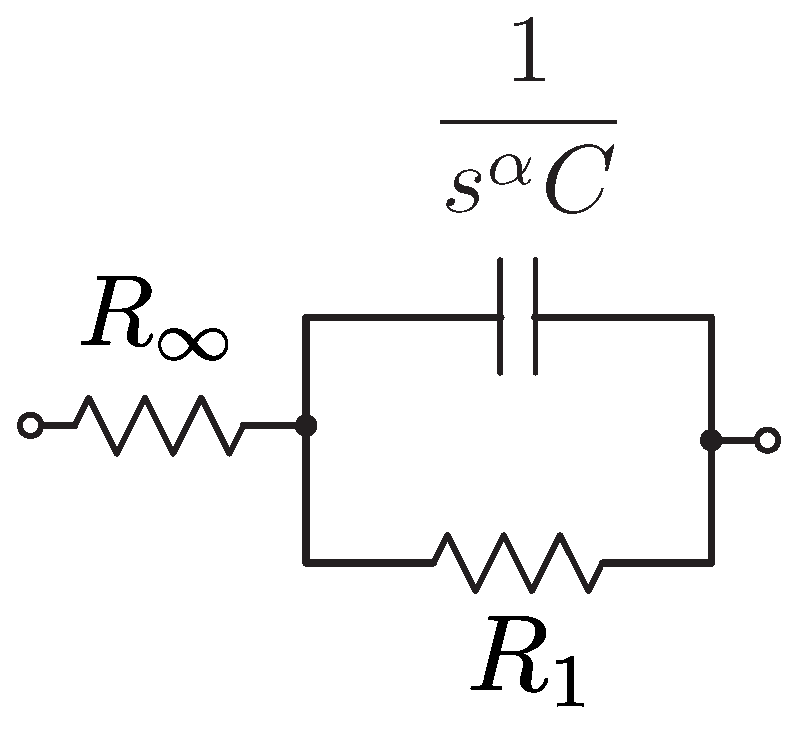
Regardless of the application, after collecting an impedance dataset (which may contain hundreds of data points at different frequencies) the data needs to be analyzed using either discrete frequencies or electrical equivalent circuit representations. Using equivalent electrical circuits can reduce a dataset from the potentially hundreds of datapoints to a smaller set (dependent on the number of circuit components in the model). This reduction is aimed at decreasing the complexity of tracking changes in the measured tissues. While there are many equivalent circuits that have been used to represent bioimpedance datasets [9], one of the most widely used is referred to as the Cole-impedance model [10], given in Figure 1. This model is composed of three hypothetical circuit elements. A high-frequency resistor $R_{\infty }$, a resistor $R_1$, and a Constant Phase Element (CPE). The impedance of a CPE is $Z_{CPE}=1/C{s}^{\alpha }$ where $s^{\alpha }={\left(j\omega \right)}^{\alpha }={\omega }^{\alpha }\left[cos(\alpha \pi /2)+jsin(\alpha \pi /2)\right]$. The value C is often referred to as a pseudo-capacitance with units Farad sec${}^{(\alpha -1)}$. The impedance of the Cole-model is given by:

$$Z\left(s\right)=R_{\infty }+\frac{R_1}{1+s^{\alpha }{R}_{1}C}$$

(1)

Recent studies have utilized the Cole-impedance model in biologic applications including: Characterizing the electrical impedance of blood for potential monitoring of thrombus formation [11], predicting myofiber size in mice [12], modeling the electrical impedance of botanical elements [13]. While this is not an exhaustive list, it does highlight the varied applications of the Cole-impedance model in biology. It is important to note that using a CPE (with the $s^{\alpha }$ term) implies a fractional derivative of order $0<\alpha <1$, with the current-voltage relationship for this component defined as:

$$i\left(t\right)=C\frac{d^{\alpha }v\left(t\right)}{d{t}^{\alpha }}$$

(2)

where $i\left(t\right)$ and $v\left(t\right)$ are the time-dependent current and voltage, respectively. This therefore places the Cole-impedance model within the domain of fractional-order systems. This field incorporates concepts from fractional calculus [14,15], the branch of mathematics concerning non-integer differentiation and integration, and is being widely explored to model biological phenomena [9,16,17,18]. One definition of a fractional derivative of order $\alpha$ is given by the Grünwald-Letnikov definition [19] as

$${}_a{D}^{\alpha }f\left(x\right)=\underset{h\to 0}{lim}\frac{1}{h^{\alpha }}\sum _{m=0}^{\left[\frac{x-a}{h}\right]}{\left(-1\right)}^m\frac{\Gamma \left(\alpha +1\right)}{m!\Gamma \left(\alpha -m+1\right)}f\left(x-mh\right)$$

(3)

where $\Gamma (·)$ is the gamma function and $n-1\le \alpha \le n$. Applying the Laplace transform to the fractional derivative of (3) with zero initial conditions yields

$$\mathcal{L}\left\{D_t^{\alpha }f\left(t\right)\right\}=s^{\alpha }F\left(s\right)$$

(4)

though other definitions, such as the Riemann-Liouville and Caputo definitions, are also available. While the fractional derivative given by (3) is not often referenced in studies of bioimpedance using the Cole-impedance model, it is still important to understand the underlying fractional-theory behind it.

When calculating (2) using sinusoidal voltages, for it to yield sinusoids requires the fractional derivative to be defined on the whole real line, as is typical of many bioimpedance applications. Therefore, the Grünwald-Letnikov, Riemann-Liouville, and Caputo on $\mathbb{R}$ definitions of fractional derivatives must be used [20]. This is important for impedance applications that are collected in experimental setups that apply a sinusoidal excitation signal and measure the corresponding sinusoidal output. For these cases, the correct definition must be used or else the fractional-order impedance model and experimental results will contradict each other. Fractional derivatives, upon which the Cole-impedance model is built, capture phenomena across multiple time scales overcoming the need to define tissue properties at the cellular level. Instead, these models assume that the behaviour is captured in the fractal structure of the tissue [16,17]. Recent research has shown the relationship between fractals and fractional calculus, based on physical and geometric considerations [21]. It was noted in [17] that muscle fibers, tendon, and nerve fibers exhibit patterns that support the dynamics of these multiscale structures expressed by fractional-order models. While these fractional-models fail to describe the underlying physiological mechanisms at the unit or cellular level that contribute to the impedance behavior of a tissue, recent works using fractional-order models to represent three-dimensional resistor-capacitor ($RC$) networks [22] support their application to model biological tissues; which are complex 3D structures of cells with both resistive and capacitive behaviour. Often, the bioimpedance of a tissue is described as being related to the extracellular fluid and intracellular fluid, with measurements at low frequency dependent on the extracellular fluids (attributed to low excitation frequencies failing to penetrate the cellular membranes of cells in the tissue) and high frequency measurements dependent on both intracellular and extracellular fluids (at frequencies where the excitation is able to penetrate the cellular membranes). Based on this interpretation, the model parameters $R_{\infty }$ and $R_1$ of the Cole-impedance model are associated with the tissue fluids and C, $\alpha$ are associated with the cellular membranes of the tissues.

While it has been previously shown that the bioimpedance at discrete frequencies (10 kHz, 50 kHz, and 100 kHz) of the biceps tissue does change due to exercise-induced fatigue [8] and that the biceps tissue bioimpedance can be well represented by the Cole-impedance model [23]; the changes in the Cole-impedance parameters that result from fatigue have not been deeply investigated. This study evaluates the parameters of the Cole-model equivalent electrical circuit that can represent bioimpedance datasets collected from the biceps tissues of participants immediately prior to and immediately post completion of a fatiguing exercise protocol; expanding on those analyses presented in [8,23]. In this work, the Cole-impedance parameters ($R_{\infty }$, $R_1$, C, $\alpha$) that represent the tissue bioimpedance of the left and right arms of 18 participants, separated into two different exercise intensity groups, are determined using numerical least squares optimization routines. These results of these optimization analyses are presented with statistical tests comparing the pre and post-fatigue measures executed to evaluate those changes that were statistically significant with discussions of these results and their implications.

2. Methods

2.1. Study Participants

This study collected measurements from the left and right biceps of 18 participants (15 males, 3 females, with an average age of $22.2\pm 3.2$ years) immediately prior to and immediately after completing an exercise protocol to fatigue the biceps brachii muscles. This study was reviewed and approved by the institutional review board of The University of Alabama (16-OR-234). All study participants were recruited from The University of Alabama and were screened prior to participation using a health questionnaire. Those participants who had any reported muscle or joint problems or who had any recent adverse reactions to exercise were excluded. Informed written consent was obtained from each participant prior to their inclusion in the study.

2.2. Exercise Protocol

Each participant executed a fatiguing exercise protocol using dumbbell biceps curls at either $60\%$ ($N=10$) or $75\%$ ($N=8$) of their previously assessed one-repetition maximum (1-RM) until task failure. The 1-RM value for each participant is the maximum weight that they were able to successfully lift for the dumbbell biceps curl exercise. The grouping of participants by intensity relative to their 1-RM weight was introduced to control for differences between the relative strengths of each participant, which could have an impact on the exercise induced changes. During this protocol, participants completed repetitions of the exercise until failure (this series of repetitions will be referred to as one set). After a two-minute rest the participants completed an additional set. This process continued until the participants had completed ten sets at which point the protocol was terminated.

2.3. Localized Electrical Impedance Measurements

The localized electrical impedance measurements were collected from each participant using a tetrapolar electrode configuration in which two current injection electrodes (I+, I−) were placed on the lateralis side of the biceps, 14 cm apart with the voltage sensing electrodes (V+, V−) placed $4.67$ cm apart. This electrode configuration is given in Figure 2. A fixed distance electrode configuration was used in this work over a configuration relative to each participants biceps dimensions to emulate expected configurations if this technique is integrated into wearable systems not tailored to each participants specific dimensions. For all collected measurements, participants were in a standing position and asked to relax their muscles with their arms resting naturally at the sides of their body. The impedance measures immediately prior to completed the protocol and immediately post-completion were collected using a Keysight E4990A impedance analyzer (Keysight Technologies: Santa Rosa, CA, USA) with a custom-interface to adapt the BNC-connectors of the E4990A to a cable-set with the required snap connectors for the Ag/AgCl electrodes. Using this setup, which is detailed in Figure 2, measurements were collected from 10 kHz to 100 kHz at 67 logarithmically spaced frequencies. This frequency range was selected because it is widely employed in bioimpedance applications [6]. It should be noted that before data collection, the Keysight E4990A was calibrated using the open/short/load procedure with the developed interface. Further details of this interface and its accuracy evaluation are detailed in [8]. Examples of the impedance collected from the left and right biceps of two participants are given in Figure 3 as solid lines, with the pre-fatigue values given as black lines and the post-fatigue values as blue lines.

2.4. Nonlinear Least Squares Fitting

The Cole-impedance parameters ($R_{\infty }$, $R_1$, C, $\alpha$) that best fit the model given by (1) for each collected dataset in this study were determined using a nonlinear least squares fitting (NLSF) procedure. This procedure iteratively attempts to numerically solve the problem

$$\begin{array}{ccc}\hfill \underset{x}{min}{f}_0\left(x\right)& =& \sum _{j=1}^n{\left(Z(x,{\omega }_j)-y_j\right)}^2\hfill \\ \hfill \mathrm{s}.\mathrm{t}.x& >& 0\hfill \end{array}$$

(5)

where x is the set of impedance parameters ($R_{\infty }$, $R_1$, C, $\alpha$) to minimize $f_o\left(x\right)$ (the objective function), $Z(x,{\omega }_j)$ is the impedance of (1) at frequency ${\omega }_j$, $y_j$ is the collected impedance at frequency ${\omega }_j$, and n is the total number of data points in the collected response. A constraint is added to the problem to limit the possible solutions to real values; because negative resistance and capacitance values are not physically possible. However, because the impedance is a complex value, many numerical solvers are not able to solve this problem and it requires that the objective function given in (5) be revised to separate and fit the real and imaginary components of the impedance. Applying this separation to (5) yields:

$$\begin{array}{ccc}\hfill \underset{x}{min}{f}_0\left(x\right)& =& \sum _{j=1}^n{\left(\Re \{Z(x,{\omega }_j)-y_j\}+\Im \{Z(x,{\omega }_j)-y_j\}\right)}^2\hfill \\ \hfill \mathrm{s}.\mathrm{t}.x& >& 0\hfill \end{array}$$

(6)

where $\Re \{·\}$ and $\Im \{·\}$ denote the real and imaginary components, respectively. There are a variety of solvers available for this class of problem, which include the MATLAB optimization functions (lsqcurvefit, fmincon, fminsearch). The least squares method is not the only optimization method available for this class of problem; methods including particle swarm optimization and other biologically inspired algorithms having been investigated [24,25,26]. Now while those alternative methods have shown very good results in terms of both accuracy and execution speed [26], the least squares method is applied in this work because of its widely available MATLAB implementation.

Algorithm 1 Sample MATLAB Code to Extract Cole-Impedance Parameters from Experimental Impedance Data

% Requires:    %          Experimental impedance (Ohms) stored in variable Z    %          Frequency range (Hz) of Z stored in variable f            % Step 1: Setup function (ColeZ) to generate Cole-impedance   % P(1) → R_\infty, P(2) → R1, P(3) → C, P(4) → alpha        w = 2 ∗ pi ∗ f;        ColeZ = @(P) (P(1) + P(2)./(1 + (1i ∗ w).${}^{\wedge }$P(4) ∗ P(2) ∗ P(3)));           % Step 2: Setup objective function to minimize (Least Squares)        objfun = @(P) sum((real(Z) − real(ColeZ(P))).${}^{\wedge }$2 + (imag(Z) − imag(ColeModel(P))).${}^{\wedge }$2);           % Step 3: Setup constraints for fmincon         A = []; b = []; Aeq = []; beq = []; nonlcon = [];        lb = [0, 0, 0, 0];                                 % Lower search boundary        ub = [inf, inf, inf, inf];                    % Upper search boundary        options = optimoptions(’fmincon’);           % Step 4: Generate random initial iterates for solver        InitialIterates = 100;        x0 = zeros(InitialIterates, 4);        lb2 = [1 1 −9 0.5];        for k = 1:1:4               x0(:,k) = lb2(k) + (ub2(k)-lb2(k)). ∗ rand(InitialIterates,1);        end         x0(:,3) = 10.${}^{\wedge }$x0(:,3);            % Step 5: Execution of optimization search for Cole parameters        MinError = inf        for m = 1:1:InitialIterates              [ColeParameters, ObjFunValue]=fmincon(objfun, x0, A, b, Aeq, beq, lb, ub, nonlcon, options);              if (ObjFunValue < MinError)                      BestFitCole = ColeParameters;                      MinError = ObjFunValue;              end        end

The NLSF is susceptible to the local minima problem, where a solution that is not the global solution may meet the stopping criteria of the solver. To overcome this challenge, the solver was applied 100 times to the simulated dataset using a different initial iterate for each execution. This method was previously implemented in [27], with the execution that yielded the lowest objective function selected as the global solution. Each of the initial iterates were randomly generated within the ranges $1\Omega <R_{0,1}<50\Omega$, $0.1\mathrm{nF}<C<100\mu \mathrm{F}$, and $0.5<\alpha <1$. The intent of this approach is for at least one of the generated initial iterates to be very close to the global solution, which improves the likelihood of returning the global solution and avoiding a local minima when the ending criteria of the solver are satisfied. A sample of MATLAB code (Algorithm 1) is presented to detail this setup of the required functions to use the fmincon function. This implementation takes advantage of the inbuilt MATLAB functions real and imag to separate the real and imaginary components of both experimental measurements and the Cole-impedance model; which eliminates the need to determine the algebraic representations of the real and imaginary components of (1) to implement the objective function to minimize.

3. Results

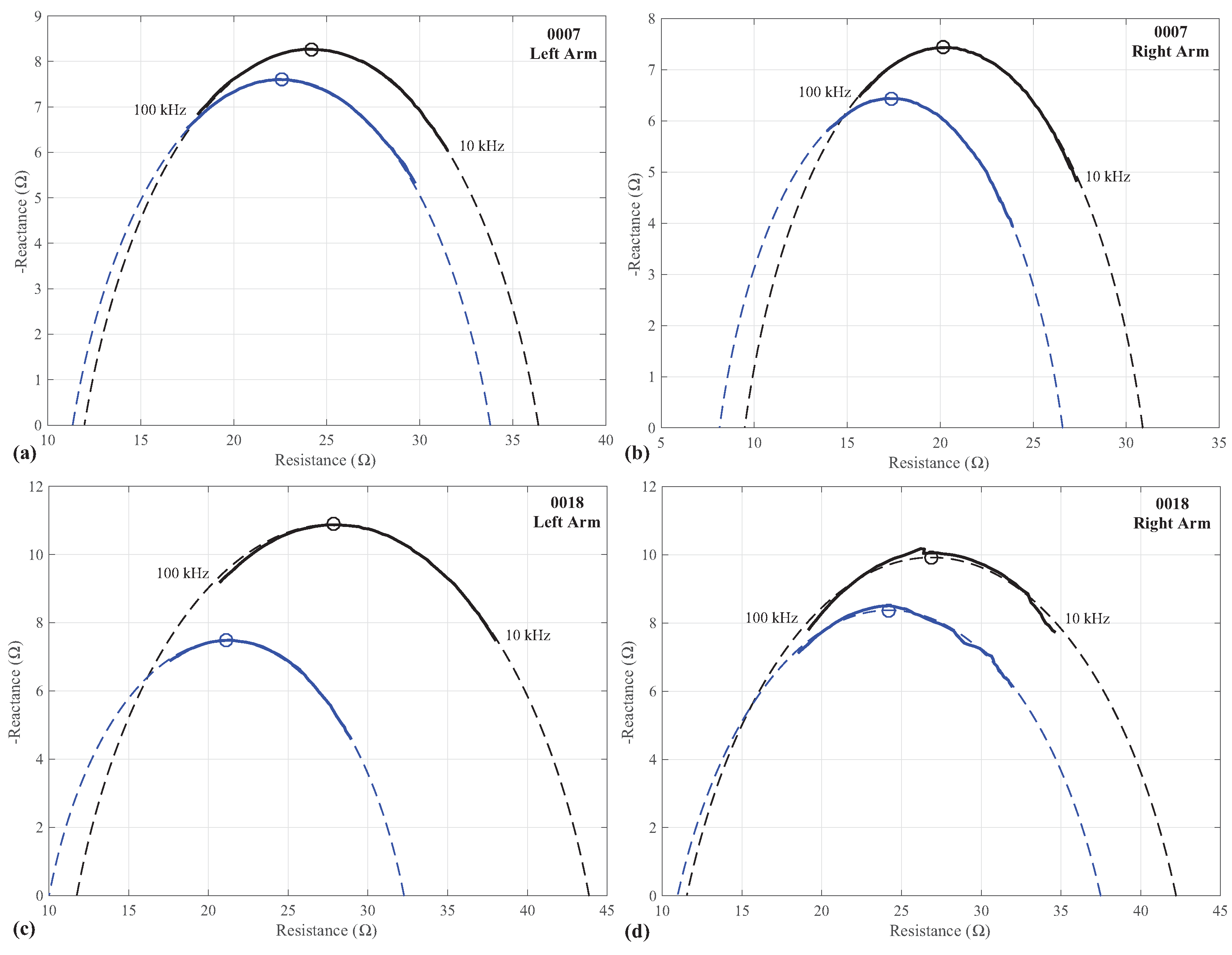
The complete set of Cole-impedance parameters extracted from the pre- and post-fatigue measurements of participants in the $60\%$ and $75\%$ exercise-intensity groups are given in

Table 1. Extracted equivalent circuit parameters from pre- and post-fatigue impedance measured from the left and right biceps of participants in the $60\%$ one-repetition maximum (1-RM) group.

Participant	${\mathit{R}}_{\mathbf{\infty }}$ ($\mathsf{\Omega }$)		${\mathit{R}}_1$ ($\mathsf{\Omega }$)		C (F sec${}^{(\mathit{\alpha }-1)}$)		$\mathit{\alpha }$		${\mathit{f}}_{\mathit{p}}$ (kHz)
	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post
Left Biceps
0001	$14.9$	$13.3$	$30.3$	$27.2$	$3.41\mu$	$2.05\mu$	$0.733$	$0.741$	$43.8$	$51.2$
0002	$17.4$	$15.6$	$40.1$	$34.4$	$1.70\mu$	$1.86\mu$	$0.768$	$0.759$	$42.5$	$53.4$
0003	$15.5$	$14.6$	$23.4$	$21.4$	$2.55\mu$	$2.34\mu$	$0.758$	$0.766$	$59.1$	$65.1$
0004	$28.2$	$28.5$	$36.4$	$29.1$	$5.06\mu$	$3.52\mu$	$0.676$	$0.719$	$52.7$	$55.8$
0005	$18.7$	$15.8$	$32.3$	$27.1$	$1.76\mu$	$1.82\mu$	$0.756$	$0.755$	$65.4$	$80.6$
0006	$15.0$	$15.5$	$33.6$	$29.1$	$3.75\mu$	$2.49\mu$	$0.717$	$0.753$	$43.4$	$50.0$
0007	$22.4$	$21.8$	$25.9$	$22.8$	$4.07\mu$	$2.69\mu$	$0.722$	$0.737$	$51.4$	$53.5$
0008	$15.4$	$14.0$	$34.8$	$29.2$	$1.88\mu$	$1.81\mu$	$0.759$	$0.768$	$51.6$	$58.5$
0009	$12.3$	$9.9$	$31.5$	$22.5$	$2.23\mu$	$3.36\mu$	$0.768$	$0.747$	$40.5$	$52.4$
0010	$28.0$	$27.3$	$36.4$	$36.7$	$6.39\mu$	$8.87\mu$	$0.658$	$0.627$	$53.3$	$58.4$
Right Biceps
0001	$10.9$	$9.3$	$26.3$	$25.7$	$3.24\mu$	$4.27\mu$	$0.745$	$0.723$	$45.7$	$47.6$
0002	$15.5$	$14.8$	$31.4$	$24.6$	$1.98\mu$	$2.08\mu$	$0.779$	$0.779$	$40.1$	$51.7$
0003	$16.5$	$14.7$	$24.9$	$23.2$	$1.95\mu$	$1.95\mu$	$0.781$	$0.776$	$53.5$	$62.6$
0004	$30.5$	$30.0$	$38.7$	$33.2$	$8.20\mu$	$6.58\mu$	$0.632$	$0.655$	$55.0$	$62.2$
0005	$16.6$	$15.4$	$31.1$	$24.5$	$1.75\mu$	$1.75\mu$	$0.761$	$0.774$	$64.1$	$69.7$
0006	$10.5$	$10.7$	$26.8$	$24.4$	$2.80\mu$	$2.28\mu$	$0.741$	$0.760$	$59.3$	$63.0$
0007	$20.0$	$19.1$	$25.5$	$22.1$	$4.40\mu$	$2.67\mu$	$0.719$	$0.736$	$49.3$	$57.6$
0008	$14.4$	$13.8$	$34.6$	$30.5$	$2.64\mu$	$2.68\mu$	$0.747$	$0.748$	$41.1$	$46.4$
0009	$11.4$	$10.9$	$30.9$	$26.6$	$4.45\mu$	$5.33\mu$	$0.727$	$0.715$	$32.6$	$38.4$
0010	$28.6$	$28.3$	$41.9$	$36.7$	$11.4\mu$	$9.83\mu$	$0.604$	$0.619$	$50.7$	$58.5$
Mean	$18.1$	$17.2{}^{*}$	$31.8$	$27.6{}^{*}$	$3.78\mu$	$2.47\mu$	$0.728$	$0.733$	$49.8$	$56.8{}^{*}$
Std. Dev.	$6.21$	$6.51$	$5.30$	$4.76$	$2.40\mu$	$2.32\mu$	$0.049$	$0.047$	$8.56$	$9.15$

Note: (${}^{*}$) denotes that there is a statistically significant ($p<0.05$) difference between the pre-fatigue and post-fatigue means.

and

Table 2. Extracted equivalent circuit parameters from pre- and post-fatigue impedance measured from the left and right biceps of participants in the $75\%$ 1-RM group.

Participant	${\mathit{R}}_{\mathbf{\infty }}$ ($\mathsf{\Omega }$)		${\mathit{R}}_1$ ($\mathsf{\Omega }$)		C (F sec${}^{(\mathit{\alpha }-1)}$)		$\mathit{\alpha }$		${\mathit{f}}_{\mathit{p}}$ (kHz)
	Pre	Post	Pre	Post	Pre	Post	Pre	Post	Pre	Post
Left Biceps
0011	$20.5$	$19.6$	$28.1$	$25.4$	$8.88\mu$	$10.1\mu$	$0.666$	$0.659$	$40.8$	$44.7$
0012	$13.5$	$14.4$	$33.3$	$25.3$	$6.48\mu$	$2.98\mu$	$0.704$	$0.779$	$25.5$	$30.9$
0013	$12.0$	$11.2$	$24.4$	$22.8$	$3.38\mu$	$3.82\mu$	$0.760$	$0.750$	$27.4$	$41.4$
0014	$32.3$	$33.0$	$50.8$	$44.8$	$13.1\mu$	$14.6\mu$	$0.552$	$0.552$	$90.2$	$93.8$
0015	$19.4$	$15.5$	$26.5$	$27.2$	$16.3\mu$	$13.2\mu$	$0.584$	$0.584$	$91.5$	$125.7$
0016	$13.3$	$12.7$	$34.3$	$31.1$	$2.70\mu$	$2.70\mu$	$0.755$	$0.756$	$34.9$	$39.1$
0017	$20.2$	$18.1$	$34.2$	$24.0$	$4.47\mu$	$3.56\mu$	$0.697$	$0.734$	$45.8$	$55.9$
0018	$24.0$	$23.2$	$24.7$	$22.0$	$6.38\mu$	$5.67\mu$	$0.704$	$0.713$	$40.0$	$47.7$
Right Biceps
0011	$20.7$	$18.6$	$25.1$	$21.3$	$6.81\mu$	$7.53\mu$	$0.706$	$0.702$	$34.2$	$40.7$
0012	$16.6$	$14.9$	$33.3$	$33.0$	$3.67\mu$	$3.41\mu$	$0.747$	$0.746$	$27.5$	$31.4$
0013	$9.5$	$8.0$	$21.4$	$18.5$	$2.83\mu$	$2.94\mu$	$0.774$	$0.775$	$44.9$	$51.0$
0014	$34.4$	$33.3$	$38.8$	$34.3$	$6.76\mu$	$7.26\mu$	$0.624$	$0.628$	$86.6$	$87.6$
0015	$28.8$	$29.0$	$31.5$	$33.2$	$6.74\mu$	$9.09\mu$	$0.625$	$0.602$	$118.9$	$112.0$
0016	$15.0$	$13.4$	$40.1$	$32.5$	$2.39\mu$	$2.03\mu$	$0.753$	$0.779$	$34.5$	$37.0$
0017	$20.3$	$18.8$	$33.3$	$27.1$	$2.56\mu$	$2.50\mu$	$0.731$	$0.742$	$59.0$	$65.9$
0018	$24.9$	$23.0$	$28.9$	$24.7$	$6.39\mu$	$5.42\mu$	$0.690$	$0.705$	$41.3$	$49.7$
Mean	$20.3$	$19.2{}^{*}$	$31.8$	$27.9{}^{*}$	$6.24\mu$	$6.05\mu$	$0.692$	$0.700$	$53.3$	$59.7{}^{*}$
Std. Dev.	$7.18$	$7.48$	$7.33$	$6.55$	$3.88\mu$	$3.92\mu$	$0.066$	$0.073$	$27.8$	$29.3$

Note: (${}^{*}$) denotes that there is a statistically significant ($p<0.05$) difference between the pre-fatigue and post-fatigue means.

, respectively. To visualize the agreement between simulations using the extracted parameters and the measured impedance, two representative cases are provided in Figure 3 for participants 0007 and 0018. These particular datasets were selected because they represent the best and worst fittings, as evaluated by the average absolute error of the simulations compared to the experimental data. The simulations using the Cole-impedance parameters are presented in Figure 3 as dashed lines, with the experimental data presented as solid lines. The Cole-impedance model was simulated from 1 mHz to 100 MHz to highlight the impedance-arc which is not fully captured in the experimental data frequency range of 10 kHz to 100 kHz. This visualizes how using the Cole-impedance model parameters supports extrapolating the theoretical low and high frequency impedance values.

Additionally, the frequency at which the reactance reaches its peak value ($f_p={\omega }_p/2\pi =1/2\pi {\left(R_{1}C\right)}^{(1/\alpha )}$) was determined using the extracted Cole-impedance model parameters for the left and right arms of each participant. These values are also given in Table 1 and Table 2. Samples of these calculated peak reactances using the values in Table 1 and Table 2 are given in Figure 3 as (o) symbols.

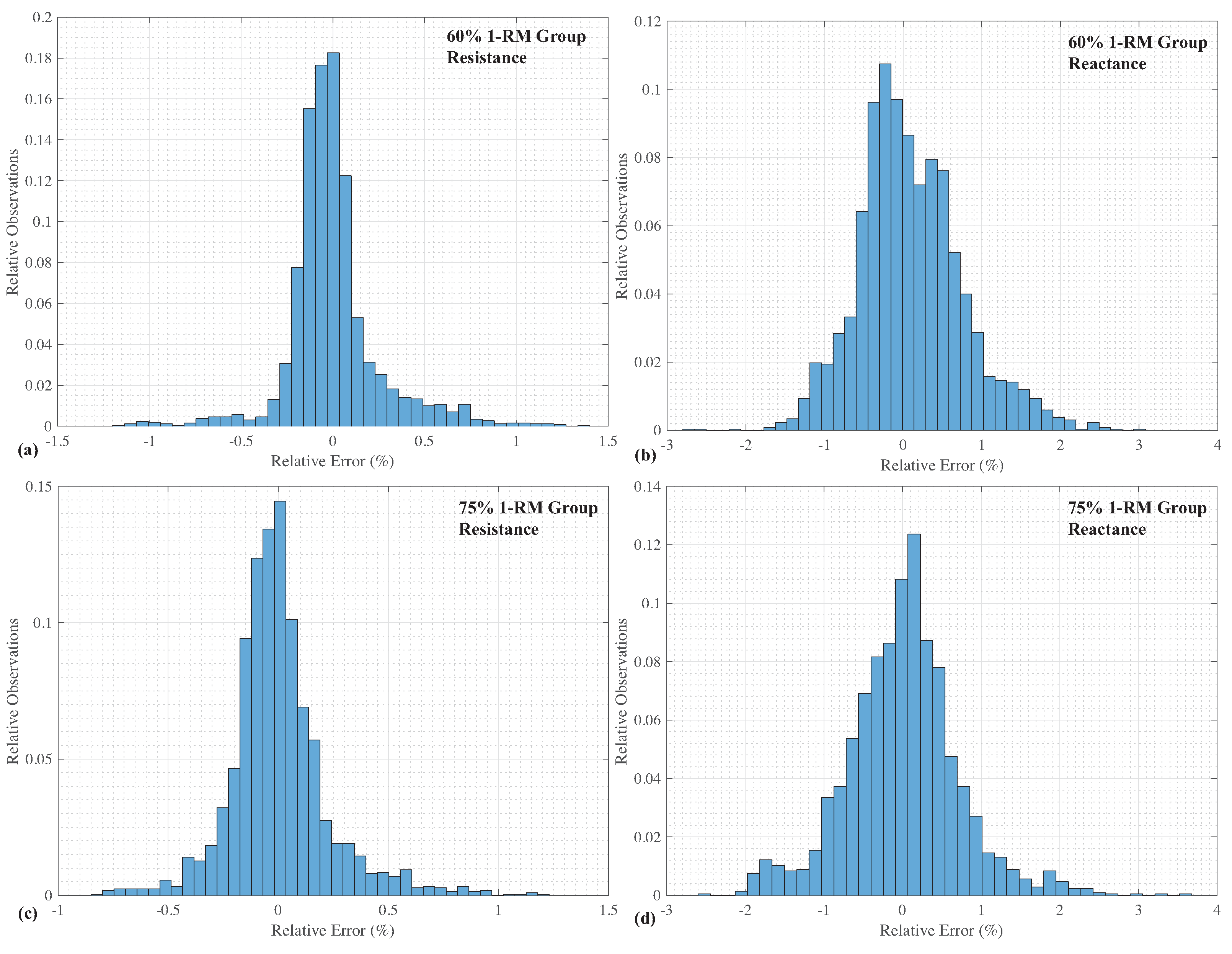
To fully detail the agreement between the experimental data and simulations using the extracted circuit parameters, relative error distributions of the resistance and reactance of both groups of participants are given in Figure 4. From these distributions, the relative errors of the resistances (given in Figure 4a,c) are predominately grouped between $\pm 0.5\%$, while the reactances (given in Figure 4b,d) show a wider grouping between $\pm 2\%$. This supports that the fitting process achieves better agreement with the resistance data than the reactance data, but both still show very good agreement with the experimental data.

Statistical Tests

Paired-samples t-tests (SPSS, IBM Inc.) were used to determine whether there was a statistically significant ($p<0.05$) difference between the mean values of the Cole-impedance model parameters extracted from the pre-fatigue and post-fatigue datasets for both the $60\%$ and $75\%$ groups of participants. These tests were applied to those datasets that did not violate the assumption of normality as assessed by the Shapiro-Wilk’s test. Based on these tests, there were statistically significant differences between the pre/post fatigue $R_{\infty }$ ($p<0.0005,p=0.001$), $R_1$ ($p<0.0005,p<0.0005$), and $f_p$ ($p<0.0005,p=0.008$) means for both the $60\%$ and $75\%$ groups. There were no statistically significant differences between the pre/post fatigue means of C ($p=0.603$) and $\alpha$ ($p=0.223$) for the $60\%$ group.

It should be noted that the C and $\alpha$ datasets for the $75\%$ 1-RM group violated the assumption of normality as assessed by the Shapiro-Wilk’s test with $p=0.007$ and $p<0.0005$, respectively. Due to these violations of normality, the statistical comparisons of the pre- and post-fatigue values were tested using a Wilcoxon signed-rank test. Using this test it was determined that there were no statistically significant differences in the median values of both C ($p=0.612$) and $\alpha$ ($p=0.160$) in this group, similar to the testing of the $60\%$ group. All post-fatigue means that show a statistically significant difference are denoted using the (${}^{*}$) symbol in Table 1 and Table 2.

4. Discussion

In this work, a total of 72 impedance datasets (18 participants with two biceps each and two measurements per biceps) were fit to the Cole-model given by (Figure 1), expanding on the preliminary fitting of five datasets in [23]. The low errors of both resistance and reactance between the Cole-impedance model using the extracted parameters and the experimental measurements, observed in the relative error distribution of Figure 4, continues to support that this model is a very good choice for representing biological tissue impedance in this frequency range (1 kHz to 100 kHz). This highlights that this fractional-order model can accurately represent the frequency-dependent impedance behaviour of these tissues. The range of extracted values of $\alpha$, $0.552\le \alpha \le 0.781$ support that these tissues are well represented by a fractional-order, as these values are far from the integer order case of $\alpha =1$ that would occur otherwise.

From the experimental measurements, there are changes in resistance and reactance comparing the pre and post fatigue measurements of the participants biceps tissues. Samples of these changes were given in Figure 3 for participants 0007 and 0018. These changes result in differences of the Cole-impedance parameters that represent these impedance datasets in the pre and post fatigue states. Based on the statistical testing of the extracted model parameters, only $R_{\infty }$, $R_1$, and $f_p$ show a statistically significant ($p<0.05$) difference between the pre-fatigue and post-fatigue states for both groups of participants. The resistance parameters of the $60\%$ group had mean decreases of $5.0\%$ and $13.2\%$ for $R_{\infty }$ and $R_1$, respectively, with the $75\%$ group having mean decreases of $5.4\%$ and $12.3\%$. The decrease in resistance parameters is consistent with the previous studies investigating skeletal muscle fatigue using bioimpedance measurements [6,7]. These studies hypothesized that the decreases in resistance may be the result of mechanisms that include: (i) increased blood flow to the muscle due to the hemodynamic response to exercise [7], (ii) heat dissipation in the tissue increasing cutaneous blood flow and vasodilation [7], and (iii) an increase in metabolites in the tissue increasing its electrical conductivity [6]. An increase in muscle edema paired with a decrease in muscle quality has been hypothesized as the reason for decreased muscular strength following exercise [28]. Localized edema is expected to increase the available charge carriers in the region resulting in the decreased tissue resistance observed after the participants completed the exercise protocol. However, a limitation of this study is that the circumference of each participants biceps pre and post fatigue were not measured to quantify the association between the resistance parameters in the Cole-impedance model and swelling.

It is interesting to note that the C and $\alpha$ parameters did not have a statistically significant change between the immediately pre and immediately post exercise data in either of the groups measured in this study. While the discrete 10 kHz, 50 kHz, and 100 kHz reactance measurements did show a statistically significant difference between pre and post-fatigue measurements in the study participants [8], this may be an effect of the interactions between the resistive and capacitive components contributing to the overall real and imaginary components of the impedance. To highlight the complex interactions between components, the real and imaginary components of the Cole-impedance given by (1) have been separated to yield the expression:

$$Z=\left[R_{\infty }+\frac{R_1\left(1+{\omega }^{\alpha }{R}_{1}Ccos\left(\frac{\alpha \pi }{2}\right)\right)}{1+2{\omega }^{\alpha }{R}_{1}Ccos\left(\frac{\alpha \pi }{2}\right)+{\omega }^{2\alpha }{R}_1^2{C}^2}\right]-j\left[\frac{R_1\left(w^{\alpha }{R}_{1}Csin\left(\frac{\alpha \pi }{2}\right)\right)}{1+2{\omega }^{\alpha }{R}_{1}Ccos\left(\frac{\alpha \pi }{2}\right)+{\omega }^{2\alpha }{R}_1^2{C}^2}\right]$$

(7)

Note that the imaginary term in (7) has contributions from $R_1$, C, and $\alpha$, so that changes in the measured reactance are not a result of only changes in C and $\alpha$. Therefore, changes in $R_1$ will result reactance changes without changes in C or $\alpha$, which could explain the significant changes in reactance reported in [8] without the significant changes in this analysis. 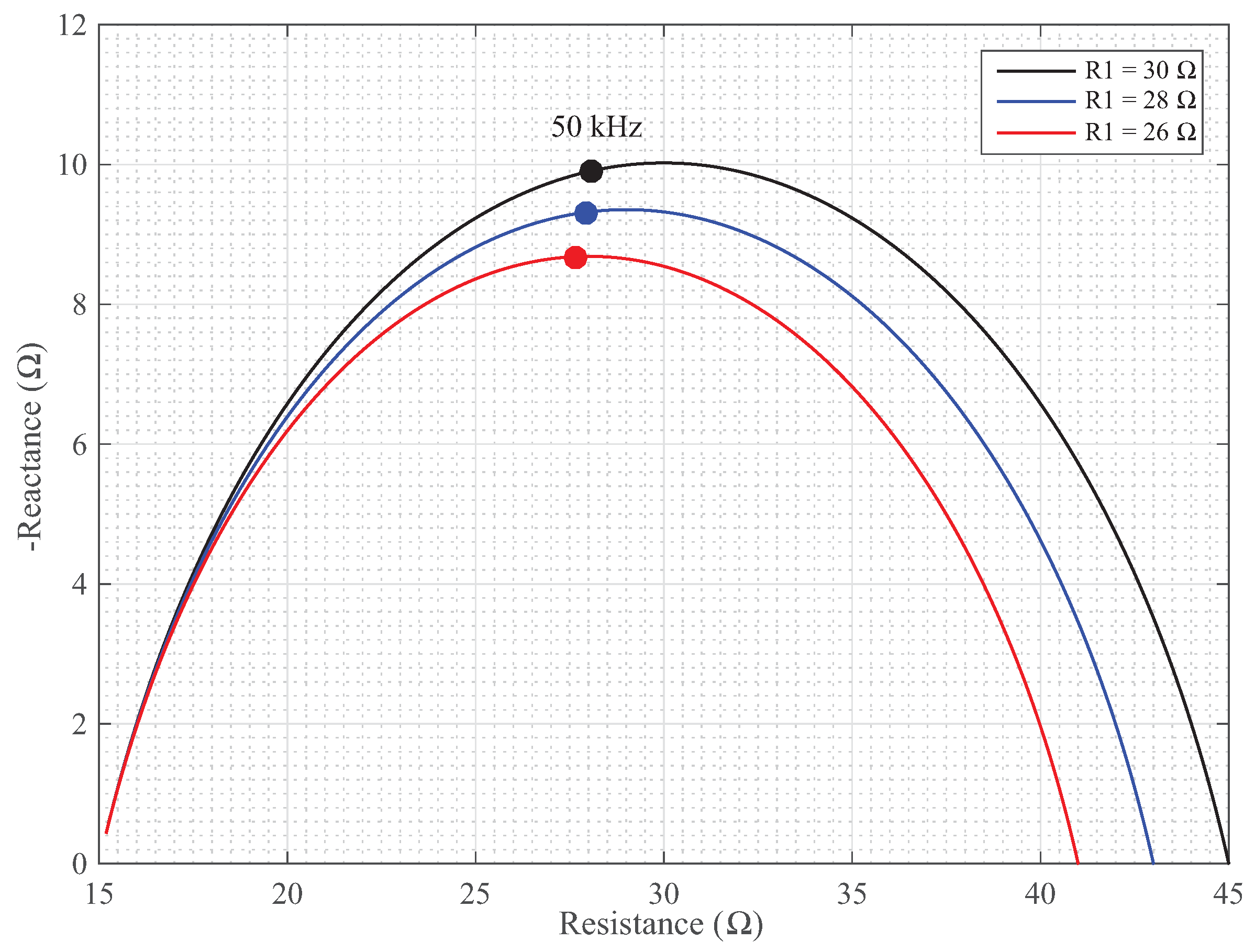To highlight this, a simulation of (7) with $R_{\infty }=15$ $\Omega$, $C=3$ $\mu$F sec${}^{(\alpha -1)}$, $\alpha =0.75$ and $R_1=30$ $\Omega$, 28 $\Omega$, and 26 $\Omega$ are given in Figure 5. Each of these simulations have different reactances even though only the $R_1$ value is varied. Further, the impedances at 50 kHz are given on each simulation case as a solid (·), which show a decrease with the decreasing $R_1$ values.

This also raises questions about which component of measured bioimpedance is the most appropriate marker to monitor changes that are a result of muscle damage, discrete reactances or capacitive components of electrical circuit representations. Previous work by Sanchez et al. investigating the bioimpedance changes in mice after injury supports that the capacitive component of the Cole-model is sensitive to changes from injury [29], which could indicate that the exercise protocol in this study, while fatiguing the participants, did not induce detectable levels of skeletal muscle damage. However, since this work did not collect markers to assess the localized tissue damage in participants it cannot be determined and will require follow-up investigations that collect further markers of tissue damage in addition to the participant bioimpedance measures. While the C and $\alpha$ changes in this study were not significant, the trend of decreasing resistance components and increases in the peak reactance frequency are consistent with changes that were observed in [29].

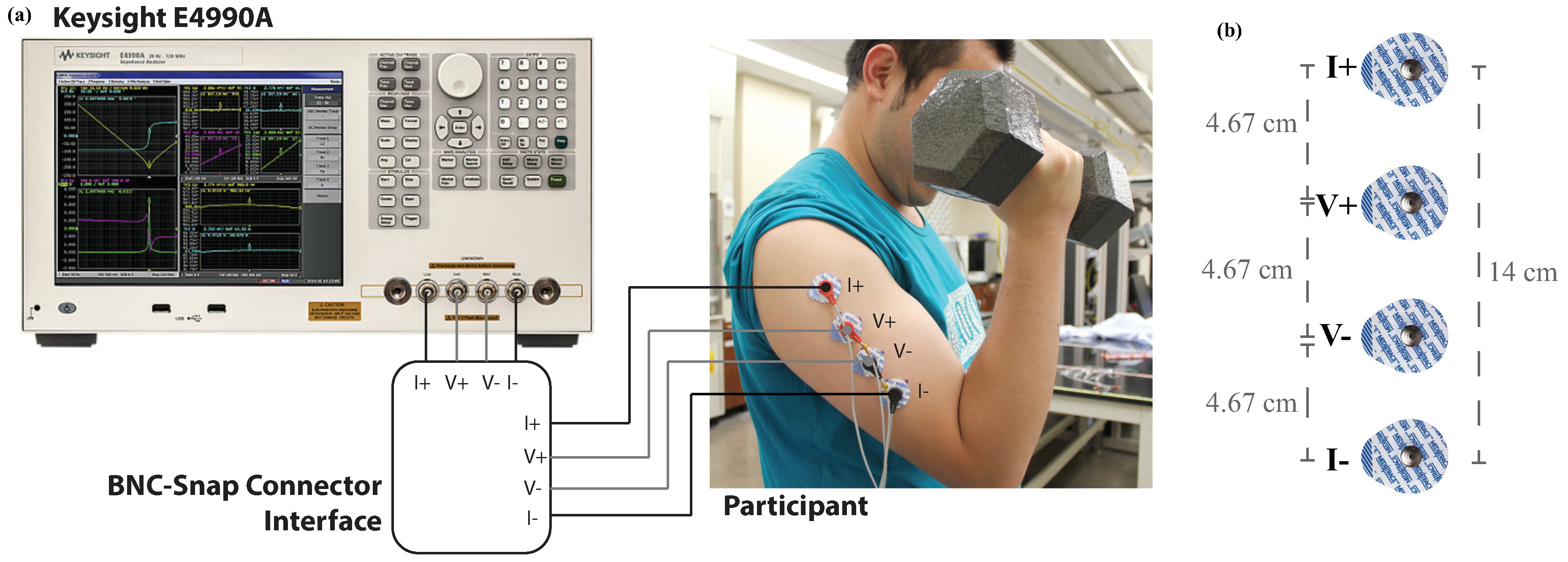
It is important to note that electrode positioning has a significant impact on the measured electrical impedance of localized tissues [30] yet there is no widely adopted process to standardize electrode placement for localized bio-impedance measurements; though recent guidelines have been proposed [31]. A limitation of this work is that the use of only a single-electrode configuration on the study participants fails to provide the data necessary to evaluate the optimum configuration to detect changes in the localized tissues due to exercise and fatigue.

Referring to the distortions that are observed in the impedance measures of the right arm of participant 0018, given in Figure 3d, these distortions may be an artifact of the measurement setup, specifically, resulting from the time required to apply the stepped-sine excitations to collect the measurements from 10 kHz to 100 kHz. For this series of tests, the Keysight E4990A was configured to measure at its highest accuracy setting, which required $0.2$ s per measured frequency for a total of $13.6$ s for the measurement from 10 kHz to 100 kHz. Even though participants were asked to relax their arms and remain motionless, there could have been variations in arm position and changes in the contraction of muscles which could have altered the electrical impedance of the tissue at each instant. This is a known limitation of the measurement of impedances using stepped sines for time-invariant impedances [32]. To reduce the potential impact of the time variant measures for future studies using the Keysight E4990A for bioimpedance studies, the measurement time could be reduced. However, this will reduce the accuracy of collected measurements and needs to be investigated to determine the correct balance of measurement time/accuracy for these applications. Also, additional sensor data could be collected during bioimpedance measures to assess motion and posture to evaluate windows during which movement artifacts will not be impacting the bioimpedance data; with this approach having been implemented for wearable systems to assess knee joint health [33].

5. Conclusions

We conclude that the Cole-impedance model does provide a very good fit to the measured electrical impedance of the biceps tissues from 10 kHz to 100 kHz of the participants in this study during both rested and fatigued states. This model shows very good agreement with the experimental data with less than $\pm 0.5\%$ and $\pm 2\%$ relative errors comparing the simulations using the Cole-model and extracted parameters to the experimental data, continuing to support the use of fractional-order circuit models to represent the frequency-dependent behaviour of biological tissues. The $R_{\infty }$, $R_1$, and $f_p$ components of the Cole-model each exhibited statistically significant differences comparing pre and post-fatigue data in both groups of participants, supporting that these components may be an effective marker of fatigue-induced changes of the skeletal muscle. The changes in resistance parameters $R_{\infty }$ and $R_1$ are expected to be a result of the localized tissue edema after the exercise protocol, but further studies are required to quantify this association.