Minkowski Dimension and Explicit Tube Formulas for p-Adic Fractal Strings

Abstract

The theory of complex dimensions describes the oscillations in the geometry (spectra and dynamics) of fractal strings. Such geometric oscillations can be seen most clearly in the explicit volume formula for the tubular neighborhoods of a p-adic fractal string ${\mathcal{L}}_p$, expressed in terms of the underlying complex dimensions. The general fractal tube formula obtained in this paper is illustrated by several examples, including the nonarchimedean Cantor and Euler strings. Moreover, we show that the Minkowski dimension of a p-adic fractal string coincides with the abscissa of convergence of the geometric zeta function associated with the string, as well as with the asymptotic growth rate of the corresponding geometric counting function. The proof of this new result can be applied to both real and p-adic fractal strings and hence, yields a unifying explanation of a key result in the theory of complex dimensions for fractal strings, even in the archimedean (or real) case.

Nature is an infinite sphere of which the center is everywhere and the circumference nowhere.

Blaise Pascal (1623–1662)

1. Introduction

An ordinary real (or archimedean) fractal string is a bounded open subset of the real line, with fractal boundary. It provides a complementary perspective to the notion of a self-similar fractal, in the sense that every self-similar string determines a self-similar set in $\mathbb{R}$, viewed as the boundary of the string. Moreover, it is noteworthy that the geometric zeta function of a fractal string determines the fractal (i.e., Minkowski) dimension of the corresponding fractal set. Following the examples of the a-string and of the archimedean Cantor string given by the first author in [1,2,3], the notion of an archimedean fractal string was conceived and defined by Michel Lapidus and Carl Pomerance in their investigation of the one-dimensional Weyl–Berry conjecture for fractal drums and its connection with the Riemann zeta function [4]. The Riemann hypothesis turned out to be equivalent to the solvability of the corresponding inverse spectral problem for fractal strings, as was established by Michel Lapidus and Helmut Maier in [5]. The heuristic notion of complex dimensions then started to emerge and was used in a crucial way, at least heuristically, in their spectral reformulation of the Riemann hypothesis. The precise notion of complex dimensions, defined as the poles of a certain geometric zeta function associated with the fractal string, was crystallized and rigorously developed by Michel Lapidus and Machiel van Frankenhuijsen in the research monograph Fractal Geometry and Number Theory [6] and then significantly further extended in the book Fractal Geometry, Complex Dimensions and Zeta Functions [7].

The work of Lapidus and Maier mentioned above can be summarized as follows:

The inverse spectral problem for a fractal string can be solved if and only if its dimension is not $1/2$.

The inverse spectral problem for a fractal string is not solvable in dimension 1/2 because the Riemann zeta function $\zeta \left(s\right)=1+1/2^s+1/3^s+\cdots$ vanishes (infinitely often) on the critical line $\Re \left(s\right)=1/2$. Therefore, the inverse spectral problem is solvable in dimension $D\ne 1/2$ if and only if the Riemann zeta function does not vanish off the critical line $\Re \left(s\right)=1/2$ or, equivalently, if and only if the Riemann hypothesis is true. In order to understand why dimension $1/2$ is so special, Michel Lapidus [8] (building, in particular, on earlier work in [4,5]), as well as Michel Lapidus and Machiel van Frankenhuijsen [7], were led to a definition of the dual of a fractal string, interchanging the dimensions D and $1-D$. A partial answer to the question why $1/2$ is singled out is that if a fractal string is self-dual, then its dimension is $1/2$. The concept of the dual of a fractal string provides a geometric way to take the functional equation of the Riemann zeta function into consideration in the theory of complex dimensions. Such considerations would not be complete if they did not also involve the Euler product of the Riemann zeta function. The spectral operator was introduced semi-heuristically in [7] as the map that sends the geometry of a fractal string onto its spectrum. Formally, the spectral operator admits an (operator-valued) Euler product. In [9,10,11], Hafedh Herichi and Michel Lapidus have rigorously defined and studied the spectral operator, within a proper functional analytic setting. They have also reformulated the above criterion for the Riemann hypothesis in terms of a suitable notion of invertibility of the spectral operator; see also [12,13] for a corresponding asymmetric criterion, expressed in terms of the usual notion of invertibility of the spectral operator. Furthermore, they have shown that the (operator-valued or “quantized”) Euler product for the spectral operator also converges inside the critical strip $0<\Re \left(s\right)<1,$ where all the (nontrivial) complex zeros of the Riemann zeta function reside.

In order to extend the framework of the theory of complex dimensions, with an aim towards applying ideas and techniques from number theory to the inverse spectral problem, it is therefore natural to attempt developing a theory of p-adic fractal strings, and then globally, an adèlic theory of fractal strings. Further laying out the foundations for such a theory is one of the main long-term goals of this paper.

We note that nonarchimedean p-adic analysis has been used in various areas of mathematics, such as arithmetic geometry, number theory and representation theory, as well as of mathematical and theoretical physics, such as string theory, cosmology, quantum mechanics, relativity theory, quantum field theory, statistical and condensed matter physics; see, e.g., [14,15,16,17,18] and the relevant references therein. (See also, e.g., [19,20,21,22,23].) In Number Theory as the Ultimate Physical Theory, [24], Igor V. Volovich has suggested that p-adic numbers can possibly be used in order to describe the geometry of spacetime at very high energies (and hence, very small scales, i.e., below the Planck or the string scale) because the measurements in the ‘archimedean’ geometry of spacetime at fine scales do not have any certainty. Furthermore, several authors, including Stephen W. Hawking, have also suggested that the fine scale structure of spacetime may be fractal; see, e.g., [8,25,26,27,28]. Therefore, a geometric theory of p-adic fractal strings and their complex dimensions might be helpful in the quest to explore the geometry and fine scale structure of spacetime at high energies.

On the other hand, in the book entitled In Search of the Riemann Zeros: Strings, Fractal Membranes and Noncommutative Spacetimes [8], Michel Lapidus has suggested that fractal strings and their quantization, fractal membranes, may be related to aspects of string theory and that p-adic (and possibly, adèlic) analogs of these notions would be useful in this context in order to better understand the underlying noncommutative spacetimes and their moduli spaces ([8,29]). The theory of p-adic fractal strings, once suitably ‘quantized’, may be helpful in further developing some of these ideas and eventually providing a framework for unifying the real and p-adic fractal strings and membranes.

In this paper, we further develop the geometric theory of p-adic (or nonarchimedean) fractal strings, which are bounded open subsets of the p-adic ${\mathbb{Q}}_p$ with a fractal “boundary”, along with the associated theory of complex dimensions and, especially, of fractal tube formulas in the nonarchimedean setting. This theory, which was first developed by Michel Lapidus and Lũ’ Hùng in [30,31,32], as well as later, by those same authors and Machiel van Frankenhuijsen in [33], extends the theory of real (or archimedean) fractal strings and their complex dimensions in a natural way. Following [30,31,32,33], we introduce suitable geometric zeta functions for p-adic fractal strings whose poles play the role of complex dimensions for the standard real fractal strings. We also discuss the explicit fractal tube formulas in the general case of (languid) p-adic fractal strings and in the special case of p-adic self-similar strings. Throughout this paper, these various results are illustrated in the case of the nonarchimedean self-similar Cantor and the Fibonacci strings (introduced in [30,31]), as well as in the case of the p-adic Euler string (introduced in [32,33]), which (strictly speaking) is not self-similar. Some particular attention is devoted to the 3-adic Cantor string (introduced and studied in [30]), whose ‘metric’ boundary is the 3-adic Cantor set [30], which is naturally homeomorphic to the classic ternary Cantor set.

The rest of this paper is organized as follows: In Section 2 and Section 3, we recall the definition of an arbitrary p-adic fractal string along with its associated geometric zeta function and complex dimensions, as well as the corresponding notions of Minkowski dimension and content. Furthermore, in Section 4, we discuss the important, but more technical, question of how to suitably define and calculate the volume of the ‘inner’ $\epsilon$-neighborhood of a p-adic fractal string. The definitions and proofs given in Section 4 depend crucially on the nonarchimedean (specifically, p-adic) nature of the underlying geometry. In Section 5, we then introduce a proper notion in this context of Minkowski dimension and Minkowski content, building on the results of Section 4. Moreover, we obtain the nonarchimedean analog of a key result in (archimedean) fractal string theory, showing that the Minkowski dimension of a p-adic fractal string coincides with the abscissa of convergence of its geometric zeta function. (In the process, we show that this common value coincides with the asymptotic growth rate of the geometric counting function of the fractal string, a result which is new even in the archimedean setting, even though it may be implicit in [4].) Our proof also provides a new and unified derivation of the archimedean result for real fractal strings ([2,3,6,7]), by placing the archimedean and the nonarchimedean settings on the same footing; see Section 5.1. In Section 6, we then use our previous results (in Section 4 and Section 5) to express the volume of the inner tube of a p-adic fractal string as an infinite sum over all the underlying complex dimensions, thereby obtaining a nonarchimedean analog of the ‘fractal tube formula’ obtained for real (or archimedean) fractal strings in [6,7]. (See, especially, [7] (Chapter 8)) We illustrate this formula in Section 6 by providing (as well as deriving via a direct computation) the fractal tube formula for the p-adic Euler string, the definition of which is given in Section 2.3. Many further illustrations of our nonarchimedean fractal tube formula are provided in [33] for the important case of general p-adic self-similar strings, including the 3-adic Cantor string (Example 2 below) and the 2-adic Fibonacci string. In Section 7, we briefly discuss possible future research directions connected with the theory developed in this paper and its predecessors, [30,31,32,33]. Finally, in Section 8, we reveal the existence of p-adic fractal strings of any rational dimension between 0 and 1 and a possible connection between their construction and the Riemann hypothesis for the Riemann zeta function. We also discuss some constructions of adèlic fractal strings and a geometric zeta function for the adèlic Euler–Riemann string.

For more information about the theory of fractal strings (or sprays) and their complex dimensions, beside the books [6,7,8,34], we refer to [2,3,4,5,9,10,11,12,13,29,30,31,32,33,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54], as well as the relevant references therein.

2. Nonarchimedean Fractal Strings

2.1. p-Adic Numbers

Given a fixed prime number p, any nonzero rational number x can be written as $x=p^v·a/b$, for some integers a and b and a unique exponent $v\in \mathbb{Z}$ such that p does not divide a or b. The p-adic absolute value is the function ${|·|}_p:\mathbb{Q}\to [0,\infty )$ given by ${\left|x\right|}_p=p^{-v}$ and ${\left|0\right|}_p=0$. It satisfies the strong triangle inequality: for every $x,y\in \mathbb{Q}$,

$${|x+y|}_p\le {max\left\{\right|x|}_p{,\left|y\right|}_p\}.$$

Relative to the p-adic absolute value, $\mathbb{Q}$ does not satisfy the archimedean property because for every $x\in \mathbb{Q}$, ${\left|nx\right|}_p$ will never exceed ${\left|x\right|}_p$ for any $n\in \mathbb{N}$. The metric completion of $\mathbb{Q}$ with respect to the p-adic absolute value ${|·|}_p$ is the field of p-adic numbers ${\mathbb{Q}}_p$. More concretely, every p-adic number $z\in {\mathbb{Q}}_p$ has a unique p-adic expansion

$$z=a_v{p}^v+\cdots +a_0+a_{1}p+a_2{p}^2+\cdots ,$$

for some $v\in \mathbb{Z}$ and digits $a_i\in \{0,1,\cdots ,p-1\}$ for all $i\ge v$ and $a_v\ne 0$. An important subset of ${\mathbb{Q}}_p$ is the unit ball, ${\mathbb{Z}}_p=\{x\in {\mathbb{Q}}_p{:\left|x\right|}_p\le 1\}$, which can also be represented as follows:

$${\mathbb{Z}}_p=\left\{a_0+a_{1}p+a_2{p}^2+\cdots :a_i\in \{0,1,\cdots ,p-1\}\mathrm{for}\mathrm{all}i\ge 0\right\}.$$

Using this p-adic expansion, one sees that

$${\mathbb{Z}}_p=\bigcup _{a=0}^{p-1}(a+p{\mathbb{Z}}_p),$$

(1)

where $a+p{\mathbb{Z}}_p=\{y\in {\mathbb{Q}}_p{:|y-a|}_p\le 1/p\}$. Thus the p-adic ball ${\mathbb{Z}}_p$ is self-similar to p scaled (by the factor 1/p) copies of itself. Note that ${\mathbb{Z}}_p$ is compact and thus complete. Also, ${\mathbb{Q}}_p$ is a locally compact group, and hence admits a unique translation invariant Haar measure ${\mu }_H,$ normalized so that ${\mu }_H\left({\mathbb{Z}}_p\right)=1$. In particular, ${\mu }_H(a+p^n{\mathbb{Z}}_p)=p^{-n}$ for every $n\in \mathbb{Z}$. For general references on p-adic analysis, we point out, e.g., [55,56,57,58,59,60].

Remark 1.

(a) 

The distance $d_p$ defined on ${\mathbb{Q}}_p$ by $d_p(x,y)={|x-y|}_p$ is called an ultrametric, since it satisfies the counterpart of the above strong triangle inequality:

$$d_p(x,z)\le max\{d_p(x,y),d_p(y,z)\}$$

(2)

for all $x,y,z\in {\mathbb{Q}}_p$. Consequently, every triangle in ${\mathbb{Q}}_p$ is isosceles with the two longer sides having the same length:

$$\begin{array}{c}If{d}_p(x,y)>d_p(y,z)\mathit{then}{d}_p(x,z)=d_p(x,y).\end{array}$$

(3)

It follows that the center can be chosen anywhere within the p-adic ball B. Moreover, given any two balls $B_1$ and $B_2$, either they are disjoint or one is entirely contained in the other (i.e., $B_1\subseteq B_2$ or $B_2\subseteq B_1$). These special properties are common to all ultrametric spaces (i.e., all metric spaces for which the ultrametric triangle inequality (2) holds).

(b) 

By definition, ${\mathbb{Z}}_p$ is the (closed) unit ball of (${\mathbb{Q}}_p,d_p$). Moreover, ${\mathbb{Z}}_p$ has the remarkable property of being a ring (since for all $x,y$ in ${\mathbb{Z}}_p$, by (2) again, ${|x+y|}_p\le {max\left(\right|x|}_p{,\left|y\right|}_p)\le 1$, and ${\left|xy\right|}_p={\left|x\right|}_p{\left|y\right|}_p\le 1$). This is to be contrasted with the fact that $[-1,1]$, the unit ball of $\mathbb{R}$, is not stable under addition (although it is obviously stable under multiplication); see [61]. Finally, since translations are homeomorphisms, every closed ball $B=B(a,r)$ in ${\mathbb{Q}}_p$ with center a has a radius r of the form $r=p^n$,

$$B(a,r)=a+p^{-n}{\mathbb{Z}}_p=\{x\in {\mathbb{Q}}_p{:|x-a|}_p\le r\}$$

(4)

for some $r\in p^{\mathbb{Z}}$, the valuation group of the nonarchimedean field ${\mathbb{Q}}_p$. We leave it to the reader to investigate the converse statement according to which every convex subset of ${\mathbb{Q}}_p$ is a metric ball (i.e., an interval); see, e.g., [59].

(c) 

(p-adic intervals). In the sequel (as well as in part of the literature on p-adic analysis, see, e.g., [55]), the metric balls $B=a+r{\mathbb{Z}}_p$ (with $a\in {\mathbb{Q}}_p$ and $r\in p^{\mathbb{Z}}$, as in (4) just above), are sometimes called the ‘intervals’ of ${\mathbb{Q}}_p$. Note that they are not connected, in the usual topological sense, but that they are ‘convex’, in the following sense: for each $x,y\in B$ and $\alpha \in {\mathbb{Z}}_p$, we have that $\alpha x+(1-\alpha )y\in B$. (Here and henceforth, it is useful to think of ${\mathbb{Z}}_p\subset {\mathbb{Q}}_p$ as being the analogue of the unit interval $[0,1]\subset \mathbb{R}$, rather than of $[-1,1]$.)

(d) 

(The archimedean/nonarchimedean dichotomy). A beautiful and classical theorem of Alexander Ostrowski states that each nontrivial absolute value on the field of rational numbers $\mathbb{Q}$, is either equivalent to the standard archimedean absolute value on $\mathbb{Q}$ or to the nonarchimedean p-adic absolute value ${|·|}_p$ for some prime p. (Recall that two absolute values are said to be equivalent if they induce the same topology on $\mathbb{Q}$; this is the case if and only if one is a power of the other.) Therefore, infinitely many completions of $\mathbb{Q}$ (one for each prime p) are nonarchimedean and $\mathbb{R}$ is the only completion of $\mathbb{Q}$ that is archimedean. For this reason, one sometimes writes $\mathbb{R}={\mathbb{Q}}_{\infty }$ and refers to (the equivalence class of) the absolute value $|·|$ as the ‘place at infinity’, associated with the ‘prime at infinity’ or the ‘real prime’; see [61]. (We note that Ostrowski’s Theorem is usually expressed in terms of valuations rather than of absolute values. Accordingly, a place of $\mathbb{Q}$ is generally defined as an equivalence class of valuations on $\mathbb{Q}$.) With this notation in mind, we see that the field ${\mathbb{Q}}_{\infty }$ is archimedean, whereas for any (finite) prime p, ${\mathbb{Q}}_p$ is a nonarchimedean field. The theory of p-adic fractal strings developed in [30,31,32,33] is aimed, initially, at finding suitable definitions and obtaining results that parallel those corresponding to the theory of real (or archimedean) fractal strings developed in [7], for example. As we will see, however, although there are many analogies between the archimedean and nonarchimedean theories of fractal strings, there are also some notable differences between them; see, especially, [32], along with [30,33].

2.2. p-Adic Fractal Strings

Let $\mathsf{\Omega }$ be a bounded open subset of ${\mathbb{Q}}_p$. Then it can be decomposed into a countable union of disjoint open balls with radius $p^{-n_j}$ centered at $a_j\in {\mathbb{Q}}_p$,

$$a_j+p^{n_j}{\mathbb{Z}}_p=B(a_j,p^{-n_j})=\{x\in {\mathbb{Q}}_p\left|\right|x-a_j{|}_p\le p^{-n_j}\},$$

where $n_j\in \mathbb{Z}$ and $j\in {\mathbb{N}}^{*}$. (We shall often call a p-adic ball an interval. By ‘ball’ here, we mean a metrically closed and hence, topologically open and closed ball.) There may be many different such decompositions since each ball can always be decomposed into smaller disjoint balls [55]; see Equation (1). However, there is a canonical decomposition of $\mathsf{\Omega }$ into disjoint balls with respect to a suitable equivalence relation, as we now explain.

Definition 1.

Let U be an open subset of ${\mathbb{Q}}_p$. Given $x,y\in U,$ we write that $x\sim y$ if and only if there is a ball $B\subseteq U$ such that $x,y\in B$.

It is clear from the definition that the relation ∼ is reflexive and symmetric. To prove the transitivity, let $x\sim y$ and $y\sim z$. Then there are balls $B_1$ containing $x,y$ and $B_2$ containing $y,z$. Thus $y\in B_1\cap B_2$; so it follows from the ultrametricity of ${\mathbb{Q}}_p$ that either $B_1\subseteq B_2$ or $B_2\subseteq B_1.$ In any case, x and z are contained in the same ball; so $x\sim z$. Hence, the above relation ∼ is indeed an equivalence relation on the open set U. By a standard argument (and since $\mathbb{Q}$ is dense in ${\mathbb{Q}}_p$), one shows that there are at most countably many equivalence classes.

Remark 2 (Convex components).

The equivalence classes of ∼ can be thought of as the ‘convex components’ of U. They are an appropriate substitute in the present nonarchimedean context for the notion of connected components, which is not useful in ${\mathbb{Q}}_p$ since ${\mathbb{Z}}_p$ (and hence, every interval) is totally disconnected. Note that given any $x\in U,$ the equivalence class (i.e., the convex component) of x is the largest ball containing x (or equivalently, centered at x) and contained in U.

Definition 2.

A p-adic (or nonarchimedean) fractal string ${\mathcal{L}}_p$ is a bounded open subset Ω of ${\mathbb{Q}}_p$.

Thus it can be written, relative to the above equivalence relation, canonically as a disjoint union of intervals or balls:

$${\mathcal{L}}_p=\bigcup _{j=1}^{\infty }(a_j+p^{n_j}{\mathbb{Z}}_p)=\bigcup _{j=1}^{\infty }B(a_j,p^{-n_j}).$$

Here, $B(a_j,p^{-n_j})$ is the largest ball centered at $a_j$ and contained in $\mathsf{\Omega }$. We may assume that the lengths (i.e., Haar measure) of the intervals $a_j+p^{n_j}{\mathbb{Z}}_p$ are nonincreasing, by reindexing if necessary. That is,

$$p^{-n_1}\ge p^{-n_2}\ge p^{-n_3}\ge \cdots >0.$$

(5)

Note that, more generally, a p-adic fractal string can be defined as an open subset $\mathsf{\Omega }$ of ${\mathbb{Q}}_p$ such that ${\mu }_H\left(\mathsf{\Omega }\right)<\infty .$

Definition 3.

The geometric zeta function of a p-adic fractal string ${\mathcal{L}}_p$ is defined as

$${\zeta }_{{\mathcal{L}}_p}\left(s\right):=\sum _{j=1}^{\infty }{\left({\mu }_H(a_j+p^{n_j}{\mathbb{Z}}_p)\right)}^s=\sum _{j=1}^{\infty }{p}^{-n_{j}s}$$

(6)

for all $s\in \mathbb{C}$ with $\Re \left(s\right)$ sufficiently large.

Remark 3.

The geometric zeta function ${\zeta }_{{\mathcal{L}}_p}$ is well defined since the decomposition of ${\mathcal{L}}_p$ into the disjoint intervals $a_j+p^{n_j}{\mathbb{Z}}_p$ is unique. Indeed, these intervals are the equivalence classes of which the open set Ω (defining ${\mathcal{L}}_p$) is composed. In other words, they are the p-adic “convex components” (rather than the connected components) of Ω. Note that in the real (or archimedean) case, there is no difference between the convex or connected components of Ω, and hence the above construction would lead to the same sequence of lengths as in [7] (Section 1.2).

2.3. Example: p-Adic Euler String

The following p-adic Euler string is a new example of p-adic fractal string, which is not self-similar (in the sense of [31,33]). It is a natural p-adic counterpart of the elementary prime string, which is the local constituent of the completed harmonic string; cf. [7] (Section 4.2.1).

Let $X=p^{-1}{\mathbb{Z}}_p$. Then, by the ‘self-duplication’ Formula (1),

$$X=\bigcup _{\xi =0}^{p-1}(\xi p^{-1}+{\mathbb{Z}}_p).$$

We now keep the first subinterval ${\mathbb{Z}}_p$, and then decompose the next subinterval further. That is, we write

$$p^{-1}+{\mathbb{Z}}_p=\bigcup _{\xi =0}^{p-1}(p^{-1}+\xi +p{\mathbb{Z}}_p).$$

Again, iterating this process, we keep the first subinterval $p^{-1}+p{\mathbb{Z}}_p$ in the above decomposition and decompose the next subinterval, $p^{-1}+1+p{\mathbb{Z}}_p$. Continuing in this fashion, we obtain an infinite sequence of disjoint subintervals ${\left\{a_n+p^n{\mathbb{Z}}_p\right\}}_{n=0}^{\infty },$ where ${\left\{a_n\right\}}_{n=0}^{\infty }$ satisfies the following initial condition and recurrence relation:

$$a_0=0\mathrm{and}{a}_n=a_{n-1}+p^{n-2}\mathrm{for}\mathrm{all}n\ge 1.$$

We call the corresponding p-adic fractal string,

$${\mathcal{E}}_p=\bigcup _{n=0}^{\infty }(a_n+p^n{\mathbb{Z}}_p),$$

the p-adic Euler string.

The geometric zeta function of the p-adic Euler string ${\mathcal{E}}_p$ is

$${\zeta }_{{\mathcal{E}}_p}\left(s\right)=\sum _{n=0}^{\infty }{\left({\mu }_H(a_n+p^n{\mathbb{Z}}_p)\right)}^s=\sum _{n=0}^{\infty }{p}^{-ns}=\frac{1}{1-p^{-s}},\mathrm{for}\Re \left(s\right)>0.$$

Therefore, ${\zeta }_{{\mathcal{E}}_p}$ has a meromorphic extension to all of $\mathbb{C}$ given by the last expression, which is the classic p-Euler factor (i.e., the local Euler factor associated with the prime p):

$${\zeta }_{{\mathcal{E}}_p}\left(s\right)=\frac{1}{1-p^{-s}},\mathrm{for}\mathrm{all}s\in \mathbb{C}.$$

(7)

Hence, the set of complex dimensions of ${\mathcal{E}}_p$ is given by

$${\mathcal{D}}_{{\mathcal{E}}_p}=\{D+i\nu \mathbf{p}|\nu \in \mathbb{Z}\},$$

(8)

where $D=\sigma =0$ and $\mathbf{p}=2\pi /\log p.$

Remark 4 (The punctured unit ball).

The unit ball minus the origin is not a ball itself, but instead the infinite union

$${\mathbb{Z}}_p\backslash \left\{0\right\}=\bigcup _{n=0}^{\infty }\bigcup _{k=1}^{p-1}k{p}^n+p^{n+1}{\mathbb{Z}}_p,$$

where every time, a small punctured neighborhood of 0, namely $p^n{\mathbb{Z}}_p\backslash \left\{0\right\}$, is subdivided into smaller balls. This union is isomorphic to the Euler string:

$${\mathcal{E}}_p=\frac{1}{p}{\mathbb{Z}}_p\backslash \left\{\frac{1}{p(1-p)}\right\}.$$

Remark 5 (Adèlic Euler string).

Note that ${\zeta }_{{\mathcal{E}}_p}$ is the p-Euler factor of the Riemann zeta function; i.e.,

$$\prod _{p<\infty }{\zeta }_{{\mathcal{E}}_p}\left(s\right)=\prod _{p<\infty }\frac{1}{1-p^{-s}}=\sum _{n=1}^{\infty }\frac{1}{n^s}=\zeta \left(s\right)for\Re \left(s\right)>1.$$

Recall that the meromorphic continuation ξ of the completed Riemann zeta function has the same (critical) zeros as ζ and satisfies the functional equation $\xi \left(s\right)=\xi (1-s)$.

We aim to form a certain ‘adèlic product’ over all p-adic Euler strings (including the prime at infinity) so that the geometric zeta function of the resulting adèlic Euler string $\mathcal{E}$ is the completed Riemann zeta function. Formally, the adèlic Euler string may be written as

$$\mathcal{E}=\underset{p\le \infty }{⨂}{\mathcal{E}}_p$$

and its geometric zeta function ${\zeta }_{\mathcal{E}}\left(s\right)$ would then coincide with the completed Riemann zeta function ξ (see [62,63]):

$${\zeta }_{\mathcal{E}}\left(s\right)=\xi \left(s\right):={\pi }^{-s/2}\mathsf{\Gamma }(s/2)\prod _{p<\infty }\frac{1}{1-p^{-s}}.$$

Remark 6 (Comparison with the archimedean theory)

From the geometric point of view, the nonarchimedean Euler string ${\mathcal{E}}_p$ is more natural than its archimedean counterpart, the p-elementary prime string $h_p$, described in [7] (Section 4.2.1). Indeed, as we have just seen, ${\mathcal{E}}_p$ has a very simple geometric definition. Since, by construction, ${\mathcal{E}}_p$ and $h_p$ have the same sequence of lengths ${\left\{p^{-n}\right\}}_{n=0}^{\infty },$ they have the same geometric zeta function, namely, the p-Euler factor

$${\zeta }_p\left(s\right):=\frac{1}{1-p^{-s}}$$

(9)

of the Riemann zeta function $\zeta \left(s\right),$ and hence, the same set of complex dimensions

$${\mathcal{D}}_p=\left\{i\nu \frac{2\pi }{\log p}:\nu \in \mathbb{Z}\right\}.$$

(10)

An ‘adèlic version’ of the ‘harmonic string’ h, a generalized fractal string whose geometric zeta function is ${\zeta }_h\left(s\right)=\zeta \left(s\right)$, or rather, of its completion $\tilde{h}$ (so that ${\zeta }_{\tilde{h}}\left(s\right)=\xi \left(s\right)$), is provided in [7] (Section 4.2.1). In particular, with each term being interpreted as a positive measure on $(0,\infty )$ and the symbol ∗ denoting multiplicative convolution on $(0,\infty )$, we have that

$$h={*}_{p<\infty }{h}_{p}and\tilde{h}={*}_{p\le \infty }{h}_p.$$

(11)

Furthermore, a noncommutative geometric version of this construction is provided in [8] in terms of the ‘prime fractal membrane’; see especially, [8], Chapters 3 and 4, along with [29]. Heuristically, a ‘fractal membrane’ (as introduced in [8]) is a kind of adèlic, noncommutative torus of infinite genus. It can also be thought of as a ‘quantized fractal string’; see [8], Chapter 3. It is rigorously constructed in [29] using Dirac-type operators, Fock spaces, Toeplitz algebras [64], and associated spectral triples (in the sense of [65]); see also [8], Section 4.2. We hope in the future to obtain a suitable nonarchimedean version of that construction. It is possible that in the process, we will establish contact with the physically motivated work in [14] involving p-adic quantum mechanics.

3. The Geometric Zeta Function

The screen S is the graph (with the vertical and horizontal axes interchanged) of a real-valued, bounded and Lipschitz continuous function $S\left(t\right)$:

$$S:=\left\{S\right(t)+it|t\in \mathbb{R}\}.$$

The window W is the part of the complex plane to the right of the screen S (see Figure 1):

$$W:=\{s\in \mathbb{C}|\Re \left(s\right)\ge S(\Im (s\left)\right)\}.$$

Let

$$infS:=\underset{t\in \mathbb{R}}{inf}S\left(t\right)\mathrm{and}supS:=\underset{t\in \mathbb{R}}{sup}S\left(t\right),$$

and assume that $supS\le \sigma ,$ where $\sigma ={\sigma }_{{\mathcal{L}}_p}$ is the abscissa of convergence of ${\zeta }_{{\mathcal{L}}_p}$ (to be precisely defined in (13) below).

Definition 4.

Let ${\mathcal{L}}_p$ be a p-adic fractal string. If ${\zeta }_{{\mathcal{L}}_p}$ has a meromorphic continuation to an open connected neighborhood of $W\subseteq \mathbb{C}$, then

$${\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right):=\{\omega \in W|\omega isapoleof{\zeta }_{{\mathcal{L}}_p}\}$$

(12)

is called the set of visible complex dimensions of ${\mathcal{L}}_p$. If no ambiguity may arise or if $W=\mathbb{C}$, we simply write ${\mathcal{D}}_{{\mathcal{L}}_p}={\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)$ and call it the set of complex dimensions of ${\mathcal{L}}_p$.

Moreover, the abscissa of convergence of ${\zeta }_{{\mathcal{L}}_p}$ (where ${\mathcal{L}}_p$ is defined in Equation (6)) is denoted by $\sigma ={\sigma }_{{\mathcal{L}}_p}$. Recall that it is defined by (see, e.g., [60])

$${\sigma }_{{\mathcal{L}}_p}:=inf\left\{\alpha \in \mathbb{R}:\sum _{j=1}^{\infty }{p}^{-n_j\alpha }<\infty \right\}.$$

(13)

Remark 7.

In particular, if ${\zeta }_{{\mathcal{L}}_p}$ is entire (which occurs only in the trivial case when ${\mathcal{L}}_p$ is given by a finite union of intervals), then ${\sigma }_{{\mathcal{L}}_p}=-\infty .$ Otherwise, ${\sigma }_{{\mathcal{L}}_p}\ge 0$ (since ${\mathcal{L}}_p$ is composed of infinitely many intervals) and we will see in Theorem 3 that ${\sigma }_{{\mathcal{L}}_p}<\infty$ since ${\sigma }_{{\mathcal{L}}_p}\le D_M\le 1,$ where $D_M=D_{M,{\mathcal{L}}_p}$ is the Minkowski dimension of ${\mathcal{L}}_p$, to be introduced in Section 5. Furthermore, it will follow from Theorem 3 that for a nontrivial p-adic fractal string, ${\sigma }_{{\mathcal{L}}_p}=D_M.$

Observe that since ${\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)$ is defined as a subset of the poles of a meromorphic function, it is at most countable and forms a discrete subset of $\mathbb{C}$.

Finally, we note that it is well known that ${\zeta }_{{\mathcal{L}}_p}$ is holomorphic for $\Re \left(s\right)>{\sigma }_{{\mathcal{L}}_p};$ see, e.g., [60]. Hence,

$${\mathcal{D}}_{{\mathcal{L}}_p}\subseteq \{s\in \mathbb{C}:\Re \left(s\right)\le {\sigma }_{{\mathcal{L}}_p}\}.$$

Remark 8 (Archimedean fractal strings).

Archimedean or real fractal strings are defined as bounded open subsets of the real line $\mathbb{R}={\mathbb{Q}}_{\infty }.$ They were initially defined in [4], following an early example in [1], and have been used extensively in a variety of settings; see, e.g., [1,2,3,5,9,10,11,12,13,34,35,36,38,39,40,41,42,43,44,45,46,47,48,49,50,51,53] and the books [6,7,8,34]. Since an open set $\mathsf{\Omega }\subset \mathbb{R}$ is canonically equal to the disjoint union of finitely or countably many open and bounded intervals (namely, its connected components), say $\mathsf{\Omega }={\bigcup }_{j=1}^{\infty }{I}_j,$ we may also describe a real fractal string by a sequence of lengths $\mathcal{L}={\left\{l_j\right\}}_{j=1}^{\infty },$ where $l_j={\mu }_L\left(I_j\right)$ is the length or 1-dimensional Lebesgue measure of the interval $I_j$, written in nonincreasing order:

$$l_1\ge l_2\ge l_3\ge \cdots .$$

(A justification for this identification is provided by the formula for the volume $V_{\mathcal{L}}\left(\epsilon \right)$ of ε-inner tubes of Ω, as given by Equation (27) below.) Note that since ${\mu }_L\left(\mathsf{\Omega }\right)<\infty ,l_j\to 0$ as $j\to \infty$, except in the trivial case when Ω consists of finitely many intervals. Also observe that the 1-dimensional Lebesgue measure ${\mu }_L$ is nothing but the Haar measure on $\mathbb{R}={\mathbb{Q}}_{\infty }$, normalized so that ${\mu }_L\left([0,1]\right)=1.$

All of the definitions given above for p-adic fractal strings have a natural counterpart for real fractal strings. For instance, the geometric zeta function of $\mathcal{L}$ is initially defined by

$${\zeta }_{\mathcal{L}}\left(s\right)=\sum _{j=1}^{\infty }{\left({\mu }_L\left(I_j\right)\right)}^s=\sum _{j=1}^{\infty }{l}_j^s,$$

(14)

for $\Re \left(s\right)>{\sigma }_{\mathcal{L}},$ the abscissa of convergence of ${\zeta }_{\mathcal{L}}$, and for a given screen S and associated window W, the set ${\mathcal{D}}_{\mathcal{L}}={\mathcal{D}}_{\mathcal{L}}\left(W\right)$ of visible complex dimensions of $\mathcal{L}$ is given exactly as in (12) of Definition 4, except with ${\mathcal{L}}_p$ and ${\zeta }_{{\mathcal{L}}_p}$ replaced with $\mathcal{L}$ and ${\zeta }_{\mathcal{L}}$, respectively. Similarly, ${\sigma }_{\mathcal{L}}$, the abscissa of convergence of ${\zeta }_{\mathcal{L}}$ is given as in (13), except with the lengths of $\mathcal{L}$ instead of those of ${\mathcal{L}}_p$. Moreover, it follows from [7] (Theorem 1.10) that for any nontrivial real fractal string $\mathcal{L}$, we have ${\sigma }_{\mathcal{L}}=D_M$, the Minkowski dimension of $\mathcal{L}$ (i.e., of its topological boundary $\partial \mathsf{\Omega }$). This latter result will be given a new proof in Section 5.1.

We refer the interested reader to the research monographs [6,7] for a full development of the theory of real fractal strings and their complex dimensions.

Languid and Strongly Languid p-Adic Fractal Strings

In Section 6, we will obtain explicit tube formulas for p-adic fractal strings, with and without error term. (See Theorem 5 and Corollary 3.) We will then apply the tube formula without error term (the strongly languid case of Theorem 5) to the p-adic Euler string discussed in Section 2.3 and revisited in Example 1 (at the end of Section 6).

In order to state the explicit formulas with (or without) error term, we need to assume the following technical hypotheses (see [7] (Definitions 5.2 and 5.3) and recall the definition of the screen S given in Section 2, just before Definition 4).

Definition 5.

A p-adic fractal string ${\mathcal{L}}_p$ is said to be languid if its geometric zeta function ${\zeta }_{{\mathcal{L}}_p}$ satisfies the following growth conditions: There exist real constants κ and $C>0$ and a two-sided sequence ${\left\{T_n\right\}}_{n\in \mathbb{Z}}$ of real numbers such that $T_{-n}<0<T_n$ for $n\ge 1$, and

$$\underset{n\to \infty }{lim}{T}_n=\infty ,\underset{n\to \infty }{lim}{T}_{-n}=-\infty ,\underset{n\to \infty }{lim}\frac{T_n}{|T_{-n}|}=1,$$

such that

• $\mathbf{L}\mathbf{1}$ For all $n\in \mathbb{Z}$ and all $u\ge S\left(T_n\right),$

  $$|{\zeta }_{{\mathcal{L}}_p}(u+i{T}_n)|\le C(|T_n{|+1)}^{\kappa },$$
• $\mathbf{L}\mathbf{2}$ For all $t\in \mathbb{R},\left|t\right|\ge 1,$

  $$|{\zeta }_{{\mathcal{L}}_p}{(S\left(t\right)+it)|\le C|t|}^{\kappa }.$$

We say that ${\mathcal{L}}_p$ is strongly languid if its geometric zeta function ${\zeta }_{{\mathcal{L}}_p}$ satisfies the following conditions, in addition to $\mathbf{L}\mathbf{1}$ with $S\left(t\right)\equiv -\infty :$ There exists a sequence of screens $S_m:t\mapsto S_m\left(t\right)$ for $m\ge 1,t\in \mathbb{R}$, with $sup{S}_m\to -\infty$ as $m\to \infty$ and with a uniform Lipschitz bound ${sup}_{m\ge 1}\left|\right|S_m{\left|\right|}_{Lip}<\infty$, such that

• $\mathbf{L}{\mathbf{2}}^{\prime }$ There exist constants $A,C>0$ such that for all $t\in \mathbb{R}$ and $m\ge 1$,

  $$|{\zeta }_{{\mathcal{L}}_p}(S_m\left(t\right)+it)|\le C{A}^{|S_m\left(t\right)|}{\left(\right|t|+1)}^{\kappa }.$$

Remark 9.

(a) 

Intuitively, hypothesis $\mathbf{L}\mathbf{1}$ is a polynomial growth condition along horizontal lines (necessarily avoiding the poles of ${\zeta }_{{\mathcal{L}}_p}$), while hypothesis $\mathbf{L}\mathbf{2}$ is a polynomial growth condition along the vertical direction of the screen.

(b) 

Clearly, condition $\mathbf{L}{\mathbf{2}}^{\prime }$ is stronger than $\mathbf{L}\mathbf{2}$. Indeed, if ${\mathcal{L}}_p$ is strongly languid, then it is also languid (for each screen $S_m$ separately).

(c) 

Moreover, if ${\mathcal{L}}_p$ is languid for some κ, then it is also languid for every larger value of κ. The same is also true for strongly languid strings.

(d) 

Finally, hypotheses $\mathbf{L}\mathbf{1}$ and $\mathbf{L}\mathbf{2}$ require that ${\zeta }_{{\mathcal{L}}_p}$ has an analytic (i.e., meromorphic) continuation to an open, connected neighborhood of $\Re \left(s\right)\ge {\sigma }_{{\mathcal{L}}_p}$, while $\mathbf{L}{\mathbf{2}}^{\prime }$ requires that ${\zeta }_{{\mathcal{L}}_p}$ has a meromorphic continuation to all of $\mathbb{C}$.

4. Volume of Thin Inner Tubes

In this section, we provide a suitable analog in the p-adic case of the ‘boundary’ of a fractal string and of the associated inner tubes (or “inner $\epsilon$-neighborhoods”). Moreover, we give the p-adic counterpart of the expression that yields the volume of the inner tubes (see Theorem 2). This result will serve as a starting point in §6 for proving the distributional explicit tube formula obtained in Theorem 5.

Definition 6.

Given a point $a\in {\mathbb{Q}}_p$ and a positive real number $r>0$, let $B=B(a,r)=\{x\in {\mathbb{Q}}_p||x-a{|}_p\le r\}$ be a metrically closed ball in ${\mathbb{Q}}_p,$ as above. (Recall that it follows from the ultrametricity of ${|·|}_p$ that B is topologically both closed and open (i.e., clopen) in ${\mathbb{Q}}_p$.) We call $S=S(a,r)=\{x\in {\mathbb{Q}}_p||x-a{|}_p=r\}$ the sphere of B. (In our sense, S also coincides with the ‘metric boundary’ of B, as given in the next definition.)

Let ${\mathcal{L}}_p={\bigcup }_{j=1}^{\infty }B(a_j,r_j)$ be a p-adic fractal string. We then define the metric boundary $\beta {\mathcal{L}}_p$ of ${\mathcal{L}}_p$ to be the disjoint union of the corresponding spheres, i.e.,

$$\beta {\mathcal{L}}_p=\bigcup _{j=1}^{\infty }S(a_j,r_j).$$

Given a real number $\epsilon >0$, define the thick p-adic ‘inner ε-neighborhood’ (or ‘inner tube’) of ${\mathcal{L}}_p$ to be

$${\mathcal{N}}_{\epsilon }={\mathcal{N}}_{\epsilon }\left({\mathcal{L}}_p\right):=\{x\in {\mathcal{L}}_p|d_p(x,\beta {\mathcal{L}}_p)<\epsilon \},$$

(15)

where $d_p(x,E)={inf\left\{\right|x-y|}_p|y\in E\}$ is the p-adic distance of $x\in {\mathbb{Q}}_p$ to a subset $E\subseteq {\mathbb{Q}}_p$. Then the volume ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$ of the thick inner ε-neighborhood of ${\mathcal{L}}_p$ is defined to be the Haar measure of ${\mathcal{N}}_{\epsilon }$, i.e., ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)={\mu }_H\left({\mathcal{N}}_{\epsilon }\right).$

Lemma 1.

Let $B=B(a,r)$ and $S=S(a,r)$, as in Definition 6. Then, for any positive number $\epsilon <r$, we have

$${\mathcal{N}}_{\epsilon }\left(B\right):=\{x\in B|d_p(x,S)<\epsilon \}=S.$$

(16)

Further, if $r=p^{-m}$ for some $m\in \mathbb{Z},$ then for all $\epsilon <r,$

$${\mu }_H\left(\{x\in B|d_p(x,S)<\epsilon \}\right)={\mu }_H\left(S\right)=(1-p^{-1})p^{-m}.$$

(17)

Proof. 

Clearly $S\subseteq \{x\in B|d_p(x,S)<\epsilon \}$ since for any $x\in S$, $d_p(x,S)=0$. Next, fix $\epsilon$ with $0<\epsilon <r$ and let $x\in B$ be such that $d_p(x,S)<\epsilon .$ Then there must exist $y\in S$ such that ${|x-y|}_p<\epsilon .$ But, since ${|y-a|}_p=r,$ we deduce from the fact that every “triangle” in ${\mathbb{Q}}_p$ is isosceles ([55], p. 6) that ${|x-a|}_p={|y-a|}_p$ and thus $x\in S$. This completes the proof of (16).

We next establish Formula (17). In light of Equation (16), it suffices to show that

$${\mu }_H\left(S\right)=(1-p^{-1})p^{-m}.$$

(18)

Let $S^1=S(0,1)=\{x\in {\mathbb{Q}}_p{\left|\right|x|}_p=1\}$ denote the unit sphere in ${\mathbb{Q}}_p$. Since $S=S(a,p^{-m})=a+p^m{S}^1,$ we have that ${\mu }_H\left(S\right)={\mu }_H\left(S^1\right)p^{-m}.$ Next we note that

$$B(0,1)=\bigcup _{m\ge 0}S(0,p^{-m})$$

is a disjoint union. Hence, by taking the Haar measure of $B(0,1),$ we deduce that

$$1=\left(\sum _{m=0}^{\infty }{p}^{-m}\right){\mu }_H\left(S^1\right)=\frac{1}{1-p^{-1}}{\mu }_H\left(S^1\right),$$

(19)

from which (18) and hence, in light of the first part, (17) follows. ☐

Theorem 1 (Volume of thick inner tubes).

Let ${\mathcal{L}}_p={\bigcup }_{j=1}^{\infty }B(a_j,p^{-n_j})$ be a p-adic fractal string. Then, for any $\epsilon >0,$ we have

$$\begin{array}{cc}\hfill {\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)& =(1-p^{-1})\sum _{j=1}^k{p}^{-n_j}+\sum _{j>k}{p}^{-n_j}\hfill \end{array}$$

(20)

$$\begin{array}{c}={\zeta }_{{\mathcal{L}}_p}\left(1\right)-\frac{1}{p}\sum _{j=1}^k{p}^{-n_j},\hfill \end{array}$$

(21)

where $k=k\left(\epsilon \right)$ is the largest integer such that $p^{-n_k}\ge \epsilon$.

Proof. 

In light of the definition of ${\mathcal{N}}_{\epsilon }={\mathcal{N}}_{\epsilon }\left({\mathcal{L}}_p\right)$ given in Equation (15) and the definition of k given in the theorem, we have that

$${\mathcal{N}}_{\epsilon }=\bigcup _{j=1}^k{S}_j\cup \bigcup _{j>k}{B}_j,$$

where $B_j:=B(a_j,p^{-n_j})$ and $S_j:=S(a_j,p^{-n_j})$ for each $j\ge 1$.

We then apply Lemma 1 to deduce the expression of ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)={\mu }_H\left({\mathcal{N}}_{\epsilon }\right)$ stated in Equations (20) and (21). ☐

Note that ${\zeta }_{{\mathcal{L}}_p}\left(1\right)={\sum }_{j=1}^{\infty }{p}^{-n_j}$ is the volume of ${\mathcal{L}}_p$ (or rather, of the bounded open subset $\mathsf{\Omega }$ of ${\mathbb{Q}}_p$ representing ${\mathcal{L}}_p$):

$${\zeta }_{{\mathcal{L}}_p}\left(1\right)={\mu }_H\left({\mathcal{L}}_p\right)<\infty .$$

It is clearly independent of the choice of $\mathsf{\Omega }$ representing ${\mathcal{L}}_p$, and so is ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$ in light of either (20) or (21).

Corollary 1.

The following limit exists in $(0,\infty ):$

$$\underset{\epsilon \to 0^{+}}{lim}{\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)={\mu }_H\left(\beta {\mathcal{L}}_p\right)=(1-p^{-1}){\zeta }_{{\mathcal{L}}_p}\left(1\right).$$

(22)

Proof. 

This follows by letting $\epsilon \to 0^{+}$ in either (20) and (21) and noting that $k=k\left(\epsilon \right)\to \infty .$ ☐

Corollary 1, combined with the fact that $\beta {\mathcal{L}}_p\subset {\mathcal{N}}_{\epsilon }\left({\mathcal{L}}_p\right)$ for any $\epsilon >0,$ naturally leads us to introduce the following definition.

Definition 7.

Given $\epsilon >0,$ the thin p-adic ‘inner ε-neighborhood’ (or ‘inner tube’) of ${\mathcal{L}}_p$ is given by

$$N_{\epsilon }=N_{\epsilon }\left({\mathcal{L}}_p\right):={\mathcal{N}}_{\epsilon }\left({\mathcal{L}}_p\right)\backslash \beta {\mathcal{L}}_p.$$

(23)

Then, in light of Corollary 1, the volume $V_{{\mathcal{L}}_p}\left(\epsilon \right)$ of the thin inner ε-neighborhood of ${\mathcal{L}}_p$ is defined to be the Haar measure of $N_{\epsilon }$ and is given by

$$V_{{\mathcal{L}}_p}\left(\epsilon \right):={\mu }_H\left(N_{\epsilon }\right)={\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)-{\mu }_H\left(\beta {\mathcal{L}}_p\right).$$

(24)

Note that, by construction, we now have ${lim}_{\epsilon \to 0^{+}}{V}_{{\mathcal{L}}_p}\left(\epsilon \right)=0.$

We next state the counterpart (for thin inner tubes) of Theorem 1, which is the key result that will enable us to obtain an appropriate p-adic analog of the fractal tube formula (in Section 6) as well as of the notions of Minkowski dimension and content (in Section 5).

Theorem 2 (Volume of thin inner tubes).

Let ${\mathcal{L}}_p={\bigcup }_{j=1}^{\infty }B(a_j,p^{-n_j})$ be a p-adic fractal string. Then, for any $\epsilon >0,$ we have

$$\begin{array}{cc}\hfill V_{{\mathcal{L}}_p}\left(\epsilon \right)& =p^{-1}\sum _{j>k}{p}^{-n_j}=p^{-1}\sum _{j:p^{-n_j}<\epsilon }{p}^{-n_j}\hfill \end{array}$$

(25)

$$\begin{array}{c}=p^{-1}\left({\zeta }_{{\mathcal{L}}_p}\left(1\right)-\sum _{j=1}^k{p}^{-n_j}\right),\hfill \end{array}$$

(26)

where $k=k\left(\epsilon \right)$ is the largest integer such that $p^{-n_k}\ge \epsilon$, as before.

Proof. 

In view of Theorem 1 and Corollary 1, the result follows immediately from Equation (24) in Definition 7. ☐

Remark 10.

Observe that because the center a of a p-adic ball $B=B(a,p^{-n})$ can be chosen arbitrarily without changing its radius $p^{-n},$ the metric boundary of a ball, $\beta B=S=S(a,p^{-n}),$ depends on the choice of a. Note, however, that in view of Equation (17) in Lemma 1, its volume ${\mu }_H\left(S\right)$ depends only on the radius of B. Similarly, even though the decomposition of a p-adic fractal string Ω (i.e., ${\mathcal{L}}_p$) into maximal balls $B_j=B_j(a_j,p^{-n_j})$ is canonical, ‘the’ metric boundary of ${\mathcal{L}}_p,$ $\beta {\mathcal{L}}_p={\bigcup }_{j=1}^{\infty }S(a_j,r_j),$ depends on the choice of the centers $a_j$. However, according to Corollary 1, ${\mu }_H\left(\beta {\mathcal{L}}_p\right)$ is independent of this choice and hence, neither ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)={\mu }_H\left({\mathcal{N}}_{\epsilon }\left({\mathcal{L}}_p\right)\right)$ nor $V_{{\mathcal{L}}_p}\left(\epsilon \right)={\mu }_H\left(N_{\epsilon }\left({\mathcal{L}}_p\right)\right)$ depends on the choice of the centers. Indeed, in light of Theorems 1 and 2, ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$ and $V_{{\mathcal{L}}_p}\left(\epsilon \right)$ depend only on the choice of the p-adic lengths $p^{-n_j},$ and hence solely on the p-adic fractal string ${\mathcal{L}}_p$, viewed as a nonincreasing sequence of positive numbers, and not on the geometric representation Ω of ${\mathcal{L}}_p$, let alone on the choice of the centers of the balls of which Ω is composed.

Although it is not entirely analogous to it, this situation is somewhat reminiscent of the fact that the volume $V_{\mathcal{L}}\left(\epsilon \right)$ of the inner ε-neighborhoods of an archimedean fractal string depends only on its lengths ${\left\{l_j\right\}}_{j=1}^{\infty }$ and not on the representative Ω of $\mathcal{L}$ as a bounded open set; see Equation (27) and the discussion surrounding it in Remark 11.

Remark 11 (Comparison between the archimedean and the nonarchimedean cases).

Recall that ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$ does not tend to zero as $\epsilon \to 0^{+},$ but that instead it tends to the positive number $(1-p^{-1}){\zeta }_{{\mathcal{L}}_p}\left(1\right),$ whereas $V_{{\mathcal{L}}_p}\left(\epsilon \right)$ does tend to zero. This is the reason why the Minkowski dimension must be defined in terms of $V_{{\mathcal{L}}_p}\left(\epsilon \right)$ (as will be done in Section 5) rather than in terms of ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right).$ Indeed, if ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$ were used instead, then every p-adic fractal string would have Minkowski dimension 1. This would be the case even for a trivial p-adic fractal string composed of a single interval, for example. This is also why, in the p-adic case, we will focus only on the tube formula for $V_{{\mathcal{L}}_p}\left(\epsilon \right)$ rather than for ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$, although the latter could be obtained by means of the same techniques.

Note the difference between the expressions for $V_{\mathcal{L}}\left(\epsilon \right)$ in the case of an archimedean fractal string $\mathcal{L}$ and for its nonarchimedean thin (resp., thick) counterpart $V_{{\mathcal{L}}_p}\left(\epsilon \right)$ (resp., ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$) in the case of a p-adic fractal string ${\mathcal{L}}_p$. Compare Equation (8.1) of [7] (which was first obtained in [4]),

$$V_{\mathcal{L}}\left(\epsilon \right)=\sum _{j:l_j\ge 2\epsilon }2\epsilon +\sum _{j:l_j<2\epsilon }{l}_j,$$

(27)

with Equations (25) and (26) in Theorem 2. (Here, we are using the notation of Remark 8, to which the reader is referred to for a brief introduction to real fractal strings.) It follows, in particular, that $V_{\mathcal{L}}\left(\epsilon \right)$ is a continuous function of ε on $(0,\infty )$, whereas ${\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)$ (and hence also $V_{{\mathcal{L}}_p}\left(\epsilon \right)$) is discontinuous (because it is a step function with jump discontinuities at each point $p^{-n_j},forj=1,2,\dots$). The above discrepancies between the archimedean and the nonarchimedean cases help explain why the tube formula for real and p-adic fractal strings have a similar form, but with different expressions for the corresponding ‘tubular zeta function’ (in the sense of [41,42]). We note that a minor aspect of these discrepancies is that $2\epsilon$ is now replaced by $\epsilon .$ Interestingly, this is due to the fact that the unit interval $[0,1]$ has inradius 1/2 in $\mathbb{R}={\mathbb{Q}}_{\infty }$ whereas ${\mathbb{Z}}_p$ has inradius 1 in ${\mathbb{Q}}_p.$ Recall that the inradius of a subset E of a metric space is the supremum of the radii of the balls entirely contained in E.

Finally, we note that for an archimedean fractal string $\mathcal{L}$, there is no reason to distinguish between the ‘thin volume’ $V_{\mathcal{L}}$ and the ‘thick volume’ ${\mathcal{V}}_{\mathcal{L}}$, as we now explain. Indeed, the archimedean analogue $\beta \mathcal{L}$ of the metric boundary is a countable set, and hence has measure zero, no matter which geometric realization Ω one chooses for $\mathcal{L}$. More specifically, in the notation of Remark 8, $\beta \mathcal{L}$ consists of all the endpoints of the open intervals $I_j$ (the connected components of Ω, or equivalently, its convex components). Hence, ${\mu }_L\left(\beta \mathcal{L}\right)=0$ and so

$$V_{\mathcal{L}}\left(\epsilon \right):={\mathcal{V}}_{\mathcal{L}}\left(\epsilon \right)-{\mu }_L\left(\beta \mathcal{L}\right)={\mathcal{V}}_{\mathcal{L}}\left(\epsilon \right),$$

as claimed.

For example, if $\mathcal{L}$ is the ternary Cantor string $\mathcal{CS}$, then $\beta \mathcal{L}$ is the countable set consisting of all the endpoints of the ‘deleted intervals’ in the construction of the real Cantor set $\mathcal{C}$. In other words, $\beta \mathcal{L}$ is the set $\mathcal{T}$ of ternary points (which has measure zero because it is countable). Hence, the metric boundary $\beta \mathcal{L}$ of $\mathcal{CS}$ is dense in $\partial \mathcal{L}$, the topological boundary of $\mathcal{CS}$, and which in the present case, coincides with the ternary Cantor set $\mathcal{C}$. Also note that the fact that $\mathcal{C}=\partial \mathcal{L}$ (and not $\mathcal{T}=\beta \mathcal{L}$) has measure zero is purely coincidental and completely irrelevant here. Indeed, the same type of argument would apply if $\mathcal{L}$ were any archimedean fractal string, even if ${\mu }_L(\partial \mathcal{L})>0$ as is the case for example, if $\partial \mathcal{L}$ is a ‘fat Cantor set’ (i.e., a Cantor set of positive measure) or, more generally, if $\partial \mathcal{L}$ is a ‘fat fractal’ (in the sense of [66,67]). The underlying reason is that in the archimedean case, the topological boundary $\partial \mathcal{L}=\partial \mathsf{\Omega }$ is disjoint from Ω (since Ω is open), and hence, does not play any role in the computation of $V_{\mathcal{L}}\left(\epsilon \right)$ or of ${\mathcal{V}}_{\mathcal{L}}\left(\epsilon \right)$. By contrast, it is not true that the metric boundary $\beta \mathcal{L}$ and the geometric representation Ω are disjoint (since, in fact, $\beta \mathcal{L}\subseteq \mathsf{\Omega }$), but what is remarkable is that the Minkowski dimension of $\beta \mathcal{L}$ coincides with that of its closure, and hence (in most cases of interest), with $D_{M,\mathcal{L}}$.

4.1. Example: The Euler String

As a first application of Theorem 2, we can obtain, via a direct computation, a tube formula for the p-adic Euler string ${\mathcal{E}}_p$; that is, an explicit formula for the volume of the thin inner $\epsilon$-neighborhood, $V_{{\mathcal{E}}_p}\left(\epsilon \right)$, as given in Definition 7.

Let ${\mathcal{E}}_p$ be the p-adic Euler string defined in Section 2.3. Given $\epsilon >0$, let k be the largest integer such that ${\mu }_H(a_k+p^k{\mathbb{Z}}_p)=p^{-k}\ge \epsilon$; then $k=\left[{\log }_p{\epsilon }^{-1}\right]$. (Here, for $x\in \mathbb{R}$, we write $x=\left[x\right]+\left\{x\right\},$ where $\left[x\right]$ is the integer part and $\left\{x\right\}$ is the fractional part of x; i.e., $x\in \mathbb{Z}$ and $0\le \left\{x\right\}<1$.) Thus, by Equation (25) of Theorem 2, we have,

$$V_{{\mathcal{E}}_p}\left(\epsilon \right)=p^{-1}\sum _{n=k+1}^{\infty }{p}^{-n}=\frac{p^{-1}}{p-1}{p}^{-k}=\frac{p^{-1}}{p-1}{p}^{-{\log }_p{\epsilon }^{-1}}{\left(\frac{1}{p}\right)}^{-\left\{{\log }_p{\epsilon }^{-1}\right\}},$$

since $k={\log }_p{\epsilon }^{-1}-\left\{{\log }_p{\epsilon }^{-1}\right\}$. Next, the Fourier series expansion for $b^{-\left\{x\right\}}$ is given by (see [7] (Equation (1.13)))

$$b^{-\left\{x\right\}}=\frac{b-1}{b}\sum _{n\in \mathbb{Z}}\frac{e^{2\pi inx}}{\log b+2\pi in},$$

(28)

Applying it with $b=1/p$ and $x={\log }_p{\epsilon }^{-1}$, we find

$$\begin{array}{cc}\hfill V_{{\mathcal{E}}_p}\left(\epsilon \right)& =\frac{p^{-1}}{p-1}\frac{p-1}{\log p}\sum _{n\in \mathbb{Z}}\frac{{\epsilon }^{1-in\mathbf{p}}}{1-in\mathbf{p}}\hfill \\ & =\frac{1}{p\log p}\sum _{\omega \in {\mathcal{D}}_{{\mathcal{E}}_p}}\frac{{\epsilon }^{1-\omega }}{1-\omega }.\hfill \end{array}$$

(29)

Finally, in the last equality, we have used Equation (8) for the set of complex dimensions ${\mathcal{D}}_{{\mathcal{E}}_p}$ of ${\mathcal{E}}_p$.

5. Minkowski Dimension

In the sequel, the (inner) Minkowski dimension and the (inner) Minkowski content of a p-adic fractal string ${\mathcal{L}}_p$ (or, equivalently, of its metric boundary $\beta {\mathcal{L}}_p$, see Definition 6) is defined exactly as the corresponding notion for a real fractal string (see [7] (Definition 1.2)), except for the fact that we now use the definition of $V\left(\epsilon \right)=V_{{\mathcal{L}}_p}\left(\epsilon \right)$ provided in Equation (24) of Definition 7. (For reasons that will be clear to the reader later on in this section, we denote by $D_M=D_{M,{\mathcal{L}}_p}$ instead of by $D=D_{{\mathcal{L}}_p}$ the Minkowski dimension of ${\mathcal{L}}_p.$) More specifically, the Minkowski dimension of ${\mathcal{L}}_p$ is given by

$$D_M=D_{M,{\mathcal{L}}_p}:=inf\left\{\alpha \ge 0|V_{{\mathcal{L}}_p}\left(\epsilon \right)=O\left({\epsilon }^{1-\alpha }\right)\mathrm{as}\epsilon \to 0^{+}\right\}.$$

(30)

Furthermore, ${\mathcal{L}}_p$ is said to be Minkowski measurable, with Minkowski content $\mathcal{M}$, if the limit

$$\mathcal{M}=\underset{\epsilon \to 0^{+}}{lim}{V}_{{\mathcal{L}}_p}\left(\epsilon \right){\epsilon }^{-(1-D_M)}$$

(31)

exists in $(0,\infty ).$

Remark 12.

Note that since $V_{{\mathcal{L}}_p}\left(\epsilon \right)={\mathcal{V}}_{{\mathcal{L}}_p}\left(\epsilon \right)-{\mu }_H\left(\beta {\mathcal{L}}_p\right)$, the above definition of the Minkowski dimension is somewhat analogous to that of “exterior dimension”, which is sometimes used in the archimedean case to measure the roughness of a ‘fat fractal’ (i.e., a fractal with positive Lebesgue measure). The notion of exterior dimension has been useful in the study of aspects of chaotic nonlinear dynamics; see, e.g., [66] and the survey article [67].

The goal of the rest of this section is to establish the following theorem, which is the exact analogue for p-adic fractal strings of [7], Theorem 1.10, which was first observed in [2,3] by using a result of [68]. (Recall that ${\sigma }_{{\mathcal{L}}_p}$ is defined in Equation (13) of Section 3. Also note that we need to assume that ${\mathcal{L}}_p$ has infinitely many lengths since if ${\mathcal{L}}_p$ is composed of finitely many intervals, then ${\sigma }_{{\mathcal{L}}_p}=-\infty$ and $D_M=D=0$; see Formula (36) below for the definition of D).

Theorem 3.

Let ${\mathcal{L}}_p$ be a p-adic fractal string composed of infinitely many intervals. Then the Minkowski dimension $D_M=D_{M,{\mathcal{L}}_p}$ of ${\mathcal{L}}_p$ equals the abscissa of convergence ${\sigma }_{{\mathcal{L}}_p}$ of the geometric zeta function ${\zeta }_{{\mathcal{L}}_p}$. That is, $D_M={\sigma }_{{\mathcal{L}}_p}$.

Theorem 3 will be established in Theorem 4 below in greater generality, namely for any summable sequence of positive numbers $l_j$. This is the object of the technical Lemma 2, which is of independent interest.

When applied to a p-adic fractal string, the following lemma relates the thin volume with the zeta function. For completeness, but independently of this, we also formulate the counterpart for the counting function of the reciprocal lengths of an arbitrary fractal string. The lemma holds in general, independently of the fact that in the present situation, the lengths are powers of p. Recall from (25) that

$$V\left(\epsilon \right)=\frac{1}{p}\sum _{j:l_j\le \epsilon }{l}_j,$$

writing V instead of $V_{{\mathcal{L}}_p}$ since what follows holds for arbitrary infinite sequences of positive numbers $l_j$ such that ${\sum }_{j=1}^{\infty }{l}_j$ is convergent. Also, the geometric counting function of $\mathcal{L}:={\left\{l_j\right\}}_{j=1}^{\infty }$,

$$\begin{array}{c}N\left(x\right):=\sum _{l_j\ge 1/x}1,\end{array}$$

(32)

is the number of reciprocal lengths up to $x>0$, and

$$\begin{array}{c}{\zeta }_{\mathcal{L}}\left(s\right):=\sum _{j=1}^{\infty }{l}_j^s,\end{array}$$

(33)

at least for all $s\in \mathbb{C}$ such that $\mathfrak{R}s>1$.

Lemma 2.

We have the following two expressions for ${\zeta }_{\mathcal{L}}\left(s\right):$

$$\begin{array}{c}{\zeta }_{\mathcal{L}}\left(s\right)={\zeta }_{\mathcal{L}}\left(1\right)l_1^{s-1}+(1-s){\int }_0^{l_1}pV\left(\epsilon \right){\epsilon }^{s-2}d\epsilon ,\end{array}$$

(34)

and

$$\begin{array}{c}{\zeta }_{\mathcal{L}}\left(s\right)=s{\int }_0^{\infty }N\left(x\right)x^{-s-1}dx.\end{array}$$

(35)

Both expressions converge exactly when ${\sum }_{j=1}^{\infty }{l}_j^s$ converges.

Proof. 

For $n>0$, we compute

$$\begin{array}{cc}\hfill (1-s){\int }_{l_n}^{l_1}pV\left(\epsilon \right){\epsilon }^{s-2}d\epsilon & =\sum _{j=1}^{n-1}(1-s){\int }_{l_{j+1}}^{l_j}pV\left(\epsilon \right){\epsilon }^{s-2}d\epsilon \hfill \\ & =\sum _{j=1}^{n-1}\sum _{k=j+1}^{\infty }{l}_k(1-s){\int }_{l_{j+1}}^{l_j}{\epsilon }^{s-2}d\epsilon ,\hfill \end{array}$$

since for $l_{j+1}\le \epsilon <l_j$, the function $pV\left(\epsilon \right)$ is constant, equal to ${\sum }_{k>j}{l}_k$. We compute the integral to obtain

$$\begin{array}{c}\hfill (1-s){\int }_{l_n}^{l_1}pV\left(\epsilon \right){\epsilon }^{s-2}d\epsilon =\sum _{j=1}^{n-1}\sum _{k=j+1}^{\infty }{l}_k\left(l_{j+1}^{s-1}-l_j^{s-1}\right).\end{array}$$

Next, we split the sum and interchange the order of summation, to obtain

$$\sum _{j=2}^n\sum _{k=j}^{\infty }{l}_k{l}_j^{s-1}-\sum _{j=1}^{n-1}\sum _{k=j+1}^{\infty }{l}_k{l}_j^{s-1}=\sum _{k=2}^{\infty }{l}_k\sum _{j=2}^{min\{k,n\}}{l}_j^{s-1}-\sum _{k=2}^{\infty }{l}_k\sum _{j=1}^{min\{k,n\}-1}{l}_j^{s-1}.$$

In this formula, the two double sums clearly converge, since ${\sum }_{k\ge 1}{l}_k$ converges. Simplifying, we obtain

$$\begin{array}{cc}\hfill (1-s){\int }_{l_n}^{l_1}pV\left(\epsilon \right){\epsilon }^{s-2}d\epsilon & =\sum _{k=2}^{\infty }{l}_k{l}_{min\{k,n\}}^{s-1}-\sum _{k=2}^{\infty }{l}_k{l}_1^{s-1}\hfill \\ & =\sum _{k=2}^{n-1}{l}_k^s+\sum _{k=n}^{\infty }{l}_k{l}_n^{s-1}-l_1^{s-1}\sum _{k=2}^{\infty }{l}_k.\hfill \end{array}$$

Now, $l_k{l}_n^{s-1}\le l_k^s$ for $k\ge n$ (if $s\ge 1$, we estimate instead $l_n^{s-1}\le 1$, provided n is so large that $l_n\le 1$). Hence we can let n approach infinity if and only if ${\sum }_{k=2}^{\infty }{l}_k^s$ converges, and then the middle sum converges to zero. In that case, we obtain ${\sum }_{k\ge 1}{l}_k^s-l_1^{s-1}{\zeta }_{\mathcal{L}}\left(1\right)={\zeta }_{\mathcal{L}}\left(s\right)-{\zeta }_{\mathcal{L}}\left(1\right)l_1^{s-1}$ for the limit.

In a similar way, we compute

$$\begin{array}{c}\hfill s{\int }_0^{l_n^{-1}}N\left(x\right)x^{-s-1}dx=\sum _{j=1}^{n-1}s{\int }_{l_j^{-1}}^{l_{j+1}^{-1}}N\left(x\right)x^{-s-1}dx=\sum _{j=0}^{n-1}j\left(l_j^s-l_{j+1}^s\right),\end{array}$$

since $N\left(x\right)=0$ for $x<l_1^{-1}$, and $N\left(x\right)=j$ for $l_j^{-1}\le x<l_{j+1}^{-1}$. We find

$$\begin{array}{c}\hfill s{\int }_0^{l_n^{-1}}N\left(x\right)x^{-s-1}dx=\sum _{j=1}^{n-1}j{l}_j^s-\sum _{j=1}^n(j-1)l_j^s=\sum _{j=1}^n{l}_j^s-n{l}_n^s.\end{array}$$

Now, $n{l}_n^s\le 2{\sum }_{j=[n/2]}^n{l}_j^s$, provided $s\ge 0$, so we can let n approach infinity if and only if ${\sum }_{j=1}^{\infty }{l}_j^s$ converges, in which case we find the value ${\zeta }_{\mathcal{L}}\left(s\right)$ for the limit, again since the tail ${\sum }_{j=[n/2]}^{\infty }{l}_j^s$ converges to zero.  ☐

Recall that the Minkowski dimension $D_M$ was defined in (30) above. We also define the growth rate of $\mathcal{L}$ (or asymptotic growth rate of the geometric counting function $N:=N_{\mathcal{L}}$) by

$$\begin{array}{c}D:=inf\left\{\alpha \ge 0|N\left(x\right)=O\left(x^{\alpha }\right)\mathrm{as}x\to \infty \right\}.\end{array}$$

(36)

Theorem 4.

Assume that the hypotheses of Theorem 3 are satisfied. Then ${\sigma }_{\mathcal{L}}$, the abscissa of convergence of ${\zeta }_{\mathcal{L}}$, coincides with $D_M$ and with D. That is, $D_M={\sigma }_{\mathcal{L}}=D$.

Proof. 

Let $\alpha >D_M.$ Since, by definition of $D_M,V\left(\epsilon \right)\le A{\epsilon }^{1-\alpha }$, then

$$(1-s){\int }_0^{l_1}V\left(\epsilon \right){\epsilon }^{s-2}d\epsilon \le A(1-s){\int }_0^{l_1}{\epsilon }^{s-\alpha -1}d\epsilon .$$

(Here, A is some suitable positive constant.) This integral converges for all real numbers $s>\alpha$; hence, by the foregoing lemma (Lemma 2), $\sigma \le \alpha$, where (for notational simplicity) $\sigma ={\sigma }_{\mathcal{L}}$ denotes the abscissa of convergence of $\mathcal{L}:={\left\{{\ell }_j\right\}}_{j=1}^{\infty }$. Since this holds for all $\alpha \in \mathbb{R}$ such that $\alpha >D_M$, we conclude that $\sigma \le D_M$. Conversely, if $\alpha <D_M$, then $V\left(\epsilon \right)$ is not $O\left({\epsilon }^{1-\alpha }\right)$ as $\epsilon \to 0^{+}$. This means that there exists a sequence ${\left\{{\epsilon }_n\right\}}_{n=0}^{\infty }$ converging to $0,$ with $l_1\ge {\epsilon }_0>{\epsilon }_1>{\epsilon }_2>\cdots$ and such that $V\left({\epsilon }_j\right)\ge {\epsilon }_j^{1-\alpha }$ for every $j\ge 1$. Moreover, we may choose the sequence to be exponentially decreasing; say, ${\epsilon }_{n+1}<{\epsilon }_n/2$ for every $n\ge 1$. Then, for $s\le 1$,

$$(1-s){\int }_0^{l_1}V\left(\epsilon \right){\epsilon }^{s-2}d\epsilon \ge \sum _{j=1}^{\infty }(1-s){\int }_{{\epsilon }_j}^{{\epsilon }_{j-1}}{\epsilon }_j^{1-\alpha }{\epsilon }^{s-2}d\epsilon ,$$

since $V\left(\epsilon \right)$ is increasing. We then estimate

$$(1-s){\int }_{{\epsilon }_j}^{{\epsilon }_{j-1}}{\epsilon }^{s-2}d\epsilon ={\epsilon }_j^{s-1}-{\epsilon }_{j-1}^{s-1}\ge {\epsilon }_j^{s-1}\left(1-2^{s-1}\right),$$

to obtain

$$(1-s){\int }_0^{l_1}V\left(\epsilon \right){\epsilon }^{s-2}d\epsilon \ge \sum _{j=1}^{\infty }{\epsilon }_j^{s-\alpha }\left(1-2^{s-1}\right).$$

For all $s\in \mathbb{R}$ such that $s\le \alpha$, this sum diverges. Again by Lemma 2, we conclude that $\sigma \ge \alpha$. This holds for all $\alpha <D_M$; hence, $\sigma \ge D_M$. Together with the first part, we conclude that $\sigma =D_M$.

Next, we show that $\sigma =D$. If $\alpha >D$, then $N\left(x\right)\le A{x}^{\alpha }$ for some $A>0$. Then for all $s\in \mathbb{R}$ such that $s>\alpha$, and noting that $N\left(x\right)$ vanishes for $x<l_1^{-1}$, we have that

$$s{\int }_{l_1^{-1}}^{\infty }N\left(x\right)x^{-s-1}dx\le \frac{A}{s-\alpha }{l}_1^{s-\alpha }.$$

Hence, according to Lemma 2, $\sigma \le \alpha$. Since this holds for all $\alpha >D$, we conclude that $\sigma \le D$.

Conversely, if $\alpha <D$, then $N\left(x\right)$ is not $O\left(x^{\alpha }\right)$. This means that there exists an unbounded sequence ${\left\{x_j\right\}}_{j=0}^{\infty }$ tending to ∞, with $l_1^{-1}\le x_0<x_1<x_2<\cdots$ and such that $N\left(x_j\right)\ge x_j^{\alpha }$ for every j. Moreover, we choose the sequence to be exponentially increasing, $x_{n+1}>2x_n$. Then, for $s\ge 0$,

$$s{\int }_{l_1^{-1}}^{\infty }N\left(x\right)x^{-s-1}dx\ge \sum _{j=0}^{\infty }s{\int }_{x_j}^{x_{j+1}}{x}_j^{\alpha }{x}^{-s-1}dx,$$

since $N\left(x\right)$ is increasing. We estimate $s{\int }_{x_j}^{x_{j+1}}{x}^{-s-1}dx\ge x_j^{-s}\left(1-2^{-s}\right),$ to obtain

$$s{\int }_{l_1^{-1}}^{\infty }N\left(x\right)x^{-s-1}dx\ge \sum _{j=1}^{\infty }{x}_j^{\alpha -s}\left(1-2^{-s}\right).$$

For $s\le \alpha$, this sum diverges. We conclude that $\sigma \ge \alpha$. This holds for all $\alpha <D$, hence $\sigma \ge D$, and it follows that $\sigma =D$.

Combining all of the above steps, we conclude that $\sigma =D_M=D,$ as desired.  ☐

Corollary 2.

For any p-adic fractal string ${\mathcal{L}}_p$ with infinitely many lengths, we have $0\le D_M={\sigma }_{{\mathcal{L}}_p}\le 1$. Furthermore, we have that $D_M={\sigma }_{{\mathcal{L}}_p}=D,$ where D is the growth rate of ${\mathcal{L}}_p$ defined by (36).

5.1. The Real Case

For (ordinary) archimedean fractal strings, the Minkowski dimension also determines the abscissa of convergence of the geometric zeta function, in an analogous manner. The advantage of our new proof is that it yields a unified approach to both the archimedean and nonarchimedean (or p-adic) cases. It also establishes in the process the new result according to which $D_M$ is not only equal to ${\sigma }_{\mathcal{L}}$ (the abscissa of convergence of $\mathcal{L}$) but also to D (the asymptotic growth rate of $\mathcal{L}$), a useful fact which was only implicit in earlier work (such as [2,3,4,6,7]), even for real (or archimedean) fractal strings and is explicitly needed, for example, in [9,10,11].

We provide here the details of our unified approach, but by focusing, of course, on the real (or archimedean) case.

The geometric zeta function of a real fractal string $\mathcal{L}={\left\{{\ell }_j\right\}}_{j=1}^{\infty },$ with $l_1\ge l_2\ge l_3\ge \cdots \to 0$, is given by (33), just as in the p-adic case, with an abscissa of convergence defined by

$${\sigma }_{\mathcal{L}}=inf\left\{\alpha \in \mathbb{R}:\sum _{j=1}^{\infty }{l}_j^{\alpha }<\infty \right\},$$

(37)

entirely analogous to (13). We assume an infinite number of positive lengths with a finite total length,

$${\zeta }_{\mathcal{L}}\left(1\right)=\sum _{j=1}^{\infty }{l}_j<\infty ;$$

so that $0\le {\sigma }_{\mathcal{L}}\le 1$.

Since both in the archimedean and in the nonarchimedean case, the geometric zeta function and geometric counting function $N_{\mathcal{L}}$ (and hence D) are defined in the same way, it immediately follows that (35) holds in the archimedean case as well, and consequently, ${\sigma }_{\mathcal{L}}=D$.

On the other hand, the formula for the volume of the tubular neighborhoods is different, due to the different geometry of the boundary of balls in ${\mathbb{Q}}_p$ (as we have seen in Section 4) and of intervals in $\mathbb{R}$. In particular, the real unit interval $[0,1]$ has inradius 1/2 in $\mathbb{R}={\mathbb{Q}}_{\infty }$ whereas the p-adic unit ball ${\mathbb{Z}}_p$ has inradius 1 in ${\mathbb{Q}}_p$ (see also Remark 11). For real fractal strings, $V_{\mathcal{L}}\left(\epsilon \right)$ is given by (27), and hence the formula corresponding to (34) is

$$\begin{array}{c}{\zeta }_{\mathcal{L}}\left(s\right)=s{\zeta }_{\mathcal{L}}\left(1\right)l_1^{s-1}+2s(1-s){\int }_0^{l_1/2}{V}_{\mathcal{L}}\left(\epsilon \right){\left(2\epsilon \right)}^{s-2}d\epsilon ,\end{array}$$

(38)

valid for $\Re s>D_M$, where $D_M$ is defined by (30). This can be proved by a method similar to the proof of Lemma 2, but we give here an alternative proof. The function $V_{\mathcal{L}}=V_{\mathcal{L}}\left(\epsilon \right)$ is continuous and piecewise differentiable for $\epsilon >0$, with derivative

$$V_{\mathcal{L}}^{\prime }\left(\epsilon \right)=2N_{\mathcal{L}}\left(\frac{1}{2\epsilon }\right).$$

Integrating by parts, we obtain

$$\begin{array}{cc}\hfill 2s(1-s){\int }_0^{l_1/2}{V}_{\mathcal{L}}\left(\epsilon \right)& {\left(2\epsilon \right)}^{s-2}d\epsilon \hfill \\ & =-s{\left[V_{\mathcal{L}}\left(\epsilon \right){\left(2\epsilon \right)}^{s-1}\right]}_0^{l_1/2}+2s{\int }_0^{l_1/2}{N}_{\mathcal{L}}(1/2\epsilon ){\left(2\epsilon \right)}^{s-1}d\epsilon \hfill \\ & =-s{\zeta }_{\mathcal{L}}\left(1\right)l_1^{s-1}+s{\int }_{l_1^{-1}}^{\infty }{N}_{\mathcal{L}}\left(x\right)x^{-1-s}dx,\hfill \end{array}$$

which by (35) equals $-s{\zeta }_{\mathcal{L}}\left(1\right)l_1^{s-1}+{\zeta }_{\mathcal{L}}\left(s\right)$ since $N_{\mathcal{L}}\left(x\right)=0$ for $x<l_1^{-1}$.

Remark 13.

As an alternative, the zeta function is also given by

$${\zeta }_{\mathcal{L}}\left(s\right)=2s(1-s){\int }_0^{\infty }{V}_{\mathcal{L}}\left(\epsilon \right){\left(2\epsilon \right)}^{s-2}d\epsilon .$$

This expression only converges for $D_M<\Re s<1$.

As was already pointed out earlier, the above formula converges for $\Re s>D_M$. In addition, it follows from the proof that the formula converges if and only if the series for ${\zeta }_{\mathcal{L}}$ converges. This implies that ${\sigma }_{\mathcal{L}}\le D_M$. In order to prove the converse inequality, we construct, just as in the proof of Theorem 4, a sequence of positive $\epsilon$-values decreasing exponentially fast to zero in order to show that (38) does not converge for $\Re s<D_M$. It follows that ${\sigma }_{\mathcal{L}}=D_M$.

We conclude that for a real (or archimedean) fractal string, we have $D_M={\sigma }_{\mathcal{L}}=D$, just as was shown in the first part of this section for a p-adic (or nonarchimedean) fractal string, and thereby completing the statement and the proof of Theorems 3 and 4 (now extended to the real case), as well as providing a unified treatment of both the archimedean and nonarchimedean cases.

6. Explicit Tube Formulas for $\mathbf{p}$-adic Fractal Strings

The following result is the counterpart in this context of Theorem 8.1 of [7], the distributional tube formula for real fractal strings. It is established by using, in particular, the extended distributional explicit formula of [7], Theorems 5.26 and 5.27, along with the expression for the volume of thin inner $\epsilon$-tubes obtained in Theorem 2.

We now state our general nonarchimedean (or p-adic) fractal tube formula in this context.

Theorem 5 (p-adic explicit tube formula).

(i) 

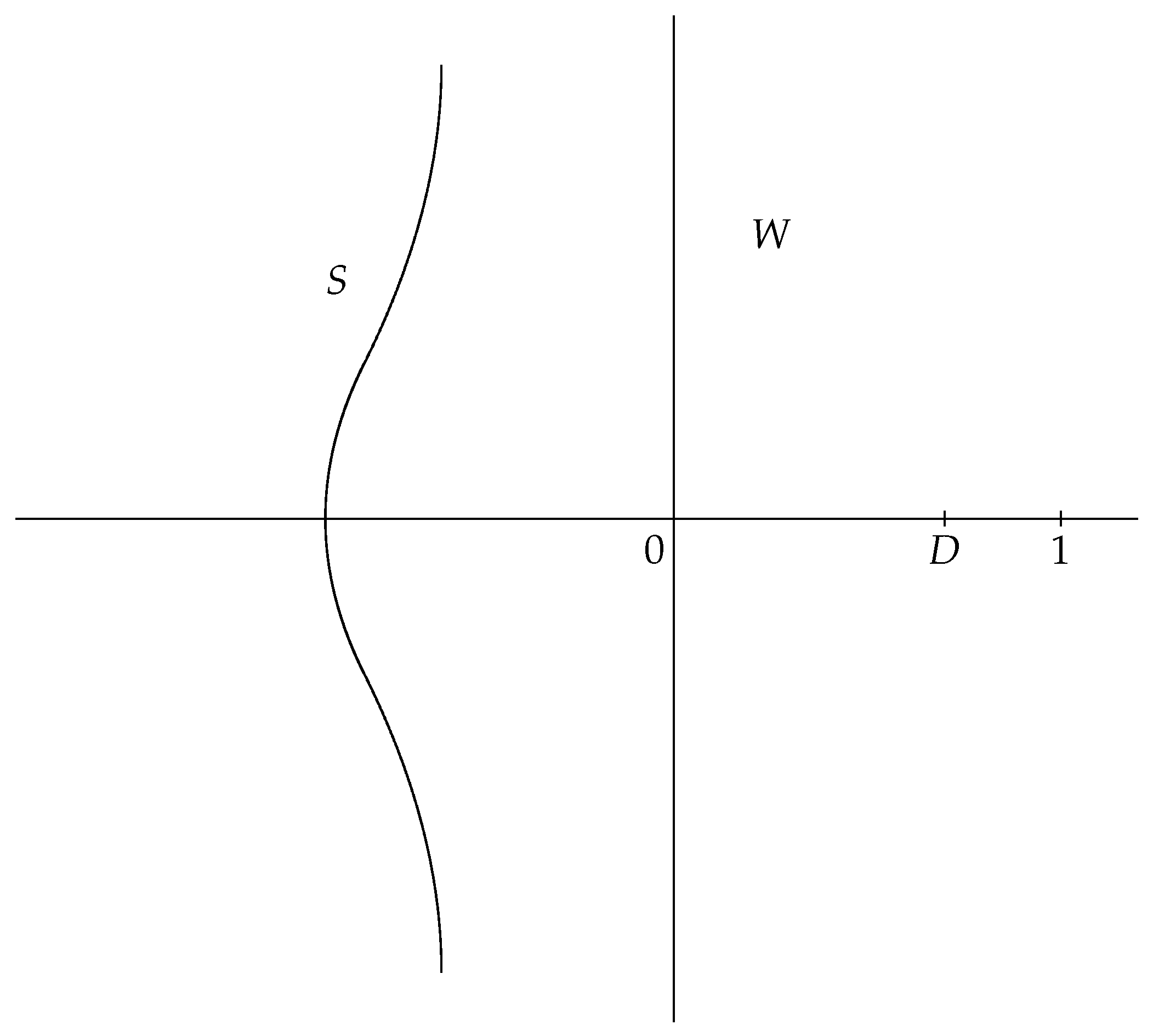
Let ${\mathcal{L}}_p$ be a languid p-adic fractal string (as in the first part of Definition 5 of Section 3), for some real exponent κ and a screen S that lies strictly to the left of the vertical line $\Re \left(s\right)=1$. Further assume that ${\sigma }_{{\mathcal{L}}_p}<1.$(Recall from Corollary 2 that we always have ${\sigma }_{{\mathcal{L}}_p}\le 1$. Moreover, if ${\mathcal{L}}_p$ is self-similar, then ${\sigma }_{{\mathcal{L}}_p}<1.)$ Then the volume of the thin inner ε-neighborhood of ${\mathcal{L}}_p$ is given by the following distributional explicit formula, on test functions in $\mathbf{D}(0,\infty )$, the space of $C^{\infty }$ functions with compact support in $(0,\infty ):$

$$V_{{\mathcal{L}}_p}\left(\epsilon \right)=\sum _{\omega \in {\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)}\mathrm{res}\left(\frac{p^{-1}{\zeta }_{{\mathcal{L}}_p}\left(s\right){\epsilon }^{1-s}}{1-s};\omega \right)+{\mathcal{R}}_p\left(\epsilon \right),$$

(39)

where ${\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)$ is the set of visible complex dimensions of ${\mathcal{L}}_p$(as given in Definition 4$).$ Here, the distributional error term is given by

$${\mathcal{R}}_p\left(\epsilon \right)=\frac{1}{2\pi i}{\int }_S\frac{p^{-1}{\zeta }_{{\mathcal{L}}_p}\left(s\right){\epsilon }^{1-s}}{1-s}ds$$

(40)

and is estimated distributionally (in the sense of [7], Definition 5.29) by

$${\mathcal{R}}_p\left(\epsilon \right)=O\left({\epsilon }^{1-supS}\right),\mathrm{as}\epsilon \to 0^{+}.$$

(41)

(ii) 

Moreover, if ${\mathcal{L}}_p$ is strongly languid (as in the second part of Definition 5), then we can take $W=\mathbb{C}$ and ${\mathcal{R}}_p\left(\epsilon \right)\equiv 0$, provided we apply this formula to test functions supported on compact subsets of $[0,A)$. The resulting explicit formula without error term is often called an exact tube formula in this case.

Proof. 

Since the proof of Theorem 5 parallels that of its counterpart for real fractal strings (see [7], Theorem 8.7), we only provide here the main steps. We will explain, in particular, why the p-adic tube formula takes a different form than in the real case. As will be clear from the proof, it all goes back to the difference between Theorem 2 and its archimedean analogue (see Equation (27) above or [7], Equation (8.1)).

According to Theorem 2,

$$\begin{array}{c}\hfill V_{{\mathcal{L}}_p}\left(\epsilon \right)=\frac{1}{p}\sum _{j:p^{-n_j}<\epsilon }{p}^{-n_j}=\frac{1}{p}{\int }_{1/\epsilon }^{\infty }\frac{1}{x}\eta \left(dx\right)=\langle {\mathcal{P}}_{\eta }^{\left[0\right]},v_{\epsilon }\rangle ,\end{array}$$

where ${\mathcal{P}}_{\eta }^{\left[0\right]}=\eta :={\sum }_{j=1}^{\infty }{\delta }_{\left\{p^{n_j}\right\}}$ is viewed as a distribution and

$$v_{\epsilon }\left(x\right):=\left\{\begin{array}{cc}0\hfill & \mathrm{if} x\le 1/\epsilon \hfill \\ 1/\left(px\right)\hfill & \mathrm{if} x>1/\epsilon .\hfill \end{array}\right.$$

Fix $\phi \in \mathbf{D}(0,\infty )$. Then

$$\begin{array}{cc}\hfill {\int }_0^{\infty }\phi \left(\epsilon \right)v_{\epsilon }\left(x\right)d\epsilon & =\frac{1}{px}{\int }_{1/x}^{\infty }\phi \left(\epsilon \right)d\epsilon \hfill \\ & =p^{-1}{\phi }_1\left(x\right),\hfill \end{array}$$

where ${\phi }_1$ is a smooth, but not compactly supported, test function, given by

$${\phi }_1\left(x\right):=\frac{1}{x}{\int }_{1/x}^{\infty }\phi \left(\epsilon \right)d\epsilon .$$

Thus

$$\begin{array}{cc}\hfill \langle V_{{\mathcal{L}}_p}\left(\epsilon \right),\phi \rangle & ={\int }_0^{\infty }\phi \left(\epsilon \right){\int }_0^{\infty }{v}_{\epsilon }\left(x\right)\eta \left(dx\right)d\epsilon \hfill \\ & =〈{\mathcal{P}}_{\eta }^{\left[0\right]},p^{-1}{\phi }_1\left(x\right)〉.\hfill \end{array}$$

(42)

The Mellin transform of ${\phi }_1$ is computed to be

$$\begin{array}{c}{\tilde{\phi }}_1\left(s\right)=\frac{1}{1-s}\tilde{\phi }(2-s)\mathrm{for}\Re s<1.\end{array}$$

(43)

Furthermore, by analytic continuation, and since $\tilde{\phi }\left(s\right)$ is entire for $\phi \in \mathbf{D}(0,\infty )$, the equality in (43) continues to hold for all $s\in \mathbb{C}.$

Now, let $\mathsf{\Psi }=p^{-1}{\phi }_1$. Its Mellin transform is

$$\tilde{\mathsf{\Psi }}\left(s\right)=\frac{p^{-1}}{1-s}\tilde{\phi }(2-s),$$

which holds for all $s\in \mathbb{C}$. Note that it follows from our previous discussion that $\tilde{\mathsf{\Psi }}\left(s\right)$ is meromorphic in all of $\mathbb{C}$, with a single, simple pole at $s=1$.

Next, we deduce from (42) and [7], Theorem 5.26 (the extended distributional explicit formula) that

$$\begin{array}{cc}\hfill \langle V_{{\mathcal{L}}_p}\left(\epsilon \right),\phi \rangle & =\sum _{\omega \in {\mathcal{D}}_{{\mathcal{L}}_p}}\mathrm{res}\left({\zeta }_{{\mathcal{L}}_p}\left(s\right)\tilde{\mathsf{\Psi }}\left(s\right);\omega \right)+{\mathcal{R}}_p\left(\epsilon \right)\hfill \\ & ={\int }_0^{\infty }\sum _{\omega \in {\mathcal{D}}_{{\mathcal{L}}_p}}\mathrm{res}\left(\frac{{\zeta }_{{\mathcal{L}}_p}\left(s\right){\epsilon }^{1-s}}{p(1-s)};\omega \right)\phi \left(\epsilon \right)d\epsilon +{\int }_0^{\infty }{\mathcal{R}}_p\left(\epsilon \right)\phi \left(\epsilon \right)d\epsilon .\hfill \end{array}$$

Therefore,

$$V_{{\mathcal{L}}_p}\left(\epsilon \right)=\sum _{\omega \in {\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)}\mathrm{res}\left(\frac{{\zeta }_{{\mathcal{L}}_p}\left(s\right){\epsilon }^{1-s}}{p(1-s)};\omega \right)+{\mathcal{R}}_p\left(\epsilon \right),$$

where the distribution ${\mathcal{R}}_p\left(\epsilon \right)$ is given by (40) and is estimated distributionally as in (41).

In closing this proof, we note that in the strongly languid case, we use [7], Theorem 5.27 in order to conclude that (39) holds with ${\mathcal{R}}_p\left(\epsilon \right)\equiv 0.$ ☐

Remark 14.

We may rewrite the (typically infinite) sum in (39) as follows:

$$\sum _{\omega \in {\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)}\mathrm{res}({\zeta }_{{\mathcal{L}}_p}(\epsilon ;s);s=\omega ),$$

(44)

where (by analogy with the definitions and results in [41,42]),

$${\zeta }_{{\mathcal{L}}_p}(\epsilon ;s):=\frac{p^{-1}{\zeta }_{{\mathcal{L}}_p}\left(s\right){\epsilon }^{1-s}}{1-s}$$

(45)

is called the nonarchimedean tubular zeta function of the p-adic fractal string ${\mathcal{L}}_p$.

By contrast, the archimedean tubular zeta function (in the present one-dimensional situation) of a real fractal string $\mathcal{L}$ is given by

$${\zeta }_{\mathcal{L}}(\epsilon ;s):=\frac{{\zeta }_{\mathcal{L}}\left(s\right){\left(2\epsilon \right)}^{1-s}}{s(1-s)},$$

(46)

and the analog of the above sum in the archimedean tube formula of [7] (as rewritten in [41]) is given as in (44), except with ${\mathcal{L}}_p$ replaced by $\mathcal{L}$ and with ${\mathcal{D}}_{\mathcal{L}}\left(W\right)\cup \left\{0\right\}$ instead of ${\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)$. Note that ${\zeta }_{\mathcal{L}}(\epsilon ;s)$ typically has a pole at $s=0$, whereas ${\zeta }_{{\mathcal{L}}_p}(\epsilon ;s)$ does not.

Corollary 3 (p-adic fractal tube formula).

If, in addition to the hypotheses in Theorem 5, we assume that all the visible complex dimensions of ${\mathcal{L}}_p$ are simple, then

$$V_{{\mathcal{L}}_p}\left(\epsilon \right)=\sum _{\omega \in {\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)}{c}_{\omega }\frac{{\epsilon }^{1-\omega }}{1-\omega }+{\mathcal{R}}_p\left(\epsilon \right),$$

(47)

where $c_{\omega }=p^{-1}\mathrm{res}\left({\zeta }_{{\mathcal{L}}_p};\omega \right)$. Here, the error term ${\mathcal{R}}_p$ is given by (40) and is estimated by (41) in the languid case. Furthermore, we have ${\mathcal{R}}_p\left(\epsilon \right)\equiv 0$ in the strongly languid case, provided we choose $W=\mathbb{C}$.

Remark 15.

In [7], Chapter 8, under different sets of assumptions, both distributional and pointwise tube formulas are obtained for archimedean fractal strings (and also, for archimedean self-similar fractal strings). (See, in particular, Theorems 8.1 and 8.7, along with Section 8.4 in [7].) At least for now, in the nonarchimedean case, we limit ourselves to discussing distributional explicit tube formulas. We expect, however, that under appropriate hypotheses, one should be able to obtain a pointwise fractal tube formula for p-adic fractal strings and especially, for p-adic self-similar strings. In fact, for the simple examples of the nonarchimedean Cantor, Euler and Fibonacci strings, the direct derivation of the fractal tube Formula (47) yields a formula that is valid pointwise and not just distributionally. (See, in particular, Section 4.1 and Example 2.) We leave the consideration of such possible pointwise extensions to a future work.

Example 1 (Fractal tube formula for the p-adic Euler string).

We now explain how to recover from Theorem 5 (or Corollary 3) the tube formula for the Euler string ${\mathcal{E}}_p$ obtained via a direct computation in Section 4.1. Indeed, it follows from Corollary 3 (applied with $W=\mathbb{C}$) that

$$V_{{\mathcal{E}}_p}\left(\epsilon \right)=\frac{1}{p}\sum _{\omega \in {\mathcal{D}}_{{\mathcal{E}}_p}}\mathrm{res}({\zeta }_{{\mathcal{E}}_p};\omega )\frac{{\epsilon }^{1-\omega }}{1-\omega },$$

(48)

which is exactly the expression obtained for $V_{{\mathcal{E}}_p}\left(\epsilon \right)$ in Formula (29) of Section 4.1 since

$$\mathrm{res}({\zeta }_{{\mathcal{E}}_p};\omega )=\frac{1}{\log p}$$

for all $\omega \in {\mathcal{D}}_{{\mathcal{E}}_p}.$ (This latter observation follows easily from the expression of ${\zeta }_{{\mathcal{L}}_p}$ obtained in Equation (7).) Note that Corollary 3 can be applied here in the strongly languid case when $W=\mathbb{C}$ and ${\mathcal{R}}_p\left(\epsilon \right)\equiv 0$ since, in light of the discussion in Section 2.3, all the complex dimensions of ${\mathcal{E}}_p$ are simple and ${\zeta }_{{\mathcal{E}}_p}$ is clearly strongly languid of order $\kappa :=0$ and with the constant $A:=p^{-1}.$ Furthermore, Formula (48) can be rewritten in the following more concrete form:

$$V_{{\mathcal{E}}_p}\left(\epsilon \right)=\frac{1}{p\log p}\sum _{n\in \mathbb{Z}}\frac{{\epsilon }^{1-in\mathbf{p}}}{1-in\mathbf{p}},$$

(49)

since ${\mathcal{D}}_{{\mathcal{E}}_p}=\{in\mathbf{p}:n\in \mathbb{Z}\}$ and $\mathbf{p}=2\pi /\log p$ (as in Equation (8) of Section 2.3).

Finally, note that since the series

$$\sum _{n\in \mathbb{Z}}\frac{{\epsilon }^{1-in\mathbf{p}}}{1-in\mathbf{p}}$$

converges pointwise because the associated Fourier series ${\sum }_{n\in \mathbb{Z}}\frac{e^{2\pi inx}}{1-in\mathbf{p}}$ is pointwise convergent on $\mathbb{R}$, it follows that the p-adic fractal tube Formulas (48) and (49) actually converge pointwise rather than just distributionally.

Example 2 (The tube formula for the nonarchimedean Cantor string).

In this example, we explain how to derive the exact fractal tube formula for ${\mathcal{CS}}_3$, the 3-adic Cantor string introduced in [30] and further studied in [31,32,33].

By construction, the complement of ${\mathcal{CS}}_3$ in ${\mathbb{Z}}_3$ is the 3-adic Cantor set ${\mathcal{C}}_3$, which is a nonarchimedean self-similar set (as introduced in [30,31]); so that ${\mathcal{C}}_3$ is the unique nonempty compact subset K of ${\mathbb{Z}}_3$ (or of ${\mathbb{Q}}_3$) which is the solution of the fixed point equation

$$K={\phi }_1\left(K\right)\cup {\phi }_2\left(K\right),$$

(50)

for some suitable affine similarity transformations ${\phi }_1,{\phi }_2$ from ${\mathbb{Z}}_3$ to itself; more specifically, we have that ${\phi }_1\left(x\right)=3x$ and ${\phi }_2\left(x\right)=2+3x$, for all $x\in {\mathbb{Z}}_3$. We refer to [30,31,32] for more information concerning the properties of ${\mathcal{C}}_3$ and ${\mathcal{CS}}_3$ as well as for corresponding figures. (See [69] for the general definition of self-similar sets in complete metric spaces, and [70] for a detailed discussion in the usual case of Euclidean spaces.)

Let $\epsilon >0$. We have that

$${\zeta }_{{\mathcal{CS}}_3}\left(s\right)=\frac{3^{-s}}{1-2·3^{-s}},foralls\in \mathbb{C}$$

and hence

$${\mathcal{D}}_{{\mathcal{CS}}_3}=\{D+i\nu \mathit{p}|\nu \in \mathbb{Z}\},$$

will all the complex dimensions being simple and where $D:={\log }_{3}2$ and $\mathit{p}:=2\pi /\log 3$. Furthermore, we have that

$$\mathrm{res}({\zeta }_{{\mathcal{CS}}_3};\omega )=\frac{1}{2\log 3},$$

independently of $\omega \in {\mathcal{D}}_{{\mathcal{CS}}_3}$, and so the exact fractal tube formula for the nonarchimedean Cantor string is found to be

$$V_{{\mathcal{CS}}_3}\left(\epsilon \right)=\frac{1}{3}\sum _{\omega \in {\mathcal{D}}_{{\mathcal{CS}}_3}}\mathrm{res}({\zeta }_{{\mathcal{CS}}_3};\omega )\frac{{\epsilon }^{1-\omega }}{1-\omega }.$$

(51)

Note that since ${\mathcal{CS}}_3$ has simple complex dimensions, we may also apply Corollary 3 (in the strongly languid case when $W=\mathbb{C}$) in order to precisely recover Equation (51).

We may rewrite (51) in the following form:

$$V_{{\mathcal{CS}}_3}\left(\epsilon \right)={\epsilon }^{1-D}{G}_{{\mathcal{CS}}_3}\left({\log }_3{\epsilon }^{-1}\right),$$

where $G_{{\mathcal{CS}}_3}$ is the nonconstant periodic function (of period 1) on $\mathbb{R}$ given by

$$G_{{\mathcal{CS}}_3}\left(x\right):=\frac{1}{6\log 3}\sum _{n\in \mathbb{Z}}\frac{e^{2\pi inx}}{1-D-in\mathbf{p}}.$$

Finally, we note that since the Fourier series

$$\sum _{n\in \mathbb{Z}}\frac{e^{2\pi inx}}{1-D-in\mathbf{p}}$$

is pointwise convergent on $\mathbb{R}$, the above direct computation of $V_{{\mathcal{CS}}_3}\left(\epsilon \right)$ shows that (51) actually holds pointwise rather than just distributionally.

In closing this example, we note that we could similarly use Theorem 5 (or Corollary 3) to obtain an exact fractal tube formula for the 5-adic Cantor set recently introduced in [71] and defined in a way analogous to the 3-adic Cantor set from [30].

Remark 16.

The 3-adic Cantor string discussed in Example 2 is an example of a p-adic (here, 3-adic) self-similar string. Another example of a p-adic (or nonarchimedean) self-similar string is the 2-adic Fibonacci string, whose complex dimensions are distributed periodically along two vertical lines (instead of a single one as in the case of a 3-adic Cantor string). (See [31,32]; furthermore, see [33] for the corresponding exact pointwise tube formula.) In general, a (nontrivial) p-adic self-similar string ${\mathcal{L}}_p$ is always lattice (that is, its scaling ratios are all integer powers of a single number, necessarily p; see [31,32]. Therefore, unlike for real (or archimedean) fractal strings (compare with [7], Chapters 2 and 3), which can be either lattice or nonlattice, the complex dimensions of ${\mathcal{L}}_p$ are always periodically distributed along finitely many vertical lines, the right most of which is the vertical line $\{\mathfrak{R}s=D_M\}$, where $D_M$ is the Minkowski dimension of ${\mathcal{L}}_p$. The corresponding fractal tube formulas, illustrating our main theorem in this section (Theorem 5) in order to obtain fractal tube formulas for general p-adic self-similar fractal strings, are provided in [33].

In order to avoid unnecessary repetitions, we refer the interested reader to [32,33] for those special but important examples of fractal tube formulas. We only mention the following two interesting facts:

(i) 

Because on each relevant vertical line, the complex dimensions form an arithmetic progression (with a progression or period independent of the line) and have the same multiplicities, the corresponding term in the associated fractal tube formula can be written as a suitable power function times a periodic function (of $x:=\log \left({\epsilon }^{-1}\right)$). (This is so assuming that the complex dimensions on that line are simple, which is always the case, for instance, of the right most vertical line $\{\mathfrak{R}s=D_M\}$).

(ii) 

In all of the concrete examples of p-adic self-similar strings studied in [32,33], including the 3-adic Cantor string and the 2-adic Fibonacci string, the corresponding exact fractal tube formula can be shown to converge pointwise (rather than distributionally, as in Theorem 5). We conjecture that at least in the case of simple complex dimensions, the exact fractal tube formula of a p-adic self-similar string always converges pointwise (and not just distributionally, as in Theorem 5). (Such a result is established in [7], Section 8.4 for general real or archimedean self-similar strings, whether or not all of the complex dimensions are simple.) Accordingly, it would be very interesting to establish that conjecture as well as to obtain a pointwise counterpart of Theorem 5; that is, a fractal tube formula for p-adic (not necessarily self-similar) fractal strings, with or without an error term, which (under suitable hypotheses) would be valid pointwise. We note that in the archimedean case (i.e., for real fractal strings) such a pointwise fractal tube formula is available under rather general conditions; see [7], Section 8.1.1, esp., Theorem 8.7 and Corollary 8.10. We leave the investigation of these issues to some future work or to the interested reader.

7. Possible Extensions

We close this paper by providing possible directions for future investigations in this area. In Remark 16, we have already mentioned the problem of obtaining a pointwise fractal tube formula, analogous to our distributional fractal tube formula (Theorem 5) in the archimedean case and to the pointwise tube formula obtained in the nonarchimedean case in [7], Section 8.1.1 (for general real fractal strings, under suitable hypotheses) and (without any assumptions) in [7], Section 8.4 for general real self-similar fractal strings. We next point out other possible problems and research directions.

7.1. Adèlic Fractal Strings and Their Spectra

It would be interesting to unify the archimedean and nonarchimedean settings by appropriately defining adèlic fractal strings, and then studying the associated spectral zeta functions (as is done for standard archimedean fractal strings in [2,3,4,5,6,7,43]). To this aim, the spectrum of these adèlic fractal strings should be suitably defined and its study may benefit from Dragovich’s work [14] on adèlic quantum harmonic oscillators. In the process of defining these adèlic fractal strings, we expect to make contact with the notion of a fractal membrane (or “quantized fractal string”) introduced in [8], Chapter 3 and rigorously constructed in [29] as a Connes-type noncommutative geometric space [65]; see also [8], Section 4.2. The aforementioned spectral zeta function of an adèlic fractal string would then be viewed as the (completed) spectral partition function of the associated fractal membrane, in the sense of [8]. (See also Remark 6 above.) We note that a geometric construction of certain adèlic fractal strings is proposed in the epilogue (Section 8) below.

7.2. Nonarchimedean Fractal Strings in Berkovich Space

As was shown in [31] and recalled in Remark 16, there can only exist lattice p-adic self-similar strings, because of the discreteness of the valuation group of ${\mathbb{Q}}_p$. However, in the archimedean setting, there are both lattice and nonlattice self-similar strings; see [7], Chapters 2 and 3. We expect that by suitably extending the notion of p-adic self-similar string to Berkovich’s p-adic analytic space [19,23], it can be shown that p-adic self-similar strings are generically nonlattice in this broader setting. Furthermore, we conjecture that every nonlattice string in the Berkovich projective line can be approximated by lattice strings with increasingly large oscillatory periods (much as occurs in the archimedean case [7], Chapter 3). Finally, we expect that, by contrast with what happens for p-adic fractal strings, the volume $V_{{\mathcal{L}}_p}\left(\epsilon \right)$ will be a continuous function of $\epsilon$ in this context. (Compare with Remark 11.)

7.3. Higher-Dimensional Fractal Tube Formulas

We expect that the higher-dimensional tube formulas obtained by Lapidus and Pearse in [40,41] (as well as, more generally, by those same authors and Winter in [42]) for archimedean self-similar sprays and the associated tilings [53] in ${\mathbb{R}}^d$ have a natural nonarchimedean counterpart in the d-dimensional p-adic space ${\mathbb{Q}}_p^d,$ for any integer $d\ge 1$. In the latter p-adic case, the corresponding ‘tubular zeta function’ ${\zeta }_{{\mathcal{T}}_p}(\epsilon ;s)$ (when $d=1$, see Remark 14) should have a more complicated expression than in the one-dimensional situation, and should involve both the inner radii and the ‘curvature’ of the generators (see [41,42], as described in [7], Section 13.1, for the archimedean case) of the tiling (or p-adic fractal spray) ${\mathcal{T}}_p.$ Moreover, by analogy with what is expected to happen in the Euclidean case [41,42], the coefficients of the resulting higher-dimensional tube formula should have an appropriate interpretation in terms of yet to be suitably defined ‘nonarchimedean fractal curvatures’ associated with each complex and integral dimension of ${\mathcal{T}}_p$. Finally, by analogy with the archimedean case (for $d\ge 1$, see [41,42]), the p-adic higher-dimensional fractal tube formula should take the same form as in Equation (44), except with ${\zeta }_{{\mathcal{L}}_p}(\epsilon ;s)$ given by a different expression from the one in (45) where $d=1$, and with ${\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)$ replaced by ${\mathcal{D}}_{{\mathcal{L}}_p}\left(W\right)\cup \{0,1,\dots ,d\}$, as well as (for nonarchimedean self-similar tilings) with $W=\mathbb{C}$ and ${\mathcal{R}}_p\left(\epsilon \right)\equiv 0$ in the counterpart of Equation (45) or (46). In the future, we plan to investigate the above problems along with related question pertaining to fractal geometry and geometric measure theory in nonarchimedean spaces.

In closing Section 7.3, we mention that recently, the first author, Goran Radunovi$\grave{\mathrm{c}}$ and Darko Žubrinic have developed a general theory of fractal zeta functions and complex dimensions (see, e.g., the book [34]) valid in Euclidean spaces ${\mathbb{R}}^N$ of any dimension and for arbitrary bounded subsets of ${\mathbb{R}}^N$. In the process, they have very significantly extended the theory of fractal tube formulas obtained originally for fractal strings in [6,7] and then for higher-dimensional fractal sprays (especially, self-similar sprays) in [40,41,42]; see, especially, [46,47] and [34], Chapter 5. Accordingly, it is natural to wonder whether the general theory of fractal zeta functions and fractal tube formulas developed in [34,46,47,48,49] can be applied and suitably adapted in order to obtain concrete nonarchimedean tube formulas valid (under appropriate hypotheses) for arbitrary compact subsets of p-adic space ${\left({\mathbb{Q}}_p\right)}^N$ (or more general ultrametric spaces), and, in particular, for arbitrary p-adic self-similar sets in ${\left({\mathbb{Q}}_p\right)}^N$.

8. Epilogue

In looking for a simple geometric way to create an adèlic fractal string and a global theory of complex fractal dimensions, we found a very natural construction of p-adic fractal strings of any rational dimension between 0 and 1. The simplest example is of dimension $D=\frac{1}{2}$, which is particularly interesting since it involves the diagonal of the digits. This reminds one of the intersections of the graph of the Frobenius with the diagonal in Enrico Bombieri’s proof of the Riemann hypothesis for curves over finite fields. It may give rise to a fractal approach to translating his proof for curves over finite fields to the curve spec $\mathbb{Z}$ over the rationals, which is the case of the famous Riemann hypothesis for the Riemann zeta function. However, we caution the reader that this possibility is far from being realized for now.

We found another natural way to create an infinite family of p-adic Cantor strings ${\mathcal{CS}}_p$ in the nonarchimedean ring of p-adic integers ${\mathbb{Z}}_p$ and simultaneously their exact counterparts in the archimedean unit interval $[0,1]$, the p-inary Cantor strings ${\mathcal{CS}}_p^{*}$. The Minkowski dimensions of the nonarchimedean and archimedean Cantor strings vary from 0 to 1 as p varies from 2 to $\infty .$ Directly above and below the Minkowski dimension lie infinitely many complex fractal dimensions, periodically distributed along a discrete vertical line. The periodic distribution of the complex fractal dimensions, being discrete near dimension 0, become denser as the Minkowski dimension tends to 1.

The simplest way to unify all infinitely many p-adic Cantor strings ${\mathcal{CS}}_p$ together with the ordinary real Cantor string $\mathcal{CS}$ is to form an infinite product

$$\mathcal{CS}\times \prod _{p<\infty }{\mathcal{CS}}_p,$$

which is a self-similar string in the set of integral adèles ${\mathbb{A}}_{\mathbb{Z}}$.

An even more harmonious and symmetric way to unify all the nonarchimedean Cantor strings together with their corresponding archimedean counterpart is first to pair each p-adic Cantor string ${\mathcal{CS}}_p$ together with the p-inary Cantor string ${\mathcal{CS}}_p^{*}$ by taking the Cartesian product ${\mathcal{CS}}_p\times {\mathcal{CS}}_p^{*}\subset {\mathbb{Q}}_p\times \mathbb{R}$. Then we can imagine the infinite direct product

$$\prod _{p<\infty }({\mathcal{CS}}_p\times {\mathcal{CS}}_p^{*})$$

as being an ‘adèlic’ Cantor string in a new ‘adèlic’ space

$$\prod _{p<\infty }({\mathbb{Q}}_p\times \mathbb{R})$$

with infinitely many archimedean components. (We put ‘adèlic’ in quotes because this space has infinitely many real components, one for every prime number, whereas the ring of adèles has only one real component, corresponding to the archimedean valuation of $\mathbb{Q}$.)

We note, however, that our constructions of adèlic fractal strings do not give the Riemann zeta function as the geometric zeta function. It would be interesting to have a natural construction of an adèlic fractal string with the Riemann zeta function as its geometric zeta function.

We conclude these comments with a construction that gives the square of the Riemann zeta function. Let ${\mathcal{E}}_p$ be the p-adic Euler string and h be the real harmonic string, then the infinite direct product

$$h\times \prod _{p<\infty }{\mathcal{E}}_p$$

can be considered as an adèlic fractal string in the set of integral adèles ${\mathbb{A}}_{\mathbb{Z}}$. Let ${\zeta }_{{\mathcal{E}}_p}$ be the geometric zeta function of ${\mathcal{E}}_p$ and ${\zeta }_h$ be the geometric zeta function of the harmonic string; then, the infinite product of complex meromorphic functions

$${\zeta }_h\times \prod _{p<\infty }{\zeta }_{{\mathcal{E}}_p}$$

is equal to the square of the Riemann zeta function.