Abstract
The highlight presented in this short article is about the power laws with respect to fractional capacitance and fractional inductance in terms of frequency.
1. Introduction
Let ic and uc be the current and voltage through and over a capacitor C, with the constant capacitance denoted by C again. Then, one says that Cf stands for a pseudo-capacitance in the sense that
where denotes the fractional derivative of order α of uc [1]. One calls Cf the pseudo-capacitance of a capacitor because its unit is Farad × s1−α instead of Farad [1]. In this article, we call it fractional capacitance of order α of a capacitor. Similarly, the fractional inductance of order β, denoted by Lf, is in the sense that
where uL and iL are the voltage and current over and through an inductor L with the constant inductance denoted again by L. The unit of Lf is Henry × s1−β. It is also called the pseudo-inductance [1,2].
Fractional elements, including a fractional capacitor and a fractional inductor, attract research interests in engineering. The literature about their analysis and applications is rich, see References [1,2,3,4,5,6,7,8,9,10], referring [11,12,13,14] to some recent work on fractional calculus. However, reports about power laws that fractional elements follow are rarely seen. This short article aims at expounding the power laws that fractional elements follow.
In the rest of this article, we present the results in Section 2, which is followed by concluding remarks.
2. Results
Denoted by X(ω) the Fourier transform of x(t). Then, one has, for α > 0,
where . Consequently,
see Miller and Ross [15], Uchaikin [16] (Section 4.5.3) and Lavoie [17] (p. 246).
Following Miller and Ross [15], Raina and Koul [18], we explain our research in the domain of generalized functions. Thus, any function considered in this article is differentiable of any times and its Fourier transform exists (Gelfand and Vilenkin [19]).
Theorem 1.
The fractional capacitance Cf may be expressed by
Cf = (jω)1−αC.
Proof.
The Fourier transform of in Equation (1) is given by
where Uc(ω) = F[uc(t)]. On the other hand, doing the Fourier transform of in Equation (1) produces
Thus, according to Equation (1) and from Equations (6) and (7), we have (jω)αCfUc(ω) = jωCUc(ω). Therefore, we have Cf = (jω)1−αC. Hence, Theorem 1 holds. ☐
Note 1.
Cf reduces to C if α → 1. We use the symbol Cf to represent either fractional capacitance or fractional capacitor.
Corollary 1.
Denote the capacitance ratio by
Rc = C/Cf.
Then, Rc follows the power law in the form
Proof.
From Equation (2.3), we have . The proof completes. ☐
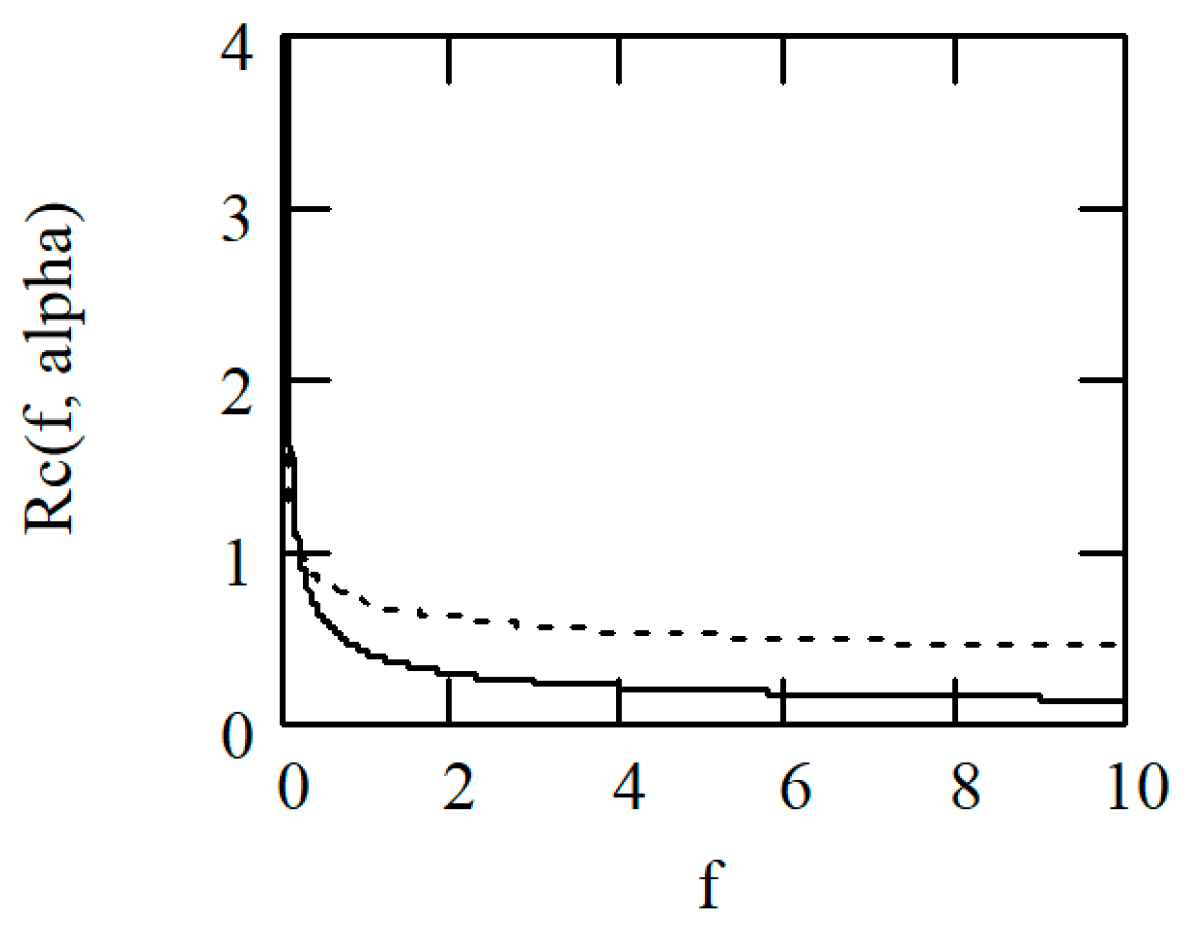
Corollary 1 suggests a power law of Rc in terms of frequency with respect to the fractional capacitor Cf. The unit of Rc is Hertzα−1. Figure 1 shows the plots of |Rc(f, α)| = (2πf )α−1.
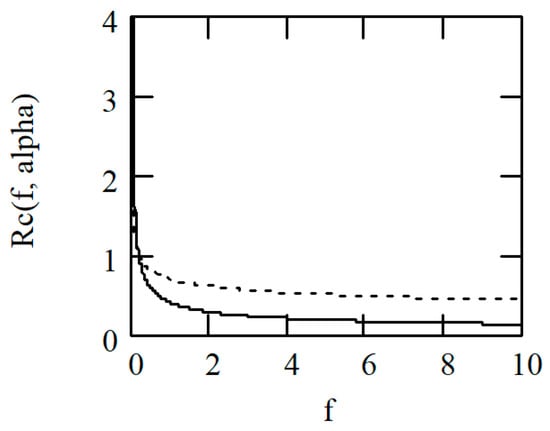
Figure 1.
The plots of |Rc(f, α)|. Solid line: α = 0.5. Dot line: α = 0.8.
Theorem 2.
The fractional inductance Lf may be in the form
Lf = (jω)1−βL.
Proof.
The Fourier transform of in Equation (2) is in the form
where IL(ω) = F[iL(t)]. On the other side, in Equation (2), we have
From Equation (2) and according to Equations (11) and (12), we have . Thus, we have Lf = (jω)1−βL. This completes the proof. ☐
Note 2.
The fractional inductance Lf degenerates to L when β → 1. The symbol Lf stands for both fractional inductance and fractional inductor.
Corollary 2.
Let Rl be the inductance ratio in the form
Rl = L/Lf.
Then, it follows the power law in the form
Proof.
From Equation (10), we have . This completes the proof. ☐
Corollary 2 exhibits a power law of Rl in terms of frequency with respect to Lf. The unit of Rl is Hertzβ−1.
3. Concluding Remarks
We have presented Theorems 1 and 2 to express the fractional capacitance and fractional inductance, respectively. In addition, power laws in terms of frequency with respect to fractional capacitance and fractional inductance have been given in Corollaries 1 and 2. To be precise, for a fractional capacitor (inductor) of order α, the ratio of C (L) to Cf (Lf) obeys (j2πf )α−1 with the unit Hertzα−1. Specifically for a fractional capacitor, due to 0 < α < 1, the power law described by Corollary 1 reveals that Cf → ∞ when f → 0. Note that a key property of a supercapacitor or an ultracapacitor utilized in batteries is that it has an infinitely large capacitance for f → 0 [20,21,22]. Therefore, the power law presented in Corollary 1 provides a new explanation about that as an application in the case of supercapacitors.
Funding
This work was supported in part by the National Natural Science Foundation of China under the project grant numbers 61672238 and 61272402.
Conflicts of Interest
The author declares no conflicts of interest.
References
- Sarafraz, M.S.; Tavazoei, M.S. Passive realization of fractional-order impedances by a fractional element and RLC components: Conditions and procedure. IEEE Trans. Circuits Syst. I 2017, 64, 585–595. [Google Scholar] [CrossRef]
- Sarafraz, M.S.; Tavazoei, M.S. Passively realisable impedance functions by using two fractional elements and some resistors. IET Circuits Devices Syst. 2018, 12, 280–285. [Google Scholar]
- Malek, H.; Dadras, S.; Chen, Y.-Q. Fractional order equivalent series resistance modelling of electrolytic capacitor and fractional order failure prediction with application to predictive maintenance. IET Power Electron. 2016, 9, 1608–1613. [Google Scholar] [CrossRef]
- Tsirimokou, G.; Psychalinos, C.; Freeborn, T.J.; Elwakil, A.S. Emulation of current excited fractional-order capacitors and inductors using OTA topologies. Microelectron. J. 2016, 55, 70–81. [Google Scholar] [CrossRef]
- Ionescu, C.M. Emerging tools in engineering: Fractional order ladder impedance models for respiratory and neural systems. IEEE J. Emerg. Sel. Top. Circuits Syst. 2013, 3, 425–431. [Google Scholar] [CrossRef]
- Pu, Y.-F.; Yuan, X.; Yu, B. Analog circuit implementation of fractional-order memristor: Arbitrary-order lattice scaling fracmemristor. IEEE Trans. Circuits Syst. I 2018, 65, 2903–2916. [Google Scholar] [CrossRef]
- Ionescu, C.M.; Machado, J.A.T.; Keyser, R.D. Modeling of the lung impedance using a fractional-order ladder network with constant phase elements. IEEE Trans. Biomed. Circuits Syst. 2011, 5, 83–89. [Google Scholar] [CrossRef] [PubMed]
- Beaulieu, A.; Bosse, D.; Micheau, P.; Avoine, O.; Praud, J.-P.; Walti, H. Measurement of fractional order model parameters of respiratory mechanical impedance in total liquid ventilation. IEEE Trans. Biomed. Eng. 2012, 59, 323–331. [Google Scholar] [CrossRef] [PubMed]
- Radwan, A.G.; Shamim, A.; Salama, K.N. Theory of fractional order elements based impedance matching networks. IEEE Microw. Wirel. Compon. Lett. 2011, 21, 120–122. [Google Scholar] [CrossRef]
- Martynyuk, V.; Ortigueira, M.; Fedula, M.; Savenko, O. Methodology of electrochemical capacitor quality control with fractional order model. AEU Int. J. Electron. Commun. 2018, 91, 118–124. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Decolonisation of fractional calculus rules: Breaking commutativity and associativity to capture more natural phenomena. Eur. Phys. J. Plus 2018, 133, 1–22. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Fractional derivatives with no-index law property: Application to chaos and statistics. Chaos Solitons Fract. 2018, 114, 516–535. [Google Scholar] [CrossRef]
- Morales-Delgado, V.F.; Taneco-Hernández, M.A.; Gómez-Aguilar, J.F. On the solutions of fractional order of evolution equations. Eur. Phys. J. Plus 2017, 132. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.F.; Baleanu, D.; Córdova-Fraga, T.; Escobar-Jiménez, R.F.; Olivares-Peregrino, V.H.; Al Qurashi, M.M. Bateman–Feshbach Tikochinsky and Caldirola–Kanai oscillators with new fractional differentiation. Entropy 2017, 19, 55. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; John Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Uchaikin, V.V. Fractional Derivatives for Physicists and Engineers; Springer: Berlin, Germany, 2013; Volume I. [Google Scholar]
- Lavoie, J.L.; Osler, T.J.; Tremblay, R. Fractional derivatives and special functions. SIAM Rev. 1976, 18, 240–268. [Google Scholar] [CrossRef]
- Raina, R.K.; Koul, C.L. On Weyl fractional calculus. Proc. Am. Math. Soc. 1979, 73, 188–192. [Google Scholar] [CrossRef]
- Gelfand, I.M.; Vilenkin, K. Generalized Functions; Academic Press: New York, NY, USA, 1964; Volume 1. [Google Scholar]
- Zhang, L.; Hu, X.; Wang, Z.; Sun, F.; Dorrell, D.G. Fractional-order modeling and state-of-charge estimation for ultracapacitors. J. Power Sources 2016, 314, 28–34. [Google Scholar] [CrossRef]
- Kanoun, H.; Gabano, J.-D.; Poinot, T. Fractional modeling of ultracapacitors dynamic behavior. IFAC Proc. Vol. 2011, 44, 13978–13983. [Google Scholar] [CrossRef]
- Zou, C.; Zhang, L.; Hu, X.; Wang, Z.; Pecht, M. A review of fractional-order techniques applied to lithium-ion batteries, lead-acid batteries, and supercapacitors. J. Power Sources 2018, 390, 286–296. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).