Option Pricing Models Driven by the Space-Time Fractional Diffusion: Series Representation and Applications
Abstract
:1. Introduction
2. Option Pricing
2.1. The Risk-Neutral Approach
2.2. Black–Scholes Model
2.3. Finite-Moment Lévy-Stable Model
2.4. Space-Time Option Pricing Model
3. Series Representation of the Pricing Formulas under the Space-Time Fractional Diffusion
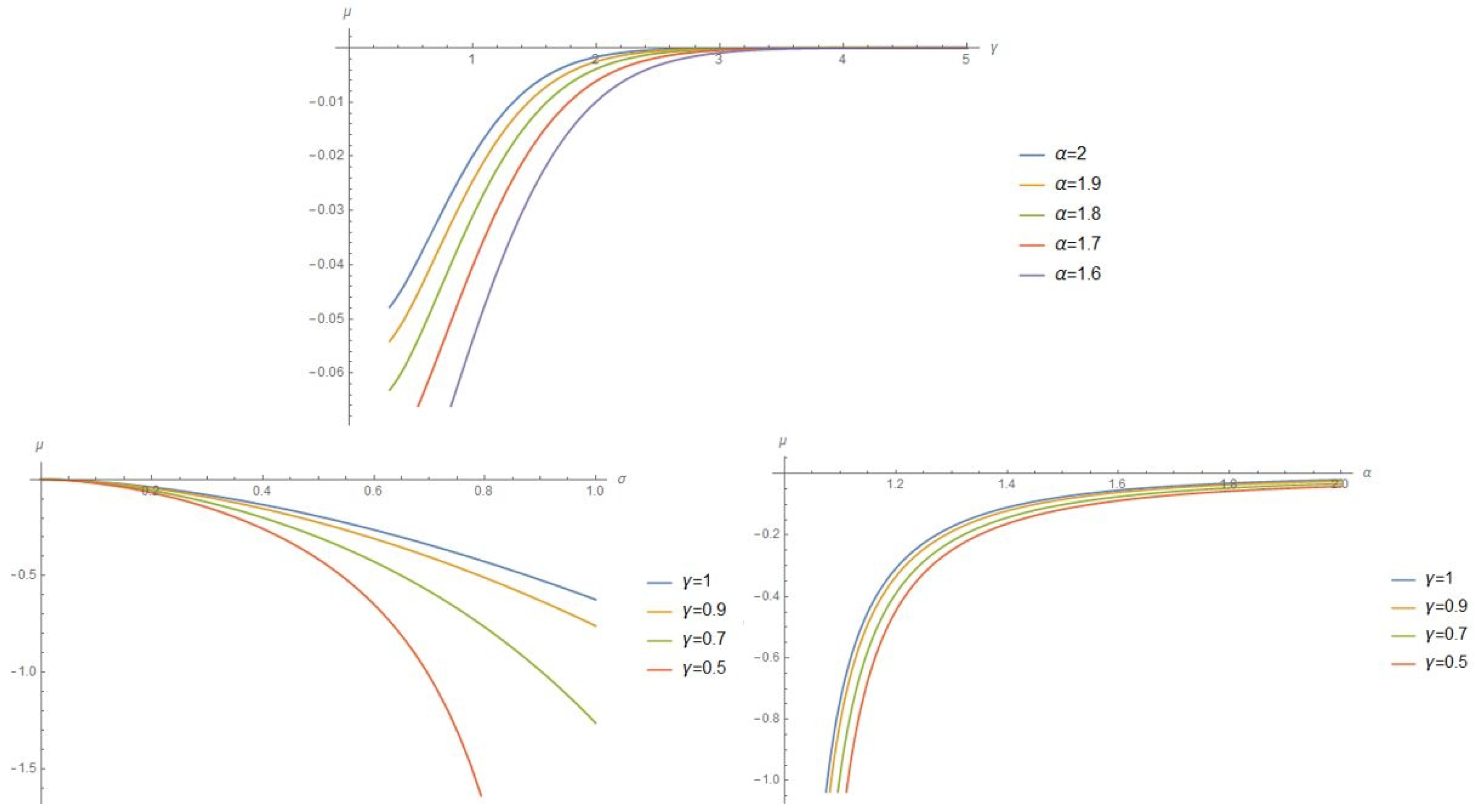
3.1. Risk-Neutral Parameter
3.1.1. Mellin–Barnes Representation of the Risk-Neutral Parameter
3.1.2. Series Representation of the Risk-Neutral Parameter
3.2. Option Price
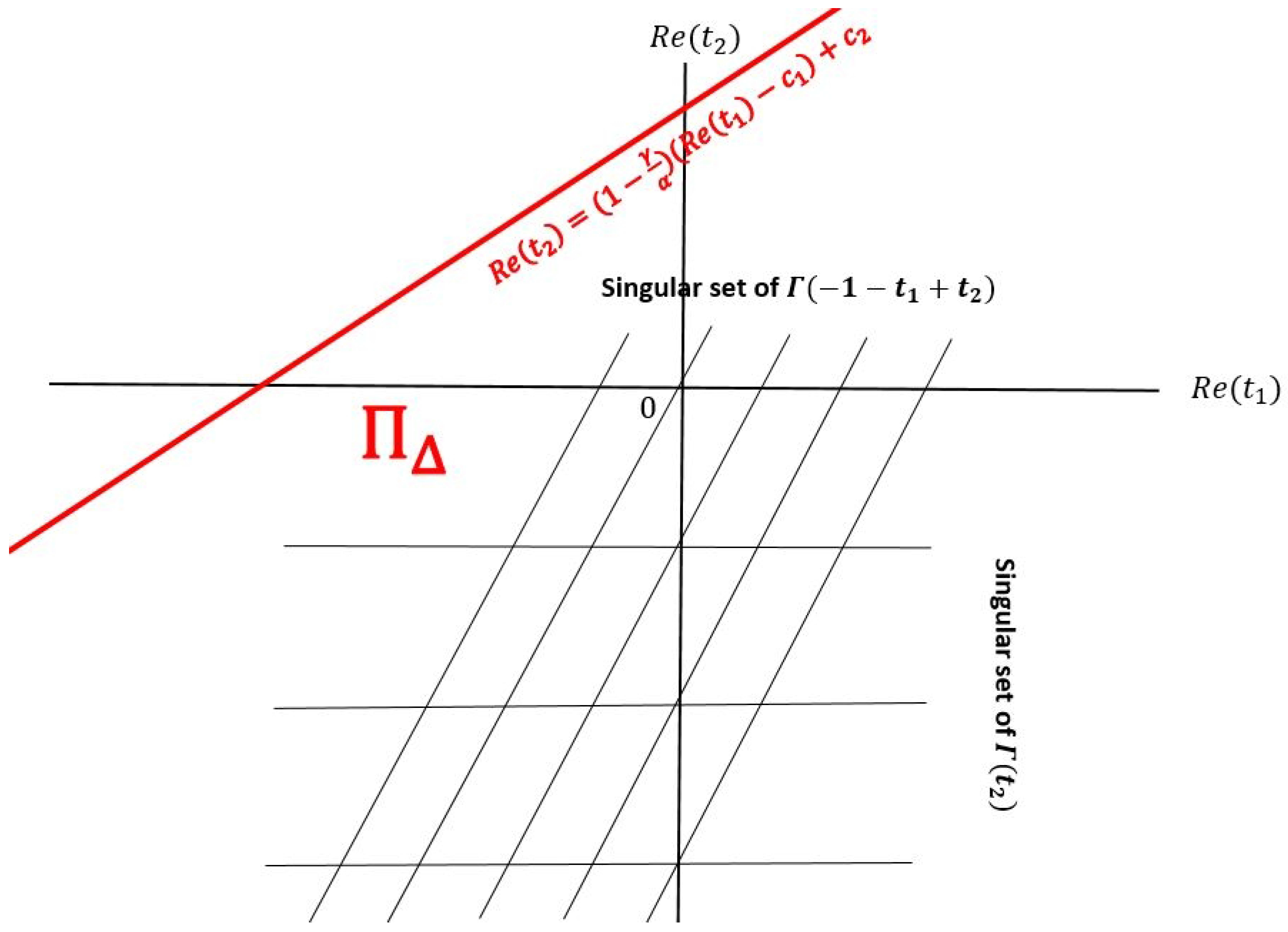
3.2.1. Mellin–Barnes Representation of the Option Price
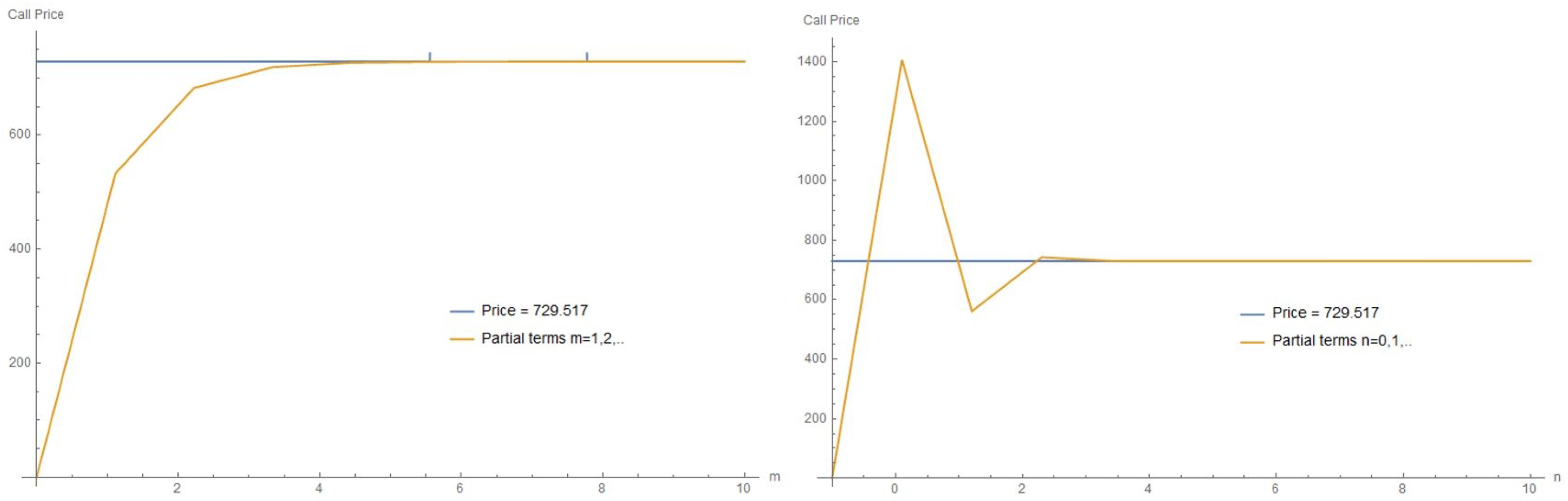
3.2.2. Series Representation of the Option Price
4. Applications
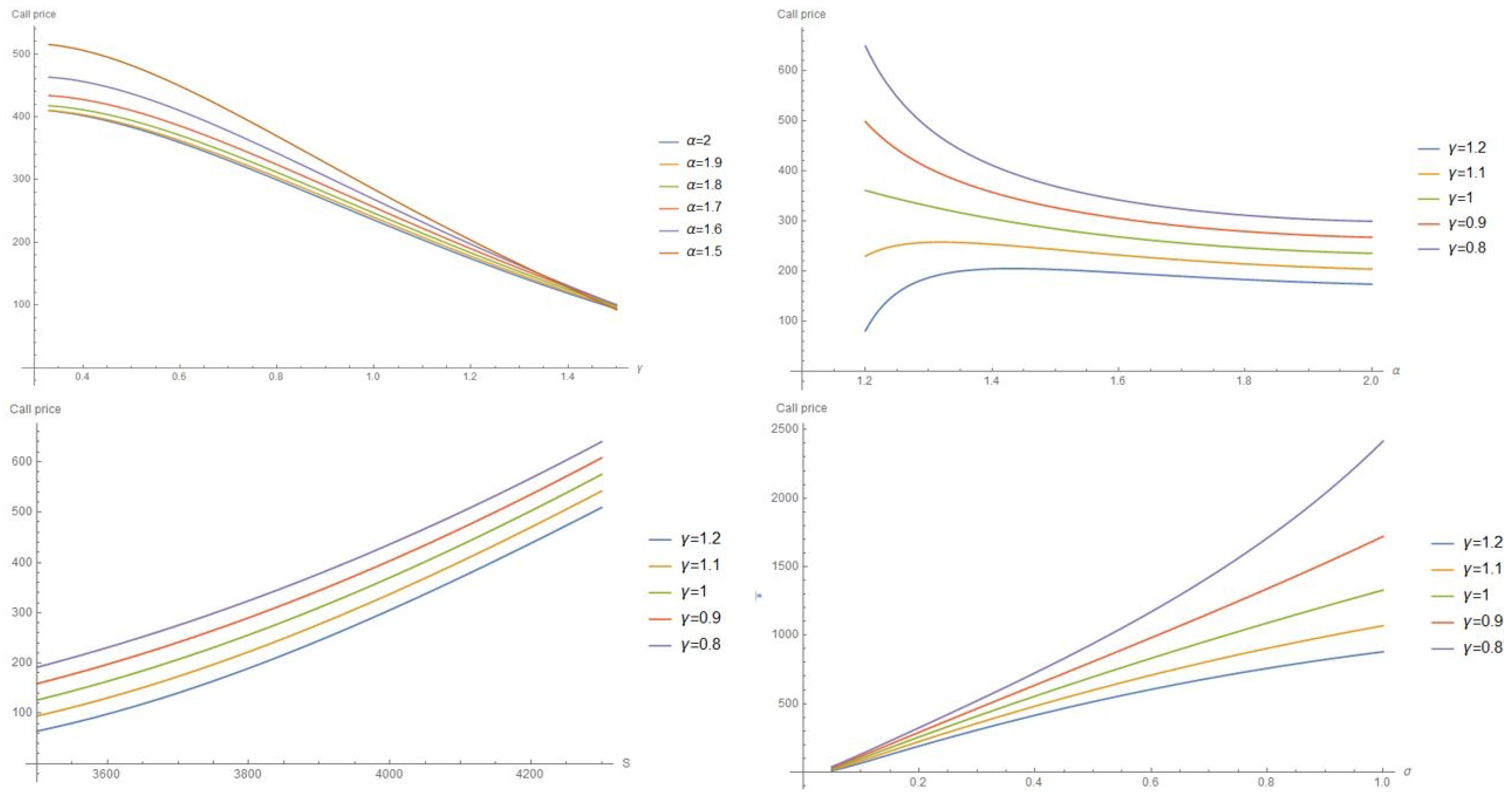
4.1. Call Price
4.2. Implied Volatility
4.2.1. At-the-Money Volatility
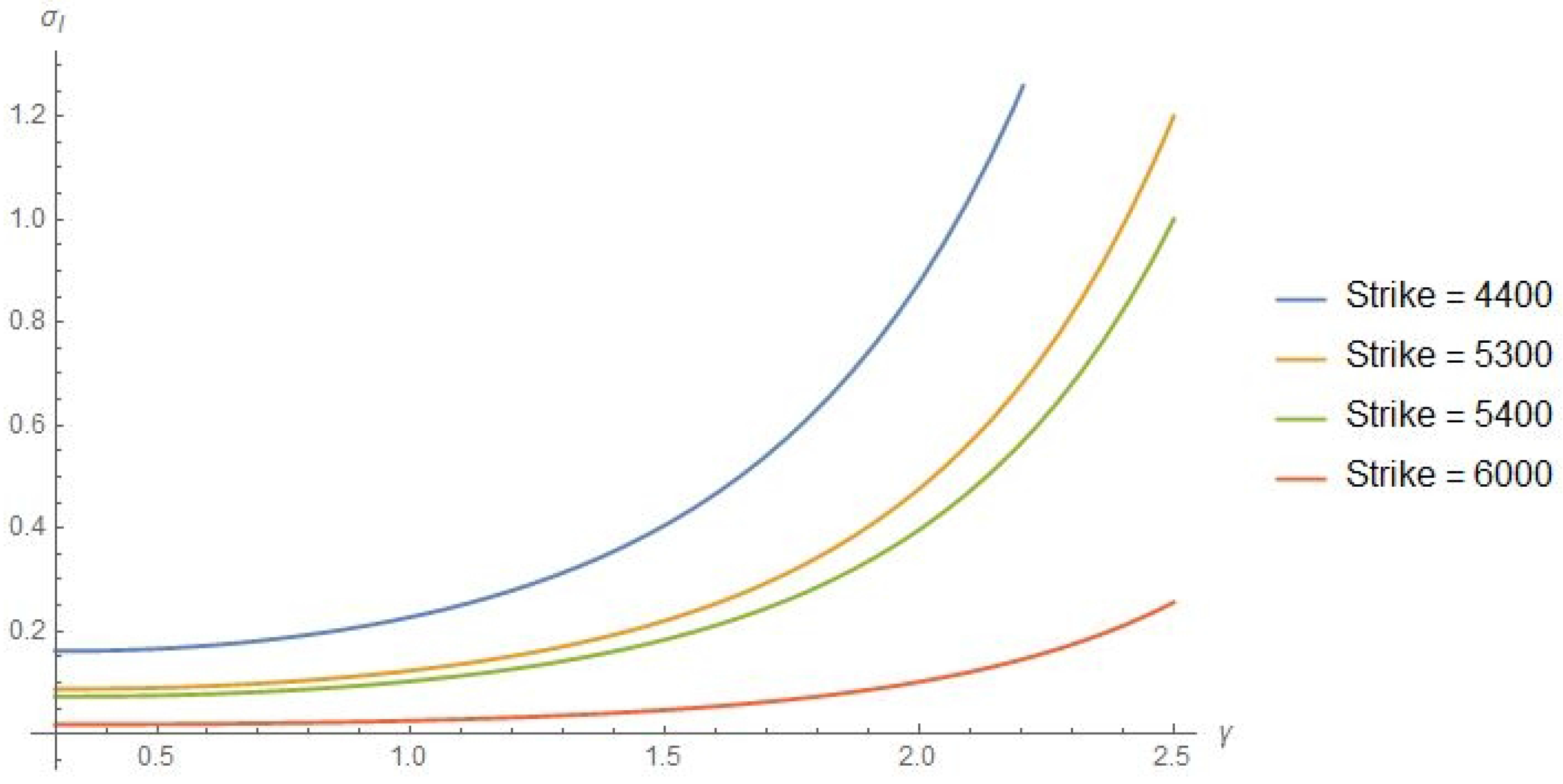
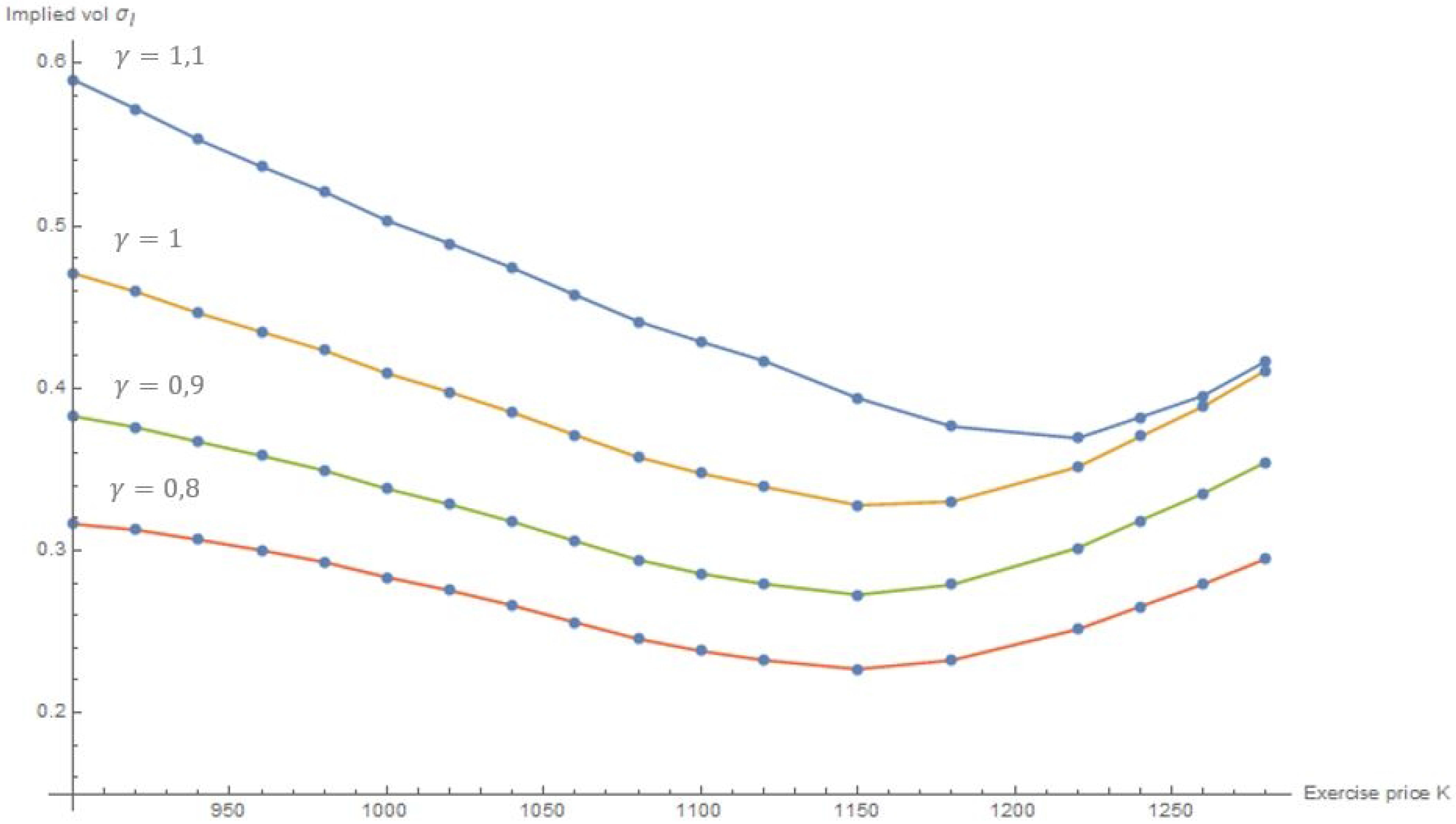
4.2.2. Volatility Smile
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Black, F.; Scholes, M. The pricing of options and corporate liabilities. J. Political Econ. 1973, 81, 637–654. [Google Scholar] [CrossRef]
- Taleb, N.N. The Black Swan: The Impact of the Highly Improbable; Random House Publishing Group: New York, NY, USA, 2010. [Google Scholar]
- Calvet, L.; Fisher, A. Multifractal Volatility: Theory, Forecasting, and Pricing; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Heston, S.L. A Closed-Form Solution for options with stochastic volatility with applications to bond and currency options. Rev. Financ. Stud. 1993, 6, 327–343. [Google Scholar] [CrossRef]
- Tankov, P.; Cont, R. Financial Modelling with Jump Processes; Chapman & Hall/CRC Financial Mathematics Series; Taylor & Francis: London, UK, 2003. [Google Scholar]
- Mainardi, F.; Luchko, Y.; Pagnini, G. The fundamental solution of the space-time fractional diffusion equation. Fract. Calc. Appl. Anal. 2001, 4, 153–192. [Google Scholar]
- Kleinert, H.; Korbel, J. Option pricing beyond Black–Scholes based on double-fractional diffusion. Phys. A 2016, 449, 200–214. [Google Scholar] [CrossRef]
- Korbel, J.; Luchko, Y. Modeling of financial processes with a space-time fractional diffusion equation of varying order. Fract. Calc. Appl. Anal. 2016, 19, 1414–1433. [Google Scholar] [CrossRef]
- Aguilar, J.-P.; Coste, C.; Korbel, J. Series representation of the pricing formula for the European option driven by space-time fractional diffusion. Fract. Calc. Appl. Anal. 2017, arXiv:1712.04990. [Google Scholar]
- Wilmott, P. Paul Wilmott on Quantitative Finance; Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Privault, N. Stochastic Finance; Chapman & Hall: Boca Raton, FL, USA, 2014. [Google Scholar]
- Gerber, H.; Hans, U.; Shiu, E. Option Pricing by Esscher Transforms; HEC Ecole des Hautes Études Commerciales: Jouy-en-Josas, France, 1993. [Google Scholar]
- Øksendal, B. Stochastic Differential Equations: Introduction with Applications, 5th ed.; Springer: Berlin, Germany, 2000. [Google Scholar]
- Carr, P.; Wu, L. The Finite Moment Log Stable Process and Option Pricing. J. Financ. 2003, 58, 753–778. [Google Scholar] [CrossRef]
- Zolotarev, V.M. One-Dimensional Stable Distributions; American Mathematical Society: Providence, RI, USA, 1986. [Google Scholar]
- Fama, E.F. The behavior of stock market prices. J. Bus. 1965, 38, 34–105. [Google Scholar] [CrossRef]
- Mandelbrot, B. The variation of certain speculative prices. J. Bus. 1963, 36, 394–419. [Google Scholar] [CrossRef]
- Aguilar, J.-P.; Coste, C.; Korbel, J. Non-Gaussian analytic option pricing: A closed formula for the Lévy-stable model. 2017; arXiv:1609.00987. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations (Matehmatics in Science and Engineering); Academic Press: Cambridge, MA, USA, 1998; Volume 198. [Google Scholar]
- Samo, S.; Kilbas, A.; Marichev, O. Fractional Integrals and Derivatives: Theory and Applications; Gordon & Breach Science Publishers: Philadelphia, PA, USA, 1993. [Google Scholar]
- Bouchaud, J.-P.; Sornette, D. The Black–Scholes option pricing problem in mathematical finance: Generalization and extensions for a large class of stochastic processes. J. Phys. I EDP Sci. 1994, 4, 863–881. [Google Scholar] [CrossRef]
- Kleinert, H.; Zatloukal, V. Green function of the double-fractional Fokker-Planck equation: Path integral and stochastic differential equations. Phys. Rev. E 2013, 88, 52106. [Google Scholar] [CrossRef] [PubMed]
- Gorenflo, R.; Luchko, Y.; Mainardi, F. Analytical properties and applications of the Wright function. Fract. Calc. Appl. Anal. 1999, 2, 383–414. [Google Scholar]
- Mainardi, F.; Mura, A.; Pagnini, G. The M-Wright function in time-fractional diffusion precesses: A tutorial survey. Int. J. Differ. Equ. 2010, 2010, 104505. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions; Dover Publications: Mineola, NY, USA, 1972. [Google Scholar]
- Passare, M.; Tsikh, A.; Zhdanov, O. A multidimensional Jordan residue lemma with an application to Mellin–Barnes integrals. In Contributions to Complex Analysis and Analytic Geometry. Aspects of Mathematics; Vieweg+Teubner Verlag: Wiesbaden, Germany, 1994; Volume E26, pp. 233–241. [Google Scholar] [CrossRef]
- Passare, M.; Tsikh, A.; Cheshel, A.A. Multiple Mellin–Barnes integrals as periods of Calabi–Yau manifolds with several moduli. Theor. Math. Phys. 1997, 109, 1544–1555. [Google Scholar] [CrossRef]
- Brenner, M.; Subrahmanyam, M.G. A simple approach to option valuation and hedging in the Black–Scholes model. Financ. Anal. J. 1994, 50, 25–28. [Google Scholar] [CrossRef]
| All Options | |||
| Parameter | Black–Scholes | Lévy Stable | Double-Fractional |
| - | 1.493(0.028) | 1.503(0.037) | |
| - | - | 1.017(0.019) | |
| 0.1696(0.027) | 0.140(0.021) | 0.143(0.030) | |
| AE | 8240(638) | 6994(545) | 6931(553) |
| Call Options | |||
| Parameter | Black–Scholes | Lévy Stable | Double-Fractional |
| - | 1.563(0.041) | 1.585(0.038) | |
| - | - | 1.034(0.024) | |
| 0.140(0.021) | 0.118(0.026) | 0.137(0.020) | |
| AE | 3882(807) | 3610(812) | 3550(828) |
| Put Options | |||
| Parameter | Black–Scholes | Lévy Stable | Double-Fractional |
| - | 1.493(0.031) | 1.508(0.036) | |
| - | - | 1.047(0.017) | |
| 0.193(0.039) | 0.163(0.034) | 0.163(0.037) | |
| AE | 3741(711) | 3114(591) | 2968(594) |
| Strike | Call Price | BS Vol | F-BS Vol () | F-BS Vol () | F-BS Vol () |
|---|---|---|---|---|---|
| 900 | 118.9 | 0.4708 | 0.3163 | 0.3827 | 0.5900 |
| 940 | 92.7 | 0.4462 | 0.3066 | 0.3670 | 0.5330 |
| 980 | 69.5 | 0.4232 | 0.2929 | 0.3493 | 0.5210 |
| 1020 | 49.2 | 0.3976 | 0.2754 | 0.3284 | 0.4891 |
| 1060 | 32.3 | 0.3711 | 0.2557 | 0.3058 | 0.4574 |
| 1100 | 19.5 | 0.3475 | 0.2380 | 0.2857 | 0.4186 |
| 1150 | 8.9 | 0.3279 | 0.2269 | 0.2727 | 0.3938 |
| 1180 | 5.1 | 0.3301 | 0.2324 | 0.2789 | 0.3764 |
| 1220 | 2 | 0.3514 | 0.2514 | 0.3015 | 0.3692 |
| 1280 | 0.25 | 0.4110 | 0.2949 | 0.3544 | 0.4166 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, J.-P.; Korbel, J. Option Pricing Models Driven by the Space-Time Fractional Diffusion: Series Representation and Applications. Fractal Fract. 2018, 2, 15. https://doi.org/10.3390/fractalfract2010015
Aguilar J-P, Korbel J. Option Pricing Models Driven by the Space-Time Fractional Diffusion: Series Representation and Applications. Fractal and Fractional. 2018; 2(1):15. https://doi.org/10.3390/fractalfract2010015
Chicago/Turabian StyleAguilar, Jean-Philippe, and Jan Korbel. 2018. "Option Pricing Models Driven by the Space-Time Fractional Diffusion: Series Representation and Applications" Fractal and Fractional 2, no. 1: 15. https://doi.org/10.3390/fractalfract2010015
APA StyleAguilar, J.-P., & Korbel, J. (2018). Option Pricing Models Driven by the Space-Time Fractional Diffusion: Series Representation and Applications. Fractal and Fractional, 2(1), 15. https://doi.org/10.3390/fractalfract2010015






