Some Properties of Positive Solutions for Nonlinear Systems Involving Pseudo-Relativistic Operators

Abstract

In this paper, we mainly investigate the radial symmetry and monotonicity of positive solutions for a nonlinear system involving pseudo-relativistic operators and fractional derivatives of order $(0,1)$. First, we prove a more general Narrow Region Principle and a Decay at Infinity Principle, which are essential for nonlocal pseudo-relativistic operators. Then, by using the direct method of moving planes, we prove the radial symmetry and radial monotonicity of positive solutions for the nonlinear system in the bounded domain $B_1\left(0\right)$ and the whole space, respectively. Finally, we show that the positive solutions of the system are strictly monotonically increasing in a Lipschitz coercive epigraph.

1. Introduction

The pseudo-relativistic Schrödinger equation accounts for a variety of physical phenomena; for example, the propagation characteristics of light beams. Nevertheless, nonlinear effects may arise from the interaction of light with different media. The nonlocal operator ${(-\Delta +m^2)}^s$ (where $s\in (0,1)$ and the mass $m>0$) finds extensive applications across multiple research fields, such as the anomalous diffusion of plasmas, probability theory, finance, and population dynamics (see [1] and the references therein). Notably, as $m\to 0^{+}$, the operator ${(-\Delta +m^2)}^s$ reduces to the well-known fractional Laplacian ${(-\Delta )}^s$, whose standard definition is available in [2,3,4] and the relevant references. When $s={\displaystyle \frac{1}{2}}$, the operator ${(-\Delta +m^2)}^s$ reduces to the pseudo-relativistic Schrödinger operator $\sqrt{-\Delta +m^2}$, which is associated with the Hamiltonian $\mathcal{H}=\sqrt{p^2{c}^2+m^2{c}^4}$ of a free relativistic particle of mass m via the standard quantization rule $p\to i\hslash \Delta$, where $i=\sqrt{-1}$, ℏ reduced Planck constant, defined as $\hslash ={\displaystyle \frac{h}{2\pi }}$, where h is the Planck constant. ℏ is a more commonly used form in quantum theory. A wealth of important properties of the pseudo-relativistic Schrödinger operator $\sqrt{-\Delta +m^2}$ have been established in the literature, and detailed discussions can be found in [5].

The pseudo-relativistic Schrödinger equation:

$$i{\partial }_t\mathrm{\Psi }=\sqrt{-c^2\Delta +m^2{c}^4}\mathrm{\Psi }-m{c}^2\mathrm{\Psi }-f\left({\left|\mathrm{\Psi }(t,x)\right|}^2\right)\mathrm{\Psi },\forall (t,x)\in {\mathbb{R}}_{+}\times {\mathbb{R}}^N,$$

(1)

where c denotes the speed of light, $m>0$ is the particle mass, $\mathrm{\Psi }(t,x)$ is a complex-valued wave function, and $f:[0,\infty )\to \mathbb{R}$ is a nonlinear function. This equation characterizes the physical evolution of systems consisting of spinless relativistic bosons (e.g., boson stars). Rigorous derivations and analyses of the equation’s dynamical properties are presented in [6,7]. Equation (1) is referred to as a pseudo-relativistic Schrödinger equation in the sense that it reduces to the well-known nonlinear Schrödinger equation in the limit as the speed of light $c\to \infty$,

$$i{\partial }_t\mathrm{\Psi }=-{\displaystyle \frac{1}{2m}}\Delta \mathrm{\Psi }-f\left({\left|\mathrm{\Psi }(t,x)\right|}^2\right)\mathrm{\Psi },\mathrm{in}{\mathbb{R}}_{+}\times {\mathbb{R}}^N,$$

(2)

which serves as the non-relativistic limit of (1) (see [8]).

By assuming a standing wave solution of the form $\mathrm{\Psi }(t,x)=e^{i\omega t}u\left(x\right)$ in (1) (where $\omega \in \mathbb{R}$ is the frequency and $u\left(x\right)$ is a real-valued function), the original Equation (1) can be transformed into a stationary semi-linear elliptic equation, for all $x\in {\mathbb{R}}^N$,

$$\sqrt{-c^2\Delta +m^2{c}^4}u+(\omega -m{c}^2)u=f\left({\left|u\left(x\right)\right|}^2\right)u\left(x\right),$$

which are the relativistic version of the limit equations:

$$-{\displaystyle \frac{1}{2m}}\Delta u+\omega u=f\left({\left|u\left(x\right)\right|}^2\right)u\left(x\right).$$

In addition, we will also examine the 3D pseudo-relativistic Hartree equation.

$$i{\displaystyle \frac{\partial \mathrm{\Psi }}{\partial t}}=\sqrt{-c^2\Delta +m^2{c}^4}\mathrm{\Psi }-m{c}^2\mathrm{\Psi }-\left({\displaystyle \frac{1}{\left|x\right|}}\ast {\left|\mathrm{\Psi }\right|}^2\right)\mathrm{\Psi },\mathrm{in}{\mathbb{R}}_{+}\times {\mathbb{R}}^3,$$

(3)

where $\mathrm{\Psi }(t,x)$ denotes a complex-valued wave field, and the convolution symbol ∗ signifies convolution over ${\mathbb{R}}^3$. The operator $\sqrt{-c^2\Delta +m^2{c}^4}-m{c}^2$ describes the kinetic energy of a relativistic particle of mass $m>0$, while the convolution kernel ${\displaystyle \frac{1}{\left|x\right|}}$ models the Newtonian gravitational potential in suitable physical units. From a physical perspective, this equation arises as an effective dynamical description for an N-body quantum system of relativistic bosons interacting via two-body Newtonian gravitational forces [9,10]. As such, it provides a theoretical framework for studying pseudo-relativistic boson stars.

Recently, fractional operators have garnered growing attention in the research community. Nevertheless, the pseudo-relativistic operator ${(-\Delta +m^2)}^s$ lacks invariance under Kelvin-type transformations or scaling transformations. Dai, Qin, and Wu [11] established a series of maximum principles, and subsequently applied the direct method of moving planes as well as the sliding method to investigate the solution properties of various equations involving the operator ${(-\Delta +m^2)}^s$.

Motivated by the work of [11], we focus on the solution properties of a nonlinear system involving the pseudo-relativistic operator, and prove the monotonicity and symmetry of its solutions under weaker conditions. In this paper, we mainly consider the following nonlinear system with pseudo-relativistic operators:

$$\left\{\begin{array}{c}{(-\Delta +m^2)}^{s}u\left(x\right)=f(u,v),\hfill \\ {(-\Delta +m^2)}^{t}v\left(x\right)=h(u,v),\hfill \end{array}\right.$$

(4)

where $0<s,t<1$, $m>0$ is the particle mass, $f(·)$ and $h(·)$ are Lipschitz continuous about $u,v$ respectively, and

(a)

${\displaystyle \frac{\partial f}{\partial u}=o\left(u^{p-1}{v}^q\right),\frac{\partial h}{\partial v}=o\left(u^k{v}^{l-1}\right),\mathrm{as}(u,v)\to (0^{+},0^{+});}$

(b)

${\displaystyle \frac{\partial f}{\partial v}=o\left(u^p{v}^{q-1}\right),\frac{\partial h}{\partial u}=o\left(u^{k-1}{v}^l\right),\mathrm{as}(u,v)\to (0^{+},0^{+});}$

(c)

${\displaystyle \frac{\partial f}{\partial v}(u,v)>0,\frac{\partial h}{\partial u}(u,v)>0,\forall (u,v)\in ({\mathbb{R}}^{+},{\mathbb{R}}^{+}).}$

The pseudo-relativistic operator ${(-\Delta +m^2)}^s$ is defined in nonlocal way by (see [12,13,14])

$${(-\Delta +m^2)}^{s}u\left(x\right)=C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}P.V.{\int }_{R^n}{\displaystyle \frac{u\left(x\right)-u\left(z\right)}{{|x-z|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}\left(m\right|x-z\left|\right)dz+m^{2s}u\left(x\right),$$

(5)

where $0<s<1$, $P.V.$ stands for the Cauchy principal value, and

$$C_{n,s}=2^{1-{\displaystyle \frac{n}{2}}+s}{\pi }^{-{\displaystyle \frac{n}{2}}}{\displaystyle \frac{s(1-s)}{\mathrm{\Gamma }(2-s)}}>0$$

with $\mathrm{\Gamma }\left(t\right)={\int }_0^{\infty }{s}^{t-1}{e}^{-s}ds$ as the Gamma function. In (5), the function $K_{\nu }\left(r\right)$ denotes the modified Bessel function of second kind with order $\nu$ (see [12,13,14]), which satisfies the following equation:

$$r^2{K}_{\nu }^{″}\left(r\right)+r{K}_{\nu }^{\prime }\left(r\right)-(r^2+{\nu }^2)K_{\nu }\left(r\right)=0,$$

(6)

and satisfies the following integral representation

$$K_{\nu }\left(r\right)={\int }_0^{\infty }{e}^{-rcosht}cosh\left(\nu t\right)dt.$$

We can verify that $K_{\nu }\left(r\right)>0$ is a real function, which has the following important properties:

(i)

$K_{\nu }^{\prime }\left(r\right)<0$, $\forall r>0$;

(ii)

$K_{\nu }\left(r\right)=K_{-\nu }\left(r\right)$, for $\nu <0$;

(iii)

For $\nu >0$, $K_{\nu }\left(r\right)\sim {\displaystyle \frac{\mathrm{\Gamma }\left(\nu \right)}{2}}{\left({\displaystyle \frac{r}{2}}\right)}^{-\nu }$, as $r\to 0$;

(iv)

For $\nu >0$, $K_{\nu }\left(r\right)\sim {\displaystyle \frac{\sqrt{\pi }}{\sqrt{2}}}{r}^{-{\displaystyle \frac{1}{2}}}{e}^{-r}$, as $r\to \infty$.

From Property $\left(iii\right)$, for $K_{\nu }\sim {\displaystyle \frac{\mathrm{\Gamma }\left(\nu \right)}{2}}{\left({\displaystyle \frac{r}{2}}\right)}^{-\nu }$ as $r\to 0$, where “∼” means that ${lim}_{r\to 0}{\displaystyle \frac{K_{\nu }}{\frac{\mathrm{\Gamma }\left(\nu \right)}{2}{\left(\frac{r}{2}\right)}^{-\nu }}}=1$. By the definition of asymptotic equivalence, for any $\epsilon >0$, there exists a large $r_0=r_0(\epsilon ,\nu )>0$ and two constants $C_0>C_1>0$ such that

$${\displaystyle \frac{C_1}{r^{\nu }}}={\displaystyle \frac{(1-\epsilon )\frac{\mathrm{\Gamma }\left(\nu \right)}{2}{2}^{\nu }}{r^{\nu }}}\le K_{\nu }\left(r\right)\le {\displaystyle \frac{(1+\epsilon )\frac{\mathrm{\Gamma }\left(\nu \right)}{2}{2}^{\nu }}{r^{\nu }}}={\displaystyle \frac{C_0}{r^{\nu }}},r\le r_0.$$

Then, the inequality can be rewritten in the simplified form, and we can conclude that there exists a sufficiently small constant $r_0>0$ and two constants $C_0>C_1>0$ such that

$${\displaystyle \frac{C_1}{r^{\nu }}}\le K_{\nu }\left(r\right)\le {\displaystyle \frac{C_0}{r^{\nu }}},\forall r\le r_0$$

(7)

From Property $\left(iv\right)$, for $K_{\nu }\sim \sqrt{\pi /\left(2r\right)}{e}^{-r}$ as $r\to \infty$, where “∼” means that ${lim}_{r\to \infty }{\displaystyle \frac{K_{\nu }}{\sqrt{\pi /\left(2r\right)}{e}^{-r}}}=1$. By the definition of asymptotic equivalence, for any $\epsilon >0$, there exists a large $R_{\infty }=R_{\infty }(\epsilon ,\nu )>0$ and two constants $C_{\infty }>c_{\infty }>0$ such that

$${\displaystyle \frac{c_{\infty }}{r^{1/2}{e}^r}}={\displaystyle \frac{(1-\epsilon )\sqrt{\pi /2}}{r^{1/2}{e}^r}}\le K_{\nu }\left(r\right)\le {\displaystyle \frac{(1+\epsilon )\sqrt{\pi /2}}{r^{1/2}{e}^r}}={\displaystyle \frac{C_{\infty }}{r^{1/2}{e}^r}},r\ge R_{\infty }.$$

Then, the inequality can be rewritten in the simplified form

$${\displaystyle \frac{c_{\infty }}{r^{\frac{1}{2}}{e}^r}}\le K_{\nu }\left(r\right)\le {\displaystyle \frac{C_{\infty }}{r^{\frac{1}{2}}{e}^r}},\forall r\ge R_{\infty }.$$

(8)

Throughout this paper, we require that

$$u\in {\mathcal{L}}_s\left({\mathbb{R}}^n\right)\cap C_{\mathrm{loc}}^{1,1}\left({\mathbb{R}}^n\right),v\in {\mathcal{L}}_t\left({\mathbb{R}}^n\right)\cap C_{\mathrm{loc}}^{1,1}\left({\mathbb{R}}^n\right)$$

where ${\mathcal{L}}_s\left({\mathbb{R}}^n\right),{\mathcal{L}}_t\left({\mathbb{R}}^n\right)$ have the same definition as in [11]

$${\mathcal{L}}_s\left({\mathbb{R}}^n\right)=\{u:{\mathbb{R}}^n\to R\mid {\int }_{{\mathbb{R}}^n}{\displaystyle \frac{e^{-\left|x\right|}\left|u\left(x\right)\right|}{1+{\left|x\right|}^{\frac{n+1}{2}+s}}}dx<\infty \}$$

and

$${\mathcal{L}}_t\left({\mathbb{R}}^n\right)=\{v:{\mathbb{R}}^n\to R\mid {\int }_{{\mathbb{R}}^n}{\displaystyle \frac{e^{-\left|x\right|}\left|u\left(x\right)\right|}{1+{\left|x\right|}^{\frac{n+1}{2}+t}}}dx<\infty \}.$$

And $C_{\mathrm{loc}}^{1,1}\left({\mathbb{R}}^n\right)$: the space of local $1,1$-Hölder continuous differentiable functions on ${\mathbb{R}}^n$. Precisely, $u\in C_{\mathrm{loc}}^{1,1}\left({\mathbb{R}}^n\right)$ if $u\in C^1\left({\mathbb{R}}^n\right)$ and for every compact set $K\subset {\mathbb{R}}^n$, for all $x,y\in K$ and $i=1,\dots ,n$, there exists $C_K>0$ such that

$$|{\partial }_{x_i}u\left(x\right)-{\partial }_{x_i}u\left(y\right)|\le C_K|x-y|.$$

Guo and Peng [13] studied the pseudo-relativistic equation with Choquard term

$${(-\Delta +m^2)}^{s}u+\omega u=R_{N,t}({\displaystyle \frac{1}{{|x-y|}^{N-2t}}}\ast u^p)u^q,x\in {\mathbb{R}}^N,$$

where $0<s,t<1,m>0,\omega >-m^{2s},2<p<\infty ,0<q\le p-1$ and

$$R_{N,t}={\displaystyle \frac{\mathrm{\Gamma }\left(\frac{N-t}{2}\right)}{\mathrm{\Gamma }\left(\frac{t}{2}\right){\pi }^{\frac{N}{2}}{2}^t}},$$

$${\displaystyle \frac{1}{{|x-y|}^{N-2t}}}\ast u^p={\int }_{{\mathbb{R}}^N}{\displaystyle \frac{1}{{|x-y|}^{N-2t}}}·u^p\left(y\right)dy$$

where ${\displaystyle \frac{1}{{|x-y|}^{N-2t}}}$ is the Greens function associated with the fractional Laplacian operator ${(-\Delta )}^t$. They established the narrow region principle and the decay at infinity principle, and then employed the direct method of moving planes to prove the radial symmetry and monotonicity of the solutions.

Very recently, H. Bueno et al. [15] established a Pohozaev identity for the problem ${(-\Delta +m^2)}^{s}u\left(x\right)=f\left(u\right)$ in both ${\mathbb{R}}^N$ and ${\mathbb{R}}_{+}^{N+1}$. They developed a specific Fourier transform theory for the fractional operator ${(-\Delta +m^2)}^s$, and then utilized the Pohozaev-type identity to prove two results:

(i)

The non-existence of solutions when $f\left(u\right)={\left|u\right|}^{p-2}u$ with $p\ge 2_s^{\ast }$;

(ii)

The existence of a ground state, along with the radial symmetry of positive solutions to the equation.

In [14], Wang established a Hopf-type lemma and a point-wise estimate for the pseudo-relativistic operator equation ${(-\Delta +m^2)}^{s}u\left(x\right)=f(x,u)$, and further proved the radial symmetry and monotonicity of positive solutions in the whole space.

Liu and Ma in [16] studied

$$\left\{\begin{array}{cc}{(-\Delta )}^{{\displaystyle \frac{\alpha }{2}}}u\left(x\right)=f(u,v),\hfill & x\in {\mathbb{R}}^n,\hfill \\ {(-\Delta )}^{{\displaystyle \frac{\alpha }{2}}}v\left(x\right)=g(u,v),\hfill & x\in {\mathbb{R}}^n,\hfill \\ u\left(x\right)>0,v\left(x\right)>0,\hfill & x\in {\mathbb{R}}^n,\hfill \end{array}\right.$$

where $\alpha \in (0,2)$. They established the maximum principle and then derived the symmetry results for solutions to the fractional Laplacian system. In [17], Wang and Wang studied a weighted fractional system given by

$$\left\{\begin{array}{c}{\mathcal{A}}_{\alpha }u\left(x\right)=f(u,v),\hfill \\ {\mathcal{B}}_{\beta }v\left(x\right)=g(u,v),\hfill \end{array}\right.$$

where they proved the relevant maximum principle, obtained symmetry results for its solutions in $B_1$ and ${\mathbb{R}}^n$, and ultimately verified the nonexistence of nonnegative solutions in the positive half-space ${\mathbb{R}}_n^{+}$.

As $m\to 0^{+}$, the general pseudo-relativistic operators ${(-\Delta +m^2)}^s$ reduce to the well-known fractional Laplacian ${(-\Delta )}^s$. This is a nonlocal integro-differential operator, whose definition reads (see, e.g., [2,3,4] and the references therein)

$${(-\Delta )}^{s}u\left(x\right)=C_{n,s}P.V.{\int }_{{\mathbb{R}}^n}{\displaystyle \frac{u\left(x\right)-u\left(y\right)}{{|x-y|}^{n+2s}}}dy.$$

The fractional Laplacian ${(-\Delta )}^s$ for $0<s<1$ is well defined for any function $u\in C_{\mathrm{loc}}^{1,1}\left({\mathbb{R}}^n\right)\cap {\dot{L}}_s\left({\mathbb{R}}^n\right)$, where the function space ${\dot{L}}_s\left({\mathbb{R}}^n\right)$ is defined as

$${\dot{L}}_s\left({\mathbb{R}}^n\right):=\left\{u:{\mathbb{R}}^n\to \mathbb{R}|{\int }_{{\mathbb{R}}^n}{\displaystyle \frac{\left|u\right(x\left)\right|}{1+{\left|x\right|}^{n+2s}}}dx<+\infty \right\}.$$

However, due to the non-locality of the pseudo-relativistic operator ${(-\Delta +m^2)}^s$, many traditional methods are not directly applicable. To circumvent this difficulty, Caffarelli and Silvestre [18] (see also [19,20]) established the extension method, which reduces this nonlocal problem to a local one in higher-dimensional spaces. Thus, the pseudo-relativistic operator ${(-\Delta +m^2)}^s$ can be defined rigorously via this extension method. Another effective approach is the integral equation method (see [4,21,22,23] and the references therein). Specifically, one can establish the equivalence between the differential equation and its corresponding integral equation. Then, by applying the integral-form moving plane method, the scaling sphere method, or the regularity lifting method, the symmetry and regularity of solutions to equations involving ${(-\Delta +m^2)}^s$ can be derived. These methods have been widely used in the study of equations involving the fractional Laplacian, yielding a series of fruitful results (see [21,24,25,26] and the references therein). Nevertheless, when using the above two approaches, we often need to impose additional conditions on the solutions—conditions that would be unnecessary if we consider the integro-differential equation directly. Furthermore, these two approaches fail for fully nonlinear nonlocal operators, such as the fractional p-Laplacian (see [27]).

To the best of our knowledge, few results exist on the radial symmetry and monotonicity of solutions to the pseudo-relativistic system. This pseudo-relativistic operator has no invariance properties under Kelvin-type or scaling transforms. Inspired by [11,13,16,17], we directly study the pseudo-relativistic equation. We do not impose additional conditions on the solutions. We establish results on radial symmetry and monotonicity under weaker assumptions. In [28], the authors focused on rigidity results for mean field-type equations with multiple exponential terms. These equations include the sinh-Gordon and Tzitzeica equations. This study was conducted on closed two-dimensional manifolds with positive Ricci curvature bounds. Their research strategy was based on two nonlinear transformations and a geometric identity. Different from our present work, they considered a Laplace–Beltrami operator in local coordinates. They also obtained the existence of constant solutions. In [29], the authors investigated a parabolic equation with general nonlinearity. They used the method of moving planes in their study. They established results on the monotonicity and nonexistence of solutions. This research line can be extended in future work. The extension aims to establish a bifurcation-type theorem related to global existence. Moreover, the monotonicity and nonexistence of positive solutions for pseudo-relativistic parabolic equations or systems are still open problems. This is also the direction of our future research.

The mathematical rigor of a fractional derivative definition is critically important. In the most general mathematical terms, the fractional derivative can be interpreted as the fractional power of the infinitesimal generator of the corresponding semigroup (see [30] for further details). This conclusion is backed by both theoretical reasoning and practical observations. Many well-known derivatives (e.g., the Riemann–Liouville fractional derivative [31]) and integral operators (including the Riesz potential [32,33]) can be represented as fractional powers of the corresponding semigroup generators. Accordingly, the semigroup-based approach offers a convincing and promising framework. It is combined with the integral kernel analysis associated with the Sonin condition, as introduced in the cited references. This framework helps enhance the theoretical rigor of fractional derivative definitions. This research direction is highly consistent with the long-term development of our work. In future studies, we plan to explore the connections between our fractional derivative model, semigroup theory, and Sonin-type kernels.

2. Preliminaries

In this section, we review some useful knowledge of the method of moving planes and prove some maximum principles.

We first introduce some notations $T_{\lambda },{\mathrm{\Sigma }}_{\lambda },x^{\lambda }$ as in [2,3,4].

Without loss of generality, we choose the first coordinate as the $x_1$ direction. For some $\lambda \in \mathbb{R},$ let

$$T_{\lambda }=\{x\in {\mathbb{R}}^n|x_1=\lambda \}$$

be the moving plane,

$${\mathrm{\Sigma }}_{\lambda }=\{x\in {\mathbb{R}}^n|x_1<\lambda \}$$

be the region to the left of the plane, and

$$x^{\lambda }=(2\lambda -x_1,x_2,\dots ,x_n)$$

be the reflection of x about the plane $T_{\lambda }$, and $y^{\lambda }=(2\lambda -y_1,y_2,\dots ,y_n)$ is the reflection of y about the plane $T_{\lambda }$.

We denote $u\left(x^{\lambda }\right)=u_{\lambda }\left(x\right)$ and $v\left(x^{\lambda }\right)=v_{\lambda }\left(x\right)$; let

$$U_{\lambda }\left(x\right)=u_{\lambda }\left(x\right)-u\left(x\right),V_{\lambda }\left(x\right)=v_{\lambda }\left(x\right)-v\left(x\right).$$

After a direct calculation, we derive that $U_{\lambda }\left(x^{\lambda }\right)=-U_{\lambda }\left(x\right)$ and $V_{\lambda }\left(x^{\lambda }\right)=-V_{\lambda }\left(x\right)$; hence, they are anti-symmetric.

Denote

$${\mathrm{\Sigma }}_{\lambda }^{U_{\lambda }^{-}}=\{x\in {\mathrm{\Sigma }}_{\lambda }|U_{\lambda }\left(x\right)<0\},$$

$${\mathrm{\Sigma }}_{\lambda }^{V_{\lambda }^{-}}=\{x\in {\mathrm{\Sigma }}_{\lambda }|V_{\lambda }\left(x\right)<0\}.$$

Lemma 1

(Decay at Infinity). Let Λ be an unbounded open set in ${\mathrm{\Sigma }}_{\lambda }$. If $u\in {\mathcal{L}}_s\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}\left(\mathrm{\Lambda }\right)$ and $v\in {\mathcal{L}}_t\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}\left(\mathrm{\Lambda }\right)$ are lower semi-continuous on $\overline{\mathrm{\Lambda }}$, and $(U_{\lambda },V_{\lambda })$ is a pair of solutions for

$$\left\{\begin{array}{cc}{(-\Delta +m^2)}^s{U}_{\lambda }\left(x\right)+C_1\left(x\right)U_{\lambda }\left(x\right)+C_2\left(x\right)V_{\lambda }\left(x\right)\ge 0,\hfill & x\in \mathrm{\Lambda }\cap {\mathrm{\Sigma }}_{\lambda }^{U_{\lambda }^{-}},\hfill \\ {(-\Delta +m^2)}^t{V}_{\lambda }\left(x\right)+C_3\left(x\right)V_{\lambda }\left(x\right)+C_4\left(x\right)U_{\lambda }\left(x\right)\ge 0,\hfill & x\in \mathrm{\Lambda }\cap {\mathrm{\Sigma }}_{\lambda }^{V_{\lambda }^{-}},\hfill \\ U_{\lambda }\left(x^{\lambda }\right)=-U_{\lambda }\left(x\right),V_{\lambda }\left(x^{\lambda }\right)=-V_{\lambda }\left(x\right),\hfill & x\in {\mathrm{\Sigma }}_{\lambda },\hfill \\ U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\hfill & x\in {\mathrm{\Sigma }}_{\lambda }\setminus \mathrm{\Lambda }.\hfill \end{array}\right.$$

(9)

Let $C_1\left(x\right),C_3\left(x\right)$ fulfill the lower bound conditions given in

$$\underset{\begin{array}{c}x\in {\mathrm{\Sigma }}_{\lambda }\\ \left|x\right|\to \infty \end{array}}{lim\; inf}(C_1\left(x\right)+m^{2s})\ge 0,\underset{\begin{array}{c}x\in {\mathrm{\Sigma }}_{\lambda }\\ \left|x\right|\to \infty \end{array}}{lim\; inf}(C_3\left(x\right)+m^{2t})\ge 0$$

(10)

and $C_2\left(x\right)<0$, $C_4\left(x\right)<0$ obey the asymptotic decay estimates

$$C_2\left(x\right)=o({\displaystyle \frac{1}{{\left|x\right|}^{\frac{1-n}{2}+s}{e}^{\eta \left|x\right|}}}),C_4\left(x\right)=o({\displaystyle \frac{1}{{\left|x\right|}^{\frac{1-n}{2}+t}{e}^{\eta \left|x\right|}}}),as\left|x\right|\to \infty$$

(11)

with $4m<\eta <\sigma min\{p+q-1,k+l-1\}$. Then, there exists a constant $R_0>0$ which is dependent on $u,v$ but independent of λ, such that, if there exist points $\overline{x}\in {\mathrm{\Sigma }}_{\lambda }$ and $\tilde{x}\in {\mathrm{\Sigma }}_{\lambda }$ such that

$$U_{\lambda }\left(\overline{x}\right)=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{U}_{\lambda }<0,V_{\lambda }\left(\tilde{x}\right)=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{V}_{\lambda }<0.$$

then

$$|\overline{x}|\le R_{0}or\left|\tilde{x}\right|\le R_0.$$

(12)

Proof. 

We prove this result by contradiction. If the inequality (12) is not true, then by using the assumption of Lemma 1, we have

$$U_{\lambda }\left(\overline{x}\right)=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{U}_{\lambda }<0,V_{\lambda }\left(\tilde{x}\right)=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{V}_{\lambda }<0.$$

From the definition of the operator ${(-\Delta +m^2)}^s$, we obtain that

$$\begin{array}{ccc}\hfill & {(-\Delta +m^2)}^s{U}_{\lambda }\left(\overline{x}\right)\hfill & \\ \hfill =& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{R^n}{\displaystyle \frac{U_{\lambda }\left(\overline{x}\right)-U_{\lambda }\left(y\right)}{|\overline{x}{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y|)dy+m^{2s}{U}_{\lambda }\left(\overline{x}\right)\hfill \\ \hfill =& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{U_{\lambda }\left(\overline{x}\right)-U_{\lambda }\left(y\right)}{|\overline{x}{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y|)dy\hfill \\ & +C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathbb{R}}^n\setminus {\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{U_{\lambda }\left(\overline{x}\right)-U_{\lambda }\left(y\right)}{|\overline{x}{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y|)dy+m^{2s}{U}_{\lambda }\left(\overline{x}\right)\hfill \\ \hfill =& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{U_{\lambda }\left(\overline{x}\right)-U_{\lambda }\left(y\right)}{|\overline{x}{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y|)dy\hfill \\ & +C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{U_{\lambda }\left(\overline{x}\right)-U_{\lambda }\left(y^{\lambda }\right)}{|\overline{x}-y^{\lambda }{|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y^{\lambda }|)dy+m^{2s}{U}_{\lambda }\left(\overline{x}\right)\hfill \\ \hfill \le & C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}\left\{{\displaystyle \frac{U_{\lambda }\left(\overline{x}\right)-U_{\lambda }\left(y\right)}{|\overline{x}-y^{\lambda }{|}^{\frac{n}{2}+s}}}+{\displaystyle \frac{U_{\lambda }\left(\overline{x}\right)+U_{\lambda }\left(y\right)}{|\overline{x}-y^{\lambda }{|}^{\frac{n}{2}+s}}}\right\}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y^{\lambda }|)dy\hfill \\ \hfill & +m^{2s}{U}_{\lambda }\left(\overline{x}\right)\hfill \\ \hfill \le & 2U_{\lambda }\left(\overline{x}\right)C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{1}{|\overline{x}-y^{\lambda }{|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y^{\lambda }|)dy+m^{2s}{U}_{\lambda }\left(\overline{x}\right)\hfill \end{array}$$

(13)

where we used the fact $|\overline{x}-y|<|\overline{x}-y^{\lambda }|$ (see Figure 1) and the property of function $K_{\nu }$ in (i). Now, we estimate the part of the integral in (13), noting that $x\in \mathrm{\Lambda }\cap {\mathrm{\Sigma }}_{\lambda }^{U_{\lambda }^{-}}$ and $\lambda \le 0$, it follows that $B_{|\overline{x}|}\left(\widehat{x}\right)\subset {\mathrm{\Sigma }}_{\lambda }^c={\mathbb{R}}^n\setminus {\mathrm{\Sigma }}_{\lambda },$ where $\widehat{x}:=\left(3\right|\overline{x}|+{\overline{x}}_1,{\overline{x}}^{\prime })$. Thus, we derive that, if $|\overline{x}|\ge {\displaystyle \frac{R_{\infty }}{4m}}$, we have

$$\begin{array}{cc}\hfill & m^{{\displaystyle \frac{n}{2}}+s}{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{1}{|\overline{x}-y^{\lambda }{|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y^{\lambda }|)dy\hfill \\ \hfill =& m^{{\displaystyle \frac{n}{2}}+s}{\int }_{{\mathrm{\Sigma }}_{\lambda }^c}{\displaystyle \frac{1}{|\overline{x}{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|\overline{x}-y|)dy\hfill \\ \hfill \ge & m^{{\displaystyle \frac{n}{2}}+s}{\int }_{B_{|\overline{x}|}\left(\widehat{x}\right)}{\displaystyle \frac{K_{\frac{n}{2}+s}(m|\overline{x}-y|)}{|\overline{x}{-y|}^{\frac{n}{2}+s}}}dy\hfill \\ \hfill \ge & m^{{\displaystyle \frac{n}{2}}+s}{\int }_{B_{|\overline{x}|}\left(\widehat{x}\right)}{\displaystyle \frac{K_{\frac{n}{2}+s}(4m|\overline{x}|)}{4^{\frac{n}{2}+s}{|\overline{x}|}^{\frac{n}{2}+s}}}dy\hfill \\ \hfill \ge & {\displaystyle \frac{c_{\infty }{m}^{\frac{n-1}{2}+s}{\omega }_n}{4^{\frac{n}{2}+s}{|\overline{x}|}^{\frac{1-n}{2}+s}{e}^{4m|\overline{x}|}}}\hfill \end{array}$$

(14)

where ${\omega }_n$ is the volume of unit sphere. A direct calculation yields

$$|\overline{x}-y|\le |\overline{x}-\widehat{x}|+|\widehat{x}-y|\le 3|\overline{x}|+|\overline{x}|=4|\overline{x}|,$$

combining properties of function $K_{\nu }$ in (i) and (8), we can derive the above inequality.

From (10), we infer that there exists an $R_1$ sufficiently large such that, for any $x\in \mathrm{\Lambda }\cap {\mathrm{\Sigma }}_{\lambda }^{U_{\lambda }^{-}}$ satisfying $\left|x\right|>R_1$, it holds $\underset{\begin{array}{c}x\in {\mathrm{\Sigma }}_{\lambda },\left|x\right|\to \infty \end{array}}{lim\; inf}(C_1\left(x\right)+m^{2s})\ge 0$. Take $R_0=max\{{\displaystyle \frac{R_{\infty }}{4m}},R_1\}$; if $|\overline{x}|>R_0$, we can deduce from (9), (13), and (14) that

$$\begin{array}{cc}\hfill -C_2\left(\overline{x}\right)V_{\lambda }\left(\overline{x}\right)& \le {(-\Delta +m^2)}^s{U}_{\lambda }\left(\overline{x}\right)+C_1\left(\overline{x}\right)U_{\lambda }\left(\overline{x}\right)\hfill \\ \hfill & \le [{\displaystyle \frac{c_{\infty }{m}^{\frac{n-1}{2}+s}{\omega }_n}{4^{\frac{n}{2}+s}{\left|\overline{x}\right|}^{\frac{1-n}{2}+s}{e}^{4m|\overline{x}|}}}+C_1\left(\overline{x}\right)+m^{2s}]U_{\lambda }\left(\overline{x}\right)\hfill \\ \hfill & \le {\displaystyle \frac{C}{|\overline{x}{|}^{\frac{1-n}{2}+s}{e}^{4m|\overline{x}|}}}{U}_{\lambda }\left(\overline{x}\right)\hfill \end{array}$$

(15)

for $C_2\left(\overline{x}\right)<0$, we have

$$\begin{array}{c}\hfill U_{\lambda }\left(\overline{x}\right)\ge -C{\left|\overline{x}\right|}^{{\displaystyle \frac{1-n}{2}}+s}{e}^{4m|\overline{x}|}{C}_2\left(\overline{x}\right)V_{\lambda }\left(\overline{x}\right),\end{array}$$

(16)

then, $V_{\lambda }\left(\overline{x}\right)<0$. Furthermore, there exists $\tilde{x}$ such that

$$V_{\lambda }\left(\tilde{x}\right)=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{V}_{\lambda }<0.$$

By a similar estimate in (13) and (14), we have

$$\begin{array}{c}\hfill {(-\Delta +m^2)}^t{V}_{\lambda }\left(\tilde{x}\right)\le \left[{\displaystyle \frac{c_{\infty }{m}^{\frac{n-1}{2}+t}{\omega }_n}{4^{\frac{n}{2}+t}{\left|\tilde{x}\right|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}+m^{2t}\right]V_{\lambda }\left(\tilde{x}\right).\end{array}$$

(17)

Combining (9), (16), (17), and $C_4\left(\tilde{x}\right)<0$, for $|\overline{x}|>R_0,\left|\tilde{x}\right|>R_0$ sufficiently large, we obtain that

$$\begin{array}{cc}\hfill 0& \le {(-\Delta +m^2)}^t{V}_{\lambda }\left(\tilde{x}\right)+C_3\left(\tilde{x}\right)V_{\lambda }\left(\tilde{x}\right)+C_4\left(\tilde{x}\right)U_{\lambda }\left(\tilde{x}\right)\hfill \\ \hfill & \le \left[{\displaystyle \frac{c_{\infty }{m}^{\frac{n-1}{2}+t}{\omega }_n}{4^{\frac{n}{2}+t}{\left|\tilde{x}\right|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}+C_3\left(\tilde{x}\right)+m^{2t}\right]V_{\lambda }\left(\tilde{x}\right)+C_4\left(\tilde{x}\right)U_{\lambda }\left(\tilde{x}\right)\hfill \\ \hfill & \le \left[{\displaystyle \frac{c_{\infty }{m}^{\frac{n-1}{2}+t}{\omega }_n}{4^{\frac{n}{2}+t}{\left|\tilde{x}\right|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}+C_3\left(\tilde{x}\right)+m^{2t}\right]V_{\lambda }\left(\tilde{x}\right)+C_4\left(\tilde{x}\right)U_{\lambda }\left(\overline{x}\right)\hfill \\ \hfill & \le {\displaystyle \frac{C}{|\tilde{x}{|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}{V}_{\lambda }\left(\tilde{x}\right)-C{\left|\overline{x}\right|}^{{\displaystyle \frac{1-n}{2}}+s}{e}^{4m|\overline{x}|}{C}_2\left(\overline{x}\right)V_{\lambda }\left(\overline{x}\right)C_4\left(\tilde{x}\right)\hfill \\ \hfill & \le {\displaystyle \frac{C}{|\tilde{x}{|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}{V}_{\lambda }\left(\tilde{x}\right)-C{\left|\overline{x}\right|}^{{\displaystyle \frac{1-n}{2}}+s}{e}^{4m|\overline{x}|}{C}_2\left(\overline{x}\right)V_{\lambda }\left(\tilde{x}\right)C_4\left(\tilde{x}\right)\hfill \\ \hfill & ={\displaystyle \frac{C{V}_{\lambda }\left(\tilde{x}\right)}{|\tilde{x}{|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}\left[1-|\overline{x}{|}^{{\displaystyle \frac{1-n}{2}}+s}{e}^{4m|\overline{x}|}{C}_2\left(\overline{x}\right){\left|\tilde{x}\right|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|\tilde{x}|}{C}_4\left(\tilde{x}\right)\right]<0,\hfill \end{array}$$

(18)

the last inequality is true. By assumption (11), we have

$$\begin{array}{cc}\hfill & |\overline{x}{|}^{{\displaystyle \frac{1-n}{2}}+s}{e}^{4m|\overline{x}|}{C}_2\left(\overline{x}\right)|\tilde{x}{|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|\tilde{x}|}{C}_4\left(\tilde{x}\right)\hfill \\ \hfill =& |\overline{x}{|}^{{\displaystyle \frac{1-n}{2}}+s}{e}^{4m|\overline{x}|}·o\left({\displaystyle \frac{1}{|\overline{x}{|}^{\frac{1-n}{2}+s}{e}^{\eta |\overline{x}|}}}\right)·{|\tilde{x}|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|\tilde{x}|}·o\left({\displaystyle \frac{1}{|\tilde{x}{|}^{\frac{1-n}{2}+t}{e}^{\eta |\tilde{x}|}}}\right)\hfill \\ \hfill =& o\left({\displaystyle \frac{1}{e^{(\eta -4m)|\overline{x}|}}}\right)·o\left({\displaystyle \frac{1}{e^{(\eta -4m)|\tilde{x}|}}}\right)\hfill \\ \hfill <& 1\hfill \end{array}$$

as $|\overline{x}|>R_0$ and $|\tilde{x}|>R_0$ sufficiently large.

This is a contradiction. Therefore, at least one of $|\overline{x}|\le R_{0}or\left|\tilde{x}\right|\le R_0$ holds. This completes the proof of Lemma 1. □

Remark 1.

If $U_{\lambda }\left(x\right)$ has a negative minimum at $\overline{x}$ in ${\mathrm{\Sigma }}_{\lambda }$, then $V_{\lambda }\left(x\right)$ can also attain its negative minimum at $\tilde{x}$ in ${\mathrm{\Sigma }}_{\lambda }$, and vice versa.

Lemma 2

(Narrow Region Principle). Let Λ be a bounded open set in ${\mathrm{\Sigma }}_{\lambda }$, which is contained in the region $\{x\mid \lambda -\delta <x_1<\lambda \}$ with $\delta >0$ small. If $u\in {\mathcal{L}}_s\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}\left(\mathrm{\Lambda }\right)$ and $v\in {\mathcal{L}}_t\left({\mathbb{R}}^n\right)\cap C_{\mathrm{loc}}^{1,1}\left(\mathrm{\Lambda }\right)$ are lower semi-continuous on $\overline{\mathrm{\Lambda }}$, and $(U_{\lambda },V_{\lambda })$ is a pair of solutions for

$$\left\{\begin{array}{cc}{(-\Delta +m^2)}^s{U}_{\lambda }\left(x\right)+C_1\left(x\right)U_{\lambda }\left(x\right)+C_2\left(x\right)V_{\lambda }\left(x\right)\ge 0,\hfill & x\in \mathrm{\Lambda }\cap {\mathrm{\Sigma }}_{\lambda }^{U_{\lambda }^{-}},\hfill \\ {(-\Delta +m^2)}^t{V}_{\lambda }\left(x\right)+C_3\left(x\right)V_{\lambda }\left(x\right)+C_4\left(x\right)U_{\lambda }\left(x\right)\ge 0,\hfill & x\in \mathrm{\Lambda }\cap {\mathrm{\Sigma }}_{\lambda }^{V_{\lambda }^{-}},\hfill \\ U_{\lambda }\left(x^{\lambda }\right)=-U_{\lambda }\left(x\right),V_{\lambda }\left(x^{\lambda }\right)=-V_{\lambda }\left(x\right),\hfill & x\in {\mathrm{\Sigma }}_{\lambda },\hfill \\ U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\hfill & x\in {\mathrm{\Sigma }}_{\lambda }\setminus \mathrm{\Lambda },\hfill \end{array}\right.$$

(19)

where $C_1\left(x\right),C_2\left(x\right),C_3\left(x\right),C_4\left(x\right)$ are uniformly bounded from below, $C_2\left(x\right)<0$, $C_4\left(x\right)<0$, and if we assume that there exist constants $C_{n,s}$ and $C_{n,t}$ such that $C_1\left(x\right),C_3\left(x\right)$ obey the inequalities

$$(-\underset{\{x\in \mathrm{\Lambda }\mid U_{\lambda }\left(x\right)<0\}}{inf}{C}_1\left(x\right)-m^{2s}){\delta }^{2s}<C_{n,s},(-\underset{\{x\in \mathrm{\Lambda }\mid V_{\lambda }\left(x\right)<0\}}{inf}{C}_3\left(x\right)-m^{2t}){\delta }^{2t}<C_{n,t}.$$

(20)

Then

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,x\in \mathrm{\Lambda }.$$

(21)

Furthermore, if $U_{\lambda }\left(x\right)=0$ or $V_{\lambda }\left(x\right)=0$ at some point in Λ, then we can obtain

$$U_{\lambda }\left(x\right)=V_{\lambda }\left(x\right)\equiv 0,x\in {\mathbb{R}}^n.$$

(22)

If Λ is an unbounded domain, the conclusion in (21) also holds under the additional conditions

$$\underset{\left|x\right|\to \infty }{lim\; inf}{U}_{\lambda }\left(x\right)\ge 0and\underset{\left|x\right|\to \infty }{lim\; inf}{V}_{\lambda }\left(x\right)\ge 0.$$

(23)

Proof. 

If inequality (21) does not hold, we may assume that $U_{\lambda }\left(x\right)<0$ at some point $x\in \mathrm{\Lambda }$ (the same conclusion holds if we instead assume $V_{\lambda }\left(x\right)<0$ at some point in $\mathrm{\Lambda }$). Then, by the properties of $U_{\lambda }\left(x\right)$ on $\overline{\mathrm{\Lambda }}$, there exists some $x^0\in \mathrm{\Lambda }$ such that

$$U_{\lambda }\left(x^0\right)=\underset{\mathrm{\Lambda }}{min}{U}_{\lambda }\left(x\right)<0.$$

From the definition of the operator ${(-\Delta +m^2)}^s$, we obtain that

$$\begin{array}{ccc}\hfill & {(-\Delta +m^2)}^s{U}_{\lambda }\left(x^0\right)\hfill & \\ \hfill =& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{R^n}{\displaystyle \frac{U_{\lambda }\left(x^0\right)-U_{\lambda }\left(y\right)}{|x^0{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y|)dy+m^{2s}{U}_{\lambda }\left(x^0\right)\hfill \\ \hfill =& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{U_{\lambda }\left(x^0\right)-U_{\lambda }\left(y\right)}{|x^0{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y|)dy\hfill \\ \hfill & +C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{U_{\lambda }\left(x^0\right)-U_{\lambda }\left(y^{\lambda }\right)}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y^{\lambda }|)dy+m^{2s}{U}_{\lambda }\left(x^0\right)\hfill \\ \hfill \le & C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}\left\{{\displaystyle \frac{U_{\lambda }\left(x^0\right)-U_{\lambda }\left(y\right)}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}+{\displaystyle \frac{U_{\lambda }\left(x^0\right)+U_{\lambda }\left(y\right)}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}\right\}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y^{\lambda }|)dy\hfill \\ \hfill & +m^{2s}{U}_{\lambda }\left(x^0\right)\hfill \\ \hfill \le & 2U_{\lambda }\left(x^0\right)C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{1}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y^{\lambda }|)dy+m^{2s}{U}_{\lambda }\left(x^0\right).\hfill \end{array}$$

(24)

Let

$$D=\{y=(y_1,y^{\prime })\in {\mathbb{R}}^n|\delta <y_1-{\left(x^0\right)}_1<2\delta ,|y^{\prime }-{\left(x^0\right)}^{\prime }|<{\displaystyle \frac{r_0}{2m}}\}\subset {\mathrm{\Sigma }}_{\lambda }^c,$$

then, we can derive that $m|y-x^0|<r_0$ for all $y\in D$.

Let $\xi :=y_1-{\left(x^0\right)}_1,\zeta :=|y^{\prime }-{\left(x^0\right)}^{\prime }|$, then, using the properties of function $K_{\nu }$ of (7), and from [11,13,17], we have

$$\begin{array}{cc}\hfill & C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{1}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y^{\lambda }|)dy\hfill \\ \hfill =& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }^c}{\displaystyle \frac{K_{\frac{n}{2}+s}(m|x^0-y|)}{|x^0{-y|}^{\frac{n}{2}+s}}}dy\hfill \\ \hfill \ge & C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_D{\displaystyle \frac{K_{\frac{n}{2}+s}(m|x^0-y|)}{|x^0{-y|}^{\frac{n}{2}+s}}}dy\hfill \\ \hfill \ge & C_0{\int }_D{\displaystyle \frac{1}{|x^0{-y|}^{n+2s}}}dy\hfill \\ \hfill =& C_0{\int }_{\delta }^{2\delta }{\int }_0^{{\displaystyle \frac{r_0}{2m}}}{\displaystyle \frac{{\omega }_{n-1}{\zeta }^{n-2}d\zeta }{{({\xi }^2+{\zeta }^2)}^{\frac{n}{2}+s}}}d\xi \hfill \\ \hfill =& C_0{\int }_{\delta }^{2\delta }{\int }_0^{{\displaystyle \frac{r_0}{2m\xi }}}{\displaystyle \frac{{\omega }_{n-1}{\left(\xi \rho \right)}^{n-2}\xi d\rho }{{\xi }^{n+2s}{(1+{\rho }^2)}^{\frac{n}{2}+s}}}d\xi \hfill \\ \hfill =& C_0{\int }_{\delta }^{2\delta }{\displaystyle \frac{1}{{\xi }^{1+2s}}}{\int }_0^{{\displaystyle \frac{r_0}{2m\xi }}}{\displaystyle \frac{{\omega }_{n-1}{\rho }^{n-2}d\rho }{{(1+{\rho }^2)}^{\frac{n}{2}+s}}}d\xi \hfill \\ \hfill \ge & C_0{\int }_{\delta }^{2\delta }{\displaystyle \frac{1}{{\xi }^{1+2s}}}{\int }_0^1{\displaystyle \frac{{\omega }_{n-1}{\rho }^{n-2}d\rho }{{(1+{\rho }^2)}^{\frac{n}{2}+s}}}d\xi \hfill \\ \hfill \ge & C_{n,s}{\int }_{\delta }^{2\delta }{\displaystyle \frac{1}{{\xi }^{1+2s}}}d\xi ={\displaystyle \frac{C}{{\delta }^{2s}}}.\hfill \end{array}$$

(25)

Combining (19), (20), (24), and (25), we have

$$\begin{array}{cc}\hfill -C_2\left(x^0\right)V_{\lambda }\left(x^0\right)& \le {(-\Delta +m^2)}^s{U}_{\lambda }\left(x^0\right)+C_1\left(x^0\right)U_{\lambda }\left(x^0\right)\hfill \\ \hfill & \le \left({\displaystyle \frac{C}{{\delta }^{2s}}}+m^{2s}+\underset{\{x\in \mathrm{\Lambda }|U_{\lambda }\left(x\right)<0\}}{inf}{C}_1\left(x^0\right)\right)U_{\lambda }\left(x^0\right)\hfill \\ \hfill & <0.\hfill \end{array}$$

(26)

Due to $C_2\left(x^0\right)<0$, then we can get

$$V_{\lambda }\left(x^0\right)<0,$$

(27)

the assumption of $V_{\lambda }\left(x\right)$, that there exists some $x^1$, satisfies

$$V_{\lambda }\left(x^1\right)=\underset{\mathrm{\Lambda }}{min}{V}_{\lambda }\left(x\right)<0.$$

(28)

By the similar estimate in (24) and (25), we have

$${(-\Delta +m^2)}^t{V}_{\lambda }\left(x^1\right)\le \left({\displaystyle \frac{C}{{\delta }^{2t}}}+m^{2t}\right)V_{\lambda }\left(x^1\right).$$

(29)

One can easily see that $\nabla U_{\lambda }\left(x^0\right)=0$, choosing $\widehat{x}\in T_{\lambda }$; then, by Taylor expansion, we can derive that

$$0=U_{\lambda }\left(\widehat{x}\right)=U_{\lambda }\left(x^0\right)+\nabla U_{\lambda }\left(x^0\right)(\widehat{x}-x^0)+o(|\widehat{x}-x^0|).$$

(30)

Then, we have

$$U_{\lambda }\left(x^0\right)=o(|\widehat{x}-x^0|)=o\left(1\right){\delta }_{x^0},$$

(31)

for sufficiently small ${\delta }_{x^0}$. From the assumption of $C_1\left(x\right),C_2\left(x\right),C_3\left(x\right),C_4\left(x\right)$, which are uniformly bounded from below, we then combine (19), (20), and $C_4\left(x\right)<0$, and can deduce that

$$\begin{array}{ccc}\hfill 0& \le {(-\Delta +m^2)}^s{V}_{\lambda }\left(x^1\right)+C_3\left(x^1\right)V_{\lambda }\left(x^1\right)+C_4\left(x^1\right)U_{\lambda }\left(x^1\right)\hfill & \\ \hfill & \le \left({\displaystyle \frac{C}{{\delta }^{2t}}}+m^{2t}+\underset{\{x\in \mathrm{\Lambda }|U_{\lambda }\left(x\right)<0\}}{inf}{C}_3\left(x^1\right)\right)V_{\lambda }\left(x^1\right)+C_4\left(x^1\right)U_{\lambda }\left(x^0\right)\hfill \\ \hfill & \le \left({\displaystyle \frac{C}{{\delta }^{2t}}}+m^{2t}+\underset{\{x\in \mathrm{\Lambda }|U_{\lambda }\left(x\right)<0\}}{inf}{C}_3\left(x^1\right)\right)V_{\lambda }\left(x^1\right)+C_4\left(x^1\right)o\left(1\right){\delta }_{x^0}\hfill \\ \hfill & <0.\hfill \end{array}$$

(32)

This is a contradiction, and thus inequality (21) holds.

Now, we prove inequality (22) by considering two cases.

Case 1: If there exists $x^0\in \mathrm{\Lambda }$, such that $U_{\lambda }\left(x^0\right)=0$. Then, we can see that $x^0$ is a minimum point of $U_{\lambda }$. That is, $U_{\lambda }\left(x^0\right)=0=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{U}_{\lambda }\left(x\right)$. Combining the definition of ${(-\Delta +m^2)}^s$, we have

$$\begin{array}{cc}\hfill {(-\Delta +m^2)}^s{U}_{\lambda }\left(x^0\right)=& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{R^n}{\displaystyle \frac{U_{\lambda }\left(x^0\right)-U_{\lambda }\left(y\right)}{|x^0{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y|)dy\hfill \\ \hfill =& -C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{R^n}{\displaystyle \frac{U_{\lambda }\left(y\right)}{|x^0{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y|)dy\hfill \\ \hfill =& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{-U_{\lambda }\left(y\right)}{|x^0{-y|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y|)dy\hfill \\ \hfill & +C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}{\displaystyle \frac{U_{\lambda }\left(y\right)}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y^{\lambda }|)dy\hfill \\ \hfill <& C_{n,s}{m}^{{\displaystyle \frac{n}{2}}+s}PV{\int }_{{\mathrm{\Sigma }}_{\lambda }}\left\{{\displaystyle \frac{-U_{\lambda }\left(y\right)}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}+{\displaystyle \frac{U_{\lambda }\left(y\right)}{|x^0-y^{\lambda }{|}^{\frac{n}{2}+s}}}\right\}{K}_{{\displaystyle \frac{n}{2}}+s}(m|x^0-y^{\lambda }|)dy\hfill \\ \hfill =& 0\hfill \end{array}$$

where we used the fact $|x^0-y|<|x^0-y^{\lambda }|$ and the property of function $K_{\nu }$ in (i). If $U_{\lambda }\left(x\right)\not\equiv 0$, from the first inequality in (19), we can deduce that

$$-C_2\left(x^0\right)V_{\lambda }\left(x^0\right)\le {(-\Delta +m^2)}^s{U}_{\lambda }\left(x^0\right)<0.$$

Since $C_2\left(x\right)<0$, we conclude that $V_{\lambda }\left(x^0\right)<0$. This contradicts (21), so we conclude that $U_{\lambda }\left(x\right)\equiv 0$ in ${\mathrm{\Sigma }}_{\lambda }$. Since $U_{\lambda }\left(x^{\lambda }\right)=-U_{\lambda }\left(x\right)$ for all $x\in {\mathrm{\Sigma }}_{\lambda }$, we further obtain that

$$U_{\lambda }\left(x\right)\equiv 0,\forall x\in {\mathbb{R}}^n.$$

We can also infer from (19) that

$$V_{\lambda }\left(x^0\right)\le 0.$$

Combining inequality (21), we get $V_{\lambda }\left(x^0\right)=0$ in ${\mathrm{\Sigma }}_{\lambda }$. Since $V_{\lambda }\left(x^{\lambda }\right)=-V_{\lambda }\left(x\right)$ for all $x\in {\mathrm{\Sigma }}_{\lambda }$, it follows that

$$V_{\lambda }\left(x\right)\equiv 0,\forall x\in {\mathbb{R}}^n.$$

Case 2: Suppose there exists $x^1\in \mathrm{\Lambda }$ such that $V_{\lambda }\left(x^1\right)=0$. By a similar argument, we have $V_{\lambda }\left(x\right)\equiv 0$, for all $x\in R^n$, and thus the conclusion $U_{\lambda }\left(x\right)\equiv 0$, for all $x\in {\mathbb{R}}^n$ still holds. □

Remark 2.

(I) If $U_{\lambda }\left(x\right)$ attains a negative minimum at $\overline{x}$ in ${\mathrm{\Sigma }}_{\lambda }$, then $V_{\lambda }\left(x\right)$ also attains a negative minimum at $\tilde{x}$ in ${\mathrm{\Sigma }}_{\lambda }$, and vice versa.

• (II) From the proofs of Lemmas 1 and 2, we can infer that the assumption

$$\left\{\begin{array}{c}{(-\Delta +m^2)}^s{U}_{\lambda }\left(x\right)+C_1\left(x\right)U_{\lambda }\left(x\right)+C_2\left(x\right)V_{\lambda }\left(x\right)\ge 0,x\in \Omega \cap {\mathrm{\Sigma }}_{\lambda }^{U_{\lambda }^{-}},\hfill \\ {(-\Delta +m^2)}^t{V}_{\lambda }\left(x\right)+C_3\left(x\right)V_{\lambda }\left(x\right)+C_4\left(x\right)U_{\lambda }\left(x\right)\ge 0,x\in \Omega \cap {\mathrm{\Sigma }}_{\lambda }^{V_{\lambda }^{-}},\hfill \end{array}\right.$$

can be weakened to

$$\left\{\begin{array}{c}{(-\Delta +m^2)}^s{U}_{\lambda }\left(x\right)+C_1\left(x\right)U_{\lambda }\left(x\right)+C_2\left(x\right)V_{\lambda }\left(x\right)\ge 0,where{U}_{\lambda }=\underset{{\mathrm{\Sigma }}_{\lambda }}{inf}{U}_{\lambda }<0,\hfill \\ {(-\Delta +m^2)}^t{V}_{\lambda }\left(x\right)+C_3\left(x\right)V_{\lambda }\left(x\right)+C_4\left(x\right)U_{\lambda }\left(x\right)\ge 0,where{V}_{\lambda }=\underset{{\mathrm{\Sigma }}_{\lambda }}{inf}{V}_{\lambda }<0,\hfill \end{array}\right.$$

and the conclusions in Lemmas 1 and 2 remain valid.

3. Main Results

In this section, we focus on the study of the following nonlinear pseudo-relativistic operators:

$$\left\{\begin{array}{cc}{(-\Delta +m^2)}^{s}u\left(x\right)=f(u,v),\hfill & x\in B_1\left(0\right),\hfill \\ {(-\Delta +m^2)}^{t}v\left(x\right)=h(u,v),\hfill & x\in B_1\left(0\right),\hfill \\ u\left(x\right)=0,v\left(x\right)=0,\hfill & x\in B_1^c\left(0\right),\hfill \end{array}\right.$$

(33)

$$\left\{\begin{array}{cc}{(-\Delta +m^2)}^{s}u\left(x\right)=f(u,v),\hfill & x\in {\mathbb{R}}^n,\hfill \\ {(-\Delta +m^2)}^{t}v\left(x\right)=h(u,v),\hfill & x\in {\mathbb{R}}^n,\hfill \\ u\left(x\right)>0,v\left(x\right)>0,\hfill & x\in {\mathbb{R}}^n,\hfill \end{array}\right.$$

(34)

$$\left\{\begin{array}{cc}{(-\Delta +m^2)}^{s}u\left(x\right)=f(u,v),\hfill & x\in \Omega ,\hfill \\ {(-\Delta +m^2)}^{t}v\left(x\right)=h(u,v),\hfill & x\in \Omega ,\hfill \\ u\left(x\right)>0,v\left(x\right)>0,\hfill & x\in \Omega ,\hfill \\ u\left(x\right)=0,v\left(x\right)=0,\hfill & x\in {\Omega }^c,\hfill \end{array}\right.$$

(35)

where $\Omega =\{x=(x^{\prime },x_n)\in {\mathbb{R}}^n|x_n>\phi \left(x^{\prime }\right)\}$ is a Lipschitz-coercive epigraph, that is $\phi :{\mathbb{R}}^{n-1}\to \mathbb{R}$ is a continuous function satisfying $\underset{|x^{\prime }|\to \infty }{lim}\phi \left(x^{\prime }\right)=+\infty$. A canonical example of such an epigraph is the upper half-space ${\mathbb{R}}_{+}^n$.

Theorem 1.

Let $0<s,t<1$ and $m>0$. Assume that $u\in {\mathcal{L}}_s\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}\left(B_1\left(0\right)\right)$ and $v\in {\mathcal{L}}_t\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}\left(B_1\left(0\right)\right)$ are positive solutions to system (33). Suppose further that $f(·)$ and $h(·)$ are Lipschitz continuous with respect to u and v, respectively, and that the cross-partial derivatives satisfy ${\displaystyle \frac{\partial f}{\partial v}}(u,v)>0$ and ${\displaystyle \frac{\partial h}{\partial u}}(u,v)>0$, respectively. Then, the pair $(u,v)$ is radially symmetric about the origin and monotonically decreasing in the radial direction.

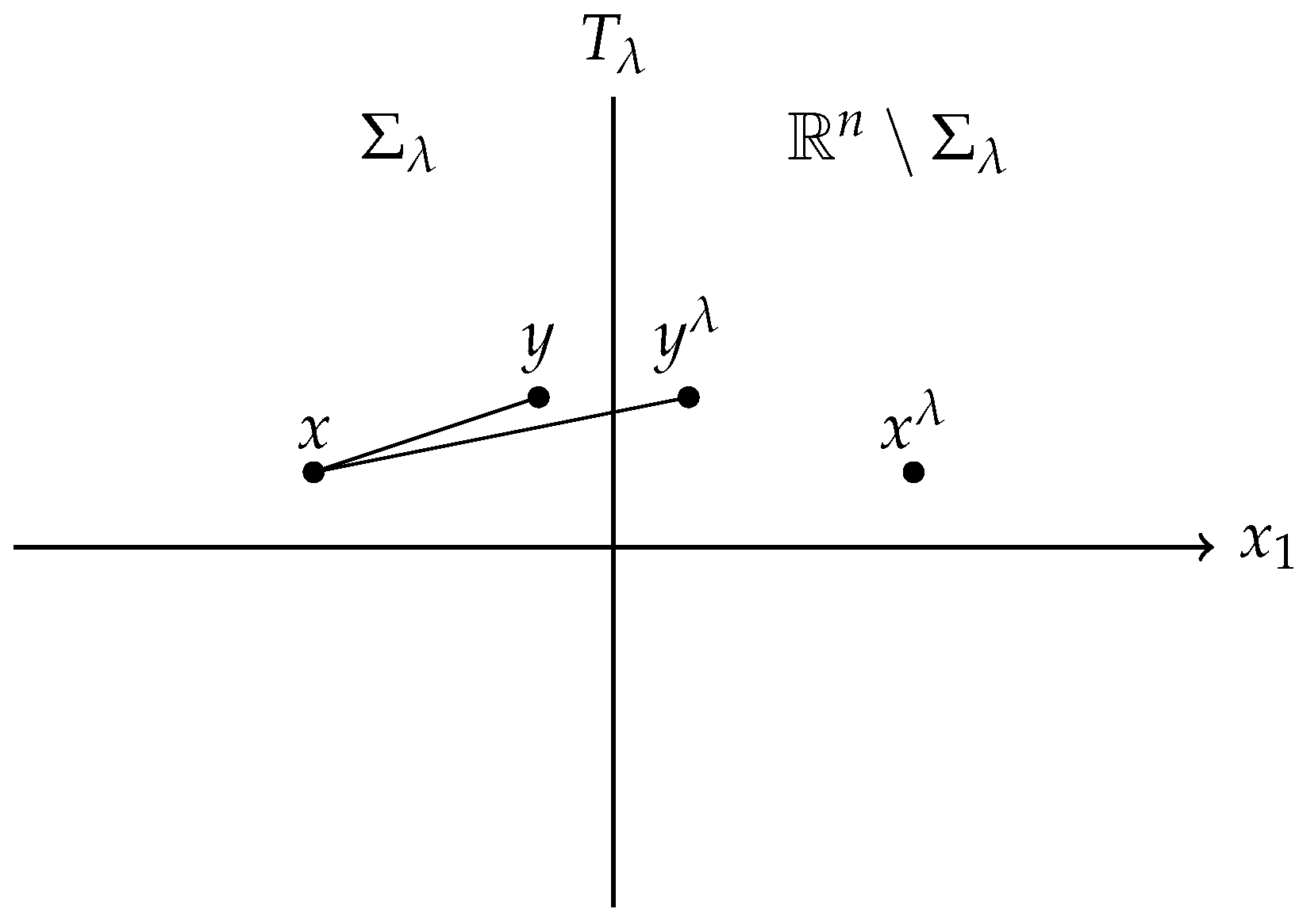
Proof. 

Choose an arbitrary direction to be the $x_1$-axis direction. Define

$$T_{\lambda }^{B_1}=\{x\in B_1\left(0\right)|x_1=\lambda \},$$

$${\mathrm{\Sigma }}_{\lambda }^{B_1}=\{x\in B_1\left(0\right)|x_1<\lambda \}.$$

Step 1. In this step, we show that for $\lambda$ sufficiently close to $-1$, the following holds:

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }^{B_1}.$$

(36)

From Equation (4), we deduce that

$$\begin{array}{cc}\hfill {(-\Delta +m^2)}^s{U}_{\lambda }\left(x\right)=& f(u_{\lambda }\left(x\right),v_{\lambda }\left(x\right))-f(u\left(x\right),v\left(x\right))\hfill \\ \hfill =& {\displaystyle \frac{f(u_{\lambda }\left(x\right),v_{\lambda }\left(x\right))-f(u,v_{\lambda }\left(x\right))}{u_{\lambda }\left(x\right)-u\left(x\right)}}{U}_{\lambda }\left(x\right)\hfill \\ \hfill & +{\displaystyle \frac{f(u\left(x\right),v_{\lambda }\left(x\right))-f(u\left(x\right),v\left(x\right))}{v_{\lambda }\left(x\right)-v\left(x\right)}}{V}_{\lambda }\left(x\right)\hfill \\ \hfill =& {\displaystyle \frac{\partial f({\xi }_{\lambda }^1\left(x\right),v_{\lambda }\left(x\right))}{\partial u}}{U}_{\lambda }\left(x\right)+{\displaystyle \frac{\partial f(u\left(x\right),{\zeta }_{\lambda }^1\left(x\right))}{\partial v}}{V}_{\lambda }\left(x\right),\hfill \end{array}$$

(37)

$$\begin{array}{cc}\hfill {(-\Delta +m^2)}^t{V}_{\lambda }\left(x\right)=& h(u_{\lambda }\left(x\right),v_{\lambda }\left(x\right))-h(u\left(x\right),v\left(x\right))\hfill \\ \hfill =& {\displaystyle \frac{h(u_{\lambda }\left(x\right),v_{\lambda }\left(x\right))-h(u,v_{\lambda }\left(x\right))}{u_{\lambda }\left(x\right)-u\left(x\right)}}{U}_{\lambda }\left(x\right)\hfill \\ \hfill & +{\displaystyle \frac{h(u\left(x\right),v_{\lambda }\left(x\right))-h(u\left(x\right),v\left(x\right))}{v_{\lambda }\left(x\right)-v\left(x\right)}}{V}_{\lambda }\left(x\right)\hfill \\ \hfill =& {\displaystyle \frac{\partial h({\xi }_{\lambda }^2\left(x\right),v_{\lambda }\left(x\right))}{\partial u}}{U}_{\lambda }\left(x\right)+{\displaystyle \frac{\partial h(u\left(x\right),{\zeta }_{\lambda }^2\left(x\right))}{\partial v}}{V}_{\lambda }\left(x\right)\hfill \end{array}$$

(38)

where ${\xi }_{\lambda }^1\left(x\right),{\xi }_{\lambda }^2\left(x\right)$ lie between $u_{\lambda }\left(x\right)$ and $u\left(x\right)$, and ${\zeta }_{\lambda }^1\left(x\right),{\zeta }_{\lambda }^2\left(x\right)$ lie between $v_{\lambda }\left(x\right)$ and $v\left(x\right)$.

We denote

$$C_1\left(x\right)=-{\displaystyle \frac{\partial f({\xi }_{\lambda }^1\left(x\right),v_{\lambda }\left(x\right))}{\partial u}},C_2\left(x\right)=-{\displaystyle \frac{\partial f(u\left(x\right),{\zeta }_{\lambda }^1\left(x\right))}{\partial v}},$$

and

$$C_3\left(x\right)=-{\displaystyle \frac{\partial h(u\left(x\right),{\zeta }_{\lambda }^2\left(x\right))}{\partial v}},C_4\left(x\right)=-{\displaystyle \frac{\partial h({\xi }_{\lambda }^2\left(x\right),v_{\lambda }\left(x\right))}{\partial u}}.$$

By the assumptions that $f(·)$ and $h(·)$ are Lipschitz continuous with respect to u and v, respectively, and that ${\displaystyle \frac{\partial f}{\partial v}}(u,v)>0$ and ${\displaystyle \frac{\partial h}{\partial u}}(u,v)>0$, it follows that $C_2\left(x\right)<0$ and $C_4\left(x\right)<0$. When $\lambda$ is sufficiently close to $-1$, the domain ${\mathrm{\Sigma }}_{\lambda }^{B_1}$ is a narrow region. Then, by Lemma 2, we obtain

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,x\in {\mathrm{\Sigma }}_{\lambda }^{B_1}.$$

(39)

Step 2. We move the plane $T_{\lambda }$ to the right until it reaches its limiting position. More precisely, we define

$${\lambda }_0=sup\left\{\lambda |U_{\mu }\left(x\right)\ge 0,V_{\mu }\left(x\right)\ge 0,x\in {\mathrm{\Sigma }}_{\mu }^{B_1},\forall \mu \le \lambda \right\}.$$

We then show that

$${\lambda }_0=0.$$

(40)

Suppose for contradiction that ${\lambda }_0<0$. Then, there exists a small constant $ϵ>0$ such that inequality (39) holds for all $\lambda \in [{\lambda }_0,{\lambda }_0+ϵ)$, which contradicts the definition of ${\lambda }_0$.

We know that $U_{{\lambda }_0}\left(x\right)\ge 0$ and $V_{{\lambda }_0}\left(x\right)\ge 0$, with $U_{{\lambda }_0}\left(x\right)\not\equiv 0$ and $V_{{\lambda }_0}\left(x\right)\not\equiv 0$. By Lemma 2, we conclude that

$$U_{{\lambda }_0}\left(x\right)>0,V_{{\lambda }_0}\left(x\right)>0,\forall x\in {\mathrm{\Sigma }}_{{\lambda }_0}^{B_1}.$$

Then, there exists a constant $c>0$ such that

$$U_{{\lambda }_0}\left(x\right)\ge c,V_{{\lambda }_0}\left(x\right)\ge c,\forall x\in {\overline{\mathrm{\Sigma }}}_{{\lambda }_0-\delta }^{B_1}.$$

Since $U_{\lambda }$ and $V_{\lambda }$ are continuous with respect to $\lambda$, we can deduce that there exists a small constant $ϵ>0$, such that for all $\lambda \in [{\lambda }_0,{\lambda }_0+ϵ)$,

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\overline{\mathrm{\Sigma }}}_{{\lambda }_0-\delta }^{B_1}.$$

(41)

The region ${\mathrm{\Sigma }}_{\lambda }^{B_1}\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta }^{B_1}$ is a narrow region; thus, we apply the result from Lemma 2 to obtain

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }^{B_1}$$

for all $\lambda \in [{\lambda }_0,{\lambda }_0+ϵ)$. This contradicts the definition of ${\lambda }_0$. Therefore, we have ${\lambda }_0=0$.

From the preceding proof, we conclude that

$$U_0\left(x\right)\ge 0,V_0\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_0^{B_1},$$

which is equivalent to

$$u_0\left(x\right)=u(-x_1,x_2,\dots ,x_n)\ge u(x_1,x_2,\dots ,x_n)=u\left(x\right),-1<x_1<0.$$

(42)

Since the $x_1$-axis was chosen to be an arbitrary direction, inequality (42) implies that $u\left(x\right)$ and $v\left(x\right)$ are radially symmetric about the origin. Monotonicity can be deduced from the fact that $U_{\lambda }\left(x\right)\ge 0$, $V_{\lambda }\left(x\right)\ge 0$ for all $x\in {\mathrm{\Sigma }}_{\lambda }^{B_1}$ and $\lambda \in (-1,0]$. □

Theorem 2.

Let $0<s,t<1$ and $m>0$. Suppose that $u\in {\mathcal{L}}_s\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}\left({\mathbb{R}}^n\right)$ and $v\in {\mathcal{L}}_t\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}\left({\mathbb{R}}^n\right)$ are positive solutions to system (34), satisfying the decay conditions

$$u\left(x\right)=o\left({\displaystyle \frac{1}{{\left|x\right|}^{\gamma }{e}^{\sigma \left|x\right|}}}\right),v\left(x\right)=o\left({\displaystyle \frac{1}{{\left|x\right|}^{\tau }{e}^{\sigma \left|x\right|}}}\right),\mathrm{as}\left|x\right|\to \infty ,$$

(43)

where $\gamma ,\tau ,\sigma >0$. Assume further that $f,h\in C^1\left([0,\infty )\times [0,\infty ),\mathbb{R}\right)$ fulfill the following assumptions:

(a)

${\displaystyle \frac{\partial f}{\partial u}=o\left(u^{p-1}{v}^q\right),\frac{\partial h}{\partial v}=o\left(u^k{v}^{l-1}\right),\mathrm{as}(u,v)\to (0^{+},0^{+});}$

(b)

${\displaystyle \frac{\partial f}{\partial v}=o\left(u^p{v}^{q-1}\right),\frac{\partial h}{\partial u}=o\left(u^{k-1}{v}^l\right),\mathrm{as}(u,v)\to (0^{+},0^{+});}$

(c)

${\displaystyle \frac{\partial f}{\partial v}(u,v)>0,\frac{\partial h}{\partial u}(u,v)>0,\forall (u,v)\in ({\mathbb{R}}^{+},{\mathbb{R}}^{+}).}$

Let $p,q,k,l\ge 1$. If s and t lie within the bounds

$$s<\gamma p+\tau (q-1)+{\displaystyle \frac{n-1}{2}}\mathrm{and}t<\gamma (k-1)+\tau l+{\displaystyle \frac{n-1}{2}},$$

then the pair $(u,v)$ is radially symmetric about some point in ${\mathbb{R}}^n$ and monotonically decreasing in the radial direction.

Remark 3.

Due to the properties of the pseudo-relativistic operator ${(-\Delta +m^2)}^s$, which does not possess invariance under Kelvin-type or scaling transformations, we must impose the decay condition (43) on u and v as $\left|x\right|\to \infty$. In the special case when $m=0$ and $s=t$, Theorem 1.2 reduces to Theorem 1 in [16].

Proof. 

To establish that the pair $\left(u\right(x),v(x\left)\right)$ is radially symmetric about some point in ${\mathbb{R}}^n$, we employ the moving plane method by translating the hyperplane $T_{\lambda }$ along the $x_1$-axis from $-\infty$ to the right. Our key objective is to prove that

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }.$$

(44)

The decay condition (43) implies the following crucial fact: if there exists a point $x\in {\mathrm{\Sigma }}_{\lambda }$ such that $U_{\lambda }\left(x\right)<0$, then $U_{\lambda }\left(x\right)$ attains its negative minimum in the interior of ${\mathrm{\Sigma }}_{\lambda }$. Similarly, if there exists a point $x\in {\mathrm{\Sigma }}_{\lambda }$ such that $V_{\lambda }\left(x\right)<0$, then $V_{\lambda }\left(x\right)$ attains its negative minimum in the interior of ${\mathrm{\Sigma }}_{\lambda }$. We split the subsequent proof into two steps.

Step 1. In this step, we show that as $\lambda \to -\infty$, the following inequality holds:

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }.$$

(45)

To verify this, we choose $\lambda <-R_0$ where $R_0$ is sufficiently large. Suppose for contradiction that (45) fails for such $\lambda$, i.e., there exists a point $\overline{x}\in {\mathrm{\Sigma }}_{\lambda }$ such that $U_{\lambda }\left(\overline{x}\right)={min}_{{\mathrm{\Sigma }}_{\lambda }}{U}_{\lambda }<0$. By Lemma 1, it follows that $V_{\lambda }\left(\overline{x}\right)<0$, which implies that $V_{\lambda }$ also attains its negative minimum at some point $\tilde{x}\in {\mathrm{\Sigma }}_{\lambda }$.

Following the same estimates as in (37) and (38), we obtain

$${(-\Delta +m^2)}^s{U}_{\lambda }\left(\overline{x}\right)=-C_1\left(\overline{x}\right)U_{\lambda }\left(\overline{x}\right)-C_2\left(\overline{x}\right)V_{\lambda }\left(\overline{x}\right)$$

(46)

and

$${(-\Delta +m^2)}^t{V}_{\lambda }\left(\tilde{x}\right)=-C_3\left(\tilde{x}\right)V_{\lambda }\left(\tilde{x}\right)-C_4\left(\tilde{x}\right)U_{\lambda }\left(\tilde{x}\right).$$

(47)

Based on the decay condition (43) and assumptions (a)–(c), we have the asymptotic behaviors

$$C_1\left(\overline{x}\right)=-{\displaystyle \frac{\partial f({\xi }_{\lambda }^1\left(\overline{x}\right),v_{\lambda }\left(\overline{x}\right))}{\partial u}}=o\left({\displaystyle \frac{1}{|\overline{x}{|}^{\gamma (p-1)+\tau q}{e}^{\sigma (p+q-1)|\overline{x}|}}}\right)\mathrm{as}\left|\overline{x}\right|\to \infty ,$$

$$C_2\left(\overline{x}\right)=-{\displaystyle \frac{\partial f(u\left(\overline{x}\right),{\zeta }_{\lambda }^1\left(\overline{x}\right))}{\partial v}}=o\left({\displaystyle \frac{1}{|\overline{x}{|}^{\gamma p+\tau (q-1)}{e}^{\sigma (p+q-1)|\overline{x}|}}}\right)=o\left({\displaystyle \frac{1}{|\overline{x}{|}^{s+\frac{1-n}{2}}{e}^{\eta |\overline{x}|}}}\right)\mathrm{as}\left|\overline{x}\right|\to \infty ,$$

$$C_3\left(\tilde{x}\right)=-{\displaystyle \frac{\partial h(u\left(\tilde{x}\right),{\zeta }_{\lambda }^2\left(\tilde{x}\right))}{\partial v}}=o\left({\displaystyle \frac{1}{|\tilde{x}{|}^{\gamma k+\tau (l-1)}{e}^{\sigma (k+l-1)|\tilde{x}|}}}\right)\mathrm{as}\left|\tilde{x}\right|\to \infty ,$$

$$C_4\left(\tilde{x}\right)=-{\displaystyle \frac{\partial h({\xi }_{\lambda }^2\left(\tilde{x}\right),v_{\lambda }\left(\tilde{x}\right))}{\partial u}}=o\left({\displaystyle \frac{1}{|\tilde{x}{|}^{\gamma (k-1)+\tau l}{e}^{\sigma (k+l-1)|\tilde{x}|}}}\right)=o\left({\displaystyle \frac{1}{|\tilde{x}{|}^{t+\frac{1-n}{2}}{e}^{\eta |\tilde{x}|}}}\right)\mathrm{as}\left|\tilde{x}\right|\to \infty ,$$

together with the sign conditions

$$C_2\left(x\right)<0,C_4\left(x\right)<0.$$

We further derive that

$$\underset{|\overline{x}|\to \infty }{lim\; inf}\left(C_1\left(\overline{x}\right)+m^{2s}\right)=\underset{|\overline{x}|\to \infty }{lim\; inf}\left({\displaystyle \frac{1}{|\overline{x}{|}^{\gamma (p-1)+\tau q}{e}^{\sigma (p+q-1)|\overline{x}|}}}+m^{2s}\right)\ge 0,$$

$$\underset{|\tilde{x}|\to \infty }{lim\; inf}\left(C_3\left(\tilde{x}\right)+m^{2t}\right)=\underset{|\tilde{x}|\to \infty }{lim\; inf}\left({\displaystyle \frac{1}{|\tilde{x}{|}^{\gamma k+\tau (l-1)}{e}^{\sigma (k+l-1)|\tilde{x}|}}}+m^{2t}\right)\ge 0.$$

Using the decay at infinity, we conclude that

$$|\overline{x}|\le R_0\mathrm{or}\left|\tilde{x}\right|\le R_0.$$

Finally, as $\lambda \to -\infty$, we must have

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }.$$

We claim that if $U_{\lambda }\left(x\right)\ge 0$ in ${\mathrm{\Sigma }}_{\lambda }$, then it follows that $V_{\lambda }\left(x\right)\ge 0$ in ${\mathrm{\Sigma }}_{\lambda }$.

Suppose for contradiction that this is not the case; then there exists a point $\tilde{x}\in {\mathrm{\Sigma }}_{\lambda }$ such that

$$V_{\lambda }\left(\tilde{x}\right)<0.$$

From (17), we obtain

$${(-\Delta +m^2)}^t{V}_{\lambda }\left(\tilde{x}\right)\le \left[{\displaystyle \frac{c_{\infty }{m}^{\frac{n-1}{2}+t}{\omega }_n}{4^{\frac{n}{2}+t}{|\tilde{x}|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}+m^{2t}\right]V_{\lambda }\left(\tilde{x}\right).$$

Furthermore, we deduce the inequality

$${(-\Delta +m^2)}^t{V}_{\lambda }\left(\tilde{x}\right)+C_3\left(\tilde{x}\right)V_{\lambda }\left(\tilde{x}\right)\le \left[{\displaystyle \frac{c_{\infty }{m}^{\frac{n-1}{2}+t}{\omega }_n}{4^{\frac{n}{2}+t}{\left|\tilde{x}\right|}^{\frac{1-n}{2}+t}{e}^{4m|\tilde{x}|}}}+m^{2t}+C_3\left(\tilde{x}\right)\right]V_{\lambda }\left(\tilde{x}\right)<0.$$

(48)

However, from Equation (47) and the fact that $C_4\left(x\right)<0$, we have

$${(-\Delta +m^2)}^t{V}_{\lambda }\left(\tilde{x}\right)+C_3\left(\tilde{x}\right)V_{\lambda }\left(\tilde{x}\right)=-C_4\left(\tilde{x}\right)U_{\lambda }\left(\tilde{x}\right)\ge 0.$$

This is a contradiction. Therefore, we conclude that $V_{\lambda }\left(x\right)\ge 0$ in ${\mathrm{\Sigma }}_{\lambda }$.

By symmetry, if we assume $V_{\lambda }\left(x\right)\ge 0$ in ${\mathrm{\Sigma }}_{\lambda }$, we can similarly derive that $U_{\lambda }\left(x\right)\ge 0$ in ${\mathrm{\Sigma }}_{\lambda }$.

Step 2. We continue translating the hyperplane $T_{\lambda }$ to its limiting position. To be precise, we define

$${\lambda }_0=sup\left\{\lambda |U_{\mu }\left(x\right)\ge 0,V_{\mu }\left(x\right)\ge 0,x\in {\mathrm{\Sigma }}_{\mu },\forall \mu \le \lambda \right\}.$$

By Lemma 1, we have ${\lambda }_0<\infty$, and thus

$$U_{{\lambda }_0}\left(x\right)\equiv 0,V_{{\lambda }_0}\left(x\right)\equiv 0,\forall x\in {\mathrm{\Sigma }}_{{\lambda }_0}.$$

(49)

Suppose for contradiction that $U_{{\lambda }_0}\left(x\right)\not\equiv 0$ and $V_{{\lambda }_0}\left(x\right)\not\equiv 0$ in ${\mathrm{\Sigma }}_{{\lambda }_0}$. We proceed to show that

$$U_{{\lambda }_0}\left(x\right)>0,V_{{\lambda }_0}\left(x\right)>0,\forall x\in {\mathrm{\Sigma }}_{{\lambda }_0}.$$

(50)

Indeed, if (50) fails to hold, then by Lemma 2, the vanishing of either $U_{\lambda }\left(x\right)$ or $V_{\lambda }\left(x\right)$ at any point in ${\mathrm{\Sigma }}_{\lambda }$ implies that

$$U_{\lambda }\left(x\right)=V_{\lambda }\left(x\right)\equiv 0,\forall x\in {\mathbb{R}}^n.$$

This yields a contradiction, so (50) must hold true.

From (50) and the choice of sufficiently large $R_0$ in Lemma 1, there exists a small constant $\delta >0$ and a constant $c_0>0$ such that

$$U_{{\lambda }_0}\left(x\right)\ge c_0,V_{{\lambda }_0}\left(x\right)\ge c_0,\forall x\in \overline{{\mathrm{\Sigma }}_{{\lambda }_0-\delta }\cap B_{R_0}\left(0\right)}.$$

Since $U_{\lambda }$ and $V_{\lambda }$ are continuous with respect to $\lambda$, there exists a small constant $ϵ>0$ satisfying $ϵ<\delta$ such that for all $\lambda \in ({\lambda }_0,{\lambda }_0+ϵ)$, we deduce that

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in \overline{{\mathrm{\Sigma }}_{{\lambda }_0-\delta }\cap B_{R_0}\left(0\right)}.$$

(51)

By applying Lemma 1, we deduce that for all $\lambda \in ({\lambda }_0,{\lambda }_0+ϵ)$, the negative minimum of either $U_{\lambda }\left(x\right)$ or $V_{\lambda }\left(x\right)$ is attained in the set $({\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta })\cap B_{R_0}\left(0\right)$. That is, there exists a point $x^0\in {\mathrm{\Sigma }}_{\lambda }$ such that

$$U_{\lambda }\left(x^0\right)=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{U}_{\lambda }<0.$$

From Lemmas 1 and 2 and Step 1, it follows that $V_{\lambda }\left(x^0\right)<0$; furthermore, there exists a point $x^1\in {\mathrm{\Sigma }}_{\lambda }$ such that

$$V_{\lambda }\left(x^1\right)=\underset{{\mathrm{\Sigma }}_{\lambda }}{min}{V}_{\lambda }<0.$$

We thus obtain the key bound $|x^0|<R_0$ or $|x^1|<R_0$.

Suppose now that $|x^0|<R_0$. By inequality (51), we have

$$x^0\in ({\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta })\cap B_{R_0}\left(0\right).$$

(52)

It then necessarily follows that

$$x^1\in ({\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta })\cap B_{R_0}\left(0\right).$$

(53)

Suppose for contradiction that (53) fails, so $x^1\in {\mathrm{\Sigma }}_{\lambda }\cap B_{R_0}^c\left(0\right)$. On the one hand, from the derivation of (15) and (16), for any $|x^1|\ge R_0$, we establish the estimate

$$V_{\lambda }\left(x^1\right)\ge -C{\left|x^1\right|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|x^1|}{C}_4\left(x^1\right)U_{\lambda }\left(x^1\right).$$

(54)

On the other hand, since $({\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta })\cap B_{R_0}\left(0\right)$ is a narrow region containing $x^0$, we derive the chain of inequalities

$$\begin{array}{cc}\hfill 0& \le {(-\Delta +m^2)}^s{U}_{\lambda }\left(x^0\right)+C_1\left(x^0\right)U_{\lambda }\left(x^0\right)+C_2\left(x^0\right)V_{\lambda }\left(x^0\right)\hfill \\ & \le \left({\displaystyle \frac{C}{{(ϵ+\delta )}^{2s}}}+m^{2s}+C_1\left(x^0\right)\right)U_{\lambda }\left(x^0\right)+C_2\left(x^0\right)V_{\lambda }\left(x^1\right)\hfill \\ & \le \left({\displaystyle \frac{C}{{(ϵ+\delta )}^{2s}}}+m^{2s}+C_1\left(x^0\right)\right)U_{\lambda }\left(x^0\right)\hfill \\ & -C_2\left(x^0\right)C{\left|x^1\right|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|x^1|}{C}_4\left(x^1\right)U_{\lambda }\left(x^1\right)\hfill \\ & \le \left({\displaystyle \frac{C}{{(ϵ+\delta )}^{2s}}}+m^{2s}+C_1\left(x^0\right)\right)U_{\lambda }\left(x^0\right)\hfill \\ & -C_2\left(x^0\right)C{\left|x^1\right|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|x^1|}{C}_4\left(x^1\right)U_{\lambda }\left(x^0\right).\hfill \end{array}$$

(55)

Rearranging this inequality yields

$${\displaystyle \frac{C}{{(ϵ+\delta )}^{2s}}}+m^{2s}+C_1\left(x^0\right)\le C_2\left(x^0\right)C{\left|x^1\right|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|x^1|}{C}_4\left(x^1\right).$$

For $|x^1|\ge R_0$, the decay assumption on $C_4\left(x^1\right)$ implies that $|x^1{|}^{{\displaystyle \frac{1-n}{2}}+t}{e}^{4m|x^1|}{C}_4\left(x^1\right)$ becomes arbitrarily small as $|x^1|\to \infty$. Since $C_2\left(x^0\right)$ is bounded from below, this leads to a contradiction for sufficiently small $ϵ$ and $\delta$. We therefore conclude that (53) must hold.

Next, note that $\Omega ={\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta }$ is a narrow region. The lower bounds for $C_1\left(x\right),C_2\left(x\right),C_3\left(x\right),C_4\left(x\right)$ follow directly from the proof of Lemma 2. Applying the narrow region principle, we obtain

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta }.$$

(56)

Combining (50), (51), and (56), we find that for all $\lambda \in ({\lambda }_0,{\lambda }_0+ϵ)$,

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }.$$

This contradicts the definition of ${\lambda }_0$ as the supremum. We thus have

$$U_{{\lambda }_0}\left(x\right)\equiv 0,V_{{\lambda }_0}\left(x\right)\equiv 0,\forall x\in {\mathrm{\Sigma }}_{{\lambda }_0}.$$

We may also translate the hyperplane starting from $+\infty$ and derive the identical conclusion $U_{{\lambda }_0}\left(x\right)\equiv 0$, $V_{{\lambda }_0}\left(x\right)\equiv 0$ for all $x\in {\mathrm{\Sigma }}_{{\lambda }_0}$. It follows that the pair $(u,v)$ is symmetric about the hyperplane $T_{{\lambda }_0}$. Since the $x_1$-axis was chosen to be an arbitrary direction, we conclude that the positive solutions $(u,v)$ are radially symmetric and monotonically decreasing about some point in ${\mathbb{R}}^n$. □

Theorem 3.

Let $0<s,t<1$ and $m>0$. Assume that $u\in {\mathcal{L}}_s\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}(\Omega )$ and $v\in {\mathcal{L}}_t\left({\mathbb{R}}^n\right)\cap C_{\mathit{loc}}^{1,1}(\Omega )$ are positive solutions to system (35). Suppose further that f and h are nonnegative, u and v are lower semi-continuous on $\overline{\Omega }$, and the following conditions are satisfied:

1.

The decay condition (43);

2.

The regularity conditions (a), (b), and (c);

3.

The exponent conditions $s<\gamma p+\tau (q-1)+{\displaystyle \frac{n-1}{2}}$ and $t<\gamma (k-1)+\tau l+{\displaystyle \frac{n-1}{2}}$.

• Then, the pair $(u,v)$ is strictly monotonically increasing along the $x_n$-axis direction.

Proof. 

To establish that the pair $\left(u\right(x),v(x\left)\right)$ is monotonically increasing along the $x_n$-axis direction, we need to verify the inequality

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }.$$

We split the proof into two steps.

Step 1. We show that as $\lambda \to 0^{+}$, the following holds:

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }.$$

(57)

Indeed, as $\lambda \to 0^{+}$, the region ${\mathrm{\Sigma }}_{\lambda }\cap \Omega$ becomes a narrow region. We thus apply Lemma 2 to deduce the validity of (57).

Step 2. Building on inequality (57), we continue translating the hyperplane $T_{\lambda }$ to the right as long as (57) remains valid. This procedure will allow us to conclude that $(u,v)$ is monotonically increasing along the $x_n$-axis direction. To formalize this, we define the supremum

$${\lambda }_0=sup\left\{\lambda |U_{\mu }\left(x\right)\ge 0,V_{\mu }\left(x\right)\ge 0,x\in {\mathrm{\Sigma }}_{\mu }\cap \Omega ,\forall 0<\mu \le \lambda \right\}.$$

Our goal is to show that

$${\lambda }_0=\infty .$$

(58)

Suppose for contradiction that $0<{\lambda }_0<\infty$. If this were true, there would exist a small constant $\epsilon >0$, such that the inequality

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }\cap \Omega$$

fails to hold for some $\lambda \in [{\lambda }_0,{\lambda }_0+\epsilon ]$.

By the definition of ${\lambda }_0$, we have $U_{{\lambda }_0}\left(x\right)\ge 0$ and $V_{{\lambda }_0}\left(x\right)\ge 0$ in ${\mathrm{\Sigma }}_{{\lambda }_0}\cap \Omega$. Recalling that $u>0$, $v>0$ in $\Omega$ and $u\left(x\right)=v\left(x\right)=0$ in ${\Omega }^c$, we deduce that $U_{{\lambda }_0}\left(x\right)>0$ and $V_{{\lambda }_0}\left(x\right)>0$ in ${\Omega }^{{\lambda }_0}\setminus \Omega$, where ${\Omega }^{{\lambda }_0}$ denotes the reflection of $\Omega$ with respect to the hyperplane $T_{{\lambda }_0}$. Applying Lemma 2, we further obtain the strict positivity

$$U_{{\lambda }_0}\left(x\right)>0,V_{{\lambda }_0}\left(x\right)>0,\forall x\in {\mathrm{\Sigma }}_{{\lambda }_0}\cap \Omega .$$

It follows that there exists a small constant $\delta >0$ and a constant $c_0>0$ such that

$$U_{{\lambda }_0}\left(x\right)\ge c_0,V_{{\lambda }_0}\left(x\right)\ge c_0,\forall x\in \overline{{\mathrm{\Sigma }}_{{\lambda }_0-\delta }}\cap \Omega .$$

Since $U_{\lambda }$ and $V_{\lambda }$ are continuous with respect to $\lambda$, there exists a small constant $ϵ>0$ satisfying $ϵ<\delta$ such that for all $\lambda \in ({\lambda }_0,{\lambda }_0+ϵ)$, we have

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in \overline{{\mathrm{\Sigma }}_{{\lambda }_0-\delta }}\cap \Omega .$$

(59)

Next, note that $({\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta })\cap \Omega$ is a narrow region. The lower bounds for $C_1\left(x\right),C_2\left(x\right),C_3\left(x\right),C_4\left(x\right)$ are given in the proof of Lemma 2. Applying the narrow region principle, we derive

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in ({\mathrm{\Sigma }}_{\lambda }\setminus {\mathrm{\Sigma }}_{{\lambda }_0-\delta })\cap \Omega .$$

(60)

Combining (59) and (60), we find that for all $\lambda \in ({\lambda }_0,{\lambda }_0+ϵ)$,

$$U_{\lambda }\left(x\right)\ge 0,V_{\lambda }\left(x\right)\ge 0,\forall x\in {\mathrm{\Sigma }}_{\lambda }\cap \Omega .$$

This contradicts the definition of ${\lambda }_0$ as the supremum. We therefore conclude that ${\lambda }_0=\infty$.

We now establish the strict positivity of $U_{\lambda }$ and $V_{\lambda }$. Suppose for contradiction that this is not the case; then, there exists a point $x^0\in {\mathrm{\Sigma }}_{{\lambda }_0}\cap \Omega$ such that

$$U_{{\lambda }_0}\left(x^0\right)=\underset{{\mathrm{\Sigma }}_{{\lambda }_0}}{min}{U}_{{\lambda }_0}\left(x\right)=0.$$

By Lemma 2, this implies the trivial solution

$$U_{{\lambda }_0}\left(x\right)=V_{{\lambda }_0}\left(x\right)\equiv 0,\forall x\in {\mathbb{R}}^n.$$

However, we have already shown that $U_{{\lambda }_0}\left(x\right)>0$ and $V_{{\lambda }_0}\left(x\right)>0$ in ${\Omega }^{{\lambda }_0}\setminus \Omega$, which yields a contradiction. Thus, we have

$$U_{{\lambda }_0}\left(x\right)>0,V_{{\lambda }_0}\left(x\right)>0,\forall x\in {\mathrm{\Sigma }}_{{\lambda }_0}\cap \Omega .$$

This completes the proof that $(u,v)$ is strictly monotonically increasing along the $x_n$-axis direction. □

4. Conclusions

Firstly, the pseudo-relativistic system we investigate generalizes various classical operators (e.g., $-\Delta ,{(-\Delta )}^s$). Secondly, the nonlinear terms we consider (e.g., $u^p,v^q$) are more general in form, which broadens the applicability of our analytical results. On this foundation, we establish the radial symmetry and monotonicity of positive solutions to the system, with results covering both the bounded domain $B_1\left(0\right)$ and the entire space. Finally, by means of the moving plane method, we prove that the solutions are strictly monotonically increasing in the epigraph of a Lipschitz coercive function. Moreover, unlike the fractional Laplacian with a homogeneous kernel, the pseudo-relativistic operator has a non-homogeneous kernel containing a relativistic correction term. This necessitates us to reconstruct the integral representation of the operator and reprove the Narrow Region Principle with adjusted parameters; these steps are not straightforward extensions of existing techniques. The derivation of the lower bound estimate for the integral at negative minimum points, as well as the treatment of nonlinear coupling terms in the system, depends on a series of refined estimates tailored to the pseudo-relativistic kernel. These estimates fill the gap between the classical fractional setting and the relativistic framework, and can serve as a technical reference for subsequent studies on similar nonlocal operators.

In our future work, we plan to pursue the following research directions:

1.

Extend the symmetry results established in this paper apply to pseudo-relativistic systems with inhomogeneous potentials or singular nonlinearities, which requires further refinement of the existing moving plane method framework;

2.

Generalize the current theoretical framework to higher-dimensional systems and nonlocal operators with more general kernels;

3.

Investigate the asymptotic behavior of solutions to time-dependent pseudo-relativistic equations by virtue of the symmetry properties derived in this work, and analyze the nonexistence of solutions for such equations;

4.

Explore the applicability of the refined technical estimates to other nonlocal operators with relativistic correction terms;

5.

Establish explicit connections between the fractional derivative model proposed in this paper, semigroup theory, and Sonin-type kernels.