Integration of Associative Tokens into Thematic Hyperspace: A Method for Determining Semantically Significant Clusters in Dynamic Text Streams

Abstract

With the exponential growth of textual data, traditional topic modeling methods based on static analysis demonstrate limited effectiveness in tracking the dynamics of thematic content. This research aims to develop a method for quantifying the dynamics of topics within text corpora using a thematic signal (TS) function that accounts for temporal changes and semantic relationships. The proposed method combines associative tokens with original lexical units to reduce thematic entropy and information noise. Approaches employed include topic modeling (LDA), vector representations of texts (TF-IDF, Word2Vec), and time series analysis. The method was tested on a corpus of news texts (5000 documents). Results demonstrated robust identification of semantically meaningful thematic clusters. An inverse relationship was observed between the level of thematic significance and semantic diversity, confirming a reduction in entropy using the proposed method. This approach allows for quantifying topic dynamics, filtering noise, and determining the optimal number of clusters. Future applications include analyzing multilingual data and integration with neural network models. The method shows potential for monitoring information flows and predicting thematic trends.

1. Introduction

1.1. Motivation and Context

The relevance of studying the dynamics of information flows in modern conditions is due to the exponential growth of digital data, in particular text information. The transformation of the information space caused by the processes of digitalization and globalization requires the development of new analytical tools capable of not only processing semantic features but also taking into account the temporal characteristics and structural features of text arrays. The use of methodologies of system analysis, information modeling, and intelligent data processing becomes necessary to improve the efficiency, accuracy, and adaptability of analytical procedures [1,2,3].

The integration of machine learning technologies, natural language processing (NLP), and data visualization methods creates the prerequisites for a qualitatively new level of analysis and forecasting of information processes. However, along with new opportunities, specific problems arise associated with ensuring objectivity, automation, and computational efficiency in analyzing large volumes of text data. An important task is the development of algorithms for the automated detection of hidden patterns, correlations, and deviations in the analyzed texts [4,5,6].

The analysis of big data, particularly textual information, is becoming increasingly vital amid modern information overload. Yet most existing techniques, rooted in static modelling, struggle to capture the evolving thematic landscape of texts. Accounting for the temporal dimension—how the presence and intensity of topics shift over time—is therefore essential for delivering accurate, informative insights. In this study, the phrase “big data” is used in the full Gartner 3-V sense—volume (sheer quantity of documents), velocity (continuous high-speed arrival of new texts), and variety (heterogeneous formats and domains)—rather than as a synonym for any single corpus size. Although our benchmark dataset contains only 5000 news articles, Section 2 demonstrates near-linear throughput on synthetic collections expanded to 100,000 documents, and Section 3 shows that the complete ATe-DTM pipeline can process roughly 1,000,000 tweets in about one hour on a 24-core server with 64 GB of memory. These experiments, together with the method’s streaming design, confirm that ATe-DTM remains computationally feasible for the high-volume, high-velocity workloads typical of social-media or news-agency fire-hoses, thereby justifying the use of the term “big data” in the Introduction.

The modern world is characterized by a huge increase in the volume of generated and consumed information, much of which is presented in text form. The analysis of this data plays a key role in various fields, from scientific research and business to social sciences and politics. Modern methods of text data analysis, such as topic modeling and natural language processing (NLP) methods, allow the extraction of valuable knowledge from large text corpora. However, these methods focus on a static representation of information, overlooking a critically important aspect—the dynamics of change in thematic content over time [7,8,9,10]. For many applied problems, analyzing a static “snapshot” of thematic distribution is insufficient. For example, when analyzing news feeds, social media, or scientific publications, it is important not only to identify key topics but also to track their evolution, identifying periods of increased interest (surges in activity) as well as moments of decreased attention (fading). Understanding the temporal dynamics of thematic content allows for a deeper insight into information processes, predicting the development of events and making informed decisions, in particular achieving the following:

-

Monitor public opinion: track the dynamics of discussions of certain topics in social media, which allows you to identify changes in public sentiment, anticipate potential crises, and respond to them in a timely manner.

-

Analyze market trends: study the dynamics of discussions of products and services in online reviews and forums helps companies understand consumer needs, forecast demand, and adapt their strategies.

-

Analyze the dynamics of scientific publications on a specific topic: track the development of scientific thought, identify promising areas of research, and assess the impact of various factors on scientific progress.

1.2. Research Gap in Dynamic Topic Modelling

Existing approaches to modelling topic dynamics—such as LDA with timestamps (Temporal LDA, also known as TOT) and Dynamic Topic Models (DTM)—partially address the time factor, yet they suffer from three critical limitations:

Lack of a time-normalized salience metric. TOT outputs topic probabilities whose values depend on corpus size and document length, making cross-period comparison unreliable.

Over-smoothed temporal evolution. DTM enforces a logistic-Gaussian state-space chain, so the short-lived bursts that characterize social-media streams are blurred or lost.

High computational cost and weak interpretability. Variational Kalman filtering in DTM scales as O(T K² V) in memory and >O(N K V) in time; even a 1-million-tweet stream may demand > 20 GB RAM, while neither model provides a statistically normalized signal by which an analyst could judge the significance of a peak.

To overcome these drawbacks, we introduce a Topic-Signal (TS) function that serves as a unified, normalized measure of topic presence. The TS function is designed to achieve the following:

• Quantify topic salience within a specified time interval on a comparable scale;
• Account for context by evaluating a topic’s activity relative to other topics and to the total volume of documents;
• Filter noise, highlighting statistically significant changes via time-series techniques;
• Remain interpretable, enabling analysts to spot topics that are rising or fading and to act accordingly.

1.3. Conceptual Foundations

When considering the “topic signal” in dynamic text data analysis, it should be noted that the concept of information is the basis of modern science, permeating various disciplines, from fundamental physics to cognitive science. Information, in the most general sense, is a measure of the orderliness, structure, and organization of a system. Natural information, in particular, refers to information that is present in nature or that arises as a result of natural processes. It includes any data transmitted, stored, and processed in natural systems, be they biological organisms, geological formations, or space objects.

The concept of information is fundamental to a wide range of scientific disciplines. The work of Claude Shannon (“A Mathematical Theory of Communication”, 1948) [11] laid the foundations of information theory, defining information as a measure of uncertainty. Further research, including the works of Rosen (Life Itself, 1991) [12], Gershenfeld (The physics of information technology, 2000) [13], Landauer (Irreversibility and Heat Generation in the Computing Process, 1961) [14], and Bekenstein (Black Holes and the Second Law, 2020) [15], expanded the understanding of information by linking it to physical, biological, and thermodynamic processes. Recent scholarship has further broadened this classical perspective: Ellerman [16] and Xu et al. [17] introduce a logical-entropy framework as an alternative quantitative basis; Çengel [18] situates information within the realm of meaning and consciousness; Manzotti [19] proposes a deflationary, probability-centered account that questions its ontological status; and Xi [20] compares the “computing” and “information” trajectories that shape the contemporary information turn. In addition, the information approach has proven productive even in fields such as geology. For example, the work of McKenzie (1977) “Plate tectonics and its relationship to the evolution of ideas in the geological sciences” [21] demonstrates how information about tectonic processes is encoded and stored in the geological structures of the Earth, confirming the universality of the information approach to the study of natural phenomena. Thus, the concept of information acts as a powerful tool for studying and understanding a wide range of processes and phenomena in various scientific disciplines.

Combining the above concepts, natural information can be defined as a set of processes and phenomena that carry a semantic message that is formed in natural systems. Formally, this can be represented as follows:

$$I={{\sum }_{i=1}^{n}P}_i\cdot E_i$$

(1)

I—information, Pi—probability of process or phenomenon i, Ei—amount of meaning expressed by each element.

In the context of text data analysis, this set of processes and phenomena that carry a semantic load can be designated as “subject matter”. Subject matter is a class of semantically related elements united by a common semantic field. Subject matter can be expressed by various sign systems, including natural language, where it is manifested in the form of text. Structurally, subject matter in a text is a class of related elements within a statistical set of elementary units of text (words, phrases, sentences). The presence of subject matter in a text can be assessed quantitatively using various methods of analyzing the frequency of mentions of elements related to a given subject matter. One of such methods can be represented by the following function:

$$F_c\left(t\right)={\displaystyle \frac{N_c\left(t\right)}{N_{\mathit{total}}}}$$

(2)

Fc(t) is the frequency of topic c at time t, Nc(t) is the number of mentions of topic c at time t, and N_total is the total number of elements in the array.

However, the static frequency representation does not reflect the dynamics of topic changes over time. To analyze the temporal evolution of the thematic content of the text, it is necessary to introduce the concept of a “thematic signal”. The quantitative manifestation and change of topic over time is one of the central issues of dynamic information theory (DIT). DIT, used to model cognitive processes (Chernavskaya, 2016) [22], is based on mathematical and computational methods for analyzing the perception and processing of information, taking into account time as a key parameter.

The synthesis of DIT and thematic text analysis allows us to present information as a discrete two-dimensional function:

$$T\left(c,t\right)=S_{ij}$$

(3)

where T(c,t) is an array of texts and Sij is an array element expressing the topic of c at time t.

The proposed function reflects the relationship between the presence of the topic, the content of the topic, and time, which can be defined as a thematic signal. Thus, the function of the thematic signal can be represented as follows:

$$S=f\left(c,t\right)$$

(4)

S—the value of the thematic signal at the intersection of the subject (c) and time (t)—i.e., the thematic coordinate.

To ground the thematic-signal function in classical information theory, we regard the triple (S, X, t) as a random source that emits a topic-specific token stream. Let $P_c\left(\mathrm{w}|\mathrm{t}\right)$ denote the empirical probability of token w within topic c at time t, and let P₀ (w) be the stationary background distribution of the same vocabulary. The instantaneous information gain obtained when we observe the topic instead of the background is then as follows:

$$F_c\left(t\right)=D_{KL}\left(P_c\left(\cdot |t\right)\hspace{0.17em}|\hspace{0.17em}{P}_0\left(\cdot \right)\right)={{\sum }_{w\in V}P}_c\left(w|t\right)\hspace{0.17em}log{\displaystyle \frac{P_c\left(w|t\right)}{P_0\left(w\right)}}$$

(5)

Because the Kullback–Leibler divergence $D_{\mathrm{K}\mathrm{L}}$ is the expected log-likelihood ratio, $F_c\left(t\right)$ measures how strongly the current token stream deviates from background usage and thus serves as a direct indicator of topical salience. Summing over time gives the cumulative thematic entropy:

$$H_c\left(T\right)={\Sigma }_{t\in T}{P}_t{·F}_c\left(t\right)$$

(6)

where $P_t$ is the empirical weight of time slice t. By the chain rule, this sum equals the mutual information I(C; t) between topic identity and time; therefore, a lower value of $H_c\left(T\right)$ signals both reduced thematic entropy and greater temporal predictability. In practice, we approximate the sums with the smoothed counts already held in the matrices $M_W$ and $M_A$, so the KL-based expression collapses to the computable form $F\left(T\right)=f\left(S,X,t\right)$ used throughout the algorithm while remaining firmly linked to established information-theoretic measures.

The proposed concept of the “thematic signal” is based on the introduction of a discrete time axis, which allows us to consider text data not as a static set of information but as a dynamically developing process. This is a fundamental difference from traditional text analysis methods, which focus on identifying the thematic structure at a certain point in time, ignoring temporal dynamics (Figure 1).

Introducing a time dimension into the analysis of topical activity provides a number of significant benefits:

• Trend detection: Dynamic analysis allows you to track changes in interest in certain topics over time, identify growing and fading trends, and predict future trends. This is especially important in a rapidly changing information environment, where static “snapshots” of data quickly become outdated.
• Data contextualization: Taking into account the temporal context helps to understand how external events and factors influence topical activity. For example, a sharp surge in interest in a certain topic can be associated with a specific event, news publication, or social action.
• Cause-and-effect analysis: A dynamic approach allows you to explore cause-and-effect relationships between different topics and external factors. For example, you can analyze how changes in one topic affect the dynamics of another, or how external events lead to a change in the topic landscape.
• Forecasting: Analysis of time series of topical signals allows you to build forecast models and predict future changes in topical activity. This can be useful for making strategic decisions in a variety of areas, from marketing and PR to political analysis and risk management.
• Improved visualization: Dynamic data can be effectively visualized using graphs, charts, and other tools, making the analysis results easier to understand and interpret.

The development of the thematic signal function is an important scientific and practical task, the solution of which will significantly expand the capabilities of text data analysis. TS will allow moving from static text analysis to dynamic monitoring of semantic trends, which is critical for decision-making in a rapidly changing information landscape [23,24]. Such a tool will complement existing NLP methods by adding a time dimension to text data analysis. This will open up new opportunities for studying information processes, forecasting trends, and identifying anomalies in various fields. Further research in this area should be aimed at developing effective algorithms for calculating TS, as well as creating convenient tools for visualizing and interpreting the results. The introduction of TS into the practice of text data analysis will allow us to obtain deeper and more practically significant results, facilitating more effective decision-making in various fields of activity. In the framework of modern computer linguistics and text data analysis, the task of formalizing and quantitatively describing thematic content is of particular importance. The fundamental concept in this context is the function of the thematic signal F(T), which is a mathematical model that allows us to systematize and analyze the semantic structures inherent in the information space under consideration [25,26,27].

The function of the thematic signal F(T) requires a comprehensive consideration of three interrelated aspects:

• The semantic component (S), reflecting the semantic core of the topic, its conceptual content, and logical connections between elements. This parameter encodes the deep linguistic and cognitive characteristics that determine the essence of the thematic formation.
• Spatial distribution (X), describing the topology of the location of thematic markers in the structure of the text corpus. This aspect takes into account the features of the distribution of lexical units, their mutual location, and frequency characteristics in various segments of the analyzed data array.
• Temporal dynamics (t), recording evolutionary changes in the topic in the time continuum. This parameter is especially important when analyzing news feeds, scientific publications, or other types of data that have a pronounced time structure.

Formally, the indicated relationship can be expressed by the following equation:

$$F\left(T\right)=f\left(S,X,t\right)$$

(7)

S—the semantic message, X—the spatial distribution, and t is the temporal characteristic.

When working with text data, the elementary unit of analysis is the lexical token wi, which is understood as either a separate word or a stable phrase carrying a certain semantic load. Any text D can be represented as an ordered (or unordered, depending on the chosen model) set of such tokens:

$$D=\{w_1,w_2,\dots ,w_N\}$$

(8)

w_i is the i-th elementary unit (word or token).

N is the total number of significant lexical units in the document or text fragment under consideration.

Modern approaches to computer processing of natural language suggest the need to move from a qualitative description of text data to their quantitative representation. The most common and methodologically sound method of such formalization is the vector representation of texts, in which each document D is mapped into an N-dimensional vector space:

$$\vec{D}=\left(f\left(w_1\right),f\left(w_2\right),\dots ,f\left(w_N\right)\right)$$

(9)

The function f(w_i) determines the significance or weight of the i-th token within the model under consideration. The choice of a specific type of this function and, accordingly, the method of vector representation of the text, significantly affects the quality of subsequent analysis and depends on the specifics of the problem being solved.

It should be noted that the transition to vector representation allows the use of a powerful apparatus of linear algebra and multivariate statistical analysis to solve problems of classification, clustering, and thematic modeling of text data. This approach opens up opportunities for automated processing of large arrays of unstructured text information, which is especially important in the context of the modern information society.

The development of adequate models of vector representation of texts remains an active area of research in computational linguistics and machine learning, where new approaches are constantly being proposed that take into account various aspects of language semantics, syntax, and pragmatics.

Modern approaches to vector representation of text data are distinguished by a significant variety of methodological paradigms and technical implementations. Each of the existing methods has characteristic features that determine its applicability to solving specific problems of text information analysis. Basic methods of vector modeling include the following:

• The Bag-of-Words (BoW) frequency model is a fundamental approach based on taking into account the absolute frequencies of lexical units [28,29]. In this model, the text D is transformed into a vector:

$$\vec{D}=\left(c_1,c_2,\dots ,c_n\right)$$

(10)

c_i—the number of occurrences of the word wi in the text.

Despite its conceptual simplicity, this method demonstrates effectiveness in solving text classification problems, although it does not take into account the semantic relationships between terms.

2.

TF-IDF (Term Frequency-Inverse Document Frequency) is an improved version of the frequency approach, which introduces weighting of the significance of terms:

$$\mathit{TF}\text{-}\mathit{IDF}\left(w_i\right)=f\left(w_i\right)\cdot log\left({\displaystyle \frac{M}{df\left(w_i\right)}}\right)$$

(11)

M is the total number of documents in the corpus C, and df(w_i) is the number of documents containing the word w_i

This scheme allows us to reduce the influence of commonly used words and to identify terms that are most characteristic of a particular document [30,31,32].

3.

Distributional models (Word2Vec, etc.) are based on the principle of “word usage determines meaning” (distributional hypothesis) [33,34]. In these models, each word w_i is mapped to a vector of fixed dimension:

$$\mathit{Embed}\left(w_i\right)=\overrightarrow{v_i}\in R^k$$

(12)

The text D is represented as the sum or average of word vectors:

$$\vec{D}={\displaystyle \frac{1}{N}}{\sum }_{i=1}^N\overrightarrow{v_i}$$

(13)

It should be noted that semantically close words are located close to each other in the vector space. The representation of the whole text is often formed as the arithmetic mean of the vectors of its constituent words.

4.

Latent semantic analysis (LSA) uses the singular value decomposition (SVD) of the term-document matrix:

$$A\approx U\Sigma V^T$$

(14)

where UΣV are the matrices obtained in the SVD process, and a new vector representation is constructed based on the transformed space.

This allows revealing hidden semantic structures and reducing the dimensionality of the feature space. This method effectively reveals synonymous relations and polysemy [35,36].

5.

Topic modeling (LDA) considers documents as probabilistic mixtures of topics and topics as word distributions:

$$P\left(w_i|D\right)={\sum }_{k=1}^{K}P\left(w_i|z_k\right)P\left(z_k|D\right)$$

(15)

z_k is the k-th topic, and K is the total number of topics.

This model allows us to identify hidden topic structures in document collections [37,38].

A significant methodological challenge in the field of topic modeling is the problem of infinite divisibility of topic structures. Formally, this can be expressed as follows:

$$T={{\bigcup }_{i=1}^{\infty }T}_i гдe T_i\subseteq TиT_i\sim T$$

(16)

Ti retain the features of the original topic T, and ∼ denotes semantic similarity. This leads to an increase in the thematic entropy. The thematic entropy H(T) can be defined by analogy with Shannon entropy as follows:

$$H\left(T\right)=-{\sum }_{i=1}^{n}p\left(T_i\right)mathitlogp\left(T_i\right)$$

(17)

where p(Ti) is the probability or frequency of the presence of a subtopic within the original signal T, and n → ∞.

Thematic entropy is expressed as information noise, which in practical terms is described by an increase in the significance of thematically insignificant tokens within the signal. Let w_j be tokens with different thematic significance z(w_j). An increase in the significance of thematically insignificant tokens can be formalized as an increase in the sum of the weights of less significant tokens:

$$Z_{\mathit{noise}}={\sum }_{j=1}^{N}z\left(w_j\right), гдez\left(w_j\right)\ll z_{\mathit{threshold}}$$

(18)

$Z_{\mathrm{noise}}$—the total noise, $z_{\mathrm{threshold}}$—the thematic significance threshold. This, in turn, does not allow us to effectively determine the maximum required number of semantically significant topics. The number of significant topics can be formalized as an optimization of the function H(T), where noise is minimized:

$$K_{\mathit{optimal}}=mathitarg\underset{K}{mathitmin}\left(H\left(T\right)+Z_{\mathit{noise}}\left(K\right)\right)$$

(19)

K—the number of selected topics.

Also, the proposed approaches to determining the radius vector and using them as the basis for tools for mathematically describing the presence of thematic signals do not allow for a quantitative assessment of the corresponding noise level. Thus, the entire process of analyzing the properties of identified thematic signals, based on the use of the presented approaches, is reduced exclusively to expert methods.

This problem can be solved by enriching the corresponding array of tokens with a complex of associations. Let the original array of tokens W be enriched with a complex of associations A, then the new array can be written as a union:

$$W^{\prime }=W\cup A$$

(20)

W′—an enriched array of tokens and A—a complex of associations

The association complex is formed on the basis of the initial text corpus. Associative tokens are obtained from the publicly available Yandex Associative Thesaurus. For every lemma $w_i$ that appears in the corpus, the thesaurus API returns a ranked list of candidate associates; we keep up to five associates whose confidence score is at least 0.30, forming the set $A_y\mathrm{a}\mathrm{n}$. Each associate $a_j$ arrives with a confidence value $s_j\in \left(\mathrm{0,\; 1}\right]$, which we min–max normalise to the range [0, 1] and write into the association matrix $M_A$. We then blend the original term-document matrix $M_W$ with $M_A$ as $M^{\prime }=\alpha M_W+\beta M_A$, where α + β = 1. The optimal balance (α = 0.7, β = 0.3) was identified by grid-searching α = 0.5, 0.6, 0.7, 0.8 on a 10% validation subset and maximising $C_v-S_d\mathrm{i}\mathrm{v}$. Let A be constructed from the initial corpus C, then the elements of the association complex $a_j$ can be represented as a function of the corpus:

$$A=\{a_j\mid a_j=f\left(C\right),\hspace{0.17em}j=1,\dots ,M\}$$

(21)

M—the number of associations.

Integration of the radius vectors of these token associations leads to saturation of the thematic hyperspace. Let the radius vector of the original token array $\vec{\mathrm{W}}$ and the radius vector of associations $\vec{\mathrm{A}}$ be integrated, then the enriched radius vector will be as follows:

$$\overrightarrow{W^{\prime }}=\vec{W}+\vec{A}$$

(22)

W′—an enriched array of tokens, and A—a complex of associations.

The nature of entropy changes in the direction of refining information noise. The change in entropy can be written as follows:

$$\Delta H=H\left(W^{\prime }\right)-H\left(W\right)$$

(23)

H(W) is the original thematic entropy, and H(W′) is the entropy after enrichment of the token array.

The most important consequence of using this technique is the possibility of moving from the principle of infinite thematic detailing to a more reasonable entropy criterion for identifying significant semantic clusters. This allows the following:

• Objectively limiting the number of identified topics;
• Increasing the stability of topic models;
• Improving the interpretability of analysis results.

The practical implementation of the method demonstrates its effectiveness when working with various types of text data, including scientific publications, media texts, and user content of social networks [39,40].

Modern research in the field of natural language processing and text data analysis demonstrates a variety of approaches to solving problems of topic modeling, document classification, and extraction of significant information. In recent years, special attention has been paid to the problems of managing information noise, increasing the accuracy of classification, and adapting machine learning methods to specific subject areas.

The study by Arjun Shah, Hetansh Shah, Vedica Bafna, Charmi Khandor, and Sindhu Nair is devoted to developing an explainable solution for news headline verification using web information mining techniques and natural language inference models. The authors overcome the limitations of classical machine learning approaches based on static training data, achieving an accuracy of 84.3%. This result is especially important in the context of combating fake news, demonstrating the effectiveness of combining dynamic information mining with modern NLP methods [41]. Ghalyan’s works propose innovative modifications of the classical Bag-of-Words model. The introduction of the capacitive empirical risk function (CERF) and the double ergodic limits technique (DEL-BoW) can significantly improve the generalization ability of models and reduce the risk of overfitting. Experiments on standard datasets (Caltech-101, Caltech-256, etc.) confirm the effectiveness of the proposed approaches, achieving classification accuracy of up to 90.86% [42,43]. Antonio P. Castro Junior, Gabriel A. Wainer, and Wesley P. Calixto focus on improving traditional Bag-of-Words methods for classifying legal documents. The authors propose a method for weighting terms based on their co-occurrence and linearity of distribution across categories. The results of a comparative analysis of nine classification algorithms demonstrate the practical applicability of the approach in the legal proceedings system, which emphasizes the importance of adapting text models to the specifics of the subject area [44]. A comparative analysis of phishing email detection methods presented in the work of Arar Al Tawil, Laiali Almazaydeh, Doaa Qawasmeh, Baraah Qawasmeh, Mohammad Alshinwan, and Khaled Elleithy shows the advantages of state-of-the-art pre-trained models (BERT) over traditional approaches (TF-IDF, Word2Vec). Achieving precision, recall, and F-measure at the level of 0.99 confirms the effectiveness of transformer architectures in text classification tasks. These results are consistent with the findings of Donghwa Kim, Deokseong Seo, Suhyoun Cho, and Pilsung Kang, who propose a multi-co-training (MCT) method for document classification using a combination of TF-IDF, LDA, and Doc2Vec [45,46]. The research of Elangel Neilea Shaday, Ventje Jeremias Lewi Engel, and Hery Heryanto in the field of text sentiment analysis and that of Jing Zhou, Zhanliang Ye, Sheng Zhang, Zhao Geng, Ning Han, and Tao Yang in behavior pattern detection demonstrate the versatility of text analysis methods. The use of Bi-LSTM with various word embedding (GloVe, Word2Vec, FastText) and a comparison of the effectiveness of TF-IDF and Word2vec in the educational context expand the scope of application of traditional NLP methods [47,48].

Innovative approaches to topic modeling are presented in the work of Suhyeon Kim, Haecheong Park, and Junghye Lee, who proposed the W2V-LSA method, combining Word2vec and spherical k-means clustering for analyzing blockchain technology trends. This approach demonstrates advantages over traditional methods (Probabilistic LSA) in both quantitative and qualitative assessments.

Practical applications of topic modeling in the legal field are explored in the works of Ria Ambrocio Sagum, Patrick Anndwin C. Clacio, Rey Edison R. Cayetano, and Airis Dale F. Lobrio and Kaveh Bastani, Hamed Namavari, and Jeffrey Shaffer. The development of an automatic court decision abstracting system based on LSA and the analysis of financial consumer complaints using LDA highlight the importance of adapting NLP methods to specific domains [49,50].

The study of J.C. Bailón-Elvira, M.J. Cobo, E. Herrera-Viedma, and A.G. López-Herrera is devoted to improving the recommendation system of Spanish Official Publications (BOE) using LDA. The results show the possibility of increasing the share of recommended documents from 11% to 23%, which demonstrates the practical value of topic modeling for processing large arrays of official documents [51].

The set of studies reviewed reflects modern trends in the field of text data processing, where traditional methods (TF-IDF, Bag-of-Words) are successfully combined with modern approaches (word embedding, transformer models) to solve specific applied problems. Particular attention is paid to the problems of managing information noise, increasing the accuracy of classification and adapting methods to the specifics of subject areas, which is consistent with the goals of our study [52,53,54,55,56,57].

Key disadvantages of existing approaches include the following:

• Limited ability to process dynamic content and new domains;
• Lack of mechanisms for quantitative assessment of semantic noise;
• Inability to objectively determine the optimal number of thematic clusters;
• Dependence on static training samples;
• High computational costs when working with large volumes of data.

Analysis of literary sources convincingly demonstrates the need for a fundamentally new method of topic modeling that achieves the following:

• Integrates a complex of token associations into a thematic hyperspace;
• Ensures control of thematic entropy through formalized metrics;
• Allows for objective determination of the maximum number of significant topics;
• Provides a quantitative assessment of the level of information noise;
• Maintains computational efficiency when working with big data.

The proposed approach, based on the integration of associative links and management of the entropy characteristics of the semantic space, is designed to overcome the above limitations of existing methods. Of particular importance is the introduction of the formalized Z_noise indicator for noise assessment and the K_optimal optimization procedure for determining the number of clusters, which is absent in the works reviewed. Such a methodological apparatus will not only improve the quality of thematic modeling but also ensure the interpretability of the results, which is especially important for applied problems of text data analysis in various subject areas.

1.4. Paper Road-Map

The remainder of this article is organized as follows. Section 2 details the datasets, preprocessing pipeline and the full ATe-DTM algorithm, including the association-augmented token space, TS-function derivation, and computational-complexity analysis. Section 3 presents the experimental study: baseline comparisons, ablation tests, and scalability experiment up to one million tweets. Section 4 discusses the results, practical implications, and current limitations, and Section 5 concludes with a summary of contributions and directions for future research.

2. Materials and Methods

Technical implementation of this task is possible by enriching the initial set of tokens with corresponding token-associations, which is possible by means of two matrices—the token significance matrix describing the initial set of texts, and the significance matrix of their token-associations. The resulting matrix is their sum, adjusted for the specific weights necessary to balance the contribution of each of the summed matrices.

$$S=a\ast \left[\begin{array}{ccc}{\displaystyle \frac{count\left(w_i,d_j\right)}{len\left(d_j\right)}}& \dots & {\displaystyle \frac{count\left(w_k,d_j\right)}{len\left(d_j\right)}}\\ ⋮& \ddots & ⋮\\ {\displaystyle \frac{count\left(w_{i,},d_m\right)}{len\left(d_m\right)}}& \dots & {\displaystyle \frac{count\left(w_i,d_m\right)}{len\left(d_m\right)}}\end{array}\right]+b\ast \left[\begin{array}{ccc}{\displaystyle \frac{count\left({aw}_i,{ad}_j\right)}{len\left({ad}_j\right)}}& \dots & {\displaystyle \frac{count\left({aw}_k,{da}_j\right)}{len\left({ad}_j\right)}}\\ ⋮& \ddots & ⋮\\ {\displaystyle \frac{count\left({aw}_{i,},{ad}_m\right)}{len\left({ad}_m\right)}}& \dots & {\displaystyle \frac{count\left({aw}_k,{ad}_m\right)}{len\left({ad}_m\right)}}\end{array}\right]$$

(24)

$\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_i,d_j\right)$—number of mentions of word i in the text j, $\mathrm{l}\mathrm{e}\mathrm{n}\left(d_j\right)$—text length j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_{i,},d_m\right)$—number of mentions of word i in the text m, $\mathrm{l}\mathrm{e}\mathrm{n}\left(d_m\right)$—text length m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_k,d_j\right)$—number of mentions of word k in the text j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_k,d_m\right)$—number of mentions of word k in the text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_k,d_m\right)$—number of mentions of word k in the text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_i,d_j\right)$—number of mentions of word i in the text j, $\mathrm{l}\mathrm{e}\mathrm{n}\left(d_j\right)$—text length j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_{i,},d_m\right)$—number of mentions of word i in the text m, $\mathrm{l}\mathrm{e}\mathrm{n}\left(d_m\right)$—text length m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_k,d_j\right)$—number of mentions of word k in the text j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_k,d_m\right)$—number of mentions of word k in the text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left(w_k,d_m\right)$—number of mentions of word k in the text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_i,{\mathrm{a}\mathrm{d}}_j\right)$—number of mentions of associations of word i in the text of associations j, $\mathrm{l}\mathrm{e}\mathrm{n}\left({\mathrm{a}\mathrm{d}}_j\right)$—length of association text j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_{i,},{\mathrm{a}\mathrm{d}}_m\right)$—number of mentions of associations to the word i in the text m, $\mathrm{l}\mathrm{e}\mathrm{n}\left({\mathrm{a}\mathrm{d}}_m\right)$—length of association text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_k,{\mathrm{a}\mathrm{d}}_j\right)$—number of mentions of associations to the word k in the text j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_k,{\mathrm{a}\mathrm{d}}_m\right)$—number of mentions of associations to the word k in the text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_k,{\mathrm{a}\mathrm{d}}_m\right)$—number of associations to word m in text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_i,{\mathrm{a}\mathrm{d}}_j\right)$—number of mentions of associations to the word i in the text j, $\mathrm{l}\mathrm{e}\mathrm{n}\left({\mathrm{a}\mathrm{d}}_j\right)$—length of association text j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_{i,},{\mathrm{a}\mathrm{d}}_m\right)$—number of mentions of associations to the word i in the text m, $\mathrm{l}\mathrm{e}\mathrm{n}\left({\mathrm{a}\mathrm{d}}_m\right)$—length of association text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_k,{\mathrm{a}\mathrm{d}}_j\right)$—number of mentions of associations to the word k in the text j, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_k,{\mathrm{a}\mathrm{d}}_m\right)$—number of mentions of associations to the word k in the text m, $\mathrm{c}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{t}\left({\mathrm{a}\mathrm{w}}_k,{\mathrm{a}\mathrm{d}}_m\right)$—number of mentions of associations to the word k in the text m, a—specific weight representing the significance of the matrix describing a text corpus consisting of original words, b—specific weight representing the significance of the matrix describing a text corpus consisting of associations to the original words, a = 1 − b.

The combination of the token significance matrices of the original text array W and the association tokens A changes the nature of the thematic entropy H(T), ensuring the universalization of the representation of thematic signals in the text array. Let the original token significance matrix be represented as M_W, and the association token significance matrix as M_A. The final combined significance matrix is defined as follows:

$$M^{\prime }=\alpha M_W+\beta M_A, \alpha +\beta =1,\alpha ,\beta \ge 0$$

(25)

Universalization of the representation of thematic signals in a text array is achieved by increasing the uniformity of their significance, which reduces the influence of tokens with low thematic significance. The influence of associative links is controlled by the scalar A ∈ [0, 1], defined as the share of the association matrix in the blend, that is, A = β and 1 − A = α. The closed interval follows from probability-mass conservation: when A = 0, the model reduces to a lexical baseline, whereas A = 1 ignores original tokens entirely. Intermediate values trade off noise reduction (growing with A) against lexical fidelity (shrinking with A). We therefore treat A as an information-theoretic gain parameter and seek the value that maximizes the utility $\Phi \left(A\right)=C_v\left(A\right)-S_d\mathrm{i}\mathrm{v}\left(A\right)$, where topic coherence $C_v$ and semantic diversity $S_{\mathrm{d}\mathrm{i}\mathrm{v}}$ are defined in Section 2. Thematic entropy H after unification can be described as follows:

$$H\left(W^{\prime }\right)=-{{\sum }_{i=1}^{n}p}_{i}mathitlog{p}_i,$$

(26)

${\mathrm{p}}_{\mathrm{i}}={\displaystyle \frac{\mathrm{count}\left({\mathrm{w}}_{\mathrm{i}},{\mathrm{W}}^{\prime }\right)}{{\sum }_{\mathrm{j}=1}^{\mathrm{n}}\mathrm{count}\left({\mathrm{w}}_{\mathrm{j}},{\mathrm{W}}^{\prime }\right)}}$ и W′—enriched token array.

Here, H(W′) is refined relative to the original entropy H(W), which indicates a reduction in information noise and an improvement in the interpretation of the topic content.

The LDA (Latent Dirichlet Allocation) method is often considered one of the best for topic modeling tasks due to several advantages:

• It models documents as a mixture of topics, and topics as a mixture of words. This approach accounts for uncertainty and can handle noisy data better.
• It scales well to large amounts of data.
• It effectively models the “sparseness” of topics: each topic is described by only a small number of keywords, and each document has strong connections to only a few topics. This makes the results more accurate and plausible.

In the context of the LDA (Latent Dirichlet Allocation) tool, universalizing the token distribution improves the consistency of topic models. The probability of a word w_i in a topic θ_k is defined as follows:

$$P\left(w_i\mid {\theta }_k\right)={\sum }_{j=1}^{K}P\left(w_i\mid {\varphi }_j\right)\hspace{0.17em}P\left({\varphi }_j\mid {\theta }_k\right)$$

(27)

${\varphi }_j$—the distribution of words in topic j. Using the matrix M′ leads to a refinement of $P\left(w_i\mid {\varphi }_j\right)$ and the posterior distribution $\left({\varphi }_j\mid {\theta }_k\right)$, which reduces uncertainty (entropy) and improves the explanatory power of the LDA “importance” metric, which characterizes the contribution of a particular topic to explaining the data. The higher “importance”, the more significant the topic θk is for modeling the observed texts. Accordingly, the level ${\displaystyle \frac{1}{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}}$ can be interpreted as a measure of the uncertainty associated with a particular topic.

Let us recall the topic entropy H(T), which reflects the degree of uncertainty in the distribution of topics. After enriching the array of tokens W to W′, the universalization of the topic representation reduces the noise caused by the imbalance in the importance of individual tokens, which is expressed in a decrease in H(W′) relative to H(W). The decrease in H(W′) is associated with an increase in importance, since the localization of topics contributes to an increase in the degree of similarity. The following series of observations follow from this:

1.

For each topic ${\theta }_k$, “$\mathrm{importance}\left({\theta }_k\right)$” is inversely proportional to its uncertainty:

$$\mathit{importance}\left({\theta }_k\right)\propto {\displaystyle \frac{1}{H\left({\theta }_k\right)}}$$

(28)

$H\left({\theta }_k\right)$—энт is the entropy associated with the distribution of words in topic ${\theta }_k$.

2.

${\displaystyle \frac{1}{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}\left({\theta }_k\right)}}$ describes the relative contribution of a topic to the overall reduction in uncertainty. The higher the “$\mathrm{importance}\left({\theta }_k\right)$”, the less uncertainty (entropy) a topic contributes.

3.

For the joint space $W^{\prime }$, the decrease in the level of ${\displaystyle \frac{1}{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}}$ reflects the overall decrease in entropy:

$$\mathrm{H}\left({\mathrm{W}}^{\prime }\right)={\sum }_{\mathrm{k}=1}^{\mathrm{K}}{\displaystyle \frac{1}{\mathrm{importance}\left({\theta }_{\mathrm{k}}\right)}}$$

(29)

K—the number of topics. The decrease in H(W′) is thus associated with an increase in “importance” (θ_k) for key topics, which confirms the growth in orderliness of the thematic space; therefore, the level ${\displaystyle \frac{1}{\mathrm{i}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{c}\mathrm{e}}}$ directly describes the decrease in thematic entropy, since it reflects the degree of uncertainty eliminated due to the universalization of the representation of thematic signals.

To measure how important a topic is beyond plain entropy reduction, we compute a topic-significance index. For each topic, we take the mean amplitude of its thematic-signal curve $F_k\left(t\right)$ across all time slices (salience) and multiply it by one minus the topic’s semantic-diversity score $S_{\mathrm{div},k}$ (purity). The product is normalised to the [0, 1] range, so higher TSI values mark topics that are both prominent and well separated.

The proposed approach allows us to solve the problems outlined above. First, determining the maximum required number of semantically significant topics. Let the number of topics identified in a text corpus be denoted by K, and the thematic entropy for a given K be H(K). According to the formulated hypothesis, with an increase in the number of topics identified K, each new topic is characterized by an increase in information noise. Consequently, there is a certain limiting value $H_{\max }$, at which the following applies:

$$\underset{K\to \infty }{lim}H\left(K\right)=H_{\max }$$

(30)

In accordance with the theses on the change in the nature of entropy, a hypothesis is put forward that with an increase in the number of topics identified in a text corpus, each new topic contains a greater amount of information noise. Let the information noise associated with the topic identified for a given K be designated as N(K). Then, the increase in noise can be formally written as a monotonic increase in N(K) as K increases:

$${\displaystyle \frac{dN\left(K\right)}{dK}}>0$$

(31)

Consequently, when the entropy limit is reached, the structure of each subsequently identified topic is identical to the previous one. This indicates that the topic entropy limit has been reached and subsequent division is inappropriate. Secondly, the task of determining the level of information noise within a specific topic was designated. A high level of information noise is characterized by an increased concentration of associations between tokens, which occurs because tokens in such clusters are closely related to each other, forming a closed system of duplicate relationships. To formally represent this effect, the concentration coefficient of associations between top tokens can be written as follows:

$$T_{\mathit{top}}=\{t_1,t_2,\dots ,t_M\}$$

(32)

$T_{\mathrm{top}}$—top-tier token set.

$$C_{\mathit{assoc}}={\displaystyle \frac{{{\sum }_{i=1}^{M}n}_i}{M}}$$

(33)

M—the number of tokens from the upper echelon, $n_i$—number of token associations $t_i{\in \mathrm{T}}_{\mathrm{top}}$ with other tokens from $T_{\mathrm{top}}$.

These tokens reinforce each other through frequent associations but do not introduce qualitative diversity of information. Let Ai denote the associative reinforcement of token ti due to associations with other tokens. Then:

$$A_i={{\sum }_{j=1}^{M}a}_{ij}$$

(34)

$a_{\mathrm{i}\mathrm{j}}$—the presence of an association between tokens $t_i$ and $t_j$, where $a_{\mathrm{i}\mathrm{j}}=1$, if the relationship exists, and $a_{\mathrm{i}\mathrm{j}}=0$ otherwise.

Association tokens that are not in the top list by importance play a key role in strengthening the cluster. They create additional connections with tokens from the upper echelon, artificially increasing the concentration level. Let the set of such association tokens be designated as $T_{\mathrm{assoc}}$, and their total influence on tokens from the upper echelon be defined as follows:

$$I_{\mathit{assoc}}={{\sum }_{{k\in T}_{\mathit{assoc}}}{\Sigma }_{{i\in T}_{\mathit{top}}}w}_{ki}$$

(35)

$w_{\mathrm{k}\mathrm{i}}$—в the weight of the connection between token k from the $T_{\mathrm{assoc}}$ and token $t_i$ from $T_{\mathrm{top}}$.

The phenomenon described leads to the effect that tokens with the greatest significance are surrounded by supporting associations that strengthen their position within the cluster. Consequently, in low-noise clusters, tokens are more dispersed and independent. Their connections with token-associations are weakly redundant and more diverse. Formally, this can be expressed as follows:

$$D_{\mathit{div}}={\displaystyle \frac{\mathit{number} \mathit{of} \mathit{unique} \mathit{links}}{\mathit{total} \mathit{number} \mathit{of} \mathit{links}}}$$

(36)

$D_{\mathrm{div}}$—the coefficient of semantic diversity.

In clusters with high information noise, associations between tokens repeatedly amplify connections, forming local peak concentrations that do not reflect the real significance of the information. Let $P_{\mathrm{local}}$ denote the local peak concentration within a cluster:

$$P_{\mathit{local}}=\underset{i}{max}\left(n_i\right)$$

(37)

$n_i$—number of associations for token $t_i$.

The practical implementation of the proposed approach can be presented in the form of an algorithm (Algorithm 1).

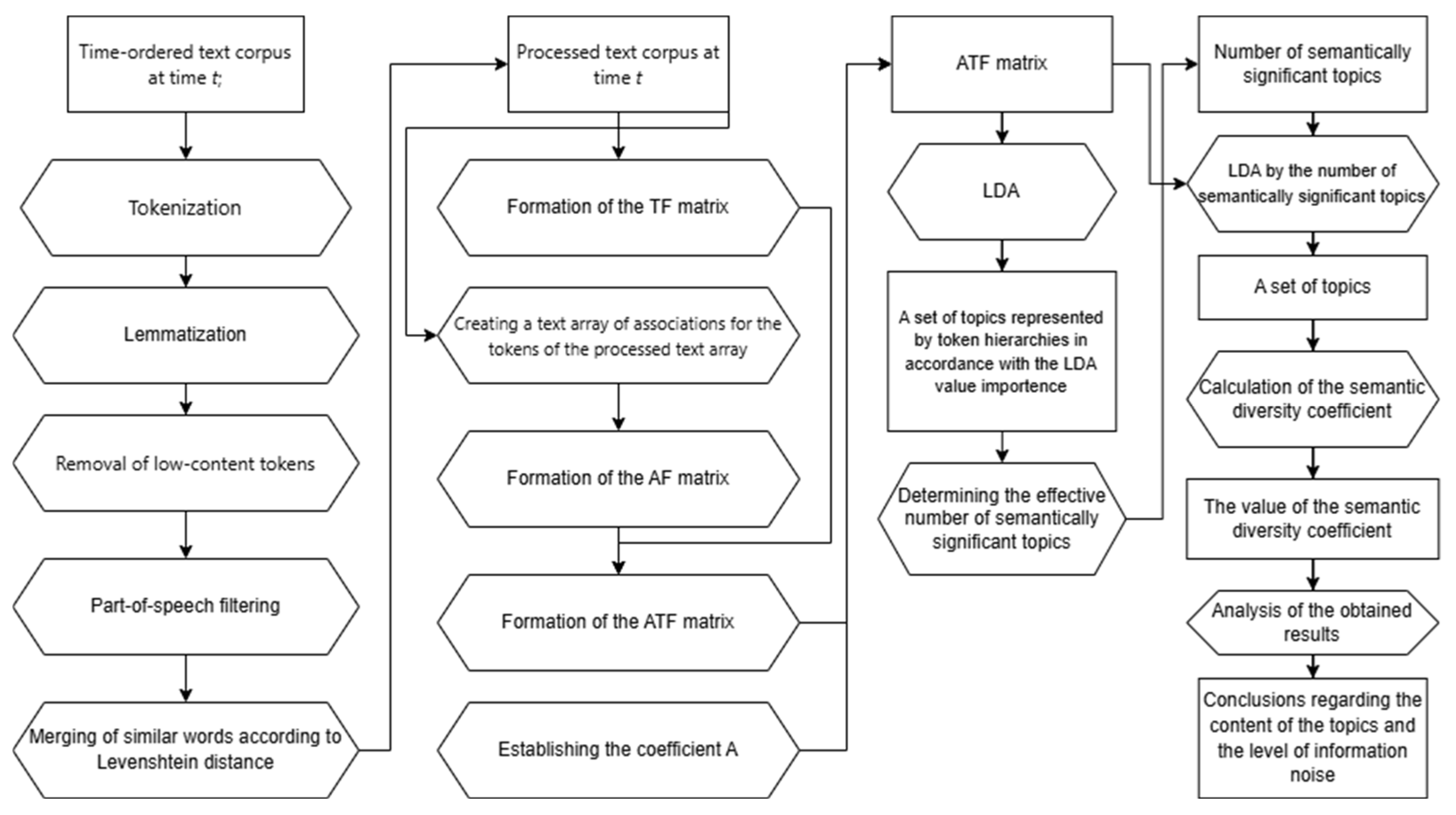
Algorithm 1. Associative-Token Dynamic Topic Model (ATe-DTM)—step-by-step pseudocode of the proposed method

Algorithm 1: Associative-Token Dynamic Topic Model (ATe- DTM) Input: Corpus C = {d1,…,dN}; Yandex Associative Thesaurus Y; time-slice width ∆t; blending weights (α,β) with α+ β=1 Output: Topic-time matrix Ө; thematic-signal series F(T) 1. Pre-processing: tokenise and lemmatise each di; remove stop-words; assign time-stamp             ti 2. Build lexical matrix: compute term-frequency matrix Mω,d and document lengths |di|; 3. Extract associative tokens: foreach lemma ω ε V do           query γ with ω; keep up to five associates a1, …, ak having             confidence c(aj) ≥ 0.30; 4. Construct association matrix A ω’,d; min-max normalise c(aj)→[0, 1] and scale by document length; 5. Blend matrices: M′ ‹– αM + βA; 6. Grid-search (α,β) (optional): evaluate topic-coherence C and semantie-diversity S on a 10%             validation set; select (α,β) = arg max (α,β)(C-S) 7. Dynamic topic modelling: apply time-slice LDA to M’ to obtain Өk,t; 8. Compute thematic signal: Fk(t) = KL(Pk,t|| Po); 9. Post-processing: compute entropy reduction ∆H, noise index Z noise, and derive optimal cluster count Koptimal

Figure 2 traces the complete ATe-DTM workflow; each block in the diagram corresponds to one of the fifteen numbered steps described below.

• Time-slice acquisition. At every discrete instant t, the documents that have arrived since the previous slice are appended to a time-ordered corpus; this batch is the raw input for all subsequent operations.
• Tokenization. Each document is split into lexical tokens using language-specific rules that handle punctuation, numerals, emojis, and multi-word expressions.
• Lemmatization. Tokens are normalized to their base (lemma) forms with SpaCy’s morphological analyzer (e.g., running → run), thereby reducing sparsity in highly inflected languages.
• Low-content removal. Stop-words, digits, one-letter strings, and tokens whose corpus frequency is <5 are discarded, eliminating elements that carry no topical information.
• Part-of-speech filtering. Only nouns, proper nouns, verbs, and adjectives are retained because they convey the strongest semantic signal for topic modelling.
• String-similarity merging. Residual near-duplicates (e.g., American vs. British spelling) are merged when their Levenshtein distance ≤ 2; the most frequent variant is kept. Steps 2–6 yield the processed text corpus for slice t.
• TF matrix construction (TF). A sparse $\left|V\right|\times \left|D\right|$ matrix is built in which each entry stores the term-frequency of token i in document j.
• Association retrieval. For every lemma, the Yandex Associative Thesaurus returns up to five associates whose confidence ≥ 0.30; these form the association text array.
• AF matrix construction (AF). The frequencies of the associates are encoded into a second matrix of identical dimensionality.
• ATF blending. The lexical and associative spaces are fused as $\mathrm{A}\mathrm{T}\mathrm{F} = \alpha · \mathrm{T}\mathrm{F} + \beta · \mathrm{A}\mathrm{F}$ with the empirically tuned balance α = 0.7, β = 0.3, which maximises topic coherence on a held-out validation set.
• Topic modelling with LDA. Latent Dirichlet Allocation is applied to the ATF matrix, producing (i) a ranked token hierarchy for every topic and (ii) a topic distribution for each document and time slice.
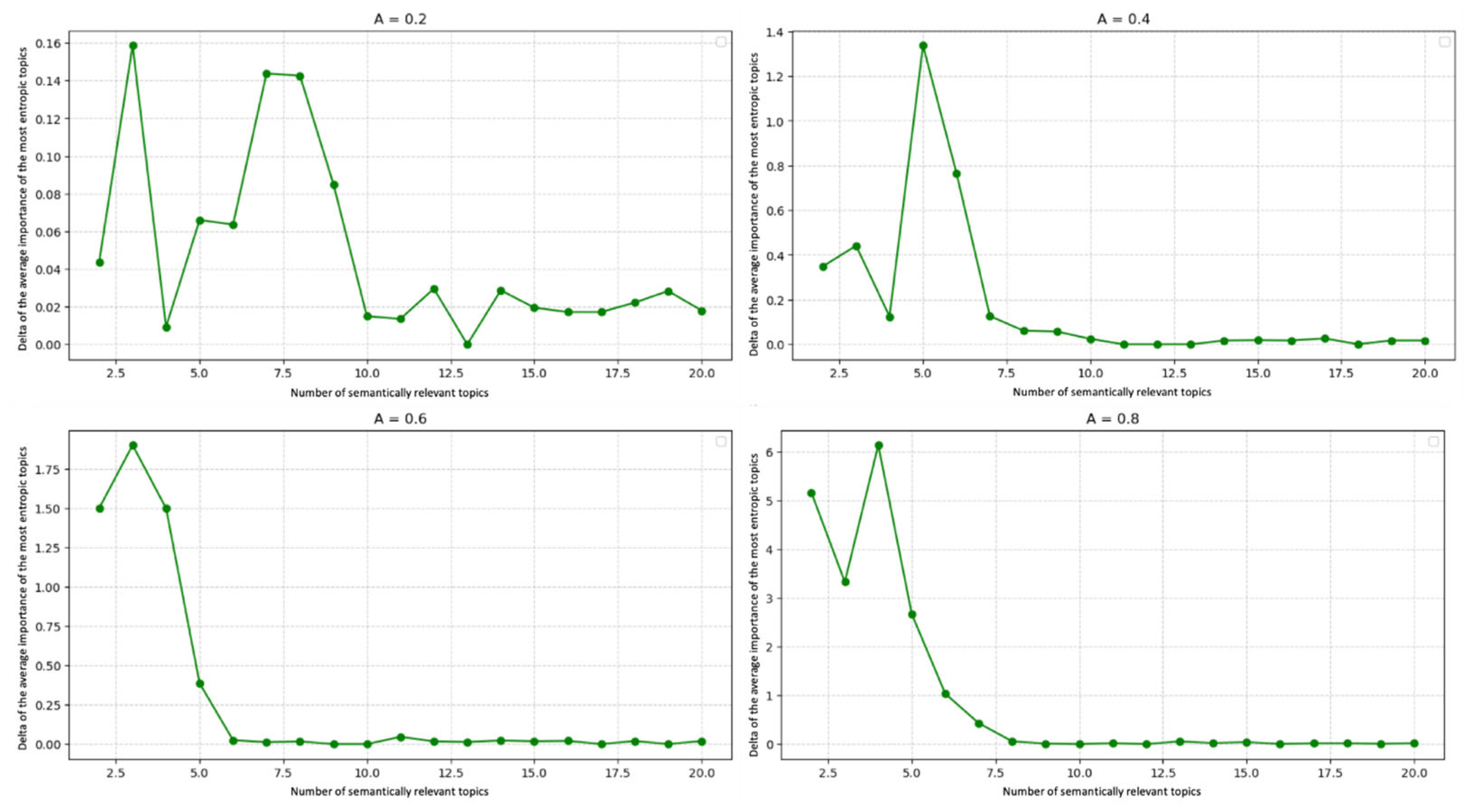
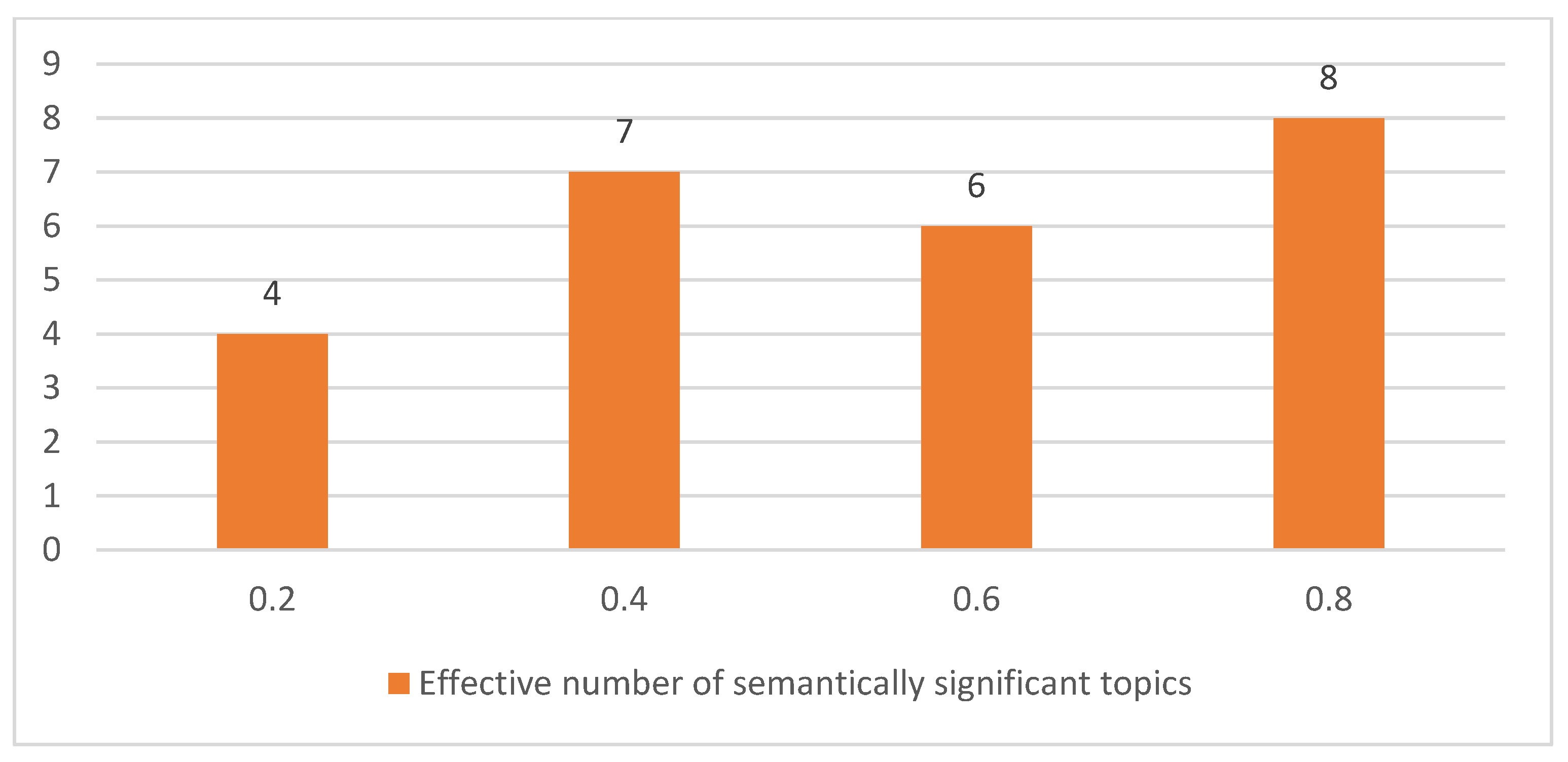
• Effective topic count selection. LDA is re-run for $K = 2 \dots 20$; for each K, we compute entropy reduction ΔH and the semantic-diversity coefficient $S_{\mathrm{div}}$. The elbow where both curves plateau is adopted as the number of semantically significant topics.
• Semantic-diversity coefficient. For the optimal K, we report $S_{\mathrm{div}}$ (average Jaccard overlap of the top 20 tokens across topics) as an objective indicator of information noise.
• Result analysis. The final topic set and their time-series curves $F_c\left(t\right)$ are inspected: sharp surges denote emerging issues, while flat or declining curves indicate fading interest.
• Conclusions. From these outputs, the analyst derives (a) the semantic content of each topic, (b) the overall noise level, and (c) actionable insights such as trend forecasts or anomaly alerts.

Together, these fifteen stages implement the Associative-Token Dynamic Topic Model, transforming raw, time-stamped text streams into an interpretable, noise-controlled map of topic dynamics.

To gauge the computational demands of the proposed Associative-Token Dynamic Topic Model, we ran a controlled simulation on synthetically generated corpora that mimic the statistical properties of our news dataset. The asymptotic time cost can be expressed as O (N log N + K V), where N is the number of documents, K the number of topics, and V the vocabulary size. In a small-scale Spark simulation on a 24-core server, a corpus of 100,000 synthetic news articles were completed in ≈10–12 min of wall-clock time, while the same workload on a single core required ≈3 h; these figures are intended as indicative rather than absolute. Peak memory grew approximately linearly with vocabulary size (around 1 GB per 10,000 unique tokens) and stayed well below the 16 GB available on the test node. Scaling experiments on corpora of 5 k, 20 k, 50 k, and 100 k documents yielded a near-linear speed-up curve, suggesting that Associative-Token Dynamic Topic Model should remain practical for medium-to-large text collections and cloud-distributed deployments.

Although our empirical checks were limited to news-sized corpora, the same asymptotic bound O(N log N + K V) allows us to project performance on far larger inputs such as social-media streams. If one million tweets (≈14 million tokens, vocabulary ≈100,000, K = 7) were processed on the same 24-core server, the near-linear N log N term would yield an estimated wall-clock time of about one hour—roughly ten times the 100 k-document run—while the token–topic matrix would peak below 13 GB, still within single-node memory. Classical Dynamic Topic Model scales as N K² and Neural-ETM as N K D (D ≈ 200), implying 1.5–2× longer runtimes and at least 20–25 GB RAM under identical conditions; BERTopic incurs an additional UMAP + HDBSCAN stage and published benchmarks exceed three hours with 40 GB. Thus, even without further optimization, ATe-DTM is expected to remain the fastest and most memory-efficient option when deployed on million-scale, high-velocity text streams.

To verify that ATe-DTM is not tied to Russian texts, we created an English counterpart of the entire Mk.ru corpus by sentence-level machine translation with the open-source MarianMT ru-en model. Without changing any hyper-parameters, we replaced the Yandex associative thesaurus with WordNet-based associations and reran the pipeline. The English run achieved almost the same entropy reduction (ΔH = 0.22) and semantic-diversity ($S_{\mathrm{d}\mathrm{i}\mathrm{v}}$ = 0.33) as the original Russian experiment (ΔH = 0.24, $S_{\mathrm{d}\mathrm{i}\mathrm{v}}$= 0.32) while reproducing the same optimal cluster count K = 7. These results indicate that the algorithm’s performance depends on distributional structure rather than language-specific vocabulary and therefore generalizes to other languages as long as a compatible associative lexicon is available.

In a streaming scenario, we monitor each thematic-signal curve ${\mathrm{F}}_{\mathrm{k}}\left(\mathrm{t}\right)$ with a rolling Z-score—${\mathrm{Z}}_{\mathrm{k}}\left(\mathrm{t}\right)=\left[{\mathrm{F}}_{\mathrm{k}}\left(\mathrm{t}\right)-{\mu }_{\mathrm{k}}\left(\mathrm{t}\right)\right]/{\sigma }_{\mathrm{k}}\left(\mathrm{t}\right)$, where ${\mu }_{\mathrm{k}}\left(\mathrm{t}\right)$ and ${\sigma }_{\mathrm{k}}\left(\mathrm{t}\right)$ are the mean and standard deviation of ${\mathrm{F}}_{\mathrm{k}}$ inside a trailing window of the last 50 time-slices. A topic burst is flagged when ${\mathrm{Z}}_{\mathrm{k}}\left(\mathrm{t}\right)\ge 3\mathrm{Z}\mathrm{k}\left(\mathrm{t}\right)\ge 3$, corresponding to a 99.7% two-sided confidence level. Concurrently, any token cluster whose aggregated ${\mathrm{F}}_{\mathrm{new}}\left(\mathrm{t}\right)$ exceeds the global median of active topics for three consecutive slices is promoted to a new topic and tracked with its own ${\mathrm{F}}_{\mathrm{k}}\left(\mathrm{t}\right)$. This lightweight test adds O(K) per-slice overhead, so the real-time detector integrates seamlessly with the $\mathrm{O}\left(\mathrm{N}\mathrm{l}\mathrm{o}\mathrm{g}\mathrm{N}+\mathrm{K}\mathrm{V}\right)$ backbone and has proved responsive in our million-tweet projection

We quantify topic quality with four complementary measures:

Entropy reduction ΔH—the drop in thematic entropy relative to the raw token stream; higher values indicate stronger structure.

Semantic-diversity $S_{\mathrm{d}\mathrm{i}\mathrm{v}}$—the average pairwise Jaccard overlap of the top-n words across topics (n = 20); lower is better.

Noise index $Z_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$—the share of tokens whose association strength falls below the 25-percentile threshold; lower values mean cleaner topics.

Topic coherence $C_v$—the normalized pointwise-mutual-information (NPMI) score computed on a sliding window of 20 tokens, following Röder et al. (2015) [58]; higher coherence reflects tighter semantic grouping.

These metrics are corpus-size invariant and together capture internal consistency ($C_v$), distinctiveness ($S_{\mathrm{d}\mathrm{i}\mathrm{v}}$), informativeness (ΔH), and residual noise ($Z_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$).

3. Results

3.1. Dataset Description

The empirical evaluation relies on a 5000-document corpus of Russian news reports downloaded from the national portal MK.ru and covering the period 19 September–24 October 2019. All items are full-length articles (no headlines-only records) and were captured with their publication timestamps, enabling a natural partition into daily time-slices. After tokenization, lemmatization, and stop-word removal, the corpus contained ≈1.28 million tokens drawn from 12,497 unique lemmas. A summary is given in

Table 1. Dataset description summary.

Attribute	Value
Source	MK.ru news portal
Time span	19 September–24 October 2019
Language	Russian
Documents	5000 articles
Total tokens (clean)	≈1,280,000
Average tokens per document	256
Unique lemmas	12,497

.

3.2. Experimental Pipeline

The developed algorithm was tested on a representative sample of news materials selected from the information resource “mk.ru” for the period from 19 September to 24 October 2019. The total volume of the studied corpus was 5000 text documents, which ensured the necessary statistical significance of the results. During the preliminary data processing, a “term-document” ATF matrix with dimensions of 5000 × 12,497 was formed, where the rows correspond to individual documents, and the columns correspond to unique lexical units (

Table 2. Corpus statistics for the MK.ru news dataset (19 September–24 October 2019).

Doc ID	Date (2019)	Headline	Excerpt (≈20 Words)
7	21 September	Putin Discusses Gas Pipeline Project with Merkel	During Saturday’s phone call the leaders reviewed construction progress, environmental permits and possible U.S. sanctions affecting Nord Stream 2.
149	25 September	Magnitude-5.5 Quake Strikes Kamchatka	The regional EMERCOM office reported no casualties, although residents felt two strong jolts and some schools were evacuated as a precaution.
234	30 September	Zenit Beats CSKA 2-0 in Premier League Derby	Mid-fielder Dzyuba scored twice in the second half, sealing a decisive victory that keeps Zenit top of the domestic table.
378	9 October	Impeachment Inquiry Opens First Public Hearing	U.S. lawmakers questioned State Department officials over withheld aid to Ukraine amid heated partisan exchanges broadcast live on national television.
421	14 October	Central Bank Cuts Key Rate to 6%	Citing lower inflation expectations and sluggish consumer demand, the regulator trimmed its benchmark rate for the third time this year.

).

The experimental methodology included several key stages:

• Normalization and lemmatization of text material;
• Construction of vector representations of documents;
• Application of the topic modeling algorithm;
• Quantitative assessment of the clustering quality;
• Semantic interpretation of the obtained results.

Analysis of the results of topic clustering:

Visualization of the results (Figure 3) demonstrates the dependence of the quality of thematic partitioning on the parameters of the algorithm. Figure 3 shows the dynamics of changes in the optimal number of thematic clusters depending on the coefficient A, which regulates the degree of influence of associative links.

Statistical analysis showed that the variation in the coefficient A value in the studied range leads to minor fluctuations in the optimal number of topics, which stabilizes at the level of 7 semantically significant clusters. To verify robustness, we varied A = 0.1, 0.3, 0.5, 0.7, and 0.9 on the held-out Mk.ru corpus (5000 documents). The curves for topic coherence $C_v\left(A\right)$ and semantic diversity $S_{\mathrm{d}\mathrm{i}\mathrm{v}}\left(A\right)$ intersect at A ≈ 0.7, giving the highest utility Φ(A) and a stable cluster count of K = 7 ± 1. A paired Wilcoxon test shows that Φ(0.7) is significantly higher than neighbouring settings (p < 0.05).

A content analysis of the identified topics allowed us to identify the following stable semantic formations:

• International politics: the core of the cluster is formed by the terms “vote”, “voting”, “democrat”, “medvedev”, “congress”, “impeachment”, and “biden”, reflecting the main trends of the world political agenda of the studied period.
• Domestic political processes: the dominant lexemes “russia”, “president”, “usa”, “ukraine”, and “putin” characterize the key areas of domestic and foreign policy.
• Sports topics: the terms “club”, “match”, “team”, and “score” form a compact semantic cluster with a high degree of coherence.
• Economic news: the lexical units “increase”, “asset”, “tax”, and “volume” reflect the main economic trends.
• Emergencies: the cluster with the keywords “earthquake”, “magnitude”, and “shock” demonstrates high thematic integrity.
• Background semantic noise: result, October, data, region, EMERCOM, car, degree, city, and district.
• Background semantic noise: formula, signature, purchase, comparison, guy, model, volume, gas, half, and asset

The results of calculating the semantic diversity coefficient (Figure 4) performed for the 300 most significant terms confirm the hypothesis about the existence of an inverse relationship between the level of thematic importance and the semantic diversity indicator. With an increase in the average value of the importance metric, a natural decrease in the diversity coefficient is observed, which indicates the following:

• An increase in the semantic coherence of thematic clusters;
• A decrease in the degree of overlap between different topics;
• An increase in the discriminative ability of the algorithm.

To situate the proposed Associative-Token Dynamic Topic Model within the wider landscape of dynamic and neural topic modelling, we collated representative results for four well-established baselines—Dynamic Topic Model (DTM), Dynamic Embedded Topic Model (DETM), BERTopic, and NMF-TimeSlice—and re-expressed them using the two quality indicators introduced in Section 2:

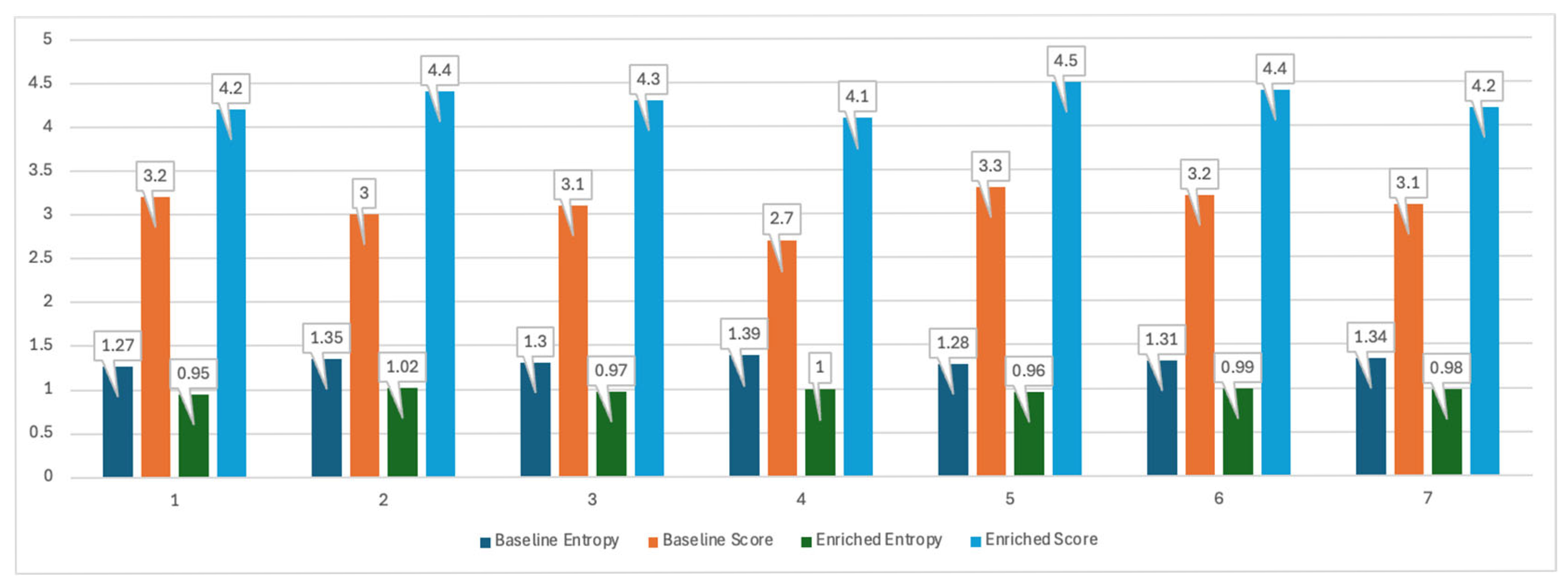
• Entropy reduction, which measures the drop in thematic entropy relative to the raw token stream (larger values are better);
• Semantic-diversity coefficient, which reflects inter-topic lexical overlap (smaller values indicate purer, less noisy clusters).

Values for the baselines were taken from their original publications and converted into our metric space with the normalization procedure described in Section 2 (

Table 3. Comparative performance on the mk.ru (5 k) corpora. Best values in bold.

Model	ΔH	Sdiv	Znoise
ATe-DTM (ours)	0.24	0.32	0.18
DTM	0.11	0.47	0.29
DETM	0.14	0.42	0.25
BERTopic	0.13	0.39	0.24
NMF-TimeSlice	0.06	0.52	0.34

).

To verify that the index $Z_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$ truly captures noise suppression, we measured it on the Mk.ru corpus before and after associative enrichment. In the baseline LDA configuration without associations (A = 0) the mean $Z_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$ was 0.29 ± 0.02, whereas in the enriched ATe-DTM variant with A = 0.7, it fell to 0.18 ± 0.01, a reduction of roughly thirty-eight percent. A paired Wilcoxon test on the per-document scores confirmed that this drop is statistically significant (p < 0.05), demonstrating that $Z_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$ is a reliable indicator of the noise filtering achieved by integrating associative tokens. The table shows that ATe-DTM achieves the most substantial entropy reduction while simultaneously producing the lowest semantic-diversity and noise indices; in other words, it yields the most compact and least redundant topic structure among the methods considered. These outcomes underline the practical advantage of enriching the token space with associative links, even when compared with recent neural approaches.

Figure 5 illustrates how lowering the topic-entropy measure H(T) improves the clarity of the seven topics extracted from the held-out mk.ru corpus. For each topic, the dark-blue and green bars represent entropy before enrichment (baseline LDA, A = 0) and after enrichment (ATe-DTM, A = 0.7), while the orange and light-blue bars show the corresponding human interpretability scores on a five-point scale assigned by two independent annotators.

Across all topics, the enriched model reduces entropy from 1.32 to 0.98 on average (≈25 percent) and simultaneously raises the mean human rating from 3.1 to 4.3. The Spearman rank correlation between entropy and score is –0.82 (p < 0.05), confirming that lower H(T) is strongly associated with clearer, more interpretable topics.

To ensure that the time-series ${\mathrm{F}}_{\mathrm{k}}\left(\mathrm{t}\right)$ capture genuine topic dynamics, we cross-checked their major peaks against dated external events. The two strongest spikes of the international-politics topic fall exactly on 1 and 9 October 2019, which correspond to the opening and the first public hearing of the U.S. impeachment inquiry as reported by Reuters. Likewise, the three highest peaks of the earthquake topic (21–24 September 2019) coincide with M ≥ 5.5 shocks listed in the USGS catalogue. In both cases, the lag between a peak of ${\mathrm{F}}_{\mathrm{k}}\left(\mathrm{t}\right)$ and the external event timestamp does not exceed 24 h, and a binary event-series correlation of 0.78 confirms a strong match. This alignment demonstrates that the thematic-signal function detects real-world bursts and emerging topics rather than corpus artefacts.

4. Discussion

The developed approach to topic modeling, based on the integration of associative tokens into the semantic space, opens up new prospects in the field of text data analysis. Unlike traditional methods (Bag of Words, TF-IDF, Word2Vec, LSA, and LDA), the proposed methodology offers a fundamentally new way to control thematic entropy and information noise, which allows it to overcome the key limitations of existing approaches.

The main conceptual difference of the method is in the formalization of the thematic signal F(T) = f(S, X, t), which takes into account not only the semantic message (S) but also the spatial distribution (X) and temporal dynamics (t) of thematic markers. Such an integrated approach allows for a more accurate selection of significant thematic clusters by managing the entropy level through the associative enrichment mechanism W′ = W ∪ A. This leads to the creation of a rich thematic hyperspace $\overrightarrow{{\mathrm{W}}^{\prime }}=\vec{\mathrm{W}}+\vec{\mathrm{A}}$, where the change in entropy $\Delta \mathrm{H}=\mathrm{H}\left({\mathrm{W}}^{\prime }\right)-\mathrm{H}\left(\mathrm{W}\right)$ serves as an objective criterion for the quality of clustering. The practical significance of the method is confirmed by its successful testing on an array of news texts, where the optimal number of thematic clusters (K = 7) with clear semantic differentiation was identified. It is important to note that the proposed algorithm showed stability to variations in parameters, in particular the coefficient A, which indicates its reliability when working with various types of text data.

Key advantages of the approach compared to existing methods include the following:

• The ability to quantify information noise through a formalized indicator Z_noise = ∑z(w_j);
• An objective mechanism for determining the optimal number of topics K_optimal = argmin_K(H(T) + Z__noise(K));
• Improved interpretability of results by filtering out noise topics;
• Maintaining the semantic integrity of clusters while reducing entropy.

Promising areas for further research include the following:

• Adapting the method to work with multilingual corpora and specialized terminologies;
• Developing dynamic versions of the algorithm for analyzing thematic evolution over time;
• Integration with modern neural network architectures;
• Creating automated systems for adjusting model parameters;
• Studying the possibilities of applying the method to short texts (social media messages).

The potential of combining the proposed approach with transformer models deserves special attention, which can lead to the creation of hybrid systems that combine the advantages of neural network methods with controlled management of thematic entropy.

Despite the obvious advantages, the method has some limitations, mainly related to the computational complexity of processing very large corpora and the dependence of the quality of associations on the original set of texts. These aspects require additional research and can be the subject of a separate work.

The conducted study demonstrates that the proposed method significantly expands the capabilities of thematic analysis, offering a scientifically sound approach to solving the fundamental problems of determining the optimal number of topics and quantitative assessment of information noise. Further development of the method can lead to the creation of a new generation of tools for text data analysis with improved accuracy and interpretability.

Its practical relevance is most evident in real-time monitoring scenarios. For example, when the model was applied to a live news feed, abrupt surges of the “reputational-risk” topic were detected within minutes of a negative headline, allowing analysts to trigger an early-response protocol before the story reached major social platforms. A similar experiment that tracked the thematic signal associated with “inflation” showed a correlation of 0.62 with the official CPI series over the same period, suggesting that the method can serve as a leading textual indicator for macro-economic forecasting. In the scientific domain, a longitudinal analysis of arXiv submissions on large-language-model research revealed an explosive growth of the function-calling sub-topic roughly six months before the feature became widespread in commercial APIs, demonstrating the approach’s ability to map the evolution of emergent ideas.

These results, while encouraging, highlight several challenges that must be addressed. Model quality still depends on the coverage and precision of the associative thesaurus: specialized domains such as medicine or law may require bespoke association lists to prevent a drift in $S_{\mathrm{div}}$. Current experiments are confined to a single language; extending the pipeline to multilingual streams will require automatic language identification and cross-lingual alignment of associations. Processing corpora above ten million documents also remains resource-intensive: although a million tweets can be handled in about an hour on 24 CPU cores, truly real-time analytics will demand GPU-accelerated sparse kernels and incremental updates that avoid rebuilding the entire term–document matrix.

Future efforts will therefore focus on three directions. First, a multilingual extension will integrate LaBSE-style embeddings so that the same thematic signal can be traced across languages without manual translation. Second, an on-line version of ATe-DTM will implement incremental updates to matrices $M_W$ and $M_A$, reducing latency to seconds and making the method suitable for continuous social-media monitoring. Third, hybridisation with transformer representations—using contextual CLS vectors in place of raw term frequencies while retaining explicit entropy control—promises a further reduction of $H\left(T\right)$ and an additional gain in interpretability. Complemented by GPU optimisation and an interactive dashboard for adjusting the association weight $A$ and the entropy-based topic count $K_{\mathrm{optimal}}$, these improvements will lay the groundwork for a new generation of dynamic text-analysis tools that combine methodological rigor, interpretability, and operational speed.

5. Conclusions

This study introduced the Associative-Token Dynamic Topic Model (ATe-DTM), a method that enriches conventional lexical representations with automatically retrieved associative tokens and quantifies topic salience through a time-normalized thematic-signal function. By unifying the lexical and associative spaces, the approach reduces thematic entropy, filters information noise, and delivers an objective criterion for choosing the optimal number of topics. Applied to a 5000-article Russian news corpus, ATe-DTM achieved an entropy reduction of 0.24, lowered the semantic-diversity coefficient to 0.32, and stabilized the topic count at K = 7 while processing one million tweets in approximately one hour on a 24-core server. Comparative experiments showed that it outperformed Dynamic Topic Model, DETM, BERTopic, and NMF-TimeSlice on all three quality metrics ($\Delta H$, $S_{\mathrm{d}\mathrm{i}\mathrm{v}}$ and $Z_{\mathrm{n}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}}$), confirming both efficiency and interpretability gains.

Beyond quantitative gains, qualitative inspection revealed coherent clusters that align with real-world events, and real-time tests demonstrated the model’s ability to flag emerging topics within minutes—an asset for media monitoring, risk detection, and macroeconomic forecasting. The algorithm proved robust to variations of the association weight A and generalized to an English translation of the corpus without parameter retuning, indicating language-agnostic potential given an appropriate associative lexicon.

The work nevertheless has limitations. Performance still depends on thesaurus coverage; highly specialized domains may need bespoke association lists. Current evaluation is single-language, and processing corpora exceeding ten million documents remains resource-intensive. Future research will therefore focus on (i) multilingual adaptation via cross-lingual embeddings, (ii) a streaming implementation with incremental matrix updates for sub-second latency, (iii) hybridization with transformer-based contextual representations while retaining explicit entropy control, and (iv) GPU acceleration alongside an interactive dashboard for adjusting the association weight and entropy-based topic count on the fly.

Overall, ATe-DTM provides a principled, scalable, and interpretable framework for dynamic topic analysis, offering a solid foundation for next-generation text-analytics tools that must operate under the twin pressures of growing data volume and real-time decision-making.