Addressing Credit Card Fraud Detection Challenges with Adversarial Autoencoders

Abstract

The surge in credit fraud incidents poses a critical threat to financial systems, driving the need for robust and adaptive fraud detection solutions. While various predictive models have been developed, existing approaches often struggle with two persistent challenges: extreme class imbalance and delays in detecting fraudulent activity. In this study, we propose an unsupervised Adversarial Autoencoder (AAE) framework designed to tackle these challenges simultaneously. The results highlight the potential of our approach as a scalable, interpretable, and adaptive solution for real-world credit fraud detection systems.

1. Introduction

Credit card fraud is a growing global concern that poses serious threats to financial institutions and consumers. With the expansion of e-commerce and digital transactions, fraudsters are finding increasingly sophisticated ways to exploit vulnerabilities in financial systems. According to the Federal Trade Commission (FTC), over 4.8 million cases of identity theft and credit card fraud were reported in 2020, resulting in losses exceeding $4.5 billion, a 45% increase over last year [1]. Credit card fraud can be broadly categorized into three types: bankruptcy fraud, application fraud, and behavioral fraud [2,3,4] Bankruptcy fraud occurs when individuals make purchases knowing they cannot repay them. Although difficult to detect, it can be mitigated by examining historical banking behavior. Application fraud involves the use of falsified or stolen personal information to open new credit accounts. This type often involves identity theft or synthetic identities [5], and banks typically rely on cross-matching and risk scoring techniques to flag such attempts. Behavioral fraud is the most prevalent and damaging form. It includes unauthorized use of legitimate card information (e.g., in online purchases), counterfeit cards, and stolen physical cards [6,7]. This type is particularly difficult to detect in real time due to its dynamic and subtle patterns [8].

As fraud techniques evolve, traditional rule-based systems and supervised models struggle to keep up, particularly in the face of highly imbalanced datasets, where fraudulent transactions represent a tiny fraction of total transactions [9]. Moreover, delays in labeling data limit the real-time applicability of supervised learning models [4,10]. These challenges highlight the need for robust, adaptive, and interpretable unsupervised learning approaches [11].

In this study, we propose a novel approach to fraud detection using an unsupervised Adversarial Autoencoder (AAE) to tackle both the class imbalance problem and delayed label availability. Our model is evaluated on a publicly available European credit card fraud dataset and demonstrates superior performance over other unsupervised methods [12].

In addition, we integrate Shapley values derived from a tree-based model to enhance the interpretability of our approach. Interpretability is critical for financial institutions and regulators, who require transparent models to understand and justify automated decisions [13].

Figure 1 illustrates the pipeline of our proposed framework, including the AAE-based detection process and the explainability module. Note that the Adversarial Autoencoder Model predictions are explained by the computed Shapley Values, hence the red arrows are connecting the Prediction to the computed Shapley Value.

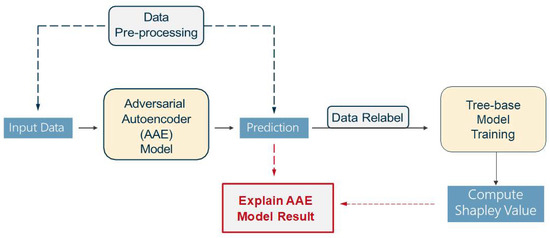
Figure 1. Paper Workflow.

The remainder of the paper is organized as follows: Section 2 reviews related work in fraud detection and unsupervised learning, Section 3 details the AAE architecture and its relevance to our problem, Section 4 presents experimental results and a feature importance analysis using Shapley values, and Section 5 concludes with a summary and directions for future work.

2. Related Work

Many studies have employed machine learning models to improve the prediction results and avoid potential risks for the behavior fraud detection problem. Classic categories include supervised and unsupervised learning models. Niu et al. [14] compared different models and concluded that supervised models would perform slightly better than unsupervised ones.

Considering supervised models requires additional label information and preprocessing procedures like outliers remove. Moreover, class balancing and unsupervised models seem to be more effective.

In supervised learning, different classifiers obtain a more accurate classification, such as Decision Tree [15], Logistic Regression [16], Support Vector Machine (SVM) [17], and Neural Networks [6]. Unsupervised learning models do not rely on labels, thus allowing for real-time detection. Since the credit card fraud data is highly imbalanced, most unsupervised models learn the structure and feature from the majority, i.e., everyday transactions, and transform the problem into an outlier detection, including One-Class SVM (OCSVM) [18], Isolation Forest [19], and Autoencoder [20]. Unlike other models, Generative Adversarial Networks (GANs) learn the distribution of normal data only, the generator learns to generate normal-like samples, while the discriminator learns to detect deviations from this distribution [21]; since anomalies are not needed during training, GANs are naturally suited for extreme imbalance.

Nowadays, Autoencoder and its variants have been widely applied and have exhibited certain advantages in fraud scenarios including accounting [22,23], telecommunication [24], transport operators [25], and credit card fraud, including Sparse Autoencoders (SAE), Denoising Autoencoder (DAE), Variational Autoencoder (VAE), and Adversarial Autoencoder (AAE). The SAE model introduces a regularized term to filter out redundant information and boost the model generalization. According to the study by Chen et al. [26], using the SAE to extract feature representations and training a discriminator to detect anomaly would outperform other models like Support Vector Data Description (SVDD) and One-class Gaussian Process (GP). The Denoising Autoencoder (DAE) enhances the model robustness and adds random noise to the traditional Autoencoder input layer. Zou et al. [27] found that DAE with oversampling increases the classification accuracy of the minority class with an appropriate threshold. VAE and AAE combine the idea of generative models with Autoencoder to learn a better representation of data, which proved to perform decently in detecting credit card fraud [23,28].

Generally, there are two major applications of Autoencoder in credit fraud detection. First, Autoencoder is employed as a dimensionality reduction method to extract key information and create important features [27,28,29,30,31,32]. It’s just like Principal Component Analysis (PCA) but can extract more nonlinear information. Based on the extracted features, other classifiers can predict whether the transaction is fraud or not. Furthermore, Misra et al. [30] found that the classifier Multilayer Perceptron (MLP) would perform better than the K- nearest Neighbors (KNN) or Logistic Regression model. The second aspect is one-class classification. An important issue in credit fraud detection is the unlabeled or imbalanced data. To solve this problem, many studies proposed Autoencoder-related methods to learn the patterns of normal transactions directly and detect anomalies by the reconstruction error [20,26,33,34].

Although the Autoencoder has achieved outstanding performance in recent years, it is less interpretable than other machine learning models such as Extreme Gradient Boosting (XGBoost). The Shapley value originated from cooperative game theory to evaluate each player’s average expected marginal contribution [35]. Machine learning provides a way to explain the prediction result by assuming each feature as a player. Specifically, when people focus more on those anomalies with high prediction probability, the Shapley value fulfills the role of interpreting anomaly detection [36,37]. The concept explains various nonlinear detection models, including the Autoencoder [38,39,40]. Antwarg et al. proposed the Shapley Additive Explanation (SHAP) [38] and kernel Shapley Additive Explanation (kernel SHAP) [39] to explore practical explanations.

3. Methods

3.1. Autoencoder

Autoencoder [41] is a model which uses neural network to learn the latent representation of the input data. As shown in Figure 2, it is similar to PCA and can be regarded as a nonlinear counterpart of PCA-based compression. There are two parts: an encoder which projects the original input into a code in the latent space and a decoder which maps the code back to the original space. The encoding function f and decoding function g are neural networks that enhance the model’s flexibility and capacity for nonlinear representation. Since redundant information in high-dimensional data can cause interference, the Autoencoder aims to identify the most relevant part of data by reconstructing the input approximately. Therefore, it trains the model by minimizing the reconstruction error

$$L\left(f,g\right)= \underset{f,g}{\mathrm{arg\; min}}{\Vert X-g\left(f\right(X\left)\right)\Vert }^2$$

(1)

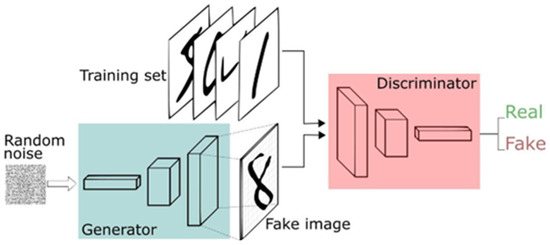
Figure 2. GAN Architecture.

The latent variable Z = f (X) is the representation that contains the most important information. The Autoencoder is an excellent method to conduct dimensionality reduction. As seen in Figure 3 below, just as the PCA performs dimensionality reduction while preserving the most important information, the AE model similarly retains the key information through its decoder

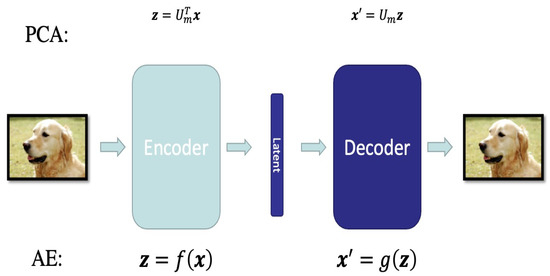
Figure 3. AE versus PCA.

3.2. Generative Adversarial Network (GAN)

Since GAN was proposed in 2014 [13], it has been widely used to complete generative tasks. The basic idea of GAN is to train a generator to generate the new data and pass the result to a discriminator to evaluate whether it is fake (generated) or actual. According to the feedback from the discriminator, the generator would adjust its mapping function from the latent space to the target space to learn more about the distribution of actual data. The training continues in an adversarial way: the generator tries to fool the discriminator while the discriminator aims to determine the data authenticity. Therefore, the training target is as follows:

$$\underset{G}{\min }\underset{D}{\max }{\mathbb{E}}_{x~p_{data\left(x\right)}}\log D\left(x\right)+{\mathbb{E}}_{z~p_{z\left(z\right)}}\left[1-\log D\left(G\left(z\right)\right)\right]$$

(2)

Which exhibits the concept of adversarial generation. D(x) is the discriminator’s estimate of the probability of whether x is real, and G(z) is the generator’s output when given noise z. As a result, the GAN would converge and reach the Nash equilibrium, which indicates that the model cannot reduce the loss or achieve a better result.

3.3. Adversarial Autoencoder

The AAE model combines the Autoencoder and GAN model, which includes two phases [42]. Figure 4 below shows the architecture of the Adversarial Autoencoder where, first is the reconstruction phase which uses the encoder to learn the latent code vector Z and uses the decoder to reconstruct X. The unique design is that the encoder is also the generator in the second phase. The adversarial regulation phase aims to train the encoder to learn a posterior distribution q(z) similar to p(z) that fools the discriminator network. The loss function is simply the addition of the reconstruction loss and the adversarial training loss.

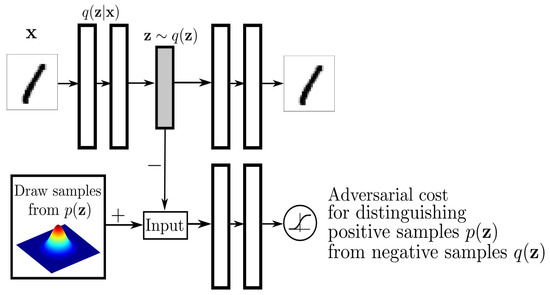
Figure 4. AAE Architecture.

As Marco et al. [23] suggested, we set the prior latent space distributions as a mixture of Gaussians with different centers and unit standard deviation N (µ, I) where µ = u1, …, u5 that divide the space equally. The GAN model would force the generator(encoder) to map the original data into a similar distribution with the mixed Gaussians. To overcome the imbalance per class, the AAE has separate class conditional priors, where we assign one Gaussian per class to encourage balanced representation. This helps to encode the minority class into a distinct well-structured region of the latent space by sampling from the minority class and then decoding into synthetic minority class examples and using these synthetic minority class examples to rebalance the training set for downstream tasks.

Due to internal structural differences, anomalies are detected as their distribution in the hidden space is different from that of most normal points. In addition, since the AAE model involves an Auto-encoder, an abnormally high reconstruction, the error also indicates potential fraud data.

3.4. Other Unsupervised Models

Other unsupervised models for fraud detection include the Isolation Forest [19] and One-Class SVM [43]. The Isolation Forest is an algorithm that uses Isolation to detect anomalies. Liu et al., proposed the concept of Isolation, which indicates how far a data point is from the rest of the data [44]. It assumes that the anomalies will divide separately when the tree splits nodes. Based on the splits of multiple trees (the forest), the anomaly score is calculated to identify the isolation points as anomalies. Its outstanding advantage lies in the linear time complexity and high parallel computing capability. However, it does not apply to particularly high-dimensional data. Since each split only involves two dimensions, many dimensions will remain unused, resulting in reduced reliability of the algorithm. In this case, the One-Class SVM is preferred.

One Class SVM [45] learns the features of the standard category and determines whether the new data belongs to this category to realize the anomaly detection. Therefore, the information of only one class is available for training on the boundary line distinguishing two classes. It works similarly to the traditional SVM but is an unsupervised model. Without the information of labels, it needs some special modeling tricks and produces various algorithms. For example, Support Vector Domain Description (SVDD) trains a minimal hypersphere to wrap all data. If the new data point falls out of the hypersphere, it will classify as anomaly data.

In a nutshell, the proposed Adversarial Autoencoder (AAE) framework integrates the reconstruction capability of autoencoders with the regularization strength of adversarial training. This design offers the following key advantages:

• It enables unsupervised fraud detection without reliance on labeled data.
• It is robust to extreme class imbalance, as it learns exclusively from the majority (normal) class.
• It can detect emerging fraud patterns, effectively addressing concept drift by identifying deviations from learned normal behavior.
• The structured latent space enhances both anomaly separation and interpretability.

4. Experiments

4.1. Dataset

The European credit fraud dataset consists of two-day transactions made by credit cards in September 2013 by European cardholders. As the statistics show, there is a total of 492 frauds out of 284,807 transactions, which indicates a highly imbalanced class. The dataset contains 28 anonymous continuous features obtained by the Principal Component Analysis (PCA) method to protect user privacy. Another two features are the timestamp and the transaction amount. The transaction amount follows a highly skewed distribution, which could potentially affect the learning dynamics of the model. To address this, we applied standardization to normalize the input features, including the transaction amount, allowing the model to learn from features on a comparable scale. To achieve faster and more stable convergence of the model, we standardize the 30 numerical features.

4.2. Model Optimization

To ensure the effectiveness of the Adversarial Autoencoder (AAE), extensive tuning was conducted on architectural depth, layer sizes, learning rates, and batch size. The final encoder–decoder architecture was selected based on its ability to minimize reconstruction loss while preserving separation in the latent space. A deeper encoder (29-256-64-16-4-2) enabled the extraction of high-level features, while a symmetrical decoder preserved the information for accurate reconstruction. The discriminator was tuned with a smaller learning rate (10⁻⁵) compared to the encoder and decoder (10⁻³) to prevent the generator from overpowering the discriminator during adversarial training. We also experimented with different batch sizes and found that a batch size of 128 balanced computational efficiency with stable convergence. These design choices collectively led to a more structured latent space and enhanced the model’s capacity to detect subtle deviations indicative of fraud.

Specifically, we generated five groups of data following a normal distribution which would divide the space equally into five parts. After adjusting the parameters, we finally selected:

• Encoder: 4 layers of 29-256-64-16-4-2,
• Decoder: 4 layers of 2-4-16-64-256-29,
• Discriminator: 4 layers of 2(hidden variable Z)-256-16-4-2-1,
• Learning rate of Encoder, Decoder and Discriminator: e⁻³, e⁻³ and e⁻⁵,
• Batch size: 128.

4.3. Results

After training the model using 1200 epochs, the loss stabilized, as shown in Figure 5. Figure 6 displays the data representation in the latent space, where the encoder found the differences in the internal structure between the fraud data and the standard normal data and successfully separated them. We calculated the distance of the latent data from the centers of 5 groups, which are expressed as

$$D\left(z^j,u^i\right)={‖z^j-u^i‖}^2,i=\mathrm{1,2},\mathrm{3,4},5$$

(3)

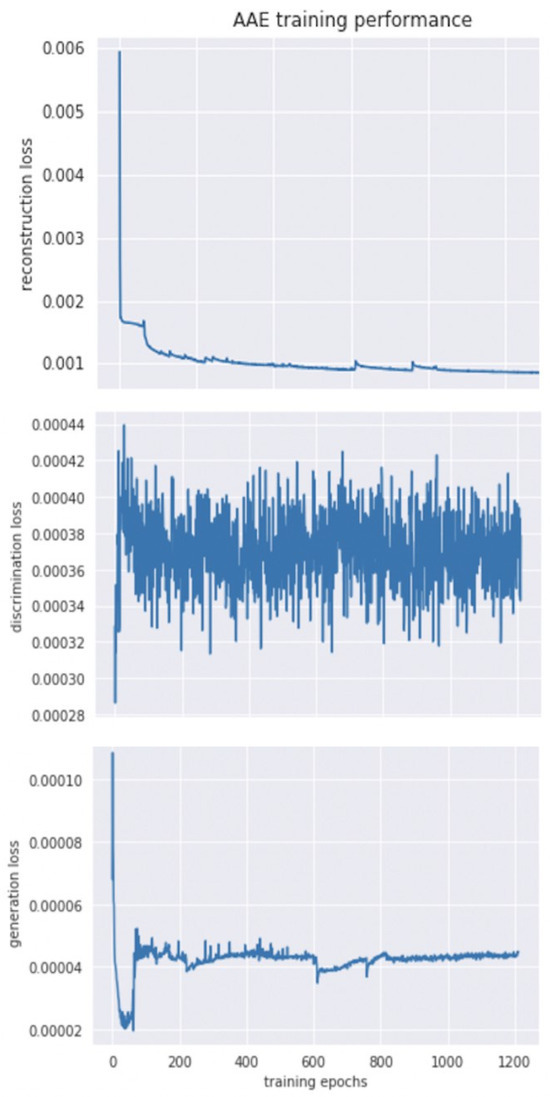
Figure 5. Loss Curves.

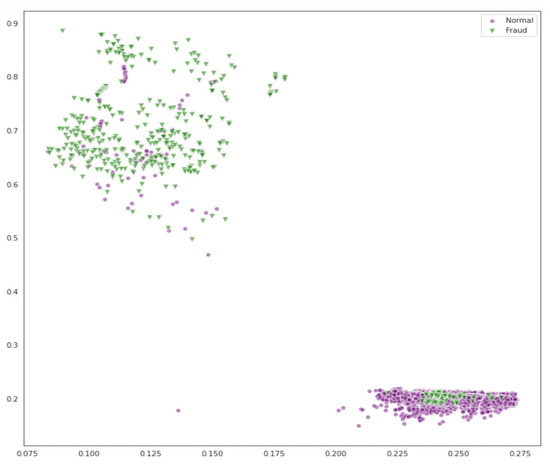
Figure 6. Representation of Latent Space.

We selected the group i with the smallest distance D(z^j, uⁱ) as the group to which z^j belongs. The group of minority points classifies the fraud data as negative samples. Since the data has a severe imbalance issue, we did not simply calculate the “Accuracy” but focused more on the Recall and F1 Score. As shown in Table 1, the model outperformed other unsupervised methods with a recall of 0.8 and an F1-Score of 0.81.

Table 1. Evaluation Metrics.

Evaluation Metrics	Methods
	Adversarial Autoencoder	Autoencoder	Isolation Forest	One Class SVM
Accuracy	0.9994	0.9878	0.9931	0.9870
Precision	0.8295	0.322	0.4695	0.1646
Recall	0.8008	0.791	0.4695	0.2439
F1 Score	0.8149	0.458	0.4695	0.1966

As the AAE model is an unsupervised neural network, it is challenging to compute the Shapley value for features directly. Therefore, we re-label the data according to the AAE prediction results and train a tree-based model to fit it. Figure 6 presents the training loss curves of the AAE model after this preprocessing step. The steady decrease and eventual stabilization of both reconstruction and adversarial loss confirm that the model has effectively learned to reconstruct normal transaction patterns while maintaining the latent space regularization. Therefore, Figure 6 validates the success of model training on the standardized, imbalanced dataset.

The performance of our AAE model was compared with other commonly used unsupervised methods: traditional Autoencoder, Isolation Forest, and One-Class SVM. As shown in Table 1, the AAE achieves the highest F1-score (0.81) and Recall (0.80), significantly outperforming the others, particularly in fraud detection sensitivity. While the standard Autoencoder relies solely on reconstruction error, it lacks the adversarial regularization that enforces structured latent representations. As a result, it shows moderate recall but poor precision. Isolation Forest and One-Class SVM, on the other hand, are sensitive to high-dimensional data and lack the deep feature extraction capacity of neural models. Their inability to model complex data distributions explains their lower recall and precision. In contrast, our AAE’s use of a Gaussian mixture prior in the latent space allows it to model multiple subpopulations within the normal class, improving anomaly separability. These results highlight the AAE’s superior adaptability, making it a more reliable choice in highly imbalanced and complex fraud detection settings.

Figure 6 above illustrates the distribution of transaction data in the latent space learned by the AAE model. Here, the encoder projects high-dimensional input into a low-dimensional representation, allowing us to observe clear separation between normal and fraudulent samples. Fraud data points cluster in more isolated regions, distinct from the denser normal data regions, which validates the AAE’s ability to learn meaningful internal representations without labeled supervision. This separation indicates that the model has effectively captured structural differences between the classes—a capability less visible in conventional Autoencoders or statistical anomaly detectors, which often produce overlapping latent distributions.

Records predicted as fraud by the AAE model are assigned a one, otherwise a zero. The Shapley value computed by the tree-based model explains how each feature drives the model to obtain the Autoencoder result. Shapley values interpretability and provides insight into how to interpret the Autoencoder prediction. In addition, tree-based SHAP is a faster implementation than kernel SHAP, which shows a significant advantage in the dataset with a large magnitude.

Alternative model options include XGBoost, Gradient Boosting Machine (GBM), and Generalized Random Forests (GRF). Take XGBoost as an example. Setting the actual label as the prediction result of the Autoencoder, the XGBoost can achieve a 0.999 AUC on the test dataset. Since the focus lies in the fraud data (anomaly), we draw a Force Plot for the 10 most important features related to the predicted ’anomaly’ in the Autoencoder and the XGBoost. Figure 7 below presents a SHAP force plot that visually highlights the top features contributing to the predicted anomalies. This plot was generated using a tree-based model (XGBoost) trained on the output labels of the AAE. The SHAP values quantify how much each feature contributes to the anomaly classification, with features like V17 and V12 playing particularly significant roles. This level of interpretability is crucial for real-world fraud detection systems, as it enables financial analysts to understand and validate why a transaction was flagged, something traditional models like One-Class SVM and Isolation Forest typically lack.

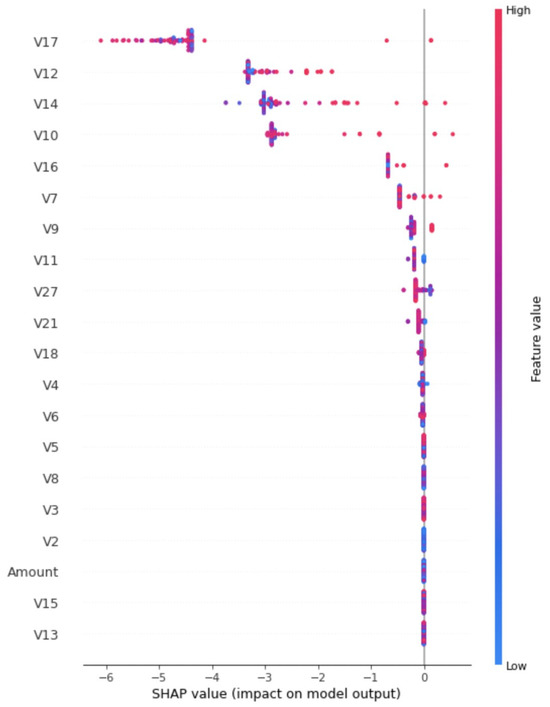
Figure 7. Force Plot of Predicted ‘Anomaly’ Points.

The horizontal coordinate represents the Shapley value of each sample, and the color indicates the magnitude of the feature value.

As illustrated, V17 and V12 are the most important features and have a negative effect. As illustrated in Figure 8 below, the points predicted as anomalies in the test set are primarily identified using features V12 and V17, highlighting their importance in the AAE model. As mentioned above, when we apply our AAE model to a real-world dataset with clearly defined variable meanings, we can use Shapley values to estimate feature importance and provide a meaningful explanation for the fraud prediction.

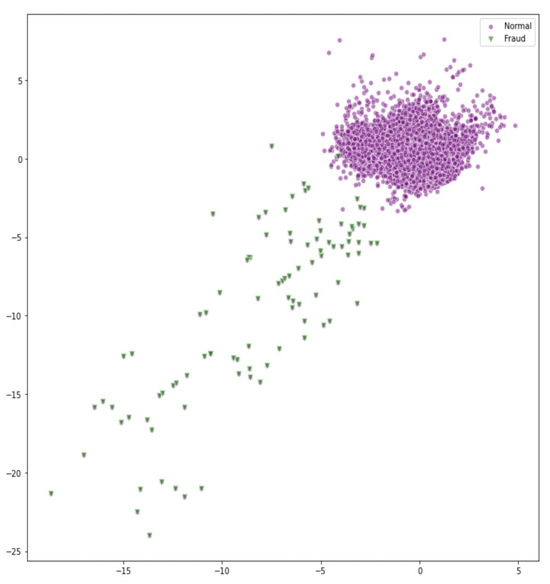
Figure 8. Test Dataset on V12 and V17 (Green: Predicted ‘Anomaly’ Points; Purple: Others).

Figure 8 further enhances interpretability by mapping the test samples based on the two most influential features identified, V12 and V17. Fraudulent transactions (shown as green points) predicted by the AAE model are visually distinguishable from the rest (purple points), supporting the SHAP analysis presented in Figure 7. This visualization confirms that these features play a significant role in anomaly detection and that the model is not arbitrarily labeling transactions. In contrast, models such as Isolation Forest and One-Class SVM lack this level of feature-specific interpretability, as they treat all dimensions uniformly, often resulting in less targeted and less explainable outcomes. Our model demonstrates superior performance compared to other state-of-the-art unsupervised methods, particularly in scenarios with limited labeled data. To enhance the transparency of the detection process, we integrate Shapley value-based explainability, enabling a deeper understanding of the model’s decision-making by identifying the most influential features contributing to fraud detection. These results demonstrate the AAE’s effectiveness in handling highly imbalanced datasets and its ability to generalize to previously unseen fraud types, affirming its robustness to concept drift and limited labels. One problem lies in that GAN training is prone to pattern collapse. Several tricks can be employed to improve the issue, but it still lacks a guarantee of convergence to the optimal point. Another problem is the poor performance of AAE on a small dataset, which may be related to the insufficient information to learn the appropriate hidden representations. We will devote more energy to solving these issues in our future work.

In comparison to other unsupervised models, the AAE offers superior interpretability and more structured latent space representation. While traditional Autoencoders also project data into latent space, they lack the structured regularization introduced by adversarial training. Likewise, models such as Isolation Forest and One-Class SVM are limited in their ability to explain predictions based feature contributions. By integrating SHAP with the AAE, we gain clearer insights for feature influence, which enhances transparency and supports more informed decision-making in fraud detection scenarios.

5. Conclusions

This research combines two unsupervised models, the Generative Adversarial Network (GAN) and Autoencoder, into the Adversarial Autoencoder (AAE) model for final fraud prediction. In this study, Generative Adversarial Networks (GANs) and Adversarial Autoencoders (AAEs) offer clear advantages in handling the key challenges of fraud detection, namely, extreme class imbalance and the lack of labeled data. GANs proved to be effective because they learned the underlying distribution of normal transactions and detected anomalies as deviations from this learned distribution, without needing labeled fraud data. The AAEs built on this by combining reconstruction-based learning with adversarial regularization, resulting in a more structured latent space that enhanced the anomaly detection. The study further improved the AAE framework by integrating Shapley value-based explanations, which added interpretability by identifying the most influential features driving the model’s predictions.

In summary, this paper highlights the following: (1) The model does not require actual labels, enabling real-time fraud detection. (2) The AAE model learns the internal distinctions between “normal” and anomalous data (fraud), which allows it to perform effectively even when trained solely on normal data. (3) The class imbalance issue has minimal impact on fraud predictions, making the model robust. (4) When new types of fraud data emerge, the AAE model continues to detect them, as it does not rely on pre-training but identifies structural differences. (5) Post-modeling analysis with the Shapley Additive Explanation (SHAP) algorithm to assess predictor importance provides valuable insights, improving the interpretability of fraud data.

Experimentally, our proposed AAE model achieved superior recall and F1 scores compared to traditional unsupervised methods like Isolation Forest and One-Class SVM. These results highlight the AAE’s technical strength as a scalable, interpretable, and adaptive solution for real-world fraud detection. Our findings highlight that the AAE’s unsupervised nature, resilience to imbalance, and capacity to detect emerging fraud patterns make it particularly well-suited for real-world fraud detection systems. The application of our AAE model to real-world datasets generated by banks or corporations will not only enhance fraud detection but also provide actionable advice for preventing fraud.