A Comparative Study of Ensemble Machine Learning and Explainable AI for Predicting Harmful Algal Blooms

Abstract

Harmful algal blooms (HABs), driven by environmental pollution, pose significant threats to water quality, public health, and aquatic ecosystems. This study enhances the prediction of HABs in Lake Erie, part of the Great Lakes system, by utilizing ensemble machine learning (ML) models coupled with explainable artificial intelligence (XAI) for interpretability. Using water quality data from 2013 to 2020, various physical, chemical, and biological parameters were analyzed to predict chlorophyll-a (Chl-a) concentrations, which are a commonly used indicator of phytoplankton biomass and a proxy for algal blooms. This study employed multiple ensemble ML models, including random forest (RF), deep forest (DF), gradient boosting (GB), and XGBoost, and compared their performance against individual models, such as support vector machine (SVM), decision tree (DT), and multi-layer perceptron (MLP). The findings revealed that the ensemble models, particularly XGBoost and deep forest (DF), achieved superior predictive accuracy, with R² values of 0.8517 and 0.8544, respectively. The application of SHapley Additive exPlanations (SHAPs) provided insights into the relative importance of the input features, identifying the particulate organic nitrogen (PON), particulate organic carbon (POC), and total phosphorus (TP) as the critical factors influencing the Chl-a concentrations. This research demonstrates the effectiveness of ensemble ML models for achieving high predictive accuracy, while the integration of XAI enhances model interpretability. The results support the development of proactive water quality management strategies and highlight the potential of advanced ML techniques for environmental monitoring.

1. Introduction

Environmental pollution has considerably elevated the amount of cyanobacterial biomass in aquatic systems, leading to degraded water quality all around the world. The increase in harmful algal blooms (HABs), especially those involving cyanobacteria, has become a major global issue. The term “bloom” denotes the rapid proliferation of blue-green algae or cyanobacteria, which are hazardous due to the toxins they produce [1]. These blooms deteriorate water quality, threaten public health, and disrupt aquatic ecosystems, and their growth is driven by nutrient pollution from agricultural runoff [2]; industrial waste; and climate changes, such as rising water temperatures [3,4]. HABs generate harmful toxins, impair waterway aesthetics, and complicate the provision of clean drinking water [5].

Grasping the underlying factors for HABs is critical for informing public and decision-makers [6], as it empowers them to make informed interventions and policy decisions based on a transparent understanding of the causes and dynamics of harmful algal blooms [7]. Communicating these insights through novel information and communication systems [8], such as virtual reality, can further enhance understanding by providing immersive and interactive experiences [9] that vividly illustrate complex data and predictive outcomes.

Lake Erie, part of the Great Lakes system, serves as a critical case study for examining both the causes and consequences of these events. The Great Lakes constitute the largest and most biodiverse freshwater reserve on Earth [10,11]. The basin encompasses both industrial facilities focused on manufacturing and areas dedicated to agriculture. Lake Erie is the shallowest and smallest lake in terms of water volume, but the fourth largest in terms of area. It is ecologically, culturally, and economically significant to the approximately 12.5 million people who live within its watershed. Each year, Lake Erie supports nearly 14,000 tons of harvested fish, over 33 million tons of transferred cargo, and over USD 1.5 million in recreational businesses [12]. However, it experiences significant challenges from nutrient overload, especially in its western basin, due to its geographical location [13]. Since 2002, the Chl-a concentration, a commonly used indicator of potential upcoming HABs, has dramatically increased annually in Lake Erie, reaching unprecedented levels in recent years [13,14]. Humans can be exposed to harmful algae through the ingestion of contaminated fish and drinking water and inhalation and dermal exposure during recreational events, such as swimming and boating [15,16]. Given the potential threats HABs pose to humans, the economy, and the environment, the accurate prediction of HAB occurrences is essential. Identifying the key factors influencing these blooms is crucial for implementing preventive measures to mitigate potential losses [17].

Recent years have seen a sharp rise in HAB events due to population growth, agriculture [18], pollution, and climate change [19]. This trend highlights the need to enhance HAB monitoring, modeling, and prediction to protect water resources and public health [20,21,22,23]. The direct measurement of algal concentrations is labor-intensive, so chlorophyll-a (Chl-a) is often used as a proxy for indicating algal blooms and water quality [24,25,26]. HAB formations often result from eutrophication [27], poor water quality [28], and climate change [29,30,31].

Studies that focus on individual factors, like nutrients, land use, or climate drivers, often lead to oversimplified predictions [32,33,34,35]. Effective HAB monitoring requires laboratory analysis of a variety of indicators, like chlorophyll-a, cyanobacteria, and algal toxins [36,37,38], using techniques such as microscopy, spectrophotometry, liquid chromatography, and biochemical assays [39]. Remote sensing using satellites and UAVs provides valuable spatial data on HAB spread [40,41,42,43]. Addressing algal blooms requires an understanding of their causes and implementing effective management strategies, including the timely prediction of HABs to protect ecological and human health.

In recent decades, advanced machine learning (ML) algorithms have been employed to predict water quality [44], including chlorophyll-a (Chl-a) concentrations [45]. Wu [46] used artificial neural networks (ANNs) to predict the daily Chl-a in a German lowland river by utilizing climate and water quality data as the independent input variables. Similarly, Huang [47] employed ANNs to predict the monthly Chl-a in a lake. A support vector machine (SVM) is another ML algorithm used to predict water quality information, including total nitrogen, total phosphorus (TP), and Chl-a [48,49]. Additionally, Derot [50] applied a random forest (RF) model to predict cyanobacteria concentrations, while Busari [51] predicted Chl-a using an RF, multi-layer perceptron (MLP), and support vector regression (SVR), and Jeong [52] used an RF and eXtreme gradient boosting (XGB) model to forecast algal blooms. Furthermore, Shin [53] used a variety of decision tree-based classifiers to forecast the occurrence of HABs in harmful bodies of water. Recently, Ai [54] used nine widely employed ML-based classification and regression models, such as ANN, BA, RF, GB, and KNN for HAB prediction, demonstrating the capabilities of several models for algal bloom predictions.

Various tree-based ensemble algorithms have been applied to predict water quality information [45,55]. Ensemble ML models use a group of models composed of multiple weaker learners to enhance the accuracy of the outcome or prediction of the final fused model, making it more accurate [56]. Random forests (RFs) and gradient-boosted decision trees (GBDTs) are commonly used tree-based ensemble models where the decision tree models serve as the weak learners. XGB is among the more popular and widely used GBDT models [52,57]. Lin [58] also demonstrated the use of other ensemble ML algorithms, such as AdaBoost, LightGBM, and a stacking regressor, in addition to other common ensemble ML algorithms. Despite their potential, these models face challenges, such as the black-box nature of predictions, requiring explainable artificial intelligence (XAI) to enhance their interpretability and usability.

All the ML models previously discussed exhibit black-box characteristics. This means that the end user has access only to the input data and final prediction outputs of the models [59]. Consequently, the users are often unaware of the reasoning behind the predictions made by complex AI systems and algorithms. Recently, explainable artificial intelligence (XAI) has emerged to overcome the ‘black-box’ nature of ML models [60]. Among the various explanation techniques, Shapley additive explanation (SHAP) is the most representative post hoc analysis technique [61]. SHAP can estimate the magnitude of the positive or negative contribution of the input features to a model’s output [62]. Unlike traditional feature importance techniques, SHAP offers a unified framework that assigns consistent and interpretable impact scores to the input variables, allowing researchers and environmental policy-makers to identify the most influential factors governing HAB dynamics. Additionally, SHAPs are commonly utilized in the field of hydrology because they can effectively visualize the importance and effect of various factors on water quality. For example, Cha [63] estimated the contributions of environmental factors on species distributions, while Kim [64] analyzed the spectral bands on satellite images to predict the Chl-a values in lake water. Finally, Jeong [52] identified the relative water quality feature importance for HAB predictions using SHAP.

Despite the increasing prevalence of SHAPs in hydrology, there is still limited research on it in the field of HABs [45,65]. While ML models have been widely used across various domains, their application to HAB prediction, particularly in Lake Erie, is still relatively underexplored. Most previous studies on Lake Erie have primarily relied on field measurements, statistical methods, and single ML model approaches. However, these methods often fail to fully capture the complex interactions among multiple environmental parameters. In addition to traditional ML models, researchers have also explored deep learning (DL) techniques, which have recently gained popularity due to their ability to model temporal dynamics and effectively handle complex feature interactions. Despite their advantages, DL models require large datasets and substantial computational resources. Given these constraints, this study emphasizes the evaluation of ensemble ML models, which offer a balance between accuracy and interpretability for HAB prediction. Moreover, the existing research has largely focused on HAB prediction performance, with limited attention to the influence of the individual variables on the predicted chlorophyll-a values.

To address this gap, this study employs a comprehensive ensemble ML approach, integrating RF, DF, XGB, and stacking and voting algorithms, along with an XAI technique to enhance both the interpretability and predictive accuracy. Another key distinction of this study is its unique dataset, which incorporates physical, chemical, and biological water quality parameters collected from multiple monitoring stations across the western part of Lake Erie over an extended period (2013–2020). Unlike prior research that primarily relied on either satellite-based monitoring or localized in situ measurements, this study combines multi-source data to develop a more generalized predictive framework. By integrating ensemble ML techniques with SHAP-based feature interpretation, this research provides a more transparent and actionable understanding of the key environmental drivers influencing HAB occurrences. To the best of our knowledge, such a detailed and comprehensive study, specifically of Lake Erie, using ensemble ML models in combination with an XAI analysis, has not been extensively documented in the literature. The objectives of this study are to (1) utilize extensive datasets that include physical, chemical, and biological water quality parameters from multiple monitoring stations; (2) predict the occurrence of HABs using ensemble-based ML models; and (3) identify the relative feature importance for HAB occurrence predictions using SHAP. The insights provided by this research will contribute to improving HAB monitoring strategies and offer a novel, interpretable, and scalable framework for water quality prediction in freshwater ecosystems.

This paper is structured as follows: Section 2 describes the methodology, including the data collection and ensemble-based ML model implementation. Section 3 presents the results and discussion, highlighting the effectiveness of SHAP for interpreting the models. Section 4 concludes with insights into the implications of the findings and suggestions for future research.

2. Methodology

2.1. Study Areas

In this study, we used water quality data collected from 7 monitoring stations (Figure 1) by National Oceanic and Atmospheric Administration (NOAA) Great Lakes Environmental Research Laboratory (GLERL) on the western side of Lake Erie. We used publicly available water quality data collected by the NOAA Great Lakes Environmental Research Laboratory (GLERL) from 2013 to 2020 [13]. Measurements were recorded at a near-daily frequency during the bloom-prone months (typically May through September). A comprehensive description of the sampling methodology, instrumentation, and quality control procedures is provided by Boegehold et al. [13]. These stations were selected to represent different nutrients, sediment, and hydrological inputs into the western basin of Lake Erie and are located in areas consistently susceptible to HABs. The selected water quality parameters measured at these stations included Secchi Depth (m), CTD temperature (°C), CTD specific conductivity (µS/cm), CTD dissolved oxygen (mg/L), turbidity (NTU), total phosphorus (µg P/L), total dissolved phosphorus (µg P/L), ammonia (µg N/L), nitrate + nitrite (mg N/L), particulate organic carbon (mg/L), particulate organic nitrogen (mg/L), total suspended solids (mg/L), and chlorophyll-a (µg/L). The dataset included measurements from CTD (conductivity–temperature–depth) sensors, which captured vertical profiles of water column conditions. CTD variables—such as temperature, conductivity, and depth—play a critical role in HAB prediction by influencing physical mixing, nutrient transport, and stratification patterns that directly impact chlorophyll-a dynamics. The primary objective was to predict chlorophyll-a concentration as a key indicator of HABs. All data preprocessing was performed by the authors and included the removal of duplicate entries, handling of missing values, and consistency checks to ensure high-quality inputs for machine learning analysis. In terms of missing data handling, records with missing values for the target variable (Chl-a) or for any of the input variables were excluded from the analysis. Due to the high temporal resolution of the NOAA monitoring dataset, these omissions represented a small fraction of the total data and did not introduce significant bias. We opted not to perform imputation to avoid introducing artificial variance or assumptions into the regression models.

Table 1. Data description and summary statistics (mean and S.D.).

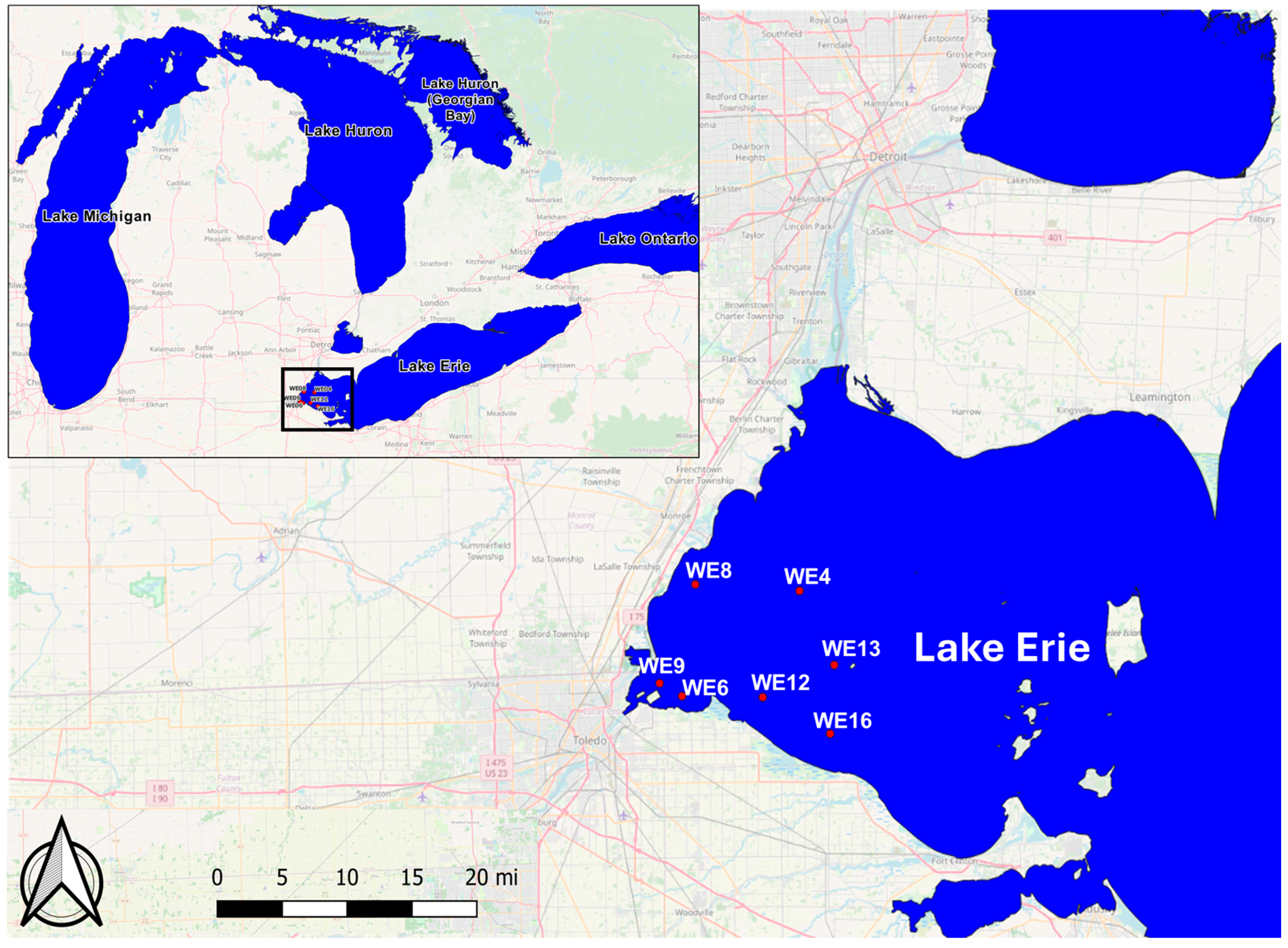
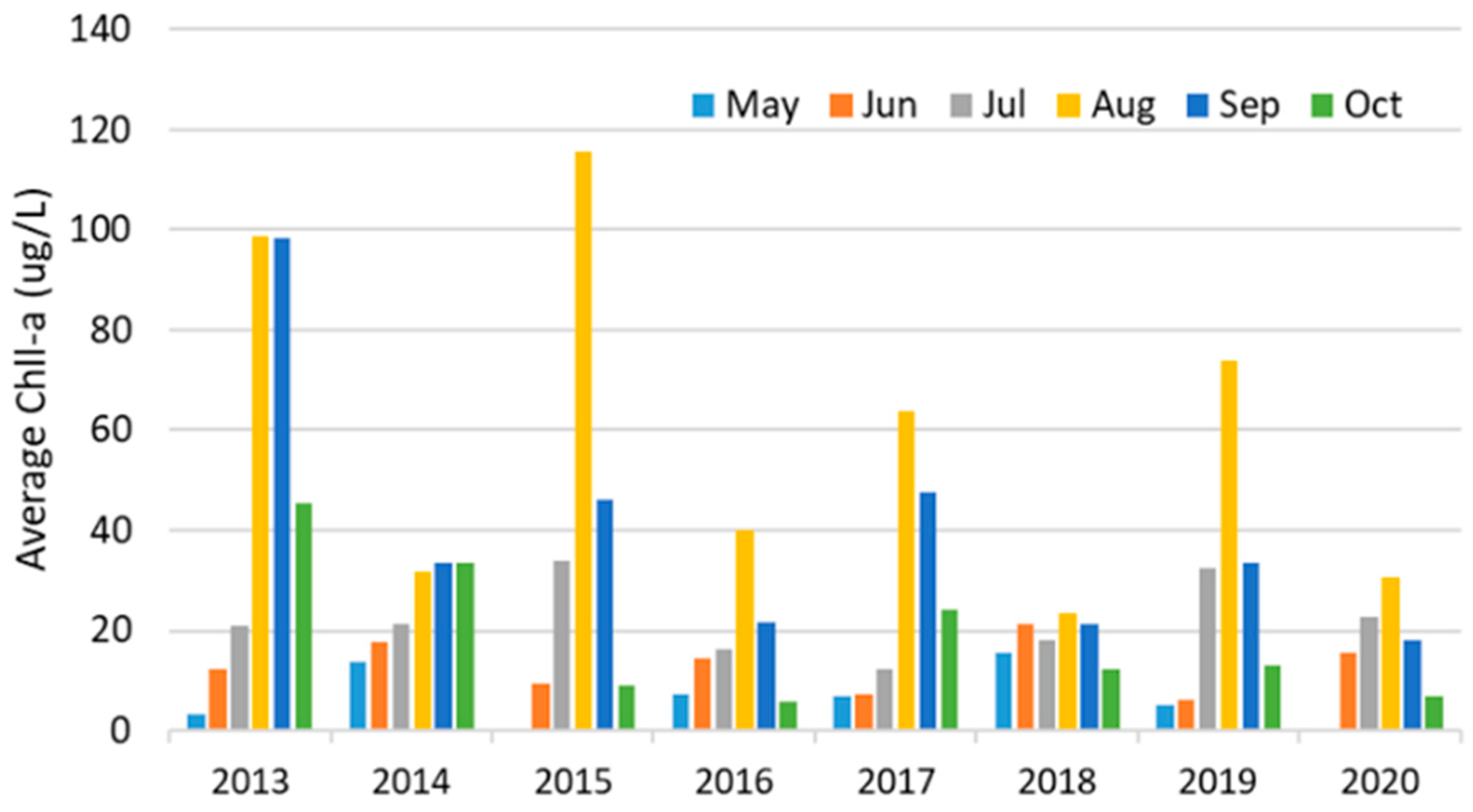
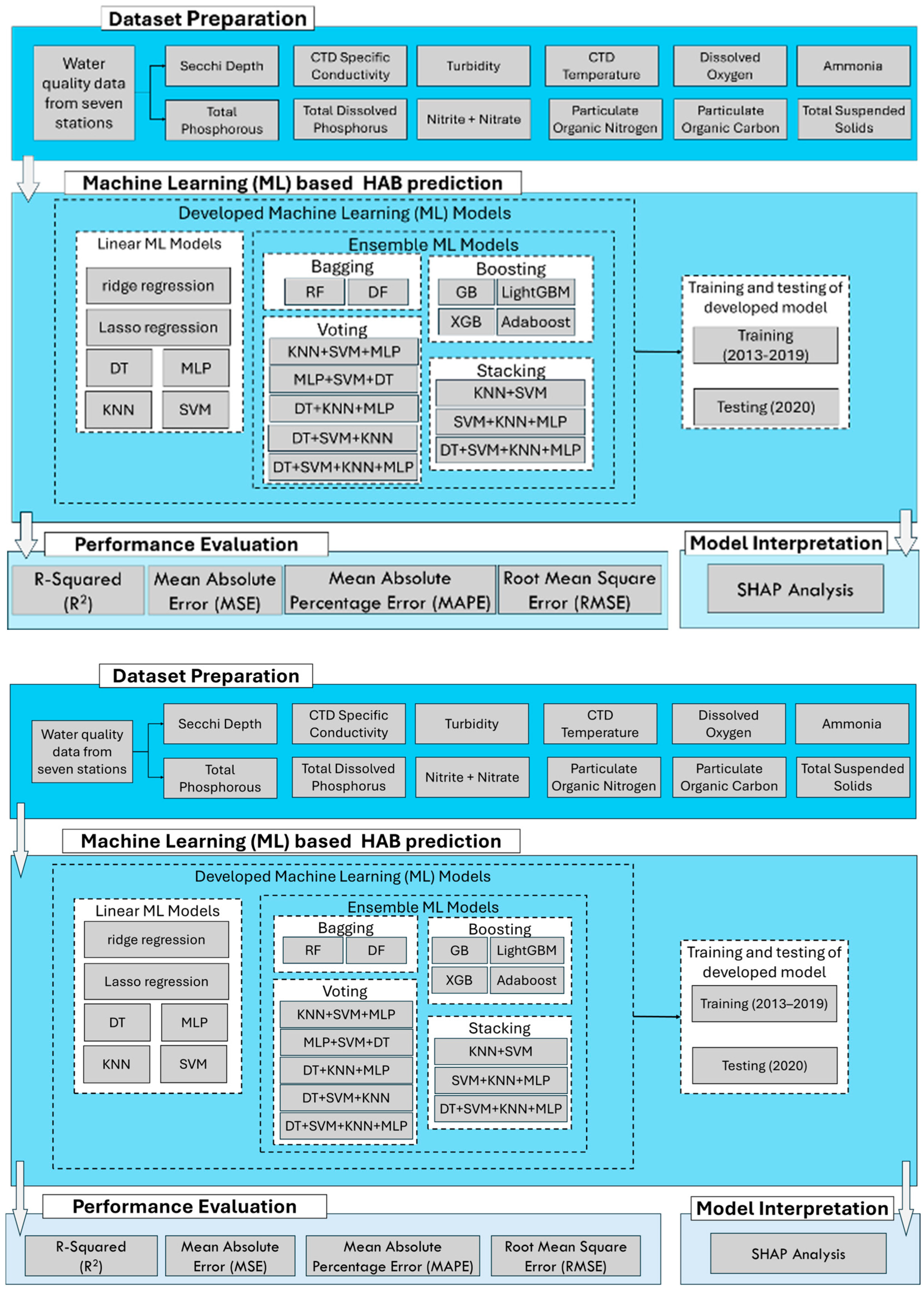
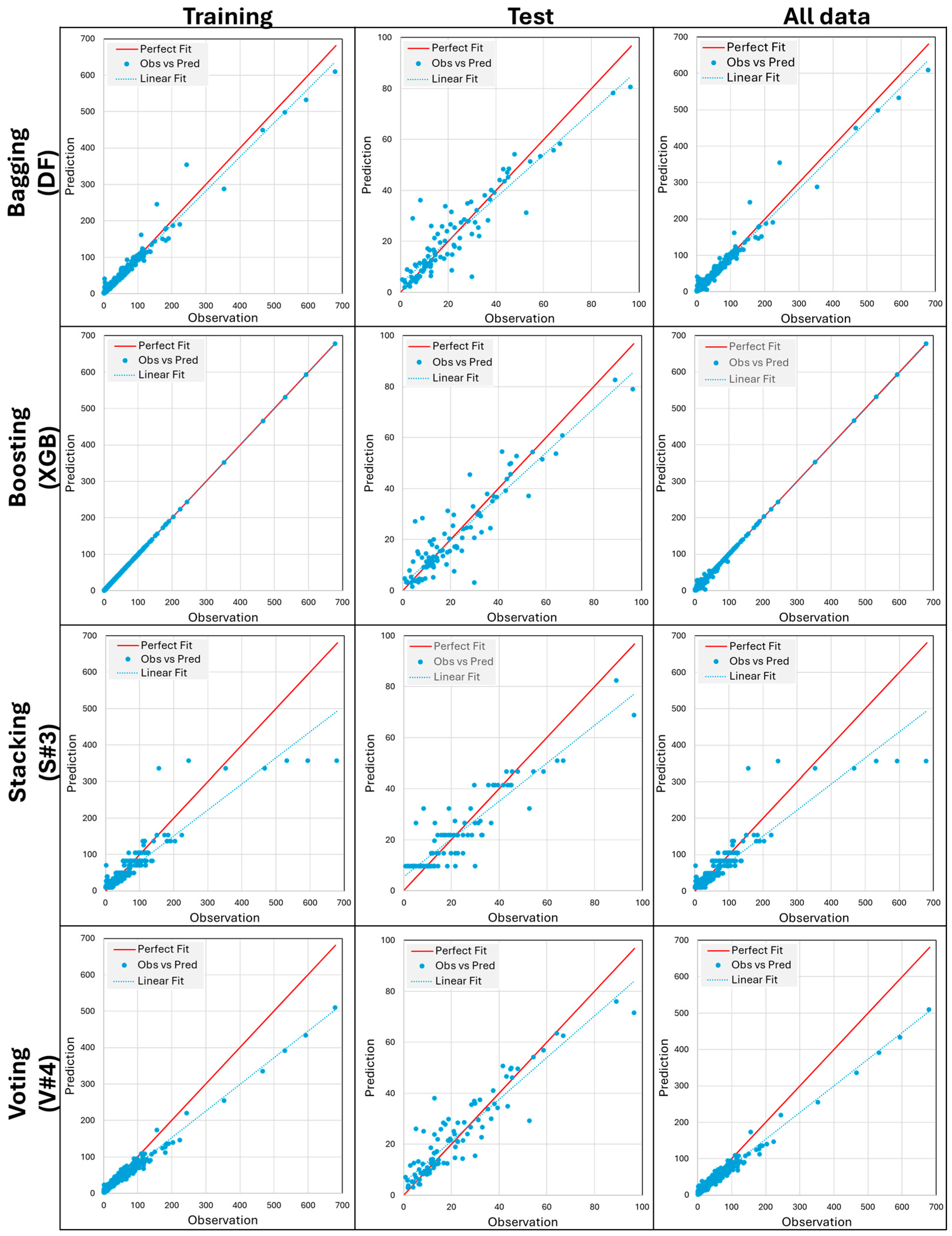
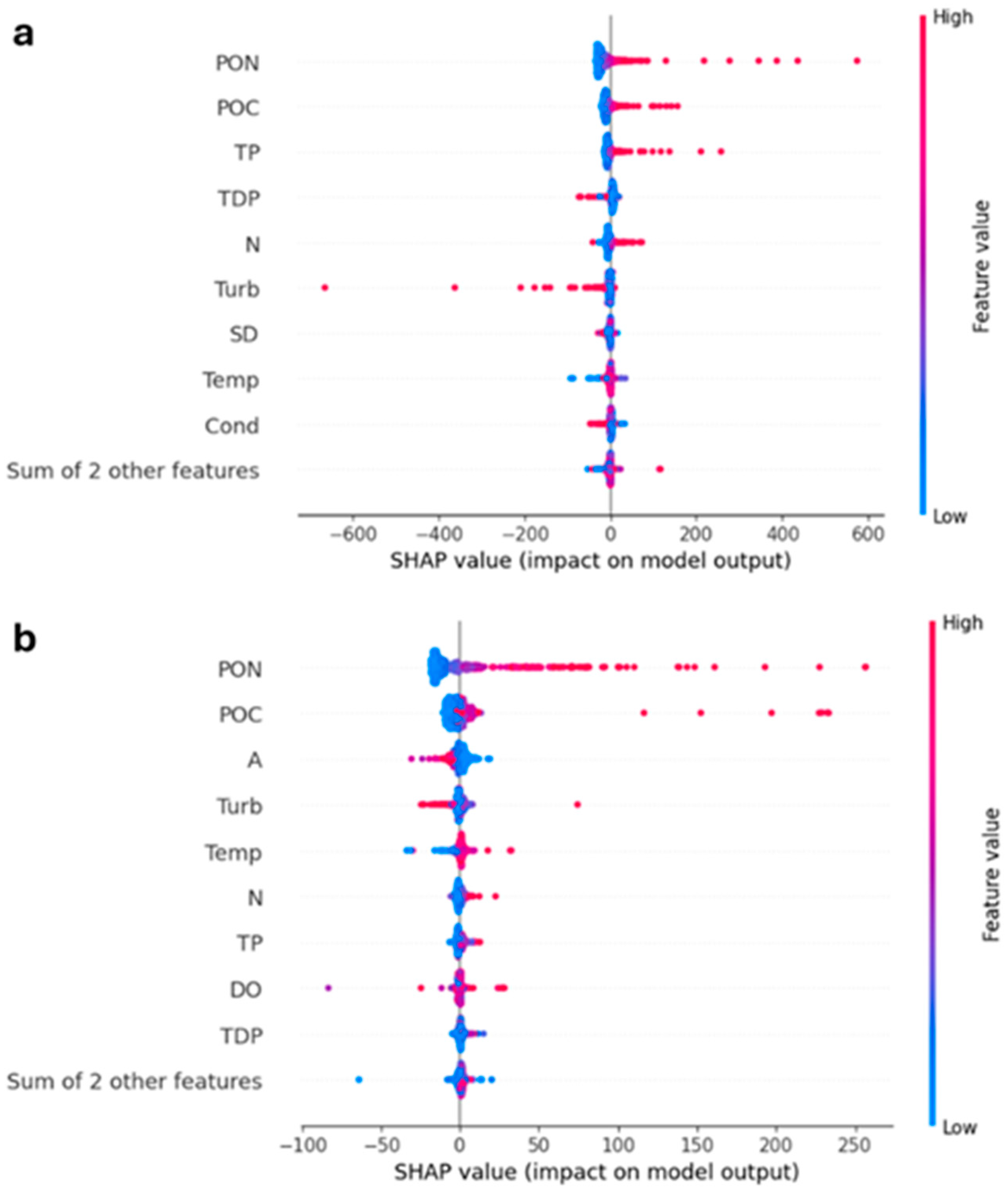
Variables		WE4	WE6	WE8	WE9	WE12	WE13	WE16
Independent variables	SD	1.96 (0.95)	0.69 (0.51)	1.14 (0.85)	0.36 (0.18)	0.88 (0.65)	1.57 (0.93)	1.38 (1.02)
	T	21.73 (3.61)	21.85 (4.31)	21.98 (4.14)	22.73 (4.07)	21.89 (3.77)	21.96 (3.47)	22.77 (3.14)
	Cond	245.49 (23.54)	350.34 (59.38)	298.18 (50.51)	388.2 (69.46)	282.91 (47.43)	249.57 (26.55)	275.6 (32.19)
	DO	7.69 (1.07)	7.6 (1.24)	7.72 (1.21)	7.09 (1.3)	7.61 (1.02)	7.74 (1.01)	7.21 (0.95)
	Turb	5.59 (6.8)	32.06 (72.07)	21.64 (94.48)	40.37 (49.34)	17.5 (21.68)	9.75 (19.08)	8.73 (7.08)
	TP	24.26 (16.2)	127.03 (146.9)	83.24 (225.15)	168.9 (123.17)	65.91 (55.52)	32.27 (29.07)	36.24 (21.28)
	TDP	5.93 (5.36)	35.03 (38.11)	18.36 (25.69)	45.91 (34.4)	18.89 (23.1)	7.48 (9.04)	11.88 (15.62)
	A	25.71 (49.08)	35.79 (50.74)	29.6 (41.98)	72.56 (84.5)	36.47 (183.73)	18.12 (32.78)	18.64 (21.21)
	N	0.37 (0.3)	1.52 (1.85)	0.83 (1)	1.85 (2.05)	0.73 (1.16)	0.34 (0.37)	0.44 (0.56)
	POC	1.08 (1.13)	4.53 (17.85)	3.66 (16.63)	3.24 (3.84)	1.62 (1.36)	1.3 (1.49)	1.18 (0.7)
	PON	0.18 (0.19)	0.74 (2.83)	0.65 (3.34)	0.56 (0.67)	0.27 (0.23)	0.22 (0.24)	0.2 (0.12)
	TSS	6.18 (6.01)	29.02 (50.1)	15.78 (36.6)	37.93 (41.6)	17.17 (20.51)	10.03 (16.97)	8.95 (6.2)
Dependent variable	Chl-a	15.22 (20.16)	50.4 (63.9)	37.49 (70.9)	47.09 (65.35)	22.53 (26.84)	17.11 (22.29)	15.5 (11.12)

provides descriptive statistics (mean and standard deviation) for the selected physical, chemical, and biological water quality parameters across seven monitoring stations located in the western basin of Lake Erie. These parameters served as input features for the machine learning models used in this study, with chlorophyll-a (Chl-a) as the output variable. Notably, considerable spatial variability was observed in key indicators, such as turbidity, total phosphorus (TP), and ammonia (A), suggesting heterogeneous environmental conditions across stations. For instance, WE9 showed the highest average TP (168.9 µg/L), while WE6 exhibited the greatest turbidity (32.06 NTU). Chl-a concentrations also varied significantly, with WE6 reporting the highest mean (50.40 µg/L), indicative of more intense algal bloom activity. These variations emphasize the importance of incorporating multi-station data to capture the complex dynamics driving HAB occurrences in Lake Erie.

Figure 2 shows the average chlorophyll-a concentrations at seven stations across Lake Erie, spanning from 2013 to 2020. The data is presented on a monthly scale, with distinct bars representing the average concentrations for each month from May through October. The figure provides valuable insight into the temporal dynamics of algal blooms in Lake Erie, highlighting both seasonal and interannual variations in Chl-a concentrations. The peak in August for several years suggests that monitoring efforts during late summer are crucial for understanding and managing HABs. Additionally, the marked variability across years underscores the need for continuous monitoring to capture the complex interplay of factors driving algal blooms in the lake.

2.2. Machine Learning Models

The linear models selected were Ridge and Lasso regressions, SVM, MLP, DT, and KNN. Each of these models has been proven to be well suited for all sorts of regression tasks, including for predicting algae blooms. These models were compared based on their performance and were also tested for their efficiency, since real-time forecasting is also highly important.

Linear Regression: The Ridge and Lasso regression methods are two commonly used linear regression methods developed for a variety of forecasting tasks. Ridge regression works through using a parameter estimation method to reduce the effect of collinearity, a common problem that occurs when there is a high correlation between two variables. Through reducing collinearity, it increases the reliability of a regression model. The Ridge regression method also has the capability of penalizing outliers in data, which further helps to create an accurate linear regression model.

Thus, Ridge regression has been commonly applied in a wide variety of tasks, ranging from genetic studies to finance [66,67]. Lasso regression is also an extension of the ordinary least squares method, and it reduces error by shrinking some of the coefficients of features to zero to find the most optimal method [68]. By doing so, Lasso regression can select features more accurately. Finally, Lasso regression also utilizes the L1 regularization method, which introduces another penalty using the absolute value of coefficients. This method has been applied for rainfall modeling [69], and both models have been proven to have some success when dealing with regression tasks.

Multi-Layer Perceptron (MLP): A multi-layer perceptron (MLP) is a deep neural network algorithm capable of performing both classification and regression tasks, which also adapts well to linear and non-linear data. It contains three main layers: an input layer, hidden layers, and output layers. The hidden layers are all fully connected with each other and contain an activation function, which transports inputs to outputs. Each layer contains a different number of perceptrons, which make the calculations in the model. The perceptrons use a weighted-average method to mimic the neurons in a human brain, and if a certain weighted average exceeds a certain threshold, then that information is passed to the other perceptrons. MLPs have been successful at a wide variety of tasks, including for predicting chlorophyll-a values [70].

Support Vector Machine (SVM): A support vector machine is another commonly used machine learning method that works by finding the decision boundary that best separates different data points, allowing it to classify or predict outcomes effectively [71]. To find the hyperplane, a kernel, which transforms data to the required form, can be utilized without increasing the computation cost. In regression tasks, a similar method is used, except hyperplanes represent the best-fit line with a threshold value between decision boundaries. Through doing so, it is also commonly used in regression tasks such as algae blooms, and it is relatively memory efficient compared to other models [72].

Decision Trees: Decision trees are a popular machine learning algorithm, which can be used in both classification and regression tasks [73]. The key features of decision tree are splitting and pruning. Splitting in a decision tree works by dividing the dataset into subsets based on the value of the selected feature, and the process is repeated recursively to build the tree. A decision tree is built through various nodes with each node representing a decision as a result of a question, and the leaf nodes represent the value that is produced as a result of that decision. Each additional branch that is added to a decision tree is another possible route that can be taken within the decision tree to reach a final solution. Another part of a decision tree is pruning. Pruning works to reduce overfitting in decision trees by removing any unnecessary branches or nodes, since decision trees are traditionally significantly impacted by noisy data. Decision trees have recently been applied to form new ensemble algorithms (i.e., random forest) and other classification and regression tasks [74].

K-Nearest Neighbors (KNN): A KNN is a commonly used machine learning algorithm that works by categorizing data points with similar values [75]. The tuning of the parameter of the K-nearest neighbors is utilized to make predictions, with a smaller K leading to noisy predictions, while a larger K leads to overfitting of the model. The K-nearest neighbors of a certain data point are determined based on a distance metric, which computes the distance between every data point in a dataset, where the distance metric used is often dependent on the dataset itself. Then, for regression tasks, the algorithm averages the values of the K-nearest neighbors for the final prediction after calculating the distance between that point and other points. KNNs have been used successfully for algae bloom predictions in previous works [76,77].

2.3. Ensemble Learning Models

Ensemble learning is a machine learning method where multiple different learners are fused together to form a large model. This technique is especially important in environmental engineering because it helps reduce uncertainty in models and improve redundancy and accuracy. The ensemble methods can be split into four main categories: bagging, boosting, voting, and stacking. The detailed algorithms are further discussed below.

Bagging Algorithms

Random Forest (RF): A random forest is a bagging ensemble method based on the ensemble of multiple different decision trees, where the combination of multiple weak learners and decision trees increases model performance [78]. Bagging uses bootstrapping, where models are trained on subsets of a dataset and the final predictions from each model are fused together. The split of a node in a tree relies on random subsets of features, and this is continued until the entire tree is built. The key features of a random forest model are its diversity and robustness, since each model is trained on a separate section of data, and the random forest can be easily scaled to larger datasets. However, the algorithm is sensitive to noisy data, since it is not distributed evenly, and the individual decision trees must be sufficiently deep. Thus, a random forest can handle continuous variables, making them suitable for regression tasks. The random forest is one of the most utilized machine learning algorithms in multiple domains, including algae bloom prediction.

Deep Forest (DF): A deep forest (DF) is a novel method developed by Zhou [79], which utilizes the stacking ensemble method through a cascade structure, implementing deep learning without requiring extensive parameter tuning. The final structure is similar to that of a neural network, but instead of neurons, layers of random forests are built. A sliding window is used to scan the raw features of the deep forest. Each layer of the deep forest contains multiple random forests as learners. The algorithm takes inspiration from stacking ensemble methods, where using an abundance of weaker learners for a fully ensemble algorithm is an important concept. Thus, model diversity plays a key role in stacking algorithms, and a deep forest emphasizes that concept through having each model search through different subsets of the training dataset. Moreover, a deep forest is also ideal for training since it requires a small number of hyperparameters. This novel method has had limited applications, especially in the field of environmental science and algae blooms.

Boosting Algorithms

Gradient Boosting (GB): A gradient boosting algorithm is another decision tree-based model, but it utilizes the boosting technique in ensemble learning [80]. The boosting technique is where a model is trained initially, and a second model is trained based on the errors of the first model. Instead of training models separately, each new model focuses on correcting errors made by previous ones, resulting in highly accurate predictions. Through each iteration, the weights in the model are adjusted to improve performance. Then, the gradient descent in the model optimizes loss by decreasing it as much as possible when new weaker learners are added to the full model throughout the training process. The gradient boosting algorithm is used as a method of fusion for the individual models.

Extreme Gradient Boosting (XGBoost): An extreme gradient boosting algorithm is an extension of a gradient boosting algorithm, which reduces overfitting during training using regularization penalties [81]. Similarly to a gradient boosting algorithm, XGBoost sequentially and iteratively adds learners, such as decision trees, to a model, and newer learners focus on the errors of previous learners. However, the main difference between XGBoost and standard gradient boosting is that it uses enhanced regularization techniques, improving the generalization capabilities of the model. XGBoost is also highly efficient, even across larger datasets. Recently, XGBoost has been applied to a variety of fields, from diabetes detection [82] to algae bloom prediction [83]. This algorithm is also used for the fusion of multiple other models in this study.

Light Gradient Boosting (LightGBM): A light gradient boosting algorithm is another commonly applied gradient boosting method in machine learning [84]. First, data are split into different bins of multiple data points instead of individual data points, allowing for training times to decrease. Like other gradient boosting algorithms, a LightGBM iteratively adds learners to an ensemble of decision trees. However, the key difference is that LightGBM builds its tree leaf-wise rather than depth-wise to achieve lower loss and improve efficiency, allowing it to be faster than XGBoost. Finally, LightGBM uses gradient one-sided sampling in order to focus on data points with higher prediction errors. LightGBM is used as an individual model in this study and has been applied in the past mainly for tasks which require high efficiency.

Adaptive Boosting Algorithm (Adaboost): An Adaboost, or adaptive boosting algorithm, is an ensemble algorithm which combines multiple weaker learners into one strong learner and assigns more weight to difficult-to-predict cases in each new iteration. A weak learner is a classifier that performs only slightly better than random guessing, and Adaboost starts by training multiple numbers of these learners on weighted versions of training data. First, all samples in a dataset are assigned the same weight. Adaboost uses the boosting method through iteratively focusing on incorrect predictions from the model and improving them accordingly. After the training process, new weights are assigned to each classifier based on their accuracy. Finally, every weak learner is combined and normalized to make the final output or prediction. Adaboost algorithms have seen usage in medical fields, among many others [85].

Voting Algorithms:

A voting classifier is another type of ensemble learning method which combines the predictions of multiple individual classifiers to improve performance [86]. It works similarly to how multiple people voting on a decision lead to a more balanced result. It can fuse multiple different methods and models, and it takes a weighted average of all different inputs. These weights can be trained and fitted based on the input data. The main advantage of a voting classifier is that it has improved generalization performance over that of individual models. There are two main types of voting used in a voting classifier: hard voting and soft voting. Hard voting is where the instance with the most votes is the final output, while soft voting, which is implemented in this research, uses a weighted average and is more suitable for regression tasks.

Stacking Algorithms:

Stacking is another ensemble method for combining the predictions of individual classifiers [87]. The key difference between stacking and voting is that it uses a final estimator, which interprets the meta-features of several base estimators trained on the original dataset. Thus, during the prediction process, each individual base estimator first makes its prediction, and the final estimator combines the results of these several models to make the final prediction. One advantage of stacking is that a variety of diverse models can be fused, which helps improve the robustness and accuracy of the method. Recently, stacking ensembles have been applied and were successful at predicting algal blooms with improved accuracy [88].

2.4. Model Development

Figure 3 presents a comprehensive workflow diagram for an ML-based HAB prediction. As shown in the figure, the initial step involved obtaining raw water quality data from seven monitoring stations located on the western basin of Lake Erie operated by NOAA-GLERL, followed by extensive data preparation, including data preprocessing. Preprocessing was critical to ensure that the input data fed into the ML models were consistent, complete, and high-quality. The data preprocessing steps conducted by the authors included the following: (1) the removal of duplicate records, (2) exclusion of entries with missing values in either the dependent variable (Chl-a) or any input features, and (3) consistency checks to ensure feature alignment across all stations. For handling missing values, we chose a conservative approach by excluding samples with missing entries rather than imputing values [89,90]. This decision aimed to avoid introducing artificial variance or assumptions into the model training process. Due to the high temporal frequency of the NOAA dataset, these omissions accounted for only a minor fraction of the dataset and were not expected to introduce significant bias.

After data cleaning, all input features were normalized using the Min-Max scaling method to rescale values into a [0, 1] range. This normalization step was essential to eliminate potential biases caused by differences in feature units or magnitudes, and to improve model training convergence and performance [89].

Subsequently, the processed data were split into training and testing subsets. Data from 2013 to 2019 were used for training, while 2020 data served as the independent testing set to evaluate model performance. This setup allowed the models to be trained on historical patterns and tested on unseen data, simulating real-world forecasting scenarios. Since our dataset contained a greater number of samples than features, we deliberately retained all input variables and were careful not to reduce the number of features too much. This strategy helped us ensure that important information influencing HAB dynamics was preserved while maintaining the robustness and interpretability of the models.

In this study, we implemented a wide range of machine learning models—including linear regression models (Ridge and Lasso), non-linear models (KNN, SVM, decision tree, and MLP), and ensemble models (RF, DF, GB, XGB, LightGBM, and AdaBoost)—to predict chlorophyll-a concentrations. To ensure fair comparison and model robustness, hyperparameter tuning was conducted using grid search combined with five-fold cross-validation, using root mean square error (RMSE) as the performance criterion. This process aimed to identify parameter combinations that minimized prediction errors on the training dataset while ensuring generalization to unseen data. For ensemble models, such as stacking and voting, multiple combinations of base learners were explored to evaluate performance variability. The weights used in soft-voting ensembles were empirically determined, and in stacking, the KNN algorithm was selected as the meta-learner for its non-parametric nature and ability to generalize across base model outputs. Hyperparameters for linear models with limited parameter spaces, such as Ridge and Lasso, were manually tuned based on validation results. All final hyperparameter configurations are summarized in

Table 2. Summary of the main hyperparameters tuned for each ML model. Parameters not listed were used with default values from the relevant Python 3.10.12 libraries.

Models	Parameters
Ridge Regression	Alpha = 100
Lasso Regression	Alpha = 100
KNN	N_neighbors = 30
DT	Min_samples_split = 2; min_samples_leaf = 1
MLP	Epochs = 2000; learning rate = 0.001; batch size = 32
SVM	Kernel = rbf; c = 100,000
LightGBM	Leaves: 31; learning_rate: 0.05; rounds: 100; feature_fraction: 0.9
RF	N_estimators = 1000
AdaBoost	N_estimators = 100; learning_rate = 0.1
DF	N_estimators = 50
GB	N_estimators = 1000
XGBoost	Num_rounds = 100; learning_rate = 0.05

for reference. All other parameters were maintained at their default values as implemented in the respective ML libraries to ensure consistency and reproducibility.

Following the model training, performance was evaluated based on several statistical metrics (R², MAE, RMSE, and MAPE). Finally, model interpretation was conducted using SHAP analysis, which provided insights into the relative importance and contribution of each input feature to the model’s predictions. This step enhanced the transparency and explainability of the models, aiding in a more interpretable understanding of HAB dynamics.

2.5. Model Evaluation

We calculated the values of R-squared ${(\mathrm{R}}^2)$, mean absolute error (MSE), mean absolute percentage error (MAPE), and root mean square error (RMSE) for evaluating the model performance, which are widely accepted metrics. These metrics have been extensively applied in HAB prediction research due to their interpretability and ability to capture different aspects of model performance.

R² quantifies the proportion of variance in the observed data explained by the model, with values ranging from 0 to 1. In other words, ${\mathrm{R}}^2$ tells us how well the model’s predictions match the actual values. In this work, measured and predicted chlorophyll-a concentrations were taken as the dependent and independent variables, respectively, and ${\mathrm{R}}^2$ was determined by applying linear regression analysis. A higher ${\mathrm{R}}^2$ indicates a stronger correlation between predicted and actual values, meaning the model captures more variability in the dataset. An ${\mathrm{R}}^2$ value of 1 represents a perfect model fit, while 0 indicates that the model performs no better than predicting the mean of the target variable. The formula for ${\mathrm{R}}^2$ is shown as follows:

$${\mathrm{R}}^2=1-{\displaystyle \frac{\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}{\sum _{i=1}^n{\left(y_i-\overline{y}\right)}^2}}$$

(1)

where $y_i$ is the ith actual value and $\widehat{y}$ is the ith predicted value of the dependent variable, and $\overline{y}$ is the mean of $y_i$.

Root mean square error (RMSE), which indicates the mean error between the predicted and measured values, is one of the most widely used performance indicators to express the general performance of prediction model [89]. RMSE measures the average magnitude of prediction errors, with lower values indicating better model accuracy. In this study, we calculated the mean error between the measured chlorophyll-a concentration and that predicted by the model. Since RMSE depends on the scale of the target variable (chlorophyll-a concentration in µg/L), it is presented in its original units rather than being normalized. Unlike ${\mathrm{R}}^2$, RMSE is not unitless and is best used for comparing models trained on the same dataset rather than across different datasets. The equation is given below:

$$\mathrm{R}\mathrm{M}\mathrm{S}\mathrm{E}=\sqrt{{\displaystyle \frac{1}{n}}\sum _{i=1}^n{\left(y_i-\widehat{y_i}\right)}^2}$$

(2)

where $y_i$ is the ith actual value and $\widehat{y_i}$ is the ith predicted value of the dependent variable, and n is the number data points.

Mean absolute error (MAE) is also a widely used performance metric to provide an intuitive and easily interpretable measure of prediction model’s performance [89]. The mean absolute error between the measured and predicted chlorophyll-a concentrations were computed without considering their directions. A lower MAE indicates a better model fit, showing that the model’s predictions are closer to the true values. It is also beneficial when comparing different models on the same dataset, as it can help identify the model with the most accurate predictions.

$$\mathrm{M}\mathrm{A}\mathrm{E}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|\left(y_i-\widehat{y_i}\right)\right|$$

(3)

Mean absolute percentage error (MAPE) is also widely used to interpret model performance [23]. It emphasizes smaller relative errors, and it is not based on different scaling of the input feature variables. Smaller MAPE values indicate enhanced accuracy and stronger predictive capabilities of the model.

$$\mathrm{M}\mathrm{A}\mathrm{P}\mathrm{E}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left|\left({\displaystyle \frac{y_i-\widehat{y_i}}{y_i}}\right)\right|\times 100\%$$

(4)

2.6. Model Interpretation Using XAI

The effects of the water quality parameters on the HAB prediction were explained using the SHAP method due to its consistency, strong theoretical foundations in game theory, and suitability for tree-based ensemble models. SHapley Additive exPlanation (SHAP), which is a post hoc and model-agnostic technique, unifies multiple interpretability methods under the concept of Shapley values [62,91]. It establishes a new explanatory model, for a given black-box system, by uncovering associations between the feature values and the output of the black-box system [92]. This method is based on coalitional game theory and Shapley values help explain which factors influence the model’s predictions the most, similar to how a coach evaluates the contribution of each player in a team’s performance [61]. SHAP was preferred over methods like Local Interpretable Model-Agnostic Explanations (LIME) because it provides a unified measure of feature importance across all possible model outputs, ensuring consistency.

In this study, TreeSHAP was used to estimate the SHAP value which represents the importance of the input variables for predicting the results using machine learning models. The ‘shap.TreeExplainer’ function enabled us to plot feature importance for global explainability, facilitating a better understanding of decision-making within our models. This analysis compensates for the black-box type shortcomings of the machine learning model and indicates the extent to which each variable affects the objective variable after being entered into the model.

3. Results and Discussion

All the reported performance metrics are based on the test dataset (2020), which was held out during model training. This approach was used to evaluate the generalization ability of the models. While training metrics can be useful for overfitting analysis, our primary focus was on predictive performance for real-world scenarios. The performance metrics of the various individual ML models, as summarized in

Table 3. Summary of performance metrics of linear ML models.

Model	R2	MAE	MAPE	RMSE
Ridge Regression	0.419	11.609	1.364	13.948
Lasso Regression	0.423	11.590	1.367	13.907
KNN	0.604	8.848	0.907	11.513
DT	0.719	6.169	0.469	9.703
MLP	0.766	6.340	0.406	8.606
SVM	0.816	5.108	0.428	7.851

, highlight the effectiveness of the different linear machine learning models in terms of their predictive accuracy and error rates. R², or the coefficient of determination, measures the proportion of variance in the Chl-a concentrations that is predictable from the independent variables. Higher R² values indicate better model performance. According to the observed R² values in the table, the SVM stands out with the highest R² of 0.816, indicating that it explained approximately 82% of the variance in the Chl-a concentrations, making it the most predictive model among those evaluated.

The MAE and RMSE are both measures of prediction error, with the MAE representing the average absolute error and the RMSE providing a measure that penalizes larger errors more than the MAE. Lower values for both metrics are preferred as they indicate higher accuracy. The SVM had the lowest MAE of 5.108 and RMSE of 7.8508, which suggests that its predictions were closest to the actual Chl-a concentrations, and that it handled larger errors better than the other models. The MAPE, which indicates the average percentage error between the predicted and actual values, further supports this, showing the SVM’s effectiveness with its relatively low value of 0.4279.

Comparatively, the Ridge and Lasso Regression models, with R² values around 0.42 and higher MAE and RMSE values, demonstrated moderate performance, making them less preferable for the high-accuracy requirements of Chl-a prediction. The KNN model improved upon these, but the DT and MLP models offered substantial improvements, as evidenced by their higher R² values and lower error metrics.

Table 4. Summary of performance metrics for ensemble models.

Ensemble Models		Performance Metrics
		R2	MAE	MAPE	RMSE
Bagging	RF	0.848	4.776	0.414	7.312
	DR	0.854	4.537	0.403	6.983
Boosting	GB	0.724	7.297	0.597	9.617
	XGB	0.852	4.919	0.427	7.047
	LightGBM	0.783	5.227	0.467	8.525
	Adaboost	0.787	6.839	0.954	8.442
Stacking	S#1 (KNN + SVM)	0.799	5.397	0.471	8.203
	S#2 (SVM + KNN + MLP)	0.811	5.234	0.469	7.951
	S#3 (DT + SVM + MLP + KNN)	0.823	5.043	0.447	7.696
Voting	V#1 (MLP + SVM +KNN)	0.769	6.558	0.691	8.798
	V#2 (MLP + SVM + DT)	0.836	5.066	0.529	7.413
	V#3 (MLP + KNN + DT)	0.763	6.512	0.725	8.919
	V#4 (SVM + KNN + DT)	0.845	4.921	0.483	7.202
	V#5 (MLP + SVM + KNN + DT)	0.645	8.764	1.148	10.907

presents a comprehensive summary of the performance metrics for the various ensemble models used to predict the chlorophyll-a values. In the bagging category, both the RF and DF exhibited a strong predictive performance. The DF model slightly outperformed the RF model, achieving an R² of 0.8544 compared to the RF’s 0.8481. Additionally, the DF had a lower MAE (4.5366) and RMSE (6.9827), indicating better accuracy and a lower prediction error than the RF, which had an MAE of 4.7761 and an RMSE of 7.312. The MAPE values also show that the DF (0.4026) provided more precise predictions than the RF (0.4137).

Among the boosting models, the XGB stood out as the top performer, with an R² of 0.8517, surpassing the other boosting models, like GB, LightGBM, and AdaBoost. The XGB also had a lower MAE (4.9188) and RMSE (7.0473) compared to the GB, which had a notably lower R² of 0.7239 and a higher MAE (7.2972) and RMSE (9.6167). The LightGBM and AdaBoost showed moderate performance, with the LightGBM having an R² of 0.7830 and the AdaBoost having an R² of 0.7872, though both had higher MAE and RMSE values compared to the XGB.

In this study, the stacking models were developed using a KNN algorithm as a meta-learning model because it does not require much training and can handle both continuous and discrete data. The models with the highest R² score were chosen and paired with a KNN and, based on the results obtained, we realized that combining a strong model with a KNN increases its R² value. The combination of DT, SVM, MLP, and KNN performed well, achieving an R² of 0.8232, compared to the other combinations. We also developed the same combinations with Lasso and Ridge regressions as the meta-learning model instead of the KNN, and observed similar performance metrics. We then decided to pair a strong model with a weak model and realized an increase in predictive performance.

The voting ensembles displayed mixed results, with some combinations performing significantly better than others. The ensemble of SVM, KNN, and DT achieved a high R² of 0.8451, with an MAE of 4.9211 and an RMSE of 7.2024, showing its effectiveness. In contrast, the ensemble including MLP, SVM, KNN, and DT underperformed, with a lower R² of 0.6449 and higher errors (MAE of 8.7638 and RMSE of 10.9070), suggesting that adding more models to a voting ensemble does not necessarily improve performance and can sometimes lead to worse results. In this case, we observed that any combination of any model with a strong model increased its predictive performance.

One key advantage of ensemble models, particularly XGB and DF, is their ability to capture complex, non-linear relationships between the input features, such as nutrient concentrations and chlorophyll-a levels. Unlike linear models, which assume a fixed relationship between features, tree-based ensembles dynamically adjust to the data structure, making them better suited for dynamic environmental processes like HAB formation. Additionally, models like RF and DF have demonstrated high resilience to missing or noisy data, a frequent challenge in environmental monitoring. The averaging mechanism in bagging-based models reduces the influence of outliers, while boosting models, such as XGB, iteratively correct misclassified instances, leading to more robust predictions.

Figure 4 presents a detailed comparison of the performance of the top-performing ensemble ML models (DF, XGB, S#3, and V#4) corresponding to each subcategory—bagging, boosting, voting, and stacking—across the training, testing, and combined datasets. These plots provide a visual diagnostic of the relationship between the observed and predicted chlorophyll-a (Chl-a) concentrations, enabling the assessment of each model’s predictive accuracy and generalization capabilities.

In each plot, the x-axis represents the observed values, while the y-axis represents the values predicted by the model. The solid-red diagonal line labeled “Perfect Fit” illustrates the ideal scenario where the model’s predictions perfectly match the observed values. The blue dots (scatter points) show the actual data points, while the dotted blue line represents the best linear fitting regression line between the observed and predicted values. The scatter points reveal the accuracy of the predictions, with deviations from the red line indicating the prediction errors. The closer the scatter points cluster around the perfect-fit line, the better the model’s predictive accuracy.

Notably, both the DF and XGB models demonstrated a strong alignment with the ideal 1:1 line, particularly across the full range of Chl-a concentrations. The scatter points for these models were densely clustered around the diagonal reference line, suggesting high predictive accuracy and minimal bias. The closeness of the dotted best-fit regression line to the 1:1 line further supports the robust performance of these models on both the training and test scenarios. These results underscore the ensemble models’ capacity to capture the non-linear relationships between various physicochemical features and Chl-a levels, thereby effectively modeling the dynamic behavior of harmful algal blooms (HABs).

The stacking model (S#3), while performing commendably, exhibited more dispersed scatter points, particularly at higher Chl-a values, indicating its tendency to underestimate the peak concentrations. This discontinuous pattern may be due to potential instability in how the meta-learner combined the predictions from the base learners. This could have reduced the model’s robustness at capturing extreme HAB conditions. Similarly, the voting model (V#4) showed improved accuracy compared to S#3, especially in the mid-range of the Chl-a distribution; however, it too struggled with higher concentration values, which may have been a result of over-smoothing during the ensemble averaging process.

Overall, Figure 5 and Table 4 emphasize that the bagging- and boosting-based ensembles (DF and XGB, respectively) outperformed the other ensemble strategies by maintaining a higher consistency between the predicted and actual values. The stacking and voting ensembles also demonstrated potential, especially when optimally combining complementary models, but their performance varied widely based on the specific combination of strong and weak models used. The bagging and boosting ensembles models were not only capable of minimizing the overall prediction error, but were also resilient to variability in the data distribution, making them highly suitable for real-world applications in environmental monitoring and decision support systems.

Table 5. Training times of each optimized model in seconds.

Model	Training Runtime
Lasso	1.0 s
Ridge	1.0 s
MLP	144.9 s
RF	5.2 s
LightGBM	7.0 s
SVM	12.7 s
Adaboost	5.2 s
DT	1.0 s
KNN	0.5 s
DF	561.8 s
GB	1.0 s
XGBoost	1.0 s

summarizes the training times (in seconds) for the various ensemble and individual ML models used to predict the chlorophyll-a values. These times highlight each model’s computational efficiency, which is crucial for real-time or resource-constrained applications. Among the individual models, the KNN exhibited the fastest training time of just 0.5 s, followed by the Lasso, Ridge, and GB, each taking 1 s. These models are thus suitable for applications where rapid model deployment or retraining is required. Among the ensemble methods, the RF (training time of 5.2 s) and LightGBM (7.0 s) showed moderate training times, balancing strong predictive performance with computational feasibility. The XGB stood out for combining both efficiency and performance, with a training time of 1.0 s, making it an attractive option for applications needing both high accuracy and low computational cost. A more complex model, like DF, required a significantly longer training time of 561.8 s due to its cascade structure. While the DF achieved an excellent predictive performance (R² = 0.8544), its resource demands may limit its practicality for real-time applications unless computational resources are abundant. These findings highlight the important trade-offs between model accuracy and computational cost, offering practical guidance for selecting models based on available resources and operational constraints.

In this study, we utilized SHAP to analyze the relative importance of the input features within various ML models for predicting HABs. The relative importance values (i.e., the mean |SHAP| value) provide insights into the contribution of each feature to the model’s predictions, enabling us to understand the driving factors behind the predictions.

Table 6. SHAP values of the 5 most important features in each ML model for HAB prediction.

ML Models	Input Features (Mean |SHAP|)
Lasso	TP (25)	Turb (6.5)	A (2.0)	TDP (1.5)	POC (0.5)
Ridge	TP (35)	Turb (10)	A (2.5)	TDP (2.0)	POC (0.7)
KNN	N (6.0)	TDP (3.5)	DO (2.5)	Temp (2.0)	Cond (1.1)
DT	PON (20.0)	POC (6.0)	A (4.0)	Turb (2.5)	DO (2.0)
MLP	TP (15.0)	Turb (12.2)	A (10.0)	POC (5.3)	PON (2.0)
AdaBoost	PON (14.5)	POC (2.2)	A (1.8)	Temp (0.3)	N (0.1)
LightGBM	PON (17.7)	POC (7.5)	A (2.8)	Turb (2.7)	TP (2.5)
RF	PON (9.5)	POC (6.0)	A (2.5)	Turb (1.8)	Temp (1.5)
SVM	PON (24)	POC (12)	TP (7.5)	TDP (6.0)	N (5.9)
GB	PON (25)	POC (6)	TP (5)	Turb (5)	A (4.5)
XGBoost	PON (18)	POC (7)	A (3)	Turb (2.7)	Temp (2.5)
DF	PON (14)	POC (5)	A (2)	Turb (1.5)	N (1)

presents the mean |SHAP| values of the five most important input features in each ML model used in our study. This table offers a critical lens into how the different models internally weigh the various water quality variables when predicting chlorophyll-a (Chl-a) concentrations, providing both interpretability and ecological insight into the harmful algal bloom (HAB) dynamics in Lake Erie.

Across nearly all the models, the particulate organic nitrogen (PON) and particulate organic carbon (POC) consistently ranked among the most influential variables, with the PON emerging as the dominant predictor in the tree-based ensemble models, such as RF, GB, XGB, DF, and AdaBoost. These results align with prior ecological findings that have highlighted the role of organic nitrogen and carbon in fueling primary production and phytoplankton growth [93]. In particular, the PON likely represents a key proxy for biological activity, serving both as a nutrient source and an indicator of particulate biomass associated with bloom formation [94,95].

The total phosphorus (TP) also exhibited a strong influence across the models, particularly in the Lasso, Ridge, MLP, and GB. As a well-established eutrophication agent, the TP contributes directly to algal proliferation by promoting nutrient-enriched conditions that favor phytoplankton growth [96,97]. The consistent importance of the TP across the linear and non-linear models underscores its foundational role in predicting Chl-a concentrations, reinforcing its status as a primary control variable in freshwater ecosystem models.

Ammonia (A) and turbidity also appeared frequently among the top-ranked predictors. Ammonia, a bioavailable form of nitrogen, is critical for algal metabolism and has demonstrated a consistently positive influence on Chl-a predictions [98]. Its significance is particularly pronounced in models such as MLP, LightGBM, and XGB, where its |SHAP| values rank in the top three. Turbidity, while not a direct nutrient, can indirectly affect bloom dynamics by influencing light availability and sediment–nutrient interactions. Its prominence in models like Lasso, Ridge, and MLP suggests its value as an auxiliary indicator of bloom-supportive conditions.

Interestingly, while the ensemble models generally converged on a consistent subset of high-importance features (PON, POC, TP, and A), individual models, such as KNN and DT, displayed more variability in their top feature selections. For instance, the KNN model identified nitrate + nitrite (N), temperature, and conductivity as the significant predictors—features that may reflect the sensitivity of distance-based models to scaling and local data distribution. Similarly, the DT model highlighted dissolved oxygen (DO), which may be indicative of the biological oxygen demand associated with bloom decomposition phases, although it is less prominent in the other models.

This divergence in feature rankings highlights the complementary strengths of different algorithms and underscores the utility of ensemble modeling. Ensemble methods, particularly those incorporating multiple learners (e.g., XGB and DF), benefit from aggregating diverse feature perspectives, thereby producing more stable and ecologically plausible interpretations. Importantly, SHAP not only quantifies the magnitude of each feature’s influence but also enables the exploration of feature interactions and directionality, as further illustrated in Figure 5.

In summary, the SHAP-based feature importance analysis in Table 6 provides valuable ecological and operational insights. It confirms that particulate organic matter and nutrient-related variables are the primary drivers of HAB dynamics in western Lake Erie. These findings reinforce the need for targeted nutrient reduction strategies—especially concerning organic nitrogen and phosphorus inputs—as part of effective HAB mitigation efforts. Furthermore, the consistency of the SHAP results across the model types strengthens confidence in the robustness and ecological relevance of the predictive framework presented in this study.

The SHAP analysis provides the direction of the contribution to the prediction results in addition to the magnitude. Figure 5 represents a SHAP summary plot for two selected machine learning models—SVM (Figure 5a) and XGB (Figure 5b)—highlighting the relative contribution and directional impact of each input variable on the models’ predictions. These plots serve as a critical interpretability component by demonstrating how the different water quality variables influence the predicted Chl-a concentrations. In this figure, the input features are sorted by their SHAP values so that a feature with a greater effect on the model’s performance is shown at a higher position. The colored dots represent the SHAP value of each sample in the data, whereas the color hue represents the actual value of the observed data, from high (red) to low (blue) values.

In both models, the particulate organic nitrogen (PON) emerges as the most influential predictor, with a clear positive correlation between high feature values (indicated in red) and increased SHAP values. This relationship suggests that higher PON levels strongly contribute to elevated Chl-a concentrations, aligning with prior ecological studies that have identified organic nitrogen as a key nutrient supporting algal proliferation [95]. Similarly, the particulate organic carbon (POC) and total phosphorus (TP) are consistently ranked among the top features, corroborating their known roles as eutrophication drivers in aquatic ecosystems [99].

A closer examination of the SHAP value distribution reveals nuanced interactions. For instance, ammonia (A) also exerted a substantial positive influence on the Chl-a predictions, particularly when its concentrations were high. In contrast, turbidity and temperature exhibited more complex, bidirectional patterns in the XGB model, indicating that their impact may be context-dependent or interact with other variables in the predictive process. The broader spread of SHAP values for these features highlights the heterogeneity of their influence across different data points, emphasizing the need for adaptive modeling frameworks that can account for such variability. While the SHAP values are model-specific, we observed strong agreement across multiple models in the ranking of the key features, such as PON, TP, and POC. Among these, the XGB model was selected for a detailed SHAP interpretation due to its high predictive accuracy, stability, and native compatibility with SHAP’s TreeExplainer. As a result, its interpretations are considered the most reliable among the ensemble of models examined.

Overall, Figure 5 and Table 6 not only validate the ecological relevance of the input features selected for modeling, but also demonstrate the value of integrating XAI methodologies. Although ensemble models, such as RF, DF, and XGB, are typically more complex than single decision trees, they achieved high predictive accuracy while maintaining strong interpretability, as shown through the SHAP analysis. In particular, the XGB and DF demonstrated that strong model performance (R² = 0.8517 and 0.8544, respectively) can be achieved without significantly compromising explainability. Simpler models, like the individual DT, offered greater inherent model transparency but with lower predictive performance (R² = 0.719), highlighting the classical trade-off between simplicity and predictive strength. In terms of interpretability, SHAP provides both global explanations (overall feature importance rankings across the dataset) and local explanations (how individual features contribute to specific predictions). This dual perspective is critical for real-world applications, where stakeholders may require both high-level understanding and case-specific insights. The ability of SHAP to offer both global and local interpretability of ensemble models strengthen the argument for explainable AI adoption, enabling the deployment of high-performing, transparent, and trustworthy HAB prediction systems in operational settings.

4. Conclusions

Predicting HABs is a major concern for devising a proper management strategy for governmental decision-making processes. Thus, the accurate prediction of HABs would allow the government to take proactive measures against these potential hazards. In recent years, advanced ML algorithms have been increasingly used for HAB prediction, and it is necessary to improve the practical applicability of these models. In this study, we presented a comprehensive and comparative analysis of ensemble ML methods for predicting chlorophyll-a concentrations, representing a significant shift from traditional methods by developing a model capable of providing integrated predictions across multiple monitoring stations rather than focusing on single-location predictions or satellite imagery.

We investigated the effectiveness of ensemble ML algorithms for predicting chlorophyll-a (Chl-a) concentrations in the western basin of Lake Erie over an eight-year period (2013–2020). Then, we studied model fusion based on stacking and voting strategies, aimed at improving the performance of weak ML algorithms. The high-performance ensemble ML models were then explained or interpreted using a SHAP analysis. For the linear ML models, the most accurate model was the SVM, with an R² value of 0.8160. The ensemble methods were, in general, able to achieve higher accuracies than the linear ML models, with the highest performing being the XGB and DF, with R² values of 0.8517 and 0.8544, respectively.

The fusion of weaker learners, such as the KNN and DT with R² values of 0.6044 and 0.7190, respectively, using the voting or stacking strategies can lead to a significant improvement in accuracy. However, the fusion of stronger learners often does not improve accuracy significantly, as demonstrated by the fusion of the MLP, KNN, SVM, and DT using the voting method. Our analysis revealed that several features significantly influence the Chl-a concentrations in Lake Erie, identifying the particulate organic carbon (POC), particulate organic nitrogen (PON), and total phosphorus (TP) as the most critical. We also found a correlation between increases in these factors and rising Chl-a concentrations, suggesting a potential link that warrants further investigation.

In summary, this study not only highlights the efficacy of the various ML models for HAB prediction but also contributes significantly to the field of environmental modeling by showing the potential of advanced ensemble machine learning techniques to enhance prediction accuracy and interpretability. The integration of explainable AI methodologies ensures that the model’s predictions are transparent and actionable, facilitating better management strategies for mitigating the impacts of HABs. Moreover, we also determined the effect of the fusion of multiple weaker and stronger models on their predictive accuracy regarding chlorophyll-a concentrations.

Although the overall prediction performance provided valuable insights, it is essential to recognize certain limitations of our study. The model was developed using only a limited number of stations due to missing data, and the training period was relatively short. Future studies should explore the integration of additional in situ measurements and remote sensing observations to enhance the data availability and improve model robustness. This would create opportunities for deep learning applications that could capture more intricate patterns in the HAB dynamics. Additionally, hybrid ML-DL approaches could be explored to leverage the strengths of both methodologies, combining the efficiency and interpretability of ensemble models with the advanced pattern recognition capabilities of deep learning. These advancements would contribute to more scalable and accurate HAB prediction frameworks. Additionally, incorporating parameters, such as meteorological data (e.g., air temperature, wind speed, precipitation, and solar irradiance) and hydrodynamic data (e.g., water level and flow rate) would enhance the model generalization and improve prediction accuracy by capturing the external drivers of HAB dynamics. It is important to note that generalizing these ML models to other environmental conditions or geographic areas would require caution. Regional differences in nutrient dynamics, hydrological processes, and biological responses may necessitate model retraining or the application of transfer learning techniques. Future studies should explore the adaptability of ensemble models to diverse aquatic environments by incorporating broader and more heterogeneous datasets.

Moreover, to support real-time deployment in field monitoring systems, future research should explore the development of lightweight and computationally efficient machine learning architectures. Techniques, such as model quantization, knowledge distillation, and neural network pruning, could reduce the computational demands while maintaining a high predictive performance. Additionally, integrating ensemble ML models with real-time remote sensing platforms and Internet of Things (IoT)-based monitoring networks could further enhance early-warning capabilities for HABs across diverse aquatic ecosystems. Designing an early-warning system for HAB onset would require redefining the problem as a classification task, establishing region-specific alert thresholds, and restructuring the data for time-lagged or lead-time prediction. These steps represent an important future direction for adapting ML models to real-time HAB risk forecasting and management.

Computational efficiency and feasibility in resource-constrained environments are critical considerations for practical deployment. High-accuracy models, such as DF and XGB, require substantial computational resources, which may limit their direct application in real-time settings. Potential solutions include model optimizing models, through pruning and quantization, and leveraging cloud–edge hybrid frameworks for distributed processing and implementing adaptive data sampling strategies that prioritize high-risk bloom periods. Furthermore, the application of transfer learning and domain adaptation could improve model generalization under conditions of limited or evolving data availability. Addressing these challenges will enhance the operational viability and scalability of ensemble ML models for real-time HAB monitoring and management.

In addition to addressing interpretability through XAI, we also considered the role of traditional process-based ecological models. While process-based models like EFDC, WASP, and QUAL2K offer valuable causal insights, they often require extensive data, complex calibration, and may struggle to maintain predictive accuracy under varied conditions. In this study, we addressed interpretability by combining ensemble ML models with explainable AI (SHAP), providing both global and local feature explanations without relying on process assumptions. This approach balances predictive performance with operational transparency, while future work may explore complementary comparisons with process-based models.

The methodology proposed in this study, integrating ensemble machine learning models with explainable AI (XAI), is highly adaptable and could be applied to various ecosystems and environmental challenges beyond HAB prediction in Lake Erie. The ensemble models used in this research are designed to handle complex, multivariate datasets, making them well suited for other water quality monitoring applications, such as detecting hypoxia, turbidity fluctuations, or chemical pollution events in different freshwater and marine systems. Additionally, the feature-importance analysis using SHAP provides insights that are valuable for understanding the environmental drivers in diverse contexts, including air pollution forecasting, soil contamination assessment, and ecological risk prediction. Given the increasing availability of remote sensing and in situ environmental data, the proposed approach could be extended to the large-scale, real-time monitoring of ecological systems across different geographic regions. Future work could explore the integration of additional environmental factors (such as meteorological and hydrodynamic variables), predictive uncertainty approaches (such as ensemble spread, quantile regression, or Bayesian machine learning), to further enhance model reliability and applicability in decision-making and early-warning systems, particularly in high-stakes environmental applications.