Machine Learning-Based Classification of Sulfide Mineral Spectral Emission in High Temperature Processes
Abstract
1. Introduction
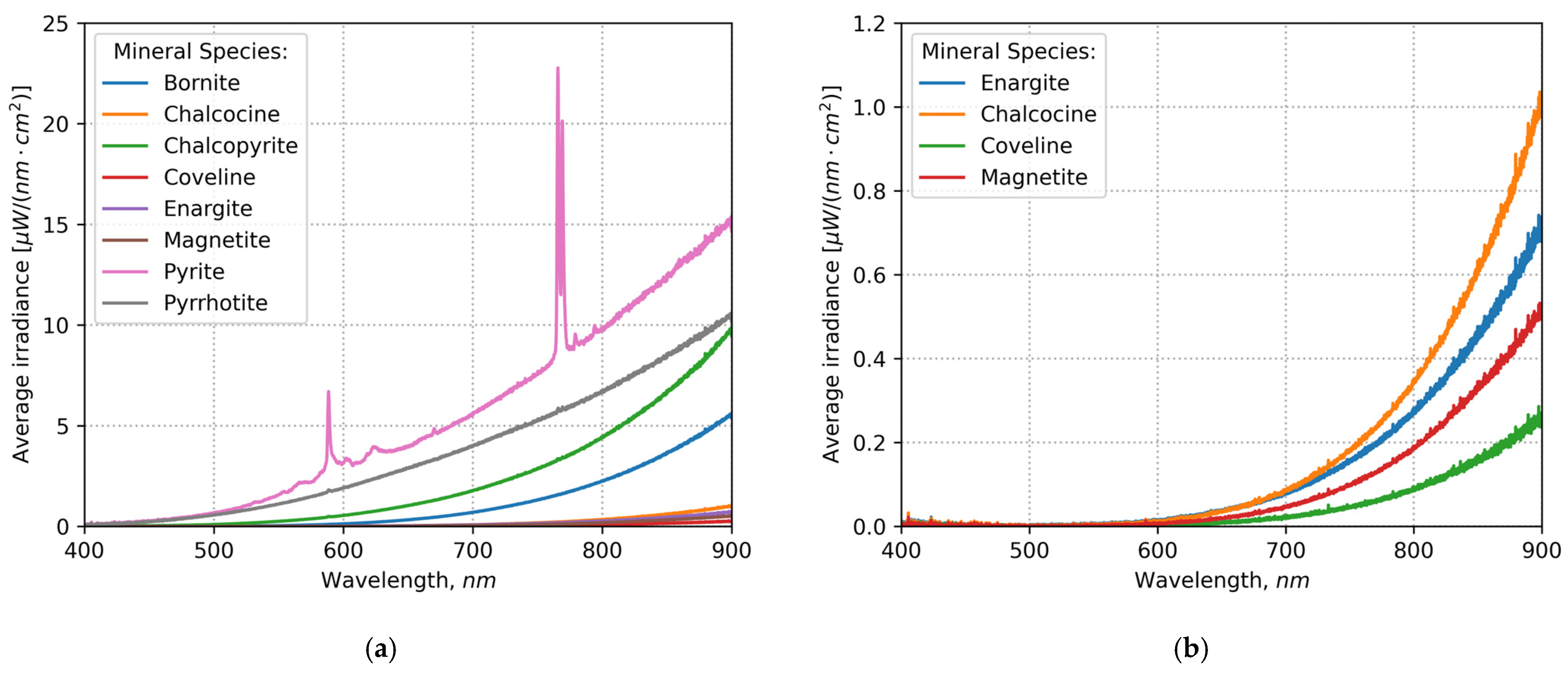
- Collection of a VIS-NIR emission spectral dataset of high-grade sulfide minerals during combustion. The dataset comprises 8294 spectral signals in the spectral range from 400 to 900 nm with a total of 2576 intensity samples, and it includes spectra from eight mineral species: bornite, chalcocine, chalcopiryte, coveline, enargite, magnetite, pyrite and pyrrhotite.
- Development of machine and deep learning models for the classification of emission spectral data. We implement and compare multiple classification approaches, including traditional machine learning and deep learning architectures such as 1D-CNNs. Emphasis is placed on model selection, hyperparameter tuning, and validation procedures to ensure generalization.
- Application of an adapted explainability method to enhance model interpretability. To address the black-box nature of deep learning models, we incorporate Grad-CAM as a post-hoc interpretability method. We generate heatmaps over the spectral input space, allowing us to visualize which spectral regions of the spectrum contributed most to the model’s classification decisions, and to correlate these identified features with known chemical emission lines and oxidation patterns of the sulfide minerals.
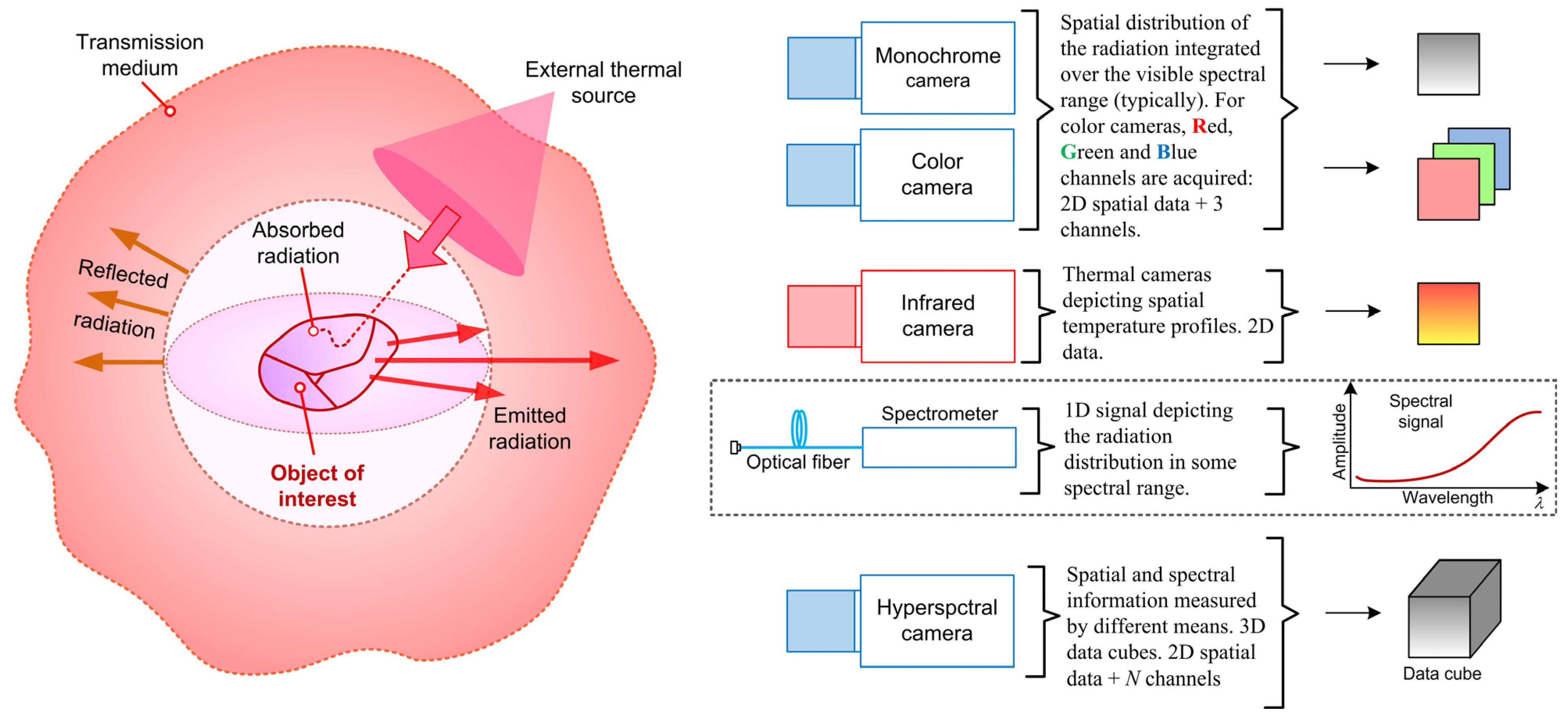
2. Background and Related Work
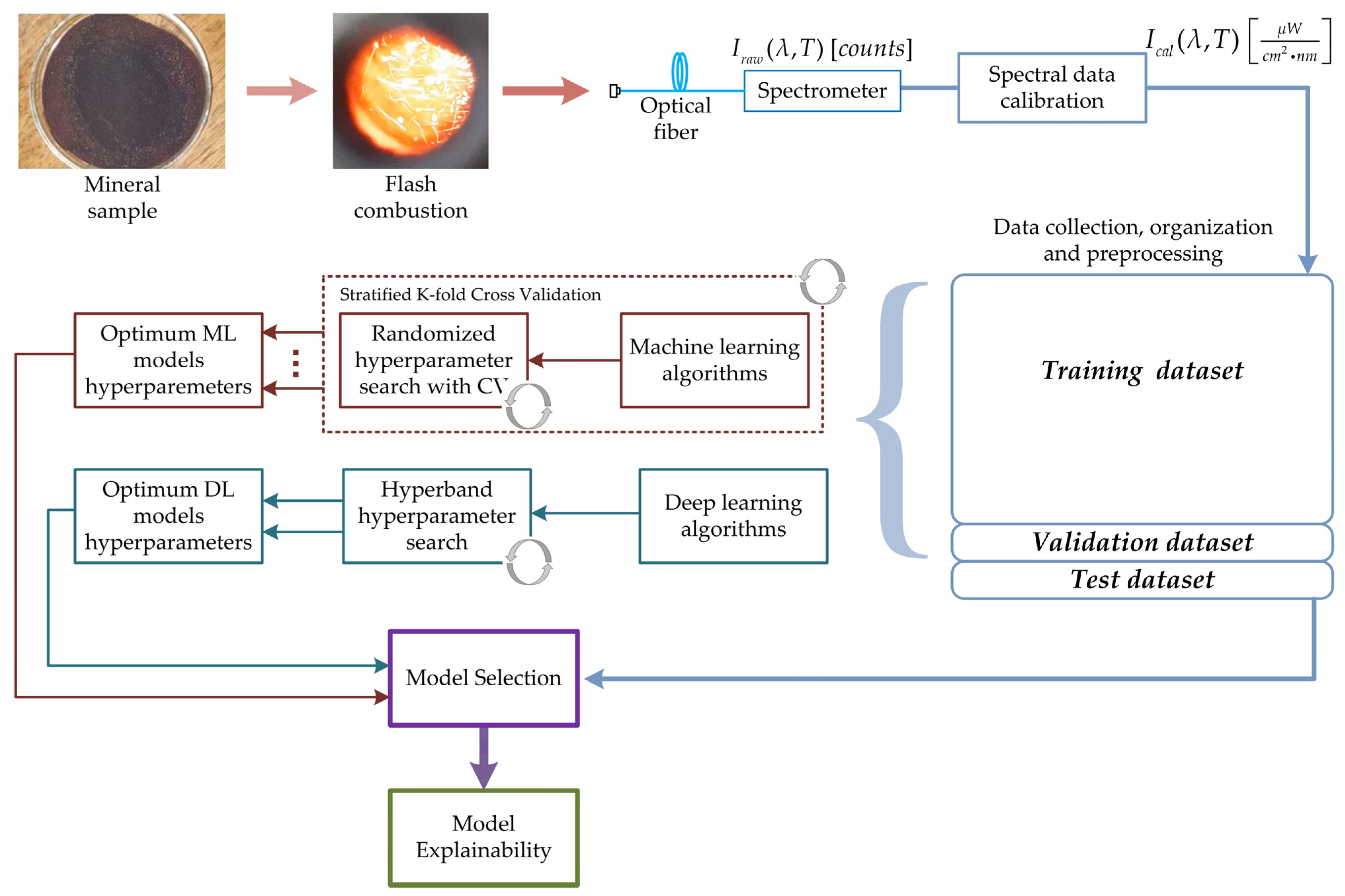
3. Materials and Methods
3.1. Experimental Setup and Spectral Acquisition
3.2. Spectral Signal Processing
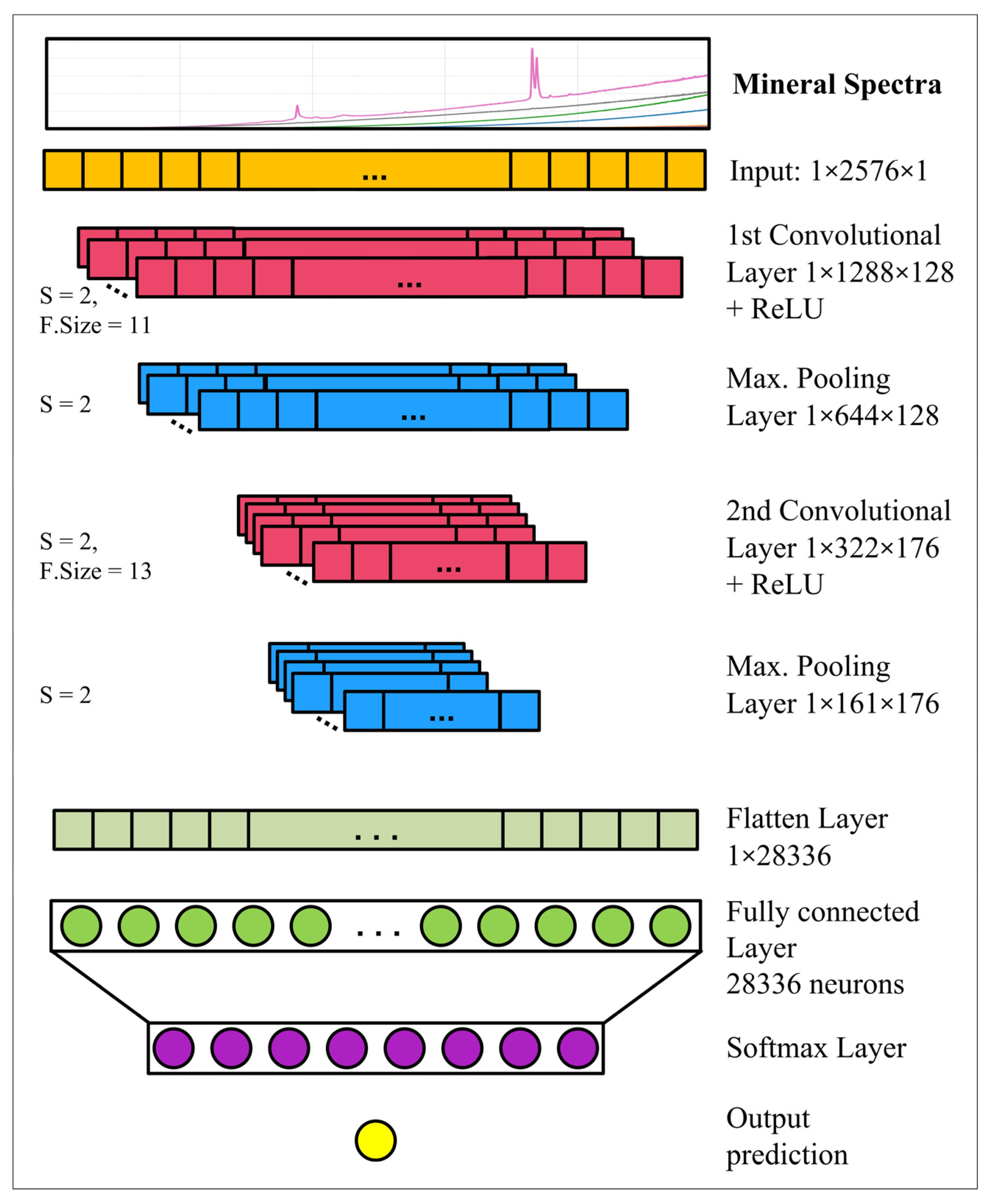
3.3. Machine and Deep Learning Modeling Strategies
- ▪
- K = Number of classes
- ▪
- = True Positives for class i, i.e., correctly classified instances of class i,
- ▪
- = False Negatives for class i, i.e., Instances of class i wrongly classified as another class.
| Metric | Definition | Formula |
|---|---|---|
| Accuracy (Acc) | Proportion of correctly predicted instances among all predictions | |
| Precision | Proportion of correctly predicted instances among all predicted positives ( is the number of false positives for class i) | |
| Recall | Proportion of correctly predicted instances among all actual positives | |
| F1-score | Harmonic mean of Precision and Recall |
4. Results and Discussion
4.1. Mineral Spectral Emission Data
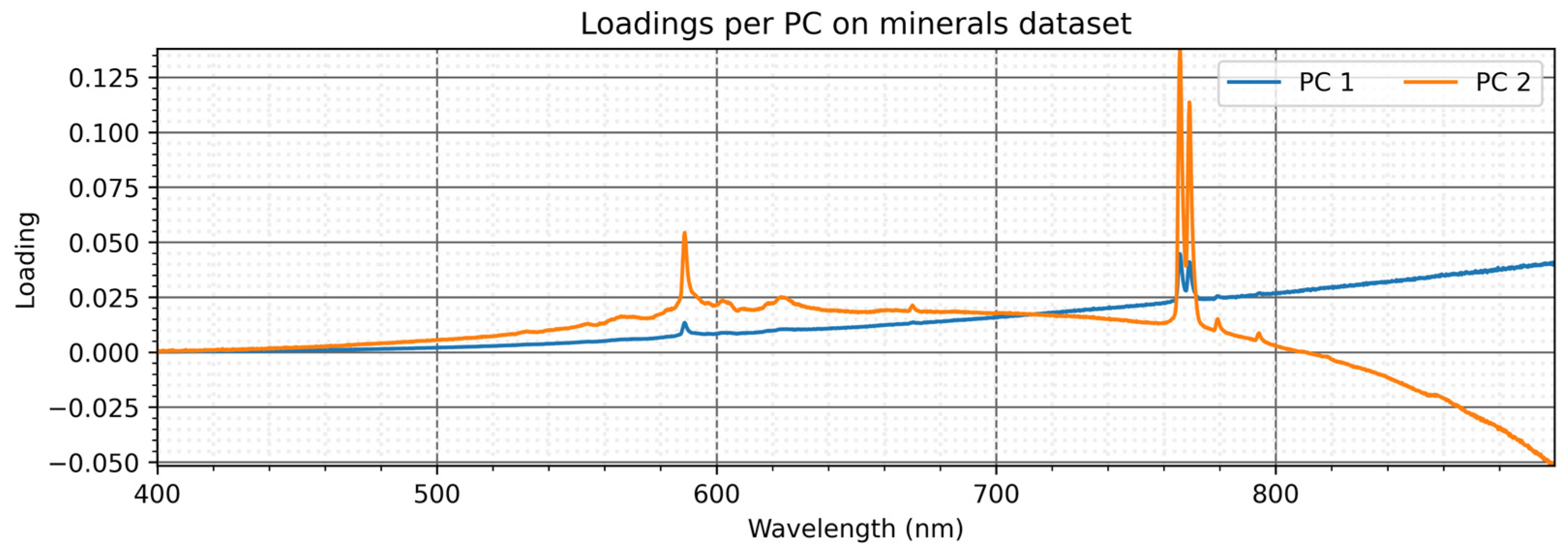
4.2. Principal Component Analysis
4.3. Classification Algorithms Evaluation
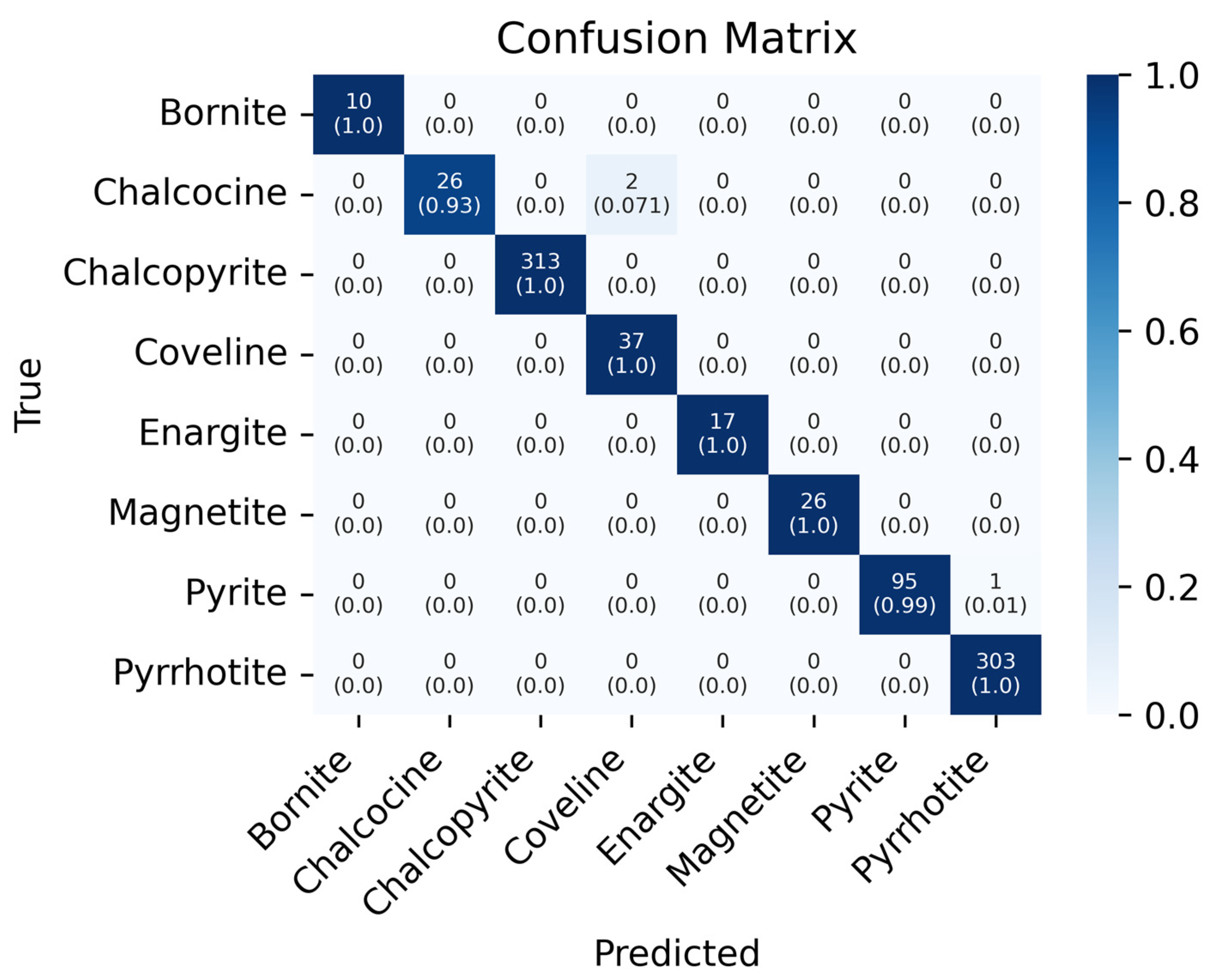
4.4. Discussion of the Optimized 1D-CNN Architecture
4.5. 1D-CNN Model Explainability
4.6. Limitations and Future Resarch Directions
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VIS | Visible |
| NIR | Near-Infrared |
| 1D-CNN | One-dimensional Convolutional Neural Network |
| Grad-CAM | Gradient-weighted Class Activation Mapping |
| FTIR | Fourier Transform Infrared |
| PCA | Principal Component Analysis |
| Adam | Adaptive Moment Estimation |
| SNR | Signal-to-Noise-Ratio |
| ANN | Artificial Neural Network |
| KNN | K-Nearest Neighbors |
| SVM | Support Vector Machine |
| DT | Decision Tree |
| HB | Histogram Boosting |
| RF | Random Forest |
| RAM | Random Access Memory |
| CPU | Central Processing Unit |
| GPU | Graphics Processing Unit |
| CV | Cross-Validation |
| Acc | Accuracy |
| BAcc | Balanced Accuracy |
References
- Schlesinger, M.E.; Sole, K.C.; Davenport, W.G.I.; Flores, G.R.F.A. Extractive Metallurgy of Copper; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar] [CrossRef]
- Davenport, W.G.; Jones, D.M.; King, M.J.; Partelpoeg, E.H. Flash Smelting: Analysis, Control and Optimization, 2nd Revised ed.; Wiley-Tms: Warrendale, PA, USA, 2004. [Google Scholar]
- Bacedoni, M.; Moreno-Ventas, I.; Ríos, G. Copper Flash Smelting Process Balance Modeling. Metals 2020, 10, 1229. [Google Scholar] [CrossRef]
- Kemori, N.; Ojima, Y.; Kondo, Y. Variation of the Composition and Size of Copper Concentrate Particles in the Reaction Shaft. In Proceedings of the Flash Reaction Processes; Center for Pyrometallurgy Conference, University of Missouri-Rolla: Rolla, MO, USA; University of Utah: Salt Lake City, UT, USA, 1988; pp. 47–68. [Google Scholar]
- Jokilaakso, A.; Suominen, R.; Pekka, T.; Lilius, K. Oxidation of Chalcopyrite in Simulated Suspension Smelting Conditions. Trans. Instit. Min. Metall.(Sect. C Mineral Process. Extr. Metall.) 1991, 100, C79–C90. [Google Scholar]
- Ahokainen, T.; Jokilaakso, A.; Vaarno, J.; Jarvi, J. Modelling Chalcopyrite Combustion Together with Fluid Flow Simulation. In Proceedings of the International Conference on CFD in the Mineral & Metal Processing and Power Generation, Melbourne, Australia, 3–4 July 1997; pp. 213–221. [Google Scholar]
- Pérez-Tello, M.; Parra, V.; Sánchez, V.; Gómez, A.; Brown, F.; Parra, R.; Balladares, E.; Araneda, E. Evolution of Size and Chemical Composition of Copper Concentrate Particles Oxidized Under Simulated Flash Smelting Conditions. Met. Mater. Trans. B 2018, 49, 627–643. [Google Scholar] [CrossRef]
- Jorgensen, F.R.A. Combustion of Pyrite Concentrate under Simulated Flash-Smelting Conditions. Trans. Inst. Mining Metall. 1981, 90, C1–C9. [Google Scholar]
- Jorgensen, F.R.A. Single-Particle Combustion of Chalcopyrite. Proc. Australas. Inst. Min. Metall. 1983, 288, 37–46. [Google Scholar]
- Jorgensen, F.R.A.; Moyle, F.J.; Wadsley, M.W. Structural Changes Associated with the Ignition of Pyrite and Chalcopyrite during Flash Smelting. In Process Mineralogy IX: Applications to Mineral Beneficiation, Metallurgy, Gold, Diamonds, Ceramics, Environment and Health; Minerals, Metals & Materials Society: Warrendale, PA, USA, 1989; pp. 323–341. [Google Scholar]
- Kemori, N.; Akada, A.; Kondo, Y. Development of a Concentrate Burner for Industrial Oxygen Flash Smelting. In Copper 91, Pyrometallurgy of Copper; Pergamon Press: Oxford, UK, 1991; pp. 141–154. [Google Scholar]
- Chen, H.R.; Mei, C.; Xie, K.; Li, X.; Zhou, J.; Wang, X.; Ge, Z. Operation Optimization of Concentrate Burner in Copper Flash Smelting Furnace. Trans. Nonferrous Met. Soc. China 2004, 14, 631–636. [Google Scholar]
- Jorgensen, F.R.A.; Campbell, A.; Taylor, R.; Washington, B. Sampling and Measurements in the Reaction Shaft at Olympic Dam. In Proceedings of the First Extractive Metallurgy Operators’ Conference, Melbourne, Australia, 7–8 November 2005; pp. 87–93. [Google Scholar]
- Parada, R.; Parra, R.; Wilkomirsky, I. Dynamic Simulation of a Flash Furnace. Can. Metall. Q. 2004, 43, 561–569. [Google Scholar] [CrossRef]
- Solnordal, C.B.; Jorgensen, F.R.A.; Koh, P.T.L.; Hunt, A. CFD Modelling of the Flow and Reactions in the Olympic Dam Flash Furnace Smelter Reaction Shaft. Appl. Math. Model. 2006, 30, 1310–1325. [Google Scholar] [CrossRef][Green Version]
- Jorgensen, F.R.A.; Zuiderwyk, M. Two-Colour Pyrometer Measurement of the Temperature of Individual Combusting Particles. J. Phys. E Sci. Instrum. 1985, 18, 486. [Google Scholar] [CrossRef]
- Tuffrey, N.E.; Richards, G.G.; Brimacombe, J.K. Two-Wavelength Pyrometry Study of the Combustion of Sulfide Minerals: Part I. Apparatus and General Observations. Metall. Materi. Trans. B 1995, 26, 929–942. [Google Scholar] [CrossRef]
- Morgan, G.J.; Brimacombe, J.K. Kinetics of the Flash Converting of MK (Chalcocite) Concentrate. Met. Mater. Trans B 1996, 27, 163–175. [Google Scholar] [CrossRef]
- Laurila, T.; Hernberg, R.; Oikari, R.; Joutsenoja, T.; Mikkola, P.; Ranki-Kilpinen, T.; Taskinen, P. Pyrometric temperature and size measurements of chalcopyrite particles during flash oxidation in a laminar flow reactor. Metall. Materi. Trans. B 2005, 36, 201–208. [Google Scholar] [CrossRef]
- Reyes, G. Desarrollo y Aplicación de un Sensor Optoelectrónico Para el Monitoreo de la Operación de un Horno de Fusión Flash de Concentrados de Cobre. Ph.D. Thesis, Universidad de Concepción, Concepción, Chile, 2021. Available online: https://repositorio.udec.cl/items/189dfe19-e58e-4aae-a714-e032da37799f (accessed on 12 May 2025).
- Díaz, W.; Toro, C.; Balladares, E.; Parra, V.; Coelho, P.; Reyes, G.; Parra, R. Spectral Characterization of Copper and Iron Sulfide Combustion: A Multivariate Data Analysis Approach for Mineral Identification on the Blend. Metals 2019, 9, 1017. [Google Scholar] [CrossRef]
- Toro, C.; Torres, S.; Parra, V.; Fuentes, R.; Castillo, R.; Díaz, W.; Reyes, G.; Balladares, E.; Parra, R. On the Detection of Spectral Emissions of Iron Oxides in Combustion Experiments of Pyrite Concentrates. Sensors 2020, 20, 1284. [Google Scholar] [CrossRef] [PubMed]
- Jahoda, P.; Drozdovskiy, I.; Payler, S.J.; Turchi, L.; Bessone, L.; Sauro, F. Machine learning for recognizing minerals from multispectral data. Analyst 2021, 146, 184–195. [Google Scholar] [CrossRef]
- Es-sahly, S.; Elbasbas, A.; Naji, K.; Lakssir, B.; Faqir, H.; Dadi, S.; Rabie, R. NIR-Spectroscopy and Machine Learning Models to Pre-concentrate Copper Hosted Within Sedimentary Rocks. Min. Metall. Explor. 2024, 41, 1979–1995. [Google Scholar] [CrossRef]
- Kok, M.; Sarjant, S.; Verweij, S.; Vaessen, S.F.C.; Ros, G.H. On-site soil analysis: A novel approach combining NIR spectroscopy, remote sensing and deep learning. Geoderma 2024, 446, 116903. [Google Scholar] [CrossRef]
- Smith, R.; Spano, T.L.; McDonnell, M.; Drane, L.; Gibbs, I.; Miskowiec, A.; Niedziela, J.L.; Shields, A.E. Interpretable Machine Learning Models Classify Minerals, Spectroscopy. Sci. Rep. 2025, 15, 15807. [Google Scholar] [CrossRef]
- Bernicky, A.R.; Davis, B.; Kadiyski, M.; Loock, H.-P. Mineralogical Analysis of Solid-Sample Flame Emission Spectra by Machine Learning. Anal. Chem. 2024, 96, 19330–19338. [Google Scholar] [CrossRef]
- Yang, B.; Yang, Z.; Xu, Y.; Cheng, W.; Zhong, F.; Ye, D.; Weng, H. A 1D-CNN model for the early detection of citrus Huanglongbing disease in the sieve plate of phloem tissue using micro-FTIR. Chemom. Intell. Lab. Syst. 2024, 252, 105202. [Google Scholar] [CrossRef]
- Li, X.; Wu, J.; Bai, T.; Wu, C.; He, Y.; Huang, J.; Li, X.; Shi, Z.; Hou, K. Variety classification and identification of jujube based on near-infrared spectroscopy and 1D-CNN. Comput. Electron. Agric. 2024, 223, 109122. [Google Scholar] [CrossRef]
- Sang, X.; Zhou, R.; Li, Y.; Xiong, S. One-Dimensional Deep Convolutional Neural Network for Mineral Classification from Raman Spectroscopy. Neural Process. Lett. 2022, 54, 677–690. [Google Scholar] [CrossRef]
- Qi, Y.; Hu, D.; Zheng, M.; Jiang, Y.; Chen, Y.P. Deep learning assisted Raman spectroscopy for rapid identification of 2D materials. Appl. Mater. Today 2024, 41, 102499. [Google Scholar] [CrossRef]
- Contreras, J.; Bocklitz, T. Explainable artificial intelligence for spectroscopy data: A review. Pflug. Arch. Eur J Physiol. 2024, 477, 603–615. [Google Scholar] [CrossRef]
- Beć, K.; Grabska, J.; Huck, C. Interpretability in near-infrared (NIR) spectroscopy: Current pathways to the long-standing challenge. TrAC-Trend. Anal. Chem. 2025, 189, 118254. [Google Scholar] [CrossRef]
- Xia, J.; Li, J.; Wang, X.; Li, Y.; Li, J. Enhanced cancer classification and critical feature visualization using Raman spectroscopy and convolutional neural networks. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2025, 326, 125242. [Google Scholar] [CrossRef]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-CAM: Visual Explanations from Deep Networks via Gradient-Based Localization. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar] [CrossRef]
- Shi, G.-Y.; Wu, H.-P.; Luo, S.-H.; Lu, X.-Y.; Ren, B.; Zhang, Q.; Lin, W.-Q.; Chen, R.-Y.; Guo, P.; Chen, H.-B.; et al. 1D Gradient-Weighted Class Activation Mapping, Visualizing Decision Process of Convolutional Neural Network-Based Models in Spectroscopy Analysis. Anal. Chem. 2023, 95, 9959–9966. [Google Scholar] [CrossRef]
- Wang, X.; Ni, L.; Zhang, C.; Xu, Q.; Ye, S. Using a one-dimensional convolutional neural network on FTIR spectroscopy to measure the thickness of composite plastic films. Infrared Phys. Technol. 2025, 147, 105777. [Google Scholar] [CrossRef]
- Szeghalmy, S.; Fazekas, A. A Comparative Study of the use of Stratified Cross-Validation and Distribution-Balanced Stratified Cross-Validation in Imbalanced Learning. Sensors 2023, 23, 2333. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Jamieson, K.; DeSalvo, G.; Rostamizadeh, A.; Talwalkar, A. Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization. J. Mach. Learn. Res. 2018, 18, 1–52. [Google Scholar]
- Zeng, F.; Peng, W.; Kang, G.; Feng, Z.; Yue, X. Spectral Data Classification by One-Dimensional Convolutional Neural Networks. In Proceedings of the 2021 IEEE International Performance, Computing, and Communications Conference (IPCCC), Austin, TX, USA, 29–31 October 2021. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Toro, C. Dataset of Spectral Emission of Mineral Species during Combustion. Figshare Dataset 2025. [Google Scholar] [CrossRef]
- Kokaly, R.F.; Clark, R.N.; Swayze, G.A.; Livo, K.E.; Hoefen, T.M.; Pearson, N.C.; Wise, R.A.; Benzel, W.M.; Lowers, H.A.; Driscoll, R.L.; et al. USGS Spectral Library Version 7 Data: U.S. Geological Survey Data Release; U.S. Geological Survey Data Release: Reston, VA, USA, 2017. [CrossRef]
- Kiranyas, S.; Abdeljaber, O.; Avci, O.; Gabbouj, M. 1-D Convolutional Neural Networks for Signal Processing Applications. In Proceedings of the 2019 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brighton, UK, 12–17 May 2019. [Google Scholar] [CrossRef]
- Gole, J.L. Toward the Modeling of the Oxidation of Small Metal and Metalloid Molecules. In Gas Phase Metal Reactions; Elsevier: Amsterdam, The Netherlands, 1992; pp. 573–604. ISBN 978-0-444-89070-2. [Google Scholar]



| Model | Hyperparameters | Values |
|---|---|---|
| KNN | K (n_neighbors) | 1 to 15 |
| Distance metrics (metric) | Minkowski, euclidian, manhattan, cosine | |
| SVM | Kernel function (kernel) | Linear, radial basis function (rbf), polynomial (poly), sigmoid |
| Regularization (C) | 1, 10, 100, 1000 | |
| Class Weight (class_weight) | Balanced, None | |
| Gamma | Scale, auto, 2 | |
| DT | Max depth | 5, 10, 15 |
| Max leaf nodes (max_leaf_nodes) | 2 to 20 with steps of 2 | |
| Min samples leaf (min_samples_leaf) | 1 to 10 with steps of 2 | |
| Min samples split (min_samples_split) | 2 to 10 with steps of 2 | |
| Impurity measure (criterion) | Entropy, gini | |
| HB | Maximum number of iterations (max_iter) | 50, 100, 150 |
| RF | N° estimators (n_estimators) | 10, 20, 50 |
| Model | Optimal Hyperparameters | Acc/BAcc (± σ) in Train | Acc/BAcc in Test | Precision a/w * in Test | Recall a/w * in Test | F1-Score a/w * in Test |
|---|---|---|---|---|---|---|
| KNN | K = 3 neighbors Distance metric: Minkowski | 0.878/ 0.884 ± 0.010 | 0.864/0.879 | 0.874/0.913 | 0.879/0.864 | 0.811/0.848 |
| SVM | Linear kernel Regularization: C = 1000 | 0.998/ 0.983 ± 0.004 | 0.983/0.980 | 0.987/0.983 | 0.980/0.983 | 0.983/0.982 |
| DT | Max depth = 10 Max leaf nodes = 16 Min samples leaf = 7 Min samples split = 10 Impurity measure: Entropy | 0.945/ 0.886 ± 0.016 | 0.914/0.876 | 0.887/0.925 | 0.886/0.920 | 0.878/0.917 |
| HB | Max iter = 100 | 0.999/ 0.985 ± 0.006 | 0.993/0.982 | 0.991/0.993 | 0.982/0.993 | 0.986/0.993 |
| RF | N° estimators = 50 | 0.999/ 0.973 ± 0.009 | 0.989/0.977 | 0.984/0.989 | 0.977/0.989 | 0.980/0.989 |
| Model | Optimal Hyperparameters | Training Acc/BAcc | Testing Acc/Bacc | Precision a/w in Test | Recall a/w in Test | F1-Score a/w in Test |
|---|---|---|---|---|---|---|
| ANN | N° hidden layers = 3 Neurons per layer = {640, 1408, 1920} Activation function = ReLu Learning rate = 0.0001 | 0.978/0.899 | 0.961/0.898 | 0.880/0.960 | 0.860/0.960 | 0.870/0.960 |
| 1D-CNN | N° conv. layers = 2 N° filters per layer = {128, 176} Filters size per layer = {11, 13} Stride = 2 for all layers Learning rate = 0.0001 Activation function = ReLu | 0.997/0.991 | 0.996/0.990 | 0.990/1.00 | 0.990/1.00 | 0.990/1.00 |
| Model Pair | BAcc Difference | McNemar’s Test (p-Value) * |
|---|---|---|
| 1D-CNN vs ANN | 0.092 | 4.336 × 10−63 |
| 1D-CNN vs HB | 0.008 | 5.152 × 10−3 |
| HB vs ANN | 0.084 | 7.521 × 10−57 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toro, C.; Díaz, W.; Reyes, G.; Peña, M.; Caselli, N.; Taramasco, C.; Ormeño-Arriagada, P.; Balladares, E. Machine Learning-Based Classification of Sulfide Mineral Spectral Emission in High Temperature Processes. Big Data Cogn. Comput. 2025, 9, 130. https://doi.org/10.3390/bdcc9050130
Toro C, Díaz W, Reyes G, Peña M, Caselli N, Taramasco C, Ormeño-Arriagada P, Balladares E. Machine Learning-Based Classification of Sulfide Mineral Spectral Emission in High Temperature Processes. Big Data and Cognitive Computing. 2025; 9(5):130. https://doi.org/10.3390/bdcc9050130
Chicago/Turabian StyleToro, Carlos, Walter Díaz, Gonzalo Reyes, Miguel Peña, Nicolás Caselli, Carla Taramasco, Pablo Ormeño-Arriagada, and Eduardo Balladares. 2025. "Machine Learning-Based Classification of Sulfide Mineral Spectral Emission in High Temperature Processes" Big Data and Cognitive Computing 9, no. 5: 130. https://doi.org/10.3390/bdcc9050130
APA StyleToro, C., Díaz, W., Reyes, G., Peña, M., Caselli, N., Taramasco, C., Ormeño-Arriagada, P., & Balladares, E. (2025). Machine Learning-Based Classification of Sulfide Mineral Spectral Emission in High Temperature Processes. Big Data and Cognitive Computing, 9(5), 130. https://doi.org/10.3390/bdcc9050130












