Identifying Influential Nodes in Complex Networks via Transformer with Multi-Scale Feature Fusion
Abstract
1. Introduction
- (1)
- We construct global and local feature maps based on node-level global and local metrics, as well as their one-hop adjacency matrix, enabling multi-scale feature input.
- (2)
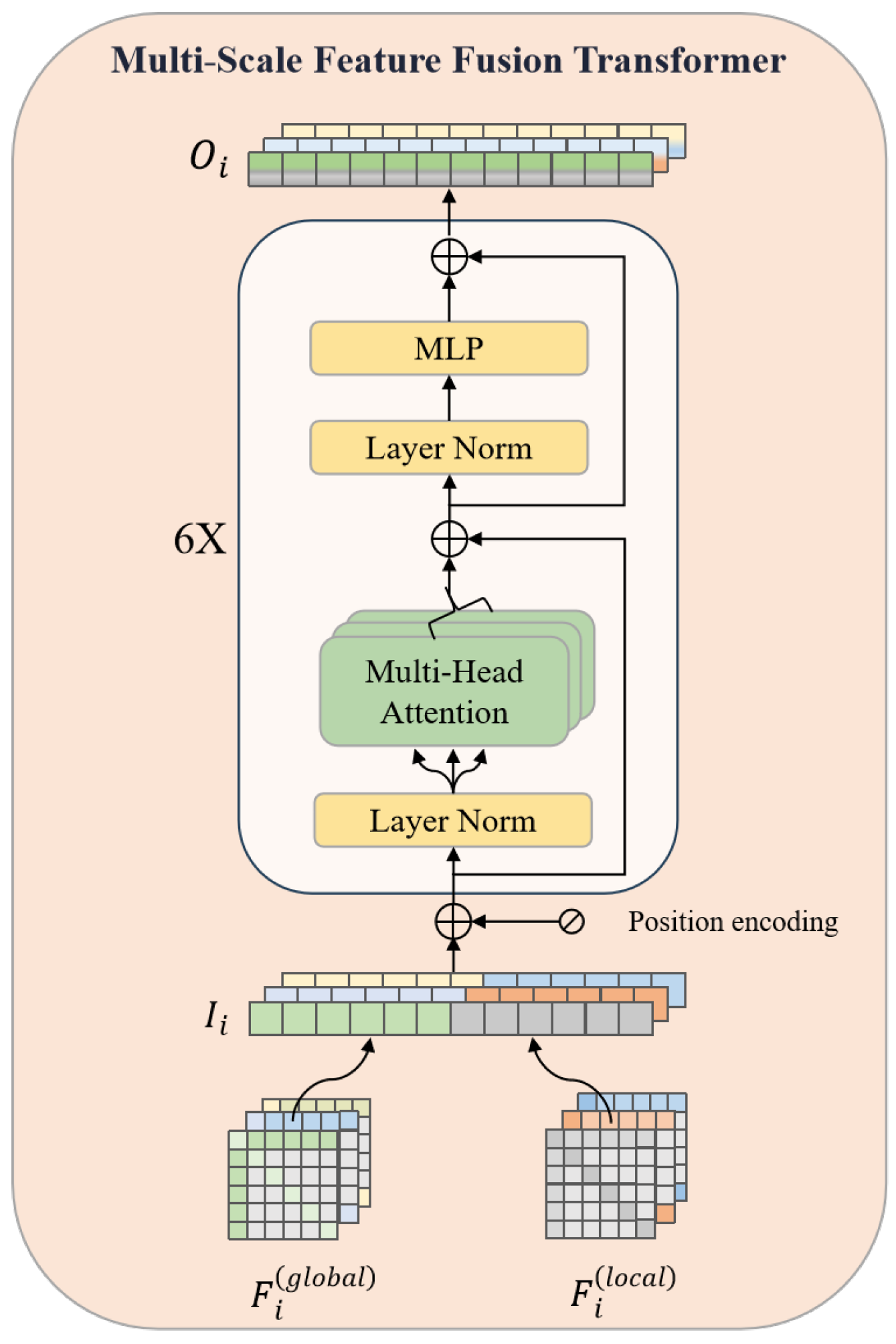
- We introduce a multi-scale fusion transformer module for feature analysis, combining both global and local node information to achieve more precise identification of node influence.
- (3)
- We conduct parameter optimization analysis to determine the optimal configuration that balances model performance with computational cost, improving prediction accuracy.
- (4)
- We evaluate MSF-Former on nine distinct network datasets (three synthetic, six real-world), and the experimental findings reveal that it outperforms seven baseline approaches in identifying influential nodes under diverse infection scenarios.
2. Notations and Acronyms
3. Related Works
3.1. Centrality-Based Approaches
3.2. Machine Learning- and Deep Learning-Based Approaches
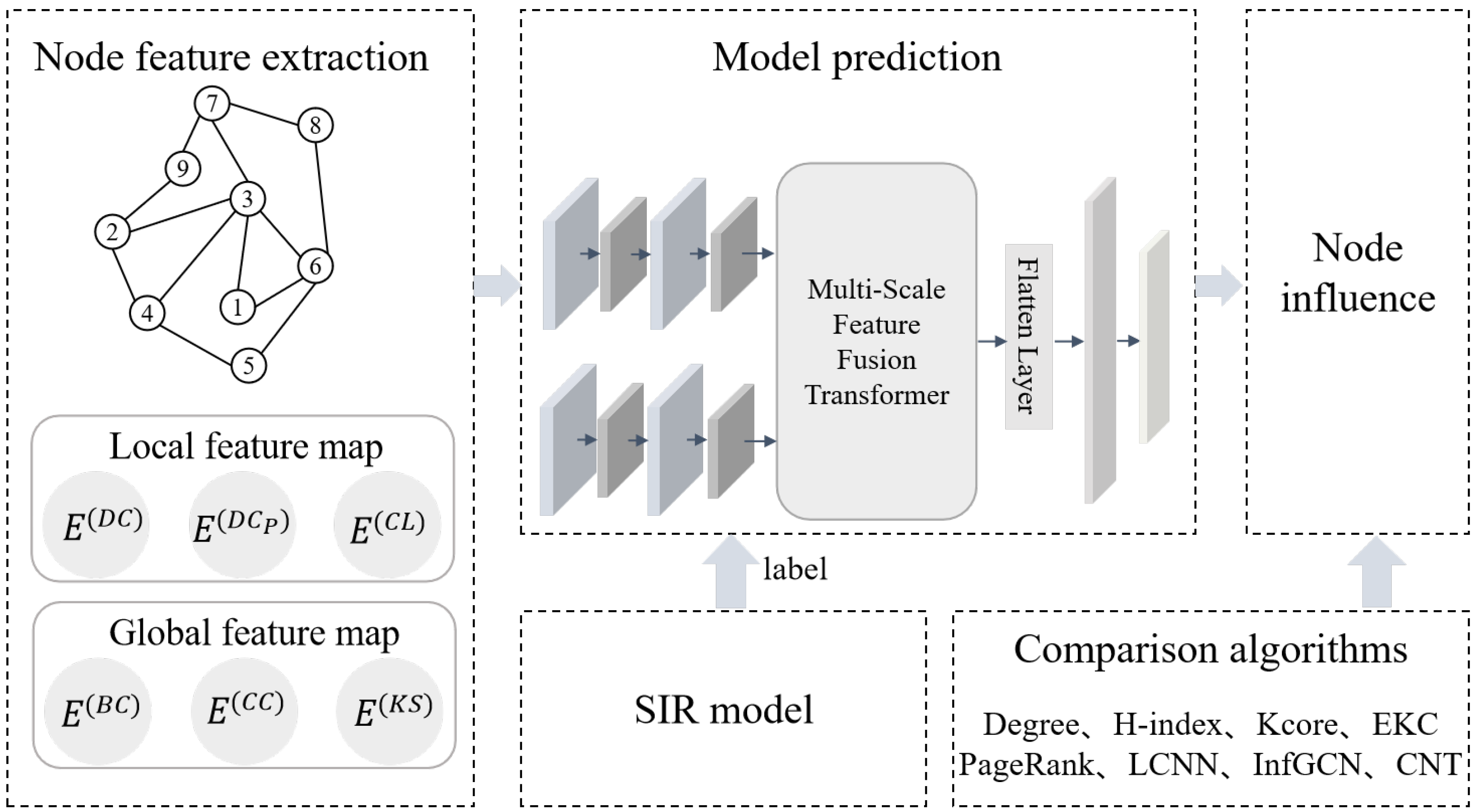
4. Methodology
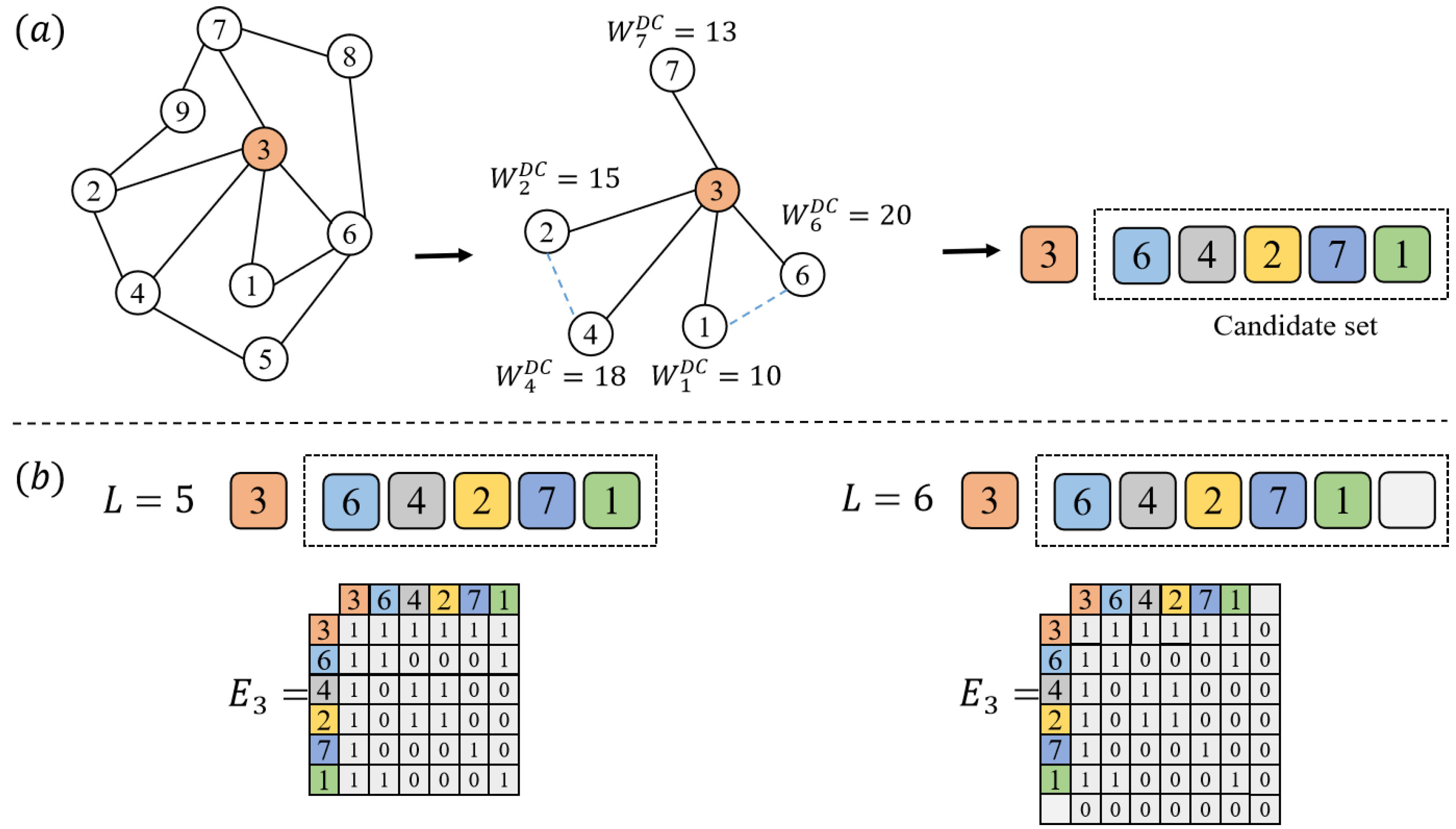
4.1. Node Feature Extraction
4.2. Label
4.3. Model Prediction
5. Experiment
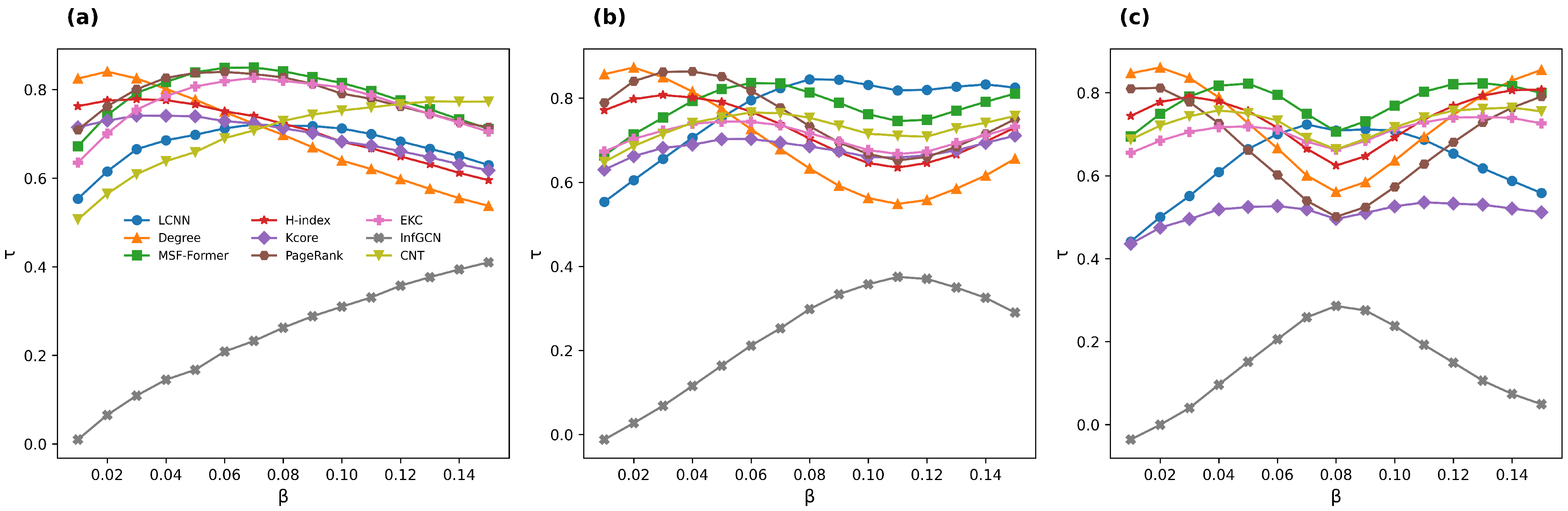
5.1. Kendall Correlation Coefficient
5.2. Datasets
5.3. Benchmark Methods
- (1)
- Degree centrality
- (2)
- K-core centrality
- (3)
- H-index
- (4)
- PageRank centrality
- (5)
- EKC
- (6)
- InfGCN
- (7)
- LCNN
- (8)
- CNT
5.4. Implementation Details
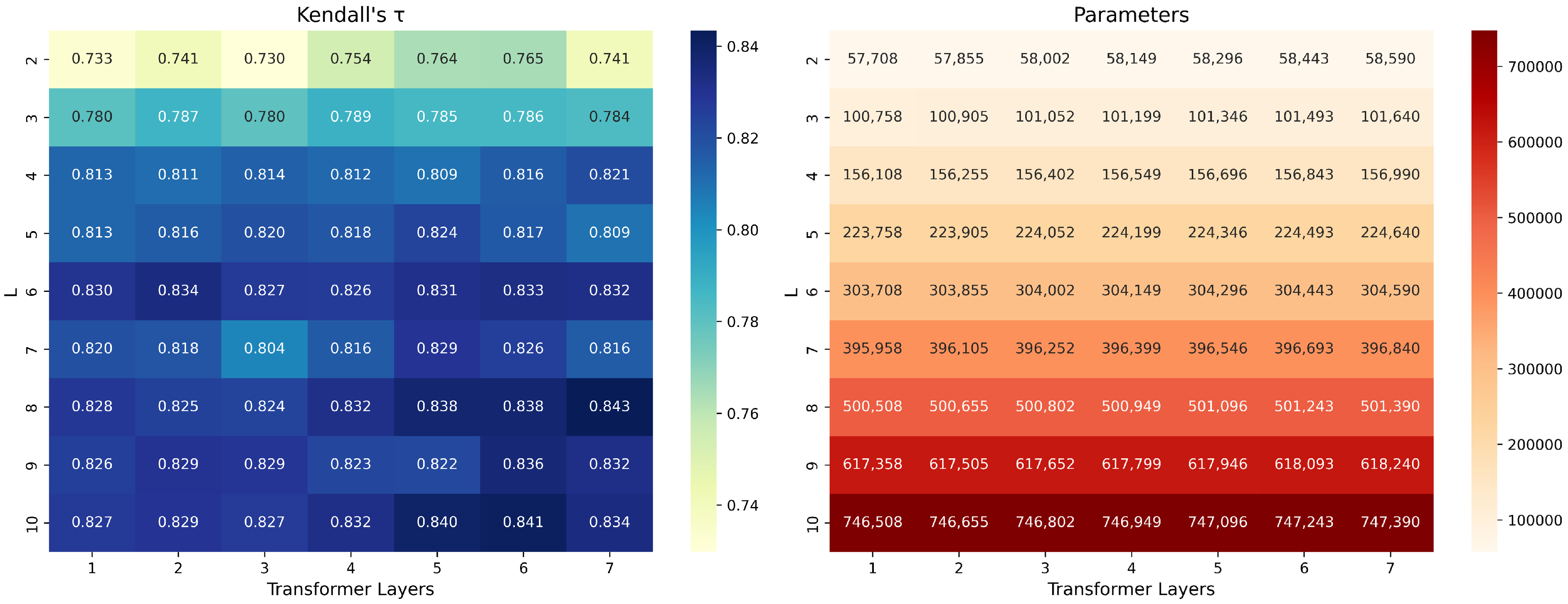
5.5. Model Parameter Analysis
5.6. Experimental Results
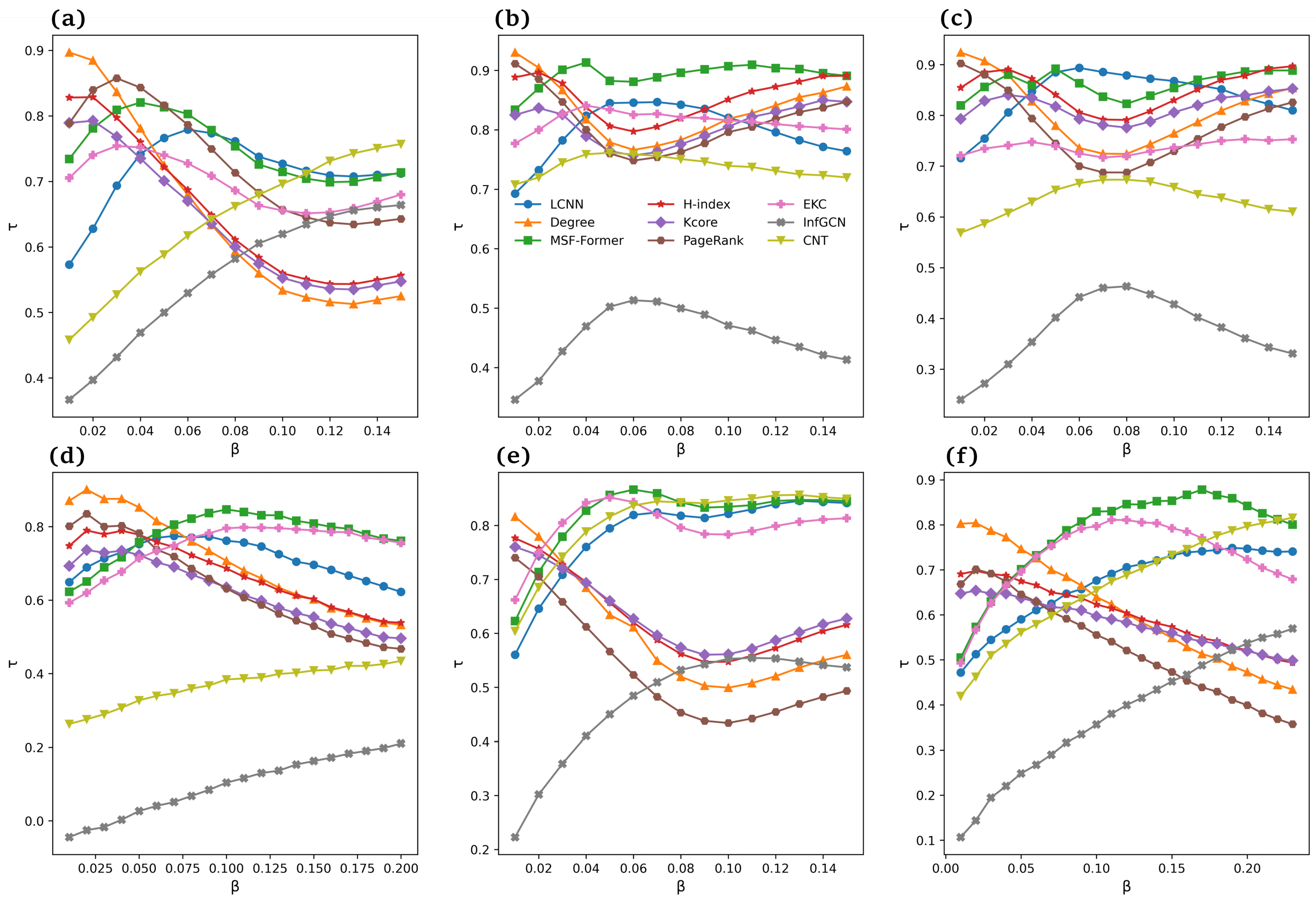
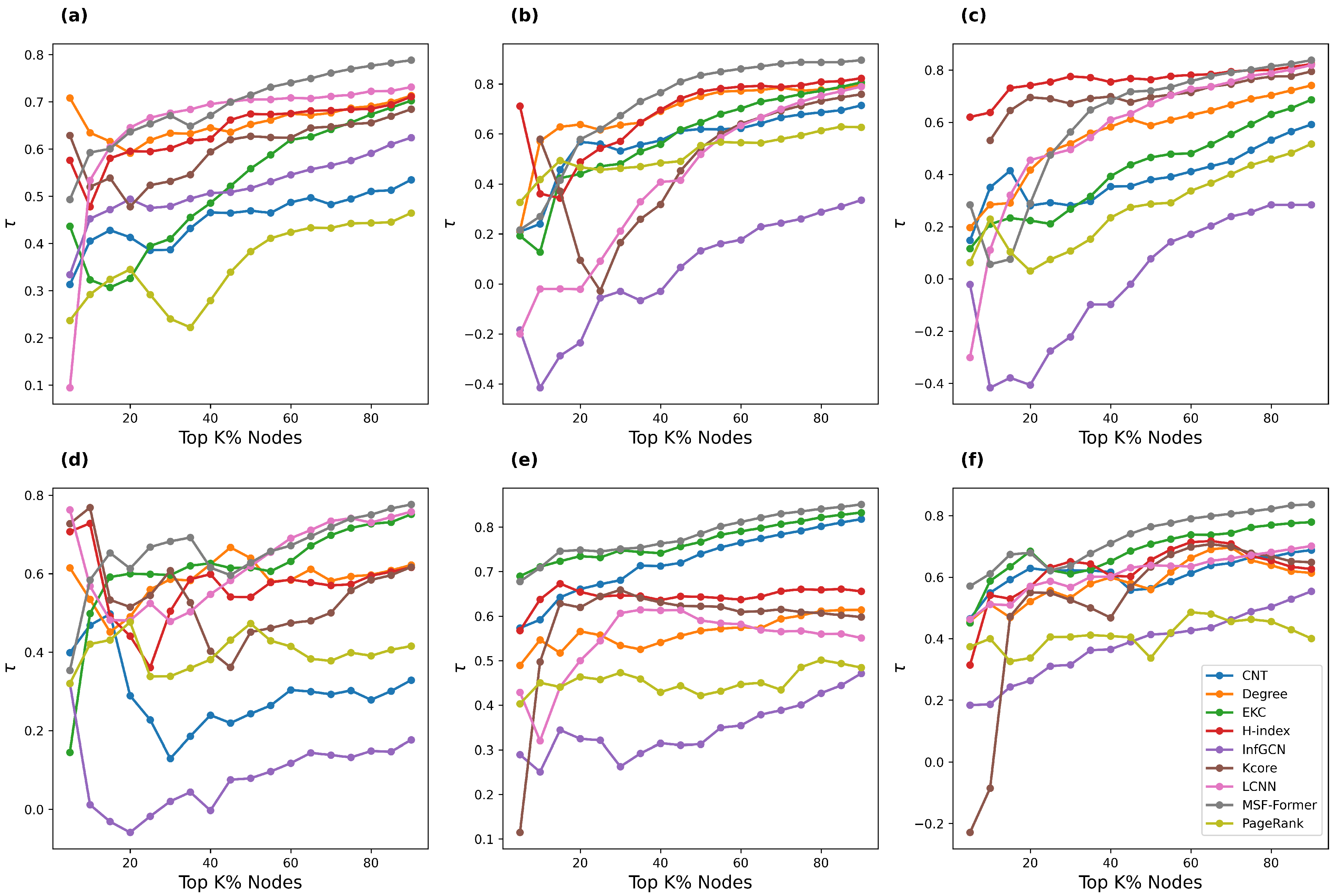
5.6.1. Synthetic Networks
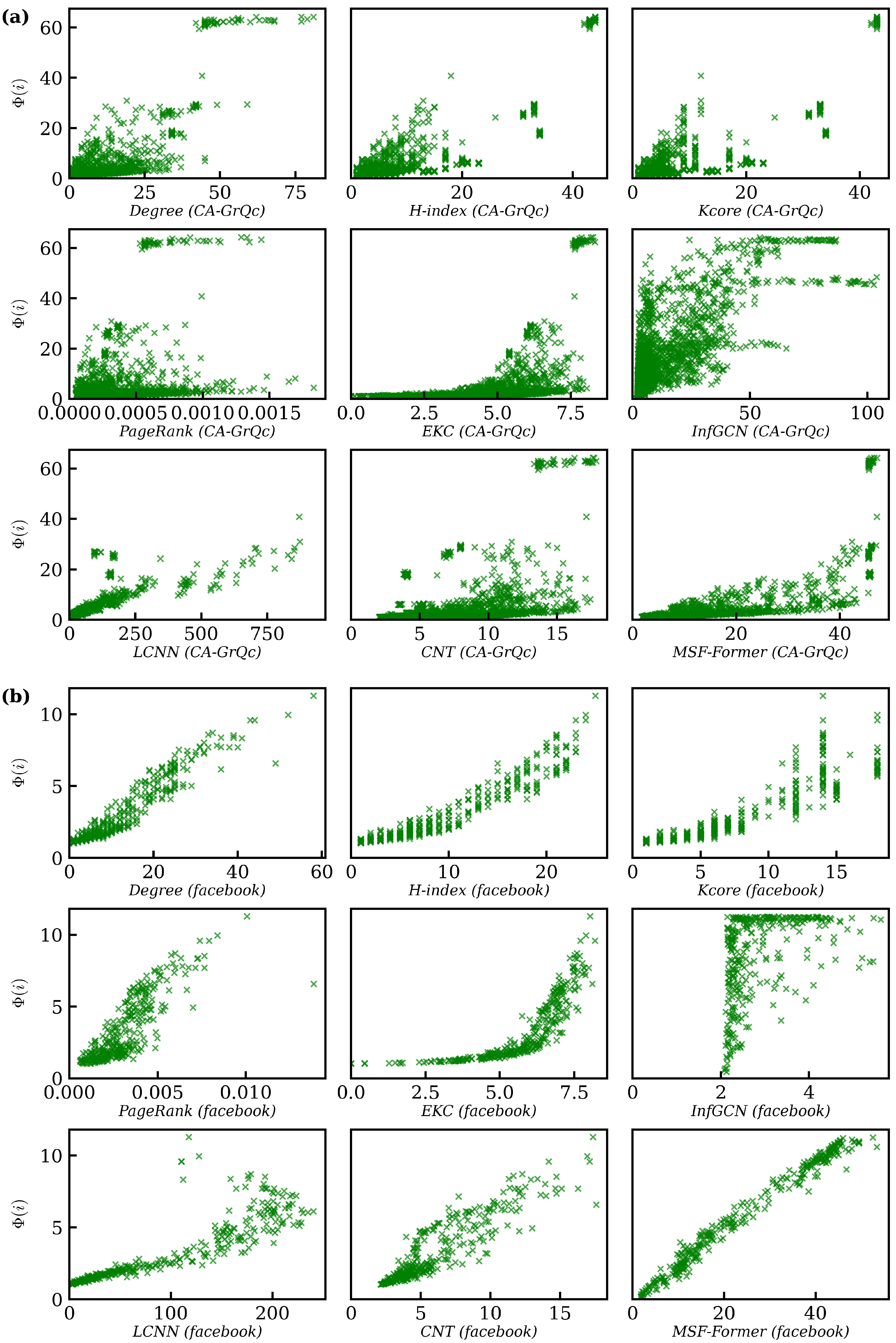
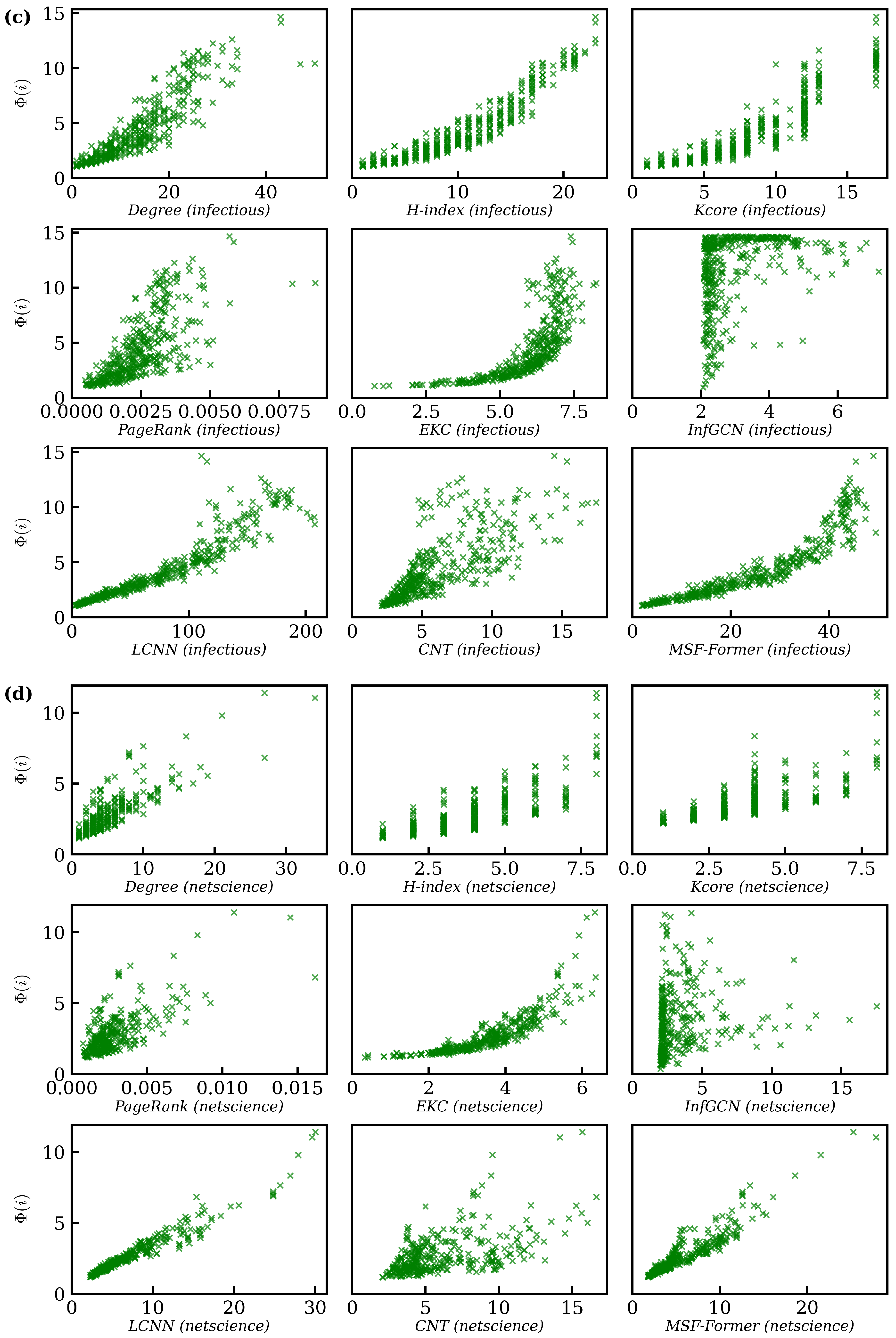
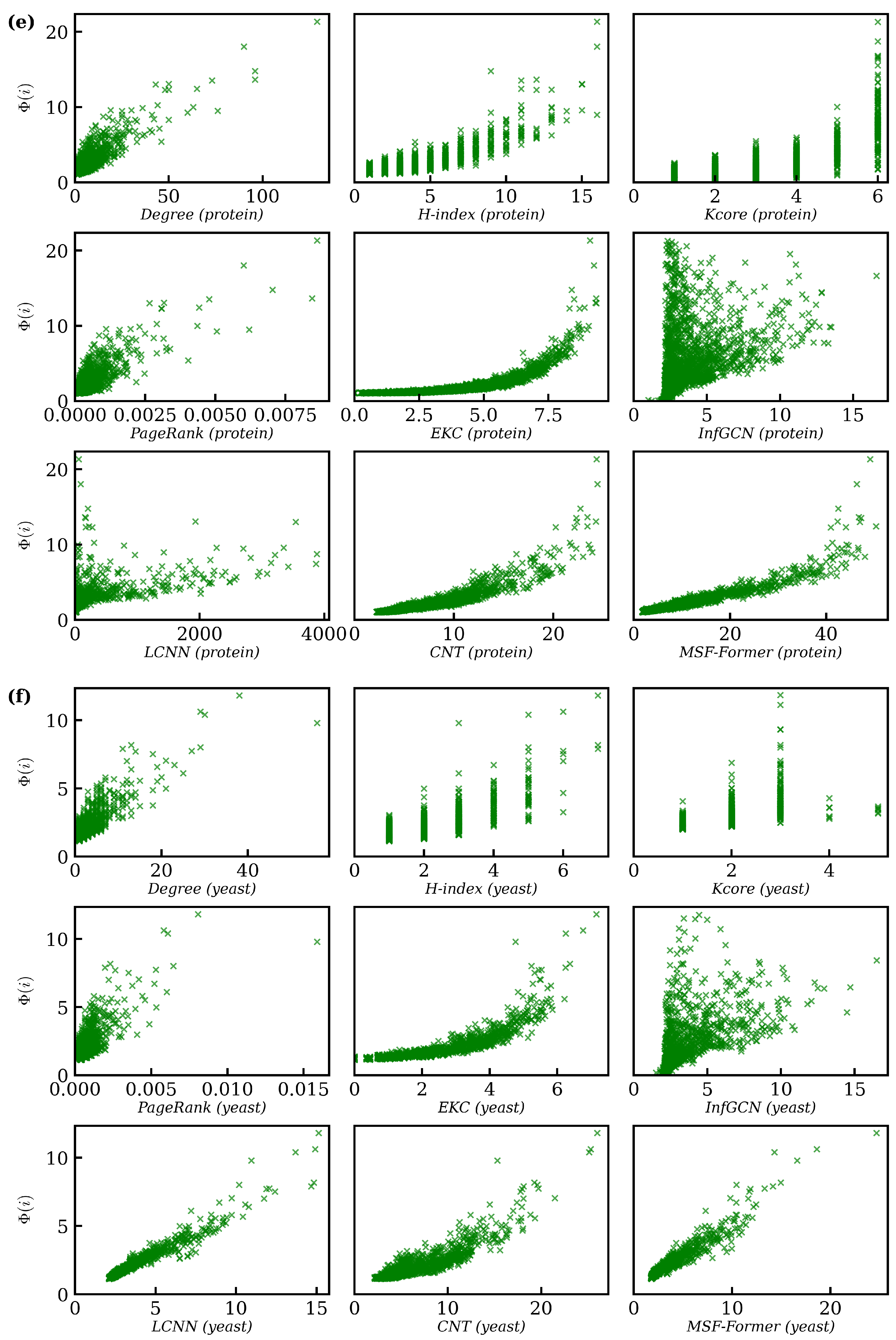
5.6.2. Real-World Network Validation
5.6.3. Computational Complexity
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lü, L.; Chen, D.; Ren, X.L.; Zhang, Q.M.; Zhang, Y.C.; Zhou, T. Vital nodes identification in complex networks. Phys. Rep. 2016, 650, 1–63. [Google Scholar] [CrossRef]
- Pastor-Satorras, R.; Vespignani, A. Epidemic spreading in scale-free networks. Phys. Rev. Lett. 2001, 86, 3200. [Google Scholar] [CrossRef] [PubMed]
- Albert, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Mod. Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Zeng, Y. Evaluation of node importance and invulnerability simulation analysis in complex load-network. Neurocomputing 2020, 416, 158–164. [Google Scholar] [CrossRef]
- Albert, R.; Jeong, H.; Barabási, A.L. Diameter of the world-wide web. Nature 1999, 401, 130–131. [Google Scholar] [CrossRef]
- Freeman, L.C. A set of measures of centrality based on betweenness. Sociometry 1977, 40, 35–41. [Google Scholar] [CrossRef]
- Sabidussi, G. The centrality index of a graph. Psychometrika 1966, 31, 581–603. [Google Scholar] [CrossRef]
- Lü, L.; Zhou, T.; Zhang, Q.M.; Stanley, H.E. The H-index of a network node and its relation to degree and coreness. Nat. Commun. 2016, 7, 10168. [Google Scholar] [CrossRef] [PubMed]
- Kitsak, M.; Gallos, L.K.; Havlin, S.; Liljeros, F.; Muchnik, L.; Stanley, H.E.; Makse, H.A. Identification of influential spreaders in complex networks. Nat. Phys. 2010, 6, 888–893. [Google Scholar] [CrossRef]
- Wen, X.; Tu, C.; Wu, M.; Jiang, X. Fast ranking nodes importance in complex networks based on LS-SVM method. Phys. A Stat. Mech. Its Appl. 2018, 506, 11–23. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Z.; Liu, J.; Gai, K. A new complex network robustness attack algorithm. In Proceedings of the 2019 ACM International Symposium on Blockchain and Secure Critical Infrastructure, Auckland, New Zealand, 8 July 2019; pp. 13–17. [Google Scholar] [CrossRef]
- Zhao, G.; Jia, P.; Huang, C.; Zhou, A.; Fang, Y. A machine learning based framework for identifying influential nodes in complex networks. IEEE Access 2020, 8, 65462–65471. [Google Scholar] [CrossRef]
- Fan, C.; Zeng, L.; Sun, Y.; Liu, Y.Y. Finding key players in complex networks through deep reinforcement learning. Nat. Mach. Intell. 2020, 2, 317–324. [Google Scholar] [CrossRef]
- Yu, E.Y.; Wang, Y.P.; Fu, Y.; Chen, D.B.; Xie, M. Identifying critical nodes in complex networks via graph convolutional networks. Knowl.-Based Syst. 2020, 198, 105893. [Google Scholar] [CrossRef]
- Tang, J.; Qu, J.; Song, S.; Zhao, Z.; Du, Q. GCNT: Identify influential seed set effectively in social networks by integrating graph convolutional networks with graph transformers. J. King Saud Univ.-Comput. Inf. Sci. 2024, 36, 102183. [Google Scholar] [CrossRef]
- Ye, L.; Rochan, M.; Liu, Z.; Wang, Y. Cross-modal self-attention network for referring image segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 10502–10511. [Google Scholar]
- Tzinis, E.; Wisdom, S.; Jansen, A.; Hershey, S.; Remez, T.; Ellis, D.P.; Hershey, J.R. Into the wild with audioscope: Unsupervised audio-visual separation of on-screen sounds. arXiv 2020, arXiv:2011.01143. [Google Scholar] [CrossRef]
- Gabeur, V.; Sun, C.; Alahari, K.; Schmid, C. Multi-modal transformer for video retrieval. In Proceedings of the European Conference on Computer Vision, Glasgow, UK, 23–28 August 2020; Springer: Cham, Switzerland, 2020; pp. 214–229. [Google Scholar]
- Dzabraev, M.; Kalashnikov, M.; Komkov, S.; Petiushko, A. Mdmmt: Multidomain multimodal transformer for video retrieval. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3354–3363. [Google Scholar]
- Iashin, V.; Rahtu, E. Multi-modal dense video captioning. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 14–19 June 2020; pp. 958–959. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Opsahl, T.; Agneessens, F.; Skvoretz, J. Node centrality in weighted networks: Generalizing degree and shortest paths. Soc. Netw. 2010, 32, 245–251. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, J.; Li, X.; Li, M.; Di, Z.; Fan, Y. Clustering coefficient and community structure of bipartite networks. Phys. A Stat. Mech. Its Appl. 2008, 387, 6869–6875. [Google Scholar] [CrossRef]
- Zhao, G.; Jia, P.; Zhou, A.; Zhang, B. InfGCN: Identifying influential nodes in complex networks with graph convolutional networks. Neurocomputing 2020, 414, 18–26. [Google Scholar] [CrossRef]
- Li, Y.; Cai, W.; Li, Y.; Du, X. Key node ranking in complex networks: A novel entropy and mutual information-based approach. Entropy 2019, 22, 52. [Google Scholar] [CrossRef]
- Chen, L.; Xi, Y.; Dong, L.; Zhao, M.; Li, C.; Liu, X.; Cui, X. Identifying influential nodes in complex networks via Transformer. Inf. Process. Manag. 2024, 61, 103775. [Google Scholar] [CrossRef]
- Ahmad, W.; Wang, B.; Chen, S. Learning to rank influential nodes in complex networks via convolutional neural networks. Appl. Intell. 2024, 54, 3260–3278. [Google Scholar] [CrossRef]
- Bonacich, P. Power and centrality: A family of measures. Am. J. Sociol. 1987, 92, 1170–1182. [Google Scholar] [CrossRef]
- Xu, X.; Zhu, C.; Wang, Q.; Zhu, X.; Zhou, Y. Identifying vital nodes in complex networks by adjacency information entropy. Sci. Rep. 2020, 10, 2691. [Google Scholar] [CrossRef]
- Brin, S.; Page, L. The anatomy of a large-scale hypertextual web search engine. Comput. Netw. ISDN Syst. 1998, 30, 107–117. [Google Scholar] [CrossRef]
- Lü, L.; Zhang, Y.C.; Yeung, C.H.; Zhou, T. Leaders in social networks, the delicious case. PLoS ONE 2011, 6, e21202. [Google Scholar] [CrossRef]
- Curado, M.; Tortosa, L.; Vicent, J.F. A novel measure to identify influential nodes: Return random walk gravity centrality. Inf. Sci. 2023, 628, 177–195. [Google Scholar] [CrossRef]
- Ullah, A.; Wang, B.; Sheng, J.; Long, J.; Khan, N.; Sun, Z. Identifying vital nodes from local and global perspectives in complex networks. Expert Syst. Appl. 2021, 186, 115778. [Google Scholar] [CrossRef]
- Liu, W.; Lu, P.; Zhang, T. Identifying influential nodes in complex networks from semi-local and global perspective. IEEE Trans. Comput. Soc. Syst. 2023, 11, 2105–2120. [Google Scholar] [CrossRef]
- Ullah, A.; Meng, Y. Finding influential nodes via graph embedding and hybrid centrality in complex networks. Chaos Solitons Fractals 2025, 194, 116151. [Google Scholar] [CrossRef]
- Rezaei, A.A.; Munoz, J.; Jalili, M.; Khayyam, H. A machine learning-based approach for vital node identification in complex networks. Expert Syst. Appl. 2023, 214, 119086. [Google Scholar] [CrossRef]
- Zhang, M.; Wang, X.; Jin, L.; Song, M.; Li, Z. A new approach for evaluating node importance in complex networks via deep learning methods. Neurocomputing 2022, 497, 13–27. [Google Scholar] [CrossRef]
- Kermack, W.O.; McKendrick, A.G. A contribution to the mathematical theory of epidemics. Proc. R. Soc. London. Ser. A Contain. Pap. Math. Phys. Character 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Bae, J.; Kim, S. Identifying and ranking influential spreaders in complex networks by neighborhood coreness. Phys. A Stat. Mech. Its Appl. 2014, 395, 549–559. [Google Scholar] [CrossRef]
- Maas, A.L.; Hannun, A.Y.; Ng, A.Y. Rectifier nonlinearities improve neural network acoustic models. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 16–21 June 2013; Volume 30, p. 3. [Google Scholar]
- Hendrycks, D.; Gimpel, K. Gaussian error linear units (gelus). arXiv 2016, arXiv:1606.08415. [Google Scholar] [CrossRef]
- Barabási, A.L.; Albert, R. Emergence of scaling in random networks. Science 1999, 286, 509–512. [Google Scholar] [CrossRef] [PubMed]
- Kendall, M.G. A new measure of rank correlation. Biometrika 1938, 30, 81–93. [Google Scholar] [CrossRef]
- Batagelj, V.; Mrvar, A. Pajek-program for large network analysis. Connections 1998, 21, 47–57. [Google Scholar]
- Newman, M.E. Finding community structure in networks using the eigenvectors of matrices. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2006, 74, 036104. [Google Scholar] [CrossRef]
- Leskovec, J.; Mcauley, J. Learning to discover social circles in ego networks. Adv. Neural Inf. Process. Syst. 2012, 25, 1–28. [Google Scholar]
- Isella, L.; Stehlé, J.; Barrat, A.; Cattuto, C.; Pinton, J.F.; Van den Broeck, W. What’s in a crowd? Analysis of face-to-face behavioral networks. J. Theor. Biol. 2011, 271, 166–180. [Google Scholar] [CrossRef] [PubMed]
- Jeong, H.; Mason, S.P.; Barabási, A.L.; Oltvai, Z.N. Lethality and centrality in protein networks. Nature 2001, 411, 41–42. [Google Scholar] [CrossRef] [PubMed]
- Rual, J.F.; Venkatesan, K.; Hao, T.; Hirozane-Kishikawa, T.; Dricot, A.; Li, N.; Berriz, G.F.; Gibbons, F.D.; Dreze, M.; Ayivi-Guedehoussou, N.; et al. Towards a proteome-scale map of the human protein–protein interaction network. Nature 2005, 437, 1173–1178. [Google Scholar] [CrossRef] [PubMed]
- Leskovec, J.; Kleinberg, J.; Faloutsos, C. Graph evolution: Densification and shrinking diameters. ACM Trans. Knowl. Discov. Data 2007, 1, 2-es. [Google Scholar] [CrossRef]
- Bellingeri, M.; Bevacqua, D.; Sartori, F.; Turchetto, M.; Scotognella, F.; Alfieri, R.; Nguyen, N.; Le, T.; Nguyen, Q.; Cassi, D. Considering weights in real social networks: A review. Front. Phys. 2023, 11, 1152243. [Google Scholar] [CrossRef]
| Acronym | Meaning | Reference |
|---|---|---|
| - | A transformer framework with multi-scale feature fusion | – |
| Degree centrality | [5] | |
| Betweenness centrality | [6] | |
| Weighted degree centrality | [22] | |
| Closeness centrality | [7] | |
| K-shell index | [9] | |
| Clustering coefficient | [23] | |
| K-core centrality | [9] | |
| H-index | [8] | |
| GCN model predicting node influence based on centrality features | [24] | |
| Enhances K-core by integrating neighbors’ K-core values | [25] | |
| Transformer model identifying influential nodes via dynamic feature sequences | [26] | |
| CNN model ranking node importance from local feature maps | [27] |
| Network | N | E | C | |||||
|---|---|---|---|---|---|---|---|---|
| LFR2000-k5 | 2000 | 10,034 | 5.69836 | 0.09836 | 0.09 | 5 | 0.37739 | 8 |
| LFR2000-k10 | 2000 | 20,634 | 4.47204 | 0.07227 | 0.07 | 10 | 0.41041 | 11 |
| LFR2000-k15 | 2000 | 30,350 | 3.92303 | 0.05772 | 0.05 | 20 | 0.4239 | 11 |
| Network | N | E | C | |||||
|---|---|---|---|---|---|---|---|---|
| CA-GrQc | 4158 | 13,422 | 6.04938 | 0.05561 | 0.05 | 6.456 | 0.55688 | 43 |
| 324 | 2218 | 3.05374 | 0.04662 | 0.04 | 13.691 | 0.46581 | 18 | |
| infectious | 410 | 2765 | 3.63085 | 0.05343 | 0.05 | 13.488 | 0.45582 | 17 |
| netscience | 379 | 914 | 6.04187 | 0.12468 | 0.12 | 4.823 | 0.74123 | 8 |
| protein | 783 | 6726 | 4.83984 | 0.06339 | 0.06 | 4.317 | 0.07152 | 6 |
| yeast | 1458 | 1948 | 6.81237 | 0.14031 | 0.14 | 2.672 | 0.07083 | 5 |
| Model | Netscience | CA-GrQc | Infectious | Protein | Yeast | LFR2000-k5 | LFR2000-k10 | LFR2000-k15 | |
|---|---|---|---|---|---|---|---|---|---|
| InfGCN | 0.0071 | 0.0778 | 0.0035 | 0.0286 | 0.0123 | 0.0027 | 0.0169 | 0.0169 | 0.0169 |
| LCNN | 0.0611 | 0.0611 | 0.0611 | 0.0611 | 0.0611 | 0.0611 | 0.0611 | 0.0611 | 0.0611 |
| CNT | 0.0042 | 0.4233 | 0.0049 | 0.1279 | 0.0718 | 0.0042 | 0.1331 | 0.1331 | 0.1331 |
| MSF-Former | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 | 0.0004 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, T.; Ruan, Y.; Yu, T.; Bai, L.; Yuan, Y. Identifying Influential Nodes in Complex Networks via Transformer with Multi-Scale Feature Fusion. Big Data Cogn. Comput. 2025, 9, 129. https://doi.org/10.3390/bdcc9050129
Jiang T, Ruan Y, Yu T, Bai L, Yuan Y. Identifying Influential Nodes in Complex Networks via Transformer with Multi-Scale Feature Fusion. Big Data and Cognitive Computing. 2025; 9(5):129. https://doi.org/10.3390/bdcc9050129
Chicago/Turabian StyleJiang, Tingshuai, Yirun Ruan, Tianyuan Yu, Liang Bai, and Yifei Yuan. 2025. "Identifying Influential Nodes in Complex Networks via Transformer with Multi-Scale Feature Fusion" Big Data and Cognitive Computing 9, no. 5: 129. https://doi.org/10.3390/bdcc9050129
APA StyleJiang, T., Ruan, Y., Yu, T., Bai, L., & Yuan, Y. (2025). Identifying Influential Nodes in Complex Networks via Transformer with Multi-Scale Feature Fusion. Big Data and Cognitive Computing, 9(5), 129. https://doi.org/10.3390/bdcc9050129






