Robust Anomaly Detection of Multivariate Time Series Data via Adversarial Graph Attention BiGRU
Abstract
1. Introduction
- (1)
- Existing MTSD typically use dimension shifting and scaling to eliminate data size, increasing training speed. However, due to the inconsistent influence of different dimensional data on the results, failure to fully consider the spatial correlation characteristics between different dimensional data leads to inadequate model performance [11]. However, due to the complex change patterns of MTSD and the inclusion of both continuous and discrete variables, it is difficult to make the model compatible with historical data and the current task, while adequately extracting spatially relevant features. Thus, the optimal scheme for compatible hybrid temporal and spatial feature extraction has yet to be investigated.
- (2)
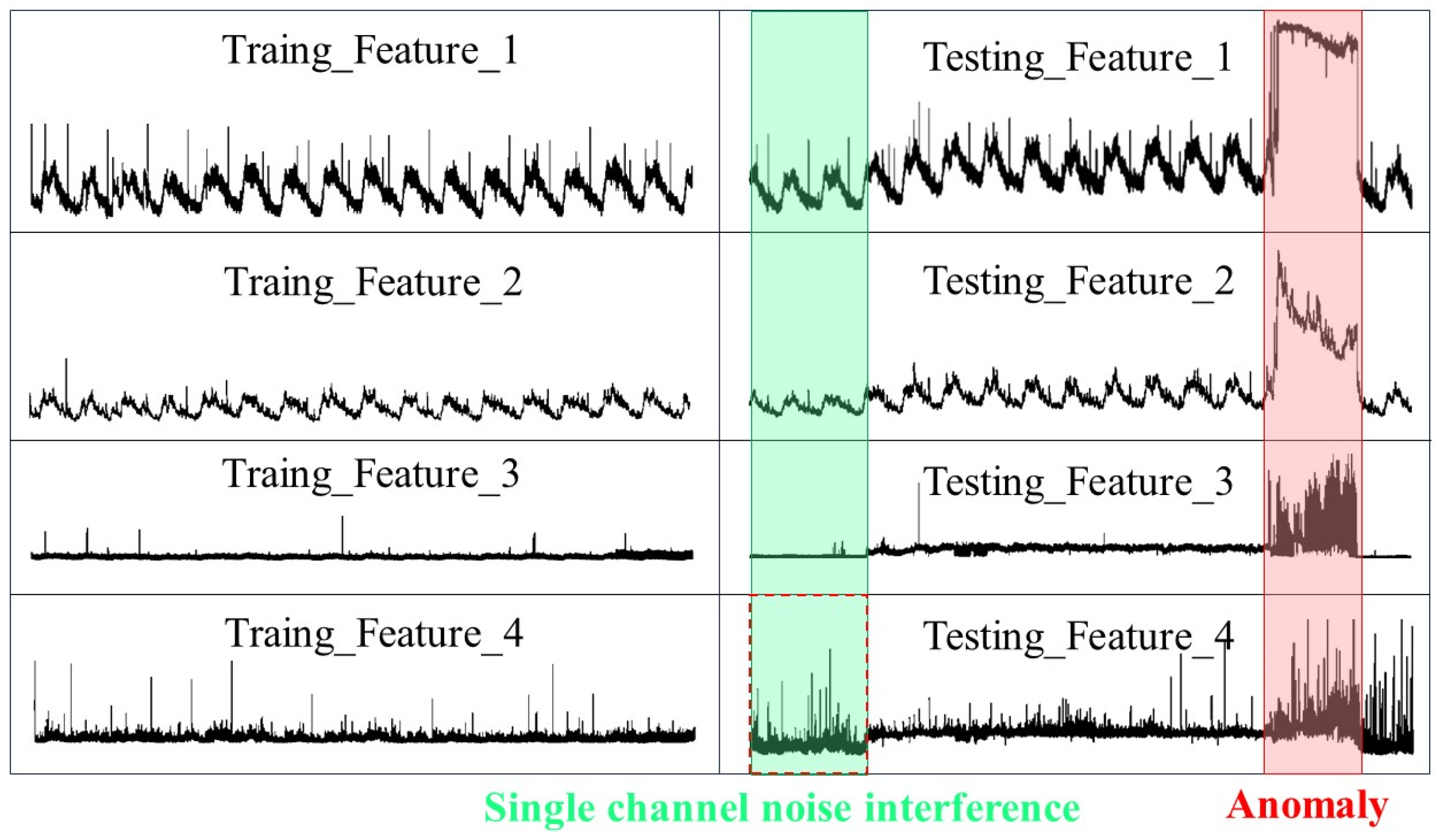
- Extracting potential representations from MTSD is susceptible to noise interference and fluctuations in the training set. As shown in Figure 1 (green indicates fluctuation, red indicates abnormality), the collected data contain a significant amount of noise, visualizing considerable noise in a real dataset, which is a common phenomenon in the real world. Existing methods lack the robustness to deal with MTSD in the face of noise and anomalous contamination. Hence, it is difficult for the model to achieve the expected results due to large errors caused by noise and interference during data reconstruction.
- (1)
- A parallel improved graph attention (PGAT) is proposed to analyze temporal dependence and spatial correlation in MTSD without any prior knowledge, thereby avoiding misclassification of normal fluctuations as anomalies.
- (2)
- Integrating deep learning technology, BiGRU model is selected to learn the spatio-temporal features of dimensional time series data. In addition, the context-dependent features are obtained to prevent information loss and enhance the robust performance of the model.
- (3)
- The advantages of predictive and reconstructive models are combined by introducing joint optimization. The reconstructed noise samples are used for adversarial training to improve the robustness of the model in the face of contaminated data. The performance and explanatory power of the model are tested on three public datasets, proving that the proposed method outperforms eight typical baseline models. Finally, the proposed model is applied to anomaly detection in laboratory equipment, validating the effectiveness of the method.
2. Related Work
2.1. MTSD Fusion
2.2. Anomaly Detection
3. PGAT-BiGRU-NRA Framework
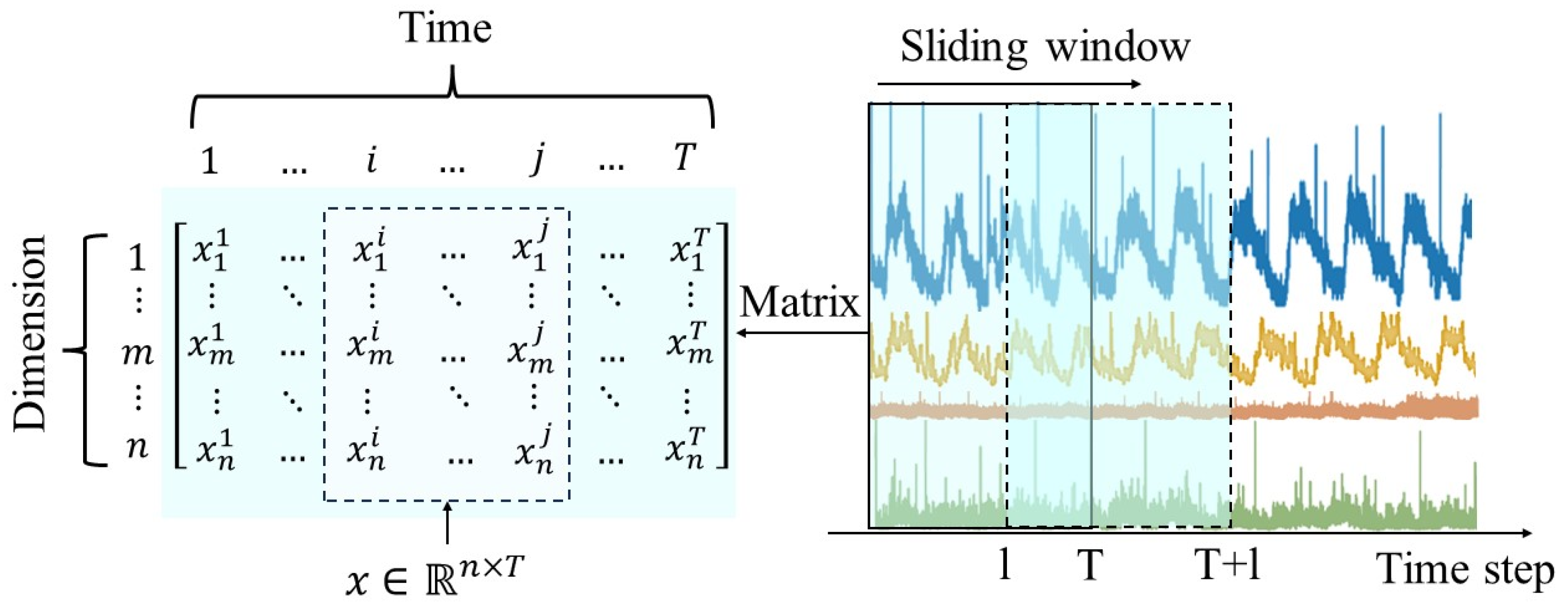
3.1. Description of the Problem
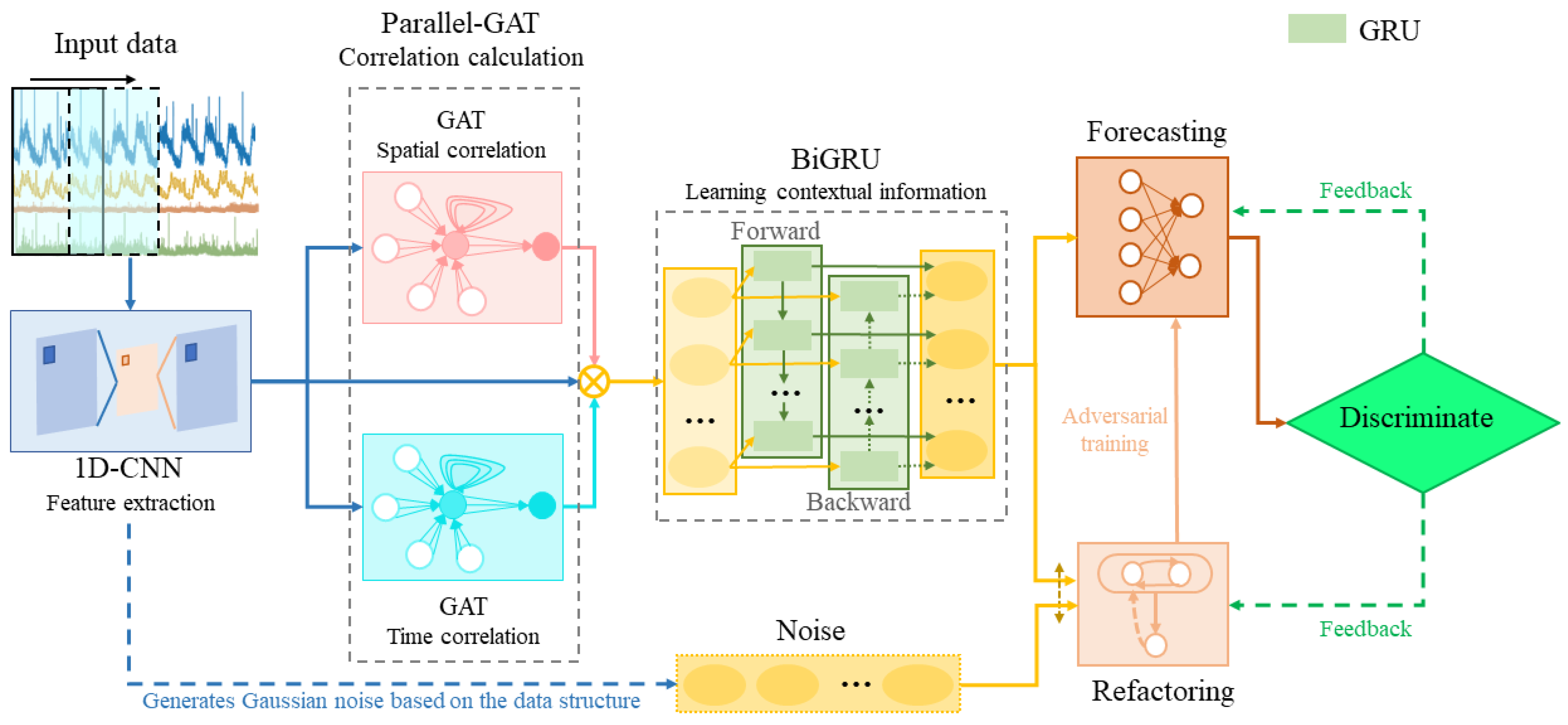
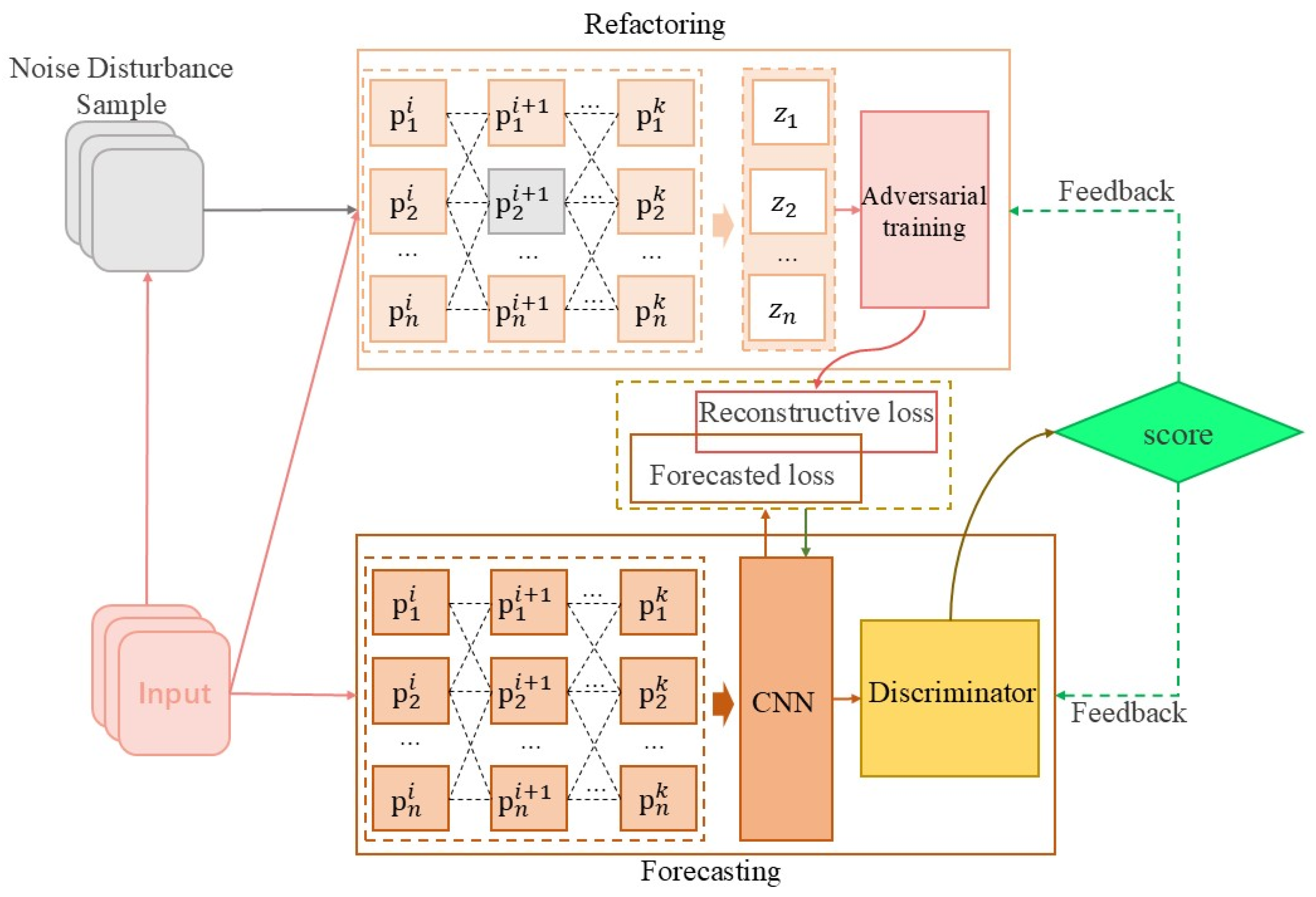
3.2. Overall Framework
- (1)
- Data Preprocessing: data preprocessing is performed for MTSD to select normalization methods according to the requirements, and 1D-CNN is applied to extract high-level local features of each time series in the preprocessed data;
- (2)
- Fusion of Multidimensional Data: parallel GATv2 is used to learn data dependencies from both the temporal dimension and the spatial feature dimension, emphasizing the fusion of multiple features with different weights;
- (3)
- Learning-Fused Feature Patterns: the BiGRU layer connects the outputs of 1D-CNN and parallel GATv2 to extract contextual information from MTSD and capture time-dependent sequential pattern features;
- (4)
- Robust Anomaly Detection and Interpretation: VAE reconstructs the model and adds noise countermeasures to improve the robustness of the fully connected network’s joint predictive modeling and obtain the result.
3.3. Key Technologies
3.3.1. Data Preprocessing
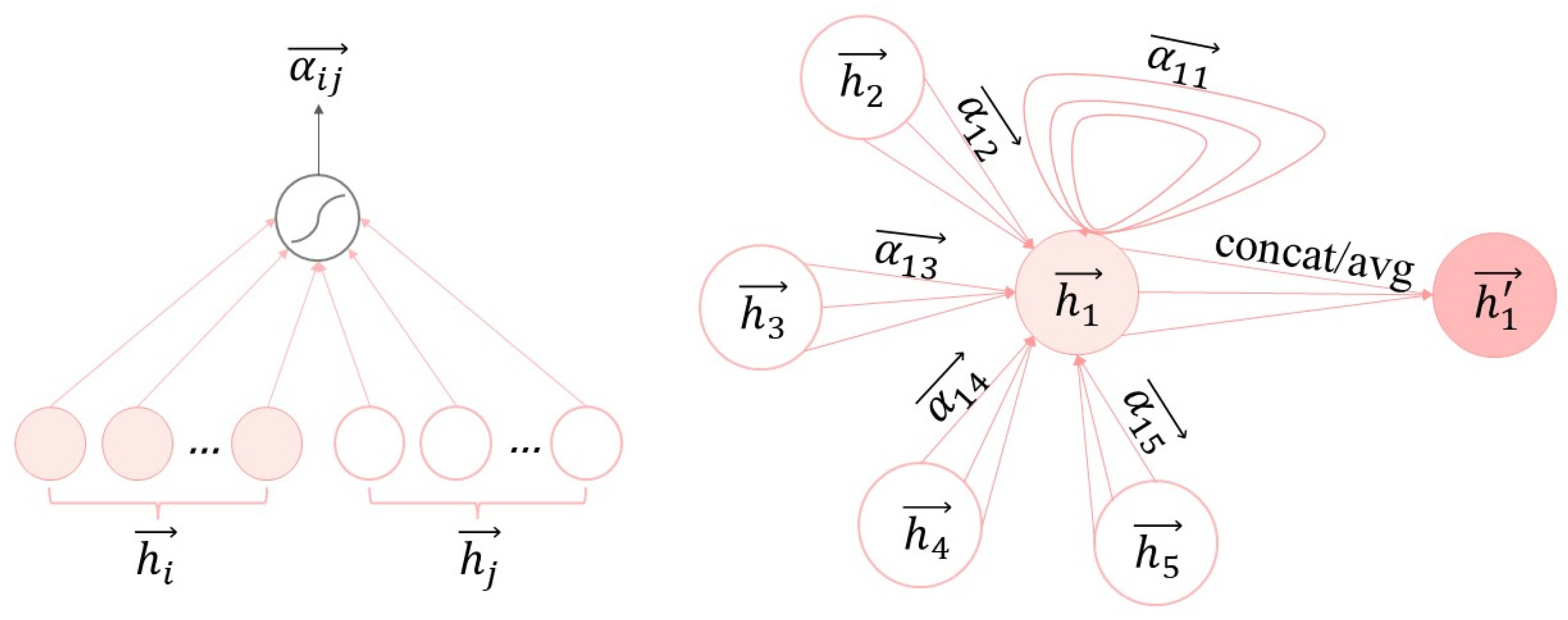
3.3.2. Parallel Improvement of Graph Attention Mechanisms
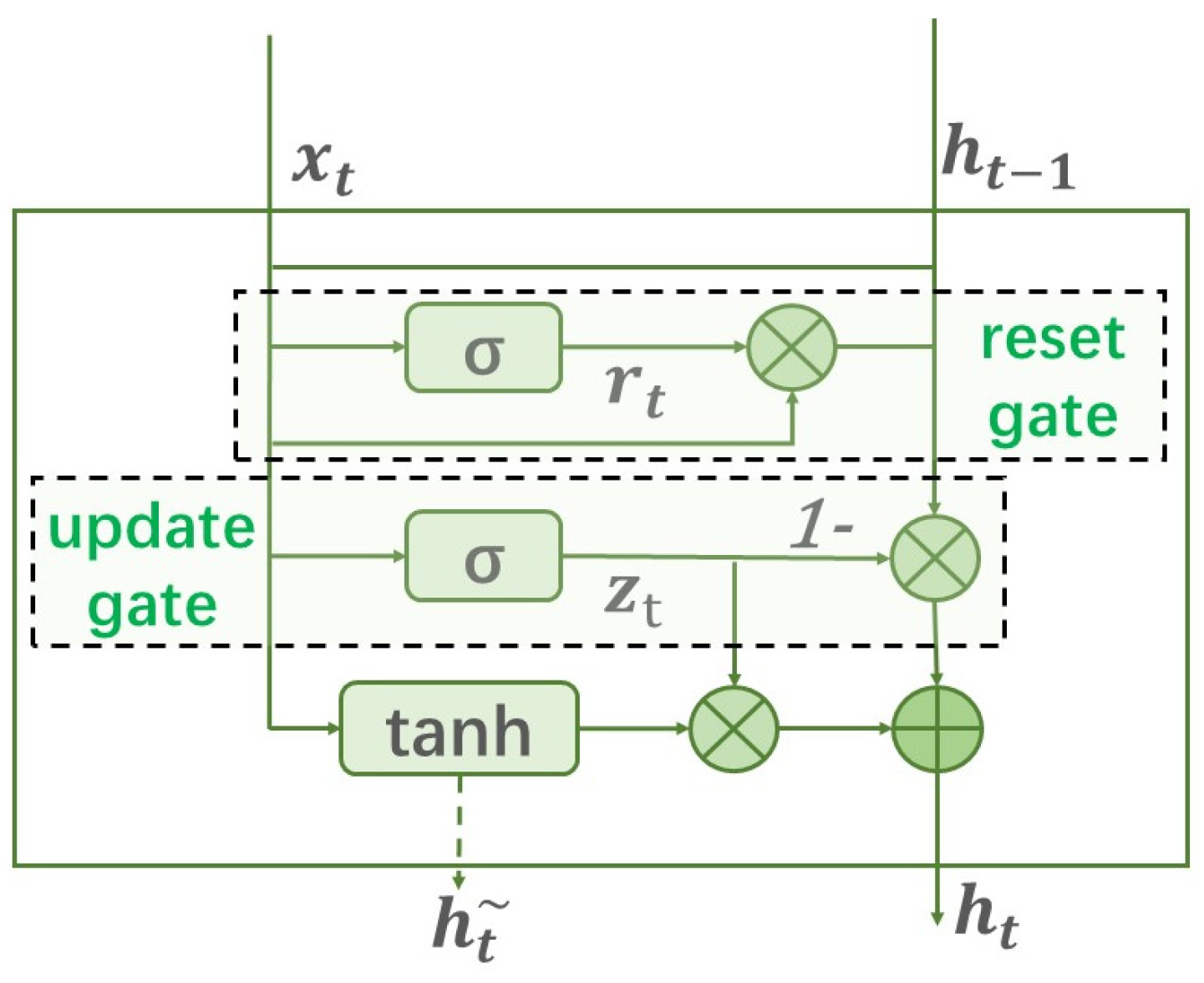
3.3.3. Bi-Directional Gated Recurrent Unit
3.3.4. Robust Joint Adversarial Optimization
3.3.5. Anomaly Detection
1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24. 25. 26. 27. 28. 29. 30. 31. |
4. Experimental Results and Analysis
4.1. Description of Datasets
4.2. Experimental Setup
4.2.1. Evaluation Metrics
4.2.2. Comparative Methods
- (1)
- OC-SVM [33] maps the samples through the kernel function to a higher dimensional space to delineate normal and abnormal boundaries;
- (2)
- LOF [34] detects anomalies using the local density deviation of the target data relative to the neighborhood;
- (3)
- BeatGAN [35] is based on an adversarial self-encoder and adds a discriminator to improve the formality of the reconstructed samples;
- (4)
- CAE-AD [28] enhances data feature representation using a self-encoder combined with contextual information for comparative learning;
- (5)
- IForest [36] isolates anomalies in the data by modeling the integration of randomly selected features on the division of observations;
- (6)
- OmniAnomaly [29] considers time-dependent, potentially spatially stochastic modeling to capture complex data distributions;
- (7)
- DeepSVDD [37] employs a co-training network to learn single-classified target data features for spherical mapping to normal data;
- (8)
- MAD-GAN [38] is based on recurrent neural networks to capture multivariate temporal distribution features while considering discriminative and generative loss detection anomalies.
4.2.3. Experimental Realization Details
4.3. Experimental Results
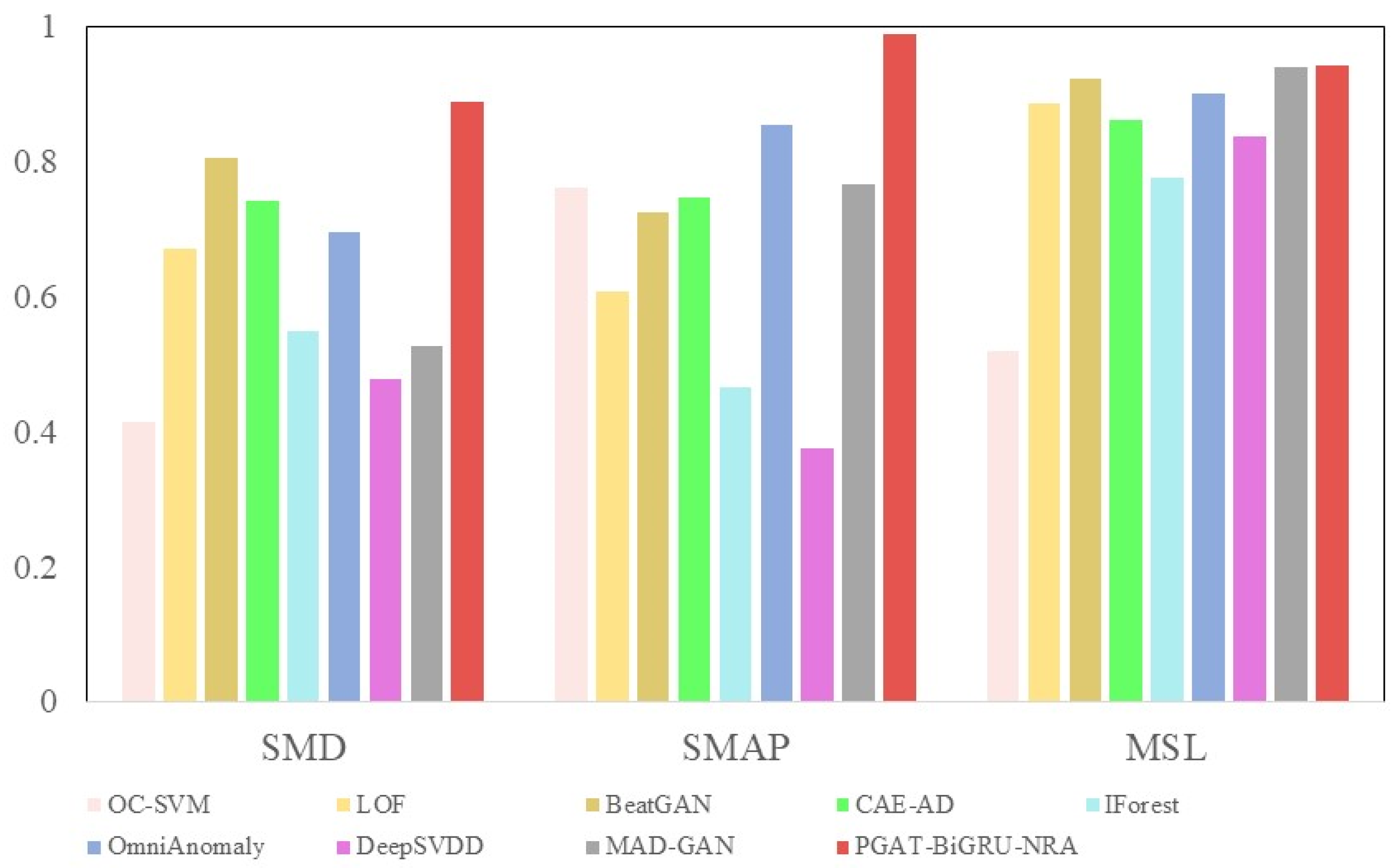
4.3.1. Analysis of Experimental Results
4.3.2. Sensitivity Experiments on PGAT-BiGRU-NRA Parameters
4.3.3. Ablation Experiment
4.4. Model Performance Analysis
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MTSD | Multivariate time series data |
| PGAT | Parallel graph attention |
| NAR | Noise Reconstruction Adversarial Training |
References
- Mutawa, A.M. Predicting Intensive Care Unit Admissions in COVID-19 Patients: An AI-Powered Machine Learning Model. Big Data Cogn. Comput. 2025, 9, 13. [Google Scholar] [CrossRef]
- Wang, Z.; Shrestha, R.M.; Roman, M.O.; Kalb, V.L. NASA’s Black Marble Multiangle Nighttime Lights Temporal Composites. IEEE Geosci. Remote Sens. Lett. 2022, 19, 2505105. [Google Scholar] [CrossRef]
- Lei, Z.; Shi, J.; Luo, Z.; Cheng, M.; Wan, J. Intelligent Manufacturing From the Perspective of Industry 5.0: Application Review and Prospects. IEEE Access 2024, 12, 167436–167451. [Google Scholar] [CrossRef]
- Yao, H.; Liu, C.; Zhang, P.; Wu, S.; Jiang, C.; Yu, S. Identification of Encrypted Traffic Through Attention Mechanism Based Long Short Term Memory. IEEE Trans. Big Data 2022, 8, 241–252. [Google Scholar] [CrossRef]
- Wan, J.; Li, D.; Tu, Y.; Liu, J.; Zou, C.; Chen, R. A General Test Platform for Cyber Physical Systems: Unmanned Vehicle with Wireless Sensor Network Navigation. In Proceedings of the 2011 International Conference on Computers, Communications, Control and Automation (CCCA 2011), Hokkaido, Japan, 1–2 February 2011; Volume III, pp. 165–168. [Google Scholar]
- Blazquez-Garcia, A.; Conde, A.; Mori, U.; Lozano, J.A. A Review on Outlier/Anomaly Detection in Time Series Data. ACM Comput. Surv. 2022, 54, 56. [Google Scholar] [CrossRef]
- Santamaria-Bonfil, G.; Reyes-Ballesteros, A.; Gershenson, C. Wind speed forecasting for wind farms: A method based on support vector regression. Renew. Energy 2016, 85, 790–809. [Google Scholar] [CrossRef]
- Deng, H.; Runger, G.; Tuv, E.; Vladimir, M. A time series forest for classification and feature extraction. Inf. Sci. 2013, 239, 142–153. [Google Scholar] [CrossRef]
- Yan, H.; Tan, J.; Luo, Y.; Wang, S.; Wan, J. Multi-Condition Intelligent Fault Diagnosis Based on Tree-Structured Labels and Hierarchical Multi-Granularity Diagnostic Network. Machines 2024, 12, 891. [Google Scholar] [CrossRef]
- Yan, S.; Shao, H.; Xiao, Y.; Zhou, J.; Xu, Y.; Wan, J. Semi-supervised fault diagnosis of machinery using LPS-DGAT under speed fluctuation and extremely low labeled rates. Adv. Eng. Inform. 2022, 53, 101648. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, Y.; Wang, J.; Pan, Z. Unsupervised Deep Anomaly Detection for Multi-Sensor Time-Series Signals. IEEE Trans. Knowl. Data Eng. 2021, 35, 2118–2132. [Google Scholar] [CrossRef]
- Tan, J.; Wan, J.; Chen, B.; Safran, M.; AlQahtani, S.A.; Zhang, R. Selective Feature Reinforcement Network for Robust Remote Fault Diagnosis of Wind Turbine Bearing Under Non-Ideal Sensor Data. IEEE Trans. Instrum. Meas. 2024, 73, 3515911. [Google Scholar] [CrossRef]
- Gao, J.; Li, P.; Chen, Z.; Zhang, J. A Survey on Deep Learning for Multimodal Data Fusion. Neural Comput. 2020, 32, 829–864. [Google Scholar] [CrossRef] [PubMed]
- Wei, Q.; Dobigeon, N.; Tourneret, J.-Y. Fast Fusion of Multi-Band Images Based on Solving a Sylvester Equation. IEEE Trans. Image Process. 2015, 24, 4109–4121. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, X.; Lv, C.; Wu, J.; Li, L.; Ding, D. An innovative information fusion method with adaptive Kalman filter for integrated INS/GPS navigation of autonomous vehicles. Mech. Syst. Signal Process. 2018, 100, 605–616. [Google Scholar] [CrossRef]
- Wu, J.; Lin, Z.; Zha, H. Essential Tensor Learning for Multi-View Spectral Clustering. IEEE Trans. Image Process. 2019, 28, 5910–5922. [Google Scholar] [CrossRef]
- Pan, Y.; Zhang, L.; Li, Z.; Ding, L. Improved Fuzzy Bayesian Network-Based Risk Analysis With Interval-Valued Fuzzy Sets and D–S Evidence Theory. IEEE Trans. Fuzzy Syst. 2020, 28, 2063–2077. [Google Scholar] [CrossRef]
- Zhu, C.; Xiao, F.; Cao, Z. A Generalized Renyi Divergence for Multi-Source Information Fusion with its Application in EEG Data Analysis. Inf. Sci. 2022, 605, 225–243. [Google Scholar] [CrossRef]
- Fu, H.; Sun, G.; Ren, J.; Zhang, A.; Jia, X. Fusion of PCA and Segmented-PCA Domain Multiscale 2-D-SSA for Effective Spectral-Spatial Feature Extraction and Data Classification in Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5500214. [Google Scholar] [CrossRef]
- Liang, W.; Xiao, L.; Zhang, K.; Tang, M.; He, D.; Li, K.-C. Data Fusion Approach for Collaborative Anomaly Intrusion Detection in Blockchain-Based Systems. IEEE Internet Things J. 2022, 9, 14741–14751. [Google Scholar] [CrossRef]
- Xie, T.; Huang, X.; Choi, S.-K. Intelligent Mechanical Fault Diagnosis Using Multisensor Fusion and Convolution Neural Network. IEEE Trans. Ind. Inform. 2022, 18, 3213–3223. [Google Scholar] [CrossRef]
- Baldauf, D.; Desimone, R. Neural Mechanisms of Object-Based Attention. Science 2014, 344, 424–427. [Google Scholar] [CrossRef] [PubMed]
- He, C.; Zhang, X.; Song, D.; Shen, Y.; Mao, C.; Wen, H.; Zhu, D.; Cai, L. Mixture of Attention Variants for Modal Fusion in Multi-Modal Sentiment Analysis. Big Data Cogn. Comput. 2024, 8, 14. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, S.; Xu, Y.; Miao, C.; Wu, M.; Zhang, J. Contextualized Graph Attention Network for Recommendation With Item Knowledge Graph. IEEE Trans. Knowl. Data Eng. 2023, 35, 181–195. [Google Scholar] [CrossRef]
- Ding, C.; Sun, S.; Zhao, J. MST-GAT: A multimodal spatial–temporal graph attention network for time series anomaly detection. Inf. Fusion 2023, 89, 527–536. [Google Scholar] [CrossRef]
- Nguyen, H.D.; Tran, K.P.; Thomassey, S.; Hamad, M. Forecasting and Anomaly Detection approaches using LSTM and LSTM Autoencoder techniques with the applications in supply chain management. Int. J. Inf. Manag. 2021, 57, 102282. [Google Scholar] [CrossRef]
- Ding, N.; Gao, H.; Bu, H.; Ma, H.; Si, H. Multivariate-Time-Series-Driven Real-time Anomaly Detection Based on Bayesian Network. Sensors 2018, 18, 3367. [Google Scholar] [CrossRef]
- Zhou, H.; Yu, K.; Zhang, X.; Wu, G.; Yazidi, A. Contrastive autoencoder for anomaly detection in multivariate time series. Inf. Sci. 2022, 610, 266–280. [Google Scholar] [CrossRef]
- Su, Y.; Zhao, Y.; Niu, C.; Liu, R.; Sun, W.; Pei, D. Robust Anomaly Detection for Multivariate Time Series through Stochastic Recurrent Neural Network. In Proceedings of the KDD ’19: The 25th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 2828–2837. [Google Scholar] [CrossRef]
- Audibert, J.; Michiardi, P.; Guyard, F.; Marti, S.; Zuluaga, M.A. USAD: UnSupervised Anomaly Detection on Multivariate Time Series. In Proceedings of the KDD ’20: The 26th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, Virtual Event. 6–10 July 2020; pp. 3395–3404. [Google Scholar] [CrossRef]
- Li, W.; Zhong, X.; Shao, H.; Cai, B.; Yang, X. Multi-mode data augmentation and fault diagnosis of rotating machinery using modified ACGAN designed with new framework. Adv. Eng. Inform. 2022, 52, 101552. [Google Scholar] [CrossRef]
- Kong, F.; Li, J.; Jiang, B.; Wang, H.; Song, H. Integrated Generative Model for Industrial Anomaly Detection via Bidirectional LSTM and Attention Mechanism. IEEE Trans. Ind. Inform. 2023, 19, 541–550. [Google Scholar] [CrossRef]
- Lyu, S.; Farid, H. Steganalysis using higher-order image statistics. IEEE Trans. Inf. Forensics Secur. 2006, 1, 111–119. [Google Scholar] [CrossRef]
- Breunig, M.M.; Kriegel, H.-P.; Ng, R.T.; Sander, J. LOF: Identifying density-based local outliers. In Proceedings of the 2000 ACM SIGMOD International Conference on Management of Data, Dallas, TX, USA, 15–18 May 2020; Volume 29, pp. 93–104. [Google Scholar] [CrossRef]
- Bin, Z.; Liu, S.; Hooi, B.; Cheng, X.; Ye, J. BeatGAN: Anomalous Rhythm Detection using Adversarially Generated Time Series. In Proceedings of the Twenty-Eighth International Joint Conference on Artificial Intelligence, Macao, China, 10–16 August 2019; pp. 4433–4439. [Google Scholar]
- Liu, F.T.; Ting, K.M.; Zhou, Z.-H. Isolation-Based Anomaly Detection. ACM Trans. Knowl. Discov. Data 2012, 6, 3. [Google Scholar] [CrossRef]
- Zhang, Z.; Deng, X. Anomaly detection using improved deep SVDD model with data structure preservation. Pattern Recognit. Lett. 2021, 148, 1–6. [Google Scholar] [CrossRef]
- Zhou, Y.; Song, Y.; Qian, M. Unsupervised Anomaly Detection Approach for Multivariate Time Series. In Proceedings of the 2021 IEEE 21st International Conference on Software Quality, Reliability and Security Companion (QRS-C), Hainan, China, 6–10 December 2021; IEEE: New York, NY, USA; pp. 229–235. [Google Scholar] [CrossRef]



| Methods | Models | Implementation | Limitations |
|---|---|---|---|
| Probability | Bayesian [14] | Circulant matrix derivation | Difficulty in obtaining a priori probabilities and modeling data when dealing with high-dimensional complex data. |
| Kalman filtering [15] | Attenuation factor perturbs weights | ||
| Markov model [16] | Singular value decomposition norm | ||
| D-S Evidence Theory | D-SBNs [17] | Feature fuzzy prior probability | The quality function is difficult to define, and the model is not robust enough. |
| BRDD-S [18] | Renyi divergence belief entropy | ||
| Knowledge | PCASVM [19] | Principal component analysis | Sensitive to noise points and performs poorly in the face of unbalanced datasets. |
| C-clustering [20] | Multiple rounds of clustering | ||
| CNN [21] | Convert to RGB image |
| Datasets | SMD | SMAP | MSL | platform |
|---|---|---|---|---|
| Features | 38 | 25 | 55 | 4 |
| Training size | 23,696 | 135,183 | 58,317 | 500,240 |
| Testing size | 23,696 | 427,617 | 73,729 | 500,131 |
| Abnormal Rate (%) | 4.16 | 13.13 | 10.27 | 15.3 |
| Method | SMD | SMAP | MSL | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | P | R | F1 | |
| OC-SVM | 0.432 | 0.362 | 0.415 | 0.452 | 0.236 | 0.761 | 0.524 | 0.423 | 0.520 |
| LOF | 0.600 | 0.761 | 0.671 | 0.435 | 0.999 | 0.607 | 0.854 | 0.925 | 0.886 |
| BeatGAN | 0.694 | 0.712 | 0.806 | 0.832 | 0.926 | 0.724 | 0.903 | 0.853 | 0.921 |
| CAE-AD | 0.639 | 0.626 | 0.741 | 0.821 | 0.812 | 0.746 | 0.756 | 0.645 | 0.861 |
| IForest | 0.602 | 0.505 | 0.549 | 0.302 | 0.999 | 0.465 | 0.668 | 0.931 | 0.775 |
| OmniAnomaly | 0.701 | 0.731 | 0.696 | 0.758 | 0.976 | 0.853 | 0.883 | 0.900 | 0.901 |
| DeepSVDD | 0.778 | 0.334 | 0.479 | 0.456 | 0.276 | 0.376 | 0.981 | 0.742 | 0.837 |
| MAD-GAN | 0.731 | 0.409 | 0.527 | 0.608 | 0.999 | 0.765 | 0.935 | 0.944 | 0.940 |
| PGAT-BiGRU-NRA | 0.764 | 0.883 | 0.887 | 0.980 | 0.997 | 0.988 | 0.905 | 0.982 | 0.942 |
| Method | SMD | SMAP | MSL | ||||||
|---|---|---|---|---|---|---|---|---|---|
| P | R | F1 | P | R | F1 | P | R | F1 | |
| Delete Time-GAT | 0.763 | 0.889 | 0.876 | 0.953 | 0.972 | 0.956 | 0.916 | 0.947 | 0.932 |
| Delete Space-GAT | 0.759 | 0.872 | 0.865 | 0.983 | 0.976 | 0.961 | 0.909 | 0.953 | 0.919 |
| BiGRU-NRA | 0.696 | 0.743 | 0.739 | 0.937 | 0.944 | 0.963 | 0.856 | 0.966 | 0.908 |
| PGAT-NRA | 0.732 | 0.865 | 0.884 | 0.974 | 0.982 | 0.961 | 0.879 | 0.952 | 0.914 |
| PGAT-BiGRU | 0.702 | 0.814 | 0.793 | 0.936 | 0.892 | 0.829 | 0.883 | 0.894 | 0.889 |
| PGAT-BiGRU-NRA | 0.764 | 0.883 | 0.887 | 0.980 | 0.997 | 0.988 | 0.905 | 0.982 | 0.942 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xing, Y.; Tan, J.; Zhang, R.; Wan, J. Robust Anomaly Detection of Multivariate Time Series Data via Adversarial Graph Attention BiGRU. Big Data Cogn. Comput. 2025, 9, 122. https://doi.org/10.3390/bdcc9050122
Xing Y, Tan J, Zhang R, Wan J. Robust Anomaly Detection of Multivariate Time Series Data via Adversarial Graph Attention BiGRU. Big Data and Cognitive Computing. 2025; 9(5):122. https://doi.org/10.3390/bdcc9050122
Chicago/Turabian StyleXing, Yajing, Jinbiao Tan, Rui Zhang, and Jiafu Wan. 2025. "Robust Anomaly Detection of Multivariate Time Series Data via Adversarial Graph Attention BiGRU" Big Data and Cognitive Computing 9, no. 5: 122. https://doi.org/10.3390/bdcc9050122
APA StyleXing, Y., Tan, J., Zhang, R., & Wan, J. (2025). Robust Anomaly Detection of Multivariate Time Series Data via Adversarial Graph Attention BiGRU. Big Data and Cognitive Computing, 9(5), 122. https://doi.org/10.3390/bdcc9050122







