Margin-Based Training of HDC Classifiers

Abstract

The explicit kernel transformation of input data vectors to their distributed high-dimensional representations has recently been receiving increasing attention in the field of hyperdimensional computing (HDC). The main argument is that such representations endow simpler last-leg classification models, often referred to as HDC classifiers. HDC models have obvious advantages over resource-intensive deep learning models for use cases requiring fast, energy-efficient computations both for model training and deploying. Recent approaches to training HDC classifiers have primarily focused on various methods for selecting individual learning rates for incorrectly classified samples. In contrast to these methods, we propose an alternative strategy where the decision to learn is based on a margin applied to the classifier scores. This approach ensures that even correctly classified samples within the specified margin are utilized in training the model. This leads to improved test performances while maintaining a basic learning rule with a fixed (unit) learning rate. We propose and empirically evaluate two such strategies, incorporating either an additive or multiplicative margin, on the standard subset of the UCI collection, consisting of 121 datasets. Our approach demonstrates superior mean accuracy compared to other HDC classifiers with iterative error-correcting training.

1. Introduction

Simple linear classifiers are receiving increased attention for use cases requiring fast and energy-efficient computations. The co-design of linear classifiers and hardware, intensively researched within the framework of hyperdimensional computing (HDC), has already demonstrated promising results in this direction [1,2].

The basic HDC classifier is a simple classical prototype/centroid model [3,4]. In these prototype models, per-class data vectors of the training set are averaged to obtain a single prototype per class, possibly followed by a prototype quantization step. While this is a computationally efficient approach in terms of training and predicting [5,6,7,8,9], the classification results are modest, since the features (i.e., the individual components of data vectors) are not weighted to reflect the actual structure (e.g., covariance) of the classes.

HDC adds to the picture the non-linear transformation of vector data to a high-dimensional vector space, resulting in hypervectors. This is beneficial for linear classification of input data with classes that are not linearly separable in the input space, as well as for other similarity-based tasks/applications. To improve performance, HDC classifiers are commonly trained using misclassified training samples [10,11,12,13,14,15,16]. The landscape of HDC applications for solving classification tasks is broad, starting from language detection with HDC-represented N-grams [17] to classification of arrhythmia types [6], time series classification [18,19], classification of medical data [20,21,22], and others [23] (see also [24,25,26,27] for a comprehensive overview).

Recent approaches to training HDC classifiers often involve various approaches to selecting the individual learning rate for only incorrectly classified samples. Unlike these approaches, we propose alternative strategies to make a decision about classification error using a margin on the classifier scores to improve test performance while using a basic learning rule with a fixed (and unit) learning rate. Class prototypes are thus adjusted to better classify not only wrongly classified samples but also correctly classified samples within the margin, so that a better classification performance is expected. Our contributions are as follows:

• Establishment of criteria and decision rules to trigger the refinement of HDC classifiers, based on the confidence levels of individual sample classifications.
• Development of HDC classifiers trained using either a multiplicative or additive margin applied to confidence scores, which operate on quantized class prototypes, and a comparative analysis of these methods.
• Configuration and enhancement of margin-based HDC classifiers for scalability, enabling effective operation on larger and more diverse datasets, exemplified by experimentation on 121 UCI datasets.
• Comprehensive experimental evaluation across 121 UCI datasets, demonstrating improved mean accuracy of the proposed HDC classifiers compared to other HDC models.
• Assessment of the impact of design choices on the classification performance of the proposed HDC classifiers.

The paper is organized as follows. Section 2 provides background on HDC. Related works are presented and discussed in Section 3. The article continues by describing the methods and experiments in Section 4 and Section 5, respectively. The results are presented in Section 6. Finally, Section 7 concludes this article.

2. Background on HDC and Basic HDC Classifiers

2.1. Formation of HDC Representations

In HDC, input data are transformed into a hyperdimensional vector (hypervector; HV) representation space in which the number of components of the HVs (i.e., the dimensionality) ranges from hundreds to tens of thousands. The key task in applications of HDC is to transform instances of the various fundamental data types of computer science, such as scalars, vectors, sequences, graphs, into HV representations. To be useful in various similarity-based tasks, the similarity of the obtained HVs should reflect the similarity of the input data objects (see Section 2.3).

These hypervectors could be real-valued, as in holographic reduced representations (HRRs) [28]; complex-valued, as in Fourier HRR [29]; bipolar vectors, as in multiply–add–permute (MAP) [30]; dense binary vectors, as in binary spatter code (BSC) [31,32]; or sparse binary vectors, as in sparse binary distributed representations (SBDRs) [33]. Each of these HDC frameworks has its own basic operations of binding and superposition; see, e.g., Section 2.2. Despite the heterogeneity of data transformation approaches, they can all be used in similar applications, such as solving classification tasks.

In this paper, we consider only dense binary HV representations, i.e., with vector components of either 0 or 1, and about half of the components are 1. This is the most commonly used variant because of its efficiency of working with binary vectors.

2.2. HDC Operations

Compositional HDC representations are produced using two fundamental HDC operations, superposition and binding, which are mathematical operators on the vector space. These operations do not change the dimensionality D of their input HVs.

The superposition operation combines several HVs into a single HV, which is used to represent (multi)sets. It is commonly implemented via component-wise addition. For dense binary HVs, component-wise addition is used to superimpose vectors followed by a majority vote (denoted as $[.]$) to binarize the vector components and where ties are broken pseudo-randomly. The binding operation associates HVs with each other. HDC allows considerable latitude in the details of binding implementation. For dense binary representations, the component-wise XOR operation (denoted as ⊕) is the common choice that we use here.

2.3. Hypervector Representation of Scalars and Numerical Vectors

In this paper, we are concerned with the representation of scalar values and numerical vectors and employ the compositional approach [34], proposed in [35,36,37], for the construction of their HVs.

Using this approach, it is desirable to map similar numerical values to similar HVs, rather than numerical values that are further apart; that is, the HVs should preserve the similarity between numerical values. One of the possible ways to transform numerical scalars to HVs is “linear mapping” [23,38]. Namely, after quantizing the numerical scalars to the range of integer values $[0,Q]$, the lowest quantization level is assigned a randomly generated HV. Then, an HV for each consecutive quantization level is obtained by flipping a certain fixed number of bits in the HV of the previous quantization level without flipping those bits that have already been flipped [23]. As a result, the similarity value to the lowest quantization level decreases linearly from the lowest level up to the highest level. Now, let us represent a numerical vector $\mathbf{x}\in {\mathbb{R}}^d$ consisting of d scalar features (i.e., $\mathbf{x}=[x_1,x_2,\cdots ,x_d]$) as HV ${\mathbf{v}}_{\mathbf{x}}\in {\mathbb{B}}^D$.

This is achieved in the following way:

• Quantizing the numerical values of each feature to the range of values $[0,Q]$ such that $x\in {[0,Q]}^d$.
• Representing the quantized feature values as their HVs ${\mathbf{v}}_{x_j}$ using linear mapping.
• Assigning a random HV ${\mathbf{v}}_{f_j}$ to each of the d features $f_j$.
• Binding each feature value HV with its corresponding feature HV using the component-wise XOR, i.e., ${\mathbf{v}}_{x_j}\oplus {\mathbf{v}}_{f_j}$.
• Finally, obtaining the HV ${\mathbf{v}}_{\mathbf{x}}$ by the addition of all d bound feature–value pairs followed by a majority vote:

$${\mathbf{v}}_{\mathbf{x}}=[{\mathbf{v}}_{x_1}\oplus {\mathbf{v}}_{f_1}+{\mathbf{v}}_{x_2}\oplus {\mathbf{v}}_{f_2}+\dots +{\mathbf{v}}_{x_d}\oplus {\mathbf{v}}_{f_d}]=[\sum _{j=1}^d({\mathbf{v}}_{x_j}\oplus {\mathbf{v}}_{f_j})].$$

(1)

2.4. Basic HDC Classifiers

The simplest HDC classifier is prototype HDC classifier (Prot-HDCL), which creates K class prototypes (also referred to as centroids), with K being the number of classes in the dataset. This is achieved by superimposing all sample HVs ${\mathbf{v}}_{\mathbf{x},i}$ of the training set that belong to the same class to obtain the class prototype for that class:

$${\mathbf{P}}_k=\sum _{i=1}^N\left\{{\mathbf{v}}_{\mathbf{x},i}\right|y_i=k\}\mathrm{for}k=1\cdots K.$$

(2)

In (2), $y_i$ is the label of the ith sample’s class. In the variant with further binarization of prototypes, a counter variable keeps track of the number of sample HVs that are included in each class prototype:

$$n_k=\sum _{i=1}^{N}I(y_i=k)\mathrm{for}k=1\cdots K,$$

(3)

where $I(.)$ is the indicator function.

The class prototype ${\mathbf{P}}_k$ is then binarized with a majority vote by the threshold $n_k/2$:

$${\mathbf{p}}_k=\left[{\mathbf{P}}_k\right].$$

(4)

Those binarized prototypes are used for classification, i.e., class prediction on new input samples.

Building on the basic structure of the HDC classifier described earlier, various training strategies can be employed to enhance classification performance. The simplest of these is the prototype refinement rule, which we denote here as HDC classifier with prototype refinement (Ref-HDCL):

• For the current training sample i, predict its class using the classifier.
• If the prediction is incorrect, then update both the correct class prototype and the incorrect class prototype.
• If the prediction is correct, leave all class prototypes unchanged.

An important variant of Ref-HDCL, which includes class prototype binarization, operates as follows: In step 1, class prediction is made by calculating the similarity values between the input sample’s HV ${\mathbf{v}}_{\mathbf{x},i}$ and all binarized class prototypes ${\mathbf{p}}_k$. The predicted class ${\widehat{y}}_i$ is the class associated with the binary prototype that has the highest similarity score to the sample’s HV, calculated with the employed similarity measure:

$${\widehat{y}}_i={\mathrm{argmax}}_k\mathrm{sim}({\mathbf{v}}_{\mathbf{x},i},{\mathbf{p}}_k)\mathrm{for}k=1\cdots K.$$

(5)

In step 2, the update of class prototypes is triggered in case of a prediction mistake:

$${\widehat{y}}_i\ne y_i.$$

(6)

The following learning rule is applied to update the non-binary prototypes. The sample’s HV is added to the prototype of the correct class ${\mathbf{P}}_{y_i}$ and subtracted from the prototype of the misclassified class ${\mathbf{P}}_{{\widehat{y}}_i}$. Additionally, the class counters are updated by incrementing $n_{y_i}$ and decrementing $n_{{\widehat{y}}_i}$. This update process is described by the following expressions:

$${\mathbf{P}}_{y_i}={\mathbf{P}}_{y_i}+{\mathbf{v}}_{\mathbf{x},i};{\mathbf{P}}_{{\widehat{y}}_i}={\mathbf{P}}_{{\widehat{y}}_i}-{\mathbf{v}}_{\mathbf{x},i}.$$

(7)

$$n_{y_i}=n_{y_i}+1;n_{{\widehat{y}}_i}=n_{{\widehat{y}}_i}-1.$$

(8)

When all training samples are processed, and thus one epoch is completed, the obtained non-binary class prototypes ${\mathbf{P}}_k$ are binarized with the corresponding updated thresholds $n_k/2$ to produce binary class prototypes to be used in the next epoch. This iterative training procedure is performed for a predefined number of epochs or until a predefined accuracy on the training set is reached.

After training completion, the binarized class prototypes are used for prediction. As stated above, classification in HDC is achieved based on the similarity values (i.e., class scores) between the input sample HV and the $binarized$ class prototypes. The choice of the similarity measure (sim) employed influences the classification results.

3. Related Work

3.1. Prototype Classifiers

The simplest form of an HDC classifier, as described in [23], is the prototype/centroid classifier [3,4]. In this approach, class prototypes are constructed by averaging the data vectors for each class in the training set, producing a single prototype per class, with an option to quantize these prototypes. We refer to this approach as Prot-HDCL, as mentioned above. While this method is computationally efficient for both training and prediction, its classification performance is often modest. This is due to the fact that the features (or components of the data HVs) are not weighted according to their relative importance in distinguishing between classes.

3.2. Prototype Refinement

Several variations of HDC classifiers employing “prototype refining” approaches essentially implement different versions of the perceptron algorithm. In VoiceHD [39], error correction is applied with a single pass through the dataset, resulting in non-binary (integer) weights. In contrast, ref. [40] explores an approach where the weights are binarized after multiple training epochs.

In BinHD [41], binary class prototypes are used for prediction, but in the event of a classification error, the non-binary prototypes are updated and subsequently binarized. This method also uses multiple training epochs. Similarly, QuantHD [42] maintains two sets of prototypes—one non-quantized and one quantized—with quantization occurring after each epoch. Quantization in this case can include either binarization or ternarization.

This approach, referred to as Ref-HDCL above, has been employed in many HDC-related studies, such as [43]. It does not incorporate the notion of confidence in prediction.

3.3. Classification Scores and Confidence in Classification Results

In the data-dependent mode of AdaptHD [44], the learning rate is adjusted based on the difference between class scores for the correct and misclassified classes. After training, the class prototypes are binarized. In OnlineHD [45], non-binary data HVs are used to improve classification accuracy, with no mention of prototype quantization. Like AdaptHD [44], the learning rate in OnlineHD [45] is adapted according to the confidence in the class scores.

In TD-HDC [46], both integer and binary prototypes are supported. During training, integer prototypes are updated in case of a misclassification by either the binary or integer classifier, with final binarized prototypes obtained after training. During inference, they use a “classification confidence” measure, defined as the difference between the two smallest Hamming distances between the input HV and the class prototypes of the binary classifier. If this confidence value falls below a predefined threshold (or margin), the integer classifier is employed to make the prediction. Thus, all of the HDC classifiers mentioned above update prototypes only when the highest class score is provided for an incorrect class.

In RefineHD [47], the authors also mention using the difference between the top two class scores for the prototype update decision.

The works most relevant to this paper in the context of HDC classification are Confidence Centroid (CONFcentroid) [48] and linear classifiers [49,50,51]. These approaches utilize the confidence in class scores to determine when to update class prototypes. However, the mentioned linear classifiers do not address the case of binary prototypes, and none of the previous works explore setups involving multiple diverse datasets.

3.4. Other HDC Classifiers

In the context of HDC classifiers, the use of randomized non-linear transformations of input data into HVs followed by a linear classifier was initially proposed in [35,36] for a distributed representation of class labels. Since then, large-margin linear classifiers have been employed, with their first explicit mention in English appearing in [49,50], and further development in [51]. For comprehensive reviews on HDC classifiers, please see [25,26,27].

4. Methods

In this work, we propose a novel approach for improving the quality of HDC classifiers by introducing unified criteria for deciding when to update class prototypes during the training process. The decision rule for refining class prototypes given the HV of the input data sample during training is different from that of Ref-HDCL as presented above in expressions (5) and (6).

The different decision rules are based on the notion of the confidence level $c_i$ with which the input sample i belonging to class $y_i$ is classified given its HV ${\mathbf{v}}_{\mathbf{x},i}$. It is defined as the difference between the similarity of the data sample HV and the correct class prototype and its similarity to the most similar class prototype of any other class:

$$c_i=\mathrm{sim}({\mathbf{v}}_{\mathbf{x},i},{\mathbf{p}}_{y_i})-\underset{k\ne y_i}{max}\mathrm{sim}({\mathbf{v}}_{\mathbf{x},i},{\mathbf{p}}_k).$$

(9)

Here, $\mathrm{sim}({\mathbf{v}}_{\mathbf{x},i},{\mathbf{p}}_k)$, $k=1\cdots K$, are the class scores given the input HV ${\mathbf{v}}_{\mathbf{x},i}$ to be classified. They evidently depend on the employed similarity measure (sim).

Then, various decision rules for prototype updates can be constructed by comparing the confidence margin value with specific threshold values, which can be defined in different ways. It is important to note that while the confidence margin $c_i$ is calculated based on the similarity between the input HV and the binarized class prototypes, the updates are performed on the second set of non-binarized prototypes (which are integer in the setup we consider, though other setups may use different representations).

In the following subsections, we present two instances of our approach, each resulting in different update decision rules. Additionally, we outline essential design choices for the deployment of margin-based HDC classifiers based on our approach.

4.1. HDC Classifiers with Additive Margin

The additive margin strategy results in a family of HDC classifiers with additive margin (AM-HDCL). An instance of this family is the CONFcentroid classifier [48]. AM-HDCL will not update the class prototypes in the training mode when

$$c_i>\alpha ,0\le \alpha <1,$$

(10)

where $\alpha$ is some constant predefined threshold. Therefore, to avoid the prototype update, the difference in class scores of the correct class and any other class should not only be positive, but also greater than $\alpha$. In case of an update (when $c_i\le \alpha$), it is performed by (7) and (8), with ${\widehat{y}}_i$ = ${\mathrm{argmax}}_{k\ne y_i}\mathrm{sim}({\mathbf{v}}_{\mathbf{x},i},{\mathbf{p}}_k)$. This is different from the update decision rule of Ref-HDCL, where correct classification when training (and hence no update of class prototypes) requires $c_i>0$, taking into account (5) and (6).

In the case of $\alpha =0$, AM-HDCL becomes Ref-HDCL. However, when $\alpha >0$, we expect more updates from AM-HDCL, as some samples that Ref-HDCL would not update are treated as requiring an update by AM-HDCL. Evaluation of the trained AM-HDCL classifier is performed by (5) and (6), equivalent to setting $\alpha =0$ in (10).

4.2. HDC Classifiers with Multiplicative Margin

The multiplicative margin strategy results in a family of HDC classifiers with multiplicative margin (MM-HDCL). It is instantiated by the classifiers considered in [49,50,51]. MM-HDCL avoids update only in the case that

$$c_i>\alpha ·\mathrm{sim}({\mathbf{v}}_{\mathbf{x},i},{\mathbf{p}}_{y_i}),0\le \alpha <1.$$

(11)

That is, the similarity margin should be larger than a fraction $\alpha$ of the correct class score.

This approach enables more frequent weight updates compared to Ref-HDCL, converging slower but towards a solution that ensures a relative (multiplicative) margin. Prototype updates follow the same procedure as in Ref-HDCL, which is also equivalent to updates in AM-HDCL. Setting $\alpha =0$ recovers the behavior of Ref-HDCL.

When the training set is correctly classified with $\alpha >0$, we anticipate an improved test set accuracy for AM-HDCL and MM-HDCL compared to a correct classification with $\alpha =0$, implying better generalization performance [52,53].

4.3. Design Choices

The performance of machine learning models is influenced by specific design choices made during the implementation of their methods. In this section, we isolate particular design choices for the methods applied at different stages of HDC classifiers.

4.3.1. Input Data Preprocessing/Standardization

Input data preprocessing and standardization are essential for the performance of machine learning models, including HDC classifiers.

The initial step is standardizing input features before transforming them into HVs. A common approach is per-feature z-score standardization, which scales each feature to have a mean of 0 and a standard deviation of 1, preserving the relative positioning of data points within their distributions. This method is useful for datasets that approximate a normal distribution and when there are outliers or features with varying variances.

After standardization, input data should be quantized in order to apply the compositional method for transforming input data into hypervectors.

A further decision involves how to standardize the resulting HVs of data samples.

4.3.2. Initialization of Class Prototypes

An important factor influencing the performance of HDC classifiers is the choice of how to initialize class prototypes before starting error-driven iterative training. This concerns the two sets of prototypes: integer and quantized. The three straightforward options are (1) initializing with zeros, (2) initializing randomly, and (3) initializing with “incremental” prototypes resulting from Prot-HDCL.

4.3.3. Quantization of Class Prototypes

The primary distinction between the HDC classifiers being examined and other linear classifiers lies in the learning of binary prototypes. This is accomplished by maintaining two sets of prototypes: an “original” set, similar to the weights in traditional linear classifiers; and a quantized (binarized, in this paper) set. Unlike post-training quantization of prototypes, which can significantly degrade accuracy, we apply quantization during the training process, as explained in Section 2.4.

This opens up several related design choices, from which we here consider just two: when to quantize; and how to quantize. The simplest alternative for when to quantize is quantization after each epoch, as given in Section 3 and employed in the CONFcentroid model [48]. The primary alternatives for how to quantize involve component-wise thresholding with a zero threshold, or component-wise thresholding using half-values of per-class counters (8).

4.3.4. Similarity Measures Between Hypervectors and Prototypes

Linear models are evidently based on the dot-product similarity ${\mathrm{sim}}_{\mathrm{dot}}(\mathbf{a},\mathbf{b})=\langle \mathbf{a},\mathbf{b}\rangle ={\sum }_{j=1}^D{a}_j{b}_j$. On the other side, a number of HDC classification models operating with binary HVs and prototypes, including CONFcentroid as the instance of AM-HDCL, use the Hamming distance ${\mathrm{dist}}_{\mathrm{Ham}}$ to compute class scores: ${\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b})={\sum }_{j=1}^{D}I(a_j\ne b_j)$, where $I(.)$ is the indicator function.

Here, we analyze the implications for ranking the class prototypes when using ${\mathrm{sim}}_{\mathrm{dot}}$ versus ${\mathrm{dist}}_{\mathrm{Ham}}$. Consider the following identities for binary $\{0,1\}$ vectors:

$${\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b})={\mathrm{dist}}_{\mathrm{Euc}}^2(\mathbf{a},\mathbf{b})=\left|\right|\mathbf{a}-{\mathbf{b}\left|\right|}^2={\left|\right|\mathbf{a}\left|\right|}^2+{\left|\right|\mathbf{b}\left|\right|}^2-2\langle \mathbf{a},\mathbf{b}\rangle ,$$

(12)

where ${\left|\right|\mathbf{a}\left|\right|}^2=\left|\mathbf{a}\right|$ is equal to the number of ones in $\mathbf{a}$. The Hamming similarity is then

$${\mathrm{sim}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b})=D-{\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b}).$$

(13)

Taking into account that ${\mathrm{sim}}_{\mathrm{dot}}(\mathbf{a},\mathbf{b})=\langle \mathbf{a},\mathbf{b}\rangle ={\sum }_{j=1}^{D}I(a_j=1\&b_j=1)=|\mathbf{a}\&\mathbf{b}|$, with & being the component-wise conjunction, we obtain

$$2\langle \mathbf{a},\mathbf{b}\rangle =\left|\mathbf{a}\right|+\left|\mathbf{b}\right|-{\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b}).$$

(14)

Therefore, generally, the ranking of class prototypes by the value of $\langle \mathbf{a},\mathbf{b}\rangle$ would not be identical to that by $-{\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b})$ due to varied $\left|\mathbf{a}\right|+\left|\mathbf{b}\right|$. On the other hand, those rankings by ${\mathrm{sim}}_{\mathrm{dot}}$ and ${\mathrm{sim}}_{\mathrm{Ham}}$ would be identical if the binarization of prototypes and encodings of input vectors ensured a constant value of the sum of the number of ones in them: $\left|\mathbf{a}\right|+\left|\mathbf{b}\right|=const$. The most straightforward way to ensure this is to binarize both prototypes and sample HVs such that the number of ones in both is $D/2$. Then, the total number of ones is $\left|\mathbf{a}\right|+\left|\mathbf{b}\right|=D$, and we obtain

$$2\langle \mathbf{a},\mathbf{b}\rangle ={\mathrm{sim}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b}).$$

(15)

In this case, the ranking by similarity values of ${\mathrm{sim}}_{\mathrm{dot}}$ and ${\mathrm{sim}}_{\mathrm{Ham}}$ is identical. Note that in dense binary randomly generated vectors, $p\left(1\right)=1/2$, hence $\mathrm{mean}\left(\right|\mathbf{a}\left|\right)=D/2$. The coefficient of variation of $\left|\mathbf{a}\right|$ decreases as $1/\sqrt{D}$, and so with increasing D, $\left|\mathbf{a}\right|+\left|\mathbf{b}\right|$ becomes relatively closer to D, and we could expect closer similarity ranking results for HVs of larger D. Similar reasoning is also applicable to real-valued vectors, which we do not consider in this paper.

Importantly, in the case of bipolar {−1,+1} HVs, which are often used in HDC instead of binary {0,1}, we have ${\left|\right|\mathbf{a}\left|\right|}^2=D$ and $4{\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b})={\mathrm{dist}}_{\mathrm{Euc}}^2(\mathbf{a},\mathbf{b})=\left|\right|\mathbf{a}-{\mathbf{b}\left|\right|}^2$. Therefore, we obtain exact equality $4{\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b})=2D-2\langle \mathbf{a},\mathbf{b}\rangle$, $2{\mathrm{dist}}_{\mathrm{Ham}}(\mathbf{a},\mathbf{b})=D-\langle \mathbf{a},\mathbf{b}\rangle$ and, as such, identical ranking for any bipolar HVs of any D.

4.3.5. The Training Procedure

For both AM-HDCL and MM-HDCL, the simplest update rule we use is given by (7). However, decisions regarding the stopping criterion and selection of class prototypes for the evaluation phase play a crucial role in achieving robust classifier performance.

A straightforward stopping criterion is to halt training after a predefined number of epochs. Another common approach is early stopping, triggered when a specified accuracy threshold on the training set is reached.

Upon completion of training, the choice of which set of class prototypes to use in evaluation becomes pertinent. While it is straightforward to use the final prototypes obtained at the end of training, this can lead to challenges, especially in determining the optimal number of training epochs on a per-dataset basis. This issue is exacerbated when handling two sets of class prototypes, one integer and one binary.

4.3.6. The Choice of Design Setup for Experiments

In this section, we outline the finalized design setup chosen for our instantiations of AM-HDCL and MM-HDCL, selected from the numerous combinations of design choices, as defined above.

• Input data standardization: Per-feature z-score standardization. In preliminary evaluations, we investigated more intensive approaches for managing outliers; however, these yielded inconsistent effects across datasets. Consequently, we adopt the standard z-score approach for consistency.
• Input data quantization: Uniform quantization into the [0, Q] range. We use $Q=100$.
• Input data transformation to hypervectors (Section 2.3): Here, instead of flipping $D/\left(2Q\right)$ bits per quantization level as in our previous work [48], we adopt a scheme that flips $D/Q$ bits to generate HVs for scalar values. This effectively halves the dimensionality of the hypervectors.
• Hypervector standardization: We maintain the binary format of generated HVs by avoiding further standardization.
• Prototypes initialization: Before starting error-driven iterative training to refine class prototypes, we initialize the two sets of prototypes (integer and quantized) using the initial “incremental” prototypes from Prot-HDCL.
• The similarity measures between HVs and class prototypes: For AM-HDCL, we use the Hamming similarity normalized by the HV dimensionality, and for MM-HDCL, we apply dot-product similarity.
• Selection of $\mathsf{\alpha }$ values: The hyperparameter $\alpha$ is evaluated over the range of [0.00, 0.02, 0.04, 0.06, 0.08, 0.10, 0.12, 0.15, 0.2, 0.25, 0.3, 0.4, 0.5, 0.7] for both AM-HDCL and MM-HDCL.
• Integer prototype update rule: According to rule (7).
• Binary prototype update rule: Binarization of integer prototypes is applied after each epoch. For AM-HDCL, binarization is achieved by thresholding based on class counter values, while for MM-HDCL, the thresholding is performed with zero values.
• Training stopping: In contrast to [48], we significantly reduce the number of training epochs from 2500 to 100, making training feasible for the large collection of 121 UCI datasets. Additionally, we halt training early if the training accuracy reached 0.9999.
• Selection of class prototypes for deployment: Upon completion of the training, we do not use the final class prototypes for testing. Nor do we apply any procedure or validate some hyperparameters to select some intermediate set of prototypes. Instead, we select the prototypes obtained at the epoch with the highest training accuracy, as in our previous work [48]. While this method may not always be optimal (we observed that maximum testing accuracy often occurs in earlier epochs, before potential “overtraining”), it remains reasonable since prototypes obtained after the training completion may lead to worse performance.

5. Experiments

The AM-HDCL and MM-HDCL instances are distinguished by their respective strategies based on the different types of confidence margin, as well as the design choices specified above. In this section, we describe the experimental setup for evaluating the performance of AM-HDCL and MM-HDCL. The performance was measured as classification accuracy. For performance comparison, we include AM-HDCL with $\alpha =0$ (AM-HDCL $\alpha$ = 0) and MM-HDCL with $\alpha =0$ (MM-HDCL $\alpha$ = 0) as baselines, along with corresponding versions of Prot-HDCL, which are prototype classifiers without prototype refinement.

We experimented with 121 UCI benchmark datasets from [54] (see Appendix A), containing the training/validation/testing dataset splits of 121 UCI datasets proposed in [54]. Though those splits themselves have drawbacks from the point of view of classic ML basic principles (see also [55]), they are widely used and selected by us to ensure better compatibility with the existing performance results.

For the encoding part, we experimented with the influence of the dimensionality D = {200, 1000, 4000, 10,000} of HVs on the classification performance.

Since HDC relies on random initialization of HVs, which influences performance, experiments with HDC were repeated for multiple realizations of randomly generated HVs, i.e., with multiple seeds for initializing a random number generator. For each seed, we transformed the initial data from the splits into their HVs. We conducted experiments with ten different seeds for each classification setup/configuration.

To select the $\alpha$ value to be used for training/testing, we trained/tested on the HVs of the validation split obtained for each seed at each combination of hyperparameter value from its range at the particular design setup. Thereafter, the obtained validation accuracies for each design setting/hyperparameter value were averaged across all seeds. The value of $\alpha$ providing the highest mean validation accuracy was selected for each dataset.

In the final training/testing, the selected hyperparameter value was used to train and test the final (selected) model for each seed. As such, a test accuracy averaged across the multiple seeds (for the “separated” datasets) or a test accuracy averaged across the four test folds and multiple seeds (for the “non-separated” datasets) was obtained for each dataset.

Setting the single value $\alpha =0$ gave us marginless versions AM-HDCL $\alpha$ = 0 and MM-HDCL $\alpha$ = 0 of AM-HDCL and MM-HDCL, respectively. Since the AM-HDCL $\alpha$ = 0 and MM-HDCL $\alpha$ = 0 classifiers did not need selection of the hyperparameter $\alpha$, only their final training/testing was performed.

6. Results and Discussion

Table 1. Mean test accuracies (in %) across all 121 datasets and seeds, reported for the best $\alpha$ value obtained through validation. The results are presented for Prot-HDCL ${\mathrm{sim}}_{\mathrm{Ham}}$, Prot-HDCL ${\mathrm{sim}}_{\mathrm{dot}}$, AM-HDCL $\alpha$ = 0, MM-HDCL $\alpha$ = 0, AM-HDCL, and MM-HDCL at various HV dimensionalities D. Standard deviations are provided in brackets, with the highest mean accuracy in bold.

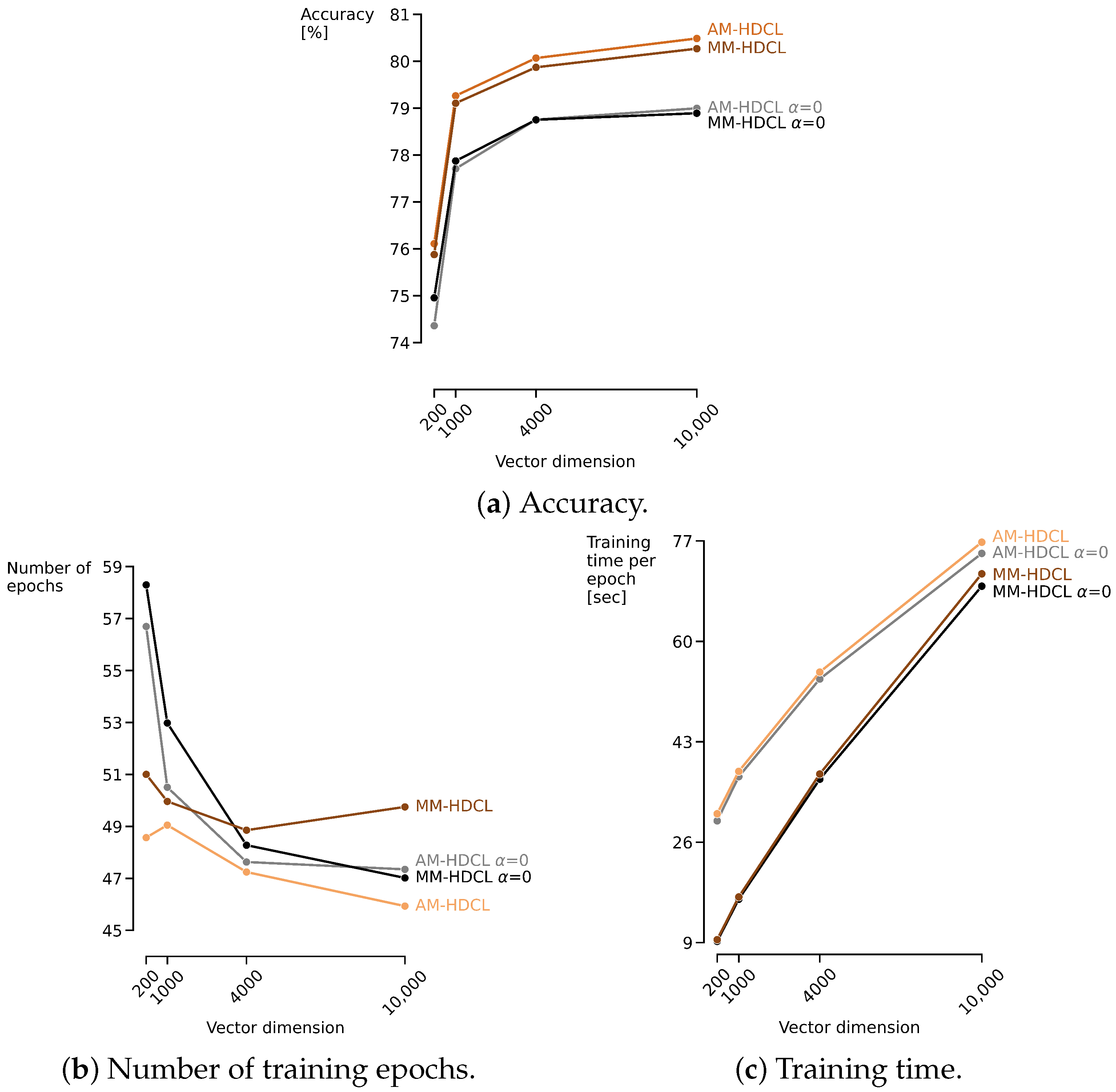
D	200	1000	4000	10,000
Classifier
Prot-HDCL ${\mathrm{sim}}_{\mathrm{Ham}}$	66.36 (±16.28)	69.70 (±15.96)	70.66 (±15.98)	70.92 (±16.05)
Prot-HDCL ${\mathrm{sim}}_{\mathrm{dot}}$	61.36 (±19.10)	65.73 (±19.20)	66.99 (±19.46)	67.43 (±19.35)
AM-HDCL $\alpha$ = 0	74.36 (±17.11)	77.71 (±16.64)	78.75 (±16.45)	79.00 (±16.55)
MM-HDCL $\alpha$ = 0	74.95 (±16.90)	77.87 (±16.45)	78.75 (±16.27)	78.89 (±16.32)
AM-HDCL	76.11 (±16.18)	79.26 (±15.62)	80.07 (±15.59)	80.49 (±15.40)
MM-HDCL	75.88 (±16.54)	79.10 (±15.59)	79.87 (±15.61)	80.27 (±15.25)

reports the mean test classification accuracies of the Prot-HDCL ${\mathrm{sim}}_{\mathrm{Ham}}$, Prot-HDCL ${\mathrm{sim}}_{\mathrm{dot}}$, AM-HDCL $\alpha$ = 0, MM-HDCL $\alpha$ = 0, AM-HDCL, and MM-HDCL classifiers, averaged across all 121 UCI datasets and seeds (detailed results per dataset can be found in Appendix B). Figure 1a further shows how varying the HV dimensionality D influences the final test accuracy, corresponding to the data in Table 1. Figure 1b presents the mean number of training epochs required to reach the best training accuracy, while Figure 1c provides the mean training time per epoch measured when running our python scripts in a distributed system of a set of heterogeneous clusters (consisting of NVIDIA A100 80 GB PCIe, Quadro RTX 4000, Tesla V100-SXM2-32 GB and Tesla V100-SXM3-32 GB) using five CPUs.

As indicated in Table 1 and Figure 1a, the mean classification accuracy improves with increasing HV dimensionality. The results for both AM-HDCL $\alpha$ = 0 and MM-HDCL $\alpha$ = 0, as well as AM-HDCL and MM-HDCL, are quite similar, with AM-HDCL and MM-HDCL consistently outperforming their marginless variants. Notably, even the marginless prototype refinement classifiers AM-HDCL $\alpha$ = 0 and MM-HDCL $\alpha$ = 0 yield substantially higher accuracy than the Prot-HDCL variants.

Figure 1b,c illustrate that the mean number of training epochs needed to achieve the highest accuracy on the training set decreases with increasing HV dimensionality. Furthermore, AM-HDCL and MM-HDCL generally require fewer epochs compared to the marginless variants AM-HDCL $\alpha$ = 0 and MM-HDCL $\alpha$ = 0. In contrast, the mean training time increases significantly with HV dimensionality. Although AM-HDCL $\alpha$ = 0 and AM-HDCL generally take longer to train than MM-HDCL $\alpha$ = 0 and MM-HDCL, this time difference diminishes as the HV dimensionality increases. Notably, with D = 10,000, the additional time required results in only a marginal accuracy improvement over $D=4000$. Thus, $D=4000$ may provide a practical trade-off between accuracy and computational complexity.

Figure 2 presents a comparison between AM-HDCL and MM-HDCL at D = 10,000, indicating the number of datasets where AM-HDCL performs better, equally well, or worse than MM-HDCL. The datasets are grouped based on the number of features, number of classes, number of samples, and the ratio of the number of features to the number of samples. The comparison shows that AM-HDCL outperforms MM-HDCL on datasets with more than 30 features, on datasets with two classes, and on datasets with more than 3000 samples. Additionally, AM-HDCL achieves better performance on datasets with a feature-to-sample ratio smaller than 0.05.

Figure 3 compares the performance of AM-HDCL and MM-HDCL at D = 10,000 against other HDC classifiers on the 121 UCI datasets. The results from [27,47] are displayed in gray, while those from [56,57] are shown in light gray. The figure highlights that AM-HDCL and MM-HDCL outperform other HDC classifier variants. Specifically, the highest-performing HDC classifier in the literature, RefineHD [47], achieves a mean accuracy of 76.7%. In comparison, AM-HDCL and MM-HDCL achieve accuracies of 80.49% and 80.27%, respectively. Notably, AM-HDCL reaches an accuracy of 76.11% even with low HV dimensionality, $D=200$ (Table 1).

Additionally, it is worth noting that our results are better than previously reported accuracies obtained using Ridge classifier (79.82% for IntRVFL [56], 78.24% for sparseRP [57], and 79.54% for SparseBlock [57]). Ridge classifier utilizes real-valued instead of binary prototypes, as well as integer-valued rather than binary hypervectors. The closeness of their results to each other also underscores the difficulty in improving upon this task for the HDC approach.

Our HDC classifiers leverage binary class prototypes and hypervectors, enabling extremely efficient deployment. In prediction mode, the core operation reduces to simply counting the number of 1-bits in machine words—a computation highly optimized on modern hardware and efficiently implemented on chips. This efficiency is particularly beneficial in scenarios with limited computational resources or where online and real-time performance is required. Moreover, the inherent simplicity of binary representations and the lightweight nature of HDC classifiers address the growing demand for fast, resource-constrained machine learning solutions, such as those needed for IoT, EdgeAI, and AIoT applications.

However, HDC classifiers with binary vectors and prototypes require larger dimensionality to achieve high classification performance and currently do not reach the top results achieved by some non-HDC classifiers. Additionally, there remains a notable gap in the theoretical understanding of these methods.

In contrast, non-HDC classifiers typically rely on real-valued vector representations and classifier parameters, with algorithms that demand significantly greater computational resources and extensive training. Although these models may achieve higher performance—as demonstrated by the top classifiers on the 121 UCI datasets in [54], including non-linear SVMs, Random Forests, and Boosting methods—they are tailored for applications where high predictive accuracy is paramount and ample computational power is available. Furthermore, deep neural networks require large datasets for extensive co-training of features and classifiers, and they are commonly employed in complex tasks like image recognition and natural language processing, where the extra computational cost and energy consumption are acceptable trade-offs for enhanced accuracy.

7. Conclusions

This work proposed an approach to training HDC classifiers which leverages confidence-triggered refinement of class prototypes based on certainty levels in individual sample classifications. The enhancement of classification accuracy is demonstrated in comparison with results obtained from classical marginless HDC counterparts and has been validated across a diverse set of 121 UCI datasets. We show that applying either additive or multiplicative margin-based training strategies results in a good performance, with the additive margin configuration yielding slightly higher results. Both strategies consistently outperform alternative modifications of classical HDC classifiers, given the results available in the literature on the same set of UCI datasets.

Additionally, we achieved better results compared to the HDC approach using a Ridge classifier, which operates with real-valued prototypes and integer-valued hypervectors rather than binary ones.

By operating with quantized and ultimately binary data and class prototype vector representations—particularly in prediction mode—our approach remains inherently fast, hardware- and energy-efficient, and well suited for resource-constrained, online, and real-time classification applications.

Promising directions for future research include exploring the combination of our confidence margin-based training with existing HDC classifiers that incorporate learning rate adjustments, which could potentially complement each other to further enhance performance. Another important avenue is investigating whether this or other improvements to HDC classifiers could enable them to achieve the performance of top non-HDC classifiers on the 121 UCI datasets while preserving the efficiency benefits of binary vectors and weights. Additionally, developing hardware implementations optimized in terms of gate efficiency and energy consumption presents a valuable direction for further research. Conducting a theoretical analysis of the proposed approach would also provide deeper insights into its fundamental properties and potential improvements.