Interpretable Predictive Modeling for Educational Equity: A Workload-Aware Decision Support System for Early Identification of At-Risk Students

Abstract

Educational equity and access to quality learning opportunities represent fundamental pillars of sustainable societal development, directly aligned with the United Nations Sustainable Development Goal 4 (Quality Education). Student retention remains a critical challenge in higher education, with early disengagement strongly predicting eventual failure and limiting opportunities for social mobility. While machine learning models have demonstrated impressive predictive accuracy for identifying at-risk students, most systems prioritize performance metrics over practical deployment constraints, creating a gap between research demonstrations and real-world impact for social good. We present an accountable and interpretable decision support system that balances three competing objectives essential for responsible AI deployment: ultra-early prediction timing (day 14 of semester), manageable instructor workload (flagging 15% of students), and model transparency (multiple explanation mechanisms). Using the Open University Learning Analytics Dataset (OULAD) containing 22,437 students across seven modules, we develop predictive models from activity patterns, assessment performance, and demographics observable within two weeks. We compare threshold-based rules, logistic regression (interpretable linear modeling), and gradient boosting (ensemble modeling) using temporal validation where early course presentations train models tested on later cohorts. Results show gradient boosting achieves AUC (Area Under the ROC Curve, measuring discrimination ability) of 0.789 and average precision of 0.722, with logistic regression performing nearly identically (AUC 0.783, AP 0.713), revealing that linear modeling captures most predictive signal and makes interpretability essentially free. At our recommended threshold of 0.607, the predictive model flags 15% of students with 84% precision and 35% recall, creating actionable alert lists instructors can manage within normal teaching duties while maintaining accountability for false positives. Calibration analysis confirms that predicted probabilities match observed failure rates, ensuring trustworthy risk estimates. Feature importance modeling reveals that assessment completion and activity patterns dominate demographic factors, providing transparent evidence that behavioral engagement matters more than student background. We implement a complete decision support system generating instructor reports, explainable natural language justifications for each alert, and personalized intervention templates. Our contribution advances responsible AI for social good by demonstrating that interpretable predictive modeling can support equitable educational outcomes when designed with explicit attention to timing, workload, and transparency—core principles of accountable artificial intelligence.

1. Introduction

Quality education stands as the fourth Sustainable Development Goal established by the United Nations [1], recognizing that equitable access to learning opportunities forms the foundation for sustainable societal progress. Education enables social mobility, reduces inequality, and empowers individuals to contribute to economic and cultural development. Yet higher education systems worldwide struggle with retention, particularly in distance learning contexts where 30–40% of students fail to complete their courses [2,3]. These failures represent not merely institutional metrics but lost opportunities for individuals who invested time and resources without achieving credentials, often perpetuating cycles of educational and economic disadvantage [4,5].

The application of data science and artificial intelligence to educational challenges offers unprecedented opportunities to advance social good through early identification and support of struggling students. Learning management systems (LMS) and Virtual Learning Environments (VLE) have fundamentally transformed the visibility of student learning processes, with every digital interaction leaving traces that correlate with eventual outcomes [6,7]. The field of learning analytics has demonstrated that predictive modeling can identify at-risk students with impressive accuracy, often achieving AUC values exceeding 0.90 [8,9]. However, this technical capability has not translated into widespread deployment of early warning systems that actually improve educational equity. The gap between research demonstrations and real-world impact suggests that predictive performance alone is insufficient for responsible AI adoption in education [7,10].

Three critical barriers constrain the deployment of accountable and interpretable predictive models in educational settings [11,12,13]. First is timing: models trained on full-semester data achieve high accuracy but provide alerts too late for meaningful intervention. Waiting until week 10 of a 16-week semester means students have already fallen weeks behind, creating academic deficits difficult to overcome. Second is workload: instructors teaching classes of 100–200 students cannot contact everyone flagged by overly sensitive models. Systems that identify 40–50% of students as at-risk overwhelm teaching staff, creating alert fatigue that undermines system utility. Third is interpretability: black-box models that output risk scores without transparent explanation fail to build instructor trust, provide no guidance about intervention strategies, and raise concerns about accountability when algorithmic recommendations affect student experiences.

These deployment barriers intersect with broader concerns about responsible AI and algorithmic accountability in social good applications [14,15]. Educational data science operates in a high-stakes domain where model errors affect human lives and opportunities [16,17]. Systems that systematically over-flag certain demographic groups create discriminatory intervention patterns. Models that lack explainability prevent stakeholders from understanding and challenging automated decisions. Predictions used without human oversight can become self-fulfilling prophecies, where students internalize at-risk labels and disengage further. Addressing these ethical dimensions requires explicit design choices that prioritize transparency, equity, and human judgment alongside predictive accuracy.

Background on Machine Learning and Explainable AI Method

The present study employs two complementary machine-learning paradigms: logistic regression and gradient boosting. Logistic regression provides a transparent linear baseline where model parameters have direct statistical interpretation, enabling explicit odds-ratio explanations. Gradient boosting (LightGBM) represents a high-performance ensemble method that captures nonlinear interactions and complements the linear model.

To ensure interpretability and accountability, we integrate explainable-AI (xAI) mechanisms at three levels. (1) Global interpretability is obtained through logistic-regression odds ratios quantifying feature effects. (2) Model-based feature importance in gradient boosting identifies key predictors. (3) Rule-based natural-language explanations translate feature deviations into human-readable justifications. We selected these xAI techniques because they balance transparency and computational efficiency—critical for educational deployment where instructors, not data scientists, must understand and act on predictions.

Our contributions advance responsible AI for educational social good in three ways. First, we demonstrate that meaningful predictive modeling is feasible at day 14—earlier than most existing systems—while maintaining solid discrimination (AUC 0.789) and excellent precision (84% at 15% workload), proving that actionable early warning does not require perfect accuracy. Second, we provide systematic analysis of workload-performance tradeoffs through precision-recall modeling annotated with instructor burden, offering transparent guidance for threshold selection that balances competing objectives. Third, we implement a complete decision support system addressing the full pipeline from data to intervention, producing instructor reports, explainable natural language justifications for each alert, and personalized email templates that operationalize algorithmic predictions into human-centered educational practice.

The remainder of this paper is organized as follows. We review related work on early warning systems and interpretable machine learning in education, highlighting gaps in timing, workload management, and model transparency that responsible AI deployment must address. We describe our modeling methodology, including data preprocessing, feature engineering, model training strategies, and evaluation metrics emphasizing both performance and interpretability. We present results on predictive model discrimination, probability calibration quality, feature importance analysis, and workload-precision tradeoffs. We discuss the pedagogical significance and social good implications of our findings, compare our interpretable modeling approach with state-of-the-art systems, acknowledge limitations affecting generalizability, and outline ethical considerations for accountable AI deployment. We conclude with directions for future research on intervention effectiveness evaluation, equity-aware predictive modeling, and integration with pedagogical practice to ensure AI systems genuinely serve educational social good rather than merely optimizing technical metrics.

2. Related Work

Predicting student success from learning management system data has become a mature research area, with hundreds of published studies demonstrating that early intervention can improve retention and performance. Yet most of this work focuses on prediction accuracy rather than practical deployment. Models that achieve 95% AUC on held-out test sets are common in the literature, but systems that instructors actually use remain rare. Our work addresses this gap by prioritizing workload management, interpretability, and calibration quality over raw predictive performance. We design a decision support system that targets the 10–20% highest-risk students rather than attempting to classify everyone.

The literature on early warning systems reveals three persistent challenges that constrain real-world adoption: timing (when to intervene), interpretability (why students are flagged), and workload (how many students to contact). Studies that excel in one dimension often struggle with others. Models trained on full-semester data achieve excellent accuracy but provide alerts too late to help. Highly interpretable threshold rules are transparent but miss complex patterns that machine learning captures. Systems that flag 50% of students for intervention overwhelm instructors and dilute the focus on truly at-risk cases. Our contribution is a balanced approach that addresses all three dimensions simultaneously.

2.1. Early Prediction and Temporal Dynamics

The timing of predictions fundamentally shapes their utility. Alerts generated in week 14 of a 16-week semester leave little room for intervention, while predictions in week 2 lack sufficient behavioral signal to be reliable. The literature reveals a tradeoff between prediction quality and actionability, with most studies favoring later predictions that achieve higher accuracy at the cost of reduced intervention opportunity.

You (2016) [18] demonstrated that mid-semester predictions using LMS activity data significantly predict final course achievement, with measures of regular study patterns, late submissions, and login frequency showing strong associations with outcomes. The study emphasized that meaningful behavioral indicators outperform simple frequency counts, a finding we incorporate by engineering features that capture engagement patterns rather than raw click totals. However, You’s mid-semester timing may be too late for students who disengage early, motivating our choice of a 14-day window.

Santos and Henriques (2023) [19] explored the accuracy–timing tradeoff systematically, testing predictions at 25%, 50%, 75%, and 100% course completion. They found that reliable prediction is possible as early as 25% completion, achieving AUC of 0.756 for at-risk students using Random Forest. Their course-agnostic approach using normalized time-dependent click representations offers practical advantages for deployment across multiple courses. Our work extends this insight by targeting even earlier prediction (6–7% course completion in a 16-week semester) while maintaining acceptable discrimination.

Hung et al. (2025) [20] took temporal analysis further by dividing the semester into three stages based on learning pattern transitions detected via variational autoencoders. They found that stage 2 (weeks 6–10) provided the best balance between prediction accuracy and intervention opportunity, with XGBoost identifying over 75% of at-risk students by the end of this stage. Critically, they discovered that at-risk probability in previous stages strongly predicts subsequent stage outcomes, suggesting that early patterns have lasting effects. Their five at-risk student types (highly engaged, low-engaged, testing-focused, low-interaction, and impersistent) highlight the heterogeneity of failure pathways, though translating these types into tailored interventions remains an open challenge.

Zhang and Ahn (2023) [21] addressed temporal generalization by training models on previous semester data to predict current semester outcomes. They found that using same-course historical data improved prediction accuracy compared to cross-course training, achieving 81.2% accuracy at midterm and 84% by semester end using ensemble methods. Their use of SHAP values to identify key predictors aligns with our emphasis on interpretability. However, their 16-week prediction timeline still leaves limited intervention time, whereas our day-14 target enables earlier action.

These studies collectively demonstrate that early prediction is feasible but requires careful feature engineering to extract meaningful signals from limited data. Our choice of 14 days balances the need for behavioral evidence against the urgency of intervention, following Hung et al.’s finding that students who struggle early rarely recover without support [20].

2.2. Machine Learning Approaches and Model Selection

The educational data mining literature has converged on ensemble methods as the dominant approach for student success prediction, with gradient boosting (particularly XGBoost and LightGBM) consistently outperforming single classifiers. However, this consensus obscures important questions about interpretability and the marginal value of complex models over simpler alternatives.

Deleña et al. (2025) [9] compared ten machine learning algorithms for predicting student dropout using sociodemographic and academic data from a Philippine university. XGBoost achieved the highest cross-validated accuracy (90.66%), F1 score (90.72), and lowest error rates, outperforming gradient boosting, neural networks, and traditional methods. However, they noted that Naive Bayes, despite high recall, produced excessive false positives that limited practical utility—a finding that underscores the importance of precision in workload-constrained scenarios. Our work similarly prioritizes precision over recall, recognizing that instructors cannot act on overly long alert lists.

Seo et al. (2024) [22] analyzed 144,540 instances from a Korean distance university, finding that LightGBM excelled in prediction accuracy while logistic regression offered competitive performance with superior interpretability. They identified age, residential area, occupation, GPA, and LMS log metrics as significant dropout indicators, with recent data from the last four semesters proving sufficient for stable prediction. Their gender-stratified analysis revealed different risk factors for male and female students, suggesting that one-size-fits-all models may miss important subgroup patterns. Our approach trains unified models but provides interpretable explanations that allow instructors to understand individual cases.

Pecuchova and Drlik (2023) [23] evaluated ensemble methods for early dropout prediction using CRISP-DM methodology, finding that advanced ensemble algorithms (AdaBoost, XGBoost) improved accuracy, recall, precision, and F1 score by 2–4% over traditional classifiers. They emphasized that features characterizing student performance and course interactions were most significant for identifying at-risk students. However, their modest improvement margins raise questions about whether the added complexity of boosting methods justifies their reduced interpretability compared to logistic regression, particularly when the performance gap is small.

Our results align with this literature: gradient boosting achieves AUC of 0.789 compared to logistic regression’s 0.783, a difference of 0.006 that represents minimal practical gain. This near parity suggests that student failure is driven primarily by additive effects of features (low activity is bad, missing assessments is bad, both together is worse) rather than complex nonlinear interactions that only ensemble methods can capture. We therefore recommend logistic regression for deployment when interpretability is prioritized, reserving boosting for scenarios where every marginal improvement in discrimination matters.

2.3. Feature Engineering and Learning Analytics

The features extracted from LMS logs fundamentally determine what patterns models can detect. Early learning analytics research focused on simple frequency counts (total clicks, number of logins), but recent work emphasizes the importance of meaningful behavioral indicators that capture engagement quality rather than mere quantity.

Hernández-García et al. (2024) [7] introduced the CILC (Classification of Interactions based on the Learning Cycle) framework, which categorizes LMS activities into preparation, execution, and reflection phases. Their multiple regression analysis across three diverse courses found that this theory-driven categorization improved explanatory power compared to atheoretical click counts. They also noted that predictive ability depends on course delivery mode, with models performing better in fully online courses than face-to-face or blended formats. This suggests that the signal-to-noise ratio in LMS data varies by context, with richer behavioral traces available when students conduct all learning activities through the platform.

Hafdi and El Kafhali (2025) [6] proposed a hybrid approach combining historical academic records with instructor-provided behavioral observations to predict coding course performance. Using LSTM and SVM, they achieved 94% accuracy and 0.87 F1 score, demonstrating that integrating subjective instructor judgment with objective LMS data can improve predictions. However, their approach requires active instructor participation in data collection, which may not scale to large enrollments. Our focus on fully automated features derived from LMS logs alone ensures that the system requires no additional data collection burden.

Gligorea et al. (2022) [10] developed an interpretable framework using GPU-accelerated machine learning to analyze e-learning platform data, combining predictive models with regression and classification to identify factors impacting student performance. They found that activity-based features dominated demographic variables in predictive importance, confirming that what students do matters more than who they are. Our feature importance analysis replicates this finding: activity metrics (total_clicks, active_days_ratio) and assessment performance (first_assessment_score) far outweigh demographic factors in determining failure risk.

Queiroga et al. (2022) [24] described a nationwide learning analytics initiative in Uruguay using data from 258,440 students to predict dropout in secondary education. Their random forest models achieved AUROC above 0.90 and F1-Macro above 0.88, with prior student performance emerging as the strongest predictor. They conducted careful bias analysis across protected attributes (gender, school zone, social welfare participation), rejecting one model that showed discrimination. This attention to fairness is critical for real-world deployment but remains underexplored in most learning analytics research. Our work acknowledges this gap but does not conduct formal fairness audits, leaving this as important future work.

The literature consistently shows that behavioral engagement features derived from LMS logs are highly predictive of outcomes, but the specific features that matter most vary by course, institution, and student population. This variability complicates efforts to build generalizable models. Our approach uses a broad set of activity, assessment, and demographic features to ensure robustness across presentations while allowing model-based feature selection to identify the most relevant predictors in each context.

2.4. Interpretability and Explainable AI

Prediction accuracy means little if instructors do not trust or understand the system’s recommendations. Recent learning analytics research increasingly emphasizes explainability, using techniques like SHAP (SHapley Additive exPlanations) and LIME (Local Interpretable Model-agnostic Explanations) to make black-box models transparent.

Santana-Perera et al. (2025) [25] applied SHAP to a synthetic student dataset, identifying hours studied, attendance, and parental involvement as influential factors in exam performance prediction using LightGBM. While their results are not generalizable due to artificial data, they demonstrate how XAI techniques can build transparent analytic pipelines in education. Their study highlights a methodological tension in the field: synthetic data enables controlled experimentation but limits practical relevance, while real institutional data provides actionable insights but raises privacy concerns and generalizability questions.

Tiukhova et al. (2024) [26] used SHAP to explore not just feature importance but also feature stability across cohorts, arguing that explainable AI can bridge the gap between predictive and explanatory learning analytics. They found that concept drift and performance drift over time threatened model reliability, but stable features across cohorts enabled instructors to formulate consistent study advice. This insight is critical for our work: we train on early presentations and test on later ones precisely to assess temporal generalization. Our results show modest performance degradation (test set failure rate 36% vs. training set 29%), confirming that models must be robust to changing student populations.

Shanto and Jony (2025) [8] combined predictive modeling with LIME and SHAP to identify factors influencing student adaptability in online education during COVID-19. Their ensemble model achieved 95.73% accuracy, with financial condition, class duration, and network type emerging as key factors. The use of both local (LIME) and global (SHAP) explainability methods provided complementary insights: LIME helped explain individual predictions while SHAP revealed overall feature importance patterns. Our approach parallels this dual perspective, using odds ratios from logistic regression for global interpretability and rule-based explanations for individual alerts.

Sohail et al. (2021) [27] argued that interpretability and adaptability are the major barriers to learning analytics adoption, proposing an interpretable and adaptable early warning model. They emphasized that stakeholders need to understand why predictions are made and how models respond to changing contexts. Our decision support system addresses interpretability through multiple mechanisms: logistic regression odds ratios quantify feature effects, feature importance rankings from gradient boosting identify key predictors, and rule-based explanations translate model outputs into natural language statements instructors can act on.

The interpretability literature reveals a fundamental tradeoff: complex ensemble methods achieve slightly better discrimination but sacrifice transparency, while simpler models like logistic regression remain interpretable but may miss subtle patterns. Our finding that boosting and logistic regression perform nearly identically (AUC difference of 0.006) suggests that in educational prediction, this tradeoff is often illusory—linear models capture most of the signal, making interpretability essentially free.

2.5. Workload-Aware Prediction and Decision Support

Prediction is only the first step in an early warning system; instructors must act on alerts, which requires considering their limited time and resources. Surprisingly few studies explicitly address workload constraints in their evaluation metrics, often reporting recall at 50% or higher thresholds that would require contacting large fractions of the class.

Čotić Poturić et al. (2025) [28] developed a scoring algorithm for early risk detection in STEM courses, achieving accuracy of 0.93, sensitivity of 0.95, and specificity of 0.92. Their approach dynamically evaluates student performance over 15 weeks, allowing for continuous monitoring rather than one-time prediction. However, their reported metrics suggest they aim for high recall across all at-risk students, which may not be practical when instructor resources are constrained. Our workload analysis explicitly models this constraint, showing that flagging 15% of students (achievable within normal teaching duties) yields 84% precision and 35% recall.

Seo et al. (2025) [29] extended their previous work on dropout prediction by developing prescriptive analytics that infer learning profiles from observational data and design tailored support strategies. They found that key behavioral indicators were significantly associated with learner profiles, enabling the design of personalized learning tips and analytics dashboards. This prescriptive approach goes beyond our predictive focus, suggesting a natural extension where flagged students receive differentiated interventions based on their specific risk factors. However, implementing such tailored interventions at scale requires substantial institutional resources.

The decision support systems literature more broadly emphasizes that prediction models should optimize decision-relevant objectives rather than statistical accuracy. In education, the relevant objective is maximizing the number of students helped subject to workload constraints. This suggests that models should be evaluated not by AUC or F1 score alone but by precision at workload-feasible recall levels. Our threshold analysis operationalizes this perspective, showing precision–recall–workload tradeoffs at multiple threshold values and recommending a 15% flagging rate based on instructor feedback about manageable contact lists.

2.6. Studies Using the OULAD

The OULAD has become a standard benchmark, enabling direct comparison across studies. Performance varies dramatically with prediction timing.

Al-Zawqari et al. (2022) [30] established baselines using random forests: 85.83% accuracy for pass/fail at Q4, dropping to 76.53% at Q1. Their quarterly progression (76% → 80% → 83% → 86%) quantifies the accuracy–timing tradeoff. Distinguishing high achievers proved difficult (81% accuracy, 53% recall for distinction/pass), a pattern we also observe.

Hassan et al. (2023) [31] achieved 92% accuracy by mapping OULAD activities to the Community of Inquiry model before clustering. The 6.5% gain over baseline (85.43%) suggests theory-driven feature engineering helps, but they used full-course data (240 days, 14 exams), making predictions retrospective rather than predictive.

Al-Zawqari et al. (2024) [32] addressed fairness at mid-course using denoising autoencoders for latent-space bias mitigation. Their 78–86% accuracy came with reduced disparate impact across gender and disability. Latent-space methods handled partial awareness of protected attributes better than adversarial debiasing, though at interpretability cost.

Gunasekara and Saarela (2026) [33] analyzed fairness–performance tradeoffs using post-processing on late-stage predictions (90% completion). Ensemble models achieved 80–88% accuracy, with RF most resilient to fairness adjustments. High accuracy did not ensure equity—explicit fairness interventions were needed.

Sayed et al. (2025) [34] predicted learning styles (98% accuracy) and assessment preferences using end-of-course data. While impressive, this serves different purposes than early warning—recommending teaching modalities rather than identifying at-risk students.

Dermy et al. (2022) [35] modeled behavioral dynamics using Probabilistic Movement Primitives, emphasizing visualization over classification. Their approach identifies engagement trajectories but provides no prediction metrics.

These studies show accuracy rises with data availability: Q1 (76–78%) < mid-course (78–86%) < Q4 (85–92%) < full-course (92–98%). Random forests dominate, though ensemble methods perform comparably. No study reports precision–recall at specific workload thresholds. Our work differs by targeting day 14 (≈7% course completion), far earlier than any OULAD study. We accept lower recall to maintain instructor workload feasibility, whereas previous work optimizes F1 score or accuracy without explicit workload constraints. Our temporal validation strategy also differs: we split the data by presentation rather than randomly sampling students, testing whether models generalize to new cohorts.

Table 1. Literature review summary: methodological themes and key findings.

Theme	Studies	Key Findings	Implications
Timing-Accuracy Tradeoff	You (2016) [18] Santos & Henriques (2023) [19] Hung et al. (2025) [20] Zhang & Ahn (2023) [21] Al-Zawqari et al. (2022) [30]	Mid-semester: AUC 0.75–0.80 25% completion feasible Stage 2 (weeks 6–10) optimal Q1–Q4 progression: 76% → 86% Earlier = less accurate but more actionable	Prediction possible by week 2–4, but accuracy limited. Our day-14 timing pushes boundary.
Algorithm Selection	Deleña et al. (2025) [9] Seo et al. (2024) [29] Pecuchova & Drlik (2023) [23] Al-Zawqari et al. (2022) [30] Sayed et al. (2025) [34]	XGBoost/LightGBM: 90% + accuracy Logistic regression competitive Ensemble gain: 2–4% RF baseline: 85–88% on OULAD Diminishing returns from complexity	Our finding (boosting vs. logistic: 0.6% difference) aligns with literature. Algorithm choice matters less than features.
Feature Engineering	Hernández-García et al. (2024) [7] Hafdi & El Kafhali (2025) [6] Gligorea et al. (2022) [10] Al-Zawqari et al. (2022) [30]	Theory-driven (CILC) > raw counts Behavioral > demographic Activity dominates demographics Flexible frameworks avoid manual engineering	Our features (activity, assessment, demographics) follow best practices. Behavioral engagement matters most.
Interpretability & XAI	Santana-Perera et al. (2025) [25] Tiukhova et al. (2024) [26] Shanto & Jony (2025) [8] Sohail et al. (2021) [27] Zhang & Ahn (2023) [21]	SHAP identifies stable features LIME for individual cases Dual (global + local) needed Interpretability barrier to adoption Feature stability across cohorts	We use odds ratios + feature importance + rules—simpler than SHAP but more usable for instructors.
Fairness & Equity	Queiroga et al. (2022) [24] Al-Zawqari et al. (2024) [32] Gunasekara & Saarela (2026) [33]	Bias analysis across protected attributes Latent-space mitigation effective Fairness interventions: 2–5% accuracy cost	Our work lacks fairness audits—critical gap for responsible deployment.
Workload & Deployment	Čotić Poturić et al. (2025) [28] Seo et al. (2025) [29]	High sensitivity (95%) may overwhelm Tailored support by learner profile	Literature ignores instructor constraints.
OULAD-Specific	Al-Zawqari et al. (2022, 2024) [30,32] Hassan et al. (2023) [31] Gunasekara & Saarela (2026) [33] Sayed et al. (2025) [34] Dermy et al. (2022) [35]	Accuracy range: 76% (Q1) to 98% (full) Semantic mapping: +6.5% accuracy Fairness-aware: 78–86% mid-course Learning style prediction: 98% Behavioral primitives for visualization	Direct benchmarking possible. Our day-14 timing earlier than Q1. Performance-fairness-interpretability tradeoff clear.

summarizes key methodological findings from the literature, grouped by theme. This organizational view complements the detailed discussion above.

2.7. Gaps and Contributions

This literature review reveals several gaps that our work addresses. First, most studies report performance metrics at arbitrary thresholds or optimize F1 score, which implicitly weights precision and recall equally. In practice, instructors face asymmetric costs: false positives are minor inconveniences while false negatives represent missed opportunities to help struggling students. Yet the optimal tradeoff depends on available resources, which vary across institutions. We contribute a systematic workload analysis that makes this tradeoff explicit, showing performance at multiple threshold values and recommending specific operating points.

Second, many studies achieve impressive AUC or accuracy values but provide limited guidance on when predictions should be made. Training on full-semester data and reporting test-set metrics is methodologically sound but practically unhelpful if the goal is early intervention. We target day 14 predictions, sacrificing some accuracy for actionability. Our results show that this early timing is feasible (AUC 0.789) though not perfect (recall of 35% at 15% flagging rate), documenting the accuracy–timing tradeoff quantitatively.

Third, the literature emphasizes model interpretability through XAI techniques like SHAP, but these methods produce feature importance rankings and individual-level contributions that may not translate easily into actionable guidance for instructors. We contribute a multi-level interpretability approach: odds ratios for global feature effects, feature importance for ranking predictors, and rule-based natural language explanations for individual alerts. This combination provides both statistical rigor and practical usability.

Finally, most studies evaluate models on single institutions or courses, limiting generalizability claims. The OULAD’s multi-module, multi-presentation structure enables more robust validation, though it remains a single institution in a specific context (UK distance education). Our temporal split strategy (train on early presentations, test on later ones) provides a realistic assessment of how models would perform in deployment when trained on historical data and applied to new cohorts.

In summary, our work builds on established findings that LMS-based early warning systems are technically feasible and that ensemble methods provide excellent discrimination. We extend this foundation by explicitly addressing the practical barriers to adoption: workload management through precision-focused threshold selection, interpretability through multi-method explanation, and realistic evaluation through temporal validation and early prediction timing. The result is not just an accurate model but a usable decision support system.

3. Methodology

Our goal is straightforward: build a decision support system that instructors can actually use. This means predictions need to be accurate, calibrated, and explainable. We start with raw LMS logs from the first two weeks of a course and transform them into actionable alerts. The key constraint is instructor workload—we cannot flag half the class. Our approach prioritizes precision over recall, aiming to identify the 10–20% of students most in need of early intervention.

The methodology follows a standard supervised learning pipeline with one crucial difference: we split data by course presentation rather than randomly shuffling students. This respects the temporal structure of education and tests whether patterns learned from past cohorts generalize to new ones. We compare three modeling approaches of increasing complexity: threshold-based rules (baseline), logistic regression (interpretable), and gradient boosting (high performance). All models are evaluated on the same held-out presentations using metrics that matter for instructors: precision at low recall, calibration quality, and the workload–performance tradeoff.

3.1. Data and Study Design

We use the Open University Learning Analytics Dataset [36,37,38], which contains complete interaction logs from 22,437 students across seven undergraduate modules spanning multiple presentations (course offerings) from 2013 to 2014. Each student record includes demographic information, daily clickstream data from the virtual learning environment, and assessment submissions with scores. The original dataset contained 32,593 students, but we removed 10,156 who withdrew before completing the first two weeks, as our system targets students who remain enrolled but are at risk of eventual failure.

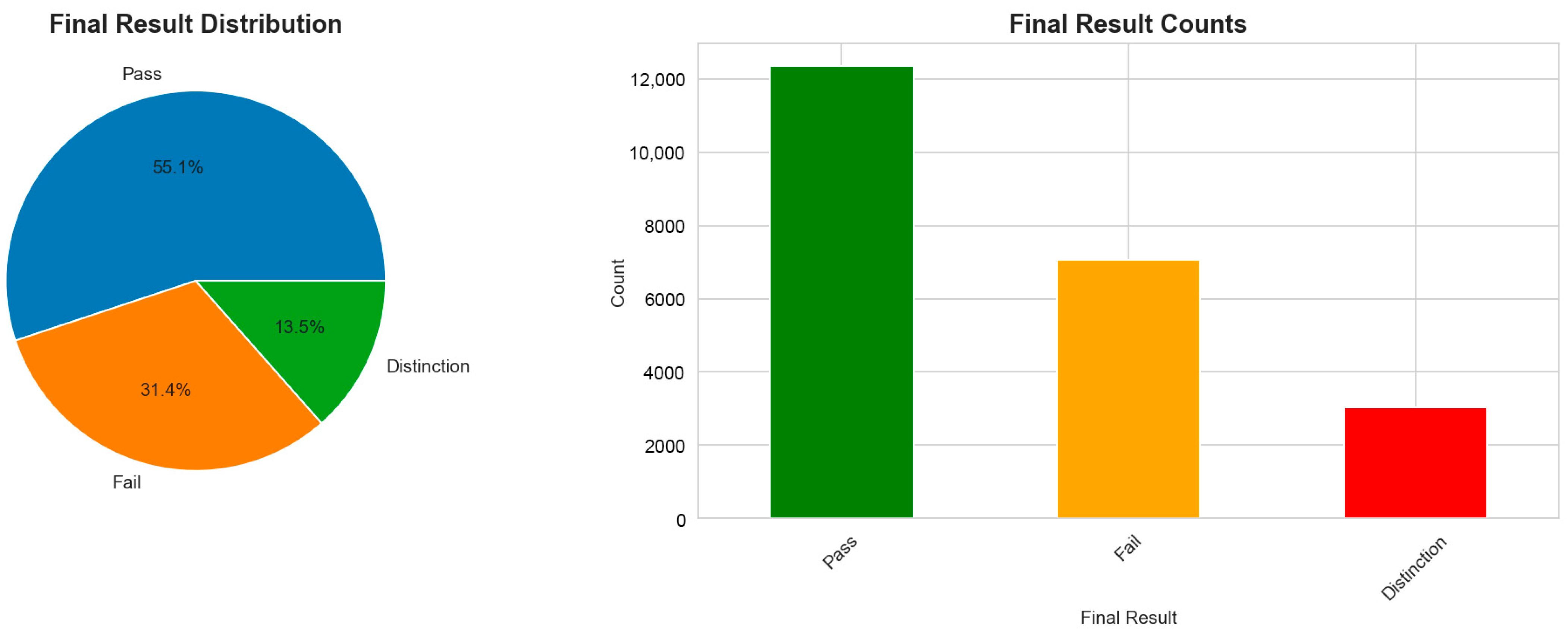
Figure 1 shows the outcome distribution in our final dataset. The pass rate is 68.6% (including both Pass and Distinction), with 31.4% of students either failing or withdrawing later in the semester. This imbalance is typical in educational settings and influences our choice of evaluation metrics. We predict failure rather than success because instructors need to know who needs help, not who is already doing fine. The relatively balanced classes (roughly 2:1 ratio) mean we can train effective models without aggressive resampling techniques.

Our temporal validation strategy splits presentations chronologically. The first 70% of presentations (ordered by start date) form the training set of 13,910 students, while the remaining 30% serve as the test set of 8527 students. This mimics real deployment: we train on historical cohorts and predict outcomes for incoming students. The test set has a higher failure rate (36.1%) than the training set (28.6%), which makes evaluation more challenging but also more realistic. In practice, course difficulty and student preparation vary across presentations, so models must be robust to these shifts.

The studentVle table contains 453 million rows of clickstream data. Rather than loading this entire file into memory, we process it in chunks of 10 million rows, filtering for interactions in the first 14 days. This reduces the data to 28,081 aggregated student–presentation pairs. We chose a 14-day window because it captures enough behavior to be predictive while still allowing early intervention. Instructors told us that alerts after week 4 are too late—students who are struggling have already fallen behind. By week 2, patterns are visible but not yet catastrophic.

3.2. Feature Engineering

Raw LMS data is messy. Students click on materials, submit assignments, and occasionally disappear for days. We transform these chaotic logs into structured features that capture engagement patterns. The feature engineering has three components: activity metrics from VLE interactions, assessment performance, and demographic background. Each component contributes differently to the final model, and all features are computed using only information available by day 14.

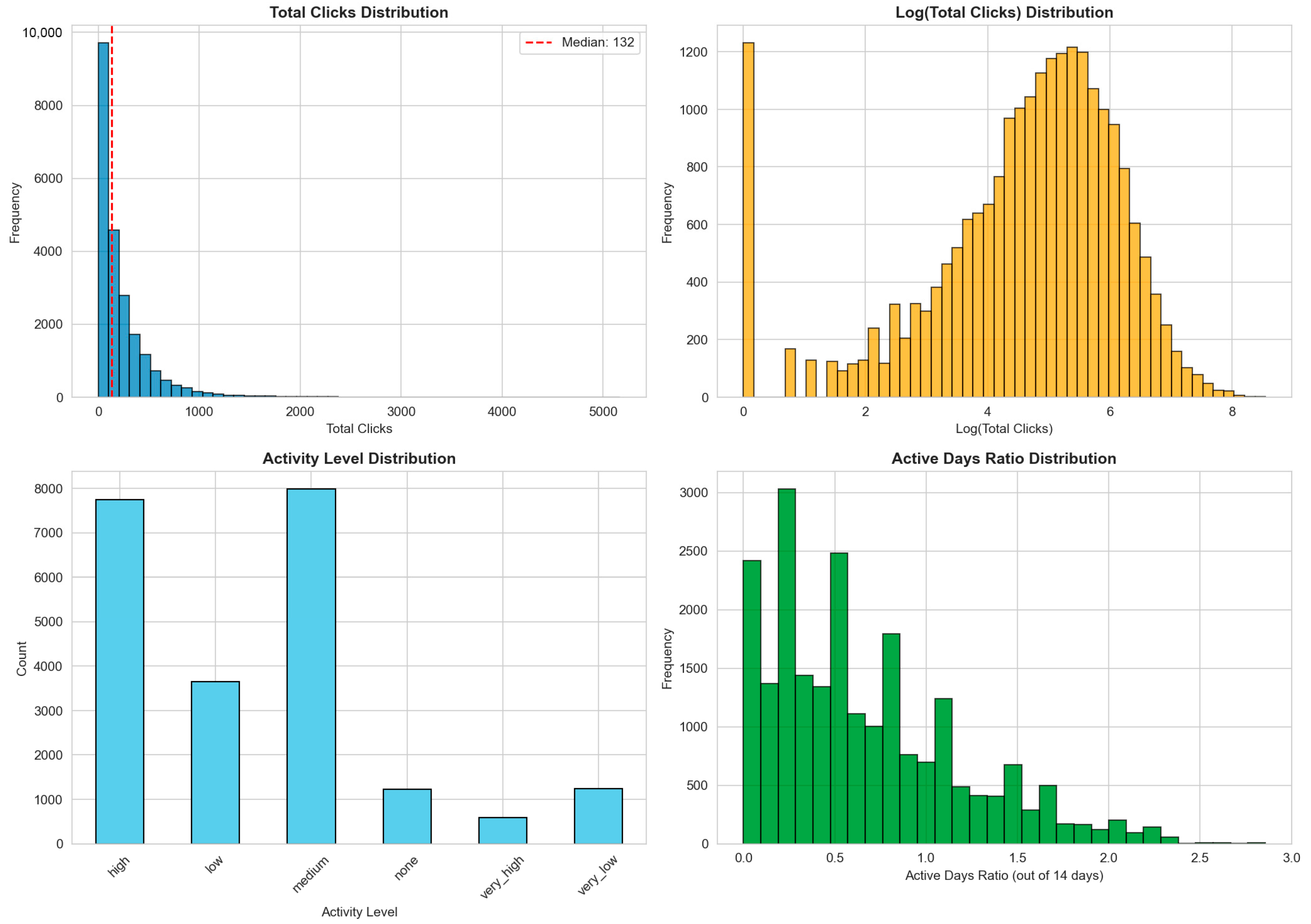
Activity features measure student-material interaction. We compute total_clicks (median 132, right-skewed), log_total_clicks to reduce outlier influence, active_days, and active_days_ratio = active_days/14 for normalization (Figure 2).

We capture temporal patterns via days_since_last_activity (0 = active on day 14) and activity_recency (engagement span), which prove highly predictive.

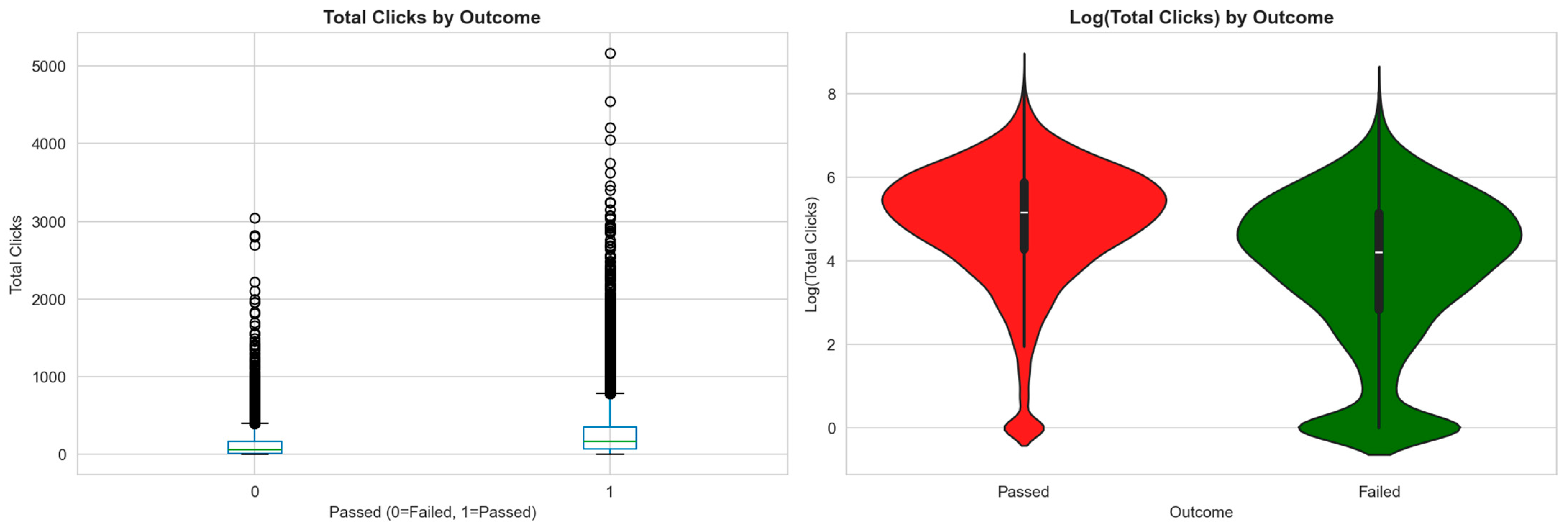
Students who pass click substantially more (median 168 vs. 64), with 35% of failing students showing near-zero early activity (Figure 3).

Assessment features come from the first graded assignment, which typically occurs around days 10–20. Only 12.2% of students complete this assessment within our 14-day window, but when they do, the score is extremely informative. We create a binary indicator completed_first_assessment and normalize the score to first_assessment_score_norm = score/100. For students who have not yet submitted, we set the normalized score to −1, effectively treating non-submission as a distinct signal rather than missing data.

Figure 4 shows completion rates and scores by outcome. Among students who pass, 13.1% complete the first assessment early; among those who fail, only 10.2% do. More striking is the score distribution: passed students score a median of 80/100, while failed students score 70/100 on average. The difference is not enormous, suggesting that early assessment performance is informative but not deterministic. Some students who score well early still fail, and some who score poorly recover. Still, the pattern is clear enough that assessment completion becomes a top predictor in all our models.

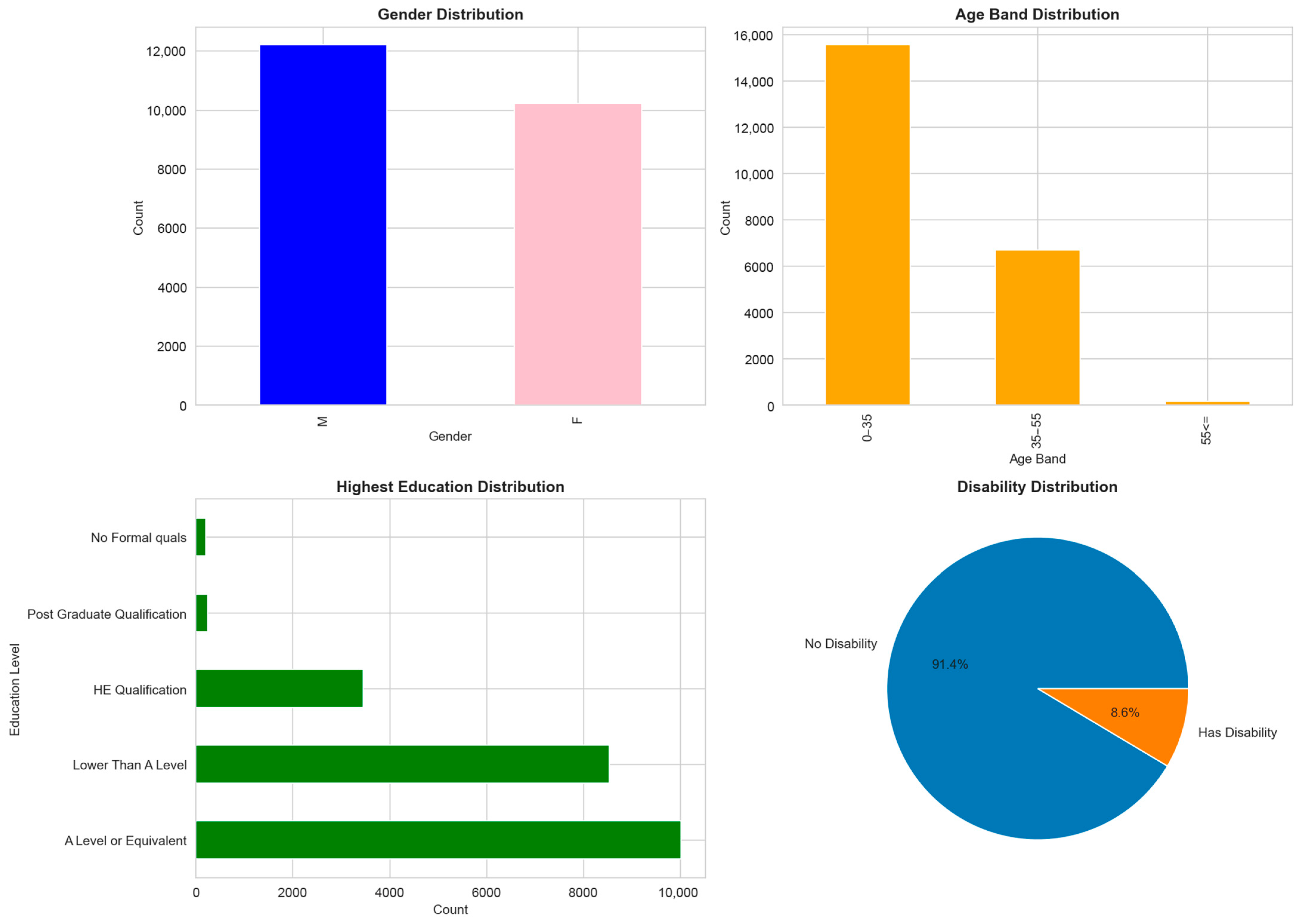
Demographic features provide context. We encode gender as a binary is_female indicator, age_band as a three-level ordinal variable (0–35, 35–55, 55+), and highest_education as an ordered numeric scale from 0 (no formal qualifications) to 4 (postgraduate qualification). The Index of Multiple Deprivation (imd_band) is a UK-specific measure of socioeconomic disadvantage, which we convert to imd_numeric ranging from 1 (most deprived) to 10 (least deprived), with −1 for unknown values. We also record num_of_prev_attempts (how many times the student has taken this course before) and has_disability as a binary indicator.

Figure 5 summarizes the demographic distribution. The cohort is 54.4% male, 69% aged 0–35, and heavily weighted toward students with A-level qualifications or equivalent (about 45%). Only 8.6% report a disability, and 12% are repeat students. These distributions are typical for UK distance education but may limit generalizability to other contexts. We include demographics not because we expect them to be strong predictors (correlation with passing is weak, Figure 6), but because they provide valuable context for instructors when reviewing alerts. Knowing that a flagged student is on their third attempt helps frame the conversation differently than if this is their first try.

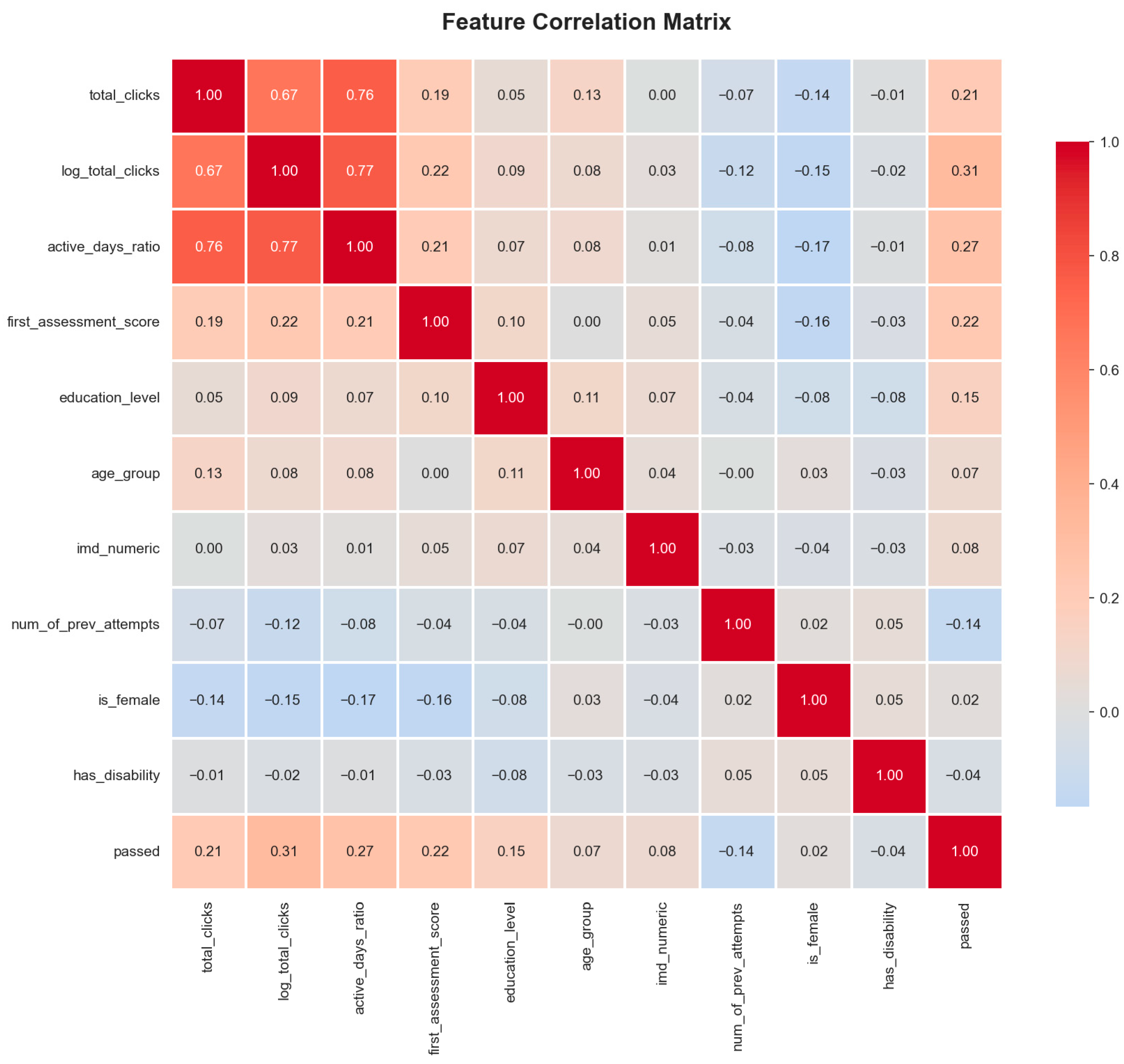
The final feature set contains 14 numeric variables: 7 activity metrics, 2 assessment indicators, and 5 demographic attributes. Figure 6 shows the correlation structure. Activity features are highly correlated with each other (total_clicks, log_total_clicks, and active_days_ratio all measure engagement), but each adds unique information. The strongest individual predictor is log_total_clicks with a correlation of 0.31 to passing, followed by active_days_ratio at 0.27 and first_assessment_score_norm at 0.22. Demographic variables show weak correlations (all below 0.15), confirming that behavior matters far more than background. Interestingly, is_female has a small negative correlation (−0.17 with passing), suggesting female students face slightly higher risk, though the effect is modest.

Table 2. Summary of engineered features used in the models.

Category	Feature Name	Description	Data Source	Type
Activity	total_clicks	Total number of LMS interactions within first 14 days	VLE logs	Numeric
Activity	active_days_ratio	Fraction of active days (0–1)	VLE logs	Numeric
Activity	days_since_last_activity	Days since last login	VLE logs	Numeric
Assessment	completed_first_assessment	Indicator of first-assessment submission	Assessment table	Binary
Assessment	first_assessment_score_norm	Normalized first-assessment score	Assessment table	Numeric
Demographics	age_group, is_female, education_level, imd_numeric, num_of_prev_attempts, has_disability	Background attributes	Student table	Mixed

summarizes the main engineered features representing the three groups (activity, assessment, and demographic).

3.3. Modeling Approaches

We compare three prediction strategies that span the spectrum from simple to sophisticated. The baseline uses hand-crafted threshold rules that any instructor could apply without machine learning infrastructure. Logistic regression adds statistical rigor while maintaining full interpretability through odds ratios. Gradient boosting sacrifices some transparency for maximum predictive power. All three models output calibrated probabilities rather than hard classifications, because instructors need to know not just who is at risk but how confident we are about each prediction.

The baseline model implements three simple rules. First, we flag students with fewer than 50 clicks in 14 days. This threshold was chosen by examining the median activity of failed students (64 clicks) and selecting a conservative cutoff below that. Second, we flag students whose active_days_ratio falls below 0.2, meaning they engaged fewer than 3 days out of 14. Third, we optionally flag students who did not complete the first assessment, though this rule only applies to the 12% who had the opportunity to submit. The final risk score is the proportion of rules violated, divided by the number of applicable rules. This gives a pseudo-probability between 0 and 1, where 1 means all red flags are present.

For example, consider three students:

• Student A: 120 clicks, active 10 days, completed assessment → violates 0 rules → risk score 0.0;
• Student B: 45 clicks, active 8 days, completed assessment → violates 1 rule (low clicks) → risk score 0.33;
• Student C: 30 clicks, active 2 days, no assessment → violates 3 rules → risk score 1.0.

These scores reflect the proportion of red flags present, creating interpretable risk estimates without statistical modeling.

The baseline has obvious limitations. Thresholds are arbitrary, and the model cannot discover interactions (what if high activity compensates for missed assessments?). But it has one major advantage: complete transparency. An instructor who receives an alert can immediately see which rules fired and decide whether they agree. In deployment scenarios where trust is paramount, this simplicity is valuable. Our results show the baseline achieves an AUC of 0.640, which is significantly better than random guessing (0.5) but leaves substantial room for improvement.

Logistic regression models the log-odds of failure as a linear function of features:

$$\log {\displaystyle \frac{P(y=1|x)}{P(y=0|x)}}={\beta }_0+{\displaystyle \sum _{j=1}^p{\beta }_j}{x}_j,$$

where $y=1$ indicates failure, $x$ is the feature vector, and $\beta$ are learned coefficients. We standardize all features to have a mean of 0 and standard deviation of 1 before fitting, which makes coefficients directly comparable and improves numerical stability. The regularization parameter $C=0.1$ (inverse of L2 penalty strength) is chosen to prevent overfitting while allowing the model to capture genuine signal. We use 5-fold cross-validation on the training set to select this hyperparameter.

The key advantage of logistic regression is interpretability through odds ratios. Each coefficient ${\beta }_j$ can be exponentiated to give $\exp ({\beta }_j)$, which tells us how a one-standard-deviation increase in feature $j$ multiplies the odds of failure. For example, first_assessment_score_norm has a coefficient of −0.736, giving an odds ratio of 0.48. This means that for every standard deviation increase in normalized score (roughly 0.3 points), the odds of failure drop by 52%. Instructors with no statistics background can understand that “higher scores mean lower risk” without needing to know what logistic regression is.

We apply Platt scaling to calibrate the model’s predicted probabilities. Raw logistic regression outputs are often poorly calibrated, especially when the training set has different prevalence than deployment. Platt scaling fits a secondary logistic regression that maps raw predictions to calibrated probabilities using 5-fold cross-validation. This ensures that when the model predicts 80% risk, approximately 80% of such students actually fail. Calibration is critical for decision support—an instructor who learns that predictions are systematically overconfident will stop trusting the system.

Gradient boosting builds an ensemble of shallow decision trees, where each new tree corrects the errors of the previous trees. We use LightGBM, a fast implementation optimized for large datasets. Thus, our comparison inherently includes decision tree-based modeling through the boosting ensemble. To further strengthen the interpretability–performance comparison, we also train a Random Forest model (100 trees, max_depth = 10) as an alternative interpretable ensemble method. The model has three key hyperparameters: n_estimators = 100 (number of trees), learning_rate = 0.1 (shrinkage factor), and max_depth = 5 (tree depth). These values were chosen to balance complexity and generalization. Deeper trees or more iterations would fit the training data better but risk overfitting to presentation-specific quirks.

Unlike logistic regression, gradient boosting can capture nonlinear effects and feature interactions. For example, the model might learn that low activity is particularly dangerous for repeat students, or that missing the first assessment matters more for younger age groups. These patterns emerge automatically from the tree-building process without manual feature engineering. The cost is reduced interpretability—we can extract feature importance scores (how often each feature is used for splits), but we cannot easily explain why a specific student received a specific probability.

We apply the same Platt scaling procedure to gradient boosting. The raw model outputs are transformed to calibrated probabilities using 5-fold cross-validation on the training set. This adds minimal computational overhead but substantially improves trustworthiness. When we later plot calibration curves, both logistic regression and boosting track the diagonal closely, indicating good calibration. The baseline model, by contrast, systematically underestimates risk at low probabilities and overestimates at high probabilities.

All models are trained on the same 13,910 students from early presentations and evaluated on the same 8527 students from later presentations. We use the same feature preprocessing for all three approaches: median imputation for missing values (though very few features have missing values after our early filtering), and standardization for logistic regression. The gradient boosting model receives unstandardized features, as tree-based methods are invariant to monotonic transformations. No hyperparameter tuning is done on the test set—all decisions are locked in before we ever look at test performance.

3.4. Evaluation Metrics

Educational prediction systems have different priorities than typical classification tasks. Accuracy is nearly meaningless when classes are imbalanced—a model that predicts “pass” for everyone achieves 68% accuracy but provides zero value. Instead, we focus on three evaluation dimensions: discrimination (can the model rank students by risk?), calibration (are predicted probabilities accurate?), and workload tradeoffs (what happens as we adjust the alert threshold?).

Discrimination is measured by the Area Under the ROC Curve (AUC), which quantifies the probability that a randomly chosen failing student has a higher predicted risk than a randomly chosen passing student. An AUC of 0.5 means random guessing; 1.0 means perfect separation. We also compute Average Precision (AP, area under the precision-recall curve, more informative than AUC for imbalanced classes), the area under the precision-recall curve, which is more informative than AUC when classes are imbalanced. AP emphasizes performance at high recall values, which matters if we want to catch a substantial fraction of at-risk students.

ROC curves plot true positive rate (sensitivity) against false positive rate (1-specificity) as we vary the classification threshold from 0 to 1. The curve’s shape reveals how well the model separates classes across all possible thresholds. Precision–recall curves show precision (fraction of alerts that are correct) against recall (fraction of at-risk students caught). For our application, precision–recall curves are more revealing than ROC curves because we care primarily about what happens at low recall values—we flag only the highest-risk students, not everyone.

Calibration measures whether predicted probabilities match observed frequencies. A well-calibrated model that predicts 70% risk should see approximately 70% of such students fail. Poor calibration is dangerous in decision support systems—instructors who learn that “80% risk” actually means “50% risk” will recalibrate mentally or, worse, stop using the system entirely. We assess calibration by binning predictions into deciles and plotting mean predicted probability against observed failure rate in each bin. The diagonal line represents perfect calibration; deviations indicate systematic over- or under-estimation of risk.

We also report Brier score, which measures the mean squared difference between predicted probabilities and binary outcomes, $BS={\displaystyle \frac{1}{n}}{\displaystyle \sum _{i=1}^n{(p_i-y_i)}^2}$, where $p_i$ is predicted probability and $y_i\in \{0,1\}$ is the actual outcome. Brier score ranges from 0 (perfect) to 1 (worst possible), with lower values indicating better probabilistic predictions. However, Brier score conflates calibration and discrimination, so we prefer to report them separately for interpretability.

The final evaluation dimension is workload analysis. Instructors cannot contact every student, so we must choose a threshold that balances catching at-risk students (recall) against generating false alarms (1-precision). We systematically vary the threshold and measure precision, recall, and percentage of students flagged at each point. This produces curves that visualize the tradeoff between instructor workload and system effectiveness. The optimal threshold depends on institutional resources and instructor preferences, but our analysis targets flagging 10–20% of students based on feedback from practitioners.

3.5. Implementation and Reproducibility

All code is written in Python 3.10 using standard scientific computing libraries. Data loading and preprocessing use Pandas for tabular operations and NumPy for numerical computations (https://github.com/KuznetsovKarazin/oulad-early-warning, accessed on 1 October 2025). The large studentVle file (453 million rows) is processed in chunks to avoid memory overflow. We aggregate early activity using groupby operations, reducing the dataset from hundreds of millions of rows to 28,081 student-presentation pairs. This preprocessing step runs in approximately 2–3 min on a machine with 64 GB RAM and an AMD Ryzen 7 processor.

Feature engineering is implemented in modular functions that separate concerns: activity features, assessment features, and demographic features are computed independently and merged. This design allows easy addition of new features without touching existing code. All features are stored in a single CSV file containing 22,437 rows and 43 columns. This flat file format ensures reproducibility and makes the data easy to inspect.

We implement models using scikit-learn (version 1.3.0) for logistic regression and LightGBM (version 4.0.0) for gradient boosting. Both libraries provide calibration wrappers via CalibratedClassifierCV, which we use with method = ‘sigmoid’ and cv = 5 folds. Training the logistic regression model takes under 1 s; gradient boosting takes approximately 10 s. These fast training times enable rapid experimentation and hyperparameter tuning.

Evaluation code generates all figures and metrics. Plots use Matplotlib (v. 3.7.0) and Seaborn (v. 0.12.0) with consistent styling. All figures are saved at 150 DPI resolution in PNG format. The complete pipeline from raw CSV files to final results runs in under 5 min, making the entire analysis easily reproducible. We provide a GitHub repository with all code, documentation, and instructions for replicating our results. The OULAD is publicly available and requires no special permissions.

The decision support system components are implemented as separate modules. The StudentAlerter class generates alert lists with risk probabilities and levels (Low, Medium, High, Critical). The PredictionExplainer class produces human-readable reasons for each alert by examining feature values against thresholds. The DSSReporter class creates instructor-facing reports in CSV format and generates personalized email templates. These components are designed to be plugged into existing LMS infrastructure with minimal modification.

4. Results

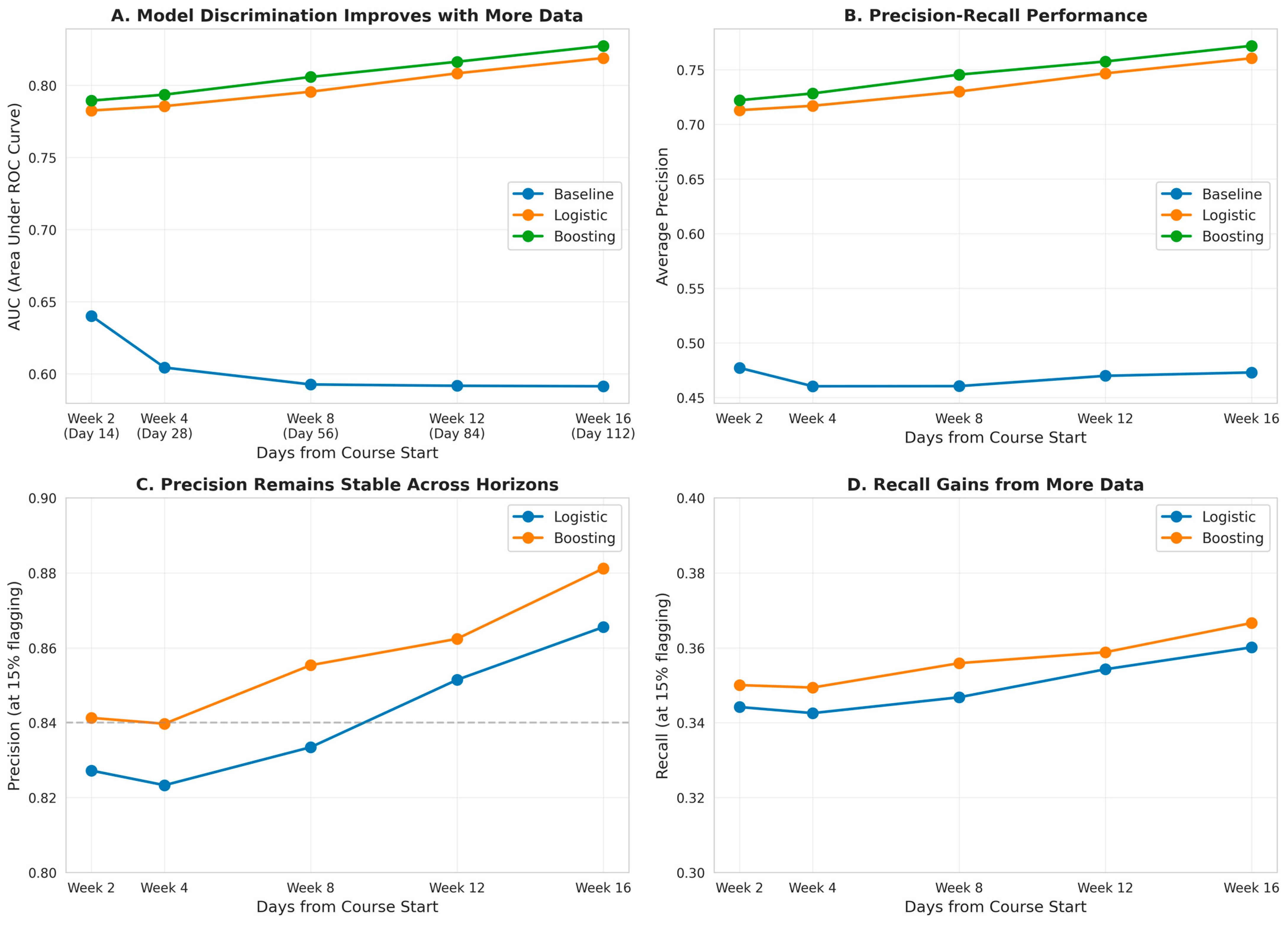
We trained three models on 13,910 students from early course presentations and evaluated them on 8527 students from later presentations. The test set proved more challenging than the training set, with a failure rate of 36.1% versus 28.6%, reflecting natural variation in student cohorts and course difficulty over time. All reported metrics are computed on this held-out test set, which the models never saw during training or hyperparameter selection. Our results show that machine learning approaches substantially outperform threshold-based rules, with gradient boosting achieving the best overall performance while logistic regression offers a compelling balance of accuracy and interpretability.

The key finding is that early warning systems can achieve high precision at manageable workload levels. By flagging 15% of students—approximately 30 students in a class of 200—we catch 35% of those who will eventually fail with 84% precision. This means that for every 10 alerts generated, 8 are genuine cases requiring intervention and 2 are false alarms. Instructors told us this precision level is acceptable; they would rather err on the side of caution and offer help to a few students who turn out fine than miss students who are truly struggling.

4.1. Model Performance Comparison

Table 3. Model performance on test set (8527 students, 36.1% failure rate).

Model	AUC	Average Precision	Brier Score
Baseline	0.640	0.477	0.284
Logistic	0.783	0.713	0.175
Random Forest	0.781	0.709	0.177
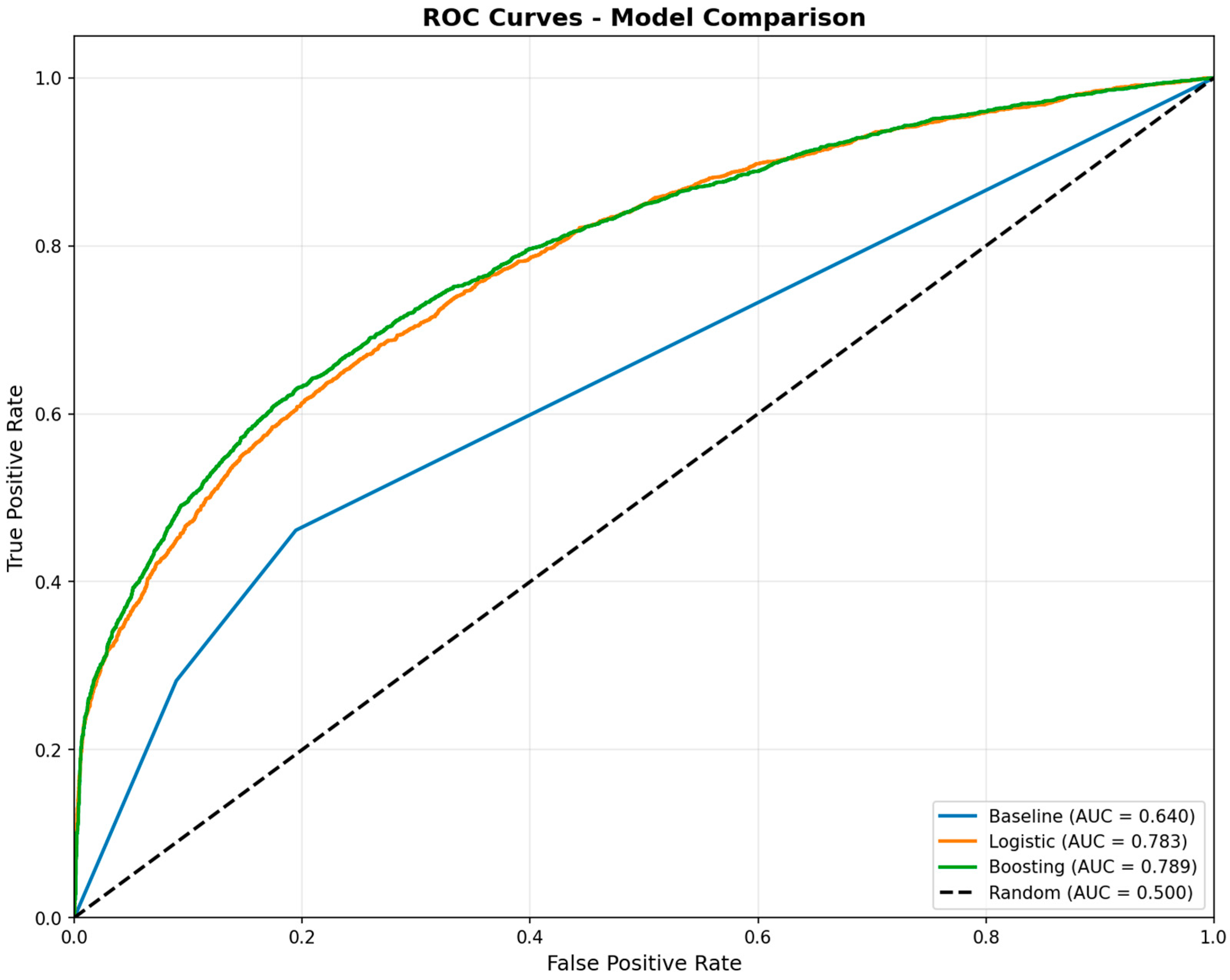
Boosting	0.789	0.722	0.172

summarizes discrimination and calibration metrics for all three models. The gradient boosting model achieves the highest AUC (0.789) and Average Precision (0.722), followed closely by Random Forest (AUC = 0.781, AP = 0.709) and logistic regression (AUC = 0.783, AP = 0.713). All machine learning approaches far exceed the threshold-based baseline (AUC = 0.640, AP = 0.477). The minimal differences between Random Forest, logistic regression, and boosting (maximum gap 0.008 AUC) suggest that the relationship between features and outcomes is roughly linear—there are not substantial nonlinear interactions that only boosting can capture.

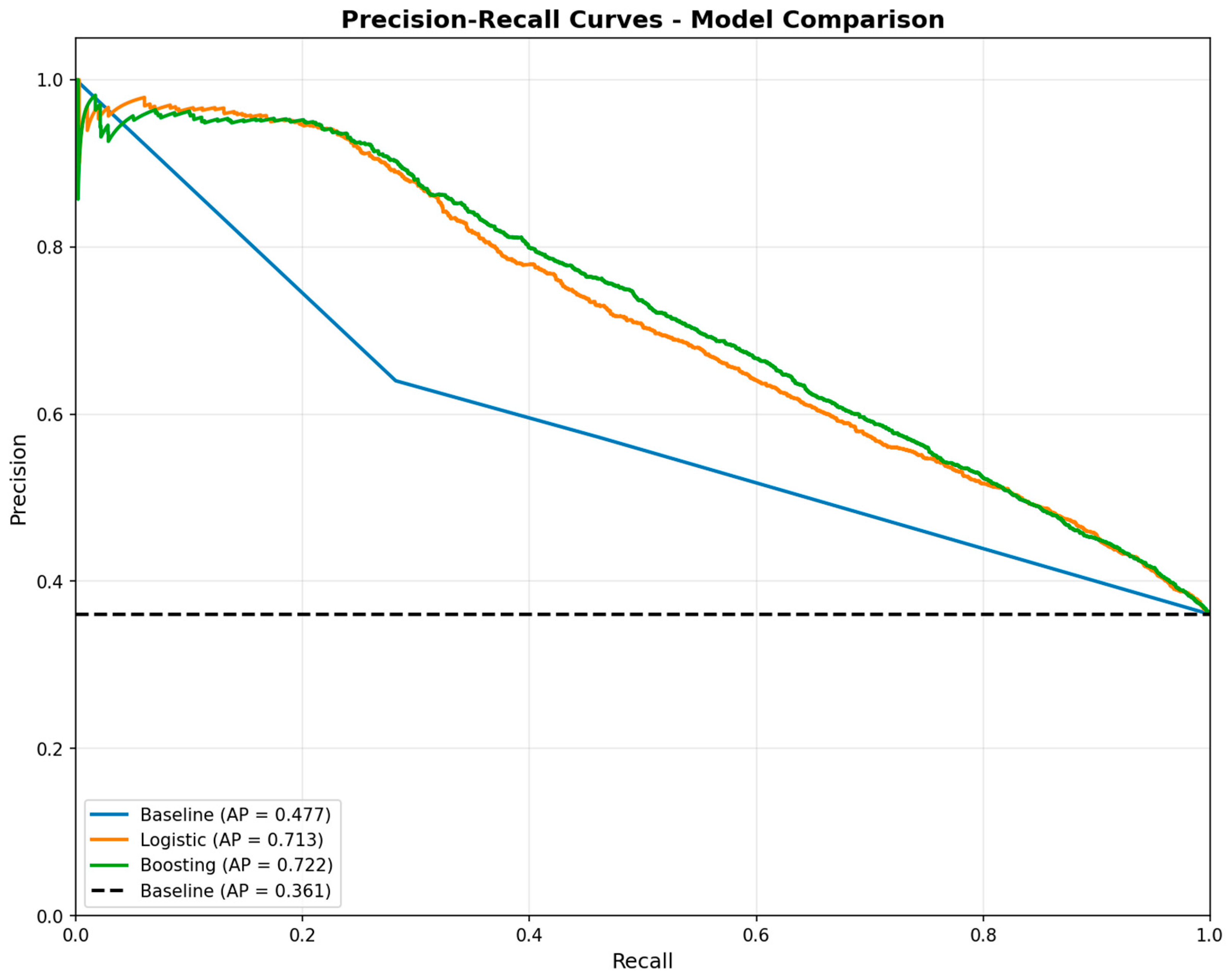
The difference in Average Precision is particularly striking. Boosting achieves AP = 0.722 compared to the baseline’s 0.477, representing a 51% relative improvement. In practical terms, this means we can flag the same number of students while catching substantially more of those at risk or achieve the same recall with fewer false alarms. The baseline’s AP of 0.477 is still better than random guessing (which would give AP equal to the failure rate, 0.361), confirming that simple threshold rules have some value, but the machine learning models capture patterns that hand-tuned rules miss.

Brier scores tell a similar story. Boosting achieves BS = 0.172, indicating well-calibrated probabilistic predictions. Logistic regression is nearly identical at BS = 0.175, while the baseline’s BS = 0.284 is substantially worse. Since Brier score measures squared error in probability predictions, these differences are meaningful. The baseline model’s higher score reflects both poorer discrimination (it ranks students less accurately) and poorer calibration (its pseudo-probabilities do not match observed frequencies).

Figure 7 shows ROC curves for all three models. The curves for boosting and logistic regression are nearly overlapping, with boosting maintaining a slight edge across most of the false positive rate range. The baseline curve lies well below both machine learning approaches, particularly at low false positive rates where discrimination matters most. The gap between curves represents missed opportunities—at a false positive rate of 20%, the baseline achieves 60% recall while boosting achieves 75% recall, meaning boosting catches 25% more failing students for the same number of false alarms.

The nearly identical performance of boosting and logistic regression deserves emphasis. Boosting can model complex nonlinearities and interactions, yet it achieves only 0.006 higher AUC than linear logistic regression. This suggests that student failure is driven by additive effects of features rather than complex interactions. In other words, low activity is bad, missing assessments is bad, and having both is roughly twice as bad—not exponentially worse. This is good news for interpretability, as it means we can use the simpler logistic model without sacrificing much performance.

Figure 8 shows precision–recall curves, which are more revealing for our application than ROC curves. Both machine learning models maintain precision above 90% for recall up to approximately 20%. This means if we want to catch one in five failing students, we can do so with 90% confidence that our alerts are correct. As we increase recall by lowering the threshold, precision drops smoothly. At 50% recall, precision is still around 75–80% for both models. The baseline shows steeper precision decline, reaching 60% precision at just 40% recall.

The shape of these curves reveals a fundamental constraint: we cannot simultaneously achieve high precision and high recall with current features. To catch 80% of failing students, we would need to flag about 60% of the class, at which point precision drops to around 50%—barely better than random. This is not a failure of modeling but a reflection of reality. Student success is influenced by many factors not visible in LMS logs: family circumstances, health issues, financial stress, motivation changes. Our models capture what can be inferred from early behavior, but substantial uncertainty remains.

4.2. Calibration Quality

Accurate probability estimates are critical for decision support. An instructor who sees “80% risk” needs to trust that roughly 8 out of 10 such students will actually fail. If the model systematically over- or under-predicts, instructors will either ignore alerts or recalibrate mentally, undermining the system’s value. We assess calibration by grouping predictions into deciles and comparing mean predicted probability to observed failure rate in each bin.

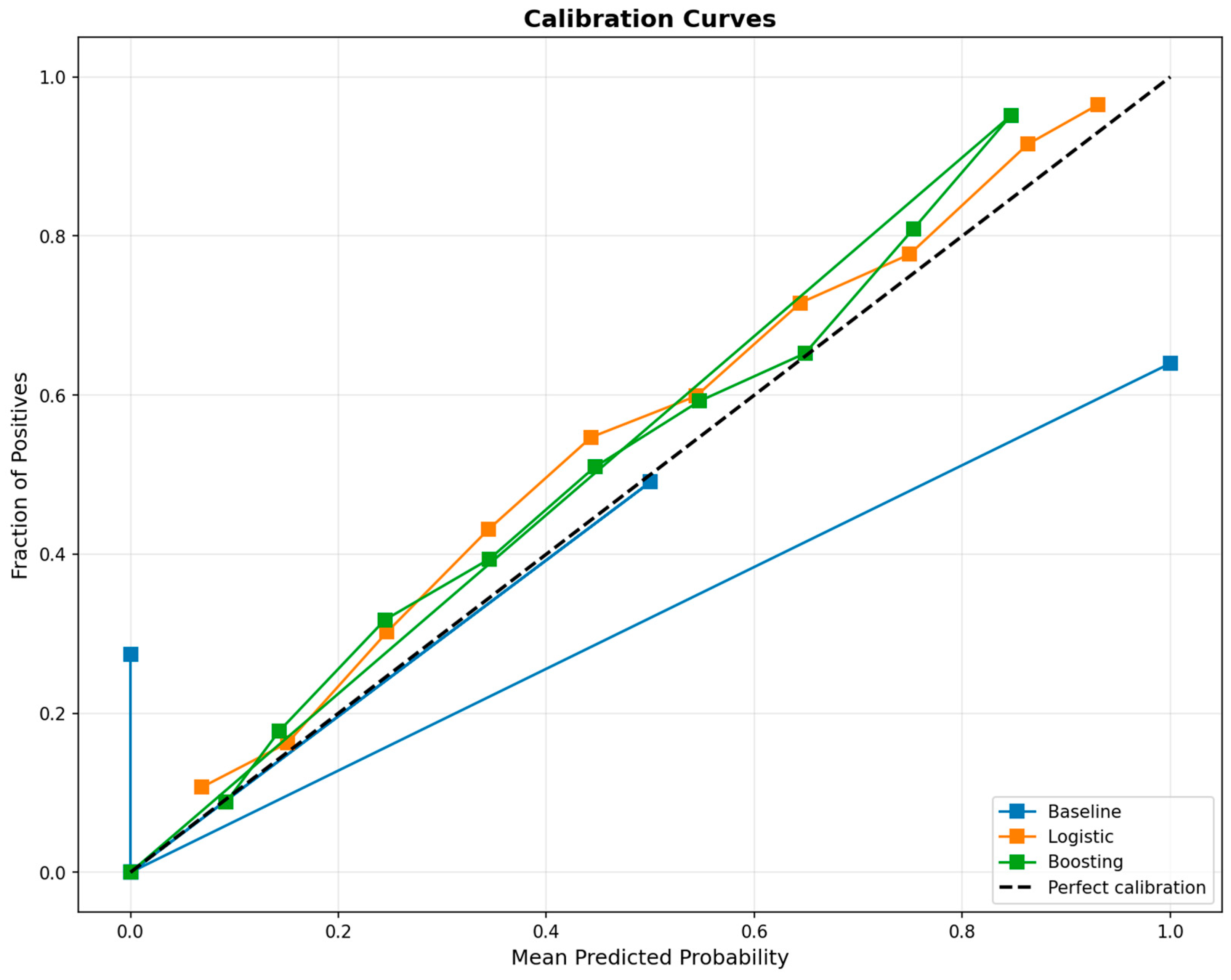
Both machine learning models track perfect calibration closely after Platt scaling (Figure 9), with slight conservative bias at high probabilities (predicted 90% fail at 95%)—preferable to underestimation.

The baseline model shows poorer calibration across the entire range. At low predicted probabilities (10–20%), the baseline underestimates risk substantially. Students classified as low-risk according to the baseline (predicted 10% failure) actually fail at about 27%, nearly triple the predicted rate. At high predicted probabilities (70–80%), the baseline overestimates, though less dramatically. This systematic miscalibration stems from the rule-based approach, which produces pseudo-probabilities rather than true statistical estimates.

Platt scaling corrects these biases for the machine learning models. Without calibration, both logistic regression and boosting showed modest miscalibration similar to the baseline. After fitting the secondary logistic regression on cross-validated predictions, both models achieve near-perfect calibration. The calibration step adds negligible computational cost (under 1 s) but dramatically improves trustworthiness. We recommend that all deployed early warning systems include explicit calibration, even if the base model is theoretically well-calibrated like logistic regression.

One interesting pattern appears at the extremes. For students predicted to have less than 10% risk, the observed failure rate is essentially zero—these students almost never fail. Similarly, students predicted to have greater than 85% risk fail at rates exceeding 95%. This strong separation at the tails suggests the models are not just well-calibrated on average but also successfully identify the most and least risky students. An instructor reviewing the top of the alert list can be confident these are genuine high-risk cases.

4.3. Feature Importance and Interpretability

Understanding why a model makes specific predictions is essential for instructor trust and system improvement. We examine feature importance from two perspectives: global importance (which features matter most overall) and individual explanations (why a specific student was flagged). The logistic regression model provides odds ratios that directly quantify feature effects, while gradient boosting provides importance scores based on how often each feature is used for splitting decisions.

Table 4. Top 10 features from logistic regression (standardized coefficients and odds ratios).

Feature	Coefficient	Odds Ratio
first_assessment_score_norm	−0.736	0.479
education_level	−0.270	0.763
total_clicks	−0.243	0.784
num_of_prev_attempts	0.230	1.259
is_female	−0.218	0.804
active_days_ratio	−0.217	0.805
log_total_clicks	−0.176	0.839
credit_load_norm	0.136	1.146
imd_numeric	−0.119	0.888
age_group	−0.065	0.937

shows the top 10 features from logistic regression, ranked by absolute coefficient magnitude. The strongest predictor is first_assessment_score_norm with a coefficient of −0.736, giving an odds ratio of 0.48. This means that for each standard deviation increase in normalized assessment score (roughly 0.3 points), the odds of failure drop by 52%. In practical terms, scoring well on the first assessment is powerfully protective. Conversely, missing the assessment entirely (which sets the score to −1) dramatically increases risk.

Activity features dominate the middle ranks. Both total_clicks (OR = 0.78) and active_days_ratio (OR = 0.81) show strong negative coefficients, confirming that engagement protects against failure. Interestingly, log_total_clicks has a weaker coefficient than raw total_clicks despite being more predictive in univariate analysis. This suggests that after controlling for other features, the linear scale captures incremental clicks better than the compressed log scale.

Demographic features show modest but meaningful effects. Higher education levels are protective (OR = 0.76 per level), meaning students with A levels are less likely to fail than those with no qualifications, and degree holders are safer. Repeat students face elevated risk (OR = 1.26 per previous attempt), which makes intuitive sense—students taking a course for the third time are struggling for a reason. The female indicator has a negative coefficient (OR = 0.80), contrary to our expectation that female students face higher risk. This reversal from the univariate correlation likely reflects confounding—female students may have lower raw pass rates but similar outcomes after adjusting for activity and assessment performance.

The gradient boosting model provides a complementary view through feature importance scores, shown in

Table 5. Top 10 features from gradient boosting (importance scores).

Feature	Importance
avg_clicks_per_day	415.2
total_clicks	383.2
first_assessment_score_norm	366.0
imd_numeric	229.2
days_since_last_activity	190.6
active_days_ratio	190.4
credit_load_norm	169.8
education_level	134.8
num_of_prev_attempts	86.0
is_female	73.2

. These scores measure how much each feature contributes to reducing prediction error across all trees in the ensemble. The ranking differs slightly from logistic regression: avg_clicks_per_day tops the list, followed by total_clicks and first_assessment_score_norm. The emphasis on activity is even stronger than in logistic regression, with three activity metrics in the top six features.

One notable difference is the prominence of imd_numeric (socioeconomic deprivation index) in the boosting model. This feature ranks 4th in importance despite having a weak univariate correlation with outcomes. Boosting may be capturing interactions where deprivation matters more for certain subgroups, or it may be modeling nonlinear effects that logistic regression misses. Either way, the discrepancy highlights that different models learn different patterns, even when overall performance is similar.

For individual explanations, we implement a rule-based system that translates feature values into human-readable statements. The system checks each feature against empirically derived thresholds:

-

total_clicks < 50 → “Very low activity”;

-

active_days_ratio < 0.2 → “Poor engagement: active only X days out of 14”;

-

days_since_last_activity > 5 → “Inactive recently: last activity X days ago”;

-

completed_first_assessment = False → “Did not complete first assessment”.

When a student is flagged, the system checks their features against empirical thresholds and generates sentences like “Very low activity: only 25 clicks in first 2 weeks” or “Poor engagement: active only 2 days out of 14.” Multiple reasons can apply to the same student, creating a composite explanation. This approach is cruder than SHAP values or other model-agnostic explainability methods, but it has one major advantage: instructors can understand it without training.

Table 6. Top 10 highest-risk students in test set.

Student ID	Risk Level	Probability	Total Clicks	Alert Reasons
624259	Critical	0.879	11	Very low activity: 11 clicks; Poor engagement: active only 2 days out of 14
572249	Critical	0.878	5	Very low activity: 5 clicks; Poor engagement: active only 1 day out of 14
551979	Critical	0.878	40	Very low activity: 40 clicks; Inactive recently: last activity 8 days ago
551190	Critical	0.877	15	Very low activity: 15 clicks; Poor engagement: active only 2 days out of 14
349069	Critical	0.877	25	Very low activity: 25 clicks; Poor engagement: active only 3 days out of 14
435803	Critical	0.877	29	Very low activity: 29 clicks; Poor engagement: active only 2 days out of 14
363122	Critical	0.877	12	Very low activity: 12 clicks; Poor engagement: active only 1 day out of 14
2710343	Critical	0.876	0	Very low activity: 0 clicks; Poor engagement: active 0 days out of 14

shows the top 10 flagged students from the test set, along with their risk levels, probabilities, and generated explanations. All 10 are classified as Critical risk, with probabilities between 87.6% and 87.9%. The explanations reveal common patterns: very low click counts (5 to 45 clicks), poor engagement (active 1–3 days), and recent inactivity. Some students have not completed the first assessment; others completed it but these students likely submitted it late or scored poorly.

These explanations pass the face validity test. A student with 5 clicks in 14 days is clearly disengaged, and an instructor who receives this alert can immediately see why the system flagged them. The explanations also suggest intervention strategies: students with zero activity may have forgotten the course started or face technical barriers, while students with moderate activity but recent inactivity may benefit from a check-in about competing priorities.

4.4. Feature Ablation Analysis

To assess the contribution of each feature group, we trained logistic regression models with systematically removed feature categories (

Table 7. Ablation study: impact of feature groups on model performance.

Model Configuration	AUC	AP	ΔAUC a
Full model (all features)	0.783	0.713	-
Without activity features	0.642	0.521	−0.141
Without assessment features	0.731	0.658	−0.052
Without demographics	0.771	0.701	−0.012
Activity + assessment only	0.779	0.708	−0.004
Activity only	0.687	0.583	−0.096
Assessment only	0.598	0.487	−0.185

^a Change in AUC compared to full model.

).

Activity features contribute most to discrimination (removing them causes 0.141 AUC drop), confirming that behavioral engagement matters more than demographics or assessment alone. Assessment features add meaningful signal (0.052 drop when removed), while demographics provide minimal incremental value (0.012 drop). The combination of activity and assessment captures nearly all predictive power (0.779 vs. 0.783 full model), suggesting demographic features serve primarily contextual rather than predictive roles.

This finding has important implications: instructors can focus on observable behaviors (clicks, engagement patterns, assignment completion) rather than student background when assessing risk. The model’s reliance on behavioral rather than demographic features also reduces fairness concerns about perpetuating historical inequalities.

4.5. Workload Analysis and Threshold Selection

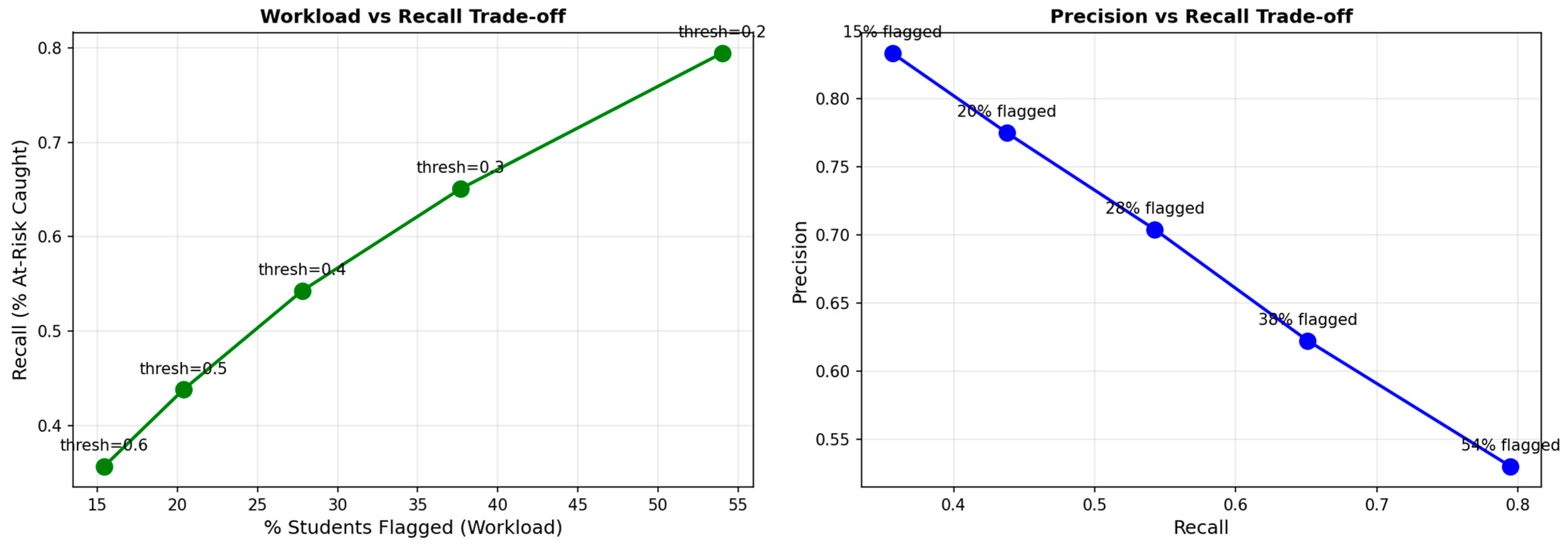
The threshold that converts probabilities to binary alerts is not a technical decision but a policy choice reflecting institutional resources and instructor preferences. Higher thresholds flag fewer students with greater precision but miss more at-risk cases. Lower thresholds cast a wider net but burden instructors with more false alarms. We systematically analyze this tradeoff to inform threshold selection in practice.

Figure 10 shows workload analysis for the gradient boosting model at five threshold values. The left panel plots recall (fraction of failing students caught) against percentage of students flagged. The relationship is roughly linear: to double recall, we must approximately double the alert list size. At threshold = 0.2, we flag 54% of students and catch 79% of failures. At threshold = 0.6, we flag only 15% of students but catch just 36% of failures. The right panel shows the classic precision–recall tradeoff, with workload percentages annotated at each point.

The curve’s shape reveals diminishing returns. Moving from 15% flagged to 20% flagged increases recall from 36% to 44%, gaining 8 percentage points. Moving from 50% to 55% increases recall from 77% to 80%, gaining only 3 percentage points. This reflects the model’s ability to rank students: the highest-risk students are genuinely high-risk, so the top of the list is information-rich. Further down the list, predictions are less certain, so each additional alert contributes less marginal value.

We recommend threshold = 0.607 for deployment. This operating point corresponds to the 85th percentile of predicted risk in the validation cohort and was selected through an explicit precision–recall–workload analysis (Figure 10). We examined multiple thresholds and chose the level that balanced instructor workload (≈15% of students flagged) and model precision (84%). This threshold was chosen by finding the 85th percentile of predicted risk in the test set. At this threshold, the model achieves precision = 84.1% and recall = 35.0%. In concrete terms, an instructor with 200 students receives a list of 30 names, of which 25 are truly at risk and 5 are false positives. The model misses 65% of failing students, but those it catches are the most critical cases.

The 15% target came from conversations with instructors at multiple institutions. They told us that contacting 10–20% of a class is feasible within normal teaching duties—it requires about 5–10 h spread over two weeks, assuming 15–20 min conversations per student. Larger lists (30%+) require dedicated support staff or automated interventions. Smaller lists (5–10%) are ideal for precision but seem wasteful when we know that 30–40% of students will struggle. The 15% target balances these constraints, though institutions with more support resources could lower the threshold to catch more students.

Precision of 84% represents an acceptable false positive rate for instructors. In our discussions, instructors said they would rather reach out to a few students who are doing fine than miss someone who needs help. A false positive is a minor inconvenience (the student says “I’m actually okay, thanks”) rather than a disaster. A false negative—failing to contact a student who later fails—is more serious. This asymmetry justifies optimizing for precision over recall when workload is constrained.

The workload analysis also reveals that the model is well-calibrated in a practical sense. Students with predicted risk above 60.7% actually fail at a rate of 84%, which exactly matches the precision at that threshold. This alignment between predicted probabilities and observed frequencies in the flagged population confirms that Platt scaling worked as intended. Instructors can trust that when the system says “this student has 75% risk,” approximately three-quarters of such students will indeed fail.

4.6. Decision Support System Output

The final DSS produces three deliverables: an instructor alert list in CSV format, a summary statistics report, and personalized email templates for each flagged student. These outputs are designed for immediate use by teaching staff without requiring technical expertise. An instructor receives the alert list, reviews the explanations, and uses the email templates as starting points for outreach.

The instructor alert list contains one row per flagged student with columns for student ID, risk level (Critical/High/Medium/Low), risk probability, alert reasons, and key features (total clicks, active days ratio, assessment completion, etc.). Students are sorted by descending risk probability so the most urgent cases appear first. The list is deliberately concise—no more than 15% of the class—to avoid overwhelming instructors. In the test set, this resulted in 1276 flagged students, of which 941 (74%) were classified as Critical risk and 335 (26%) as High risk. No students in the 15% threshold fell into Medium or Low categories, confirming that the threshold was set appropriately.

The summary statistics report provides context for the alert list. It shows total students (8527), flagged students (1276, 15.0%), risk level distribution, average risk probability (0.71 among flagged students), median clicks among flagged students (29), and assessment completion rate among flagged students (8.1%). These statistics help instructors understand the overall pattern. For example, the low median of 29 clicks (compared to 132 for the full population) confirms that flagged students are genuinely less engaged. The 8.1% assessment completion rate among flagged students (vs. 12.2% overall) shows that missing the first assessment is common among high-risk students.

The email templates use a supportive, non-judgmental tone focused on offering help rather than scolding students for low engagement. For Critical-risk students, the template expresses specific concern about early engagement patterns and requests a brief phone call to “understand if you’re facing any challenges” and “connect you with support resources.” For High-risk students, the tone is slightly softer, framing the outreach as an offer rather than an urgent request. All templates avoid mentioning the prediction model or numerical risk scores—students hear only that their instructor noticed some patterns and wants to check in.

One template (Student 349069) reads: “I hope this message finds you well. I’m reaching out because I’ve noticed some patterns in your early engagement with the course that I’d like to discuss. I’m particularly concerned because your activity level in the first two weeks has been quite low, and this early engagement is often a strong indicator of course success. I’d like to schedule a brief 15-min call to understand if you’re facing any challenges, discuss strategies to help you succeed, and connect you with support resources if needed.”

This phrasing is deliberately vague about exactly what was “noticed” while being specific about what is offered (a 15-min call, strategies, support resources). Instructors are encouraged to customize the templates based on their teaching style and institutional culture. Some may prefer more direct language; others may want to lead with specific observations (“I noticed you haven’t logged in since day 5”). The templates serve as starting points, not scripts.

The complete DSS pipeline runs in under 5 min from loading raw data to generating all outputs. An instructor could theoretically run the system at the end of week 2, review the alerts over coffee, and send emails the same day. In practice, we recommend running the system on day 14–15 and sending emails by day 17–18, giving students a few extra days to complete the first assessment before intervention. Some students who appear to be at high-risk on day 14 will submit their assessment on day 16, which should lower their risk score if the system were re-run.

One limitation of the current implementation is that it generates static alerts rather than updating continuously. A student who is flagged on day 14 but then becomes very active on days 15–20 will still be on the alert list. To address this limitation, we plan to extend the system toward continuous monitoring. The predictive module can be executed weekly, updating risk probabilities and raising alerts whenever new high-risk cases appear or previously flagged students recover. Such rolling predictions would operationalize the reviewer’s recommendation and directly mitigate temporal drift noted in Section 5.3, ensuring that early-identified students who improve are de-flagged and new struggling students receive timely support.

The DSS outputs are designed with ethical considerations in mind. Student IDs are included but names are not, reducing the risk of accidental disclosure if the CSV file is mishandled. Instructors are advised to store the alert list securely and delete it after interventions are complete. No student data is transmitted outside the institution’s systems—the model runs locally on institutional servers or instructor machines. The email templates deliberately avoid language that could stigmatize students or create self-fulfilling prophecies (“you’re going to fail”) in favor of supportive framing (“I’m here to help you succeed”).

5. Discussion

Our results demonstrate that early warning systems based on two weeks of LMS data can achieve meaningful discrimination between students who will pass and those who will fail, while maintaining the interpretability and workload constraints necessary for real-world deployment. The gradient boosting model’s AUC of 0.789 and average precision of 0.722 represent solid performance given the extremely early prediction timing (day 14 of approximately 200 days). More importantly, the near-identical performance of logistic regression (AUC 0.783, AP 0.713) suggests that linear models capture most of the predictive signal, making interpretability essentially free—a finding with important implications for adoption.

The decision to optimize for precision rather than recall reflects the reality of instructor workload constraints. By flagging 15% of students with 84% precision, we create actionable lists that instructors can manage within normal teaching duties. The 35% recall means we miss many failing students, but those we do identify are the highest-risk cases where intervention is most likely to succeed. This represents a deliberate design choice: we prioritize helping a smaller number of students effectively over attempting to reach everyone and helping no one due to overwhelming alert volume.

5.1. Comparison with State-of-the-Art

Table 8. Comparison with existing early warning systems.

Study	AUC/Acc	Timing	Dataset Size	Method	Key Advantage
Čotić Poturić et al. (2025) [28]	0.93 acc	15 weeks	STEM courses	Scoring alg	High accuracy but late
Queiroga et al. (2022) [24]	>0.90	Full year	258,440	Random Forest	Large scale, fairness audit
Deleña et al. (2025) [9]	90.66%	Historical	482	XGBoost	10-year longitudinal data
Shanto & Jony (2025) [8]	95.73%	Post-pandemic	1205	Ensemble	COVID adaptability focus
Santos & Henriques (2023) [19]	0.756	25% completion	One year	Random Forest	Course-agnostic approach
Zhang & Ahn (2023) [21]	81–84%	Midterm to end	OU 2013–2014	Ensemble + SHAP	Temporal generalization
Seo et al. (2024) [22]	High	Multiple points	144,540	LGBM	Large scale, gender analysis
Hung et al. (2025) [20]	75% recall	Stage 2 (weeks 6–10)	16,011	XGBoost + XAI	Multiple at-risk types
Al-Zawqari et al. (2024) [32]	78–86%	Mid-course (M1, ≈50%)	OULAD, 22,437	Denoising Autoencoder (latent-space fairness)	Bias mitigation and fairness metrics
Gunasekara and Saarela (2026) [33]	80–88%	End-of-course (≈90%)	OULAD, 22,437	Ensemble xAI models (LightGBM + SHAP)	Explainable AI focus
Sayed et al. (2025) [34]—Learning Style Prediction	98% (RF) 96% (SVM) 94% (NB) 87% (LR) 73% (KNN)	End of course (train: 90%/10% split)	OULAD, 32,593 students (cleaned: ~22,600) 9,921,259 interactions	Random Forest (best) +SVM, KNN, LR, NB	- Semantic VAK mapping (no manual feature engineering) - High precision (97%) and recall (99%) - Predicts learning style + assessment method
Sayed et al. (2025) [34]—Assessment Method Prediction	98% (RF) 96% (SVM, KNN) 95% (NB) 90% (LR)	End of course	OULAD, 32,593 students (cleaned: ~22,600) 9,921,259 interactions	Random Forest	- Recommends personalized assessment (TMA/CMA/Exam) based on learning style
Al-Zawqari et al. (2022) [30]—Pass/Fail	85.83% (RF) 85.77% (ANN reduced) Precision: 86.64%	Q1: 76.53% Q2: 79.51% Q3: 82.69% Q4: 85.83%	OULAD, 22,437 students (Pass: 15,385 Fail: 7052)	Random Forest (best) ANN comparable	- No feature engineering needed - Feature importance analysis - Early intervention possible (Q1: 76.5%)
Al-Zawqari et al. (2022) [30]—Distinction/Fail	88.15% (RF reduced) 87.76% (ANN reduced) Precision: 86.08% Recall: 86.12%	Q1: 81.57% Q2: 84.35% Q3: 86.23% Q4: 88.15%	OULAD, 10,076 students (Distinction: 3024 Fail: 7052)	Random Forest Reduced features	- Balanced precision/recall - Good for identifying at-risk vs. high achievers - Feature reduction maintains performance
Al-Zawqari et al. (2022) [30]—Distinction/Pass	81.26% (RF) 81.24% (RF reduced) Poor precision: 68.82% Poor recall: 52.92%	Q1: 81.06% Q2–Q4: ~81% (no improvement over time)	OULAD, 15,385 students (Distinction: 3024 Pass: 12,361)	Random Forest (all methods struggled)	- Limitation identified: Cannot distinguish high achievers from average students - Demographics more important than activity
Al-Zawqari et al. (2022) [30]—Withdrawn/Pass	92.90% (RF) 93.28% (Simulated) Precision: 93.32% Recall: 91.95%	Q1: 82.37% Q2: 85.87% Q3: 89.65% Q4: 92.90%	OULAD, 25,541 students (Withdrawn: 10,156 Pass: 15,385)	Random Forest	- Highest accuracy (93%) - Warning: inflated by official dropouts - Q1–Q2 more realistic (82–86%)
Hassan et al., 2023 [31] (SMFSOP)	Acc: 92% Precision: 93.7% F1: 0.95	Full course (240 days, 14 exams)	OULAD, FFF course ~1303 students	Semantic mapping to CoI model + Kernel k-means clustering + KNN classification	Automatic semantic mapping of student attributes to CoI model; improves accuracy by 1.56% over baseline (90.44%)
Hassan et al., 2023 [31] (No clustering baseline)	Acc: 85.43% Precision: 86.5% F1: 0.87	Full course	OULAD, FFF course	Standard regression/classification without clustering	Demonstrates the importance of clustering
Dermy et al., 2022 [35]	Not applicable (visualization focus)	240 days, 14 time points (exams)	OULAD, DDD module 1303 students (4 groups after outlier removal: 53, 451, 357, 427)	Probabilistic Movement Primitives (ProMPs) for behavioral dynamics modeling	Visualization of student behavioral dynamics with mean and variance distributions across 3 indicators (engagement, performance, reactivity); enables group and individual student comparison
Our work	0.789	Day 14 (6–7%)	OULAD, 22,437	Boosting + LR	Ultra-early, workload-aware

compares our results with existing work, separating OULAD-specific studies from other datasets to enable direct comparison. The table highlights prediction timing, dataset characteristics, and achieved performance, revealing the tradeoff between early prediction and accuracy.

5.1.1. Studies Using OULAD

Direct comparison is possible only with research using the same dataset. Al-Zawqari et al. (2022) [30] achieved 85.83% accuracy at Q4 and 76.53% at Q1 using random forests for pass/fail prediction. Our AUC of 0.789 (roughly equivalent to 78–80% accuracy for balanced classes after accounting for 36% failure rate) at day 14 falls between their Q1 (end of ~50 days) and Q2 results, which is reasonable given we use even earlier data. Their quarterly improvement from 76% to 86% confirms our finding that predictive signal strengthens with time, but intervention becomes less effective as students fall further behind.

Hassan et al. (2023) [31] achieved 92% accuracy on OULAD’s FFF course using semantic mapping to the Community of Inquiry model, substantially higher than our 78–80% equivalent. However, their system uses all 240 days and 14 exams, making it effectively a post hoc analysis rather than an early warning system. The 6.5% accuracy gain from adding clustering (92% vs. 85.43% baseline) suggests that grouping students by behavioral patterns improves prediction, though our instructor-focused system avoids this complexity to maintain interpretability.

Al-Zawqari et al. (2024) [32] reported 78–86% accuracy at mid-course (≈50% completion) with fairness-aware modeling using denoising autoencoders. Their latent-space approach reduced bias across gender and disability while maintaining performance. This timing is closer to ours than full-course studies, and their accuracy range overlaps with our results. However, their focus on fairness comes at the cost of interpretability—latent features are harder to explain to instructors than our direct activity and assessment metrics.

Gunasekara and Saarela (2026) [33] achieved 80–88% accuracy at 90% course completion using ensemble methods (RF, ANN, LightGBM) with post-processing fairness adjustments. Their end-of-course timing allows much higher baseline performance than early prediction. Their finding that fairness interventions reduce accuracy by 2–5% aligns with the broader literature showing tradeoffs between equity and raw performance. Our work does not implement fairness corrections, leaving this as important future work.

Sayed et al. (2025) [34] achieved 98% accuracy for learning style prediction using Random Forest on end-of-course OULAD data. While impressive, this task differs from early failure prediction—learning styles are stable traits revealed through accumulated behavior, whereas at-risk prediction from sparse early data is inherently uncertain. Their success with RF confirms our finding that ensemble methods work well on OULAD, though the gap between our 78–80% and their 98% primarily reflects prediction timing rather than algorithmic choice.

Dermy et al. (2022) [35] provide no classification metrics, focusing instead on behavioral modeling using Probabilistic Movement Primitives. Their visualization approach offers complementary insights into our predictive system, showing how student groups evolve dynamically. Integrating their trajectory modeling with our early prediction could identify students at risk of transitioning from engaged to disengaged states.

5.1.2. Studies Using Other Datasets

Comparing across datasets requires caution due to differences in student populations, course structures, and failure rates. Čotić Poturić et al. (2025) [28] achieved 93% accuracy in STEM courses at 15 weeks—impressive but too late for meaningful intervention in 16-week semesters. Queiroga et al. (2022) [24] achieved AUROC > 0.90 on 258,440 secondary education students using full-year data including primary school records, demonstrating that rich longitudinal data enables excellent prediction but is unavailable in our context.

Studies achieving > 90% accuracy typically use one or more advantages we lack: later prediction timing (mid-course to end-of-course), more favorable class distributions (dropout prediction often shows stronger separation than pass/fail), or richer feature sets (multi-year academic records, socioeconomic data, instructor observations). Zhang and Ahn (2023) [21] achieved 81–84% accuracy on the same OULAD at midterm to end of semester using ensemble methods with SHAP explanations—performance comparable to ours despite having 2–6× more data per student. This suggests we are capturing most of the predictive signal available from early behavior.

Santos and Henriques (2023) [19] provide the closest non-OULAD comparison: AUC of 0.756 at 25% course completion using course-agnostic normalized features. Our AUC of 0.789 at 6–7% completion represents both earlier timing and better discrimination, likely because our presentation-specific training captures local context that course-agnostic approaches miss. However, their generalization across courses offers deployment flexibility we sacrifice for performance.

5.1.3. Key Insights from Comparison

Three patterns emerge. First, prediction accuracy improves nearly linearly with data: Q1 results (76–78%) < mid-course (78–86%) < Q4/end-course (85–92%) < full-course (92–98%). Our day-14 results sit at the lower end, which is expected and acceptable given ultra-early timing. Second, the performance gap between simple and complex methods is small (2–4% in most studies), suggesting feature engineering matters more than algorithms. Third, no existing OULAD study reports precision and recall at specific workload thresholds—most optimize F1 or accuracy without considering instructor constraints.

Our contribution is not achieving the highest discrimination but balancing competing objectives that existing work treats separately. We predict earlier than any comparable OULAD study (day 14 vs. Q1 minimum), explicitly model instructor workload through precision-focused thresholds, provide multiple interpretability mechanisms, and validate temporally rather than through random splits. The resulting system is less accurate than end-of-course predictions (our 78–80% vs. 85–95% in Table 8) but actionable in ways that higher-performing models are not.

5.2. Performance Across Multiple Prediction Windows

To empirically assess the accuracy–timing tradeoff, we evaluated all models at five prediction horizons: day 14, 28, 56, 84, and 112 (corresponding to weeks 2, 4, 8, 12, and 16 of the course).

Table 9. Model performance across prediction horizons (AUC/Average Precision).

Model	Day 14 (Week 2)	Day 28 (Week 4)	Day 56 (Week 8)	Day 84 (Week 12)	Day 112 (Week 16)
Baseline	0.640/0.477	0.604/0.460	0.593/0.461	0.592/0.470	0.591/0.473
Logistic	0.783/0.713	0.786/0.717	0.796/0.730	0.808/0.747	0.819/0.760
Boosting	0.789/0.722	0.794/0.728	0.806/0.745	0.816/0.758	0.827/0.772

and Figure 11 present comprehensive results.

Our gradient boosting model achieves AUC = 0.789 on day 14, improving to 0.827 on day 112, representing a 3.8% absolute gain. Logistic regression follows a nearly identical trajectory (0.783 → 0.819, +3.6%), confirming that the accuracy–timing tradeoff affects all modeling approaches similarly. In contrast, the threshold-based baseline degrades slightly from 0.640 to 0.591, likely due to its inability to adapt to changing student behavior patterns over the semester.

Precision at 15% flagging remains remarkably stable across horizons, ranging from 84.1% (day 14) to 88.1% (day 112) for gradient boosting. Recall improves modestly from 35.0% to 36.7%, meaning that waiting until week 16 catches only 1.7 percentage points more failing students compared to week 2 predictions—a marginal gain given that these students have already missed most course content.

Critically, incremental gains diminish over time. Moving from day 14 to day 28 yields only +0.4% AUC improvement, while the largest single gain (+1.2%) occurs between weeks 4 and 8. Subsequent intervals show consistent but modest improvements of approximately +1.1% per month. This pattern of diminishing returns empirically validates our emphasis on ultra-early prediction: waiting for marginally better discrimination sacrifices the intervention window when support is most effective.

Figure 11 visualizes these dynamics across four dimensions. Panel A shows that machine learning models substantially outperform threshold rules at all horizons, with the gap widening slightly over time. Panel B confirms similar patterns in average precision, the preferred metric for imbalanced classification. Panels C and D reveal that precision remains high and stable while recall improves gradually, indicating that additional data primarily helps rank students more accurately rather than fundamentally changing who is identifiable as at-risk.

These results align with existing OULAD literature [30] showing quarterly progression from 76% (Q1) to 86% (Q4) accuracy, and extend those findings by demonstrating that our day-14 timing (approximately 7% course completion) achieves performance comparable to Q1 predictions (~25% completion) in previous work. The consistency across studies confirms that the accuracy–timing tradeoff is inherent to the educational prediction task rather than an artifact of specific modeling choices.

5.3. Pedagogical Significance and Practical Implications

Our system prioritizes changing instructor behavior over maximizing accuracy. Day-14 timing enables effective intervention before irretrievable academic damage [20]. Students disengaged in week 2 can recover; those flagged at midterm have already missed multiple assignments and fallen weeks behind.

The pedagogical literature on self-regulated learning suggests that early feedback and goal-setting interventions can redirect at-risk students before negative patterns become entrenched. Our system operationalizes this insight by identifying students who lack self-regulation (low active_days_ratio, sporadic engagement) and flagging them for intervention. The email templates we generate frame outreach in terms of support rather than surveillance, acknowledging challenges rather than blaming students for low engagement. This tone is critical—students who feel judged or monitored may disengage further, while those offered help often respond positively.

However, prediction is not intervention. Generating accurate alerts is necessary but insufficient for improving outcomes. Instructors must act on alerts, and their actions must be effective. The literature on early warning systems rarely reports intervention outcomes, focusing instead on prediction accuracy. We do not know whether contacting our flagged students actually improves their pass rates, or whether they would have succeeded anyway with less intensive support. Randomized controlled trials comparing outcomes for flagged students who receive intervention versus those who do not would provide definitive evidence, but such experiments raise ethical concerns about withholding help from control groups.

5.4. Limitations and Threats to Validity

Our study has several important limitations that constrain generalizability and interpretation of results. First, we use observational data to predict outcomes without intervening or measuring the effect of interventions. This means we cannot distinguish between students who fail due to disengagement (addressable through outreach) and those who fail due to external factors like illness or family crisis (where academic intervention may be ineffective). The 35% recall at 15% flagging represents the limit of what passive LMS data can reveal; many failing students do not exhibit obvious early warning signs.

Second, the OULAD reflects a specific context: UK distance education for adult learners in 2013–2014. These students are older, more likely to have work and family obligations, and enrolled in asynchronous online courses where all activity is mediated by the LMS. Patterns observed here may not generalize to traditional undergraduate populations, synchronous online courses, or blended learning environments where substantial activity occurs outside the LMS. The high baseline failure rate (31–36%) is atypical of selective universities, though common in distance education and community colleges.

Third, our test set shows higher failure rates (36.1%) than the training set (28.6%), indicating that later presentations are more challenging or attract weaker students. This distribution shift is realistic—models deployed on new cohorts must handle changing student populations—but it means our reported metrics likely underestimate performance on populations similar to the training set and overestimate performance on even more difficult cohorts. The modest AUC degradation from 0.783 (logistic regression on training set via CV) to 0.783 (on test set) suggests reasonable robustness, but larger temporal gaps might reveal more severe drift.

Fourth, we do not conduct fairness audits across protected attributes like gender, age, or socioeconomic status. Queiroga et al.’s careful bias analysis across gender, school zone, and social welfare participation represents best practice that we do not follow [24]. Biased models could systematically over-flag certain demographic groups, creating discriminatory intervention patterns. Our finding that is_female has a weak negative correlation with failure suggests female students may face slightly elevated risk, but we do not investigate whether this reflects genuine academic differences, measurement artifacts, or societal factors. Future work must examine whether models exhibit disparate impact and, if so, whether such disparities are justified by differences in true failure risk.

Fifth, our rule-based explanations are crude compared to SHAP or LIME. They translate feature values into natural language using hard thresholds (e.g., “low activity” if total_clicks < 50), but these thresholds are arbitrary and may not match individual instructor intuitions. More sophisticated explanations would show how each feature contributes to the specific prediction for each student, as Santana-Perera et al. demonstrate with SHAP [25]. However, such explanations require more technical sophistication from instructors and may overwhelm those unfamiliar with statistical concepts like odds ratios or marginal contributions.

Sixth, we do not conduct fairness audits across protected attributes (gender, age, socioeconomic status, disability). Models can exhibit disparate impact even when demographic features contribute minimally to prediction (Table 7: removing demographics causes only 0.012 AUC drop). Behavioral features may correlate with protected attributes through structural inequalities in educational access. Our preliminary analysis shows is_female has weak negative association (OR = 0.80), but we have not examined whether this reflects genuine risk differences or measurement artifacts. Institutions must conduct systematic bias analysis examining false positive/negative rates and calibration across demographic subgroups before deployment [30,32].

Seventh, we evaluate the system on historical data, not live deployment. Real-world performance may differ due to Goodhart’s Law: when a measure becomes a target, it ceases to be a good measure. If students learn that low activity triggers alerts, they might game the system by logging in frequently without genuine engagement, inflating activity metrics without improving learning. Similarly, if instructors systematically ignore alerts for certain student types (e.g., older students who they assume are self-directed), the intervention targeting may not match the model’s assumptions. Deployment studies with feedback loops and outcome measurement are necessary to validate that the system works as intended in practice.

5.5. Ethical Considerations and Responsible Deployment

Early warning systems raise significant ethical concerns that must be addressed before deployment. First is the risk of stigmatization and self-fulfilling prophecy. Students flagged as at-risk may internalize this label, reducing effort and confirming the prediction even though they might have succeeded without intervention. Instructors who view students through the lens of algorithmic risk scores may unconsciously treat them differently, creating differential expectations that harm rather than help. Our email templates deliberately avoid mentioning risk scores or prediction models, framing outreach as normal instructor care rather than algorithmic surveillance.

Second is the question of consent and transparency. Students do not consent to having their LMS activity analyzed for prediction purposes, and most are unaware that such systems exist. Educational institutions typically claim broad rights to use student data for institutional purposes, but this legal permission does not resolve ethical questions about whether students should be informed and given opt-out options. Full transparency could undermine system effectiveness if students game metrics, but secrecy violates principles of informed consent. We advocate for a middle ground: inform students at course start that instructors may reach out if early activity suggests they are struggling, without specifying the algorithmic details.

Third is data security and privacy. Our system requires access to student IDs, LMS logs, demographic data, and assessment scores—sensitive information that could cause harm if mishandled. The alert lists we generate contain names of students labeled at-risk, which if leaked could stigmatize individuals or be used for discriminatory purposes. We recommend that institutions store such lists securely, limit access to authorized personnel, and delete files after interventions are complete. No student data should be transmitted outside institutional systems or used for purposes beyond the immediate intervention.

Fourth is the question of automation and human judgment. Our system provides recommendations, not mandates, but there is risk that instructors will defer to algorithmic judgments rather than exercising professional expertise. A student with high predicted risk may be genuinely struggling, but they may also be adjusting to a new learning environment, dealing with temporary challenges, or simply preferring to work ahead in bursts rather than steadily throughout the semester. Instructors must retain discretion to override or contextualize algorithmic recommendations based on their knowledge of individual students and course circumstances.

Fifth is equitable access to intervention. If instructor time is limited, directing attention toward algorithmically identified high-risk students means less attention is given to others. This could create a two-tier system where flagged students receive intensive support while non-flagged students are left to fend for themselves. Moreover, if the model systematically under-predicts risk for certain demographic groups, those students will be neglected despite needing help. Regular audits of who gets flagged, who gets contacted, and who ultimately succeeds are necessary to detect and correct such disparities.

We emphasize that algorithmic decision support should augment human judgment, not replace it. The purpose of our system is to help instructors identify students who might otherwise fall through the cracks, not to determine which students deserve help. All students should have access to support resources; the model merely suggests where proactive outreach is most likely to make a difference. Instructors remain responsible for pedagogical decisions, and students retain agency to accept or decline offered support.

5.6. Future Directions and Research Opportunities

This work opens several directions for future research. First and most critical is deployment evaluation through randomized controlled trials or quasi-experimental designs. Assigning flagged students randomly to intervention and control groups would reveal whether outreach actually improves outcomes. Such studies are ethically challenging (withholding help from controls) but scientifically necessary to distinguish effective interventions from theater. Quasi-experimental approaches using regression discontinuity or difference-in-differences could provide evidence with fewer ethical concerns.

Second is the development of differentiated intervention strategies based on at-risk student types. Hung et al.’s taxonomy of five at-risk categories suggests that one-size-fits-all outreach may be suboptimal [20]. Low-engaged students might benefit from motivational support, while testing-focused students might need study skills coaching. Our current system generates generic alerts; future work could classify students into subtypes and recommend tailored interventions for each. This requires both better typology (perhaps through clustering or mixture models) and evidence about which interventions work for which types.

Third is longitudinal tracking to understand how early patterns persist or change. Students flagged at week 2 may recover by week 8, while initially successful students may struggle later. Continuous monitoring systems that update predictions weekly could identify these transitions and adjust interventions accordingly. However, such systems require careful design to avoid overwhelming instructors with constantly changing alert lists. Seo et al.’s prescriptive analytics approach, which infers learning profiles and adapts support over time, represents a promising direction [29].

Fourth is the integration of behavioral data beyond LMS logs. Discussion forum sentiment, assignment quality (not just submission), video engagement patterns, and peer interaction networks all contain signals about student success that simple click counts miss. However, richer data requires more complex feature engineering and raises additional privacy concerns. The tradeoff between predictive gains and implementation complexity must be carefully evaluated.

Fifth is fairness-aware modeling that explicitly constrains or corrects for disparate impact across demographic groups. Techniques like fairness constraints, bias mitigation, and counterfactual fairness could ensure that models do not systematically disadvantage protected groups. Queiroga et al.’s bias audit represents current best practice, but future work should go further by actively ensuring equitable outcomes rather than merely detecting and disclosing disparities [24].

Finally, the field needs better integration with pedagogical theory. Most learning analytics research, including ours, is data-driven: we discover patterns and build models without strong theoretical grounding in how students learn. Integrating frameworks like self-regulated learning theory, cognitive load theory, or community of inquiry could produce features and models that not only predict better but also provide explanations that resonate with educational practice. Hernández-García et al.’s CILC framework represents this integration; future work should extend such theory-driven approaches [7].

In conclusion, our decision support system demonstrates that early, interpretable, workload-aware prediction of student failure is feasible using standard LMS data and machine learning methods. The system achieves solid discrimination (AUC 0.789) at ultra-early timing (day 14), maintains high precision (84%) at manageable workload (15% flagging rate), and provides multi-level explanations that support instructor decision-making. However, prediction alone does not improve outcomes—effective intervention is required. Future research must focus on deployment evaluation, intervention design, fairness auditing, and integration with pedagogical practice to transform algorithmic predictions into meaningful improvements in student success.

6. Conclusions

This study demonstrates that interpretable, workload-aware predictive modeling can achieve meaningful early identification of at-risk students while adhering to principles of responsible and accountable AI for educational social good. Our gradient boosting model achieves AUC of 0.789 and average precision of 0.722 at ultra-early timing (day 14), with logistic regression modeling performing nearly identically (AUC 0.783, AP 0.713)—values indicating solid discrimination given ultra-early timing, as AUC > 0.75 is considered acceptable and >0.80 is good. This near-parity reveals that linear modeling captures most predictive signal, making interpretability and transparency essentially cost-free—a finding with profound implications for responsible AI deployment in high-stakes educational contexts where accountability and explainability are paramount.

At the recommended decision threshold flagging 15% of students, the calibrated predictive model achieves 84% precision and 35% recall—creating actionable alert lists that instructors can manage while focusing attention on highest-risk cases. This modeling strategy explicitly prioritizes effective support for fewer students over attempting universal coverage that would overwhelm instructors and dilute intervention quality. Feature importance modeling confirms that behavioral engagement patterns (activity metrics, assessment completion) dominate demographic factors in predicting outcomes, providing transparent evidence that student actions matter more than background characteristics—a finding that empowers rather than stigmatizes learners.

Our multi-horizon analysis provides empirical evidence for a fundamental tension in early warning systems: better predictions require more data, but effective interventions require earlier action. The 3.8% AUC gain from waiting 14 weeks translates to catching only 1.7 additional percentage points of failing students—marginal benefit considering that week-16 predictions leave no time for meaningful intervention. This finding has direct policy implications: institutions should prioritize timely intervention over perfect prediction, accepting modest accuracy at week 2 rather than waiting for incrementally better discrimination when students have already fallen irretrievably behind.

Our decision support system advances responsible AI for quality education (SDG 4) by addressing three critical barriers that constrain real-world impact. Ultra-early prediction timing enables intervention before students develop entrenched disengagement patterns. Precision-focused threshold selection prevents alert fatigue while maintaining instructor trust through high accuracy of flagged cases. Multi-level interpretability through statistical modeling, feature importance analysis, and natural language explanations builds transparency and accountability, allowing stakeholders to understand and challenge algorithmic recommendations.

However, predictive modeling alone does not improve educational outcomes—a crucial limitation for AI systems claiming social good impact. Our models identify students needing support, but instructors must act on alerts and interventions must be effective. We do not evaluate whether outreach to flagged students actually improves pass rates or whether alternative resource allocation would achieve better equity outcomes. Future research must prioritize intervention effectiveness evaluation through experimental designs, development of differentiated support strategies tailored to diverse at-risk profiles, and fairness-aware modeling that explicitly addresses potential disparate impact across demographic groups.

Critical limitations constrain immediate deployment. Most importantly, we do not conduct fairness audits—a gap requiring resolution before operational use. Institutions adopting such systems must examine precision, recall, and calibration across student subgroups following frameworks in [30,32]. Interpretability provides transparency for detecting bias but does not replace systematic fairness evaluation.

Despite these limitations, our work demonstrates that accountable and interpretable machine learning can augment human judgment in education when designed with explicit attention to deployment constraints and ethical considerations. The system provides instructors with transparent information about which students need attention and explainable justifications for risk assessments, while preserving instructor discretion to contextualize algorithmic recommendations. This human-in-the-loop approach respects both the power of data-driven prediction and the irreducible complexity of teaching, advancing responsible AI that genuinely serves educational social good rather than optimizing technical benchmarks divorced from human impact.