Fast Adaptive Approximate Nearest Neighbor Search with Cluster-Shaped Indices

Abstract

In this study, we propose a novel adaptive algorithm for approximate nearest neighbor (ANN) search, based on the inverted file (IVF) index (cluster-based index) and online query complexity classification. The concept of the classical IVF search implemented in vector databases is as follows: all data vectors are divided into clusters, and each cluster is assigned to its central point (centroid). For an ANN search query, the closest centroids are determined, and the further search continues in the corresponding clusters only. In our study, the complexity of each query is assessed and classified with the use of results of an initial trial search in a limited number of clusters. Based on this classification, the algorithm dynamically determines the presumably sufficient number of clusters which is sufficient to achieve the desired Recall value, thereby improving vector search efficiency. Our experiments show that such a complexity classifier can be built with the use of a single feature, and we propose an algorithm for its training. We studied the impact of various features on the query processing and discovered a strong dependence on the number of clusters that contains at least one nearest neighbor (productive clusters). The new algorithm is designed to be implemented on top of the IVF search which is a well-known algorithm for approximate nearest neighbor search and uses existing IVF indexes that are widely used in the most popular vector database management systems, such as pgvector. The results obtained demonstrate a significant increase in the speed of nearest neighbor search (up to 35%) while maintaining a high Recall rate of 0.99. Additionally, the search algorithm is deterministic, which might be extremely important for tasks where the reproducibility of results plays a crucial role. The developed algorithm has been tested on datasets of varying sizes up to one billion data vectors.

1. Introduction

Modern data collection tools enable us to accumulate large volumes of multidimensional information on the object of study. This information becomes a valuable source of knowledge about the object when processed with the use of methods and algorithms of intelligent data analysis. Nearest neighbor search (NNS) is an optimization problem that involves finding the data vector most similar to a given vector (query vector) in the original dataset. Similarity is generally given by a dissimilarity function that determines the distance between vectors and classes in a space $R^D$. This space consists of a set of vectors with a distance function $d(x_i,q_i)$. The greater the value of the distance function, the lower the similarity between the query vector and a vector from the original dataset. To measure the distance of order p between two data vectors, Minkowski distance functions (also called l_p norms) are usually applied: $d_P\left(x_i,q_i\right)={\left({\sum }_{i=1}^M{\left|x_i-q_i\right|}^P\right)}^{{\displaystyle \frac{1}{P }}}$ [1]. Here, x and q are vectors of dimension D. Parameter p is chosen by the analyst and regulates the relative weight of each coordinate. Well-known special cases of this function are obtained for specific values of P [1,2].

The NNS problem is defined within a metric space (N, d), where N is a finite set of vectors, and $d\left(x_i,q_i\right)$ is the distance function that is reflexive, non-negative, symmetrical, and satisfying the triangle inequality [1,3,4]. In practice, most studies consider the Euclidean case (l₂ norm) [1].

The Exact NNS requires constructing a data structure that returns the element $p\in N$ with the minimum distance to a given query vector $q\in R^M$. This approach achieves sublinear (or even logarithmic) query processing time for small datasets with low dimensionality. However, when applied to massive datasets with high dimensionality, the query time grows very rapidly, making it impractical for real-world use. Approximation methods can significantly reduce this computational cost, enabling much faster searches [5,6].

The Approximate NNS introduces a relaxation approach: given a query vector q, the algorithm may return any vector within distance not greater than $c·d(q,p)$, where p is the true nearest neighbor [1,5]. Here, $c\ge 1$ is the approximation factor: when $c=1$, the problem reduces to the exact NNS, while larger values of c enable us to search faster with a reduced precision [1,5].

For the approximate NNS, the most frequently used quality measure is Recall (denoted as Recall@K), which is the rate of the true (exact) nearest neighbors among K found neighbors.

Modern research proposes various methods for solving the nearest neighbor search problem, with the use of both exact approaches (such as linear search and space partitioning) and approximate approaches (proximity graph methods, hashing-based techniques, vector approximation files, compression and clustering-based search).

The linear approach sequentially computes the distance from the query vector to each vector in the dataset, with complexity O(DN), where D is the vector dimensionality and N is the number of vectors [7,8]. Performance degrades as dimensionality increases [8]. Heuristic algorithms can reduce costs [5,6]; nevertheless, the method scales poorly for large and high-dimensional datasets.

To improve similarity search in high-dimensional spaces, tree-based structures such as KD-trees [9,10,11,12,13], R-trees [14,15,16,17], B+-trees [18,19,20], and Cover-trees [21,22] partition the space to limit candidate points. Distances are computed only for neighbors in the same partition as the query vector. While these methods reduce the search space, their efficiency also declines with high dimensionality and large datasets due to the overhead of constructing and storing the trees [7].

In [23], the authors investigate the impact of dimensionality on the nearest neighbor search efficiency. In high-dimensional spaces, the contrast between the closest and farthest points diminishes, illustrating the so-called “curse of dimensionality”. To overcome the curse of dimensionality, the approximate nearest neighbor search (ANN) approaches were proposed. The key advantage of the ANN is its ability to efficiently compute approximate solutions, leading to substantial improvements in speed and reduced memory usage compared to exact nearest neighbor search methods. In certain cases, the dataset size makes the full exact search computationally infeasible within a reasonable time. In other situations, the difference between the exact and the approximate nearest neighbor search results may be minimal or insignificant.

In [3,24,25,26], the authors introduced proximity graph methods such as Navigable Small Worlds (NSW) and later extended this approach with Hierarchical Navigable Small Worlds (HNSW) in [27,28]. These methods are based on the small world concept, which refers to a property of graphs where each node has short-range connections to its neighbors (typically around log(N) steps), as well as several long-range connections that facilitate efficient global exploration. The HNSW algorithm constructs a multi-layer hierarchical graph structure to efficiently index and search for nearest neighbors in high-dimensional spaces. Unlike exact K-Nearest Neighbors method (KNN) [28], which performs a complete search in the data, the HNSW scales well for large datasets.

Hashing-based learning represents an approach to the ANN search problem [29]. These methods transform high-dimensional points into compact binary or integer representations, known as hash codes, which are significantly shorter than the original feature vectors. While this encoding enhances computational efficiency and reduces memory requirements, it inevitably introduces some information loss, especially when the original high-dimensional points are compressed into a lower-dimensional space. Hashing-based ANN techniques are generally divided into two main types: data-independent approaches (locality-sensitive hashing, LSH) [30,31], and data-dependent approaches (locality-preserving hashing, LPH) [27,28]. LSH [30,31] accelerates similarity search in large databases by increasing the likelihood of hash collisions among nearby points. As a randomized algorithm, it does not guarantee exact results deterministically, but it provides a high probability of retrieving either the exact nearest neighbor or a sufficiently accurate approximation.

In [32,33], the authors introduced an efficient indexing technique for multidimensional databased on the Vector Approximation File (VA-File) method. This filtering approach supports effective nearest neighbor search by partitioning the vector space with the use of hyperplanes to approximate distances between clusters of data vectors. Other researchers introduced the partial vector approximation file approach [34], which is designed to handle partial similarity queries in a subspace, even when the specific subspace is not known in advance.

Another class of ANN search methods for high-dimensional data relies on encoding vectors into compact representations using vector quantization [35]. This approach, often referred to as compression or clustering-based search, is founded on partitioning the data space into several low-dimensional subspaces and then quantizing the points within each subspace independently [36]. A large body of research on ANN search has been developed around product quantization (PQ), which has demonstrated strong efficiency and accuracy for large-scale high-dimensional datasets [36,37,38,39,40,41,42].

In [43], the authors introduced an approach to adaptive ANN search that uses only static features of the query (Tao method). Unlike AdaptNN [44], which relies on runtime characteristics, Tao method predicts search termination conditions based on the local intrinsic dimensionality (LID) of the query before the query processing begins. This eliminates the laborious feature selection process and simplifies the model training. Tao method is integrated with two leading ANN indexing approaches: IMI (Inverted Multi-Index) [44,45] and HNSW (Hierarchical Navigable Small World) [46,47].

NNS methods are widely applied in various domains, including traffic simulation systems [20], database research [19], image processing [13,14], pattern recognition, information retrieval [18], object classification, and similarity search. In these tasks, objects are represented as vectors describing their parameters, and NNS is performed within the corresponding vector space.

In vector databases (like PostgreSQL pgvector [48] and others), the search involves finding data with approximate matches to the query vector [49]: the goal is to identify data vectors that are closest to the query vector using ANN algorithms [50]. The primary advantage of this approach is its ability to enhance search performance significantly with only a slight compromise in query accuracy.

Unlike standalone ANN search algorithms, an ANN search algorithm implemented as a part of a relational database management system (RDBMS) cannot keep the data as well as supplementary data structures (indexes) entirely in the RAM since the RDBMS may experience heavy parallel workloads involving many different data tables and indexes. Moreover, RDBMS often reads data from disk through its buffer manager in small blocks (4–16 KB). Blocks of this size cannot store a lot of high-dimensional float point 32-byte (FP32) vectors (a block of 8 KB can only store 15 128-dimensional FP32 vectors). This raises the problem of vector data compression in ANN search indexes. Solving this problem may lead to more efficient vectors per index storage and thus save costly disk read operations.

Existing studies [51] show that one of the most important factors affecting the ANN search speed is the quality of the constructed index (supplementary data structure used to search faster). For example, achieving target Recall levels may require varying numbers of vector-vector distance computations. In our study, we focus on problems that must be solved with a high Recall value (0.99 for 100 nearest neighbors). This requirement limits the range of algorithm types [51,52]. In the worst case, an algorithm has to perform N distance calculations (where N is the number of vectors in the indexed dataset), which means the index is practically useless. The rapid growth of artificial intelligence and machine learning methods determines the high demand in the RDBMS and approximate nearest neighbor search algorithms.

The goal of our research is to develop a fast approximate nearest neighbor search algorithm that provides high Recall rates (Recall@100 ≥ 0.99) to be embedded into exiting software solutions. High Recall values are essential for benchmarking approximate nearest neighbor search as they indicate how effectively the algorithm retrieves true closest matches from a dataset. Low Recall may negatively impact user experience and security in applications like recommendation systems and fraud detection, making it crucial to ensure the result quality. Our hypothesis is that in addition to the quality of the constructed index and the organization of the data structure, the result of query processing can be improved at the stage of search through the constructed index by estimating the complexity level of the search query. For the clustering-based search, we introduce the rate of the productive clusters (i.e., clusters which give us at least one nearest neighbor) among all scanned clusters as a new criterion to estimate the complexity level at the first stage of search.

The structure of this article is as follows: In Section 2, we observe approaches to approximate nearest neighbor search in vector datasets. In Section 3, we present the adaptive search in the Inverted File Index with a meta-classifier. In Section 4, we describe the results of our computational experiments on various datasets. In Section 5, we give a short conclusion.

2. Approximate Nearest Neighbors Search Methods

In this section, we observe approaches to the approximate vector search, which may be divided into several categories according to the type of the supplementary data structure (index) used.

Hashing-based methods [53,54,55,56,57,58] assign data vectors to buckets using specific hash functions, increasing the collision probability for nearby vectors, thus facilitating quicker retrieval. Quantization-based methods [36,59,60,61,62], including IVF [35] and IMI [44,45], compress vectors into shorter codes, significantly reducing storage and computational requirements. Facebook’s Faiss approach [63] employs product quantization (PQ) methods, achieving high speed efficiency in large-scale applications. Tree-based methods, such as KD-tree [64] and R*-tree [65], divide the data space hierarchically into regions represented by tree leaves, restricting searches to promising regions only, thereby enhancing search speed. Flann [66] is a KD-tree-based library that has been widely adopted for its efficiency. Despite these advances, graph-based methods have demonstrated superior performance by requiring fewer data points to achieve the same Recall rates [67,68,69,70]. Additionally, various accelerators, such as FPGA [71] and GPU [63], NPUs [72], which can dramatically improve the efficiency of ANN searches.

2.1. Graph-Based Search

Graph-based techniques leverage the inherent structure of data by representing it as a graph, where nodes correspond to data points and edges signify proximity or similarity.

Navigating Spreading-out Graph (NSG) [69] stands as a leading graph-based indexing method, designed to closely approximate the Monotonic Relative Neighborhood Graph (MRNG) while ensuring search performance close to logarithmic complexity and relatively low construction overhead. NSG, along with other graph-based methods like FANNG [73], NSW [26], and HNSW [46], employs best-first search for query processing. Additional graph-based methods include [70,74,75,76,77]. These methods focus primarily on the construction and optimization of the graph index itself.

DiskANN [78] integrates an incremental graph-based ANN algorithm operating in memory with a storage layer that maintains the graph structure on solid-state drives. DiskANN is a cutting-edge ANNS system designed to operate efficiently on SSDs, leveraging a novel graph-based indexing algorithm known as Vamana.

Vamana is a graph-indexing algorithm with a smaller diameter than NSG and HNSW, which enables DiskANN to reduce sequential disk reads during search. Vamana graphs also perform competitively in memory, matching or surpassing state-of-the-art methods. For large datasets, DiskANN can build smaller Vamana indices on data partitions and merge them into a single structure, achieving near -full index performance while handling data exceeding memory limits. The system integrates vector compression, storing both the index and full-precision vectors on disk, while keeping compressed vectors in memory to balance efficiency and storage. Powered by Vamana, DiskANN scales to billion-vector datasets with 100-dimensional vectors on a 64 GB RAM workstation, reaching over 95% Recall@1 with sub-5 ms query latency [79].

HNSW algorithm [46,47] incrementally builds a multi-level structure similar to a skip list. Each layer in this hierarchy corresponds to an NSW graph [3,26]. In such a graph, nodes are linked mainly to nearby neighbors, while the overall topology ensures that any node can be reached within only a few traversal steps.

HNSW builds a hierarchy of NSW graphs, where each layer is a superset of the one above and the base layer includes all data vectors. This design, similar to skip lists, enables efficient navigation through the graph.

The hierarchical clustering-based nearest neighbor graph (HCNNG) [80] employs a clustering-based methodology. This method involves randomly selecting two vectors (p and p′) and partitioning the input data based on proximity to these vectors. Clusters are formed when the number of vectors within a partition falls below a specified threshold. Within each leaf cluster, a local approximate nearest neighbor graph is constructed as a degree-bounded minimum spanning tree (MST), where each point has a maximum degree of K. Redundant edges are then pruned to refine the graph.

PyNNDescent [81] combines random-hyperplane clustering with iterative refinement. Initially, each cluster connects points to their K nearest neighbors; then nearest neighbor descent progressively improves the graph by exploring two-hop neighborhoods and pruning long edges.

2.2. Parallel Graph Systems

Shared-memory systems, which process in-memory datasets within a single computation node, include notable examples such as Galois [82], Ligra [83,84], Polymer [85], GraphGrind [86], GraphIt [87], and Graptor [88]. These systems are designed to leverage multicore architectures for enhanced performance. Distributed systems like Pregel [89,90], GraphLab [91], and PowerGraph [92] handle large-scale graph processing across multiple nodes, ensuring scalability and robustness. Out-of-core designs, such as GraphChi [93] and X-Stream [94], process massive graphs with disk support, overcoming memory limitations. GPU-based graph frameworks like CuSha [95], Gunrock [96], GraphReduce [97], and Graphie [98] exploit the parallel processing power of GPUs for accelerated graph computation. These systems typically adhere to a vertex-centric model [89,90] or its variants, such as edge-centric [94], within the Bulk Synchronous Parallel (BSP) model [99]. Unlike these systems, which often involve synchronous processing, Speed-ANN employs delayed synchronization inspired by the stale synchronization model [100]. This approach allows worker threads to operate asynchronously before synchronization, maintaining high parallelism while minimizing distance computations.

2.3. Parallel and General Search Techniques

These approaches encompass efforts to parallelize various search algorithms: breadth-first search (BFS) [83,94], depth-first search (DFS) [101], and beam search [102]. These advancements have significantly influenced the development of parallel neighbor expansion techniques. The optimization and acceleration of search processes are based on the following key insights [103]: (1) recognizing that the convergence bottleneck in ANN search arises from the need to identify numerous targets; and (2) implementing optimizations specifically designed to reduce the number of distance computations and synchronization overheads in parallel neighbor expansion. These optimizations include staged search, which reduces redundant computations, and redundant-expansion aware synchronization, which adaptively adjusts synchronization frequency to balance accuracy and performance.

Parallel graph systems and generic search schemes provide a foundation for developing advanced search algorithms like Speed-ANN [103], which addresses specific bottlenecks in ANN search through innovative parallel techniques and optimizations. By understanding and leveraging these various methods, Speed-ANN aims to significantly improve the efficiency and scalability of similarity graph searches, particularly for large-scale datasets.

In the next subsections, several methods based on quantization are observed. Among them, the most common and popular are product quantization and inverted file index algorithms. The next sections disclose these methods and the principles of vector indexing and data compression algorithms by which they solve the problem of determining neighbors.

2.4. Vector Quantization and Compression Algorithms

Quantization-based methods represent a cutting-edge solution for scalable search of maximum inner products in massive databases.

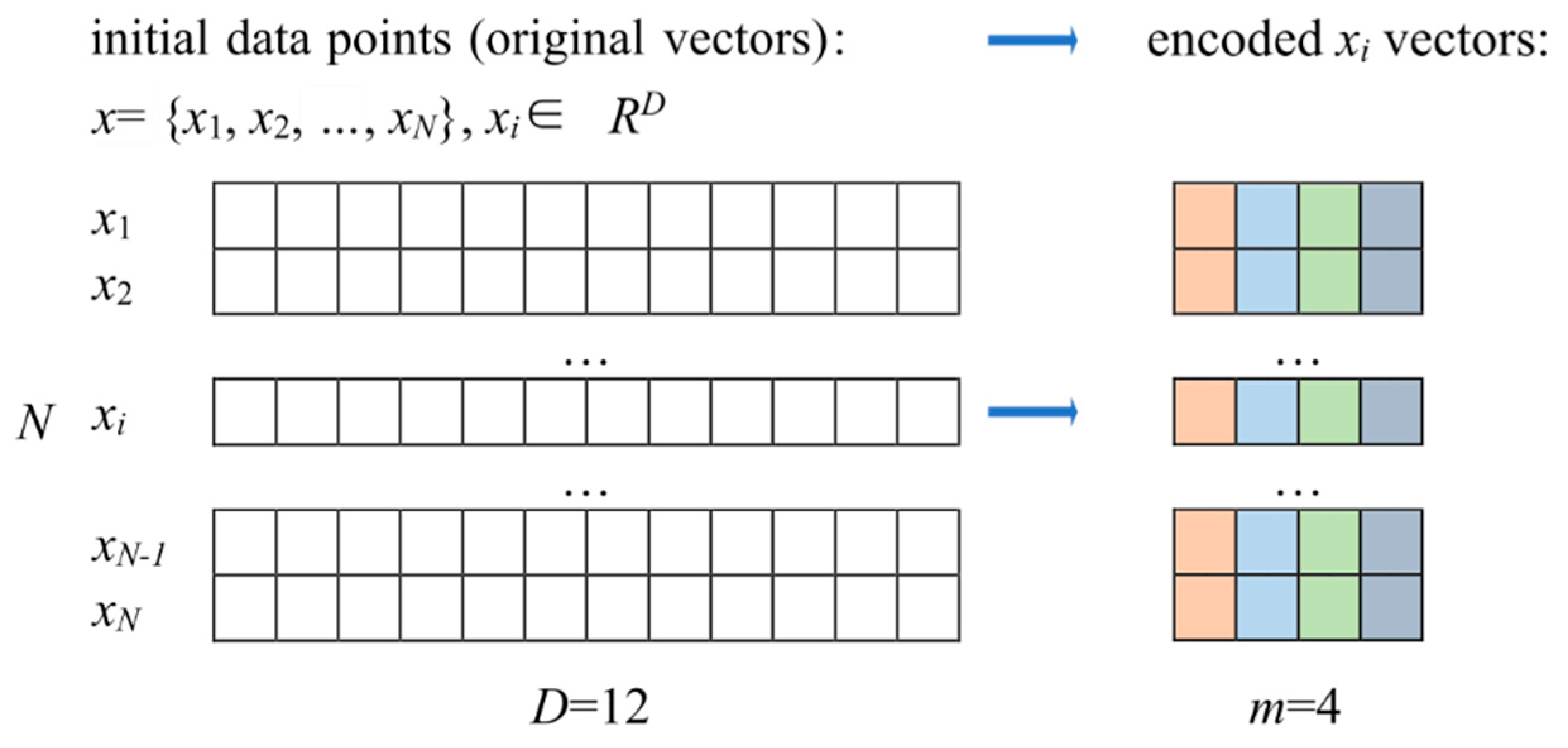
Vector quantization (VQ) [35,104] is a data compression technique used in various fields such as image and video compression [105], audio and signal processing [106,107], pattern recognition, and data analysis. VQ is also applied in machine learning, particularly in the classification and clustering of vectors (data points) for handling large datasets and feature extraction. The core idea of vector quantization is to represent multidimensional data using a finite set of vectors, known as code vectors. Essentially, VQ partitions the feature space into groups (clusters), with each group represented by its corresponding code vector. This approach reduces the amount of stored information.

The VQ process consists of the following stages: training (clustering, codebook generation, vector assignment, quantization), encoding, and decoding. During the training stage, a clustering algorithm is first applied to find the cluster centers (centroids), followed by codebook generation and quantization. In the encoding stage, each original data vector is mapped to the nearest (corresponding) code vector. In the decoding stage, each original vector is reconstructed from the code vectors.

The goal of Vector Quantization (VQ) is to minimize the distortion between the original input vectors and the codebook vectors, thereby achieving compact data representation while preserving as much information as possible.

In [35], the authors defined the goal of VQ as follows: VQ purpose is to reduce the cardinality of the representation space, in particular when the input data is real-valued. They also provided the definition for quantizer: “…a quantizer is a function q mapping a D-dimensional vector $x\in R^D$ to a vector $q\left(x\right)\in C=\{c_i,i\in I\}$, where the index set I is from now on assumed to be finite: I = 0… k−1. The values $c_i$ are called centroids. The set of values C is the codebook of size k”. The set of vectors mapped to a given index i is called a Voronoi cell and defined as [35]

$$V_i\triangleq \left\{x\in R^D:q\left(x\right)=c_i\right\}.$$

Thus, all vectors mapped to a given index i are reconstructed using the same vector from the codebook (the centroid). The quality of quantization can be measured by MSE between the vector x and its quantized representation q(x).

The storage requirement for representing the index alone, without applying any entropy coding, is $\left[{log}_{2}k\right]$ bits.

Many methods use VQ as their basis; this is a crucially important concept for approximate nearest neighbors search.

2.5. Scalar Quantization

Scalar quantization (SQ), also known as integer quantization, is a data compression technique that converts floating-point values into integers. The core idea of SQ is to transform each real-valued dimension z of a vector into an integer value [108]. This process involves truncating and scaling each dimension z of the vector [109]. SQ uses n bits to represent each dimension of the vector z as an integer within the range [0, 2n−1] (typically n = 8, n = 6, or n = 4) [63]. Each dimension is transformed as follows:

$$z\to \left[{\displaystyle \frac{\left(2^{b-1}\right)min(max\left(z,a\right),b)}{b-a}}\right],$$

where [⋅] denotes the nearest integer value. Usually, values a and b are selected based on the percentiles of the distribution. For example, when encoding with n = 4 bits, each dimension z is represented as an integer in the range [0, 15].

The primary drawback of SQ is its inability to account for the distribution of values within each dimension. An alternative approach, product quantization (PQ), which is also designed for data compression, may be used independently of the distribution of vector data.

Many studies focus on approximate nearest neighbor search based on PQ [35,36,39,40,41,42]. PQ was introduced by the authors of [35] and significantly reduces the amount of stored information while accelerating the nearest-neighbor search process. This makes it particularly useful in the fields of machine learning and information retrieval.

2.6. Product Quantization

PQ is a technique for dimensionality reduction and speeding up searches in large datasets with high-dimensional spaces. PQ is especially prevalent in machine learning tasks. The approach is based on compression or clustering. Initially, the data space is first divided into a Cartesian product of multiple low-dimensional subspaces, after which each subspace is quantized independently [35,36]. Unlike VQ, PQ uses multiple code vectors for each group of sub-vectors, which enhances quantization efficiency and reduces the volume of stored information.

The memory cost of a PQ-code is mlog₂k^* bits [110]. The parameters m and k* therefore control the trade-off between reconstruction quality and memory.

The NNS is based on computing distances between the query and dataset vectors. In [111], two approaches for comparing vectors based on their quantization indices are presented: symmetric distance computation (SDC) and asymmetric distance computation (ADC). The authors recommend using ADC for nearest neighbor search, as it provides lower distortion in distance measurement. The search using ADC is faster compared to direct linear (exact) search but still becomes slower with very large datasets.

The authors in [110] noted three positive properties of PQ: PQ compresses the original vector into a short code; the computation of approximate distance using ADC between the original vector and the compressed PQ code is efficient; and due to their simplicity, these structures and encoding algorithms can be combined with alternative indexing techniques.

2.7. Approximate Search with the Use of the Inverted File Based on Standard Quantization

For a large dataset, an inverted file (IVF) is constructed using standard quantization over a codebook of codewords (centroids), which are representative vectors typically obtained by clustering the original data [44,45]. The inverted file then maintains a list of vectors that are close to each code vector (belonging to the Voronoi cell, Figure 1).

Figure 1. Creating a codebook for the IVF search.

The goal of IVF-based or standard quantization is to identify dataset vectors close to a given query vector. When a query is performed, either the closest codeword or a set of several closest codewords is determined. When processing a query, the algorithm first selects the nearest codeword (or a small group of nearest codewords) and then merges the corresponding lists of vectors to generate the final results (Figure 2).

Figure 2. Generating a list of nearest vectors to a query in the IVF search.

However, in this approach, when dealing with a large dataset (ranging from hundreds of millions to billions of vectors), there is a high likelihood of generating an excessively large (inefficient) list of dataset vectors that are close to the query vector. This can be a consequence of imprecise initial distribution (partitioning) of the original set of vectors into groups (clusters), i.e., spatial decomposition has a significant impact on search accuracy [36]. If the number of centroids (code vectors) is increased for a more accurate distribution of the original dataset, then both query time and index construction time increase [111]. To address this issue, PQ may be proposed. Optionally, the IVF index may store the lists of complete vectors which for each of centroids. This enables us to compute the exact distances to the query vector while scanning the index. This step, referred to as re-ranking, can enhance the accuracy of the search results [112]. Compared to the exhaustive search, retrieval is significantly accelerated, which addresses one of the challenges when working with millions of vectors.

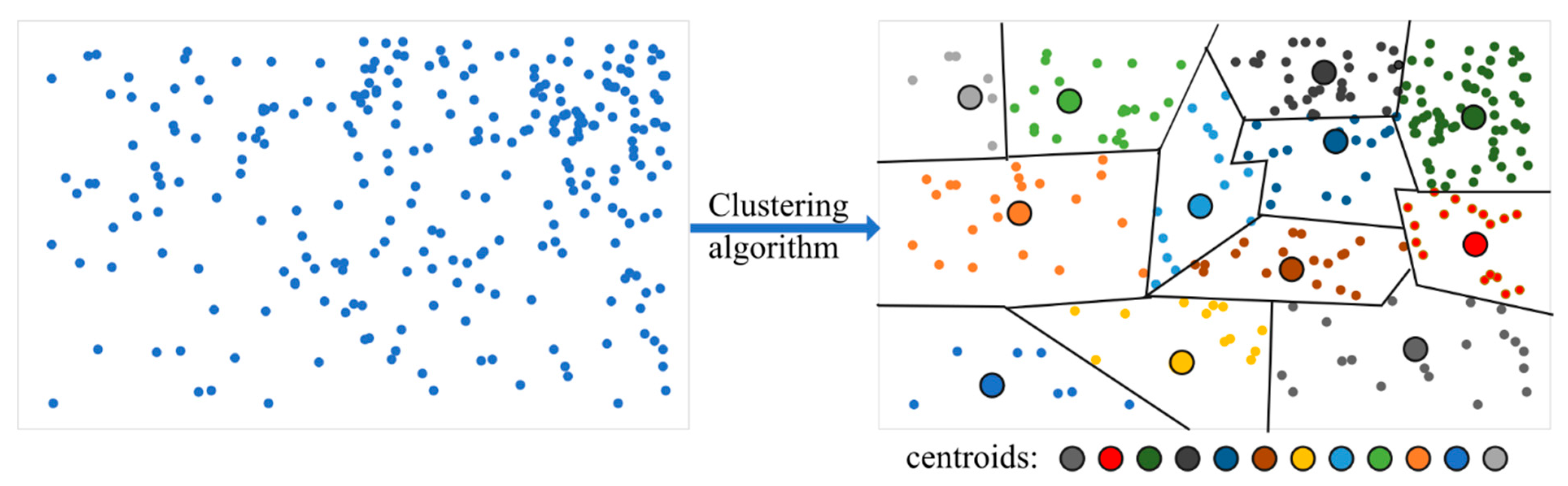
The concept of an IVF-based search algorithm is as follows: group the original set of vectors (vector space) into clusters using a clustering algorithm, such as k-means or its modifications, and then assign a centroid (code vector) to each group, which serves as the chosen center for the cluster (Figure 3). For each centroid (code vector), the index contains information about all the vectors belonging to its cluster, thus forming the codebook (Figure 4).

Figure 3. Spatial decomposition of vectors.

Figure 4. Matching vectors to centroids (codebook vectors).

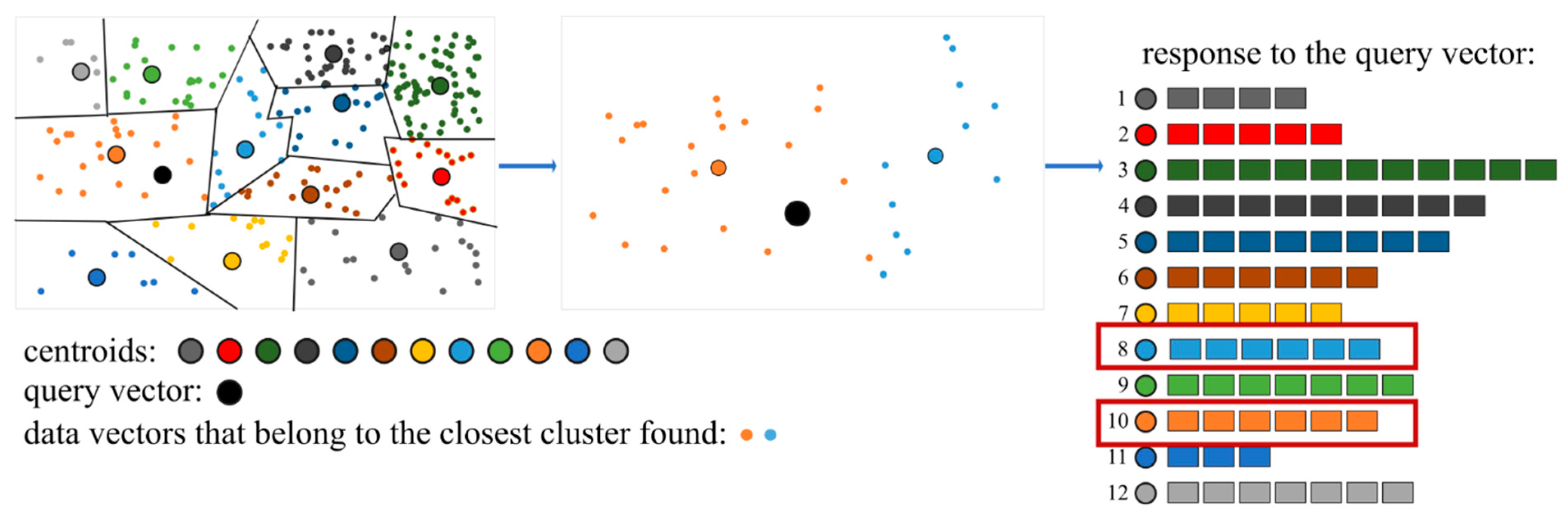
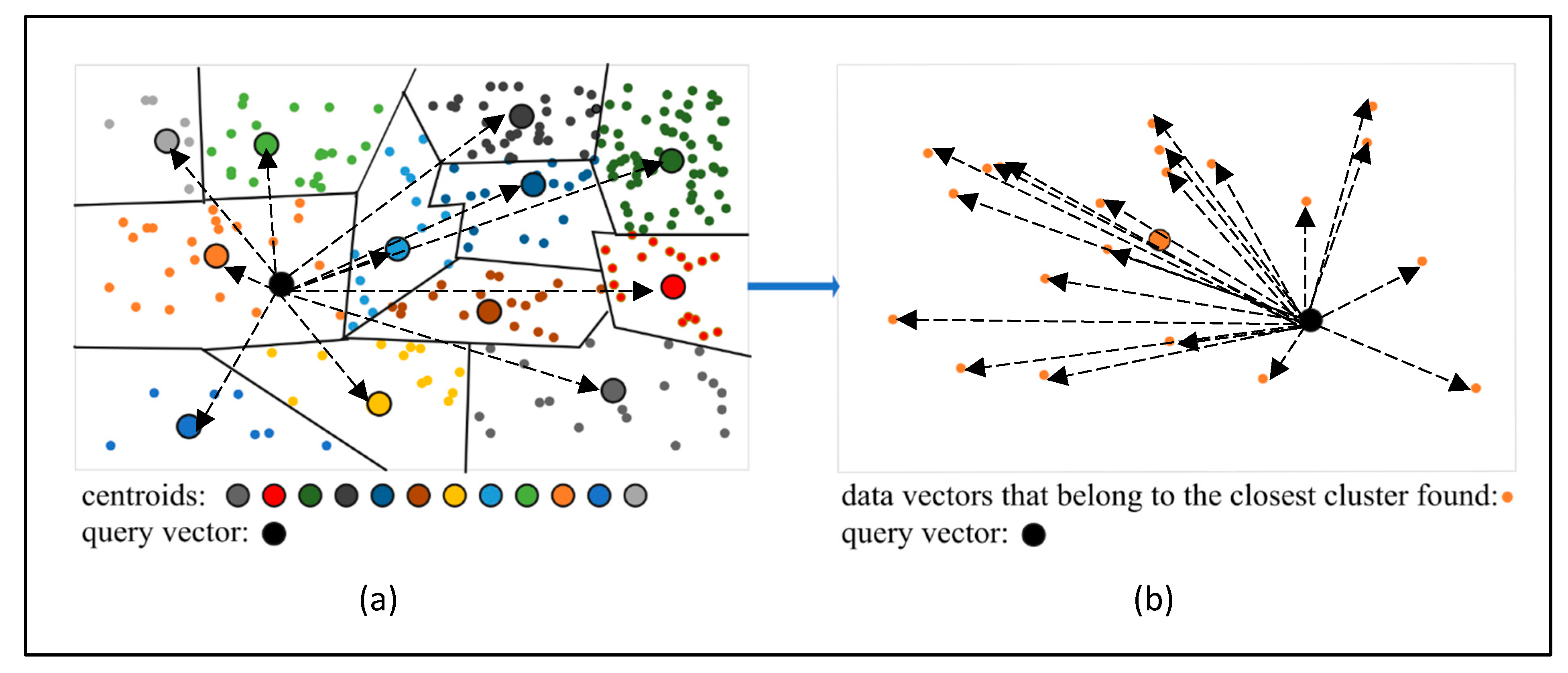
Next, the nearest neighbor search is performed for the query vector. Rather than scanning the entire dataset, the algorithm first identifies the centroid closest to the query vector (Figure 5a) by minimizing the distance between the query vector and all centroids. The actual nearest neighbor (or neighbors) is then retrieved from the vectors belonging to the cluster associated with the selected centroid (Figure 5b), thereby restricting the search space. The number of centroids is typically chosen heuristically. For instance, in widely used approaches such as FAISS [63], the authors recommend setting $k=\sqrt{N}$, where N is the number of vectors in the index. This choice provides a balanced two-level search: first, among $\sqrt{N}$ centroids, and second, among approximately $\sqrt{N}$ vectors in each cluster.

Figure 5. Nearest neighbors are searched among the data vectors contained in the cluster closest to the query. (a) The algorithm first identifies the centroid closest to the query vector by minimizing the distance between the query vector and all centroids.(b) The actual nearest neighbor (or neighbors) is then retrieved from the vectors belonging to the cluster associated with the selected centroid.

It is worth mentioning that there is a high likelihood that the query vector is located near the edge of a cluster, with its nearest neighbor located in an adjacent cluster. This issue is known as the edge problem [113]. While KNN compares the query vector against all N data vectors (each of dimensionality D, resulting in a time complexity of O(ND)), ANN with IVF restricts the search to only the subset of points within the nearest clusters, leading to the following reduced time complexity: O(KD + ND/K) [114], where K is the number of clusters (groups) that can variate. In the first step (matching with all centroids), the time complexity is O(KD), and in the second step (searching for the nearest neighbor within the closest cluster), it is O(ND/K).

Therefore, to achieve a tradeoff between high search quality and performance we need not only a capable clustering but also a careful parameter K adjustment.

2.8. Selecting a Search Algorithm Under Established Requirements

In the realm of ANN search, the selection of an appropriate algorithm is critical to achieving specific performance metrics, particularly in terms of Recall rate. Our study targets high Recall values for large K values, which encouraged an evaluation of available methodologies. We use an average Recall rate of 0.99 on 100 nearest neighbors as an example.

Among the above-mentioned algorithms, product quantization (PQ) emerges as a potentially viable option due to its efficiency in data storage and rapid query execution. However, the application of PQ may compromise search accuracy (Table 1), failing to meet the stringent requirements outlined in our research objectives, and also need fine tuning of its parameters.

Table 1. Comparison of existing algorithms performance on datasets of embeddings, 1 million instances and 128 dimensions.

Algorithm	Source	Recall at K = 100	Dataset	Note
Symmetric Distance Computation	Herve Jegou, Matthijs Douze, and Cordelia Schmid [35]	0.45	GIST [115]
Asymmetric Distance Computation		0.65	GIST
PQ+IVFADC (k’ = 1024, w = 64)		0.74	GIST	This approach requires setting the codebook size k’ and the number of neighboring cells w. Recall@100 depends on these parameters, and increasing the code length is ineffective when w is small.
PQ+IVFADC (k′ = 8192, w = 64)		0.61	GIST
PQ+IVFADC (k′ = 1024, w = 8)		0.68	GIST
PQ+IVFADC (k′ = 8192, w = 8)		0.52	GIST
Faiss-GPU w/IVFFlat	Peng, Zhen et al. [103]	0.52	SIFT	The results presented are taken from a table comparing latency.
Speed-ANN-32T on KNL		0.91	SIFT
LSH	FAISS: The missing manual [113]	0.4 to 0.85	SIFT	Suitable for small or low dimensional datasets.
HNSW		0.5 to 0.95	SIFT	High speed and quality usage, uses a lot of memory.
IVF		0.7 to 0.95	SIFT	High quality, high speed, easily scalable.

In recent advancements, graph-based search algorithms have garnered significant attention within the scientific community, demonstrating promising efficiency and performance characteristics. These methods provide a compelling alternative that balances high computational performance with necessary precision; however, they use a lot of memory, which may be an issue when the ANN queries are processed by a RDBMS.

Table 1 presents comparative results of various approximate nearest search algorithms. IVF and HNSW show the best results among other algorithms, however inverted file index is more scalable and stable.

Taking into consideration the specific goals of our study (i.e., high Recall values and low memory usage), the implementation of an Inverted File Index is a relevant choice. This indexing methodology facilitates the effective organization of data, enabling high-accuracy retrieval and making it acceptable for applications necessitating an elevated Recall. This method has a wide field of improvement of both clustering for index constructing and search procedure. Thus, the Inverted File Index can be used for our goal of maximizing search quality. Moreover, IVF is implemented in many vector databases, such as pgvector (an open-source PostgreSQL extension), making possible further implementation and practical use of the algorithm developed in this research. The principle of online query complexity estimation might probably be used with the other ANN search techniques such as HNSW and PQ. However, in this study, we focus on the IVF as one of the most popular ones of the existing RDBMSs. The implementation of our approach does not require any changes in the IVF index structure.

3. IVF-Based Adaptive Search with Query Complexity Classification

The structure of the IVF search method consists of two stages: creating an IVF index and search with the use of the constructed index. In this research, we focus on the second stage. The IVF index is a supplementary data structure which consists of a list of k clusters. Each cluster has its centroid C_i which is a point (vector) in the same space as data vectors. Each of data vectors is assigned to a cluster having the centroid nearest to this data vector. Thus, the clusters are lists of the data vectors assigned to centroids. The IVF query processing starts from searching for the centroids which are nearest to the query vector q. The number of such centroids (and corresponding clusters) is limited to a natural number nprobe < k. Then, all data vectors in nprobe clusters are scanned to find the nearest K neighbors of q. Our idea is to start the search procedure with some minimum number of closest centroids and their clusters, then estimate the preliminary search results, and continue the search (if needed) so that the final nprobe value depends on the results of the preliminary search.

As mentioned above, the goal of this research is to develop an approximate nearest neighbor search algorithm that provides a high Recall rate (at least 0.99). The Recall metric in ANN query processing is a standard quality measure. It highly depends on the quality of the centroids: all modern efficient algorithms for centroid search are heuristic random search algorithms which do not guarantee an optimal result [116,117,118,119,120]. However, it also depends on the number of clusters obtained by the clustering algorithm, and also on the number of clusters scanned during the query processing K.

For our preliminary experiments intended to understand the dependence of the query processing results on the features of a single query, let us consider the SIFT1M dataset [103,113] (1 million of 128-dimensional data vectors) divided into 4096 clusters taken as an example in all our preliminary experiments. As our preliminary experiments with various nprobe values demonstrate, to obtain Recall@100 = 0.99 (in average), the IVF search algorithm must scan approximately 5% of clusters (this is about 200 clusters) which leads to processing approximately 50,000 data vectors in each ANN query. When the number of clusters is reduced to 3% of the total (127 clusters), the resulting Recall values vary across different queries.

The idea of our method is to classify the queries: distinguish the “simple” queries and “complex” queries after processing a limited number of clusters. The “simple” queries are those requiring smaller numbers of clusters processed with a high Recall. For the SIFT1M example, let the queries for which the Recall value reaches 1.0 or 0.99 after processing 3% of clusters be classified as simple (Table 2). If the Recall falls below these thresholds after processing 3% of clusters, let such queries be considered complex. For simple queries in the SIFT1M dataset, scanning 127 clusters is sufficient to achieve high Recall. In our SIFT1M dataset, the true neighbors are pre-calculated for a special list of query vectors. In real-world datasets, true neighbors are unknown and thus real Recall values cannot be calculated exactly. However, they may be approximated through an extensive search for some limited number of queries (training sample of queries). After processing a reasonable number of queries, our classifier must be capable of recognizing the simple and complex queries. For complex queries, the search must be continued.

Table 2. The results of query processing (SIFT1M dataset), where l₂ is distance to the data vector selected as the nearest neighbor, l_c is the distance to the cluster center of a data vector selected as its nearest neighbor, n_res is the number of clusters in which nearest neighbors were found, and Recall is the fraction of correctly determined neighbors among the100 predicted.

Number of Query	<l2>	σ(l2)	max(l2)	<lc>	σ(lc)	max(lc)	nres	Recall
0	78,725.8	5723.66	83,582	82,588.8	10,322.3	103,515	41	0.97
1	62,840.1	3453.5	66,853	54,277.1	10,035.0	75,566.6	28	0.96
2	41,863.3	3374.59	45,862	43,334.7	8653.09	62,068.9	23	0.99
3	41,260.5	3038.36	44,852	43,877.7	4615.84	70,784.3	14	1.00
4	62,709.1	4470.44	67,477	63,630.6	19,619.1	93,600.6	29	0.97
5	81,312.2	5371.47	87,644	86,521.2	12,956.8	108,471	42	0.88
6	61,879.8	3354.74	66,123	61,033.3	9810.32	78,267.6	43	0.94
7	36,848.8	4143.73	41,901	33,443.5	12,430.3	73,763.8	16	1.00
8	60,241.2	3521.91	64,914	57,454.6	12,061.0	81,352.5	30	0.94
9	58,733.8	3965.1	63,567	61,073.5	11,142.1	84,609.7	32	1.00
10	79,190.0	6635.88	86,494	85,952.2	8779.93	106,106.0	44	0.93
11	44,841.0	3336.09	48,074	44,711.4	6757.47	58,723.0	26	0.97
12	53,708.8	3670.09	57,272	56,956.6	7524.57	70,652.4	32	0.98
13	57,174.1	3635.02	61,995	54,672.5	13,568.5	83,061.7	30	0.95
14	69,782.6	4423.02	74,929	65,107.2	15,021.9	90,432.0	36	0.94
15	55,450.7	3565.02	59,554	58,087.5	7800.52	74,834.5	30	1.00
16	51,708.7	3701.75	55,406	49,710.7	7565.09	69,743.6	38	0.99
17	57,093.6	3028.29	60,511	56,592.3	6949.12	72,847.6	36	0.94
18	62,165.1	3509.82	66,257	65,344.1	9005.28	84,700.5	44	0.98
19	46,533.5	2720.02	49,592	44,272.4	6638.65	58,191.4	32	0.97

As mentioned in Section 2.7, IVF algorithms (as well as the new one proposed in this study) suffer from the edge problem: there is a high likelihood that the query vector is located near the edge of a cluster, with its nearest neighbor located in an adjacent cluster. Since ANN with IVF restricts the search to only the subset of points within the nearest clusters, there is no guarantee that the clusters with the true nearest neighbors are scanned. Nevertheless, in the case of our adaptive search algorithm, the number of clusters to be scanned depends on the results of the early stage of cluster scanning. For more complex queries, the edge problem leads to often incorrect cluster identification. In our study, we assume that the higher the of error ratio in identifying clusters by distances to their centroids (i.e., the higher is the complexity of the query), the greater the diversity in the numbers of those clusters that provide the nearest neighbors at the early search stage. We use this parameter (the number of effective clusters in the early stages of the search) in our query complexity classifier and adaptive IVF search algorithm.

The algorithm proposed in this study is an adaptive method based on the IVF, and it suffers from the same edge problem. However, we believe that the edge problem is more important for the queries, which we classify as complex.

The query processing results can be measured by several statistical values. For example, the average distance from the query to its nearest neighbors may differ, and the deviation of such a distance differs. We have conducted preliminary experiments to build a classifier capable of recognizing the simple queries based on the features listed in Table 2. Calculating these values requires processing some initial number of clusters.

Complex queries are characterized by the need to search across a larger number of clusters to achieve high Recall. These queries are a challenge in approximate nearest neighbor search. The primary goal in handling such queries is to maximize Recall, ensuring that as many relevant results as possible are retrieved, while maintaining strict precision constraints to avoid a surge in false positives. This balance is critical for delivering accurate and reliable search results, particularly in applications where complex queries often hold significant importance.

To achieve this goal, the system must focus on reducing the likelihood of missing relevant results for complex queries. This involves employing advanced techniques, such as dynamic query expansion, adaptive resource allocation, or query-specific search strategies, to ensure that these challenging queries are handled effectively. Our research is focused on a new adaptive search strategy that processes each query taking into account its complexity.

Section 3.1 and Section 3.2 describe a series of our preliminary experiments on a comparatively small dataset (1,000,000 data vectors), which enables us to detect the most important features (metrics) of an ANN query and estimate its complexity level. Based on the results of these preliminary experiments, in Section 3.3, we propose an adaptive IVF search algorithm, which includes the query complexity classifier and an algorithm for training this classifier.

3.1. Data Processing Query Complexity Analysis

To analyze the dependence of the query complexity and the expected Recall value on various factors, we conducted several preliminary experiments that differed in the number of clusters processed (nprobes) for the same queries. When the search algorithm receives a query vector q, it searches for K nearest neighbors in nprobe clusters which are closest to q. We summarized the data obtained after an experiment on a series of queries, including various metrics and characteristics of the query: the average distance to the data vector of the chosen neighbor, the standard deviation of those distances, the maximum of those distances, the average distance to the centroid of the data vector of the chosen neighbor, the standard deviation of those distances, the maximum of those distances, the number of clusters in which the nearest neighbors were found, and the Recall values for searching one, five, ten, twenty, fifty, and one hundred nearest neighbors. Each query was performed with various values of nprobe.

After each experiment, the Recall value was calculated. For each query, we fixed the minimum nprobe value, which is needed to achieve the desired Recall (Recall@100 = 0.99). The results enable us to analyze how various characteristics of a query affect the number of clusters query needed to process in order to achieve high Recall values.

The accumulated data is enough to examine how query complexity depends on the characteristics and statistics calculated on the early stages of query processing (after searching in comparatively small number of clusters). This analysis allowed us to create a predictive model that may classify queries on the first stages of neighbors search and decide whether or not the algorithm should proceed the survey.

One of the important features in such data is the number of clusters that contain at least one found nearest neighbor (effective clusters). This feature is referred to as n_res (see Table 2). We have studied the dependence of n_res on nprobe. This supplementary research on the same SIFT1M dataset with the same IVF index (4096 clusters) required another preliminary experiment: our analysis is based on the results of ANN search with fixed nprobe values ranging from 1% to 7% of the total number of clusters (40 < nprobe < 287), where 1% ensures minimal valuable result and 7% provides the extensive search quality. 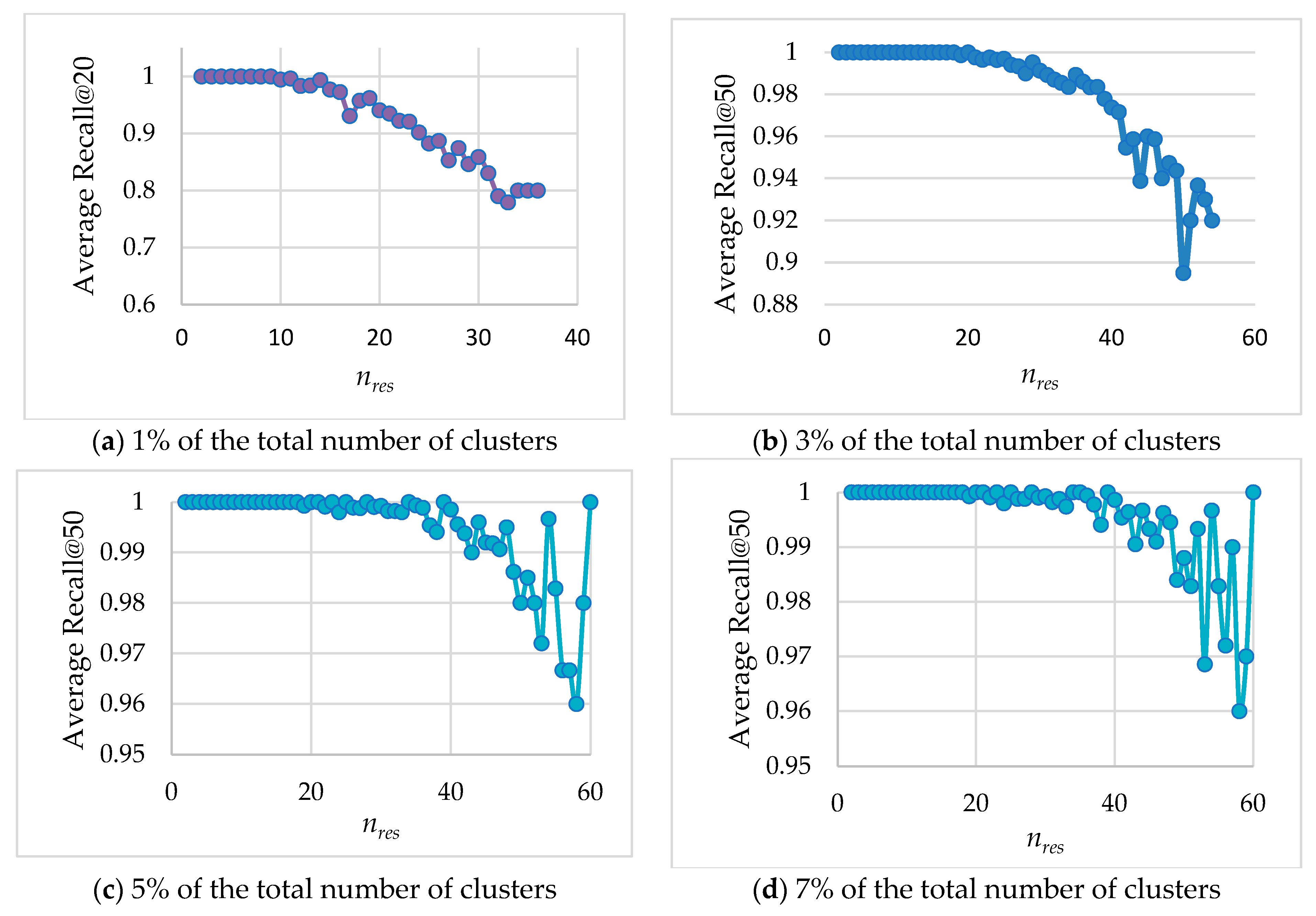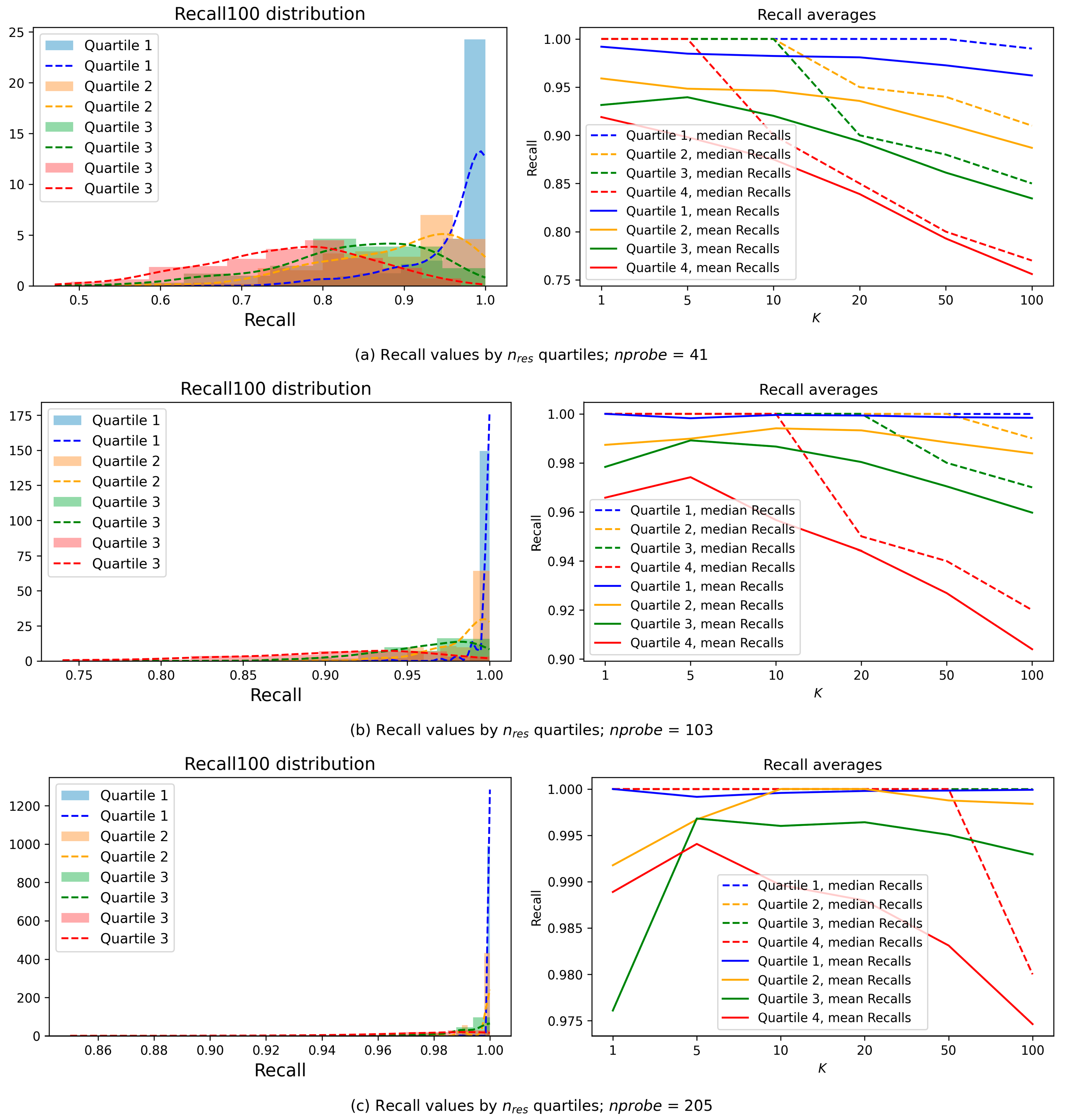Figure 6 presents the average Recall values (y-axis) for subsets of queries with identical n_res values (x-axis), measured at fixed nprobe values that are approximately 1%, 3%, 5%, and 7% of the total number of clusters.

Figure 6. Dependence of average Recall on the number of effective clusters n_res.

Figure 6 shows that the decrease in n_res leads to higher Recall, which means that simple queries (for which searching in a small number of clusters is sufficient) generally provide better solutions. We categorize queries based on the complexity of their processing. Simple queries are those whose results are concentrated within a small number of clusters (low n_res values) and still achieving high Recall value. Complex queries, on the other hand, have their results distributed across a larger number of clusters (high n_res values). For such queries, Recall may decrease due to the increased search complexity, although for some queries, high Recall can still be maintained.

This classification enables us to optimize query performance by classifying queries into simple and complex ones after the first stages of the search process.

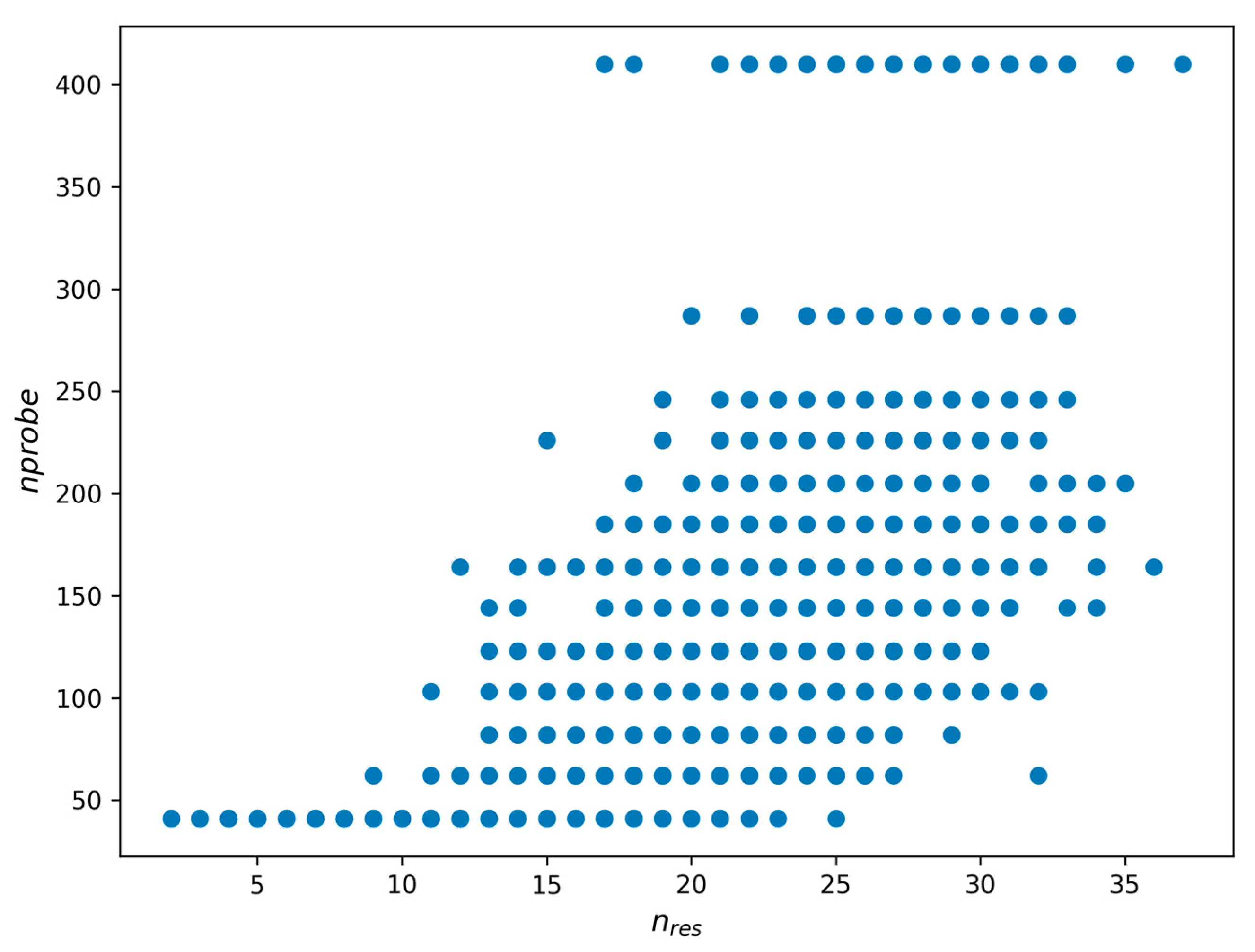
The query processing result values are represented as follows (Figure 7): on the y-axis, we demonstrate the nprobe value required to achieve a specified Recall level. The x-axis shows the corresponding n_res value. This scatter plot highlights the relation (dependency) between nprobe and n_res.

Figure 7. The relationship between the number of effective clusters n_res and the number of processed clusters nprobe, scatter plot. SIFT1M dataset, IVF index on 4096 clusters.

Figure 7 shows us that we may estimate the query complexity as a numeric value that depends on n_res.

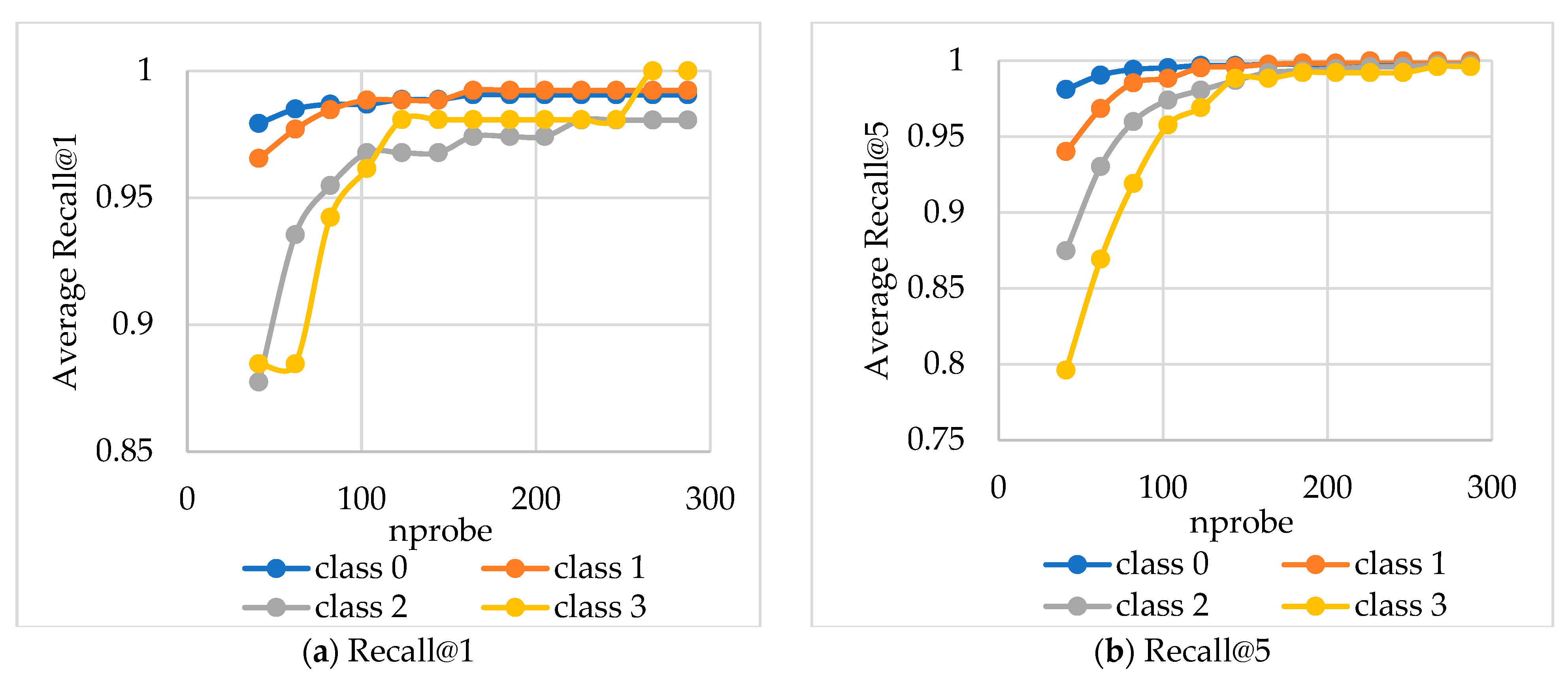
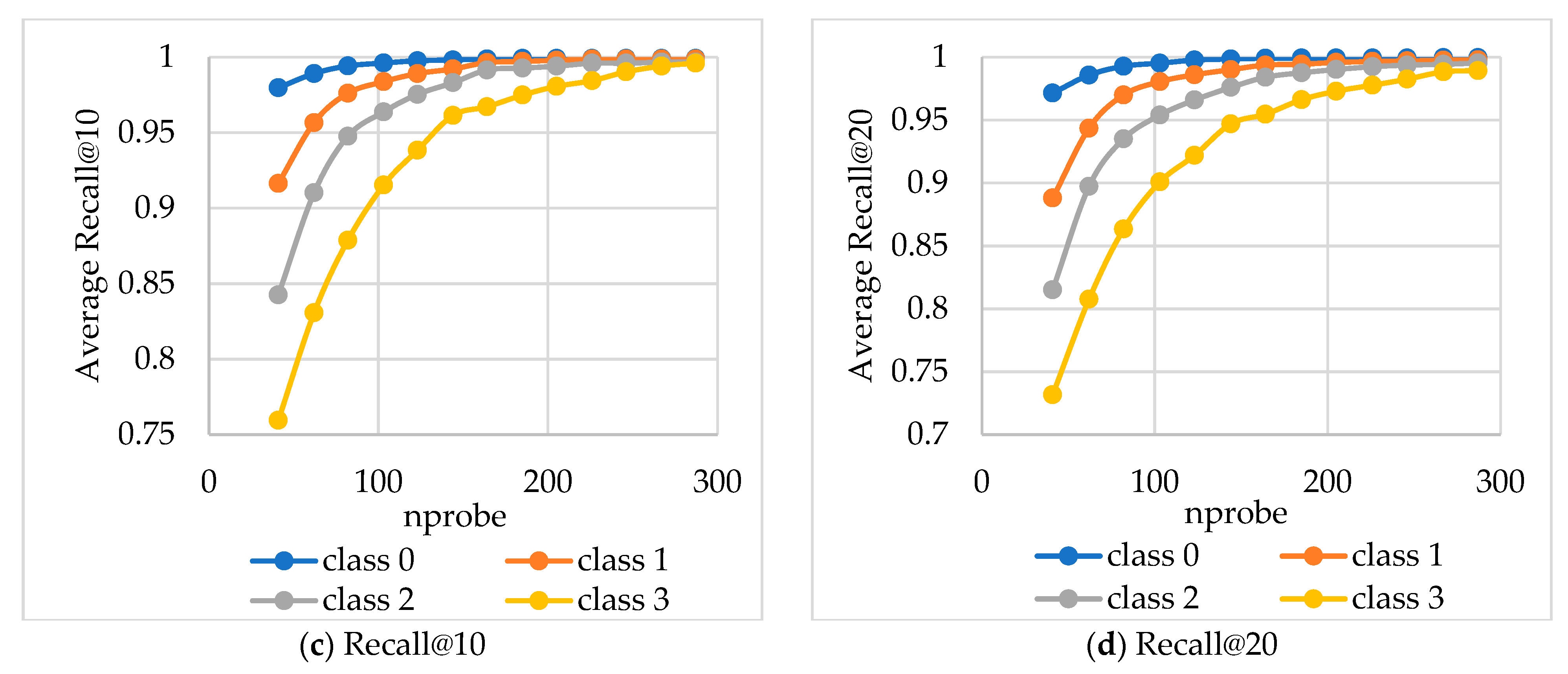
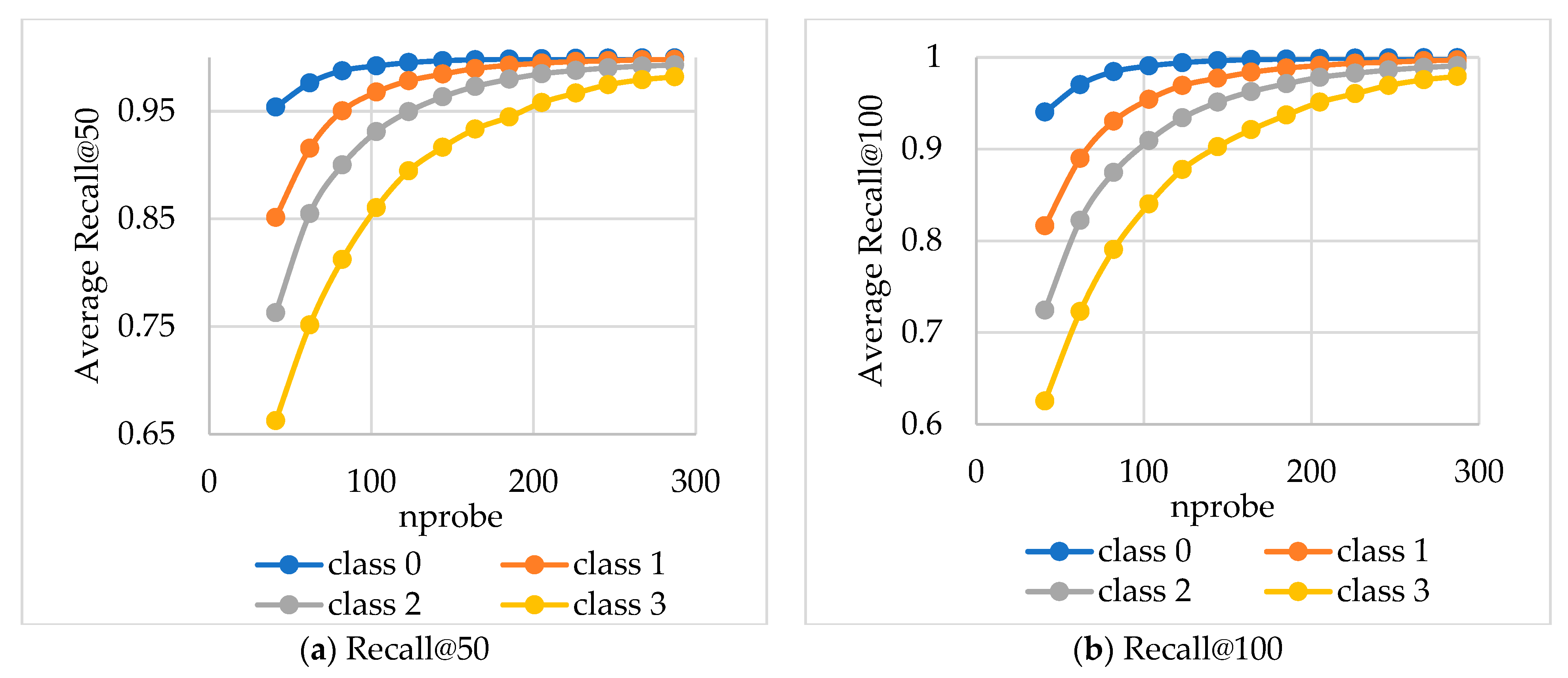
The average Recall values were calculated based on nprobe values for queries grouped into four equal complexity classes (Figure 8 and Figure 9).

Figure 8. Dependence of the average Recall values on the number of processed clusters nprobe for 4 query complexity classes. Recall@1-Recall@20. SIFT1M dataset, IVF index on 4096 clusters.

Figure 9. Dependence of the average Recall values on the number of processed clusters nprobe for 4 query complexity classes. Recall@50-Recall@100.SIFT1M dataset, IVF index on 4096 clusters.

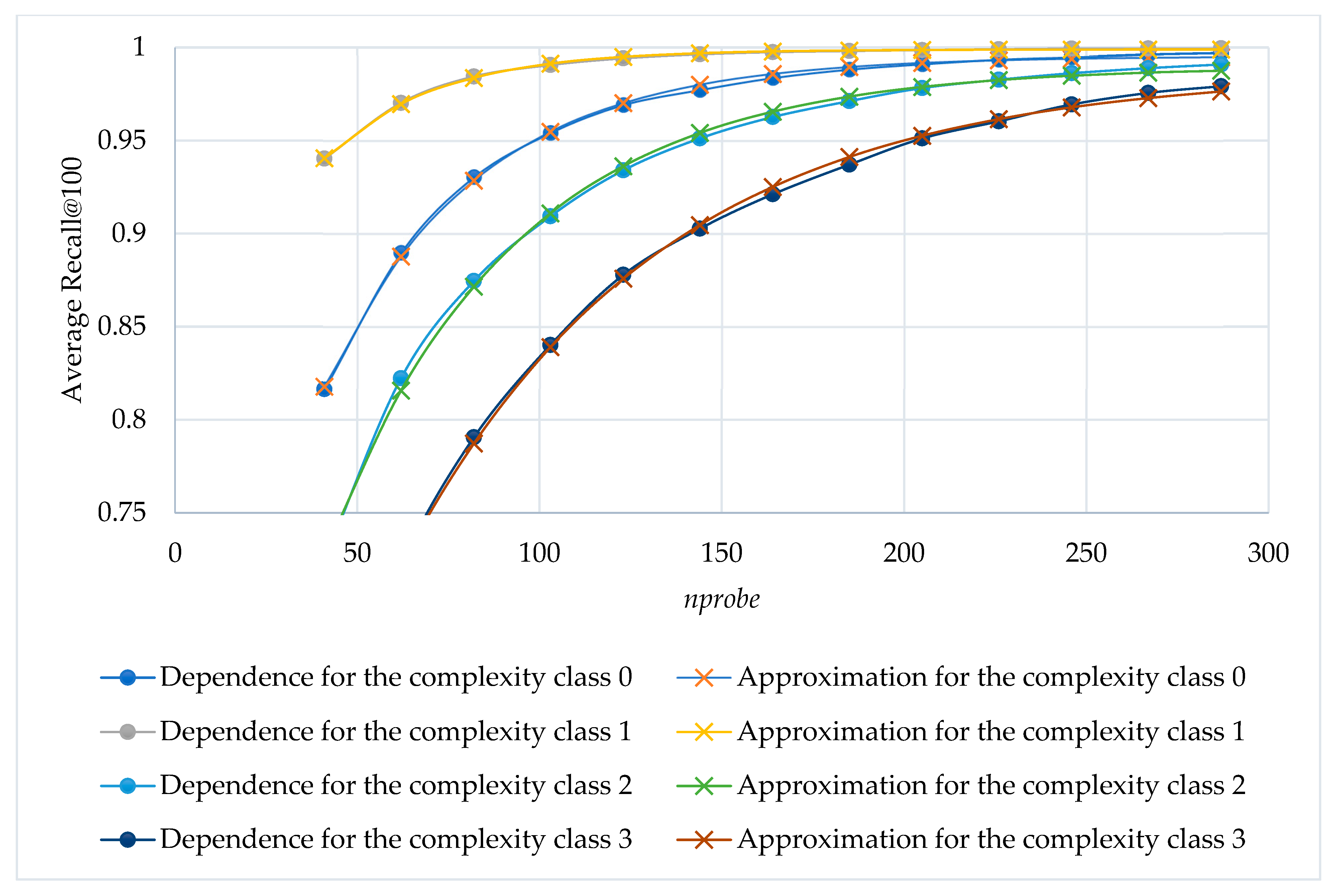
A computational experiment was carried out to assess the average Recall@100 across varying nprobe values. Subsequently, an analytical model was constructed to approximate the resulting dependencies for four complexity classes (Figure 10). The analytical form of the model is given by exponential expressions $c-a·e^{(1-x)/b}$. For each complexity class, the corresponding model coefficients along with the root mean square deviation (RMSD) were determined and are reported in Table 3.

Figure 10. Dependence of average Recall@100 on nprobe.

Table 3. Parameters of the resulting dependencies approximation for four complexity classes (see Figure 10).

Complexity Class Number	A	b	c	RMSD
class 0	0.216248	30.53076	0.998972	3.68 × 10−6
class 1	0.460257	41.96785	0.995304	3.48 × 10−5
class 2	0.565668	51.76675	0.989846	1.19 × 10−4
class 3	0.635409	70.00414	0.987077	8.45 × 10−5

Figure 8, Figure 9 and Figure 10 show us that presumably sufficient values of nprobe can be obtained through approximation. Since we can accumulate some characteristics and statistics of the query classes after preliminary search, the construction of a supervised learning model is possible. We have considered four different classifiers: decision tree, random forest, SVM, and linear regression. The random forest and SVM did not yield comparatively good results for our query classification problem. Moreover, they consume significantly more computational resources for training and processing. The constructed decision tree enabled us to determine the importance of the factors (features) that influence the model’s prediction (feature importance). The obtained feature importance is shown in Table 4.

Table 4. The importance of query processing result features for the query complexity classification.

Feature	Importance
nres	0.68
σ(l2)	0.12
<lc>	0.09
Big5	0.05
<l2>	0.04
max(l2)	0.02

The most important factor in classifying the query is the number of effective clusters (n_res). Thus, this most important feature of the query was used to build our query classifier and further adapt the search process depending on the classification results.

As mentioned above, IVF-based ANN search methods suffer from the edge problem: if centroid c₁ is the closest centroid to a query vector q, a data vector of another cluster may be located in a periphery of its cluster, and it may occur closer to a query vector than the closest data vectors of the cluster associated with the closest centroid c₁. To avoid the edge problem, the separation of a “core” and “edge” (periphery) of a cluster seems to be relevant. As shown below, this idea gives us only a minimum practical effect.

In Figure 11, q is a query vector, c₁ is its nearest centroid, and c₂ is another centroid. Denote the distances $D_1= ‖q-c_1‖$ and $D_2= ‖q-c_2‖$. Then, within the radius D₂ − D₁ around centroid c₂, no nearest neighbor of q can reside. Such an area around c₂ may be defined as a core area of the cluster assigned to c₂.

Figure 11. The edge problem illustration.

To avoid scanning data vectors in the core areas of the clusters, in an IVF index, we may precompute the distances from each data vector to its nearest centroid d_k. Then, after computing the distance D* from the incoming query q to its nearest centroid, we may partially ignore data vectors belonging to other cluster cores: for the jth cluster, given the distance D_j from the query vector to centroid c_j, we can exclude from consideration those elements of the jth cluster for which $d_k\le D_j-D^{*}$. Thus, the radius $d_j-D^{*}$ outlines the core parts of clusters (with respect to a specific query q), and within this radius, the edge problem does not arise. Clearly, clusters for which $D_j>{2D}^{*}$ may also be safely excluded from query processing when searching for the single nearest neighbor.

Moreover, if the query falls inside the hypersphere centered at the nearest centroid with radius ${\displaystyle \frac{1}{4}}{D}^{\prime }$, where D′ is the distance from the nearest centroid to its closest neighboring centroid (these distances may also be computed during IVF index construction), then the search for the single nearest neighbor to q can be restricted to the interior of this hypersphere. That is, if $D^{*}<{\displaystyle \frac{1}{4}}{D}^{\prime }$, then the nearest neighbor is guaranteed to lie in the cluster associated with the nearest centroid.

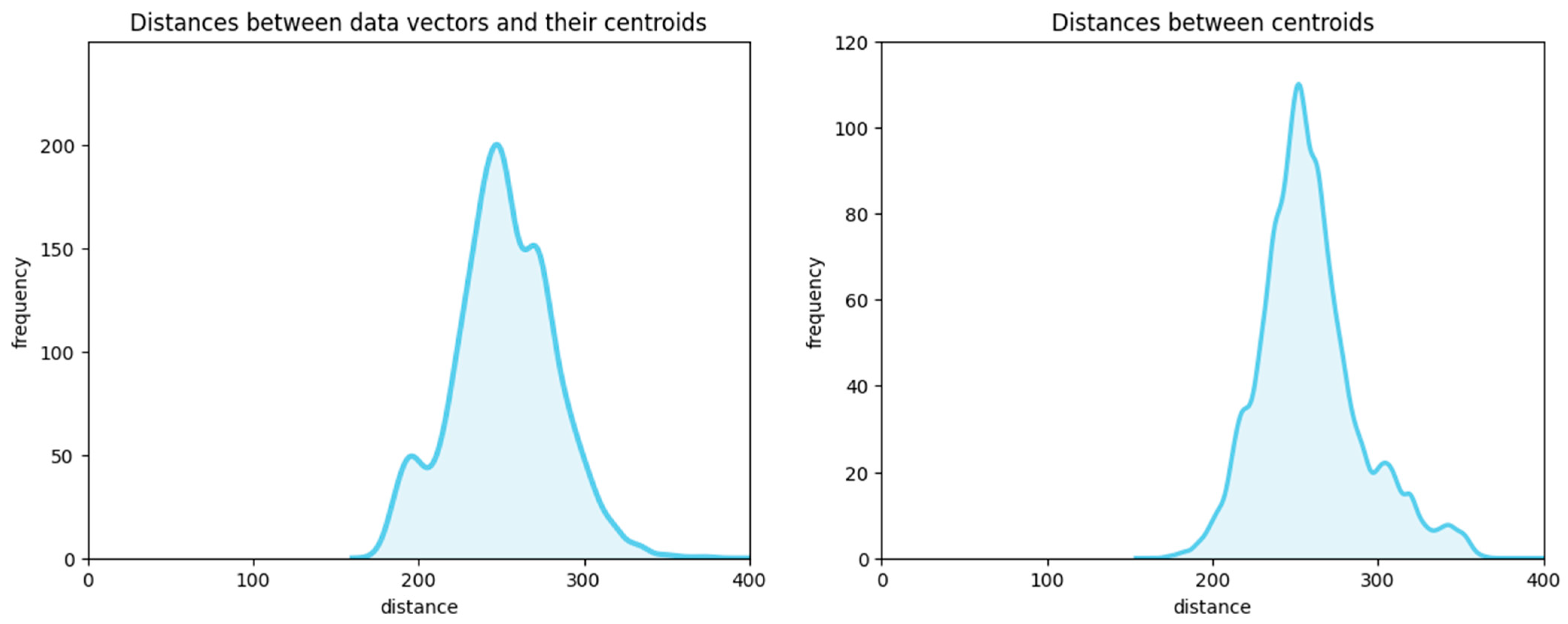
However, using this principle when ANN search is performed over multidimensional embeddings is practically useless. Figure 12 illustrates that both the inner-cluster distances d_k and the inner-centroid distances D′ are concentrated within a narrow range (distributed with low variance). In fact, in a high-dimensional space, such as our 128-dimensional dataset of embeddings (SIFT), nearly all pairwise distances are approximately equal. Therefore, condition $d_k\le D_j-D^{*}$ defines a hypersphere of a negligibly small volume, as well as hyperspheres defined by condition $D^{*}<{\displaystyle \frac{1}{4}}{D}^{\prime }$.

Figure 12. Distributions of inner-cluster and inter-centroid distances.

Our preliminary experiments aimed at accelerating search by precomputing distances to centroids and inter-centroid distances for the SIFT1M dataset, and by checking conditions $d_k\le D_j-D^{*}$ and $D^{*}<{\displaystyle \frac{1}{4}}{D}^{\prime }$, showed that these conditions hold for fewer than 0.35% of the test queries provided with this dataset. Therefore, attempts to delimit “core” and “edge” cluster regions, within which the edge problem does not arise, and filtering data using these conditions only slow down the search (due to condition checking).

This also explains the limited informativeness of those query features (Table 2) that encode various distance-based quantities.

In many clustering problems, methods based on relative distances are also commonly used. For example, Elkan’s algorithm [120] and approaches exploit the so-called “cluster cores.” These techniques rely on comparing distances among query vectors, data vectors, and centroids. However, the results shown in Table 4 illustrate that distance-based features play only a minor role. Our results with Elkan’s algorithm implemented for clustering (instead of k-means) demonstrate no difference in results.

At the same time, the edge problem reflected in the diversity of clusters in which the nearest neighbors are found can be inferred from the outcomes of early search stages. Accordingly, the feature n_res is substantially more informative than the “geometric” features based on distances, such as <l₂>, σ(l₂), max(l₂), <l_c>, σ(l_c), and max(l_c).

3.2. Approximation of Cluster Number to Be Processed (nprobe) as a Function of Number of Effective Clusters (n_res)

In this subsection, we explored the dependency between n_res and nprobe. Figure 13 demonstrates the average growth in the number of effective clusters as the total number of processed clusters increases. By determining the nature of this dependence, we can predict the required number of clusters for achieving a high Recall value. Analysis of this trend enables us to assess the impact of nprobe selection on the model’s performance.

Figure 13. Mean n_res value, first, second, and third quartiles of n_res values depending on nprobe.

We can see that the dependency is non-linear. As the number of nprobes increases, the relative impact of additional search decreases. This means that scanning only a limited number of clusters is usually enough to achieve high Recall values.

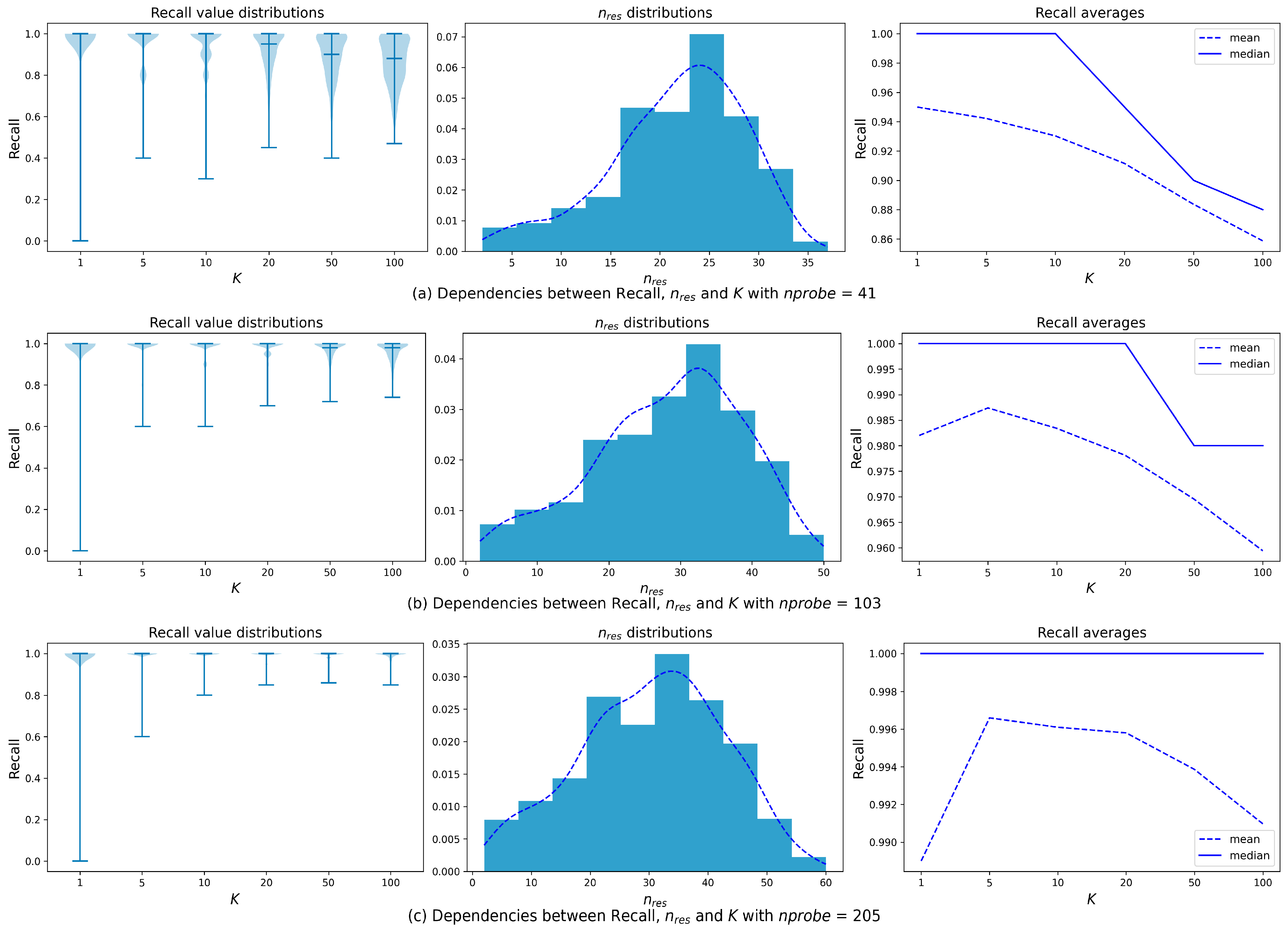
Figure 14 demonstrates that when the nprobe parameter increases, the variance of the Recall value decreases. At low nprobe values, an increase in K leads to a decline in average Recall. This observation emphasizes the importance of adaptive algorithm implementation, as different queries require varying amounts of computational resources. Distribution patterns in histograms demonstrate that the dataset can be effectively segmented into several balanced complexity classes. These classes can be delineated by establishing specific n_res thresholds that serve as markers for different classes of complexity. This approach allows for more efficient resource allocation based on query difficulty.

Figure 14. Distribution of values of achieved Recall and the number of successful clusters for different nprobe values.

Figure 15 shows the distribution of Recall values across the classes of complexity, defined as quartiles of the n_res values.

Figure 15. Distributions of n_res values and expected Recall values by quartiles.

After the analysis above, we constructed a series of simple classifiers based on logical rules: not deep and very simple decision trees. The logical rule-based binary classifier is an illustrative model used in our research to demonstrate how the quality of the constructed model depends on the size of the training sample and the input features provided to it. We used the random data vectors as ANN queries. Depending on the number of queries used to train this binary classifier, we obtained simpler or more complex rules for the query recognition. The rules may include the average distances and their standard deviations; however, the most important feature is the number of clusters where at least one of the nearest neighbors was found. We scanned 127 out of 1024 clusters (nprobe = 127) in the SIFT1M dataset, and the number of clusters that gave us the nearest neighbors varied from 13 to approximately 70.

An example of the Logical Rules (SIFT1M, nprobe = 127) for identifying complex queries is as follows (Example Classifier 1):

• If n_res ≤ 19, then q is simple;
• If n_res ≤ 21 and σ(l₂) ≥ 4980.56, then q is simple;
• If n_res ≤ 28 and σ(l_c) ≥ 9593.3, then q is simple;
• If n_res ≤ 33 and <l₂> ≤ 48,853.7 and max(l_c) ≥ 77,234.4, then q is simple;
• If n_res ≤ 34 and <l₂> ≤ 37,432.2 and <l_c> ≤ 36,761.1, then q is simple;
• Otherwise, q is complex.

If we build an index for an approximate vector search, for training a classifier, we must know the true Recall values which is a computationally complex problem since it requires an exact search to identify the true nearest neighbors. Thus, the query complexity classifier should be trained on a reasonable number of queries in order to reduce extensive search during the index construction process.

Based on only 100 processed query samples, the logical rule approach resulted in such Simplified Rules (an example based on training the classifier with, SIFT1M, nprobe = 127) is as follows (Example Classifier 2):

• If n_res ≤ 21, then q is simple;
• If n_res ≤ 30 and the number of vectors processed ≥ 31,676, then q is simple;
• Otherwise, q is complex.

Thus, our preliminary experiments demonstrate that an effective classifier may be trained using a minimal training sample: on the SIFT1M dataset with a 1024-cluster index, a binary classifier trained on just 10 data vectors using the n_res feature produces satisfactory results. This illustrative model generates a single logical rule that accurately classifies query complexity: if the number of clusters containing neighbors is less than 28, the query is considered simple; otherwise, it is classified as complex.

As we can see, in both examples of the query classifier listed above, all the logical rules include the n_res feature, which is compared to a series of constants (boundaries).

If we use a smaller number of queries to construct the classifier, it includes only the n_res feature. An example of the simplest rule (based on training the illustrative binary classifier with 10 query samples) is as follows (Example Classifier 3):

• If n_res ≤ 28 then q is simple.

Table 5 illustrates that even one feature (n_res) can show the complexity of a query quite accurately. The accuracy of the simplest binary classifier above is 0.85 for the SIFT1M dataset, and the accuracy of more complex classifiers is insignificantly higher. Also, training such a classifier requires significantly less training data, so it is less computationally expensive. Thus, the classifier with only one feature is largely accurate, and its essential feature is n_res.

Table 5. Comparison of the Example Classifiers based on logical rules.

Classifier	Accuracy
Example Classifier 1, 6 logical rules	0.91
Example Classifier 2, 3 logical rules	0.83
Example Classifier 3, 1 logical rule	0.85

Therefore, after our preliminary experiments, we came up with a simple model of binary classifier to test our findings.

Let us construct the simplest adaptive two-stage IVF search algorithm with a binary query complexity classifier. At the first stage, for each query, our algorithm processes the minimum number of clusters (127 clusters for our example with the SIFT1M dataset). After processing the minimum number of clusters, we use our classifier for each query. If the query seems to be simple, then the search algorithm stops and returns the nearest neighbors obtained from the minimum number of clusters. Otherwise, the adaptive algorithm doubles the number of the scanned clusters (Algorithm 1).

Algorithm 1. Simplified adaptive approximate nearest neighbors search.

Required: Built IVF index, query vector q, ratio of clusters for preliminary search n1, ratio of clusters for additional search n2, and maximal number of effective clusters for a query to be considered simple M.

Process IVF search in n1 clusters that have the centroids closest to the query q. Calculate nres as the number of effective clusters. If nres < M, then STOP. Otherwise, search in n2 additional clusters having the centroids closest to the query q.

Table 6 shows a comparison of the two algorithms applied to the SIFT1M dataset: the first algorithm process is a classical IVF search with the fixed nprobe value. In our example, it processed nprobe = 184 clusters for each query at once. The second algorithm performs our simplest adaptive IVF search. It processes 127 clusters, then estimates n_res, classifies the query, and processes 127 clusters more if necessary.

Table 6. The comparison of the adaptive search with binary two-stage classifier and the standard IVF search.

Method	Number of Clusters Processed for Each Query (avg.)	Number of Data Vectors Processed for Each Query (avg.)	Recall@100 (avg., 10,000 Queries)
Processing 4.5% of clusters (classical IVF search)	184	45,519.1015625	98.842%
Processing 3% of clusters, then recognition, then processing additional 3% of clusters (Algorithm 1)	182.96	45,498.7109375	99.149%

In our experiment, quantities of clusters processed (184 clusters for the first algorithm and 127 + 127 clusters for the second one) were selected so that both algorithms processed approximately the same amount of data in each query (exactly 184 for the first algorithm and approx. 183 for the second one). The second algorithm processes even less data on average. For simple queries, it processes 127 clusters, and for the complex queries, twice as much. The average computation complexity is approximately the same; however, the average Recall for the second approach is much better. The error rate reduction is about 26%. Thus, this approach may increase the average Recall or significantly save time for query processing. The results have shown that this simplest classifier has obtained certain improvements, and the concept of classifying query complexity is promising.

In this simplest example, we used a classifier with only two classes. In the example presented in Figure 15, we divided the queries into four classes based on the achieved n_res values.

Thus, our preliminary experiments with the SIFT1M dataset show the fundamental possibility of constructing a search algorithm based on the IVF index with adaptive nprobes values and the fairly high comparative efficiency of the simplest of such algorithms. In the next subsection, we propose an algorithm with four query complexity classes and an algorithm for training the classifier. These algorithms were used for larger datasets, up to one billion data vectors.

3.3. Query Complexity Classifier Based on the Number of Effective Clusters

Based on the findings presented in Section 3.1 and Section 3.2, we propose a classifier that splits queries into two or four groups based on the number of effective clusters n_res after processing some small reasonable number of clusters. Let us denote this number as n_minchecked. The first class represents the queries for which n_minchecked is sufficient to reach the target Recall value (on average), and the extensive search is not needed. Other classes are determined by dividing the distribution of rest of the queries into subsets of approximately equal cardinalities based on n_res. Let the class mark indicate how many additional clusters need to be considered for each query to achieve the desired Recall value. Having forecasted the number of scanned clusters needed for achieving the desired Recall value for each of the classes (on average), we may improve the overall performance of the ANN search algorithm depending on the query complexity class.

Algorithm 2 is designed to determine the presumably sufficient number of clusters to be processed (nprobe) to achieve a specified level of Recall in the approximate nearest neighbors search.

To train the classifier, we use a sample consisting of randomly selected data vectors contained in the database. As shown in the previous subsection, it is sufficient to have a relatively small sample for training the classifier, although the sample size certainly affects the accuracy of the classifier. Consequently, it should impact the efficiency of query processing. For each of the data vectors included in such a sample, the value of n_res must be determined. Within this process, the algorithm must repeatedly calculate the obtained Recall values. This requires the true nearest neighbors to be defined for each of the data vectors included in the classifier training sample, which brings significant computational costs. Thus, a tradeoff between the training sample size and the accuracy of the resulting classifier must be found. The issue of the required sample size was not studied in detail within the scope of this research, so it requires a separate investigation. In the experiments below, we used samples of 200 data vectors (queries). As our research results show, such a sample size is sufficient to achieve a significant increase in the performance of the approximate nearest neighbor search algorithm through the use of a query classifier based on complexity class. Classifier training algorithm requires expected Recall value Recall@K, the number of nearest neighbors K, training sample size, and a variable n_minchecked as hyperparameters.

Next, true nearest neighbors for each query in the set Q are defined with the use of the exact search. For each query q_i from Q, the counter nprobe is initialized to zero. The algorithm then enters iteration, where the value of nprobe is increased until the target level of Recall@K is reached.

The training sample of queries is divided into four groups (classes) of approximately equal size based on the values of nclust. Class1 is determined by the n_minchecked value, which is the minimal amount of clusters to be processed. Classes Class2–Class4 must be approximately of the same size.

Finally, the average values of nprobe for each of the four classes are calculated to predict the optimal parameter value of the ANN search (optimal nprobe value for each class).

Algorithm 2. Classifier training algorithm (determining query complexity classes and selecting the presumably sufficient nprobe value for each class)

Required: Training set of queries Q as a random sample of data vectors, expected Recall@K value, number of nearest neighbors K, minimum number of clusters to be scanned nminchecked.

1. Calculate true nearest neighbors with an extensive search for each query q from the set Q.   2. For each qi in Q, search in nminchecked clusters, and calculate the nres.   3. for each qi in Q do   4. nprobe:= 0.   5. nprobe:= nprobe + 1.   6. Estimate the Recall value Recall(qi)@K obtained after scanning nprobes clusters.   7. if Recall(qi)@K ≥ Recall@K then go to step 5.   8. nprobe@qi:= nprobe.   9. end for. 10. Divide Q into four subsets based on nprobes@qi, determine complexity classes boundaries according to nminchecked and nprobes@qi as follows: M1:= nminchecked. Class1:= {qi|nprobe@qi ≤ nminchecked}, Classes234:= Q\Class1. M2:= percentile33(Classes234). //Here, M2 is the 33rd percentile of the nres value among Classes234. M3:= percentile66(Classes234). Class2:= {qi | M1 < nprobe@qi ≤ M2}. Class3:= {qi | M2 < nprobe@qi ≤ M3}. Class4:= {qi | nprobe@qi > M3}. 11. Calculate the average nprobe@qi at which the required Recall value is achieved for each complexity class i ∈ {1,2,3,4} as parameters S1, S2, S3, S4. 12. Return M1, M2, M3, S1, S2, S3, S4.

Algorithm 3 outlines a process for querying a vector and determining the nearest neighbors based on specific parameters. Initially, the process begins with receiving a query vector q, a specified number of nearest neighbors K, and an expected Recall value. Next, it checks whether the classifier has been trained. If the classifier is not trained, the default ANNS procedure starts. However, if the classifier is trained, the algorithm proceeds to find the K nearest neighbors in baseline number of clusters, denoted as n_minchecked. The value nprobe is adjusted based on the outcomes of this search.

Algorithm 3. The process of requesting a vector and determining the nearest neighbors based on specific parameters.

Required: query vector q, number of desired nearest neighbors K, nminchecked, complexity classes borders M1, M2, M3, nprobes values for each complexity class S1, S2, S3, S4, trained classifier for K, nminchecked and expected Recall@K (see Algorithm 2).

If the classifier for K, nminchecked and expected Recall@K is not trained, then run default ANN search procedure and stop. Find K nearest neighbors in fixed minimal number of clusters nminchecked. Calculate nres. If nres ≤ M1, then nprobes:= S1. If M1< nres ≤ M2, then nprobes:= S2. If M2 < nres ≤ M3, then nprobes:= S3. If nres > M3, then nprobes:= S4. Perform the search process in (nprobes − nminchecked) more clusters.

Then, we analyzed the changes in query processing results with the number of neighbors K set to 100, depending on various stages of processing and the number of processed clusters nprobe. We investigated the impact by varying the number of processed clusters on the quality and efficiency of the results, which is an important aspect of optimizing data processing algorithms. The findings contribute to a deeper understanding of the relationship between the number of clusters and processing outcomes, holding both theoretical and practical significance for further research.

The values expected K, expected recall@ K, n_minchecked, M1, M2, M3, S1-S4 (Algorithm 2) constitute a supplement to the IVF index. Expected K represents the number of neighbors for which the index is built. Expected recall@ K indicates the anticipated Recall level for those K neighbors. Initially, n_minchecked refers to the number of clusters processed to calculate the n_res values. M1, M2, and M3 serve as the boundaries between classes. Additionally, S1–S4 are the average values of nprobe at which expected recal@K is successfully achieved.

Algorithm 2, which should be run after building the IVF index, provides almost all the parameters for Algorithm 3, which performs the adaptive IVF query processing. However, the parameter n_minchecked (minimal number of clusters to be scanned) must be set in advance. On the one hand, this parameter determines the relative size of complexity class Class1 (the simplest queries). Thus, the value for n_minchecked should be chosen so that the ratio of this class is approximately equal to the other classes., i.e., scanning n_minchecked clusters must be sufficient to achieve the desired Recall value for ¼ (25%) of queries (approximately). On the other hand, the choice of n_minchecked value is essential for the correct work of our classifier which is based on the n_res value. If the total number of clusters in the IVF index is small, then a small number of scanned clusters provide the desired Recall for 25% of queries. In this case, since n_res values are integers, the discrete nature of these values may result in us getting the same M1–M3 values for different query classes. From our experiments, this happens if n_minchecked does not exceed 20. The question of the minimum acceptable values for n_minchecked remains open. However, since our research is our study aims to achieve high Recall values for fairly large datasets, we assume that the IVF index contains at least several thousand clusters, and thus the number of the scanned clusters is at least several dozen, which is sufficient for Algorithm 2 to set different values of parameters M1–M3 for the complexity classes.

4. Computational Experiments

In our adaptive search algorithm, queries are divided into four groups based on their complexity. Classifying queries by complexity enables optimization of the search process: more complex queries are assigned by a higher nprobe value, while simpler queries use a lower nprobe value. This approach maintains the required level of Recall.

We implemented Algorithms 2 and 3 for larger datasets of various sizes.

For all datasets, after building the IVF index, we ran Algorithm 2 to train the query complexity classifier and determine M1–M3 and S1–S4 values.

For the experiments presented below, we used the SIFT10M, the 10-million subset of the first 10,000,000 records of the 128-dimensional SIFT1B dataset [33] (which is also known as BIGANN). The dataset consists of typical pre-trained embeddings for approximate nearest neighbor search using the Euclidean distance and consists of 10,000,000 objects. The SIFT1B dataset, as well as its subsets, are traditionally used for the purpose of estimating the RDBMS efficiency. All these datasets are provided along with the standard sets of test queries [33] which we used in our experiments.

The experiments were conducted using the Euclidean distance metric (l₂ norm), with the following settings: number of parallel processes (Parallel on) allowed for the RDBMS query processing, number of nearest neighbors to be found K = 100, and n_minchecked used for Recall evaluation. In the experiments below, n_minchecked = 40.

The technical characteristics of the computational equipment are as follows:, 8× Ascend 910B4 chips, 1.5 TB DDR4 RAM, 7 TB NVMI disk.

The results of the computational experiments aimed at evaluating the stability and effectiveness of the implemented adaptive nprobe algorithm (Algorithm 3), with various parameter values (M1, M2, M3, S1, S2, S3, and S4), are presented in Table 1, Table 2, Table 3, Table 4, Table 5, Table 6, Table 7, Table 8, Table 9, Table 10 and Table 11.

Table 7. Comparative results for the adaptive nprobe algorithm. Dataset: SIFT10M (10,000,000 data vectors); data sample size for clustering algorithm is 10,000.

	Index 1		Index 2		Index 3		Index 4		Index 5
Run number	1	2	1	2	1	2	1	2	1	2
Top K	100	100	100	100	100	100	100	100	100	100
Parallel processes	100	100	100	100	100	100	100	100	100	100
M1	17	17	17	17	17	17	17	17	17	17
M2	22	22	22	22	22	22	22	22	22	22
M3	29	29	29	29	29	29	29	29	29	29
M1/nminchecked	0.43	0.43	0.43	0.43	0.43	0.43	0.43	0.43	0.43	0.43
M2/nminchecked	0.55	0.55	0.55	0.55	0.55	0.55	0.55	0.55	0.55	0.55
M3/nminchecked	0.73	0.73	0.73	0.73	0.73	0.73	0.73	0.73	0.73	0.73
S1	40	40	40	40	40	40	40	40	40	40
S2	100	100	100	100	100	100	100	100	100	100
S3	141	141	141	141	141	141	141	141	141	141
S4	185	185	185	185	185	185	185	185	185	185
Recall@100	0.9913	0.9913	0.9912	0.9912	0.9913	0.9913	0.9910	0.9910	0.9912	0.9912
Latency	227.77	222.5	235.17	232.34	224.73	222.63	225.52	226	238.61	227.7
QPS	436.59	446.87	422.13	427.46	442.22	446.85	437.02	440.29	415.28	433.66
nlist	3150	3150	3150	3150	3150	3150	3150	3150	3150	3150

Table 8. Comparative results of the experiment with the standard IVF algorithm, fixed nprobe= 125. Dataset: SIFT10M; data sample size for clustering algorithm is 10,000.

	Index 1		Index 2		Index 3		Index 4		Index 5
Run number	1	2	1	2	1	2	1	2	1	2
nprobe	125	125	125	125	125	125	125	125	125	125
Top K	100	100	100	100	100	100	100	100	100	100
Parallel processes	100	100	100	100	100	100	100	100	100	100
Recall@100	0.9912	0.9912	0.9911	0.9911	0.9913	0.9913	0.9912	0.9912	0.9912	0.9912
Latency	296.53	288.4	294.87	315.64	319.58	271.42	297.33	286.06	297.8	286.17
QPS	335.61	344.78	337.15	314.85	310.92	366.25	334.37	347.47	333.79	347.36
nlist	3150	3150	3150	3150	3150	3150	3150	3150	3150	3150

Table 9. Averaged parameter values from experiment series with various M1, M2, M3, S1, S2, S3, and S4 parameter settings. Dataset: SIFT10M.

	Series
	1	2
Top K	100	100
Parallel processes	100	100
M1	10	10
M2	18	17
M3	23	23
S1	12	9
S2	47	37
S3	82	88
S4	158	163
Recall@100	0.99004 (avg.), std.dev. = 0.0002	0.99072 (avg.), std.dev. = 0.0002
Latency	227.428 (avg.), std.dev. = 14.135	246.847 (avg.), std.dev. = 14.623
QPS (avg.)	437.622	404.823
Nlist	3150	3150

Table 10. Comparative results of the adaptive nprobe algorithm compared to standard IVF search. Dataset: SIFT100M (100,000,000 data vectors); the data sample size for the clustering algorithm is 100,000.

Algorithm, Index	Brute Force	Standard IVF, Averaged for Six Runs with Four Indexes	Adaptive IVF, Index 1 (Two Runs)		Adaptive IVF, Index 2 (Two Runs)		Adaptive IVF, Index 3	Adaptive IVF, Index 4
Top K	100	100	100	100	100	100	100	100
Parallel processes	100	100	100	100	100	100	100	100
M1	-	-	15	15	15	15	15	15
M2	-	-	23	23	23	23	23	23
M3	-	-	27	27	27	27	27	27
M1/nminchecked	-	-	0.38	0.38	0.38	0.38	0.38	0.38
M2/nminchecked	-	-	0.58	0.58	0.58	0.58	0.58	0.58
M3/nminchecked	-	-	0.68	0.68	0.68	0.68	0.68	0.68
S1	-	-	40	40	40	40	40	40
S2	-	-	85	85	85	85	85	85
S3	-	-	140	140	140	140	140	140
S4	-	-	255	255	255	255	255	255
Recall@100	1.00	0.9863	0.9904	0.9902	0.9902	0.9901	0.9901	0.9906
Latency	-	719.8	660.54	602.82	572.32	670.82	673.5	679.2
QPS	19.61	136.21	147.14	158.3	167.32	145.21	145.02	144.88
nlist	-	10,000	10,000	10,000	10,000	10,000	10,000	10,000
nprobe	-	120	Adaptive (avg. 106.4)	Adaptive (avg. 106.4)	Adaptive (avg. 106.4)	Adaptive (avg. 106.3)	Adaptive (avg. 106.4)	Adaptive (avg. 106.4)

Table 11. Comparative results of the adaptive nprobe algorithm (Algorithm 3). Dataset: SIFT1B (1,000,000,000 data vectors); the data sample size for clustering algorithm is 1,000,000.

	Recall100@100	Latency, ms	QPS
Standard IVF	0.9904 (avg.), std.dev. = 0.0002	7959 (avg.), std.dev. = 356	6.08 (avg.)
Adaptive IVF (Algorithm 3)	99.05 (avg.), std.dev. = 0.0002	5607 (avg.), std.dev. = 380	8.47 (avg.)
Avg. improvement, %		29.6%	39.3%

We used five versions of the IVF index to estimate the comparative efficiency of our approach (Algorithm 3) since the search efficiency depends on the quality of the IVF index (which is out of scope of this research).

For the RDBMSs, the most practically important metrics are average latency (amount of time since the ANN query arrives until its processing finishes) and QPS (queries per second).

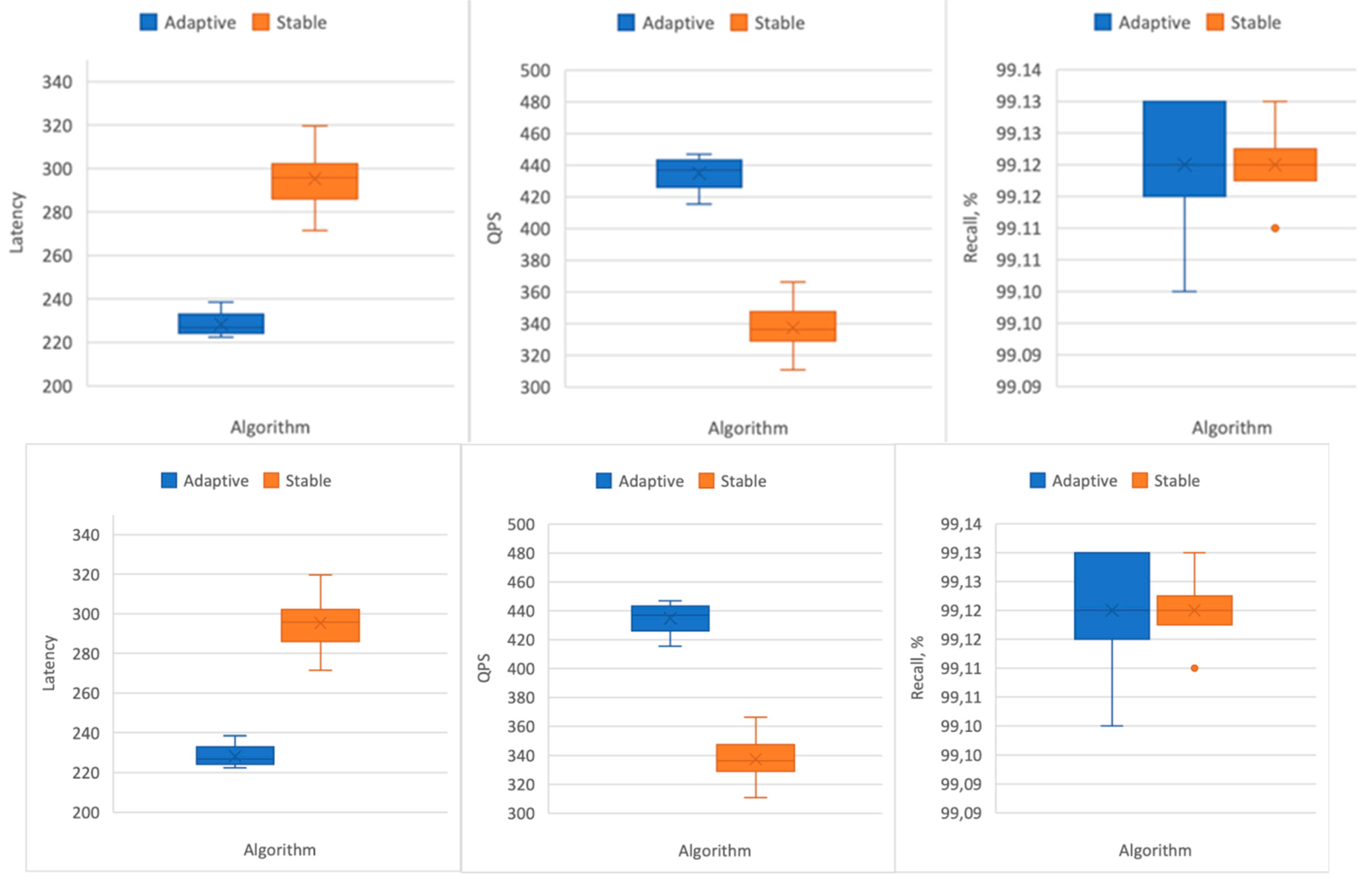
The averaged key metrics from the first experiment (Table 7) are Recall@100 = 0.9912, QPS = 434.84.

To obtain the centroids of the clusters, the IVF index-building algorithms (which are out of the scope of this paper) may use the standard k-means clustering algorithm (Indexes 3–5 in Table 7 and Table 8) and more sophisticated algorithms, including greedy agglomerative clustering [119,120] (Indexes 1 and 2 in Table 7 and Table 8). As we can see, the quality of the index does not affect the search efficiency significantly.

Clustering algorithms are computationally expensive, especially agglomerative clustering algorithms. Therefore, sampling is traditionally used to construct IVF indexes on large datasets. In our case, random sampling was used to find the centroids, and the cluster structure for the SIFT10M dataset was built using 10,000 data vectors (0.1% from the whole dataset). After finding the positions of all centroids, each data vector from the whole dataset was assigned to its nearest centroid. This may have slightly reduced the overall quality of the index; however, this sampling enabled us to reduce the indexing time. In several experiments, we used greedy agglomerative clustering algorithms, which result in a better objective function value of the k-means clustering problem (i.e., better squared distance sum value); however, this did not lead to a significant increase in the ANN search performance.

Table 8 presents the results of the experiment on the same dataset with the standard IVF search algorithm with the fixed nprobe = 125. Aggregated key metrics from this experiment are Recall with an average value of 99.12 and QPS with an average value of 337.26. In these—as well as future—experiments with the standard IVF search algorithm, we selected the minimum nprobe value, which provided the desired Recall value (in the case of SIFT10M dataset with nlist = 3150, this minimum value was 125).

The experimental results from Table 7 and Table 8 demonstrate the superiority of the proposed adaptive nprobe algorithm compared to the standard IVF search algorithm with the stable nprobe: latency is reduced by 23%, while QPS (queries per second) increases by 25%, all while maintaining the required Recall level above 0.99 (Figure 16).

Figure 16. Latency, QPS, and Recall comparison: adaptive IVF search algorithm (Algorithm 3) compared to standard (stable) IVF search. SIFT10M dataset.

Algorithm 2 returns seven search parameters (M1–M3 and S1–S4); however, the class boundary values M1–M3 can be tuned manually. Table 9 shows how fine-tuning of these parameters may affect the search quality and performance. The presented results are averaged metrics obtained by 10 launches on 10 different indexes. We can see that manual fine-tuning can lead to further improvement of efficiency—which indicates the need for further clarification of the nature of the relation between the required nprobe values and n_res—and, consequently, further improvement of Algorithm 2.

Our experiments on larger datasets (Table 10 and Table 11) demonstrate that the comparative advantage of the adaptive algorithm remains if we process really big data.

The results (Table 10) show that our adaptive approximate nearest neighbors search can reach the Recall value of 0.99 on large datasets and increase the search speed.

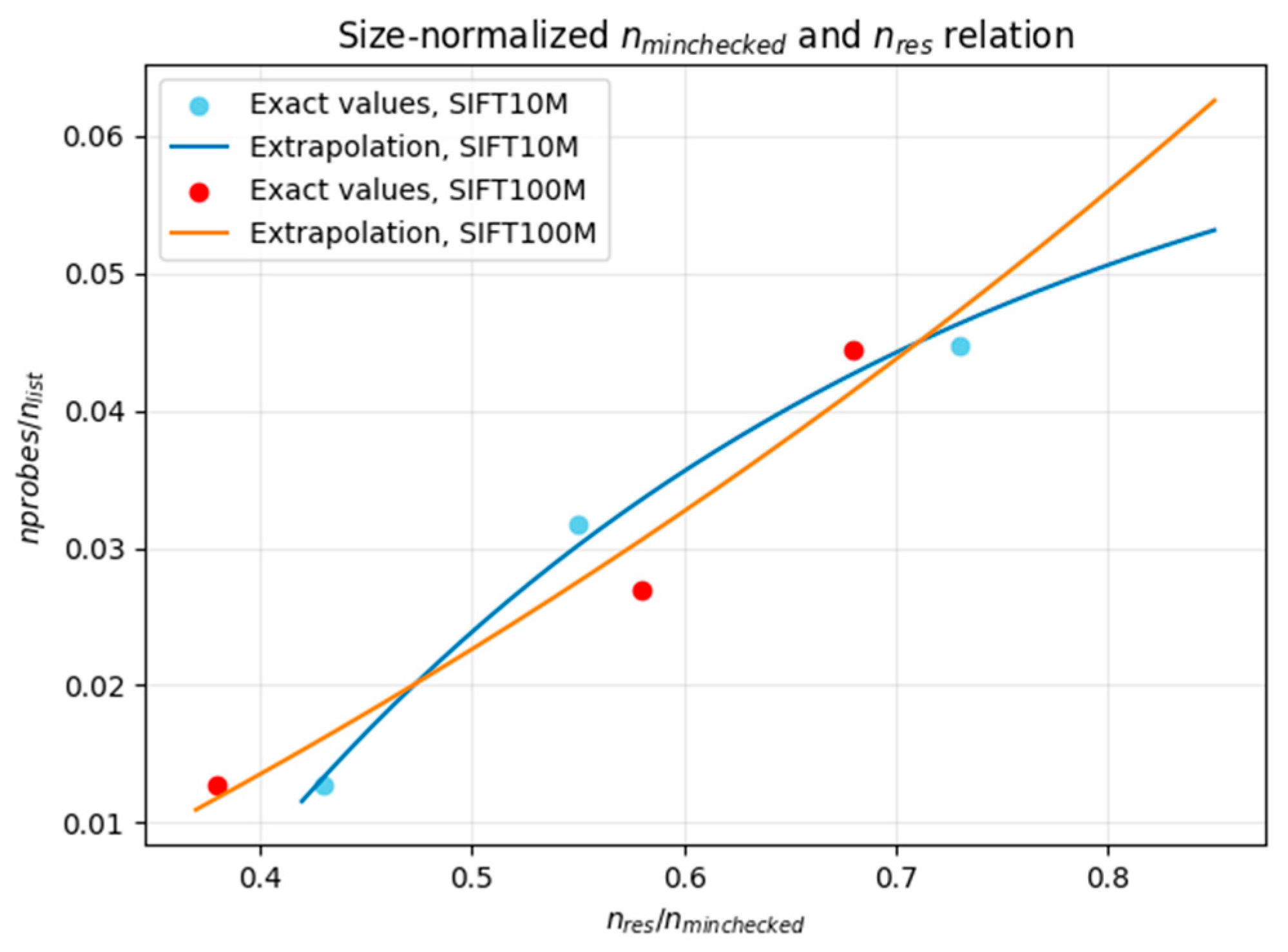
Figure 17 illustrates the relation between the ratio of resultative clusters in the first search stage (n_res/n_minchecked) and the ratio of clusters to be scanned for various query complexity classes. As we can see, the dependencies of various datasets differ. Therefore, our attempts to find a function that approximates the query complexity measure (nprobes) based on the ratio n_res/n_minchecked failed, and we did not find a universal approximation for an arbitrary dataset. Therefore, further research may be warranted in the future.

Figure 17. Dependency of values nprobes/n_list (median values for each complexity class) and n_res/n_minchecked, where n_list is the number of constructed clusters.

For the results in Table 10, the average adaptive nprobe is 106.4 (1.106% of all clusters). In comparison with the standard IVF search with fixed nprobe = 120 (1.2% of all clusters), the number of clusters (and data vectors) to be scanned was reduced by a factor of 1.127. The average QPS value (151.31 for the adaptive search and 136.21 for the standard IVF search) was increased by a factor of 1.11. Thus, the reduction in the volume of scanned data is proportional to the increase in search speed. In [90], the authors report that their version of the HNSW search requires only 0.03% of data vectors to be processed (which is 338,739 times less than the brute force requires), while the QPS value increases only by a factor of 6.86 (in comparison with the brute force). Unlike more sophisticated index structures—such as HSNW—the IVF index has a very simple structure: lists of data vectors grouped into clusters. In the case of large datasets, the clusters are relatively big data arrays that occupy sequentially located areas on the disk drive which are processed in a very simple way: simply reading and calculating the distances. In fact, the speed of such processing depends almost only on the disk drive performance. Thus, despite our new search algorithm requiring much more data vectors to be scanned than graph-based methods, it enables us to achieve a significant increase in search speed (compared to the brute-force search; see Table 10). Figure 18 gives us an idea of how the Recall value increases with an increase in the ratio of scanned data vectors in our adaptive search algorithm.

Figure 18. Dependency of Recall values on the ratio of scanned data vectors. SIFT10M dataset; 10,000,000 data vectors; adaptive IVF.

Table 11 summarizes the results of measuring our approach on the largest SIFT1B dataset (one billon data vectors). The algorithms for building IVF indexes capable of processing the largest datasets are still under development in RDBMSs such as pgvector, and we had no opportunity to run Algorithms 2 and 3 with various IVF indexes. Table 11 demonstrates the averaged comparative results of five runs of Algorithm 3 with the same IVF index. The data demonstrates that the search performance improvement grows as the dataset grows, showing ~40% improvement at the billion-scale data size.

The results presented in Table 11 illustrate a significant improvement in search performance achieved by our adaptive algorithm when applied to the dataset of one billion data vectors. This underscores the algorithm’s capability to handle large-scale data effectively while ensuring high Recall rates.

5. Conclusions

The central contribution of this work is the introduction of a query-adaptive paradigm for approximate nearest neighbor search (ANNS) within inverted file index (IVF) structures. In this paradigm, the search effort is dynamically calibrated to the intrinsic complexity of individual queries rather than being fixed a priori for all requests.

A key methodological innovation is a replacement of the heuristic static nprobe selection with a lightweight classifier-driven decision mechanism. Unlike prior adaptive approaches—such as Tao [43] or AdaptNN [74], which rely on pre-computed static features like local intrinsic dimensionality—or runtime monitoring of distance distributions, our method leverages empirically observable metrics derived directly from the IVF structure. These metrics include the number of effective clusters (n_res), the variance of distances to retrieved neighbors (σ(l₂)), and the proximity to cluster centroids. This design makes the classifier independent of external assumptions about data geometry and computationally inexpensive to evaluate crucial properties for integration into RDBMS environments such as pgvector, where both memory and latency budgets are constrained.

We propose an adaptive ANN search algorithm that includes the query complexity prediction and dynamic tuning of the nprobes parameter. The proposed adaptive nprobes algorithm dynamically determines the presumably sufficient number of clusters to process based on the complexity of each individual query, achieving a balanced trade-off between Recall and QPS.

The obtained results confirm the effectiveness of the developed algorithm. At a required Recall value greater than 0.99, it achieved an up to 28.93% increase in query processing speed (QPS) and up to 22.7% reduction in average latency compared to the standard IVF algorithm. The high stability of the Recall metric demonstrates the reliability of the approach under varying query complexities. The experiments conducted with the greedy agglomerative clustering algorithm showed that this method provides a narrower range of Recall variation compared to the standard algorithm, indicating improved stability and predictability of the results. Scalability analysis demonstrated that the proposed approaches maintain their effectiveness on large-scale datasets (100 million data points).

Our adaptive search algorithm’s efficiency proves that the result of query processing can be improved at the stage of searching through constructed index without any additions to the index-constructing process or changing the structure of data.

We recognize several limitations and directions for future work. First, the classifier requires a training phase with exact nearest neighbor annotations for a representative query sample. While we demonstrate that even 100–200 samples are sufficient to achieve satisfactory performance (Section 3.2), this still introduces non-trivial overhead during index construction. Future extensions could investigate semi-supervised or online learning strategies that enable incremental refinement of the classifier during production use. Second, the current implementation assumes a single fixed Recall target (Recall@100 ≥ 0.99). Extending the framework to support multi-objective optimization—for example, balancing Recall against latency under dynamic SLAs—would broaden its applicability in cloud-native vector databases. Third, although our experiments focus on Euclidean distance and IVF-Flat, the underlying principle of early termination based on predictive complexity estimation generalizes to other quantization schemes (such as PQ+IVF) and indexing structures (such as HNSW), provided that similar early-stage diagnostic features can be extracted.

The proposed approach resolves the long-standing assumption in the ANNS literature that higher Recall necessarily requires probing more clusters. We demonstrate that statistically guided sampling enables near-optimal Recall with substantially fewer distance computations. This result challenges the prevailing view that performance improvements in IVF require larger codebooks or more aggressive pruning that increase index size and construction time. By decoupling accuracy from search breadth, our method becomes particularly appealing for environments constrained by disk I/O, where each cluster scan may trigger a page read or memory bandwidth.

In addition, unlike graph-based methods such as HNSW and NSG or hashing-based approaches such as LSH, which often entail high memory overheads and complex graph maintenance, our solution operates entirely within the standard IVF framework. It requires no structural modifications to the index, only lightweight metadata augmentation (classifier parameters M₁–M₃, S₁–S₄) and a minor adjustment to the query execution pipeline. This property makes the method well suited for seamless integration into existing vector database engines such as pgvector and Pinecone, where backward compatibility and operational simplicity are paramount.

In conclusion, the proposed adaptive IVF search represents a pragmatic, efficient, and deployable evolution of the IVF paradigm. By recognizing that not all queries are equal, and by leveraging simple, interpretable features derived from early-stage search outcomes, we achieve substantial performance gains without sacrificing accuracy, determinism, or compatibility. This approach offers a scalable, low-overhead path toward high-performance ANNS in real-world vector databases, making it a compelling candidate for adoption in next-generation AI infrastructure.