A Complex Network Science Perspective on Urban Parcel Locker Placement

Abstract

The rapid rise of e-commerce is intensifying pressure on last-mile delivery networks, making the strategic placement of parcel lockers an urgent urban challenge. In this work, we adapt multilayer two-mode Social Network Analysis to the parcel-locker siting problem, modeling city-scale systems as bipartite networks linking spatially resolved demand zones to locker locations using only open-source demographic and geographic data. We introduce two new Social Network Analysis metrics, Dual centrality and Coverage centrality, designed to identify both structurally critical and highly accessible lockers within the network. Applying our framework to Milan, Rome, and Naples, we find that conventional coverage-based strategies successfully maximize immediate service reach, but tend to prioritize redundant hubs. In contrast, Dual centrality reveals a distinct set of lockers whose presence is essential for maintaining overall connectivity and resilience, often acting as hidden bridges between user communities. Comparative analysis with state-of-the-art multi-criteria optimization baselines confirms that our network-centric metrics deliver complementary, and in some cases better, guidance for robust locker placement. Our results show that a network-analytic lens yields actionable guidance for resilient last-mile locker siting. The method is reproducible from open data (potential-access weights) and plug-in compatible with observed assignments. Importantly, the path-based results (Coverage centrality) are adjacency-driven and thus largely insensitive to volumetric weights.

1. Introduction

The rapid growth of e-commerce in recent years has placed unprecedented strain on last-mile delivery infrastructure worldwide. The “last mile”, i.e., the final leg of a parcel’s journey to the customer, is widely recognized as the most costly and inefficient segment of the supply chain. Estimates suggest that last-mile delivery can account for as much as 35–50% of total shipping costs (https://www.amcsgroup.com/resources/blogs/last-mile-delivery-gaining-efficiencies-and-reducing-operating-costs, accessed on 8 July 2025) and around 30% of urban transport emissions (https://transport.ec.europa.eu/document/download/b818ff86-2463-4949-9413-d3ca559f60b9_en, accessed on 8 July 2025). These challenges are driving the exploration of more sustainable and efficient delivery models. In particular, out-of-home delivery options such as parcel pickup points and automated parcel lockers have gained traction as promising solutions to consolidate deliveries and reduce doorstep failures. Parcel lockers (secure, self-service kiosks for parcel pickup) were first introduced roughly two decades ago and have seen steady adoption since, yet their full benefits and best deployment strategies remain underexplored [1]. According to the World Economic Forum, the broad use of parcel lockers could cut global last-mile delivery costs by 2–12% and reduce emissions by 5–18% by 2030. By avoiding repeated delivery attempts and enabling route consolidation, lockers can mitigate many inefficiencies of traditional home delivery. Recent empirical studies provide supportive evidence; for example, a field trial in Seattle found that installing a common carrier locker in a residential building significantly decreased in-building delivery time for couriers (improving efficiency), albeit with only a modest reduction in vehicle dwell time at the curb [2]. Multiple environmental assessments likewise indicate that locker-based deliveries, when well utilized, can lower overall delivery vehicle travel and emissions [3,4,5]. One study in Germany found up to 11% cost savings and 2.5% ${\mathrm{CO}}_2$ reduction from using lockers in urban areas [6], while a simulation in Norway concluded that converting a large share of home deliveries to lockers could cut emissions by as much as 30% [7]. These gains, however, are highly sensitive to placement and usage rates; poorly sited lockers that force customers into long detours can negate benefits, underscoring the importance of strategic network design [8].

Despite the clear potential of parcel lockers for last-mile logistics, planning robust locker networks remains a complex challenge. Most existing approaches in both industry and academia focus on optimizing locker locations using classical facility location models or heuristic algorithms. Typical objectives include maximizing coverage of customers, minimizing distance or travel time, or reducing operational costs. While such models are valuable for initial deployment, they often treat facilities in isolation and do not capture the network characteristics of the system, such as how lockers collectively connect different communities, or how resilient the network is to disruptions. Our work aims to fill this gap by adopting a complex network science perspective on the parcel locker system. We model the locker network as a two-layer graph (bipartite network) linking demand zones with locker locations, which allows us to apply techniques from Social Network Analysis (SNA) to identify key structural properties. By representing users (or neighborhoods) and lockers as nodes in an integrated network, we can move beyond simple point location optimization and instead analyze the connectivity, centrality, and vulnerability of the entire delivery infrastructure. In this study, we introduce two novel network-based metrics, Dual centrality and Coverage centrality, to evaluate the importance of parcel locker nodes from complementary angles. Dual centrality rates lockers as important if they serve many high-demand user areas and rates user areas as important if they access key lockers (this iterative “mutual importance” concept is akin to two-mode Bonacich centrality in social networks [9]). Coverage centrality, by contrast, is a path-based measure that assesses how crucial a given locker is for connecting different user zones to each other, by counting the pairs of zones that a locker connects on the shortest paths. By applying these metrics to the parcel locker networks of three major cities, we are able to uncover critical insights that traditional models might miss. For instance, we find that the lockers with the widest immediate coverage (serving the most people) are not necessarily the most structurally critical for network connectivity and resilience. In fact, our analysis reveals a stark trade-off: strategies that simply prioritize the highest-demand lockers can leave the network fragile, highly vulnerable to the removal of a few hubs, whereas considering network centrality highlights less-obvious lockers whose presence is vital to maintaining system-wide connectivity.

The novelty and significance of this work lie in bridging the gap between conventional location optimization and complex network analysis for urban logistics. To our knowledge, prior multilayer and two-mode methods have not been applied specifically to city-scale parcel-locker siting with open-data inputs and locker-focused diagnostics; our contribution is to tailor and validate that framework for parcel lockers via Dual and Coverage centralities and a robustness-oriented siting workflow. This approach provides a richer understanding of the system’s behavior under strain (e.g., failures or surges in demand) and offers urban planners tangible guidance on building more robust and equitable last-mile networks. Our methodology relies solely on open data, high-resolution gridded population, and open maps of locker locations, making it broadly applicable to different cities without proprietary datasets. Despite the rapid growth of out-of-home delivery, most parcel-locker siting studies rely on static facility location and MCDM formulations that optimize coverage, distance, or cost, with limited attention to the two-mode (users–lockers) network structure and to system-wide robustness under failures. Recent reviews confirm this methodological emphasis and note that dynamic or time-varying models remain uncommon in the locker literature, while equity assessments are only beginning to appear empirically (e.g., spatial accessibility/inequity of Amazon lockers) [1,10]. This leaves a gap for open-data, generalizable methods that diagnose both fairness and resilience from a network perspective. Our contribution is to (i) model city-wide locker systems as a bipartite multilayer network built solely from open data; (ii) introduce two complementary centralities (Dual centrality and Coverage centrality) tailored to the two-mode topology; (iii) benchmark against one-mode/weighted baselines, including robustness under targeted vs. random failures; and (iv) translate diagnostics into an executable planning workflow with feasibility screening (zoning, utilities, and transit accessibility). This network-centric approach addresses documented limitations of static siting models and targets the policy motivation of improving last-mile efficiency while safeguarding resilience [11,12,13].

The remainder of this paper is organized as follows. Section 2 reviews the state of the art on parcel lockers in last-mile logistics, traditional locker location models, and the use of network science in logistic systems, highlighting how our approach departs from and adds to existing work. Section 3 then details our multilayer network model formulation and the proposed centrality metrics, along with the experimental design. Section 4 presents the empirical findings from Milan, Rome, and Naples, comparing the insights from Dual vs. Coverage centrality and evaluating network robustness. Section 5 interprets the implications of these results for urban logistics planning and outlines limitations and future research directions. Finally, Section 6 summarizes the key contributions and recommendations of this study.

2. Related Literature

This literature review is organized into four streams to clarify contributions and limits: (i) empirical/impact studies quantifying costs, time, and emissions of locker use; (ii) classical facility location models (e.g., p-median and variants with capacity or bi-level choice) that optimize distance/cost given candidate sites; (iii) multi-criteria decision-making (MCDM) rankings that blend accessibility, safety, cost, and policy judgments (e.g., AHP/SFAHP); and (iv) network-oriented work using SNA or multilayer formalisms mostly outside lockers but relevant to last-mile resilience. We next summarize each stream, then critically assess drawbacks and open problems that motivate our two-mode, multilayer approach.

The rise of e-commerce has spurred extensive research into last-mile delivery innovations, among which parcel lockers have emerged as a prominent solution. A growing body of literature documents the operational benefits of parcel lockers in urban logistics. By consolidating multiple deliveries at a single secure location, lockers can significantly reduce failed home delivery attempts and enable couriers to serve more customers per trip. Delivery failure rates in home delivery are non-trivial because missed deliveries not only inconvenience consumers but also incur extra costs and emissions due to repeat attempts. Parcel lockers directly tackle this issue by providing guaranteed delivery points, thus virtually eliminating the risk of a failed drop-off. Moreover, because one locker can serve dozens of recipients, delivery routes can be made denser and more efficient. Industry analyses and pilots have reported meaningful improvements; for example, the World Economic Forum estimated substantial savings in delivery cost and emissions from locker adoption at scale. Research case studies align with this view. The authors of [2] deployed a common-carrier locker in Seattle and observed faster deliveries inside residential buildings and positive reception from users. Likewise, various simulation studies in Europe have quantified moderate-to-large environmental gains when lockers replace doorstep deliveries under the right conditions [3,4,5,6,7]. A recent review of locker implementations notes that while lockers were first introduced around 2001–2002 (e.g., by postal operators in Europe and Asia), their adoption has accelerated in the past few years in response to the pandemic-fueled e-commerce boom [1]. Today, major e-retailers and logistics providers worldwide (Amazon, Alibaba, DHL, InPost, etc.) are rolling out expansive locker networks, and municipalities are recognizing lockers as an element of sustainable urban mobility plans.

However, the literature also highlights several nuanced challenges associated with parcel lockers. One key issue is user acceptance and accessibility: lockers only deliver benefits if customers are both willing and able to use them. Multiple studies have identified factors such as convenient access, perceived security, and proximity to one’s home or daily travel routes as critical for encouraging locker use [14,15]. If lockers are sited in inconvenient or unsafe locations—for example, placed far from residential areas or lacking secure 24/7 access—their intended consolidation benefits can be undermined. In such cases, customers might end up driving personal vehicles to retrieve parcels or simply avoid the locker option altogether. Indeed, research cautions that poorly placed lockers can increase overall travel distances (and emissions) by forcing significant detours for couriers or consumers [3]. Another concern is equity of service: recent spatial analyses have examined whether locker networks fairly serve different neighborhoods. For example, a study of Amazon’s lockers in Portland, Oregon, found that many lockers were clustered in central commercial areas, whereas some lower-income and outer suburban communities had significantly fewer lockers available per resident [10]. These findings indicate that, despite the clear systemic advantages of parcel lockers, careful planning and placement are required to ensure broad accessibility and to avoid simply shifting burdens onto end-users. Our work contributes to this discussion by providing a framework to evaluate how well a given locker network connects disparate user zones and by identifying which locations are structurally critical for maintaining accessible service across an entire city.

Given the importance of good placement, numerous studies have addressed the parcel locker location problem using traditional operations research and multi-criteria decision methods. In general, these approaches formulate locker siting as an optimization problem; typically, to minimize overall delivery distance or cost or to maximize coverage of demand, subject to various constraints (e.g., budget or number of lockers to open). A common model is the p-median (or facility location) formulation, where the goal is to select p locker sites such that the sum of distances from customers to their nearest locker is minimized. The authors of [16] adopt this approach in a data-driven study for Shenzhen, China, using taxi trip data to optimally place lockers at transit stations. Due to the large candidate pool (thousands of locations), they introduce a sampling heuristic to solve the p-median efficiently, and their results highlight the benefit of situating lockers at central transit hubs to enable ride-pooling deliveries. Other researchers have enriched location models with additional real-world factors. Capacity constraints are one example. The authors of [17] propose a variant of the locker location problem that considers different locker sizes and heterogeneous customer demand, optimizing not only which locations to open but also the module size at each location. This reflects practical trade-offs in locker deployments, e.g., balancing a few large lockers versus many small ones. Similarly, the authors of [18] formulate a bi-level program for locker placement and capacity planning, capturing both the strategic decision of a planner and the operational response of customers (which locker they choose). Their model tries to anticipate customer preferences, aiming to place lockers where they will attract the most usage while also relieving delivery costs. Very recent works have explored graph neural networks (GNNs) to approximate network-wide shortest-distance structure and enable hazard-aware routing. In particular, [19] proposes a GNN that, after training, approximates single-source shortest distances and supports route recommendation under probabilistic hazards (e.g., flood scenarios), showing strong accuracy with substantial inference-time speedups relative to classical SSSP routines.

Beyond mathematical programming, multi-criteria decision-making (MCDM) techniques have been applied to incorporate qualitative or strategic considerations into locker siting. For instance, the authors of [20] develop a hybrid analytic hierarchy process (AHP) model to rank potential locker locations in Dublin, Ireland. They evaluate each site on multiple criteria, such as population density, safety, accessibility, and implementation cost, by gathering expert judgments, and then derive an overall score using a fuzzy AHP approach. This kind of MCDM reflects the reality that city planners may value criteria other than pure distance efficiency, including community acceptance and urban design factors. In a related vein, the authors of [21] examine locker placement considering both transportation impacts and urban planning perspectives. They emphasize the need for cooperation between logistics firms and municipalities, suggesting multi-level governance approaches to integrate locker networks into city land-use policy.

Overall, the traditional literature on parcel locker placement provides a rich toolkit of optimization models and decision frameworks. These studies have shown how optimal or near-optimal solutions can substantially improve delivery performance; for example, by cutting total distance traveled or ensuring most customers have a locker within a short radius. However, a limitation of many such models is that they focus on static, one-to-one allocations (each customer to the nearest facility) and often yield a solution set of locker sites without examining the interactions among those sites. In other words, classic models might tell us where to put lockers, but not which of those lockers become linchpins of the system or how the network would reconfigure if certain lockers fail or are removed. This is where a network science perspective can complement existing methods: by treating the entire set of lockers and their served areas as an interconnected graph, we can evaluate properties like redundancy, reachability, and criticality that are not directly captured by solitary optimization objectives. In the past decade, multilayer network models have gained prominence as a way to represent complex systems with different interacting components [13,22,23,24,25]. A multilayer (or multi-modal) network allows nodes to belong to different layers or types, with connections both within and across layers. This framework has been applied in domains ranging from social media analysis to transportation systems, because it preserves the inherent heterogeneity of real-world networks (e.g., people vs. events, or bus routes vs. road networks) [26,27,28]. In the context of logistics and urban mobility, multilayer network approaches are gaining traction due to their ability to model interactions across different actor sets or transport modes. For instance, co-modal delivery systems can be represented as two-layer networks: one layer modeling public transit stops and another modeling logistics depots, with inter-layer edges capturing parcel flows between them. Such structures can significantly improve the realism and granularity of the model, enabling planners to assess how parcels transfer from freight networks to passengers’ transit systems. Recent studies demonstrate the power of this perspective: the multilayer formalism has been successfully used to analyze multimodal transport systems, e.g., integrating bus, metro, and pedestrian layers in urban mobility models, and to evaluate freight-transit integration scenarios, where public transport vehicles carry parcels between depots and terminal hubs [29,30,31,32]. These works highlight key benefits, such as more efficient use of existing infrastructure and reduced environmental impact, while also revealing methodological challenges, including transfer modeling, inter-layer weighting strategies, and resilience analysis. By leveraging this multilayer lens, our paper contributes to urban logistics literature by modeling parcel locker systems as two-mode networks and introducing novel centrality metrics, Dual and Coverage centrality, to assess both inter-layer connectivity and the structural resilience of locker placements.

A key set of tools for analyzing such networks comes from Social Network Analysis (SNA), which offers a rich vocabulary for node importance (centrality), community structure, and flow patterns. Centrality measures like degree, betweenness, and closeness have previously been used in transportation research to identify critical nodes or links; for instance, finding the most influential intersections in a road network or the most utilized transfer stations in a transit network [33,34,35]. In freight logistics, some studies have employed network analytics to examine supply chain connectivity and vulnerability. A recent review in [36] provides a comprehensive systematic review of 113 SNA applications in supply chain management, explicitly highlighting the use of centrality measures (degree, betweenness, closeness) to identify vulnerable or influential nodes whose failure can cascade through supply networks. The authors of [37] catalog studies applying centrality in logistics contexts and call for new metrics tailored to supply chain resilience. Further, focused analyses, such as the one in [38], confirm that reliance on highly central nodes can both improve information flow and increase systemic risk, reflecting that “the most connected” is not always “the most important” in a functional sense. These insights align with our findings for parcel lockers, where structural centrality offers a distinct perspective from mere connectivity volume.

In summary, the convergence of multilayer network modeling and logistics is an exciting development that allows researchers to capture complexity beyond what single models or aggregate metrics can offer. Our approach builds on this by explicitly modeling the two-layer structure of the problem (demand and supply) and harnessing SNA metrics to yield actionable insights. This contributes to the literature by demonstrating the value of network science methods in an applied logistics scenario, specifically, showing how they can diagnose network robustness and equity in ways that complement classical optimization results. We posit that as last-mile systems evolve (with increasing integration of crowd-sourced delivery, drones, urban hubs, etc.), such network-oriented analyses will become increasingly important to guide design and policy. By applying and validating these concepts on real city data, our work lays the groundwork for a new perspective on an established problem, highlighting novel strategies to make urban delivery networks both efficient and resilient. Across streams, evidence shows that lockers deliver time/cost/emissions gains when well used [1,2,3,4,5,6,7], but empirical studies are site-specific and give little guidance on where to place lockers or how robust a network remains under failures. Facility location models (e.g., p-median and capacitated/bi-level variants [8,16,17,18]) produce efficient initial deployments but treat facilities largely in isolation, rely on one-to-nearest assignment, and rarely evaluate system connectivity, resilience, or equity; one-mode projections further hide two-mode structure. MCDM rankings (AHP/SFAHP [20,21]) are transparent and policy-tunable but are weight-sensitive, typically static, and align closely with coverage/popularity without testing network-wide cohesion. Network/SNA work in transport and supply chains [33,34,35,36,37] captures bridges and redundancy, yet lockers are sparsely treated; common one-mode projections inflate cliques and lose bipartite constraints, and path-based diagnostics for two-mode locker systems are largely absent. Therefore, key open problems are as follows: (i) siting rules that improve resilience as well as reach; (ii) identifying “hidden bridges” versus high-reach hubs in a two-mode (users–lockers) topology; (iii) robustness evaluation under targeted vs. random failures; (iv) equity/coverage summaries that are reproducible from open data; and (v) plug-in compatibility with observed flows, capacity, and temporal variation.

Table 1. Concise synthesis of locker siting literature: performance signals and recurring drawbacks.

Stream	Typical Objective	Representative Approaches	How They Perform (and Recurring Drawbacks)
(i) Empirical impacts	Measure delivery time, costs, emissions.	Field studies and assessments [1,2,3,4,5,6,7]	Show non-trivial savings and emission cuts when utilization is high; drawbacks: often site-specific; little guidance on where to place lockers; robustness/equity seldom tested.
(ii) Facility location	Min distance/cost, max coverage.	p-median/capacitated/bi-level choice [8,16,17,18]	Produce efficient initial deployments; drawbacks: treat facilities mostly in isolation; rely on one-to-nearest assignment; limited view of system connectivity and failure resilience; projection effects hide two-mode structure.
(iii) MCDM ranking	Blend accessibility, safety, cost, policy.	AHP/(S)Fuzzy AHP, expert weights [20,21]	Transparent and policy-tunable; aligns with coverage/popularity; drawbacks: sensitive to weights; typically static; does not evaluate network-wide cohesion or vulnerability.
(iv) Network	Identify critical nodes/links; resilience.	SNA on transport/supply chains; multilayer modeling [13,33,34,35,36,37]	Captures bridges and redundancy; drawbacks: two-mode lockers sparsely treated; common one-mode projections inflate cliques and lose bipartite constraints.

shows a summary of the approaches discussed in this literature review.

We address these gaps by (1) modeling city-scale locker systems as an open-data, two-mode multilayer network; (2) introducing Dual and Coverage centralities tailored to lockers to separate bridges from hubs; (3) benchmarking against one-mode/weighted baselines with robustness tests (targeted vs. random removals); and (4) translating diagnostics into an executable siting workflow with feasibility screening.

3. Methods

3.1. Multilayer Network Model Formulation

We propose a multilayer network model to represent the parcel locker system as a two-mode (bipartite) network connecting demand zones (or individual customers) with parcel lockers. This model captures the interactions between users and lockers in a flexible way, and it can be adapted to different data granularities (individual or aggregated by area) without altering the core formulation. The network is defined as follows:

• User layer (demand side), consisting of nodes representing e-commerce customers. If individual-level data is available, each customer is a node. If not, customers can be aggregated by geographic zones (e.g., city districts or postal code areas), and each zone node represents the collective customers in that area. Using zones reduces complexity and preserves privacy while still capturing spatial demand patterns. For example, we may use zones such as city neighborhoods or municipalities. Each zone node can be associated with attributes like population or parcel volume demand.
• Locker layer (supply side), consisting of nodes representing the parcel lockers (automated parcel pickup stations). Each locker node is defined by its location (geographic coordinates) and possibly capacity or operator.
• Inter-layer connections, i.e., edges that exist between the user layer and the locker layer (there are no direct user–user or locker–locker edges in the basic bipartite representation). An edge connects a user (or zone) node i to a locker node j if that user (or someone in that zone) has used or can use locker j for parcel deliveries. These edges can be weighted. A natural weighting $w_{ij}$ is the frequency or volume of parcels delivered from zone i to locker j (or the count of distinct customers in zone i who use locker j). An unweighted edge simply indicates a possible usage relationship. For example, if residents of Zone A picked up 500 parcels from Locker X in a given period, we set an edge $(\mathrm{Zone}\mathrm{A},\mathrm{Locker}\mathrm{X})$ with weight $w=500$.

Formally, let Z be the set of zone (or customer) nodes and L the set of locker nodes. We define a bipartite graph $G=(Z\cup L,E)$ where $E\subseteq Z\times L$ consists of edges between zones and lockers. The incidence can be described by a matrix $B=\left[b_{ij}\right]$ of size $\left|Z\right|\times \left|L\right|$, where $b_{ij}>0$ if zone i is connected to locker j (e.g., $b_{ij}=w_{ij}$ could represent parcel flow).

This formulation allows meaningful projections onto single layers by algebraic transformations of the bipartite incidence matrix.

Let

$$B=\left[b_{ij}\right]\in {\mathbb{R}}^{\left|Z\right|\times \left|L\right|},b_{ij}=\left\{\begin{array}{cc}{w}_{ij}>0,\hfill & (z_i,l_j)\in E,\hfill \\ 0,\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

where Z is the set of demand zones and L the set of lockers. The first projection we can obtain is zone–zone projection:

$$P_Z=B{B}^{\top }\in {\mathbb{R}}^{\left|Z\right|\times \left|Z\right|},{\left(P_Z\right)}_{ik}=\sum _{j=1}^{\left|L\right|}{B}_{ij}{B}_{kj},$$

where an edge exists between zones $z_i$ and $z_k$ if ${\left(P_Z\right)}_{ik}>0$. The other projection enabled by this model is locker–locker projection:

$$P_L=B^{\top }B\in {\mathbb{R}}^{\left|L\right|\times \left|L\right|},{\left(P_L\right)}_{jm}=\sum _{i=1}^{\left|Z\right|}{B}_{ij}{B}_{im},$$

where an edge exists between lockers ${\ell }_j$ and ${\ell }_m$ if ${\left(P_L\right)}_{jm}>0$. These projections enable the following:

• Analysis of demand-zone connectivity via $P_Z$;
• Study of facility overlap and redundancy via $P_L$.

In our baseline, we collapse all operators into a single locker layer (common-carrier); if lockers are non-interoperable across operators, the same metrics can be computed per operator by restricting L and B to a given brand, in which case, redundancy is lower and locker criticality/rankings may change.

3.2. On the Choice of a Two-Mode (Bipartite) Network Model

We represent parcel lockers as a two-mode (bipartite) network linking demand zones (or individual customers) to lockers because this formulation preserves the heterogeneity of actors and the semantics of interactions. Collapsing the system into a single layer, whether unweighted or weighted, forces zone–zone or locker–locker ties that are merely artifacts of sharing counterparts, with well-documented distortions for two-mode data: clique inflation, effective degree-squaring, and the loss of asymmetric coupling between demand and supply [39,40,41,42]. In practice, these distortions bias centrality estimates and path structures, altering robustness and coverage conclusions drawn from the network.

A weighted one-mode projection summarizes overlap (e.g., zones sharing lockers) but cannot encode cross-type constraints and feasibility that are intrinsic to parcel locker systems. Capacities, service radii, time-distance thresholds, operator-specific availability, and assignment rules are naturally attached to locker nodes or zone–locker edges; after projection, operationally distinct bipartite configurations can collapse into identical one-mode patterns, obscuring which lockers can actually serve which populations. This loss of identifiability matters for planning and policy: two cities with different zone–locker relations can look indistinguishable once projected.

Formally, information loss is structural: there exist distinct incidence matrices $B\ne \tilde{B}$ that yield the same one-mode summaries $P_Z=B{B}^{\top }$ (and analogously $P_L=B^{\top }B$). Any analysis defined solely on $P_Z$ or $P_L$, therefore, cannot, in general, recover the underlying two-mode relations. By working directly on the bipartite graph, we retain the true two-mode topology, preserve demand–supply asymmetries, and can incorporate operational constraints without ambiguity. As a remark, consider the two incidence matrices $B=\left[\begin{array}{ccc}1& 0& 0\\ 1& 1& 0\end{array}\right],\tilde{B}=\left[\begin{array}{ccc}1& 0& 0\\ 1& 0& 1\end{array}\right].$ Both yield the same zone–zone summary $B{B}^{\top }=\tilde{B}{\tilde{B}}^{\top }=\left[\begin{array}{cc}1& 1\\ 1& 2\end{array}\right],$ yet they encode different zone–locker relations. Analyses defined only on $P_Z$ therefore cannot, in general, recover the underlying two-mode structure.

3.3. Social Network Analysis Metrics

Having formulated the parcel locker system as a network, we next define metrics to analyze the importance of nodes in this multilayer context. Traditional social network analysis (SNA) offers many centrality measures (degree, betweenness, closeness, eigenvector, etc.), but here, we introduce two metrics tailored to our two-layer network: Dual centrality and Coverage centrality. These metrics are designed to capture the influence of a node (particularly a locker) in connecting users and facilitating coverage of service. Both metrics are novel adaptations in the context of parcel locker networks, providing insights that go beyond simple degree counts. Below, we formally define each measure and discuss its interpretation.

3.3.1. Dual Centrality

Dual centrality is a centrality measure for two-mode networks that assigns an importance score to nodes in each layer by considering their mutual reinforcement. In essence, a zone is central if it is connected to many important lockers, and a locker is central if it is used by many important zones. This captures the intuitive “dual” notion that highly influential lockers and user groups confer importance on each other. Our Dual centrality measure extends the concept of eigenvector centrality to a bipartite setting (also known as a two-mode eigenvector centrality or a “Bonacich Dual centrality” approach [9]).

Mathematically, let $C_i^{\left(Z\right)}$ be the centrality score of zone i and $C_j^{\left(L\right)}$ the centrality of locker j. We define them to satisfy the coupled equations:

$$C_i^{\left(Z\right)}={\displaystyle \frac{1}{\lambda }}\sum _{j\in L}{b}_{ij}{C}_j^{\left(L\right)},C_j^{\left(L\right)}={\displaystyle \frac{1}{\lambda }}\sum _{i\in Z}{b}_{ij}{C}_i^{\left(Z\right)},$$

where $b_{ij}$ is the weight of the edge between zone i and locker j (from the incidence matrix B), and $\lambda$ is a scaling constant (the leading eigenvalue). In matrix form,

$${\mathbf{C}}^{\left(Z\right)}={\displaystyle \frac{1}{\lambda }}B{\mathbf{C}}^{\left(L\right)},{\mathbf{C}}^{\left(L\right)}={\displaystyle \frac{1}{\lambda }}{B}^{\top }{\mathbf{C}}^{\left(Z\right)}.$$

Substituting yields ${\mathbf{C}}^{\left(Z\right)}={\displaystyle \frac{1}{{\lambda }^2}}B{B}^{\top }{\mathbf{C}}^{\left(Z\right)}$ and ${\mathbf{C}}^{\left(L\right)}={\displaystyle \frac{1}{{\lambda }^2}}{B}^{\top }B{\mathbf{C}}^{\left(L\right)}$, meaning ${\mathbf{C}}^{\left(Z\right)}$ is an eigenvector of $B{B}^T$; similarly, ${\mathbf{C}}^{\left(L\right)}$ is an eigenvector of $B^{T}B$. In practice, we find the principal eigenvector of $B{B}^T$ to obtain zone centralities and of $B^{T}B$ to obtain locker centralities. By construction, these centralities are positive and mutually consistent: a zone gets a high score if it heavily uses lockers that themselves have high scores, and a locker gets a high score if it is utilized by high-scoring zones.

Dual centrality provides a simultaneous, mutually-reinforced ranking of both user zones and lockers within the bipartite network. Unlike standard eigenvector centrality or PageRank, which are defined for single-layer (one-mode) networks and measure node importance based solely on their connections within a single set, Dual centrality explicitly accounts for the two-mode (bipartite) structure of the parcel locker system. Here, the centrality score of each locker is not just a function of the number or prestige of its direct connections, but also of the collective importance of the user zones it serves, and vice versa. This means that a locker achieves high Dual centrality if it is used by multiple zones that themselves are “important” (i.e., zones with high centrality in terms of their connections to other pivotal lockers), creating a recursive reinforcement across both layers. Conversely, a zone’s centrality is elevated when it relies on lockers that are themselves highly central. As a result, Dual centrality reveals lockers that are structurally indispensable for network cohesion, even if they are not the most frequently used or simply the best-connected in terms of raw degree. This makes Dual centrality particularly powerful for highlighting “hidden hubs” in the system, facilities that underpin robust connectivity among diverse user communities but might be overlooked by conventional centrality metrics. In this sense, Dual centrality uncovers the “core” backbone of the locker network and helps identify both facilities and user zones that are critical for maintaining overall accessibility and resilience, thus offering strategic insights not captured by traditional single-layer metrics.

3.3.2. Coverage Centrality

Coverage centrality is a shortest-path-based centrality metric that evaluates a node’s importance as a bridge connecting other nodes in the network. In classic terms, the Coverage centrality of a node v is defined as the number of distinct pairs of other nodes for which v lies on at least one shortest path between them [43]. It is similar in spirit to betweenness centrality, but instead of summing fractions of paths, it simply counts each pair that is connected through v (hence measuring how many pairs “coverage” is provided by that node). We adapt this concept to the parcel locker network to quantify how well a given locker connects disparate user communities.

In our bipartite context, we focus on Coverage centrality for locker nodes. Consider two distinct user zones a and b. In the two-layer graph $G=(Z\cup L,E)$, these zones may be connected by a path that goes through one or more lockers. If zone a and zone b share a common locker j that they both use, then a shortest path from a to b in the graph is $a\to j\to b$ (two hops, via locker j). In that case, locker j lies on this shortest path. If a and b do not directly share a locker, they might still be connected through a sequence of zone–locker–zone–locker hops; for example, $a\to j\to c\to k\to b$, where c is another intermediate zone, j is used by a and c, and k is used by c and b. In that scenario, locker j is on one of the shortest paths between a and b as well (along with locker k). We say a locker covers a pair of zones if it lies on a shortest path between them in the bipartite network. The Coverage centrality $C_{\mathrm{cov}}\left(j\right)$ of locker j is then

$$C_{\mathrm{cov}}\left(j\right)=\sum _{\begin{array}{c}\{a,b\}\subset Z\\ a\ne b\end{array}}\mathbf{1}\left(d(a,b)=d(a,j)+d(j,b)\right),$$

where

• Z is the set of zone nodes;
• $d(x,y)$ is the shortest path length between x and y in G;
• $\mathbf{1}(·)$ is the indicator function (it is 1 if the condition is true, 0 otherwise);
• the sum is over the unordered sets $\{a,b\}$ to count each pair only once.

In other words, we count how many pairs $\{a,b\}$ satisfy $d(a,b)=d(a,j)+d(j,b)$; that is, where j is on at least one shortest path between a and b. Intuitively, $C_{\mathrm{cov}}\left(j\right)$ counts how many pairs of user communities rely on locker j as a critical intermediary. If multiple shortest paths exist, we still count the pair for j as long as j is on one of the shortest paths (even if other alternate routes also exist). In practice, for efficiency, one can compute Coverage centrality by analyzing the zone-projection network or performing all-pairs shortest paths in the bipartite graph and counting those that go through each locker. For a simpler interpretation, if a locker j is used by k different zones, then any pair of those zones $(a,b)$ has a two-hop connection via j; locker j thus immediately covers $\left({\displaystyle \genfrac{}{}{0pt}{}{k}{2}}\right)$ zone-pairs through direct sharing. Furthermore, locker j might also lie on longer shortest paths for zones that are indirectly connected (as in the example with an intermediate zone c). The Coverage centrality measure will account for both direct and indirect cases through the formal shortest-path definition.

Coverage centrality offers a distinct perspective from traditional metrics by directly measuring how many pairs of user zones depend on a given locker to stay connected within the network. Unlike degree or eigenvector centrality, which count connections or recursively measure importance, Coverage centrality asks, “for how many pairs of zones does this locker sit on a shortest path between them?”. In other words, it captures the bridging function of a locker in facilitating indirect access across the urban area, not just its immediate popularity or prominence. For example, a locker with a high degree might simply serve a densely populated area, but a locker with high Coverage centrality is one whose presence is crucial for linking together otherwise separated communities. If such a locker were removed, many pairs of zones would be disconnected, fragmenting the network structure. This makes Coverage centrality especially powerful for identifying “single points of failure” and evaluating network resilience: a locker with exceptionally high Coverage centrality represents a critical bottleneck, while a more even distribution of coverage scores suggests greater redundancy and robustness. Thus, Coverage centrality is not just a measure of traffic or local influence, but a strategic indicator of how the entire city’s parcel access depends on particular infrastructure nodes. This focus on network-wide shortest paths makes Coverage centrality conceptually and computationally different from standard betweenness, which distributes credit across all paths, whereas Coverage centrality simply counts pairs for which a locker is essential. By prioritizing lockers with high Coverage centrality for upgrades or redundancy, planners can directly target improvements that will most enhance city-wide connectivity and service equity.

3.4. Mathematical Properties of the Two Indicators

We summarize key theoretical properties that ensure the two proposed metrics are well posed, stable, and computationally tractable.

For Dual centrality, let $B\ge 0$ be the $\left|Z\right|\times \left|L\right|$ incidence matrix, $A_L=B^{\top }B$ and $A_Z=B{B}^{\top }$. (i) Well-posedness and positivity: $A_L$ and $A_Z$ are symmetric-positive semidefinite. If the bipartite graph is connected on the locker (resp. zone) side-equivalently, $A_L$ (resp. $A_Z$) is irreducible; then, by the Perron–Frobenius theorem, the largest eigenvalue is simple and admits a strictly positive eigenvector. The resulting locker (resp. zone) Dual centralities are unique up to scaling. (ii) Invariances: for any $\alpha >0$, replacing B by $\alpha B$ leaves the eigenvectors of $A_L$ and $A_Z$ unchanged (eigenvalues scale by ${\alpha }^2$). Rankings are invariant to permutations of nodes. (iii) Stability: let $\tilde{B}=B+\Delta B$ and ${\tilde{A}}_L={\tilde{B}}^{\top }\tilde{B}=A_L+E$. Davis–Kahan bounds imply that the angle between the Perron eigenvectors of $A_L$ and ${\tilde{A}}_L$ is $O(\parallel E{\parallel }_2/({\lambda }_1-{\lambda }_2))$; thus, small perturbations of B produce small changes in the ranking when a spectral gap exists. (iv) Relation to known methods: Dual centrality coincides with the leading right/left singular vectors of B and with the limit of the HITS iteration $u\leftarrow B^{\top }v$, $v\leftarrow Bu$ (with normalization). On a one-mode projection, it reduces to eigenvector centrality on $A_L$ or $A_Z$, but without information loss from projection. (v) Complexity: power iteration on $A_L$ (or the two-step $u\leftarrow B^{\top }\left(Bu\right)$) uses only sparse matrix–vector products; each iteration costs $O\left(\right|E\left|\right)$ and converges linearly at rate ${\lambda }_2/{\lambda }_1$. As a sketch of proof, (i) and (ii) follow directly from Perron–Frobenius and the scaling identity ${\left(\alpha B\right)}^{\top }\left(\alpha B\right)={\alpha }^2{B}^{\top }B$. For property (iii), write $E=B^{\top }\mathsf{\Delta }B+\mathsf{\Delta }{B}^{\top }B+\mathsf{\Delta }{B}^{\top }\mathsf{\Delta }B$ and apply the Davis–Kahan $sin\mathsf{\Theta }$ theorem. In property (iv), the normalized iteration $u^{(t+1)}\propto B^{\top }B{u}^{\left(t\right)}$ is power iteration on $A_L$; $v^{\left(t\right)}\propto B{u}^{\left(t\right)}$ recovers the dual scores on Z. Finally, property (v) uses standard sparse MVM costs. These stability guarantees support replacing potential-access weights with observed or model-based assignments: if two-mode neighborhoods are preserved and re-weightings are bounded, rankings vary smoothly and the hub/bridge separation is retained.

For Coverage Centrality, for a locker j we define

$$C_{\mathrm{cov}}\left(j\right)=\left|\{\{a,b\}\subset Z:d(a,b)=d(a,j)+d(j,b)\}\right|,$$

i.e., the number of unordered zone pairs whose at least one shortest path passes through j. (i) Bounds and normalization: one has $0\le C_{\mathrm{cov}}\left(j\right)\le \left({\displaystyle \genfrac{}{}{0pt}{}{\left|Z\right|}{2}}\right)$; moreover, $C_{\mathrm{cov}}\left(j\right)\ge \left({\displaystyle \genfrac{}{}{0pt}{}{{deg}_Z\left(j\right)}{2}}\right)$ from the length-2 paths induced by zones directly sharing j. For cross-city comparability, we use the normalized value $C_{\mathrm{cov}}\left(j\right)/\left({\displaystyle \genfrac{}{}{0pt}{}{\left|Z\right|}{2}}\right)$. (ii) Invariances: the score is invariant under node relabeling and under any strictly monotone transformation of edge lengths that preserves the set of shortest paths (hence the coverage relation). (iii) Relation to betweenness: let $BC\left(j\right)={\sum }_{a<b}{\sigma }_{ab}\left(j\right)/{\sigma }_{ab}$ be the (unnormalized) betweenness, where ${\sigma }_{ab}$ is the number of shortest a-b paths and ${\sigma }_{ab}\left(j\right)$ those that traverse j. Then, $BC\left(j\right)\le C_{\mathrm{cov}}\left(j\right)$, with equality on trees (unique shortest paths). Coverage counts how many pairs rely on j (pair count), and betweenness measures how much of each pair’s geodesic flow traverses j (path share). (iv) Monotonicity: adding an edge incident to j cannot decrease $C_{\mathrm{cov}}\left(j\right)$. Adding edges elsewhere can only decrease it if and only if they create strictly shorter a-b routes that bypass j, a desirable sensitivity to added redundancy. (v) Complexity: in the unweighted case, a Brandes-style dynamic program restricted to zone sources evaluates $C_{\mathrm{cov}}$ in $O\left(\right|Z\left|\right|E\left|\right)$ time and $O\left(\right|E\left|\right)$ memory; with positive weights, Dijkstra-based variants yield $O\left(\right|Z\left|\right|E|log|V\left|\right)$. As a sketch of proof, properties (i) and the local lower bound follow since any two neighbors of j form a length-2 shortest path via j and at most $\left({\displaystyle \genfrac{}{}{0pt}{}{\left|Z\right|}{2}}\right)$ pairs can be covered. Property (ii) is immediate because coverage depends only on membership in the shortest-path set. For (iii), each pair contributes ${\sigma }_{ab}\left(j\right)/{\sigma }_{ab}\le 1$ to betweenness but contributes 1 to coverage whenever ${\sigma }_{ab}\left(j\right)>0$, with equality when ${\sigma }_{ab}\equiv 1$. Property (iv) follows by comparing distances before/after the edge update and noting that only strictly shorter bypasses can remove coverage. Finally, (v) adapts Brandes’ predecessor DAG and dependency accumulation to record whether j lies on some shortest path from each source; weighted complexities follow by replacing BFS with Dijkstra. Because $C_{\mathrm{cov}}$ is driven by geodesic adjacency, any weighting that preserves zone–locker adjacency (e.g., replacing population with observed counts on the same edges) leaves its qualitative conclusions essentially unchanged.

3.5. Computational Complexity of the Proposed Metrics

Let $V=Z\cup L$ be the node set ($\left|V\right|=\left|Z\right|+\left|L\right|$) and $E\subseteq Z\times L$ the bipartite edges. We store the incidence $B\in {\mathbb{R}}^{\left|Z\right|\times \left|L\right|}$ in sparse CSR/CSC and avoid forming dense projections.

3.5.1. Dual Centrality

Locker (resp. zone) scores are the Perron eigenvectors of $A_L=B^{\top }B$ (resp. $A_Z=B{B}^{\top }$). We compute them with power iteration using the two-step multiplication $u\leftarrow B^{\top }\left(Bu\right)$ (and symmetrically on Z), which performs only sparse MVMs. Each iteration costs $O\left(\right|E\left|\right)$ time and $O\left(\right|V|+|E\left|\right)$ space; convergence is linear with rate ${\lambda }_2/{\lambda }_1$, hence total time

$$T_{\mathrm{Dual}}=O\left(\left|E\right|T_{\epsilon }\right),T_{\epsilon }=O\left({\displaystyle \frac{log(1/\epsilon )}{log({\lambda }_1/{\lambda }_2)}}\right),$$

where $\epsilon$ is the stopping tolerance.

3.5.2. Coverage Centrality

For each zone source $a\in Z$, we build the shortest-path DAG on the bipartite graph and mark lockers $j\in L$ that lie on at least one geodesic to any $b\in Z$ (Brandes-style dependency accumulation). In the unweighted case (BFS per source), the total cost is

$$T_{\mathrm{Cov}}^{\mathrm{unw}}=O\left(\right|Z\left|\right|E\left|\right),\mathrm{space}O\left(\right|E\left|\right).$$

With positive weights (Dijkstra per source with binary heaps),

$$T_{\mathrm{Cov}}^{\mathrm{w}}=O\left(\right|Z\left|\right|E|log|V\left|\right),\mathrm{space}O\left(\right|E\left|\right).$$

A cheap lower bound $C_{\mathrm{cov}}\left(j\right)\ge \left({\displaystyle \genfrac{}{}{0pt}{}{{deg}_Z\left(j\right)}{2}}\right)$ is computable in $O\left(\right|E\left|\right)$ time and can be used as a screen.

3.5.3. Remarks

All kernels are near-linear in $\left|E\right|$ per iteration/source and never require materializing $A_L=B^{\top }B$ or $A_Z=B{B}^{\top }$. On our spatial bipartite graphs (sparse, small effective diameter) these bounds are tight in practice. When needed, weighted variants replace BFS with Dijkstra in the Coverage centrality kernel, leaving other costs unchanged. The asymptotic time and space costs for all kernels (sparse implementations) are summarized in

Table 2. Asymptotic complexity (sparse implementation).

Kernel	Time	Space
Dual centrality (power iter.)	$O\left(\right|E\left|T_{\epsilon }\right)$	$O\left(\right|V|+|E\left|\right)$
Coverage (unweighted)	$O\left(\right|Z\left|\right|E\left|\right)$	$O\left(\right|E\left|\right)$
Coverage (weighted)	$O\left(\right|Z\left|\right|E|log|V\left|\right)$	$O\left(\right|E\left|\right)$

.

3.6. Flow-, Capacity-, and Time-Aware Variants

Our baseline uses open data and treats $w_{ij}$ as a potential-access weight (population of zone i within radius of locker j). When richer inputs are available, the same bipartite formulation $B=\left[w_{ij}\right]$ extends as follows:

• Observed parcel flows. Replace $w_{ij}$ with observed zone–locker counts $F_{ij}$ (e.g., parcels per period). Dual and Coverage centralities operate identically on the weighted B.
• Locker capacity. Let ${\mathrm{cap}}_j$ be the effective throughput (parcels per period) of locker j and ${\lambda }_j={\sum }_i{w}_{ij}$ the incoming load. A simple saturation factor

  $$s_j=min\left\{1,\frac{{\mathrm{cap}}_j}{{\lambda }_j+\epsilon }\right\},w_{ij}^{\prime }=w_{ij}{s}_j,$$

  downweights overloaded lockers; alternatively, use a penalty $\varphi \left({\rho }_j\right)$ with ${\rho }_j={\lambda }_j/{\mathrm{cap}}_j$ (e.g., $\varphi \left(\rho \right)=e^{-\gamma max(0,\rho -1)}$). Centralities and robustness are then computed on $B^{\prime }=\left[w_{ij}^{\prime }\right]$. Sites with ${\rho }_j>1$ are flagged for upgrades in the planning workflow.
• Temporal usage. Build time-sliced networks $B\left(t\right)$ (e.g., hour/day/season). Compute centralities and robustness per slice to obtain $C_j^{\left(L\right)}\left(t\right)$ and summary statistics such as ${\overline{C}}_j^{\left(L\right)}={\mathbb{E}}_t\left[C_j^{\left(L\right)}\left(t\right)\right]$ or worst-case metrics (e.g., ${min}_t{\mathrm{AUC}}_k\left(t\right)$). Selection can use a temporal aggregate (mean or $\alpha$-quantile) of the policy mix $S_{\alpha }$ introduced in Section 5.
• Estimating flows when unpublished. If $F_{ij}$ are unavailable, one may estimate them via a gravity/logit assignment, $F_{ij}\propto {\mathrm{pop}}_{i}exp(-\beta d_{ij})exp\left({\theta }^{\top }{X}_j\right)$, where $X_j$ encodes attributes (e.g., transit proximity, hours).
• Behavioral choice models. When stated or revealed-preference data are available, zone→locker weights can be generated via a discrete-choice model. Let $U_{ij}={\beta }_d{d}_{ij}+{\beta }_t{t}_{ij}+{\beta }_h{\mathrm{hours}}_j+{\beta }_s{\mathrm{safety}}_j+{\beta }_a{\mathrm{amenities}}_j+{\epsilon }_{ij}$ denote the utility of locker j for residents in zone i (attributes illustrative). A multinomial (or nested) logit yields $p_{ij}=exp\left(U_{ij}\right)/{\sum }_{m\in L_i}exp\left(U_{im}\right)$ and flows $F_{ij}=D_i{p}_{ij}$ with $D_i$ demand in i. Capacity-aware variants include a congestion term, e.g., $U_{ij}\leftarrow U_{ij}+\gamma \psi \left({\rho }_j\right)$ with ${\rho }_j={\lambda }_j/{\mathrm{cap}}_j$, ${\lambda }_j={\sum }_i{F}_{ij}$, and $\psi (·)$ monotone decreasing, iterated to fixed point. Set $B=\left[w_{ij}\right]$ with $w_{ij}=F_{ij}$ (or its capacity-saturated $w_{ij}^{\prime }$) and recompute centralities/robustness unchanged. Agent-based models (ABMs) can likewise generate time-sliced $B\left(t\right)$ by simulating individual agents’ daily activity chains and locker choices (using the same utility). Aggregating $F_{ij}\left(t\right)$ over time windows yields $B\left(t\right)$ for temporal Dual/Coverage analyses; summary scores can be formed by means or worst-case across t.

In the absence of operator data, we use potential access as an open-data proxy: an edge $(i,j)$ exists when zone i can reach locker j within 500 m (walkable network distance), and $w_{ij}$ is proportional to the resident mass in i. This upper-bounds feasible demand and foregrounds the two-mode topology (who can reach whom), which drives our structural findings. Two properties mitigate the lack of flows: (i) Coverage centrality is adjacency-driven and lower-bounded by locker degree on sparse, locally clustered graphs; (ii) Dual centrality (leading singular vectors of B) is stable under bounded re-weightings when a spectral gap exists. Hence, replacing “population within 500 m” with observed assignments $F_{ij}$ or gravity/logit weights typically rescales B without altering which lockers act as hubs vs. bridges; magnitudes may shift, but qualitative conclusions persist. Our code accepts B from observed flows, and capacity saturation can be applied via $w_{ij}^{\prime }=w_{ij}{s}_j$.

3.7. Experimental Plan

The experimental plan was designed to provide a comprehensive and reproducible comparison of parcel locker network structure and centrality-based selection strategies across three major Italian cities. Our approach consisted of the following steps:

• Dataset construction. For Milan, Rome, and Naples, we construct high-resolution grid-based bipartite networks, using open demographic data and open-source locker locations.
• Network Characterization. We compute key topological properties of each multilayer network, including node counts, average degrees, densities, and spatial patterns.
• Centrality Metrics. For each network, we calculate both Dual centrality and Coverage centrality for lockers, analyzing their distributions and spatial patterns.
• Vulnerability Analysis. We assess robustness under (i) random failures (uniform without replacement) and (ii) targeted removals by each ranking (Dual, Coverage, PageRank, betweenness). After each removal, we track LCC share, pair reachability, average path length, and efficiency; robustness is summarized via normalized ${\mathrm{AUC}}_k$ up to $k\in \{5,10,15,20\}$.
• Comparative Evaluation. We compare locker rankings across Dual, Coverage, PageRank, and betweenness (overlap@k, Spearman/Kendall, partial correlations controlling for degree), and benchmark robustness via ${\mathrm{AUC}}_k$; statistical tests use paired Wilcoxon with Holm–Bonferroni correction.
• Evaluation and Comparison with Baselines. To highlight the practical relevance of our approach, we directly compared our network centrality metrics with classic centrality measures and multi-criteria methods. Specifically, we analyzed how the top-ranked lockers identified by each method overlapped and compared the results.

3.8. Baselines and Comparative Protocol

We evaluate whether operating on the two-mode topology yields more reliable structural inferences than single-layer/weighted alternatives under identical decision budgets. As baselines, we derive one-mode weighted projections $P_Z=B{B}^{\top }$ (zone–zone) and $P_L=B^{\top }B$ (locker–locker) from the incidence matrix B and compute degree/strength, weighted betweenness, eigenvector, and PageRank on each. Because zone-based rankings do not directly select facilities, we map zone scores to lockers through their bipartite neighborhood using both max and sum aggregators. We also include a coverage-driven multi-criteria baseline (SFAHP, when available) built on the same spatial inputs, together with two naïve references (random top-k and bipartite degree on B). Our methods under test are Dual centrality and Coverage centrality as defined previously; all methods receive the same graph, weights, and service radius, and return a ranking over lockers.

The comparison is conducted city by city to avoid cross-city confounding and uses identical top-k budgets ($k\in \{5,10,15,20\}$) for all methods. To assess robustness, we perform targeted removals by deleting lockers in ranking order and track the drop in the largest connected component, the fraction of reachable zone pairs, the average path length, and the network efficiency; performance is summarized via fragmentation curves and area-under-curve statistics. Agreement and divergence among rankings are quantified through overlap@k ($|A\cap B|/k$), as well as Spearman’s $\rho$ and Kendall’s $\tau$ between per-locker scores, including partial correlations controlling for degree. Statistical evidence is assessed with pooled one-sided Wilcoxon signed-rank tests across cities; given the small sample, we report effect sizes and unadjusted p-values. Implementation relies on weighted Dijkstra distances and Brandes’ algorithm for betweenness; eigenvector and PageRank use sparse power iteration (tolerance ${10}^{-8}$, maximum 1000 iterations).

3.9. Dataset Description

We built three city-level datasets (Milan, Rome, Naples) entirely from open sources by combining official geography/demography with open points of interest. For each city, we import ISTAT municipal boundaries and resident population (Com01012025_WGS84) and generate a 100 m grid covering the urban area. Population is allocated proportionally to grid-area intersections to preserve privacy while retaining spatial detail. We then query OpenStreetMap (Overpass) for parcel lockers, locker vending machines, and post offices, reproject the points to a metric CRS, and connect each grid centroid to all lockers within 500 m. Consequently, all experiments, including locker removals, assume instantaneous local rerouting within the policy radius: when a locker is deleted, a demand cell retains edges to any surviving lockers within 500 m. The resulting bipartite incidence matrix B has one mode for demand cells and one for lockers; nonzero entries encode potential access weighted by cell population. This standardized workflow yields three open, reproducible, and structurally comparable datasets that capture resident-locker relations at city-block resolution and support the multilayer analysis that follows.

We used a regular 100 m grid to aggregate residents because it approximates the urban block scale in European cities, preserves intra-neighborhood variation, and keeps the bipartite graph sparse. In our datasets, this yields average zone degree ≈1–1.2 and very low bipartite density (

Table 3. Key multilayer network characteristics for each Italian city dataset.

Multilayer Network Characteristic	Milan	Rome	Naples
Number of demand zones	10,776	15,545	3446
Number of locker nodes	169	219	48
Average zone degree	1.22	1.10	1.08
Average locker degree	77.70	78.29	77.31
Bipartite density	0.0072	0.0050	0.0224
Zone projection density	0.0077	0.0052	0.0233
Locker projection density	0.0087	0.0034	0.0142

), ensuring that SNA scores are not driven by clique inflation. From a spatial analysis standpoint, this choice balances the modifiable areal unit problem (MAUP) [44,45]: very coarse zones obscure local access, whereas very fine zones escalate $\left|Z\right|$ and can inflate the number of zone–locker edges without adding behavioral signal. A 500 m network-distance radius (roughly a 5–7 min walk) is widely used as an access threshold in urban transport and land use (typical walk-to-transit ranges are 400–800 m) [46,47,48]. We compute $d_{ij}$ as street-network distances (Dijkstra), not straight-line. Two design choices reduce sensitivity to zone size: (i) path-based scores use a normalized form; (ii) edges carry demand weights, so subdividing a zone does not mechanically up-weight lockers unless the subdivision adds genuinely new accessibility.

We rely on the most recent ISTAT release (2025) and an OSM snapshot retrieved contemporaneously with the analysis; processed datasets and scripts are archived with the code for full reproducibility. Preliminary network statistics (Table 3) show 10,776/15,545/3446 demand cells and 169/219/48 lockers in Milan/Rome/Naples, respectively, with very low bipartite density (<0.03) and average zone degree around 1–1.2, confirming sparsity and locality of access. Preprocessing includes geometry reprojection and validation, removal of out-of-boundary or invalid points, de-duplication of coincident POIs, and coordinate consistency checks. Missing OSM attributes (e.g., capacity) are not used by our structural analysis; zero-population cells carry zero weight. Uncovered cells (no locker within 500 m) are retained and can be explicitly counted in accessibility analyses; in this paper, we focus on robustness.

This experimental plan ensures that findings on locker criticality, network resilience, and metric comparison are not artifacts of arbitrary modeling decisions.

4. Results

4.1. Multilayer Network Characteristics

Table 3 summarizes the structural properties of the multilayer (bipartite) networks built for Milan, Rome, and Naples using our reproducible grid-based methodology. Overall, we observe a clear urban scaling effect: Rome presents the highest number of demand zones (over 15,500) due to its larger surface and administrative fragmentation, followed by Milan (over 10,700 zones), and Naples (about 3400 zones). The number of locker nodes roughly reflects each city’s population and coverage, with Rome again leading and Naples being the smallest among the three. When it comes to connectivity, all three cities show very low average zone degrees (around 1–1.2), meaning that, on average, each 100 m cell is connected to just one or two nearby lockers. This is a direct consequence of both the granularity of our grid and the actual locker distribution, and it highlights how sparse and local these access points are in Italian cities. Conversely, average locker degree is much higher (about 77–78 in all cases), since each locker node is “claimed” by multiple overlapping demand cells within the buffer radius, especially in denser or more centrally located areas. The bipartite density (i.e., the ratio of realized to possible links in the user–locker network) remains very low overall (<0.01), except in Naples, where the combination of fewer zones and slightly higher overlap results in a somewhat denser structure. Projection densities (both zone and locker) are similarly small, indicating that the projected (single-layer) user–user and locker–locker networks are also sparse. This sparsity is natural in such spatial systems, where connections emerge mostly due to geographic proximity rather than dense cross-linking. In short, these network characteristics reveal that Italian parcel locker systems are highly localized, with many demand cells but relatively few lockers serving each one. The approach flexibly adapts to different city shapes and locker distributions, making it a solid foundation for downstream SNA analyses.

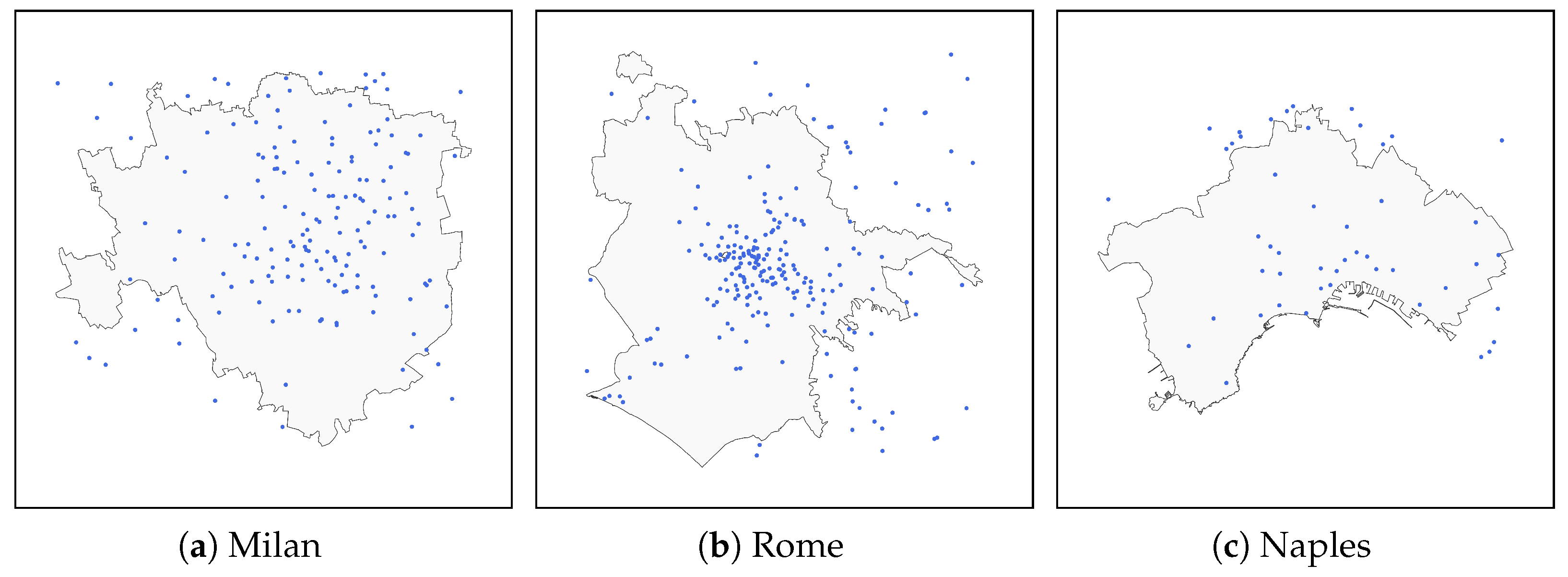
To complement the quantitative network statistics, Figure 1a–c visually depict the spatial distribution of parcel lockers (blue dots) overlaid on the administrative boundaries of Milan, Rome, and Naples, respectively. These maps clearly highlight several key features already anticipated by the tabular results. First of all, in all cities, lockers are heavily clustered in and around the city center, while peripheral zones and administrative boundaries show a much sparser distribution (with some cells not covered at all). Second, the buffer method ensures that even with a limited number of lockers, a substantial fraction of the territory falls within the catchment area of at least one facility. However, especially in Naples and certain suburban areas of Rome, some demand cells remain relatively isolated. Finally, locker placement visually follows the population density and city shape. For example, Milan shows a fairly even “radial” coverage, Rome is more polycentric, while Naples is more elongated and coastal, with locker clusters following the built environment. Overall, these spatial plots make the sparsity and local character of the locker networks immediately apparent, as well as the dependence on actual locker locations, factors that will significantly affect centrality and coverage metrics discussed in the following sections.

4.2. Analysis of Proposed Centrality Metrics

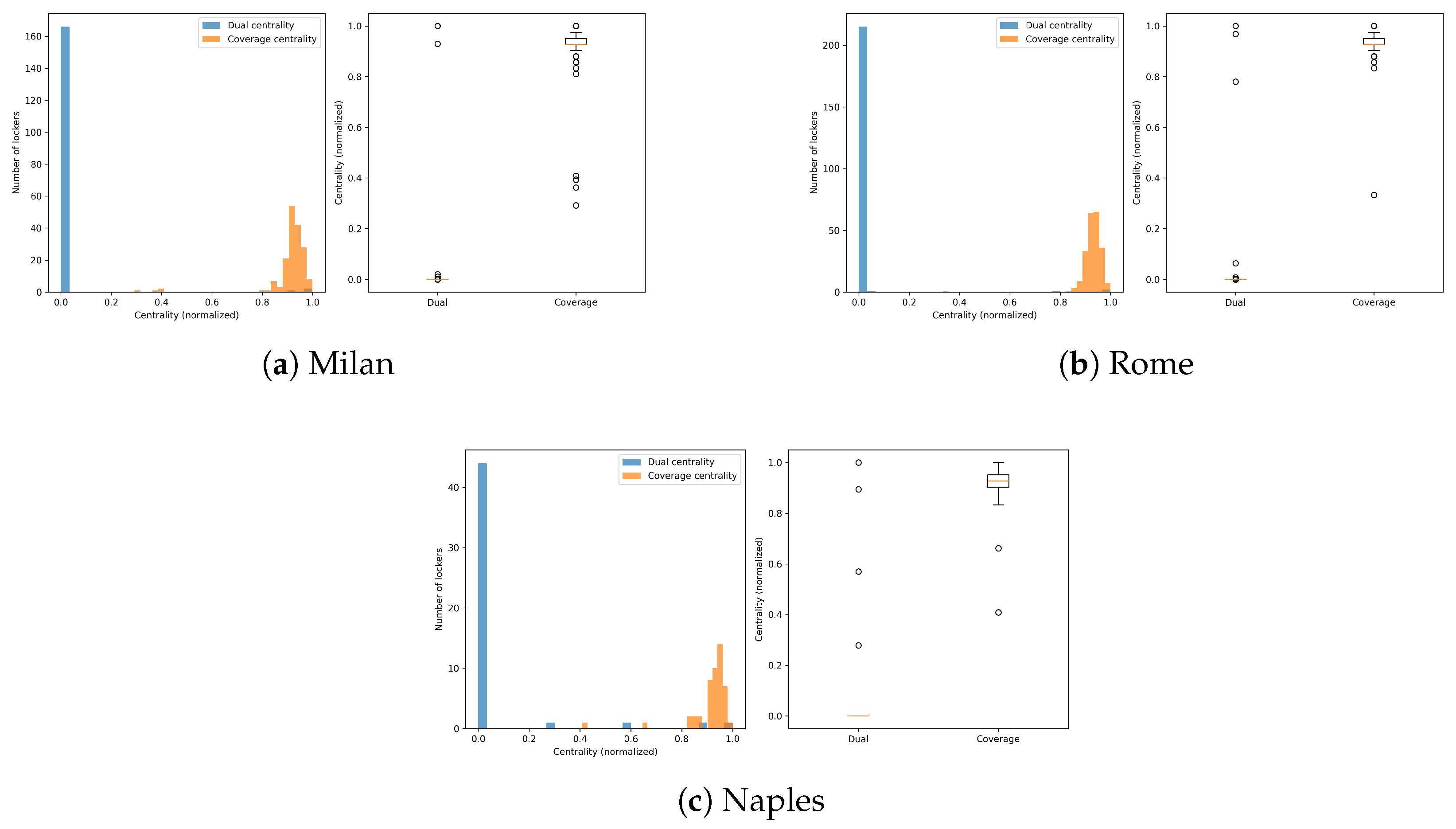
In this section, we analyze both Dual centrality and Coverage centrality for each locker in Milan, Rome, and Naples. Note that in all experiments, Coverage centrality is computed on the bipartite graph with unweighted hop distances (zone–locker edges of unit length); Dijkstra-weighted distances are used only for one-mode baselines (e.g., betweenness/PageRank on $P_L$). Figure 2 displays the distributions of these centrality scores, using both histogram and boxplot representations for each city. As shown in the left panels of the figure, the vast majority of lockers exhibit very low Dual centrality, with their scores clustering sharply near zero. This confirms that most lockers serve relatively peripheral or redundant roles in the network, being used by only a few demand zones or by zones that themselves are not central. In all three cities, only a handful of lockers emerge with high Dual centrality. These outliers represent the pivotal infrastructure points that link multiple high-demand user zones and therefore play a key role in maintaining the network’s cohesion. Coverage centrality, by contrast, shows a distinctly different pattern. While most lockers still have moderate to low coverage, a nontrivial subset of lockers attains very high Coverage centrality values (normalized close to one). This reflects the presence of strategic lockers that act as essential connectors between large numbers of zone pairs, i.e., they are traversed on the shortest paths between many demand cells, thus functioning as structural “bridges” in the system. The distribution is highly skewed, with a heavy tail: in each city, only a few lockers are responsible for a disproportionate share of network connectivity among users. The boxplots on the right further highlight this disparity: Dual centrality values are tightly concentrated at the lower end, with occasional outliers representing the key “core” lockers. Coverage centrality, on the other hand, displays greater variance and a visibly higher median, indicating that a relatively larger fraction of lockers contribute meaningfully to overall network coverage, even though the most critical coverage is still provided by a minority of nodes. This dual characterization reinforces the complementary nature of the two metrics: Dual centrality is highly selective, pinpointing the absolute most important nodes by mutual reinforcement, whereas Coverage centrality is more sensitive to redundancy and spatial overlap in service provision. Together, these plots reveal that the locker networks in all three Italian cities are strongly hierarchical and highly localized: most lockers are marginal, but a small elite subset is truly essential to ensuring connectivity and robustness of parcel access across the urban area.

To further enrich this quantitative and spatial picture, Figure 3 presents a detailed cartographic view of the most central lockers in each city, overlaying the top-five lockers by Dual and Coverage centrality on the urban context. These visualizations offer immediate insight into the functional geography of parcel access across Milan, Rome, and Naples. Notably, the top-ranked lockers (according to either metric) tend to cluster around areas of high urban density, major transport corridors, and prominent transit nodes. This spatial selection aligns well with intuition: lockers that act as pivotal bridges between multiple demand zones, or that provide the shortest paths connecting distant parts of the city, are typically located at infrastructural or demographic hubs. The Dual centrality highlights those lockers that are most deeply embedded in the core of the network, acting as essential connectors for the entire system’s cohesion. Coverage centrality, on the other hand, often identifies lockers positioned at strategic edges or crossroads, ensuring robust connectivity even towards the urban periphery. Visual inspection of the maps also reveals interesting differences between cities. In Milan, the top lockers are well distributed around the radial and dense central districts, reflecting the city’s compact form and multimodal transport axes. Rome’s most central lockers, by contrast, cluster around the historic core and a few suburban transfer points, in line with its polycentric and administratively fragmented urban structure. Naples, with its more linear, coastal form, sees the highest-centrality lockers positioned both near the waterfront and at gateway points linking different urban segments. Across all cases, these maps make clear that network structure and city morphology jointly shape which lockers emerge as the most critical from a centrality perspective.

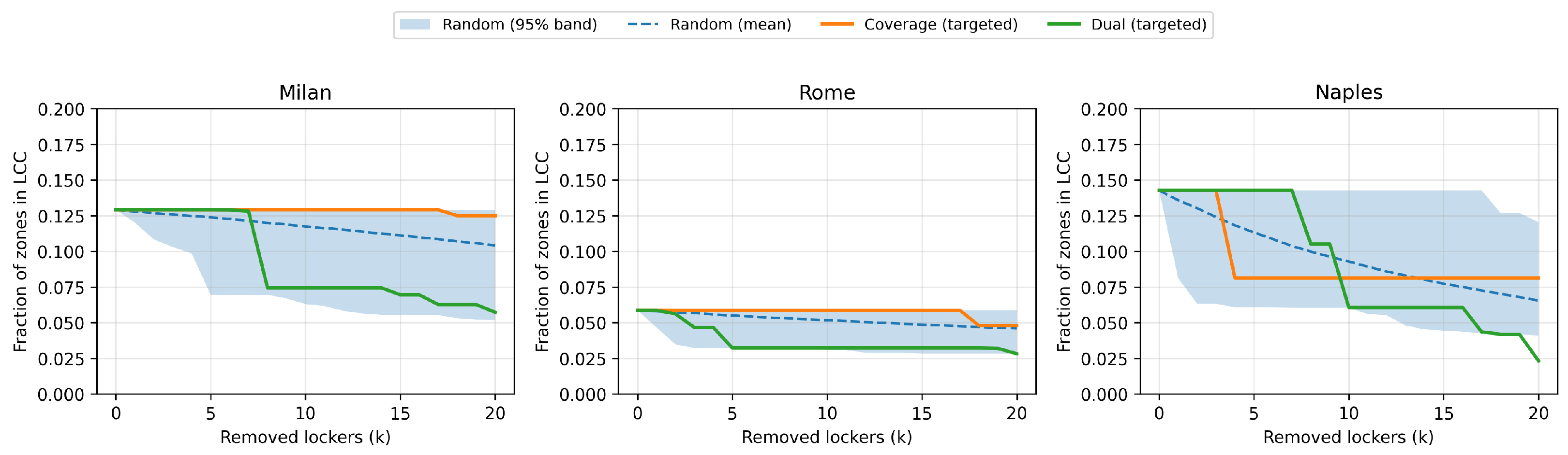
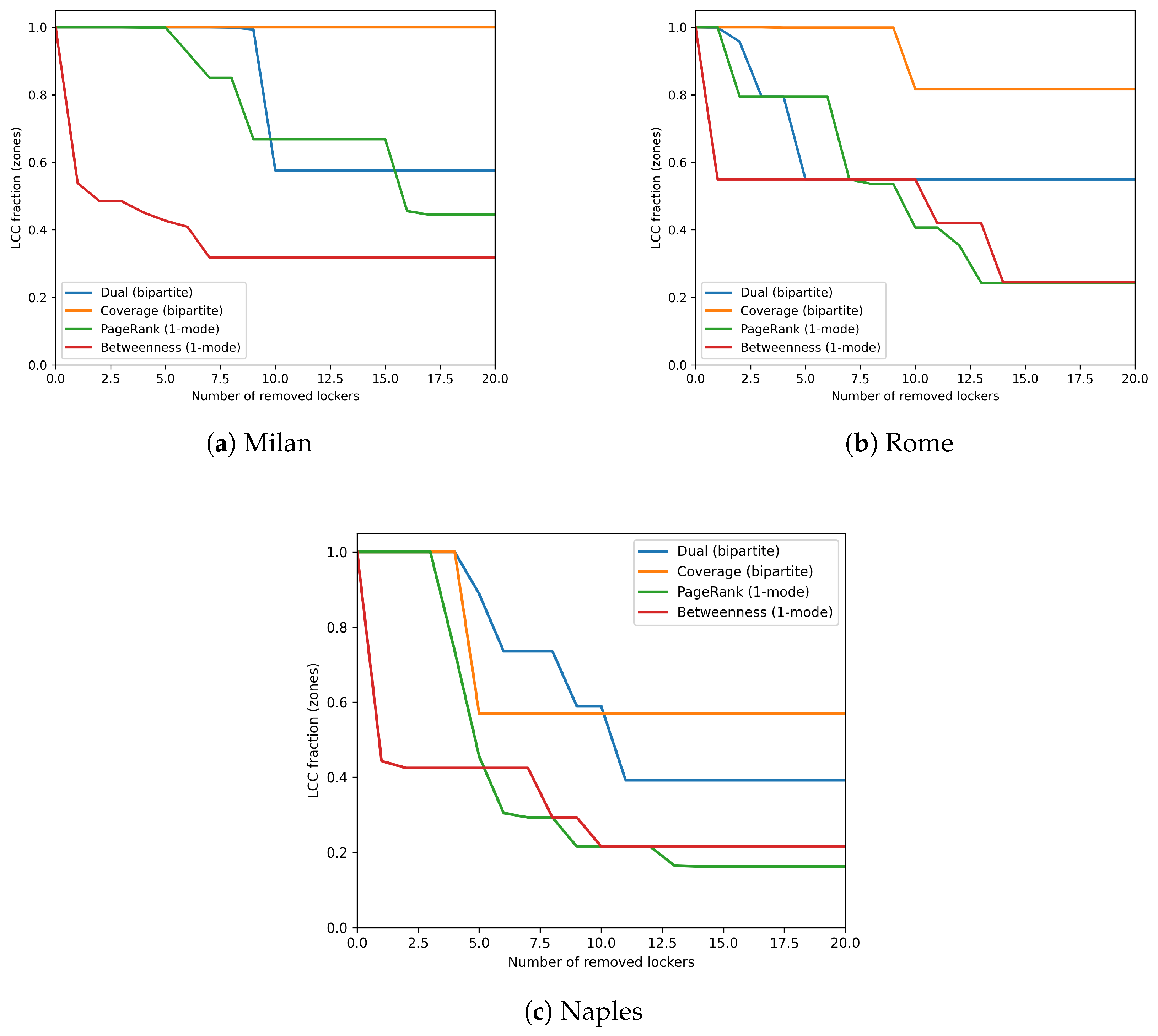
To assess the resilience of parcel locker networks under targeted disruption, we performed a vulnerability analysis in which lockers were sequentially removed according to their Coverage centrality ranking. Figure 4 shows, for each city, how fragmentation evolves as increasingly many top-coverage lockers are removed. Across all three cases, targeting high-reach hubs does not precipitate an immediate breakdown of global connectivity. In Milan, removing the first few hubs produces only a modest rise in the number of small components, while the largest connected component (LCC) remains nearly unchanged up to an inflection point, evidence of substantial local redundancy around dense cores. Rome exhibits a similarly buffered response: fragmentation increases gradually, and the LCC stays high until larger removal budgets, consistent with its polycentric structure and multiple alternative paths. Naples is more sensitive: after the first two to three removals, the curves show a steeper LCC decline and a visible proliferation of small, isolated clusters, in line with its elongated morphology and sparser redundancy. Overall, the curves indicate that coverage-oriented hubs concentrate immediate access yet are embedded in neighborhoods that provide short detours; their removal mainly trims peripheral reach rather than shattering the backbone. This points to a practical design rule: combine broad-reach siting with explicit hardening of bridge-like lockers (identified by Dual centrality), add backup options in morphologically constrained corridors, and diversify placement where the curves exhibit early, steep drops.

Finally, to complement the targeted-removal analysis, we simulate random failures by deleting lockers uniformly at random (without replacement) for $k\in \{5,10,15,20\}$. For each city and for each k, we run $R=1000$ Monte Carlo replicates, record after every removal the fraction of demand zones that remain in the largest connected component (LCC), and summarize robustness with the (normalized) area under the LCC curve up to k removals (${\mathrm{AUC}}_k$). As a reference, we display the Monte Carlo mean together with the 2.5–97.5% quantile band. Statistical significance is assessed with a one-sided Monte Carlo test that compares the targeted curve (Coverage or Dual centrality) against the random baseline,

$$p={\displaystyle \frac{1+\#\{r:{\mathrm{AUC}}_k^{\left(r\right)}\le {\mathrm{AUC}}_k^{\mathrm{targeted}}\}}{R+1}},$$

which estimates the probability that random failures are at least as damaging as the targeted attack. We also report the effect size $\mathsf{\Delta }{\mathrm{AUC}}_k={\mathrm{AUC}}_k^{\mathrm{targeted}}-\mathbb{E}\left[{\mathrm{AUC}}_k^{\mathrm{rand}}\right]$.

Figure 5 overlays, for each city, the random-failure envelope (mean ±95% band over $R=1000$ runs) and the targeted curves (Coverage/Dual). Two patterns emerge. First, targeting lockers ranked by Dual centrality appears more damaging than random in Milan and Rome, with marginal evidence ($\mathsf{\Delta }{\mathrm{AUC}}_{20}=-0.025$, $p\approx 0.072$; $-0.015$, $p\approx 0.059$). This is indicative evidence that Dual centrality pinpoints vulnerability-critical bridges. Second, targeting top lockers by Coverage centrality is not worse than random in Milan and Rome ($\mathsf{\Delta }{\mathrm{AUC}}_{20}=+0.011$ and $+0.005$; $p=0.914$ and $0.652$), indicating that high-reach hubs are largely redundant for global cohesion. In Naples, both strategies are statistically indistinguishable from random (Coverage: $\mathsf{\Delta }{\mathrm{AUC}}_{20}=-0.004$, $p=0.456$; Dual: $\mathsf{\Delta }{\mathrm{AUC}}_{20}=-0.004$, $p=0.462$), which we attribute to the city’s elongated, fragmented morphology and the wider random envelope.

Overall, these results confirm the complementary roles of the two metrics: Dual centrality surfaces structurally critical connectors whose failure fragments access, whereas Coverage centrality highlights popular hubs whose removal has limited impact on system-wide connectivity.

4.3. Comparative Robustness Across Selection Strategies

To directly compare our two-mode formulation with single-layer alternatives, we stress-test the network by targeted removals of lockers following each method’s ranking. Intuitively, a ranking is more robust if the network of demand zones remains largely connected even after the top-k lockers it prioritizes are removed. We track the fraction of zones in the largest connected component (LCC) as removals proceed; higher curves thus indicate better robustness of the residual user network. Figure 6 shows the resulting fragmentation curves for the three cities, while

Table 4. Comparative robustness under targeted removal.

City and k	Bipartite (Dual)	Bipartite (Coverage)	One-Mode (PageRank)	One-Mode (Betweenness)
Milan, $k=10$	0.978	1.000	0.983	0.517
Rome, $k=10$	0.707	0.990	1.000	0.572
Naples, $k=10$	1.000	0.763	0.492	0.436
Pooled p (Wilcoxon)	[0.392] vs. PR	[<0.05] vs PR	—	—

summarizes a normalized area-under-curve (AUC, ↑) up to $k=10$ removals (trapezoidal rule) and pooled one-sided Wilcoxon tests against the 1-mode PageRank baseline.

In Milan, bipartite Coverage attains the highest AUC (1.0), with an almost perfectly flat curve up to $k=20$; bipartite Dual and 1-mode PageRank closely follow (0.978 and 0.983, respectively), while 1-mode betweenness is clearly more fragile (0.517). The flat Coverage curve indicates that the lockers it prioritizes concentrate immediate reach within already well-interconnected clusters; their removal barely affects global zone connectivity, revealing that these are high-reach but structurally redundant sites. In Rome, a polycentric city, 1-mode PageRank slightly leads (AUC $=1.0$), and bipartite Coverage is nearly indistinguishable (0.990), whereas Dual scores lower (0.707), and betweenness is the weakest (0.572). Here, PageRank and Coverage tend to select lockers embedded in dense cores with multiple alternative paths; by contrast, Dual surfaces bridge-like sites that actually hold communities together, so removing them causes steeper LCC drops, useful diagnostic information about where resilience hinges. In Naples, with its elongated coastal morphology and patchy access, bipartite Dual clearly dominates (AUC $=1.0$), whereas 1-mode PageRank and betweenness degrade rapidly (0.492 and 0.436), and bipartite Coverage is intermediate (0.763). This is precisely the setting where preserving the two-mode structure matters most: Dual identifies the few lockers that stitch otherwise weakly connected demand clusters; projection-based baselines miss this cross-type coupling and overestimate redundancy.

Pooling cities, the one-sided Wilcoxon test against 1-mode PageRank shows that bipartite Coverage yields significantly higher robustness ($p<0.05$), while bipartite Dual is competitive overall ($p=0.392$) and decisively superior on the fragmented Naples case. Across all cities, 1-mode betweenness is consistently the least robust. Taken together, these experiments demonstrate that operating on the bipartite topology produces selections that are at least as robust as, and often more robust than, single-layer baselines, while also revealing structurally critical lockers invisible to one-mode projections. The two bipartite metrics serve complementary roles. Coverage maximizes immediate reach and, as the flat curves show, tends to pick hubs whose failure does not shatter connectivity, useful when the objective is equitable access with ample local redundancy. Dual pinpoints the bridges that sustain system-wide cohesion; hardening or adding redundancy around these sites directly increases resilience where it actually matters. Because the overlap between the two selections is small (see Section 4.4), a hybrid policy can secure both short-term reach and global robustness. Because the robustness curves are topology-driven, a capacity-aware run amounts to replacing B with the saturated $B^{\prime }$ (see Section 3.6); this typically lowers absolute robustness but preserves the relative pattern: Coverage prioritizes high-reach hubs, whereas Dual pinpoints bridge-like lockers that govern cohesion.

4.4. Comparative Evaluation with Other Centralities

To rigorously evaluate our centrality metrics, we compared the top-five lockers selected by Coverage centrality and Dual centrality for each city. The results, summarized in

Table 5. Overlap among top-five lockers selected by Dual centrality and Coverage centrality in each city.

City	Overlap (Cov ∩ Dual)	All Top-Five
Milan	0/5	0
Rome	1/5	1
Naples	1/5	1

, show a striking contrast: in all three cities, Coverage centrality persistently highlights the lockers with the largest user base, while Dual centrality identifies a mostly disjoint set of structurally strategic lockers. Notably, the overlap between Coverage and Dual centrality is minimal, underscoring the fact that Dual centrality captures a fundamentally different network property, prioritizing lockers that bridge otherwise distant or weakly connected zones, not just those with the highest immediate usage.

This consistent pattern demonstrates the added value of Dual centrality: it selects lockers with unique structural importance, often missed by coverage-based or popularity-based rankings. While Coverage centrality is practical for identifying the most “popular” lockers, Dual centrality brings to light those nodes that are irreplaceable for network-wide connectivity, which is critical for ensuring resilience and redundancy. In denser or more interconnected bipartite networks, Coverage centrality can reveal non-obvious “bridge” lockers that play a unique structural role. However, in our datasets, characterized by high sparsity and strong local clustering, Coverage centrality essentially reduces to a popularity ranking, focusing primarily on the largest hubs, similar to degree. As a result, for these Italian city cases, Dual centrality emerges as the metric among those tested that consistently highlights lockers with a distinct, non-redundant network role. Specifically, those that act as critical connectors between otherwise weakly linked demand zones. We note, however, that this outcome may depend on network topology, and in other spatial or organizational contexts, Coverage centrality could provide additional insights beyond simple degree.

To further qualify the comparative value of our centrality metrics, we performed an explicit spatial and quantitative analysis of the top lockers identified by Coverage, betweenness, PageRank, and Dual centrality for each city. The resulting maps, shown in Figure 7, provide an immediate visual intuition for the way each metric captures distinct structural features of the urban locker network. In all three cities, Coverage centrality consistently identifies the main urban hubs, i.e., those lockers located at the heart of the densest neighborhoods or major access corridors. These nodes maximize the number of users that can reach a locker within the shortest distance, and unsurprisingly, they often overlap with the lockers selected by PageRank, as both metrics are sensitive to high user flow and central positioning within the network. This overlap is particularly evident in Milan and Naples, where four or even five of the top lockers coincide across these two metrics, underscoring the spatial concentration of demand around a few prominent sites.

However, a very different picture emerges when considering betweenness and Dual centrality. Betweenness centrality highlights lockers that serve as bridges between otherwise separated parts of the city; these are often found at peripheral or transitional locations, well away from the main clusters. The spatial spread of the top betweenness lockers is clear in each map, and their minimal overlap with the coverage-based selection confirms that they are structurally important in a different sense, crucial for maintaining network-wide connectivity, not just serving the largest number of users. Dual centrality, on the other hand, identifies lockers with a unique role in the network’s core structure, often located at non-redundant positions that may be missed by other rankings. While Dual centrality is mathematically related to eigenvector-based rankings, in practice, it tends to select a set of lockers that are not only influential due to direct connections, but also structurally irreplaceable for the overall cohesion of the network. These contrasts are particularly visible in Milan, where the Coverage and PageRank lockers form a tight, central cluster, while top betweenness and Dual lockers are more widely scattered. In Rome, the picture is more complex, with some lockers appearing in multiple top-five lists, reflecting the city’s polycentric form and multiple important corridors. Naples, with its elongated coastal form, shows the clearest separation: top-Coverage lockers are found in central and highly accessible locations, while top betweenness lockers are distributed at the periphery, ensuring connectivity across the fragmented urban landscape.

These findings suggest that for the highly sparse and locally clustered locker networks observed in Italian cities, Coverage centrality primarily recovers the most popular and centrally located lockers, closely matching PageRank. Betweenness and Dual centrality, instead, surface lockers whose network roles would otherwise remain hidden, those whose removal would most severely disrupt overall accessibility or fragment the network. The complementary perspectives afforded by these different metrics reveal both the dominant hubs and the “hidden bridges”, providing urban planners and logistics operators with robust, evidence-based criteria for prioritizing interventions and strengthening the resilience of last-mile delivery infrastructures. Quantitatively, this multi-metric analysis demonstrates that no single centrality captures all dimensions of network importance. Coverage-based rankings are ideal for maximizing direct access and service efficiency, but can overlook structurally critical nodes that are essential for redundancy and resilience. Dual and betweenness centralities, by contrast, bring to light those lockers whose removal would most severely fragment the network or reduce access for otherwise underserved areas. The joint analysis of these metrics thus provides a far more complete and actionable perspective for both operational planning and strategic investment in urban parcel locker systems.

In addition, we examine the relationship between our two metrics and established centralities and test whether they anticipate robustness outcomes. For convergent/discriminant validity, we compute Spearman’s $\rho$, Kendall’s $\tau$, and degree-controlled partial Spearman correlations between Coverage centrality and Dual centrality vs. bipartite degree/strength on B and one-mode betweenness and PageRank on the locker projection, city by city.

Table 6. Rank correlations between proposed indicators and classic centralities. “—” indicates not applicable.

City	Target	Baseline Centrality	Spearman $\mathit{\rho }$	Kendall $\mathit{\tau }$	Partial Spearman $\mathit{\rho }$ (Deg-Controlled)
Milan	Coverage	Bipartite degree/strength	1.000 [0.000]	0.989 [0.000]	0.697
Milan	Coverage	one-mode betweenness	0.670 [0.000]	0.556 [0.000]	0.386
Milan	Coverage	one-mode PageRank	0.724 [0.000]	0.550 [0.000]	0.474
Milan	Dual	Bipartite degree/strength	−0.036 [0.640]	−0.009 [0.908]	—
Milan	Dual	one-mode betweenness	0.644 [0.000]	0.462 [0.000]	0.402
Milan	Dual	one-mode PageRank	0.764 [0.000]	0.581 [0.000]	0.560
Rome	Coverage	Bipartite degree/strength	1.000 [0.000]	0.989 [0.000]	0.718
Rome	Coverage	one-mode betweenness	0.658 [0.000]	0.516 [0.000]	0.382
Rome	Coverage	one-mode PageRank	0.714 [0.000]	0.544 [0.000]	0.470
Rome	Dual	Bipartite degree/strength	−0.026 [0.702]	−0.012 [0.873]	—
Rome	Dual	one-mode betweenness	0.611 [0.000]	0.438 [0.000]	0.355
Rome	Dual	one-mode PageRank	0.744 [0.000]	0.568 [0.000]	0.529
Naples	Coverage	Bipartite degree/strength	1.000 [0.000]	0.986 [0.000]	0.701
Naples	Coverage	one-mode betweenness	0.655 [0.000]	0.518 [0.000]	0.380
Naples	Coverage	one-mode PageRank	0.732 [0.000]	0.553 [0.000]	0.489
Naples	Dual	Bipartite degree/strength	−0.012 [0.932]	−0.014 [0.898]	—
Naples	Dual	one-mode betweenness	0.728 [0.000]	0.552 [0.000]	0.486
Naples	Dual	one-mode PageRank	0.809 [0.000]	0.642 [0.000]	0.617

shows that Coverage centrality is almost perfectly aligned with bipartite degree/strength in all cities (e.g., $\rho =1.0$, $\tau \approx 0.99$), and its association with PageRank and betweenness is weak-to-modest once degree is controlled, and consistent with the lower bound $C_{\mathrm{cov}}\left(j\right)\ge \left({\displaystyle \genfrac{}{}{0pt}{}{{deg}_Z\left(j\right)}{2}}\right)$ on sparse, locally clustered graphs. Dual centrality displays low correlation with degree (near zero) and moderate-to-strong positive association with PageRank and betweenness (e.g., Milan ${\rho }_{\mathrm{PR}}=0.764$, ${\rho }_{\mathrm{BW}}=0.644$; Naples ${\rho }_{\mathrm{PR}}=0.809$, ${\rho }_{\mathrm{BW}}=0.728$), which remains appreciable after degree control, indicating that Dual centrality captures global two-mode structure beyond local popularity. For predictive validity, we summarize fragmentation curves by ${\mathrm{AUC}}_k$ under targeted removals and run paired one-sided Wilcoxon tests (pooled across cities) comparing Coverage centrality and Dual centrality against Degree, betweenness, and PageRank for $k\in \{5,10,15,20\}$ (see

Table 7. Predictive validity.

k	Target	Baseline	Wilcoxon Stat	p (One-Sided)
5	Coverage	Degree	0.000	1.000
5	Coverage	betweenness	6.000	0.125
5	Coverage	PageRank	6.000	0.125
5	Dual	Degree	2.500	0.605
5	Dual	betweenness	6.000	0.125
5	Dual	PageRank	6.000	0.125
10	Coverage	Degree	0.000	1.000
10	Coverage	betweenness	6.000	0.125
10	Coverage	PageRank	6.000	0.125
10	Dual	Degree	2.000	0.688
10	Dual	betweenness	6.000	0.125
10	Dual	PageRank	5.000	0.250
15	Coverage	Degree	0.000	1.000
15	Coverage	betweenness	6.000	0.125
15	Coverage	PageRank	6.000	0.125
15	Dual	Degree	1.000	0.875
15	Dual	betweenness	6.000	0.125
15	Dual	PageRank	5.000	0.250
20	Coverage	Degree	0.000	1.000
20	Coverage	betweenness	6.000	0.125
20	Coverage	PageRank	6.000	0.125
20	Dual	Degree	0.000	1.000
20	Dual	betweenness	6.000	0.125
20	Dual	PageRank	5.000	0.250

). With the current sample, AUC differences are consistently non-negative in the direction of our indicators and often larger against betweenness/PageRank; with $N=3$ cities, the pooled tests are under-powered and p-values do not always cross conventional thresholds. We therefore interpret these as directional evidence, consistent with the descriptive robustness advantages documented in Section 4.3.

4.5. Comparative Evaluation with Baseline Methods

To rigorously evaluate the effectiveness and practical value of our proposed network-centric centrality metrics for parcel locker placement, we benchmarked them against a state-of-the-art location optimization method from recent literature: the multi-criteria decision-making (MCDM) approach using the Spherical Fuzzy Analytic Hierarchy Process (SFAHP) introduced by [20]. For each Italian city in our study (Milan, Rome, Naples), we implemented the SFAHP model using available criteria (e.g., population buffer, proximity to public transport) adapted to the Italian urban context and the open data at our disposal. We then compared the resulting SFAHP locker rankings with those obtained from our centrality-based approaches, namely Dual centrality and Coverage centrality, focusing on three key aspects: (i) the overlap among the top-five lockers selected by each method, (ii) the spatial and network roles of the selected lockers, and (iii) the implications for equity and resilience.

Table 8. Top-five overlap between SFAHP, Coverage Centrality, and Dual Centrality for each city.

City	SFAHP ∩ Coverage	SFAHP ∩ Dual	Coverage ∩ Dual
Milan	5/5	1/5	1/5
Rome	5/5	1/5	1/5
Naples	4/5	0/5	1/5

summarizes the rankings and overlaps between the SFAHP method and the network-based metrics in each city. Strikingly, in both Milan and Rome, the top-five lockers selected by SFAHP are identical to those identified by Coverage centrality, confirming that SFAHP essentially prioritizes lockers serving the highest population within the buffer, i.e., the “most popular” or accessible locations. By contrast, the overlap between SFAHP and Dual centrality is minimal (only 1/5 lockers in Milan and Rome, and 0/5 in Naples), highlighting the conceptual distinction between structural network roles (Dual centrality) and simple user coverage. In all cities, Dual centrality systematically identifies lockers that are structurally pivotal, acting as bridges or “glue” within the locker-user network, while not necessarily serving the largest population. This demonstrates that Dual centrality provides a complementary and previously unaddressed perspective on network resilience and redundancy.

While SFAHP (and by extension, Coverage centrality) reliably prioritizes lockers at locations such as post offices, public transport stops, and commercial centers, aligning with classical accessibility and expert-driven criteria, our network-centric metrics reveal lockers with unique structural importance. In particular, Dual centrality surfaces lockers that, although less obvious from a classical planning perspective, are essential for maintaining network connectivity, preventing fragmentation, and ensuring that no single failure disconnects large user segments. Lockers selected by Dual and Coverage centrality are associated with higher network coverage and larger connected user components, especially in spatially fragmented cities such as Naples. Our results demonstrate that network-based analysis is not simply an alternative to established multi-criteria methods, but an essential complement. By uncovering infrastructure points invisible to classical MCDM or population-driven heuristics, network centrality metrics provide actionable insights for resilient, equitable, and future-proof locker network design.

5. Discussion

The results of this study provide a nuanced perspective on the design and optimization of urban parcel locker networks, highlighting both practical implications and methodological contributions. By modeling the system as a multilayer (bipartite) network and introducing novel centrality metrics, Dual centrality and Coverage centrality, we offer a more holistic understanding of locker importance than traditional approaches based solely on usage or proximity. The consistent finding that Dual centrality identifies structurally critical but not necessarily popular lockers, while Coverage centrality mainly recovers the largest hubs, suggests that a multi-metric approach is essential for supporting resilient and equitable urban logistics.

A key implication of these findings is the need to move beyond naive optimization criteria, such as maximizing direct coverage or serving the highest population density, when planning locker deployments. Our vulnerability analysis demonstrates that networks optimized solely for coverage are highly vulnerable to targeted disruptions: the removal of just a few top-coverage lockers can rapidly fragment service, disconnecting large portions of the urban area. Conversely, lockers with high Dual or betweenness centrality play a disproportionate role in holding the network together, and their identification provides actionable guidance for both redundancy planning and capacity upgrades. For practitioners, this means that combining centrality-driven insights with traditional demand modeling can yield more robust and future-proof parcel infrastructures, especially in complex urban environments characterized by polycentricity and heterogeneous access needs.

Among the strengths of the proposed framework is its generality and reproducibility. The model is entirely data-driven, requiring only open geographic and demographic datasets, and is scalable to other cities or regions with minimal adaptation. The grid-based methodology for defining demand zones preserves both privacy and spatial detail, enabling high-resolution analyses without relying on proprietary user data. The open-source release of all datasets and code further supports transparency and reuse, allowing researchers and planners to replicate or extend the analyses.

Our network-centric rankings are structural signals, not permits to build. We therefore treat top-ranked lockers as candidate locations that must be screened against standard siting layers: (i) land-use/zoning compliance and right-of-way; (ii) utility availability (grid and telecom backhaul) and basic security (lighting, CCTV); and (iii) multimodal accessibility (walkability, bike lanes, proximity to public transport stops). This two-stage workflow preserves generality and reproducibility while ensuring implementability. In our maps, the highest-scoring sites cluster around mixed-use, transit-rich areas, which qualitatively supports transport accessibility; however, detailed power and permitting checks are outside the scope of our open-data analysis and should be performed by the planning authority during the screening step.

Regarding fairness against resilience, these are not inherently antagonistic because they measure different facets of performance. We do not employ socio-demographic attributes in the reported experiments. In our work, “fairness” denotes dispersion of spatial accessibility (e.g., uncovered-population share or the population-weighted Gini of distance-to-nearest-locker); socio-demographic disparity analysis is out of scope. Fairness can be assessed with coverage and dispersion of access (e.g., share of population within radius r, uncovered zones, and the population-weighted Gini of distance-to-nearest-locker), while resilience is summarized by ${\mathrm{AUC}}_k$ of the LCC under failures/attacks. Coverage-oriented choices typically raise near-term access and reduce inequality, whereas Dual centrality candidates strengthen system cohesion by safeguarding bridges. Whether a tension emerges is an empirical property of each city’s topology. We therefore propose a simple quantitative diagnostic without new data: sweep a convex policy mix

$$S_{\alpha }\left(j\right)=\alpha \widehat{\mathrm{Dual}}\left(j\right)+(1-\alpha )\widehat{\mathrm{Coverage}}\left(j\right),\alpha \in [0,1],$$

rank by $S_{\alpha }$, and trace the Pareto curve $(\mathrm{Fairness}\mathrm{metric},{\mathrm{AUC}}_k)$ across $\alpha$. A flat or outward-bulging frontier indicates complementarity; a pronounced trade-off signals where to add redundancy or adjust budgets. Finally, we outline a three-step, executable recipe for planners:

• Anchor and reach. Select a small set of resilience anchors among the top Dual centrality lockers and ensure each large demand cluster is linked to at least one anchor (with a backup within 200–400 m).
• Equity fill-in. Add top Coverage centrality lockers to lift population coverage and reduce the Gini of access, prioritizing underserved zones until equity targets are met.
• Feasibility screen and iterate. Apply a GIS-based pass/fail (zoning, utilities, sidewalk width, public transport proximity), re-score surviving candidates with $S_{\alpha }$, and re-check robustness (${\mathrm{AUC}}_k$) and fairness targets.

This workflow turns structural diagnostics into siting shortlists that satisfy land-use, power, and accessibility constraints while making the fairness-resilience trade-offs explicit and tunable.

Most existing parcel-locker siting studies are static (facility location or scenario analyses); to our knowledge, explicitly dynamic/temporal network models for lockers are still uncommon. Where operator data exist, our bipartite weights can be replaced by observed flows and rescaled for capacity (Section 3.6); time-sliced $B\left(t\right)$ allows computing fairness/robustness in peak vs. off-peak conditions, with selections based on mean or worst-case performance. Our bipartite framework is compatible with dynamics via a time-indexed incidence $B\left(t\right)$ (e.g., hour/day/season or scenarios), applying the same centralities and robustness metrics per time slice or over distributions. The method also transfers to other last-mile assets (parcel shops/pick-up points, micro-hubs, express/automatic distribution stations) by replacing the locker layer and keeping user-facility edges; the same feasibility screening (zoning, utilities, accessibility) applies. In addition, our bipartite formulation is plug-in compatible with discrete-choice and agent-based demand models: a calibrated logit/nested-logit produces $p_{ij}$ and flows $F_{ij}=D_i{p}_{ij}$ that simply populate B (or $B\left(t\right)$), while ABM produces time-sliced assignments $F_{ij}\left(t\right)$ reflecting daily activity patterns and mode availability. Because Coverage centrality is adjacency-driven and Dual centrality is stable under bounded re-weightings (see Section 3.4), behaviorally refined B typically changes magnitudes rather than overturning the hub–bridge separation; capacity-aware utilities can be iterated to equilibrium and then analyzed with the same robustness tests. This enables policy experiments (e.g., extended hours, new transit stop, perceived safety improvements) by perturbing utilities and re-scoring lockers without altering the network workflow. Finally, scalability to different city sizes is practical because computations are near-linear in the number of edges; small/medium towns can use coarser grids or tighter radii, and large metros are supported by our sparse pipeline.

Nevertheless, some limitations must be acknowledged. First, our edges encode potential access (population within 500 m) rather than observed assignments. While this abstracts from behavioral choice, two features mitigate the limitation: (i) Coverage centrality is adjacency-driven and lower-bounded by degree; (ii) Dual centrality (principal singular vectors) is stable under bounded re-weightings when a spectral gap exists. In practice, observed flows usually rescale B without altering the hub/bridge contrast; magnitudes may change, but not the qualitative interpretation. When operator data are available, our pipeline directly accepts observed $F_{ij}$ (or gravity/logit estimates) and capacity-aware adjustments. Secondly, this study relies on static spatial data and does not capture temporal fluctuations in demand, delivery schedules, or user preferences, factors that can significantly impact real-world network dynamics. The focus on spatial proximity as the sole criterion for user–locker association may overlook social, behavioral, or economic barriers to access. Moreover, while the bipartite model accurately represents the structure of current locker systems, it does not account for potential locker-to-locker transfers or multimodal integration with other urban transport layers, which are becoming increasingly relevant in advanced last-mile logistics. While our analysis is intentionally grounded in spatial accessibility to ensure transparency and reproducibility, it does not explicitly capture important real-world factors such as user preferences, behavioral biases, operational costs, or locker capacity limitations. In practice, locker selection and usage are shaped by a mix of psychological, social, and economic drivers, not just proximity. Future research should address these limitations by integrating empirical usage data (e.g., operator records, surveys, or mobile app traces) to calibrate demand more realistically, simulating behavioral responses with agent-based or discrete-choice models, and modeling capacity or operational constraints directly within the network. Furthermore, advancing the framework to include temporal variability, dynamic demand, and multi-modal integration (such as connections to home delivery, retail points, or micro-mobility) would better reflect the complexity of urban logistics. These enhancements would not only strengthen the practical relevance of centrality-based planning, but also open new directions for data-driven, equitable, and resilient last-mile delivery optimization. A further limitation concerns external validity. Our empirical scope is restricted to three Italian cities; however, they were deliberately selected to span distinct urban archetypes: Milan (compact, monocentric core), Rome (larger, polycentric, and administratively fragmented), and Naples (elongated, coastal/topography-constrained), thus covering diverse geography, demography, and transport structures. The mechanisms we study are structural (two-mode incidence, redundancy vs. bridging), and our results are robust across modeling choices, which supports transferability. Because the pipeline relies only on open demographic and POI data and a bipartite formulation, it is readily replicable in other European and non-European contexts. A broader cross-city panel, explicitly stratified by morphology and transit supply, is a valuable direction for future work.

In summary, the multilayer network approach advanced in this paper provides a robust foundation for analyzing, optimizing, and future-proofing parcel locker systems. It offers urban planners and logistics operators new tools to assess network robustness, identify hidden vulnerabilities, and design interventions that enhance both efficiency and resilience. Future research should aim to incorporate temporal data, model adaptive user behaviors, and explore integration with broader urban mobility systems to fully capture the complexity and potential of next-generation last-mile delivery infrastructures.

6. Conclusions

This work presents a unified, data-driven framework for the quantitative analysis and strategic planning of urban parcel locker networks, grounded in multilayer network theory. By combining high-resolution spatial grids with open-source demographic and locker data, and by introducing both Dual and Coverage centrality metrics, we provide a flexible and reproducible methodology that captures the structural complexity of real-world last-mile delivery systems.

The main contributions are twofold. Methodologically, we demonstrate how advanced network analysis can reveal hidden structural vulnerabilities and inform more resilient deployment strategies, insights that go far beyond what can be achieved through simple demand or degree-based heuristics. Empirically, our application to Milan, Rome, and Naples reveals the limitations of coverage, or popularity-driven optimization: while maximizing user reach is important, true network resilience depends on the strategic role of a small set of structurally critical lockers, as revealed by Dual and Coverage centrality.

For practitioners and policymakers, these findings highlight the importance of combining classic service metrics with network-based diagnostics when designing or upgrading parcel infrastructure. Prioritizing interventions based solely on coverage risks exposing urban systems to targeted disruptions and service fragmentation. Instead, a multi-criteria approach can support more robust and adaptable locker networks, benefiting operators, city planners, and end users alike.

Looking forward, future research should strengthen this framework by directly incorporating dynamic demand patterns, behavioral and socio-economic factors, and multimodal integration with other urban mobility systems. Applying the model to new cities and regulatory settings will help test its generalizability and adaptability. Integrating real-time or longitudinal usage data, modeling operational constraints such as locker capacity and costs, and considering environmental or equity impacts would further boost the practical and policy relevance of this approach. By evolving toward more data-driven, behaviorally realistic, and multi-modal planning, the methods presented here can support both academic research and the design of resilient and efficient last-mile logistics in rapidly changing urban environments.