Abstract
Anomaly detection in multivariate time series (MTS) remains challenging due to the presence of complex and dynamic spatiotemporal dependencies. To address this, we propose the Dynamic Spatiotemporal Graph Mixed Network (DTS-MixNet), which takes a sliding window data as input to predict the next time series data and determine its state. The model comprises five blocks. The Temporal Graph Structure Learner (TGSL) generates the attention-weighted graphs via two types of neighbor relationships and the multi-head-attention-based neighbor degrees. Then, the Cross-Temporal Dynamic Encoder (CTDE) aggregates the cross-temporal dependencies from attention-weighted graphs, and encodes them into a proxy multivariate sequence (PMS), which is fed into the proposed Cross-Variable Dynamic Encoder (CVDE). Subsequently, the CVDE captures the sensors-among spatial relationship through multiple local spatial graphs and a global spatial graph, and produces a spatial graph sequence (SGS). Finally, the Spatiotemporal Mixer (TSM) mixes PMS and SGS to build a spatiotemporal mixed sequence (TSMS) for downstream tasks, e.g., classification or prediction. We evaluate on two industrial control datasets and discuss applicability to non-industrial multivariate time series. The experimental results on benchmark datasets show that the proposed DTS-MixNet is encouraging.
1. Introduction
In the Industry 4.0 era, the complexity and criticality of infrastructures, such as industrial equipment, IoT systems, and transportation networks, have significantly increased. These infrastructures commonly generate vast amounts of multivariate time series (MTS) data, characterized by nonlinearity, nonstationarity, and inter-sensor coupling (also called inter-variable coupling). For example, in steel production, there exist various types of sensors including temperature, density, oxygen consumption, pressure, and so on. And a change in one sensor’s measured value may propagate to others, leading to correlated anomalies. Hence, it is very important to carry out system monitoring with high reliability.
Multivariate time series anomaly detection (AD-MTS), which aims to identify potential abnormal behaviors or time points requiring corrective actions, is thus a critical technique for ensuring system safety. Unlike traditional anomaly detection methods designed for static data, e.g., statistical [1,2,3] or distance-based [4,5] approaches, AD-MTS must address the inherent temporal dynamics and complex inter-variable interactions, which is called spatiotemporal dependencies. To illustrate these dependencies, we employ the Secure Water Treatment (SWaT) dataset [6], an industrial control system benchmark in which each variable is denoted by a sensor tag (e.g., LIT101, a water level indicator in Tank 1; P102, a pump; AIT201, an analyzer; MV101, a motorized valve). As shown in Figure 1, anomalies are highlighted in red: (1) temporal dependencies (including lag effects): the impact of anomalies can propagate over time, showing sequential and lagged effects, e.g., an initial change in LIT101 followed by deviations in P102 and AIT201. (2) Inter-sensor (spatial) dependencies (coupling): anomalies in certain sensors can trigger cascading effects in related sensors, e.g., a change in LIT101 leading to anomalies in MV101 and P101. Capturing such spatiotemporal dependencies is important for AD-MTS.
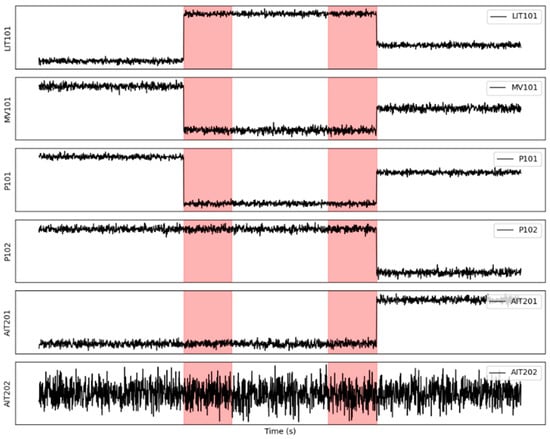
Figure 1.
An illustrative example on SWaT dataset, where the red areas indicate anomalous events.
Recent advances in deep learning have shown promise in AD-MTS. Convolutional Neural Networks (CNNs) and Stacked Autoencoders (SAEs) [7,8,9] excel at extracting complex and nonlinear features. Generative Adversarial Networks (GANs) [10] can learn the distribution of non-anomalous data, and Long Short-Term Memory networks (LSTMs) [11] are widely used to capture long-range temporal dependencies. However, these methods largely focus on the internal patterns of individual time series and fail to adequately capture interactions among multiple series. To model inter-variable relationships, Graph Neural Networks (GNNs) have been introduced to AD-MTS. For instance, GDN [12] uses GNNs to predict non-anomalous behavior and detect deviations, while GReLeN [13] and DyGraphAD [14] explore learning dynamic graph structures to capture time-varying relationships. Despite the potential of GNN-based methods for modeling inter-sensor relationships, existing approaches still struggle to simultaneously and dynamically capture spatiotemporal dependencies. Specifically, most approaches lack the capability to dynamically capture evolving dependencies and over-time interaction among sensors, which are critical for identifying anomalies driven by complex coupling effects.
To address the aforementioned challenge, this work proposes DTS-MixNet for multivariate time series anomaly detection. It aims to adaptively learn the patterns evolving in the temporal dimension and capture the sensors-among spatial relationship in the variable dimension, which are synergistically fused to improve the accuracy and robustness of anomaly detection. The architecture of the proposed DTS-MixNet is presented in Figure 2, which contains five parts. Now, the main contributions are summarized as follows:
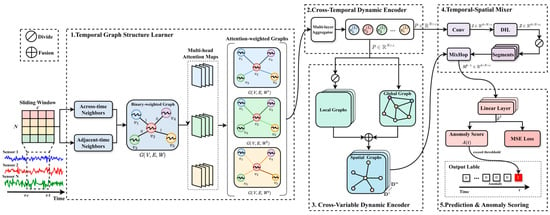
Figure 2.
The structural diagram of our proposed framework.
- We propose a novel deep learning architecture, called DTS-MixNet, for multivariate time series anomaly detection. It uniquely integrates dynamic graph learning across both temporal dimension and spatial (variable) one.
- Temporal Graph Structure Learner (TGSL) discovers evolving temporal dependencies by identifying across-time and adjacent-time neighbors and assigning attention-based edge weights via multi-head attention.
- The framework further includes the Cross-Temporal Dynamic Encoder (CTDE) and the Cross-Variable Dynamic Encoder (CVDE). The CTDE aggregates temporal dependencies within the sliding window to generate a proxy multivariate sequence (PMS), whereas the CVDE integrates both local and global inter-sensor dependencies to construct a spatial graph sequence (SGS).
- Spatiotemporal Mixer (TSM) is designed to effectively fuse the learned dynamic temporal features and the dynamic spatial graph structures. This enables the model to capture higher-order interaction patterns across both time and variables and lead to a more comprehensive representation for downstream tasks.
The rest of this article is organized as follows. Section 2 surveys related methods for time series anomaly detection. The proposed DTS-MixNet is introduced in Section 3. Section 4 discussed anomaly scores and complexity analysis. Experimental results are presented in Section 5. Finally, the conclusion is given in Section 6.
2. Related Works
In this section, we first review the current state of research in anomaly detection and analyze the developments in multivariate time series processing techniques. Since our work relies on Graph Neural Networks (GNNs), we also provide a summary related to GNNs.
2.1. Anomaly Detection
In the field of data-driven anomaly detection and diagnostics, Multivariate Statistical Process Monitoring (MSPM) methods have garnered significant attention and are considered some of the most widely studied and applied techniques. Among these, Principal Component Analysis (PCA), Partial Least Squares (PLS) and Canonical Variable Analysis (CVA) [15,16,17] are widely used for anomaly detection. These techniques are based on linear dimensionality reduction, detecting anomalies by monitoring deviations in key features within the reduced-dimensional space. However, these methods often overlook the nonlinear relationships and temporal dependencies inherent in the data, which may result in a failure to accurately capture potential anomalies in complex dynamic processes.
In addition, deep learning has been widely adopted in anomaly detection due to its powerful nonlinear modeling capabilities. Deep learning models can automatically extract complex features from data and handle large datasets, significantly enhancing the accuracy and robustness of anomaly detection. Notable methods include Autoencoders, Generative Adversarial Networks (GANs) and Convolutional Neural Networks (CNNs) [18,19,20,21]. Autoencoders identify anomalies by reconstructing input data and detecting reconstruction errors. GANs, through adversarial training between a generator and a discriminator, can generate samples that resemble the real data distribution, identifying anomalies by comparing the differences. CNNs excel at handling high-dimensional and spatiotemporal data, significantly improving anomaly detection performance in complex data scenarios. These deep learning approaches have advanced the field by addressing some of the limitations of traditional linear methods, particularly in capturing the intricate nonlinear relationships and temporal dynamics present in modern industrial and sensor-driven data.
2.2. Multivariate Time Series
Multivariate time series signals are sequences of multidimensional vector observations collected over time, generated by numerous physical and virtual sensors. To effectively process such data, researchers have published a large number of studies in recent years. Among traditional machine learning methods, the Autoregressive Model (AR) [22] is a statistical model used for time series analysis. It predicts future values based on past values, assuming that the current value is a linear combination of several previous values. By analyzing historical data and examining its correlation coefficients, an appropriate regression model can be constructed. The Autoregressive Integrated Moving Average Model (ARIMA) [23] is a classical statistical model used for time series forecasting. It predicts future values by modeling the differences between successive observations rather than the raw values themselves. Support Vector Regression (SVR) [24] is a powerful nonlinear regression method that can be used to analyze multivariate time series data. Although SVR was initially designed to solve univariate regression problems, it can be extended to handle multivariate time series data. However, traditional analytical tools like these often struggle to handle complex relationships in time series data, such as nonlinearity and inter-variable dependencies. This complexity can lead to less accurate predictions, especially when the relationships between variables are intricate or when the data exhibits nonlinear behavior. As a result, while these traditional methods have been foundational in time series analysis, they often fail to apply in complex application scenarios.
Due to the excellent performance of artificial neural networks in handling complex feature dependencies and nonlinear relationships, an increasing number of researchers have begun using artificial neural networks for modeling and analyzing multivariate time series. Recurrent Neural Networks (RNNs) [25] are a common approach in multivariate time series analysis, effectively handling time-dependent data by maintaining temporal dependencies through recurrent connections. However, RNNs suffer from the long-term dependency problem, where early information may be forgotten as the number of time steps increases. The advent of deep learning has led to the development of various neural networks based on Convolutional Neural Networks (CNNs) [26,27] and Transformers [28], which have shown significant advantages in modeling real-world time series data. One of the major limitations of these methods is their inability to effectively utilize long-term historical data. To address this issue, researchers have turned to Long Short-Term Memory networks (LSTMs) [29], an improved version of RNNs that introduces gating mechanisms to solve the long-term dependency problem. Gated Recurrent Units (GRUs) [30], a similar recurrent neural network architecture to LSTMs, can also be used to analyze multivariate time series data. GRUs have a simpler structure than LSTMs but still effectively capture long-term dependencies in time series. However, the relationships between variables in multivariate time series often exhibit graph-like structures. The aforementioned methods do not explicitly model the spatial relationships that exist between time series in non-Euclidean spaces, which limits their expressiveness. In real-world applications, the interactions between different time series are often complex and structured, and ignoring these spatial dependencies can result in models that fail to capture the full extent of the data’s underlying patterns. To overcome this limitation, recent approaches have incorporated Graph Neural Networks (GNNs) into time series analysis to capture complex graph-structured relationships among variables. This integration allows for more accurate and comprehensive modeling of multivariate time series data, taking into account both temporal dynamics and spatial interactions between variables.
In recent years, Graph Neural Networks (GNNs) [31] have emerged as a powerful tool for learning representations of non-Euclidean data, paving the way for modeling real-world time series data. GNNs can capture various complex relationships, such as inter-variable connections within multivariate sequences and temporal dependencies across time points. Given the inherent spatiotemporal dependencies in real-world scenarios, a series of studies have combined GNNs with temporal modeling frameworks to better capture these dependencies, showing promising results in multivariate time series anomaly detection. Among these, GNN-GRUAD [32], MGUAD [33] and DuoGAT [34] are some of the classic methods used for multivariate time series anomaly detection.
2.3. Graph Neural Network
Due to the widespread presence of graph-structured data in the real world—such as traffic networks, molecular structures, and social networks—there is a need to handle complex and diverse relationships within this data. Traditional deep learning models struggle to effectively process graph data in non-Euclidean spaces, where many learning tasks require dealing with intricate relational information between elements [35]. This challenge led to the emergence of Graph Neural Networks (GNNs). GNNs are specifically designed to model the spatial relationships within data and are well-suited for handling graph-structured data in non-Euclidean spaces, a task that traditional and other deep neural network-based methods find difficult. GNNs have distinct advantages and have been widely applied in various fields, including recommendation systems, social network analysis, bioinformatics, intelligent transportation, and time series anomaly detection. Their ability to explicitly model the spatial relationships in data makes them uniquely powerful for these applications.
The concept of Graph Neural Networks (GNNs) was first introduced by Gori et al. [36]. Early research focused on learning the representation of target nodes through an iterative process that propagated information from neighboring nodes using a recurrent neural architecture, continuing until a stable fixed point was reached. This process generally required substantial computation. To handle graph-structured data, researchers were inspired by convolutional networks and sought to redefine convolution for graphs. For instance, Bruna et al. [37] developed a variant of graph convolution based on Spectral Graph Theory, designing a learnable diagonal matrix filter. However, this variant of graph convolution was computationally inefficient, and the filters were not spatially localized. In response, Henaff et al. [38] attempted to localize the spectral filters spatially by introducing smoothness coefficients. Subsequently, Defferrard et al. [39] proposed ChebNet, which simplified the computation by approximating the filter up to the th order using the truncated expansion of Chebyshev polynomials. Later, Kipf and Welling [40] introduced Graph Convolutional Networks (GCNs), which leveraged the adjacency relationships between nodes to learn node representations, enabling end-to-end learning on graph data. As GNNs have evolved, there has been a surge in time series analysis methods based on GNNs. These methods explicitly model relationships across time and variables, paving the way for modeling real-world time series data. GNN-based approaches have proven particularly effective in capturing the complex dependencies in time series, including both temporal dependencies and spatial ones, making them well-suited for a wide range of applications, from anomaly detection to forecasting.
3. Methodology
3.1. Problem Statement
Let denote the training data, which is acquired from sensors over equispaced time steps, and denote the training data at time . Let denote the test data over equispaced time steps, which is also acquired from the same sensors, and our objective is to detect anomalies in the test data. In addition, a sliding window of size serves as a processing unit and the data of a sliding window at time is denoted as follows:
Note that adjacent sliding windows are allowed to overlap.
will be used to predict the values of the sensors at time . The deviation between the actual data and the predicted data is treated as the loss in the training phase and as an anomaly score in the testing phase. We note that these deviations may exhibit temporal correlation due to the underlying dynamics of multivariate time series. Unlike classical control-chart methods that assume independent residuals, our approach calibrates anomaly thresholds on validation data, which inherently accounts for such correlations. About the application of deviation, we will provide a detailed explanation in Section 3.6 and Section 4.1. The notation used in this paper is listed in Table 1.

Table 1.
The symbolic notations and their descriptions.
3.2. Temporal Graph Structure Learner
As mentioned above, multivariate time series typically exhibit evolving relationships in the temporal dimension. When all sensors are considered together, the data at each time step can be represented as a node. Consequently, sequential nodes form connections across time, involving both across-time and adjacent-time relationships. In graph theory, such relationships can be characterized through neighbor attribution, which consists of neighbor relationships and neighbor degrees. To capture these temporal patterns, we propose the Temporal Graph Structure Learner (TGSL), which is designed to model evolving dependencies. Specifically, it identifies and refines the candidate neighbors for each node, including both across-time and adjacent-time neighbors. The neighbor relationship is denoted as a binary-weighted graph , where is a vertex set, is an edge set and is a binary matrix. Then, the graph is fed into a multi-head attention net with heads, and it ultimately generates weighted graphs, called attention-weighted graphs and denoted ,…,, respectively. As a result, the dependencies of multivariate time series are evaluated with attention-weighted graphs, which reflects different attention perspectives. Since the adjacent sliding windows in our work are allowed to overlap, without loss of generality, the data in a sliding window takes into consideration. Now, we provide the design process of the proposed learner.
- (1)
- Capture Neighbor Relationship
Without loss of generality, the data in a sliding window is taken into consideration. Given the data of a sliding window at time , i.e., , if each sample is considered as a node, i.e., is corresponding to , then we can obtain a node set . Because the nodes may exhibit temporal transitivity or coupling, their neighbor relationships cannot be simple checked by Euclidean distance. To ensure consistent input dimensionality and enable efficient batch training, a fixed sliding window of length is adopted. To this end, we define two learnable vectors, and , which will be continuously refined through iterative optimization, and they are used to potentially represent the neighbor relationships as follows:
where is a relationship matrix, the function ensures that the edge values are all positive, and the function guarantees that the sum of the weights corresponding to relevant time steps is equal to 1. If is larger, the relationship between and is closer. Thus, the nearest nodes of can be obtained by
is the set of ’s -nearest neighbors. In this paper, this type of neighbors is called across-time neighbors, which aims to distinguish it from another type, called adjacent-time neighbors and denoted as :
Obviously, is the set of ’s two adjacent points and they have strong associations with the node . Now, we combine these two types of neighbors to form the final nearest neighbors as follows:
Next, the neighbor relationship is denoted as a binary-weighted graph , in which is a vertex set, is an edge set and there is an edge if the vertex is one of ’s neighbors, and is a binary matrix and its entry is given by
- (2)
- Evaluate Neighbor Degree
Although the binary-weighted graph describes the neighbor relationship of nodes, it can not reflect their neighbor degree. To reliably evaluate the neighbor degree, we introduce a Graph Attention Network [41] to adaptively optimize their edge weights. First, the binary-weighted graph is fed into a multi-head attention net with heads, and then we compute their compatibility score between the neighbors to obtain their edge weights. Specifically, for the -th attention head, a learnable mapping matrix transforms the fed nodes into a new space for obtaining more tight representations. Then, an optimized vector is introduced to score the neighbor degree in the new space, which is formulated as:
where ‘’ denotes vector concatenation, and is an activation function. Next, the score is normalized to the edge weights as follows:
Through different attention heads, we can obtain weighted graphs, denoted as
Here, is called attention-weighted graph and is the -th attention weight. Note that each graph is corresponding to an attention perspective and it focuses on a distinct relationship based on its specific attention mechanism. So far, the temporal graph structure is represented by attention-weighted graphs.
3.3. Cross-Temporal Dynamic Encoder
Obviously, the attention-weighted graph demonstrates the -type complex and spreading dependencies. To use all dependencies, i.e., types of dependencies, we propose Cross-Temporal Dynamic Encoder (CTDE), which aggregates the dependencies from attention-weighted graphs and encodes all nodes into the new representations.
All nodes are fed into an -layer aggregator. Let denote the -th layer output of the node , then the outputs of the subsequent layers are as follows:
where is an activation function, and , , is a learnable mapping matrix for effective dependency aggregation form the attention-weighted graph . The output of the final layer, i.e., , is the new representation of node . As a result, a new sequence can be obtained, i.e., , and here it is called Proxy Multivariate Sequence (PMS). For brevity, we use the matrix form to denote the PMS as follows:
where is the new representation after aggregation, represents the feature dimension aggregated for each timestamp, and represents the number of timestamps.
3.4. Cross-Variable Dynamic Encoder
The Proxy Multivariate Sequence (PMS), generated by the proposed TGSL and CTDE, has captured the dependencies in the temporal dimension. However, there also exists rich spatial information in multivariate time series data, i.e., among sensors or variables. To mine useful information, we design a block, called Cross-Variable Dynamic Encoder (CVDE). The CVDE block utilizes PMS to construct spatial graphs and generate Spatial Graph Sequence (SGS) under local perspective and global one, respectively.
To capture the spatial relationship among variables (sensors) in Proxy Multivariate Sequence (PMS), Proxy Multivariate Sequence (PMS) is divided into non-overlapping localities with a fixed length , which generates a local sequence, denoted , . Then, in each locality, we treat a variable (a sensor) as a node and establish a spatial graph, in which the Dynamic Time Warping (DTW) distance is employed to measure the similarity between variable features in each locality and build their adjacency matrices. Specifically, for the -th locality , the local spatial adjacency matrix is computed by
where represents the feature of the -th variable, i.e., the -th row of , is the DTW distance function between two sequences and is a hyperparameter that controls the scaling of DTW distances when constructing adjacency matrices, regulating how sharply or smoothly similarities between variables decay. The DTW metric provides robustness to local misalignments by allowing elastic matching along the time axis and please see [42] for more details. Hence, the non-overlapping localities are described as local spatial graphs, which is represented by local adjacency matrices, i.e., , .
Obviously, a local adjacency matrix only reflects the spatial information of a locality. To capture the global spatial information between variables (sensors), we also use the DTW distance to define a global spatial adjacency matrix, denoted , which is formulated as
where represents the feature of the -th variable, i.e., the -th row of in and is a hyperparameter. To incorporate global spatial information into the local structures, each local adjacency matrix is combined with the global one, resulting in the following Spatial Graph Sequence (SGS):
where is a learnable parameter and . For simplification, let denote the Spatial Graph Sequence.
3.5. Spatiotemporal Mixer
The Cross-Temporal Dynamic Encoder (CTDE) and the Cross-Variable Dynamic Encoder (CVDE), respectively, generate the Proxy Multivariate Sequence (PMS) and the Spatial Graph Sequence (SGS). To make full use of the complementary information from both sequences, we design the Spatiotemporal Mixer (TSM), which takes PMS and SGS as input and integrates them into a new sequence, referred to as the Spatiotemporal Mixed Sequence (TSMS). TSMS will be used for downstream tasks, e.g., classification task or prediction task. The designed TSM contains two processes as follows.
- (1)
- Generating Hidden Representations
A 2D convolutional layer, with a convolutional kernel and channels, is used to extract a richer feature representation from the Proxy Multivariate Sequence . Here, the kernel ensures that the convolution operation focuses on feature transformation, and the channels aim to obtain a higher-dimensional embedding. Note that the intrinsic aggregation information existing in may be decomposed in higher-dimensional embedding space. Thus, it is necessary to re-aggregate the information of nearby points from the feature representation . To this end, the feature representation is fed into the Dilated Inception Layer (DIL) to aggregate nearby points, which can use various kernel sizes to capture similarities between pairs of sequences. See [43] for more detail. As a result, a hidden representation is generated.
- (2)
- Mixing Temporal and Spatial Information
First, the hidden representation is divided into non-overlapping segments, i.e., and , along the temporal dimension. Then, and correspond one-to-one. Now, we employ MixHop module for mixing temporal and spatial information, which is formulated as:
where represents the feature matrix of the -th segment. In fact, the MixHop [44] function can not only realize the interaction of spatiotemporal signals, but also capture higher-order relationship of neighbors through multiple orders. Next, we concatenate these feature matrices as follows:
where is the final representation of a sliding window at time . Hence, over time steps, we can gain Spatiotemporal Mixed Sequence (TSMS), i.e.,
3.6. Neural Network Prediction
The function is composed of a series of linear layers in a neural network. These layers process the concatenated input , ultimately producing the predicted target values for each sensor at time , i.e., as follows:
It should be noted that our approach requires labeled data during training. The model is optimized by minimizing the prediction error with respect to ground-truth labels, ensuring that the learned representations are aligned with the actual system behavior. This design follows the supervised anomaly detection setting, as in benchmark datasets such as SWaT and WADI, where attack periods are explicitly annotated. Extending the framework to fully unsupervised scenarios without labels is an interesting direction for future work.
To train the model, we adopt the mean squared error (MSE) as the loss function. Although MSE is equivalent to assuming that the residuals follow an approximately Gaussian distribution, it remains one of the most widely used and effective objectives in multivariate time series modeling. This choice is motivated by its computational simplicity, stability in optimization, and interpretability as a measure of deviation between predicted and observed values. Moreover, prior studies on SWaT and WADI have also employed MSE under similar settings, which ensures comparability with existing baselines. While other robust losses (e.g., L1 loss or Huber loss) could potentially relax the Gaussian assumption, we empirically found MSE sufficient to achieve strong performance in our experiments. The loss function is therefore defined as the deviation between the predicted output and the observed data :
Note that these deviations may exhibit temporal correlation due to the dynamics of multivariate time series. Unlike traditional control-chart methods that assume independent residuals, our approach calibrates anomaly thresholds on validation data, which implicitly accounts for such correlations.
The pseudo-code of the training phase is summarized in Algorithm 1.
| Algorithm 1: Pseudo-code of Training Phase |
| Input: Input signal: , Sliding window size: , Ground truth data at time : . Initialize model parameters end for Backpropagate loss and update model parameters using Adam optimizer. Output: Epoch loss end for Return trained model parameters |
4. Discussion
In this section, we discuss the key insights and findings from the proposed anomaly detection method. We focus on several important aspects, including anomaly scoring, time complexity, scalability, threshold calibration, and the challenges of deploying the model in dynamic, real-world environments. We also highlight potential optimizations and adaptations that can improve the model’s performance and applicability across various domains.
4.1. Anomaly Scoring
In the testing phase, the deviation between the observed data and the model prediction is used as the anomaly score. Because these deviations may exhibit temporal correlation, we do not assume independence as in classical control-chart methods. Instead, the detection threshold is calibrated on a held-out validation set, so that the correlation structure of the residuals is implicitly taken into account. At time , the deviation for the -th sensor is computed as
Since the distribution of errors can be skewed, each sensor’s deviation is normalized in a robust manner:
where and denote the median and the interquartile range (IQR) of the error distribution for the -th sensor, respectively. This construction is essentially a robust Z-score, making it less sensitive to skewness and outliers compared to variance-based normalization. The system-level anomaly score is then defined as the maximum normalized deviation across sensors:
This heuristic highlights the strongest signal among all sensors, which works effectively in practice but does not explicitly capture cross-sensor correlations. Incorporating more rigorous multivariate control statistics, such as Hotelling’s , is a promising direction for future work.
The pseudo-code of the testing phase is summarized in Algorithm 2.
| Algorithm 2: Pseudo-code of Testing Phase |
| Input: Input signal: , Sliding window size: , Ground truth data at time t: . Output: Anomaly detection result . Initialize trained model parameters . The detection threshold is calibrated on a held-out validation set by sweeping candidate values and selecting the one that maximizes the F1-score. Append to end for Return |
4.2. Time Complexity Analysis
In this section, we analyze the time complexity of our proposed model during both the training phase and testing phase. The complexity is influenced by several factors, including the number of time steps (for training) and (for testing), the sliding window size , and the number of sensors . Below, we provide a detailed breakdown of the time complexity for each operation involved in both phases. Table 2 summarizes the time complexity of each operation in both the training and testing phases.

Table 2.
Time complexity per module.
The time complexity of the training phase depends on several components. Each operation, including the Temporal Graph Structure Learner (TGSL), Cross-Temporal Dynamic Encoder (CTDE), Cross-Variable Dynamic Encoder (CVDE), Spatiotemporal Mixer (TSM), and the neural network prediction, involves processing data at each time step. Thus, the total time complexity for the training phase is .
The testing phase follows a similar structure to the training phase, but without backpropagation. Each operation in the testing phase has the same complexity as in the training phase, but we only perform forward passes. Therefore, the total time complexity for the testing phase is .
The time complexity analysis shows that the model’s complexity scales quadratically with the number of sensors and is linearly dependent on the sliding window size and the number of time steps in both the training and testing phases. The training complexity is higher due to the iterative process over multiple epochs, while the testing phase involves only forward passes, making it less computationally intensive. This analysis quantifies the computational demands of our approach and informs assessments of scalability. Nevertheless, practical limitations are more likely to arise from theoretical aspects—e.g., robustness to distribution shift and threshold calibration—than from computation; strengthening these aspects will be a focus of future work.
4.3. Scalability and Optimization
The time–complexity analysis indicates that the dominant cost grows quadratically with the number of sensors (due to variable–variable interactions) and approximately linearly with the window length and the number of time steps in both training and testing. While this characterization clarifies computational demands, it also highlights potential challenges when scaling to hundreds or thousands of sensors in large IoT/industrial systems.
To mitigate these costs, the following strategies can be applied in practice or explored in future work; they target either the variable–variable terms, the temporal mixing cost, or both.
- Sparse/dilated temporal neighbors. In temporal modules, restrict attention to adjacent time steps plus at most across-time links (e.g., dilated offsets). This replaces dense interactions with .
- Approximate similarity for CVDE. When CVDE relies on DTW, employ a Sakoe–Chiba band or soft-DTW with a small bandwidth , optionally preceded by piecewise aggregate approximation (PAA). This changes per-pair cost from to with .
- Low-rank/linear attention. Replace quadratic attention with kernelized/low-rank variants so a layer scales as with small rank , rather than
- Group-level mixing. Cluster sensors into functional groups (via long-term correlation/MI or domain taxonomy), perform mixing at the group level (), then refine within groups.
Several of them are compatible with the current framework and can be combined; a systematic study of the accuracy–efficiency trade-offs is a promising direction for future work.
4.4. Domain Applicability and Adaptation
Our experiments use industrial control datasets, where variables correspond to sensors/actuators with relatively regular sampling. Applying DTS-MixNet to non-industrial multivariate time series (e.g., healthcare, finance) raises distinct challenges: irregular sampling and missingness, non-stationarity/regime shifts, heterogeneous variable semantics, and privacy constraints. We outline adaptations within our framework:
- Domain priors for spatial graphs. Augment dynamically learned graphs with prior structure (e.g., clinical ontologies, market sector/industry taxonomies) via Laplacian or edge-level regularization, yielding prior-regularized dynamic graphs that respect domain knowledge while remaining adaptive.
- Shift-robust thresholding. Instead of a single fixed threshold, employ validation-based quantile calibration or conformal prediction for per-deployment calibration; update thresholds online with a small sliding validation buffer to accommodate regime changes.
- Self-supervised pretraining. Pretrain TGSL/CTDE with masked forecasting/reconstruction on large heterogeneous MTS, then fine-tune on the target domain; this preserves the architecture and improves data efficiency under limited labels.
Although we report results only on ICS benchmarks, a more comprehensive evaluation on out-of-domain datasets (such as healthcare, finance, etc.) will be an important direction for future work.
4.5. Threshold Calibration and Adaptation
The fixed threshold used in our offline evaluation (selected on a held-out validation split and fixed for the test set) ensures comparability across methods. In dynamic deployments, however, normal behavior may drift over time, suggesting the use of adaptive calibration. Let denote a sliding calibration buffer of size , which stores recent anomaly scores. We outline practical, model-agnostic strategies that are compatible with our scoring framework:
- (1)
- Rolling quantile calibration (lightweight).
Populate with predicted-normal windows (e.g., ) and update the threshold as
where denotes the empirical -quantile of the scores in and is a safety margin. When (cold start), fall back to the validation-tuned . Here, denotes the minimum buffer size required for reliable recalibration, typically set between and .
- (2)
- Conformal prediction with a sliding calibration set.
Treat as a nonconformity score and maintain a calibration set of size . At each time step, compute the conformal -value as
An anomaly is flagged if . Here, denotes the target significance level, which controls the tolerated false alarm rate when interpreting . This procedure provides finite-sample error control under exchangeability assumptions, and effectively replaces a fixed threshold with a time-varying decision rule without changing the underlying model.
4.6. Real-Time Deployment and Challenges
In real-world industrial applications, real-time deployment introduces several critical challenges that must be addressed to ensure the practical usability of anomaly detection models. These include issues related to inference latency, streaming data processing, and robustness to missing sensor values. Below, we outline these aspects and how they might be addressed within the context of DTS-MixNet.
Inference Latency: Real-time systems require that anomaly detection models make predictions with minimal latency to allow for timely intervention. While the current DTS-MixNet architecture may involve complex graph computations, which can be computationally intensive, we propose the following approaches to optimize latency: (i) model pruning, where less critical parts of the graph are simplified, (ii) batching inputs in streaming settings to reduce the overhead of graph-based computations, and (iii) parallelization techniques such as multi-threading or GPU acceleration to speed up inference times. We plan to assess these optimization strategies in future work to improve real-time deployment performance.
Handling Streaming Data: In real-world settings, anomaly detection must often be performed on streaming data, where new sensor readings are continuously fed into the system. Our current approach handles sliding windows of fixed length, but for a true real-time deployment, future work will focus on extending this model to work with online learning techniques. This would allow the model to update its parameters incrementally as new data arrives, ensuring that it remains adaptable to changes in the system over time.
Robustness to Missing Sensor Values: Missing sensor values are a common challenge in industrial systems due to sensor failures, communication issues, or temporary disconnects. To enhance the robustness of DTS-MixNet, we will explore imputation strategies (e.g., mean imputation,-NN imputation, or even model-based imputation via auxiliary models). Additionally, we will investigate the possibility of masking missing values during the graph construction and learning process to prevent them from adversely affecting the model’s predictions.
Addressing these challenges is crucial for ensuring that DTS-MixNet can be deployed in dynamic, real-world environments. Future work will investigate these aspects in more detail, potentially through experiments and optimization techniques tailored for real-time performance.
5. Experiments
5.1. Dataset
This paper utilizes two real-world benchmark datasets to evaluate multivariate time series anomaly detection methods: SWaT [6] and WADI [45]. SWaT (Secure Water Treatment) and WADI (Water Distribution) are two widely used industrial control system (ICS) datasets for cybersecurity and anomaly detection research. They are primarily employed to detect and study potential attacks or anomalous behaviors in industrial systems.
- SWaT is a model of a small-scale water treatment plant, simulating six stages of a real-world water treatment process, including chemical treatment, filtration, and purification. The plant is equipped with various sensors and actuators. The dataset consists of time series data from multiple sensors and actuators, capturing both non-anomalous operations and attack scenarios.
- WADI is a model of a water distribution network that simulates the water distribution process in the real world, covering multiple stages from water storage to distribution. This system is more complex than SWaT and involves larger-scale operations. The WADI dataset records sensor readings and actuator states, with the data also being time series, encompassing both non-anomalous operations and intentionally injected attack behaviors.
The specific details about above two datasets are summarized in Table 3.

Table 3.
Statistics about two datasets.
5.2. Baseline Methods
We compared the performance of our method with seven popular anomaly detection methods, including:
- LSTM-VAE (Long Short-Term Memory Variational Autoencoder) [46]: This model combines Long Short-Term Memory (LSTM) networks with a Variational Autoencoder (VAE), primarily used for anomaly detection in time series data. The model leverages LSTM’s ability to capture temporal dependencies and VAE’s capability in generating and modeling complex data distributions.
- DAGMM (Deep Autoencoding Gaussian Mixture Model) [47]: A deep learning method for anomaly detection that integrates an Autoencoder with a Gaussian Mixture Model (GMM). It is effective in detecting anomalies in high-dimensional data.
- MAD-GAN (Multivariate Anomaly Detection using Generative Adversarial Networks) [48]: A GAN-based method for anomaly detection in multivariate time series. MAD-GAN uses a generator-discriminator architecture to learn the distribution of time series data, detecting anomalies based on the discriminator’s ability to distinguish between non-anomalous and anomalous data.
- MTAD-GAT (Multivariate Time-series Anomaly Detection using Graph Attention Networks) [49]: This method uses Graph Attention Networks (GAT) for multivariate time series anomaly detection. It efficiently captures the complex dependencies between variables in time series data and detects anomalies by modeling dynamic changes over time.
- GDN (Graph Deviation Network) [12]: A multivariate time series anomaly detection method based on Graph Neural Networks (GNN). GDN builds and learns a relational graph between different variables in time series data, capturing the dependencies between them to detect anomalies. It identifies anomalies by learning deviations from non-anomalous behavior using GNNs.
- GRN (GRU-based Interpretable Multivariate Time Series Anomaly Detection Model) [50]: GRN is a deep learning model that combines GRU (Gated Recurrent Unit) and interpretability techniques, designed to handle multivariate time series data from multiple sensors in industrial control systems. The model learns the temporal dependencies within the time series to capture non-anomalous patterns and identifies anomalies by calculating the prediction error.
- ECNU-GNN (Edge Conditional Node Update Graph Neural Network) [51]: This model is a graph neural network-based model for multivariate time series anomaly detection, which captures complex temporal and relational dependencies by conditionally updating node states. The model represents time series data as a graph, where each node corresponds to a time step or sensor, and edges represent the relationships between them. By conditionally updating node states based on edge features, ECNU-GNN can more accurately learn non-anomalous behavior patterns and effectively detect anomalies in systems, making it particularly useful for anomaly detection in complex environments like sensor networks and industrial control systems.
5.3. Evaluation Metrics
We evaluate the performance of our method and other baseline models using precision (Prec), recall (Rec), and F1-score (F1) on the test dataset for anomaly detection. These metrics are defined as follows:
Precision (Prec): Precision is the ratio of true anomalies correctly identified by the model to the total number of data points predicted as anomalies.
It measures the model’s ability to avoid false positives, indicating how accurate the anomaly predictions are.
Recall (Rec): Recall is the ratio of true anomalies correctly identified by the model to the total number of actual anomalies in the dataset.
It evaluates the model’s capability to detect as many true anomalies as possible, focusing on minimizing false negatives.
F1-Score (F1): The F1-score is the harmonic mean of precision and recall. It balances the trade-off between precision and recall, especially when dealing with imbalanced data.
A higher F1-score reflects an improved harmonic mean of precision and recall, indicating that the model is simultaneously achieving higher detection coverage and lower false alarms. Nonetheless, the F1-score has inherent limitations: it implicitly weights precision and recall equally and may be misleading in skewed or safety-critical scenarios. Therefore, while F1 provides a convenient summary metric for comparative evaluation, it should be interpreted alongside precision and recall rather than as a definitive indicator of performance.
Moreover, while precision, recall, and F1-score are widely used in machine learning evaluations and facilitate direct comparison with prior anomaly detection studies, they do not fully capture the asymmetric importance of false alarms versus missed detections in industrial control systems. In statistical process monitoring, thresholds are often chosen to control the false alarm rate (FAR) or the in-control average run length (IC ARL). In our framework, the threshold is tuned on a validation set to maximize the F1-score, ensuring consistency with existing baselines. Extending the framework to incorporate FAR- or ARL-based thresholding criteria should be an important direction for future research.
5.4. Experimental Setup
- (1)
- Parameter Selection
Our model was trained end-to-end using the Adam optimizer with a learning rate set to . Training was conducted for epochs, and of the training samples were reserved as a validation set to monitor convergence and prevent overfitting. The number of nearest across-time neighbors was set to for the SWaT dataset and for the WADI dataset. The number of attention heads in the Temporal Graph Structure Learner (TGSL) was set to . The parameter , used for constructing the local graph, was set to for SWaT and WADI, while , used for constructing the global graph, was set to for SWaT and WADI. The Dilated Inception Layer (DIL) within the Spatiotemporal Mixer (TSM) utilized a kernel size combination of . The hidden channel dimension for intermediate representations was configured to . For all datasets, the time window length was set to , the number of sub-blocks was set to , and the sub-block length was set to . This configuration ensures consistency across datasets while allowing the model to adapt to the unique characteristics of each one.
All hyperparameters were tuned on a held-out validation split using a grid search with a blocked temporal split (train validation test) to avoid temporal leakage. For each candidate configuration, the model was trained for up to epochs with early stopping on the validation loss. After training, the anomaly detection threshold was calibrated on the validation set by sweeping candidate values and selecting the one that maximized the validation F1-score, balancing false positives and false negatives. The best configuration was then re-trained on the combined training and validation sets, and the fixed was applied for testing. This procedure ensures comparability with existing baselines while preventing information leakage.
The specific grid ranges explored for each hyperparameter are summarized in Table 4. We focus the sensitivity analysis on the sliding-window length and the number of attention heads (see Section 5.9), as these parameters directly control the temporal receptive field and attention capacity of TGSL/CTDE. Other hyperparameters were fixed to the values yielding the best validation performance for fairness and computational efficiency.

Table 4.
Hyperparameter search ranges.
- (2)
- Baseline Setup.
All reproduced baselines were trained under a unified configuration: epochs, window length , stride , and—where applicable—attention heads . We used the Adam optimizer with a fixed learning rate across reproduced methods. All models shared the same train/validation/test splits and Z-score normalization (statistics from training only). To avoid threshold-selection artifacts, the decision threshold for each method was tuned on a held-out validation split by maximizing F1 and then kept fixed for the test set.
5.5. Comparative Study
Table 5 presents the evaluation results for all compared models across the specified metrics, which is shown by the anomaly detection accuracy including precision, recall and F1-score. For ECNU-GNN, the experimental results are from the literature [51]. Notably, DTS-MixNet achieves the highest precision among the methods compared. While other graph-based methods, such as GDN, MTAD-GAT, and ECNU-GNN, also achieve commendable performance, underscoring the general effectiveness of graph structures in capturing inter-variable relationships within MTS, DTS-MixNet achieves further improvements.

Table 5.
The accuracy in terms of precision (%), recall (%) and F1-score.
While bootstrap confidence intervals could in principle provide additional statistical rigor, we follow the prevailing practice in anomaly detection benchmarks and report only point estimates for clarity and comparability.
Overall, the results indicate measurable gains of DTS-MixNet over strong graph baselines on both datasets. Consistent with common practice in anomaly detection benchmarks, we report point estimates rather than bootstrap confidence intervals for clarity and comparability.
5.6. Ablation Study
To quantitatively evaluate the impact and necessity of each core component within the proposed CDTS-MixNet framework, we conducted comprehensive ablation experiments on the SWaT and WADI datasets. In these experiments, specific modules or mechanisms were systematically removed or simplified, and the resulting impact on anomaly detection precision was measured. The detailed settings are presented below, and the results summarized in Table 6.

Table 6.
The precision (%) after removing core components.
Temporal Modeling Settings:
The Temporal Graph Structure Learner (TGSL) and Cross-Temporal Dynamic Encoder (CTDE) are designed to capture intricate dependencies along the time axis. We evaluated their importance through the following ablation settings:
- w/o Temporal Attention: The multi-head attention mechanism (Equations (7) and (8)) within TGSL was removed. Instead, the aggregation in CTDE (Equation (10)) used simpler, non-learned weights (e.g., uniform weights based on the binary graph from Equation (6)).
- w/o Across-Time Neighbors: The learned across-time neighbors (, Equation (3)) were excluded from TGSL. Only the adjacent-time neighbors (, Equation (4)) were used to construct the temporal graph.
- w/o Temporal Graph Modeling: The entire TGSL and CTDE pipeline was bypassed. The raw input sequence was directly fed into subsequent modules, isolating the contribution of dynamic temporal graph learning and encoding.
Spatial Modeling Settings:
The Cross-Variable Dynamic Encoder (CVDE) focuses on capturing relationships between sensors (variables). Its contribution was assessed via the following:
- w/o Spatial Graphs: Local and global spatial graph ( and , Equations (12)–(14)) were replaced. Instead, a single, static graph (e.g., -Nearest Neighbors approach,) was used for the spatial mixing in TSM.
- w/o TSM Feature Enhancement: The initial feature enhancement steps within the TSM specifically the Convolution and the Dilated Inception Layer (DIL) were removed. Consequently, the Proxy Multivariate Sequence , after being segmented into , was directly fed into the MixHop component.
The results demonstrate a significant performance drop across all ablation scenarios, particularly when the entire dynamic temporal modeling is removed (w/o Temporal Graph Modeling) or when dynamic spatial graphs are replaced by static ones (w/o Spatial Graphs). This confirms that explicitly modeling dynamic temporal relationships (including both adjacent and weighted across-time dependencies) is crucial. Furthermore, the decrease in precision observed in the w/o Spatial Graphs setting highlights the critical importance of adaptively capturing inter-variable relationships based on the current window’s context using DTW (via CVDE), rather than relying solely on static assumptions. The removal of TSM feature enhancement (w/o TSM Feature Enhancement) also indicates the value of refining the temporal representations before spatiotemporal fusion.
5.7. Interpretability of Model
In this section, we explore the interpretability of our model, focusing on two critical aspects: the interpretability of sensor embeddings and the interpretability of attacks. These components provide valuable insights into how the model makes decisions, enabling us to understand and trust the results of the anomaly detection process.
- (1)
- Interpretability of Embedding Vectors for Sensors
We present the t-SNE visualizations of sensor embeddings for both the SWaT and WADI datasets. These visualizations provide insight into how sensor embeddings, learned by our model, are organized in a low-dimensional space, reflecting the similarity of the sensors based on their measurements.
Figure 3a shows the t-SNE [52] representation of the learned sensor embeddings on SWaT colored by eight sensor classes. We observe that sensors such as HMI_FIT101, HMI_FIT201, and HMI_FIT301 form a distinct cluster, indicating that these sensors, which measure similar parameters in the SWaT system, are closely embedded in the low-dimensional space. This clustering highlights the model’s ability to capture the functional relationships between sensors. The inset further emphasizes this by zooming in on the cluster of HMI_FIT sensors, which are closely related.

Figure 3.
t-SNE visualizations of sensor embeddings: (a) SWaT dataset; (b) WADI dataset.
Similarly, Figure 3b illustrates the t-SNE representation for the WADI dataset, which contains sensor classes. Despite the increased complexity, clear clustering patterns are still evident. Sensors like 2_FIC_101_SP, 2_FIC_201_SP, and 2_FIC_301_SP form a compact cluster, demonstrating that the model effectively captures the functional relationships between sensors in the WADI system. The inset highlights this specific cluster of 2_FIC sensors, showing how closely they are embedded in relation to each other.
These visualizations confirm the effectiveness of the learned embeddings in capturing both temporal and spatial dependencies, as the model groups sensors that measure similar parameters together in the embedding space. The tight local clusters are a key feature, enhancing the interpretability of the sensor representations learned by the model.
- (2)
- Interpretability of Attacks
The goal of this experiment is to reveal which sensors our model flags as most anomalous during attack periods and how these sensors interact with the rest of the network. Figure 4a,b show sensor graphs for the SWaT and WADI datasets. In these graphs, each node represents a sensor, and the edges between them represent functional dependencies. The red triangles indicate the sensors with the highest anomaly scores, which are the most likely to be affected by an attack or exhibit anomalous behavior.

Figure 4.
Sensor graphs with anomaly detection: (a) SWaT dataset; (b) WADI dataset.
In Figure 4a (SWaT), HMI_MV_101_STATUS has the highest anomaly score, suggesting it could be the compromised sensor or closely related to an attacked sensor. The graph highlights the strong correlation between HMI_MV_101_STATUS and HMI_LIT_101_PV, indicating that HMI_LIT_101_PV measures and transmits information about raw water volume and valve liquid level, controlled by HMI_MV_101_STATUS. Similarly, in Figure 4b (WADI), 1_MV_001_STATUS shows the highest anomaly score, and it is strongly connected to 1_AIT_001_PV and 1_FIT_001_PV, suggesting a critical relationship between these sensors. The red triangle indicates that 1_MV_001_STATUS might be affected by an anomaly, which could propagate to related sensors.
These visualizations help identify critical sensors and their interdependencies, demonstrating the model’s ability to capture functional relationships and detect anomalies within the system.
The purpose of this experiment is to evaluate the interpretability of our model in detecting anomalous behaviors associated with potential attacks. By analyzing the predicted sensor values against the observed ones, we aim to identify which sensors exhibit anomalous behavior during the attack periods, helping us better understand the model’s decision-making process. Figure 5a,b show the predicted and observed values for sensors from the SWaT and WADI datasets, respectively. The red-highlighted areas represent the regions identified as anomalies by our model.
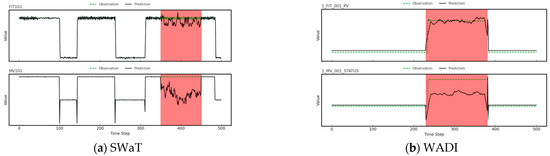
Figure 5.
Anomaly detection results: (a) SWaT dataset; (b) WADI dataset.
Figure 5a illustrates the anomaly detection for sensors in the SWaT dataset. The top plot shows the FIT101 sensor, where the prediction (solid black line) deviates significantly from the observation (dashed green line) in the red-highlighted region, indicating an anomaly. Similarly, in the bottom plot, the MV101 sensor exhibits a clear discrepancy between the predicted and observed values in the same region, further confirming the detection of an anomaly. Figure 5b presents the anomaly detection results for the WADI dataset. The top plot shows 1_FIT_001_PV, where the predicted values diverge from the observed values in the red area, signaling an anomaly. In the bottom plot, the 1_MV_001_STATUS sensor also shows a similar deviation in the red-highlighted region, identifying it as another anomalous behavior.
The red-highlighted regions in both figures represent the times when the sensors exhibit unusual behavior, which is crucial for understanding system faults or potential attacks. These visualizations demonstrate how the model identifies and isolates anomalies by comparing predicted and observed sensor readings.
- (3)
- Practical Implications and Future Work
While the embedding and attack interpretability analysis provides important insights into how our model detects anomalies, further expansion of this section could be beneficial for practitioners in real-world applications. Based on our current findings, we outline practical directions for enhancing the interpretability and utility of DTS-MixNet:
- Sensor Role Identification: By examining the clusters in the sensor embedding space, we can classify sensors based on their functional roles in the system. This could help practitioners understand which sensors are crucial for the overall system health, and prioritize them for
- Real-time Anomaly Monitoring: To improve the practical utility of our model, we are exploring ways to incorporate these interpretability features into a real-time monitoring dashboard. This would allow operators to visualize sensor embeddings, track anomalies, and identify critical sensors in the context of their system, making anomaly detection more actionable and transparent.
Future work will focus on enhancing the interpretability of the model by providing not only visualizations but also more actionable insights. This could include tools such as attribution summaries, time–sensor heatmaps, and detailed analysis of anomaly propagation, which would make the anomaly detection process more understandable and useful for practitioners.
5.8. Correlation Heatmap Analysis
It is insightful to visualize the inherent complexity of inter-sensor relationships within real-world multivariate time series data. To this end, Figure 6 presents the correlation matrix heatmap calculated for the SWaT dataset. This visualization underscores the necessity for models capable of capturing complex cross-variable interactions, motivating design choices within CDTS-MixNet, particularly the Cross-Variable Dynamic Encoder (CVDE).
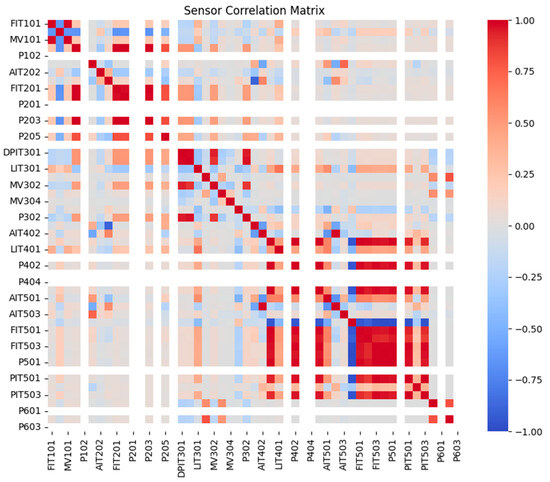
Figure 6.
Correlation matrix heatmap of SWaT dataset.
The heatmap reveals several key characteristics indicative of complex system behavior:
- Strong Correlations: Distinct blocks of strong positive (deep red) and negative (deep blue) correlations are clearly evident between various sensor pairs. For example, notable correlations exist within the AIT501-FIT503 sensor block. This signifies strong mutual influence or dependency between these sensors, highlighting that they cannot be effectively modeled in isolation.
- Group Structures: Clusters of sensors often exhibit similar correlation patterns when compared to other groups. For instance, the sensors in the PIT501-P603 group demonstrate cohesive behavior in their correlations. These groupings may hint at underlying functional modules or subsystems within the monitored physical process.
This analysis of inherent data complexity sets the stage for the subsequent ablation study. Having visually established the importance of capturing inter-sensor dependencies, we will now quantitatively assess how effectively the different components of CDTS-MixNet contribute to this goal and impact overall anomaly detection performance.
5.9. Sensitivity
In this experiment, we investigate the impact of two critical hyperparameters—sliding window length and number of attention heads —on the model performance, measured by the F1 score. We conducted experiments on two datasets, SWaT and WADI, to assess the sensitivity of the model to these hyperparameters.
- (1)
- Sliding Window Length
The sliding-window length controls the temporal receptive field: larger incorporates longer context, whereas smaller emphasizes recent dynamics with higher variance.
In Figure 7a, we show the F1 score variations for different sliding window lengths on the SWaT and WADI datasets. The selected window lengths are 10, 20, 30, 40, 50, and 60. To ensure fair comparison, the sub-block length was fixed at 5 in all settings, regardless of the value of . The F1 score increases gradually as the sliding window length increases. Notably, when the window length reaches 30, there is a significant improvement in performance. Longer windows allow the model to capture deeper temporal dependencies, thus improving the F1 score.
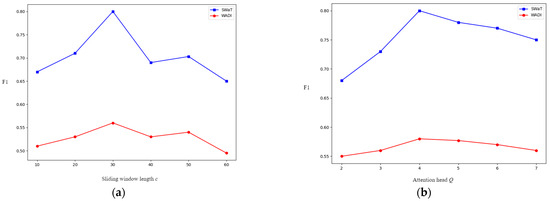
Figure 7.
Sensitivity analysis of hyperparameters: (a) sliding window length ; (b) number of attention heads .
- (2)
- Number of Attention Heads
controls the number of parallel attention distributions used to aggregate information from neighbors. A larger lets the model attend to multiple, complementary dependency patterns in parallel, but also increases computation and can introduce redundancy when different heads learn similar patterns (with fixed model width, each head receives fewer channels).
In Figure 7b, we vary . On SWaT, F1 improves from to and then saturates with small fluctuations, indicating diminishing returns beyond four heads under our protocol. On WADI, the curve is flatter: additional heads yield smaller gains, likely because higher variability reduces the benefit of adding overlapping heads. Overall, provides a reasonable trade-off between modeling diverse dependencies and computational cost.
6. Conclusions
This paper addressed the challenge of multivariate time series anomaly detection, focusing on the dynamic dependencies across both time and variables. We proposed the Dynamic Spatiotemporal Graph Mixed Network (DTS-MixNet), an effective framework designed to tackle this challenge. DTS-MixNet uniquely integrates dynamic graph learning for both temporal evolution (via TGSL and CTDE) and spatial interactions (via CVDE with DTW), followed by effective spatiotemporal fusion using a MixHop-based TSM.
Ablation studies further validated the significant contributions of its core components, confirming the importance of dynamically modeling and fusing both temporal and spatial information. While computationally more intensive than simpler models, DTS-MixNet effectively captures the intricate dynamics missed by conventional approaches. Future work could explore computational optimizations, enhanced interpretability, and applications in diverse real-world scenarios. In essence, DTS-MixNet provides a robust and effective approach for improving anomaly detection accuracy in complex, interconnected systems by adaptively learning and leveraging dynamic spatiotemporal dependencies.
Author Contributions
Conceptualization, C.T. and J.H.; methodology, C.T. and W.H.; validation, J.L.; formal analysis, C.T.; resources, M.M. and S.W.; data curation, J.L.; writing—original draft preparation, C.T. and J.H.; writing—review and editing, C.T., M.M., W.H. and S.W.; supervision, M.M., W.H. and S.W.; funding acquisition, W.H. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by grants from the National Natural Science Foundation of China (Nos. 62101189 and U20A20228).
Data Availability Statement
The data presented in this study (SWaT and WADI) are available in the public domain at https://itrust.sutd.edu.sg/itrust-labs_datasets/ (accessed on 24 July 2025).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tax, D.M.J.; Duin, R.P.W. Support vector data description. Mach. Learn. 2004, 54, 45–66. [Google Scholar] [CrossRef]
- Kim, S.; Choi, Y.; Lee, M. Deep learning with support vector data description. Neurocomputing 2015, 165, 111–117. [Google Scholar] [CrossRef]
- Zhai, S.; Cheng, Y.; Lu, W.; Zhang, Z. Deep structured energy based models for anomaly detection. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1100–1109. [Google Scholar]
- Angiulli, F.; Pizzuti, C. Fast Outlier Detection in High Dimensional Spaces. In Principles of Data Mining and Knowledge Discovery; Springer: Berlin/Heidelberg, Germany, 2002; pp. 15–27. [Google Scholar]
- Keogh, E.; Lin, J.; Fu, A. HOT SAX: Efficiently finding the most unusual time series subsequence. In Proceedings of the Fifth IEEE International Conference on Data Mining (ICDM’05), Houston, TX, USA, 27–30 November 2005. [Google Scholar]
- Mathur, A.P.; Tippenhauer, N.O. SWaT: A water treatment testbed for research and training on ICS security. In Proceedings of the 2016 International Workshop on Cyber-Physical Systems for Smart Water Networks (CySWater), Vienna, Austria, 11 April 2016; pp. 31–36. [Google Scholar]
- Choi, K.; Yi, J.; Park, C.; Yoon, S. Deep learning for anomaly detection in time-series data: Review, analysis, and guidelines. IEEE Access 2021, 9, 120043–120065. [Google Scholar] [CrossRef]
- Wen, T.; Keyes, R. Time series anomaly detection using convolutional neural networks and transfer learning. arXiv 2019, arXiv:1905.13628. Available online: https://arxiv.org/abs/1905.13628 (accessed on 13 July 2025). [CrossRef]
- An, J.; Cho, S. Variational autoencoder based anomaly detection using reconstruction probability. Spec. Lect. IE 2015, 2, 1–18. [Google Scholar]
- Akcay, S.; Atapour-Abarghouei, A.; Breckon, T.P. GANomaly: Semi-supervised anomaly detection via adversarial training. In Computer Vision—ACCV 2018; Springer: Cham, Switzerland, 2019; pp. 622–637. [Google Scholar]
- Lin, S.; Clark, R.; Birke, R.; Schönborn, S.; Trigoni, N.; Roberts, S. Anomaly detection for time series using VAE-LSTM hybrid model. In Proceedings of the ICASSP 2020—2020 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, 4–8 May 2020; pp. 4322–4326. [Google Scholar]
- Deng, A.; Hooi, B. Graph neural network-based anomaly detection in multivariate time series. In Proceedings of the AAAI Conference on Artificial Intelligence, Virtual, 2–9 February 2021; Volume 35, pp. 4027–4035. [Google Scholar]
- Zhang, W.; Zhang, C.; Tsung, F. GRELEN: Multivariate time series anomaly detection from the perspective of graph relational learning. In Proceedings of the Thirty-First International Joint Conference on Artificial Intelligence, Vienna, Austria, 23–29 July 2022; pp. 2390–2397. [Google Scholar]
- Chen, K.; Feng, M.; Wirjanto, T.S. Multivariate time series anomaly detection via dynamic graph forecasting. arXiv 2023, arXiv:2302.02051. Available online: https://arxiv.org/abs/2302.02051 (accessed on 13 July 2025). [CrossRef]
- Yin, S.; Ding, S.X.; Haghani, A.; Hao, H.; Zhang, P. A comparison study of basic data-driven fault diagnosis and process monitoring methods on the benchmark Tennessee Eastman process. J. Process Control 2012, 22, 1567–1581. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Jaeckle, C.; Kiparissides, C.; Koutoudi, M. Process monitoring and diagnosis by multiblock PLS methods. AIChE J. 1994, 40, 826–838. [Google Scholar] [CrossRef]
- Russell, E.L.; Chiang, L.H.; Braatz, R.D. Fault detection in industrial processes using canonical variate analysis and dynamic principal component analysis. Chemom. Intell. Lab. Syst. 2000, 51, 81–93. [Google Scholar] [CrossRef]
- Schlegl, T.; Seebock, P.; Waldstein, S.M.; Langs, G.; Schmidt-Erfurthb, U. f-AnoGAN: Fast unsupervised anomaly detection with generative adversarial networks. Med. Image Anal. 2019, 54, 30–44. [Google Scholar] [CrossRef]
- Zhou, C.; Paffenroth, R.C. Anomaly detection with robust deep autoencoders. In Proceedings of the 23rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Halifax, NS, Canada, 13 August 2017; pp. 665–674. [Google Scholar]
- Jang, J.; Lee, H.H.; Park, J.A.; Kim, H. Unsupervised anomaly detection using generative adversarial networks in 1H-MRS of the brain. J. Magn. Reson. 2021, 325, 106936. [Google Scholar] [CrossRef]
- Staar, B.; Lütjen, M.; Freitag, M. Anomaly detection with convolutional neural networks for industrial surface inspection. Procedia CIRP 2019, 79, 484–489. [Google Scholar] [CrossRef]
- Zivot, E.; Wang, J. Vector autoregressive models for multivariate time series. In Modeling Financial Time Series with S-PLUS®; Springer: New York, NY, USA, 2006; pp. 385–429. [Google Scholar]
- Box, G.E.; Pierce, D.A. Distribution of residual autocorrelations in autoregressive-integrated moving average time series models. J. Am. Stat. Assoc. 1970, 65, 1509–1526. [Google Scholar] [CrossRef]
- Cao, L.J.; Tay, F.E.H. Support vector machine with adaptive parameters in financial time series forecasting. IEEE Trans. Neural Netw. 2003, 14, 1506–1518. [Google Scholar] [CrossRef]
- Connor, J.T.; Martin, R.D.; Atlas, L.E. Recurrent neural networks and robust time series prediction. IEEE Trans. Neural Netw. 1994, 5, 240–254. [Google Scholar] [CrossRef]
- Zhao, B.; Lu, H.; Chen, S.; Liu, J.; Wu, D. Convolutional neural networks for time series classification. J. Syst. Eng. Electron. 2017, 28, 162–169. [Google Scholar] [CrossRef]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Conditional time series forecasting with convolutional neural networks. arXiv 2018, arXiv:1703.04691. Available online: https://arxiv.org/abs/1703.04691 (accessed on 16 July 2025). [CrossRef]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in time series: A survey. In Proceedings of the Thirty-Second International Joint Conference on Artificial Intelligence, IJCAI-23, Macao, China, 19–25 August 2023; pp. 6778–6786. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Wu, Z.; Pan, S.; Chen, F.; Long, G.; Zhang, C.; Yu, P.S. A comprehensive survey on graph neural networks. IEEE Trans. Neural Netw. Learn. Syst. 2021, 32, 4–24. [Google Scholar] [CrossRef]
- Zhang, R.; Zhou, Z.; Zuo, Y.; Cui, Y.; Zhang, Z. Multivariate time series anomaly detection based on graph neural network and grated neural network. In Proceedings of the International Conference on Cyber Security, Artificial Intelligence, and Digital Economy (CSAIDE 2023), Nanjing, China, 3–5 March 2023; Volume 12718, p. 127180R. [Google Scholar]
- Xu, K.; Li, Y.; Li, Y.; Xu, L.; Li, R.; Dong, Z. Masked graph neural networks for unsupervised anomaly detection in multivariate time series. Sensors 2023, 23, 7552. [Google Scholar] [CrossRef]
- Lee, J.; Park, B.; Chae, D.K. DuoGAT: Dual time-oriented graph attention networks for accurate, efficient and explainable anomaly detection on time-series. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management, Birmingham, UK, 21–25 October 2023; pp. 1188–1197. [Google Scholar]
- Zhou, J.; Cui, G.; Hu, S.; Zhang, Z.; Yang, C.; Liu, Z.; Wang, L.; Li, C.; Sun, M. Graph neural networks: A review of methods and applications. AI Open 2020, 1, 57–81. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Bruna, J.; Zaremba, W.; Szlam, A.; LeCun, Y. Spectral networks and locally connected networks on graphs. arXiv 2013, arXiv:1312.6203. Available online: https://arxiv.org/abs/1312.6203 (accessed on 16 July 2025).
- Henaff, M.; Bruna, J.; LeCun, Y. Deep convolutional networks on graph-structured data. arXiv 2015, arXiv:1506.05163. Available online: https://arxiv.org/abs/1506.05163 (accessed on 16 July 2025). [CrossRef]
- Defferrard, M.; Bresson, X.; Vandergheynst, P. Convolutional neural networks on graphs with fast localized spectral filtering. In Advances in Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2016; p. 29. [Google Scholar]
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. arXiv 2016, arXiv:1609.02907. Available online: https://arxiv.org/abs/1609.02907 (accessed on 16 July 2025).
- Velickovic, P.; Cucurull, G.; Casanova, A.; Romero, A.; Lio, P.; Bengio, Y. Graph attention networks. Stat 2017, 1050, 10–48550. [Google Scholar]
- Müller, M. Dynamic time warping. In Information Retrieval for Music and Motion; Springer: Berlin/Heidelberg, Germany, 2007; pp. 69–84. [Google Scholar]
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the dots: Multivariate time series forecasting with graph neural networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 753–763. [Google Scholar]
- Abu-El-Haija, S.; Perozzi, B.; Kapoor, A.; Alipourfard, N.; Lerman, K.; Harutyunyan, H.; Steeg, G.V.; Salstyan, A. MixHop: Higher-order graph convolutional architectures via sparsified neighborhood mixing. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, CA, USA, 9–15 June 2019; Volume 97, pp. 21–29. [Google Scholar]
- Ahmed, C.M.; Palleti, V.R.; Mathur, A.P. WADI: A water distribution testbed for research in the design of secure cyber physical systems. In Proceedings of the 3rd International Workshop on Cyber-Physical Systems for Smart Water Networks, Pittsburgh, PA, USA, 21 April 2017; pp. 25–28. [Google Scholar]
- Park, D.; Hoshi, Y.; Kemp, C.C. A multimodal anomaly detector for robot-assisted feeding using an LSTM-based variational autoencoder. IEEE Robot. Autom. Lett. 2018, 3, 1544–1551. [Google Scholar] [CrossRef]
- Zong, B.; Song, Q.; Min, M.R.; Cheng, W.; Lumezanu, C.; Cho, D.; Chen, H. Deep autoencoding gaussian mixture model for unsupervised anomaly detection. In Proceedings of the 6th International Conference on Learning Representations, Vancouver, BC, Canada, 30 April–3 May 2018; pp. 1–19. [Google Scholar]
- Li, D.; Chen, D.; Jin, B.; Shi, L.; Goh, J.; Ng, S.K. MAD-GAN: Multivariate anomaly detection for time series data with generative adversarial networks. In Artificial Neural Networks and Machine Learning—ICANN 2019: Text and Time Series; Springer: Cham, Switzerland, 2019; pp. 703–716. [Google Scholar]
- Zhao, H.; Wang, Y.; Duan, J.; Huang, C.; Cao, D.; Tong, Y.; Xu, B.; Bai, J.; Zhang, Q. Multivariate time-series anomaly detection via graph attention network. In Proceedings of the 2020 IEEE International Conference on Data Mining (ICDM), Sorrento, Italy, 17–20 November 2020; pp. 841–850. [Google Scholar]
- Tang, C.; Xu, L.; Yang, B.; Tang, Y.; Zhao, D. GRU-based interpretable multivariate time series anomaly detection in industrial control system. Comput. Secur. 2023, 127, 103094. [Google Scholar] [CrossRef]
- Jo, H.; Lee, S.W. Edge conditional node update graph neural network for multivariate time series anomaly detection. Inf. Sci. 2024, 679, 121062. [Google Scholar] [CrossRef]
- Maaten, L.V.D.; Hinton, G. Visualizing data using t-SNE. J. Mach. Learn. Res. 2008, 9, 2579–2605. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).