Analysis of Highway Vehicle Lane Change Duration Based on Survival Model
Abstract
1. Introduction
2. Material and Methods
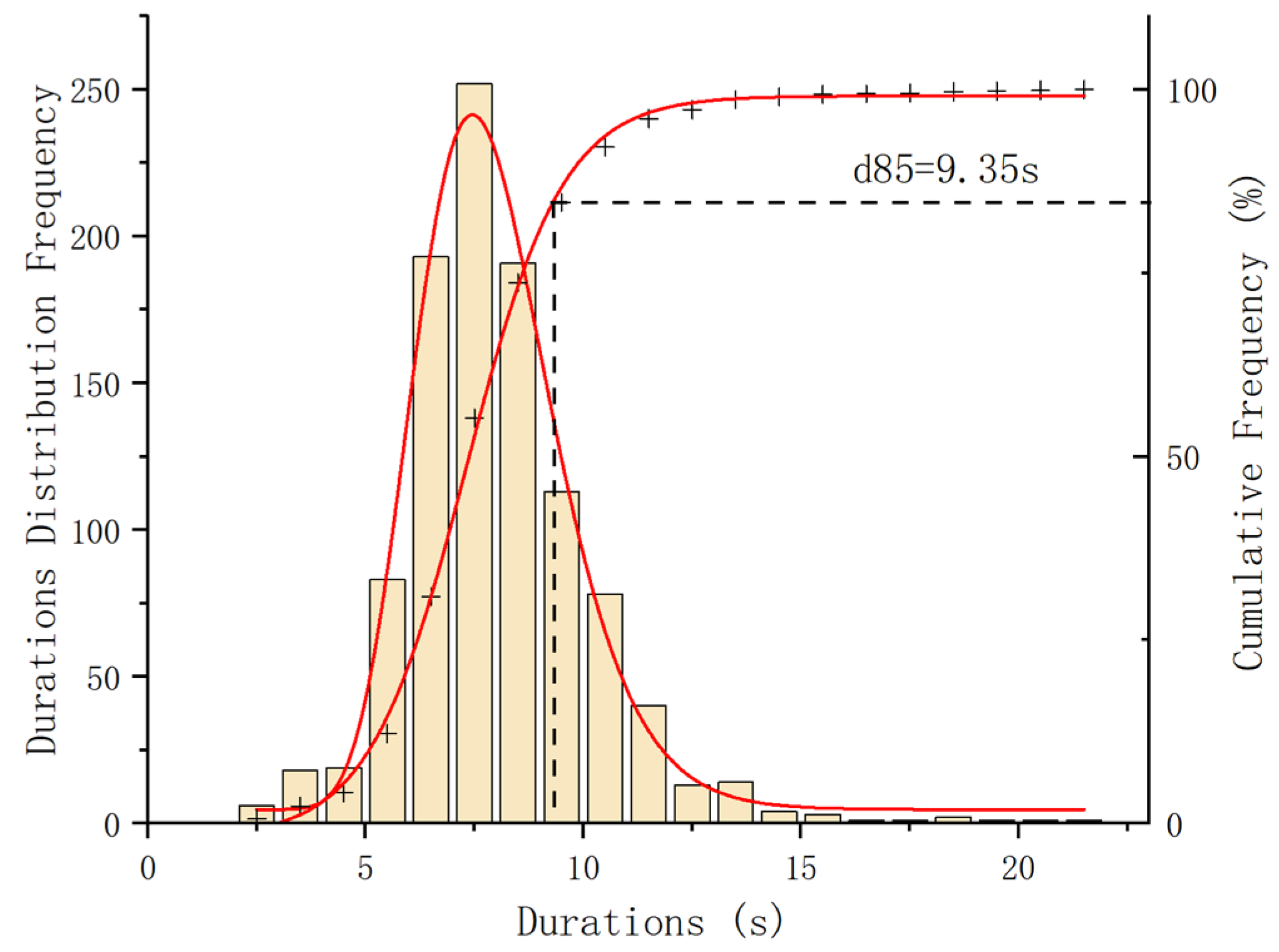
2.1. Data and Preprocessing
2.2. Methods
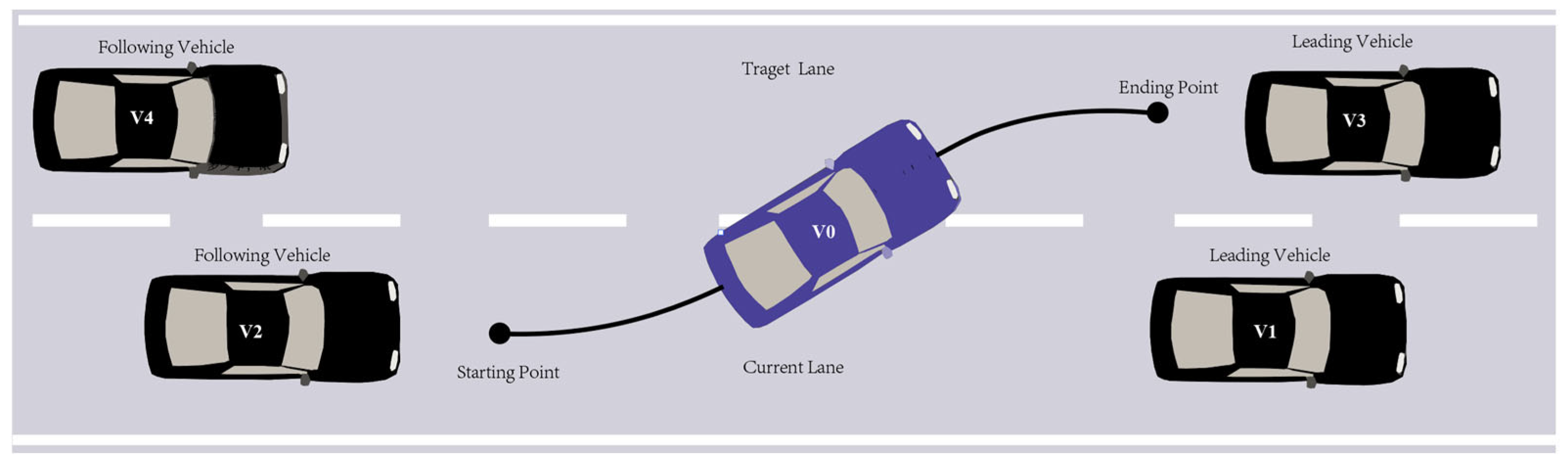
2.2.1. Problem Description
2.2.2. COX Proportional Hazards Model
2.2.3. Random Survival Forest Model
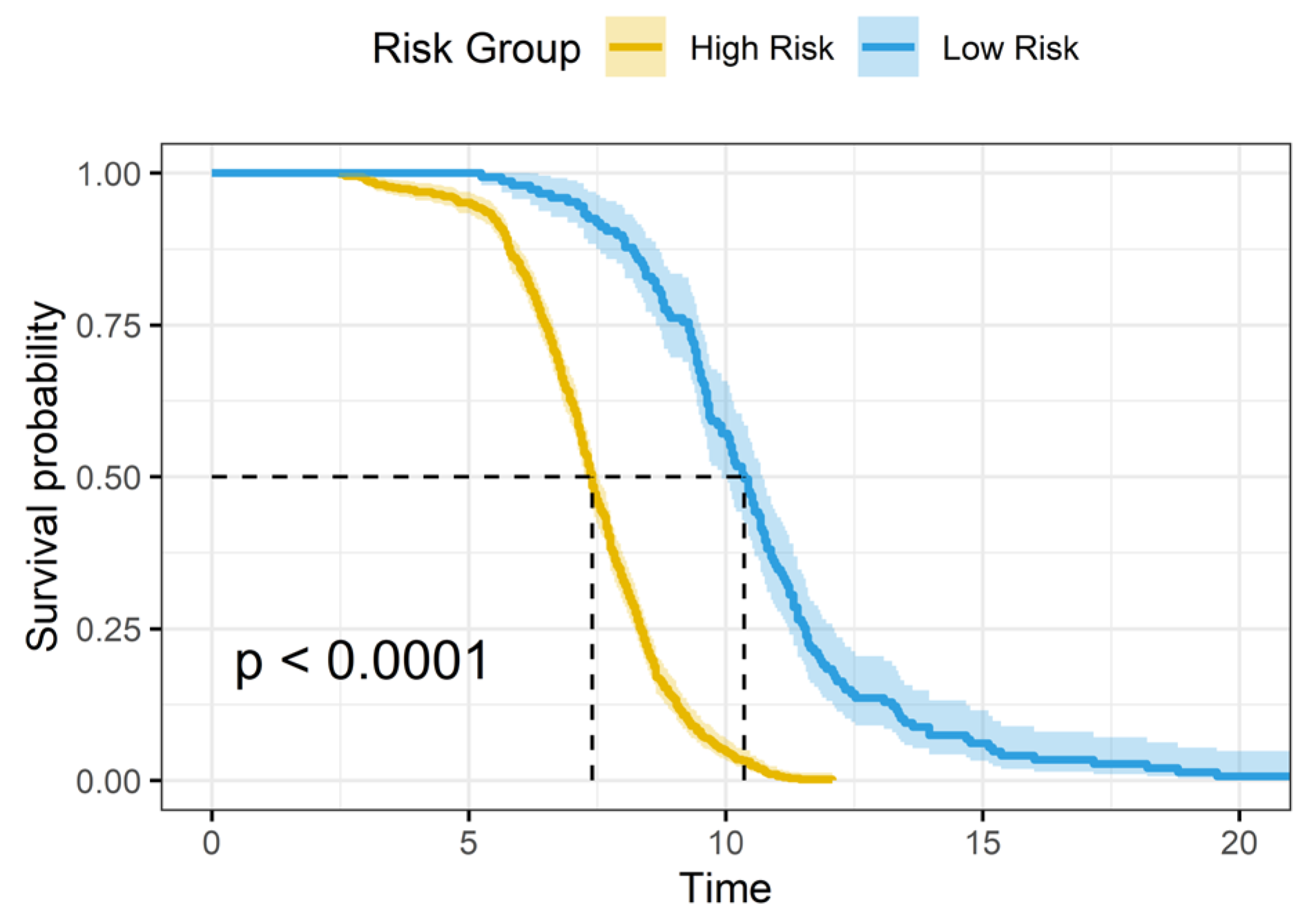
3. Results
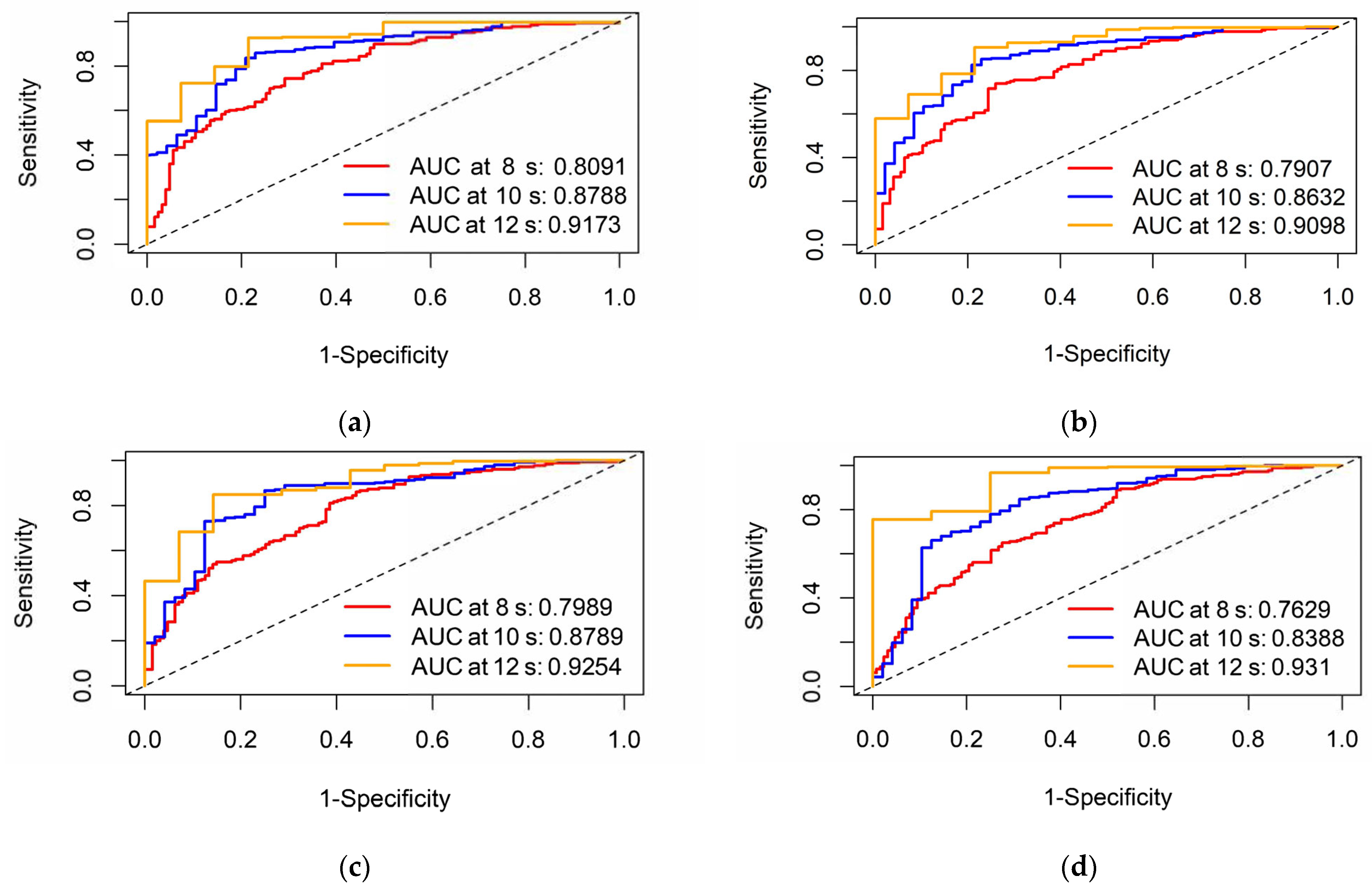
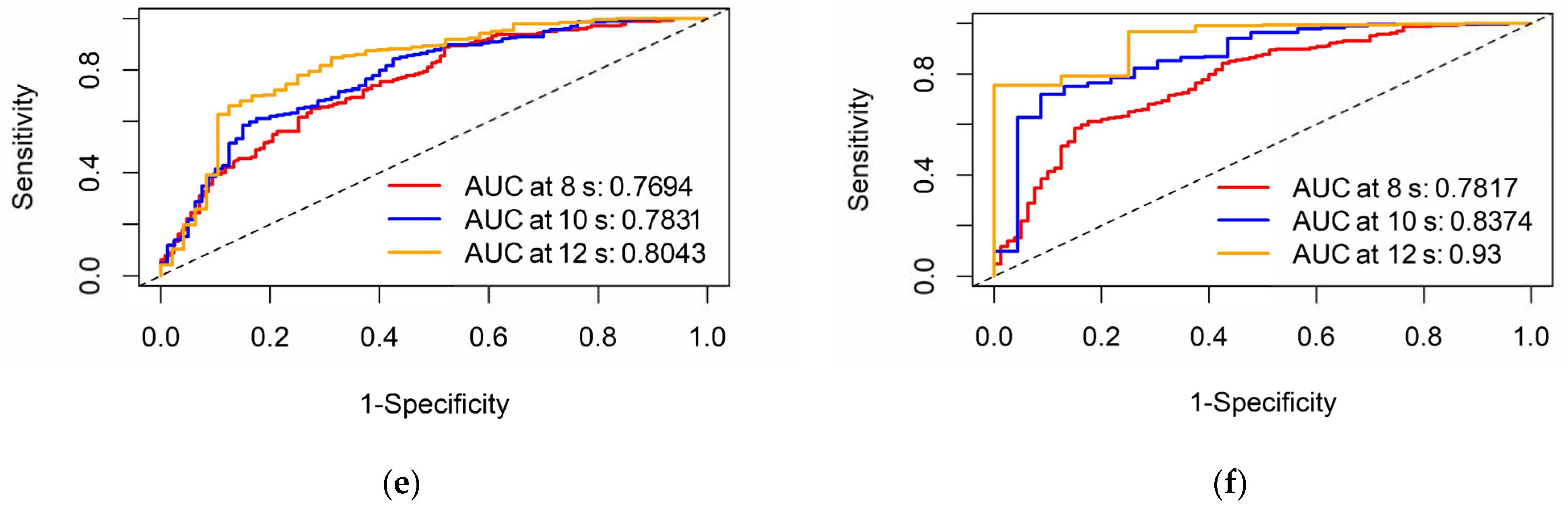
3.1. Analysis of CPH Model Results
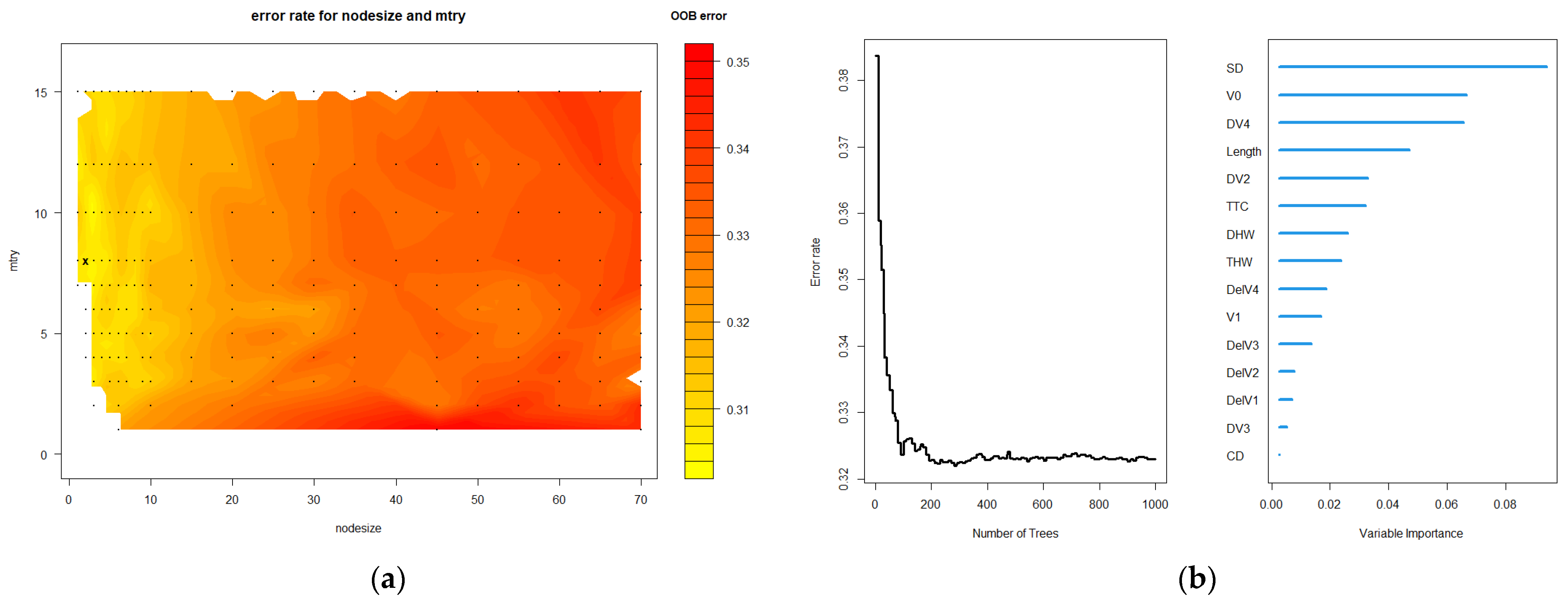
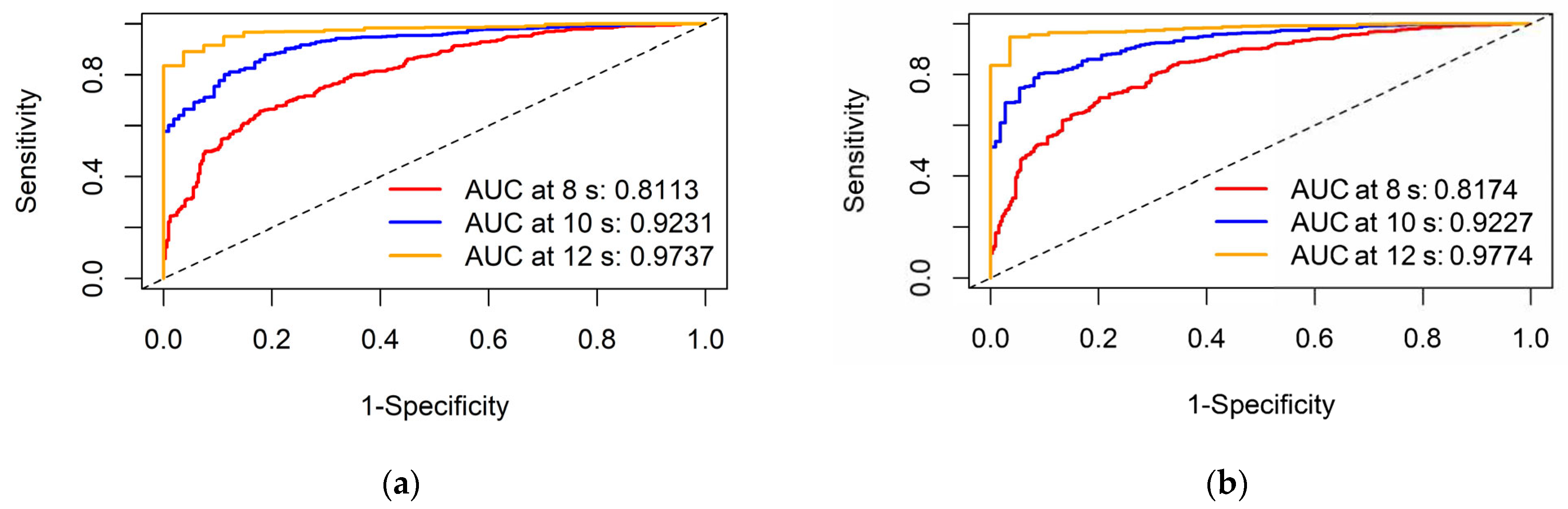
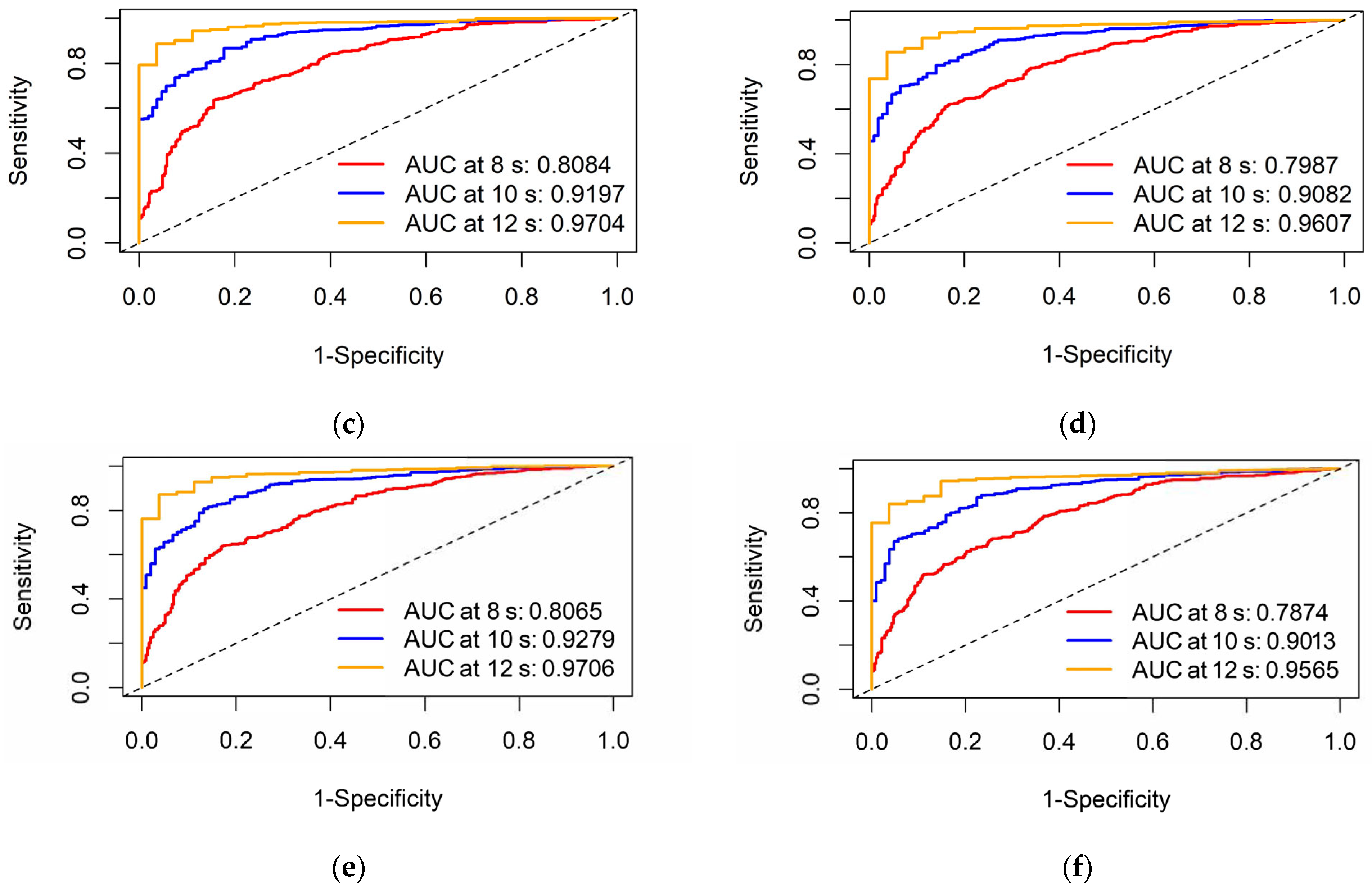
3.2. Analysis of RSF Model Results
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Nagatanit, T.; Yonekura, S. Multiple-vehicle collision induced by lane changing in traffic flow. Phys. A Stat. Mech. Its Appl. 2014, 404, 171–179. [Google Scholar] [CrossRef]
- Lisheng, J.; Wen-ping, F.; Ying-nan, Z.; Shuang-bin, Y.; Hai-jing, H. Research on safety lane change model of driver assistant system on highway. In Proceedings of the 2009 IEEE Intelligent Vehicles Symposium, Xi’an, China, 3–5 June 2009; pp. 1051–1056. [Google Scholar]
- Zheng, Z.; Ahn, S.; Monsere, C. Impact of traffic oscillations on freeway crash occurrences. Accid. Anal. Prev. 2010, 42, 626–636. [Google Scholar] [CrossRef]
- Ali, Y.; Haque, M.; Zheng, Z.; Washington, S.; Yildirimoglu, M. A hazard-based duration model to quantify the impact of connected driving environment on safety during mandatory lane-changing. Transp. Res. Part C Emerg. Technol. 2019, 106, 113–131. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Pan, Y.; Ma, J. Analysing and modelling of discretionary lane change duration considering driver heterogeneity. Transp. B Transp. Dyn. 2023, 11, 343–360. [Google Scholar] [CrossRef]
- Wen, X.; Huang, C.; Jian, S.; He, D. Analysis of discretionary lane-changing behaviours of autonomous vehicles based on real-world data. Transp. A Transp. Sci. 2023, 1–24. [Google Scholar] [CrossRef]
- Li, Y.; Wu, D.; Chen, Q.; Lee, J.; Long, K. Exploring transition durations of rear-end collisions based on vehicle trajectory data: A survival modeling approach. Accid. Anal. Prev. 2021, 159, 106271. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Fu, C.; Wang, W. Modeling duration of overtaking between non-motorized vehicles: A nonparametric survival analysis based approach. PLoS ONE 2021, 16, e0244883. [Google Scholar] [CrossRef]
- Jokhio, S.; Olleja, P.; Bärgman, J.; Yan, F.; Baumann, M. Analysis of time-to-lane-change-initiation using realistic driving data. IEEE Trans. Intell. Transp. Syst. 2023, 25, 4620–4633. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Ni, D.; Zhang, Y. Comprehensive survival analysis of lane-changing duration. Measurement 2021, 182, 109707. [Google Scholar] [CrossRef]
- Wu, J.; Zhang, S.; Singh, A.; Qin, S. Hazard-based model of mandatory lane change duration. In Proceedings of the 17th COTA International Conference of Transportation Professionals, Shanghai, China, 7–9 July 2017; pp. 805–811. [Google Scholar]
- Zeng, Q.; Wang, F.; Chen, T.; Sze, N.N. Incorporating real-time weather conditions into analyzing clearance time of freeway accidents: A grouped random parameters hazard-based duration model with time-varying covariates. Anal. Methods Accid. Res. 2023, 38, 100267. [Google Scholar] [CrossRef]
- Ali, Y.; Sharma, A.; Chen, D. Investigating autonomous vehicle discretionary lane-changing execution behaviour: Similarities, differences, and insights from Waymo dataset. Anal. Methods Accid. Res. 2024, 42, 100332. [Google Scholar] [CrossRef]
- Ali, Y.; Zheng, Z.; Haque, M.; Yildirimoglu, M.; Washington, S. Understanding the discretionary lane-changing behaviour in the connected environment. Accid. Anal. Prev. 2020, 137, 105463. [Google Scholar] [CrossRef]
- Ali, Y.; Zheng, Z.; Haque, M. Modelling lane-changing execution behaviour in a connected environment: A grouped random parameters with heterogeneity-in-means approach. Commun. Transp. Res. 2021, 1, 100009. [Google Scholar] [CrossRef]
- Li, Y.; Li, L.; Ni, D. Exploration of lane-changing duration for heavy vehicles and passenger cars: A survival analysis approach. arXiv 2021, arXiv:2108.05710. [Google Scholar]
- Li, Y.; Li, L.; Ni, D. Comparative univariate and regression survival analysis of lane-changing duration characteristic for heavy vehicles and passenger cars. J. Transp. Eng. Part A Syst. 2022, 148, 04022109. [Google Scholar] [CrossRef]
- Balal, E.; Cheu, R.; Gyan-Sarkodie, T.; Miramontes, J. Analysis of discretionary lane changing parameters on freeways. Int. J. Transp. Sci. Technol. 2014, 3, 277–296. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Z.; Li, L. Investigation of discretionary lane-change characteristics using next-generation simulation data sets. J. Intell. Transp. Syst. 2014, 18, 246–253. [Google Scholar] [CrossRef]
- Ataelmanan, H.; Puan, O.; Hassan, S. Examination of lane changing duration time on expressway. In Proceedings of the IOP Conference Series: Materials Science and Engineering, Bapatla, India, 7–8 May 2021; Volume 1144, p. 012078. [Google Scholar]
- Hamdar, S.; Mahmassani, H. Life in the fast lane: Duration-based investigation of driver behavior differences across freeway lanes. Transp. Res. Rec. 2009, 2124, 89–102. [Google Scholar] [CrossRef]
- Chauhan, P.; Kanagaraj, V.; Asaithambi, G. Understanding the mechanism of lane changing process and dynamics using microscopic traffic data. Phys. A Stat. Mech. Its Appl. 2022, 593, 126981. [Google Scholar] [CrossRef]
- Washington, S.; Karlaftis, M.; Mannering, F.; Anastasopoulos, P. Statistical and Econometric Methods for Transportation Data Analysis; Chapman and Hall/CRC: Boca Raton, FL, USA, 2020. [Google Scholar]
- Chen, Z.; Wen, H.-Y. Survival Analysis of Vehicle Lane-changing Duration on Road Segment Adjacent to Freeway Tunnels. J. Transp. Syst. Eng. Inf. Technol. 2022, 22, 210–217 and 227. [Google Scholar]
- Nan, S.; Yan, L.; Tu, R.; Li, T. Modeling lane-transgressing behavior of e-bike riders on road sections with marked bike lanes: A survival analysis approach. Traffic Inj. Prev. 2020, 22, 153–157. [Google Scholar] [CrossRef]
- Chen, H.; Zhao, X.; Li, Z.; Li, H.; Gong, J.; Wang, Q. Study on the influence factors of takeover behavior in automated driving based on survival analysis. Transp. Res. Part F Traffic Psychol. Behav. 2023, 95, 281–296. [Google Scholar] [CrossRef]
- Vlahogianni, E. Modeling duration of overtaking in two lane highways. Transp. Res. Part F Traffic Psychol. Behav. 2013, 20, 135–146. [Google Scholar] [CrossRef]
- Hou, L.; Lao, Y.; Wang, Y.; Zhang, Z.; Zhang, Y.; Li, Z. Time-varying effects of influential factors on incident clearance time using a non-proportional hazard-based model. Transp. Res. Part A Policy Pract. 2014, 63, 12–24. [Google Scholar] [CrossRef]
- Dhoke, A.; Kumar, A.; Ghosh, I. Hazard-based duration approach to pedestrian crossing behavior at signalized intersections. Transp. Res. Rec. 2021, 2675, 519–532. [Google Scholar] [CrossRef]
- Zou, Y.; Tang, J.; Wu, L.; Henrickson, K.; Wang, Y.; Sarkar, A.; Mansourkhaki, A.; Malakouti, M.; Yeganeh, S.; Zheng, X.; et al. Quantile analysis of factors influencing the time taken to clear road traffic incidents. In Proceedings of the Institution of Civil Engineers-Transport; Thomas Telford Ltd.: London, UK, 2017; Volume 170, pp. 296–304. [Google Scholar]
- Wali, B.; Khattak, A.; Liu, J. Heterogeneity assessment in incident duration modelling: Implications for development of practical strategies for small & large scale incidents. J. Intell. Transp. Syst. 2022, 26, 586–601. [Google Scholar]
- Shi, Y.; Zhang, L.; Liu, P. Survival analysis of urban traffic incident duration: A case study at shanghai expressways. J. Comput. 2014, 26, 29–39. [Google Scholar]
- Shang, T.; Lian, G.; Zhao, Y.; Liu, X.; Wang, W. Off-Ramp Vehicle Mandatory Lane-Changing Duration in Small Spacing Section of Tunnel-Interchange Section Based on Survival Analysis. J. Adv. Transp. 2022, 2022, 9427052. [Google Scholar] [CrossRef]
- Peng, J.; Wang, C.; Fu, R.; Yuan, W. Extraction of parameters for lane change intention based on driver’s gaze transfer characteristics. Saf. Sci. 2020, 126, 104647. [Google Scholar] [CrossRef]
- Ishwaran, H.; Lauer, M.S.; Blackstone, E.H.; Lu, M.; Kogalur, U.B. randomForestSRC: Random Survival Forests Vignette. Available online: https://ishwaran.org/vignettes/survival.pdf (accessed on 13 June 2024).
- Cox, D.R. Regression Models and Life-Tables on JSTOR. J. R. Stat. Soc. 1972, 34, 187–220. [Google Scholar] [CrossRef]
| Variable Name (Unit) | Symbol | Mean (Std. Dev) | Univariate Cox Regression Analysis | Multivariate Cox Regression Analysis | ||
|---|---|---|---|---|---|---|
| Coefficient of Regression a | Exp(a) | Coefficient of Regression a | Exp(a) | |||
| Length of lane-changing vehicles (m) | Length | 6.18 (3.73) | −0.044 *** | 0.957 | −0.056 *** | 0.945 |
| Speed of lane-changing vehicles (m/s) | V0 | 27.82 (6.72) | 0.071 ** | 1.073 | 0.066 *** | 1.069 |
| Distance headway (m) | DHW | 60.63 (60.25) | 0.002 ** | 1.002 | −0.001 | 0.999 |
| Time headway (s) | THW | 2.16 (2.46) | −0.026 * | 0.974 | 0.015 | 1.015 |
| Time to collision (s) | TTC | 95.72 (354.50) | 0.000 | 1.000 | 0.000 | 1.000 |
| Speed of the leading vehicle in the current lane (m/s) | V1 | 27.77 (7.59) | 0.040 *** | 1.041 | −0.0015 | 0.985 |
| Speed difference with the leading vehicle in the current lane (m/s) | DelV1 | −0.29 (2.44) | 0.010 | 1.010 | −0.002 | 0.998 |
| Speed difference with the following vehicle in the current lane (m/s) | DelV2 | 0.32 (2.27) | 0.015 | 1.015 | 0.022 | 1.022 |
| Distance to the following vehicle in the current lane (m) | DV2 | 51.62 (32.49) | 0.008 *** | 1.008 | 0.004 ** | 1.004 |
| Speed difference with the leading vehicle in the target lane (m/s) | DelV3 | 0.59 (4.53) | 0.015 * | 1.016 | 0.014 | 1.014 |
| Distance to the leading vehicle in the target lane (m) | DV3 | 77.47 (63.81) | 0.002 *** | 1.002 | 0.000 | 1.000 |
| Speed difference with the following vehicle in the target lane (m/s) | DelV4 | −0.11 (5.59) | −0.009 | 0.991 | −0.006 | 0.995 |
| Distance to the following vehicle in the target lane (m) | DV4 | 47.78 (36.59) | 0.007 *** | 1.007 | 0.007 *** | 1.007 |
| Standard deviation of lane-changing vehicle’s speed (m/s) | SD | 9.86 (8.50) | −0.041 *** | 0.960 | −0.044 *** | 0.957 |
| Lane-changing direction | CD | 1.59 (0.49) | −0.012 | 0.988 | −0.102 | 0.903 |
| Variable Group Name | Variable Composition |
|---|---|
| All-variable group | SD, V0, DV4, DHW, Length, DV2, THW, TTC, DelV4, V1, DelV3, DelV1, DelV2, DV3, CD |
| C1-variable group | SD, V0, DV4, DHW, Length, DV2, THW, TTC, DelV4, V1, DelV3, DelV1, DelV2 |
| C2-variable group | SD, V0, DV4, DHW, Length, DV2, THW, TTC, DelV4 |
| C3-variable group | SD, V0, DV4, DHW, Length, DV2, THW |
| S-variable group | SD, V0, DV4, DHW, Length, DV2, THW, V1, DelV3, DV3 |
| M-variable group | SD, V0, DV4, Length, DV2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Huang, S.; Wen, H.; Liu, W. Analysis of Highway Vehicle Lane Change Duration Based on Survival Model. Big Data Cogn. Comput. 2024, 8, 114. https://doi.org/10.3390/bdcc8090114
Zhao S, Huang S, Wen H, Liu W. Analysis of Highway Vehicle Lane Change Duration Based on Survival Model. Big Data and Cognitive Computing. 2024; 8(9):114. https://doi.org/10.3390/bdcc8090114
Chicago/Turabian StyleZhao, Sheng, Shengwen Huang, Huiying Wen, and Weiming Liu. 2024. "Analysis of Highway Vehicle Lane Change Duration Based on Survival Model" Big Data and Cognitive Computing 8, no. 9: 114. https://doi.org/10.3390/bdcc8090114
APA StyleZhao, S., Huang, S., Wen, H., & Liu, W. (2024). Analysis of Highway Vehicle Lane Change Duration Based on Survival Model. Big Data and Cognitive Computing, 8(9), 114. https://doi.org/10.3390/bdcc8090114






