Cumulative and Rolling Horizon Prediction of Overall Equipment Effectiveness (OEE) with Machine Learning
Abstract
1. Introduction
2. Materials and Methods
- a—availability (%);
- p—performance (%);
- q—quality (%).
Selection of Independent Variables for Machine Learning
3. OEE Prediction with Machine Learning
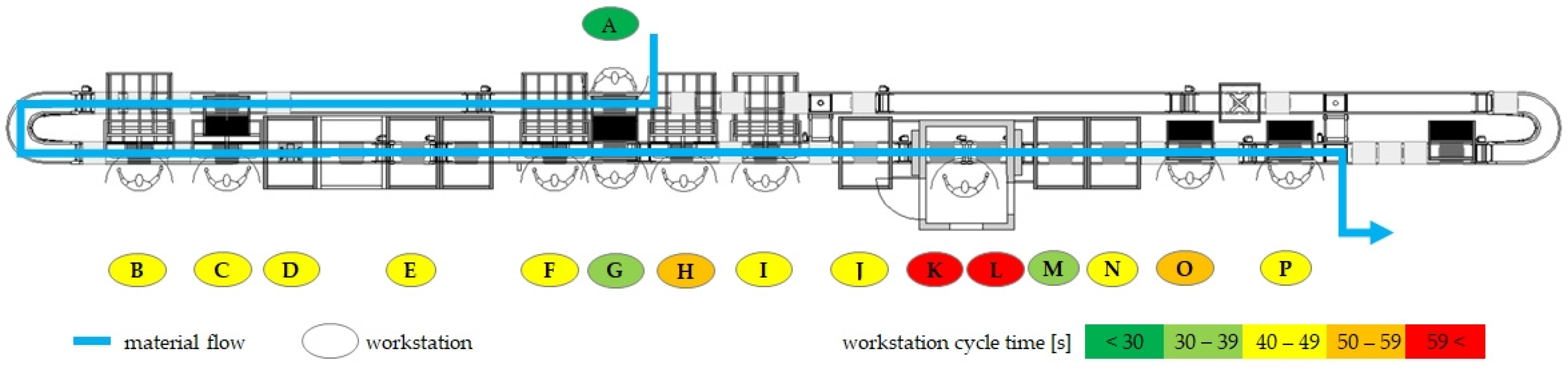
3.1. The Real Work Environment of Applied Machine Learning
- Tf—production rate;
- Q—annual volume of the production task (unit/year);
- T—working time requirement of the production task assigned to the production unit (hour/unit);
- Ipr—actually available productive time base (hour/year).
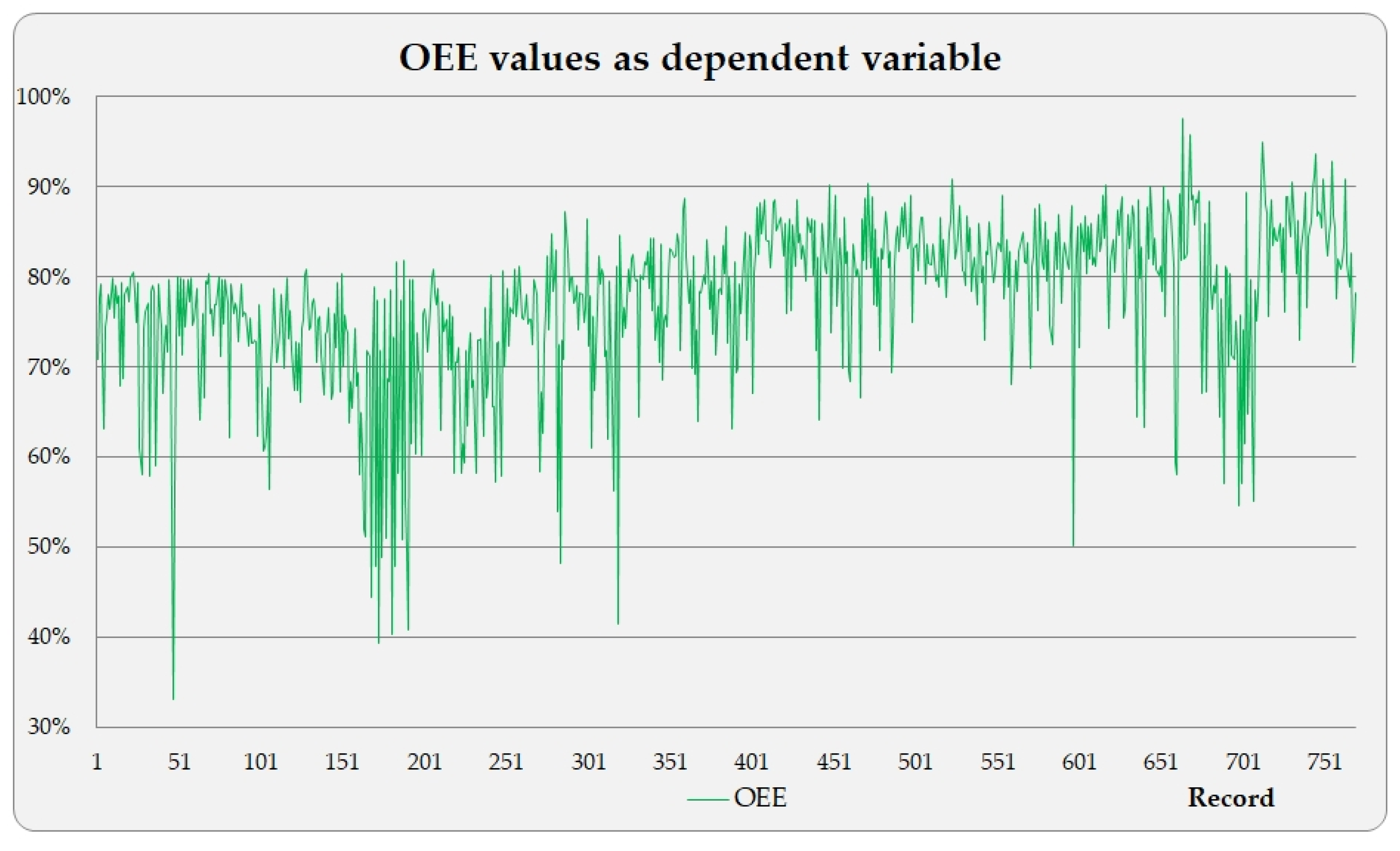
3.2. Production Data for Machine Learning
3.3. Cumulative and Rolling Horizon Prediction
- Cumulative approach;
- Rolling horizon approach;
- ○
- Fix rolling horizon;
- ○
- Changing rolling horizon.
3.4. Applied Machine Learning Methods
- Multiple linear regression (MLR);
- Polynomial regression (simple) (Pol 1);
- Polynomial regression (complex) (Pol 2);
- Lasso regression (Lasso);
- Ridge regression (Ridge);
- Random forest regression (RF);
- Gradient boost regression (GB);
- Mixed GAM computation vehicle with automatic smoothness estimation regression (MGCV).
4. Discussion
- n—number of fitted points;
- —actual value;
- —predicted value [36].
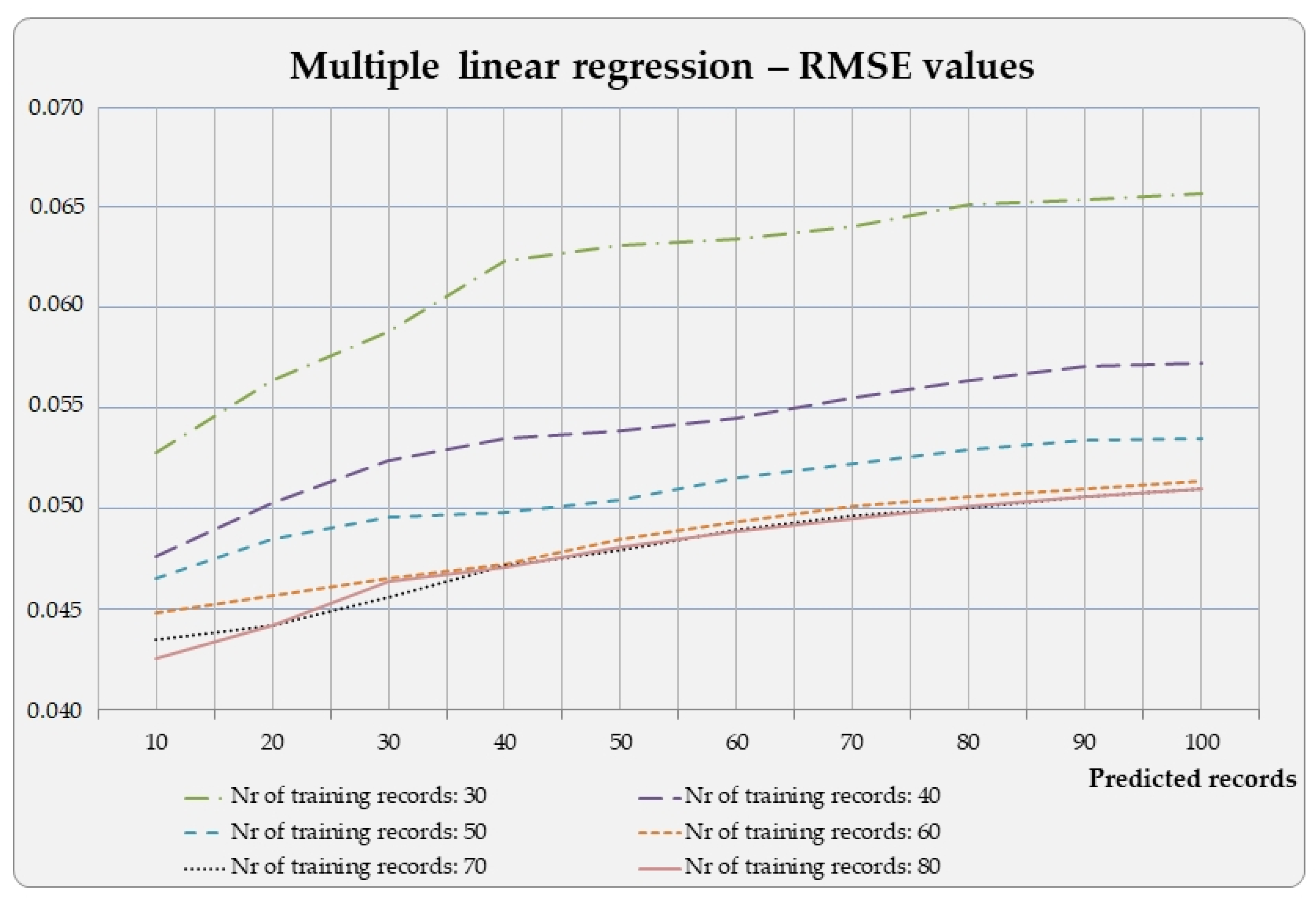
- In terms of the examined training periods, simple polynomial regression (Pol 1) showed the best average RMSE result with a fix rolling horizon (0.0545), followed by lasso (0.0555) and gradient boost regression (0.0556), although, with GB, the 10–50 training period cannot be interpreted due to the specificity of the method;
- In the case of a rolling horizon, the lowest RMSE value (0.0489) can be achieved with lasso regression set to the training parameters 70 and 80;
- Analyzing the cumulative methods, the gradient boost regression showed the best RMSE result (0.0472), followed by multiple linear regression (0.0496) and MGCV (0.0496);
- Considering the average speed of calculation, the fastest method is simple polynomial regression (4.7 s), followed by multiple linear regression (5.1 s) and random forest (9.9 s). The individual values are shown in Table 6. (The laptop used with Intel ® Celeron ® CPU N2840 @ 2.16 GHz 2.16 GHz, 4.00 GB RAM);
- The RMSE values of the examined cumulated methods are generally better than those of the fix rolling horizon methods;
- In the case of production planning, the recommended OEE prediction method is the gradient boost cumulated approach due to the most accurate RMSE value and the moderately long calculation requirement.
- Regarding the examined training periods, the gradient boost regression showed the best average RMSE result with fix rolling horizon (0.0496), followed by random forest (0.0512), multiple linear regression (0.0520) and MGCV with the same result (0.0520);
- In the case of fix rolling horizon, the lowest RMSE value (0.0450) can be achieved with gradient boost regression set to the training parameters 190;
- Analyzing the cumulative methods, the multiple linear regression showed the best RMSE result (0.0544), followed by MGCV (0.0544) and ridge regression (0.0558);
- Considering the average speed of calculation, the fastest method is multiple linear regression (2.0 s), followed by simple polynomial regression (2.7 s) and MGCV (2.9 s);
- The RMSE values of the examined fix rolling horizon methods are always better than the cumulated approach;
- In the case of industrial investment, the recommended prediction method is the gradient boost fix rolling horizon approach with 180–200 training sets, due to the most accurate RMSE value and the medium–long calculation requirement.
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Attribution | Can Be Measured by MES, ERP, SQL and Log Files | Example | A | P | Q | |
|---|---|---|---|---|---|---|
| Qualification | Education | No | - | |||
| Internal training | Yes | Other downtime, reason: planned training | x | |||
| Special knowledge | No | - | ||||
| Practical experience | Yes | Variable cycle time per station per person | x | |||
| External training | No | - | ||||
| Skills, abilities | Seeing | No | - | |||
| Hearing | No | - | ||||
| Fine movement | No | - | ||||
| Stamina | No | - | ||||
| Communication skills | No | - | ||||
| Personality, character | Punctuality | Yes | Number of assembled bad products | x | ||
| Speed | Yes | Variable cycle time per station per person | x | |||
| Compliance | No | - | ||||
| Monotony tolerance | No | - | ||||
| Conscientious work | No | - | ||||
| Motivation | Goals | Yes | Availability, performance, quality, OEE target | x | ||
| Expectations of employee | No | - | ||||
| Rewards, condemnations | No | - | ||||
| Team, company | No | - | ||||
| Work conditions | No | - | ||||
| Organization | Available staff | Yes | Other downtime, reason: missing operator | x | ||
| Improvement | Yes | Trends (OEE, scrap, etc.) | x | |||
| Leading, management | No | - | ||||
| Support | No | - | ||||
| Planning | Yes | Production and resource plan, scheduling | x | |||
| Attribution | Can Be Measured by MES, ERP, SQL and Log Files | Example | A | P | Q | |
|---|---|---|---|---|---|---|
| Work environment | Safety | No | - | |||
| Health protection | No | - | ||||
| Ergonomics | No | - | ||||
| Perceived environment | No | - | ||||
| Automatization | Yes | Manual or nonmanual (automated) assembly | x | |||
| Production environment | Complexity of technology | Yes | Assembly lines, stations, products | x | ||
| 5S | Yes | Downtime, reason: cleaning | x | |||
| Concerns of technology | No | - | ||||
| Production without waste | Yes | Downtimes, scrap | x | |||
| Visual support | Yes | OEE Andon board | x | |||
| Market environment | Oder | Yes | Production and resource plan, scheduling | x | ||
| Takt time, cycle time feasibility | Yes | Takt time, cycle time data | x | |||
| Pull system | Yes | Production plan, batch size, changeover, scheduling | x | |||
| Competition | No | - | ||||
| Production plan feasibility | Yes | Fulfilment of production plan | x | |||
| Company environment | Company, team | Yes | Staff (operator, setter, etc.) | x | ||
| Shift schedule, breaks | Yes | Downtime, reason: changeover | x | |||
| Overtime | Yes | Production and resource plan, scheduling | x | |||
| Motivation, commitment | No | - | ||||
| Employee expectations | No | - | ||||
| Worker environment | Social situation | No | - | |||
| Plant availability | No | - | ||||
| Social acceptance | No | - | ||||
| Benefits | No | - | ||||
| Expectations of employer | No | - | ||||
| Attribution | Can Be Measured by MES, ERP, SQL and Log Files | Example | A | P | Q | |
|---|---|---|---|---|---|---|
| Production technology | Assembly process | Yes | Manual or nonmanual (automated) assembly | x | ||
| Repair, rework process | Yes | Downtime, reason: quality problems | x | |||
| Checking process | Yes | Cycle time of checking station | x | |||
| Packaging process | Yes | Cycle time of packaging station | x | |||
| Automatization | Yes | Manual or non-manual (automated) assembly | x | |||
| Measurement, control | Maintenance | Yes | Downtime, reason: maintenance | x | ||
| SPC, 100% checking | Yes | In MES: SPC report | x | |||
| Six sigma | No | - | ||||
| Failure analysis, PDCA, Pareto | Yes | Pareto analysis | x | |||
| Poka yoke | Yes | Downtime, reason: Poka yoke check | x | |||
| Work process | Standard operational procedure | Yes | In MES: documents module | x | ||
| Process parameters | Yes | Time and duration data | x | |||
| Material workflow | No | - | ||||
| Best practices | Yes | In MES: documents module | x | |||
| Planned cycle time | Yes | Cycle time data per stations | x | |||
| Lean methods | Goals | Yes | Availability, performance, quality, OEE target | x | ||
| Expectations | No | - | ||||
| Rewards, condemnations | No | - | ||||
| Company, team | No | - | ||||
| Work conditions | No | - | ||||
| Material and information flow | Available workforce | Yes | Staff (operator, setter, etc.) | x | ||
| Improvement | Yes | Trends (OEE, scrap, etc.) | x | |||
| Leading, organization | No | - | ||||
| Support | No | - | ||||
| Planning | Yes | Production and resource plan, scheduling | x | |||
| Attribution | Can Be Measured by MES, ERP, SQL and Log Files | Example | A | P | Q | |
|---|---|---|---|---|---|---|
| Material failure | Material quality | Yes | Downtime, reason: quality problems | x | ||
| Surface | Yes | Downtime, reason: quality problems | x | |||
| Deficiency | Yes | Downtime, reason: quality problems | x | |||
| Surplus | Yes | Downtime, reason: quality problems | x | |||
| Color | Yes | Downtime, reason: quality problems | x | |||
| Size error | Width, length, height | Yes | Downtime, reason: quality problems | x | ||
| Diameter | Yes | Downtime, reason: quality problems | x | |||
| Out of tolerance | Yes | Downtime, reason: quality problems | x | |||
| Deformation | Yes | Downtime, reason: quality problems | x | |||
| Position problem | Yes | Downtime, reason: quality problems | x | |||
| Quantitative error | Too much, too little | Yes | Downtime, reason: logistics problem | x | ||
| Not available | Yes | Downtime, reason: logistics problem | x | |||
| Stuck together | Yes | Downtime, reason: quality problems | x | |||
| Mixed | Yes | Downtime, reason: quality problems | x | |||
| Batch failure | Yes | Downtime, reason: quality problems | x | |||
| Material handling | Damaged | Yes | Downtime, reason: logistics problem | x | ||
| Contaminated | Yes | Downtime, reason: logistics problem | x | |||
| Temperature, warranty | Yes | Downtime, reason: logistics problem | x | |||
| Not available, not accessible | Yes | Downtime, reason: logistics problem | x | |||
| Not identified | Yes | Downtime, reason: logistics problem | x | |||
| Design failure | Function problem | Yes | Downtime, reason: design failure | x | ||
| Comfort problem | Yes | Downtime, reason: design failure | x | |||
| Not controllable, not repairable | No | - | ||||
| Not durable | No | - | ||||
| Not or difficult to assemble | Yes | Significantly different cycle time, takt time | x | |||
| Attribution | Can Be Measured by MES, ERP, SQL and Log Files | Example | A | P | Q | |
|---|---|---|---|---|---|---|
| Maintenance | Maintenance plan | Yes | Downtime, reason: maintenance | x | ||
| Fulfilment of planned maintenance | Yes | Downtime, reason: maintenance | x | |||
| Assemble ability, repairability, maintainability | Yes | Downtime, reason: maintenance | x | |||
| Standard parts | No | - | ||||
| Manuals, drawings | No | - | ||||
| Machine and tool adjustment | Adjusted, validated | Yes | Downtime, reason: settings | x | ||
| Setting documentation | No | - | ||||
| Simple, fast, standardized | Yes | Downtime, reason: settings | x | |||
| Failure catalogue available | No | - | ||||
| SMED, OTED | Yes | Downtime, reason: changeover | x | |||
| Stability | Trouble proof | No | - | |||
| Energy supply continuous | Yes | Downtime, reason: technical issue | x | |||
| Machine capability, process capability | Yes | Significantly different cycle time, takt time | x | |||
| Operable | Yes | Operating and non-operating time | x | |||
| Reliable PC, PLC network | Yes | Downtime, reason: technical issue | x | |||
| Standardization | Standard parts, components | No | - | |||
| Spare parts available | Yes | Downtime, reason: maintenance | x | |||
| Available documents | No | - | ||||
| Parts of MES | Yes | Assembly line and machines exist in MES | x | |||
| Traceable, identifiable | Yes | In MES: traceability reports | x | |||
| Safety | Can be stopped, interruptible | No | - | |||
| Ergonomic | No | - | ||||
| Free of hazardous materials | No | - | ||||
| Easy to handle | No | - | ||||
| Not accidental | No | - | ||||
| Attribution | Can Be Measured by MES, ERP, SQL and Log Files | Example | A | P | Q | |
|---|---|---|---|---|---|---|
| Material checking | Quantitative control | Yes | Number of scrap pieces | x | ||
| Incoming inspection | Yes | Number of scrap pieces | x | |||
| Quality control | Yes | Number of scrap pieces | x | |||
| Traceability | Yes | In MES: traceability reports | x | |||
| Function checking | Yes | Number of scrap pieces | x | |||
| Product control | Sampling frequency | Yes | Number of checked products | x | ||
| Sampling size | Yes | Number of checked products | x | |||
| Checking functional operation | Yes | Scrap or good products | x | |||
| Sampling place | Yes | Checking station in MES | x | |||
| Documentation control | Yes | In MES: documents module | x | |||
| Machine, tool checking | Appropriate frequency | Yes | Downtime, reason: maintenance | x | ||
| Machine testing | Yes | Downtime, reason: maintenance | x | |||
| Checking maintenance | Yes | Downtime, reason: maintenance | x | |||
| Calibration | Yes | Downtime, reason: maintenance | x | |||
| Safety control | Yes | Downtime, reason: maintenance | x | |||
| Checking of assembly process | SPC | Yes | In MES: SPC report | x | ||
| Simulation control | Yes | Downtime, reason: settings | x | |||
| First and last product control | Yes | Timestamp data of first and last products | x | |||
| Type change checking | Yes | Timestamp data of changeover | x | |||
| Poka yoke control | Yes | Timestamp data of Poka yoke check | x | |||
| Measurement instruments checking | Functionality | Yes | Timestamp data of Poka yoke check | x | ||
| Reliability | No | - | ||||
| Accuracy | No | - | ||||
| Frequency | Yes | Timestamp data of Poka yoke check | x | |||
| Documents control | Yes | In MES: documents module | x | |||
References
- Backus, P.; Janakiram, M.; Mowzoon, S.; Runger, C.; Bhargava, A. Factory cycle-time prediction with a data mining approach. IEEE Trans. Semicond. Manuf. 2006, 19, 252–258. [Google Scholar] [CrossRef]
- Choudhary, A.K.; Harding, J.A.; Tiwari, M.K. Data mining in manufacturing: A review based on the kind of knowledge. J. Intell. Manuf. 2009, 20, 501–521. [Google Scholar] [CrossRef]
- Tao, F.; Qi, Q.; Liu, A.; Kusiak, A. Data-driven smart manufacturing. J. Manuf. Syst. 2018, 48, 157–169. [Google Scholar] [CrossRef]
- Nagorny, K.; Lima-Monteiro, P.; Barata, J.; Colombo, W.A. Big data analysis in smart manufacturing: A review. Int. J. Commun. Netw. Syst. Sci. 2017, 10, 31–58. [Google Scholar] [CrossRef]
- Muchiri, P.; Pintelon, L. Performance measurement using overall equipment effectiveness (OEE): Literature review and practical application discussion. Int. J. Prod. Res. 2008, 46, 3517–3535. [Google Scholar] [CrossRef]
- Harding, J.A.; Shahbaz, M.; Srinivas, S.; Kusiak, A. Data-Mining in manufacturing: A review. J. Manuf. Sci. Eng. 2006, 128, 969–976. [Google Scholar] [CrossRef]
- Wuest, T.; Weimer, D.; Irgens, C.; Thoben, K.D. Machine learning in manufacturing: Advantages, challenges, and applications. Prod. Manuf. Res. 2016, 4, 23–45. [Google Scholar] [CrossRef]
- Mantravadi, S.; Moller, C. An overview of next-generation Manufacturing Execution System: How important is MES for Industry 4.0? Procedia Manuf. 2019, 30, 588–595. [Google Scholar] [CrossRef]
- Beregi, R.; Pedone, G.; Háy, B.; Váncza, J. Manufacturing Execution System integration through the standardization of a Common Service Model for Cyber-Physical Production Systems. Appl. Sci. 2021, 11, 7581. [Google Scholar] [CrossRef]
- Wiendahl, H.P.; Reichardt, J.; Nyhuis, P. Handbook Factory Planning and Design; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- ElMaraghy, H.; Schuh, G.; ElMaraghy, W.; Piller, F.; Schönleben, P.; Tseng, M.; Bernand, A. Product variety management. CIRP Ann. 2013, 62, 629–652. [Google Scholar] [CrossRef]
- Jordan, M.I.; Mitchell, T.M. Machine learning: Trends, perspectives, and prospects. Science 2015, 349, 255–260. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Z.H. Machine Learning; Springer Nature: Singapore, 2021. [Google Scholar] [CrossRef]
- Rebala, G.; Ravi, A.; Churiwala, S. An Introduction to Machine Learning; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Oliveira, R.; Taki, S.A.; Sous, S.; Salimi, M.A. Global Process Effectiveness: When Overall Equipment Effectiveness Meets Adherence to Schedule. Procedia Manuf. 2019, 38, 1615–1622. [Google Scholar] [CrossRef]
- Corrales, L.C.; Lambán, M.P.; Korner, M.E.H.; Royo, J. Overall Equipment Effectiveness: Systematic literature review and overview of different approaches. Appl. Sci. 2020, 10, 6469. [Google Scholar] [CrossRef]
- Nakajima, S. Introduction to TPM: Total Productive Maintenance; Productivity Press: Cambridge, UK, 1988. [Google Scholar]
- Lejon, E.; Kyösti, P.; Lindström, J. Machine learning for detection of anomalies in press-hardening: Selection of efficient methods. Procedia CIRP 2018, 72, 1079–1083. [Google Scholar] [CrossRef]
- Abdelrahman, O.; Keikhosrokiani, P. Assembly line anomaly detection and root cause analysis using machine learning. IEEE Access 2020, 8, 189661–189672. [Google Scholar] [CrossRef]
- Peres, R.S.; Barata, J.; Leitao, P.; Garcia, G. Multistage quality control using machine learning in the automotive industry. IEEE Access 2019, 7, 79908–79916. [Google Scholar] [CrossRef]
- Syafrudin, M.; Alfian, G.; Fitriyani, N.L.; Rhee, J. Performance analysis of IoT-based sensor, Big Data processin, and Machine Learning model for real-time monitoring system in automotive manufacturing. Sensors 2018, 18, 2946. [Google Scholar] [CrossRef]
- Wang, T.; Chen, J.; Gao, X.; Qin, Y. Real-time monitoring for disk laser welding based on feature selection and SVM. Appl. Sci. 2017, 7, 884. [Google Scholar] [CrossRef]
- Lee, J.H.; Noh, S.D.; Kim, H.J.; Kang, Y.S. Implementation of Cyber-Physical Production System for quality prediction and operation control in metal casting. Sensors 2018, 18, 1428. [Google Scholar] [CrossRef]
- Souza, B.V.; Santos, S.R.B.; Oliveira, A.M.; Givigi, S.N. Analyzing and predicting Overall Equipment Effectiveness in manufacturing industries using machine learning. In Proceedings of the 2022 IEEE International Systems Conference (SysCon), Montreal, QC, Canada, 25–28 April 2022; pp. 1–8. [Google Scholar] [CrossRef]
- EL Mazgualdi, C.; Masrour, T.; El Hassani, I.; Khdoudi, A. Machine learning for KPIs prediction: A case study of the overall equipment effectiveness within automotive industry. Soft Comput. 2021, 25, 2891–2909. [Google Scholar] [CrossRef]
- Imane, M.; Aoula, E.S.; Achouyab, E.H. Using Bayesian Ridge Regression to predict the Overall Equipment Effectiveness performance. In Proceedings of the 2022 2nd International Conference on Innovative Research in Applied Science, Engineering and Technology (IRASET), Meknes, Morocco, 3–4 March 2022; pp. 1–4. [Google Scholar] [CrossRef]
- Imane, M.; Aoula, E.S.; Achouyab, E.H. Support Vector Regression to predict the Overall Equipment Effectiveness indicator. In Proceedings of the 2022 International Conference on Intelligent Systems and Computer Vision (ISCV), Fez, Morocco, 18–22 May 2022; pp. 1–5. [Google Scholar] [CrossRef]
- Bonada, F.; Echeverria, L.; Domingo, X.; Anzaldi, G. AI for improving the Overall Equipment Efficiency in manufacturing industry. In New Trends in the Use of Artificial Intelligence for the Industry 4.0; Martínez, L.R., Rios, R.A.O., Prieto, M.D., Eds.; IntechOpen: London, UK, 2020. [Google Scholar] [CrossRef]
- Khoudi, A.; Masrour, T. Prediction of industrial process parameters using artificial intelligence algorithms. arXiv 2019, arXiv:1812.10537v2. [Google Scholar] [CrossRef]
- Khdoudi, A.; Masrour, T.; El Mazgualdi, C. Using machine learning algorithms for the prediction of industrial process parameters based on product design. Adv. Intell. Syst. Sustain. Dev. 2019, 3, 728–749. [Google Scholar] [CrossRef]
- El Mazgualdi, C.; Masrour, T.; Barka, N.; El Hassani, I. A learning-based decision tool towards smart energy optimization in the manufacturing process. Systems 2022, 10, 180. [Google Scholar] [CrossRef]
- Khdoudi, A.; Barka, N.; Masrour, T.; El Hassani, I.; El Mazgualdi, C. Online prediction of automotive tempered glass quality using machine learning. Res. Sq. 2022. [Google Scholar] [CrossRef]
- Zouhri, W.; Rostami, H.; Homri, L.; Dantan, J.Y. A genetic-based SVM approach for quality data classification. In Artificial Intelligence and Industrial Applications; Springer International Publishing: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Dobra, P.; Jósvai, J. Overall Equipment Effectiveness (OEE) complexity for semi-automatic automotive assembly lines. Acta Polytech. Hung. 2023, 20, 63–82. [Google Scholar] [CrossRef]
- Kardos, K.; Jósvai, J. Gyártási Folyamatok Tervezése; István Széchenyi University: Győr, Hungary, 2005. (In Hungarian) [Google Scholar]
- Igual, L.; Segui, S. Introduction to Data Science, a Python Approach to Concepts, Techniques and Applications; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
| Attribution | Can Be Measured by MES, ERP, SQL and Log Files | Example | A | P | Q | |
|---|---|---|---|---|---|---|
| Qualification | Practical experience | Yes | Variable cycle time per station per person | x | ||
| Motivation | Goals | Yes | Availability, performance, quality, OEE target | x | ||
| Organization | Improvement | Yes | Trends (OEE, scrap, etc.) | x | ||
| Production technology | Assembly process | Yes | Manual or nonmanual (automated) assembly | x | ||
| Measurement, control | Maintenance | Yes | Downtime, reason: maintenance | x | ||
| Work process | Process parameters | Yes | Time and duration data | x | ||
| Material and information flow | Available workforce | Yes | Staff (operator, setter, etc.) | x | ||
| Material failure | Material quality | Yes | Downtime, reason: quality problems | x | ||
| Material handling | Not available, not accessible | Yes | Downtime, reason: logistics problem | x | ||
| Machine and tool adjustment | SMED, OTED | Yes | Downtime, reason: changeover | x | ||
| Product control | Sampling frequency | Yes | Number of checked products | x | ||
| Checking of assembly process | SPC | Yes | In MES: SPC report | x | ||
| Assembly Station | Operation by | Assembly Station | Operation by |
|---|---|---|---|
| A | human | I | human |
| B | human | J | machine |
| C | human | K | human |
| D | machine | L | human |
| E | machine | M | machine |
| F | human | N | machine |
| G | human | O | human |
| H | human | P | human |
| Types of Production Process | Production Rate |
|---|---|
| Mass production | 0.8 < Tf ≤ 1.0 |
| Large batch size | 0.6 < Tf ≤ 0.8 |
| Medium batch size | 0.4 < Tf ≤ 0.6 |
| Small batch size | 0.2 < Tf ≤ 0.4 |
| Job-shop or project production | 0 ≤ Tf < ≤ 0.2 |
| RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Step | Training | Testing | MLR | Pol 1 | Pol 2 | Lasso | Ridge | RF | GB | MGCV | Min |
| 10 | 10 | 60 | 0.3737 | 0.0587 | 0.1294 | 0.0786 | 0.0721 | 0.0701 | - | - | 0.0587 |
| 10 | 20 | 60 | 0.0881 | 0.0553 | 0.0924 | 0.0682 | 0.0676 | 0.0655 | - | 0.0882 | 0.0553 |
| 10 | 30 | 60 | 0.0635 | 0.0501 | 0.0777 | 0.0569 | 0.0582 | 0.0621 | - | 0.0635 | 0.0501 |
| 10 | 40 | 60 | 0.0545 | 0.0543 | 0.0644 | 0.0519 | 0.0534 | 0.0599 | - | 0.0545 | 0.0519 |
| 10 | 50 | 60 | 0.0516 | 0.0541 | 0.0611 | 0.0513 | 0.0524 | 0.0577 | - | 0.0516 | 0.0513 |
| 10 | 60 | 60 | 0.0493 | 0.0541 | 0.0580 | 0.0498 | 0.0517 | 0.0564 | 0.0587 | 0.0493 | 0.0493 |
| 10 | 70 | 60 | 0.0490 | 0.0543 | 0.0573 | 0.0489 | 0.0507 | 0.0549 | 0.0570 | 0.0490 | 0.0489 |
| 10 | 80 | 60 | 0.0489 | 0.0546 | 0.0569 | 0.0489 | 0.0513 | 0.0540 | 0.0559 | 0.0489 | 0.0489 |
| 10 | 90 | 60 | 0.0510 | 0.0547 | 0.0580 | 0.0497 | 0.0513 | 0.0536 | 0.0540 | 0.0491 | 0.0491 |
| 10 | 100 | 60 | 0.0514 | 0.0550 | 0.0581 | 0.0505 | 0.0516 | 0.0529 | 0.0524 | 0.0492 | 0.0492 |
| Avg. | 0.0881 | 0.0545 | 0.0713 | 0.0555 | 0.0560 | 0.0587 | 0.0556 | 0.0559 | 0.0545 | ||
| 10 | Cum. | 60 | 0.0496 | 0.0603 | 0.0604 | 0.0503 | 0.0507 | 0.0498 | 0.0472 | 0.0496 | 0.0472 |
| RMSE | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Step | Training | Testing | MLR | Pol 1 | Pol 2 | Lasso | Ridge | RF | GB | MGCV | Min |
| 50 | 100 | 150 | 0.0597 | 0.0573 | 0.0588 | 0.0555 | 0.0593 | 0.0573 | 0.0542 | 0.0597 | 0.0542 |
| 50 | 110 | 150 | 0.0619 | 0.0576 | 0.0593 | 0.0600 | 0.0631 | 0.0560 | 0.0551 | 0.0619 | 0.0551 |
| 50 | 120 | 150 | 0.0524 | 0.0565 | 0.0573 | 0.0525 | 0.0567 | 0.0528 | 0.0518 | 0.0524 | 0.0518 |
| 50 | 130 | 150 | 0.0513 | 0.0570 | 0.0578 | 0.0516 | 0.0557 | 0.0514 | 0.0494 | 0.0513 | 0.0494 |
| 50 | 140 | 150 | 0.0498 | 0.0563 | 0.0565 | 0.0513 | 0.0539 | 0.0514 | 0.0495 | 0.0498 | 0.0495 |
| 50 | 150 | 150 | 0.0496 | 0.0571 | 0.0565 | 0.0513 | 0.0540 | 0.0514 | 0.0515 | 0.0496 | 0.0496 |
| 50 | 160 | 150 | 0.0506 | 0.0585 | 0.0585 | 0.0524 | 0.0546 | 0.0522 | 0.0507 | 0.0506 | 0.0506 |
| 50 | 170 | 150 | 0.0504 | 0.0576 | 0.0576 | 0.0519 | 0.0540 | 0.0488 | 0.0472 | 0.0504 | 0.0472 |
| 50 | 180 | 150 | 0.0497 | 0.0571 | 0.0569 | 0.0513 | 0.0531 | 0.0471 | 0.0456 | 0.0497 | 0.0456 |
| 50 | 190 | 150 | 0.0482 | 0.0562 | 0.0559 | 0.0503 | 0.0512 | 0.0476 | 0.0450 | 0.0482 | 0.0450 |
| 50 | 200 | 150 | 0.0489 | 0.0570 | 0.0566 | 0.0513 | 0.0522 | 0.0476 | 0.0456 | 0.0489 | 0.0456 |
| Avg. | 0.0520 | 0.0571 | 0.0574 | 0.0527 | 0.0553 | 0.0512 | 0.0496 | 0.0520 | 0.0496 | ||
| 50 | Cum. | 150 | 0.0544 | 0.0617 | 0.0619 | 0.0562 | 0.0558 | 0.0562 | 0.0562 | 0.0544 | 0.0544 |
| Applied Regression | Production Planning | Industrial Investments | ||
|---|---|---|---|---|
| Roll. Hor. | Cum. | Roll. Hor. | Cum. | |
| Multiple linear regression | 5.1 s | 7.0 s | 2.0 s | 5.0 s |
| Polynomial regression (simple) | 4.7 s | 6.0 s | 2.7 s | 3.9 s |
| Polynomial regression (complex) | 56.3 s | 70.3 s | 14.4 s | 15.0 s |
| Lasso regression | 546.9 s | 765.9 s | 86.3 s | 117.4 s |
| Ridge regression | 17,727.3 s | 18,906.0 s | 2758.2 s | 3506.2 s |
| Random forest regression | 9.9 s | 33.9 s | 4.0 s | 6.8 s |
| Gradient boost regression | 511.2 s | 1016.7 s | 94.1 s | 152.8 s |
| MGCV | 10.5 s | 13.3 s | 2.9 s | 3.7 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dobra, P.; Jósvai, J. Cumulative and Rolling Horizon Prediction of Overall Equipment Effectiveness (OEE) with Machine Learning. Big Data Cogn. Comput. 2023, 7, 138. https://doi.org/10.3390/bdcc7030138
Dobra P, Jósvai J. Cumulative and Rolling Horizon Prediction of Overall Equipment Effectiveness (OEE) with Machine Learning. Big Data and Cognitive Computing. 2023; 7(3):138. https://doi.org/10.3390/bdcc7030138
Chicago/Turabian StyleDobra, Péter, and János Jósvai. 2023. "Cumulative and Rolling Horizon Prediction of Overall Equipment Effectiveness (OEE) with Machine Learning" Big Data and Cognitive Computing 7, no. 3: 138. https://doi.org/10.3390/bdcc7030138
APA StyleDobra, P., & Jósvai, J. (2023). Cumulative and Rolling Horizon Prediction of Overall Equipment Effectiveness (OEE) with Machine Learning. Big Data and Cognitive Computing, 7(3), 138. https://doi.org/10.3390/bdcc7030138





