Analyzing the Performance of Transformers for the Prediction of the Blood Glucose Level Considering Imputation and Smoothing
Abstract
1. Introduction
2. Related Work
3. Materials and Methods
3.1. Data Acquisition
3.2. Data Analysis
3.3. Handling the Gaps
3.3.1. Removing Missing Values
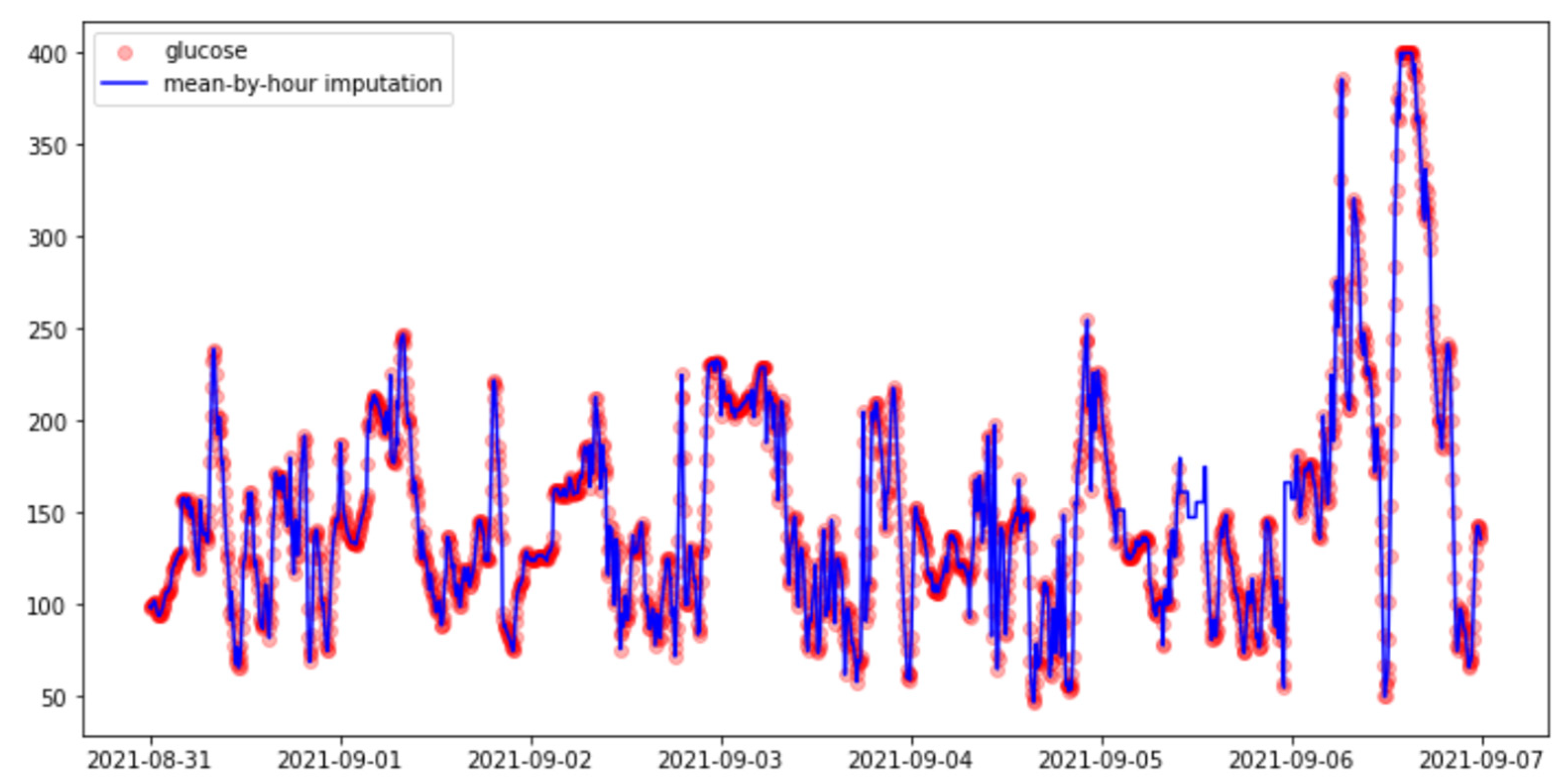
3.3.2. Imputation Methods
- (i)
- Hourly mean.
- (ii)
- Linear Interpolation.
- (iii)
- Spline Interpolation:
- (iv)
- Polynomial Interpolation.
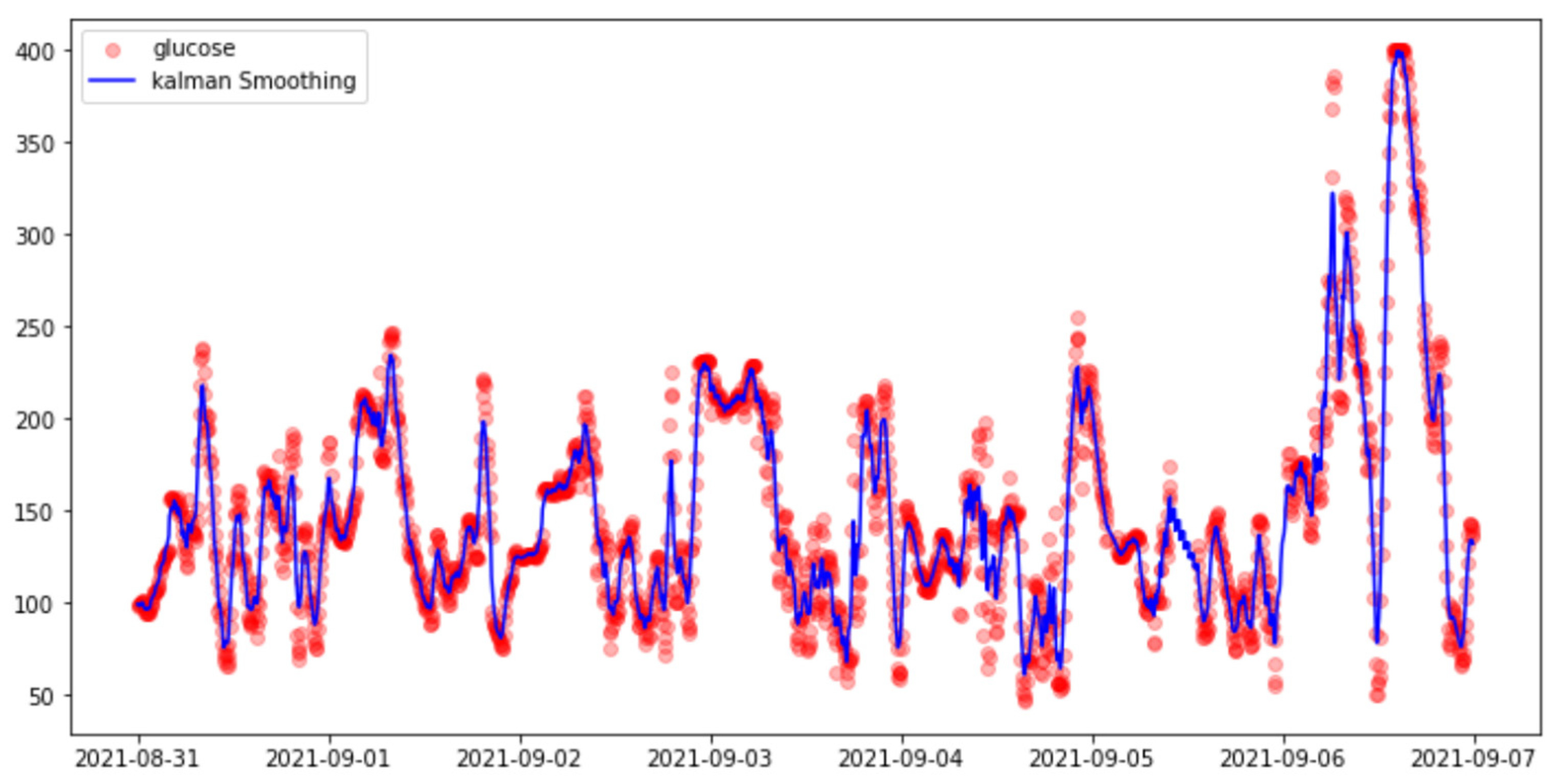
3.3.3. Smoothing Methods
- (i)
- Kalman Smoothing
- (ii)
- Smoothing Splines.
3.4. Prediction Models
3.4.1. XGBoosting
3.4.2. One-Dimensional Convolutional Neural Networks (1D-CNN)
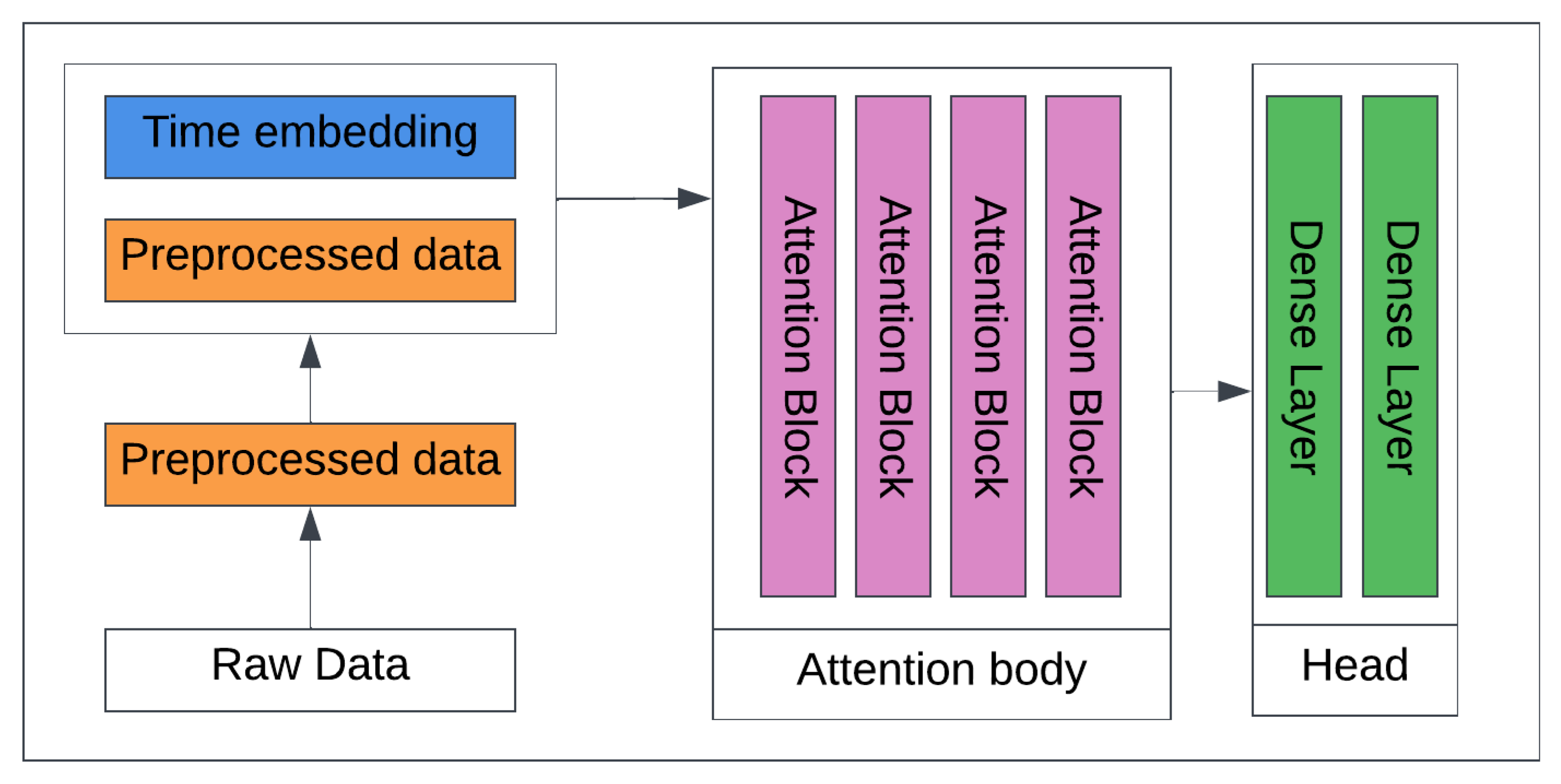
3.4.3. Transformers
4. Results and Discussion
4.1. Using Only CGM without Imputation to Predict Glucose Level
4.2. Using CGM and Meal to Predict Glucose Level
5. Conclusions and Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bertachi, A.; Biagi, L.; Contreras, I.; Luo, N.; Vehí, J. Predictions of Blood Glucose Levels and Nocturnal Hypoglycemia Using Physiological Models and Artificial Neural Networks. In Proceedings of the KDH@ IJCAI, Stockholm, Schweden, 13 July 2018; pp. 85–90. [Google Scholar]
- Atkinson, M.A. The pathogenesis and natural history of type 1 diabetes. Cold Spring Harb. Perspect. Med. 2012, 2, a007641. [Google Scholar] [CrossRef] [PubMed]
- Li, K.; Daniels, J.; Liu, C.; Herrero, P.; Georgiou, P. Convolutional Recurrent Neural Networks for Glucose Prediction. IEEE J. Biomed. Health Inform. 2020, 24, 603–613. [Google Scholar] [CrossRef] [PubMed]
- Bremer, T.; Gough, D.A. Is blood glucose predictable from previous values? A solicitation for data. Diabetes 1999, 48, 445–451. [Google Scholar] [CrossRef] [PubMed]
- Cryer, P.E.; Davis, S.N.; Shamoon, H. Hypoglycemia in diabetes. Diabetes Care 2003, 26, 1902–1912. [Google Scholar] [CrossRef] [PubMed]
- Wen, Q.; Zhou, T.; Zhang, C.; Chen, W.; Ma, Z.; Yan, J.; Sun, L. Transformers in Time series: A Survey. arXiv 2022, arXiv:2202.07125. [Google Scholar]
- Midroni, C.; Leimbigler, P.J.; Baruah, G.; Kolla, M.; Whitehead, A.J.; Fossat, Y. Predicting Glycemia in Type 1 Diabetes Patients: Experiments with XGBoost. In Proceedings of the KDH@ IJCAI, Stockholm, Schweden, 13 July 2018. [Google Scholar]
- Bhimireddy, A.; Sinha, P.; Oluwalade, B.; Gichpya, J.W.; Purkayastha, S. Blood Glucose Level Prediction as Time-Series Modeling using Sequence-to-Sequence Neural Networks. In Proceedings of CEUR Workshop Proceedings. 2020. Available online: https://scholarworks.iupui.edu/bitstream/handle/1805/30224/Bhimireddy2020Blood-NSF-AAM.pdf?sequence=1&isAllowed=y (accessed on 29 December 2022).
- Marling, C.; Bunescu, R. The OhioT1DM Dataset for Blood Glucose Level Prediction: Update 2020. In Proceedings of the 5th International Workshop on Knowledge Discovery in Healthcare Data, Santiago de Compostela, Spain, 30 August 2020. [Google Scholar]
- Martinsson, J.; Schliep, A.; Eliasson, B.; Meijner, C.; Persson, S.; Mogren, O. Automatic blood glucose prediction with confidence using recurrent neural networks. In Proceedings of the 27th International Joint Conference on Artificial Intelligence (KHD@IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 64–68. [Google Scholar]
- Zecchin, C.; Facchinetti, A.; Sparacino, G.; Cobelli, C. How Much Is Short-Term Glucose Prediction in Type 1 Diabetes Improved by Adding Insulin Delivery and Meal Content Information to CGM Data? J. Diabetes Sci. Technol. 2016, 10, 5. [Google Scholar] [CrossRef] [PubMed]
- Zecchin, C.; Facchinetti, A.; Sparacino, G.; Cobelli, C. Jump Neural Network for Online Short-time Prediction of Blood Glucose from Continuous Monitoring Sensors and Meal Information. Comput. Methods Programs Biomed. 2014, 113, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Sun, Q.; Jankovic, M.V.; Bally, L.; Mougiakakou, S.G. Predicting blood glucose with an LSTM and Bi-LSTM based deep neural network. In Proceedings of the 2018 14th Symposium on Neural Networks and Applications (NEUREL), Belgrade, Serbia, 20–21 November 2018; IEEE: New York, NY, USA, 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Zhu, T.; Li, K.; Herrero, P.; Chen, J.; Georgiou, P. A Deep Learning Algorithm for Personalized Blood Glucose Prediction. In Proceedings of the 3rd International Workshop on Knowledge Discovery in Healthcare Data co-located with the 27th International Joint Conference on Artificial Intelligence and the 23rd European Conference on Artificial Intelligence (KHD@-IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 74–78. [Google Scholar]
- Chen, J.; Li, K.; Herrero, P.; Zhu, T.; Georgiou, P. Dilated Recurrent Neural Network for Short-time Prediction of Glucose Concentration. In Proceedings of the 3rd International Workshop on Knowledge Discovery in Healthcare Data co-located with the 27th International Joint Conference on Artificial Intelligence and the 23rd European Conference on Artificial Intelligence (KHD@-IJCAI), Stockholm, Sweden, 13–19 July 2018; pp. 69–73. [Google Scholar]
- Rabby, F.; Tu, Y.; Hossen, H.; Lee, I.; Maida, A.S.; He, X. Stacked LSTM based deep recurrent neural network with Kalman smoothing for blood glucose prediction. BMC Biomed. Inform. Decis. Mak. 2021, 21, 101. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Lu, L.; Aponte, L.; Angelidi, A.M.; Novak, V.; Karniadakis, G.E.; Mantzoros, C.S. Deep transfer learning and data augmentation improve glucose levels prediction in type 2 diabetes patients. NPJ Digit. Med. 2021, 4, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Bevan, R.; Coenen, F. Experiments in non-personalized future blood glucose level prediction. CEUR Workshop Proc. 2020, 2675, 100–104. [Google Scholar]
- Joedicke, D.; Garnica, O.; Kronberger, G.; Colmenar, J.M.; Winkler, S.; Velasco, J.M.; Contador, S.; Hidalgo, J.I. Analysis of the performance of Genetic Programming on the Blood Glucose Level Prediction Challenge 2020. In Proceedings of the KDH@ ECAI, Santiago de Compostela, Spain & Virtually, 29–30 August 2020; pp. 141–145. [Google Scholar]
- Jeon, J.; Leimbigler, P.J.; Baruah, G.; Li, M.H.; Fossat, Y.; Whitehead, A.J. Predicting Glycaemia in Type 1 Diabetes Patients: Experiments in Feature Engineering and Data Imputation. J. Healthc. Inform. Res. 2020, 4, 71–90. [Google Scholar] [CrossRef] [PubMed]
- Staal, O.M.; Sælid, S.; Fougner, A.; Stavdahl, Ø. Kalman smoothing for objective and automatic preprocessing of glucose data. IEEE J. Biomed. Health Inf. 2018, 23, 218–226. [Google Scholar] [CrossRef] [PubMed]
- Sarkka, S. Bayesian Filterings and Smoothing; Cambridge University Press: Cambridge, UK, 2013. [Google Scholar]
- SimdKalman Fast Kalman filters in Python leveraging single-instruction multiple-data vectorization. Available online: https://simdkalman.readthedocs.io/en/latest/ (accessed on 29 December 2022).
- Barratt, S.T.; Boyd, S.P. Fitting a Kalman Smoother to Data. In Proceedings of the 2020 American Control Conference (ACC), Denver, CO, USA, 1–3 July 2020; IEEE: New York, NY, USA, 2020; pp. 1526–1531. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Chen, T.; Guestrin, C. XGBoost: A scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 784–785. [Google Scholar]
- Alfian, G.; Syafrudin, M.; Rhee, J.; Anshari, M.; Mustakin, M.; Fahrurozzi, I. Blood Glucose Prediction Model for Type 1 Diabetes based on Extreme Gradient Boosting. In IOP Conference Series: Material Science and Engineering, Chennai, India, 16–17 September 2020; IOP Publishing: Bristol, UK, 2020; Volume 803. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017. [Google Scholar]
- Liu, Y.; Wu, H.; Wang, J.; Long, M. Non-stationarity Transformers: Exploring the stationarity in Time Series Forecasting. arXiv 2022, arXiv:2205.14415. [Google Scholar]
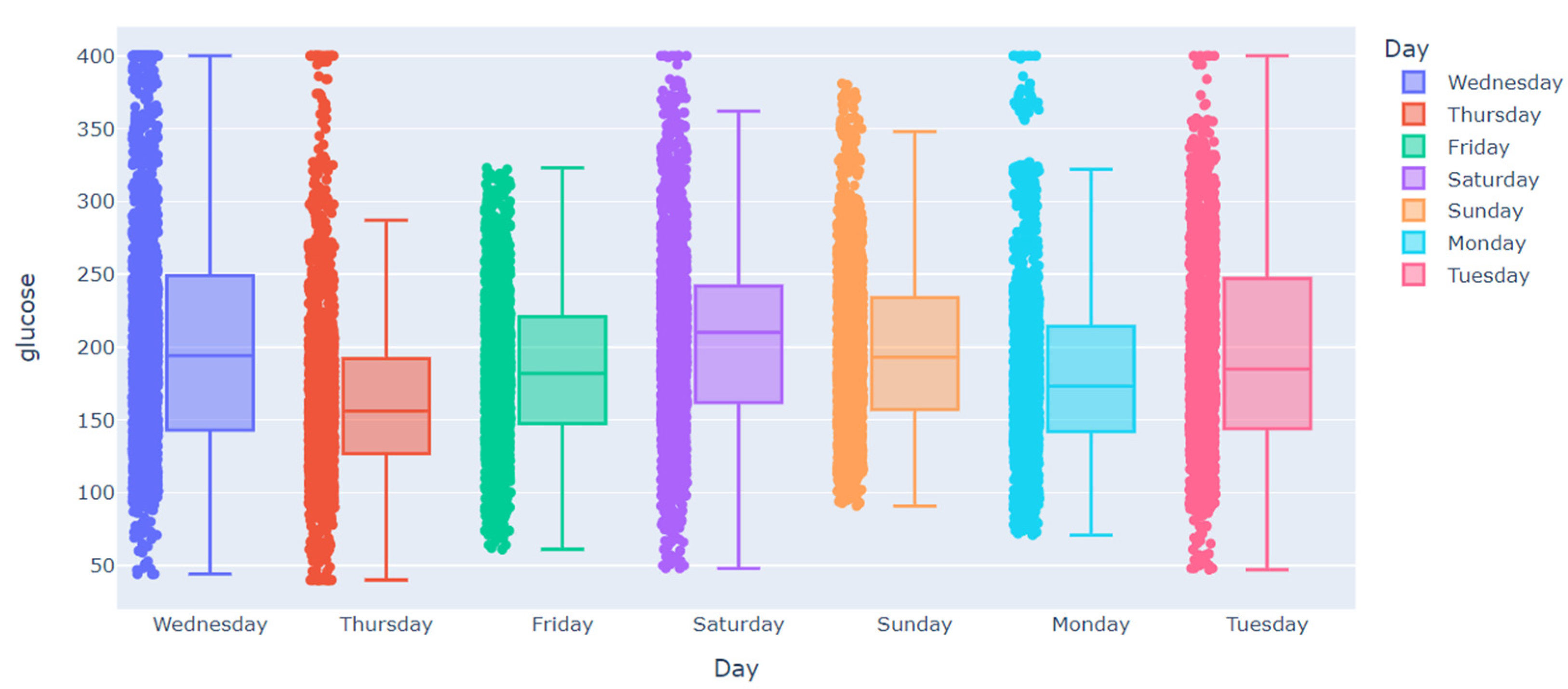
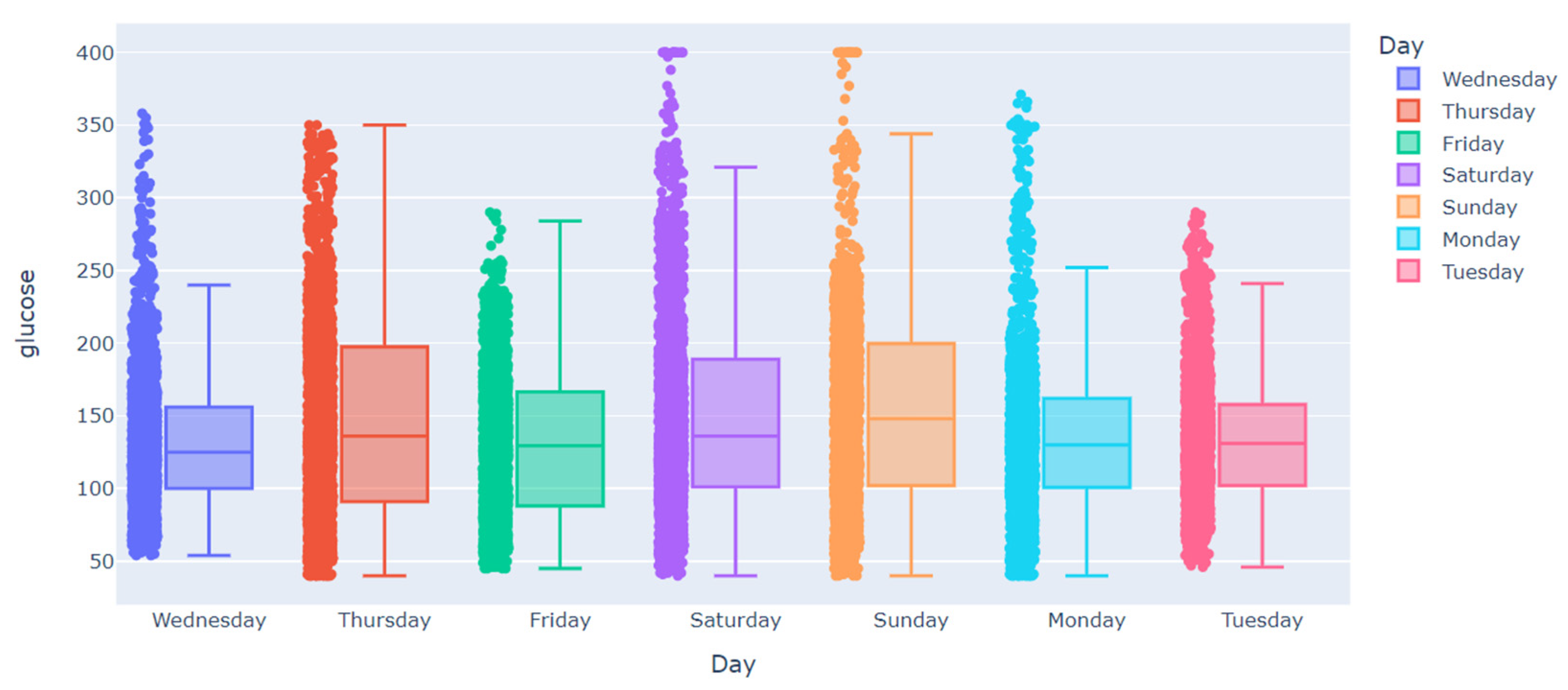
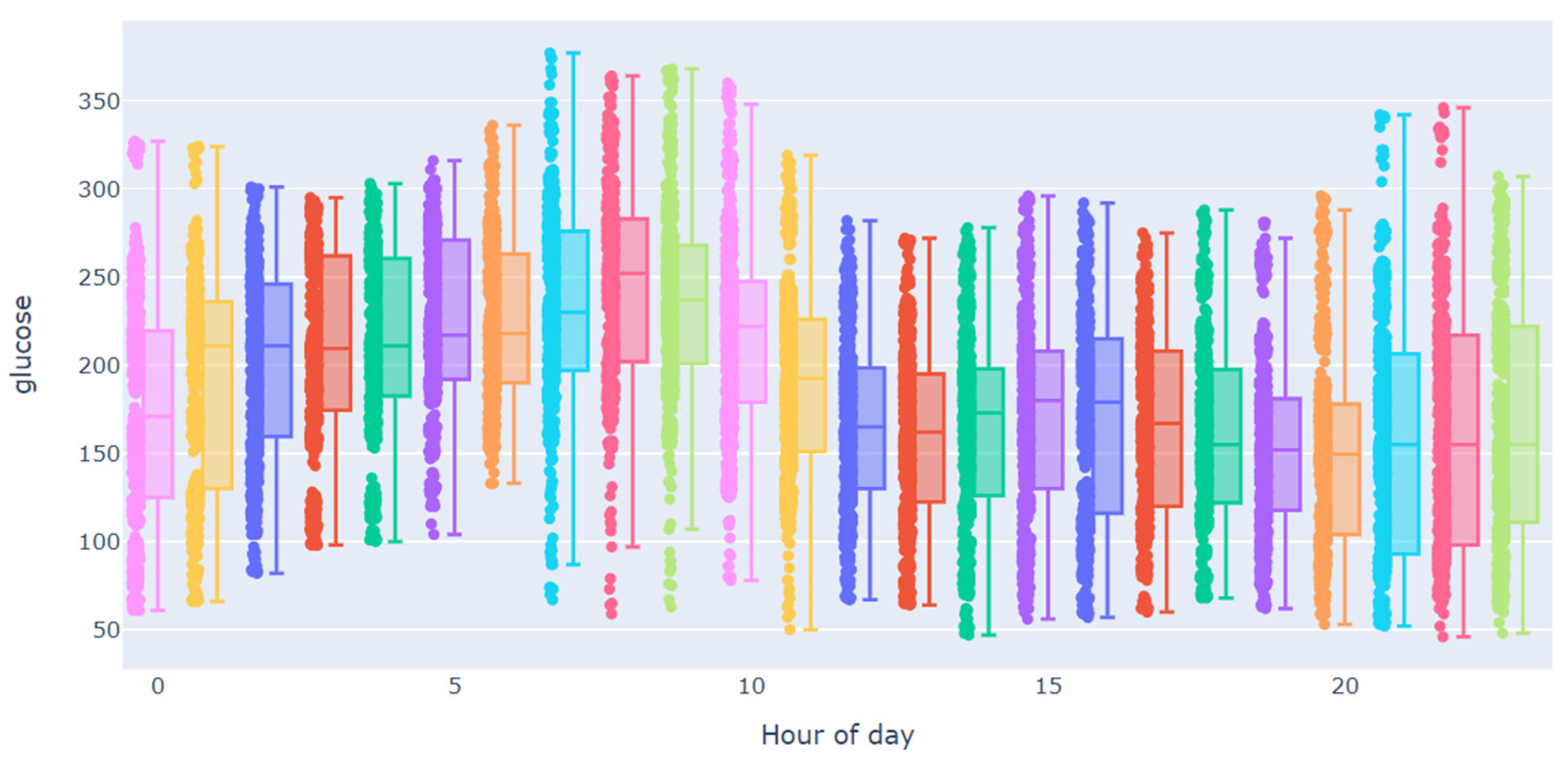
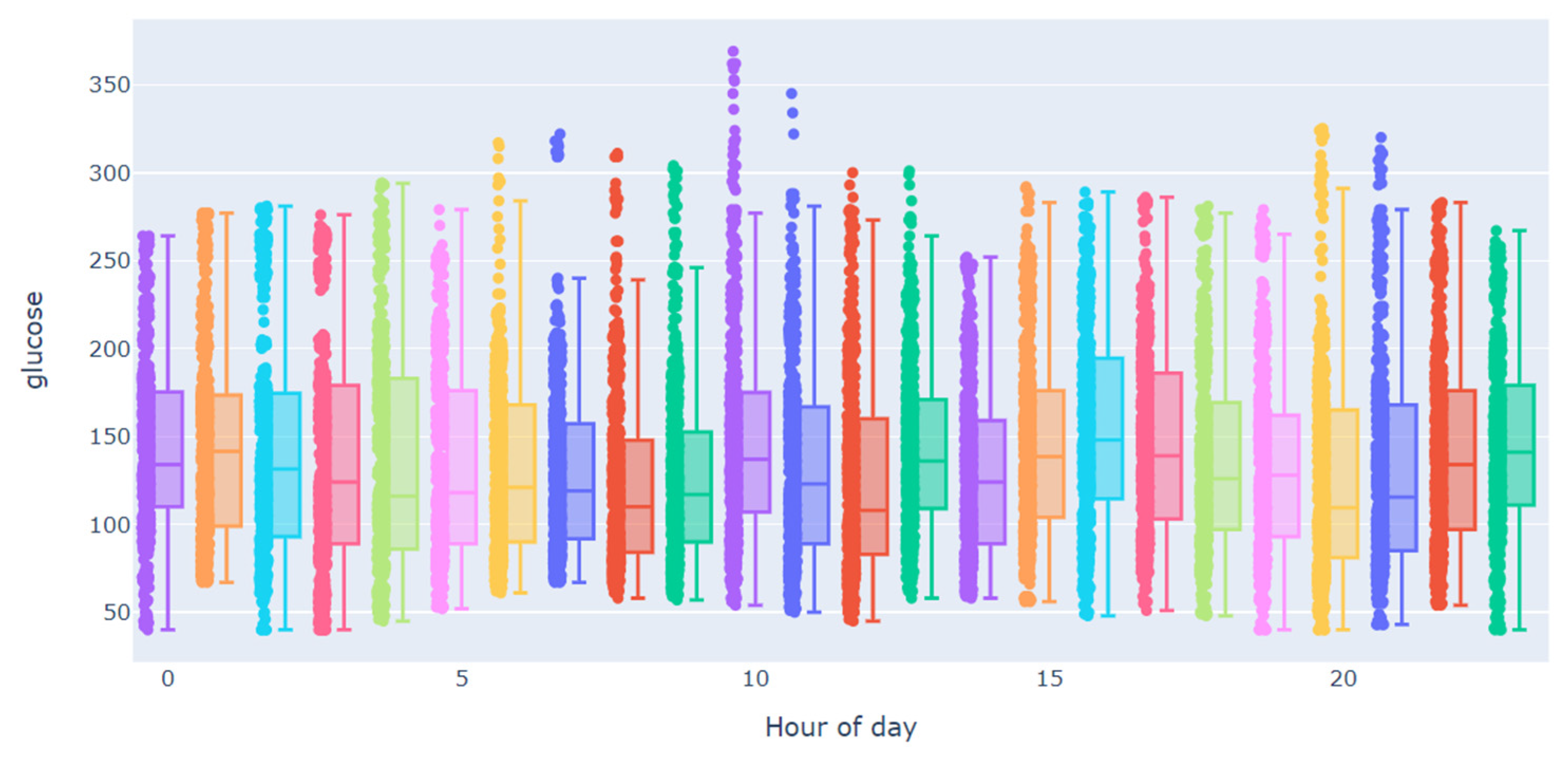




| Subject | Percentage of Missing Values in Training Dataset | Largest Gap in Training Dataset | Percentage of Missing Values in Testing Dataset | Largest Gap in Testing Dataset |
|---|---|---|---|---|
| 559 | 10.62 | 13 h 03 m (4) | 12.61 | 09 h 01 m (2) |
| 563 | 7.43 | 24 h 06 m (4) | 4.53 | 09 h 52 m (1) |
| 570 | 5.41 | 12 h 07 m (1) | 4.68 | 03 h 15 m (0) |
| 575 | 9.44 | 11 h 24 m (7) | 4.74 | 04 h 19 m (0) |
| 588 | 3.55 | 12 h 37 m (2) | 3.12 | 04 h 01 m (0) |
| 591 | 14.96 | 80 h 38 m (5) | 3.05 | 03 h 51 m (0) |
| 540 | 8.86 | 19 h 40 m (5) | 5.54 | 09 h 38 m (1) |
| 544 | 16.17 | 61 h 35 m (5) | 13.42 | 28 h 54 m (1) |
| 552 | 18.17 | 43 h 27 m (6) | 40.15 | 117 h 59 m (2) |
| 567 | 19.77 | 26 h 22 m (9) | 16.78 | 16 h 02 m (2) |
| 584 | 8.28 | 14 h 47 m (4) | 11.04 | 16 h 56 m (1) |
| 596 | 20.2 | 49 h 25 m (9) | 8.65 | 10 h 44 m (1) |
| Subject | Training | Testing | ||
|---|---|---|---|---|
| Hypoglycemic | Hyperglycemic | Hypoglycemic | Hyperglycemic | |
| 559 | 4.16% | 39.23% | 3.00% | 37.11% |
| 563 | 2.57% | 23.29% | 0.7% | 38.83% |
| 570 | 1.97% | 54.92% | 0.4% | 69.63% |
| 575 | 8.76% | 22.28% | 5.37% | 31.12% |
| 588 | 1.05% | 35.20% | 0.14% | 45.39% |
| 591 | 3.94% | 32.00% | 5.18% | 27.54% |
| 540 | 7.07% | 20.43% | 4.97% | 32.52% |
| 584 | 0.93% | 50.36% | 1.02% | 36.67% |
| Subject | XGBoosting | 1D-CNN | Transformer |
|---|---|---|---|
| 559 | 14.14 | 15.96 | 13.57 |
| 563 | 14.10 | 16.63 | 13.40 |
| 570 | 11.95 | 13.19 | 11.34 |
| 575 | 16.80 | 19.13 | 16.78 |
| 588 | 13.53 | 15.72 | 12.89 |
| 591 | 15.22 | 17.87 | 14.32 |
| 540 | 16.25 | 17.15 | 14.02 |
| 584 | 16.16 | 18.28 | 15.21 |
| Average | 14.77 | 16.74 | 13.94 |
| Subject | Smoothing | Imputation | ||||
|---|---|---|---|---|---|---|
| Interpolation | ||||||
| Kalman | Spline | Linear | Spline | Polynomial | Hourly Mean | |
| 559 | 7.07 | 11.55 | 13.16 | 13.36 | 13.60 | 16.44 |
| 563 | 6.48 | 6.38 | 13.78 | 13.71 | 13.73 | 14.17 |
| 570 | 6.39 | 7.59 | 11.91 | 11.74 | 11.51 | 16.15 |
| 575 | 8.25 | 8.45 | 16.23 | 16.20 | 16.32 | 20.38 |
| 588 | 7.00 | 7.08 | 13.46 | 13.53 | 13.68 | 13.75 |
| 591 | 7.35 | 7.46 | 15.26 | 15.34 | 15.43 | 16.56 |
| 540 | 10.13 | 16.07 | 17.87 | 17.25 | 17.57 | 31.30 |
| 584 | 7.47 | 8.97 | 15.55 | 15.46 | 15.42 | 20.23 |
| Average | 7.51 | 9.19 | 14.43 | 14.57 | 14.65 | 18.62 |
| Subject | Smoothing | Imputation | ||||
|---|---|---|---|---|---|---|
| Interpolation | ||||||
| Kalman | Spline | Linear | Spline | Polynomial | Hourly Mean | |
| 559 | 7.94 | 5.51 | 14.81 | 16.25 | 16.40 | 17.49 |
| 563 | 8.41 | 5.12 | 16.36 | 17.07 | 18.12 | 16.15 |
| 570 | 6.66 | 4.63 | 13.41 | 13.61 | 12.90 | 17.04 |
| 575 | 9.15 | 6.53 | 19.05 | 19.18 | 18.27 | 21.74 |
| 588 | 8.27 | 5.44 | 13.58 | 18.35 | 18.70 | 15.48 |
| 591 | 8.98 | 6.33 | 17.90 | 20.22 | 19.52 | 18.75 |
| 540 | 8.57 | 7.24 | 16.23 | 20.30 | 19.73 | 27.40 |
| 584 | 8.82 | 8.23 | 17.53 | 21.00 | 21.31 | 22.07 |
| Average | 8.35 | 6.12 | 16.10 | 18.24 | 18.11 | 19.51 |
| Subject | Smoothing | Imputation | ||||
|---|---|---|---|---|---|---|
| Interpolation | ||||||
| Kalman | Spline | Linear | Spline | Polynomial | Hourly Mean | |
| 559 | 6.93 | 9.30 | 12.13 | 15.31 | 15.34 | 14.87 |
| 563 | 7.40 | 9.38 | 12.95 | 13.37 | 13.26 | 13.38 |
| 570 | 7.27 | 8.96 | 11.20 | 11.87 | 11.95 | 14.91 |
| 575 | 8.57 | 12.13 | 16.11 | 17.15 | 17.09 | 19.10 |
| 588 | 7.67 | 10.48 | 12.52 | 12.91 | 13.00 | 12.91 |
| 591 | 8.78 | 11.59 | 14.41 | 14.11 | 14.95 | 15.24 |
| 540 | 8.05 | 13.08 | 13.57 | 15.04 | 15.18 | 16.19 |
| 584 | 8.85 | 14.05 | 14.51 | 19.32 | 19.25 | 18.83 |
| Average | 7.94 | 11.12 | 13.42 | 14.88 | 15.00 | 15.67 |
| Subject | Smoothing | Imputation | ||||
|---|---|---|---|---|---|---|
| Interpolation | ||||||
| Kalman | Spline | Linear | Spline | Polynomial | Hourly Mean | |
| 559 | 7.20 | 11.73 | 13.65 | 12.99 | 13.32 | 16.69 |
| 563 | 6.62 | 6.62 | 13.86 | 13.81 | 13.81 | 14.21 |
| 570 | 6.43 | 7.90 | 11.70 | 11.37 | 11.26 | 15.89 |
| 575 | 8.49 | 8.92 | 16.69 | 16.58 | 16.57 | 20.68 |
| 588 | 7.21 | 7.58 | 13.53 | 13.37 | 13.56 | 13.72 |
| 591 | 7.34 | 7.84 | 14.98 | 15.14 | 15.32 | 16.31 |
| 540 | 10.41 | 18.03 | 16.37 | 17.77 | 18.04 | 31.58 |
| 584 | 7.64 | 9.08 | 15.53 | 15.47 | 15.49 | 20.15 |
| Average | 7.66 | 9.71 | 14.53 | 14.56 | 14.67 | 18.65 |
| Subject | Smoothing | Imputation | ||||
|---|---|---|---|---|---|---|
| Interpolation | ||||||
| Kalman | Spline | Linear | Spline | Polynomial | Hourly Mean | |
| 559 | 8.53 | 5.55 | 21.12 | 24.91 | 21.86 | 25.08 |
| 563 | 8.23 | 4.76 | 20.84 | 21.19 | 18.35 | 18.60 |
| 570 | 7.18 | 4.56 | 15.47 | 15.54 | 14.72 | 18.77 |
| 575 | 9.34 | 6.89 | 22.57 | 24.43 | 21.02 | 26.16 |
| 588 | 11.03 | 5.02 | 21.14 | 22.50 | 23.00 | 21.10 |
| 591 | 9.50 | 6.16 | 21.63 | 23.06 | 21.47 | 21.62 |
| 540 | 8.64 | 7.36 | 18.26 | 24.47 | 21.88 | 27.40 |
| 584 | 8.87 | 7.31 | 18.58 | 30.55 | 24.80 | 24.08 |
| Average | 8.91 | 5.95 | 19.95 | 23.33 | 20.88 | 22.85 |
| Subject | Smoothing | Imputation | ||||
|---|---|---|---|---|---|---|
| Interpolation | ||||||
| Kalman | Spline | Linear | Spline | Polynomial | Hourly Mean | |
| 559 | 9.49 | 5.40 | 13.99 | 14.60 | 14.48 | 15.33 |
| 563 | 8.97 | 4.99 | 13.83 | 13.65 | 13.49 | 14.11 |
| 570 | 10.60 | 6.98 | 13.14 | 13.71 | 13.41 | 17.23 |
| 575 | 11.73 | 6.63 | 18.52 | 18.85 | 18.49 | 21.87 |
| 588 | 9.98 | 6.31 | 14.60 | 15.30 | 15.38 | 15.02 |
| 591 | 10.87 | 5.52 | 16.48 | 17.19 | 16.96 | 17.20 |
| 540 | 12.00 | 6.66 | 16.45 | 16.05 | 16.13 | 18.11 |
| 584 | 11.30 | 5.31 | 16.67 | 16.57 | 16.59 | 20.00 |
| Average | 10.61 | 5.97 | 15.46 | 15.74 | 15.61 | 17.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acuna, E.; Aparicio, R.; Palomino, V. Analyzing the Performance of Transformers for the Prediction of the Blood Glucose Level Considering Imputation and Smoothing. Big Data Cogn. Comput. 2023, 7, 41. https://doi.org/10.3390/bdcc7010041
Acuna E, Aparicio R, Palomino V. Analyzing the Performance of Transformers for the Prediction of the Blood Glucose Level Considering Imputation and Smoothing. Big Data and Cognitive Computing. 2023; 7(1):41. https://doi.org/10.3390/bdcc7010041
Chicago/Turabian StyleAcuna, Edgar, Roxana Aparicio, and Velcy Palomino. 2023. "Analyzing the Performance of Transformers for the Prediction of the Blood Glucose Level Considering Imputation and Smoothing" Big Data and Cognitive Computing 7, no. 1: 41. https://doi.org/10.3390/bdcc7010041
APA StyleAcuna, E., Aparicio, R., & Palomino, V. (2023). Analyzing the Performance of Transformers for the Prediction of the Blood Glucose Level Considering Imputation and Smoothing. Big Data and Cognitive Computing, 7(1), 41. https://doi.org/10.3390/bdcc7010041






