A Probabilistic Data Fusion Modeling Approach for Extracting True Values from Uncertain and Conflicting Attributes

Abstract

Real-world data obtained from integrating heterogeneous data sources are often multi-valued, uncertain, imprecise, error-prone, outdated, and have different degrees of accuracy and correctness. It is critical to resolve data uncertainty and conflicts to present quality data that reflect actual world values. This task is called data fusion. In this paper, we deal with the problem of data fusion based on probabilistic entity linkage and uncertainty management in conflict data. Data fusion has been widely explored in the research community. However, concerns such as explicit uncertainty management and on-demand data fusion, which can cope with dynamic data sources, have not been studied well. This paper proposes a new probabilistic data fusion modeling approach that attempts to find true data values under conditions of uncertain or conflicted multi-valued attributes. These attributes are generated from the probabilistic linkage and merging alternatives of multi-corresponding entities. Consequently, the paper identifies and formulates several data fusion cases and sample spaces that require further conditional computation using our computational fusion method. The identification is established to fit with a real-world data fusion problem. In the real world, there is always the possibility of heterogeneous data sources, the integration of probabilistic entities, single or multiple truth values for certain attributes, and different combinations of attribute values as alternatives for each generated entity. We validate our probabilistic data fusion approach through mathematical representation based on three data sources with different reliability scores. The validity of the approach was assessed via implementation into our probabilistic integration system to show how it can manage and resolve different cases of data conflicts and inconsistencies. The outcome showed improved accuracy in identifying true values due to the association of constructive evidence.

1. Introduction

In this era of information technology advancement, individuals and organizations must manage, process, exchange, and share information in heterogeneous environments [1,2]. To address this need, the foremost requirement is to integrate data originating from autonomous and heterogeneous sources. Data integration is the general process of producing a unified (mediated) repository from a set of heterogeneous and autonomous sources that may contain (semi-)structured or unstructured data [3,4,5,6]. Data integration represents a significant part of the activities of the global data management industry [3,7]. It provides a comprehensive yet concise overview of all available data without requiring the user to view each data source individually [1,3].

The need to access information from different sources through a uniform interface has been the driving force behind much research in the area of data integration [1]. Many approaches and tools have been proposed in recent decades to achieve integration at different schema and instance levels, with varying degrees of accuracy and success [8,9,10,11]. Such proposals have been presented in data integration systems, data management tools and techniques, and conflict resolution approaches [12,13,14,15]. This diversity of these technological solutions is the result of the adaption of diverse application domains with different needs and degrees of heterogeneity, such as the consideration of scientific data, online data, big data, and the combination of structured and unstructured data [13,16]. Issues related to overcoming data heterogeneity or the consequences of having the same information stored in different ways remain major concerns to data integration researchers [3,8,9,10,17,18]. According to Magnani and Montesi [19], Jaradat, Halimeh, Deraman and Safieddine [3], Bakhtouchi [8], and Papadakis, Skoutas, Thanos and Palpanas [9], schema mapping and entity linkage (also known as “duplicate deduction”) in diverse sources have been recognized as two major issues that must be addressed in order to integrate data into a single, consistent representation. Another major issue, named “data fusion” or “data conflict resolution”, has been recognized; this requires further research to achieve consistent, integrated data [8,9,10,20]. Data fusion is about how to find a true value from contradicting attribute values when integrating data from several sources [17,21,22]. Although the resolution of data conflicts has been mostly neglected, several approaches and techniques have evolved [2,17,23,24,25], many of which attempt to “prevent” data conflicts by focusing solely on the uncertainty of missing values, while others employ a variety of resolution strategies to “resolve” conflicts [3,9,23,24]. Accordingly, the problem regarding the lack of a proper data conflict resolution modeling approach with explicit uncertainty management and correlations has been identified in [3,8,19,24,26]. In particular, an approach is required to tackle the data fusion problem based on probabilistic data linkage results and addresses its representational and computational uncertainty management challenges. This motivates us to study the probabilistic data fusion problem based on source accuracy, probabilistic entity merging, data conflict, and uncertainty management.

This paper looks closely at a probabilistic data fusion approach for extracting true values from uncertain and conflicting attributes. To this end, we propose a new probabilistic data fusion modeling approach. The approach represents and manages the uncertain and conflicting multi-valued attributes of a generated entity named “network digital object” (nDO). An obtained nDO, with its possible alternative, is generated from the probabilistic merging of multi-corresponding entities. Our approach considers both the Open-World Assumption (OWA) and Closed-World Assumption (CWA) while constructing the possible worlds of the fused values and their probabilistic formulations. It also considers both single and multiple truth assumptions. Based on these considerations, more meaningful probabilistic data fusion answers can be obtained to fit real-world data integration and fusion scenarios. The main contributions of this paper are as follows:

(1).

Handling the data fusion representational challenge of accepting probabilistic data, i.e., reliability scores of data values and probabilistic similarity value sets, to generate probabilistic global entities with their fused data value alternatives.

(2).

A formal representation of varied data fusion cases to fit into the probabilistic data fusion problem. The formulation of data fusion cases is outlined by observing the origin of the generated data values and their uncertainty.

(3).

Incorporating data lineage into the data fusion model to trace the source of data that offers additional information with which to understand the conflict and uncertainty among the observed data and to facilitate the on-demand data fusion process.

(4).

The construction of a data fusion computational method that conditionally calculates the posterior/updated reliability score for a possible world of true fused value(s).

(5).

The implementation of the data fusion method within the probabilistic data integration system that can show the applicability of addressing on-demand probabilistic fusion for different data conflict types based on the merging of probabilistic entity alternatives.

(6).

Finally, our proposed data fusion approach is designed to cope with a dynamic, volatile and on-demand fusion environment and to support efficient modification re-execution. It provides a means of a new Decision Model (DM) logic that isolates the matching logic from the decision logic, yielding an additional efficiency advantage while dealing with dynamic data. The constructed model can work in two-fold benefit solutions; it can work as a complete probabilistic DM or replace the manual DM sub-stage in traditional DM logic.

The rest of the paper is organized as follows. Section 2 briefly reviews some literature and related work. Section 3 introduces the proposed approach. Section 4 describes our data fusion problem based on the probabilistic integration of heterogeneous data sources. In Section 5, we develop our probabilistic data fusion model and its constructed computational method. Section 6 presents a proof of concept through system implementation and mathematical proof to illustrate the validity of the proposed model. Section 7 outlines the limitations related to the proposed approach. Finally, the conclusions of this paper are given in Section 8, and some future directions for our work are identified.

2. Data Fusion Background and Related Work

In this section, we first highlight data integration in general and its related conflict resolution tasks. After that, uncertainty modeling and probabilistic databases are discussed.

2.1. Data Integration

The field of data integration has expanded in several directions as the technology and application landscapes have evolved over the years [13]. This expansion has been observed from the diverse schema and/or instance integration challenges and solution proposals. These proposals include data integration systems, conflict resolutions, and data management tools and techniques. They have evolved from precise integration systems to uncertainty management mechanisms [13]. A diverse range of technological solutions has also been required to adapt to the needs and environments of a wide range of application domains, such as the consideration of scientific data, online data, or big data, and the combination of structured and unstructured data [3,13,16]. The data integration field has been motivated toward the utilization and development of combined techniques from artificial intelligence and data uncertainty management fields [13]. The contributions of these fields were to propose data representation formalisms of heterogeneous data sources’ contents and to manage and resolve the heterogeneity of the integrated outcomes [13].

As a general view of data integration, we can state that it is the general process of producing a unified (mediated) repository from a set of multiple heterogeneous and autonomous sources that may contain (semi-)structured or unstructured data [3,4,5,27]. Data integration contributes a significant solution to the global data management industry and data quality field [3,7]. It facilitates information access and reuse through a single point, enables users to focus on specifying what they want and frees them from the tedious tasks of how to obtain the answers, and helps users gain more comprehensive information that satisfies their needs and interests [28]. Traditional integration goals are to increase the completeness, conciseness and correctness of the information available to users and to free them from the knowledge about the data sources themselves [8,23]. However, since data from various independent sources are integrated, schema and instance uncertainty are naturally inevitable at all stages of the integration process; hence, they need to be handled and managed accordingly [8,19,29]. To meet this general requirement, we need data integration that performs two integration levels (i.e., schema and instance integration levels) and three formidable conflict resolution tasks (i.e., schema mapping, entity linkage and data fusion). Figure 1 shows these integration levels and their corresponding conflict resolution tasks as the integration process proceeded from multiple heterogeneous data sources.

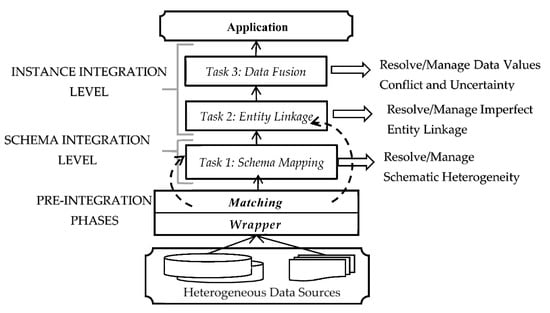
Figure 1. Data Integration level and its corresponding conflict resolution tasks.

The data integration industry has approached these tasks of generating integrated outcomes in two broad resolution strategies: (i) the precise integration strategy and (ii) the uncertainty integration management strategy. Classical data integration (CDI) approaches, such as traditional mediation, Peer-to-Peer (P2P), and warehouse, are based on the first strategy. This strategy aims to provide a high-quality end of data for well-defined and well-understood precise data integration tasks but does not cope well with uncertainty management. From the traditional perspective, CDI deals with uncertain data as something that can be avoided by unrealistic simplified and restrictive assumptions, such as sharing universal key identification and having enough data [13]. Moreover, uncertain information is ignored, avoided, manually resolved, or removed at some point through defuzzification, viewing consistent answers, using predefined thresholds, or semi-automatic choice of the most likely outcome only [8,18,19]. The recent data integration generation that represents the dataspace vision [20] and pay-as-you-go data management with their relevant principles of automation, probabilistic data representation and manipulation, and best-effort integration are all based on the uncertainty management strategy. This strategy and its approaches identified that uncertainty is inherently unavoidable in the integration process, yet uncertain information is valuable and even more useful than losing it; hence, it is an important result to be managed and viewed by the users [5,7,30,31,32].

Several data integration systems have been developed by the research committee and by the commercial industry, such as Big-Gorilla [13], Tamer [12,15], Deepdive [14], Data Civilizer [33], HUMMER [34], and FUSEM [35]. For instance, Big-Gorilla is an open-source system consisting of data integration and preparation operator modules such as string matching, entity matching, and schema matcher. At the same time, Hummer and FUSEM can be viewed as data fusion systems that contain tools for resolving data conflict (i.e., addressing the data fusion task) [13,36]. Moreover, research approaches related to probabilistic schema integration, entity linkage and data fusion have also been developed by the data integration research committee. For instance, Dong and her collaborative researchers proposed a probabilistic schema integration approach in [32], as well as data fusion approaches that consider data sources correlation in sort of data duplication [23,24,25,37]. Moreover, research efforts related to probabilistic entity linkage and resolution can be found at [9,10,38,39,40,41,42,43,44,45,46].

The uncertainty management strategy and its corresponding resolution approaches were proposed due to several reasons and motivations that have been identified by the data integration literature [13]. One reason for this proposal is information space complexity [5,11,27,47]. This complexity is related to the expanding growth, heterogeneity nature, and data quality diversity of related online information sources. Another reason is observed from the precise integration strategy limitation [18,32]. Precise integration is still a major undertaking that requires a significant upfront human intervention. Data integration literature has documented that CDI methods occupy a position at a high-cost setting up and maintenance, information loss, and misleading and error-prone results. CDI methods are also less effective for numerous or rapidly changing data resources [26,32,48]. Finally, the challenging nature of the instance integration level, as it represents the entity linkage and data fusion tasks for resolving the entity identification and data conflict problems, is another motive for the second strategy adoption [9,18]. Instance integration denotes the main purpose of the integration process as providing users with the actual comprehensive and complementary information about their requested entities throughout the generation of global entities [3]. According to the data integration industry literature, more efforts have been focused on the data integration industry literature, and more have been focused on schema integration and entity linkage. In contrast, fewer efforts were focused on the data fusion task (or data conflict resolution) based on uncertainty management [6,20,27].

2.2. Uncertainty Modeling

Uncertainty is used as the general and specific label to refer to the information items that represent multiple possible states of the external world, yet it is unknown which state corresponds to the actual situation of the world. Therefore, these types of information cannot be asserted with complete confidence of being correct. Uncertainty may concern the actual data relating to the occurrence of an event in the world and the relations among various events. Under this label, several distinct types can be observed, such as impreciseness, incompleteness, errors, vagueness and ambiguity and redundancy natures of the integrated datasets as explained further in [49]. In fact, there have been many attempts to classify various possible types of uncertain information, such as the ones presented by [50,51]. In this paper, we are concerned with four basic types, i.e., imprecise, inconsistent, incomplete and uncertain data, as illustrated next.

Imprecision means the available information is not specific enough and denotes a set of possible alternatives, where the real value is one of those alternatives. For instance, “Ali’s age is either 33 or 38” (disjunction); it is 34 ± 1 year (error margins); or we simply do not know Ali’s age (Ali’s age is NULL). A null value usually denotes that the information is unavailable (incomplete). However, it could be regarded as imprecise information from the entire domain of legal values. It may also indicate unknown or inapplicable values. Inconsistency denotes that the available information reflects conflict representations about a particular aspect and cannot be true at the same time. For example, “Ali’s age is between 33 and 38” and “Ali’s age is 40”. Finally, uncertainty expresses doubt about if our information about a particular aspect is true or not, as “Ali’s age is probably 33”. The doubt can be quantified with a confidence value as “Ali’s age is 33 with probability 0.6” [30,51,52].

Imprecision and inconsistency are relevant to the content of an attribute value of a data object. At the same time, uncertainty is relevant to the degree of truth of its existence and its attribute values. Therefore, imprecision and inconsistency induce uncertainty, and probabilistic information can combine uncertainty with imprecision or inconsistency. For instance, consider the above examples “33 or 38” and “33 with probability 0.6”. The first example is a form of impreciseness, whereas the second is a form of uncertainty. By combining these two examples: the age of Ali is 33 with a probability of 0.6 and 38 with a probability of 0.4, information expresses certainty in terms of a probability measure on each alternative, and hence, uncertainty is reduced [19].

The AI and database communities have taken into consideration several approaches, such as rule-based systems, Dempster–Shafer, and fussy sets, for modeling uncertain information [21,30,53,54]. For instance, some efforts used NULL values representation to replace all partial information about the imperfect parts of a description, and hence, uncertainty was ignored. Others suggested the use of meta-information (soundness and completeness) to declare the portion of perfect from imperfect information, and hence, uncertainty was avoided. In addition, there were solutions developed using the certainty factors, such as weights, to denote confidence about the stated facts and rules that describe real-world objects. However, declaring confidence factors is a subjective issue, and objections have been raised showing that the lack of firm semantics may lead to unintuitive results [49].

In addition, approaches based on probability theory were developed to provide a model that supports alternative results [30]. The probabilistic model has been dominant in the database community to develop probabilistic databases that capture, manage and represent uncertain data [53,54,55]. These proposals were mainly based on symbolic-qualitative and/or numeric-quantitative models [53]. Among them are the uncertain data model, probabilistic graphical model, and possible-world model [30,53]. One of the most common uncertain data models is the extension of the relational model to include c-table, ?-table, or-set table, or-set-? table, which represents uncertainty at the tuple and attribute levels [30,56]. The probabilistic graphical model handles the database as two-tuples (R, P), where R is a set of relations and P is a probabilistic graphical model presented either in Bayesian networks or Markov networks [30]. The dependency relationship between uncertain data can be addressed in this graphical representation. Each tuple or attribute in R is associated with a random variable that represents the existing probability, and each node of P is a random variable that may correspond to a certain tuple in R. The edges represent the relationship between random variables [30,57]. The typical database with uncertainty management is the probabilistic database, where the possible-world model is the base for such probabilistic representation [30,53,58], and [54]. Each possible-world instance corresponds to a certain database, where the uncertain attributes are certain values satisfying constraints [30,55]. Some typical uncertain databases and possible-world instances are formed due to the existence of attribute-level uncertainty with continues attribute values, attribute-level uncertainty with discrete attribute values, and record-level uncertainty with or without generating rules [30,59]. Correspondingly, various probabilistic databases have been proposed, such as DCAE [60] MayBMS [61], Trio [62], MCDB [63], and IMPrECISE [64,65]. For example, MayBMS, Trio, DCAE, and MCDB are probabilistic database approaches for uncertain relational data, while IMPrECISE is an approach for uncertain XML data format [60,66]. Moreover, MayBMS focused on the tuple-level uncertainty, while MCDB and DCAE focused on attribute-level uncertainty. The possible-world model is the mathematical backbone for these approaches, and they are mainly designed for single-type of data [66,67].

However, many systems based on probabilistic databases still have certain semantic deficiencies that limit their potential applications [55]. This deficiency is mainly related to the avoidance of considering the Open-World Assumption (OWA) by adopting the Closed-World Assumption (CWA) only while creating the probabilistic database. Thus, these probabilistic databases lack a suitable handling of data incompleteness [55]. CWA indicates the facts that do not appear in the database to have a probability of zero. This means that CWA assumes that the facts of a specific database domain are complete, which is not always true in real-world applications.

In contrast, the OWA does not assume the completeness of a specific database domain. It considers the possibility of having an unknown value or values outside the database domain to be true; hence, an unknown fact (i.e., also known as an open fact) that does not appear in a specific database might have a probability greater than zero. Accordingly, incompleteness is represented or handled using those probabilistic database efforts [55]. Our proposed data fusion approach considers both assumptions (i.e., OWA and CWA) while constructing the possible worlds of the fused values and their probabilistic formulations, thus addressing these concerns. Based on this consideration, more meaningful probabilistic data fusion answers can be obtained to fit real-world data integration and fusion scenarios.

2.3. Data Fusion Related Work

Data fusion is the process of reformulating objects from multiple observations [68]. Data fusion can be defined as a process of generating a single fused representation over two or more probable linked entities, which are being merged and replaced in a central repository by a new entity containing attributes values as the union of their respective sets [11,22,26,69]. It can also be defined as providing users with more trustable data with higher quality [26,70]. As a result, for each obtained attribute, there are likely to be several possible values, each of which has originated from independent or correlated sources and asserted with a different degree of confidence by correspondents with differing reliability levels [71]. Therefore, rather than just take an ad hoc or precise decision on which version is correct, it is better to absorb all opinions and make a probabilistic estimation of the likely correct one [3,18,71].

Estimating the truth while forming this fused representation requires managing several types of conflict and uncertainty at the entity and data levels since the new entity may have multi-possible worlds [69]. In fact, the fusion of multi-valid or invalid attribute values from probabilistic merged entities represents a major reconciliation challenge [3,8,19]. Therefore, proposing advanced fusion methods with the capabilities of accepting and handling uncertain data from probabilistic entities merging, considering the role of source dependence, and storing versions of data values with an associated likelihood of correctness is a crucial issue in the current age of information integration and data quality fields [3,8,11,17,19,21,26].

Over the last two decades, intensive efforts toward proposing precise and/or probabilistic data fusion approaches have been observed in the data integration community [8]. Related works that address the management of uncertain data values throughout the proposal of probabilistic data fusion solutions can be found in [8,18,21,24,25,67,68,69,70,72,73,74,75,76]. This intensive effort has been established due to the importance of obtaining quality information for the intended users. Generally, the work conducted by Bleiholder and Naumann [77], and Dong and Naumann [23] included an early survey of data fusion approaches, as typical data fusion approaches were mainly rule-based. Due to the produced results, those approaches can also be divided into deciding and mediating strategies. Deciding strategy picked a preferred value among existing values while mediating strategy produced an entirely new value such as the average of conflicting numbers. Moreover, recent research by Bakhtouchi [8] Bakhtouchi [8] and Xu, Zadorozhny and Grant [68] presented one of the latest surveys in the field of data fusion. In their papers, three data fusion or conflict handling strategies were highlighted based on the previous categorization found by Bleiholder and Naumann [77]. These strategies are conflict ignorance, conflict avoidance and conflict resolving [8,23,77]. Conflict ignorance performs no resolution over conflicting data. Sometimes, it was not even aware of the existence of conflicts. Therefore, inconsistent results have a high potential to be produced. (Pass It On) and (Consider All Possibilities) are two ignoring strategies representatives. Conflict avoidance strategies acknowledge the existence of possible conflicts, yet it does not perform individual resolution for each conflict. Instead, a single decision is made, such as using preference of a source, and applying it to all conflicts. In this case, the data that are coming from the preferred source are contained only. Take the Information, No Gossiping, and Trust Your Friends are all avoiding strategies. Finally, conflict resolution strategies provide the means for individual fusion decision for each conflict. Such a decision can be instance-based, i.e., it regards the actual conflicting values, using Cry with The Wolves, Roll the Dice, or Meet in the Middle strategies. The resolution decision can be metadata-based, such as Keep Up to Date strategy.

According to research by [23,37], none of the above strategies is perfect, and they all fall short in some or all of the following aspects. (i) Data sources are of different quality, and we often trust data from more accurate sources, but accurate sources can make mistakes as well; thus, neither treating all sources as the same nor taking all data from accurate sources without verifying is appropriate. (ii) The real world is dynamic, and the true value often evolves overtime, but it is hard to distinguish incorrect value from outdated value. Thus, taking the most common value may end up with an out-of-date value, while taking the most recent value may end up with a wrong value. (iii) Data sources can copy from each other, and errors can be propagated quickly. Thus, ignoring possible dependency among sources can lead to biased decisions. Finally, (iv) linkage decisions might be probabilistic. In this case, merging depends on the linkage context; ignoring differences leads to conflict-avoidance and wrong value consideration [26,69]. For these reasons, researchers were motivated to develop advanced strategies that rely on managing uncertainty and probability modeling to resolve conflicts. Such advance resolution strategies were based on considering the accuracy, freshness and/or correlation of the participated sources. Basically, three different categorizations of advanced fusion strategies, which conditionally consider source accuracy, data freshness, and sources correlation in terms of copying data from each other, have been outlined in [8,25].

• Conflict Resolution by Considering Accuracy of Source: Data sources have different accuracies, and some are considered more trustworthy. Therefore, a more precise decision can be obtained by considering sources’ reliability as proposed in [67,69,71,78,79]. Using this technique requires a probability model that iteratively computes the sources’ accuracy to decide the true values. Research by Panse and Ritter [69] investigated how a set of probabilistic tuples designated as duplicates can be merged by considering uncertainty on the instance and source reliability. According to [67], a general optimization framework called CRH is proposed that seamlessly integrates the truth-finding process on various data types.
• Conflict Resolution by Considering Freshness of Sources: The data is often changing dynamically in the real world. The value of being true or false can be, in a subtle case, out-of-date. Accordingly, research done in [24,80] addressed data sources’ freshness and treated incorrect and out-of-date values differently by describing their probabilistic model accordingly.
• Conflict Resolution by Considering Dependency between Sources: In many domains, especially on the Web, data sources may copy from each other for some of their data. Dependency among sources in sort of source copying has been considered in research work such as [23,24,25,70,73,81,82]. According to [23,24], source accuracy has been considered for the analysis of source dependencies. Research by [70] introduced a two-stage fusion approach based on Markov Logic Networks. Unlike current data fusion research that focuses on resolving data conflict on a single attribute, this effort considered the interrelationship of data conflict on different attributes to improve the accuracy of the fused results. These research efforts are effective in detecting positive correlation on false data but are not effective with positive correlation on true data or negative correlation. Their models also rely on a single truth assumption, as everyone has a unique birthplace. In practice there can be multiple truths for certain facts, such as someone may have multiple professions. Accordingly, [25] introduced a data fusion approach with correlation, i.e., the correlation among sources can be much broader than copying. It can be positive or negative, and caused by different reasons.

Furthermore, those advanced resolution solutions were generally classified in [24] into three categories: voting, quality-based, and relation-based. Voting is the main baseline category, where the value with the highest vote count or provided by the largest number of data sources is selected from the conflicting values. Quality-based is based on evaluating data sources’ trustworthiness. Accordingly, the value with a higher vote for a high-quality data source is computed. Based on how we measure source trustworthiness, the quality-based category can be subcategorized into Web-link-based methods, IR-based methods, graphical-model methods, and Bayesian methods. Approaches based on the Bayesian method, such as [23,24,37,78], measure the source’s trustworthiness by its accuracy, which primarily indicates the probability of each of its values being true [19]. Relation-based category extends the quality-based methods by considering the relationships between the sources. The relationship can be in a sort of copying between a pair of sources or in a sort of correlation among a subset of sources. Further discussion on these advanced methods and approaches can be found in [6,20,23,24,67,72,78,83,84,85,86].

Nevertheless, most of these advanced methods followed an iterative approach to truth-finding, data/source quality evaluation, and sources correlation detection [72]. They are primarily unsupervised or semi-supervised, as they do not use training data [84]. They were mostly considered probabilistic handling of the merged uncertain data based on certain precise linkage and entity merging results [69]. As a result, their fusion techniques were mainly designed to support offline fusion and static information that does not evolve overtime [8,24,70,73]. The research by [73] built the first online data fusion system called SOLARIS. Moreover, they mostly resolve the conflicting data by relying on either a single truth assumption or multiple truth assumptions [25]. In practice, an entity may contain attributes with a single truth value and/or multiple truth values, such as a person may have a single birth date and multiple professions. Even more, fuse multi-valid or invalid attribute values due to probabilistic linked and merged entities and over dynamic and volatile information sources have only been rarely and individually addressed in [69,70,73].

By considering source accuracy, probabilistic entity linkage nature and on-demand data fusion process, our data fusion approach is relative to the approaches proposed in [20,26,67,69,70,73,79]. Even though it is different from the above works in the following aspects. First, while our approach is based on the ‘quality-based strategy, it proposed to manage and resolve two major fusion cases. Firstly, the multi-true values (i.e., multiple truth assumptions), and inconsistent-true values (i.e., single truth assumptions) are based on closed-world and open-world assumptions. Secondly, the data fusion is processed over probabilistic entity linkage and multi-merging alternatives. Our approach can also support on-demand fusion and cope with dynamic and volatile conflicting and uncertain data by keeping and storing the reliability scores alongside its actual data values and by taking the matching and computation process as a chain of separate processes, where each one has its own inputs and outputs data [87]. Upon a user request, such a fusion process for a selected attribute and over a probabilistic global entity is initiated by matching its values from their corresponding sources and entities to form a global domain of merged attribute’s values pairs, and then the computational fusion is executed separately.

3. Preliminaries

This section introduces some background of the proposed model, including the definitions of the informative digital object (iDO) concept, the integration framework, the lineage, and the rules of possible-world semantic.

3.1. Informative Digital Object (iDO) Concept

The term informative Digital Object (iDO) describes a Real-World Object (RWO) as a person or a place that has a distinct identity locally. In fact, iDO is the ground root for proposing the network Digital Object (nDO) concept that represents a particular global entity generated from the probabilistic merging of its corresponding local iDOs.

We can define the iDO concept as a uniquely identifiable container that aggregates and presents relevant multi-entities components in terms of the actual content aspect and in the form of compound digital existence, throughout mapping the associated relationships among them with a coherent and cohesive representation of information context about a specific RWO [87]. iDO is an extended content-based model mechanism for the Digital Object (DO) concept, which consists of diverse contents of information units constructed from sequence transformation of meta-levels components of relevant data. The actual contents are grouped under varied categories to give an organized representation of an RWO’s features and to convey meaningful and comprehensive information. Thus, multi-parts components can be managed and viewed as a single entity [87].

In the iDO model, the object’s features are classified under three major categories, i.e., identification, descriptive, and supportive, and where each category consists of various subcategories due to the correlation and mapping type between a specific attribute with its corresponding iDO [3]. This categorization would provide domain-independent entity resolution rules [3]. Detailed information about iDO concept to represent the entities from the participated sources within a probabilistic data integration framework, the attribute types and categories, and the possible-world generation rules and mapping types can be found in our previous research paper as [3,88]. The iDO representation for the RWOs is given in the following definitions.

Definition 1.

The participated data sources that are required to be integrated is a set of$n$sources, where each participated source can be in a type of (semi-)structured$\left(t{p}_1\right)$, or unstructured$(t{p}_2)$, i.e.,$S=\left\{S_1,S_2,\dots ,S_n\right\}:i\in \left[1,n\right], S_i.tp\in \left\{t{p}_1,t{p}_2\right\}$. This representation helps distinguish the matching comparison process between each of these two types. For example, the participated$\left(t{p}_1\right)$ sources are assumed to contain unique objects. Hence, the internal matching comparison is not required as no duplicated objects can be found. In contrast,$\left(t{p}_2\right)$sources may contain duplicated objects, and then the comparison process proceeds internally. Detailed information about this pair-wise source-to-target matching process can be found in [3].

Definition 2.

Entities of the participated data sources for integration are considered to belong to the same domain. They are assumed to be modeled in sort of iDOs to represent persons, restaurants or any other RWOs. Each $S_i$source contains a set of$m$iDOs, where the range of$m$in the participated sources are different, i.e.,$S_i=\left\{iD{O}_{i1},iD{O}_{i2},\dots , iD{O}_{im}\right\}: 1\le h\le m$. An$(iD{O}_{ih})$is triple of a comprise set of attributes’ names$(A_k^{ih}:1\le k\le c)$, attributes’ values$(a_{k.g}^{ih}: 1\le g\le q)$, and attributes’ types$(ty\in \left\{Idn, Desc,Supp\right\})$, i.e.,$A_k^{ih}.a_{k.g}^{ih}.ty$. These attributes describe the shared features of iDOs, where an attribute may contain single or multiple data values and belongs to a specific category that encodes the attribute type$\left(ty\right)$. According to [3], a specific mapping rule based on the attribute type can be applied to obtain the possible world.

3.2. The Best-Effort Data Integration Framework

Our probabilistic data fusion approach is formulated based on the proposed best-effort data integration framework presented in [3]. This framework considers that the global schema generation and its mapping production are a priori performed. Hence, a $\left(GS\right)$ global schema consisting of global attributes is obtained before the initiating of the instance integration process, i.e., $A_k^{ih}\in \left(A_1^{GS}.ty, A_2^{GS}.ty, \dots , A_c^{GS}.ty\right)$. These generated global attributes correspond to a specific attribute that existed at the participated data sources. Each $\left(A_k^{GS}\right)$ with its mapped data sources’ attributes must belong to a specific $\left(ty\right)$ attribute’s type, such that one of these global attributes represents the main parameter, such as the name of an author or a restaurant. Thus, the type of this main parameter attribute is $\left(ty=Idn\right)$.

Despite the precise integration at the schema level, the framework takes the instance integration as a non-trivial process that requires probability management capabilities. Therefore, a probabilistic global entity named network digital object ($nD{O}_w:1\le w\le z$) is added to the traditional framework formulation. This framework aims to remove the manual interventions by allowing less precise but automatic instance integration (i.e., entity linkage and data fusion) answers. It also corresponds to the pair-wise source-to-target matching process. In this process, a participated $\left(S_i\right)$ data sources can be presented as a target data source $(T{s}_t: T{s}_t\in S)$ or a local source $(L{s}_s: L{s}_s\in S)$. Accordingly, an $iD{O}_{ih}$ that belongs to a $T{s}_t$ data source is denoted as a reference entity/instance, i.e., $rD{O}_w^{ih}:1\le w\le z$, while an $iD{O}_{ih}$ that belongs to a $L{s}_t$ data source is denoted as a possible local entity/instance that may link with a specific $rD{O}_w^{ih}$ entity/instance, i.e., $pD{O}_{wx}^{ih}:1\le x\le y$. This matching process allows a set of possible local instances to be compared and probabilistically matched against a specific reference instance based on their shared attribute values. In correspondence to the global schema generation, each participated $iD{O}_{ih}$ must have an attribute that represents the main parameter for the matching process between pairs of references to local instances, i.e., $\left(A_k^{ih}.Idn\right)$. Figure 2 illustrates the matching formulation and process between three iDOs obtained from three structured data sources $\left(tp=t{p}_1\right)$.

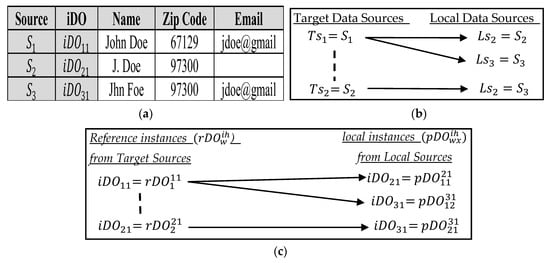
Figure 2. The pair-wise-source-to-target matching and formulation process based on the best effort data integration framework. (a) The participated iDO instances as observed from three structured data sources of $S_1.t{p}_1, S_2.t{p}_1,\& S_3.t{p}_1.$ (b) The pair-wise-source-to-target matching process for the three structured data sources of $S_1.t{p}_1, S_2.t{p}_1,\& S_3.t{p}_1$. (c) The pair-wise-source-to-target matching process for the three iDO instances according to their local instance $(pD{O}_{wx}^{ih})$ or reference instance $(rD{O}_w^{ih}$) formulations.

From the matching process, a probabilistic pair-wise entity linkage result is obtained as $rD{O}_w=\{rD{O}_w^{ih}:pD{O}_{w1}^{ih}\left[Pr\left(L_{w1,}\right)\right],pD{O}_{w2}^{ih}\left[Pr\left(L_{w2,}\right)\right],\dots ,pD{O}_{wy}^{ih}\left[\mathit{Pr}\left(L_{wy}\right)\right]\}:1\le x\le y, 0\le Pr\left(L_{wx}\right)\le 1$, and $Pr\left(L_{wx,}\right)$ is the probability linkage value for a pair of $\left(rD{O}_w^{ih}:pD{O}_{wx}^{ih}\right)$ instances as representing the same RWO. By considering the possible-worlds generation rules and the probabilistic distribution, the probabilistic entities merging can be computed to generate a global merged entity that is denoted as $\left(nD{O}_w\right)$. In correspondence, the best-effort data integration framework is four components of $\left(L{s}_s, T{s}_t, M_{s,t},nD{O}_w\right),$ where:

• $T{s}_t$ is a target data source that belongs to a $Ts$ set of $n$ target sources, i.e., $Ts=\left(T{s}_1,T{s}_2,\dots ,T{s}_n\right):t\in \left[1,n\right], T{s}_t\in Ts\in S.$ A $T{s}_t$ source can be in type of $t{p}_1 or t{p}_2.$ A reference instance is denoted as $rD{O}_w^{ih}=\{a_1^{ih}.idn, a_{2.1}^{ih}.ty,a_{2.2}^{ih}.ty,\dots ,a_{2.q}^{ih}.ty, a_{3.1}^{ih}.ty,\dots , a_{c.q}^{ih}.ty\}:g=1$ for $a_{1.g}^{ih}.idn.$
• $L{s}_s$ is a local data source that belongs to a $Ls$ set of $n$ local sources, i.e., $Ls=\left(L{s}_1,L{s}_2,\dots ,L{s}_n\right):s\in \left[1,n\right],L{s}_s\in Ls\in S.$ A $L{s}_s.tp$ source can be in a type of $t{p}_1$ or $t{p}_2.$ A local instance is denoted as $pD{O}_{wx}^{ih}=\{a_1^{ih}.idn,a_{2.1}^{ih}.ty,a_{2.2}^{ih}.ty,\dots ,a_{2.q}^{ih}.ty, a_{3.1}^{ih}.ty,\dots , a_{c.q}^{ih}.ty\}: g=1$ for $a_{1.g}^{ih}.idn.$
• $M_{s,t}$ is a triple of $(T{s}_t.rD{O}_w^{ih}.\left(a_{k.g}^{ih}.idn, \dots ,a_{c.q}^{ih}.ty\right);L{s}_s.pD{O}_{wx}^{ih}.\left(a_{k.g}^{ih}.idn, \dots ,a_{c.q}^{ih}.ty\right);$$m_{s.k~t.k})$ $M_{s,t}$ mapping is a set of one-to-one probabilistic matching for each reference attribute value $a_{k.g}^{ih}.ty\in rD{O}_w^{ih}$ against a local attribute value $a_{k.g}^{ih}.ty\in pD{O}_{wx}^{ih},$ if initially the similarity $(m_{s.k~t.k})$ value between a pair of main parameter attribute’s values originated from a reference instance with its corresponding local instance is greater than a specified threshold value, i.e., $m_{s.k~t.k}\left(pD{O}_{wx}^{ih}\left(a_k^{ih}.idn\right)\right) ~ (rD{O}_w^{ih}\left(a_k^{ih}.idn)\right)\ge \delta :rD{O}_w^{ih}\ne pD{O}_{wx}^{ih},$ and $\left(\delta \right)$ is the similarity threshold value for considering the matching between the pairs of main parameter’s data values. Thus, for each instance pairs from $iD{O}_{ih}={{\displaystyle \cup }}_{i=1}^n{{\displaystyle \cup }}_{h=1}^m{{\displaystyle \cup }}_{k=1}^c{{\displaystyle \cup }}_{g=1}^q\left(iD{O}_{ih}.a_{k.g}^{ih}.ty\right)$ there is $L{s}_s.iD{O}_{ih}$ against $T{s}_t.iD{O}_{ih}$ local source-to-target entities matching in the form of $pD{O}_{wx}^{ih}.a_{k.g}^{ih}.ty ~ rD{O}_w^{ih}.a_{k.g}^{ih}.ty: rD{O}_w^{ih}\ne pD{O}_{wx}^{ih},$ and $(~)$ denotes the pair-wise matching operation.
• $nD{O}_w$ is a set of $z$ mutual probabilistic global entities merging alternatives that are generated from merging their possible corresponding iDOs, as they have pair-wise linkage results in sort of a reference instance to its possible local instances, i.e., $rD{O}_w=\left(rD{O}_w^{ih}:pD{O}_{w1}^{ih}\left[Pr\left(L_{w1,}\right)\right],pD{O}_{w2}^{ih}\left[Pr\left(L_{w2,}\right)\right],\dots ,pD{O}_{wy}^{ih}\left[Pr\left(L_{wy,}\right)\right]\right):1\le w\le z,1\le x\le y$. A probabilistic global entity is a set of instances merged from a reference instance with its possible local instances, i.e., $nD{O}_w=\{\left(nD{O}_{w.1},Pr\left(M_{w.1}\right)\right),(nD{O}_{w.2},$ $Pr\left(M_{w.2}\right)),\dots ,\left(nD{O}_{w.f},Pr\left(M_{w.f}\right)\right)\}:1\le j\le f,{\displaystyle \sum }_{j=1}^{f}Pr\left(M_{w.j}\right)=1$. Each possible entities merging alternative has an assigned probability distribution value obtained from multiplying the probability linkages of its linked instances, i.e., $nD{O}_{w.j}=\left((rD{O}_w^{ih}:pD{O}_{w1}^{ih},pD{O}_{w2}^{ih},\dots ,pD{O}_{wy}^{ih}),\mathit{Pr}\left(M_{w.j}\right)\right)$. For each requested attribute and within each possible merge, there could be a multi-valued attribute in which each possible attribute’s value alternative is assigned with a probabilistic data fusion value obtained from updating and conditionally computing the reliability scores of its attribute’s values, i.e., $nD{O}_{w.j}.A_k^{Gs}=\left\{\left(a\left(Pw{s}_{tv.1}\right),\mu \left(a\left(Pw{s}_{tv.1}\right)\right)\right),\left(a\left(Pw{s}_{tv.2}\right),\mu \left(a\left(Pw{s}_{tv.2}\right)\right)\right),\dots ,\left(a\left(Pw{s}_{tv.P}\right),\mu \left(a\left(Pw{s}_{tv.P}\right)\right)\right)\right\}:$ $1\le l\le L, {\displaystyle \sum }_{p=1}^P\mu \left(a\left(Pw{s}_{tv.p}\right)\right)=1$. An $a\left(Pw{s}_{tv.p}\right)$ possible world may contain single or multi-possible true values, i.e., $a\left(Pw{s}_{tv.p}\right)=\left\{a_{k.1}^{w.j},a_{k.2}^{w.j},\dots ,a_{k.g}^{w.j}\right\}$.

3.3. Data Lineage

Data lineage represents a very important perspective in the integration process. In particular, while trying to resolve and manage uncertain and conflicted data contributed from matched and integrated entities that originated from heterogeneous and volatile data sources [89,90]. Data lineage would provide information on the entities and the data values’ origin, but also explanations for any generated information and returned results. In this approach, we combine lineage and uncertainty management into one data model. Lineage is closely related to uncertainty and conflicts because it is a powerful mechanism for tracing the uncertainty origin [89].

Having a model supporting lineage means it has the ability for modeling the trace to the origin of an iDO and its data values residing in a data source. It offers additional information that helps understand conflict and uncertainty. It also facilitates the correlations among the participated iDOs. For instance, suppose that entities generated from a particular structured source are distinct real-world objects. If two matched iDOs originated from the same structured source, then we know that a possible world cannot contain these references in one possible merged alternative. Thus, impossible worlds would not be included due to the construction of rules that consider the lineage of the data source and its type.

The proposed approach uses the lineage to identify and resolve conflicts that arise at the linkage and data fusion tasks. Data linage is a convenient mechanism to compute the probability for the data fused values where multi-values can exist at different sources [89,90]. We can obtain the correct reliability scores $\left({\mu }_{a_{k.g}^{ih}}\right)$ of a data by encapsulating linage to its actual value, such as having a data with linage from two data sources shows that this value is combined, hence its probabilistic fusion needs to be computed accordingly. $ih$ depicts the lineage of a specific data value $\left(a_{k.g}^{{\displaystyle \cup }ih}\right)$ as obtained from certain $S_i.tp$ data source/s and that belongs to certain $iD{O}_{ih}$ object. Due to the similar $a_{k.g}^{ih}$ values as obtained from multiple merged iDOs, ${\displaystyle \cup }ih$ may indicate the union lineages of these iDOs. Thus, the lineage of a data value ${\displaystyle \cup }ih=\left(1,2,\dots ,\left|ih\right|\right),\forall ih \in a_{k.g}^{{\displaystyle \cup }ih}$.

3.4. Possible-World Semantic

Possible world is a fundamental concept in uncertainty management research, as most of the related works are based on it. It helps manage the odds of matching outputs, linkage’s answers, merging results, and multi-valued data [19,26,91]. As the participated data sources and the matching outputs contain incomplete, imprecise or uncertain information, they implicitly represent a collection of possible appearances in a sample space, called possible-worlds or alternatives (Pws). Possible worlds describe an object or item where many possibilities may exist as an answer for that description [3].

A possible world is a hypothetical state about an object or item that represents certain and ordinary information. It is obtained from choosing one alternative among a collection of representations that form the total sample space for each item containing uncertain data [52,92]. If there is a possibility showing that none of the given answers exists or is true, this should be treated as an alternative. In order for a database to recognize this alternative, the OWA should be taken into consideration [55]. For instance, by referring to the example presented in Figure 3, we can state that the disjunctive information of (John teaches Physics or Calculus) shows imprecise information about the subject that John teaches. Does this show uncertainty about John’s attributes? If the disjunction is interpreted inclusively using the CWA, then it represents three possible worlds: one in which John teaches Physics, he teaches Calculus, or he teaches both. Under the OWA, however, there would be a fourth-world possibility, i.e., John teaches none of them (neither Calculus nor Physics). This means there is Some Other unknown Value (SOV) that John teaches. The disjunctive facts state that one of these worlds represents the actual situation, but it is unknown which one. Assigning probability values to these worlds gives them confidence degrees that measure the certainty level for each alternative being true. For example, if we know John teaches Physics with probability (0.8) or Calculus with probability (0.6), then we can be more certain that John is more likely teaches both subjects, as this alternative has the highest confidence. Figure 3 illustrates these possible-world examples according to both assumptions of CWA and OWA.

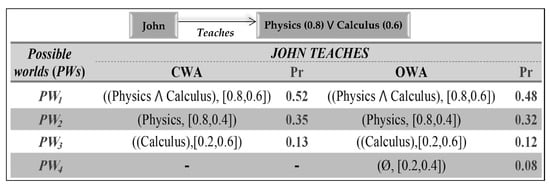
Figure 3. Possible world’s example with associated probability values.

The presence of a null value in the outcome means we have a missing value. A missing value that exists in the real world but for some reason is not available or unknown. Moreover, the missing value is characterized with respect to the presence and meaning of null values and to the validity of the CWA or the OWA [52,92]. CWA denotes that only the values actually observed from the participated data sources, and no other values present facts of the real-world [55]. Thus, the correct value must only be contained from the participated data sources. In contrast, OWA states neither the truth nor the falsity of facts not represented in the participated data sources. Therefore, primitive sources are not necessarily complete, as the correct value may not be contained in these sources [52,92].

Null or missing value comes in five different types, as stated by [52]. These types represent different interpretations, such as a value can be missing either because it exists but is unknown, because it does not exist at all, or because it may exist. However, it is not actually known whether it exists or not. Due to the scope of this research and the nature existence of the multi-valued attributes, this research restricted the null value manipulation to Atomic Existential null value to correspond to the uncertainty conflict situation based on CWA and OWA. Atomic existential value (i.e., only one value is possible), such as when the age of a person is unknown ($Null$). In the existential null, there might be supplementary knowledge concerning the unknown value that the attribute may take as having a domain of possible values [3,52]. As this paper deals with uncertain data and results, several sample spaces $\left({\Omega }^{w.j.k}\right)$ and possible worlds $\left(Pw{s}_{Tv}^{Case.w.j.k}\right)$ will be obtained to manage the uncertainty and conflicts of the data fusion results.

3.5. Probabilistic Entity Linkage Definition

In this research paper, instance integration is approached as a non-trivial integration problem where a collective iteration process is practically inapplicable and inefficiently expensive, and the manual intervention is unaccepted (impossible or hard to achieve). It also portrays the incorporation of uncertainty management in entity linkage and data fusion tasks by using the probability theory to manage uncertain and conflict items.

Probabilistic management is the process of starting with imperfect data and manipulating correlated data to generate a new probabilistic global entity by probabilistically linking and merging its represented reference entity with its possible local entities and by probabilistically fusing its generated attributes’ values (i.e., single-valued attributes value, and multi-valued attributes) [3]. The probabilistic entity is a generated global entity that contains a set of possible instances merged from the reference instance with its possible local instances, i.e., $nD{O}_w=\left\{\left(nD{O}_{w.1},\mathit{Pr}\left(M_{w.1}\right)\right),\left(nD{O}_{w.2},\mathit{Pr}\left(M_{w.2}\right)\right),\dots ,\left(nD{O}_{w.f},\mathit{Pr}\left(M_{w.f}\right)\right)\right\}$. Each possible merge has an assigned probability distribution value, i.e., $\mathit{Pr}\left(M_{w.j}\right)$ generated from multiplying the probability linkages of its possible linked local instances, i.e., $nD{O}_{w.j}=\left\{(rD{O}_w^{ih}:pD{O}_{w1}^{ih},pD{O}_{w2}^{ih},\dots ,pD{O}_{wy}^{ih}),\mathit{Pr}\left(M_{w.j}\right)\right\}:\sum _{j=1}^f\mathit{Pr}\left(M_{w.j}\right)=1$ [3].

The probabilistic data fusion task this research paper deals with is explicitly considered the pair-wise probabilistic entity linkages and their corresponding probabilistic entity merging results. Section 4 covers the probabilistic data fusion problem based on these linkages and merging results.

3.6. Probabilistic Data Fusion Assumptions

The participated sources are taken under the condition of an independent cause of the error. This is a valid condition since the participated sources are independently maintained, in which the data values in one source are not derived from the data values in other sources. Besides that, the obtained data values for multiple merged instances follow the categorical value condition, s the values that do not match exactly are considered distinct. Thus, the accuracy of the supplied data values in our fusion problem implies the assumptions below:

Assumption 1.

Each participated data value is assumed to be associated with a confidence value that indicates its probability degree of correctness, i.e., $\left({\mu }_{a_{k.g}^{ih}}\right)$.

Assumption 2.

Since the data sources’ correlation in sort of data copying is out of this research scope. Hence the errors of attribute values are independent across different data sources. In other words, for any distinct data sources of$(S_1,\dots ,S_n)$the value of$a_{k.1}^{1h}$recorded in$S_1$is not dependent on the values of$\left(a_{k.2}^{2h},\dots ,a_{k.q}^{ih}\right)$recorded in$(S_2,\dots ,S_n)$, (and so on). Once we know the true value, i.e.,$a_{k.Tv}^{w.j}$ of$A_k^{w.j}$ attribute (and vice versa). This means the reliability score of an attribute value does not depend on the reliability scores of other values, once we know the presented event that corresponds to the true world of the fused value, i.e., $\left(a_{k.Tv}^{w.j}=a_{k.q}^{ih}.T\oplus a_{k.Tv}^{w.j}=a_{k.q}^{ih}.F\right):a_{k.Tv}^{w.j}=$ the possible true data value, $T=$ being true, $F=$ being false and $\oplus$ represents an exclusive OR (XOR).

Assumption 3.

Prior probabilities of$a_{k.Tv}^{w.j}=a_{k.1}^{1h}.T=a_{k.1}^{1h}.F,a_{k.Tv}^{w.j}=a_{k.2}^{2h}.T=a_{k.2}^{2h}.F,\dots ,a_{k.Tv}^{w.j}=$ $a_{k.q}^{ih}.T=a_{k.q}^{ih}.F)$are the same and not dependent if we have no reason a priori to believe that one value is more likely to occur. These probabilities are given to$a_{k.Tv}^{w.j}$before the reliability scores of$A_k^{w.j}.a_{k.g}^{ih}$are being considered.

4. The Probabilistic Data Fusion Problem

The probabilistic data fusion problem that this paper aims to address is explicitly considered the entities linkage and merging decisions that can be resolved using probabilistic decisions. This means that the representation of entities merging’s answer could produce multi-possible alternatives, where each alternative may have different combinations of possible linked instances, which in turn may contain similar and/or distinct data values in their shared attributes. Moreover, as an attribute’s values are originated from heterogeneous data sources, they can be distinct, misspelt, incomplete, outdated, or even may contain typographical errors. They also can be more or less certain and reliable.

In fact, the quality of the participated sources affects our belief in the correctness of their information items. Often, those sources provide a degree of confidence for their contributed information as generated from statistical tools, thereby lending their prediction a probabilistic interpretation [24,25]. Consequently, multi-valid or invalid global attributes’ values can exist. The assigned data values for each global attribute can differ from one alternative to another, and each distinct value can be originated from one to multiple data sources. This consideration brings an additional representational and computational challenge to the development of the data fusion model. Accordingly, there is a need to consider the accuracy of the attribute values as originated from their data sources and their combined reliability scores based on the included instances of entities’ merging alternative.

To make a clear presentation of our fusion problem and to facilitate the understanding of the following solution space, we first highlight the data fusion cases that this paper aims to identify and address. Then, we provide a formal definition of our data fusion problem, i.e., the probabilistic fusion for multi-valued attributes based on probabilistic entities merging alternatives. The obtained attributes may contain valid or invalid data as they originated from different sources or instances with different reliability scores.

4.1. Data Fusion Cases

Among the different values that could be merged for a particular global attribute $\left(A_k^{Gs}\right)$ and within a specific set of entities merging alternative $\left(nD{O}_{w.j}\right)$, i.e., $Dom A_k^{w.j}$, one value can only be true, or multiple values can be true [7,8,19,71,77]. For example, a person can have one true age, yet they can also have multiple true phone numbers. These differences reflect two fusion cases: (i) an attribute with multi-true values, such as the phone number for global $\left(nD{O}_{w.j}\right)$ entity $(768–4001, 567–3211)$. (ii) An attribute may have inconsistent values. This case forms a conflict classified by previous research into two types of conflict: Uncertainty and Contradiction [8,23,37]. Contradiction is a type of conflict between two or more inconsistent non-null values that refer to the same object attribute, such as the merged Age values for a person from two sources is$\left(35, 37\right)$, in which a person can only have one true age, while uncertainty represents the conflict between non-null values(s) with one or more null values that refer to the same object’s attribute.

Considering the above discussion of data fusion cases, the non-null and null values, and the CWA and OWA assumptions, the data fusion challenge can be split into six different cases, as shown in Table 1. Each case depicts a specific multi-valued attribute challenge that is required to be handled accordingly. Each case is also given a specific representation, such as $\left(\mathrm{C}1.1\right)$ is the representation for the multi-true value case under the closed-world assumption (i.e., MTC-CWA), while $\left(\mathrm{C}\mathrm{2.1.2}\right)$ is the representation for the contradiction case under the open-world assumption (i.e., ITCC-OWA).

Table 1. The data fusion cases are based on the CWA or the OWA assumptions.

Multi-Valued Attribute Cases		CWA		OWA
		Case	Representation	Case	Representation
Multi-True values Case (MTC)		MTC-CWA	$\mathrm{C}1.1$	MTC-OWA	$\mathrm{C}1.2$
Inconsistent True values Case (ITC)	Contradiction case (ITCC)	ITCC-CWA	$\mathrm{C}\mathrm{2.1.1}$	ITCC-OWA	$\mathrm{C}\mathrm{2.1.2}$
	Uncertainty case (ITCU)	ITCU-CWA	$\mathrm{C}\mathrm{2.2.1}$	ITCU-OWA	$\mathrm{C}\mathrm{2.2.2}$

4.2. Problem Formulation

In this paper, the data fusion problem addresses the probabilistic fusion of multi-valid or invalid attribute values within a particular$nD{O}_w$set. This set may contain multiple alternatives of probabilistic entities merging subsets, i.e., $nD{O}_w=\left\{\left(nD{O}_{w.1},\mathit{Pr}\left(M_{w.1}\right)\right), \left(nD{O}_{w.2},\mathit{Pr}\left(M_{w.2}\right)\right),\dots ,\left(nD{O}_{w.f},\mathit{Pr}\left(M_{w.f}\right)\right)\right\}:1\le j\le f,$ to decide which attribute value’s or values’ alternative is more likely the correct answer for $nD{O}_{w.j}$ entities merging alternative. This $nD{O}_w$ alternatives set is obtained from pair-wise probabilistic linkage decision of local instances $\left(pD{O}_{wx}^{ih}\right)$ to a reference instance $\left(rD{O}_w^{ih}\right)$, i.e., $\left(rD{O}_w^{ih}:pD{O}_{w1}^{ih}\left[Pr\left(L_{w1,}\right)\right], pD{O}_{w2}^{ih}\left[Pr\left(L_{w2,}\right)\right],\dots ,pD{O}_{wy}^{ih}\left[Pr\left(L_{wy,}\right)\right]\right):1\le w\le z,1\le x\le y$. $pD{O}_{wx}^{ih}$ is a possible instance from $L{s}_s$ local data source that is probably linked to a particular $rD{O}_w^{ih}$ reference instance. $rD{O}_w^{ih}$ is an iDO instance from $T{s}_t$ target data source. Moreover, as the actual data values are assigned with reliability scores, $A_k^{Gs}.a_{k.g}$ global attribute value that is populated from similar values originating from multiple data sources, i.e., $A_k^{Gs}.a_{k.g}=A_k^{ih}.a_{k.g}^{{\displaystyle \cup }ih}$, may have multiple reliability scores at once $\left({\mu }_{A_k^{Gs}.a_{k.g}}={\displaystyle \cup }{\mu }_{a_{k.g}^{ih}}\right)$ [3]. Identifying the probabilistic true value or values of data items as obtained from independent data sources and populated based on multiple probabilistic entities merging alternatives is initiated from the following inputs:

• A set of participated$S=\left\{S_1,\dots ,S_n\right\}$ sources. Each $S_i,i\in \left[1,n\right]$ source can be either a local source $L{s}_s$, or a target source $T{s}_t$, and it contains a set of $iD{O}_{ih}$ objects that represent a particular aspect of a RWO.
• A participated $iD{O}_{ih}$ object is a triple of a comprise set of attribute’s names, values, and types, i.e., $\left(A_k^{ih}, a_{k.g}^{ih},ty\right)$, where the type of a participated attribute is obtained based on the type of its corresponding global attribute, i.e., $A_k^{ih}.ty=A_k^{Gs}.ty: ty\in \left\{Idn,Desc,Supp\right\}$, and $\exists A_k^{ih}.ty=A_k^{GS}.Idn$. An attribute may have a single data value, i.e., $\left(A_k^{ih}.a_{k.g}^{ih}=A_k^{ih}.a_{k.1}^{ih}=A_k^{ih}.a_k^{ih}\right)$, or multiple data values, i.e., $\left(A_k.a_{k.g}:1<g\le q\right)$.
• $nD{O}_w$ entities merging set obtained from $rD{O}_w$linkage set. $nD{O}_w$ consists of all the possible subsets of the entities merging alternatives $\{\left(nD{O}_{w.1},\mathit{Pr}\left(M_{w.1}\right)\right), \left(nD{O}_{w.2},\mathit{Pr}\left(M_{w.2}\right)\right),\dots , \left(nD{O}_{w.f},\mathit{Pr}\left(M_{w.f}\right)\right)\}$. A $nD{O}_{w.j}$ subset is depicted as $\left(\left(rD{O}_w^{ih}:pD{O}_{w1}^{ih},pD{O}_{w2}^{ih},\dots ,pD{O}_{wy}^{ih}\right),\mathit{Pr}\left(M_{w.j}\right) \right)$, and ${\displaystyle \sum }_{j=1}^f\mathit{Pr}\left(M_{w.j}\right)=1$. The assigned $pD{O}_{wx}^{ih}$ instances in each alternative differ from one to another. Due to the assigned $pD{O}_{wx}^{ih}$ instances in each entity merging’s alternative, each attribute may include different sets of data values.
• A confidence degree, which is referred to as a reliability score and is denoted by ${\mu }_{a_{k.g}^{ih}}$, to indicate the probability of a specific value provided by $A_k^{ih}$ attribute being true and associated with a particular $A_k^{Gs}$ global attribute. Accordingly, there is given a reliability source’s score of ${\mu }_{a_{k.g}^{ih}}$ to be associated with each $a_{k.g}^{ih}$ data value.
• A matching function returning a precise (Match, or Not Match) decision between a pair of participated data values obtained from iDOs that belong to a particular $nD{O}_w$ merging set. For a specific attribute, the generated data values are the union of all distinct values. Each obtained data value could be derived from multiple similar values originating from multiple iDOs as they are observed from a participating $rD{O}_w^{ih}$ entity with its corresponding $pD{O}_{wx}^{ih}$ instances. The matching outputs produce a data values’ domain based on the obtained global schema/attributes and the participated data sources. This domain of data values is depicted below and Figure 4d shows an example of this domain generation:
  

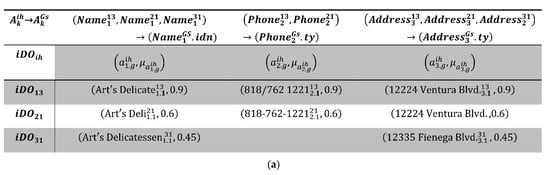
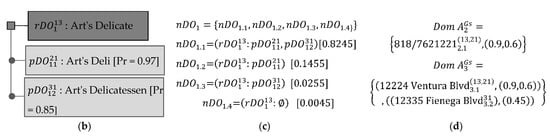  Figure 4. Example of the probabilistic data fusion problem under the existence of multi-valued attributes. (a) The participated iDO instances. (b) The pair-wise probabilistic Linkages. (c) The probabilistic entities merging alternatives from 4b instances. (d) The populated data values for the global attributes of the participated instances in 4c.

$$DOM A_k^{Gs}={{\displaystyle \cup }}_{g^w=1}^{q^w}\left(a_{k.g}^{w.{\displaystyle \cup }ih},{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}{\mu }_{a_{k.g}^{w.{\displaystyle \cup }ih}}\right):i\in \left(T{s}_t,L{s}_s\right)$$

(1)

where, within a specific $A_k^{GS}$ global attribute and $nD{O}_w$ entities merging set:

-

$a_{k.g}^{w.{\displaystyle \cup }ih}$ depicts a populated data value from its corresponding data values that existed at the participated $T{s}_t$ and $L{s}_s$ sources. $a_{k.g}^{w.{\displaystyle \cup }ih}$ may assemble a single value of $a_{k.g}^{w.{\displaystyle \cup }ih}=a_{k.1}^{ih}$, or a combined data value from its corresponding similar values as $a_{k.g}^{w.{\displaystyle \cup }ih}=\left(a_{k.1}^{ih},\dots ,a_{k.q}^{ih}\right): \forall a_{k.g}^{ih}\in nD{O}_w,\exists a_{k.1}^{ih}=a_{k.2}^{ih}=\dots =a_{k.q}^{ih}$.

-

$ih$ depicts the data lineage of each iDO in the $rD{O}_w$ set that has the attribute value. At each generated global data value, ${\displaystyle \cup }ih$ indicates the data lineage union for those similar data values as originated from the participated data sources and related to one $a_{k.g}^{w.{\displaystyle \cup }ih}$ global data value, i.e., ${\displaystyle \cup }ih=\left(1,\dots ,\left|ih\right|\right),\forall ih \in a_{k.g}^{w.{\displaystyle \cup }ih}$. Due to the similar $a_{k.g}^{ih}$ values, ${\displaystyle \cup }ih$ could indicate one or many lineages.

-

${{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}\left({\mu }_{a_{k.g}^{w.{\displaystyle \cup }ih}}\right)$ or ${\displaystyle \cup }{\mu }_{a_{k.g}^{w.{\displaystyle \cup }ih}}$ for representation simplicity, represents the reliability scores set for all included iDOs’ data values in a $a_{k.g}^{w.{\displaystyle \cup }ih}$ global data value. Depending on the observed ${\displaystyle \cup }ih$ data lineage for $a_{k.g}^{w.{\displaystyle \cup }ih}$ data value, the ${\displaystyle \cup }{\mu }_{a_{k.g}^{w.{\displaystyle \cup }ih}}$ set may have single or multiple reliability scores. This means, a generated global attribute’s value can be obtained from one or more data sources or iDOs, and hence, it can be assigned with single to multiple reliability scores.

Considering a specific $A_k^{GS}$ attribute and a $nD{O}_{w.j}$ merging alternative, the actual combination of its data values contains the union of all distinct values that are generated from the matching function and that belonged to the assigned instances in a specific $nD{O}_{w.j}$ alternative. This combination of data values for an attribute produces a data values domain as denoted by the following formulation:

$$Dom A_k^{w.j}={{\displaystyle \cup }}_{g^{w.j}=1^{w.j}}^{q^{w.j}}\left(a_{k.g}^{w.j.{\displaystyle \cup }ih},{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}\left({\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}\right)\right): Dom A_k^{w.j}\subseteq Dom A_k^{Gs.w}$$

(2)

At this domain, $a_{k.g}^{w.j.{\displaystyle \cup }ih}, {\displaystyle \cup }ih, \mathrm{and} {\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}$ are, respectively, referred to as the populated data values, lineage and reliability scores for a specific $nD{O}_{w.j}=(rD{O}_w^{ih}:pD{O}_{w1}^{ih},pD{O}_{w2}^{ih},\dots ,pD{O}_{wy}^{ih}),\mathit{Pr}\left(M_{w.j}\right)$ merging alternative. Due to null value existence, an additional challenge to generate $Dom A_k^{w.j}$ domain is observed. This occurred since one of the data values that belongs to $Dom A_k^{w.j}$ is an atomic null value, i.e., $\left(a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}\right)$. This means the null value is denoted by a domain of possible values of $Dom a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}$, such that either one or none of these possible values can be a true value. Thus, $Dom A_k^{w.j}$ in Equation (2) can be reformulated as stated in Equation (3).

$$\begin{gathered} Dom A_k^{w.j}=\left({{\displaystyle \cup }}_{g^{w.j}=1}^{q^{w.j}-\left|g.N{l}^{w.j}\right|}\left(a_{k.g}^{w.j.{\displaystyle \cup }ih},{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}\left({\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}\right)\right), \left(a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih},{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}\left({\mu }_{a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}}\right)\right)\right)= \\ \left({{\displaystyle \cup }}_{g^{w.j}=1}^{q^{w.j}-\left|g.N{l}^{w.j}\right|}\left(a_{k.g}^{w.j.{\displaystyle \cup }ih},{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}\left({\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}\right)\right), {{\displaystyle \cup }}_{Nlg=Nl1}^{Nlq}\left(a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih},{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}\left({\mu }_{a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}}\right)\right)\right): \exists a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}\in Dom A_k^{w.j} \end{gathered}$$

(3)

The example of a probabilistic instance integration process for three restaurant instances is given in Figure 4 to illustrate our data fusion problem. These iDOs originated from three structured sources ($S_1.t{p}_1, S_2.t{p}_1, and S_3.t{p}_1$), where the reliability scores for their data values are $\left({\mu }_{a_{1.1}^{13}}={\mu }_{a_{2.1}^{13}}={\mu }_{a_{3.1}^{13}}=0.9,{\mu }_{a_{1.1}^{21}}={\mu }_{a_{2.1}^{21}}={\mu }_{a_{3.1}^{21}}=0.6, \mathrm{and} {\mu }_{a_{1.1}^{31}}={\mu }_{a_{3.1}^{31}}=0.45\right)$. Moreover, the Name attribute has been recognized as the main parameter for the instance matching and integration process; hence, $ty=Idn$ for this attribute (i.e., $Nam{e}_{1.1}^{GS}.idn$). In this example, the participated iDO instances are shown in Figure 4a, whereas the produced probabilistic entity linkages and merging alternatives are shown in Figure 4b,c, respectively. In addition, the data value domains for the global Phone and Address attributes are presented in Figure 4d.

From Figure 4a, we see that Name and Address global attributes are obtained from their corresponding restaurant’s Name, and Address, as existed in three participated iDOs, where each iDO originated from a different data source, i.e., $\left(Nam{e}_1^{13}, Nam{e}_1^{21},Nam{e}_1^{31}\right)\to Nam{e}_{1.1}^{Gs}.idn, and \left(Addres{s}_3^{13},Addres{s}_3^{21},Addres{s}_2^{31}\right)\to \left(Addres{s}_3^{Gs}.ty\right)$. In contrast, the global Phone attribute is generated from its corresponding Phone attributes as existed in two participated iDOs, where each iDO belongs to a different source, i.e., $iD{O}_{13}$ from $S_1$, and $iD{O}_{21}$ from $S_2: \left(Phon{e}_2^{13},Phon{e}_2^{21}\right)\to \left(Phon{e}_2^{Gs}.ty\right)$. Due to these correspondences, we note that $Dom A_2^{Gs}$ in Figure 4d does not contain a null value since $iD{O}_{31}$ from $S_3$ do not have a Phone attribute, rather it consists of one value of $\left(818/762 {1221}_{2.1}^{\left(13,21\right)},\left(0.9,0.6\right)\right)$. This value comes with two lineages and two reliability scores as obtained from $iD{O}_{13}$ and $iD{O}_{21}$ instances. $Dom A_2^{Gs}$ domain presents the combined data values for the global Phone attribute as populated in Equation (1). In contrast, $Dom A_3^{\mathrm{Gs}}$ has two data values with different cardinality of lineages and reliability scores, i.e., $\left(\left(12335 Fienega Blv{d}_{3.2}^{31}\right),\left(0.45\right)\right)$, and $\left(\left(12335 Fienega Blv{d}_{3.2}^{31}\right),\left(0.45\right)\right)$. $Dom A_3^{Gs}$ domain depicts the combined data values for the global Address attribute as populated using Equation (1). Basically, these domains of data values comprise all distinct Phone and Address values that are obtained from running a matching function over the pair of $\left(iD{O}_{13}~iD{O}_{21}\right)$ and $\left(iD{O}_{13}~iD{O}_{31}\right)$ instances to generate $\left\{rD{O}_1^{13}:\left(pD{O}_{11}^{21}, 0.97\right), \left(pD{O}_{12}^{31},0.85\right)\right\}$ linkage set as shown in Figure 4b. These reference and local instances correspond to the participated iDOs as $rD{O}_1^{13}\equiv iD{O}_{13}, pD{O}_{11}^{21}\equiv iD{O}_{21}, \mathrm{and} pD{O}_{12}^{31}\equiv iD{O}_{31}$. Based on our data fusion problem, the data values in these domains need to be fused, i.e., finding the true data value or alternative values based on the entities merging alternatives in 4c. Accordingly, the data values domains of $Dom A_k^{w.j}$ to be fused are populated based on Equation (2) and are shown in Table 2. If the data fusion case belongs to the ITCU categories as previously presented in Table 1, the data values domains of $Dom A_k^{w.j}$ to be fused will be populated based on Equation (3).

Table 2. Example of the probabilistic data fusion problem under the existence of multi-valued attributes.

$\mathit{n}\mathit{D}{\mathit{O}}_{\mathit{w}.\mathit{j}}\in \mathit{n}\mathit{D}{\mathit{O}}_{\mathit{w}}:\mathit{w}=1$	${{\displaystyle \mathit{\bigcup }}}^{ }\mathit{i}\mathit{h}$ Lineage for w.j Merging Alternatives	$\mathit{D}\mathit{o}\mathit{m} {\mathit{A}}_2^{\left(1.1,1.2,\dots ,1.4\right)}$	$\mathit{D}\mathit{o}\mathit{m} {\mathit{A}}_3^{\left(1.1,1.2,\dots ,1.4\right)}$
$\mathit{n}\mathit{D}{\mathit{O}}_{\mathbf{1.1}}=$ $\left(\left(\mathit{r}\mathit{D}{\mathit{O}}_{\mathbf{1}}^{\mathbf{13}}:\mathit{p}\mathit{D}{\mathit{O}}_{\mathbf{11}}^{\mathbf{21}},\mathit{p}\mathit{D}{\mathit{O}}_{\mathbf{12}}^{\mathbf{31}}\right)\left[\mathbf{0.8245}\right]\right)$	$\left(13, 21, 31\right)$	$Dom A_2^{1.1}=$ $\left\{818/762 {1221}_{2.1}^{\left(13,21\right)},\left(0.9,0.6\right)\right\}$	$Dom A_3^{1.1}=\left\{\begin{array}{c}\left({12224 \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{\left(13,21\right)},\left(0.9,0.6\right)\right)\\ ,\left(12335{ \mathrm{Fienega} \mathrm{Blvd}}_{3.2}^{31},0.45\right)\end{array}\right\}$
$\mathit{n}\mathit{D}{\mathit{O}}_{\mathbf{1.2}}=\left(\left(\mathit{r}\mathit{D}{\mathit{O}}_{\mathbf{1}}^{\mathbf{13}}: \mathit{p}\mathit{D}{\mathit{O}}_{\mathbf{11}}^{\mathbf{21}}\right) \left[\mathbf{0.1455}\right]\right)$	$\left(13, 21\right)$	$Dom A_2^{1.2}=$ $\left\{818/{7621221}_{2.1}^{\left(13,21\right)},\left(0.9,0.6\right)\right\}$	$Dom A_3^{1.2}=$ $\left\{\begin{array}{c}\left({12224 \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{\left(13,21\right)},\left(0.9,0.6\right)\right)\end{array}\right\}$
$\mathit{n}\mathit{D}{\mathit{O}}_{\mathbf{1.3}}=$ $\left(\left(\mathit{r}\mathit{D}{\mathit{O}}_{\mathbf{1}}^{\mathbf{13}}: \mathit{p}\mathit{D}{\mathit{O}}_{\mathbf{12}}^{\mathbf{31}}\right) \left[\mathbf{0.0255}\right]\right)$	$\left(13, 31\right)$	$Dom A_2^{1.3}=$ $\left\{818/{7621221}_{2.1}^{\left(13\right)},\left(0.9\right)\right\}$	$Dom A_3^{1.3}=$ $\left\{\begin{array}{c}\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{\left(13\right)},0.9\right),\\ \left(12335{ \mathrm{Fienega} \mathrm{Blvd}}_{3.2}^{31},0.45\right)\end{array}\right\}$
$\mathit{n}\mathit{D}{\mathit{O}}_{\mathbf{1.4}}=$ $\left(\left(\mathit{r}\mathit{D}{\mathit{O}}_{\mathbf{1}}^{\mathbf{13}}: \mathbf{\varnothing }\right) \left[\mathbf{0.0045}\right]\right)$	$\left(13\right)$	$Dom A_2^{1.4}=$ $\left\{{818/7621221}_{2.1}^{\left(13\right)},\left(0.9\right)\right\}$	$Dom A_3^{1.4}=$ $\left\{\begin{array}{c}\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{\left(13\right)},0.9\right)\end{array}\right\}$

From $Dom A_3^{Gs}$ in Figure 4d and $Dom A_3^{1.3}$ in Table 2, we noticed that these domains share the same values, yet the linages for their first value are different. The lineage for $\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{{\displaystyle \cup }ih}\right)$ in $Dom A_3^{Gs}$ is ${\displaystyle \cup }ih=\left(13,21\right)$ but in $Dom A_3^{1.3}$ is ${\displaystyle \cup }ih=\left(13\right)$ only. This occurs since $pD{O}_{11}^{21}$ does not exist in the $nD{O}_{1.3}$ merging alternatives, as the above figure shows. The data fusion computation method will be executed based on these domains to obtain the possible true fused value or values.

It is worth stating that this problem definition copes with dynamic and volatile data values that may evolve over time. It could also correspond to the online data fusion problem since the prior entities’ linkage, and merging stages are processed separately, where each stage keeps and stores the obtained probability outcomes alongside their actual data. The fusion process is carried out on these outcomes upon a user’s request, as the obtained probabilities are stored alongside the actual data values.

5. The Probabilistic Data Fusion Model

In this section, we formally describe the data fusion solution and show how we leverage the trustworthiness of data sources and their values in truth discovery. To determine $a_{k.Tv}^{w.j}$ that might be the value(s) observed from the participated sources, the production of the data fusion sample space $\left({\Omega }^{w.j.k}\right)$ and possible worlds $\left(Pw{s}_{Tv}^{case. w.j.k}\right)$ within a particular $A_k^{w.j}$ attribute’s values, and $nD{O}_{w.j}$ merging alternative are discussed next. Then, the probabilistic data fusion method is constructed to compute the conditional probability (i.e., updated reliability score) for a possible data values’ world that is probably recognized as the true fused answer, using ${\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}$ scores and given a data fusion case to obtain a possible-worlds’ set over a domain of $Dom A_k^{w.j}$.

5.1. The Probabilistic Data Fusion Sample Space and Possible-Worlds Generation

The form of the data value and its associated reliability scores affect the data fusion sample space production. In addition, recognizing a possible-worlds set over its sample space depends on the applied data fusion case. Accordingly, the data fusion sample space production and possible-world generation are discussed next based on the identified cases in Table 1.

5.1.1. The Data Fusion Sample Space Production

Each value in $Dom A_k^{w.j}$ is assigned with a reliability score $\left(0\le {\mu }_{a_{k.g}^{ih}}\le 1\right)$ to indicate the probability of being a true fused value, i.e., $\left(a_{k.g}^{ih}.T:{\mu }_{a_{k.g}^{ih}.T}={\mu }_{a_{k.g}^{ih}}\right)$. Since ${\mu }_{a_{k.g}^{ih}}\le 1$, then $\left(\neg {\mu }_{a_{k.g}^{ih}}=1-{\mu }_{a_{k.g}^{ih}}\right)$ that indicates the probability of the data value being a false fused value, i.e., $\left(a_{k.g}^{ih}.F:{\mu }_{a_{k.g}^{ih}.F}=\neg {\mu }_{a_{k.g}^{ih}.T}=\neg {\mu }_{a_{k.g}^{ih}}\right)$. Thus, a pair of $\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}, {\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}\right)$ in $Dom A_k^{w.j}$ can be interpreted as a pair set of two mutual events. This is depicted as:

$$\begin{gathered} \left(a_{k.g}^{w.j.{\displaystyle \cup }ih},{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}\right)\to \\ \left\{\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}.T,{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T}\right),\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}.F,{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.F}\right)\right\} \end{gathered}$$

(4)

where

-

$a_{k.g}^{w.j.{\displaystyle \cup }ih}.T$ implies the event when the generated data value that belongs to $Dom A_k^{w.j}$ is a true fused value, i.e., $a_{k.Tv}^{w.j}=a_{k.g}^{w.j.{\displaystyle \cup }ih}\Rightarrow a_{k.Tv}^{w.j}\in Dom A_k^{w.j},$with a probability equals to the union of the original reliability scores for all $ih$ lineage exited in $a_{k.g}^{w.j}.T$ event, i.e., ${\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T}=\left({\mu }_{a_{k.1}^{ih}},{\mu }_{a_{k.2}^{ih}},\dots ,{\mu }_{a_{k.q}^{ih}}\right), \forall ih\in a_{k.g}^{w.j.{\displaystyle \cup }ih}$.

-

$a_{k.g}^{w.j.{\displaystyle \cup }ih}.F$ implies the event when the generated data value that belongs to $Dom A_k^{w.j}$ is a false fused value, i.e., $a_{k.Tv}^{w.j}\ne a_{k.g}^{w.j.{\displaystyle \cup }ih}\Rightarrow a_{k.Tv}^{w.j}\notin Dom A_k^{w.j}$, with probability equals to the union of the reliability score’s complements for all ${\displaystyle \cup }ih$ existed in $a_{k.g}^{w.j}.F$, i.e., ${\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.F}={\displaystyle \cup }\neg {\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T}=(\neg {\mu }_{a_{k.1}^{ih}},\dots ,\neg {\mu }_{a_{k.q}^{ih}}),\forall ih=a_{k.g}^{w.j.{\displaystyle \cup }ih}$.

-

${\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F}$ set indicates either the original reliability scores’ set or the complement scores’ set for its associated data value’s event $a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F$.

Due to the ${\displaystyle \cup }ih$observed, the data value in an event may resemble a single data value, i.e.,$a_{k.g}^{w.j}.T\backslash F=a_{k.g}^{w.j.ih}.T\backslash F$, or a combined data value from its similar $a_{k.g}^{ih}$ values, i.e., $a_{k.g}^{w.j}.T\backslash F=a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F=\left(a_{k.1}^{ih}.T|F,a_{k.2}^{ih}.T|F,\dots ,a_{k.q}^{ih}.T\backslash F\right), \forall a_{k.g}^{ih}=a_{k.g}^{w.j.{\displaystyle \cup }ih}\in nD{O}_{w.j}$. The reliability scores set assigned to a data value’s event $\left(a_{k.g}^{w.j}.T\backslash F\right)$ may also have a single reliability score of ${\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F}={\mu }_{a_{k.g}^{w.j.ih}.T\backslash F}$, or multiple reliability scores of ${\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F}=({\mu }_{a_{k.1}^{ih}.T\backslash F},{\mu }_{a_{k.2}^{ih}.T\backslash F}, \dots , {\mu }_{a_{k.q}^{ih}.T\backslash F}),\forall a_{k.g}^{ih}=a_{k.g}^{w.j.{\displaystyle \cup }ih}\in nD{O}_{w.j}$.

For a domain holding one pair of data value, i.e., $Dom A_k^{w.j}=\left\{\left(a_{k.g}^{w.j.{\displaystyle \cup }ih},{\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}}\right)\right\}$, the two events of $\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}.T, a_{k.g}^{w.j.{\displaystyle \cup }ih}.F\right)$ comprise the data fusion sample space, where each event represents a possible world of true data fused value, i.e., $\left(a_{k.Tv}^{w.j}=a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\oplus a_{k.Tv}^{w.j}=a_{k.g}^{w.j.{\displaystyle \cup }ih}.F\right)$, such that $(\oplus )$ represents an exclusive OR (i.e., XOR). This is noticed since the general data fusion’s sample space of true alternatives is obtained as: ${\mathsf{\Omega }}^{w.j.k}={{\displaystyle \cup }}_{l=1}^L{\mathsf{\Omega }}_{tv.l}:1\le l\le L,L=2^{\left|Dom A_k^{w.j}\right|}$ [3].

As multi-distinct data values are being observed in $Dom A_k^{w.j}$, the generation of the data fusion’s sample space requires considering the Cartesian product operation over the events sets that could be obtained from $Dom A_k^{w.j}$ in Equation (4). Therefore, the produced sample space over $Dom A_k^{w.j}$ is the result of the Cartesian product operation over the events’ sets of its data values pairs, as presented below in Equation (5):

$$\begin{gathered} {\mathsf{\Omega }}^{w.j.k}=\left\{\left(a_{k.1}^{w.j.{\displaystyle \cup }ih}.T,{\displaystyle \cup }{\mu }_{a_{k.1}^{w.j.{\displaystyle \cup }ih}.T}\right),\left(a_{k.1}^{w.j.{\displaystyle \cup }ih}.F,{\displaystyle \cup }{\mu }_{a_{k.1}^{w.j.{\displaystyle \cup }ih}.F}\right)\right\}\times \dots \\ \times \left\{\left(a_{k.q}^{w.j.{\displaystyle \cup }ih}.T,{\displaystyle \cup }{\mu }_{a_{k.q}^{w.j.{\displaystyle \cup }ih}.T}\right),\left(a_{k.q}^{w.j.{\displaystyle \cup }ih}.F,{\displaystyle \cup }{\mu }_{a_{k.q}^{w.j.{\displaystyle \cup }ih}.F}\right)\right\}\Rightarrow \\ {\mathsf{\Omega }}^{w.j.k}=\left({\times }_{g^{w.j}=1}^{q^{w.j}}\left\{\left(a_{k.g}^{{\displaystyle \cup }ih}.T,{\displaystyle \cup }{\mu }_{a_{k.g}^{{\displaystyle \cup }ih}.T}\right),\left(a_{k.g}^{{\displaystyle \cup }ih}.F,{\displaystyle \cup }{\mu }_{a_{k.g}^{{\displaystyle \cup }ih}.F}\right)\right\}|\begin{array}{c}{a}_{k.g}^{w.j}\in Dom A_k^{w.j}\\ \left|{\displaystyle \cup }ih\right|\ge 1\end{array}\right) \end{gathered}$$

(5)

${\mathsf{\Omega }}^{w.j.k}$ will contain multiple mutual data fusion worlds of ${\mathsf{\Omega }}_{tv.l},$ such that each data value pair included in a ${\Omega }_{tv.l}$ world is encoded by either its true or false event. Moreover, since each event is a pair of true or false forms of the actual data value with its reliability scores, the ${\Omega }_{tv.l}$ world is depicted as a pair that comprises multiple data values’ events with their associated reliability score sets. This representation of alternatives in sort of pairs form is depicted in Equation (6). From this pair representation, the mutual alternatives produced at a particular data fusion’s sample space are as shown below:

$$\begin{gathered} {\mathsf{\Omega }}^{w.j.k}=\begin{array}{c} \left(\left\{a\left({\mathsf{\Omega }}_{tv.l}\right),\mu \left({\mathsf{\Omega }}_{tv.l}\right)\right\}|\begin{array}{c}a\left({\mathsf{\Omega }}_{tv.l}\right)={{\displaystyle \cup }}_{g^{w.j}=1}^{q^{w.j}}\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F\right) \\ \mu \left({\mathsf{\Omega }}_{tv.l}\right)={{\displaystyle \cup }}_{g^{w.j}=1}^{q^{w.j}}{{\displaystyle \cup }}_{g^{ih}=1^{11}}^{q^{nm}}\left({\mu }_{a_{k.g}^{w.j.{{\displaystyle \cup }}^{ }ih}.T\backslash F}\right)\end{array}\right)\Rightarrow \end{array} \\ {\mathsf{\Omega }}^{w.j.k}=\left\{\begin{array}{c}\left\{\left(a_{k.1}^{{\displaystyle \cup }ih}.T,\dots ,a_{k.q-1}^{{\displaystyle \cup }ih}.T,a_{k.q}^{{\displaystyle \cup }ih}.T\right),\left({\displaystyle \cup }{\mu }_{a_{k.1}^{{{\displaystyle \cup }}^{ }ih}.T},\dots ,{\displaystyle \cup }{\mu }_{a_{k.q-1}^{{{\displaystyle \cup }}^{ }ih}.T},{\displaystyle \cup }{\mu }_{a_{k.q}^{{{\displaystyle \cup }}^{ }ih}.T}\right)\right\}\\ ,\dots ,\\ \left\{\left(a_{k.1}^{{\displaystyle \cup }ih}.F,\dots ,a_{k.q-1}^{{\displaystyle \cup }ih}.F,a_{k.q}^{{\displaystyle \cup }ih}.T\right),\left({\displaystyle \cup }{\mu }_{a_{k.1}^{{\displaystyle \cup }ih}.F},\dots ,{\displaystyle \cup }{\mu }_{a_{k.q-1}^{{\displaystyle \cup }ih}.F},{\displaystyle \cup }{\mu }_{a_{k.q}^{{\displaystyle \cup }ih}.T}\right)\right\}\\ \left\{\left(a_{k.1}^{{\displaystyle \cup }ih}.F,\dots ,a_{k.q-1}^{{\displaystyle \cup }ih}.F,a_{k.q}^{{\displaystyle \cup }ih}.F\right),\left({\displaystyle \cup }{\mu }_{a_{k.1}^{{\displaystyle \cup }ih}.F},\dots ,{\displaystyle \cup }{\mu }_{a_{k.q-1}^{{\displaystyle \cup }ih}.F},{\displaystyle \cup }{\mu }_{a_{k.q}^{{\displaystyle \cup }ih}.F}\right)\right\}\end{array}\right\} \end{gathered}$$

(6)

where

-

$a\left({\mathsf{\Omega }}_{tv.l}\right)$ implies the union of the true and false $\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F\right)$ data value’s events that are contained in a ${\Omega }_{tv.l}$ world. Depending on $Dom A_k^{w.j}$, the $a\left({\mathsf{\Omega }}_{tv.l}\right)$ set denotes one or more of the actual data values’ events, such that none, some or all of them can be combined data values.

-

$\mu \left({\mathsf{\Omega }}_{tv.l}\right)$ implies the reliability scores set for a ${\mathsf{\Omega }}_{tv.l}$world, as it is gained from the union of the reliability scores sets of all the distinct ${\displaystyle \cup }{a}_{k.g}^{w.{\displaystyle \cup }ih}.T/F$ events that are included in the ${\mathsf{\Omega }}_{tv.l}$ world. Depending on the participating events in an ${\mathsf{\Omega }}_{tv.l}$ alternative, i.e., all are true, some are true, or none is true (all false), the reliability score set for a data fusion alternative $\mu \left({\mathsf{\Omega }}_{tv.l}\right)$ may have the original or/and the complement reliability scores sets.

Table 3 illustrates the sample space production and is outlined based on $Dom A_3^{1.1}$ from Table 2.

Table 3. An example for sample space production.

Equation	$\mathbf{The} \mathbf{Sample} \mathbf{Space} \mathbf{Production} \left({\mathit{\Omega }}^{\mathrm{1.1.3}}\right)$$\mathbf{form} \mathit{D}\mathit{o}\mathit{m} {\mathit{A}}_3^{1.1}$
(4)	$\{\left(a_{3.1}^{1.1}.T=12224 Ventura Blvd,{\displaystyle \cup }{\mu }_{a_{3.1}^{1.1}.T}=\left(0.9,0.6\right)\right),\left(a_{3.1}^{1.1}.F \ne 12224 Ventura Blvd,{\displaystyle \cup }{\mu }_{a_{3.1}^{1.1}.F}=\left(0.1,0.4\right)\right)\}$. $\{\left(a_{3.2}^{1.1}.T=12335 Fienega Blvd,{\mu }_{a_{3.2}^{1.1}.T}=\left(0.45\right)\right),\left(a_{3.2}^{1.1}.F\ne 12335 Fienega Blvd, {\mu }_{a_{3.2}^{1.1}.F}=\left(0.55\right)\right)\}$
(5)	${\mathsf{\Omega }}^{\mathrm{1.1.3}}=2^2=4={\times }_{g=1}^2=\left\{\left(a_{3.1}^{1.1.\left(13,21\right)}.T,{\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T}\right),\left(a_{3.1}^{1.1.\left(13,21\right)}.F,{\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F}\right)\right\}\times \left\{\left(a_{3.2}^{\mathrm{1.1.31}}.T,{\mu }_{a_{3.2}^{\mathrm{1.1.31}}.T}\right),\left(a_{3.2}^{\mathrm{1.1.31}}.F,{\mu }_{a_{3.2}^{\mathrm{1.1.31}}.F}\right)\right\}$.
(6)	${\Omega }^{\mathrm{1.1.3}}=\left\{{\Omega }_{tv.1},{\Omega }_{tv.2},{\Omega }_{tv.3},{\Omega }_{tv.4}\right\}:{\Omega }_{tv.l}=\left(a\left({\Omega }_{tv.l}\right),\mu \left({\Omega }_{tv.l}\right)\right)\to$ $a\left({\Omega }_{tv.1}\right)=\left(a_{3.1}^{1.1.\left(13,21\right)}.T,a_{3.2}^{\mathrm{1.1.31}}.T\right)=\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)},12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right), \&$ $\mu \left({\Omega }_{tv.1}\right)=\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T},{\mu }_{a_{3.2}^{\mathrm{1.1.31}}.T}\right)=\left(0.9, 0.6, 0.45\right)$ $a\left({\Omega }_{tv.2}\right)=\left(a_{3.1}^{1.1.\left(13,21\right)}.T,a_{3.2}^{\mathrm{1.1.31}}.F\right)=\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)}\right), \&$ $\mu \left({\Omega }_{tv.2}\right)=\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T},{\mu }_{a_{3.2}^{\mathrm{1.1.31}}.F}\right)=\left(0.9, 0.6, 0.55\right)$ $a\left({\Omega }_{tv.3}\right)=\left(a_{3.1}^{1.1.\left(13,21\right)}.F,a_{3.2}^{\mathrm{1.1.31}}.T\right)=\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right), \&$ $\mu \left({\Omega }_{tv.3}\right)=\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F},{\mu }_{a_{3.2}^{\mathrm{1.1.31}}.T}\right)=\left(0.1, 0.4, 0.45\right)$  $a\left({\Omega }_{tv.4}\right)=\left(a_{3.1}^{1.1.\left(13,21\right)}.F,a_{3.2}^{\mathrm{1.1.31}}.F\right)=(\varnothing ),\& \mu \left({\Omega }_{tv.4}\right)=\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F},{\mu }_{a_{3.2}^{\mathrm{1.1.31}}.F}\right)=\left(0.1, 0.4, 0.55\right)$

Due to null value existence, an additional challenge to generate the ${\mathsf{\Omega }}^{w.j.k}$ sample space is observed. This challenge is related to $Dom A_k^{w.j}$ generation in Equation (3). The sample space for this domain is generated throughout the Cartesian product operations over the events pair’s sets of the non-null and the null data values’ sets based on Equation (5). However, since the atomic null indicates that at most one data value can be true, then any generated world that represents more than one data value by its true event would be an impossible world, i.e., $Iw{s}^{w.j.k\left(Null\right)}$, and it should be eliminated from the $\left({\mathsf{\Omega }}^{w.j.k\left(Null\right)}\right)$ sample space production. Thus, the sample space production due to null value presence is formulated in Equation (7).

$$\begin{array}{l}{\mathsf{\Omega }}^{w.j.k}=\left({\mathsf{\Omega }}^{w.j.k\left(\mathrm{NonNull}\right)}\times {\mathsf{\Omega }}^{w.j.k\left(\mathrm{Null}\right)}\right):\forall { \mathsf{\Omega }}_{tv.l}^{w.j.k\left(\mathrm{Null}\right)}\\ \in {\mathsf{\Omega }}^{w.j.k\left(Null\right)}, \exists \left(\left|\underset{Nlg=Nl1}{\overset{Nlq}{{\displaystyle \cup }}}{a}_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.T\right|\subseteq a\left({ \mathsf{\Omega }}_{tv.l}^{w.j.k\left(\mathrm{Null}\right)}\right)\right)\\ \le 1, {\mathsf{\Omega }}^{w.j.k\left(Null\right)}=\underset{l^{Nl}=1^{Nl}}{\overset{L^{Nl}}{{\displaystyle \cup }}}{\mathsf{\Omega }}_{tv.l^{Nl}}^{w.j.k},L^{Nl}=\left|Dom a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}\right|+1,\end{array}$$

(7)

where:

-

${\mathsf{\Omega }}^{w.j.k\left(\mathrm{NonNull}\right)}={\times }_{g^{w.j}=1}^{q^{w.j}-\left|g.N{l}^{w.j}\right|}\left\{\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}.T,{\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T}\right),\left(a_{k.g}^{w.j.{\displaystyle \cup }ih}.F,{\displaystyle \cup }{\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.F}\right)\right\}$.

-

$$\begin{gathered} {\mathsf{\Omega }}^{w.j.k\left(\mathrm{Null}\right)}={\times }_{Nlg=Nl1}^{Nlq}\left\{\left(a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.T,{\displaystyle \cup }{\mu }_{a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.T}\right),\left(a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.F,{\displaystyle \cup }{\mu }_{a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.F}\right)\right\}- \\ Iw{s}^{w.j.k\left(\mathrm{Null}\right)}:\forall a\left({\mathsf{\Omega }}_{tv.l}^{w.j.k\left(\mathrm{Null}\right)}\right)\ni \left(\left|\underset{Nlg=Nl1}{\overset{Nlq}{{\displaystyle \cup }}}{a}_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.T\right|\ge 2\right),\exists { \mathsf{\Omega }}_{tv.l}^{w.j.k\left(\mathrm{Null}\right)}\in \\ Iw{s}^{w.j.k\left(\mathrm{Null}\right).} \end{gathered}$$

Each obtained world from this operation will be represented as a pair of multi-possible values’ events with their associated reliability scores sets as previously stated in Equation (6), such that each world consists of $a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.T/F$ and ${\displaystyle \cup }{\mu }_{a_{k.g.Nlg}^{w.j.{\displaystyle \cup }ih}.T/F}$ events.

5.1.2. The Obtained Possible-Worlds Based on the Data Fusion Cases

The earlier stated sample spaces in Equations (6) and (7) will be utilized to obtain the possible-worlds sets for the data fusion cases. In fact, a possible-worlds set can be equal or lesser than its sample space due to the impossible-worlds incidents $\left(Iw{s}^{Case. w.j.k}\right)$. For instance, alternatives containing multi-true events are considered possible worlds under the MTC cases only. However, alternatives that have at most one true event are only recognized as possible worlds under the ITC cases. Due to the data fusion cases, the production of possible worlds set out of a ${\mathsf{\Omega }}^{w.j.k}$ sample space is presented in Equation (8), while Table 4 shows the possible-worlds production rules for each data fusion case presented earlier in Table 1.

Table 4. The possible-worlds generations given a data fusion case.

Data Fusion Cases	Possible Worlds Generation$\left(Pw{s}_{Tv}^{Case.w.j.k}\right)$
C1.2: MTC-OWA	$If \left({\Omega }^{w.j.k}|Case=\mathrm{C}1.2\right),then Pw{s}_{Tv}^{C1.2.w.j.k}={\Omega }^{w.j.k}$, $Pw{s}_{tv.p}^{w.j.k}\to {\mathsf{\Omega }}_{tv.l}, and P=L$. $\therefore Pw{s}_{Tv}^{C1.2.w.j.k}=\underset{p=1}{\overset{P}{{\displaystyle \cup }}}Pw{s}_{tv.p}=\underset{l=1}{\overset{L}{{\displaystyle \cup }}}{\mathsf{\Omega }}_{tv.l}$
C1.1: MTC-CWA	$If \left({\Omega }^{w.j.k}|Case=\mathrm{C}1.1\right),then \left(Pw{s}_{Tv}^{C1.1.w.j.k}={\Omega }^{w.j.k}-Iw{s}^{\mathrm{C}1.1.w.j.k}\right): \forall {\mathsf{\Omega }}_{tv.l}\in Iw{s}^{\mathrm{C}1.1.w.j.k}, \exists \left(\left|a_{k.g}^{w.j}.T\right|\in {\mathsf{\Omega }}_{tv.l}\right)\ge 1$. $\therefore Pw{s}_{Tv}^{C1.1.w.j.k}=\underset{p=1}{\overset{P}{{\displaystyle \cup }}}Pw{s}_{tv.p}:P<L, \forall Pw{s}_{tv.p}\in Pw{s}_{Tv}^{C1.1.w.j.k}, \exists Pw{s}_{tv.p}=\left({\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}1.1.w.j.k}\right)$.
C2.1.1: ITCC-CWA	$If \left({\Omega }^{w.j.k}|Case=\mathrm{C}\mathrm{2.1.1}\right), then \left(Pw{s}^{\mathrm{C}\mathrm{2.1.1}.w.j.k}={\Omega }^{w.j.k}-Iw{s}^{\mathrm{C}\mathrm{2.1.1}.w.j.k}\right):\forall {\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}\mathrm{2.1.1}.w.j.k} if only \exists \left(\left|a_{k.g}^{w.j}.T\right|\in {\mathsf{\Omega }}_{tv.l}\right)=1$. $\therefore Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.1.1}.w.j.k}=\underset{p=1}{\overset{P}{{\displaystyle \cup }}}Pw{s}_{tv.p}:P<L,\forall Pw{s}_{tv.p}\in Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.1.1}.w.j.k}, \exists Pw{s}_{tv.p}=\left({\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}2.1.w.j.k}\right)$
C2.1.2: ITCC-OWA	$If \left({\Omega }^{w.j.k}|Case=\mathrm{C}\mathrm{2.1.1}\right), then \left(Pw{s}^{\mathrm{C}\mathrm{2.1.1}.w.j.k}={\Omega }^{w.j.k}-Iw{s}^{\mathrm{C}\mathrm{2.1.2}.w.j.k}\right):\forall {\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}\mathrm{2.1.2}.w.j.k} if only \exists \left(\left|a_{k.g}^{w.j}.T\right|\in {\mathsf{\Omega }}_{tv.l}\right)\le 1$. $\therefore Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.1.2}.w.j.k}=\underset{p=1}{\overset{P}{{\displaystyle \cup }}}Pw{s}_{tv.p}:P<L, \forall Pw{s}_{tv.p}\in Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.1.2}.w.j.k}, \exists Pw{s}_{tv.p}=\left({\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}\mathrm{2.1.2}.w.j.k}\right)$.
C2.2.1: ITCU-CWA	$If \left({\Omega }^{w.j.k}|Case=\mathrm{C}\mathrm{2.2.1}\right), then \left(Pw{s}^{\mathrm{C}\mathrm{2.2.1}.w.j.k}={\Omega }^{w.j.k}-Iw{s}^{\mathrm{C}\mathrm{2.2.1}.w.j.k}\right): \forall {\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}\mathrm{2.2.1}.w.j.k} if only \exists \left(\left|a_{k.g}^{w.j}.T\right|\oplus \left|a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}.T\right|\in {\mathsf{\Omega }}_{tv.l}\right)=1, and \exists a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}.T\backslash F\in {\Omega }_{tv.l}.$  $\therefore Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.2.1}.w.j.k}=\underset{p=1}{\overset{P}{{\displaystyle \cup }}}Pw{s}_{tv.p}:P<L, \forall Pw{s}_{tv.p}\in Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.2.1}.w.j.k}, \exists Pw{s}_{tv.p}=\left({\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}\mathrm{2.2.1}.w.j.k}\right)$.
C2.2.2: ITCU-OWA	$If \left({\Omega }^{w.j.k}|Case=\mathrm{C}\mathrm{2.2.2}\right), then \left(Pw{s}^{\mathrm{C}\mathrm{2.2.2}.w.j.k}={\Omega }^{w.j.k}-Iw{s}^{\mathrm{C}\mathrm{2.2.2}.w.j.k}\right):\forall {\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}\mathrm{2.2.2}.w.j.k} if only \exists \left(\left|a_{k.g}^{w.j}.T\right|\oplus \left|a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}.T\right|\in {\mathsf{\Omega }}_{tv.l}\right)\le 1, and \exists a_{k.g.Nl}^{w.j.{\displaystyle \cup }ih}.T\backslash F\in {\Omega }_{tv.l}.$ $\therefore Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.2.2}.w.j.k}=\underset{p=1}{\overset{P}{{\displaystyle \cup }}}Pw{s}_{tv.p}:P<L, \forall Pw{s}_{tv.p}\in Pw{s}_{Tv}^{\mathrm{C}\mathrm{2.2.2}.w.j.k}, \exists Pw{s}_{tv.p}=\left({\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{\mathrm{C}\mathrm{2.2.2}.w.j.k}\right)$

$$\begin{gathered} Pw{s}_{Tv}^{Case.w.j.k}={\mathsf{\Omega }}^{w.j.k}-Iw{s}^{Case.w.j.k}\Rightarrow \\ Pw{s}_{Tv}^{Case.w.j.k}=\underset{p=1}{\overset{P}{{\displaystyle \cup }}}Pw{s}_{tv.p}:1\le p\le P, Pw{s}_{Tv}^{Case.w.j.k}\le {\mathsf{\Omega }}^{w.j.k}, \& Pw{s}_{tv.p}\to \left({\mathsf{\Omega }}_{tv.l}\notin Iw{s}^{w.j.k}\right), \\ \therefore \forall \left(Pw{s}_{Tv}^{Case.w.j.k}\ni Pw{s}_{tv.p}\in {\mathsf{\Omega }}^{w.j.k}\right), \exists Pw{s}_{tv.p}\notin Iw{s}^{w.j.k}, and a\left({\Omega }_{tv.l}\right)\to a\left(Pw{s}_{tv.p}\right), \mu \left({\Omega }_{tv.l}\right)\to \mu \left(Pw{s}_{tv.p}\right) \forall {\Omega }_{tv.l}=Pw{s}_{tv.p} \& {\Omega }_{tv.l}\in Pw{s}_{Tv}^{Case.w.j.k} \end{gathered}$$

(8)

Example 2: To illustrate the sample space and possible-worlds production based on the data fusion cases, the data value domain and sample space from$Dom A_3^{1.1}$inTable 2 and Table 3 are used. By using $Dom A_3^{1.1}$ domain in Table 2 and the sample space production in Table 3, the below sample space alternatives are generalized: ${\Omega }^{\mathrm{1.1.3}}=\left\{{\Omega }_{tv.1},{\Omega }_{tv.2},{\Omega }_{tv.3},{\Omega }_{tv.4}\right\}, where$

• ${\Omega }_{tv.1}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.T,a_{3.2}^{1.1.\left(31\right)}.T\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T},{\mu }_{a_{3.2}^{1.1.\left(31\right)}.T}\right)\right)\to {\Omega }_{tv.1}=\left(a\left({\Omega }_{tv.1}\right),\mu \left({\Omega }_{tv.1}\right)\right)\to {\Omega }_{tv.1}=\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)},12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.9,0.6,0.45\right)\right)$.
• ${\Omega }_{tv.2}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.T,a_{3.2}^{1.1.\left(31\right)}.F\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T},{\mu }_{a_{3.2}^{1.1.\left(31\right)}.F}\right)\right)\to {\Omega }_{tv.2}=\left(a\left({\Omega }_{tv.2}\right),\mu \left({\Omega }_{tv.2} \right)\right)\to {\Omega }_{tv.2}=\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6,0.55\right)\right).$
• ${\Omega }_{tv.3}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.F,a_{3.2}^{1.1.\left(31\right)}.T\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F},{\mu }_{a_{3.2}^{1.1.\left(31\right)}.T}\right)\right)\to {\Omega }_{tv.3}=\left(a\left({\Omega }_{tv.3}\right),\mu \left({\Omega }_{tv.3}\right)\right)\to {\Omega }_{tv.3}=\left(\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.1,0.4,0.45\right)\right)$.
• ${\Omega }_{tv.4}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.F,a_{3.2}^{1.1.\left(31\right)}.F\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F},{\mu }_{a_{3.2}^{1.1.\left(31\right)}.F}\right)\right)\to {\Omega }_{tv.4}=\left(a\left({\Omega }_{tv.4}\right),\mu \left({\Omega }_{tv.4}\right)\right)\to {\Omega }_{tv.4}=\left(\left(\varnothing “Unknown”\right),\left(0.1,0.4,0.55\right)\right)$

After producing the above sample space, the possible-worlds production can be generated for a data fusion case based on the production rules presented in Table 4. Accordingly, the possible-worlds sets that can be observed in a given data fusion case are listed below:

-

If the data fusion case is MTC-OWA (C1.2), then multiple data values can be true at the same time, and it is possible to have the true value that does not exist in $DOM A_3^{1.1}$ domain. Therefore, the generated possible worlds $\left(Pw{s}^{\left(C1.2\right).\left(\mathrm{1.1.3}\right)}\right)$ will be equal to the sample space of ${\Omega }^{\mathrm{1.1.3}}$ as shown below:

• $Pw{s}_{Tv}^{\left(C1.2\right).\left(\mathrm{1.1.3}\right)}={\Omega }^{\mathrm{1.1.3}}=\left\{{\Omega }_{tv.1},{\Omega }_{tv.2},{\Omega }_{tv.3},{\Omega }_{tv.4}\right\}=\left\{Pw{s}_{tv.1}, Pw{s}_{tv.2}, Pw{s}_{tv.3}, Pw{s}_{tv.4}\right\}: Pw{s}_{tv.1}={\Omega }_{tv.1}=$$\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)},12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.9,0.6,0.45\right)\right), Pw{s}_{tv.2}={\Omega }_{tv.2}=$$\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6,0.55\right)\right), Pw{s}_{tv.3}={\Omega }_{tv.3}=$$\left(\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.1,0.4,0.45\right)\right), \& Pw{s}_{tv.4}={\Omega }_{tv.4}=\left(\left(\varnothing “Unknown”\right),\left(0.1,0.4,0.55\right)\right)$.

-

If the data fusion case is MTC-OWA (C1.1), then multiple data values can be true at the same time, and it is not possible to have a true value that does not exist in $DOM A_3^{1.1}$ domain. Therefore, the generated possible worlds $\left(Pw{s}^{\left(C1.1\right).\left(\mathrm{1.1.3}\right)}\right)$ would be as shown below:

• $Pw{s}_{Tv}^{\left(C1.1\right).\left(\mathrm{1.1.3}\right)}={\Omega }^{\mathrm{1.1.3}}-Iw{s}^{\left(C1.1\right).\left(\mathrm{1.1.3}\right)}: Iw{s}^{C1.1.w.j.k}=\left\{{\Omega }_{tv.4}\right\}\Rightarrow Pw{s}_{Tv}^{\left(C1.1\right).\left(\mathrm{1.1.3}\right)}=\left\{Pw{s}_{tv.1}, Pw{s}_{tv.2}, Pw{s}_{tv.3}\right\}: Pw{s}_{tv.1}= {\Omega }_{tv.1}$$=\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)},12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.9,0.6,0.45\right)\right), Pw{s}_{tv.2}={\Omega }_{tv.2}=$$\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6,0.55\right)\right), Pw{s}_{tv.3}={\Omega }_{tv.3}=\left(\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.1,0.4,0.45\right)\right)$.

-

If the data fusion case is ITCC-CWA (C2.1.1), then one data value can be true at a time, and it is not possible to have the true value from outside $DOM A_3^{1.1}$ domain. Therefore, the generated possible worlds $\left(Pw{s}^{\left(C\mathrm{2.1.1}\right).\left(\mathrm{1.1.3}\right)}\right)$ would be as shown below:

• $Pw{s}_{Tv}^{\left(C\mathrm{2.1.1}\right).\left(\mathrm{1.1.3}\right)}={\Omega }^{\mathrm{1.1.3}}-Iw{s}^{\left(C\mathrm{2.1.1}\right).\left(\mathrm{1.1.3}\right)}:Iw{s}^{\left(C\mathrm{2.1.1}\right).\left(\mathrm{1.1.3}\right)}=\left\{{\Omega }_{tv.1},{\Omega }_{tv.4}\right\}\Rightarrow Pw{s}_{Tv}^{\left(C\mathrm{2.1.1}\right).\left(\mathrm{1.1.3}\right)}=$$\left\{Pw{s}_{tv.1}, Pw{s}_{tv.2}\right\}: Pw{s}_{tv.1}={\Omega }_{tv.2}=\left(\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6,0.55\right)\right), Pw{s}_{tv.2}={\Omega }_{tv.3}=$$\left(\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.1,0.4,0.45\right)\right)$.

-

If the data fusion case is ITCC-OWA (C2.1.2), then one data value can be true at a time, and it is possible to have the true value from outside $DOM A_3^{1.1}$ domain. Therefore, the generated possible worlds $\left(Pw{s}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}\right)$ would be as shown below:

• $Pw{s}_{Tv}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}={\Omega }^{\mathrm{1.1.3}}-Iw{s}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}:Iw{s}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}=\left\{{\Omega }_{tv.1}\right\}\Rightarrow Pw{s}_{Tv}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}=$$\left\{Pw{s}_{tv.1}, Pw{s}_{tv.2},Pw{s}_{tv.3}\right\}: Pw{s}_{tv.1}={\Omega }_{tv.2}=\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6,0.55\right)\right), Pw{s}_{tv.2}={\Omega }_{tv.3}=$$\left(\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.1,0.4,0.45\right)\right), \& Pw{s}_{tv.3}={\mathsf{\Omega }}_{tv.4}=\left(\left(\varnothing “Unknown”\right),\left(0.1,0.4,0.55\right)\right)$

To present the illustrated example for the uncertainty data fusion cases, we assume that the data value of ${\mathrm{a}}_{3.2}^{31}$ in $DOM A_3^{1.1}$ domain is null, where it comes with additional knowledge about its possible domain of values as $Dom {\mathrm{a}}_{3.2.\mathrm{Nl}}^{1.1.\left(31\right)}=\left\{a_{3.2.Nl1},a_{3.2.Nl2}\right\},$such that $a_{3.2.Nl1}=“114 Eqaila Blvd”$ and$, a_{3.2.Nl2}=“105 Eqaila Blvd”$. Based on Equation (7), the data fusion sample space’s sets under uncertainty are outlined as shown below:

${\mathsf{\Omega }}^{\mathrm{1.1.3}}=\left({\mathsf{\Omega }}^{\mathrm{1.1.3}\left(\mathrm{NonNull}\right)}\times {\mathsf{\Omega }}^{\mathrm{1.1.3}\left(\mathrm{Null}\right)}\right)$: Where

$${\mathsf{\Omega }}^{\mathrm{1.1.3}\left(\mathrm{NonNull}\right)}\begin{array}{l}=\left\{\left(a_{3.1}^{1.1}.T,{\displaystyle \cup }{\mu }_{a_{3.1}^{1.1}.T}\right),\left(a_{3.1}^{1.1}.F,{\displaystyle \cup }{\mu }_{a_{3.1}^{1.1}.F}\right)\right\}\\ =\left\{\left(12224 Ventura Blv{d}_{3.1}^{1.1},\left(0.9,0.6\right)\right),\left(\varnothing “Unknown,\left(0.1,0.4\right)\right)\right\}\end{array}$$

$${\mathsf{\Omega }}^{\mathrm{1.1.3}\left(\mathrm{Null}\right)}=\left\{\begin{array}{c}\left(\left(a_{3.2.Nl1}^{1.1.\left(31\right)}.T, a_{3.2.Nl2}^{1.1.\left(31\right)}.F\right),\left({\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.T},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F}\right)\right),\\ \left(\left(a_{3.2.Nl1}^{1.1.\left(31\right)}.F, a_{3.2.Nl2}^{1.1.\left(31\right)}.T\right),\left({\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.T}\right)\right),\\ \left(\left(a_{3.2.Nl1}^{1.1.\left(31\right)}.F, a_{3.2.Nl2}^{1.1.\left(31\right)}.F\right),\left({\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F}\right)\right)\end{array}\right\}\Rightarrow$$

$${\mathsf{\Omega }}^{\mathrm{1.1.3}\left(\mathrm{Null}\right)}=\left\{\begin{array}{c}\left(\left(114 Eqaila Blv{d}_{3.2.Nl1}\right),\left(0.45,0.55\right)\right),\\ \left(\left(105 Eqaila Blv{d}_{3.2.Nl2}\right),\left(0.55,0.45\right)\right),\\ \left(\left(\varnothing “Unknown”\right),\left(0.55,0.55\right)\right)\end{array}\right\}\Rightarrow {\mathsf{\Omega }}^{\mathrm{1.1.3}}=\left\{{\Omega }_{tv.1},{\Omega }_{tv.2},{\Omega }_{tv.3},{\Omega }_{tv.4},{\Omega }_{tv.5},{\Omega }_{tv.6}\right\}:$$

-

${\Omega }_{tv.1}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.T,a_{3.2.Nl1}^{1.1.\left(31\right)}.T, a_{3.2.Nl2}^{1.1.\left(31\right)}.F\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.T},{\mu }_{a_{3.2.Nl2}^{1.1.\left(31\right)}.F}\right)\right)=\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)},114 Eqaila Blv{d}_{3.2.Nl1}^{1.1.\left(31\right)} \right),\left(0.9,0.6, 0.45,0.55\right)\right)$.

-

${\Omega }_{tv.2}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.T,a_{3.2.Nl1}^{1.1.\left(31\right)}.F, a_{3.2.Nl2}^{1.1.\left(31\right)}.T\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F},{\mu }_{a_{3.2.Nl2}^{1.1.\left(31\right)}.T}\right)\right)=\left(\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{1.1.\left(13,21\right)},{105 \mathrm{Eqaila} \mathrm{Blvd}}_{3.2.\mathrm{Nl}2}^{1.1.\left(31\right)} \right),\left(0.9,0.6, 0.55,0.45\right)\right).$${\Omega }_{tv.3}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.T,a_{3.2.Nl1}^{1.1.\left(31\right)}.F, a_{3.2.Nl2}^{1.1.\left(31\right)}.F\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.T},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F},{\mu }_{a_{3.2.Nl2}^{1.1.\left(31\right)}.F}\right)\right)=\left(\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6, 0.55,0.55\right)\right)$.

-

${\Omega }_{tv.4}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.F,a_{3.2.Nl1}^{1.1.\left(31\right)}.T, a_{3.2.Nl2}^{1.1.\left(31\right)}.F\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.T},{\mu }_{a_{3.2.Nl2}^{1.1.\left(31\right)}.F}\right)\right)=$$\left(\left(114 Eqaila Blv{d}_{3.2.Nl1}^{1.1.\left(31\right)}\right),\left(0.1,0.4, 0.45,0.55\right)\right)$.

-

${\Omega }_{tv.5}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.F,a_{3.2.Nl1}^{1.1.\left(31\right)}.F, a_{3.2.Nl2}^{1.1.\left(31\right)}.T\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F},{\mu }_{a_{3.2.Nl2}^{1.1.\left(31\right)}.T}\right)\right)=$$\left(\left(105 Eqaila Blv{d}_{3.2.Nl2}^{1.1.\left(31\right)}\right),\left(0.1,0.4, 0.55,0.45\right)\right)$.

-

${\Omega }_{tv.6}=\left(\left(a_{3.1}^{1.1.\left(13,21\right)}.F,a_{3.2.Nl1}^{1.1.\left(31\right)}.F, a_{3.2.Nl2}^{1.1.\left(31\right)}.F\right),\left({\displaystyle \cup }{\mu }_{a_{3.1}^{1.1.\left(13,21\right)}.F},{\mu }_{a_{3.2.Nl1}^{1.1.\left(31\right)}.F},{\mu }_{a_{3.2.Nl2}^{1.1.\left(31\right)}.F}\right)\right)=\left(\left(\varnothing “Unknown”\right),\left(0.1,0.4, 0.55,0.55\right)\right)$

Below are possible worlds for the data fusion’s uncertainty cases as observed based on the above sample space sets:

-

If the data fusion case is ITCU-CWA (C2.2.1), then one data value can be true at a time, and it is not possible to have the true value from outside $DOM A_3^{1.1}$ domain. Therefore, the generated possible worlds $\left(Pw{s}^{\left(C\mathrm{2.2.1}\right).\left(\mathrm{1.1.3}\right)}\right)$ would be as shown below:

$$Pw{s}_{Tv}^{\left(C\mathrm{2.2.1}\right).\left(\mathrm{1.1.3}\right)}\begin{array}{l}={\Omega }^{\mathrm{1.1.3}}-Iw{s}^{\left(C\mathrm{2.2.1}\right).\left(\mathrm{1.1.3}\right)}:Iw{s}^{\left(C\mathrm{2.2.1}\right).\left(\mathrm{1.1.3}\right)}\\ =\left\{{\Omega }_{tv.1},{\Omega }_{tv.2},{\mathsf{\Omega }}_{tv.4}\right\}\Rightarrow Pw{s}_{Tv}^{\left(C\mathrm{2.2.1}\right).\left(\mathrm{1.1.3}\right)}=\left\{Pw{s}_{tv.1}, Pw{s}_{tv.2}, Pw{s}_{tv.3}\right\}:\end{array}$$

• $Pw{s}_{tv.1}={\Omega }_{tv.3}=\left(\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6, 0.55,0.55\right)\right),$
• $Pw{s}_{tv.2}={\Omega }_{tv.4}=\left(\left(114 Eqaila Blv{d}_{3.2.Nl1}^{1.1.\left(31\right)}\right),\left(0.1,0.4, 0.45,0.55\right)\right),$
• $Pw{s}_{tv.3}={\Omega }_{tv.5}=\left(\left({105 \mathrm{Eqaila} \mathrm{Blvd}}_{3.2.\mathrm{Nl}2}^{1.1.\left(31\right)}\right),\left(0.1,0.4, 0.55,0.45\right)\right)$

-

If the data fusion case is ITCU-OWA (C2.2.2), then one data value can be true at a time and it is possible to have the true value from outside $DOM A_3^{1.1}$ domain. Therefore, the generated possible worlds $\left(Pw{s}^{\left(C\mathrm{2.2.2}\right).\left(\mathrm{1.1.3}\right)}\right)$ would be as shown below:

$$Pw{s}_{Tv}^{\left(C\mathrm{2.2.2}\right).\left(\mathrm{1.1.3}\right)}\begin{array}{l}={\Omega }^{\mathrm{1.1.3}}-Iw{s}^{\left(C\mathrm{2.2.2}\right).\left(\mathrm{1.1.3}\right)}:Iw{s}^{\left(C\mathrm{2.2.2}\right).\left(\mathrm{1.1.3}\right)}\\ =\left\{{\Omega }_{tv.1},{\Omega }_{tv.2}\right\}\Rightarrow Pw{s}_{Tv}^{\left(C\mathrm{2.2.2}\right).\left(\mathrm{1.1.3}\right)}=\left\{Pw{s}_{tv.1}, Pw{s}_{tv.2},Pw{s}_{tv.3},Pw{s}_{tv.4}\right\}: \end{array}$$

• $Pw{s}_{tv.1}={\Omega }_{tv.3}=\left(\left(12224{ \mathrm{Ventura} \mathrm{Blvd}}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6, 0.55,0.55\right)\right),$
• $Pw{s}_{tv.2}={\Omega }_{tv.4}=\left(\left(114 Eqaila Blv{d}_{3.2.Nl1}^{1.1.\left(31\right)}\right),\left(0.1,0.4, 0.45,0.55\right)\right),$
• $Pw{s}_{tv.3}={\Omega }_{tv.5}=\left(\left({105 \mathrm{Eqaila} \mathrm{Blvd}}_{3.2.\mathrm{Nl}2}^{1.1.\left(31\right)}\right),\left(0.1,0.4, 0.55,0.45\right)\right),$
• $Pw{s}_{tv.4}={\Omega }_{tv.6}=\left(\left(\varnothing “Unknown”\right),\left(0.1,0.4, 0.55,0.55\right)\right)$

Therefore, a probabilistic global entity with its actual data values and reliability scores is created, and the updated reliability scores for those data values can be computed based on the obtained possible-worlds sets and their recognized data fusion cases. The next section shows the constructed probabilistic data fusion computational method.

5.2. The Probabilistic Data Fusion Computational Method

After conceptually representing the actual data values’ merging for a probabilistic global entity in sort of multi-alternatives of possible true data fusion answers within a $Pw{s}_{Tv}^{Case.w.j.k}$ set, in this section, we formally construct the data fusion computation method and show how we leverage the trustworthiness of sources in truth discovery.

The data fusion method is operated to compute the conditional probability, i.e., updated reliability score, for a possible data value’s or values’ world that is/are most likely recognized as the true fused answer using $\mu \left({\mathsf{\Omega }}_{tv.l_p}\right)$ scores and given a data fusion case. Thus, the conditional probability form of $\left(a_{k.Tv}^{w.j}=a\left({\mathsf{\Omega }}_{tv.l}\right)|Case\right), \mu \left(a_{k.Tv}^{w.j}=a\left({\mathsf{\Omega }}_{tv.l}\right)|Case\right):$ ${\mathsf{\Omega }}_{tv.l}\subseteq Pw{s}_{Tv}^{Case.w.j.k}, {\mathsf{\Omega }}_{tv.l}\to Pw{s}_{tv.\mathrm{p}}, a\left({\mathsf{\Omega }}_{tv.l}\right)\to a\left(Pw{s}_{tv.\mathrm{p}}\right), \& \mu \left({\mathsf{\Omega }}_{tv.l}\right)\to \mu \left(Pw{s}_{tv.\mathrm{p}}\right)$ is used to represent a possible data values’ world that is most likely recognized as the true fusion answer with its conditional probability value that required further computation. In this form,$Case$condition implies a given possible-world set in regard to the presented fusion cases in Table 1, $Case\in \{MTC-CWA,MTC-OWA,ITCC-CWA,ITCC-OWA,ITCU-CWA,ITCU-OWA\}$. In order to do that, the listed assumptions in Section 3.5 are considered.

To obtain a single reliability score, i.e., the conditional probability value, for each possible data fusion’s alternative within a particular $Dom A_k^{w.j}$ and $nD{O}_{w.j}$ alternative, the data fusion computational formula is constructed in Equation (9). This formula is constructed using Bayes’ theorem, the probability distribution from $\mu \left(Pw{s}_{tv.p}\right)$, and assumptions 1 to 3 (refer to Section 3.6) (the detailed derivations are given in Appendix A):

$$\begin{gathered} \mu \left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)|Pw{s}_{Tv}^{Case.w.j.k}\right)=\frac{\mu \left(\left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)\right){{\displaystyle \cap }}^{ }Pw{s}_{Tv}^{Case.w.j.k}\right)}{\mu \left(Case=Pw{s}_{Tv}^{Case.w.j.k}\right)}=\frac{\mu \left(\left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)\right){{\displaystyle \cap }}^{ }Pw{s}_{Tv}^{Case.w.j.k}\right)}{{{\displaystyle \sum }}^{ }\mu \left(Pw{s}_{Tv}^{Case.w.j.k}\right)}=\frac{{\displaystyle \prod }\mu \left(Pw{s}_{tv.p}\right)}{{{\displaystyle \sum }}_{p=1}^P{\displaystyle \prod }\mu \left(Pw{s}_{tv.p}\right)}=\frac{{\displaystyle \prod }\mu \left(Pw{s}_{tv.p}\right)}{{\displaystyle \prod }\mu \left(Pw{s}_{tv.1}\right)+{\displaystyle \prod }\mu \left(Pw{s}_{tv.2}\right)+\dots +{\displaystyle \prod }\mu \left(Pw{s}_{tv.P}\right)} \\ \mathrm{Substituting} \mathrm{for} {{\displaystyle \prod }}^{ }\mu \left({\mathsf{\Omega }}_{tv.l}^{w.j.k}\right)\to {{\displaystyle \prod }}^{ }\mu \left(Pw{s}_{tv.p}\right) \mathrm{from} \mathrm{Equations} \left(6\right) \mathrm{and} \left(8\right),\mathrm{we} \mathrm{get;}; \\ \mu \left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)|Pw{s}_{Tv}^{Case.w.j.k}\right)=\frac{{{\displaystyle \prod }}_{g^{w.j}=1}^{q^{w.j}}{{\displaystyle \prod }}_{g^{ih}=1^{11}}^{q^{nm}}{\left({\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F}\right)}_{tv.p}}{{\displaystyle \prod }_{g^{w.j}=1}^{q^{w.j}}{\displaystyle \prod }_{g^{ih}=1^{11}}^{q^{nm}}{\left({\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F}\right)}_{tv.1}+{\displaystyle \prod }_{g^{w.j}=1}^{q^{w.j}}{\displaystyle \prod }_{g^{ih}=1^{11}}^{q^{nm}}{\left({\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F}\right)}_{tv.2}+\dots +{\displaystyle \prod }_{g^{v.j}=1}^{q^{v.j}}{\displaystyle \prod }_{g^{ih}=1^{11}}^{q^{nm}}{\left({\mu }_{a_{k.g}^{w.j.{\displaystyle \cup }ih}.T\backslash F}\right)}_{tv.P}} \end{gathered}$$

(9)

where ${\displaystyle \sum }_{p=1}^P\mu \left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)|Pw{s}_{Tv}^{Case.w.j.k}\right)=1$.

This computation is processed to all $Pw{s}_{tv.1, tv.2,\dots , tv.P}\in Pw{s}_{Tv}^{Case.w.j.k}$ worlds that observed from ${\Omega }^{w.1.k,\dots ,w.f.k}$ sets. Thus, the possible-worlds sets of correct values and their posterior reliability scores are obtained for all merging alternatives that assemble the processed $nD{O}_w$ entity. This concludes that a probabilistic global entity with its actual values is obtained, and the updated reliability for requested attribute values are computed accordingly.

Example 3. To illustrate the computation method for finding the probabilistic true data fusion answer within a specific set of$Pw{s}_{Tv}^{Case.w.j.k}$, this example is continued based on the possible-worlds sets that are obtained in example 2 using the$ITCC-OWA$(C2.1.2), data fusion case.

Since $Pw{s}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}=\left\{Pw{s}_{tv.1}, Pw{s}_{tv.2},Pw{s}_{tv.3}\right\},\mathrm{where} Pw{s}_{tv.1}=((12224 Ventura$ $Blv{d}_{3.2}^{1.1.\left(13,21\right)}),\left(0.9,0.6,0.55\right)),Pw{s}_{tv.2}=\left(\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.1,0.4,0.45\right)\right)$, and $Pw{s}_{tv.3}=\left(\left(\varnothing “Unknown”\right),\left(0.1,0.4,0.55\right)\right)$, then the conditional probability of the updated reliability score for a specific possible-world’s data value being true is computed as below.

$$Pw{s}_{Tv}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}=\begin{array}{l}\left\{a\left(Pw{s}_{tv.p}\right), \mu \left(Pw{s}_{tv.p}\right)\right\}\\ =\left\{\begin{array}{c}\left(\left(12224 Ventura Blv{d}_{3.1}^{1.1.\left(13,21\right)}\right),\left(0.9,0.6,0.55\right)\right),\\ \left(\left(12335 Fienega Blv{d}_{3.2}^{1.1.\left(31\right)}\right),\left(0.1,0.4,0.45\right)\right),\\ \left(\left(\varnothing “Unknown”\right),\left(0.1,0.4,0.55\right)\right)\end{array}\right\}\end{array}$$

• $\mu \left(a_{k.Tv}^{v.j}=a\left(Pw{s}_{tv.1}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}\right)=\frac{\mu \left(Pw{s}_{tv.1}\right)}{\mu \left(Pw{s}_{tv.1}\right)+\mu \left(Pw{s}_{tv.2}\right)+\mu \left(Pw{s}_{tv.3}\right)}=\frac{0.9\times 0.6\times 0.55}{\left(0.9\times 0.6\times 0.55\right)+\left(0.1\times 0.4\times 0.45\right)+\left(0.1\times 0.4\times 0.55\right)}=\frac{0.297}{0.297+0.018+0.022}=\frac{0.297}{0.337}\approx 0.881$.
• $\mu \left(a_{k.Tv}^{v.j}=a\left(Pw{s}_{tv.2}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}\right)=\frac{\mu \left(Pw{s}_{tv.2}\right)}{\mu \left(Pw{s}_{tv.1}\right)+\mu \left(Pw{s}_{tv.2}\right)+\mu \left(Pw{s}_{tv.3}\right)}=\frac{0.018}{0.337}\approx 0.053$.
• $\mu \left(a_{k.Tv}^{v.j}=a\left(Pw{s}_{tv.3}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.1.2}\right).\left(\mathrm{1.1.3}\right)}\right)=\frac{\mu \left(Pw{s}_{tv.3}\right)}{\mu \left(Pw{s}_{tv.1}\right)+\mu \left(Pw{s}_{tv.2}\right)+\mu \left(Pw{s}_{tv.3}\right)}=\frac{0.022}{0.337}\approx 0.065$.

Based on the updated reliability score for each data value. The probability of $“12224$ $Ventura Blvd”$ being the true value equals to 0.881, the probability of $“12335 Fienega$ $Blvd”$ being the true value equals to 0.053, and the probability of none of these values being true equals to 0.065. We conclude that the most likely correct address’s value, i.e., the data fusion answer for the global entity of $nD{O}_{1.1}=\left(rD{O}_1^{13}:pD{O}_{11}^{21},pD{O}_{12}^{31}\right)\left[0.8245\right]\to \left(Ar{t}^{’}s Delicat{e}^{\left(13, 21,31\right)},0.8245\right)$, is $“12224 Ventura Blvd”$ with 0.881 probability.

5.3. Probability to Possibility Transformation Method

The main reason for the transformation method is to allow a user to choose the range of true data fused values’ alternatives that they are willing to retrieve and view. This method has the advantage of offering effective retrieved answers; fewer but more likely alternatives can only be retrieved using a threshold value chosen based on user selection. In addition, the possibility theory has the advantage over the probability theory of providing a more efficient information retrieval and ranking strategy by using a possibility threshold value instead of a probability threshold value [93,94].

In fact, determining a probabilistic threshold value for retrieving some alternatives is very difficult due to the variety of probability distribution values ranges. By using a possibility threshold value, the user can randomly select a possibility value to be the threshold value ($\beta$) for retrieving the data fusion answer’s alternatives. Therefore, alternatives whose possible values are equaled or exceed the selected possible threshold value would only be retrieved.

This transformation method is based on dividing the probability values for the true data fused value’s alternatives that belong to a particular possible-worlds set of ($nD{O}_{w.j}$) over the highest probability value among. Thus, the transformed possibility value for the alternative with a maximum probability distribution value will equal one. The formula below shows the transformation computation.

$$Pos\left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)|Pw{s}_{Tv}^{Case.w.j.k}\right)=\frac{\mu \left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)|Pw{s}_{Tv}^{Case.w.j.k}\right)}{Max \left(\mu \left(a_{k.Tv}^{w.j}=a \left(Pw{s}_{tv.p}\right)|Pw{s}_{Tv}^{Case.w.j.k}\right)\right)}:\forall Pw{s}_{tv.p}\in Pw{s}_{Tv}^{Case.w.j.k}$$

(10)

6. Proof of Concept: Model Implementation and Discussion

The data fusion computational method has been mathematically proved as discussed in Appendix A. This mathematical approval is established by considering the integration of data values as associated with different reliability scores and as obtained from three different data sources. The data fusion method has been implemented in our probabilistic integration system as an extended merging and computation functions that operates at the attribute level to handle the two inconsistent true value cases under the CWA (i.e., ITCC-CWA (C2.1.1) and ITCU-CWA (C2.2.1)). In this implementation, the data values for a global attribute are matched and grouped under one domain. The decision model for this data fusion method generates a set of possible worlds of fused data values’ alternatives, in which each possible world is associated with an updated reliability value, i.e., $\left(a\left(Pw{s}_{tv.p}\right),\mu \left(a_{k.Tv}^{w.j}=a\left(Pw{s}_{tv.p}\right)|Pw{s}_{Tv}^{Case.w.j.k}\right)\right)$. The updated value is computed based on Equation (9). The updated reliability values within each entities merging’s alternatives are transformed into possibility values using Equation (10). This transformation is constructed to facilitate the retrieval process based on the user’s possibility threshold values.

To see the feasibility of the proposed data fusion approach and how the data fusion results may change by obtaining new pieces of evidence, Figure 5 and Figure 6 are presented. In Figure 5, the decision outputs for the data fusion method under ITCC-CWA case are illustrated. It shows in Figure 5c, the possible fused values for City attribute at each possible entities merging alternative as produced from the entities merging set of {(RO1_(1,1,1)): PO1_(2,1,1) [1.0], PO2_(3,1,2) [1.0]}, where the participated entities with their original matching tree are presented in Figure 5a, while their probabilistic entities merging result is shown in Figure 5b. These entities originated from three participating data sources, where the reliability score for “Amsterdam” data value as originating from the first data source is equal to 0.8, and the reliability score for “Enschede” data value as originating from the second data source is equal to 0.8, and the reliability score for “Georgia” data value as originated from the third source is equal to 0.4, i.e., $a_{2.1}^{11}=\mathrm{Amsterdam}, {\mu }_{a_{2.1}^{11}}=0.8, a_{2.2}^{21}=\mathrm{Enschede}, {\mu }_{a_{2.2}^{21}}=0.8, \mathrm{and} a_{2.3}^{32}=\mathrm{Georgia}, {\mu }_{a_{2.3}^{32}}=0.4$. Using the merged entities alternative of nDO_1.1.1, and the reliability scores of the City data values that correspond to nDO_1.1.1 entities’ alternative, the updated reliability score for each possible data fused alternative is computed using Equations (9) and (10) and presented their corresponding values in the attribute’s probability and possibility columns as shown in Figure 5c.

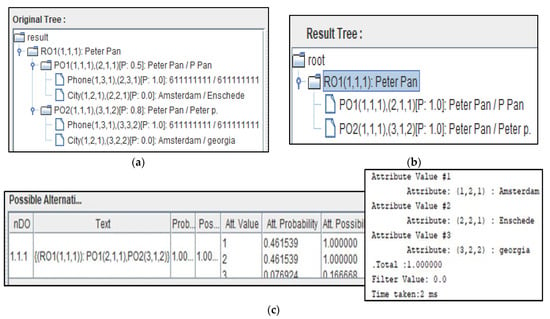
Figure 5. City data fusion alternatives’ example with their updated reliability score based on the C2.1.1 case. (a) The participated entities with their original matching tree. (b) The probabilistic entities linkage/merging results. (c) The possible data fused values for City attribute at each possible entities merging alternative as produced based on Figure 5b.

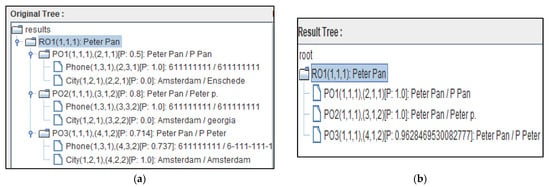
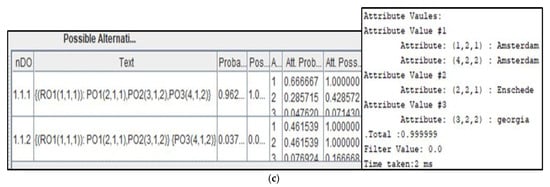
Figure 6. The updated-City data fusion alternatives’ example is based on the newly added evidence from the fourth data source. (a) The participated entities with their original matching tree. (b) The probabilistic entities linkage/merging results. (c) The possible data fused values for City attribute at each possible entities merging alternative as produced based on Figure 6b.

From Figure 5b,c, we can state that RO1, PO1, and PO2 represent the same RWO named “Peter Pan”, with three different possible alternatives of the city name where “Peter Pan” lives. The original reliability scores, as obtained from the data sources, has determined that “Amsterdam” and “Enschede” are equal to 0.8, but “Georgia” is equal to 0.4. The updated reliability scores, which is the conditional probability of having a certain attribute’s value being the true fused value as obtained based on Equation (9), is approximately equal to 0.46 for “Amsterdam” and “Enschede” values, and it is approximately equal to 0.08 for “Georgia”. Based on these updated reliability scores, the possibility values have been obtained using Equation (10) to indicate that “Amsterdam” and “Enschede” values share the same possibility of either one of them being the true fused value of where “Perter Pan” lives, i.e., $Pos\left(a_{2.Tv}^{1.1}=a\left(Pw{s}_{tv.1}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.1.1}\right).\mathrm{1.1.2}}\right)=Pos\left(a_{2.Tv}^{1.1}=a\left(Pw{s}_{tv.2}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.1.1}\right)\mathrm{.1.1.2}}\right)=1$. It also indicates the possibility of having “Peter Pan” lives in “Georgia” is very low as $Pos\left(a_{2.Tv}^{1.1}=a\left(Pw{s}_{tv.3}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.1.1}\right)\mathrm{.1.1.2}}\right)=0.08$. Based on the given evidence from the participated entities and their attribute values reliability scores, we can state that “Peter Pan” is more likely lives in either “Amsterdam” or “Enschede” with a probability of 0.46 and with a possibility of 1.0.

To show how the data fusion computational results may change according to new information/evidence, a new data source that contains information about a person named “P. Perter” is included in the participated data sources and entities of the presented example in Figure 5. This new entity has a city value of “Amsterdam” with a 0.7 original reliability score. Accordingly, the data fusion’s alternatives result after considering the additional information from the new data source are presented in Figure 6.

In Figure 6, the decision outputs for the data fusion method under ITCC-CWA case is illustrated. Figure 6c shows the possible fused values for City attribute at each possible entities merging alternative as produced from the entities merging set of {(RO1_(1,1,1)): PO1_(2,1,1) [1.0]_, PO2_(3,1,2) [1.0], PO3_(4,1,2) [0.96]}, where the participated entities with their original matching tree are presented in Figure 6a, while their probabilistic entities merging result is shown in Figure 6b. These entities originated from four participating data sources, where the reliability score for the “Amsterdam” data value as originating from the first data source is equal to 0.8, and from the fourth data source is equal to 0.7, and the reliability score for “Enschede” data value as originated from the second source is equal to 0.8, and the reliability score for “Georgia” data value as originated from the third source is equal to 0.4, i.e., $a_{2.1}^{11,42}=\mathrm{Amsterdam}, {\mu }_{a_{2.1}^{11,42}}=\left(0.8, 0.7\right), a_{2.2}^{21}=\mathrm{Enschede}, {\mu }_{a_{2.2}^{21}}=0.8,$ and $a_{2.3}^{32}=\mathrm{Georgia}, {\mu }_{a_{2.3}^{32}}=0.4$. Using the merged entities alternatives of nDO_1.1.1 and nDO_1.1.2, and the reliability scores of the City data values that correspond to nDO_1.1.1 and nDO_1.1.2 entities’ alternatives, the updated reliability score under each entities merging alternative and for each possible data fused alternative is computed using Equations (9) and (10) and presented their corresponding values in the attribute’s probability and possibility columns as shown in Figure 6c.

Figure 6c shows two possible entities merging alternatives, i.e., nDO_1.1.1 and nDO_1.1.2. For nDO_1.1.1, the four participating entities correspond to the same person of “Peter Pan”, where the “Amsterdam” value is obtained from the first source, and the new added one with a union reliability score of (0.8 and 0.7). Due to the new information from the fourth data source, the updated reliability scores shown in Figure 6c have changed from the ones presented in Figure 5c. Accordingly, the updated reliability score of having “Amsterdam” as the true fused city value for the “Peter Pan” entity is approximately equal to 0.67. Therefore, the probability for “Enschede” becomes approximately equal to 0.28, and for “Georgia” is approximately equal to 0.08. Therefore, “Amsterdam” has the highest possibility of being the true fused value of where “Peter Pan” lives, i.e., $Pos\left(a_{2.Tv}^{1.1}=a\left(Pw{s}_{tv.1}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.1.1}\right)\mathrm{.1.1.2}}\right)=1$. On the other hand, the possibility of “Enschede” or “Georgia” being the true fused value of where “Peter Pan” lives becomes equal to 0.4 or 0.07, respectively. Based on this information, we can state that “Peter Pan” is more likely to live in “Amsterdam” with a probability of 0.67 and a possibility of 1.0. For the second entity merging alternative of nDO_1.1.2, three participated entities were corresponding to the same person “Peter Pan”, while PO3_(4,1,2) entity that originated from the fourth source did not belong the generated global entity of “Peter Pan”, i.e., {(RO1_(1,1,1)): PO1_(2,1,1), PO2_(3,1,2)},{PO3_(4,1,2)}[0.037]. The participated entities in nDO_1.1.2 are the same ones presented in nDO_1.1.1 in Figure 5; hence, the update reliability scores for the City’s value alternatives within nDO_1.1.2 merging alternative are the same as the one presented in Figure 5c.

Figure 7 illustrates the decision outputs for the data fusion method under ITCU-CWA case and for the Phone attribute, where two possible entities merging alternatives were observed, i.e., nDO_1.3.1 and nDO_1.3.2. Figure 7c shows the possible fused values for the Phone attribute and for each possible entities merging alternatives as produced form the entities merging set of {(RO3_(1,1,3)): PO1_(2,1,3) [1.0], PO2_(3,1,3) [0.73]}, where the participated entities with their original matching tree are presented in Figure 7a, while their probabilistic entities merging result is shown in Figure 7b. These entities originated from three participating data sources; such that the reliability score of “622,222,222” data value as originated from the first data source is equal to 0.8, and from the second data source is equal to 0.7, while the phone value for the record obtained from the third data source is unknown, i.e., NULL, and it is reliability score is 0.8, i.e., ${\mathrm{a}}_{3.1}^{13}={\mathrm{a}}_{3.1}^{23}=622222222,{ \mathsf{\mu }}_{{\mathrm{a}}_{3.1}^{13}}=0.8,{ \mathsf{\mu }}_{{\mathrm{a}}_{3.1}^{23}}=0.7,{ \mathrm{a}}_{3.2}^{33}= \mathrm{NULL},{ \mathsf{\mu }}_{{\mathrm{a}}_{3.2}^{33}}=0.8$. Using the merged entities alternatives of nDO_1.3.1 and nDO_1.3.2. The reliability scores of the Phone data values that correspond to nDO_1.3.1 and nDO_1.3.2 entities’ alternatives, the updated reliability score under each entities merging alternative and for each possible data fused alternative is computed using Equations (9) and (10), and presented their corresponding values in the attribute’s probability and possibility columns as shown in Figure 7c.

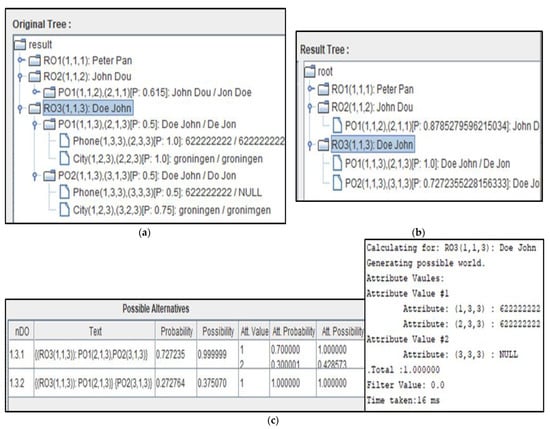
Figure 7. Phone data fusion alternatives’ example with their updated reliability score based on the C2.2.1 case. (a) The participated entities with their original matching tree. (b) The probabilistic entities linkage/merging results. (c) The possible data fused values for Phone attribute at each possible entities merging alternative as produced based on Figure 7b.

In Figure 7c, two possible entity merging alternatives were stated, and the data fusion value for the phone attribute was conditionally computed accordingly. For instance, nDO_1.3.1 alternative indicates the three participating entities correspond to the same person of “John Doe”, with an approximate probability value of 0.73 and with a possibility value of 1.0. In this alternative, the “622,222,222” phone value is obtained from the two records that belong to the first and second sources; hence, its original reliability score is (0.8, 0.7), but for the unknown “Null” value is 0.8 as it is obtained from the third data source. Accordingly, the updated reliability scores, as computed from Equation (9), is 0.7 for “622,222,222” value and it is 0.3 for the unknown “Null” value. Based on these updated scores, the possibility values have been obtained from Equation (10) to indicate that “622,222,222” has the highest possibility of being the true phone number for the “John Doe” global entity, i.e., $Pos\left(a_{3.Tv}^{3.1}=a\left(Pw{s}_{tv.1}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.2.1}\right)\mathrm{.3.1.3}}\right)=1$. The alternative of not knowing John Doe’s number has a low possibility of being true, i.e., $Pos\left(a_{3.Tv}^{3.2}=a\left(Pw{s}_{tv.1}\right)|Pw{s}_{Tv}^{\left(C\mathrm{2.2.1}\right)\mathrm{.3.2.3}}\right)=0.43$. However, the Phone data fusion value under nDO_1.3.2 alternative is different from the first alternative since the third record, i.e., PO2_(3,1,3), does not belong to the generated global entity of “John Doe”. This global entity is generated from {(RO3_(1,1,3)): PO1_(2,1,3) [1.0]} records only, hence, “622,222,222” is the only Phone value to be observed with (0.8, 0.7) reliability scores. Accordingly, the updated reliability score as computed from Equation (9) is 1.0 for the “622,222,222” value.

Based on the implementation of our fusion method within our developed probabilistic integration system and by using a sample dataset, we managed to show how our data fusion method can operate in different fusion cases and how it can cope with the dynamic nature of new information or evidence. We also managed to conclude that by using the offered fusion method, a data value with a higher confidence score and cardinality will be more likely the true value. This is observed by running varied examples related to the data conflict cases. This claim is true as independency assumption among the participated sources is assumed, in which positive evidence can be obtained from having data values with high confidence scores and existed in multiple data sources. Moreover, by considering the possibility of transformation, a better retrieval mechanism for the probable true data fusion’s answers can be achieved.

In terms of considering source accuracy, probabilistic entity linkage nature, and on-demand fusion process, our data fusion approach is relative to the approaches proposed by [26,32,48,73,76,82]. Even though we identified many aspects that make it different to the previous works. First, while our approach is based on the quality based’ strategy, it proposes to manage and resolve two major fusion cases; multi-true values (i.e., multiple truth assumptions), and inconsistent-true values (i.e., single truth assumptions) based on closed-world and open-world assumptions. Second, the data fusion is processed over probabilistic entity linkage and multi-merging alternatives. Our approach can also support on-demand fusion and cope with dynamic and volatile conflicting and uncertain data by keeping and storing the reliability scores alongside its actual data values and by taking the matching and computation process as a chain of separate processes, where each one has its own inputs and outputs data [3]. Upon a user request, such a fusion process for a selected attribute and over a probabilistic global entity is initiated by matching its values from their corresponding sources and entities to form a global domain of merged attribute’s values pairs, and then the computational fusion is executed separately.

7. Limitations

It is worth noticing that entities integration with uncertainty management is hard in general and comes in many forms due to the variety of ways to be defined and processed and the variety of uncertainty types that might be appeared; hence, no single solution addresses all challenges [19]. It does not seem possible to address the computational and representational challenges in general. Yet, we can still study these challenges for the problem with uncertainty management under specific formalizations, uncertainty cases, and scope.

Accordingly, our proposed model is constructed based on a precise mediated and centralized schema structure, where a probabilistic schema integration and a decentralized integration concern are out of this paper’s scope. Moreover, while the experiment demonstrated that our proposed process works in theory, the formula needs to be implemented in several real case scenarios, such as scientific collaborations or personal information, to determine any challenges, accuracy, and the margin of error. Another limitation in our proposed model is related to the ignorance of data sources correlation; data sources can copy from each other, and errors can be propagated quickly. Therefore, ignoring possible dependency among data sources can lead to biased decisions. Another limitation is related to the implementation of our proposed model due to the utilization of a text matching function only. Further enhancement can be added by including a function to compare and match images. Therefore, the data fused values can be found for different forms of data.

8. Conclusions

This paper presented a new probabilistic data fusion model. It described a specific scenario of a probabilistic fusion problem and solution space, where several representational and computational challenges have been identified and formulated. The problem scenario correlates to the attempts and needs to manage and resolve uncertain and conflicting data for multiple attribute values. These values originated due to the probabilistic entities’ integration outcomes over heterogeneous and autonomous data sources. The proposed data fusion method is implemented within the probabilistic integration system to verify its efficiency and feasibility in resolving different data conflict cases. This implementation demonstrated the ability of the system to manage the static and dynamic environment in managing data from a variety of sources. The method automates the homo economics decision making in selecting the most probable and true value [95]. While the experiment demonstrated that our proposed process works in theory, the formula needs to be implemented in several real case scenarios to determine any challenges, accuracy, and the margin of error.

Several challenges related to the data integration and fusion problem under uncertainty management, data correlations, multiple correspondences and probabilistic merging of correlated entities still need to be addressed, and that will continue to occupy the information integration community for a long time to come. Future works include exploring our method in other data fusion strategies, such as capturing sources and attributes correlation to identify positive and negative evidence while conditionally computing the probability of a data being true. It also includes implementing other fusion cases and allocating a suitable benchmark for evaluation purposes. With emerging approaches to data fusion, the industry is in need of a standardization testing mechanism that could also be explored. This testing mechanism would assess the output quality of such approaches in the form of an index of success rate or margin of error for a given fusion process.