Multi-State Synchronization of Chaotic Systems with Distributed Fractional Order Derivatives and Its Application in Secure Communications
Abstract
:1. Introduction
2. Problem Formulation
2.1. Distributed Fractional-Order Derivative
- (1)
- If (where is the impact function), we have the impact function based on the screening property:
- (2)
- If , then:
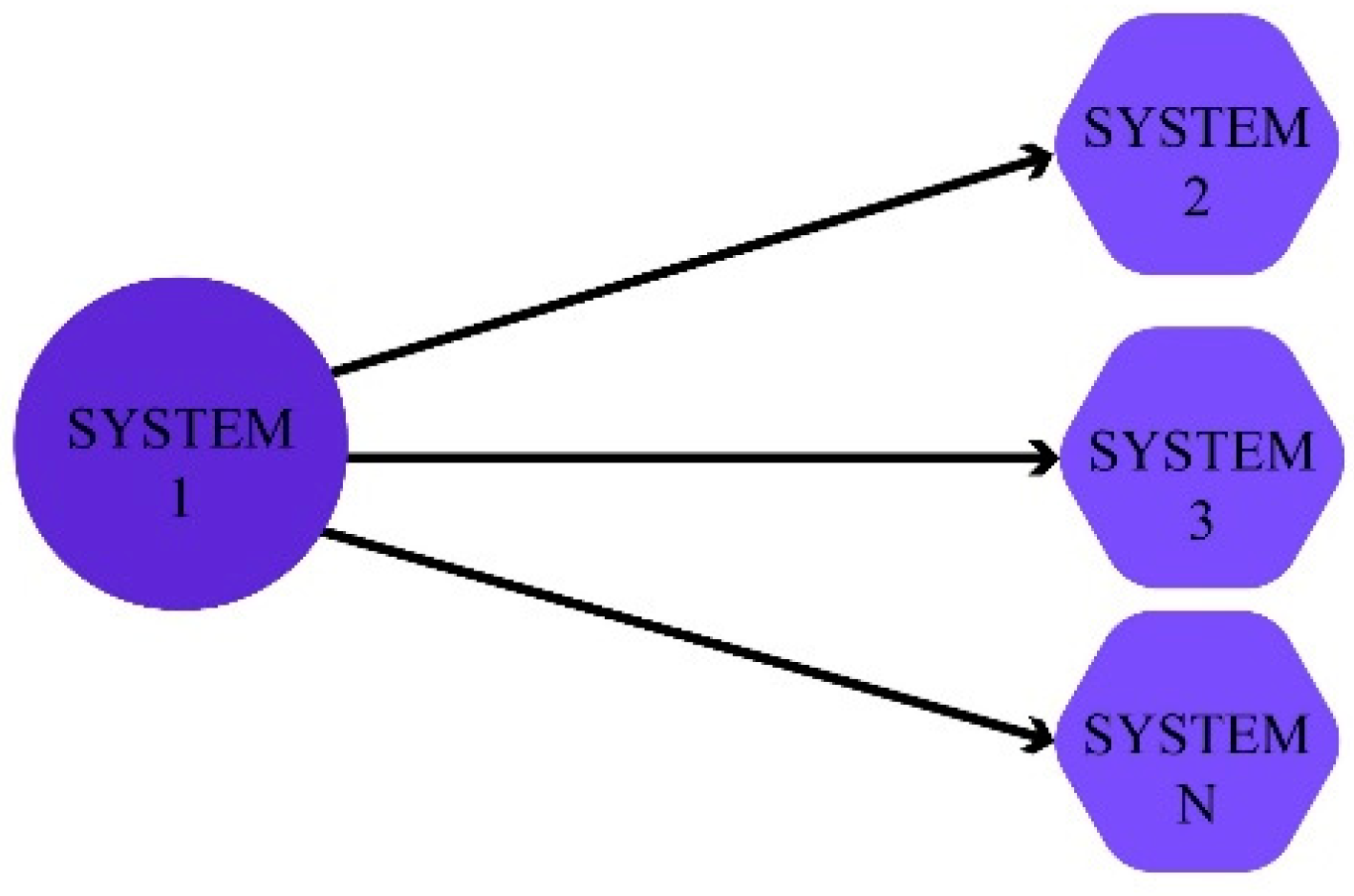
2.2. Multi-State Adaptive Synchronizations
2.3. Synchronizations of Distributed Fractional Order in the Presence of Disturbance, Unknown Time Delay and Uncertaintyin Systems
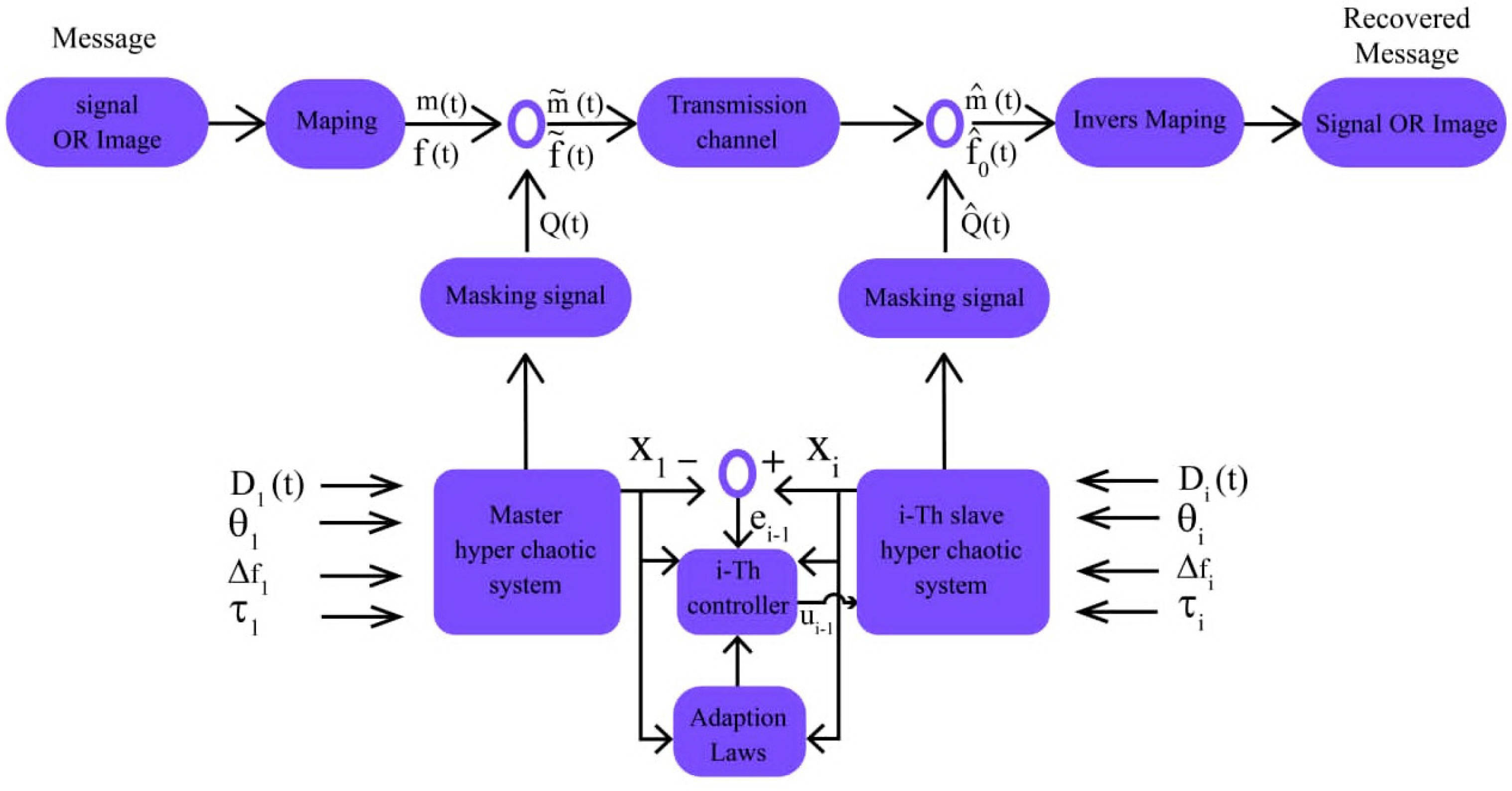
3. Encryption Method with Chaotic Masking
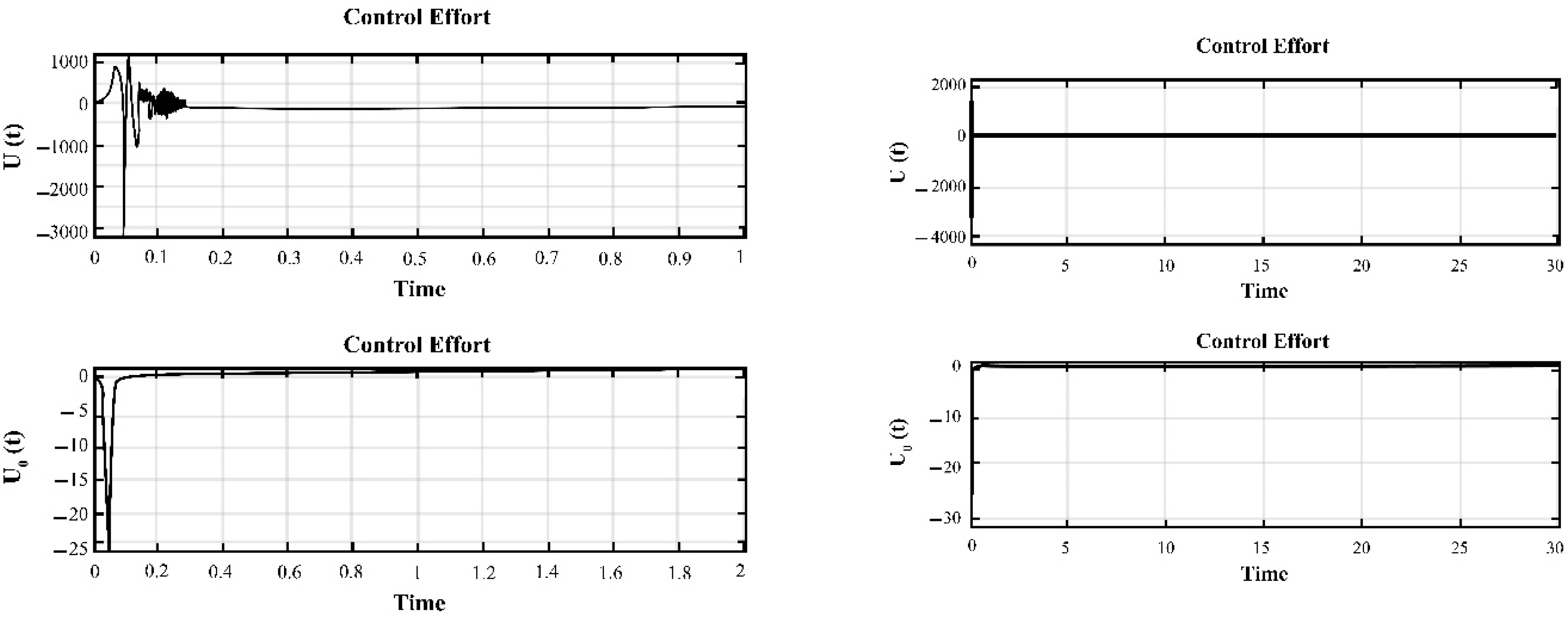
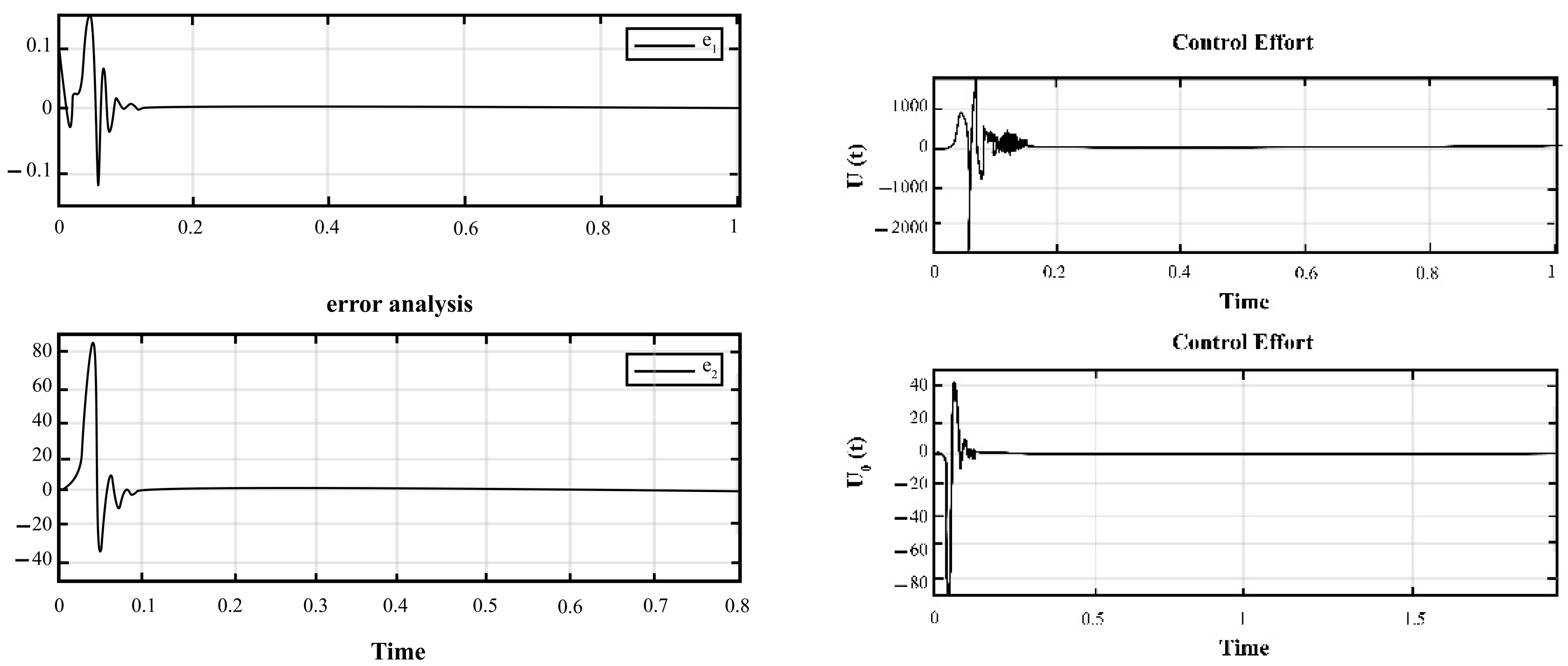
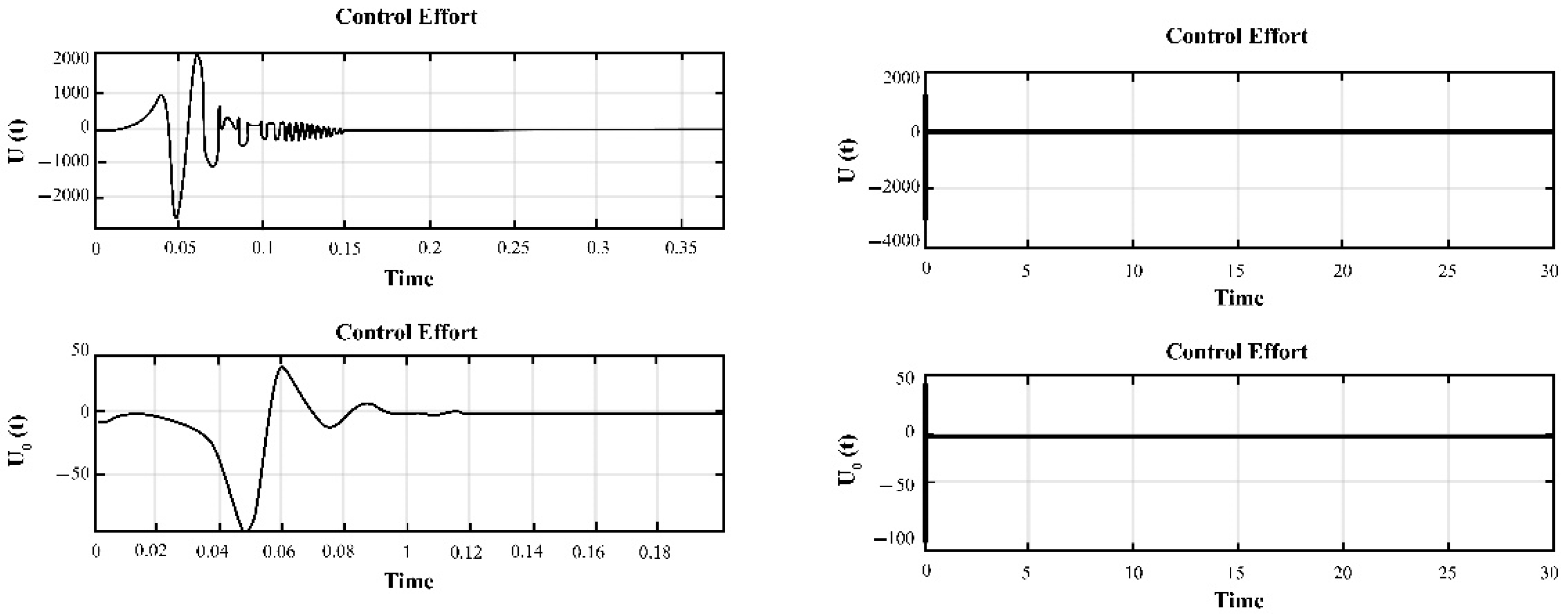
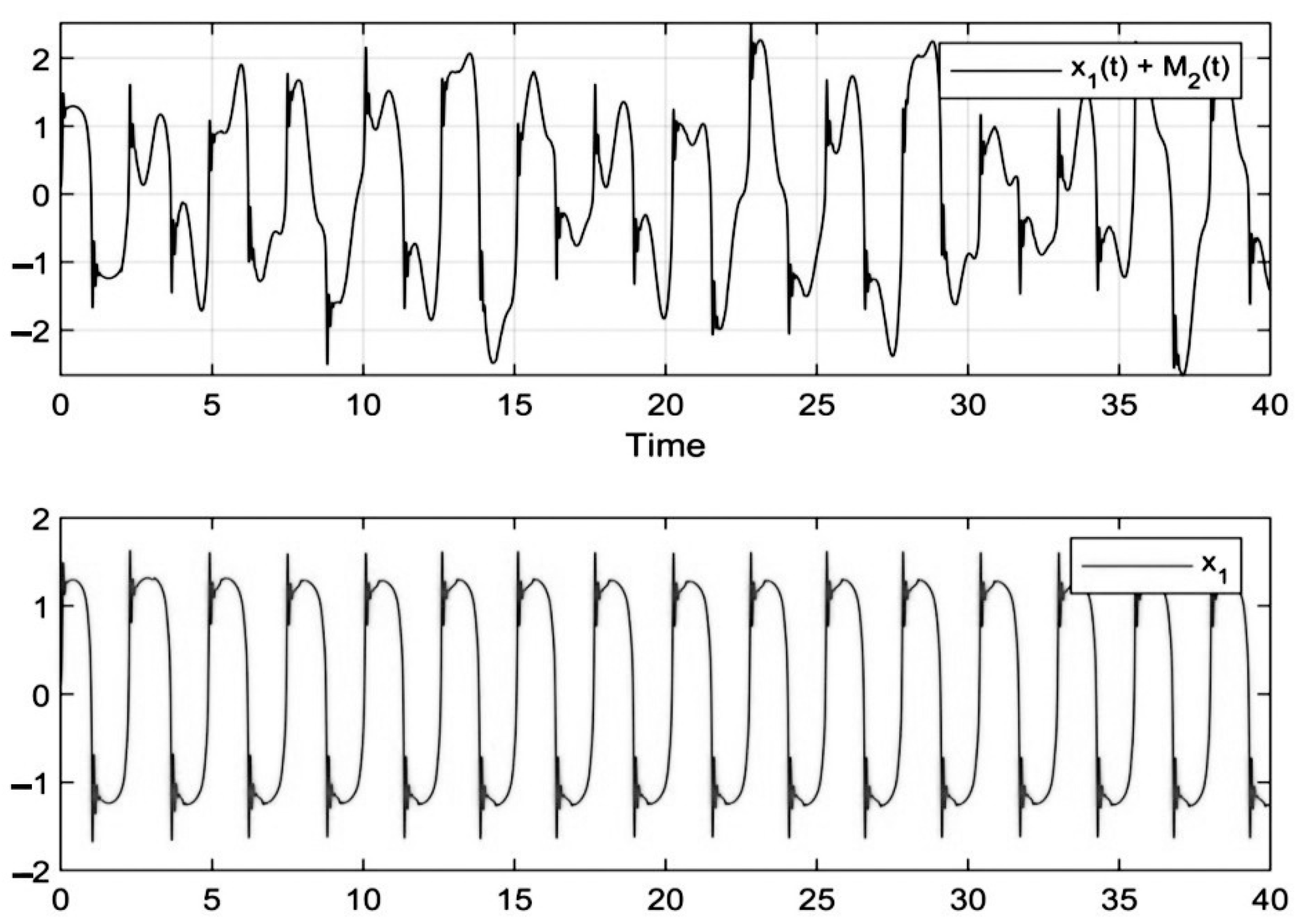
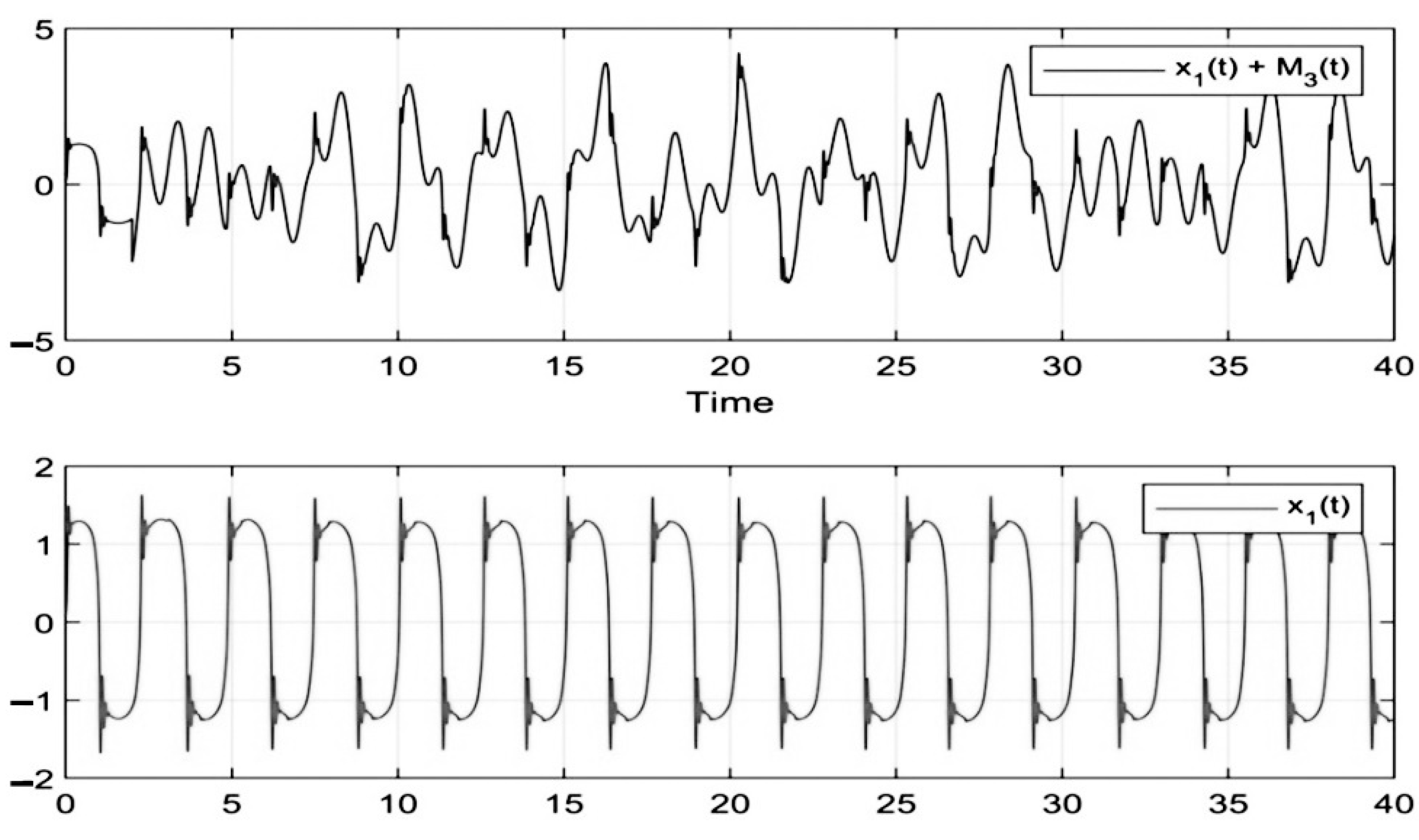
4. Simulation and Results for the Duffing Distributed Fractional Order System
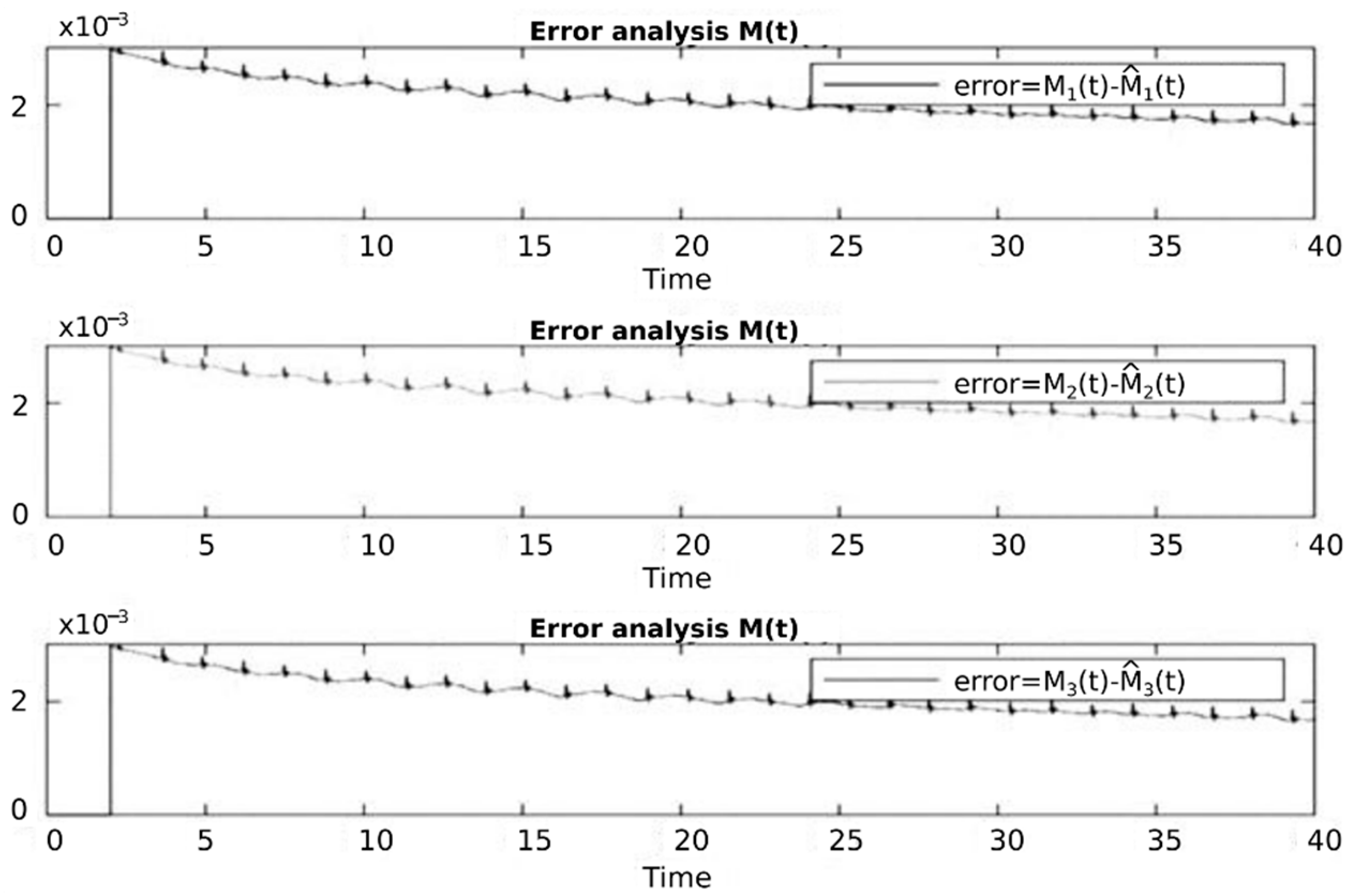
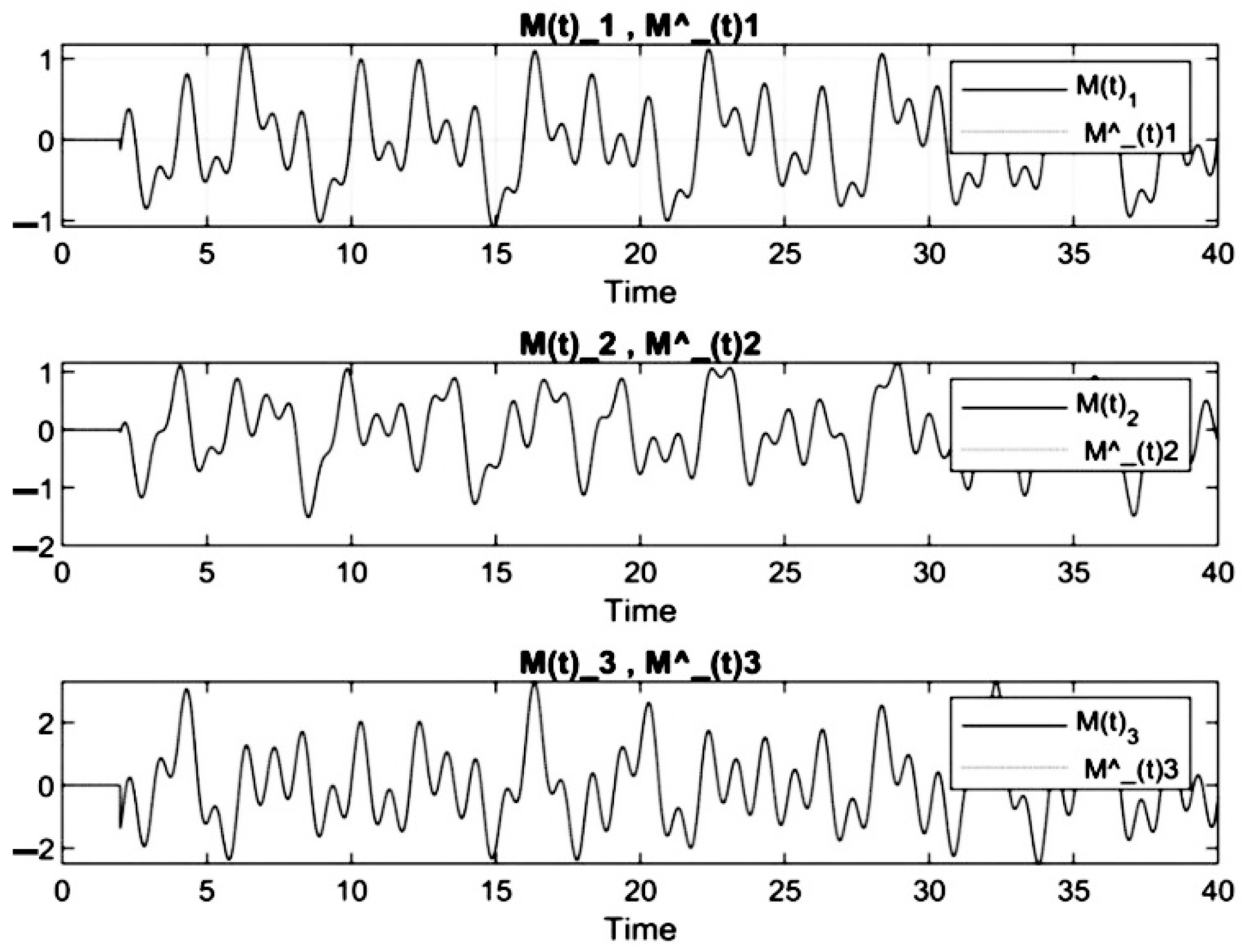
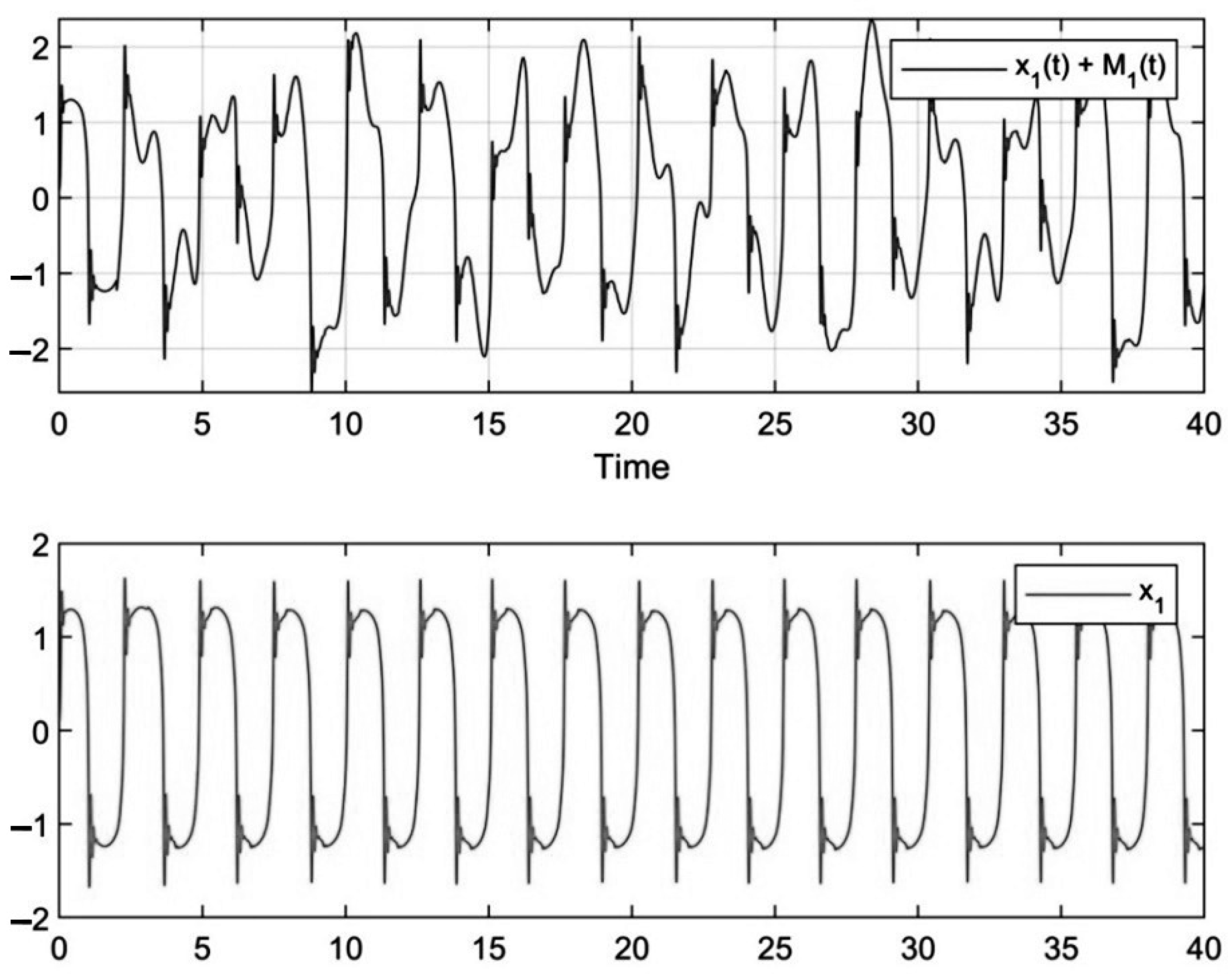
5. The Results of Chaotic Masking Experiments in Secure Communications
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lin, C.M.; Pham, D.H.; Huynh, T.T. Synchronization of chaotic system using a brain-imitated neural network controller and its applications for secure communications. IEEE Access 2021, 9, 75923–75944. [Google Scholar] [CrossRef]
- Li, Y.; Xu, M.; Sun, J.; Liu, N.; Yu, P.; Liu, P. Finite-time Synchronization of Fractional-Order Neural Networks With Time-Varying Delays. In Proceedings of the 2021 11th International Conference on Information Science and Technology (ICIST), Chengdu, China, 21–23 May 2021; pp. 668–672. [Google Scholar] [CrossRef]
- Ha, S.; Liu, H.; Li, S.; Liu, A. Backstepping-based adaptive fuzzy synchronization control for a class of fractional-order chaotic systems with input saturation. Int. J. Fuzzy Syst. 2019, 21, 1571–1584. [Google Scholar] [CrossRef]
- Rahman, Z.A.S.; Jasim, B.H.; Al-Yasir, Y.I.; Abd-Alhameed, R.A.; Alhasnawi, B.N. A new no equilibrium fractional order chaotic system, dynamical investigation, synchronization, and its digital implementation. Inventions 2021, 6, 49. [Google Scholar] [CrossRef]
- Lin, L. Projective synchronization of two coupled Lorenz chaotic systems in predefined time. Int. J. Dyn. Control 2021, 10, 1–11. [Google Scholar] [CrossRef]
- Coronel-Escamilla, A.; Gómez-Aguilar, J.F.; Torres-Jiménez, J.; Mousa, A.A.; Elagan, S.K. Fractional synchronization involving fractional derivatives with nonsingular kernels: Application to chaotic systems. Math. Methods Appl. Sci. 2021, 1–17. [Google Scholar] [CrossRef]
- Mirrezapour, S.Z.; Zare, A.; Hallaji, M. A new fractional sliding mode controller based on nonlinear fractional-order proportional integral derivative controller structure to synchronize fractional-order chaotic systems with uncertainty and disturbances. J. Vib. Control 2021, 28, 1077546320982453. [Google Scholar] [CrossRef]
- Deepika, D. Hyperbolic uncertainty estimator based fractional order sliding mode control framework for uncertain fractional order chaos stabilization and synchronization. ISA Trans. 2021, 123, 76–86. [Google Scholar] [CrossRef] [PubMed]
- Wu, X.; Bao, H.; Cao, J. Finite-time inter-layer projective synchronization of Caputo fractional-order two-layer networks by sliding mode control. J. Frankl. Inst. 2021, 358, 1002–1020. [Google Scholar] [CrossRef]
- Yadav, V.K.; Shukla, V.K.; Das, S. Exponential synchronization of fractional-order complex chaotic systems and its application. Chaos Solitons Fractals 2021, 147, 110937. [Google Scholar] [CrossRef]
- Ding, W.; Patnaik, S.; Sidhardh, S.; Semperlotti, F. Applications of distributed-order fractional operators: A review. Entropy 2021, 23, 110. [Google Scholar] [CrossRef]
- Katsikadelis, J.T. Numerical solution of distributed order fractional differential equations. J. Comput. Phys. 2014, 259, 11–22. [Google Scholar] [CrossRef]
- Li, Z.; Luchko, Y.; Yamamoto, M. Analyticity of solutions to a distributed order time-fractional diffusion equation and its application to an inverse problem. Comput. Math. Appl. 2017, 73, 1041–1052. [Google Scholar] [CrossRef]
- Aminikhah, H.; Sheikhani, A.H.R.; Houlari, T.; Rezazadeh, H. Numerical solution of the distributed-order fractional Bagley-Torvik equation. IEEECAA J. Autom. 2017, 6, 760–765. [Google Scholar] [CrossRef]
- Mashayekhi, S.; Razzaghi, M. Numerical solution of distributed order fractional differential equations by hybrid functions. J. Comput. Phys. 2016, 315, 169–181. [Google Scholar] [CrossRef]
- Najafi, H.S.; Sheikhani, A.R.; Ansari, A. Stability analysis of distributed order fractional differential equations. Abstr. Appl. Anal. 2011, 2011, 175323. [Google Scholar] [CrossRef]
- Yang, Z.; Zheng, X.; Wang, H. A variably distributed-order time-fractional diffusion equation: Analysis and approximation. Comput. Methods Appl. Mech. Eng. 2020, 367, 113118. [Google Scholar] [CrossRef]
- Meerschaert, M.M.; Nane, E.; Vellaisamy, P. Distributed-order fractional diffusions on bounded domains. J. Math. Anal. Appl. 2011, 379, 216–228. [Google Scholar] [CrossRef] [Green Version]
- Aminikhah, H.; RefahiSheikhani, A.; Rezazadeh, H. Stability analysis of distributed order fractional Chen system. Sci. World J. 2013, 2013, 645080. [Google Scholar] [CrossRef] [Green Version]
- Mahmoud, E.E.; Trikha, P.; Jahanzaib, L.S.; Matoog, R.T. Chaos control and Penta-compound combination anti-synchronization on a novel fractional chaotic system with analysis and application. Results Phys. 2021, 24, 104130. [Google Scholar] [CrossRef]
- Khan, A.; Budhraja, M.; Ibraheem, A. Multi-switching dual compound synchronization of chaotic systems. Chin. J. Phys. 2018, 56, 171–179. [Google Scholar] [CrossRef]
- Khan, A.; Khattar, D.; Prajapati, N. Adaptive multi switching combination synchronization of chaotic systems with unknown parameters. Int. J. Dyn. Control. 2018, 6, 621–629. [Google Scholar] [CrossRef]
- Khan, A.; Trikha, P. Compound difference anti-synchronization between chaotic systems of integer and fractional order. SN Appl. Sci. 2019, 1, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Matouk, A.E. Chaotic attractors that exist only in fractional-order case. J. Adv. Res. 2022, 1–10. [Google Scholar] [CrossRef]
- Matouk, A.E. (Ed.) Advanced Applications of Fractional Differential Operators to Science and Technology; IGI Global: Hershey, PA, USA, 2020. [Google Scholar] [CrossRef]
- Matouk, A.E. A Novel Fractional-Order System: Chaos, Hyperchaos and Applications to Linear Control. J. Appl. Comput. Mech. 2021, 7, 701–714. [Google Scholar]
- Baleanu, D.; Zibaei, S.; Namjoo, M.; Jajarmi, A. A nonstandard finite difference scheme for the modeling and nonidentical synchronization of a novel fractional chaotic system. Adv. Differ. Equ. 2021, 2021, 1–19. [Google Scholar] [CrossRef]
- Hassan, T.S.; Elabbasy, E.M.; Matouk, A.E.; Ramadan, R.A.; Abdulrahman, A.T.; Odinaev, I. Routh–Hurwitz Stability and Quasiperiodic Attractors in a Fractional-Order Model for Awareness Programs: Applications to COVID-19 Pandemic. Discret. Dyn. Nat. Soc. 2022, 2022, 1939260. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Yousefpour, A.; Munoz-Pacheco, J.M.; Moroz, I.; Wei, Z.; Castillo, O. A new multi-stable fractional-order four-dimensional system with self-excited and hidden chaotic attractors: Dynamic analysis and adaptive synchronization using a novel fuzzy adaptive sliding mode control method. Appl. Soft Comput. 2020, 87, 105943. [Google Scholar] [CrossRef]
- Kumar, S.; Matouk, A.E.; Chaudhary, H.; Kant, S. Control and synchronization of fractional-order chaotic satellite systems using feedback and adaptive control techniques. Int. J. Adapt. Control. Signal Process. 2021, 35, 484–497. [Google Scholar] [CrossRef]
- Matouk, A.E.; Khan, I. Complex dynamics and control of a novel physical model using nonlocal fractional differential operator with singular kernel. J. Adv. Res. 2020, 24, 463–474. [Google Scholar] [CrossRef]
- Djenina, N.; Ouannas, A.; Batiha, I.M.; Grassi, G.; Oussaeif, T.E.; Momani, S.A. Novel Fractional-Order Discrete SIR Model for Predicting COVID-19 Behavior. Mathematics 2022, 10, 2224. [Google Scholar] [CrossRef]
- Khan, A.; Jahanzaib, L.S.; Trikha, P. Secure communication: Using parallel synchronization technique on novel fractional order chaotic system. IFAC-PapersOnLine 2020, 53, 307–312. [Google Scholar] [CrossRef]
- Yu, F.; Liu, L.; He, B.; Huang, Y.; Shi, C.; Cai, S.; Wan, Q. Analysis and FPGA realization of a novel 5D hyperchaotic four-wing memristive system, active control synchronization, and secure communication application. Complexity 2019, 2019, 4047957. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Zhang, W.; Su, H.; Yang, J. Observer-based synchronization of chaotic systems satisfying incremental quadratic constraints and its application in secure communication. IEEE Trans. Syst. Man Cybern. Syst. 2018, 50, 5221–5232. [Google Scholar] [CrossRef]
- Samimi, M.; Majidi, M.H.; Khorashadizadeh, S. Secure communication based on chaos synchronization using brain emotional learning. AEU Int. J. Electron. Commun. 2020, 127, 153424. [Google Scholar] [CrossRef]
- Luo, J.; Qu, S.; Xiong, Z.; Appiagyei, E.; Zhao, L. Observer-based finite-time modified projective synchronization of multiple uncertain chaotic systems and applications to secure communication using DNA encoding. IEEE Access 2019, 7, 65527–65543. [Google Scholar] [CrossRef]
- Khan, A.; Jahanzaib, L.S.; Khan, T.; Trikha, P. Secure communication: Using fractional matrix projective combination synchronization. In AIP Conference Proceedings; AIP Publishing LLC: Melville, NY, USA, 2020; Volume 2253, p. 020009. [Google Scholar]
- Aguila-Camacho, N.; Duarte-Mermoud, M.A.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Shu, M.; Zhang, F.; Leng, S.; Sun, X. Secure communication of fractional complex chaotic systems based on fractional difference function synchronization. Complexity 2019, 2019, 7242791. [Google Scholar] [CrossRef] [Green Version]
- Chen, W.; Dai, H.; Song, Y.; Zhang, Z. Convex Lyapunov functions for stability analysis of fractional order systems. IET Control. Theory Appl. 2017, 11, 1070–1074. [Google Scholar] [CrossRef]
- Matignon, D. Stability results for fractional differential equations with applications to control processing. Comput. Eng. Syst. Appl. 1996, 2, 963–968. [Google Scholar]
- Chen, X.; Park, J.H.; Cao, J.; Qiu, J. Sliding mode synchronization of multiple chaotic systems with uncertainties and disturbances. Appl. Math. Comput. 2017, 308, 161–173. [Google Scholar] [CrossRef]
- Chen, J.; Li, C.; Yang, X. Chaos synchronization of the distributed-order Lorenz system via active control and applications in chaotic masking. Int. J. Bifurc. Chaos 2018, 28, 1850121–1850882. [Google Scholar] [CrossRef]
- KekhaJavan, A.A.; Shoeibi, A.; Zare, A.; HosseiniIzadi, N.; Jafari, M.; Alizadehsani, R.; Nahavandi, S. Design of Adaptive-Robust Controller for Multi-State Synchronization of Chaotic Systems with Unknown and Time-Varying Delays and Its Application in Secure Communication. Sensors 2021, 21, 254. [Google Scholar] [CrossRef] [PubMed]
- Kim, V.; Parovik, R. Mathematical model of fractional duffing oscillator with variable memory. Mathematics 2020, 8, 2063. [Google Scholar] [CrossRef]
- KekhaJavan, A.; Zare, A.; Alizadehsani, R. Juan Manuel Gorriz.Medical Images Encryption Based on Adaptive-Robust Multi-Mode Synchronization of Chen Hyper-Chaotic Systems. Sensors 2022, 21, 3925. [Google Scholar]
- KekhaJavan, A.; Zare, A.; Alizadehsani, R.; Balochian, S. Robust Multi-Mode Synchronization of Chaotic Fractional Order Systems in the Presence of Disturbance, Time Delay and Uncertainty with Application in Secure Communications. Big Data Cogn. Comput. 2022, 6, 51. [Google Scholar] [CrossRef]
- Jahanshahi, H.; Sajjadi, S.S.; Bekiros, S.; Aly, A.A. On the development of variable-order fractional hyperchaotic economic system with a nonlinear model predictive controller. Chaos Solitons Fractals 2021, 144, 110698. [Google Scholar] [CrossRef]




| Reference | Disturbance | Uncertainty | Type Order | Time Delay | Unknown Parameters |
|---|---|---|---|---|---|
| [45] | ✓ | Time varying-unknown | Integer-order | ✓ | ✓ |
| [47] | ✓ | × | Integer-order | × | × |
| [38] | × | × | Fractional-order | ✓ | ✓ |
| [48] | ✓ | Time varying-unknown | Fractional-order | ✓ | ✓ |
| [36] | × | × | Distributed Fractional Order | × | × |
| [19] | ✓ | × | Distributed Fractional Order | × | × |
| Proposed method | ✓ | unknown | Distributed Fractional Order | ✓ | ✓ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kekha Javan, A.A.; Zare, A.; Alizadehsani, R. Multi-State Synchronization of Chaotic Systems with Distributed Fractional Order Derivatives and Its Application in Secure Communications. Big Data Cogn. Comput. 2022, 6, 82. https://doi.org/10.3390/bdcc6030082
Kekha Javan AA, Zare A, Alizadehsani R. Multi-State Synchronization of Chaotic Systems with Distributed Fractional Order Derivatives and Its Application in Secure Communications. Big Data and Cognitive Computing. 2022; 6(3):82. https://doi.org/10.3390/bdcc6030082
Chicago/Turabian StyleKekha Javan, Ali Akbar, Assef Zare, and Roohallah Alizadehsani. 2022. "Multi-State Synchronization of Chaotic Systems with Distributed Fractional Order Derivatives and Its Application in Secure Communications" Big Data and Cognitive Computing 6, no. 3: 82. https://doi.org/10.3390/bdcc6030082
APA StyleKekha Javan, A. A., Zare, A., & Alizadehsani, R. (2022). Multi-State Synchronization of Chaotic Systems with Distributed Fractional Order Derivatives and Its Application in Secure Communications. Big Data and Cognitive Computing, 6(3), 82. https://doi.org/10.3390/bdcc6030082







