A Better Mechanistic Understanding of Big Data through an Order Search Using Causal Bayesian Networks

Abstract

Every year, biomedical data is increasing at an alarming rate and is being collected from many different sources, such as hospitals (clinical Big Data), laboratories (genomic and proteomic Big Data), and the internet (online Big Data). This article presents and evaluates a practical causal discovery algorithm that uses modern statistical, machine learning, and informatics approaches that have been used in the learning of causal relationships from biomedical Big Data, which in turn integrates clinical, omics (genomic and proteomic), and environmental aspects. The learning of causal relationships from data using graphical models does not address the hidden (unknown or not measured) mechanisms that are inherent to most measurements and analyses. Also, many algorithms lack a practical usage since they do not incorporate current mechanistic knowledge. This paper proposes a practical causal discovery algorithm using causal Bayesian networks to gain a better understanding of the underlying mechanistic process that generated the data. The algorithm utilizes model averaging techniques such as searching through a relative order (e.g., if gene A is regulating gene B, then we can say that gene A is of a higher order than gene B) and incorporates relevant prior mechanistic knowledge to guide the Markov chain Monte Carlo search through the order. The algorithm was evaluated by testing its performance on datasets generated from the ALARM causal Bayesian network. Out of the 37 variables in the ALARM causal Bayesian network, two sets of nine were chosen and the observations for those variables were provided to the algorithm. The performance of the algorithm was evaluated by comparing its prediction with the generating causal mechanism. The 28 variables that were not in use are referred to as hidden variables and they allowed for the evaluation of the algorithm’s ability to predict hidden confounded causal relationships. The algorithm’s predicted performance was also compared with other causal discovery algorithms. The results show that incorporating order information provides a better mechanistic understanding even when hidden confounded causes are present. The prior mechanistic knowledge incorporated in the Markov chain Monte Carlo search led to the better discovery of causal relationships when hidden variables were involved in generating the simulated data.

1. Introduction

The size of biomedical data, as well as the rate at which it is being produced, is increasing dramatically. The biomedical data is also being collected from many different sources, such as hospitals (clinical Big Data), laboratories (genomic and proteomic Big Data), and the internet (online Big Data). There is a growing need for statistically predictive causal discovery algorithms that incorporate the biological knowledge gained from modern statistical, machine learning, and informatics approaches used in the learning of causal relationships from biomedical Big Data comprised of clinical, omics (genomic and proteomic), and environmental components.

While earlier available studies focus on statistical methods to infer causality [1,2,3,4], recent statistical machine learning methods have been introduced which aim at analyzing big datasets [5,6,7,8,9,10,11,12,13,14,15,16,17,18]. However, given many different types of clinical, genomic, and environmental data, it is rather uncommon to see statistical machine learning methods that utilize prior knowledge relevant to the mechanisms behind the phenomena which generates those different data types. The statistical machine learning methods that recognize that there are many variables which are not collected in the data, but are still related to the mechanisms which produced the data (hidden variables), are also limited. Furthermore, there is a lack of statistical methods that evaluate how well the methods perform at inferring causality when hidden confounded variables are present.

There are many aspects of causality, from its representation (syntax) to its semantics and many different related concepts to causality, e.g., theory of inferred causation, counterfactual analyses, incomplete interventions, confounding effect, etc. [1,9]. However, in learning mechanisms from a phenomenon with collected data, the goal is to infer cause and effect relationships among complicated knitted random variables in the dataset with reasonable confidence.

Thus, the focus in this study is on the learning of causal relationships among random variables in the collected data, particularly when using causal Bayesian networks (CBNs). CBNs are directed acyclic graphs in which each arc is interpreted as a direct causal influence between a parent node and a child node relative to the other nodes in the network [19]. CBNs consist of a structure (such as an example in Figure 1) and a set of probabilities that parameterize said structure (not shown). In general, for each variable there is a conditional probability of that variable given the states of its direct causes. Thus, the probability associated with Gliomas Grade is P (Gliomas Grade|PTNP1, LPL, EGFR). That is, we provide the probability distribution over the values of the Gliomas Grade conditioned on each of the possible expression levels of the genes PTNP1, LPL, and EGFR. For variables that have no direct causes in the network, a prior probability is specified. The causal Markov condition [9] specifies the conditional independence relationships which are represented by a causal network: Let X and Y be variables. Suppose that Y is neither a direct nor an indirect effect of X. Then X is independent of Y, conditioned on any state of the direct causes of X. The causal Markov condition permits the joint distribution of the n variables in a CBN to be factored as follows [19]:

$$P(x_1,x_2,\dots ,x_n|K)={\displaystyle \prod _{i=1}^{n}P(x_i|{\pi }_i,K)}$$

(1)

where x_i denotes a state of variable X_i, π_i denotes a joint state of the parents of X_i, and K denotes background knowledge (prior probability). Since the initial research for a general Bayesian formulation for learning causal structure (including latent variables) and parameters from observational data using CBN [20,21], Bayesian causal discovery has become an active field of research in which numerous advances have been made [1,7,8,10,22,23].

CBNs have been suitable in analyzing Big Data sets consisting of different types of large data including clinical, genomic, and environmental data [8,12,23,24,25,26,27,28,29]. Such causal statistical models help to provide a more comprehensive understanding of human physiology and disease. More importantly, CBNs have been used as a natural way to express “causal” knowledge as a graph using nodes (representing random variables) and arcs (representing “causal” relationships). Indeed, there are many causal models made from existing causal knowledge—from simple and intuitive causal models (e.g., a model to predict whether neighbor is out [30], a sprinkler model [1], etc.), to expert causal models (e.g., a multiple diseases model [31], an ALARM monitoring system [32], etc.). The learning of causal relationships from data has been discussed in different articles [1,9,33], and this especially holds true for cases where researchers have used Bayesian Networks for learning structures [29,34,35,36,37]. Also, other algorithms, such as PC [9], K2 [5], and more recently the Bayesian Inference for Directed Acyclic Graphs (BiDAG) [12], have been used to learn causal relationships from data.

Earlier structure learning methods concentrated on model selection, where we select a model M* from

$$M^{*}=argma{x}_{i}P\left(D|M_i\right)$$

(2)

or

$$M^{*}=argma{x}_{i}P\left(M_i|D\right)$$

(3)

where we assume we have p number of mutually exclusive models, $M_1,M_2,\dots ,M_p$ [38]. Later methods incorporated model averaging [29], where we summarize how likely a feature F that is found in a subset of the models and is defined by a set of indices, $f\subseteq \left\{1,2,\dots ,p\right\}$ where f includes those indices of the models where F is observed. Thus, in model averaging, we calculate the probability of a feature F as the following:

$${{\displaystyle \sum }}_{f}P\left(D|M_f\right)$$

(4)

or

$${{\displaystyle \sum }}_{f}PP\left(M_f|D\right)$$

(5)

However, most of the structure learning methods do not address hidden variables. Since we cannot observe all relevant variables in a natural phenomenon, to better learn the underlying mechanistic process from Big Data, we need to address and evaluate the learning of causal relationships with hidden variables.

In this paper, we show that searching through the order (we describe further about what we mean by “order” in the method section) of variables in CBNs can help provide a better understanding of the underlying mechanistic process that generated the data even in the presence of hidden variables. In addition, we propose a novel algorithm in searching through the order (we call it the PrePrior algorithm) which evidences a promising performance when attempting to learn the underlying mechanistic process from data containing hidden variables. The algorithm utilizes model averaging techniques such as searching through a relative order (e.g., if gene A is regulating gene B, then we can say that gene A is in a higher order than gene B) and incorporates relevant prior mechanistic knowledge to guide the Markov chain Monte Carlo (MCMC) search through the order.

2. Methods

Given a CBN structure S and a dataset D, the Bayesian scoring method that assesses how well the structure fits the given data can be calculated using a closed form [39]:

$$P(D|S)={{\displaystyle \prod }}_{i=1}^n{{\displaystyle \prod }}_{j=1}^{q_i}\frac{\Gamma \left({N^{\prime }}_{ij}\right)}{\Gamma \left({N^{\prime }}_{ij}+N_{ij}\right)}{{\displaystyle \prod }}_{k=1}^{r_i}\frac{\Gamma \left({N^{\prime }}_{ijk}+N_{ijk}\right)}{\Gamma \left({N^{\prime }}_{ijk}\right)}$$

(6)

In the above scoring method, Dirichlet uniform parameter priors are used and parameter independence is assumed [40]; n represents the number of variables in the structure; q_i represents the number of configurations of the parents for a given variable Xi; and r_i represents the total amount of states for a variable Xi. For example, if Xi is a binary random variable and it has two binary random variables as direct causes (parents), then r_i is equivalent to two and q_i is equivalent to four. N_ijk represents the counts for a given variable Xi under a given parent configuration (indexed by j) and a given state (indexed by k) for variable Xi. N’_ijk represents the Dirichlet uniform prior, which in this case may be calculated as the following:

$$N{’}_{ijk}=\frac{1}{r_i{q}_i}$$

(7)

The number of possible structures increases exponentially with the number of variables, and so the above formula is sufficient for determining the best BN when the number of variables in the CBN is small. However, when the number of variables is large, it becomes impossible to determine the best structure in this manner. The problem of finding the best CBN is NP-hard [41], and thus it is not always possible to find the best CBN that fits the data. This is the key limitation of model selection methods [38] when used as a means of extending our current mechanistic understanding through the learning of causal relationships from data.

The algorithm we introduce in this paper utilizes model averaging techniques, such as searching through a relative order [29] (e.g., cause is in a higher order than effect) and incorporating prior mechanistic knowledge to guide the MCMC (Markov Chain Monte Carlo) search through the order. An order describes the relationships between variables based on describing whether a variable can be a direct cause (parent) for another variable.

Definition 1.

(Order $\succ$): $X_i\succ X_j$ iff $X_j\notin P{a}_{Xi}$.

With the above definition of the order, we are stating that X_i is considered to be of a higher order than X_j if, and only if, X_j cannot be found in the group of direct causes (parents) of X_i. A potential ordering for a list of three variables is <X₁, X₂, X₃>. This order implies that X₁ can be a direct cause (parent) of X₂ and/or X₃, but X₂ and X₃ cannot be direct causes (parents) of X₁. Similarly, X₂ can be a direct cause (parent) of X₃, but X₃ cannot be a direct cause (parent) of X₂. Note that any given order of random variables can better summarize mechanistic (causal) relationships than just one structure. For example, an order <X₁, X₂, X₃> includes the following three structures (Figure 2):

Orders are useful because, in a manner similar to structures, they can be scored. Since an order represents a set of structures, it may be scored by summing over all structures consistent with the given order. This method for scoring an order is not efficient because it would require that we have a score for all structures that meet a given order. With that being the case, we consider an alternative method for scoring orders presented by Friedman and Koller [29], which uses the direct cause (parent) sets of variables. The equation for this scoring procedure is:

$$P(D|O)={{\displaystyle \prod }}_{i=1}^n{{\displaystyle \sum }}_{U\in U_{i,o}}{{\displaystyle \prod }}_{j=1}^{q_{i,U}}\frac{\Gamma \left({N^{\prime }}_{ij}\right)}{\Gamma \left({N^{\prime }}_{ij}+N_{ij}\right)}{{\displaystyle \prod }}_{k=1}^{r_i}\frac{\Gamma \left({N^{\prime }}_{ijk}+N_{ijk}\right)}{\Gamma \left({N^{\prime }}_{ijk}\right)}$$

(8)

The above equation is an expansion of Bayesian scoring presented by Heckerman [33]. Here, O represents an ordering, U_i,o represents the possible parent-sets for a given variable under a given ordering, and q_i,U represents the possible configurations of the parents for a variable i within a parent-set U. All other parameters in the equation are represented in the same manner as in Equation (6).

The benefit in scoring orders over scoring structures is that in the case where one is dealing with two or more variables, there are more structures than orders. For example, when the number of variables equals four, there are 543 structures but only 24 different orders.

An MCMC search is used to search through the orders. At any given MCMC search process, we have a current order (denote it as o) and a proposed order (denote it as o′), and we decide whether the proposed order will take the place of the current order with a probability that is returned by a decision function $f\left(o,o^{\prime }\right)$. A proposed order is generated by either applying a local perturbation (i.e., swapping two variables in an order: for example, <X₁, X₂…X_i…X_j…X_n> to <X₁, X₂…X_j…X_i…X_n>), or a global perturbation (i.e., aka a cutting the deck, swapping groups of variables in an order: for example, <X₁, X₂…X_i, X_i+1…X_n> to < X_i+1…X_n, X₁, X₂…X_i >). Initially, a random order is generated.

Friedman and Koller [29] propose the following two algorithms for MCMC search with different $f\left(o,o^{\prime }\right)$:

o

Random Algorithm

▪

Uses $f\left(o,o^{\prime }\right)=min\left[1,\frac{P(D|o^{\prime })}{P(D|o)} \right]$

o

Prior Algorithm

▪

Uses $f\left(o,o^{\prime }\right)=min\left[1,\frac{P(D|o^{\prime })P(o^{\prime }|o)}{P(D|o)P\left(o|o^{’}\right)} \right]$

where o, o′, and D represent the current order that we are considering: a proposed order and a dataset, respectively.

We further propose a new algorithm called the PrePrior Algorithm with the following MCMC search with the same $f\left(o,o^{\prime }\right)$ as the Prior algorithm with an additional step:

o

PrePrior Algorithm

▪

Uses $P(o^{\prime }|o)$ based on user defined prior to sample o′

▪

Uses $f\left(o,o^{\prime }\right)=min\left[1,\frac{P(D|o^{\prime })P(o^{\prime }|o)}{p(D|o)P\left(o|o^{’}\right)} \right]$

Note that PrePrior algorithm generates proposed orders based on the prior, $P\left(o\right)$ and $P\left(o^{\prime }\right)$ that the user provides.

User’s Prior of an Order. To specify a prior of mechanistic causal knowledge in terms of an order o (if X is known to cause Y, we say X has a higher order than Y, i.e., $X\succ Y$) or $P\left(o\right)$, we assume the following:

i.

If no prior is provided, a uniform prior of any given order is assumed. For example, for a pairwise order of X and Y, if no prior is provided then $P\left(X\prec Y\right)=P\left(Y\prec X\right)=0.5$. In general, for n variables a uniform prior for any order o is $P\left(o\right)=\frac{1}{n!}$.

ii.

The prior of an order is specified as the probability of how likely it is compared to the uniform prior. For example, if prior publications show gene Y is regulating gene X, a user might specify $P\left(X\prec Y\right)=0.9$ and if there have been studies suggesting that gene Z is regulating gene W, a user might specify $P\left(W\prec Z\right)=0.6$.

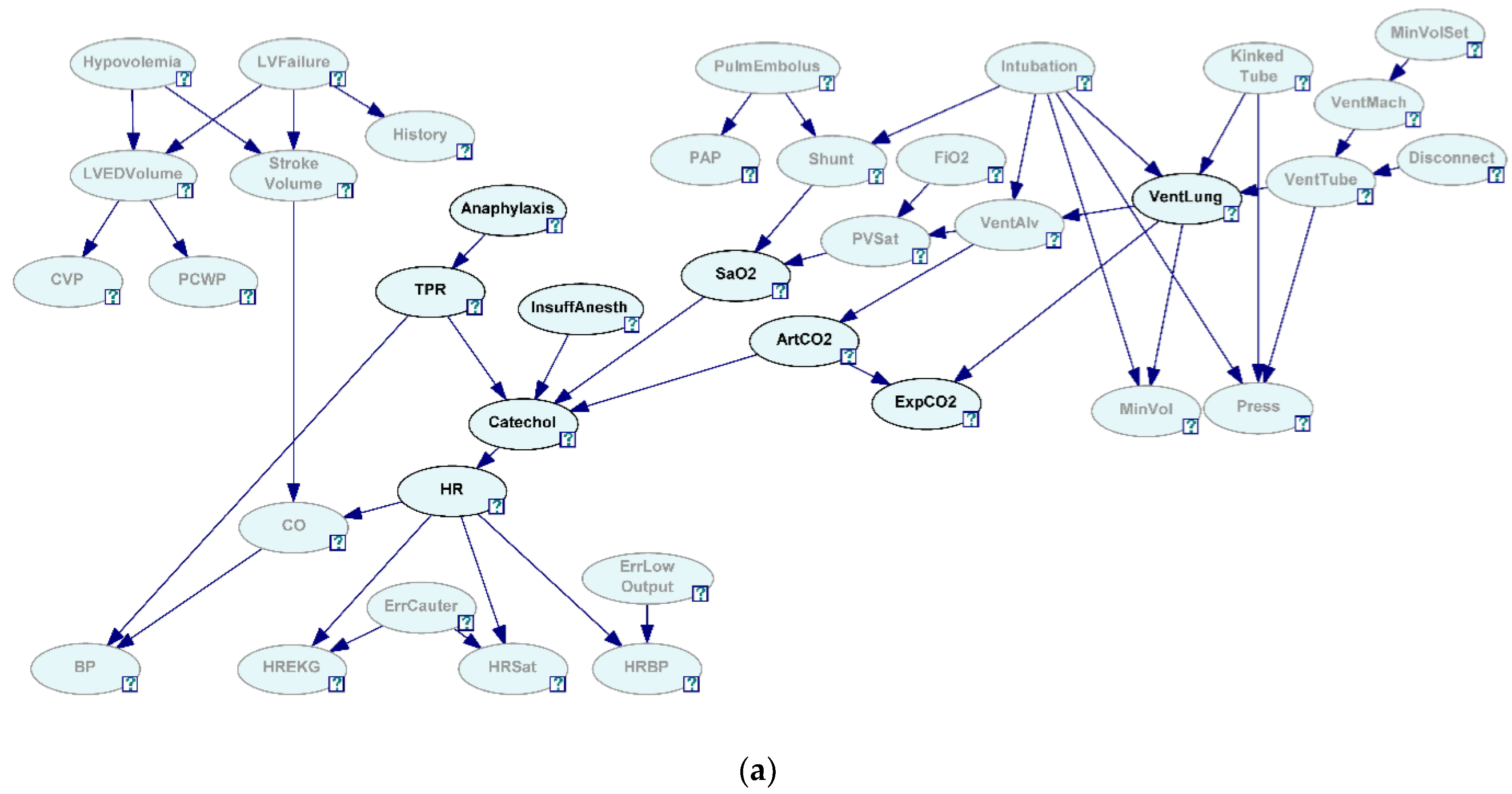
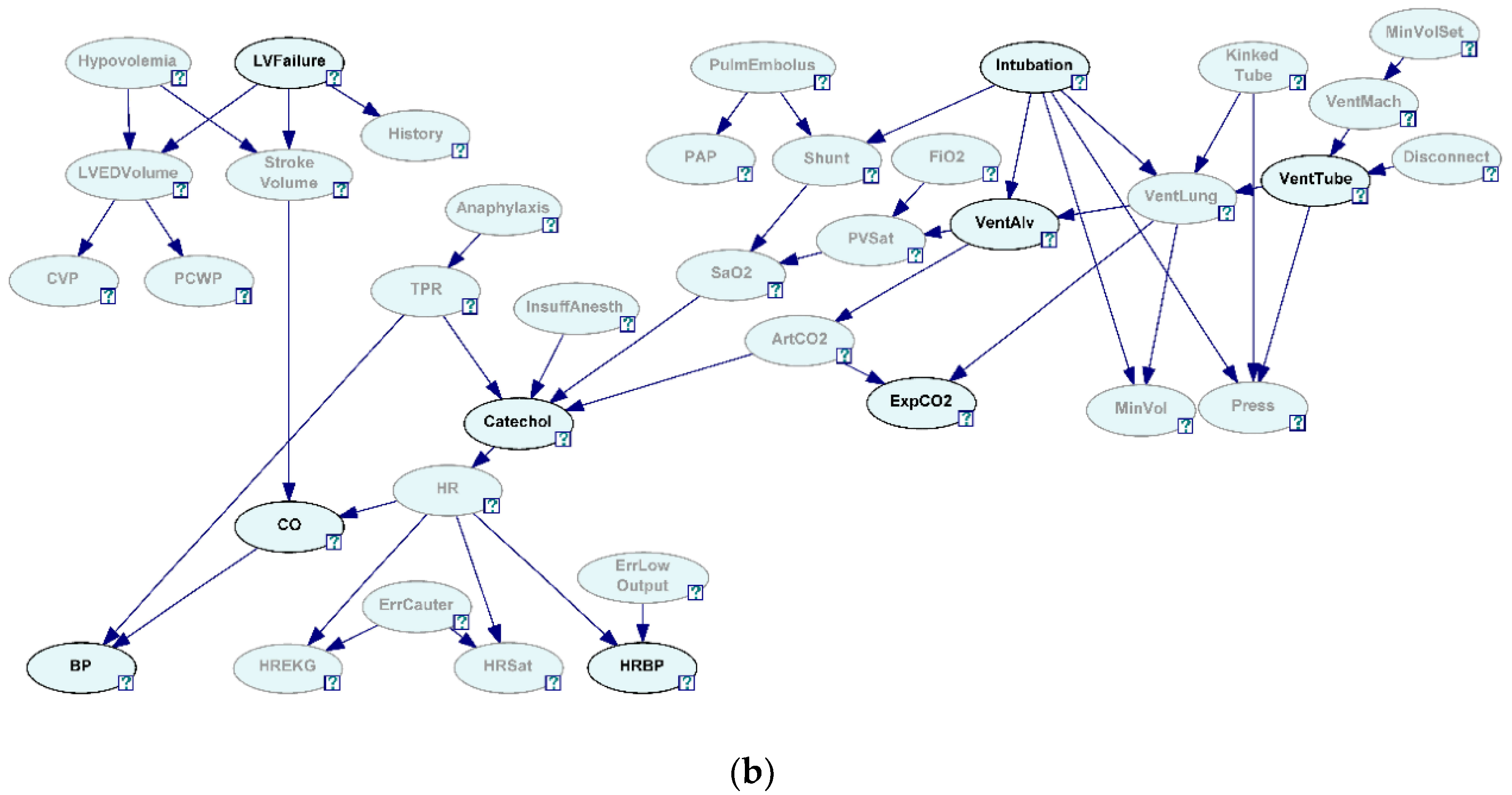
For mechanism discovery, the correct discovery of the generating structure is the most important aspect of the algorithm. Datasets consisting of 50 and 1000 simulated observational cases from the ALARM Bayesian network were generated [27]. To see how well the algorithm correctly discovered the generating structure in the presence of hidden variables, we have selected two sets of nine variables each selected from 37 variables in the network. The first variable set is referred to as Close 9 variables (C9) and was created by selecting variables that were closely situated in the network (Figure 3a, all the grayed-out variables are hidden and not selected). The second variable set is referred to as Sparse 9 variables (S9) and was created by selecting variables that were relatively situated further in the network (Figure 3b, all the grayed-out variables are hidden and not selected).

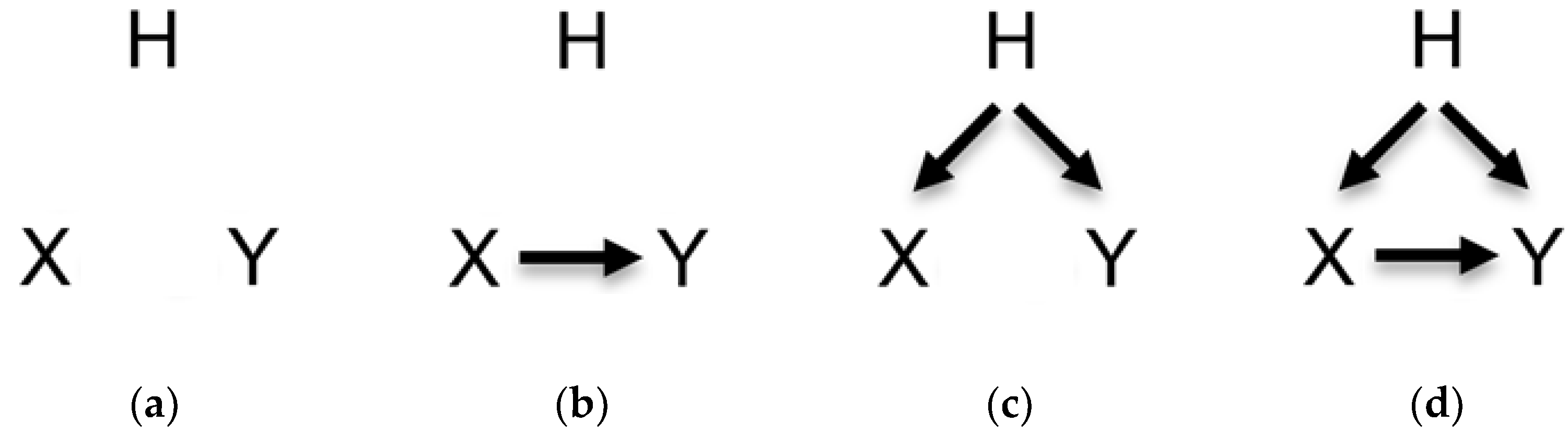
Another reason we have selected these nine variables was to see how well the causal discovery algorithms were predicting the four pairwise relationships shown in Figure 4. Distinguishing these four pairwise relationships is the first step in better understanding the mechanistic process involved in generating these datasets.

Different numbers of pairwise causal relationships are found in the Close 9 variables (C9) and Sparse 9 variables (S9) (

Table 1. Number of pairwise causal relationships in Close 9 variables (C9) and Sparse 9 variables (S9). H represents a variable that is shaded. (a) Close 9 variables (C9). (b) Sparse 9 variables (S9).

(a)
Pairwise Relationship	ØX Y	ØX→Y	HX Y	HX→Y
Count	14	8	4	10
(b)
Pairwise Relationship	ØX Y	ØX→Y	HX Y	HX→Y
Count	7	20	6	3

). For example, in C9, TPR and VentLung are not confounded nor causally related (denoted as Ø_{X Y} in Figure 4a), and TPR and HR are not confounded and causally related (denoted as Ø_X→Y in Figure 4b). In S9, ExpCO2 and Catechol are confounded but not causally related (denoted as H_{X Y} in Figure 4c, ArtCO2 being a variable as H), and ArtCO2 and VentAlv are confounded and causally related (denoted as H_X→Y in Figure 4d where VentLung takes the role of H).

Two datasets were generated from each of the two sets of variables. Two of the datasets had 50 observational cases each and were named D50C9 and D50S9 because they were generated by the C9 and S9 sets of variables, respectively. The other two datasets had 1000 observational cases each and were named D1KC9 and D1KS9 because they were generated by the C9 and S9 sets of variables, respectively. Many biological mechanistic networks are not completely connected, i.e., each variable has limited (e.g., less than five) causes. As a result, we have limited the number of possible parents to five and scored all the possible orders using Equation (8). It took roughly one month to score all of the possible orders for the four datasets. The dataset of results is referred to as Dataset Global BDe Best Order. Dataset Global BDe Best Order contains information on all of the scores for all of the possible orders, and therefore we know which is the best order (and the best Bayesian networks structure) that will be identified if the BDe metric [5] (similar to Equation (8)) is used given the dataset.

The Random, Prior, and PrePrior algorithms were independently ran three times on D50C9 and D50S9 for 1 h, 2 h, and 4 h; and on D1KC9 and D1KS9 for 2 h, 4 h, and 16 h. We have used five Linux machines to run in parallel of 522 total h (over 21 equivalent days) of runs.

The predictive performance is calculated as a pairwise causal distance from either generating the structure (denoted it as S_G and shown in Figure 5) or the Dataset Global BDe Order. For each variable pair of X and Y, let the underlying relationship between X and Y be denoted as R_X,Y where $R_{X,Y}\in \left\{X\to Y,X\leftarrow Y, X\left(none\right)Y\right\}$. Let the likelihood score of R_X,Y assessed from either the generating structure and Dataset Global BDe Order as P_G(R_X,Y) and P_G(D|R_X,Y) respectively, where $D\in \left\{\mathrm{D}50\mathrm{C}9, \mathrm{D}50\mathrm{S}9, \mathrm{D}1\mathrm{KC}9, \mathrm{D}1\mathrm{KS}9\right\}.$ Note that we calculate.

$$P_G\left(R_{X,Y}\right)=\left\{\begin{array}{c}1 if R_{X,Y}\in S_G \\ 0 if R_{X,Y}\notin S_G\end{array}\right.$$

(9)

and

$$P_G\left(D|R_{X,Y}\right)={{\displaystyle \sum }}_{o\in O}{{\displaystyle \sum }}_{S_o}{\delta }_{S_o}P\left(D|S_o\right)P(D|o)$$

(10)

$${\delta }_{S_o}=\left\{\begin{array}{c}1 if R_{X,Y}\in S_o \\ 0 if R_{X,Y}\notin S_o\end{array}\right.$$

(11)

where O is the set of orders that satisfy $\frac{{{\displaystyle \sum }}_{O}P(D|O)}{{{\displaystyle \sum }}_{{\mathsf{\Phi }}_O}P(D|{\mathsf{\Phi }}_O)}>0.99$ and S_o is the set of structures that satisfy an order $o\in O$ and $\frac{{{\displaystyle \sum }}_{S_o}P(D|S_o)}{{{\displaystyle \sum }}_{{\mathsf{\Phi }}_{S_o}}P(D|{\mathsf{\Phi }}_{S_o})}>0.99$ for all possible orders (denote them as ${\mathsf{\Phi }}_O$) and all possible structures that satisfies an order $o\in O$ (denote them as ${\mathsf{\Phi }}_{S_o}$).

Additionally, we calculate P^S_G (D|R_X,Y).

$$P^S{}_G\left(D|R_{X,Y}\right)={{\displaystyle \sum }}_S{\delta }_{S}P\left(D|S\right)$$

(12)

$${\delta }_S=\left\{\begin{array}{c}1 if R_{X,Y}\in S \\ 0 if R_{X,Y}\notin S\end{array}\right.$$

(13)

S is the set of structures that satisfies $\frac{{{\displaystyle \sum }}_{S}P(D|S)}{{{\displaystyle \sum }}_{{\mathsf{\Phi }}_S}P(D|{\mathsf{\Phi }}_S)}>0.99$ for all possible structures (denote them as ${\mathsf{\Phi }}_S$) from all possible orders.

We use P^S_G(D|R_X,Y) and P_G(D|R_X,Y) for all X and Y to generate a consensus causal structure by drawing arcs between X and Y with the thickest arc when P^S_G(D|R_X,Y) or P_G(D|R_X,Y) are above 0.9999, and with the thinnest arc when P^S_G(D|R_X,Y) or P_G (D|R_X,Y) are close to 0.0001. If P^S_G(D|X→Y) and P^S_G(D|Y→X) both are less than 0.0001, then no arcs are drawn between X and Y.

We first compare generating causal structure and Dataset Global BDe Best Order by calculating the following:

$${{\displaystyle \sum }}_{R_{X,Y}}\left(P_G\left(R_{X,Y}\right)-P_G\left(D|R_{X,Y}\right)\right)$$

(14)

$${{\displaystyle \sum }}_{R_{X,Y}}\left(P_G\left(R_{X,Y}\right)-P^S{}_G\left(D|R_{X,Y}\right)\right)$$

(15)

These results will show us how the BDe metric approximates the generated causal structure given the generated datasets. In addition to comparing the predictive ability of these algorithms, we compared the causal structure predictive ability of the algorithms that use BDe metric with the Dataset Global BDe Best Order.

We report each Dataset Global BDe Best Order prediction using a Markov blanket of a variable (Catechol) appearing both from Close 9 variables (C9) and Sparse 9 variables (S9) and compared that with the Markov blanket of the Catechol from the generating structure.

Denote the probability of R_X,Y predicted from an algorithm as P_A(D|R_X,Y) and P^S_A(D|R_X,Y). Note that P_A(D|R_X,Y) is calculated the same way we calculated P_G(D|R_X,Y) described above. We report the distance from the generating structure as

$${{\displaystyle \sum }}_{R_{X,Y}}\left(P_G\left(R_{X,Y}\right)-P_A\left(D|R_{X,Y}\right)\right)$$

(16)

$${{\displaystyle \sum }}_{R_{X,Y}}\left(P_G\left(R_{X,Y}\right)-P^S{}_A\left(D|R_{X,Y}\right)\right)$$

(17)

and the distance from the Dataset Global BDe Order as

$${{\displaystyle \sum }}_{R_{X,Y}}\left(P_G\left(D|R_{X,Y}\right)-P_A\left(D|R_{X,Y}\right)\right)$$

(18)

$${{\displaystyle \sum }}_{R_{X,Y}}\left(P^S{}_G\left(D|R_{X,Y}\right)-P^S{}_A\left(D|R_{X,Y}\right)\right)$$

(19)

Note here we consider indirect causation to assess R_X,Y, i.e., we check whether X appears as an ancestor of Y (i.e., repeatedly applying parent-of(Y) function–parent-of(parent-of(Y)), parent-of(parent-of(parent-of (Y)))…), or whether Y appears as an ancestor of X in the overall network.

We report how well algorithms predict the Markov blanket of each variable in Close 9 variables (C9) and Sparse 9 variables (S9) (denote all Markov Blankets as A_M) and compare with the Markov blanket of the variable from the Dataset Global BDe Best Order (denote all Markov Blankets as G_M) by calculating the following distance:

$${{\displaystyle \sum }}_{g_M\in G_M}{{\displaystyle \sum }}_{a_M\in A_M}d\left(g_M,a_M\right)$$

(20)

$$d\left(g_M,a_M\right)=\left\{\begin{array}{c}\left|P_G\left(D|g_M\right)-P_A\left(D|a_M\right)\right| if g_M\equiv a_M \\ P_G\left(D|g_M\right) if g_M\notin A_M\\ P_A\left(D|a_M\right) if a_M\notin G_M\\ 0 othewise\end{array}\right.$$

(21)

$${{\displaystyle \sum }}_{g_M\in G_M}{{\displaystyle \sum }}_{a_M\in A_M}{d}^S\left(g_M,a_M\right)$$

(22)

$$d^S\left(g_M,a_M\right)=\left\{\begin{array}{c}\left|P^S{}_G\left(D|g_M\right)-P^S{}_A\left(D|a_M\right)\right| if g_M\equiv a_M \\ P^S{}_G\left(D|g_M\right) if g_M\notin A_M\\ P^S{}_A\left(D|a_M\right) if a_M\notin G_M\\ 0 othewise\end{array}\right.$$

(23)

Note that $P_G\left(D|g_M\right)$ and $P_A\left(D|a_M\right)$ can be calculated by incorporating the order weight (as we calculated $P_G\left(D|R_{X,Y}\right)$ or $P_A\left(D|R_{X,Y}\right)$ by multiplying $P(D|O)$) and $P^S{}_G\left(D|g_M\right)$ and $P^S{}_A\left(D|a_M\right)$ can be calculated by not incorporating the order weight (as we calculated $P^S{}_G\left(D|R_{X,Y}\right)$ or $P^S{}_A\left(D|R_{X,Y}\right)$ by not multiplying $P(D|O)$).

We also report all algorithms’ predicted performance, as how well they predict four causal pairwise relationships–Ø_{X Y}, Ø_X→Y, H_{X Y}, and H_X→Y–introduced in Table 1 by comparing the algorithm’s prediction of R_X,Y ∈ { X→Y, X←Y, X(none)Y} with the true underlying relationships T_X,Y ∈ {Ø_{X Y}, Ø_X→Y, H_{X Y}, H_X→Y}. In addition to the predictive performance, we also report the following for each R_X,Y and for each T_X,Y:

$$P_A\left(R_{X,Y}|T_{X,Y}\right)=\frac{{{\displaystyle \sum }}_{X,Y}{\delta }_{T_{X,Y}}{P}_A\left(D|R_{X,Y}\right)}{{{\displaystyle \sum }}_{X,Y}{\delta }_{T_{X,Y}}}$$

(24)

$$P^S{}_A\left(R_{X,Y}|T_{X,Y}\right)=\frac{{{\displaystyle \sum }}_{X,Y}{\delta }_{T_{X,Y}}{P}^S{}_A\left(D|R_{X,Y}\right)}{{{\displaystyle \sum }}_{X,Y}{\delta }_{T_{X,Y}}}$$

(25)

$${\delta }_{T_{X,Y}}=\left\{\begin{array}{c}1 if true relationship is T_{X,Y} \\ 0 if true relationship is not T_{X,Y}\end{array}\right.$$

(26)

where ${{\displaystyle \sum }}_{X,Y}{\delta }_{T_{X,Y}}$ is the number of underlying true relationships (i.e., counts in Table 1). Finally, we report the percentage of the algorithm’s most probable prediction of R_X,Y given the true underlying true relationships T_X,Y by calculating the following:

$$C_A\left(R_{X,Y}|T_{X,Y}\right)=\frac{{{\displaystyle \sum }}_{X,Y}{\delta }_{R_{X,Y},T_{X,Y}}}{{{\displaystyle \sum }}_{X,Y}{\delta }_{T_{X,Y}}}$$

(27)

$${\delta }_{R_{X,Y},T_{X,Y}}=\left\{\begin{array}{c}1 if true relationship is T_{X,Y} and R_{X,Y}\equiv argma{x}_{r_{X,Y}}{P}_A\left(D|r_{X,Y}\right)\\ 0 otherwise \end{array}\right.$$

(28)

$$C^S{}_A\left(R_{X,Y}|T_{X,Y}\right)=\frac{{{\displaystyle \sum }}_{X,Y}\delta {’}_{R_{X,Y},T_{X,Y}}}{{{\displaystyle \sum }}_{X,Y}{\delta }_{T_{X,Y}}}$$

(29)

$$\delta {’}_{R_{X,Y},T_{X,Y}}=\left\{\begin{array}{c}1 if true relationship is T_{X,Y} and R_{X,Y}\equiv argma{x}_{r_{X,Y}}{P}^S{}_A\left(D|r_{X,Y}\right)\\ 0 otherwise \end{array}\right.$$

(30)

$${\delta }_{T_{X,Y}}=\left\{\begin{array}{c}1 if true relationship is T_{X,Y} \\ 0 if true relationship is not T_{X,Y}\end{array}\right.$$

(31)

We have also run other causal discovery algorithms, such as PC [9], K2 [5], and BiDAG [12] on the same datasets, i.e., 50 and 1000 cases for Sparse 9 variables (in D50S9 and D1KS9); and 50 and 1000 cases for Close 9 variables (in D50C9 and D1KC9). Since BiDAG could only incorporate binary random variables for learning, we converted all the variables in the datasets as continuous variables. This was done by adding normal noise with $\mu =0, \delta =0.01$ to each measurement of discrete data. The reason we have used these parameters for noise was that they have given the most consistent conditional independencies among the variables when we compared the original discrete data and converted continuous data.

3. Results

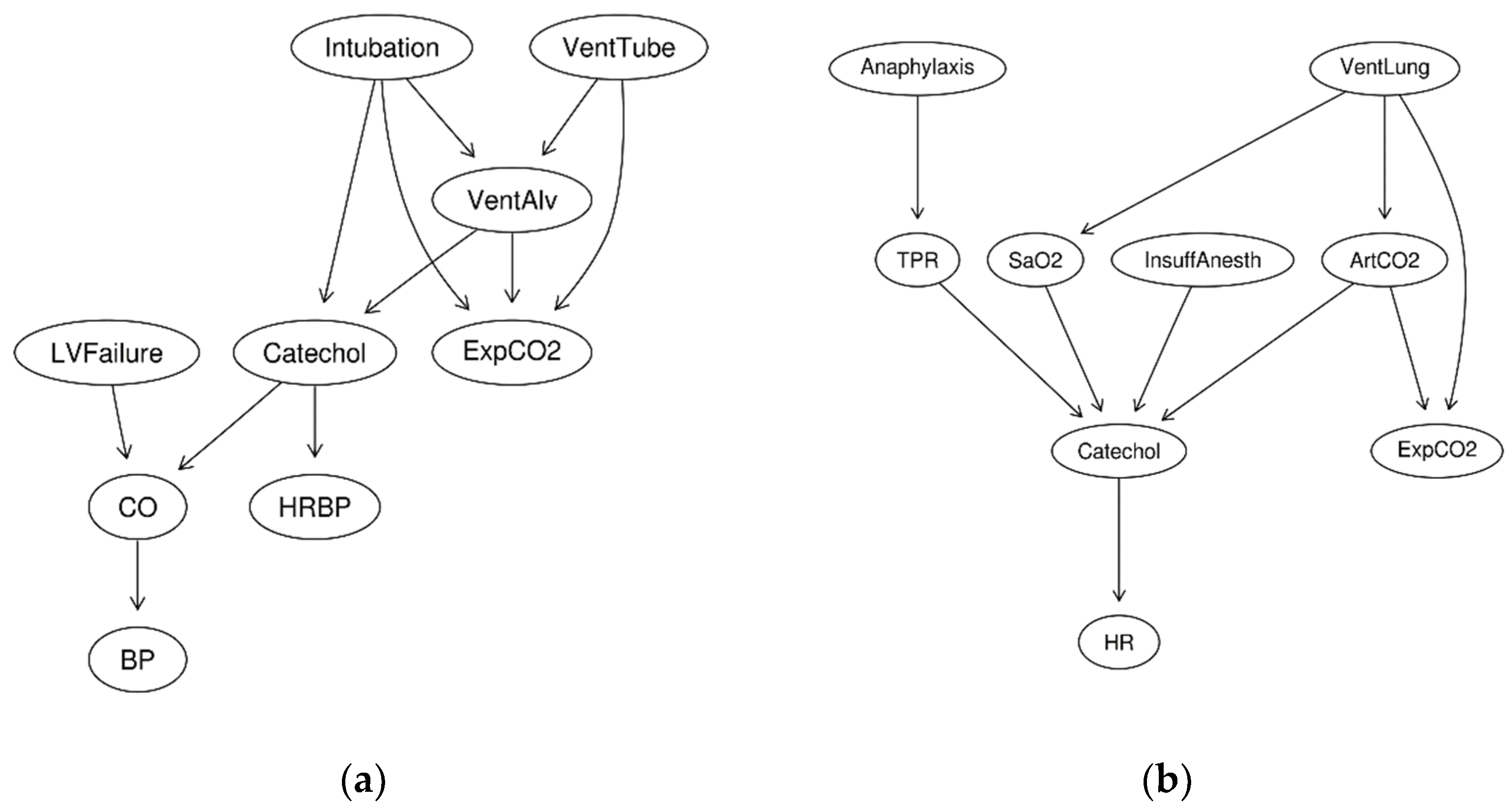
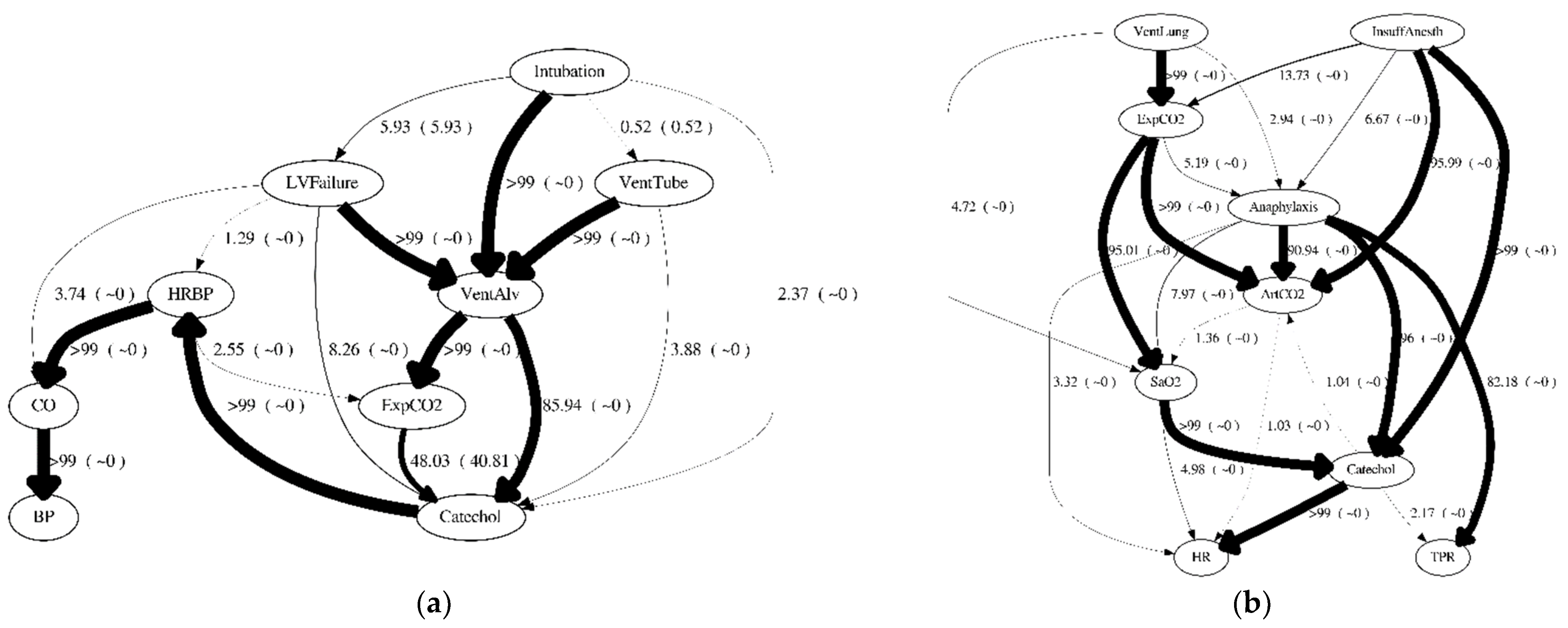
Figure 6 reports the highest scored structure reported by BDe scores for each dataset. It is interesting to note that even with a large number of samples and a significantly more likely Global BDe Structure, i.e., for 1000 cases (D1KS9) and its BDe percentage structure score of >99%, it predicts incorrect mechanisms, e.g., HRBP is predicted as a cause of CO and CO is predicted as a cause of LVFailure (Figure 6c). However, the generating structure shows that HRBP is not a cause of CO (they are confounded by Catechol), and LVFailure is a cause of CO (Figure 5a). Another interesting result to notice is that even with many cases (i.e., 1000 cases), the highest BDe scored structure may obtain a mere 4% of the total BDe structure score.

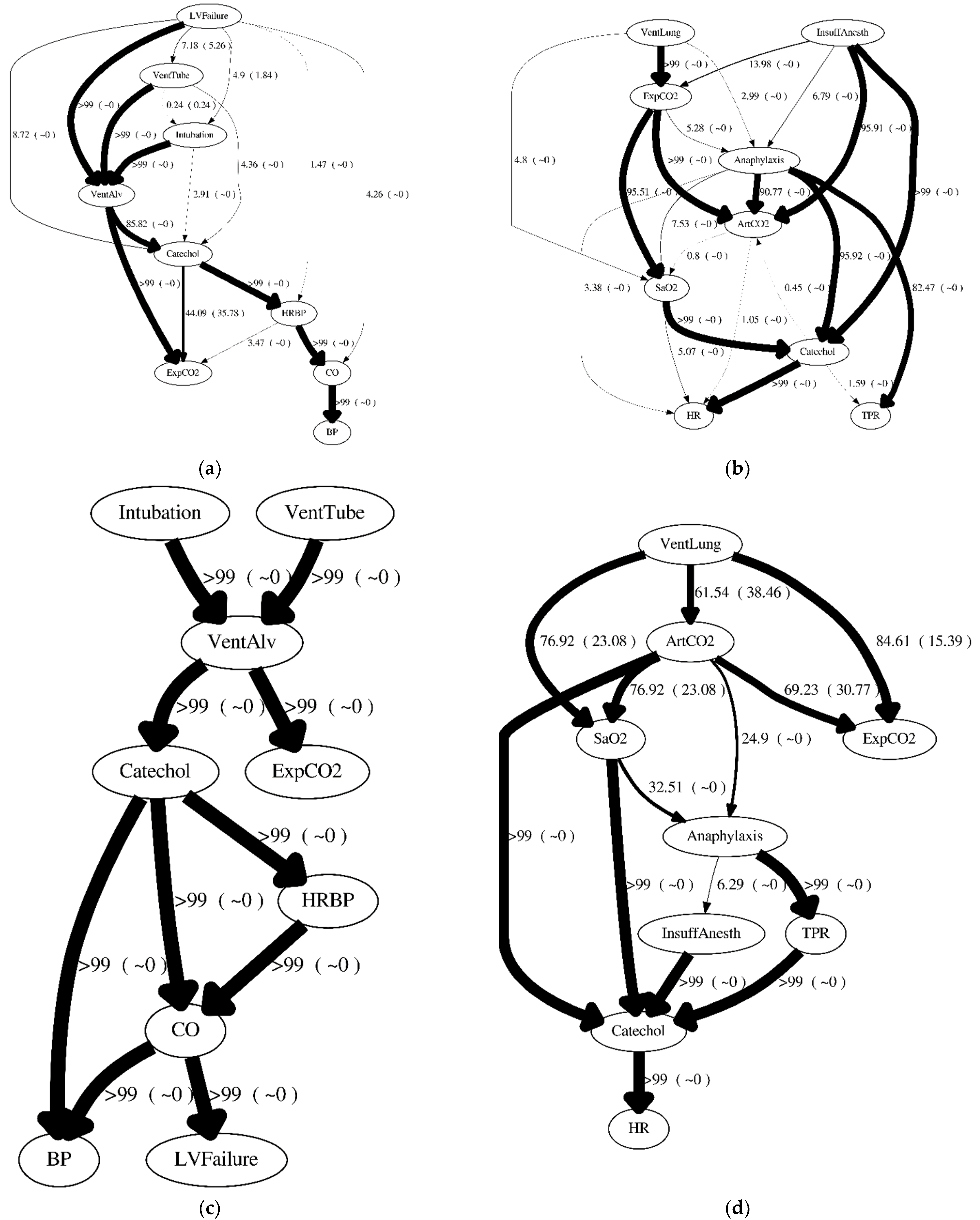
Figure 7 shows consensus structures using P^S_G(D|R_X,Y) (without incorporating the order weight) for D50S9, D50C9, D1KS9, and D1KC9. The arcs thicknesses are based on P^S_G(D|X→Y) or P^S_G(D|Y→X). If P^S_G(D|X→Y) is displayed as a percentage, then P^S_G(D|Y→X) is also displayed as a percentage in the parentheses. If P^S_G(D|X→Y) and P^S_G(D|Y→X) both are less than 0.0001, then no arcs are drawn between X and Y. >99 or ~0 indicates where the pairwise causal relationship probability is greater than 0.9999 or less than 0.0001, respectively. Similarly, Figure 8 shows consensus structures using P_G(D|R_X,Y) (with incorporating the order weight) for D50S9, D50C9, D1KS9, and D1KC9.

The Global BDe structure using D50S9 was marginally better (maximum likelihood of 0.1423) than other structures. All of the models incorrectly identified causal effects from LVFailure to VentAlv; from Catechol to ExpCO2; and from HRBP to CO when compared to the generating structure (Figure 5a). In D50S9, the consensus structures generated with the order weight (Figure 8a) and without the order weight (Figure 7a) were different than the Global BDe structure (Figure 6a). A significant difference between the consensus structures generated with the order weight (Figure 8a), and without the order weight (Figure 7a), was a causal relationship between Catechol to ExpCO2. The consensus structure generated with the order weight predicted P_G(D|ExpCO2 → Catechol) = 0.4803 as the most probable relationship; however, the consensus structure generated without the order weight predicted P_G(D|Catechol → ExpCO2) = 0.4409 as the most probable relationship, as the generating structure (Figure 3a) showed that Catechol and ExpCO2 had no direct causal influence between each other. It is also noteworthy that one of their common causes, VentAlv, was correctly predicted to be a common cause in both consensus structures. This showed that, to some extent, we can use the disagreement between the consensus structures generated with and without the order weight to identify confounded relationships without any direct causal relationship.

The Global BDe structure using D50C9 was marginally better (maximum likelihood of 0.1571) than other structures. In D50C9, the consensus structures generated with the order weight (Figure 8b) or without the order weight (Figure 7b) were slightly different than the Global BDe structure (Figure 6b). All models incorrectly identified causal effects from Anaphylaxis to ArtCO2; from InsuffAnesth to ArtCO2; and predicted a reversed causal direction of ArtCO2 and ExpCO2 compared to the generating structure (Figure 5b). Compared to the same 50 cases, D50S9, no significant differences were observed between the consensus structures generated with the order weight (Figure 8b) and without the order weight (Figure 7b).

Only in D1KS9, both consensus structures generated with (Figure 8c) or without the order weight (Figure 7c) agreed with the Global BDe structure (Figure 6c). This is not surprising because the Global BDe structure was significantly better (>0.9999) than any other structures. However, all models incorrectly predicted the following three causal relationships: between CO and LVFailure (reversed causal prediction); between Intubation and ExpCO2 (missing causal prediction); and added between Catechol and BP (unnecessary causal prediction) compared to the generating structure (Figure 5a).

The Global BDe structure using D1KC9 was marginally better (maximum likelihood of 0.0403). Among the four datasets, it resulted in the lowest maximum likelihood, making D1KC9 the most difficult dataset to learn causal relationships from. All models incorrectly identified a causal effect from ArtCO2 to SaO2 (Figure 5b). In D1KC9, the consensus structures generated with the order weight (Figure 8d) and without the order weight (Figure 7d) were different than the Global BDe structure (Figure 6d). A significant difference between the consensus structures generated with the order weight (Figure 8d) and without the order weight (Figure 7d) was the prediction of a causal relationship between VentLung and ArtCO2. The consensus structure generated with the order weight predicted P_G(D|ArtCO2 → VentLung) = 0.5556 as being the most probable relationship; however, the consensus structure generated without the order weight predicted P_G(D|VentLung → ArtCO2) = 0.6154 as being the most probable relationship. As the generating structure (Figure 3b) shows VentLung and ArtCO2 have a direct causal influence between each other and their common cause, Intubation is hidden in the dataset. This shows how difficult it is to learn reliable causal relationships among the upstream variables in which most of the confounded causes are hidden in the dataset.

We believe all these results are due to the omission of 28 variables and random sampling effects. Also, as the later results will show, with 50 cases, it is more difficult to learn the generating structure of C9, and with 1000 cases it is more difficult to learn the generating structure of S9.

Table 2. Mean and Standard Deviation (S.D.) of the Dataset Global BDe Best Order percentage score.

Dataset	D50S9	D50C9	D1KS9	D1KC9
Mean	7.1429%	7.1429%	7.1429%	7.1429%
S.D.	0.001470	0.00203	4.48 × 10−8	8.37 × 10−6

shows all the orders (from the total of 9! = 362,880 orders) that received a combined percentage score of >99%. Interestingly, the means were all 7.1429%. However, depending on the dataset, the standard deviation of the scores were different. The data sampled from S9 tended to show tighter percentage scores among the orders than the data sampled from C9. This means that order scores from S9 had less impact than those from C9.

Table 3. Structure distances between the generating causal structure and the Dataset Global BDe Best Order.

Dataset	D50S9	D50C9	D1KS9	D1KC9
Without the order weight	18.2123	21.6760	18.0000	14.2517
With the order weight	17.2238	21.6370	18.0000	13.5725

summarizes our claim that incorporating the ordering results can help us gain mechanistic knowledge. According to the distances, the BDe score had difficulties in learning the true underlying mechanisms from the generating structure with 50 cases of C9. However, by adding more samples, i.e., with 1000 cases of C9, we improved the ability to learn the true underlying mechanisms from the generating structure.

Overall, the results shown in Table 3 illustrate that order weight improves in learning the true underlying mechanisms from the generating structure. In the 1000 cases of S9 (D1KS9), as it was mentioned earlier (shown in Figure 6c), there was only one structure that was significant in terms of BDe score (i.e., >99% of the total BDe structure score). Because of this fact, all orders that were compliant with the dominating structure had a very similar score with a very tight margin, resulting in almost all the same order score (Table 2). Therefore, in this situation we can see why the order score will not improve in learning the true underlying mechanisms from the generating structure.

Table 4. Structure distances without the order weight. (a) 50 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset. (b) 1000 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset.

(a)
			D50S9				D50C9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Var	Mean	Var	Mean	Var	Mean	Var
1 h	Random		20.14	11.175	2.91	25.420	22.31	0.302	12.89	124.57
	P	SC	24.71	9.612	11.40	44.969	24.25	7.271	20.32	6.456
		WC	22.53	14.353	8.24	60.001	25.80	7.252	21.82	6.606
		SI	22.50	0.898	8.67	16.204	25.85	7.491	21.69	6.102
		WI	23.18	0.746	7.68	2.070	27.55	0.029	23.43	0.005
	PP	SC	18.21	0.000	0.00	0.000	22.32	0.315	12.95	125.70
		WC	18.21	0.000	0.00	0.000	22.65	0.001	19.17	0.077
		SI	17.36	2.204	1.46	6.416	22.34	0.327	13.00	126.82
		WI	18.21	0.000	0.00	0.000	22.34	0.327	13.00	126.82
2 h	Random		18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
	P	SC	18.13	0.019	0.15	0.071	22.67	0.000	19.51	0.000
		WC	18.14	0.016	0.14	0.059	22.68	0.000	19.29	0.143
		SI	18.14	0.016	0.14	0.059	22.67	0.000	19.51	0.000
		WI	17.36	2.204	1.46	6.416	22.68	0.000	19.29	0.143
	PP	SC	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
		WC	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
		SI	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
		WI	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
4 h	Random		18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
	P	SC	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
		WC	18.21	0.000	0.00	0.000	22.32	0.315	12.95	125.70
		SI	18.21	0.000	0.00	0.000	22.00	0.317	6.46	125.18
		WI	18.21	0.000	0.01	0.001	21.68	0.000	0.00	0.000
	PP	SC	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
		WC	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
		SI	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
		WI	18.21	0.000	0.00	0.000	21.68	0.000	0.00	0.000
BiDAG			48.00	8.000	58.94	8.957	39.00	2.000	44.24	3.068
K2			28.00	-	14.46	-	44.00	-	46.16	-
PC			40.00	-	50.98	-	33.00	-	32.85	-
(b)
			D1KS9				D1KC9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Variance	Mean	Variance	Mean	Variance	Mean	Variance
2 h	Random		39.68	58.607	42.37	71.345	25.83	201.870	26.68	200.887
	P	SC	33.11	285.037	28.44	377.926	9.14	8.136	10.86	2.249
		WC	33.81	78.699	42.54	26.088	25.20	243.398	25.39	223.036
		SI	40.67	37.333	36.00	156.000	13.52	19.847	17.25	36.087
		WI	36.67	65.333	46.00	12.000	25.34	253.669	25.40	278.016
	PP	SC	37.56	37.926	36.44	17.926	20.24	103.441	24.50	70.396
		WC	36.00	300.000	33.78	509.481	12.79	37.146	16.07	20.011
		SI	35.33	341.333	35.33	645.333	27.45	271.048	29.21	236.507
		WI	45.11	6.370	45.85	36.067	24.92	263.521	27.72	284.627
4 h	Random		41.83	14.083	40.17	116.083	13.33	35.665	14.84	92.436
	P	SC	39.00	19.000	41.00	39.000	23.34	70.611	25.36	180.337
		WC	44.00	4.000	44.67	17.333	25.01	276.117	25.79	303.470
		SI	38.61	11.122	42.77	76.699	23.80	259.143	26.79	214.084
		WI	39.39	5.106	39.33	105.333	20.45	95.313	21.83	79.829
	PP	SC	38.00	16.000	42.67	57.333	19.59	400.968	24.97	301.929
		WC	36.37	32.514	37.12	25.046	21.31	51.338	22.20	67.272
		SI	38.00	16.000	41.11	18.370	26.79	179.473	27.00	205.282
		WI	38.67	25.333	38.00	100.000	26.79	179.473	27.00	205.282
16 h	Random		37.44	17.926	37.72	48.898	11.11	3.567	9.43	9.872
	P	SC	38.76	10.313	32.90	37.027	14.69	22.697	17.57	62.939
		WC	44.67	1.333	48.57	10.122	13.95	16.385	18.71	13.462
		SI	39.33	17.333	39.00	73.000	14.44	28.325	19.52	2.893
		WI	29.67	140.333	29.67	364.333	15.46	43.441	17.66	9.317
	PP	SC	43.00	3.000	49.67	16.333	14.39	15.414	14.43	17.557
		WC	40.00	28.000	41.67	58.333	16.43	9.102	15.33	5.494
		SI	32.37	174.601	29.03	651.995	23.44	225.689	25.63	158.151
		WI	44.22	9.481	46.89	37.926	12.24	8.376	13.33	57.693
BiDAG			40.00	0.000	28.00	0.000	17.00	18.000	18.35	8.960
K2			18.00	-	0.00	-	66.00	-	60.37	-
PC			41.00	-	48.00	-	30.00	-	24.27	-

P: Prior, PP: PrePrior, SC: Strong Correct, WC: Weak Correct, SI: Strong Incorrect, WI: Weak Incorrect.

and

Table 5. Structure distances with the order weight. (a) 50 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset. (b) 1000 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset.

(a)
			D50S9				D50C9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Var	Mean	Var	Mean	Var	Mean	Var
1 h	Random		19.64	30.35	5.81	51.162	21.70	0.005	1.48	1.493
	P	SC	30.14	60.89	19.72	120.601	23.77	11.813	8.08	33.905
		WC	19.04	5.786	6.56	15.904	24.70	16.125	9.96	18.692
		SI	21.06	6.438	8.61	7.391	24.38	5.997	12.28	10.007
		WI	21.56	5.154	8.72	12.071	26.15	10.588	12.91	57.855
	PP	SC	16.86	0.097	0.84	0.454	21.88	0.090	4.46	34.262
		WC	16.95	0.073	0.63	0.342	21.80	0.011	3.73	7.171
		SI	16.32	0.697	1.97	3.170	21.99	0.115	6.74	44.955
		WI	16.86	0.027	0.82	0.107	21.90	0.084	5.20	31.125
2 h	Random		16.53	0.012	1.53	0.055	21.63	0.000	0.07	0.000
	P	SC	16.20	0.079	2.12	0.341	21.94	0.001	5.67	0.502
		WC	16.33	0.022	2.13	0.167	21.97	0.030	6.64	11.473
		SI	16.29	0.003	2.05	0.014	21.96	0.015	6.15	4.471
		WI	16.04	0.172	2.61	0.788	21.96	0.029	6.20	14.410
	PP	SC	17.04	0.024	0.43	0.111	21.63	0.000	0.05	0.000
		WC	17.04	0.025	0.43	0.105	21.62	0.000	0.07	0.000
		SI	17.04	0.024	0.43	0.112	21.63	0.000	0.06	0.000
		WI	17.03	0.101	0.43	0.453	21.64	0.001	0.09	0.002
4 h	Random		16.56	0.001	1.47	0.003	21.63	0.000	0.05	0.000
	P	SC	16.56	0.001	1.47	0.003	21.65	0.000	0.08	0.000
		WC	16.52	0.007	1.56	0.030	21.72	0.005	1.35	1.645
		SI	16.54	0.014	1.52	0.057	21.67	0.002	0.49	0.498
		WI	16.40	0.072	1.82	0.314	21.64	0.000	0.08	0.000
	PP	SC	17.22	0.000	0.04	0.000	21.62	0.000	0.06	0.000
		WC	17.22	0.000	0.04	0.000	21.63	0.000	0.05	0.000
		SI	17.22	0.000	0.05	0.000	21.63	0.000	0.07	0.000
		WI	17.22	0.000	0.04	0.000	21.64	0.000	0.06	0.000
BiDAG			48.00	8.000	58.94	8.957	39.00	2.000	44.24	3.068
K2			28.00	-	14.46	-	44.00	-	46.16	-
PC			40.00	-	50.98	-	33.00	-	32.85	-
(b)
			D1KS9				D1KC9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Variance	Mean	Variance	Mean	Variance	Mean	Variance
2 h	Random		39.59	42.692	42.97	56.086	25.56	209.278	27.13	217.735
	P	SC	33.11	285.037	28.44	377.927	8.41	4.901	10.99	0.078
		WC	34.03	76.580	42.53	27.008	25.61	226.015	26.49	246.942
		SI	40.22	46.815	35.33	185.334	13.08	25.578	17.13	56.053
		WI	36.67	65.333	46.00	12.000	25.27	243.761	26.92	279.100
	PP	SC	38.00	47.967	36.95	26.069	20.10	105.759	25.59	77.767
		WC	35.10	273.648	33.43	489.516	12.76	37.207	15.97	35.531
		SI	35.33	341.333	35.33	645.333	26.50	291.276	29.65	294.053
		WI	43.87	17.647	45.25	52.435	25.21	252.008	28.56	306.454
4 h	Random		42.10	13.594	40.57	120.587	12.87	39.938	15.80	100.781
	P	SC	39.00	19.000	41.00	39.000	23.32	71.322	26.40	192.191
		WC	44.00	4.000	44.67	17.333	25.14	271.993	26.98	289.026
		SI	37.43	5.247	41.73	79.882	23.18	279.931	27.16	239.742
		WI	39.42	5.003	39.33	105.333	18.50	12.703	21.95	40.858
	PP	SC	38.00	16.000	42.67	57.333	21.03	80.477	22.92	77.419
		WC	34.84	28.731	35.45	22.966	19.69	398.657	25.21	327.081
		SI	38.67	17.333	42.00	16.000	21.20	48.632	23.62	67.978
		WI	39.11	33.037	38.44	113.926	26.85	177.831	28.76	188.909
16 h	Random		37.10	21.481	37.85	50.113	10.50	9.386	10.13	19.393
	P	SC	38.50	20.920	33.91	55.929	14.37	25.397	18.40	64.781
		WC	44.93	0.657	48.80	12.263	14.04	15.646	19.26	14.133
		SI	39.24	18.301	39.14	69.670	14.39	28.542	19.90	5.251
		WI	29.27	157.213	29.27	390.813	16.17	39.229	18.72	11.306
	PP	SC	43.00	3.000	49.67	16.333	14.50	16.538	15.93	15.372
		WC	40.45	36.578	42.11	70.072	16.51	7.749	16.57	7.196
		SI	32.20	173.354	28.87	647.190	24.20	244.548	26.97	221.240
		WI	44.22	9.489	46.89	37.936	11.36	13.995	14.00	47.746
BiDAG			40.00	0.000	28.00	0.000	17.00	18.000	18.35	8.960
K2			18.00	-	0.00	-	66.00	-	60.37	-
PC			41.00	-	48.00	-	30.00	-	24.27	-

P: Prior, PP: PrePrior, SC: Strong Correct, WC: Weak Correct, SI: Strong Incorrect, WI: Weak Incorrect.

compare the structure distances between (1) the algorithm’s predicted structures and the generated structures (Generated δ), and (2) the algorithm’s predicted structures and the best BDe structure scores (Global BDe δ). In some sense, Generated δ measures how well the algorithm learns the underlying mechanism from a phenomenon, and Global BDe δ measures how well the algorithm estimates the best BDe (or BGe) score from the sample.

In 50 cases spanning Table 4a and Table 5a, it is clear that all the MCMC ordering algorithms (Random, Prior, and PrePrior) outperformed constrained variant algorithms (BiDAG, K2, and PC) in terms of Generated δ and Global BDe δ with datasets D50S9 and D50C9. Also, in general, algorithms with the order weight predicted better in generating structures (i.e., lower Generated δ and Global BDe δ,) with a higher confidence (i.e., lower variance.)

With the maximum hours (4 h) run, Random and PrePrior converged on their predictions; however, Prior showed some variance in performance. We note that with a lesser number of hours (1 and 2 h), PrePrior showed better performances (better predictions with confidence, i.e., less variance) than Random in D50S9 and comparable predictions in D50C9 (in 1 h run, Random Generated δ was 22.31 with variance of 0.302, and PrePrior Weak Correct achieved Generated δ 22.65 with a very low variance, 0.001 (Table 4a)).

The structure distances of 1000 cases are shown in Table 4b and Table 5b. K2 showed the best Generated δ and Global BDe δ in D1KS9; however, its performance was the lowest among all the algorithms in D1KC9. We believe this was because, in D1KS9, as it was mentioned earlier (shown in Figure 6c), there was only one structure that was significant in terms of its BDe score (>99% of the total BDe structure scores).

The BiDAG performance in Global BDe δ in D1KS9 was the second best (next to K2′s); however, Generated δ in D1KS9 was either comparable or worse than the MCMC ordering algorithms (Random, Prior, and PrePrior). It seems MCMC ordering algorithms need more than 16 h to converge, although structure distances were generally decreasing in D1KC9, however, that trend is questionable in D1KS9.

We could not find a general pattern as we saw in 50 cases that better predicted the generating structures (lower Generated δ and Global BDe δ) with a higher confidence, i.e., a lower variance with order weight in 1000 cases. We believe this fact has to do with the results that we mentioned earlier, i.e., that MCMC ordering algorithms needs more than 16 h to converge.

With the outstanding performance of K2 in D1KS9 reported earlier, however, we must also mention the outstanding performance of the Prior algorithm with the Strong Correct prior, which achieved a better performance that was statistically significant in a mere 2h run in D1KC9. In D1KC9, all algorithms showed larger than ten for Generated δ, except for Prior. Prior achieved lower than ten for Generated δ with a high confidence (variance of 8.136; significantly lower than the second lowest variance of 18.0 from BiDAG).

Table 6. Markov blanket distances without the order weight. (a) 50 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset. (b) 1000 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset.

(a)
			D50S9				D50C9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Var	Mean	Var	Mean	Var	Mean	Var
1 h	Random		16.05	0.01	0.76	1.734	16.17	0.000	4.78	17.170
	P	SC	16.14	0.01	3.14	4.233	16.28	0.048	7.68	1.059
		WC	16.14	0.02	2.45	5.900	16.40	0.047	8.28	1.077
		SI	16.04	0.00	2.57	2.746	16.40	0.045	8.26	1.048
		WI	16.11	0.00	2.01	0.166	16.53	0.000	8.93	0.001
	PP	SC	16.00	0.00	0.00	0.000	16.17	0.000	4.80	17.286
		WC	16.00	0.00	0.00	0.000	16.16	0.000	7.15	0.003
		SI	16.00	0.00	1.07	3.407	16.17	0.000	4.82	17.401
		WI	16.00	0.00	0.00	0.000	16.17	0.000	4.82	17.401
2 h	Random		16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
	P	SC	16.00	0.00	0.17	0.083	16.16	0.000	7.23	0.000
		WC	16.00	0.00	0.15	0.072	16.16	0.000	7.18	0.007
		SI	16.00	0.00	0.15	0.072	16.16	0.000	7.23	0.000
		WI	16.00	0.00	1.07	3.407	16.16	0.000	7.18	0.007
	PP	SC	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
		WC	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
		SI	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
		WI	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
4 h	Random		16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
	P	SC	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
		WC	16.00	0.00	0.00	0.000	16.17	0.000	4.80	17.286
		SI	16.00	0.00	0.00	0.000	16.18	0.000	2.39	17.170
		WI	16.00	0.00	0.02	0.001	16.19	0.000	0.00	0.000
	PP	SC	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
		WC	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
		SI	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
		WI	16.00	0.00	0.00	0.000	16.19	0.000	0.00	0.000
BiDAG			18.00	0.000	18.00	0.000	16.00	0.000	18.00	0.000
K2			16.00	-	13.79	-	18.00	-	18.00	-
PC			18.00	-	18.00	-	18.00	-	18.00	-
(b)
			D1KS9				D1KC9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Variance	Mean	Variance	Mean	Variance	Mean	Variance
2 h	Random		18.00	0.00	13.03	1.003	11.50	8.502	10.95	13.371
	P	SC	18.00	0.00	9.33	17.333	7.99	0.938	5.82	0.333
		WC	17.41	1.03	13.83	0.090	12.76	10.277	12.30	15.951
		SI	18.00	0.00	8.67	9.333	9.46	1.369	8.82	4.790
		WI	17.33	1.33	13.67	0.333	11.79	14.828	10.85	30.014
	PP	SC	18.00	0.00	11.11	2.370	12.39	7.741	12.13	14.534
		WC	18.00	0.00	10.00	9.000	9.15	0.912	8.16	2.063
		SI	18.00	0.00	11.78	25.481	12.32	8.611	11.61	17.310
		WI	18.00	0.00	11.82	0.183	12.51	6.667	11.76	21.675
4 h	Random		18.00	0.00	9.83	11.083	10.31	10.219	8.07	30.555
	P	SC	18.00	0.00	12.67	1.333	12.09	10.991	11.43	23.473
		WC	18.00	0.00	11.33	9.333	11.80	5.340	10.90	16.552
		SI	17.49	0.77	13.42	0.468	12.76	16.142	12.34	25.819
		WI	18.00	0.00	11.67	16.333	11.13	6.473	10.48	12.860
	PP	SC	18.00	0.00	12.67	1.333	10.27	13.426	9.97	15.665
		WC	18.00	0.00	12.18	1.522	11.16	11.527	10.79	20.176
		SI	18.00	0.00	12.22	0.148	12.40	2.221	11.58	10.344
		WI	18.00	0.00	10.33	14.333	12.40	2.221	11.58	10.344
16 h	Random		18.00	0.00	11.89	1.454	8.38	0.250	4.66	0.750
	P	SC	18.00	0.00	8.33	4.333	10.73	9.584	9.25	23.921
		WC	18.00	0.00	12.90	3.313	9.69	0.677	8.66	4.616
		SI	18.00	0.00	12.33	8.333	9.50	1.190	9.24	1.328
		WI	18.00	0.00	10.50	9.250	11.60	11.056	10.38	17.422
	PP	SC	16.00	12.00	12.33	0.333	9.61	0.634	8.24	4.689
		WC	16.00	12.00	11.67	2.333	9.43	1.452	7.26	1.587
		SI	16.33	8.33	8.67	57.333	12.52	6.552	11.65	19.964
		WI	18.00	0.00	12.22	4.148	9.63	5.630	7.63	15.827
BiDAG			18.00	0.000	18.00	0.000	11.00	2.000	11.13	2.000
K2			18.00	-	0.00	-	18.00	-	17.86	-
PC			18.00	-	18.00	-	18.00	-	18.00	-

P: Prior, PP: PrePrior, SC: Strong Correct, WC: Weak Correct, SI: Strong Incorrect, WI: Weak Incorrect.

and

Table 7. Markov blanket distances with the order weight. (a) 50 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset. (b) 1000 cases datasets. Dark shaded cells represent the lowest distance or variance in each timed run for the dataset; Bright shaded cells represent the second lowest distance or variance in each timed run for the dataset.

(a)
			D50S9				D50C9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Var	Mean	Var	Mean	Var	Mean	Var
1 h	Random		16.05	0.006	2.06	2.129	16.19	0.000	0.60	0.165
	P	SC	16.16	0.013	5.03	7.234	16.33	0.068	3.09	4.954
		WC	16.07	0.004	2.61	1.096	16.40	0.103	3.82	2.873
		SI	16.03	0.000	2.77	0.561	16.35	0.036	4.67	1.479
		WI	16.08	0.003	2.70	0.779	16.50	0.052	4.93	8.424
	PP	SC	16.00	0.000	0.66	0.226	16.18	0.000	1.72	4.575
		WC	16.00	0.000	0.49	0.173	16.18	0.000	1.41	0.999
		SI	16.00	0.000	1.44	1.565	16.18	0.000	2.56	5.958
		WI	16.00	0.000	0.62	0.042	16.18	0.000	1.97	4.155
2 h	Random		16.00	0.000	1.14	0.029	16.19	0.000	0.11	0.000
	P	SC	16.00	0.000	1.51	0.176	16.18	0.000	2.13	0.069
		WC	16.00	0.000	1.52	0.086	16.18	0.000	2.49	1.568
		SI	16.00	0.000	1.49	0.004	16.18	0.000	2.32	0.617
		WI	16.00	0.000	1.89	0.393	16.18	0.000	2.34	1.980
	PP	SC	16.00	0.000	0.34	0.051	16.19	0.000	0.11	0.000
		WC	16.00	0.000	0.34	0.039	16.19	0.000	0.12	0.000
		SI	16.00	0.000	0.34	0.053	16.19	0.000	0.11	0.000
		WI	16.00	0.000	0.34	0.211	16.19	0.000	0.14	0.001
4 h	Random		16.00	0.000	1.09	0.002	16.19	0.000	0.11	0.000
	P	SC	16.00	0.000	1.10	0.001	16.19	0.000	0.13	0.000
		WC	16.00	0.000	1.16	0.012	16.18	0.000	0.56	0.199
		SI	16.00	0.000	1.12	0.033	16.19	0.000	0.27	0.053
		WI	16.00	0.000	1.35	0.137	16.19	0.000	0.13	0.000
	PP	SC	16.00	0.000	0.08	0.000	16.19	0.000	0.10	0.000
		WC	16.00	0.000	0.08	0.000	16.19	0.000	0.11	0.000
		SI	16.00	0.000	0.08	0.000	16.19	0.000	0.11	0.000
		WI	16.00	0.000	0.08	0.000	16.19	0.000	0.11	0.000
BiDAG			18.00	0.000	18.00	0.000	16.00	0.000	18.00	0.000
K2			16.00	-	13.79	-	18.00	-	18.00	-
PC			18.00	-	18.00	-	18.00	-	18.00	-
(b)
			D1KS9				D1KC9
			Generated δ		Global BDe δ		Generated δ		Global BDe δ
			Mean	Variance	Mean	Variance	Mean	Variance	Mean	Variance
2 h	Random		18.00	0.000	13.07	1.014	11.33	10.106	11.20	13.067
	P	SC	18.00	0.000	9.33	17.333	7.81	0.754	5.85	0.182
		WC	17.44	0.947	13.75	0.187	12.85	10.937	12.26	19.666
		SI	18.00	0.000	8.67	9.333	9.35	1.854	8.70	8.596
		WI	17.33	1.333	13.67	0.333	11.79	14.794	11.32	26.604
	PP	SC	18.00	0.000	11.14	2.212	12.33	8.413	12.35	13.923
		WC	18.00	0.000	10.02	7.929	9.13	0.956	8.22	6.685
		SI	18.00	0.000	11.78	25.481	12.06	11.445	11.45	24.335
		WI	18.00	0.000	12.03	0.199	12.52	6.597	11.79	23.237
4 h	Random		18.00	0.000	9.71	10.526	10.24	10.616	8.23	30.807
	P	SC	18.00	0.000	12.67	1.333	11.98	12.267	11.42	27.102
		WC	18.00	0.000	11.33	9.333	11.80	5.289	11.02	16.626
		SI	17.49	0.765	13.08	0.685	12.61	18.288	12.41	25.506
		WI	18.00	0.000	11.67	16.333	10.92	7.615	10.64	13.564
	PP	SC	18.00	0.000	12.67	1.333	11.42	4.975	10.74	12.474
		WC	18.00	0.000	12.00	0.694	10.27	13.420	9.71	18.499
		SI	18.00	0.000	12.33	0.333	11.16	11.522	10.91	18.678
		WI	18.00	0.000	10.44	15.259	12.26	2.796	11.69	9.394
16 h	Random		18.00	0.000	12.03	0.481	8.25	0.529	4.80	1.709
	P	SC	18.00	0.000	8.51	4.844	10.78	8.952	9.38	22.068
		WC	18.00	0.000	12.93	4.398	9.53	1.103	8.76	4.205
		SI	18.00	0.000	12.47	6.981	9.22	0.950	9.24	1.265
		WI	18.00	0.000	10.30	11.470	12.01	9.357	10.63	16.177
	PP	SC	18.00	0.000	12.33	0.333	9.72	0.400	8.30	3.678
		WC	18.00	0.000	11.78	2.821	9.31	0.754	7.43	1.861
		SI	18.00	0.000	8.67	57.333	12.58	6.028	11.64	23.386
		WI	18.00	0.000	12.22	4.153	9.47	6.395	7.62	16.874
BiDAG			18.00	0.000	18.00	0.000	11.00	2.000	11.13	2.000
K2			18.00	-	0.00	-	18.00	-	17.86	-
PC			18.00	-	18.00	-	18.00	-	18.00	-

P: Prior, PP: PrePrior, SC: Strong Correct, WC: Weak Correct, SI: Strong Incorrect, WI: Weak Incorrect.

compare the Markov blanket distances between the algorithm’s predicted Markov blanket of each variable in the structures (for short, we refer it to MB) and MB in the generated structure (Generated δ), as well as the distance of the algorithm’s predicted MB and the MB of the best BDe structure scores (Global BDe δ).

In 50 cases from Table 6a and Table 7a, it is clear that all the MCMC ordering algorithms (Random, Prior, and PrePrior) outperformed the constrained variant algorithms (BiDAG, K2, and PC) in Generated δ and Global BDe δ with datasets D50S9. In dataset D50C9, BiDAG was slightly better (16.0 vs. 16.19) in Generated δ; however, it was significantly worse in Global BDe δ. Also, in general, Generated δ and Global BDe δ of the algorithms with the order weight did not change much because the MB distances were low to begin with (Generated δ ranged from 16.00 to 16.53, and with the order weight it ranged from 16.00 to 16.50; Global BDe δ ranged from 0.00 to 8.93, and with the order weight it ranged from 0.00 to 5.03). We note that with the order weight, the 1h runs in D50C9 showed lower Global BDe δ with a higher confidence, i.e., a lower variance.

With the maximum hour (4 h) run, Random and PrePrior predictions converged; however, Prior showed some variance in its performance. We note that with a smaller number of hours (1 and 2 h) runs, PrePrior showed better performances (better predictions with higher confidence (i.e., lower variance) than Random in D50S9, and comparable performances in D50C9 (in 1 h run, Random Generated δ was 16.17 with variance of 0.0, PrePrior Weak Correct achieved Generated δ 16.16 with a very low variance, 0.0 (Table 6a).

MB distances of 1000 cases are shown in Table 6b and Table 7b. In D1KS9, PrePrior with Strong and Weak Prior achieved the best Generated δ (16.00) with a variance of 12.0. K2 showed the best Global BDe δ (0.0) in D1KS9. Also, in general, Generated δ and Global BDe δ of the algorithms with the order weight did not change much because the MB distances were low to begin with (Generated δ ranged from 7.99 to 18.0, and with the order weight it ranged from 7.81 to 18.0; Global BDe δ ranged from 4.66 (excluding 0.0 from K2) to 13.83 (excluding 18.0 from BiDAG), and with the order weight it ranged from 4.80 (excluding 0.0 from K2) to 13.75 (excluding 18.0 from BiDAG)).

In D1KC9, most of the MCMC ordering algorithms (Random, Prior, and PrePrior) outperformed the constrained variant algorithms (BiDAG, K2, and PC) in Generated δ and Global BDe δ. In 2 h runs, Prior with Weak Correct prior achieved the best Generated δ (7.99; the runner-up was PrePrior Weak Correct prior with 9.15) and Global BDe δ (5.82; the runner-up was PrePrior Weak Correct prior with 8.16); however, the most confident prediction came from PrePrior Weak Correct prior in Generated δ (0.912; the runner-up was Prior Weak Correct prior with 0.938).

Also, in D1KC9 with 4 h runs, PrePrior with Strong Correct prior achieved the best Generated δ (10.27; the runner-up was Random with 10.31) and Random achieved the best Global BDe δ (8.07; the runner-up was PrePrior Strong Correct prior with 9.97). In 16 h runs, Random achieved the best Generated δ (8.38; the runner-up was PrePrior Weak Correct prior with 9.43) and Global BDe δ (4.66; the runner-up was PrePrior Strong Correct prior with 7.26).

Table 8. Algorithms’ predicted probabilities of four causal pairwise relationships without the order weight. (a) Dataset for Sparse 9 variable with 50 cases (D50S9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (b) Dataset for Close 9 variable with 50 cases (D50C9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (c) Dataset for Sparse 9 variable with 1000 cases (D1KS9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (d) Dataset for Close 9 variable with 1000 cases (D1KC9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship.

(a)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.168	0.342	0.152	1.000
	Y→X		0.442	0.635	0.578	0.000
	X  Y		0.390	0.023	0.270	0.000
Prior SC	X→Y		0.168	0.342	0.152	1.000
	Y→X		0.442	0.635	0.578	0.000
	X  Y		0.390	0.023	0.270	0.000
Prior WC	X→Y		0.168	0.342	0.152	1.000
	Y→X		0.442	0.635	0.578	0.000
	X  Y		0.390	0.023	0.270	0.000
PrePrior SC	X→Y		0.168	0.342	0.152	1.000
	Y→X		0.442	0.635	0.578	0.000
	X  Y		0.390	0.023	0.270	0.000
PrePrior WC	X→Y		0.168	0.342	0.152	1.000
	Y→X		0.442	0.635	0.578	0.000
	X  Y		0.390	0.023	0.270	0.000
BiDAG	X→Y		0.143	0.350	0.000	0.000
	Y→X		0.000	0.100	0.167	0.667
	X  Y		0.857	0.550	0.833	0.333
K2	X→Y		0.286	0.250	0.167	0.667
	Y→X		0.429	0.700	0.833	0.000
	X  Y		0.286	0.050	0.000	0.333
(b)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.038	0.470	0.485	0.204
	Y→X		0.156	0.253	0.244	0.601
	X  Y		0.805	0.277	0.271	0.195
Prior SC	X→Y		0.038	0.470	0.485	0.204
	Y→X		0.156	0.253	0.244	0.601
	X  Y		0.805	0.277	0.271	0.195
Prior WC	X→Y		0.032	0.474	0.393	0.402
	Y→X		0.189	0.253	0.246	0.409
	X  Y		0.779	0.274	0.361	0.189
PrePrior SC	X→Y		0.038	0.470	0.485	0.204
	Y→X		0.156	0.253	0.244	0.601
	X  Y		0.805	0.277	0.271	0.195
PrePrior WC	X→Y		0.038	0.470	0.485	0.204
	Y→X		0.156	0.253	0.244	0.601
	X  Y		0.805	0.277	0.271	0.195
BiDAG	X→Y		0.071	1.000	0.250	0.400
	Y→X		0.500	0.000	0.750	0.300
	X  Y		0.429	0.000	0.000	0.300
K2	X→Y		0.429	0.500	0.750	0.700
	Y→X		0.286	0.375	0.250	0.300
	X  Y		0.286	0.125	0.000	0.000
(c)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.139	0.371	0.269	0.935
	Y→X		0.135	0.136	0.046	0.065
	X  Y		0.726	0.493	0.685	0.000
Prior SC	X→Y		0.248	0.390	0.107	1.000
	Y→X		0.143	0.093	0.238	0.000
	X  Y		0.609	0.517	0.655	0.000
Prior WC	X→Y		0.109	0.411	0.468	0.730
	Y→X		0.048	0.163	0.071	0.270
	X  Y		0.844	0.426	0.460	0.000
PrePrior SC	X→Y		0.024	0.367	0.472	0.944
	Y→X		0.024	0.175	0.000	0.056
	X  Y		0.952	0.458	0.528	0.000
PrePrior WC	X→Y		0.156	0.340	0.139	1.000
	Y→X		0.429	0.631	0.518	0.000
	X  Y		0.415	0.028	0.343	0.000
BiDAG	X→Y		0.571	0.400	0.500	0.000
	Y→X		0.286	0.400	0.333	0.667
	X  Y		0.143	0.200	0.167	0.333
K2	X→Y		0.429	0.400	0.000	1.000
	Y→X		0.286	0.550	0.333	0.000
	X  Y		0.286	0.050	0.667	0.000
(d)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.046	0.641	0.279	0.582
	Y→X		0.046	0.287	0.205	0.374
	X  Y		0.908	0.072	0.517	0.044
Prior SC	X→Y		0.023	0.486	0.132	0.535
	Y→X		0.036	0.344	0.272	0.287
	X  Y		0.941	0.170	0.595	0.178
Prior WC	X→Y		0.012	0.433	0.122	0.645
	Y→X		0.016	0.358	0.268	0.252
	X  Y		0.972	0.209	0.610	0.103
PrePrior SC	X→Y		0.042	0.543	0.211	0.635
	Y→X		0.037	0.324	0.241	0.257
	X  Y		0.920	0.133	0.548	0.109
PrePrior WC	X→Y		0.052	0.571	0.270	0.652
	Y→X		0.061	0.320	0.329	0.237
	X  Y		0.887	0.109	0.401	0.111
BiDAG	X→Y		0.000	0.750	0.750	0.400
	Y→X		0.143	0.250	0.250	0.600
	X  Y		0.857	0.000	0.000	0.000
K2	X→Y		0.429	0.375	0.750	0.500
	Y→X		0.571	0.375	0.250	0.500
	X  Y		0.000	0.250	0.000	0.000

and

Table 9. Algorithms’ predicted probabilities of four causal pairwise relationships with the order weight. (a) Dataset for Sparse 9 variable with 50 cases (D50S9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (b) Dataset for Close 9 variable with 50 cases (D50C9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (c) Dataset for Sparse 9 variable with 1000 cases (D1KS9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (d) Dataset for Close 9 variable with 1000 cases (D1KC9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship.

(a)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.157	0.338	0.140	1.000
	Y→X		0.426	0.628	0.448	0.000
	X  Y		0.417	0.033	0.412	0.000
Prior SC	X→Y		0.157	0.338	0.140	1.000
	Y→X		0.426	0.628	0.448	0.000
	X  Y		0.417	0.033	0.412	0.000
Prior WC	X→Y		0.157	0.338	0.140	1.000
	Y→X		0.426	0.628	0.444	0.000
	X  Y		0.417	0.034	0.416	0.000
PrePrior SC	X→Y		0.156	0.340	0.139	1.000
	Y→X		0.429	0.631	0.518	0.000
	X  Y		0.415	0.028	0.343	0.000
PrePrior WC	X→Y		0.156	0.340	0.139	1.000
	Y→X		0.429	0.631	0.518	0.000
	X  Y		0.415	0.028	0.343	0.000
BiDAG	X→Y		0.143	0.350	0.000	0.000
	Y→X		0.000	0.100	0.167	0.667
	X  Y		0.857	0.550	0.833	0.333
K2	X→Y		0.286	0.250	0.167	0.667
	Y→X		0.429	0.700	0.833	0.000
	X  Y		0.286	0.050	0.000	0.333
(b)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.037	0.470	0.484	0.203
	Y→X		0.156	0.252	0.242	0.600
	X  Y		0.807	0.278	0.275	0.197
Prior SC	X→Y		0.037	0.470	0.483	0.202
	Y→X		0.156	0.252	0.242	0.600
	X  Y		0.807	0.278	0.275	0.198
Prior WC	X→Y		0.037	0.470	0.473	0.223
	Y→X		0.159	0.252	0.242	0.581
	X  Y		0.804	0.278	0.284	0.197
PrePrior SC	X→Y		0.037	0.470	0.484	0.203
	Y→X		0.156	0.252	0.242	0.600
	X  Y		0.807	0.278	0.275	0.197
PrePrior WC	X→Y		0.037	0.470	0.484	0.203
	Y→X		0.156	0.252	0.242	0.600
	X  Y		0.807	0.278	0.275	0.197
BiDAG	X→Y		0.071	1.000	0.250	0.400
	Y→X		0.500	0.000	0.750	0.300
	X  Y		0.429	0.000	0.000	0.300
K2	X→Y		0.429	0.500	0.750	0.700
	Y→X		0.286	0.375	0.250	0.300
	X  Y		0.286	0.125	0.000	0.000
(c)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.133	0.377	0.257	0.955
	Y→X		0.125	0.114	0.032	0.045
	X  Y		0.743	0.509	0.712	0.000
Prior SC	X→Y		0.232	0.390	0.121	1.000
	Y→X		0.145	0.094	0.230	0.000
	X  Y		0.622	0.517	0.649	0.000
Prior WC	X→Y		0.105	0.419	0.489	0.689
	Y→X		0.032	0.161	0.067	0.311
	X  Y		0.863	0.420	0.444	0.000
PrePrior SC	X→Y		0.024	0.367	0.472	0.944
	Y→X		0.024	0.175	0.000	0.056
	X  Y		0.952	0.458	0.528	0.000
PrePrior WC	X→Y		0.167	0.350	0.352	0.852
	Y→X		0.024	0.136	0.056	0.148
	X  Y		0.809	0.514	0.593	0.000
BiDAG	X→Y		0.571	0.400	0.500	0.000
	Y→X		0.286	0.400	0.333	0.667
	X  Y		0.143	0.200	0.167	0.333
K2	X→Y		0.429	0.400	0.000	1.000
	Y→X		0.286	0.550	0.333	0.000
	X  Y		0.286	0.050	0.667	0.000
(d)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.045	0.640	0.260	0.586
	Y→X		0.041	0.287	0.174	0.376
	X  Y		0.914	0.073	0.566	0.039
Prior SC	X→Y		0.020	0.473	0.140	0.534
	Y→X		0.035	0.349	0.245	0.301
	X  Y		0.945	0.179	0.615	0.165
Prior WC	X→Y		0.011	0.449	0.115	0.649
	Y→X		0.022	0.353	0.280	0.243
	X  Y		0.967	0.198	0.606	0.109
PrePrior SC	X→Y		0.036	0.524	0.199	0.637
	Y→X		0.037	0.331	0.236	0.248
	X  Y		0.927	0.146	0.565	0.115
PrePrior WC	X→Y		0.046	0.580	0.288	0.667
	Y→X		0.051	0.316	0.341	0.211
	X  Y		0.904	0.104	0.371	0.122
BiDAG	X→Y		0.000	0.750	0.750	0.400
	Y→X		0.143	0.250	0.250	0.600
	X  Y		0.857	0.000	0.000	0.000
K2	X→Y		0.429	0.375	0.750	0.500
	Y→X		0.571	0.375	0.250	0.500
	X  Y		0.000	0.250	0.000	0.000

show algorithm’s predicted probabilities of four causal pairwise relationships shown in Figure 4. In all four datasets, all the MCMC ordering algorithms (Random, Prior, and PrePrior) outperformed the constrained variant algorithms (BiDAG, and K2) in the confounded relationships H_{X Y} (no causal relationship) or H_X→Y (causal relationship). K2 and BiDAG incorrectly predicted (with probability of 0.0) the true underlying confounded relationships: for example, with 1000 cases, using D1KS9, BiDAG predicted all the three true H_X→Y relationships with a probability of 0.0, and using D1KC9, BiDAG, and K2 predicted all of the four true H_{X Y} relationships with probability of 0.0. Typically, algorithms with the order weight tended to perform better in correctly predicting true causally independent relationships (Ø_{X Y} and H_{X Y}) and performed worse in correctly predicting true causal predictions (Ø_X→Y and H_X→Y).

Table 10. Algorithms’ most probable prediction rates by four causal pairwise relationships without the order weight. (a) Dataset for Sparse 9 variable with 50 cases (D50S9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (b) Dataset for Close 9 variable with 50 cases (D50C9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (c) Dataset for Sparse 9 variable with 1000 cases (D1KS9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (d) Dataset for Close 9 variable with 1000 cases (D1KC9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship.

(a)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.14	0.35	0.00	1.00
	Y→X		0.43	0.65	0.50	0.00
	X  Y		0.43	0.00	0.50	0.00
Prior SC	X→Y		0.14	0.35	0.00	1.00
	Y→X		0.43	0.65	0.50	0.00
	X  Y		0.43	0.00	0.50	0.00
Prior WC	X→Y		0.14	0.35	0.00	1.00
	Y→X		0.43	0.65	0.50	0.00
	X  Y		0.43	0.00	0.50	0.00
PrePrior SC	X→Y		0.14	0.35	0.00	1.00
	Y→X		0.43	0.65	0.50	0.00
	X  Y		0.43	0.00	0.50	0.00
PrePrior WC	X→Y		0.14	0.35	0.17	1.00
	Y→X		0.43	0.65	0.33	0.00
	X  Y		0.43	0.00	0.50	0.00
BiDAG	X→Y		0.14	0.35	0.00	0.00
	Y→X		0.00	0.10	0.17	0.67
	X  Y		0.86	0.55	0.83	0.33
K2	X→Y		0.29	0.25	0.17	0.67
	Y→X		0.43	0.70	0.83	0.00
	X  Y		0.29	0.05	0.00	0.33
(b)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
Prior SC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
Prior WC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
PrePrior SC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
PrePrior WC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
BiDAG	X→Y		0.07	1.00	0.25	0.40
	Y→X		0.50	0.00	0.75	0.30
	X  Y		0.43	0.00	0.00	0.30
K2	X→Y		0.43	0.50	0.75	0.70
	Y→X		0.29	0.38	0.25	0.30
	X  Y		0.29	0.13	0.00	0.00
(c)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.14	0.40	0.17	1.00
	Y→X		0.14	0.05	0.00	0.00
	X  Y		0.71	0.55	0.83	0.00
Prior SC	X→Y		0.29	0.40	0.00	1.00
	Y→X		0.14	0.05	0.33	0.00
	X  Y		0.57	0.55	0.67	0.00
Prior WC	X→Y		0.14	0.30	0.33	1.00
	Y→X		0.00	0.15	0.00	0.00
	X  Y		0.86	0.55	0.67	0.00
PrePrior SC	X→Y		0.00	0.35	0.50	1.00
	Y→X		0.00	0.20	0.00	0.00
	X  Y		1.00	0.45	0.50	0.00
PrePrior WC	X→Y		0.14	0.30	0.33	1.00
	Y→X		0.00	0.10	0.00	0.00
	X  Y		0.86	0.60	0.67	0.00
BiDAG	X→Y		0.57	0.40	0.50	0.00
	Y→X		0.29	0.40	0.33	0.67
	X  Y		0.14	0.20	0.17	0.33
K2	X→Y		0.43	0.40	0.00	1.00
	Y→X		0.29	0.55	0.33	0.00
	X  Y		0.29	0.05	0.67	0.00
(d)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.00	0.75	0.25	0.60
	Y→X		0.00	0.25	0.00	0.40
	X  Y		1.00	0.00	0.75	0.00
Prior SC	X→Y		0.00	0.38	0.25	0.60
	Y→X		0.00	0.38	0.25	0.40
	X  Y		1.00	0.25	0.50	0.00
Prior WC	X→Y		0.00	0.38	0.00	0.70
	Y→X		0.00	0.38	0.50	0.10
	X  Y		1.00	0.25	0.50	0.20
PrePrior SC	X→Y		0.00	0.38	0.25	0.70
	Y→X		0.00	0.38	0.00	0.10
	X  Y		1.00	0.25	0.75	0.20
PrePrior WC	X→Y		0.00	0.63	0.75	0.60
	Y→X		0.00	0.38	0.25	0.40
	X  Y		1.00	0.00	0.00	0.00
BiDAG	X→Y		0.00	0.75	0.75	0.40
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.00	0.00	0.00
K2	X→Y		0.43	0.38	0.75	0.50
	Y→X		0.57	0.38	0.25	0.50
	X  Y		0.00	0.25	0.00	0.00

and

Table 11. Algorithms’ most probable prediction rates by four causal pairwise relationships with the order weight. (a) Dataset for Sparse 9 variable with 50 cases (D50S9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (b) Dataset for Close 9 variable with 50 cases (D50C9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (c) Dataset for Sparse 9 variable with 1000 cases (D1KS9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship. (d) Dataset for Close 9 variable with 1000 cases (D1KC9). Dark shaded cells represent the best prediction of the correct causal relationship; Bright shaded cells represent the second best prediction of the correct causal relationship.

(a)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.14	0.35	0.17	1.00
	Y→X		0.43	0.65	0.33	0.00
	X  Y		0.43	0.00	0.50	0.00
Prior SC	X→Y		0.14	0.35	0.17	1.00
	Y→X		0.43	0.65	0.33	0.00
	X  Y		0.43	0.00	0.50	0.00
Prior WC	X→Y		0.14	0.35	0.17	1.00
	Y→X		0.43	0.65	0.33	0.00
	X  Y		0.43	0.00	0.50	0.00
PrePrior SC	X→Y		0.14	0.35	0.17	1.00
	Y→X		0.43	0.65	0.33	0.00
	X  Y		0.43	0.00	0.50	0.00
PrePrior WC	X→Y		0.14	0.35	0.17	1.00
	Y→X		0.43	0.65	0.33	0.00
	X  Y		0.43	0.00	0.50	0.00
BiDAG	X→Y		0.14	0.35	0.00	0.00
	Y→X		0.00	0.10	0.17	0.67
	X  Y		0.86	0.55	0.83	0.33
K2	X→Y		0.29	0.25	0.17	0.67
	Y→X		0.43	0.70	0.83	0.00
	X  Y		0.29	0.05	0.00	0.33
(b)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
Prior SC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
Prior WC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
PrePrior SC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
PrePrior WC	X→Y		0.00	0.50	0.50	0.20
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.25	0.25	0.20
BiDAG	X→Y		0.07	1.00	0.25	0.40
	Y→X		0.50	0.00	0.75	0.30
	X  Y		0.43	0.00	0.00	0.30
K2	X→Y		0.43	0.50	0.75	0.70
	Y→X		0.29	0.38	0.25	0.30
	X  Y		0.29	0.13	0.00	0.00
(c)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.14	0.40	0.17	1.00
	Y→X		0.14	0.05	0.00	0.00
	X  Y		0.71	0.55	0.83	0.00
Prior SC	X→Y		0.29	0.40	0.00	1.00
	Y→X		0.14	0.05	0.33	0.00
	X  Y		0.57	0.55	0.67	0.00
Prior WC	X→Y		0.14	0.30	0.33	1.00
	Y→X		0.00	0.15	0.00	0.00
	X  Y		0.86	0.55	0.67	0.00
PrePrior SC	X→Y		0.00	0.35	0.50	1.00
	Y→X		0.00	0.20	0.00	0.00
	X  Y		1.00	0.45	0.50	0.00
PrePrior WC	X→Y		0.14	0.30	0.33	1.00
	Y→X		0.00	0.10	0.00	0.00
	X  Y		0.86	0.60	0.67	0.00
BiDAG	X→Y		0.57	0.40	0.50	0.00
	Y→X		0.29	0.40	0.33	0.67
	X  Y		0.14	0.20	0.17	0.33
K2	X→Y		0.43	0.40	0.00	1.00
	Y→X		0.29	0.55	0.33	0.00
	X  Y		0.29	0.05	0.67	0.00
(d)
Algorithm		True	ØX  Y	ØX→Y	HX  Y	HX→Y
	Prediction
Random	X→Y		0.00	0.75	0.25	0.60
	Y→X		0.00	0.25	0.00	0.40
	X  Y		1.00	0.00	0.75	0.00
Prior SC	X→Y		0.00	0.38	0.25	0.60
	Y→X		0.00	0.38	0.25	0.20
	X  Y		1.00	0.25	0.50	0.20
Prior WC	X→Y		0.00	0.38	0.00	0.70
	Y→X		0.00	0.38	0.50	0.10
	X  Y		1.00	0.25	0.50	0.20
PrePrior SC	X→Y		0.00	0.38	0.25	0.70
	Y→X		0.00	0.38	0.00	0.10
	X  Y		1.00	0.25	0.75	0.20
PrePrior WC	X→Y		0.00	0.63	0.25	0.70
	Y→X		0.00	0.38	0.25	0.10
	X  Y		1.00	0.00	0.50	0.20
BiDAG	X→Y		0.00	0.75	0.75	0.40
	Y→X		0.14	0.25	0.25	0.60
	X  Y		0.86	0.00	0.00	0.00
K2	X→Y		0.43	0.38	0.75	0.50
	Y→X		0.57	0.38	0.25	0.50
	X  Y		0.00	0.25	0.00	0.00

show the algorithm’s most probable prediction rates of four causal pairwise relationships shown in Figure 4. As it was noticed earlier in Table 8 and Table 9, in all four datasets, all the MCMC ordering algorithms (Random, Prior, and PrePrior) outperformed the constrained variant algorithms (BiDAG, and K2) in confounded relationships H_{X Y} (no causal relationship) or H_X→Y (causal relationship). Algorithms with the order weight changed most the probable prediction rates of the confounded and causally independent predictions (H_{X Y}) of MCMC ordering algorithms except PrePrior with Weak Correct prior in D50S9 (one relationship prediction of Y→X was changed to X→Y). Another change by weighing order was noticed in D1KC9. There, algorithms with the order weight changed most the probable prediction rates of the confounded and causally independent predictions (H_{X Y}), and the confounded causal predictions (H_X→Y) of PrePrior with Weak Correct prior. For H_{X Y}, five relationships prediction of X→Y were correctly changed to the true underlying relationship, X Y; and for H_X→Y, one relationship prediction of Y→X was correctly changed to the true underlying relationship, X→Y.

4. Discussion and Future Work

The results from this study show that learning causal relationships from data is difficult, especially because many variables are hidden to us whether we are aware of that or not. Many Big Data analytic methods have been dealing with Big Data characteristics, such as its large volume, its fast growth in size, or its variety of data types. However, as we have shown in this study, it is important to incorporate and develop causal discovery frameworks to discover underlying mechanistic processes from Big Data.

Searching through order of variables in CBN and incorporating likelihood of the order helped us better search through plausible underlying mechanistic processes even when hidden variables were present. Further incorporating the prior of the order in the search process (PrePrior algorithm) showed an increase in performance, especially when there were a limited number of cases available, than other published methods that did not incorporate the prior of the order. We believe combining different types of data, e.g., environmental, genomics, neurological, social media, etc., will further strengthen our capabilities of discovering underlying mechanistic processes from Big Data.

Our study was focused in discovering underlying mechanistic processes using a small number of variables, i.e., <30. It was practical to use a small number of variables because we were focused on understanding the effect of hidden variables when learning causal relationships from data. Thus, the results reported here should be interpreted under this premise. As it was pointed out earlier, our study is limited in telling what the effects of the other characteristics of Big Data can contribute to the discovery of underlying mechanistic processes. Moreover, understanding those characteristics effects and combination effects of them will lead us to develop novel methods that will revolutionize the future Big Data analytics.

PrePrior algorithm can be extended in many different directions. As it was shown, with 1000 cases, all MCMC ordering algorithm could not converge in their predictions. This aspect can be overcome by incorporating constraint-based methods in conjunction with the Bayesian MCMC sampling methods using BDe (or BGe) scores. This will enable us to analyze not only larger samples, but also larger number of variables, one of the hall mark characteristics of Big Data. Also, it will extend the causal discovery ability when we model hidden variables explicitly or implicitly into the PrePrior algorithm.

5. Conclusions

We have shown searching through order of variables in CBN and incorporating the likelihood of the order helped us better understand the underlying mechanistic process that generated the data even when hidden variables were introduced in the experimental design. Also, a novel algorithm in searching through the order we proposed (PrePrior algorithm) showed promising performance in better learning the underlying mechanistic process that generated the data, especially confounded causal relationships with a reasonable number of samples (≈50).