Gambling Strategies and Prize-Pricing Recommendation in Sports Multi-Bets
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Processing
2.2. Defining and Labeling Profitable Rounds
3. Results
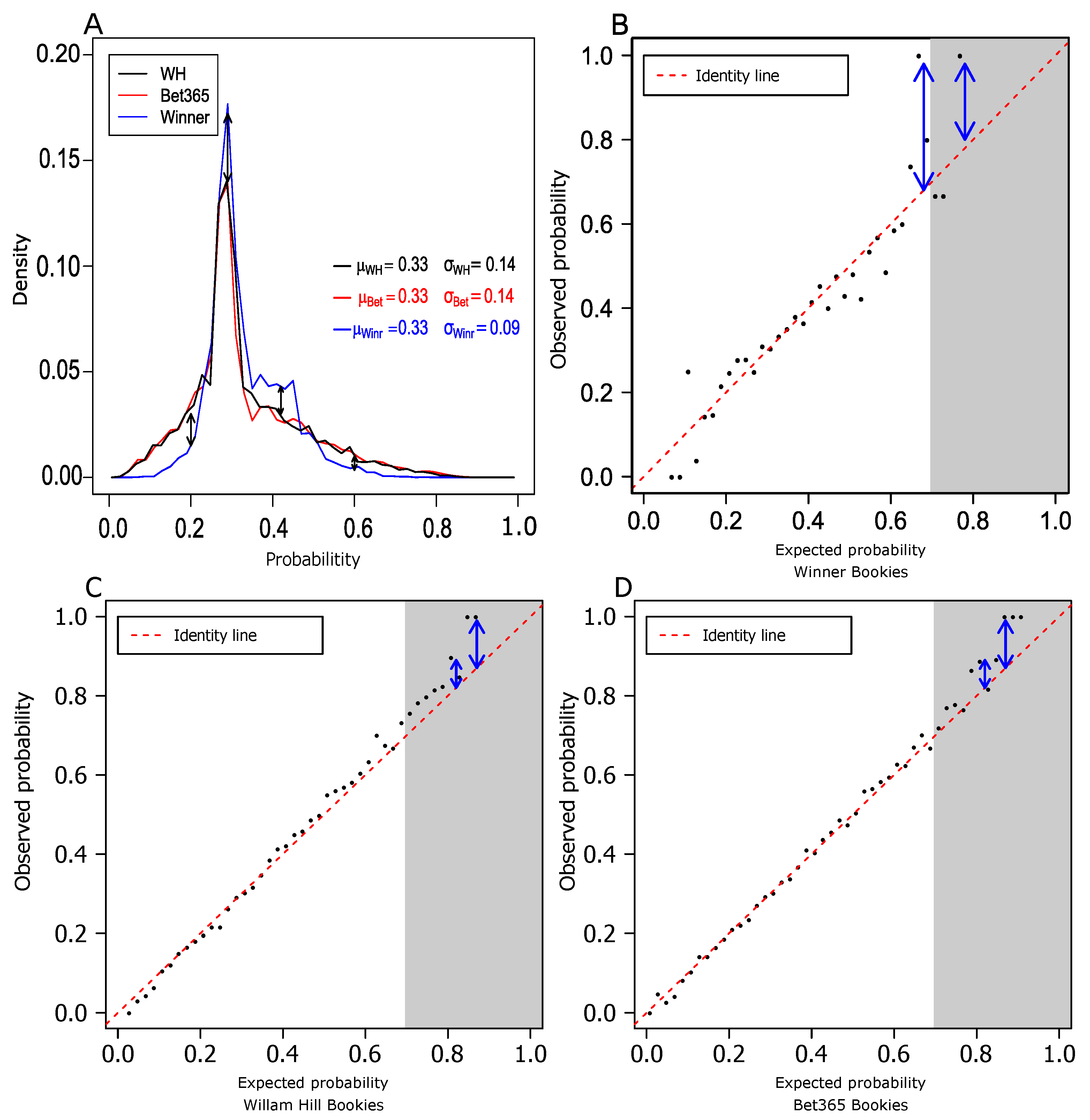
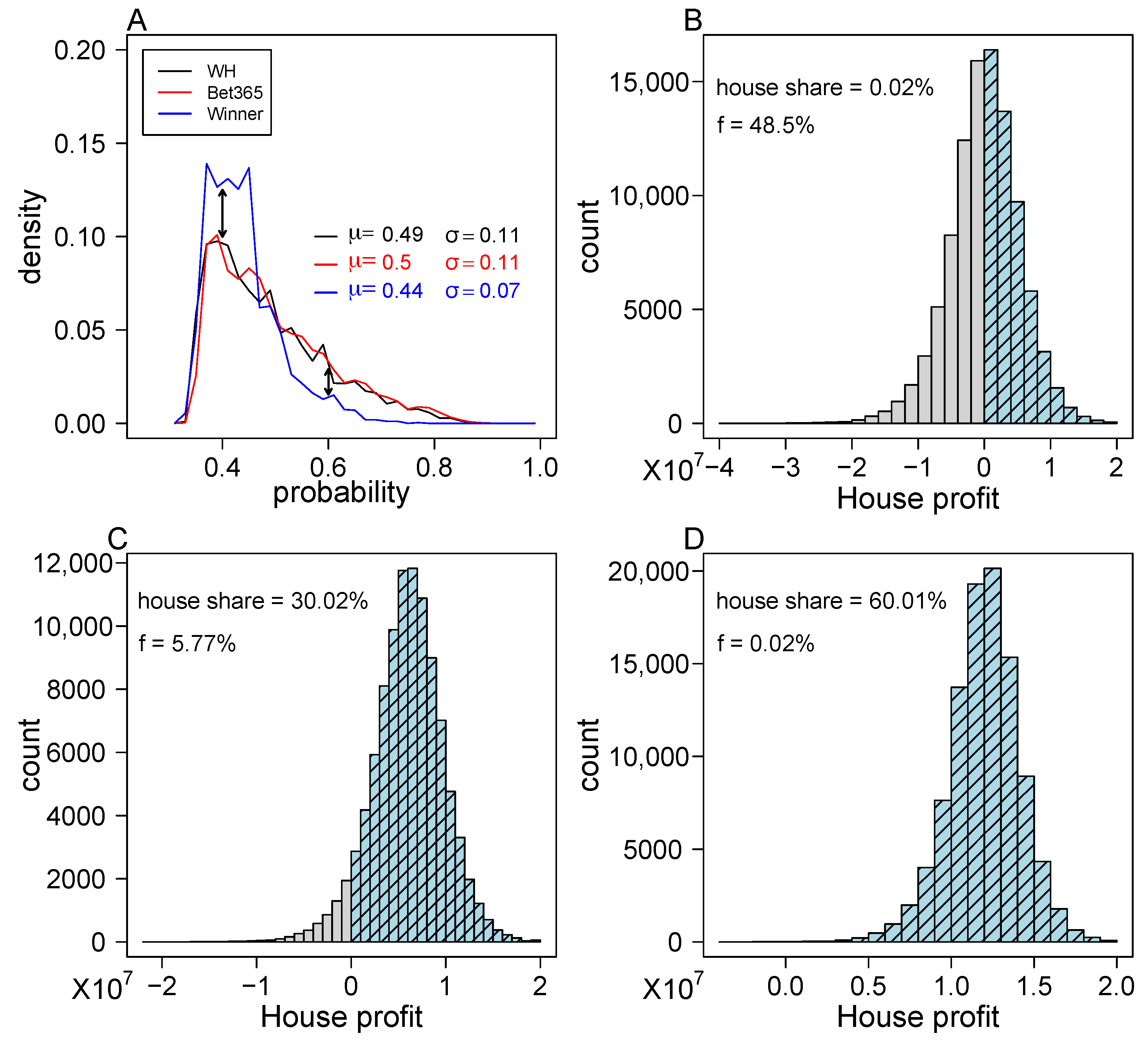
3.1. Market Efficiency of Single Bets
3.2. Single-Bet Gambling Profitable Strategy Is Hard to Find
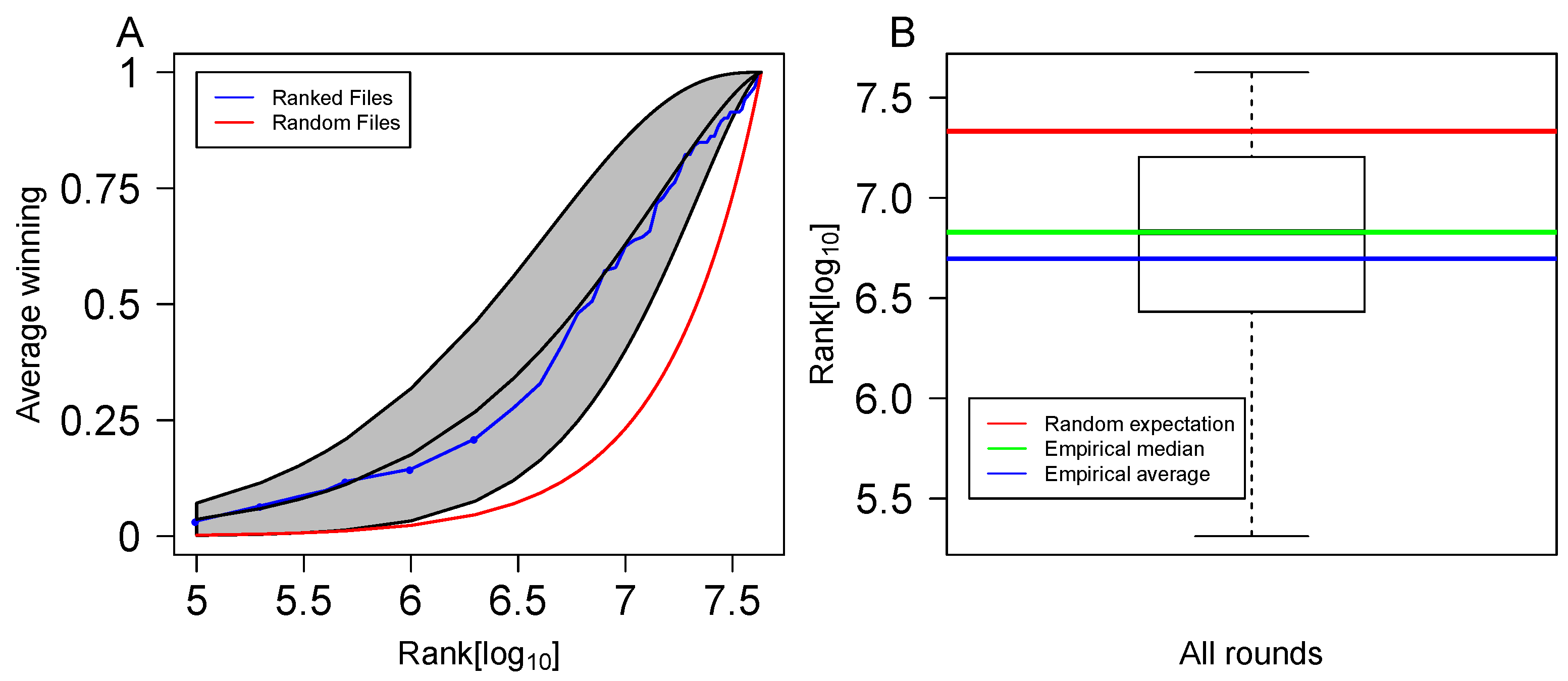
3.3. Form Ranking
3.4. Choosing the Best Rounds to Bet
3.4.1. Feature Extraction and Engineering
3.4.2. Model Selection
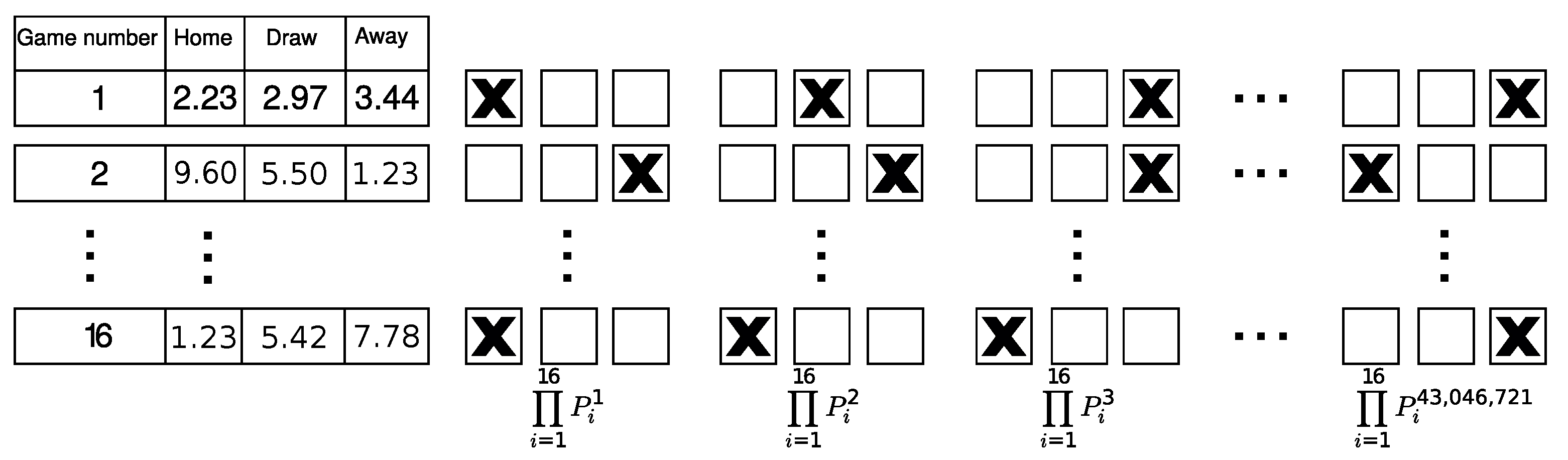
3.5. Proposed Fair Prize-Pricing Mechanism in Multi-Bets
3.5.1. Generalizing the Single-Bet Prize-Pricing Mechanism to Multi-Bets
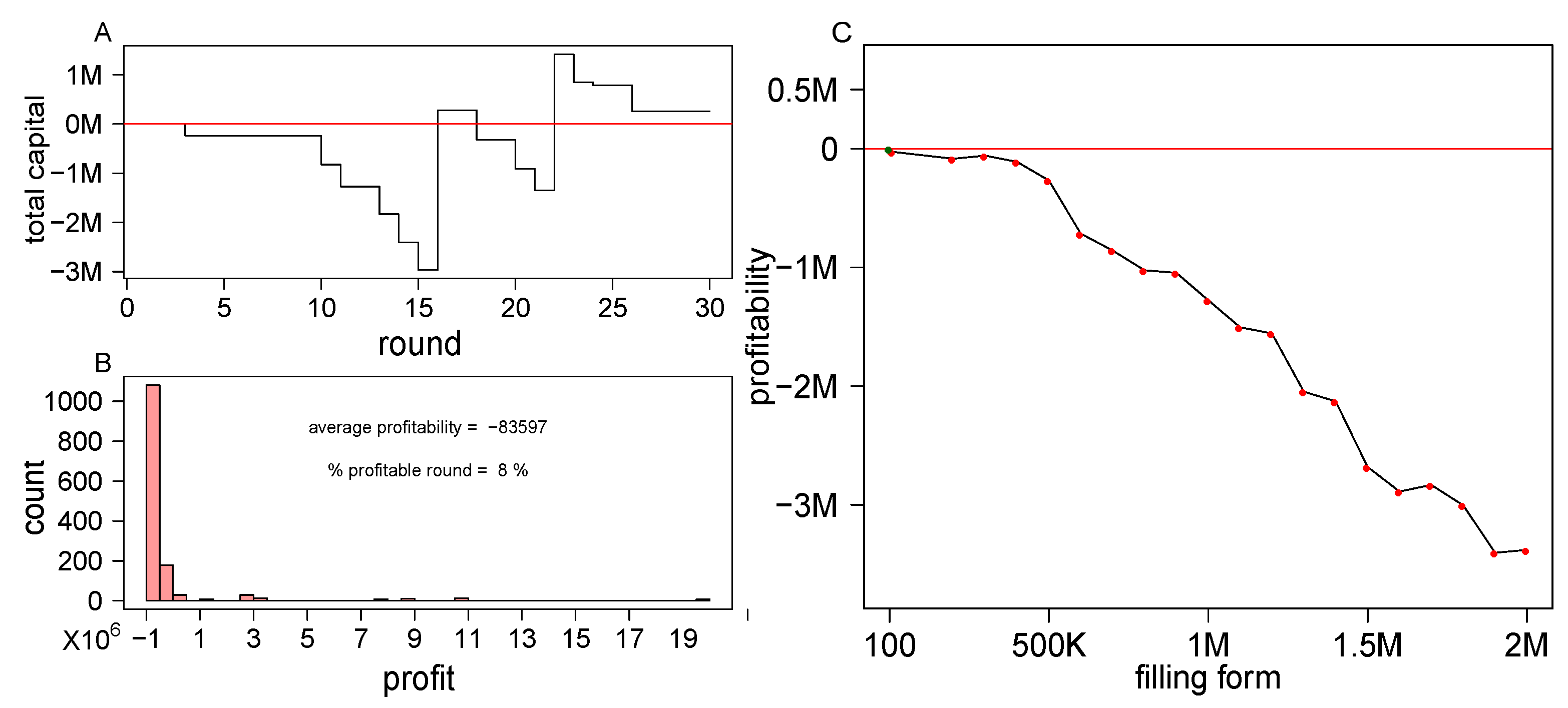
3.5.2. Risk Assessment of the Suggested Prize-Pricing Mechanism
4. Discussion
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davenport, T. Big Data at Work: Dispelling the Myths, Uncovering the Opportunities; Harvard Business Review Press: Brighton, MA, USA, 2014. [Google Scholar]
- Skinner, B.; Guy, S.J. A Method for Using Player Tracking Data in Basketball to Learn Player Skills and Predict Team Performance. PLoS ONE 2015, 10, e0136393. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Radicchi, F. Who Is the Best Player Ever? A Complex Network Analysis of the History of Professional Tennis. PLoS ONE 2011, 6, e17249. [Google Scholar] [CrossRef] [PubMed]
- Yaari, G.; Eisenmann, S. The Hot (Invisible?) Hand: Can Time Sequence Patterns of Success/Failure in Sports Be Modeled as Repeated Random Independent Trials? PLoS ONE 2011, 6, e24532. [Google Scholar] [CrossRef] [PubMed]
- Yaari, G.; David, G. “Hot Hand” on Strike: Bowling Data Indicates Correlation to Recent Past Results, Not Causality. PLoS ONE 2012, 7, e30112. [Google Scholar] [CrossRef]
- Stins, J.F.; Yaari, G.; Wijmer, K.; Burger, J.F.; Beek, P.J. Evidence for sequential performance effects in professional darts. Front. Psychol. 2018, 9, 591. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jensen, M.C. Some anomalous evidence regarding market efficiency. J. Financ. Econ. 1978, 6, 95–101. [Google Scholar] [CrossRef]
- Alper, O.; Somekh-Baruch, A.; Pirvandy, O.; Schaps, M.; Yaari, G. Effects of correlations and fees in random multiplicative environments: Implications for portfolio management. Phys. Rev. E 2017, 96, 022305. [Google Scholar] [CrossRef] [PubMed]
- Woodland, L.M.; Woodland, B.M. Market efficiency and profitable wagering in the national hockey league: Can bettors score on longshots? South. Econ. J. 2001, 983–995. [Google Scholar]
- Kelly, J. A New Interpretation of Information Rate. Bell Labs Tech. J. 1956, 35, 917–926. [Google Scholar] [CrossRef]
- Bailey, M.; Clarke, S.R. Predicting the match outcome in one day international cricket matches, while the game is in progress. J. Sport. Sci. Med. 2006, 5, 480. [Google Scholar]
- Paul, R.J.; Weinbach, A.P. An Analysis of the Last Hour of Betting in the NFL. Int. J. Sport Financ. 2011, 6, 307. [Google Scholar]
- Hucaljuk, J.; Rakipović, A. Predicting football scores using machine learning techniques. In Proceedings of the 2011 34th International Convention, Opatija, Croatia, 23–27 May 2011; pp. 1623–1627. [Google Scholar]
- Ganeshapillai, G.; Guttag, J. A data-driven method for in-game decision making in MLB. In Proceedings of the MIT Sloan Sports Analytics Conference, Chicago, IL, USA, 11–14 August 2013. [Google Scholar]
- Surowiecki, J. The Wisdom of Crowds; Anchor Books: New York, NY, USA, 2005. [Google Scholar]
- Sinha, S.; Dyer, C.; Gimpel, K.; Smith, N.A. Predicting the NFL using Twitter. arXiv 2013, arXiv:1310.6998. [Google Scholar]
- Hidayat, A. Phantom, J.S. 2011. Available online: https://github.com/ariya/phantomjs (accessed on 4 July 2016).
- Fama, E.F. Random walks in stock market prices. Financ. Anal. J. 1995, 51, 75–80. [Google Scholar] [CrossRef] [Green Version]
- Gray, P.K.; Gray, S.F. Testing market efficiency: Evidence from the NFL sports betting market. J. Financ. 1997, 52, 1725–1737. [Google Scholar] [CrossRef]
- Cortis, D. Expected values and variances in bookmaker payouts: A theoretical approach towards setting limits on odds. J. Predict. Mark. 2015, 9, 1–14. [Google Scholar] [CrossRef]
- Yaari, G.; Solomon, S. Cooperation evolution in random multiplicative environments. Eur. Phys. J. B. 2010, 73, 625–632. [Google Scholar] [CrossRef] [Green Version]
- Hassanniakalager, A.; Sermpinis, G.; Stasinakis, C.; Verousis, T. A conditional fuzzy inference approach in forecasting. Eur. J. Oper. Res. 2020, 283, 196–216. [Google Scholar] [CrossRef]
- Lunardon, N.; Menardi, G.; Torelli, N. ROSE: A Package for Binary Imbalanced Learning. R J. 2014, 6, 82–92. [Google Scholar] [CrossRef] [Green Version]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pirvandy, O.; Fridman, M.; Yaari, G. Gambling Strategies and Prize-Pricing Recommendation in Sports Multi-Bets. Big Data Cogn. Comput. 2021, 5, 70. https://doi.org/10.3390/bdcc5040070
Pirvandy O, Fridman M, Yaari G. Gambling Strategies and Prize-Pricing Recommendation in Sports Multi-Bets. Big Data and Cognitive Computing. 2021; 5(4):70. https://doi.org/10.3390/bdcc5040070
Chicago/Turabian StylePirvandy, Oz, Moti Fridman, and Gur Yaari. 2021. "Gambling Strategies and Prize-Pricing Recommendation in Sports Multi-Bets" Big Data and Cognitive Computing 5, no. 4: 70. https://doi.org/10.3390/bdcc5040070
APA StylePirvandy, O., Fridman, M., & Yaari, G. (2021). Gambling Strategies and Prize-Pricing Recommendation in Sports Multi-Bets. Big Data and Cognitive Computing, 5(4), 70. https://doi.org/10.3390/bdcc5040070





