JAMPI: Efficient Matrix Multiplication in Spark Using Barrier Execution Mode

Abstract

The new barrier mode in Apache Spark allows for embedding distributed deep learning training as a Spark stage to simplify the distributed training workflow. In Spark, a task in a stage does not depend on any other tasks in the same stage, and hence it can be scheduled independently. However, several algorithms require more sophisticated inter-task communications, similar to the MPI paradigm. By combining distributed message passing (using asynchronous network IO), OpenJDK’s new auto-vectorization and Spark’s barrier execution mode, we can add non-map/reduce-based algorithms, such as Cannon’s distributed matrix multiplication to Spark. We document an efficient distributed matrix multiplication using Cannon’s algorithm, which significantly improves on the performance of the existing MLlib implementation. Used within a barrier task, the algorithm described herein results in an up to 24% performance increase on a 10,000 × 10,000 square matrix with a significantly lower memory footprint. Applications of efficient matrix multiplication include, among others, accelerating the training and implementation of deep convolutional neural network-based workloads, and thus such efficient algorithms can play a ground-breaking role in the faster and more efficient execution of even the most complicated machine learning tasks.

1. Introduction

The past decade has seen the emergence of two immensely powerful processes in tandem: the rise of big data handling solutions, such as Apache Spark on one hand, and the apotheosis of deep learning as the tool of choice for demanding computational solutions for machine learning problems on the other hand. Yet, at its essence, big data and deep learning remain not only separate communities but also significantly separate domains of software. Despite deep learning over big data becoming a crucial tool in a range of applications, including in computer vision [1,2], bioinformatics [3,4,5,6], natural language processing (NLP) [7,8,9,10], clinical medicine [11,12,13,14,15,16], anomaly detection in cybersecurity and fraud detection [17,18,19], and collaborative intelligence/recommender systems [20,21,22,23], its full potential remains to be harnessed. The primary impediment in this respect is largely a divergence of attitudes and concerns, leading to two divergent paradigms of development:

• The big data paradigm, primarily designed around RDDs and the the DataFrame-based API. This outlook has dominated the development of Apache Spark.
• The DL/ML paradigm, which is primarily focused on efficient linear algebra operations to facilitate machine learning approaches, especially matrix algebra for deep neural networks.

The future of deep learning over big data depends greatly on facilitating the convergence of these two worlds into a single, unified paradigm: the use of well-designed big data management tools, such as Apache Spark, to interoperate with the demands of deep learning. The road towards this convergence depends on the development of efficient matrix primitives that facilitate rapid calculations over distributed networks and large data sets.

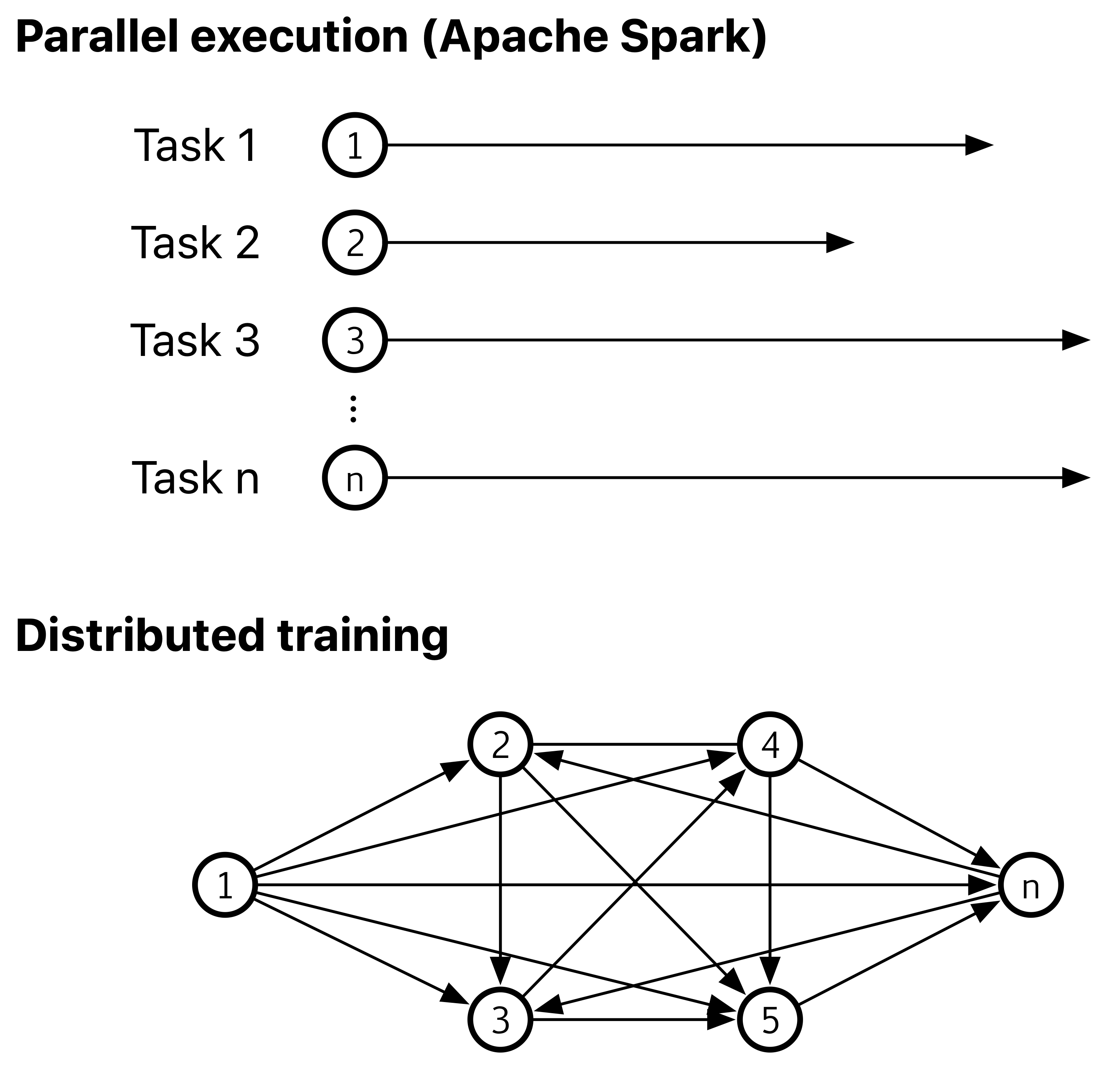
The current execution model of Apache Spark is principally focused on independent, embarrassingly parallel, tasks that are run and scaled, but the needs of deep learning are primarily focused on distributed training: the performance of completely communicating and coordinating tasks, optimized for interconnectivity rather than independent parallel running, while also maintaining scalability and efficiency. With the recent introduction of the barrier execution mode in Apache Spark, it has finally become possible to construct a computational approach that allows for such networked execution to take place, facilitating distributed training of deep neural networks (see Figure 1).

Prior work on efficient matrix algebra operations has primarily focused on spatial separation. Thus, for instance, Bosagh Zadeh et al. (2016) discuss the most frequent algorithmic approach to solving linear algebra problems in Spark: separating matrix and vector operations, retaining the latter with the driver node for single node execution and distributing the former across the cluster [24]. This is a convenient method to allow for running legacy code written for single node devices on large Spark clusters, but does not generalize to a wide range of problems. A more promising approach is Marlin, a more generic set of matrix algebra primitives (including multiplication), proposed by Gu et al. (2015) [25]. Marlin’s performance is similar to that of MLLib, and a somewhat better performance is attained by Stark, a scalable matrix multiplication primitive using Strassen’s algorithm [26]. However, the time complexity of Strassen’s algorithm is $\mathcal{O}\left(n^{2.807355}\right)$, which is inherently less advantageous than other approaches, such as Coppersmith–Vinograd (1987) [27]. Neither this nor the somewhat faster algorithm introduced by Williams (2012) leverage a large number of cores as efficiently as Cannon’s algorithm [28].

This algorithm [29] and its generalization (Lee et al., 1997) rely on a toroidal mesh of interconnected nodes [30]. While the use of MPI as the vehicle of connecting the nodes distributed along the toroidal mesh has been considered in the past (e.g., Li et al., 2012), [31] to the best of the authors’ knowledge, this is the first time such a communication interface has been natively implemented in Spark for matrix multiplication.

JAMPI (Java Assisted Matrix Product with Inter-task communication), the framework described in this paper, is an efficient and rapid solution to an aspect of efficient matrix primitives, namely matrix multiplication. By integrating JDK’s new Vector API, asynchronous network IO (nio) for distributed message passing and Spark’s barrier mode, a pure Scala implementation of Cannon’s 2.5D matrix multiplication algorithm can be devised that is significantly more efficient than MLlib’s BlockMatrix.multiply function. JAMPI thus avoids reliance on foreign, low level or native code in combination with JNI, on the one hand, being a pure Scala implementation. On the other hand, it provides a pre-written framework that integrates with Spark as a native task rather than an external MPI procedure call, and handles inter-task communication directly, yielding performance benefits that would otherwise be associated with a low-level MPI implemented resource negotiation framework.

1.1. Cannon’s Algorithm

Matrix multiplication plays a significant role in a range of practical applications, including (but not limited to) scientific computing, non-linear modeling, agent-based models and the training of deep convolutional neural networks (deep learning). The proliferation of deep learning as the cognitive technology of choice for problems with large source data sets and high-dimensional or high-order multivariate data means that efficiency gains in the underlying linear algebra primitives has the potential to enable significant performance benefits in a wide range of use cases. In particular, constructing primitives that leverage computational capacity through rapid parallel computation and efficient interchange lends itself as an avenue towards these performance gains. While packages comprising efficient matrix primitives already exist [32], these often operate at a low level and do not integrate well with existing and proven solutions to manage large computational loads.

The matrix multiplication operation ★ for an $p\times q$ matrix $\mathbf{A}$ and an $q\times r$ matrix B is defined so that for the resultant matrix $\mathbf{C}=\mathbf{A}★\mathbf{B}$, each element $c_{i,j}$ is the dot product of the i-th row of $\mathbf{A}$ and the j-th column of $\mathbf{B}$—i.e.,

$$c_{i,j}=\sum _{k=1}^n{a}_{i,k}{b}_{k,j}$$

(1)

The multiplication of square matrices constitutes a special case. For a square matrix of order n—i.e., an $n\times n$ matrix—a special case is obtained, which can be resolved efficiently using Cannon’s algorithm [29].

For a square matrix of order n—i.e., $n\times n$—Cannon’s algorithm uses a toroidally connected mesh ${\mathbf{P}}^{n\times n}$ of $n^2$ processes. Rendered in pseudocode, the algorithm (Algorithm 1) can be expressed as follows for p processors:

Algorithm 1 Cannon’s algorithm

1: for all i = 0 : $\sqrt{p}$ − 1 do   2:     CShift left A[i; :] by i   3: for all j = 0 : $\sqrt{p}$ − 1 do  4:     CShift up B[:; j] by j   5: for k = 0 : $\sqrt{p}$ − 1 do  6:     for i = 0 : $\sqrt{p}$ − 1, j = 0 : $\sqrt{p}$ − 1 do  7:         C[i, j] += A[i, j] * B[i, j]  8:         CShift left A[i; :] by 1  9:         CShift up B[:; j] by 1

Cannon’s algorithm is designed to be performed on a virtual square grid $\mathbf{P}$ of p processors (i.e., a $\sqrt{p}\times \sqrt{p}$ matrix). The multiplicand and multiplier matrices $\mathbf{A}$ and $\mathbf{B}$ are laid out on $\mathbf{P}$, after which the i-th row of $\mathbf{A}$ is circularly shifted by i to the left and the j-th column of $\mathbf{B}$ circularly shifted by j elements up. Then, n times, the two entries mapped onto $p_{i,j}$ are multiplied and added onto the running value of $p_{i,j}$, after which each row of $\mathbf{A}$ is shifted left by one element and each column of $\mathbf{B}$ is shifted up by one element.

Standard methods of multiplying dense matrices require $O\left(n^3\right)$ floating operations for an $n\times n$ matrix. Cannon’s algorithm improves on this by reducing it to $O\left(\frac{n^3}{p}\right)$. In particular, because of the fact that memory is not dependent on the number of processors, it scales dynamically with the number of processors. This makes it an attractive candidate for implementation as a high-performance distributed matrix multiplication primitive.

1.2. Spark’s Barrier Mode

Spark’s barrier mode is a new mode of execution introduced to Apache Spark as part of Project Hydrogen [33]. Barrier execution features gang scheduling on top of the MapReduce execution model to support distributed deep learning tasks that are executed or embedded as Spark steps. The current implementation ensures that all tasks (limited to mapPartitions) are executed at the same time, and collectively cancels and restarts all tasks in the case of failure events. In addition to true parallel execution, the workers’ host names and partition identifiers are accessible inside the tasks, alongside a barrier call, similar to MPI’s MPI_Barrier function [34].

While this functionality is sufficient to support the primary use case of Spark’s barrier mode—namely, executing embedded MPI or other foreign (i.e., non-Spark and non-JVM, steps within a Spark application)—it does not provide any inter-task communication primitive to implement the same algorithms within JVM/Spark native steps. In fact, the design documentation for Spark’s barrier mode clearly defines this as outside the scope of the project, stating that beyond a simple BarrierTaskContext.barrier() call, no intra-communication functionality will be part of the implementation. It is assumed that such functionality would be handled by the user program. It is our view, based on our extensive experience with implementing deep learning solutions on distributed systems, that this is a clear show-stopper: if Spark is to be a force to be reckoned with as the data layer for deep learning applications over big data, it should not force execution outside Spark’s boundaries.

2. Methods

2.1. Cannon’s Algorithm on MPI

The MPI version of the algorithm described in Section 1.1 relies on MPI’s Cartesian topology. After setting up a 2D communication grid of processors with MPI_Cart_create, processors exchange data with their neighbors by calling MPI_Sendrecv_replace. In the main loop, each processor executes a local dot product calculation, then shifts the results horizontally for matrix a and vertically for matrix b. In our benchmarks, we used MPICH version 3.3.2 as the underlying MPI implementation.

To speed up matrix multiplication, we applied -O4 -ftree-vectorize -march=native GNU C compiler flags to ensure vectorized code execution. By vectorization, we refer to using SIMD (Single Instruction, Multiple Data) CPU features, more precisely Advanced Vector Extensions (AVX-512F) that allows for the faster execution of fused multiply–add (FMAC) operations in local/partial matrix dot product steps. After compiling our code with GCC 7.3.1, we ensured that the disassembled code contains vfmadd231sd instruction for vectorized FMAC.

2.2. JAMPI

JAMPI is a de novo native Scala implementation of Cannon’s algorithm, as described in Section 1.1. For message passing, we built a nio-based asynchronous message passing library that mimics MPI’s Cartesian topology and send-receive-replace functionality. To avoid unnecessary memory copies and to optimize performance for both throughput and latency, our PeerMessage object allocates fixed 8MB off-heap buffers for both sending and receiving data. Send and receive network operations are executed asynchronously and in parallel.

The matrix multiplication is embedded into a barrier execution task, which is parametrized by the the number of partitions, the local partition ID, the hostnames for the other partitions (address from BarrierTaskContext.getTaskInfos()), as well as the local matrix pairs from the RDD.

• def dotProduct[T : ClassTag](
•   partitionId: Integer,
•   numOfPartitions: Integer,
•   hostMap: Array[String],
•   matrixA: Array[T],
•   MatrixB: Array[T]): Array[T]

JAMPI supports double, float and int Java primitive data types passed as Java Arrays.

2.3. Vectorization Using Panama OpenJDK

In order to achieve performance on par with the optimized MPI implementation for local dot product steps, we used JVM’s native vector intrinsics and super-word optimization capabilities for both JAMPI and MLlib Spark application benchmarks. The most recent and most comprehensive vectorization support in JVM is found in the Vector API module, part of OpenJDK’s Project Panama. While the Vector API module is currently in incubation status, we consider it stable enough to use for both the Spark platform and application code.

For fair benchmarking, we avoided using Vector<> objects or advanced methods, such as manual unrolling. While these techniques could potentially further improve performance, our goals were to compare the distributed algorithms’ performances with the same CPU opcodes used in local matrix multiplications. From the JIT compiler outputs, we confirmed that both Spark applications were using vfmadd231sd, just as in the GCC compiled MPI version.

To use the new vector intrinsics’ features, we built a custom OpenJDK package from the tip of the panama/dev branch (dev-442a69af7bad). The applied JVM flags were –add-modules jdk.incubator.vector and -XX:TypeProfileLevel=121 for both JAMPI and MLlib applications.

2.4. Apache Spark Mllib

We used Apache Spark MLlib’s built-in BlockMatrix.multiply() as a baseline to compare with JAMPI’s speed and resource usage. It is known that MLlib’s implementation is often faster if the number of partitions exceeds that of worker cores (typically by a factor of 2–4 at least), a scenario known as over-partitioning. To ensure that this is adequately reflected, we performed two test runs—a ‘’normal” test run, where partitions are set to equal the number of worker cores, and an ‘’over-partitioned” test run, where partitions equal four times the number of worker cores.

2.5. Test Protocols

All tests were performed on Amazon Web Services EC2 instances using m5 instance types with Intel^® Xeon^® Platinum 8175M CPUs and 4GB RAM per core. Instance configurations are described in

Table 1. Instance configurations by worker cores, nodes and partitions.

Total Worker Cores	Instance Type	Nodes	Partitions
1	m5.large	1	1
16	m5.xlarge	4	4
64	m5.2xlarge	8	8
256	m5.2xlarge	32	8

. Tests were conducted on Apache Spark 3.0.0-preview2 with a separate master node. The driver process was initiated from the master node, and its resource consumption is not included in the results. For single core tests, 2-core CPUs were used, with the second CPU core having been manually disabled in the VM. For each permutation of matrix size and number of cores, 100 runs were performed and the resulting runtimes were statistically analysed.

Applications reported only the dot product execution time. A single one-value reducer (avg) was included to trigger RDD reduction/collection on Spark without moving substantial amounts of data to the driver process. Timings thus exclude the MPI and Spark application startup times, but included the time required to establish a barrier task step during the RDD reduction step. For testing, random matrices composed of uniformly distributed 64-bit floating point elements were used. Test scenarios were performed ten times, capturing execution time, CPU and memory consumption, and mean values are reported. Test execution relied on the same set of matrices for every implementation, thereby ensuring a fair comparison. Test scenarios, as well as the original JAMPI source code, are available online [35].

2.6. Scalability Analysis

An important aspect of any distributed algorithm is its ability to scale up as the problem size increases. This is crucial for proving the value of an algorithmic solution, since it demonstrates its ability to solve increasingly complex instances of the same fundamental problem effectively. There are intrinsic issues when scaling distributed multi-processor algorithms. It is known, for instance, that the memory requirement for each processor increases as we add processors to a computation. Therefore, we must analyze the effect of problem size on the memory requirements per processor.

For Cannon’s algorithm, multiplying two square matrices of size $n\times n$, the problem size W is on the order of $n^2$—i.e.,

$$W=\mathcal{O}\left(n^2\right)$$

(2)

The sequential time, that is when p = 1, is

$$T_1\left(n\right)=\mathcal{O}\left(n^3\right)$$

(3)

For p processors, the execution time for a matrix of size $n\times n$ is given as $T_p\left(n\right)$. It follows that the parallelization of the problem yields a speed-up, calculated as $\frac{W}{T_p\left(n\right)}$.

In addition, the parallel execution of an $n\times n$ problem size over p processors will incur a performance overhead of $T_o(n,p)$, including all communication costs.

It is known that the communication cost D, which describes the amount of data being shifted across the p processors, can be calculated as

$$D=O\left(\frac{n^2}{\sqrt{p}}\right)$$

(4)

Using the following iso-efficiency relationship of parallel systems,

$$T_1\left(n\right)\ge c{T}_o(n,p)$$

(5)

Substituting Equation (3) in Equation (5), it follows that

$$n^3\ge c\sqrt{p}{n}^2\Rightarrow n\ge c\sqrt{p}$$

(6)

It thus follows from Equation (6) and the definition of W in Equation (2) that

$$\frac{M\left(c\sqrt{p}\right)}{p}=\frac{c^{2}p}{p}=c^2$$

(7)

More generally, it holds that, for a problem size W and p processors, Cannon’s Algorithm memory requirements increase by a constant factor $c^2$ that are independent of the number of processors p involved in the computation. Since the memory requirements per processor increase linearly, without a direct relationship to p, it can be said that Cannon’s algorithm is extremely scalable.

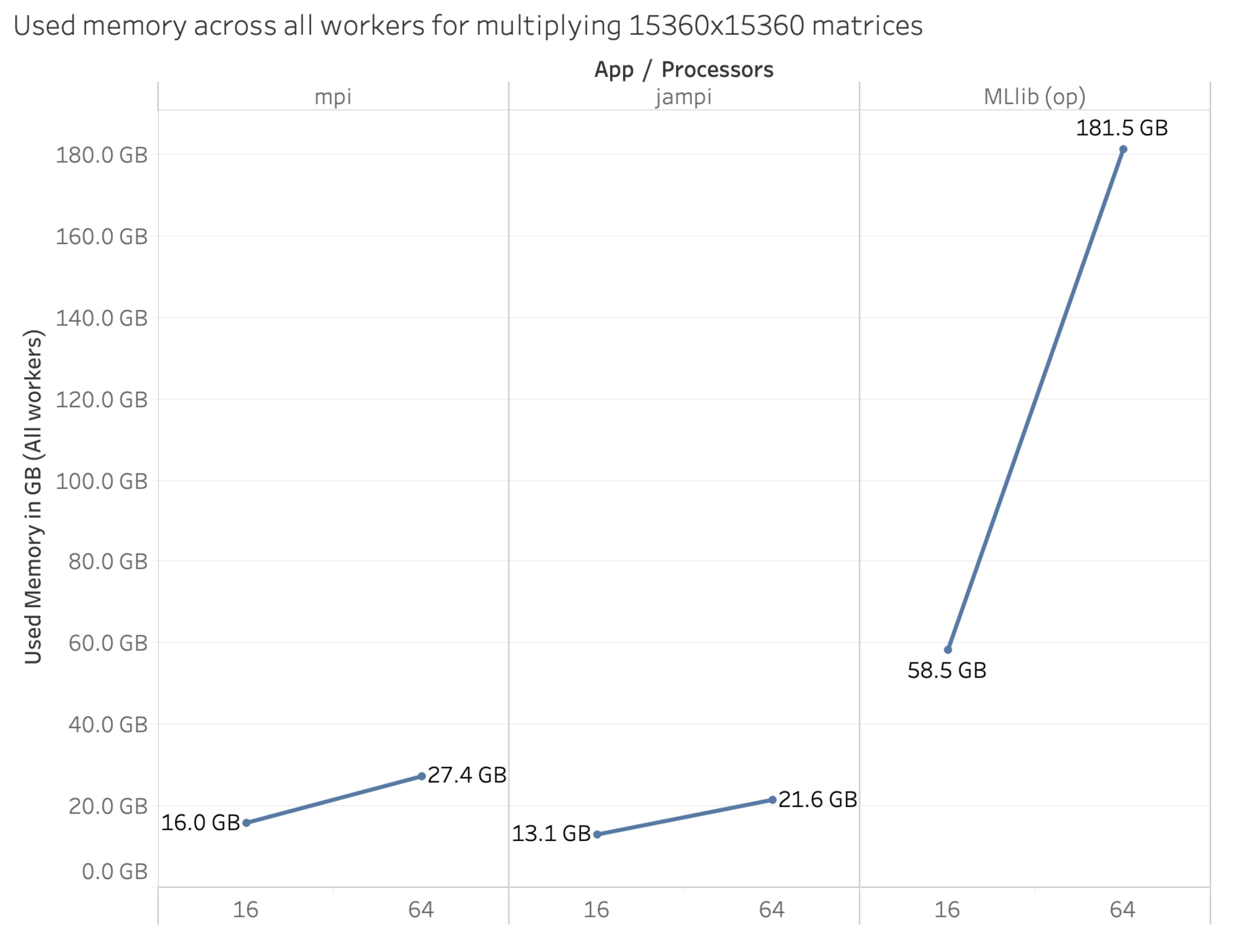
Figure 2 illustrates this scaling behavior comparatively between JAMPI, a pure MPI implementation and MLlib. JAMPI, as well as the MPI algorithm test case, are both direct implementations of Cannon’s algorithm, thus having the same scalability behavior.

It is evident from Figure 2 that MLLib’s memory requirement increases quite fast, suggesting that its scalability factor is larger than that of Cannon’s algorithm (i.e., it is less scalable). This is a key limitation of MLlib and Spark when compared to MPI and JAMPI alike, which scale better. Indeed, in some test scenarios, we have been unable to scale MLlib beyond a certain problem size, indicating that, in addition to its poor performance compared to MPI and JAMPI, it is also limited in the maximum problem size it can accommodate with a set level of resources. Neither JAMPI nor the native MPI implementation is so limited.

3. Results

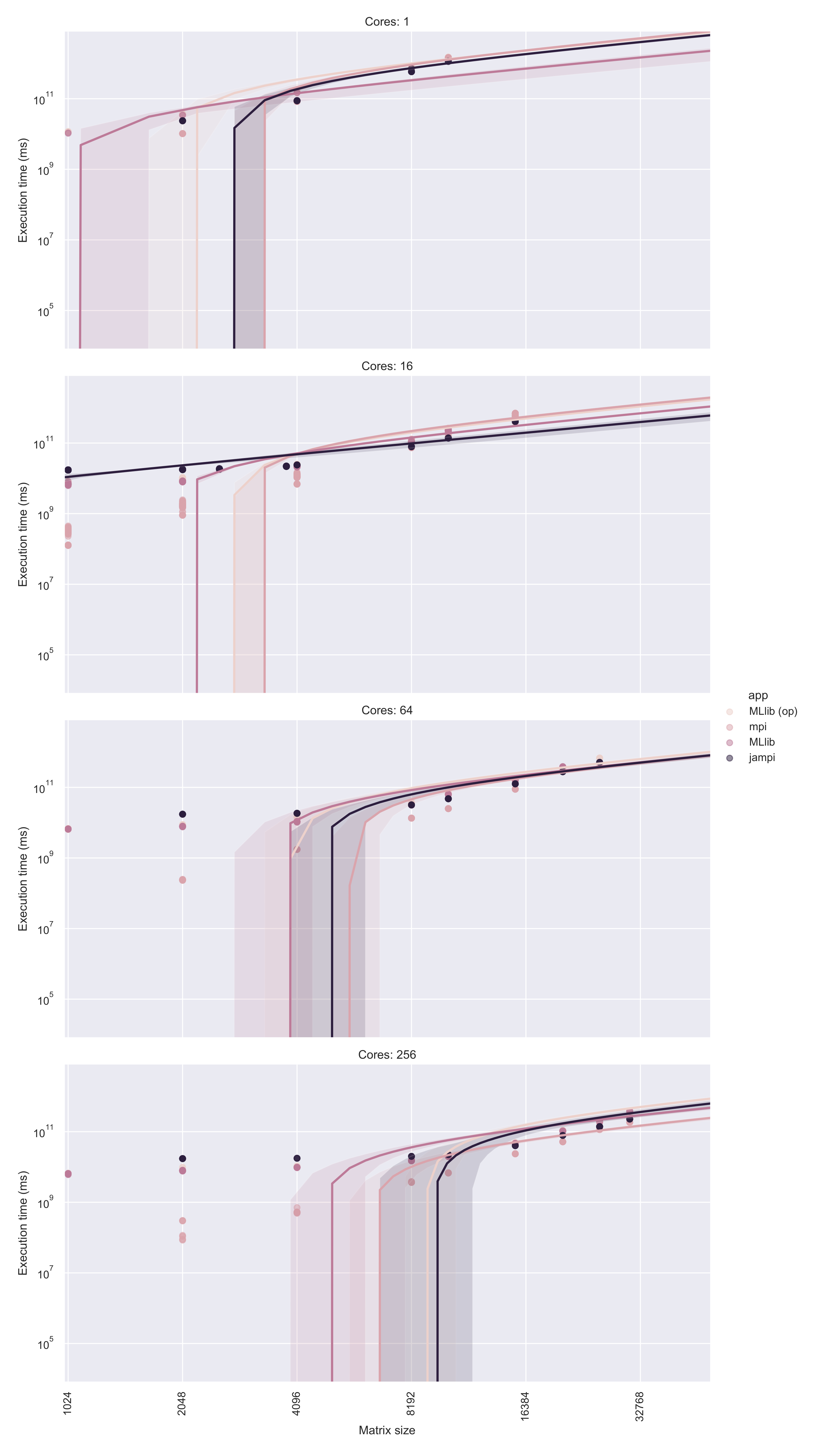
Comparative analysis of runtimes over a range of matrix sizes reveals that JAMPI is significantly superior to MLlib, even when over-partitioned (see Figure 3; over-partitioning is denoted by op). When normalized against JAMPI’s execution times over 16 and 64 cores, execution time is slower for smaller matrices (under 4096 × 4096 elements) due to the need to establish and run the barrier execution task. However, beyond a trivial problem size, JAMPI and the MPI implementation rapidly become significantly more efficient, regardless of the number of cores. Notably, plain MLlib (i.e., without over-partitioning) was unable to accommodate a problem size beyond 10,240 × 10,240 (for 16 cores) or 20,480 × 20,480 (for 64 cores).

3.1. Memory Usage

Memory usage has been a documented limiting factor, with pure MLlib reaching execution limits at relatively trivial matrix dimensions per processor (

Table 2. Out-of-memory boundary sizes for MLlib, in normal (MLlib) and over-partitioned (MLlib (op)) mode.

Cores	MLlib	MLlib (op)
1	4096	10,240
16	10,240	15,360
64	20,480	25,600
256	30,720	51,200

). While over-partitioning slightly increases the maximum matrix size, MLlib suffers from not only lower performance but also a memory consumption upper bound that limits its ability to scale to larger problem sizes.

Our research indicates that, for a 10,240 × 10,240 element standard matrix, JAMPI and MPI perform approximately equally (4889 MB vs. 5108 MB, respectively, for 256 cores), while both over-partitioned and regular MLlib execution create a marginally larger memory footprint (6049 and 6423 MB, respectively, for 256 cores). However, with increasing problem size, differences become vastly apparent: for a 30,720 × 30,720 element matrix, MPI and JAMPI continue to require a constant memory footprint (5572 and 6084 MB, respectively), while the same problem size requires 24,525 MB with over-partitioning and 29,445 MB without. In other words, JAMPI and MPI memory burden increases constantly, regardless of the number of cores, while MLLib’s memory consumption increases rapidly, as Figure 2 indicates. For instance, when processing a 30,720 × 30,720 matrix size, MLlib requires a 4.03 (with over-partitioning) to 4.84 (without over-partitioning) times larger memory allocation.

Comparative analysis of memory usage (see Figure 2) shows that JAMPI is generally on par (within 30%) of the pure MPI implementation, while MLlib typically requires approximately four times the amount of memory allocation that the MPI based approaches demand, with regular MLlib requiring typically 15% to 50% more memory than over-partitioned implementations.

3.2. Performance

Comparing performance in terms of execution time shows a similar picture in all multi-core environments. MLlib, both with and without over-partitioning, presents a lower execution time compared to JAMPI in trivial-sized matrices (4096 × 4096 for 16- and 64-core environments, 10,240 × 10,240 for 256-core environments).

However, MLlib execution times rapidly increase. At the largest matrix sizes with 256 cores, for instance, JAMPI consistently outperforms over-partitioned MLlib (see

Table 3. Large matrix runtime comparison (runtime in ${10}^{11}$ seconds) between MLlib, overpartitioned (op) MLlib, JAMPI and pure MPI.

Matrix Size	MLlib (SD)	MLlib (op) (SD)	MPI	JAMPI (SD)	% JAMPI vs. MLlib (op) Speed-Up
30,720	3.782 (0.057)	2.868 (0.0124)	1.837 (0.008)	2.284 (0.009)	25.569%
51,200	–	11.554 (0.022)	–	9.749 (0.015)	18.514%

) and while somewhat slower than a pure MPI implementation on a 30,720 × 30,720 element matrix, it does not have to contend with MPI’s out-of-memory limitation. As Figure 3 shows, a pure MPI implementation is somewhat faster than JAMPI, but JAMPI greatly outpaces (by as much as 25%) the runtime of an over-partitioned MLlib implementation over the same matrix. This demonstrates a clear benefit for large matrix operations in particular, given that this additional performance increase does not come at the cost of additional development time burden, since JAMPI is implemented in native Spark. Detailed statistics for each permutation of application, core count and matrix size are enclosed as Supplement 1.

The comparative analysis of performance indicators shows that, while a pure MPI implementation is somewhat faster than JAMPI, this difference is significantly smaller than the difference between the MLlib implementation and JAMPI, proving that JAMPI is an efficient and fast alternative to pure MPI applications without a significant performance overhead.

4. Discussion

Cannon’s algorithm can be implemented quite conveniently using a barrier task within Spark, providing a native interpretation of this highly efficient distributed linear algebra primitive. By using barrier tasks to reimplement matrix primitives with Panama’s built-in efficient vectorization and asynchronous communication (as provided by nio in this case), very significant performance gains can be effected on frequently used tasks. The proposed implementation of Cannon’s algorithm, for instance, has yielded an almost 25% decrease in execution time, and has been superior to the MLlib implementation on all core sizes above trivial matrix sizes. While this algorithm is limited to square matrices, the general effectiveness gains are indicative of a strong theoretical and practical benefit of further research in ways efficient matrix primitives can be integrated with big data solutions such as Apache Spark. Further research in this field is required to create a coherent stack of matrix primitives in order to allow for modern deep learning applications, relying greatly on such building blocks to leverage the performance benefits of big data solutions in storing and managing data as a layer of an integrated framework of large-scale machine learning.