Data Stream Clustering Techniques, Applications, and Models: Comparative Analysis and Discussion
Abstract
1. Introduction
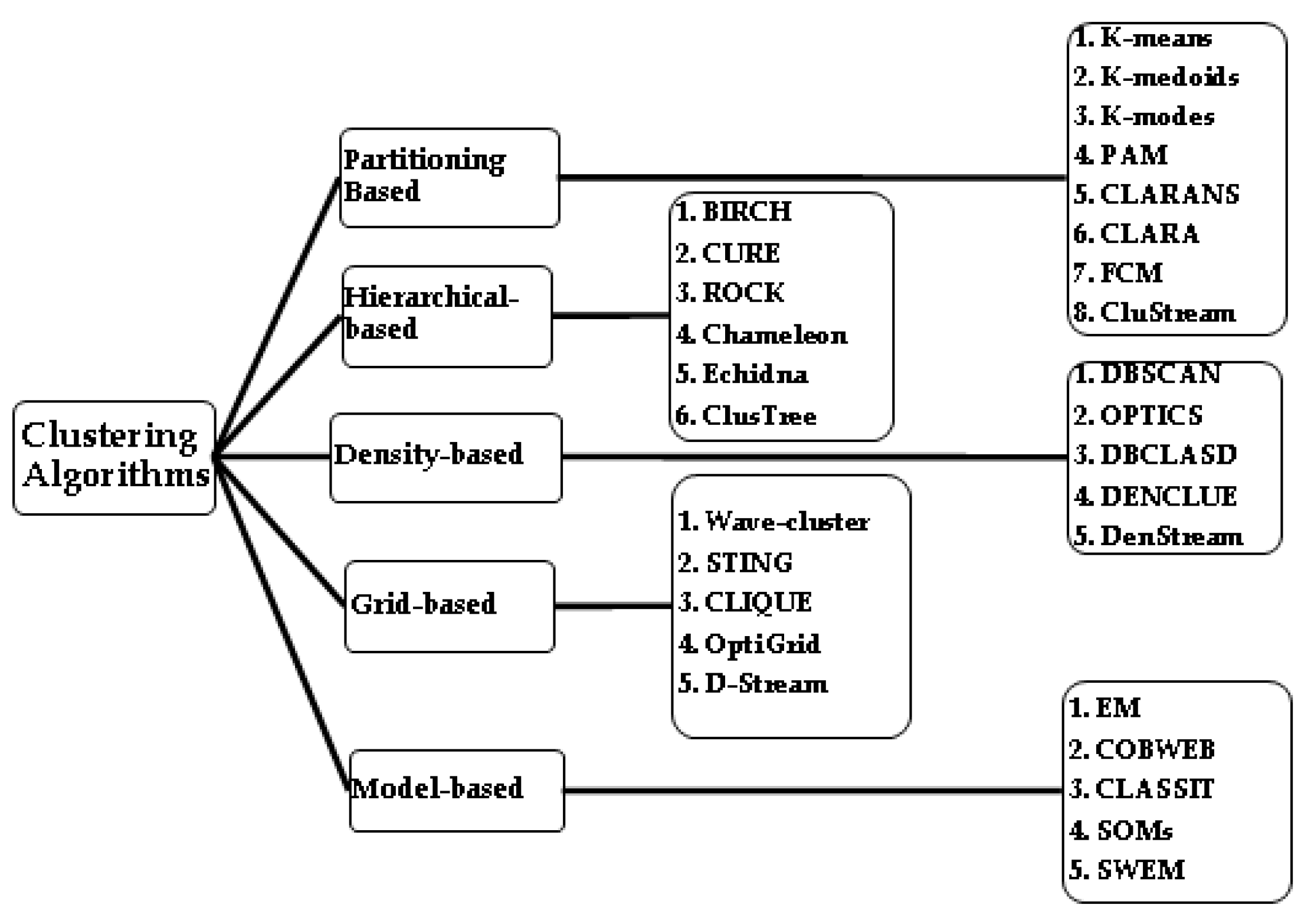
2. Clustering Techniques
2.1. Partitional Clustering
2.2. Hierarchical Clustering
2.3. Density-Based
2.4. Grid-Based
2.5. Model-Based
3. Literature Survey
3.1. Partitional Clustering Method
| Method 1: | Method 2: |
| Let d- Euclidean Distance Calculate Also, compute Then medoid of is | Let and Let If , Then call to be the Medoid of . |
| Algorithm 1. k-means |
| Data: |
| , |
| // here minimum of all distances from each mean is calculated; |
3.2. Hierarchical Clustering Method
3.3. Density-Based Clustering Method
| Basic Definition | Description |
| ε-neighborhood of a point | the neighborhood within a radius of ε. Neighborhood of a point p is denoted by : , where dist(p, q) denotes the Euclidean distance between points p and q |
| MinPts | the minimum number of points around a data point in the -neighborhood |
| core point | a point is a core point if the cardinality of whose ε-neighborhood is at least MinPts |
| border point | a point is a border point if the cardinality of its ε-neighborhood is less than MinPts and at least one of its ε-neighbors is a core point |
| noise point | a point is a noise point if the cardinality of its ε-neighborhood is less than MinPts and none of its neighbors is a core point |
| directly density reachable | a point p is directly density reachable from point q, if p is in the ε-neighborhood of q and q is a core point |
| density reachable | a point p is density reachable from point q, if p is in the ε-neighbourhood of q and q is not a core point but they are reachable through chains of directly density reachable points |
| density-connected | if two points p and q are density reachable from a core point o, p and q are density connected |
| cluster | Maximal set of density-connected points. |
- Input ;
- Generate clusters ;
- If then shall not be consider for further calculations;
- Calculate ;
- Repeat step (4) till no such union exists.
3.4. Grid-Based Clustering Method
- Neighboring Grids [40]: consider two density grids and , if there exist , , such that
- (i)
- ; and
- (ii)
- ;
then and are neighboring grids in the dimension denoted as . - Grid Group [40]: A set of density grids is a grid group if for any two grids , there exist a sequence of grids such that , , and .
- Inside and Outside Grids [40]: Consider a Grid Group and a grid , suppose , if has neighboring grid in every dimension , then is an inside grid in . Otherwise is outside grid in .
- Grid Cluster [40]: Let be grid groups, if every inside grids of are a dense grids and every outside grids are either a dense grid or a transitional grid, then is a grid cluster.
- (i)
- If , then
- (ii)
- If , then .
- (a)
- If , then .
- (b)
- If , then .
3.5. Model-Based Clustering Methods
- For each object, , and cluster, . This requirement enforces that a fuzzy cluster is fuzzy set.
- For each object, , . This requirement ensures that every object participates in clustering equivalently.
- For each cluster, . This requirement ensures that for every cluster, there is at least one object for which the membership value is nonzero.
4. Evaluation Clustering Methods
4.1. Assessing Cluster Tendency
- Sample points, , uniformly from D. The probability of inclusion of each point in is same. For each point, , the nearest neighbour of in is calculated, and let , be the distance between and its nearest neighbour in , then
- Sample points, , uniformly from . For each , calculate nearest neighbour of in , and let be the distance between and its nearest neighbour in , then
- Hopkins Statistic, , is calculated as
4.2. Determining Number of Clusters in a Data Set
4.3. Measuring Clustering Quality
4.3.1. The Internal Measures for Evaluation of Clustering Quality
Cluster Accuracy (CA)
Adjusted Rand Index (ARI)
- −
- : Number of pairs of instances that are in the same cluster in both.
- −
- : Number of pairs of instances that are in different clusters.
- −
- : Number of pairs of instances that are in the same cluster in A, but in different clusters in B. is set of cluster based on external criterion and B is set of cluster based on clustering result.
- −
- : Number of pairs of instances that are in different clusters in A, but in the same cluster in B. A is set of cluster based on external criterion and B is set of cluster based on clustering result.
Normalized Mutual Information (NMI)
Silhouette Coefficient
4.3.2. The External Measure for Evaluation of Clustering Quality
Compactness (CP)
Separation (SP)
Davies-Bouldin Index (DB)
Dunn Validity Index (DVI)
5. Challenging Issues and Comparison
- For Data stream algorithms it is necessary to specify parameters especially in case of k-means type algorithms such as; (i) the expected number of clusters (in case of k-means algorithm it is necessary to specify number of clusters) or the expected density of clusters (in case of density-based method it is required to tune minimum number of points for a given radius of the micro-clusters); (ii) the window length, whose size controls the trade-off between quality and efficiency; and (iii) the fading factor of clusters or objects, which gives more importance to the most recent objects.
- Data stream algorithms must be robust enough to deal with existence of outliers/noise. Evolving data streams are always dynamic in nature in terms of generation of new clusters and fading of old clusters. This nature of data stream imposes another challenge to deal with; algorithms should provide mechanism to identify outliers/noise in such cases.
- The window models techniques somewhat deals with challenges arise with non-stationary distributions of data streams. Still there is need to develop more and more robust data stream clustering algorithms for change detection (context) for trends analysis.
- Data type presented in many data streams are of mixed type, i.e., categorical, ordinal, etc. within several real-world application domains. This will be another challenge in data stream clustering algorithm.
- Increase in mobile applications and activities of social network have generated data streams in big size, handling such data stream is a challenge in terms of processing capability and memory space optimization. Some of the data stream algorithms tried to provide better solution for such challenges. It is also essential to evaluate such clustering algorithms to measure effectiveness, efficiency and quality of data stream clustering algorithm.
| Algorithms | Merits | Remark |
DenStream [43,44]:
|
|
|
StreamOptics [45]:
|
|
|
C-DenStream [46]:
|
|
|
rDenStream [46,47]:
|
|
|
SDStream [48]:
|
|
|
HDenStream [49]:
|
|
|
SOStream [50]:
|
|
|
HDDStream [51]:
|
|
|
PreDeConStream [52]:
|
|
|
FlockStream [53]:
|
|
|
DUCstream [54]:
|
|
|
DStream I [55]:
|
|
|
DD-Stream [56]:
|
|
|
D-Stream II [57]:
|
|
|
MR-Stream [58]:
|
|
|
PKS-Stream [59]:
|
|
|
DCUStream [60]:
|
|
|
DENGRIS-Stream [61]:
|
|
|
ExCC [62]:
|
|
|
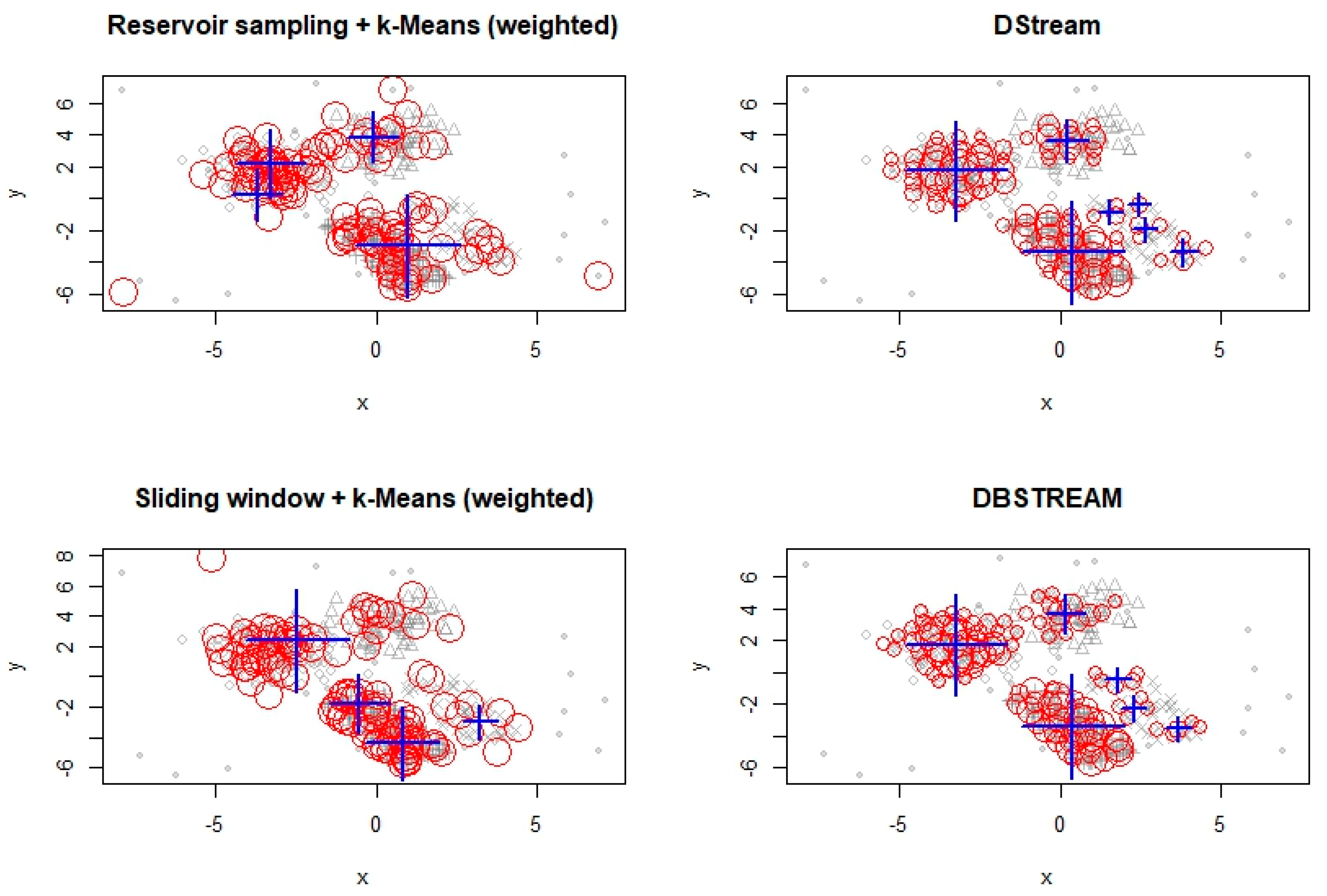
6. Experimental Results and Discussion
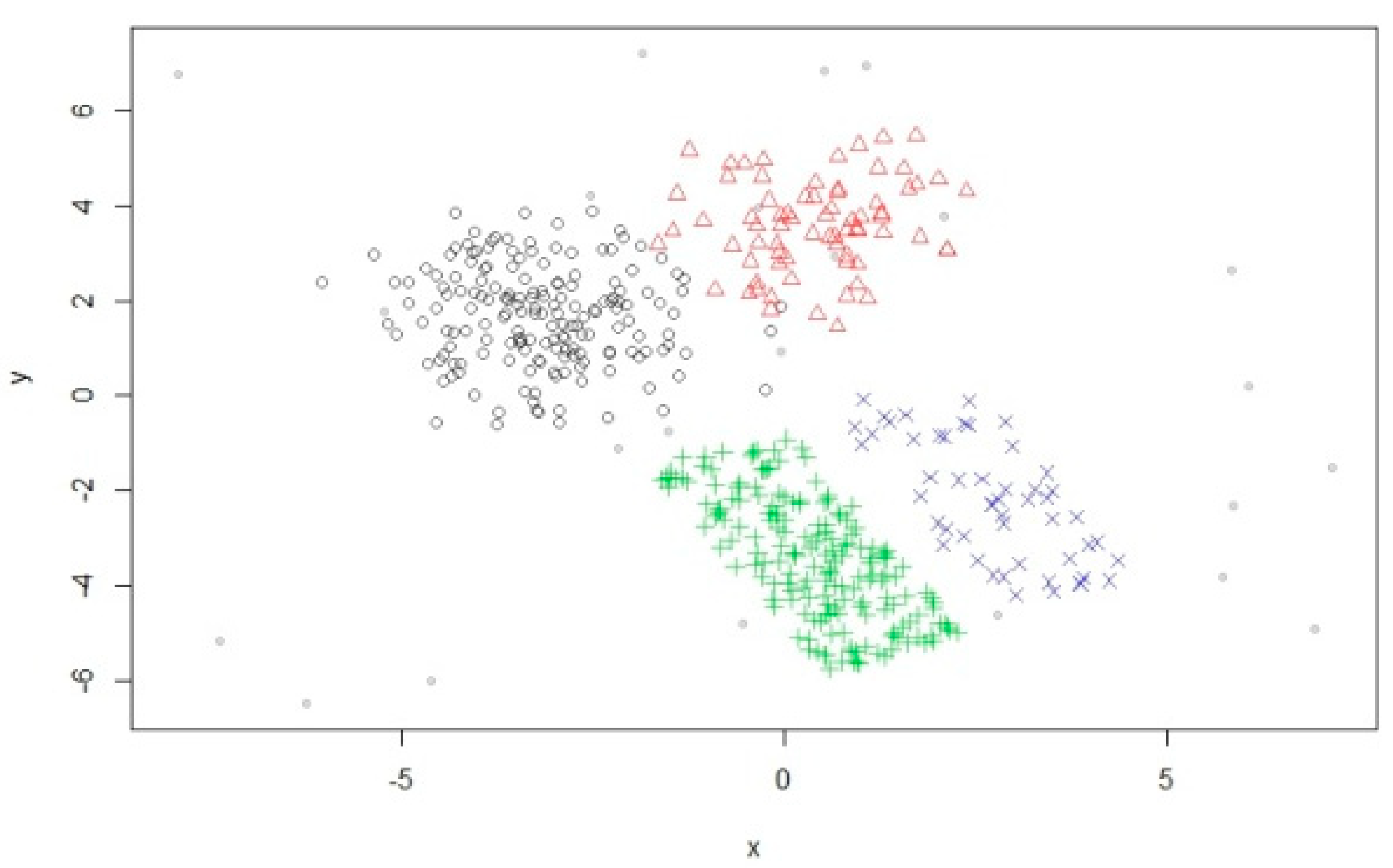
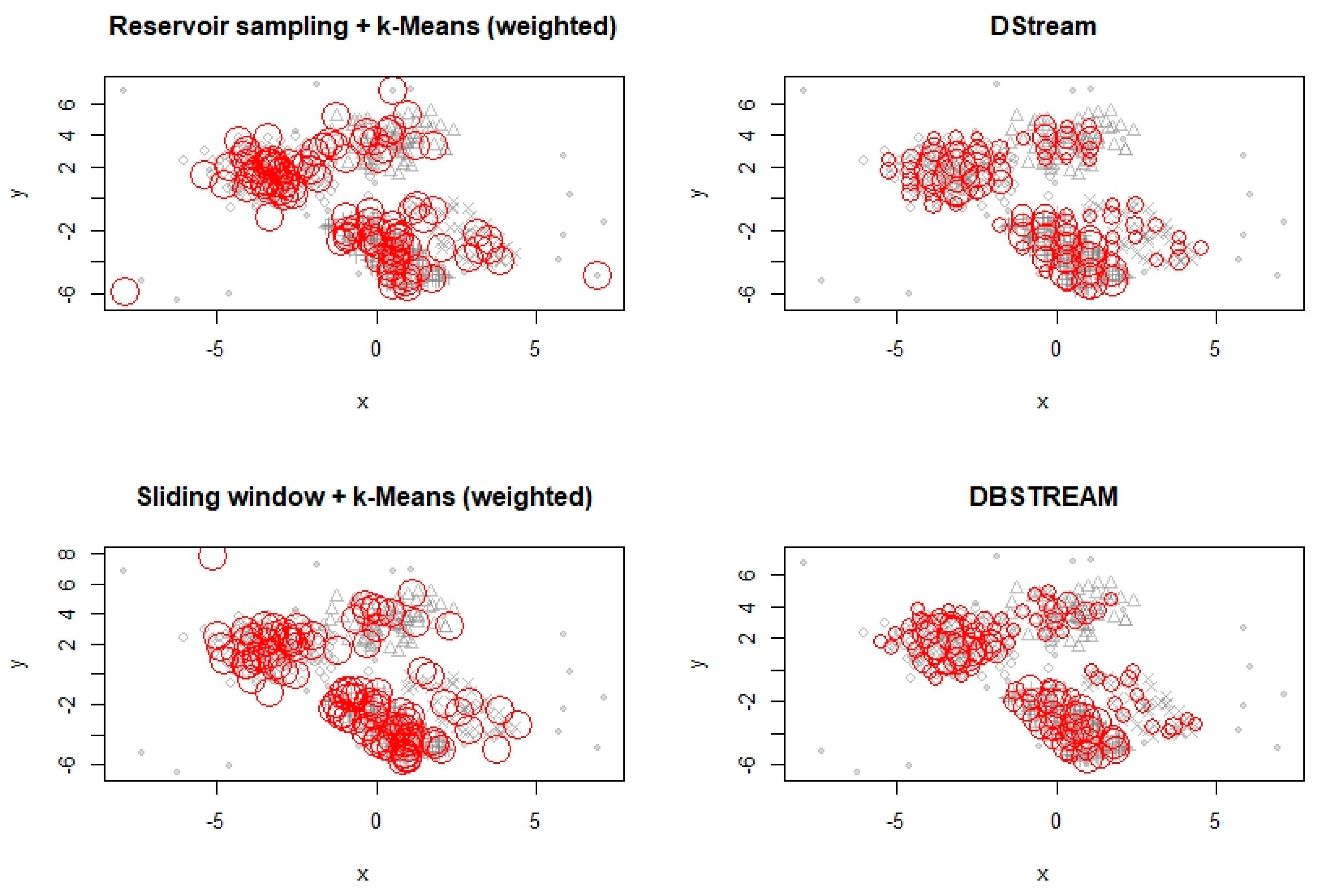
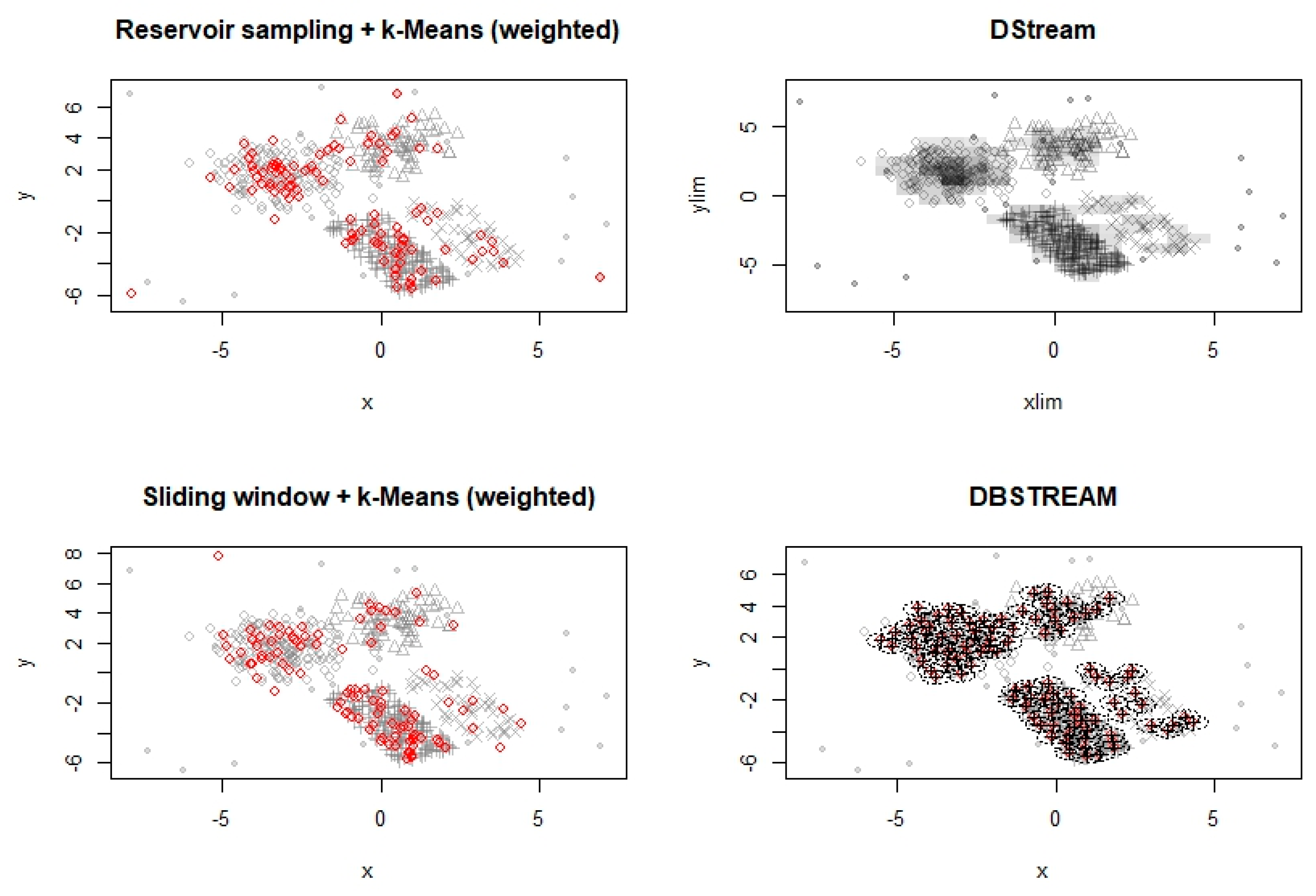
6.1. Experimentation with Data Streams
6.2. Experimentation with Evolving Data Stream
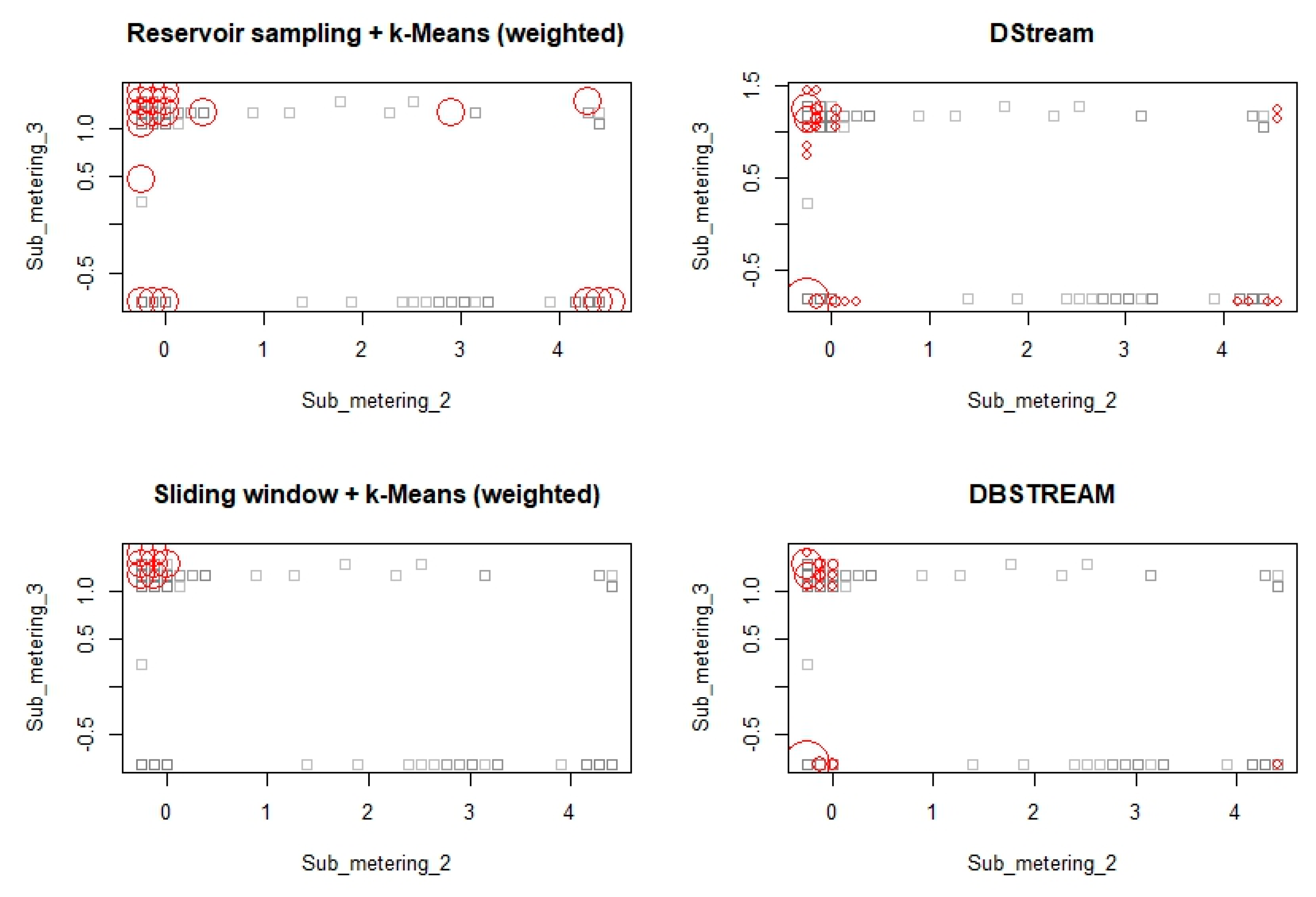
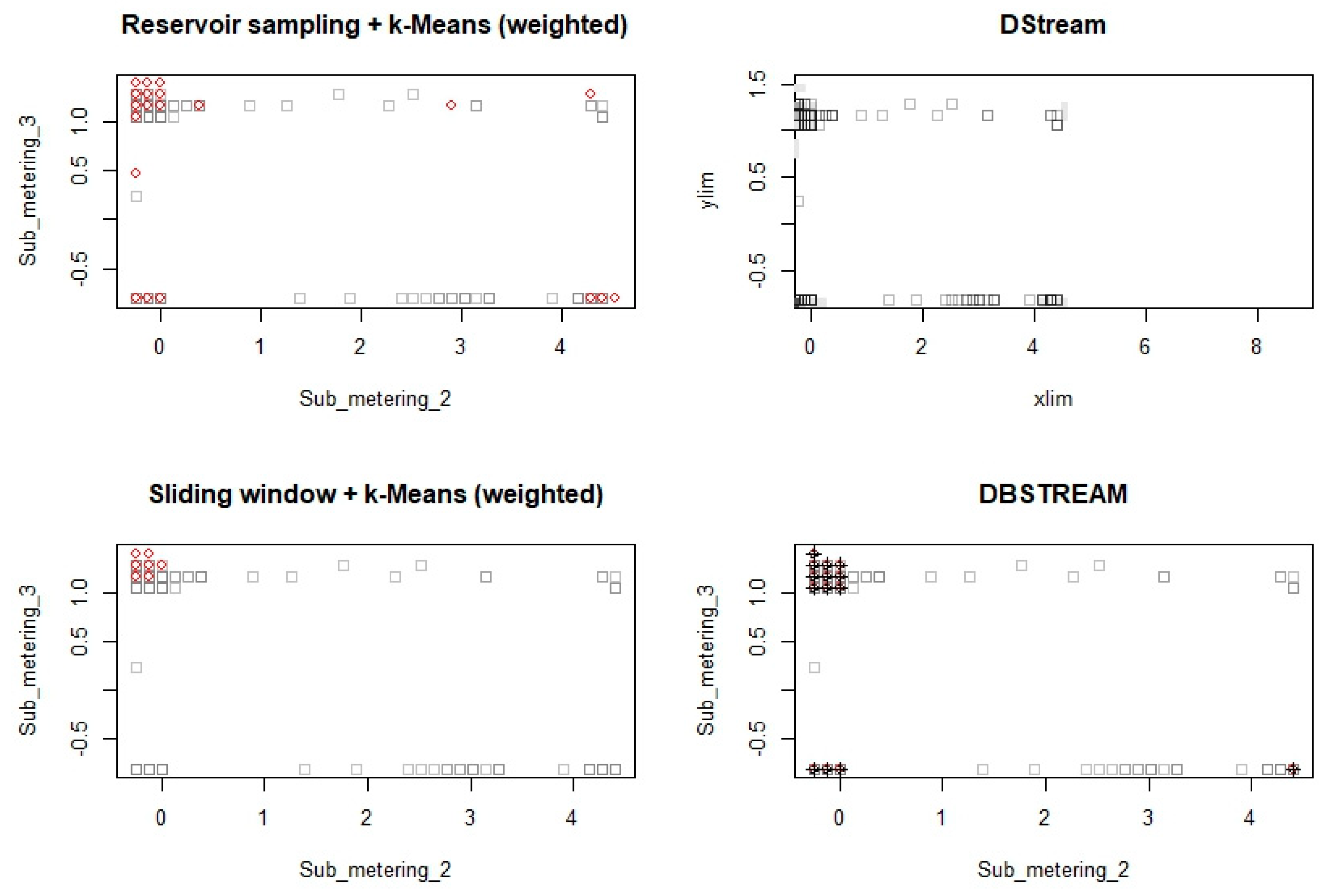
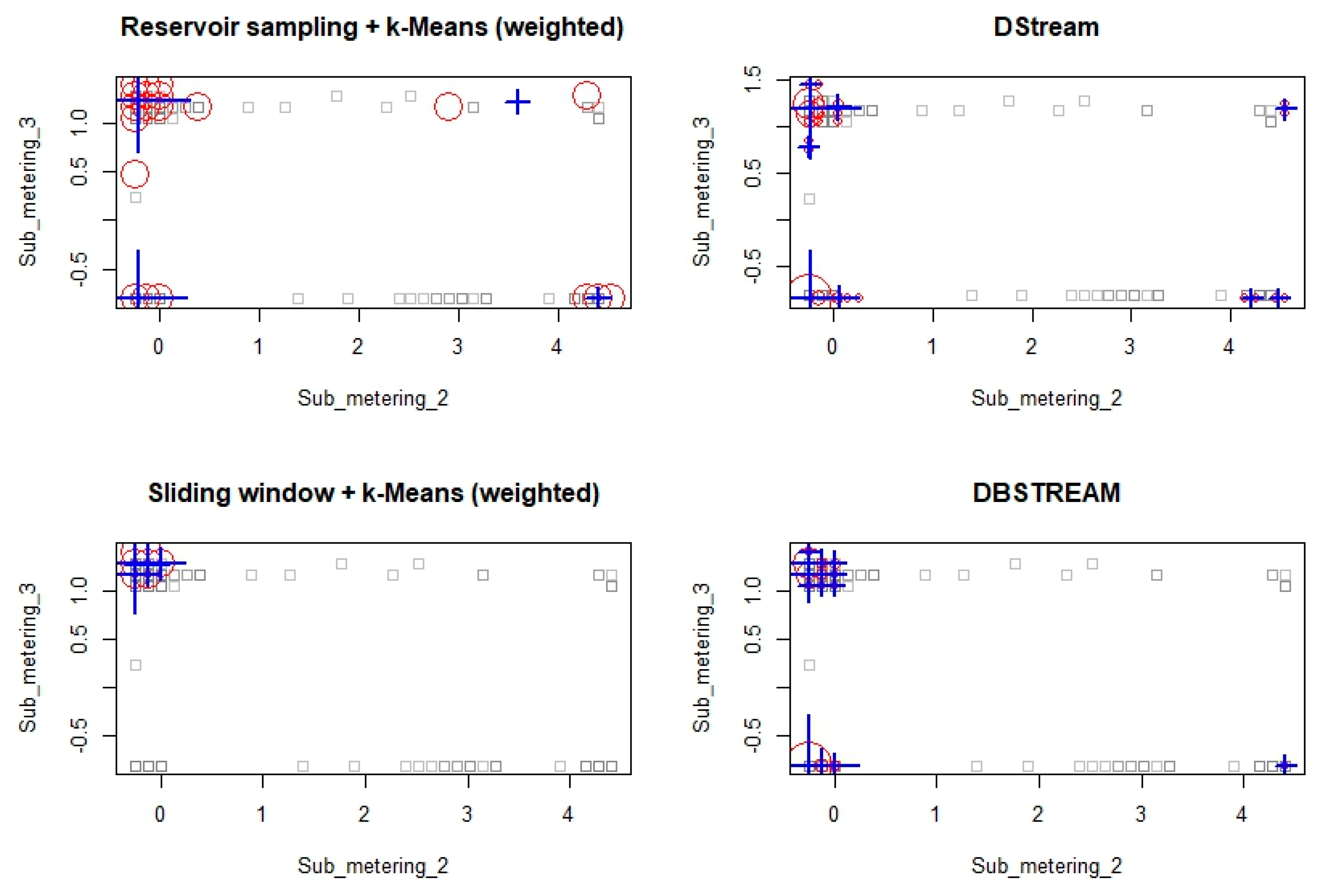
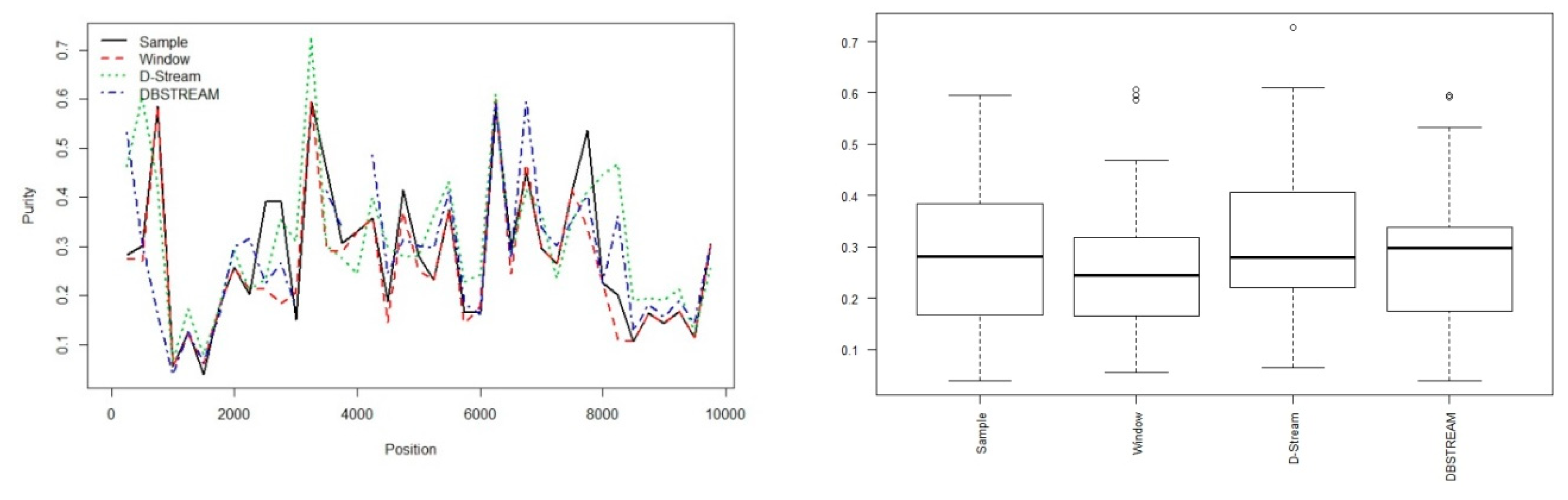
6.3. Experimentation on Real-Life Data Stream
7. Conclusions and Future Outlook
Author Contributions
Funding
Conflicts of Interest
References
- Aggarwal, C.C.A. Framework for Diagnosing Changes in Evolving Data Streams. In Proceedings of the ACM Sigmod, San Diego, CA, USA, 9–12 June 2003; pp. 575–586. [Google Scholar] [CrossRef]
- Babcock, B.; Babu, S.; Datar, M.; Motwani, R.; Widom, J. Models and Issues in Data Stream Systems. In Proceedings of the ACM PODS Conference, Madison, WI, USA, 3–5 June 2002; pp. 1–16. [Google Scholar]
- Domingos, P.; Hulten, G. Mining High-Speed Data Streams. In Proceedings of the ACM SIGKDD Conference, Boston, MA, USA, 20–23 August 2000; pp. 71–80. [Google Scholar]
- Guha, S.; Mishra, N.; Motwani, R.; O’Callaghan, L. Clustering Data Streams. In Proceedings of the IEEE FOCS Conference, Redondo Beach, CA, USA, 12–14 November 2000; pp. 1–8. [Google Scholar]
- Yan, S.; Lin, K.; Zheng, X.; Zhang, W.; Feng, X. An Approach for Building Efficient and Accurate Social Recommender Systems using Individual Relationship Networks. IEEE Trans. Knowl. Data Eng. 2016, 29, 2086–2099. [Google Scholar] [CrossRef]
- Jain, A.K.; Murty, M.N.; Flynn, P.J. Data clustering: A review. ACM Comput. Surv. 1999, 31, 264–323. [Google Scholar] [CrossRef]
- Lu, J.; Zhu, Q. Data clustering: A review. IEEE Access 2017, 5, 4991–5000. [Google Scholar] [CrossRef]
- Hahsler, M.; Bolanos, M. Clustering Data Streams Based on Shared Density between Micro-Clusters. IEEE Trans. Knowl. Data Eng. 2016, 28, 1449–1461. [Google Scholar] [CrossRef]
- Sun, Y.; Tang, K.; Minku, L.L.; Wang, S.; Yao, X. Online Ensemble Learning of Data Streams with Gradually Evolved Classes. IEEE Trans. Knowl. Data Eng. 2016, 28, 1532–1545. [Google Scholar] [CrossRef]
- Mahesh, K.; Kumar, A. Rama Mohan Reddy, A fast DBSCAN clustering algorithm by accelerating neighbour searching using Groups method. Elsevier Pattern Recognit. 2016, 58, 39–48. [Google Scholar] [CrossRef]
- Ros, F.; Guillaume, S. DENDIS: A new density-based sampling for clustering algorithm. Elsevier Expert Syst. Appl. 2016, 56, 349–359. [Google Scholar] [CrossRef]
- Wu, X.; Zhu, X.; Wu, G.; Ding, W. Data Mining with Big Data. IEEE Trans. Knowl. Data Eng. 2014, 26, 97–107. [Google Scholar]
- Amini, A.; YingWah, T.; Saboohi, H. On Density-Based Data Streams Clustering Algorithms: A Survey. J. Comput. Sci. Technol. 2014, 29, 116. [Google Scholar] [CrossRef]
- Gaber, M.; Zaslavsky, A.; Krishnaswamy, S. Mining data streams: A review. ACM Sigmod Rec. 2005, 34, 18–26. [Google Scholar] [CrossRef]
- Ikonomovska, E.; Loskovska, S.; Gjorgjevik, D. A survey of stream data mining. In Proceedings of the 8th National Conference with International Participation, Philadelphia, PA, USA, 20–23 May 2007; pp. 19–25. [Google Scholar]
- Gaber, M.; Zaslavsky, A.; Krishnaswamy, S. Data Stream Mining, DATA Mining and Knowledge Discovery Handbook; Springer: Berlin/Heidelberg, Germany, 2010; pp. 759–787. [Google Scholar]
- Jain, A.K.; Dubes, R.C. Algorithms for Clustering Data. In Algorithms for Clustering Data; Prentice-Hall, Inc.: Upper Saddle River, NJ, USA, 1988; ISBN 0-13-022278-X. [Google Scholar]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2009, 31, 651–666. [Google Scholar] [CrossRef]
- Mahdiraji, A. Clustering data stream: A survey of algorithms. Int. J. Knowl.-Based Intell. Eng. Syst. 2009, 13, 39–44. [Google Scholar] [CrossRef]
- Amini, A.; Wah, T.; Saybani, M.A. Study of density-grid based clustering algorithms on data streams. In Proceedings of the 8th International Conference on Fuzzy Systems and Knowledge Discovery, Shanghai, China, 26–28 July 2011; pp. 1652–1656. [Google Scholar]
- Chen, C.L.P.; Zhang, C. Data-intensive applications, challenges, techniques and technologies: A survey on big data. Inf. Sci. 2014, 275, 314–347. [Google Scholar] [CrossRef]
- Fahad, A.; Alshatri, N.; Tari, Z.; Alamri, A.; Khalil, I.; Zomaya, A.Y.; Foufou, S.; Bouras, A.A. survey of clustering algorithms for big data: Taxonomy and empirical analysis. Trans. Emerg. Top. Comput. 2014, 2, 267–279. [Google Scholar] [CrossRef]
- Amini, A.; Wah, T.Y. Density micro-clustering algorithms on data streams: A review. In Proceedings of the International Multiconference Data Mining and Applications, Hong Kong, China, 16–18 March 2011; pp. 410–414. [Google Scholar]
- Amini, A.; Wah, T.Y. A comparative study of density-based clustering algorithms on data streams: Micro-clustering approaches. In Intelligent Control and Innovative Computing; Springer: Berlin/Heidelberg, Germany, 2012; pp. 275–287. [Google Scholar]
- Aggarwal, C.C. A survey of stream clustering algorithms. In Data Clustering: Algorithms and Applications; CRC Press: Bocaton, FL, USA, 2013; pp. 457–482. [Google Scholar]
- Hartigan, J.A.; Wong, M.A.; Means, A.K. Clustering Algorithm. J. R. Stat. Soc. Ser. C 1979, 28, 100–108. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Cluster Analysis: Basic Concept and Methods. In Data Mining: Concept and Techniques; Morgan Kaufmann: Burlington, MA, USA, 2012; ISBN 978-0-12-381479-1. [Google Scholar]
- Xu, R.; Wunsch, D. Survey of clustering algorithms. IEEE Trans. Neural Netw. 2005, 16, 645–678. [Google Scholar] [CrossRef] [PubMed]
- O’Callaghan, L.; Mishra, N.; Meyerson, A.S.; Guha, R. Motwani Streaming-data algorithms for high-quality clustering. In Proceedings of the 18th International Conference on Data Engineering, Washington, DC, USA, 26 February–1 March 2002; pp. 685–694. [Google Scholar]
- Zhang, T.; Ramakrishnan, R.; Livny, M. BIRCH: A New Data Clustering Algorithm and Its Applications. Data Min. Knowl. Discov. 1997, 1, 141–182. [Google Scholar] [CrossRef]
- Guha, S.; Rastogi, R.; Shim, K. CURE: An efficient clustering algorithm for large databases. ACM Sigmod Rec. 1998, 27, 73–84. [Google Scholar] [CrossRef]
- Guha, S.; Rastogi, R.; Shim, K. ROCK: A robust clustering algorithm for categorical attributes. In Proceedings of the 15th International Conference on Data Engineering (Cat. No.99CB36337), Sydney, NSW, Australia, 23–26 March 1999; pp. 512–521. [Google Scholar]
- Karypis, G.; Han, E.; Kumar, V. Chameleon: Hierarchical clustering using dynamic modeling. Computer 1999, 32, 68–75. [Google Scholar] [CrossRef]
- Philipp, K.; Assent, I.; Baldauf, C.; Seidl, T. The clustree: Indexing micro-clusters for anytime stream mining. Knowl. Inf. Syst. 2011, 29, 249–272. [Google Scholar]
- Guha, S.; Meyerson, A.; Mishra, N.; Motwani, R.; O’Callaghan, L. Clustering data streams: Theory and practice. IEEE Trans. Knowl. Data Eng. 2003, 15, 515–528. [Google Scholar] [CrossRef]
- Chris, F.; Raftery, A.E. MCLUST: Software for model-based cluster analysis. J. Classif. 1999, 16, 297–306. [Google Scholar]
- Miin-Shen, Y.; Lai, C.; Lin, C. A robust EM clustering algorithm for Gaussian mixture models. Pattern Recognit. 2012, 45, 3950–3961. [Google Scholar]
- Fisher, D.H. Knowledge acquisition via incremental conceptual clustering. Mach. Learn. 1987, 2, 139–172. [Google Scholar] [CrossRef]
- Kohonen, T. The self-organizing map. Proc. IEEE 1990, 78, 1464–1480. [Google Scholar] [CrossRef]
- Chen, Y.; Tu, L. Density-based clustering for real-time stream data. In Proceedings of the 13th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Jose, CA, USA, 12–15 August 2007; pp. 133–142. [Google Scholar]
- Kranen, P.; Jansen, T.; Seidl, T.; Bifet, A.; Holmes, G.; Pfahringer, B. An Effective Evaluation Measure for Clustering on Evolving Data Streams. In Proceedings of the 17th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Diego, CA, USA, 21–24 August 2011; pp. 868–876. [Google Scholar]
- Jun, W.U.; Xiong, H.; Chen, J. Adapting the Right Measures for K-means Clustering. In Proceedings of the 15th ACM SIGKDD international conference on Knowledge discovery and data mining, Paris, France, 28 June–1 July 2009; pp. 877–886. [Google Scholar]
- Cao, F.; Ester, M.; Qian, W.; Zhou, A. Density-Based Clustering over an Evolving Data Stream with Noise. In Proceedings of the SIAM Conference on Data Mining, Bethesda, MD, USA, 20–22 April 2006; pp. 328–339. [Google Scholar]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. In Proceedings of the Second International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Tasoulis, D.K.; Ross, G.; Adams, N.M. Visualising the cluster structure of data streams. In Proceedings of the 7th International Conference on Intelligent Data Analysis, Oslo, Norway, 14–17 June 1999; pp. 81–92. [Google Scholar]
- Ruiz, C.; Menasalvas, E.; Spiliopoulo, C. DenStream: Using domain knowledge on a data stream. In Proceedings of the 12th International Conference on Discovery Science, Porto, Portugal, 3–5 October 2009; pp. 287–301. [Google Scholar]
- Liu, L.; Jing, K.; Guo, Y.; Huang, H. A three-step clustering algorithm over an evolving data stream. In Proceedings of the IEEE International Conference on Intelligent Computing and Intelligent Systems, Shanghai, China, 20–22 November 2009; pp. 160–164. [Google Scholar]
- Ren, J.; Ma, R. Density-based data streams clustering over sliding windows. In Proceedings of the Sixth International Conference on Fuzzy Systems and Knowledge Discovery, Tianjin, China, 14–16 August 2009; pp. 248–252. [Google Scholar]
- Lin, J.; Lin, H. A density-based clustering over evolving heterogeneous data stream. In Proceedings of the ISECS International Colloquium on Computing, Communication, Control, and Management, Sanya, China, 8–9 August 2009; pp. 275–277. [Google Scholar]
- Isaksson, C.; Dunham, M.H.; Hahsler, M. SOStream: Self Organizing Density-Based Clustering over Data Stream. In Machine Learning and Data Mining in Pattern Recognition; MLDM 2012. Lecture Notes in Computer Science; Perner, P., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 264–278. ISBN 978-3-642-31536-7. [Google Scholar]
- Ntoutsi, I.; Zimek, A.; Palpanas, T.; Kröger, P.; Kriegel, H.P. Density-based projected clustering over high dimensional data streams. In Proceedings of the 2012 SIAM International Conference on Data Mining, Anahelm, CA, USA, April 2012; pp. 987–998. [Google Scholar]
- Hassani, M.; Spaus, P.; Gaber, M.M.; Seidl, T. Density-based projected clustering of data streams. In Proceedings of the 6th International Conference, SUM 2012, Marburg, Germany, 17–19 September 2012; pp. 311–324. [Google Scholar]
- Forestiero, A.; Pizzuti, C.; Spezzano, G. A single pass algorithm for clustering evolving data streams based on swarm intelligence. Data Min. Knowl. Discov. 2013, 26, 1–26. [Google Scholar] [CrossRef]
- Garofalakis, M.; Gehrke, J.; Rastogi, R. Querying and mining data streams: You only get one look: A tutorial. In Proceedings of the 2002 ACM SIGMOD International Conference on Management of Data, Madison, WI, USA, 2–6 June 2002; p. 635. [Google Scholar]
- Jia, C.; Tan, C.; Yong, A. A grid and density-based clustering algorithm for processing data stream. In Proceedings of the IEEE Second International Conference on Genetic and Evolutionary Computing, Wuhan, China, 25–26 September 2008; pp. 517–521. [Google Scholar]
- Tu, L.; Chen, Y. Stream data clustering based on grid density and attraction. ACM Trans. Knowl. Discov. Data 2009, 3. [Google Scholar] [CrossRef]
- Wan, L.; Ng, W.K.; Dang, X.H.; Yu, P.S.; Zhang, K. Density-based clustering of data streams at multiple resolutions. ACM Trans. Knowl. Discov. Data 2009, 3, 14–28. [Google Scholar] [CrossRef]
- Ren, J.; Cai, B.; Hu, C. Clustering over data streams based on grid density and index tree. J. Converg. Inf. Technol. 2011, 6, 83–93. [Google Scholar]
- Yang, Y.; Liu, Z.; Zhang, J.P.; Yang, J. Dynamic density-based clustering algorithm over uncertain data streams. In Proceedings of the 9th IEEE International Conference on Fuzzy Systems and Knowledge Discovery (FSKD), Chongqing, China, 29–31 May 2012; pp. 2664–2670. [Google Scholar]
- Bhatnagar, V.; Kaur, S.; Chakravarthy, S. Clustering data streams using grid-based synopsis. Knowl. Inf. Syst. 2014, 41, 127–152. [Google Scholar] [CrossRef]
- Hahsler, M.; Bolanos, M.; Forrest, J. Introduction to stream: An Extensible Framework for Data Stream Clustering Research with R. J. Stat. Softw. 2017, 76, 1–50. [Google Scholar] [CrossRef]
- Pandove, D.; Goel, S.; Rani, R. Systematic Review of Clustering High-Dimensional and Large Datasets. ACM Trans. Knowl. Discov. Data 2018, 12, 4–68. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Wang, J.Y.; Yu, P.S. A Framework for Projected Clustering of High Dimensional Data Streams. In Proceedings of the Thirtieth International Conference on Very Large Data Bases, Toronto, ON, Canada, 31 August–3 September 2004. [Google Scholar]
- Zhou, A.; Cao, F.; Qian, W.; Jin, C. Tracking clusters in evolving data streams over sliding windows. Knowl. Inf. Syst. 2008, 15, 181–214. [Google Scholar] [CrossRef]
- Liadan, O.; Mishra, N.; Meyerson, A.; Guha, S.; Motwani, R. Streaming-data algorithms for high-quality clustering. In Proceedings of the 18th International Conference on Data Engineering, Washington, DC, USA, 26 February–1 March 2002. [Google Scholar]
- Dempster, P.A.; Laird, N.M.; Rubin, D.B. Maximum likelihood from incomplete data via the EM algorithm. J. R. Stat. Soc. Ser. B 1977, 39, 1–38. [Google Scholar]
- Dang, X.H.; Lee, V.; Ng, W.K.; Ciptadi, A.; Ong, K.L. An EM-based algorithm for clustering data streams in sliding windows. In International Conference on Database Systems for Advanced Applications; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Damminda, A.; Halgamuge, S.K.; Srinivasan, B. Dynamic self-organizing maps with controlled growth for knowledge discovery. IEEE Trans. Neural Netw. 2000, 11, 601–614. [Google Scholar]
- Toby, S.; Alahakoon, D. Growing self-organizing map for online continuous clustering. In Foundations of Computational Intelligence Volume 4; Springer: Berlin/Heidelberg, Germany, 2009; pp. 49–83. [Google Scholar]
- Chow, T.W.S.; Wu, S. An online cellular probabilistic self-organizing map for static and dynamic data sets. IEEE Trans. Circuits Syst. Regul. Pap. 2004, 51, 732–747. [Google Scholar] [CrossRef]
| Density-Based Data Stream Clustering Algorithms | |||
|---|---|---|---|
| Density Micro-Clustering Algorithms | Density Grid-Based Clustering Algorithms | ||
| DenStream (2006) | HDenStream (2009) | DUC-Stream (2005) | PKS-Stream (2011) |
| StreamOptics (2007) | SOStream (2012) | D-Stream I (2007) | DCUStream (2012) |
| C-DenStream (2009) | HDDStream (2012) | DD-Stream (2008) | DENGRIS-Stream (2012) |
| rDenStream (2009) | PreDeConStream (2012) | D-Stream II (2009) | ExCC (2013) |
| SDStream (2009) | FlockStream (2013) | MR-Stream (2009) | |
| External Measures | Internal Measures |
|---|---|
| Cluster Accuracy | Compactness |
| Random Index | Separation |
| Adjusted Random Index | Davies-Bouldin Index |
| Normalized Mutual Information | Dumm Validity Index |
| Purity (P) | Sum of Square Error |
| Precision | Silhouette |
| Recall | |
| Entropy (E) | |
| F Measure (F) |
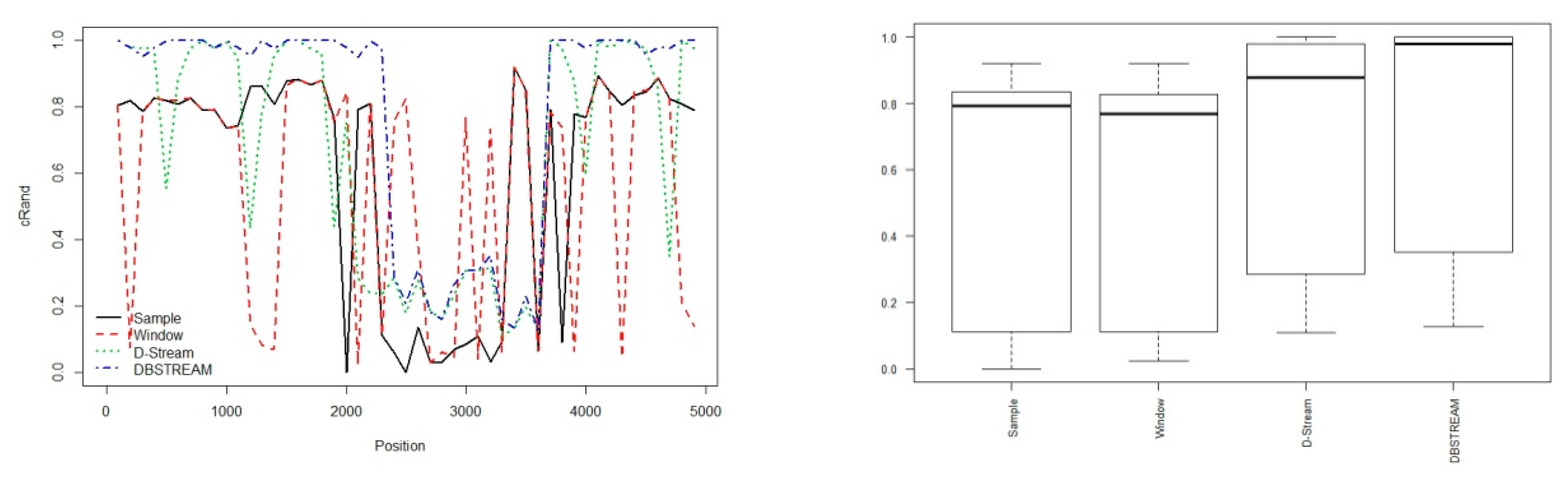
| Partition | ||||||
| Sample | Window | D-Stream | DBSTREAM | |
|---|---|---|---|---|
| numMicroClusters | 100.0000000 | 100.0000000 | 84.0000000 | 99.0000000 |
| purity | 0.9556277 | 0.9474273 | 0.9659613 | 0.9705846 |
| Sample | Window | D-Stream | DBSTREAM | |
|---|---|---|---|---|
| numMacroClusters | 4.0000000 | 4.0000000 | 7.0000000 | 6.0000000 |
| purity | 0.8697902 | 0.8325503 | 0.8926433 | 0.8758753 |
| SSQ | 1199.8108788 | 1564.1203674 | 866.9658854 | 885.5041398 |
| cRand | 0.5811980 | 0.5500995 | 0.7820541 | 0.7954812 |
| silhouette | 0.4291496 | 0.4289753 | 0.3047187 | 0.2943902 |
| Date | Time | global_active_power | global_reactive_power | Voltage | global_intensity | sub_metering_1 | sub_metering_2 | sub_metering_3 |
|---|---|---|---|---|---|---|---|---|
| Date | Numeric | Numeric | Numeric | Numeric | Numeric | Numeric | Numeric | Numeric |
| Attribute Title | Description |
|---|---|
| date | Represents Date in format dd/mm/yyyy |
| time | Represents time in format hh:mm:ss |
| global_active_power | Represents household global minute averaged active power (in kilowatt). |
| global_reactive_power | Represents household global minute averaged reactive power (in kw). |
| voltage | Represents minute-averaged voltage (in volt). |
| global_intensity | Represents household global minute-averaged current intensity (in amp). |
| sub_metering_1 | Represents energy sub-metering No. 1 (in watt-hour of active energy). It corresponds to the kitchen, containing mainly a dishwasher, an oven and a microwave (hot plates are not electric but gas powered). |
| sub_metering_2 | Represents energy sub-metering No. 2 (in watt-hour of active energy). It corresponds to the laundry room, containing a washing-machine, a tumble-drier, a refrigerator and a light. |
| sub_metering_3 | Represents energy sub-metering No. 3 (in watt-hour of active energy). It corresponds to an electric water-heater and an air-conditioner. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kokate, U.; Deshpande, A.; Mahalle, P.; Patil, P. Data Stream Clustering Techniques, Applications, and Models: Comparative Analysis and Discussion. Big Data Cogn. Comput. 2018, 2, 32. https://doi.org/10.3390/bdcc2040032
Kokate U, Deshpande A, Mahalle P, Patil P. Data Stream Clustering Techniques, Applications, and Models: Comparative Analysis and Discussion. Big Data and Cognitive Computing. 2018; 2(4):32. https://doi.org/10.3390/bdcc2040032
Chicago/Turabian StyleKokate, Umesh, Arvind Deshpande, Parikshit Mahalle, and Pramod Patil. 2018. "Data Stream Clustering Techniques, Applications, and Models: Comparative Analysis and Discussion" Big Data and Cognitive Computing 2, no. 4: 32. https://doi.org/10.3390/bdcc2040032
APA StyleKokate, U., Deshpande, A., Mahalle, P., & Patil, P. (2018). Data Stream Clustering Techniques, Applications, and Models: Comparative Analysis and Discussion. Big Data and Cognitive Computing, 2(4), 32. https://doi.org/10.3390/bdcc2040032




