Productivity Benchmarking Using Analytic Network Process (ANP) and Data Envelopment Analysis (DEA)

Abstract

Measuring productivity is the systematic process for both inter- and intra-organizational comparisons. The productivity measurement can be used to control and facilitate decision-making in manufacturing as well as service organizations. This study’s objective was to develop a decision support framework by integrating an analytic network process (ANP) and data envelopment analysis (DEA) approach to tackling productivity measurement and benchmarking problems in a manufacturing environment. The ANP was used to capture the interdependency between the criteria taking into consideration the ambiguity and vagueness. The nonparametric DEA approach was utilized to determine the input-oriented constant returns to scale (CRS) efficiency of different value-adding production units and to benchmark them. The proposed framework was implemented to benchmark the productivity of an apparel manufacturing company. By applying the model, industrial managers can gain benefits by identifying the possible contributing factors that play an important role in increasing the productivity of manufacturing organizations.

1. Introduction

To evaluate the performance of any production system, productivity measurement is essential and vital. Productivity represents the relationship between input factors (i.e., labor, capital) and output factors (e.g., goods or services produced) [1,2]. The productivity of a manufacturing process can be expressed as the combination of efficiency and effectiveness with the aim of maximizing output while minimizing the use of inputs [3,4]. Productivity provides information about the performance, quality of individuals, workgroups, and processes. The per unit production cost is reduced with the increase in the productivity, which allows the organization to remain competitive in both the inside and outside markets of the country [5,6].

The capital productivity or labor productivity is the most popular measure for any manufacturing production system. However, it represents only a partial picture of the performance [2]. Performance measurement or comparison of the production system is vital for subsequent improvement efforts. Performance measurement, especially in a complex production environment, has remained a prominent topic among researchers over the past decade. Mawson et al. [7] presented four approaches for productivity measurement: a growth accounting approach, a distance function-based approach, an index number approach, and an econometric approach. Different researchers used these methods to evaluate the technical efficiency of the manufacturing industry. For example, Ramcharran [6] estimated the productivity and efficiency of the US textile industry for the period of 1975–1993 considering a variable elasticity of substitution production function. Razzak [8] proposed an ordinary least square regression method to produce the deterministic or stochastic trend of certain total factor productivity estimates. The firm-level technical efficiency of Australian textile and clothing firms was examined by Mokhtarul Wadud [9] using a Cobb Douglas stochastic production frontier. Bhandari and Maiti [10] used a translog stochastic frontier production function for estimating the technical efficiency of Indian textile manufacturing firms. Bhandari and Ray [5] used both grand frontier and group frontier to evaluate the technical efficiency of the Indian textile industry.

Recently, the data envelopment analysis (DEA) approach has been gaining in popularity for measuring productivity in different manufacturing sectors. DEA measures the relative efficiency of decision-making units (DMUs) with multiple inputs and multiple outputs. The DEA, first proposed by Charnes et al. [11], is a well-established method for efficiency measurement or relative performance evaluation based on linear programming. Sigala [12] proposed the DEA method for measuring and benchmarking productivity in the hotel sector. Joshi and Singh [13] analyzed the relationship between input variables (i.e., raw material, net fixed assets, energy and fuel, and wages and salaries) and output variables (gross sales) using a DEA-based productivity index approach. Saricam and Erdumlu [14] provided a DEA framework to determine and compare efficiency performance of the Turkish textile and apparel industry at an industry level. Gambhir and Sharma [15] used firm-level panel data about 160 companies from 2007–2008 to 2012–2013 to analyze the productivity performance of Indian textile manufacturing industries using DEA. Erdumlu [16] evaluated the efficiency of the Turkish apparel, textile, and leather sector using measure-specific DEA. Raheli et al. [17] presented a two-stage nonparametric DEA model to evaluate the sustainability and energy efficiency of tomato production. Li and Tsai [18] used the DEA method to evaluate the apparel retail performance or efficiency at the corporate level. Most of the studies used the model proposed by Charnes et al. [11] to calculate the corresponding weights of each input and output vector and the productivity index. However, the Charnes, Cooper and Rhodes (CCR) model may provide multiple efficient alternatives, which can result in difficulties or challenges for managers or decision-makers in real-life decision-making [19,20].

To avoid this limitation, some of the studies integrated the analytic network process (ANP) with the DEA model [19,21,22,23]. The ANP is a well-known multi-criteria decision-making method, used to evaluate the relative level of importance of the criteria or factor sets along with the consideration of their importance. The ANP is an extension of the analytic hierarchy process (AHP), as AHP cannot represent the interrelationship and dependence of the higher-level criteria on lower-level criteria [22]. However, filling the supermatrix and questionnaire design for the pairwise comparison has always been challenging for decision-makers due to the large number of data involved [19,21,23]. The ANP-DEA hybrid algorithm has been recommended to eliminate both the ordering in the DEA model and the limitation of the whole hierarchy and subjective evaluations in the ANP method.

The aim of this study was to develop a hybrid ANP-DEA framework to evaluate effectively the productivity of manufacturing industries. The main advantage of the proposed ANP-DEA framework is that it can eliminate the disadvantage of multiple efficient full-ranking in the DEA method, as well as the limitations of dependency problems in the ANP method. In this study, the relative weights of different criteria or factors were calculated using the ANP method taking into consideration the interrelationships and the dependency among them. The assurance regions were then determined using the lower bound and upper bound for the weight of each input or output. Then, these assurance regions were incorporated into the DEA model by constraining the range of weights. The proposed model was subsequently applied to measure and benchmark the productivity of different units or floors of an apparel company in Bangladesh.

The apparel industries in Bangladesh suffer from poor productivity because of several factors or variables [24,25]. There are several weaknesses in the ready-made garment industry of Bangladesh, and the lack of capacity to produce export-quality fabrics and accessories is one of them. Thus, the apparel industries, and the ready-made garment industry in particular, are highly reliant on imported raw material and accessories [25]. The labor productivity in the ready-made garment sector of Bangladesh is lower compared to that of its competitors [26]. Moreover, the underdeveloped infrastructure, the shortage of power supply, and transportation and communication problems create a serious bottleneck [27]. Frequent port congestion due to inadequate port infrastructures and facilities results in shipment delays and increases the process lead time [24].

The remainder of this paper is structured as follows. The proposed hybrid ANP-DEA model is described in Section 2. Subsequently, the proposed model is applied to evaluate the floor productivity of an apparel industry in Bangladesh. The conclusions, limitations of the study and scope for further research are discussed in the final section of the paper.

2. Framework Development

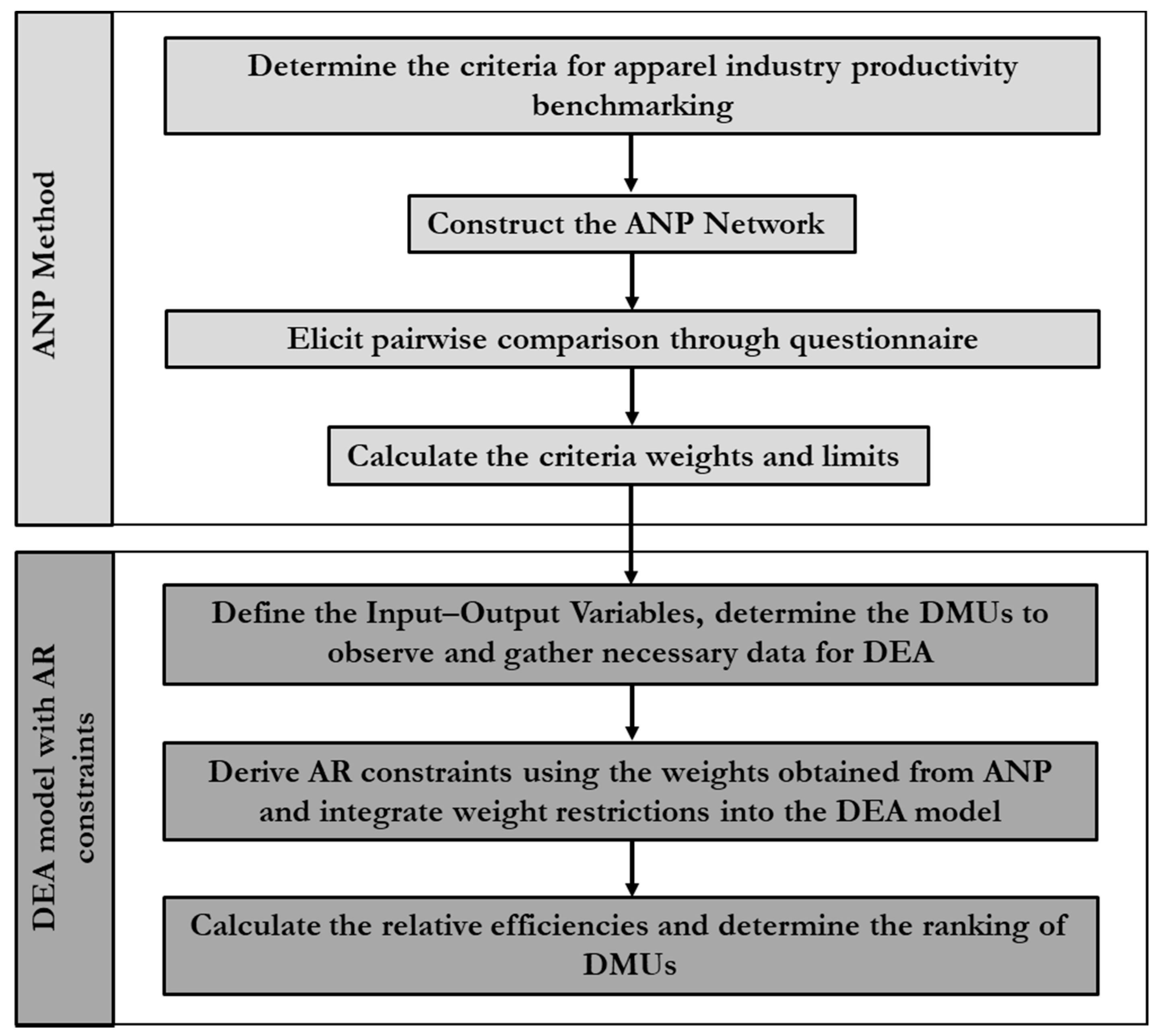
The proposed framework integrates ANP with DEA for productivity measurement. The proposed ANP-DEA based framework for productivity measurement is presented in Figure 1. The productivity measurement process contains several steps.

Step 1: The criteria are determined for the apparel industry productivity benchmarking based on the literature review and data availability.

Step 2: The ANP model is constructed based on the selected criteria.

Step 3: After developing the ANP model structure, the pairwise comparisons are performed using the decision-makers’ judgment. In general, multiple decision-makers can be involved in the decision process and the judgment can reflect the group decision-making effort.

Step 4: The weights of the various criteria or factors are determined.

Step 5: The input variables, output variables, and decision-making units (DMUs) of the DEA model are determined and the related data are collected based on the requirements.

Step 6: The decision-maker weights are considered to determine the bounds for the DEA assurance regions (AR). The lower bounds and upper bounds are calculated from the ranges of the manager importance weights.

Step 7: The DEA evaluation is completed integrating the performance data and the managerial preference bounds. The alternatives are ranked based on the relative efficiency scores from the DEA model.

The detailed methodology is described in the following subsections.

2.1. Analytic Network Process (ANP)

The AHP, a well-known and widely used multi-criteria decision-making approach, was introduced by Saaty [28]. The AHP method considers the hierarchical structure of the model and represents a one-way approach, using top-down relationships. It involves building a hierarchy of decision elements and then making comparisons between each possible pair in each cluster using a scale from 1 to 9. It then determines the weight of each element within a cluster (or level of the hierarchy). However, AHP cannot represent the interrelationship and dependency of the elements within a cluster and between the cluster.

As an improved form of AHP, the ANP can consider the interaction of elements in a level and between elements in different levels. There are feedback loops in these systems. The interdependencies among factors and subfactors can be determined by calculating the eigenvectors through several matrix transformations. According to Saaty’s method [28,29], the four main steps to calculate the relative importance weights of subcriteria are presented as follows:

Step 1: Model construction and problem structuring

The problem should be stated clearly and decomposed into a rational system like a network. The structure can be developed according to the opinions presented by decision-makers through brainstorming or other appropriate methods.

Step 2: Pairwise comparison matrix and priority vector

Like the AHP method, the pairwise comparison of the decision elements at each cluster is performed with respect to their significance toward their control criteria. The decision-makers also compare the components themselves pairwise with respect to their contribution to the goal. In general, the 1–9 scale of relative importance is used for the pairwise comparisons (see

Table 1. Saaty’s 1–9 scale for analytic hierarchy process (AHP) preference.

Intensity of Importance	Definition	Explanation
1	Equal importance	Two activities contribute equally to the objective
3	Moderate importance	Experience and judgment slightly favor one over another
5	Strong importance	Experience and judgment strongly favor one over another
7	Very strong importance	Activity is strongly favored, and its dominance is demonstrated in practice
9	Absolute importance	Importance of one over another affirmed on the highest possible order
2, 4, 6, 8	Intermediate values	Used to represent compromise between the priorities listed above
Reciprocal of above non-zero numbers	If activity i has one of the above non-zero numbers assigned to it when compared with activity j, then j has the reciprocal value when compared with i.

). Furthermore, the interdependencies between the elements of a cluster are also evaluated in pairs where the effect of each element on other elements is represented by an eigenvector.

Step 3: Supermatrix construction

To generate the weighted supermatrix, the pairwise comparison matrices are multiplied with the corresponding weights. Then, normalization is performed and the sum of the columns of the weighted supermatrix is generally equal to 1.

Step 4: Limit supermatrix calculation

In this step, the weighted supermatrix is derived with a sufficiently large power number to achieve a stable supermatrix that has a convergence on the weights. The resulting new matrix is the limit supermatrix with the same columns. The results indicate the global weights of subcriteria, and the criteria with the highest overall priority weights are the most important criteria.

Weights and Bounds Determination

The direct weights of subcriteria and their interdependencies on the final goal were considered in this study in order to get the relative importance evaluations to constrain the DEA models. For the assurance regions, the minimum and maximum values for each subcriterion from among all the decision-makers were considered in this study [19]. The tighter bounds indicated the greater agreement by the decision-makers on the importance of complexity measures, whereas the looser bounds represented more inconsistency and uncertainty regarding the importance of the measures.

2.2. Data Envelopment Analysis (DEA)

DEA is a method which can evaluate the relative efficiency of DMUs having multiple inputs and outputs. Initially, Charnes et al. [11] presented the basic DEA model which has been improved by many researchers. The relative validity or efficiency of a set of common character DMUs can be compared generating the enveloping surface of effective activities. Using the supposition that there are n DMUs or alternatives, and that each DMU has p number of inputs and q number of outputs, then the basic DEA evaluation model is as follows:

$$Max{h}_j=\frac{{{\displaystyle \sum }}_{k=1}^q{u}_k{y}_{kj}}{{{\displaystyle \sum }}_{i=1}^p{v}_i{x}_{ij}}$$

(1)

s.t.

$$\frac{{{\displaystyle \sum }}_{k=1}^q{u}_k{y}_{kj}}{{{\displaystyle \sum }}_{i=1}^p{v}_i{x}_{ij}}\le 1,j=1,2,\dots ,n$$

$$u_k\ge \epsilon ,v_i\ge \epsilon ,$$

where x_ij and v_i are the values of inputs and input weights, respectively, y_kj and u_k are the values of outputs and output weights, respectively, and ε is non-Archimedean. To solve the Equation (1), Charnes, Cooper and Rhodes (CCR) [11] developed the following linear programing model:

$$Max{h}_j={\displaystyle \sum }_{k=1}^q{u}_k{y}_{kj}$$

(2)

s.t.

$${\displaystyle \sum }_{i=1}^p{v}_i{x}_{ij}=1$$

$${\displaystyle \sum }_{k=1}^q{u}_k{y}_{kr}-{\displaystyle \sum }_{i=1}^p{v}_i{x}_{ir}\le 0,r=1,2,\dots ,n$$

$$u_r\ge \epsilon ,v_i\ge \epsilon$$

By optimizing the effective index, the corresponding weights of each input and output vector are determined. The model is able to handle the issue of unclear weight information within the inputs and outputs. However, the CCR model may give numerous efficient alternatives, which may result in challenges for the decision-makers in practice. Andersen and Petersen [30] proposed an improved method to overcome this problem as follows:

$$Max{h}_j={\displaystyle \sum }_{k=1}^q{u}_k{y}_{kj}$$

(3)

s.t.

$${\displaystyle \sum }_{i=1}^p{v}_i{x}_{ij}=1$$

$${\displaystyle \sum }_{k=1}^q{u}_k{y}_{kr}-{\displaystyle \sum }_{i=1}^p{v}_i{x}_{ir}\le 0,r=1,2,\dots ,n,r\ne k$$

$$u_r\ge \epsilon ,v_i\ge \epsilon$$

This new model formulation (also known as the super-efficiency CCR model) can discriminate among the same efficient units effectively in CCR models, as it allows for scores to be greater than 1 [19,20].

2.3. Hybrid ANP and Super-Efficiency CCR

The integrated ANP with super-efficiency CCR can overcome the limitations of both methods and provide the advantages of both ANP and DEA models. The managerial preferences can be incorporated into the super-efficiency CCR models by constraining the range of weights. To map managerial preferences effectively for the DEA, assurance regions (AR) can be used to restrict the weights. The AR can be determined considering the lower bound (LB) and upper bound (UB) for the weight of each input or output. The LB and UB can help to define constraints that relate to the weight values of different factors. These LB and UB values are obtained from the limit supermatrices of the ANP model. The LB and UB can be utilized to develop the AR constraint sets as follows [19]:

$$\frac{v_i}{v_j}\ge \frac{L{B}_i}{U{B}_j}\mathrm{and}\frac{v_i}{v_j}\le \frac{U{B}_i}{L{B}_j}$$

(4)

These constraints or the assurance regions can be integrated into the super-efficiency CCR model to form the super-efficiency CCR/AR model [20].

Relative Complexity Score

Using the super-efficiency CCR/AR model, an efficiency score is developed considering the relative value of the complexity in the floor production. The relative complexity score of floor M (between 0 and 1), comparing within the set of floors, can be expressed as follows:

$$RC{S}_M=h_M=\frac{{{\displaystyle \sum }}_{k=1}^q{u}_k{y}_{kM}}{{{\displaystyle \sum }}_{i=1}^p{v}_i{x}_{iM}}$$

(5)

According to the relative complexity scores, the floor with the highest complexity score should get more attention from the floor and production managers.

3. Implementation of the Proposed Model

The proposed model was implemented using data collected from Ananta Apparel, which is one of the leading apparel industries in Bangladesh. Ananta has an annual turnover of over $200 million and is engaged in the marketing, development, and manufacturing of apparel. The current employees number over 20,000 across the company. For this analysis, six sewing floors were selected. Two floor managers and one production manager participated in the decision-making.

3.1. ANP Model

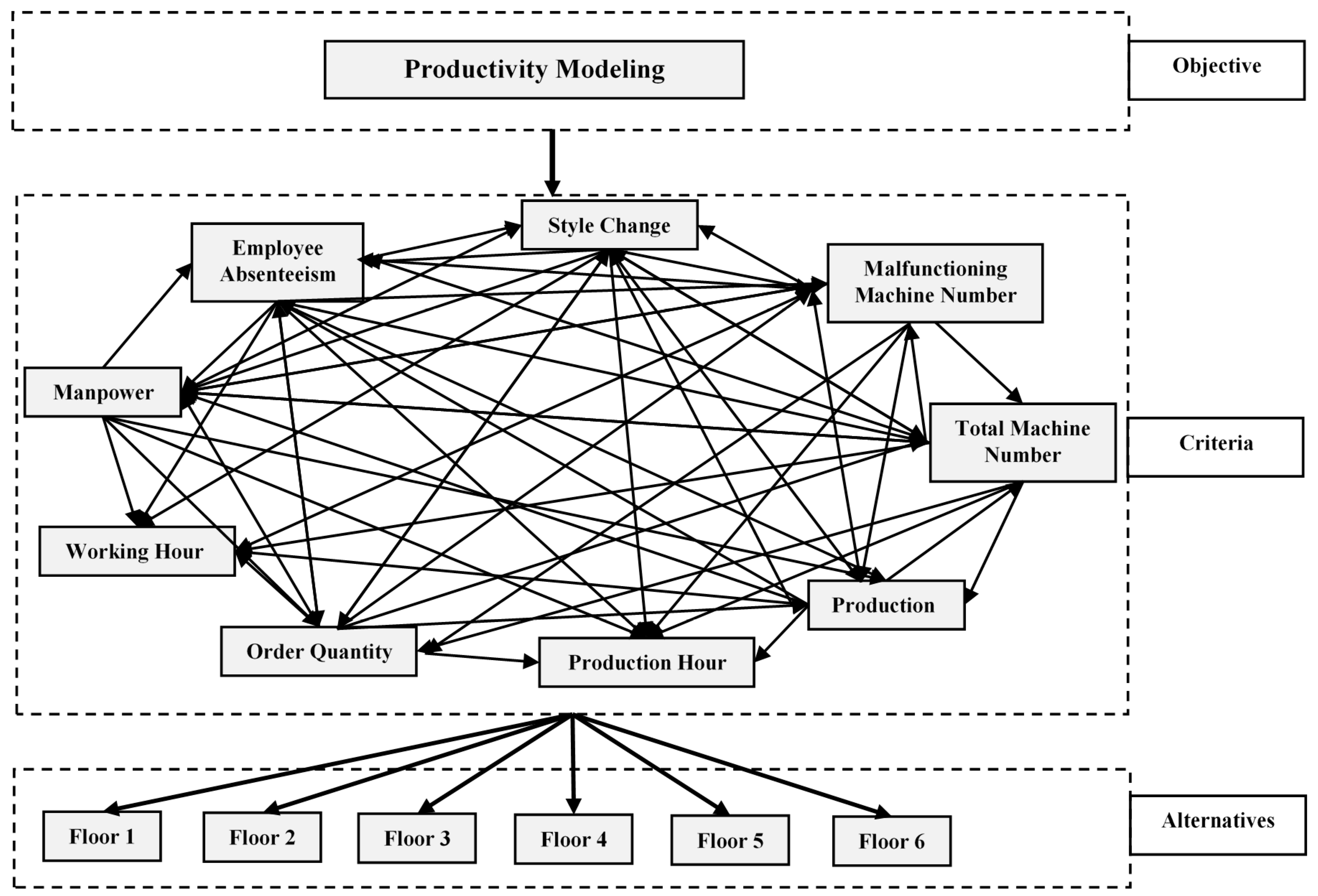
Based on the literature review and constant interaction with managers and employees of the Sewing department, nine key criteria were identified: manpower, employee absenteeism, style change, working hour, total machine number, malfunctioning machine number, production, production hour, and order quantity. The productivity evaluation based on these identified key criteria is illustrated as follows:

Manpower is closely related to productivity. If there is more manpower than is needed, the cost will increase, and it will decrease efficiency. Employee absenteeism is a curse to a company. High absenteeism causes loss to a company and reduces its productivity. If there is a frequent style change, productivity will decrease because the employee needs time to become accustomed to the changed style. To ensure high productivity, the company tries to keep a low working hour and a high production hour. In a competitive environment, the company’s main target is high production and a high order quantity received to make a profit. Total machine number and malfunctioning machine number increase costs, so these affect productivity as well.

After identifying the criteria, alternatives should be developed. Six alternatives were considered for this model, corresponding to six floors of the Sewing department, namely floor 1, floor 2, floor 3, floor 4, floor 5, and floor 6 (see Figure 2).

After developing the ANP model structure, the pairwise comparisons were performed using face-to-face interviews with the decision-makers using a comprehensive questionnaire. Based on these interviews and judgments, the weights of the main criteria were determined and supermatrices were derived.

Table A1. Unweighted Supermatrix.

Variables	Floor 1	Floor 2	Floor 3	Floor 4	Floor 5	Floor 6	Empl. Absent.	Malfunctioning Machine Number	Manpower	Order Quantity	Production Hour	Production	Style Change	Total Machine	Working Hour	Productivity Benchmarking
Floor 1	0.000	0.000	0.000	0.000	0.000	0.000	0.404	0.026	0.310	0.230	0.221	0.059	0.302	0.346	0.329	0.000
Floor 2	0.000	0.000	0.000	0.000	0.000	0.000	0.063	0.086	0.075	0.045	0.104	0.123	0.119	0.061	0.042	0.000
Floor 3	0.000	0.000	0.000	0.000	0.000	0.000	0.261	0.052	0.040	0.025	0.028	0.225	0.041	0.029	0.023	0.000
Floor 4	0.000	0.000	0.000	0.000	0.000	0.000	0.035	0.152	0.208	0.497	0.163	0.059	0.071	0.219	0.291	0.000
Floor 5	0.000	0.000	0.000	0.000	0.000	0.000	0.141	0.527	0.079	0.113	0.055	0.495	0.333	0.070	0.074	0.000
Floor 6	0.000	0.000	0.000	0.000	0.000	0.000	0.097	0.157	0.288	0.090	0.429	0.038	0.135	0.275	0.241	0.000
Employee Absenteeism	0.129	0.052	0.043	0.066	0.047	0.027	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.019
Malfunctioning Machine Number	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.133
Manpower	0.153	0.092	0.130	0.052	0.082	0.105	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.048
Order Quantity	0.116	0.189	0.142	0.096	0.151	0.156	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.104
Production Hour	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.207
Production	0.405	0.449	0.414	0.443	0.495	0.383	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.275
Style Change	0.103	0.124	0.178	0.190	0.158	0.178	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.072
Total Machine	0.038	0.037	0.047	0.126	0.036	0.118	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.070
Working Hour	0.056	0.056	0.045	0.027	0.030	0.034	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.071
Productivity Benchmarking	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

and

Table A2. Weighted Supermarix.

Variables	Floor 1	Floor 2	Floor 3	Floor 4	Floor 5	Floor 6	Empl. Absent.	Malfunctioning Machine Number	Manpower	Order Quantity	Production Hour	Production	Style Change	Total Machine	Working Hour	Productivity Benchmarking
Floor 1	0.000	0.000	0.000	0.000	0.000	0.000	0.404	0.026	0.310	0.230	0.221	0.059	0.302	0.346	0.329	0.000
Floor 2	0.000	0.000	0.000	0.000	0.000	0.000	0.063	0.086	0.075	0.045	0.104	0.123	0.119	0.061	0.042	0.000
Floor 3	0.000	0.000	0.000	0.000	0.000	0.000	0.261	0.052	0.040	0.025	0.028	0.225	0.041	0.029	0.023	0.000
Floor 4	0.000	0.000	0.000	0.000	0.000	0.000	0.035	0.152	0.208	0.497	0.163	0.059	0.071	0.219	0.291	0.000
Floor 5	0.000	0.000	0.000	0.000	0.000	0.000	0.141	0.527	0.079	0.113	0.055	0.495	0.333	0.070	0.074	0.000
Floor 6	0.000	0.000	0.000	0.000	0.000	0.000	0.097	0.157	0.288	0.090	0.429	0.038	0.135	0.275	0.241	0.000
Employee Absenteeism	0.129	0.052	0.043	0.066	0.047	0.027	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.019
Malfunctioning Machine Number	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.133
Manpower	0.153	0.092	0.130	0.052	0.082	0.105	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.048
Order Quantity	0.116	0.189	0.142	0.096	0.151	0.156	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.104
Production Hour	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.207
Production	0.405	0.449	0.414	0.443	0.495	0.383	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.275
Style Change	0.103	0.124	0.178	0.190	0.158	0.178	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.072
Total Machine	0.038	0.037	0.047	0.126	0.036	0.118	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.070
Working Hour	0.056	0.056	0.045	0.027	0.030	0.034	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.071
Productivity Benchmarking	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

present the unweighted supermatrix and the weighted supermatrix, respectively. In this study, Super Decisions software was used to solve and analyze the ANP model. It was assumed that the maximum and minimum values for each factor would provide bounds for the assurance regions, which would then be used in the next phase of the framework.

Table A3. Limit Matrix.

Variables	Floor 1	Floor 2	Floor 3	Floor 4	Floor 5	Floor 6	Empl. Absent.	Malfunctioning Machine Number	Manpower	Order Quantity	Production Hour	Production	Style Change	Total Machine	Working Hour	Productivity Benchmarking
Floor 1	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098	0.098
Floor 2	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048	0.048
Floor 3	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066	0.066
Floor 4	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077
Floor 5	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155	0.155
Floor 6	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056	0.056
Employee Absenteeism	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032	0.032
Malfunctioning Machine Number	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
Manpower	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051	0.051
Order Quantity	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069	0.069
Production Hour	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000
Production	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221	0.221
Style Change	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077	0.077
Total Machine	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031	0.031
Working Hour	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020	0.020
Productivity Benchmarking	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000	0.000

shows the limit matrix. Tighter bounds indicated better agreement among managers or decision-makers with respect to the importance of the measures, whereas looser bounds represented higher uncertainty and inconsistency.

Table 2. Priorities of the factors using ANP.

Name	Normalized by Cluster	Limiting
Floor 1	0.1958	0.0979
Floor 2	0.0958	0.0479
Floor 3	0.1324	0.0662
Floor 4	0.1541	0.0770
Floor 5	0.3099	0.1550
Floor 6	0.1121	0.0560
Employee Absenteeism	0.0637	0.0318
Malfunctioning Machine Number	0.0000	0.0000
Manpower	0.1015	0.0508
Order Quantity	0.1385	0.0693
Production Hour	0.0000	0.0000
Production (Output)	0.4418	0.2209
Style Change	0.1539	0.0769
Total Machine Number	0.0611	0.0305
Working Hour	0.0395	0.0198

indicates the priorities of the factors based on the ANP model. The results were also assessed by Super Decisions’ sensitivity analysis module to examine the reaction to change in judgments, as discussed in the next section.

3.2. DEA Model

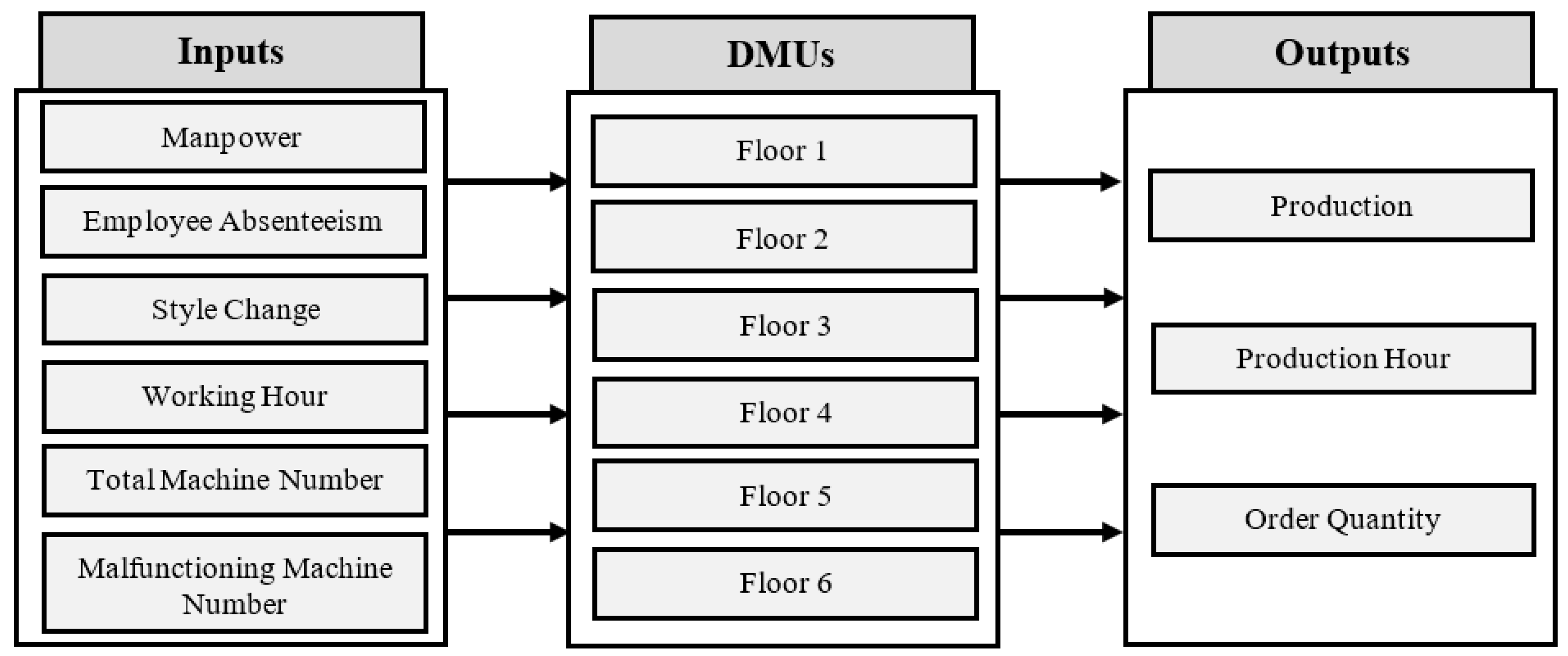
In this step, the productivity measurement of the alternatives was evaluated using DEA models. The factor weight restrictions derived from the ANP technique were found normally in DEA. In general, DEA studies consider measures with ‘‘less is better’’ as inputs and ‘‘more is better’’ as outputs. Based on this definition of inputs and outputs, a total of six inputs and three outputs were selected. The inputs were manpower, employee absenteeism, style change, working hour, total machine number, and malfunctioning machine number, whereas the outputs were production, production hour, and order quantity. To demonstrate the proposed framework, six sewing floors were considered for evaluation. Figure 3 shows the proposed DEA model. The data from the DMUs for the six floors are presented in

Table 3. Data from the DMUs.

DMU		Floor 1	Floor 2	Floor 3	Floor 4	Floor 5	Floor 6
Input	Manpower	289	259	229	282	259	283
	Employee Absenteeism	3	8	4	10	7	9
	Style Change	1	2	5	3	1	2
	Working Hour	3024	2742	2438	2874	2841	3039
	Total Machine Number	189	159	129	182	159	183
	Malfunctioning Machine Number	4	2	3	1	0	1
Output	Production	4000	4200	4300	4000	4520	3900
	Production Hour	1672	1608	1467	1669	1536	1754
	Order Quantity	175,585	113,378	107,296	235,072	153,511	152,587

.

Weight and Bounds Determination

To determine the managerial weights, pairwise comparisons were performed to represent each set of relationships and the relative efficiency scores were aggregated to generate the supermatrix. Then, a stable set of weights was determined to converge the supermatrix. After performing all the pairwise comparisons, consistency ratios of the matrices were calculated to identify possible errors in judgments. The judgments of the comparison matrices are considered consistent and reliable if the consistency ratios of all the pairwise comparison matrices are less than 0.1. In this study, the consistency ratios of all the pairwise comparison matrices were less than 0.1. Thus, the judgments were consistent and reliable.

Table 4. Weight of the criteria.

Criteria	Floor 1	Floor 2	Floor 3	Floor 4	Floor 5	Floor 6
Manpower	0.3095	0.0750	0.0398	0.2079	0.0794	0.2884
Employee Absenteeism	0.4037	0.0626	0.2609	0.0347	0.1411	0.0970
Style Change	0.3021	0.1121	0.0409	0.0705	0.3325	0.1349
Working Hour	0.3295	0.0416	0.0230	0.2907	0.0741	0.2413
Total Machine Number	0.3460	0.0609	0.0289	0.2189	0.0700	0.2413
Malfunctioning Machine Number	0.0260	0.0860	0.0522	0.1519	0.5274	0.1566
Production	0.0594	0.1227	0.2248	0.0594	0.4952	0.0384
Production Hour	0.2208	0.1042	0.0278	0.1631	0.0550	0.4292
Order Quantity	0.2296	0.0452	0.0250	0.4965	0.1132	0.0904
Lower Limit	0.0260	0.0416	0.0230	0.0347	0.0550	0.0550
Upper limit	0.4037	0.1227	0.2609	0.4965	0.5274	0.4292

shows the weights of the main criteria. These weights had an influence on the evaluation of the floor efficiency in the next stages.

The weights were calculated based on the main criteria. The weights of manpower, employee absenteeism, style change, working hour, total machine number, malfunctioning machine number, production, production hour, and order quantity were 2.1536, 3.5450, 3.6861, 3.4871, 3.5388, 3.4113, 3.5164, 3.4691, and 3.4156, respectively.

The assurance region weights were calculated from the overall weights of the floors which were within the upper and lower limit of the weights. The ranking of the six different floors using the DEA-CCR model is presented in

Table 5. DEA–Charnes, Cooper and Rhodes and assurance regions (CCR/AR) model result.

Alternatives	Normal Efficiency	Ideal Efficiency	Ranking
Floor 1	0.1958	0.6316	2
Floor 2	0.0958	0.3090	6
Floor 3	0.1325	0.4274	4
Floor 4	0.1538	0.4963	3
Floor 5	0.3100	1.0000	1
Floor 6	0.1121	0.3615	5

. Due to the maximum overall weight in the ANP model, Floor 5 was ranked as the most efficient with a score of 0.3100. Floors 1 and 4 were ranked second and third, respectively. According to Table 5, Floor 2 was ranked as the most inefficient one with an efficiency score of 0.0958. This ranking of the floors can help the decision-makers or managers make the decision of which floor is undesirable for this decision environment and which floor is not productive and needs improvement.

4. Conclusions

In this study, a decision support framework was developed integrating the ANP and DEA methods to benchmark the productivity of a manufacturing process. Both quantitative and qualitative inputs may require measuring productivity. The proposed model was able to accommodate this issue. To illustrate the proposed framework, the authors implemented it to measure the productivity of an apparel industry in Bangladesh incorporating both quantitative data about the alternatives and soft preferential information or qualitative information from the decision-makers. The ANP helps to structure the decision environment in a logical way and is able to express the interrelationship and dependencies among criteria of different levels. The DEA evaluation was performed by integrating both the floor performance data and managers’ or decision-makers’ preference bounds. The floor or alternatives were ranked based on the relative efficiency scores using the CCR/AR approach.

The proposed hybrid ANP-DEA framework combines the subjective and objective judgments in the complexity measurement. The proposed framework offers an opportunity for decision-makers to develop results that are reflective of these perceptions. The proposed framework is flexible to allow modifications in the productivity benchmarking criteria and subcriteria, such as the removal of unwanted criteria or subcriteria, the addition of new criteria or subcriteria, and alterations in the pairwise comparison judgments. The results of the proposed framework can provide managers or decision-makers the opportunity to better investigate the reasons for the poor performance of any specific floor or unit and focus on the most important activities that will improve the productivity.

This study has certain limitations, which open some avenues for future research. The results of this study are based on the judgment of a limited number of interviewed employees in a company. The applicability of the proposed framework is demonstrated using a single apparel industry in a single country context. Additional research is required to observe if the findings could be extended to other apparel industries in other developing nations. The sensitivity analysis of the proposed framework can be investigated in future research.

Although the proposed framework was implemented to measure the floor efficiency in an apparel industry, it can be applied to measure the productivity of different sections or even different organizations. The proposed framework can be used to evaluate the productivity of other types of manufacturing industries, such as food, pharmaceutical products, and furniture, with the collaboration of experts from the corresponding knowledge disciplines and by making the necessary changes in the criteria or subcriteria. In order to consider the vagueness and ambiguity of the decision-making process, the proposed framework can be further extended in the future using fuzzy ANP with DEA approaches for productivity measurement. The research can be further extended, compared, and/or validated using other hybrid network-based methods, such as a fuzzy cognitive mapping or grey-based analytic network process.