2.1. Determination of Acoustic Pump Parameters
In order to quantify the transmission and excitation parameters, the pump is interpreted as an acoustic four-pole in the frequency domain. This system-theoretic approach is applied to the experiments and CFD simulations within this study. In
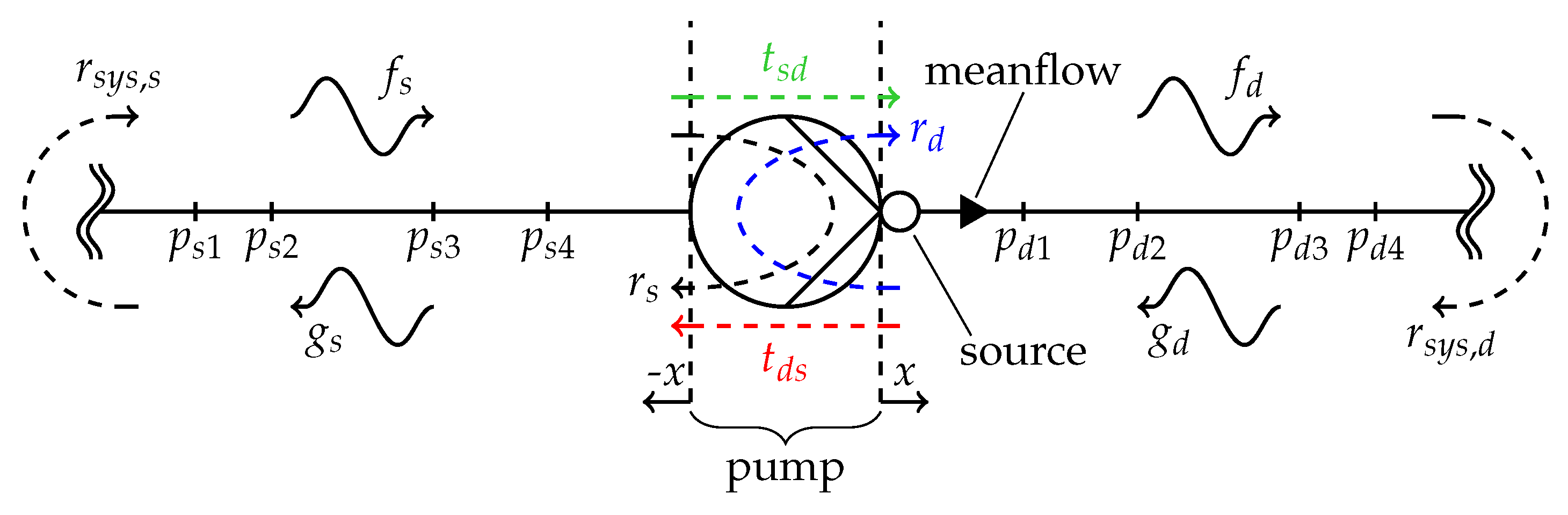
Figure 1, a schematic representation of the pump’s acoustic surrounding is shown. By means of the linear equation
the following parameters are connected:
and : up- and downstream-propagating pressure waves, with and quantifying the acoustic pressure fields on the suction (s) and discharge (d) side of the pump,
: the pump’s scattering matrix, which contains the four transmission parameters , , , and ,
and : the pump’s source (src.) parameters in the form of up- and downstream-propagating pressure waves.
Generally, if the acoustic pressure fields in the pump’s suction and discharge piping are known, the requested pump parameters can be inferred. To decompose a one-dimensional acoustic pressure field in up- and downstream-propagating waves
and
, the complex pressure amplitudes
at a minimum of two different locations along the direction of propagation
x must be known [
12]:
where
k is the frequency (
f)-dependent wave number. Wave propagation is assumed to be lossless, without convective components, and linear. The fluid is considered single-phase. The effective speed of sound in the piping
is assumed to be frequency-independent. A first and good (based on our experience in measuring the propagation of sound waves in thin-walled, water-filled steel pipes) estimation of
in an elastic, axially fixed pipe can be calculated according to [
13] by means of
where
and
are the Young’s modulus and Poisson’s ratio of the pipe material,
s is the wall thickness,
d the inner pipe diameter, and
and
are the fluid’s specific speed of sound and Young’s modulus. For compressible single-phase CFD simulations without taking FSI into account,
equals the fluid specific speed of sound
. If the number of measuring points is
, Equation (
2) becomes overdetermined. Especially for experiments, this is desirable to compensate for measurement errors. In this case,
and
need to be determined by means of a least squares method. For this, both sides of Equation (
2) are multiplied by the complex conjugate transposed (adjoint) matrix
to obtain the Gaussian normal equation
and, therefore, a solvable linear system of equations [
14]. In order to evaluate the quality of the solution found, a relative error
, based on the residuum
, is determined
Since the effective speed of sound
should be a result of the procedure as well, a superior golden-section search algorithm [
14] is prepended to the least squares method described above to find the value of
within a defined range which minimises the residuum. By means of this optimisation procedure it is now possible to evaluate
,
and
and, therefore, the requested acoustic pressure field parameters in the pump’s suction and discharge piping. Note that the system’s reflection coefficients
and
can be calculated by means of
Based on the known in- and output parameters
,
,
, and
, the four-pole’s unknown transmission parameters
,
,
, and
can be determined. It can be assumed that the transmission behaviour of the pump in standstill corresponds in a good approximation to that of the pump in operation [
15]. Since in standstill
, Equation (
1) is simplified. It is then possible to estimate
using at least two different sound configurations
on each side of the system:
The two-source method is the most effective way to create different sound configurations. By means of alternating the sources’ amplitudes and phases relative to each other it is theoretically possible to generate an infinite number of linear independent configurations [
16]. If Equation (
7) is overdetermined (
), the transmission parameters can be evaluated by means of the same least squares method approach used to solve Equation (
2) for
.
If it is additionally to be investigated whether a four-pole tends to have dissipative, passive, or active properties, the acoustic power ratio
can be calculated.
is the ratio of outgoing and incoming time-averaged acoustic powers and can be determined from the transmission parameters:
and
are the acoustic impedances within the pipes connected to the suction and discharge flange of the pump. The derivation of Equation (
8) is shown in
Appendix A. Based on the amount of
compared to one, the following conclusions can be drawn:
: the part different to one is dissipated (or transformed) within the four-pole;
: the four-pole is a purely passive acoustic element;
: the part different to one is generated (or transformed) within the four-pole.
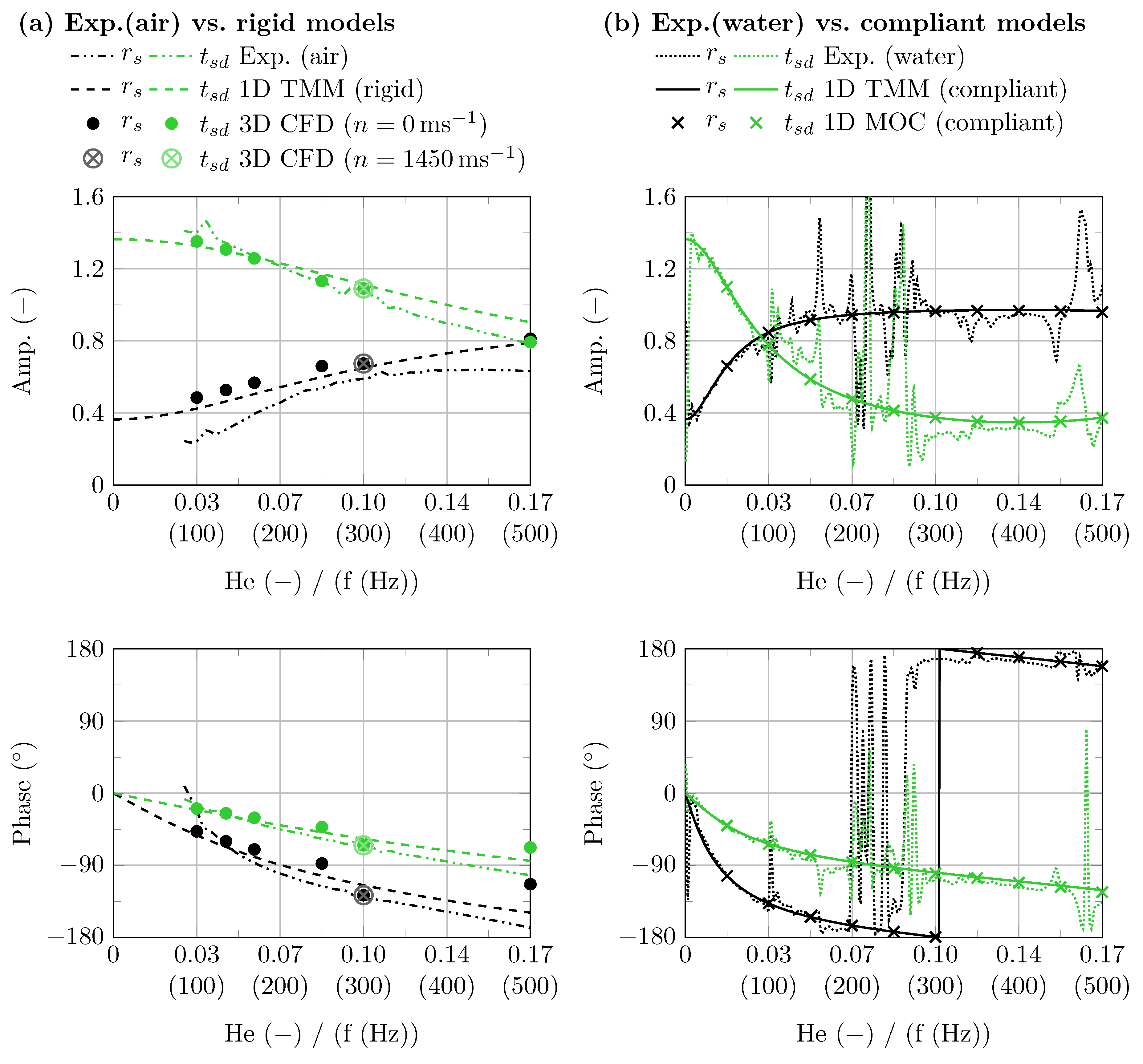
Ideally, the acoustic transmission behaviour of the pump should be purely passive. This is the special case for a pump in standstill in the absence of dissipative and FSI effects. Therefore, the evaluation of is used herein to analyse the quality of the CFD simulations regarding numerical dissipation of acoustic pressure waves and the effect of the FSI on the experimentally determined transmission parameters.
Looking back on Equation (
1), the only unknown parameters left are the up- and downstream-propagating source waves
and
. In order to estimate a set of source parameters,
,
,
, and
need to be determined while the pump works in a specific operation point. By means of the following Equation
and
can be transformed into the native acoustic sources monopole
and dipole
to allow a better physical interpretation:
where
represents the specific acoustic impedance in the source region and is calculated using the corresponding effective speed of sound
.
2.2. Experimental Approach
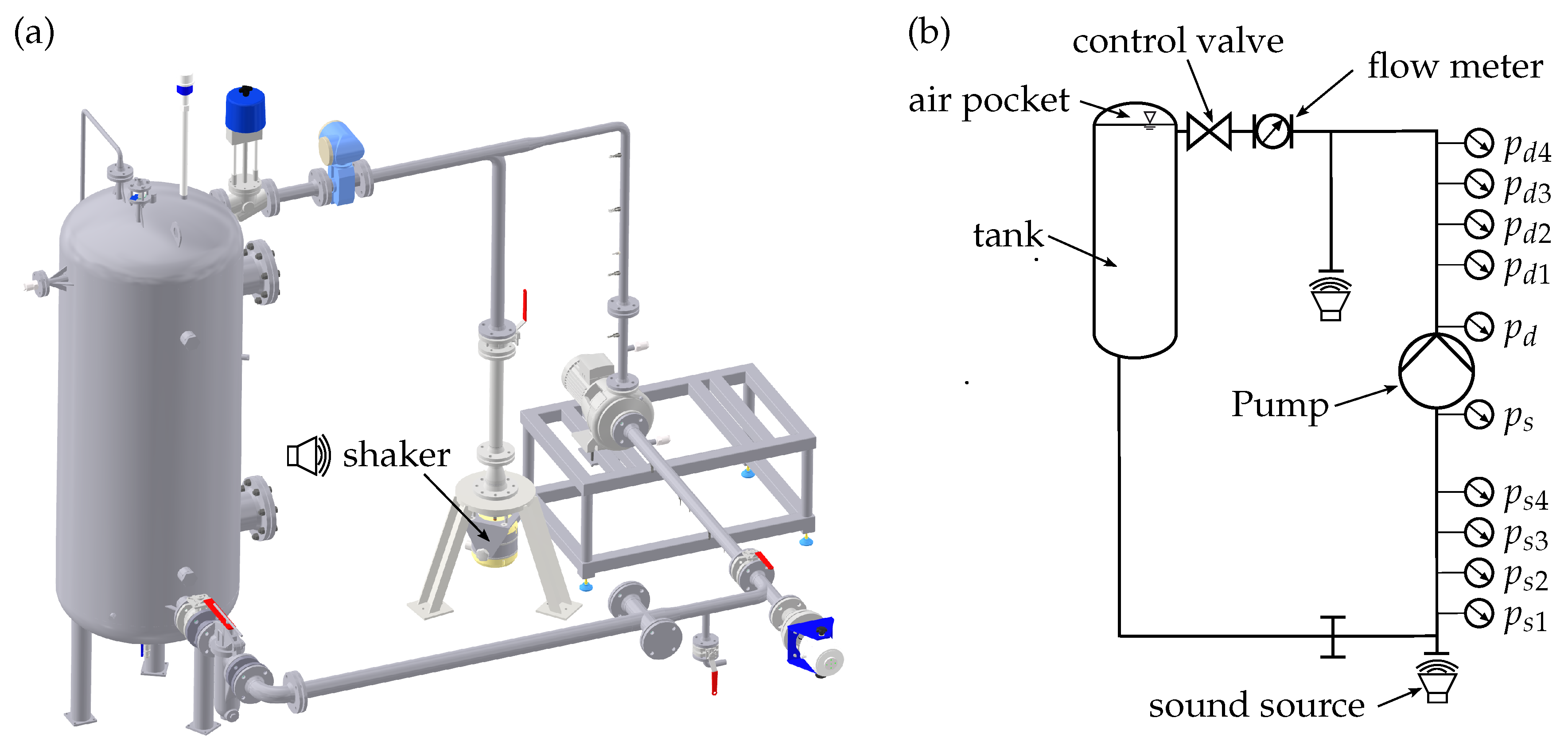
In
Figure 2, the experimental setup is illustrated. The pump under test is a radial, single-stage centrifugal pump with a volute-type casing. The pump is speed-regulated and the specifications are listed in
Table 1. For high-resolution pressure measurements in water, piezoelectric (PE) transducers Kistler™ (Winterthur, Switzerland) 7061 B/C are flush-mounted to the pipes’ inner walls on the suction (
) and discharge (
) sides of the pump.
The charge signal outputs of the PE sensors are amplified by means of Kistler™ (Winterthur, Switzerland) 5018A and 5011B charge amplifiers. For equivalent measurements in air, condenser microphones PCB™ (Depew, NY, USA) 130A23 are used. Sensor locations relative to each other are non-equidistant and optimised to the range of frequencies investigated in this study. In
Table 2, measurement positions relative to the pump’s flanges are catalogued (flow direction = positive x-direction). Two capacitive pressure sensors STS™ (Sirnach, Switzerland) ATM 1st (
) and a magnetic inductive flow meter E+H™ (Reinach, Switzerland) Promag W are used to measure the pump’s head curve. A control valve is applied to adjust the pump’s operation point. An air pocket within the tank can be pressurised to regulate the system’s net positive suction head
. The value of
was set to
to prevent cavitation in the pump as far as possible. Electromagnetic shakers (TIRA™ (Schalkau, Germany) TV 51110 and 51140-M) connected to a flexible membrane construction (water) or common loudspeakers (air) are used as optional sources of sound. All signals are further processed by means of the data acquisition devise imc™ (Berlin, Germany) Cronos Flex. Signals of PE sensors are sampled at
and further post-processed by a flat-top windowed discrete Fourier transformation (DFT) with a uniform signal length of
. The resulting frequency resolution is
. The useful frequency range of PE transducers and charge amplifiers is not limited to small frequencies, as they can also be used for quasi-static measurements. The microphones are calibrated for frequencies within 20 Hz
kHz. The relative error
(Equation (
5)) is used for a quality check of the measurement results since all further acoustic parameters are calculated based on the results for the pressure field decompositions.
The two-source method is used to evaluate the pump’s acoustic transmission characteristics (Equation (
7)). The external sound sources (shakers or loudspeakers) are fed with a white-noise signal designed for the frequency range
. An attempt was made to generate as many different sound configurations as possible in order to minimise the influence of statistic measurement errors on the requested parameters.
Therefore, the sources’ amplitudes and the correlation of signals are varied to generate a number of different cases. The evaluated results (, , , ) are filtered by means of a weighted averaging function over five data points to statistically smooth the curves. Except for a few outliers ( for frequencies around the system’s mechanical resonances) the relative error in decomposition applies for , which indicates good quality.
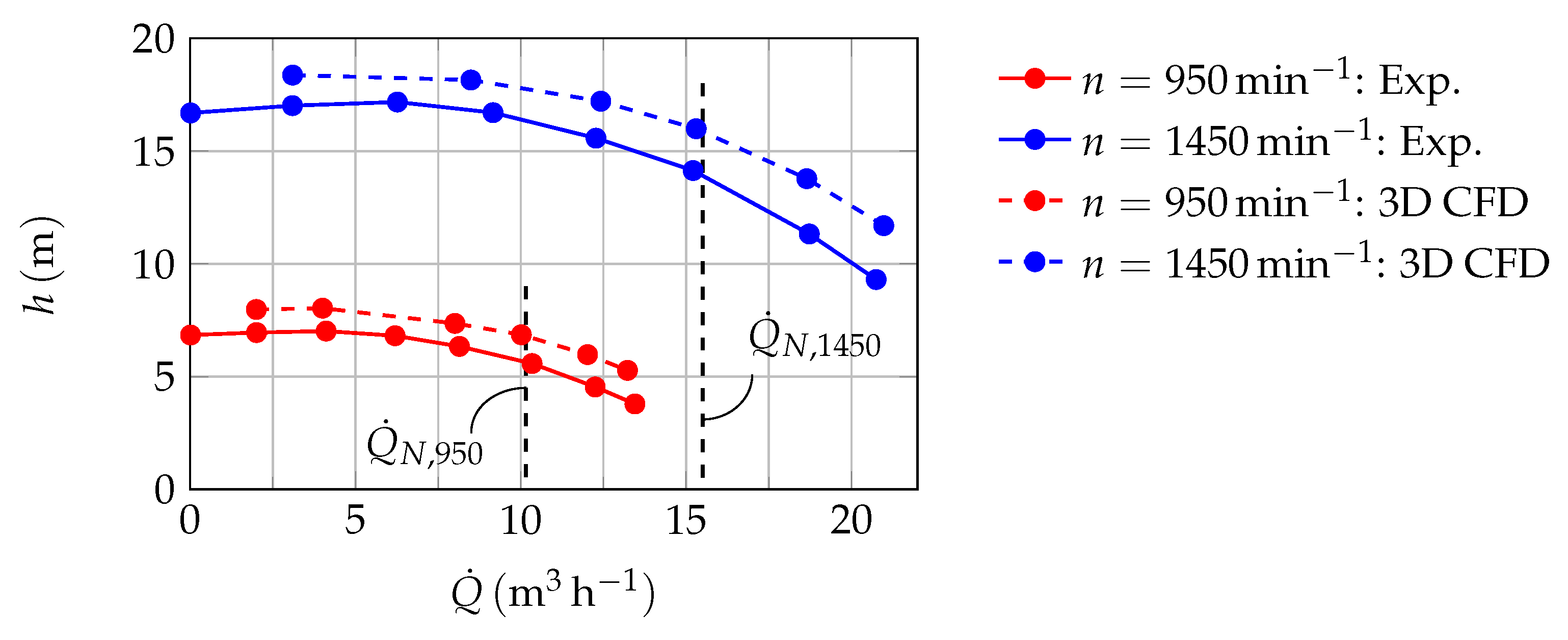
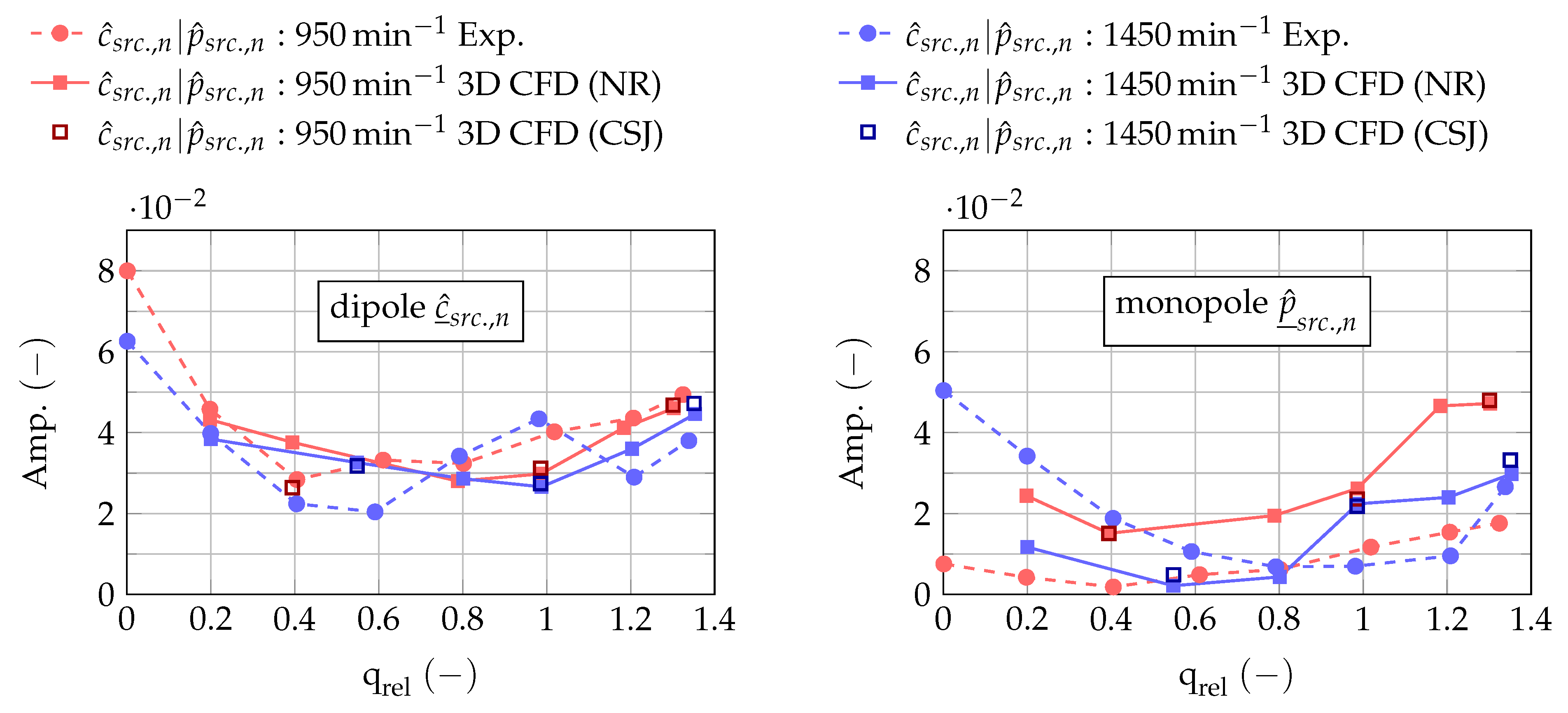
Finally, the source parameters are evaluated. The relative flow rate
is varied in equal steps
from
to the highest overload operation point of
for two different rotational speeds (
and
). For every single operation point the pressure field parameters
,
,
, and
are determined. The relative error in decomposition is again
for
. Based on that, as well as on the known transmission parameters, the up- and downstream-running source waves
and
are calculated (Equation (
1)) and further transformed into complex monopole
and dipole
amplitudes (Equations (
9) and (
10)).
2.3. 3D CFD Approach
An in-house CFD solver named
solver3D is used to calculate the pump’s flow-acoustic behaviour. It is described in detail by [
17,
18] and is summarised here only very briefly. The unsteady Reynolds-averaged Navier–Stokes (URANS) equations are solved by a cell-centred unstructured finite volume (FV) scheme. The extended SIMPLE (semi-implicit method for pressure-linked equations) algorithm for compressible flow is used. The accuracy of the interpolation approaches used is second-order in space. An implicit three-level time discretization scheme is employed, which is second-order accurate as well. The flow is further assumed to be isothermal. Single-phase flow is applied, which means that cavitation effects are omitted. The Tait equation for liquid water is applied as a barotropic equation of state (EOS). The speed of sound is assumed to be
for ambient temperature
and density
.
The simulation setup is adopted from [
19]. The statistical shear stress transport (SST) turbulence model with automatic wall treatment is used.
The 3D domain is illustrated in
Figure 3 and consists of impeller, volute casing, side chambers on the suction and pressure sides, as well as pipe sections beyond the pump’s suction and discharge flanges. The structure surrounding the fluid is considered rigid, namely, no FSI is taken into account. According to previous investigations, the pump’s head is grid-independent for a grid with about 2 million hexahedral cells when wall functions are used. The latter simplification leads to an over-prediction of the pump’s head, especially in overload operation, which can be attributed to an inaccurate reproduction of flow separations at the volute’s tongue [
19,
20]. However, the computational effort for the resolution of a viscous boundary layer (
) combined with high time resolution requirements would be exceptionally high and is, therefore, out of this research’s scope. A sliding mesh interface is used to connect the rotating impeller with the stationary casing part. A time resolution of about
impeller rotation is prescribed to ensure a proper resolution of the acoustic pressure wave propagation. This corresponds to a time step of
for
. For the lower rotational speed
, the same time-step size is adopted, leading to a time resolution of
impeller rotation. The acoustic Courant–Friedrichs–Lewy (CFL) number, calculated by means of
where
c is the mean velocity of the fluid, is about
on average and has a maximum value of
. As depicted in
Figure 3, the 3D-FV area is coupled to a 1D finite difference (FD) domain at the interface (IF). The coupling is employed since a non-reflecting (NR) boundary condition (BC) is integrated within the 1D code. The NRBC is prescribed at both ends of the 1D domain. This makes it possible to selectively adjust the system impedance by an optional cross-section jump (CSJ) before the NRBC. The numerical scheme is based on the one-dimensional conservation equations for mass and momentum in characteristic form (method of characteristics (MOC)). It is implemented in the in-house solver
FLOAT [
8]. The 3D/1D coupling in terms of the pump model used is set and analysed in detail by [
18] according to the procedure in [
21].
The method for evaluation of the acoustic parameters is adapted from experiments:
- (i)
the pump is left at standstill and treated with sound from external sources (src.) to evaluate the transmission parameters;
- (ii)
several operation points are adjusted to calculate the monopole and dipole amplitudes from the CFD simulations.
In both cases, monitor points in the 3D domain are used to record the high-resolution pressure–time signals, which are further flat-top windowed and transformed by a DFT for the acoustic pressure wave decomposition (Equation (
2) with
). Only time intervals with constant pressure amplitudes, are used for further evaluation. Each time interval has a length of 28 periods minimum. For case (i) a sinusoidal pressure signal is prescribed at one boundary while the other one is kept solely non-reflective and vice versa. It follows that for each frequency of interest two independent configurations are generated to evaluate the related transmission parameters (Equation (
7) with
). In case (ii), the pump operates either in a fully non-reflective system (no CSJ,
) or for equivalent operation conditions in a partly reflecting system (with CSJ,
) to analyse the influence of varying the system impedance. The operating points are adjusted by means of prescribed mean flow at the inlet and mean pressure at the system’s outlet. Both boundary conditions are set in addition to the NRBC. Note that the decisive criterion for the length of the signal time intervals in case (ii) is the respective blade-passing frequency
, which is
for
and
for
. As described above, a minimum of 28 periods of the signal is used for post-processing.
2.4. 1D Modelling
The approach described by [
9] is used to develop a 1D model which represents the pump’s acoustic transmission characteristics in a frequency range of
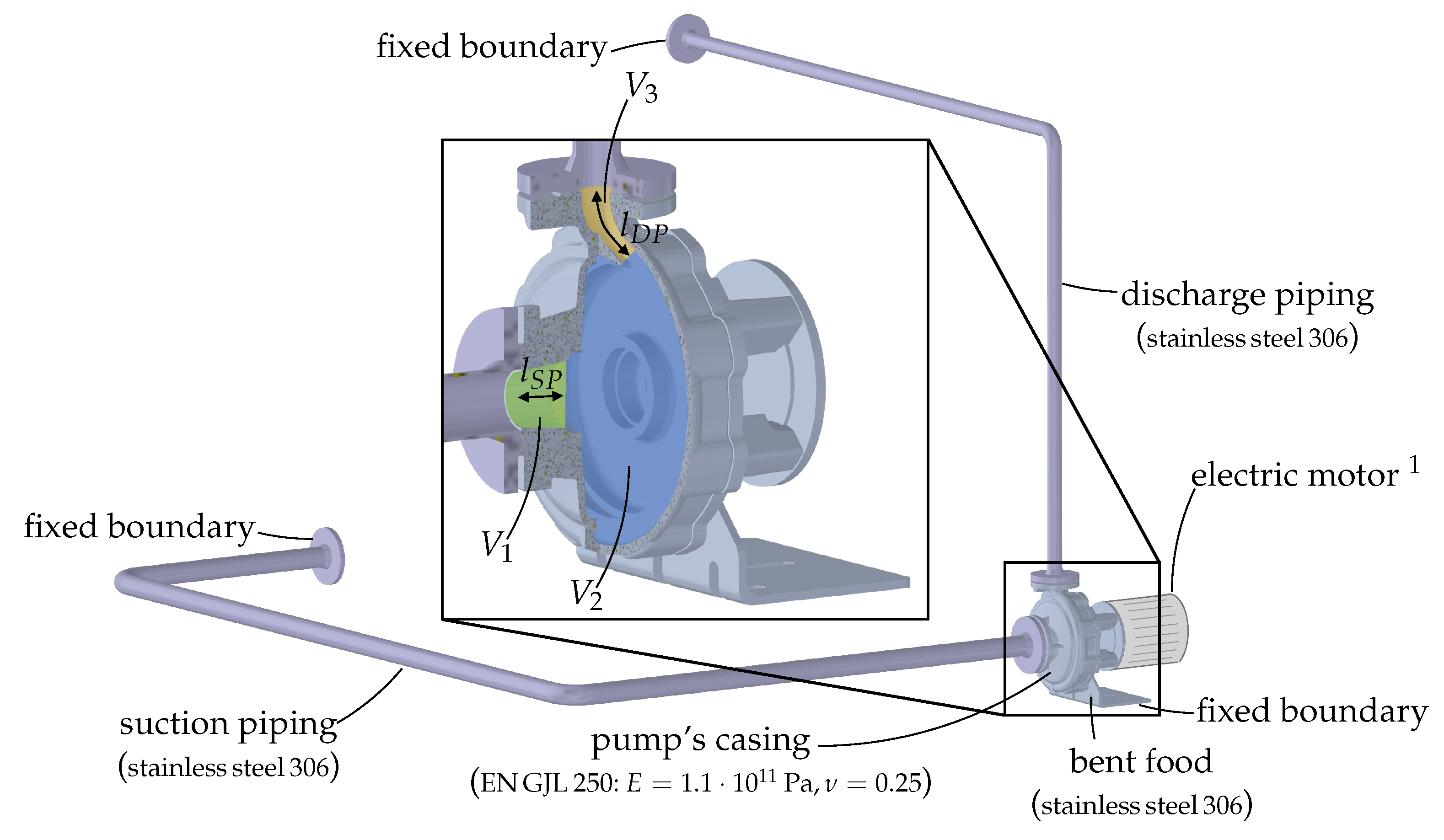
. Therefore, the geometry of the pump is simplified as a series connection of three one-dimensional elements: namely, suction port (SP), a middle part called chamber (CH), and discharge port (DP). Every element is geometrically defined via its diameter
d and length
l. The latter is to be understood as an effective acoustic length which corresponds to the average distance that pressure waves travel through the respective pump part. In the cases of the suction and discharge ports, the determination of the acoustic lengths
and
is straightforward since there is only a single path for plane pressure wave propagation. In order to calculate the acoustic length for the middle part, including the impeller and volute
, an effective acoustic length is determined. This corresponds to the average of the longest and shortest paths through the pump sections involved. The diameters of each model part
,
, and
are estimated by means of the respective fluid volumes
V and the known acoustic length:
In addition to the geometric model parameters, the effective speed of sound within the respective elements
can be adjusted to consider the compliance of the casing or the connected piping system and, therefore, the FSI. The effective speed of sound in the connected pipes
, calculated either by means of Equation (
3) or by decompositions based on experiments (see
Section 2.2), is approximately
. The effective speeds of sound within the casing, i.e.,
,
, and
, can be evaluated based on static-mechanical FEM simulations. This approach was successfully used in [
8] to determine
for centrifugal pumps with volute casings with three different specific rotational speeds. The goal, analogous to Equation (
3), is to take into account the mechanical elasticity of the pump’s casing and include this as an additional compliance in an equation for
. The consideration is exclusively quasi-static. This means that structural dynamic effects are not taken into account. According to the explanations in [
13], the following equation can be derived from the one-dimensional equation of mass conservation and the definition of the speed of sound in the fluid
:
The expression
represents an additional compliance. If
is extended by a characteristic length
l, this results in the following relationship:
Equation (
14) holds if
and provides the possibility to calculate the effective speed of sound in fluids surrounded by elastic mechanical structures that are not as simple and regular as cylindrical tubes, for example. Therefore, the undeformed inner fluid volume
V and the change in volume
due to a change in fluid pressure
must be known, which can be calculated using static FEM simulations, for example.
For the current pump under investigation a procedure according to [
8] is adopted and extended to determine, in addition to
, the effective speeds of sound in the suction and discharge ports,
and
. The commercial software
Ansys™ (with
Ansys Workbench and
Ansys Mechanical 2023R1) is used to prepare the model, perform the simulation, and post-process the results. The setup used for the FEM is depicted in
Figure 4.
The rotor (impeller, shaft, and mechanical seal) and electric motor are not considered for simplification. The pump is connected to a simplified piping system. The flanges of the piping system and the bent foot of the pump are fixed by boundary conditions. The contact elements between the respective bodies are handled as bonded. No gravity is taken into account. According to experiments, the components’ materials are chosen. The stainless steel is of type 306 (
, Young’s modulus
). The Young’s modulus of cast iron
EN GJL 250 is set to
and, therefore, to a mean value within the range of manufacturer’s specifications. The native
Ansys Mechanical mesh generator is used. The overall element size is prescribed as
. An additional refinement to
element size for the pump’s casing is considered. The calculated mesh has about 444,000 tetrahedral elements with quadratic shape functions. To effect a linear elastic deformation of the casing and, therefore, a measurable volume change, the fluid pressure in the pump is varied up to one bar gauge pressure. The total differentials are
and
(according to Equation (
14)), and so
can be linearised to
within this range of inner pressure load (this assumption was checked and confirmed within the relevant range of gauge pressure
). The resulting total displacements of the pump’s casing due to a change in fluid pressure of
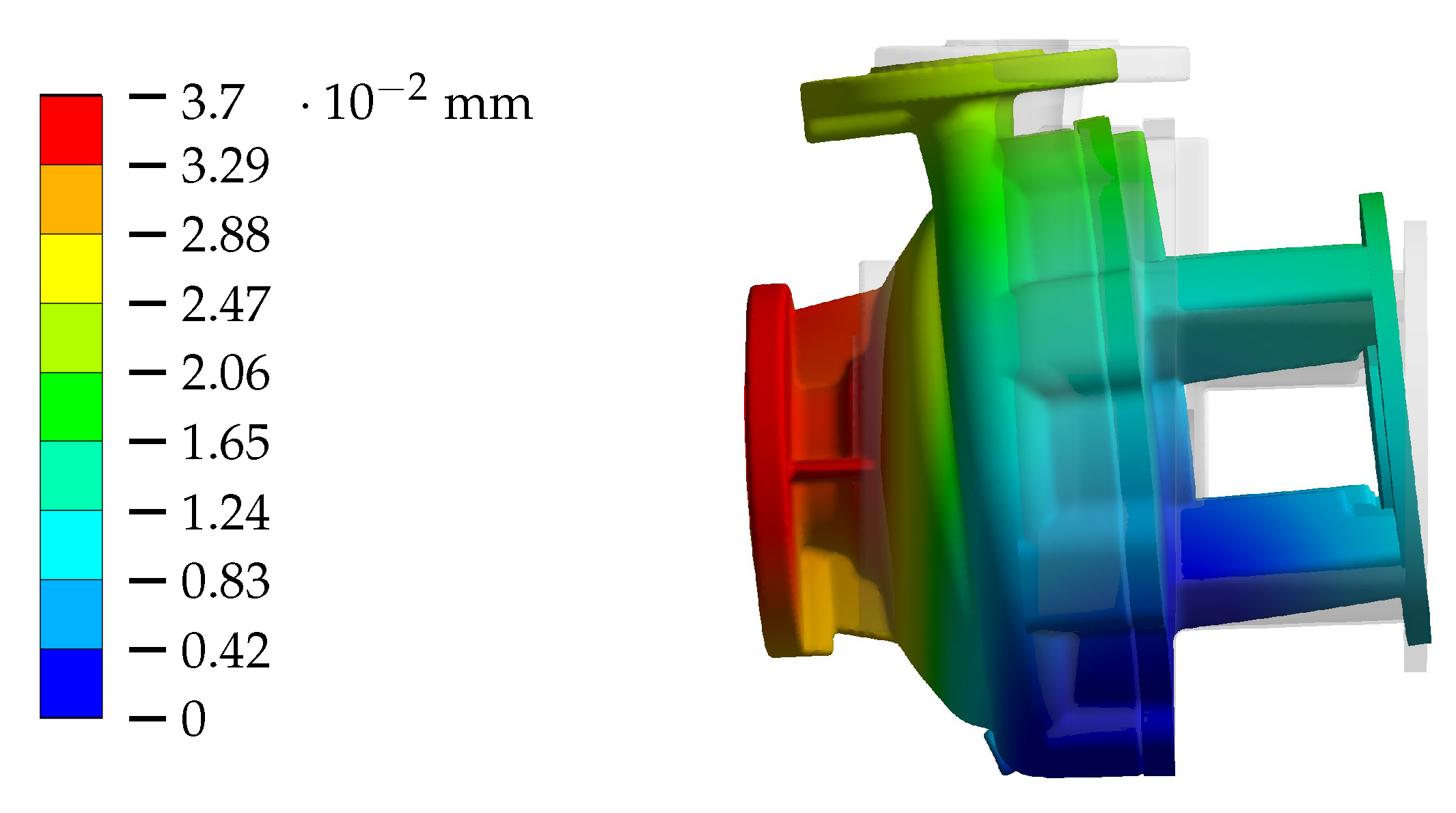
are illustrated in
Figure 5. The two main causes of displacements are a tilting movement around the pump’s foot and a deformation of the casing, mainly in the areas of the sloping walls between the suction port and spiral contour. The effective speed of sound is influenced in particular by the last mentioned deformation of the casing.
To evaluate the necessary parameters
V and
from the FEM results, the fluid volumes
,
, and
within the pump are determined in the undeformed (index 0) and deformed (index
) cases. In both cases, it is important to use the discretized model to avoid the influence of discretization errors on the target parameters. This kind of error would have a great impact since
is small and of a similar order of magnitude. The values of
and
for the middle part (volume 2) are both reduced by the rotor’s volume
. Thus, the rotor neglected for the FEM can be considered again for the calculation of
. However, the compressibility of the rotor, which is made out of cast iron, is disregarded. This simplification is legitimate since the compressibility of cast iron is
, which is almost 35 times higher compared to water (
). The volume change
for all volume parts is calculated by means of
. The resulting parameters are listed in
Table 3. The largest
due to
is calculated for volume 2. The value of
is comparable to the volume of an averaged-sized rain drop and seems, thus, rather small compared to
. However, the effective speed of sound is significantly reduced to
, and thus, the effect of the resulting additional compliance is very high. The pump’s suction and discharge ports are stiffer.
even becomes negative in volume 3, which leads to an effective speed of sound which is higher compared to
.
The resulting parameters for the compliant 1D model are listed in
Table 4. The transmission coefficients of a rigid model that is geometrically similar to the compliant one are calculated as well. In this case, no additional compliances are considered and, therefore, the speed of sound within the 1D elements equates to the speed of sound in water
. The wave propagation within the 1D pump model is assumed to be lossless.
The transmission parameters of the compliant model are calculated according to the
two-source method based on time-domain simulations by means of the MOC in-house solver
FLOAT, as described by [
9]. Since only harmonic wave propagation is considered, it is possible to calculate the model’s acoustic transmission behaviour based on the transfer matrix method (TMM) in the frequency domain as well [
22]. The transfer matrix
for one element (el.) of constant area
A connects the sound pressure
and the sound flux
at the element’s inlet and outlet, and is defined as
As lossless wave propagation is considered, the wave number
k is calculated as a function of frequency
f and the effective speed of sound in the respective element
:
The specific acoustic impedance is also a function of
:
Multiplication of the elementary transfer matrices gives the whole model’s functional
:
Finally, a change in the acoustic variables from
and
to
and
is needed to obtain the transmission parameters in the form of the scattering matrix
. The necessary conversion rules can be found in [
23]. Note that the lengths for pipes (s) and (d) are set to a negligible value of
to consider the cross-section jumps between piping and pump ports within the TMM calculations.