Influence of Spanwise and Streamwise Film Hole Spacing on Adiabatic Film Effectiveness for Effusion-Cooled Gas Turbine Blades
Abstract
:1. Introduction
- Convective cooling—between the cooling fluid and porous wall;
- Film cooling—a layer of coolant air over the blade reduces the convective heat flux from the hot gas cross flow,
2. Materials and Methods
2.1. Research Object
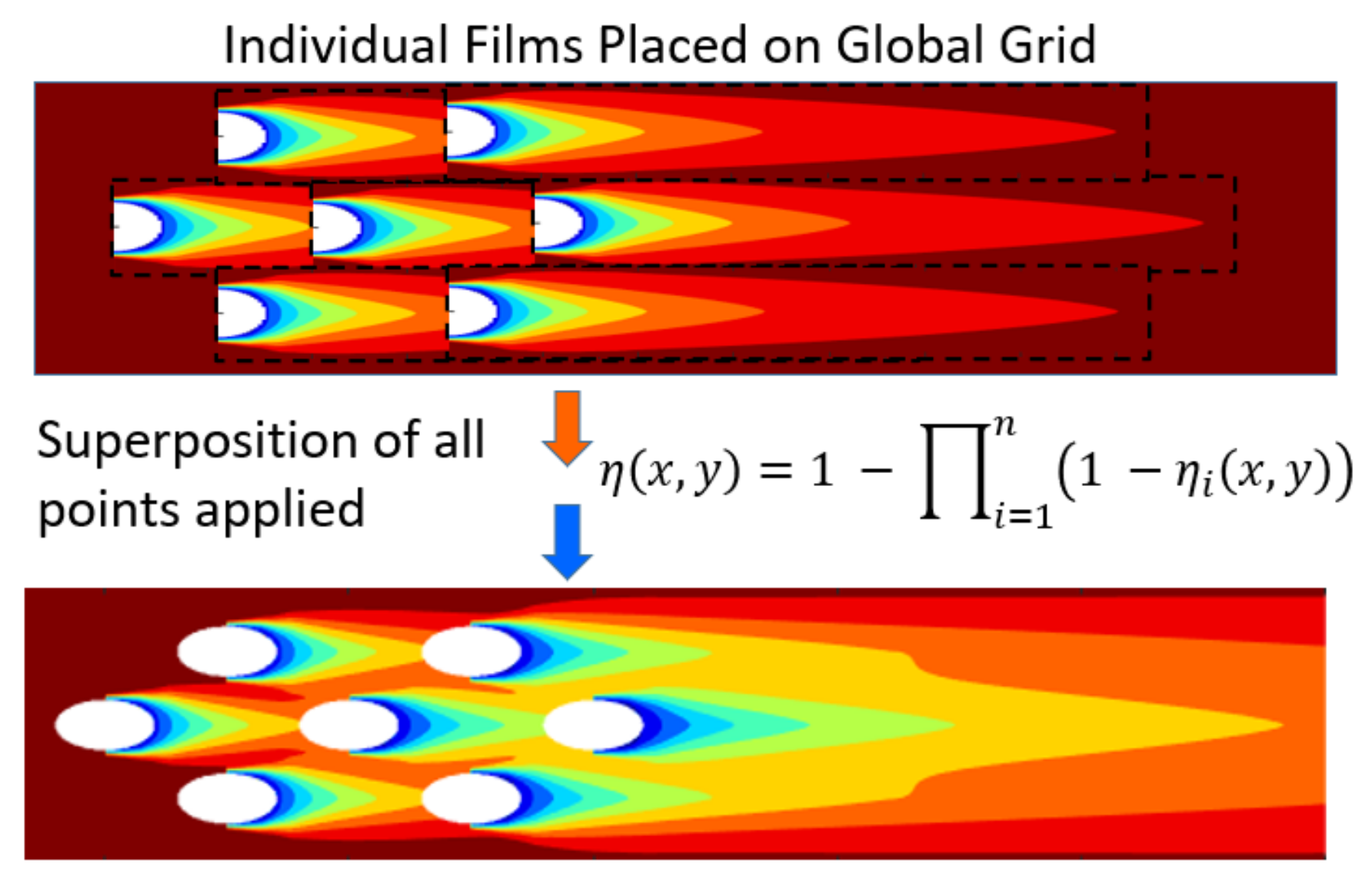
2.2. Numerical Method
2.3. Experimental Method
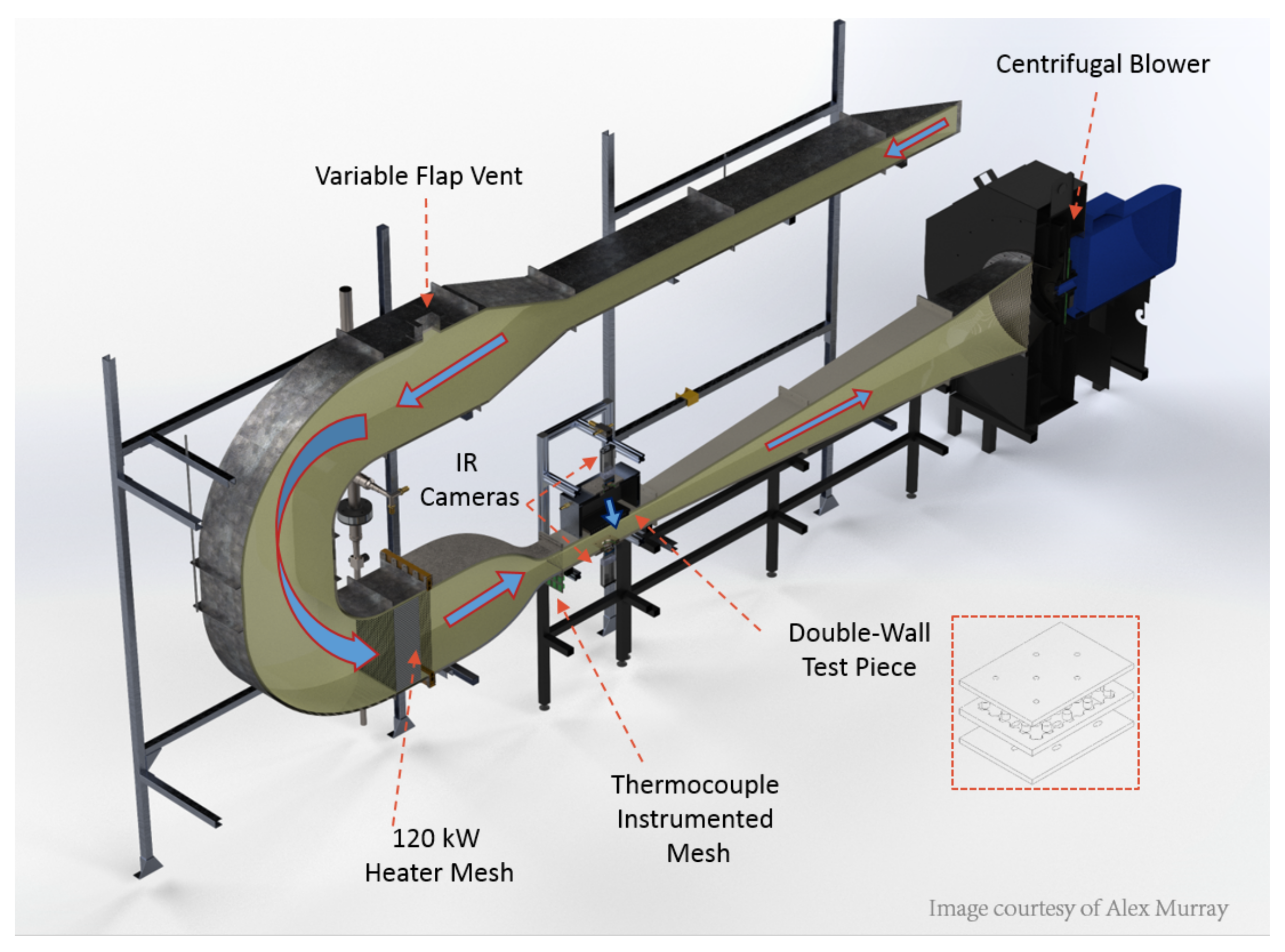
2.3.1. Experimental Facility
2.3.2. Infrared Methodology
3. Results and Discussion
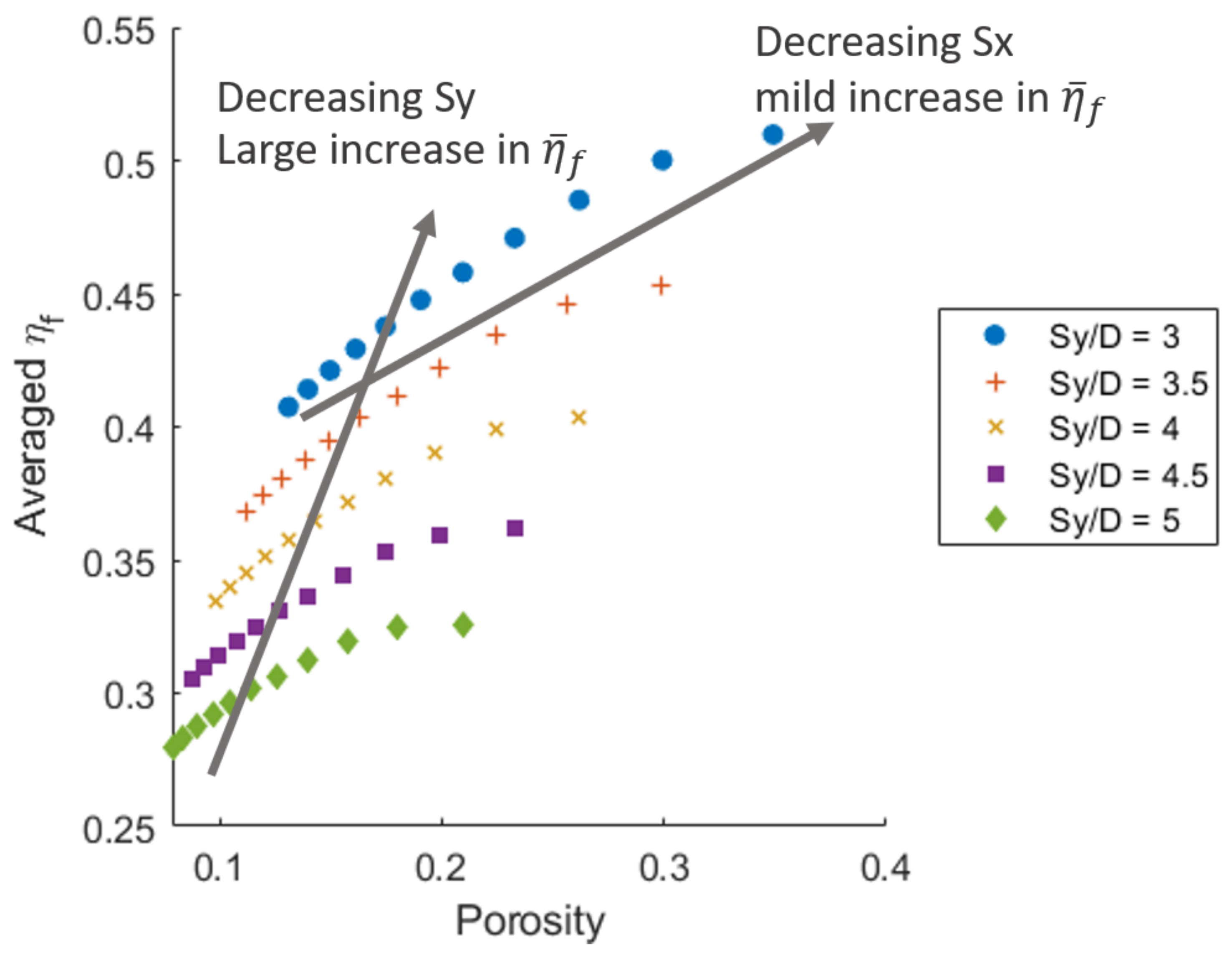
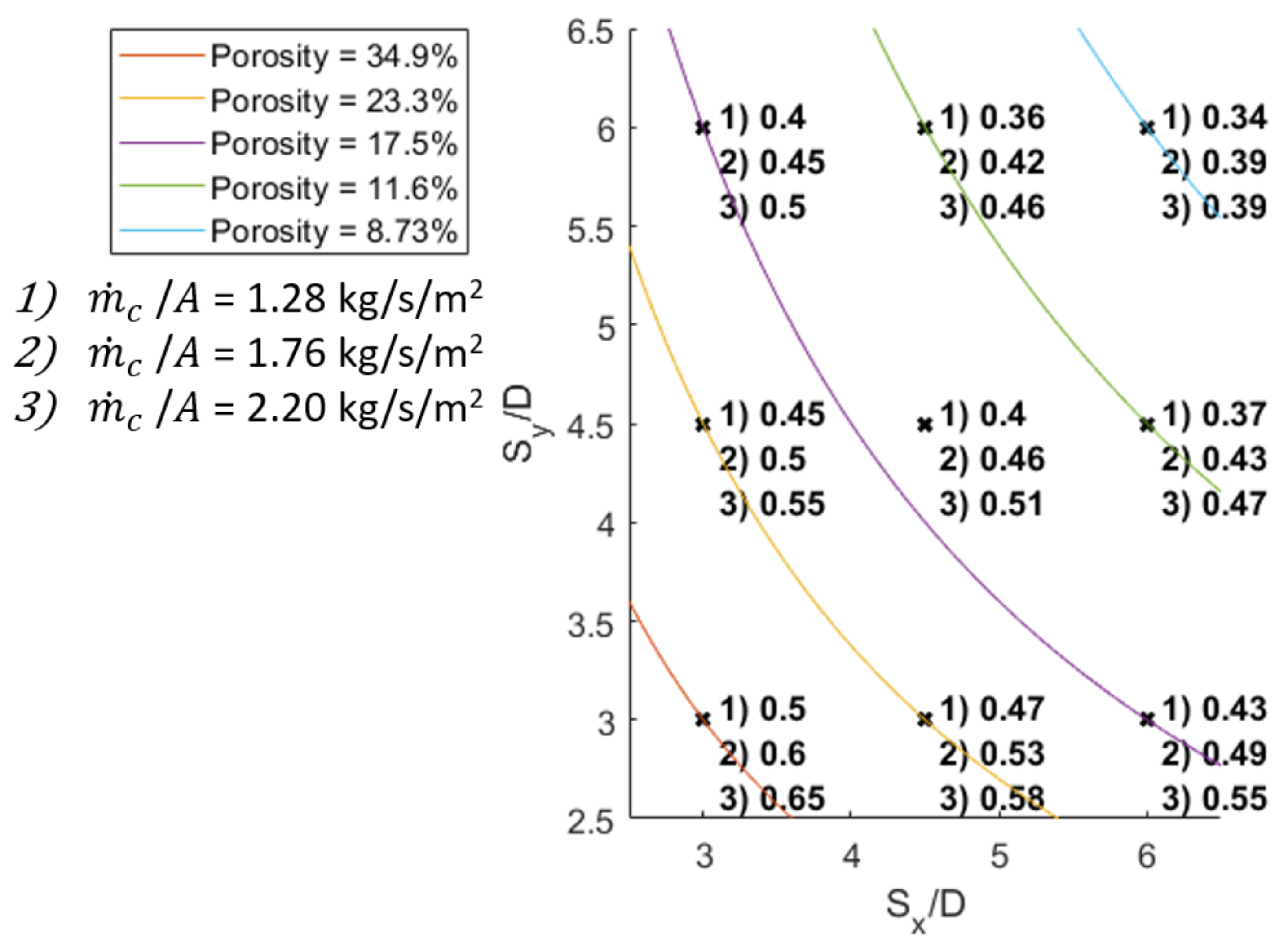
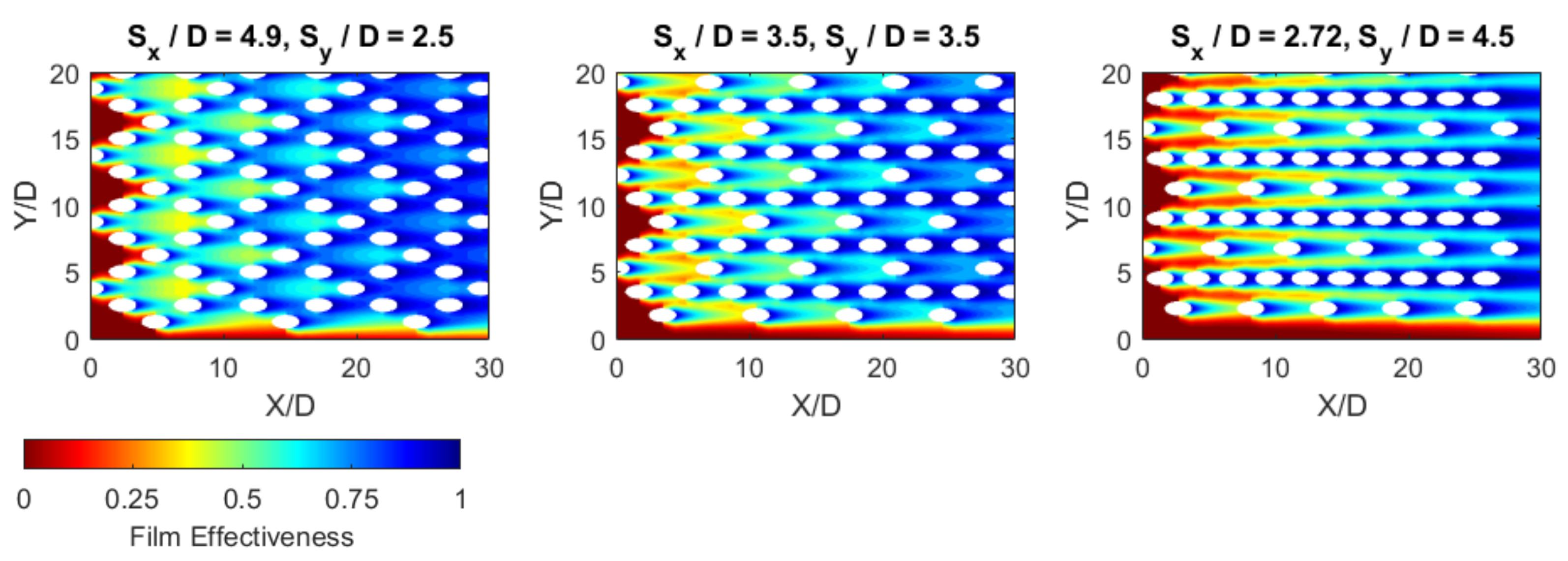
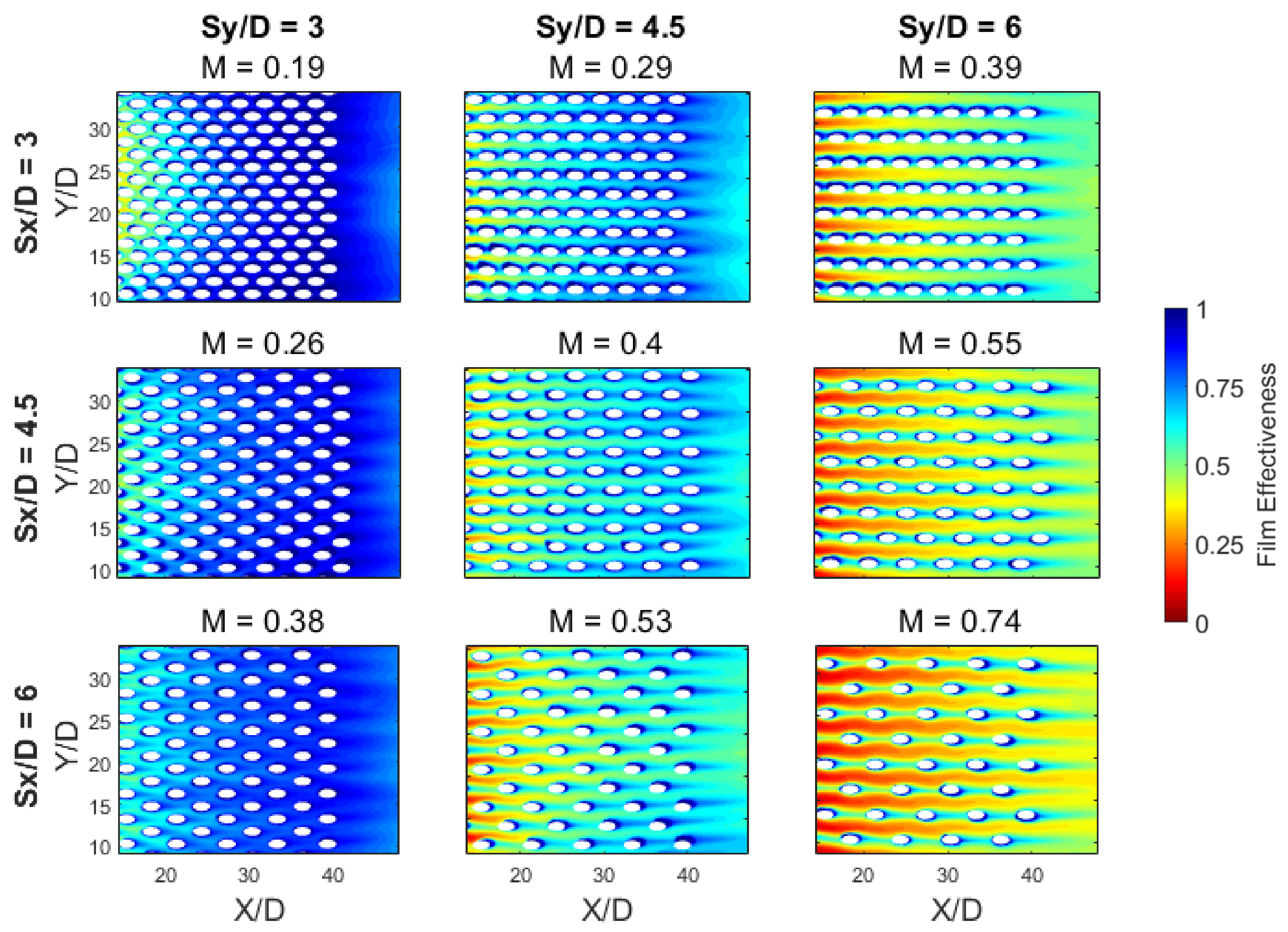
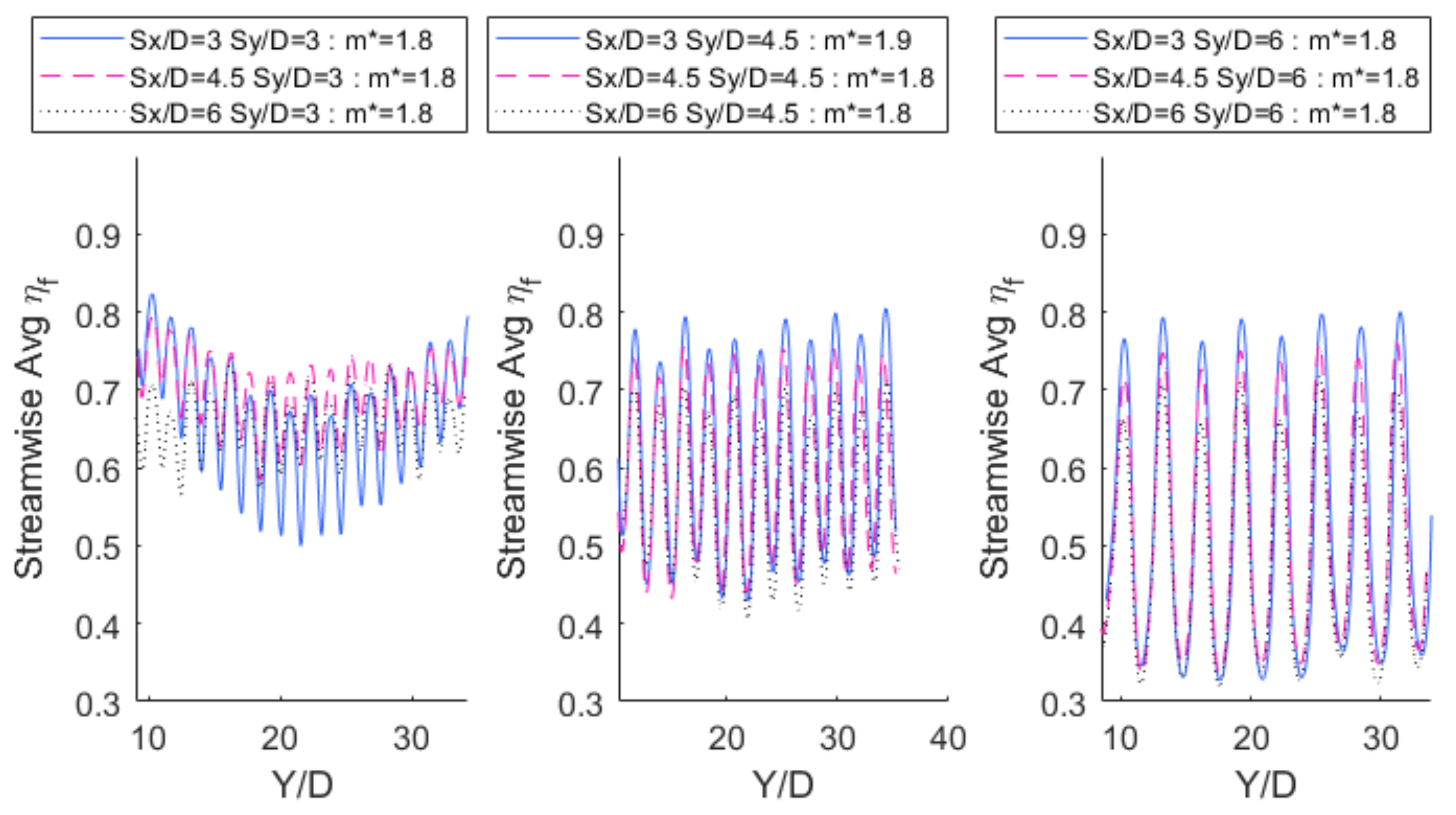
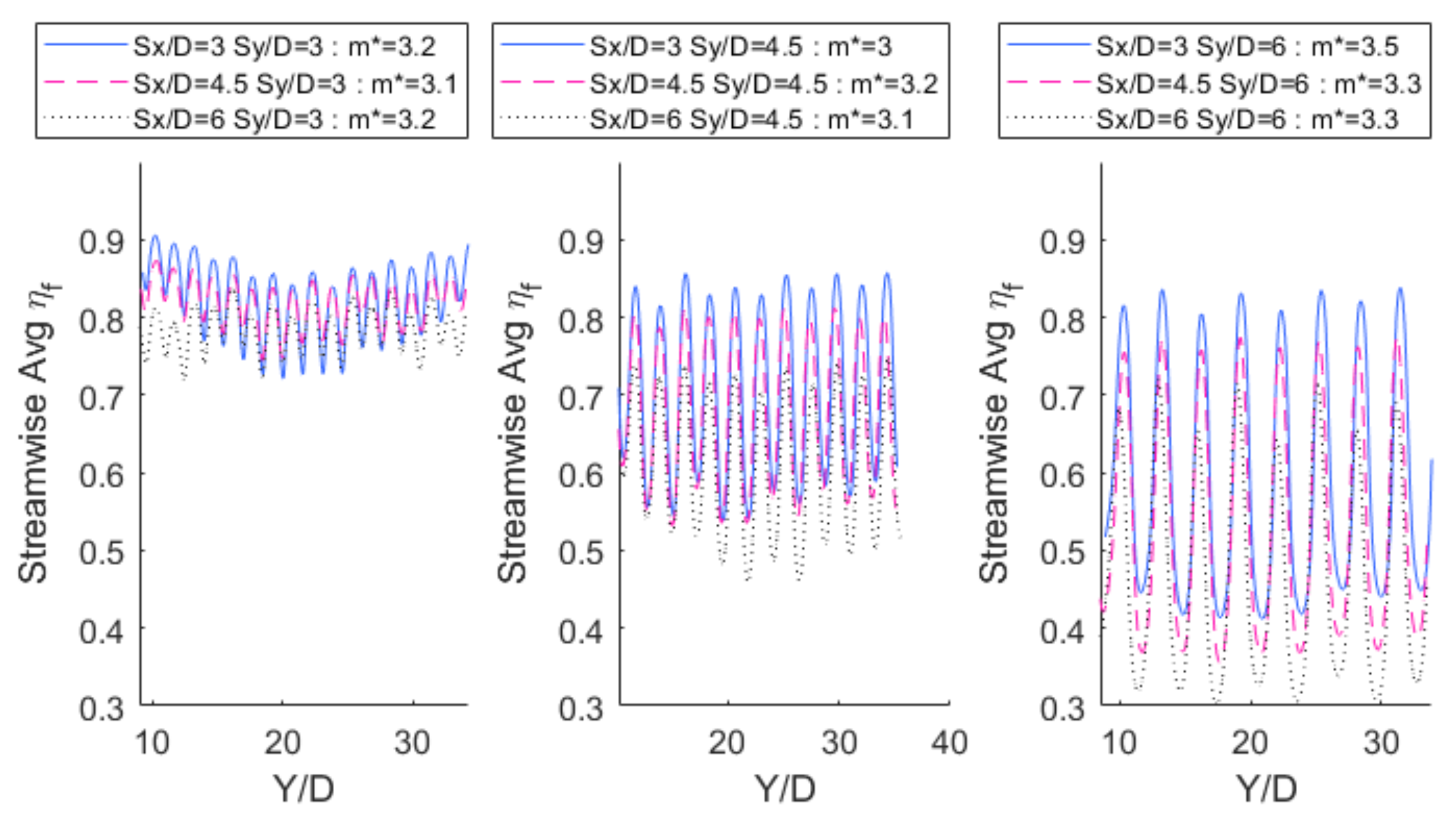
3.1. Numerical Results
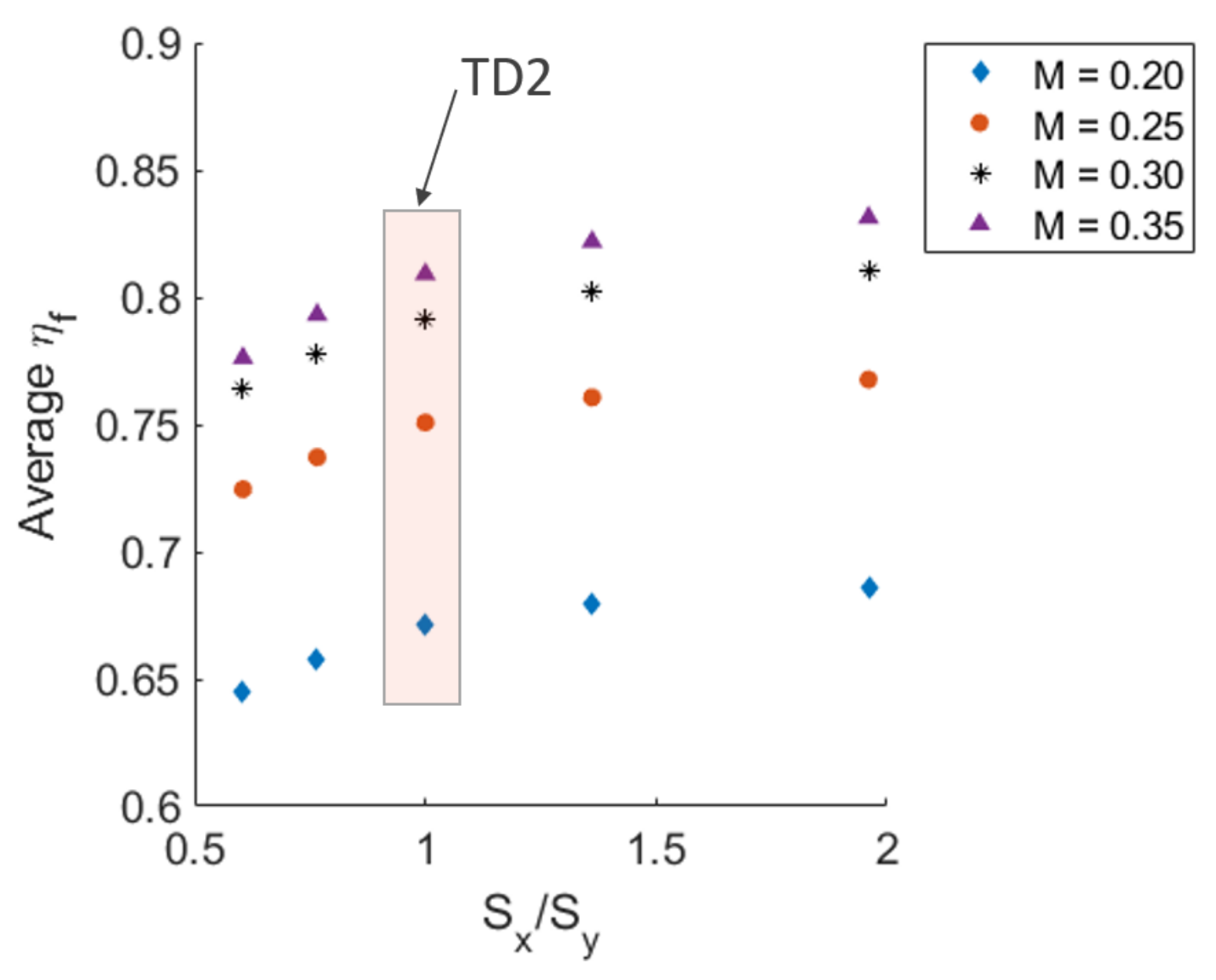
3.2. Td2 Results
3.3. Experimental Results
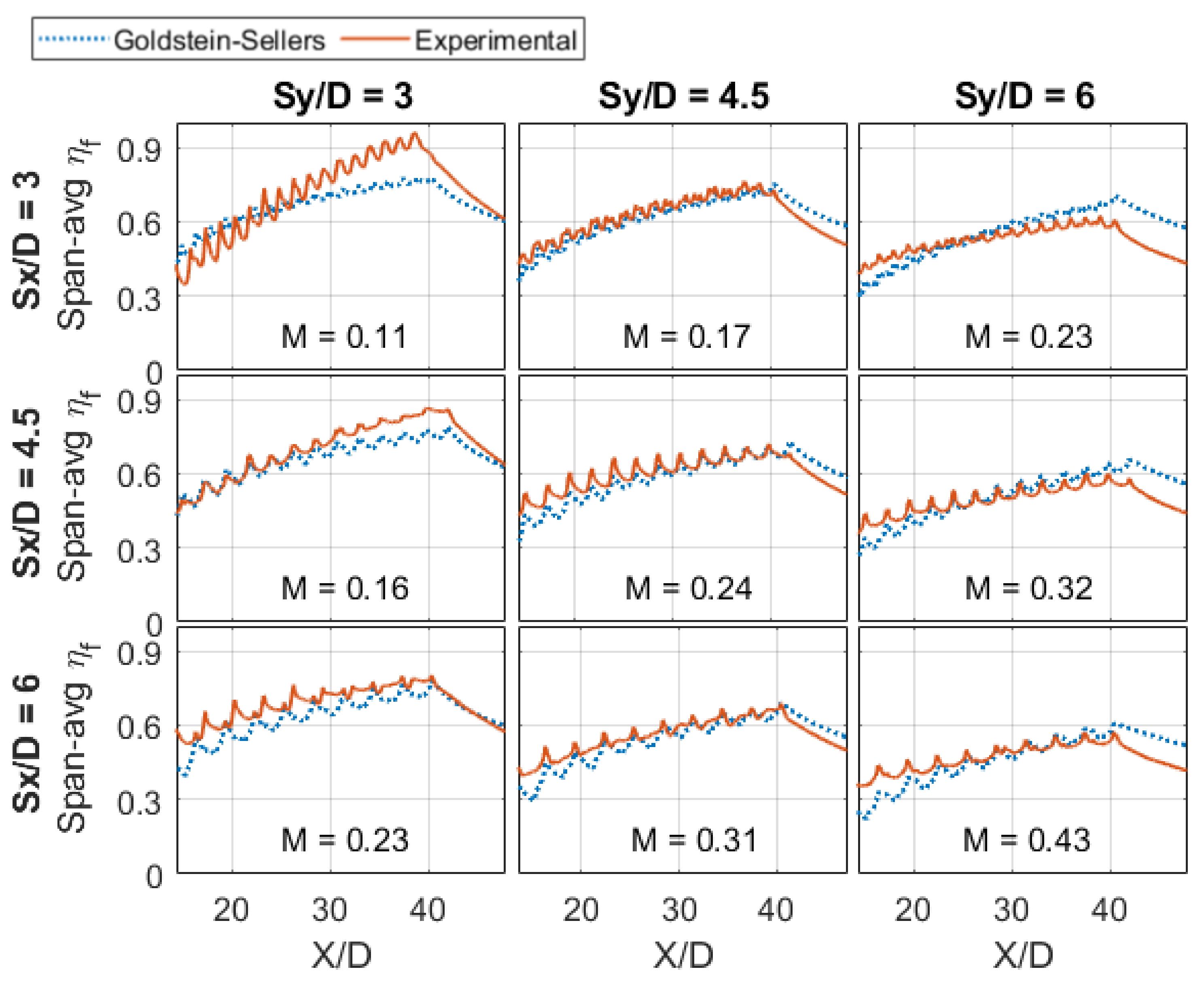
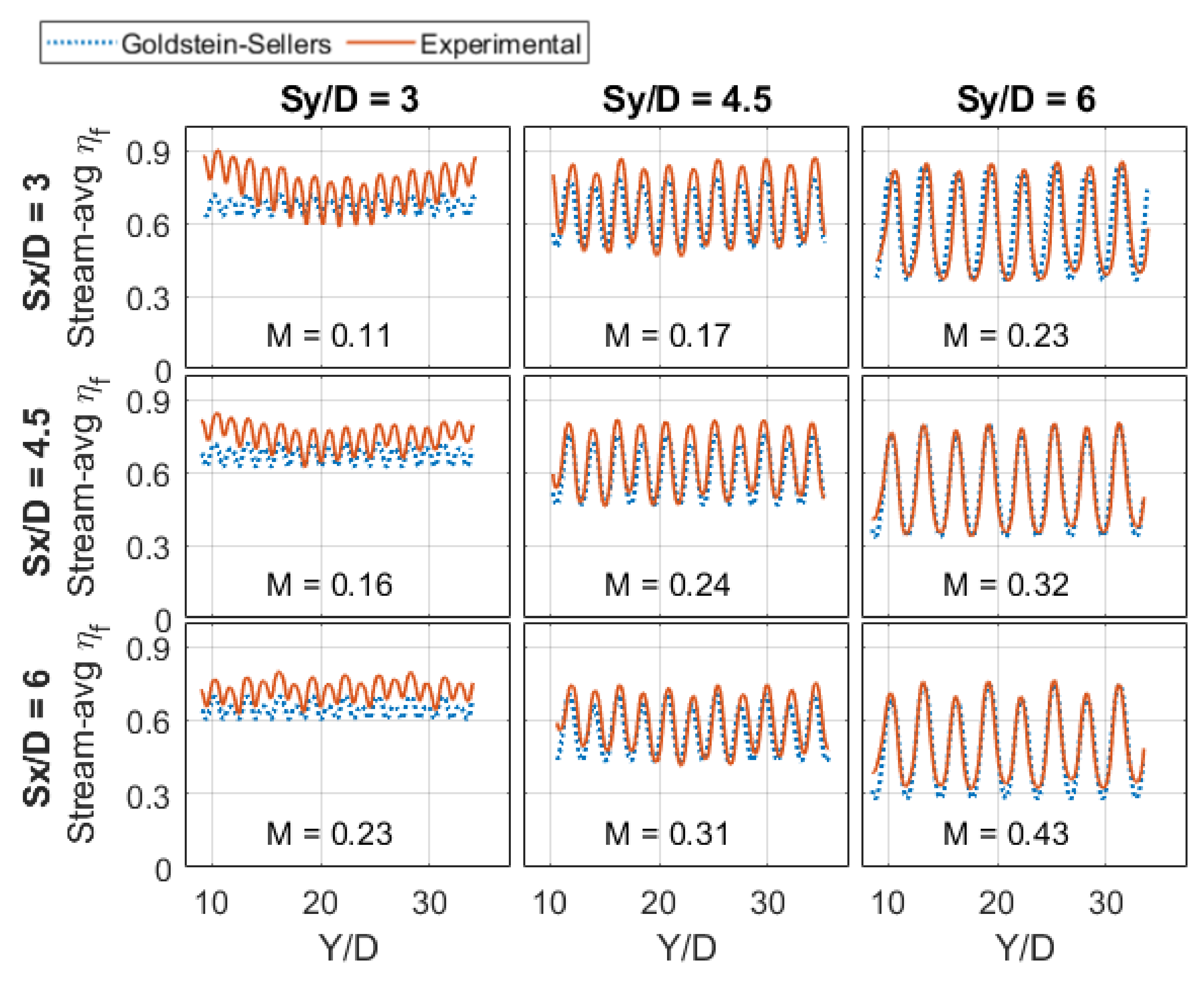
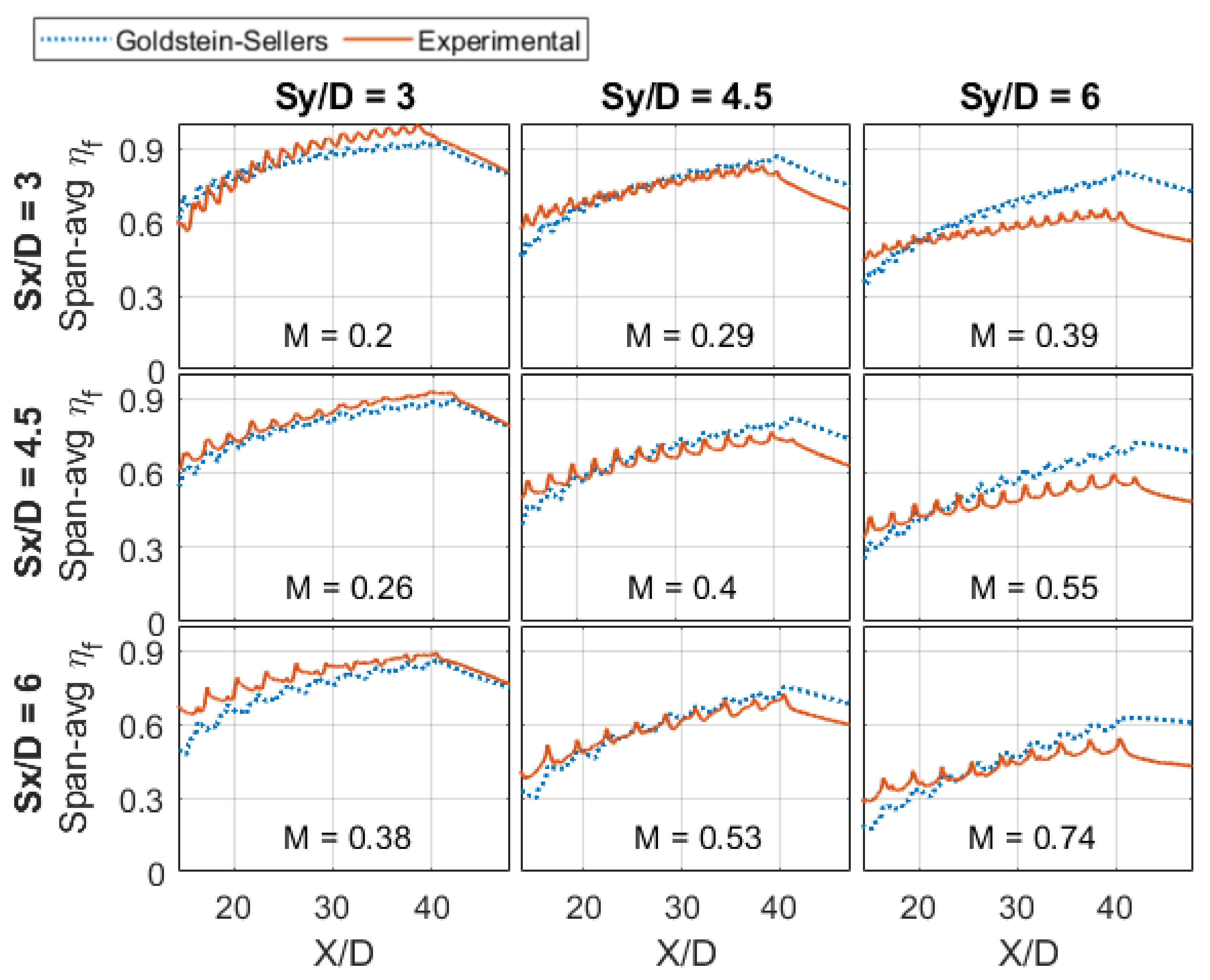
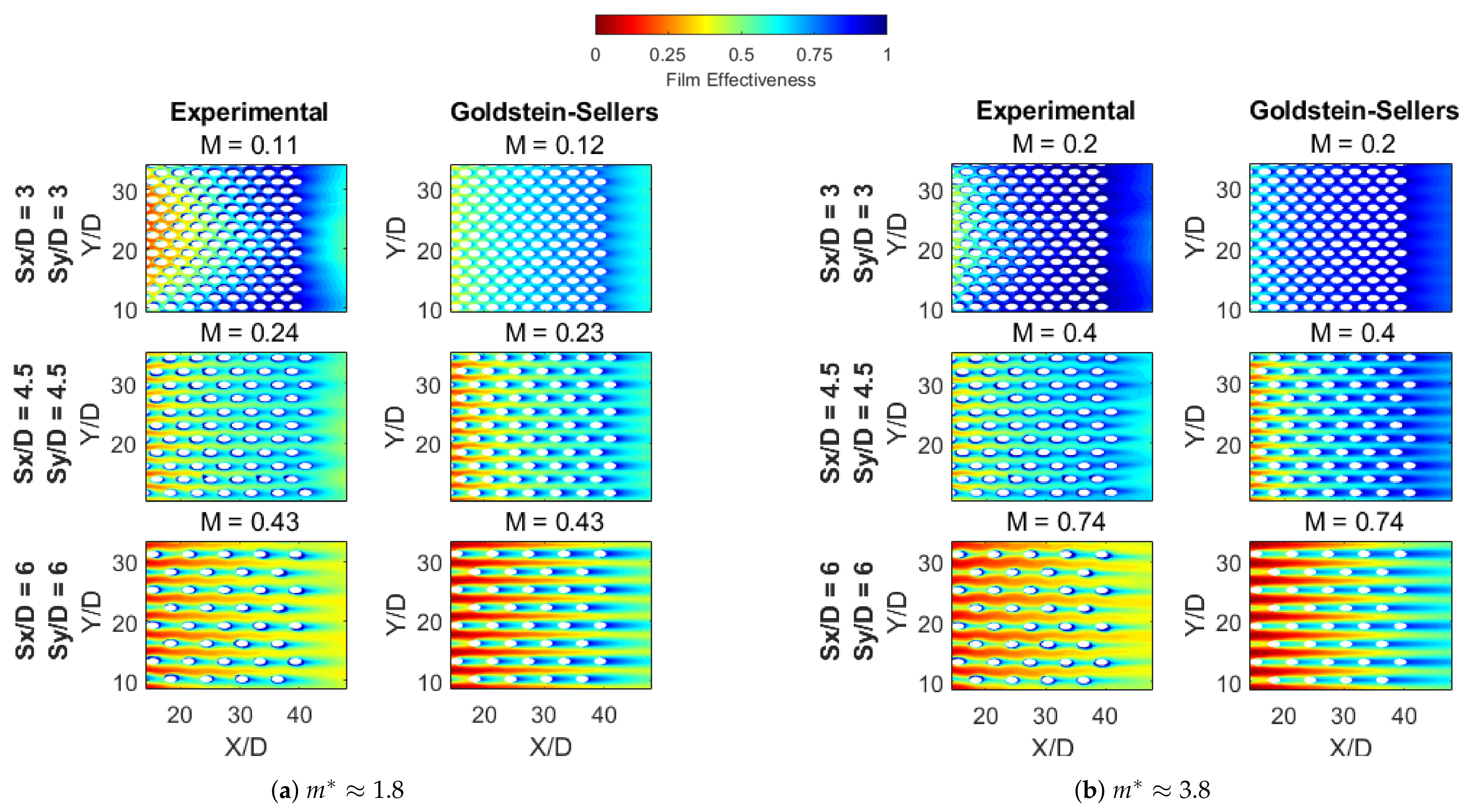
3.4. Numerical and Experimental Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Acronyms | ||
| IR | Infrared | |
| OTI | Oxford Thermofluids Institute | |
| Non-Dimensional Numbers | ||
| Film Effectiveness | ||
| Porosity | ||
| Spanwise distance constant | ||
| Spanwise shaping constant | ||
| M | Blowing ratio | |
| Non-dimensional mass flow | ||
| Streamwise distance film-decay | ||
| Properties | ||
| Turbulent thermal diffusivity | /s | |
| Mass flow rate | kg/s | |
| Hole inclination angle | deg | |
| Thermal conductivity | W/m·K | |
| Density | kg/ | |
| Hole surface area | ||
| Surface coverage of film holes | ||
| Specific heat capacity | J/kg·K | |
| D | Diameter | m |
| H | Plate thickness | m |
| h | Heat transfer coefficient | W/·K |
| k | Thermal conductivity | W/m·K |
| Streamwise spacing | m | |
| Spanwise Spacing | m | |
| T | Temperature | K |
| V | Velocity | m/s |
| Subscripts | ||
| ∞ | Free stream | |
| aw | Adiabtic wall | |
| c | coolant | |
| f | film | |
References
- Research Councils UK. Transpiration Cooling Systems for Jet Engine Turbines and Hypersonic Flight; Research Councils UK: Swindon, UK, 2018.
- Eckert, R.G.; Esgar, J.B. Survey of Advantages and Problems Associated with Transpiration Cooling and Film Cooling of Gas-Turbine Blades; NACA-RM-E50K15; National Advisory Committee for Aeronautics Research Memorandum: Washington, DC, USA, 1951.
- Polezhaev, J. Transpiration cooling for blades of high temperatures gas turbine. Energy Convers. Manag. 1997, 38, 1123–1133. [Google Scholar] [CrossRef]
- Krewinkel, R. A review of gas turbine effusion cooling studies. Int. J. Heat Mass Transf. 2013, 66, 706–722. [Google Scholar] [CrossRef]
- Battisti, L.; Fedrizzi, R.; Cerri, G. Novel Technology for Gas Turbine Blade Effusion Cooling. In Proceedings of the ASME Turbo Expo 2006: Power for Land, Sea, and Air, Barcelona, Spain, 8–11 May 2006; Volume 3, pp. 491–501. [Google Scholar]
- Rogers, N.; Ren, Z.; Buzzard, W.; Sweeney, B.; Tinker, N.; Ligrani, P.; Hollingsworth, K.; Liberatore, F.; Patel, R.; Ho, S.; et al. Effects of Double Wall Cooling Configuration and Conditions on Performance of Full-Coverage Effusion Cooling. J. Turbomach. 2017, 139, 051009. [Google Scholar] [CrossRef]
- Jiang, Y.; Murray, A.; Ireland, P.; Di Mare, L. Coolant Jets Interaction in Effusion Cooling System: Experimental and Numerical Study; American Society of Mechanical Engineers: New York, NY, USA, 2019. [Google Scholar]
- Ngetich, G.C.; Ireland, P.T.; Murray, A.V.; Romero, E. A 3D Conjugate Approach for Anaysing A Double-Walled Effusion-Cooled Turbine Blade. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Bernhard Gustafsson, K.M.; Gunnar Johansson, T. An experimental study of surface temperature distribution on effusion-cooled plates. J. Eng. Gas Turbines Power 2001, 123, 308–316. [Google Scholar] [CrossRef]
- Sellers, J.P. Gaseous Film Cooling with Multiple Injection Stations. AIAA J. 1963, 1, 2154–2156. [Google Scholar] [CrossRef]
- Muska, J.F.; Fish, R.W.; Suo, M. The Additive nature of film cooling from rows of holes. J. Eng. Gas Turbines Power 1976, 98, 457–463. [Google Scholar] [CrossRef]
- Murray, A.; Ireland, P.; Wong, T.; Tang, S.; Rawlinson, A. High Resolution Experimental and Computational Methods for Modelling Multiple Row Effusion Cooling Performance. Int. J. Turbomach. Propuls. Power 2018, 3, 4. [Google Scholar] [CrossRef] [Green Version]
- Goldstein, R.J. Film Cooling. Adv. Heat Transf. 1971, 7, 321–379. [Google Scholar] [CrossRef]
- Jiang, Y.; Capone, L.; Ireland, P.; Romero, E. A detailed study of the interaction between two rows of cooling holes. ASME J. Turbomach. 2018, 140, 041008. [Google Scholar] [CrossRef]
- Murray, A.V.; Ireland, P.T.; Rawlinson, A.J. An Integrated Conjugate Computational Approach for Evaluating the Aerothermal and Thermomechanical Performance of Double-Wall Effusion Cooled Systems. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar] [CrossRef]
- Murray, A.V.; Ireland, P.T.; Romero, E. Development of a steady-state experimental facility for the analysis of double-wall effusion cooling geometries. J. Turbomach. 2019, 141, 041008. [Google Scholar] [CrossRef]
- Baldauf, S.; Schulz, A.; Wittig, S. High resolution measurements of local effectiveness by discrete hole film cooling. In Proceedings of the ASME 1999 International Gas Turbine and Aeroengine Congress and Exhibition, Indianapolis, IN, USA, 7–10 June 1999. [Google Scholar] [CrossRef] [Green Version]
- Lutum, E.; Johnson, B.V. Influence of the Hole Length-to-Diameter Ratio on Film Cooling with Cylindrical Holes. J. Turbomach. 1999, 121, 209. [Google Scholar] [CrossRef] [Green Version]
- Murray, A.V.; Ireland, P.T.; Romero, E. Experimental and Computational Methods for the Evaluation of Double-Wall, Effusion Cooling Systems. J. Turbomach. 2020, 142, 111003. [Google Scholar] [CrossRef]
- Yang, L.; Min, Z.; Parbat, S.N.; Chyu, M.K. Effect of Pore Blockage on Transpiration Cooling with Additive Manufacturable Perforate Holes. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018; ASME: New York, NY, USA, 2018; p. V02DT47A004. [Google Scholar] [CrossRef]
- Elmukashfi, E.; Murray, A.V.; Ireland, P.T.; Cocks, A.C. Analysis of the thermomechanical stresses in double-wall effusion cooled systems. J. Turbomach. 2020, 142, 051002. [Google Scholar] [CrossRef] [Green Version]
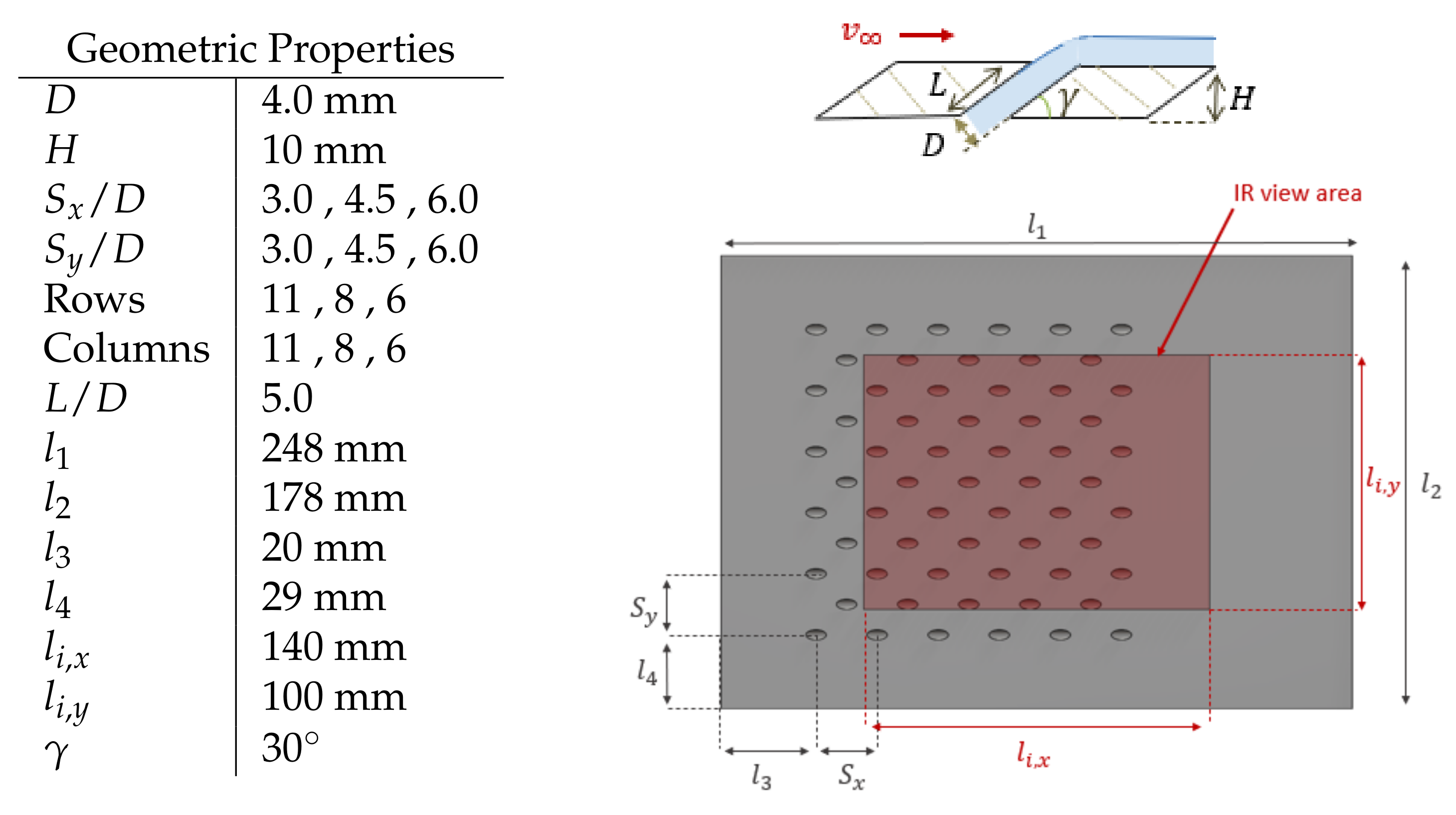





| TD2 Study Geometric Properties | |||||
|---|---|---|---|---|---|
| D | 2.0 mm | ||||
| 4.9 | 4.1 | 3.5 | 3.1 | 2.7 | |
| 2.5 | 3.0 | 3.5 | 4.0 | 4.5 | |
| 373 K | 0.8 | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Courtis, M.; Murray, A.; Coulton, B.; Ireland, P.; Mayo, I. Influence of Spanwise and Streamwise Film Hole Spacing on Adiabatic Film Effectiveness for Effusion-Cooled Gas Turbine Blades. Int. J. Turbomach. Propuls. Power 2021, 6, 37. https://doi.org/10.3390/ijtpp6030037
Courtis M, Murray A, Coulton B, Ireland P, Mayo I. Influence of Spanwise and Streamwise Film Hole Spacing on Adiabatic Film Effectiveness for Effusion-Cooled Gas Turbine Blades. International Journal of Turbomachinery, Propulsion and Power. 2021; 6(3):37. https://doi.org/10.3390/ijtpp6030037
Chicago/Turabian StyleCourtis, Matthew, Alexander Murray, Ben Coulton, Peter Ireland, and Ignacio Mayo. 2021. "Influence of Spanwise and Streamwise Film Hole Spacing on Adiabatic Film Effectiveness for Effusion-Cooled Gas Turbine Blades" International Journal of Turbomachinery, Propulsion and Power 6, no. 3: 37. https://doi.org/10.3390/ijtpp6030037
APA StyleCourtis, M., Murray, A., Coulton, B., Ireland, P., & Mayo, I. (2021). Influence of Spanwise and Streamwise Film Hole Spacing on Adiabatic Film Effectiveness for Effusion-Cooled Gas Turbine Blades. International Journal of Turbomachinery, Propulsion and Power, 6(3), 37. https://doi.org/10.3390/ijtpp6030037






