Experimental Study on Flow Behavior of Unshrouded Impeller Centrifugal Pumps under Inlet Air Entrainment Condition
Abstract
:1. Introduction
2. Experimental Set-Up
3. Experimental Uncertainties
4. Results and Discussion
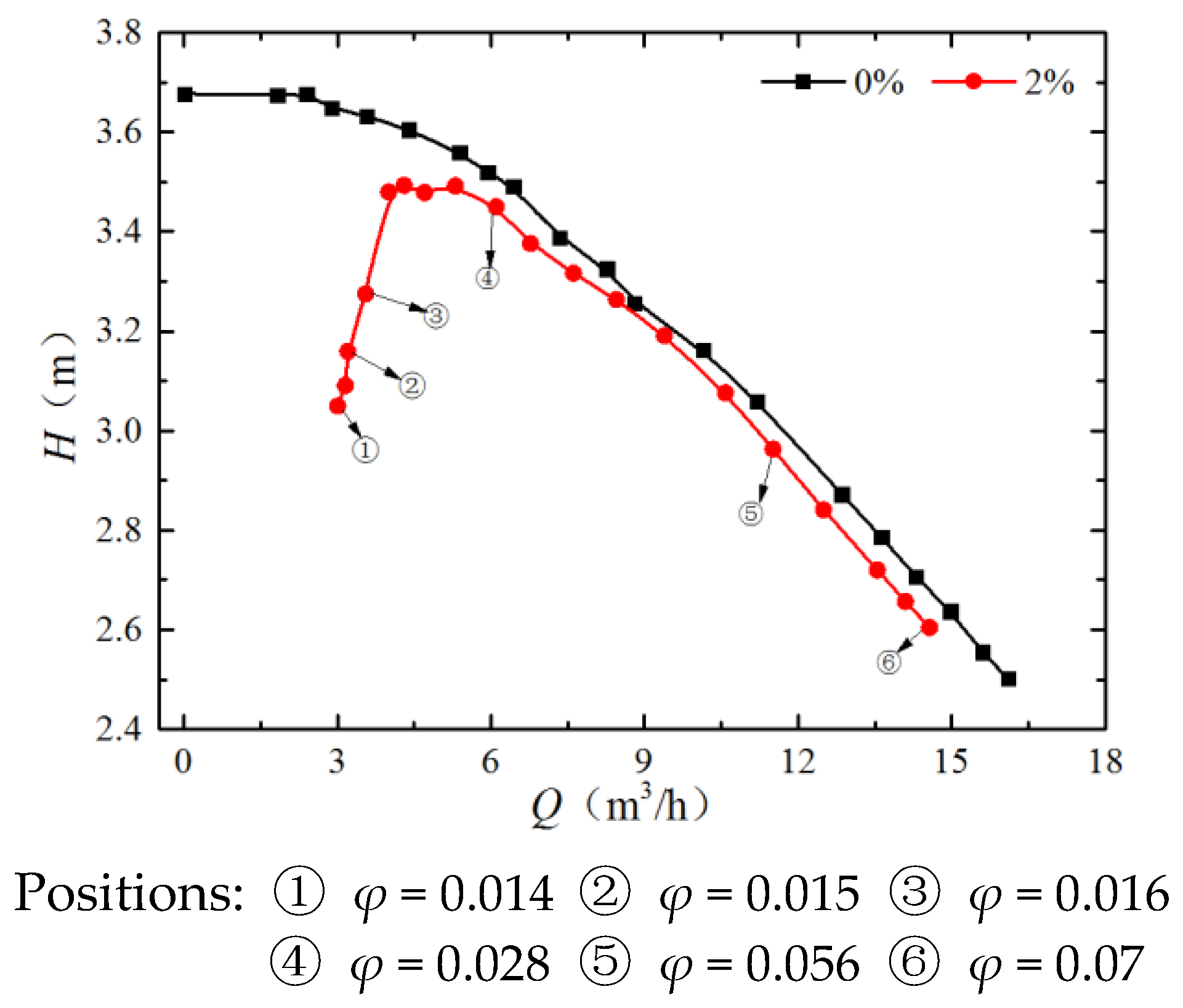
4.1. Pump Performance
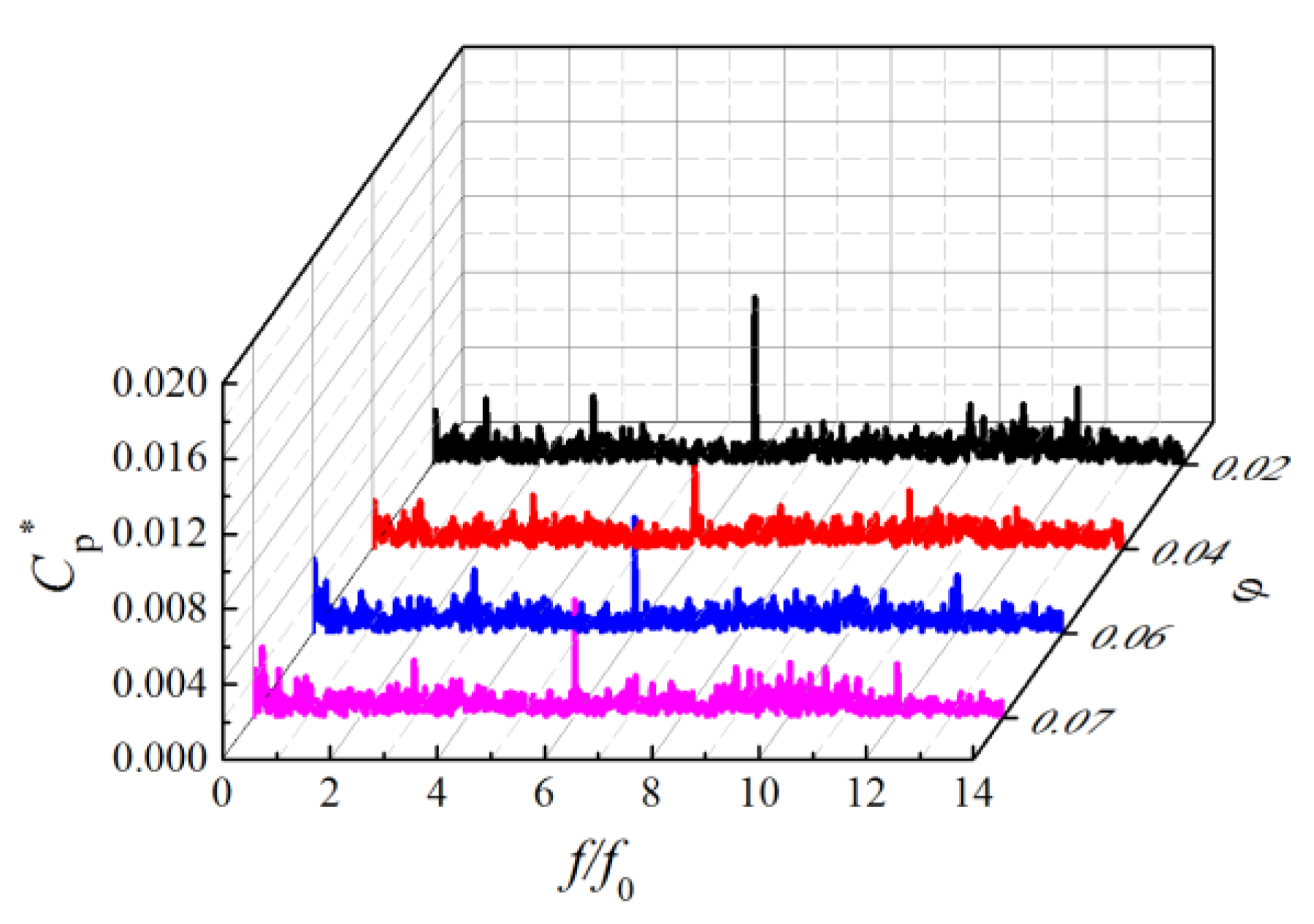
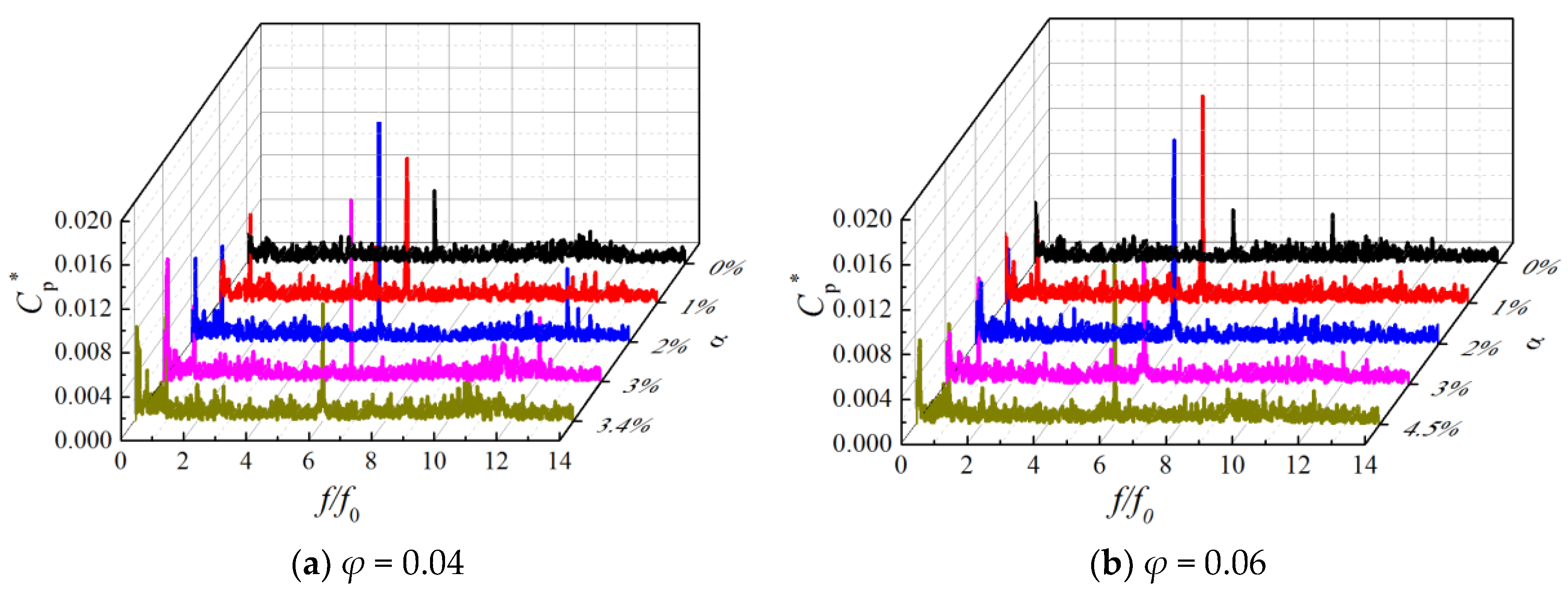
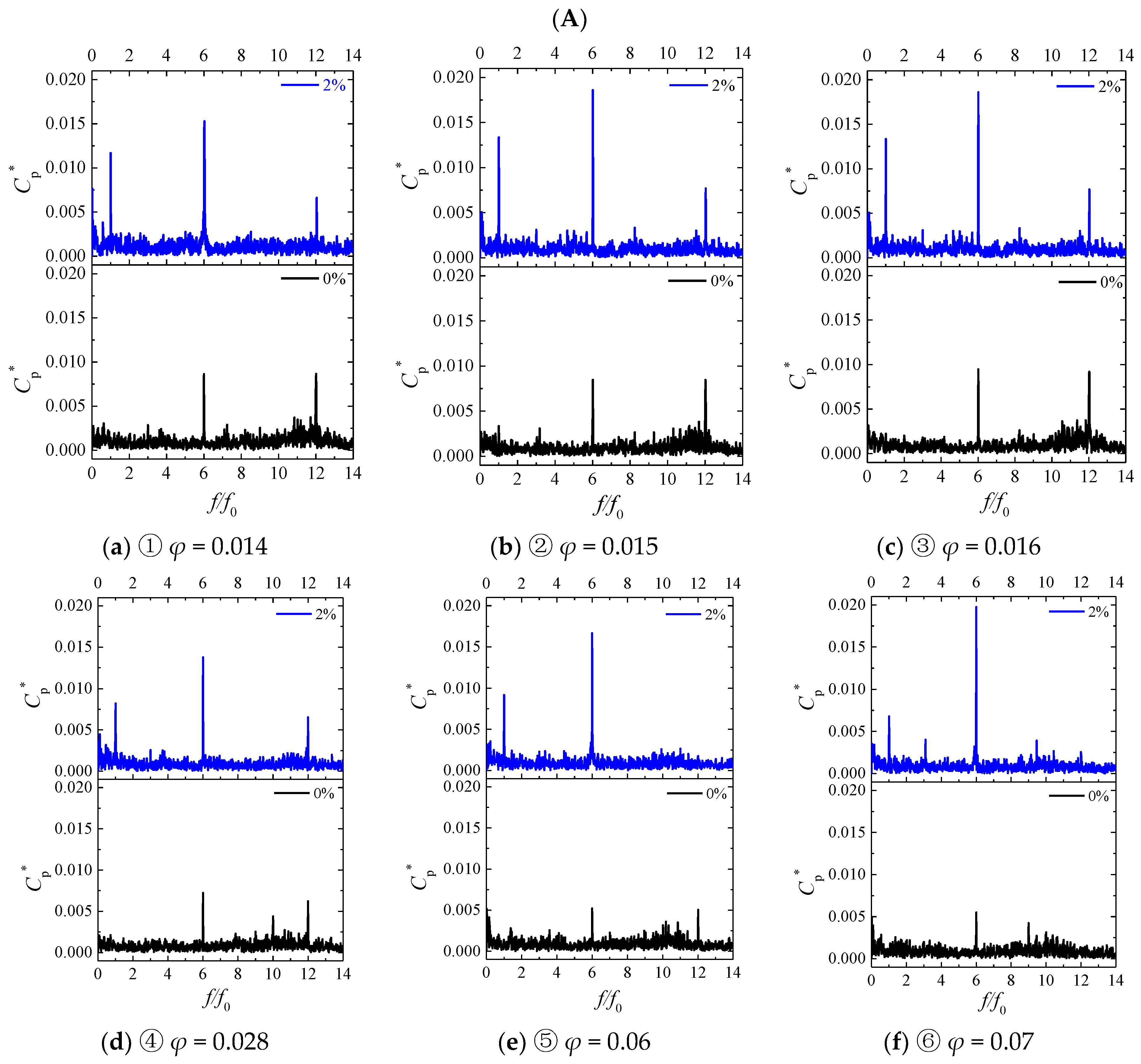
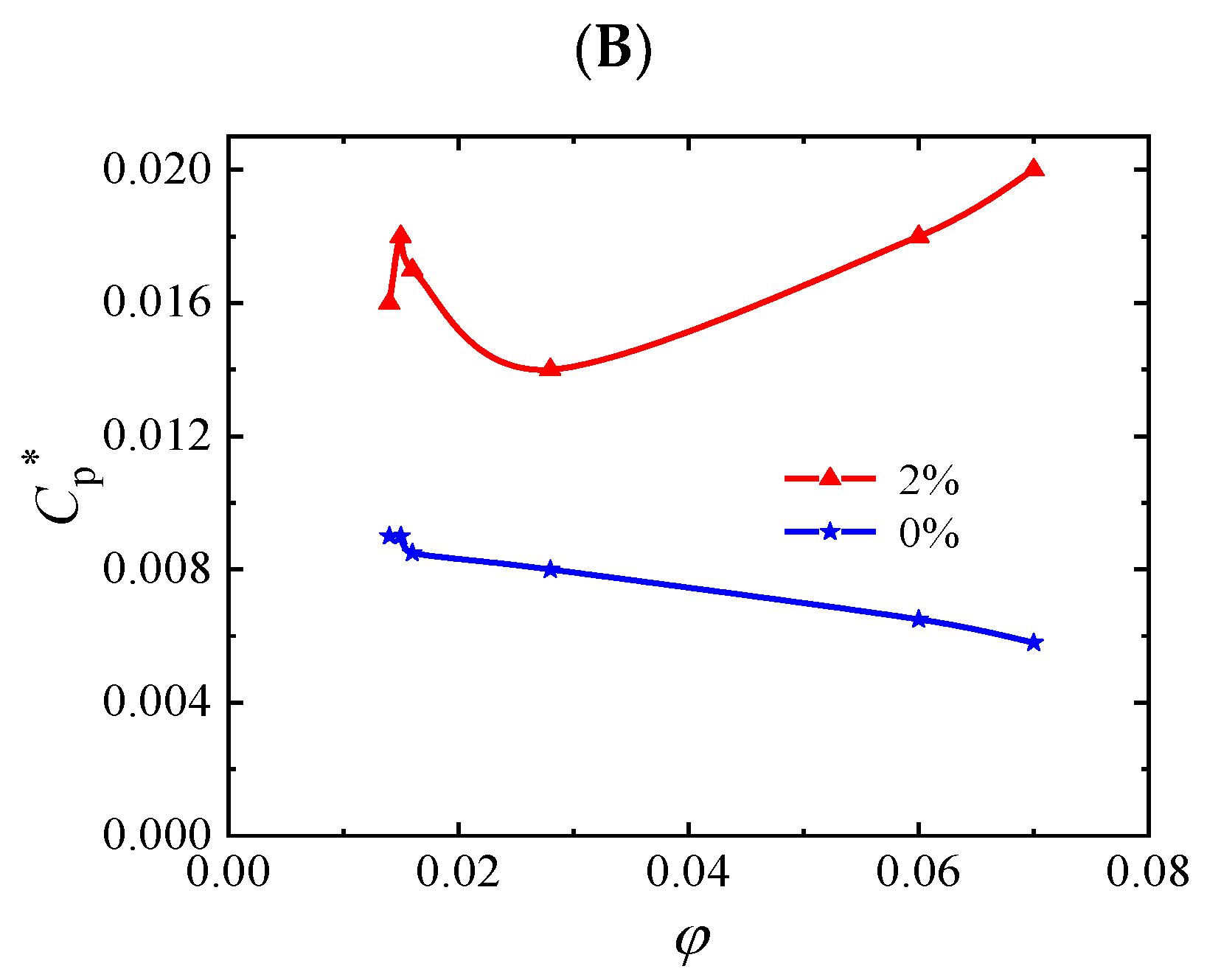
4.2. Pressure Fluctuation
4.3. Flow Visualization Inside the Impeller and Volute Channel
5. Conclusions
- (1)
- Two-phase flow pump performance degradations have been experimentally obtained for a given rotational speed of 1000 rpm and several inlet void fractions up to 4.6%.
- (2)
- For an inlet void fraction of 2%, the pump outlet pressure pulsation reaches its maximum value, which is found to be the first critical point for pump performance modification in relation with pressure pulsation amplitude evolutions.
- (3)
- Results from visualization have shown that local void fraction increases as the bubble sizes increase when decreasing flow rates. Air bubbles tend to agglomerate near the impeller suction side shroud at mid-chord and close to the pressure side close to the impeller outlet plane. The starting point of pump break down is related to a strong inward reverse flow occurring in a specific location near the shroud gap of the impeller and volute tongue region. However, it is still one question that if this phenomenon related to the low flow rate value only for pure water.
- (4)
- Additional visualization should however be performed in the whole pump area, including inlet tube flow patterns, close to the performance head curve slope modification just before pump break down starting point.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| A | Cross-sectional area |
| Cp | Pressure pulsation coefficient: |
| Cp* | Amplitude of Cp after Fast Fourier analysis |
| H | Pump head |
| P | Shaft power |
| p | Static pressure |
| Q | Volume flow rate |
| R | Radius |
| u | Impeller rotational speed: u = ω·R |
| Ω | Specific speed: Ω = ω·Q0.5/(g·H)0.75 |
| Λ | Specific radius: Λ = R·(g·H)0.25/Q0.5 |
| α | Inlet air void fraction: α = Qair/(Qair + Qwater) |
| β | Blade angle (from tangential direction) |
| ηg | Global efficiency: η =ρgQwaterH/P |
| ηint | Internal efficiency |
| φ | Flow coefficient: φ = Qwater/(2π·R2·b2·u2) |
| ψ | Head coefficient: ψ = gH/(u2)2 |
| ρ | Density of mixed fluid: ρ = ρwater × (1 − α) + ρair × α |
| ψt,int | Internal head coefficient: ψt = ψ/ηint |
| ω | Angular velocity |
| τ | Shaft power coefficient: τ = P/ρA2(u2)3 |
| 1 | Impeller inlet |
| 2 | Impeller outlet |
| t | Impeller inlet tip |
References
- Schäfer, T.; Neumann, M.; Bieberle, A.; Hampel, U. Uwe Hampel. Experimental investigations on a common centrifugal pump operating under gas entrainment conditions. Nucl. Eng. Des. 2017, 316, 1–8. [Google Scholar] [CrossRef]
- Li, X.; Jiang, Z.; Zhu, Z.; Si, Q.; Li, Y. Entropy generation analysis for the cavitating head-drop characteristic of a centrifugal pump. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018, 232, 4637–4646. [Google Scholar] [CrossRef]
- Minemura, K.; Murakami, M.; Katagiri, H. Characteristics of centrifugal pumps handling air-water mixtures and size of air bubbles in pump impellers. Bull. JSME 1985, 28, 2310–2318. [Google Scholar] [CrossRef]
- Clark, A.P. Numerical prediction of bubble flow in a centrifugal pump. Adv. Multiph. Flow 1995, 64, 175–181. [Google Scholar]
- Schäfer, T.; Bieberle, A.; Neumann, M.; Hampel, U. Application of gamma-ray computed tomography for the analysis of gas holdup distributions in centrifugal pumps. Flow Meas. Instrum. 2015, 46, 262–267. [Google Scholar] [CrossRef]
- Jiang, Q.; Heng, Y.; Liu, X.; Zhang, W.; Bois, G.; Si, Q. A review on design considerations of centrifugal pump capability for handling inlet gas-liquid two-phase flows. Energies 2019, 12, 1078. [Google Scholar] [CrossRef] [Green Version]
- Si, Q.; Cui, Q.; Zhang, K.; Yuan, J.; Bois, G. Investigation on centrifugal pump performance degradation under air-water inlet two-phase flow conditions. La Houille Blanche 2018, 3, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Müller, T. Numerical 3D RANS simulation of gas-liquid flow in a centrifugal pump with an euler-euler two-phase model and a dispersed phase distribution. In Proceedings of the 11th European Conference on Turbomachinery Fluid dynamics & Thermodynamics, ETC11, ETC2015-076, Madrid, Spain, 23–27 March 2015. [Google Scholar]
- Si, Q.R.; Bois, G.; Zhang, K.Y.; Yuan, J.P. Air-water two-phase flow experimental and numerical analysis in a centrifugal pump. In Proceedings of the 12th European Conference on Turbomachinery Fluid dynamics and Thermodynamics, ETC12, Paper ID: ETC2017-54, Stockholm, Sweden, 3–7 April 2017. [Google Scholar]
- Stel, H.; Ofuchi, E.; Sabino, R.; Ancajima, F.; Bertoldi, D.; Marcelino, N.; Morales, R. Investigation of the motion of bubbles in a centrifugal pump impeller. J. Fluids Eng. 2019, 141, 031203. [Google Scholar] [CrossRef]
- Si, Q.; Bois, G.; Liao, M.; Zhang, H.; Cui, Q.; Yuan, S. A comparative study on centrifugal pump designs and two-phase flow characteristic under inlet gas entrainment conditions. Energies 2020, 13, 65. [Google Scholar] [CrossRef] [Green Version]
- Si, Q.; Zhang, H.; Bois, G.; Zhang, J.; Cui, Q.; Yuan, S. Experimental investigations on the inner flow behavior of the centrifugal pumps under inlet air- water two-phase conditions. Energies 2019, 12, 4377. [Google Scholar] [CrossRef] [Green Version]
- ISO 9906: 2012. Rotodynamic Pumps-Hydraulic Performance Acceptance Tests—Grades 1, 2 and 3. Available online: https://max.book118.com/html/2017/0914/133901920.shtm (accessed on 31 May 2012).





| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rotating speed, n(rpm) | 1000 | Inlet diameter, D1/mm | 74 |
| Design Head, H/m | 4 | Outlet diameter, D2/mm | 174 |
| Design flow rate, Qd/m3 h−1 | 17.25 | Outlet tube diameter, DO/mm | 65 |
| Design flow coefficient | 0.1 | Impeller blade inlet angle, β1/° | 28 |
| number of blades, Z | 6 | Impeller blade outlet angle, β2/° | 30 |
| Specific speed, Ω | 0.484 | Outlet blade width, b2/mm | 12 |
| Specific radius | 3.141 | —— | —— |
| n/(rpm) | Q/Qd | α = 0% | α = 1% | α = 2% | α = 3% | α = 4% |
|---|---|---|---|---|---|---|
| 1000 | 0.3 | 3.16 | — | — | — | — |
| 0.48 | 3.35 | 3.82 | 3.42 | 3.65 | — | |
| 0.75 | 3.76 | 4.38 | 4.20 | 3.94 | 4.19 | |
| 0.87 | 3.87 | — | — | — | — |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Liao, M.; Si, Q.; Fan, M.; Wang, P.; Liu, Z.; Yuan, S.; Cui, Q.; Bois, G. Experimental Study on Flow Behavior of Unshrouded Impeller Centrifugal Pumps under Inlet Air Entrainment Condition. Int. J. Turbomach. Propuls. Power 2021, 6, 31. https://doi.org/10.3390/ijtpp6030031
Liao M, Si Q, Fan M, Wang P, Liu Z, Yuan S, Cui Q, Bois G. Experimental Study on Flow Behavior of Unshrouded Impeller Centrifugal Pumps under Inlet Air Entrainment Condition. International Journal of Turbomachinery, Propulsion and Power. 2021; 6(3):31. https://doi.org/10.3390/ijtpp6030031
Chicago/Turabian StyleLiao, Minquan, Qiaorui Si, Meng Fan, Peng Wang, Zhonghai Liu, Shouqi Yuan, Qianglei Cui, and Gérard Bois. 2021. "Experimental Study on Flow Behavior of Unshrouded Impeller Centrifugal Pumps under Inlet Air Entrainment Condition" International Journal of Turbomachinery, Propulsion and Power 6, no. 3: 31. https://doi.org/10.3390/ijtpp6030031
APA StyleLiao, M., Si, Q., Fan, M., Wang, P., Liu, Z., Yuan, S., Cui, Q., & Bois, G. (2021). Experimental Study on Flow Behavior of Unshrouded Impeller Centrifugal Pumps under Inlet Air Entrainment Condition. International Journal of Turbomachinery, Propulsion and Power, 6(3), 31. https://doi.org/10.3390/ijtpp6030031







