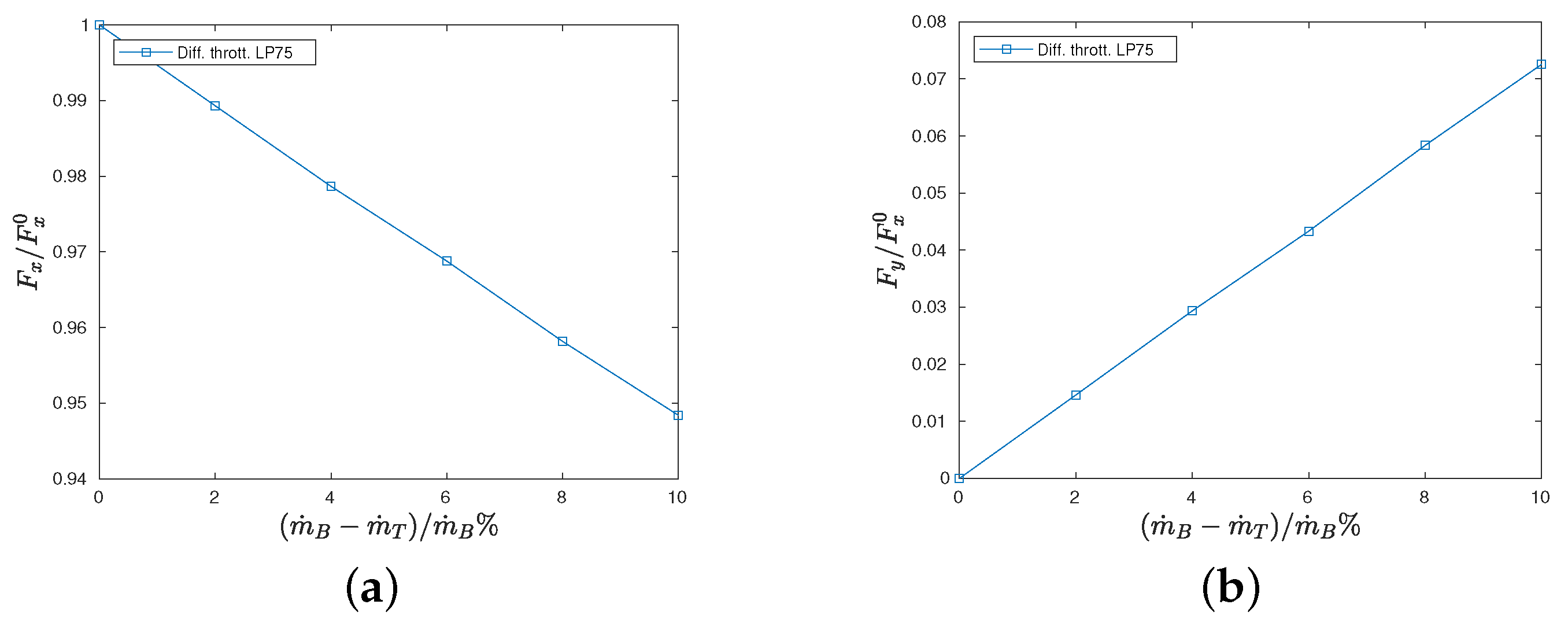Differential Throttling and Fluidic Thrust Vectoring in a Linear Aerospike

Abstract

Aerospike nozzles represent an interesting solution for Single-Stage-To-Orbit or clustered launchers owing to their self-adapting capability, which can lead to better performance compared to classical nozzles. Furthermore, they can provide thrust vectoring in several ways. A simple solution consists of applying differential throttling when multiple combustion chambers are used. An alternative solution is represented by fluidic thrust vectoring, which requires the injection of a secondary flow from a slot. In this work, the flow field in a linear aerospike nozzle was investigated numerically and both differential throttling and fluidic thrust vectoring were studied. The flow field was predicted by solving the Reynolds-averaged Navier–Stokes equations. The thrust vectoring performance was evaluated in terms of side force generation and axial force reduction. The effectiveness of fluidic thrust vectoring was investigated by changing the mass flow rate of secondary flow and injection location. The results show that the response of the system can be non-monotone with respect to the mass flow rate of the secondary injection. In contrast, differential throttling provides a linear behaviour but it can only be applied to configurations with multiple combustion chambers. Finally, the effects of different plug truncation levels are discussed.

1. Introduction

Rocket engines that are used in space launchers are usually equipped with a conventional fixed geometry bell-shaped nozzle which provide good performance and are quite reliable. In serially staged launchers, the area expansion ratio of the nozzles used in the different stages increases significantly from the first stage to the last stage: this allows operation with nearly optimum expansion ratios in the different phases of the mission. However, there are clustered launchers in which there is a core engine which works from sea-level to almost vacuum conditions, such as the Vulcain 2 engine in the Ariane 5 launcher or the Main Engine in the Space Shuttle launching system. Furthermore, Single-Stage-to-Orbit (SSTO) configurations have been also proposed. In all these configurations, a significant performance gain could be obtained by reducing the non-adaptation losses: several advanced nozzle concepts have been investigated for this purpose [1].

The aerospike nozzle represents an effective self-adapting nozzle which allows the nozzle exit pressure to be adapted according to the environment pressure without the use of any moving component. Several configurations of aerospike engines have been proposed and investigated, with both circular and linear designs [2,3,4,5,6,7]. In the 1960s, Rocketdyne developed the J-2T-200K and J-2T-250K annular engines which were based on a toroidal combustion chamber and a truncated plug [8]. These engines, which were derived from the J-2 engine used in the Saturn-family launchers, were evaluated with both cold and hot tests.

The linear aerospike engine XRS-2200 was selected as a candidate propulsion system for the Venture Star/X33 SSTO spaceplane in the 1990s [9]. The engine was based on a cluster of 20 independent combustion chambers and was successfully tested on the ground.

After these pioneering contributions, the research effort on aerospikes slowed because of the cancellation of several programs. More recently, research in the field has been led by universities and private companies. An example is the California Launch Vehicle Education Initiative (CALVEIN) as a collaboration between the California State University and Garvey Spacecraft Corporation. In the framework of the CALVEIN project, several tests on a truncated plug nozzle were performed [10].

Other attempts were performed by private companies which proposed aerospikes for the propulsion of both SSTO and Two-Stage-Two-Orbit (TSTO) configurations: Firefly Aerospace and RocketStar Space proposed a TSTO vehicle, while ARCA Space Corporation proposed a SSTO design [11]. Furthermore, the use of linear aerospike nozzles has also been investigated for high-speed aircrafts [12].

The development of aerospike engines is characterised by the need to solve several challenging aspects, from cooling issues to structural problems [1]. Furthermore, the use of an aerospike nozzle limits the possibility to perform thrust vectoring by introducing a gimballed joint, as it is done in conventional bell nozzles. This is due to the large diameter/extension of the aerospike nozzle which prevents the possibility of moving the entire nozzle. However, thrust vectoring is a key requirement for the use of aerospike nozzle in space launchers. For these reasons, several alternative thrust vectoring strategies have been investigated [11].

Among them, some possible strategies are represented by movable plugs, flaps on the plug, differential throttling and fluidic thrust vectoring [13,14,15,16,17,18,19,20,21,22]. Differential throttling is a simple control strategy which can be applied in the presence of clustered aerospike engines with multiple independent combustion chambers. Since the mass flow rate and the pressure can be controlled independently in each chamber, it is possible to generate a lateral thrust component which can be used for manoeuvring.

However, there are both annular and linear aerospike configurations in which a common combustion chamber is considered. This is particularly true for small-scale engines in which the use of multiple chambers is not convenient [16]. In this case, differential throttling is no longer an option. A possible solution is represented by fluidic thrust vectoring, which consists in injecting a secondary flow from the plug wall in order to create an obstacle for the primary flow coming from the throat. This generates a shock followed by a separation downstream to the injection point. As a consequence, an asymmetric pressure distribution is obtained on the plug wall and this generates the required lateral thrust component.

The effectiveness of the fluidic thrust vectoring is influenced by several parameters: injection location, injection mass flow rate, and nozzle pressure ratio. These effects have been widely investigated experimentally [15,23,24] and numerically [15,16,17,23,25,26,27,28,29]. Furthermore, fluidic thrust vectoring allows to avoid or reduce the size of aerodynamic control surfaces for vehicles moving in the atmosphere [30,31,32]: this possibility has been investigated for the development of low observable aircrafts [33]. Finally, fluidic thrust vectoring has been investigated for the development of high-performance Unmanned Aerial Vehicles [34,35].

In the present work, differential throttling and fluidic thrust vectoring are discussed and compared as possible strategies for thrust control in a linear aerospike. The goal of the present work is to provide a cost–benefit analysis: the performance of the different strategies is evaluated in terms of lateral and axial force components while the requirements are estimated in terms of mass flow rate unbalance or secondary mass flow rate. The results were obtained by means of numerical simulations based on the Reynolds-averaged Navier–Stokes (RANS) equations. The paper is organised as follows. In Section 2, the equations used to evaluate the thrust components in an aerospike engine are provided. In Section 3, the physical model and the numerical schemes adopted for the simulations are described. In Section 4, the numerical results are reported for two different geometries. Finally, in Section , conclusions and future perspectives are discussed.

2. Thrust Evaluation in Aerospikes

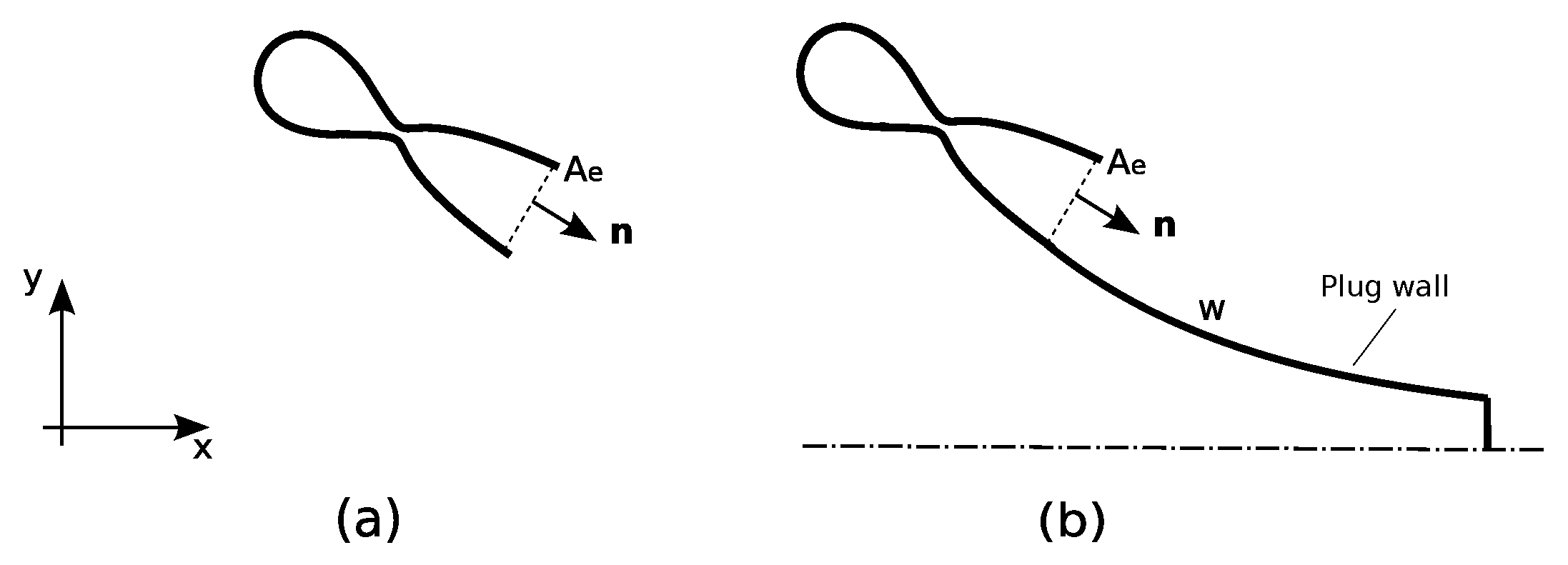
Consider the generic rocket nozzle represented in Figure 1a. The area of the exit section of the nozzle is $A_e$. The thrust $\mathit{F}$ generated by the rocket can be computed as follows:

$$\mathit{F}={({\mathit{F}}_x,{\mathit{F}}_y)}^T={\int }_{A_e}(\rho (\mathit{u}·\mathit{n})\mathit{u}+(p-p_0)\mathit{n})dA$$

(1)

where $\rho$, $\mathit{u}$, p, $p_0$ and $\mathit{n}$ represent density, velocity vector, pressure, ambient pressure and normal unit vector, respectively. According to the scheme in Figure 1a, the axis of the nozzle is assumed to be inclined with respect to the global reference system $(x,y)$.

Consider now a linear aerospike nozzle as represented in Figure 1b: the scheme shows only the upper half because of symmetry considerations. The previous expression can be updated in order to compute the force in the new configuration:

$$\mathit{F}={\int }_{A_e}(\rho (\mathit{u}·\mathit{n})\mathit{u}+(p-p_0)\mathit{n})dA+{\int }_w((p-p_0)\mathbb{I}+\mathit{\tau })·\mathit{n}dA$$

(2)

where $\mathbb{I}$ represents the identity matrix and $\mathit{\tau }$ is the viscous stress tensor at wall. The first integral in Equation (2) represents the thrust of a rocket with a nozzle truncated at section $A_e$. This term is augmented by the force that the fluid applies to the plug which contains both pressure and viscous contributions: the second integral quantifies this contribution. The integrals which appear in Equation (2) must be extended to both the nozzle exits and to the full plug surface.

The terms in Equation (2) put in evidence the different mechanisms which can be exploited in an aerospike engine to produce a lateral thrust component ${\mathit{F}}_y$. When shock vectoring is applied a fluid is injected from a slot located on one side of the plug. The injected fluid represents an obstacle for the primary supersonic flows: this generates a shock wave which alters the pressure distribution. As a result, an asymmetric pressure distribution on the two sides of the plug is obtained and the second integral in Equation (2) leads to a net lateral force component. However, the first integral in Equation (2) does contribute to this thrust vectoring strategy because the perturbations induced by the injected fluid influence only the plug region and do not affect the flow field upstream to the section $A_e$.

An alternative strategy is exploited when differential throttling is applied. In this case, a different total pressure is imposed in the combustion chambers which feed the two sides of the plug. As a consequence, both the integrals which appear in Equation (2) contribute to the generation of the lateral thrust component: the first integral takes into account the force contributions generated by the region upstream to the section $A_e$ while the second integral quantifies the pressure imbalance on the two sides of the plug. In the following, the mass flow rate provided by the top and bottom chambers will be referred to as ${\dot{m}}_T$ and ${\dot{m}}_B$, respectively. When fluidic thrust vectoring is performed, then ${\dot{m}}_T={\dot{m}}_B$ and the mass flow rate of the secondary injection will be referred to as ${\dot{m}}_i$.

3. Mathematical Model and Numerical Setup

The purpose of this work is to compare two different solutions for thrust vectoring in aerospike nozzles. A preliminary validation of the model and a grid convergence analysis was performed [21] on the results of a cold flow experimental test [1]. Since a cold flow is considered, the fluid is assumed to be air with a frozen chemical composition. This assumption is kept for all the simulations presented in this work. The flow field is described by means of the compressible Reynolds-averaged Navier–Stokes (RANS) equations with the Spalart–Allmaras closure model [36]. An ideal gas that follows the ideal gas equation of state is assumed. The specific heat ratio is assumed to be constant and set to $\gamma =1.4$. The dynamic viscosity is evaluated by means of the Sutherland’s law. All of the simulations reported in the following were performed by assuming a nozzle pressure ratio (chamber total pressure over ambient static pressure) equal to 56.7. An investigation into the effectiveness of fluidic thrust vectoring for different values of nozzle pressure ratio is reported in [21].

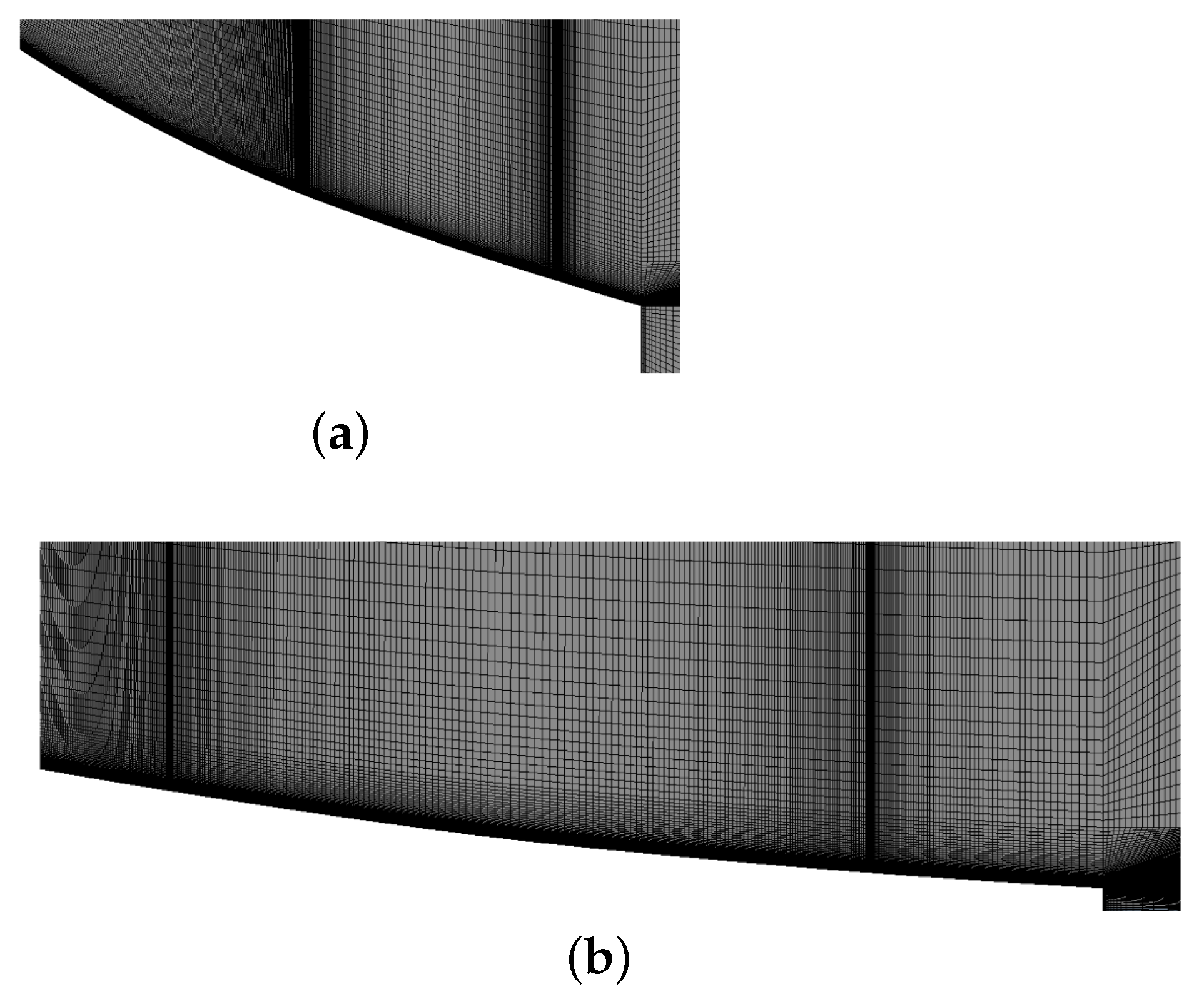
The governing equations are solved by means of a second-order accurate finite volume discretisation implemented in the Fluent solver. Convective fluxes are evaluated by means of the Roe approximate Riemann solver [37]. The governing equations are integrated in time by an implicit scheme until a steady solution is reached. The spatial domain is discretised by means of a block structured mesh, which is refined in the boundary layer region and in the injection point. Two linear aerospikes are considered in this work: the first is truncated at 40% of the full plug length (LP40) and the second at 75% of the full plug length (75%), as shown in Figure 2. The flow field in these nozzles is bidimensional for most the extension; the three-dimensional effects are confined to the extremities. For this reason, bidimensional simulations were performed in this work. The computational domain and the enforced boundary conditions for both the LP40 and LP75 geometries are reported in Figure 3. In particular, total temperature, total pressure and angle are imposed at the nozzle inlet. At the outlet, the static pressure is imposed where the local Mach number is subsonic and the solution is extrapolated from inside the domain where the local Mach number is supersonic. The mesh used for simulating the effects of differential throttling contains approximately 110,000 cells, while the mesh used for the fluidic thrust vectoring simulations contains more cells (250,000) since it is necessary to refine the grid in the injection region. This resolution level was chosen using the results from a grid convergence analysis carried out in a previous numerical study [21]. In particular, the dimensionless wall distance $y^{+}$ for the first layer of cells was chosen in order to guarantee the condition $y^{+}<5$, which is recommended for the Spalart–Allmaras model. Details of the mesh in the region near the plug are reported in Figure 4 where it is possible to observe the refinements close to the injection slots. An adiabatic wall boundary condition is applied to the plug wall while the injection slots are simulated by setting a sonic inlet boundary conditions.

4. Numerical Results

In this section, the numerical results obtained for the LP40 and LP75 geometries are reported for both differential throttling and shock vectoring. The performance of the two control systems is evaluated in terms of lateral thrust generation and axial thrust reduction. A parametric study is performed in order to quantify the mass flow rate imbalance or the secondary flow mass flow rate required to obtain an effective control.

4.1. Linear Aerospike Nozzle Truncated at $40\%$ (LP40)

A first set of simulations was performed on the LP40 geometry. This configuration is characterised by a very short plug, which is representative of a real-world application: the truncation of the spike significantly reduces the cooling problems and the axial length of the nozzle.

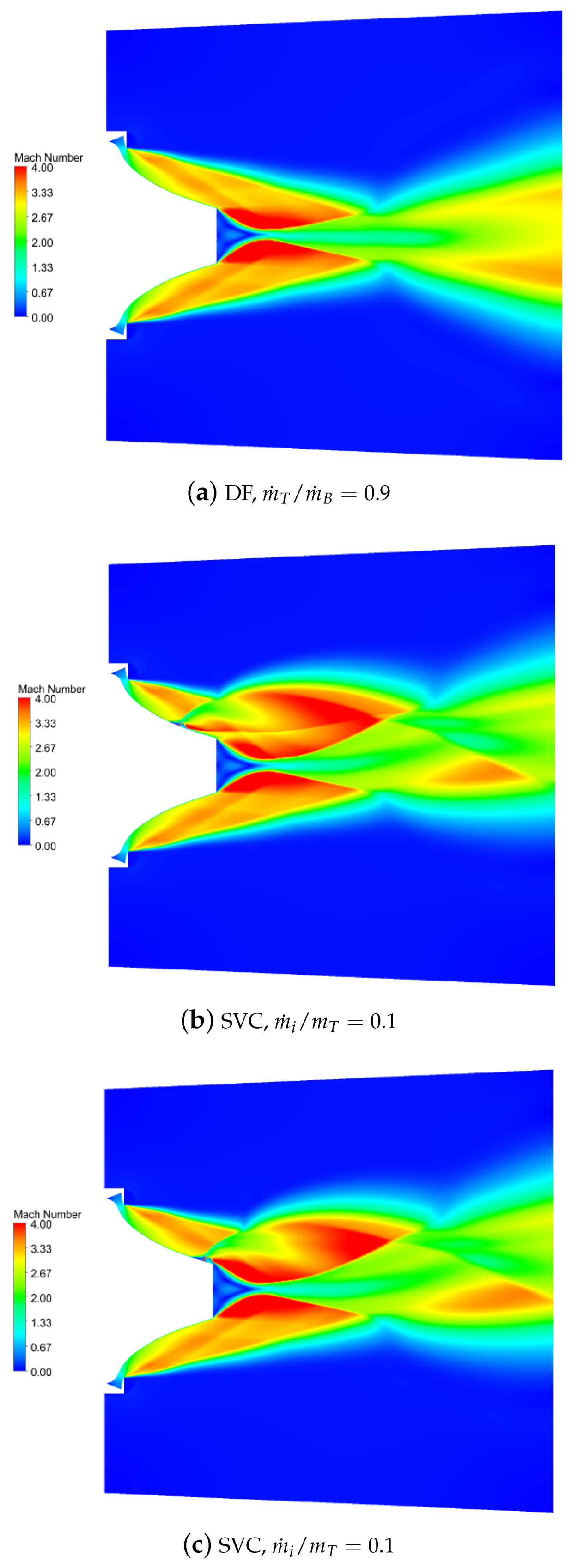
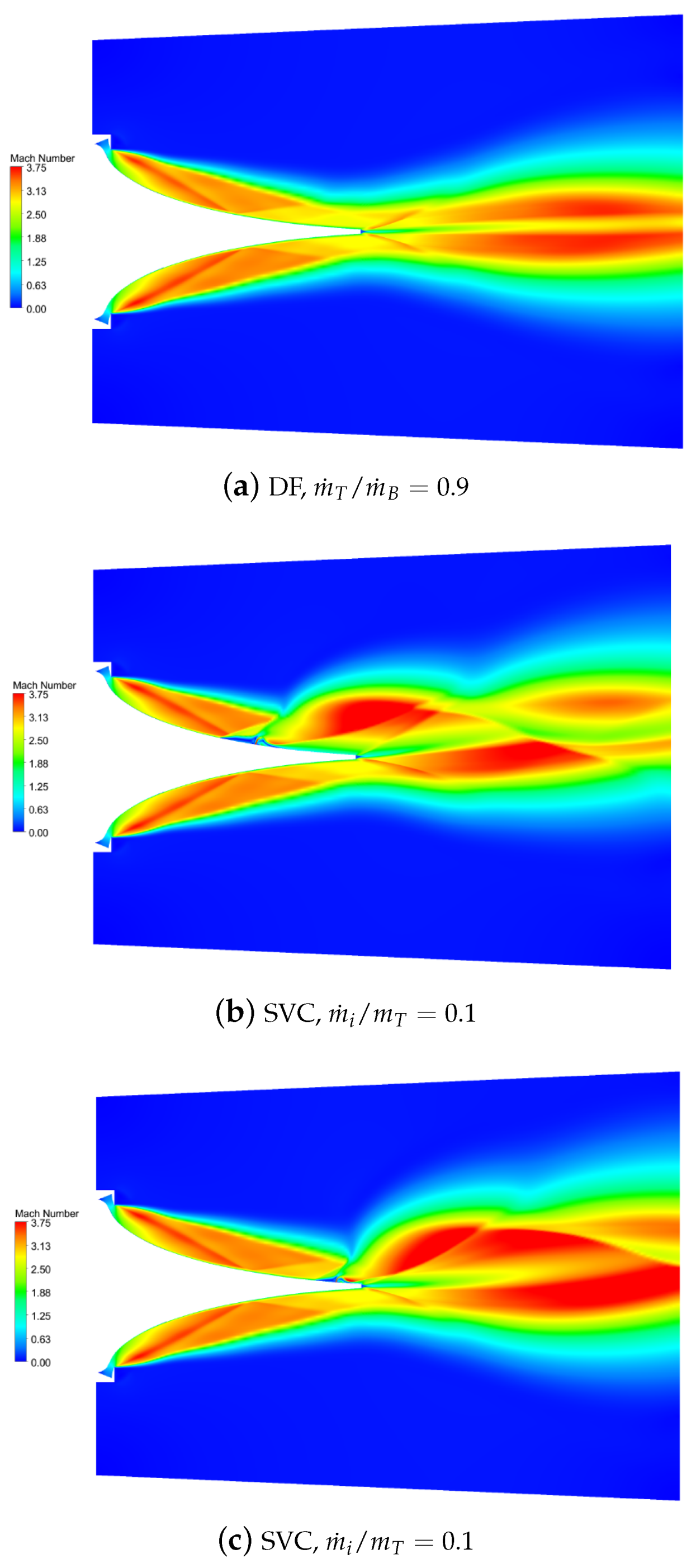
Figure 5 shows the Mach field obtained on the LP40 plug using different control strategies. In Figure 5a, the results obtained by differential throttling are reported: this solution is obtained by reducing the total pressure in the top chamber while keeping the same total temperature in both chambers. As a result, the mass flow rate from the top chamber is reduced, while the mass flow rate from the bottom chamber remains constant. In particular, the plot refers to the condition ${\dot{m}}_T/{\dot{m}}_B=0.9$.

In Figure 5b, the flow field obtained by shock vector control is reported. It is possible to clearly identify the location of the secondary injection on the upper side of the plug: the secondary flow acts as an obstacle which induces a shock wave as a separation. The separation moves upstream with respect to the injection slot and generates a sort of fluidic ramp on the wall. The Mach field shows that the flow accelerates just downstream of the injection slot and then another shock wave is generated at the end of the separation region. These results refer to the condition ${\dot{m}}_i/m_T=0.1$ and the injection slot is located at 60% of the plug length.

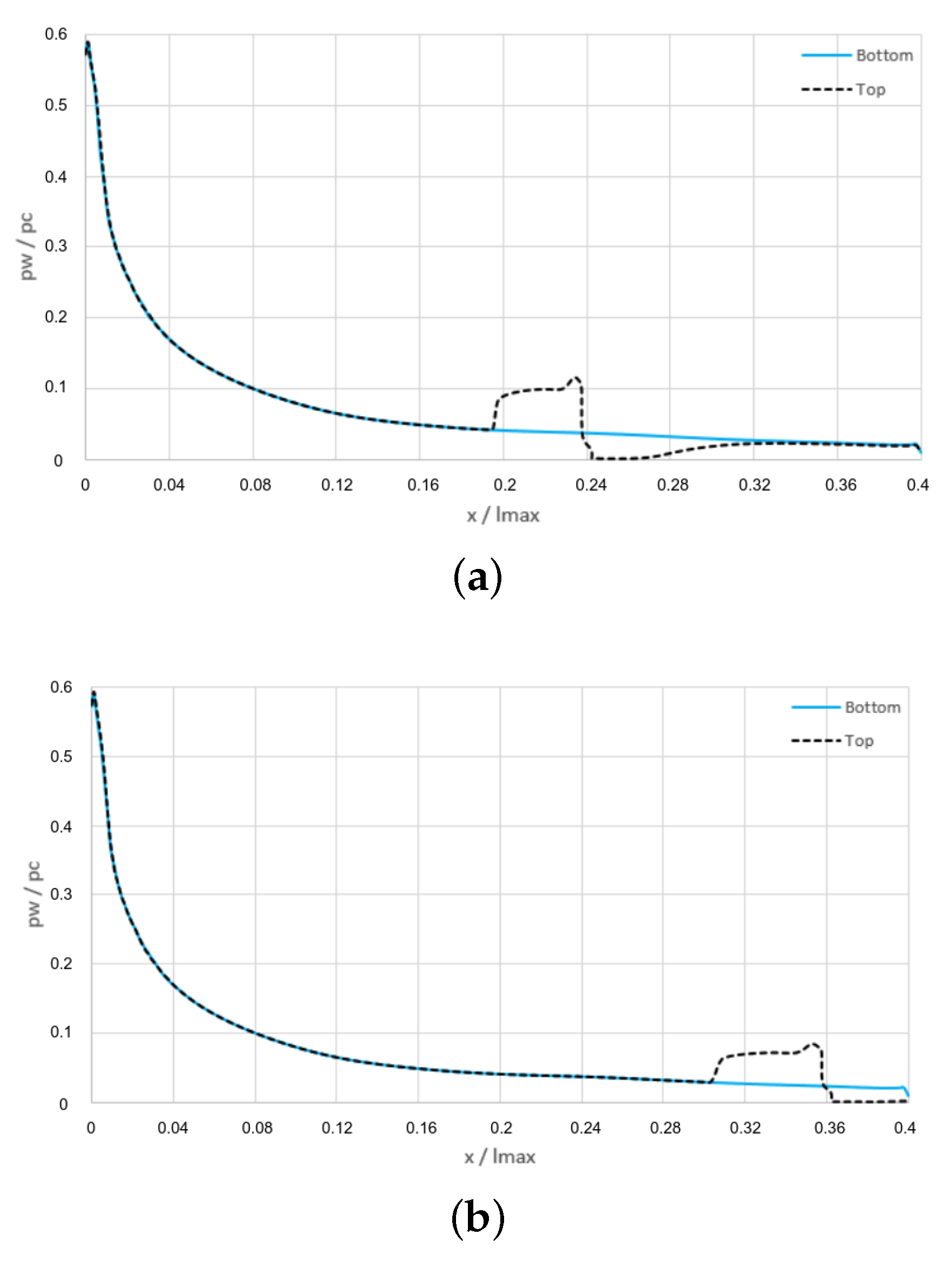
The results in Figure 5c for an injection slot located at 90% of the plug length are qualitatively similar to those observed in Figure 5b. The influence of the injection location can be seen more clearly by comparing the wall pressure distributions, which are reported in Figure 6. The results show that the secondary injection generates a shock wave in front of the injection slot. The shock wave is not exactly located on the injection slot but it is placed upstream because of the boundary layer separation. An expansion region can be observed downstream of the injection slot. The magnitude of the lateral force component is determined by the integral of the wall pressure distribution on the full plug: the compression and the expansion regions lead to opposite contributions which tend to cancel each other out. This effect is particularly evident when the injection is located at 60% of the plug length (see Figure 6a). In contrast, when the injection is performed at 90 % of the plug length, the surface affected by the expansion is reduced, as shown by Figure 6b.

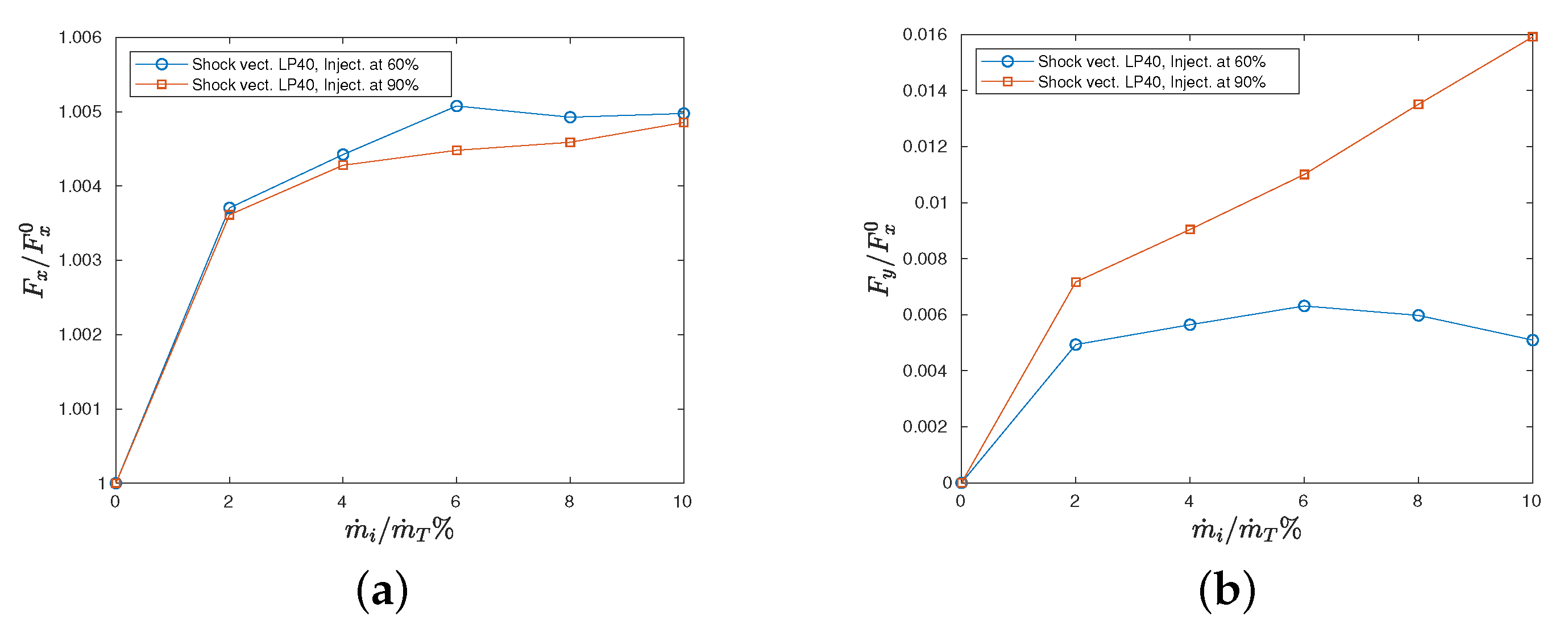
These qualitative considerations are confirmed by the computations of the thrust components reported in the plot of Figure 7. In particular, the lateral thrust component normalised with respect to the magnitude of the unperturbed thrust ${\mathit{F}}_x^0$ is shown as a function of ${\dot{m}}_i/m_T$ in Figure 7b. When the injection is performed at 90% of the plug length, the behaviour is monotone and the lateral thrust component is always higher with respect to the results obtained when the injection is performed at 60% of the plug length. This seems to be related to the fact that, when the injection is performed close to the end, the expansion acts on a small region and is not able to significantly reduce the effects generated by the compression. This behaviour is in line with the experimental findings of [23]. Furthermore, when the injection is performed at 60% of the plug length, the results are non-monotone with respect to ${\dot{m}}_i/m_T$: this could again be related to the absence of a clear net effect since both compression and expansion influence a significant portion of the plug.

The plot in Figure 7a shows the axial thrust component: its value is slightly increased when the secondary injection is introduced. This is due to the fact that the secondary injection has a small axial component and this leads to a weak increase in the axial thrust component.

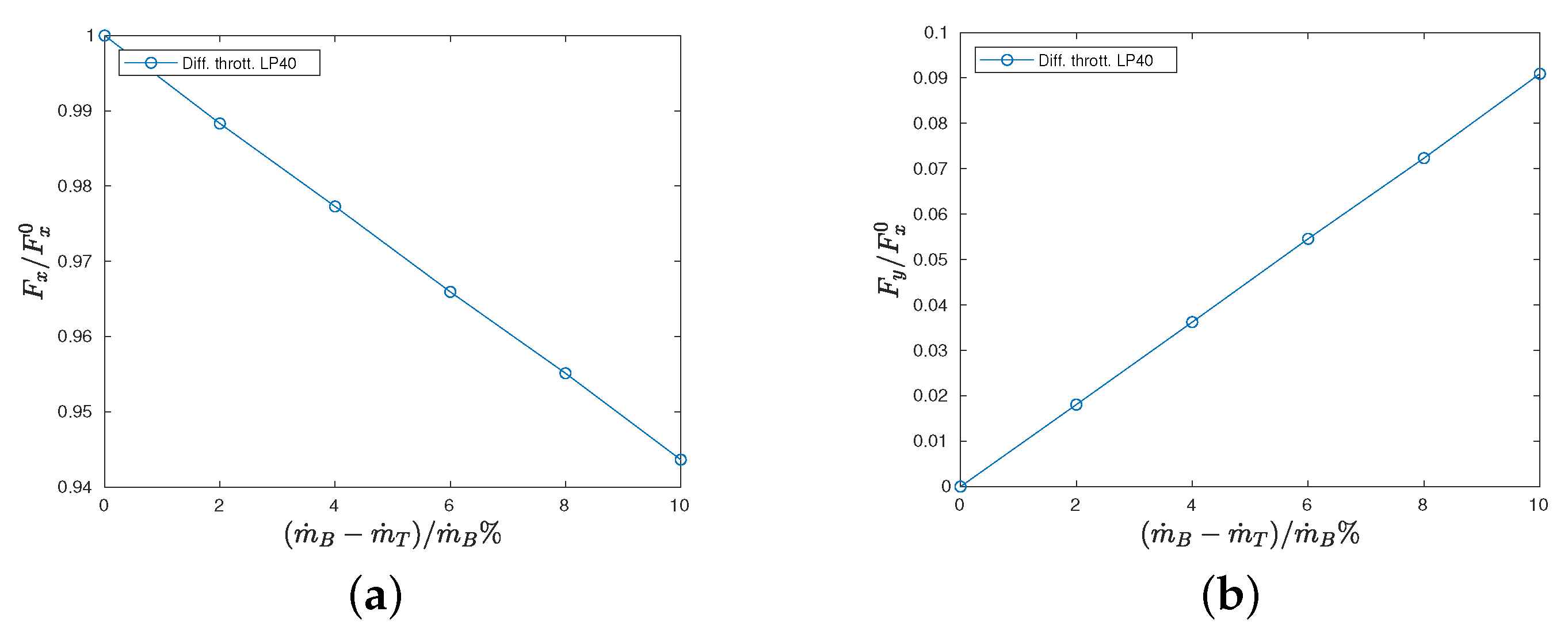
Finally, the results for differential throttling are reported in Figure 8: the trend in this case is very clear. The lateral thrust component, which is reported in Figure 8b, grows linearly with respect to $({\dot{m}}_B-{\dot{m}}_T)/{\dot{m}}_B$. In this case, the axial thrust component decreases significantly when $({\dot{m}}_B-{\dot{m}}_T)/{\dot{m}}_B$ is increased. This linear behaviour can be partially predicted by consideration of the terms that appear in the first integral of Equation (2). The throat of the nozzles is assumed to be sonic and the total temperature is kept fixed in the two chambers. In such a condition, the mass flow rate through each nozzle is directly proportional to the total pressure of the chamber. Furthermore, the speed at the section $A_e$ is fixed because the Mach number is determined by the geometric expansion ratio and the speed of sound remains constant. Finally, the static pressure at section $A_e$ is directly proportional to the total pressure of the chamber because of the constant Mach number. As a result, all of the terms that appear in the first integral of Equation (2) are directly proportional to the total pressure of the chamber or constants. It is not possible to perform similar analytical considerations for the second integral in Equation (2). However, the results reported in Figure 8 suggest that the linear behaviour of the terms in the first integral dominates the response of the system.

4.2. Aerospike Nozzle Truncated at $75\%$ (LP75)

A second set of simulations was performed on the aerospike nozzle truncated at 75% of the original spike length (LP75). The Mach field obtained by adopting differential throttling, secondary injection at 60% of the plug length and secondary injection at 90% of the plug length is reported in Figure 9. The results are qualitatively similar to the fields obtained for the LP40 but now the injection-induced separation is even more intense and it covers a larger region with respect to that for the LP40: this could be related to the fact that the injection in the LP75 is applied in a region where the wall slope is smaller with respect to the corresponding points in the LP40. A smaller wall slope is related to a smaller pressure gradient: this can influence the extension of the separation.

The wall pressure distribution obtained by using shock vector control on the LP75 is reported in Figure 10. The plot confirms that the extension of the separation region is significantly larger with respect to the LP40 since the shock is positioned significantly upstream of the injection slot. This suggests that thrust vector control on the LP75 should be more effective with respect to the LP40 configuration. This is confirmed by the plot in Figure 11b, which shows the lateral thrust component as a function of ${\dot{m}}_i/m_T$. The values observed in this configuration are larger with respect to the values obtained for the LP40: in particular, the maximum lateral thrust component is $0.02{\mathit{F}}_x^0$ for the LP75 and $0.016{\mathit{F}}_x^0$ for the LP40, where ${\mathit{F}}_x^0$ is the uncontrolled axial thrust.

Even for the LP75, the location of the injection slot represents a key parameter: the closer the slot to the end, the larger the lateral thrust component becomes. Furthermore, while the use of an injection slot at 60% of the plug length leads to a non-monotone behaviour with the LP40, a monotone behaviour is preserved with the LP75. In this configuration, the axial thrust component is slightly increased by the activation of the secondary injection.

As far as differential throttling is concerned, the results show that the lateral thrust component grows linearly with the difference between the mass flow rates. However, differential throttling seems less effective on the LP75 nozzle with respect to the LP40 nozzle: this can be deduced by comparing the plots in Figure 8b and Figure 12b, which show that the lateral thrust component is larger on the shorter nozzle. Differential throttling influences both the integrals which appear on the right-hand side of Equation (2). The term related to the momentum flux through the surface $A_e$ is not affected by the plug geometry. However, the term related to the pressure integral on the plug wall is influenced by the choice of the truncation length and the effects on the lateral force are not negligible, as shown by the comparison between Figure 8b and Figure 12b. For this geometry, the axial thrust component decreases monotonically as $({\dot{m}}_B-{\dot{m}}_T)/{\dot{m}}_B$ is increased.

5. Conclusions

Differential throttling and shock vectoring are investigated as possible solutions for providing thrust vectoring in a linear aerospike nozzle. The results show that differential throttling is a highly effective strategy: the obtained lateral thrust component varies linearly with respect to the difference between the mass flow rates from the two feeding chambers. This linear behaviour makes differential throttling very attractive from a control engineering perspective. The numerical tests show that differential throttling is more effective on shorter nozzles: this is a further advantage since aerospike nozzles are usually truncated to a small percentage of the full length in order to limit weight and cooling problems.

Fluidic thrust vectoring, and in particular, shock vectoring, represent a valid alternative that could be considered when differential throttling cannot be applied because a common combustion chamber is adopted; for example, in small-scale engines. The simulations show that the location of the injection slot is a key parameter for two reasons. The first reason is that the injection induces a compression upstream of the injection slot and an expansion downstream of the injection slot: if the slot is located far from the end of the plug, then the two effects tend to cancel each other out and this reduces the magnitude of the lateral thrust component. This numerical result is in line with the experimental findings of Eilers et al. [23], who underlined the importance of placing the injection slot close to the end of the plug.

The second reason that the injection location is critical is the relation between the lateral thrust component and the secondary mass flow rate. The results presented in this paper show that if the plug is truncated to a sufficiently large percentage of the original full spike (75% in this work), then this relation remains monotone for both the tested locations of the injection slot. However, if a shorter plug is considered (LP40), then the use of an injection slot located far from the plug end can lead to a non-monotone behaviour: the lateral thrust component grows with the secondary mass flow rate up to a certain limit and then starts to decrease. This non-monotone behaviour was observed only in one of the configurations investigated in this work. However, the possibility of having a non-monotone response requires particular attention in the implementation of this control strategy. From this perspective, the results suggest that slot positioning becomes more important when short plugs are considered.

The present study is based on RANS equations which provide only the average field and which can lead to significant modelling uncertainty in the regions characterised by separations. Future work will be devoted to the study of the same problems by means of scale-resolving simulations which allow the direct capture of the evolution of the largest turbulence scales in order to evaluate the temporal fluctuations in the thrust components.