Abstract
This paper presents an adjoint-based shape optimization framework and its demonstration in a conjugate heat transfer problem in a turbine blading. The gradient of the objective function is computed based on the continuous adjoint method, which also includes the adjoint to the turbulence model. Differences in the gradient resulting from making the frozen turbulence assumption are discussed. The developed software was used to optimize both the blade shape of the internally cooled linear C3X turbine blade and the position of cooling channels aiming at (a) minimum total pressure drop of the hot gas flow and (b) minimum highest temperature within the blade. A two-step optimization procedure was used. A free-form parameterization tool, based on volumetric NURBS, controls the blade airfoil contour, while the cooling channels are free to move following changes in the coordinates of their centers. Geometric and flow constraints are included in the performed optimizations, keeping the cooling channels away from the airfoil sides and retaining the turbine inlet capacity and flow turning.
1. Introduction
The efficient design of gas turbines with improved performance and longer lifetime, for use in aerospace and marine propulsion, land power plants, and other industrial applications, is of great importance. Gains are expected from aerodynamically optimized compressors, reduced friction in mechanical parts, optimal performance of inlet ducts and nozzles, and/or higher turbine inlet temperatures. The latter is limited by the thermal resistance of the first turbine row blades which are currently able to operate at gas temperatures exceeding the limits set by the materials thanks to internal and/or external cooling. Relevant studies account for the interaction of blades and gas flow in gas turbine components. This can be done using conjugate heat transfer (CHT) analysis and optimization.
A CHT analysis involves the strongly or loosely coupled solutions of the governing equations in the adjacent fluid and solid domains. In a strongly coupled scheme, PDEs in different domains are solved simultaneously, while in a loosely coupled one, each discipline is solved separately and communicates with the other(s) by exchanging data along their interfaces [1]. For the shape optimization of cooled blades, both stochastic and gradient-based methods have been used. The latter make use of the adjoint method to compute the gradient of quantities of interest at a cost independent of the number of design parameters. In [2], the continuous adjoint method to compute the objective function gradient in CHT shape optimizations for turbulent incompressible flows is developed in the OpenFOAM environment. There, the shape optimization of a 2D internally cooled turbine cascade and a 3D car engine cylinder cooling system are presented.
The internally cooled C3X turbine blade, reported in [3], is a well-known test case that has widely been used for validation purposes [4,5] and is used in this paper, as well. The optimization of the cooling system of the C3X blade can be found in [6,7], which both use evolutionary algorithms, and in [8] using the globally convergent method of moving asymptotes. In the latter, the objective function derivatives with respect to the design variables needed by the optimization algorithm are computed based on forward finite differences.
This paper is an extended version of [9] and deals with the continuous adjoint method for computing the gradient of the objective and constraint functions with respect to the design variables; the adjoint to the turbulence model PDE is also formulated and solved. Compared to the material presented in [9], the development of the continuous adjoint for CHT problems is presented in detail. The adjoint solver is used within a gradient-based algorithm to optimize the C3X turbine blade, aiming at minimizing the total pressure drop and the highest blade temperature, by controlling the blade shape and its cooling holes’ locations. This optimization is performed in two steps, in which constant heat transfer coefficients are imposed in the cooling holes. The latter are based on 3D CHT analysis runs instead of using the empirical expression of [3,9].
This paper is organized as follows. The governing equations and the adjoint development are presented in Section 2 and Section 3, respectively. The in-house CFD software PUMA [10], running on GPUs, is presented in Section 4 and used for the CHT analysis of the C3X turbine blade in Section 5. The adjoint-based computed sensitivity derivatives are compared with finite differences in Section 6. Section 7 presents the CHT optimization of the C3X turbine blade.
2. Governing Equations
In a 3D CHT analysis problem, the flow equations in the fluid domain are coupled with the heat conduction one in the solid domain . In , the RANS (mean-flow; ) equations for compressible fluid flows read
where are the inviscid fluxes and the viscous ones. , p and stand for the fluid’s density, pressure, and total enthalpy, respectively. are the velocity components and the Kronecker symbol. is the stress tensor based on the Boussinesq assumption. The heat fluxes are , with being the fluid’s conductivity, where and are the bulk and turbulent viscosity. is the specific heat under constant pressure, and . The dynamic viscosity depends on the fluid’s temperature [11]. Turbulence is modeled either by the one-equation Spalart–Allmaras or the two-equation SST model. The transport equations of the Spalart–Allmaras variable , the turbulent kinetic energy , and the turbulence frequency are
where and are the production and destruction of , and d stands for the distance from the nearest solid wall boundary. can be computed via
The constants , , , and along with the expressions of , , , and are given in [12]. The last two quantities are functions of vorticity , where . Constants , , , the expression for the production of k, and those of , , , , , and can be found in [13]. In Equation (5), S stands for the strain rate magnitude. The distance field , which affects the production and destruction terms of and the solid wall condition for , is computed by solving the Eikonal equation,
The last state equation, which stands for the heat conduction equation over , reads
where are heat fluxes and is the thermal conductivity of the solid. The flow and heat conduction solvers communicate across the fluid–solid interface (FSI), where and must be satisfied. , are the normal vectors to the FSI pointing toward and , respectively.
3. Continuous Adjoint Formulation
In this work, two objective functions and two flow constraints are considered. The total pressure drop and the highest temperature of the blade are the two objective functions. The inlet capacity and hot gas exit flow angle are the two flow constraints. These quantities are
where the highest blade temperature is approximated by the above differentiable expression where takes on a large value. , , are the massflow and the mass-averaged total pressure and total temperature at the hot gas inlet, respectively, and , , stand for the mass-averaged total pressure and velocity components at the hot gas exit. Gradient-based optimization algorithms require the gradient of both the objective and constraint functions; thus, in the remainder of this section, the continuous adjoint method for a generic function F (standing for , , , or ) is formulated. In continuous adjoint, F is augmented () by the field integrals of the product of the state equations’ residuals with the adjoint variable fields over and . For the development of the adjoint method, only the Spalart–Allmaras turbulence model is used. Differentiating with respect to the design variables gives
where , , and are the nth adjoint flow fields (n = 1,…,5), the adjoint Spalart–Allmaras, and adjoint distance fields, respectively, all defined in . stands for the adjoint temperature and is defined in . By definition, and are the same. For any function of the state variables, the expression
correlates its total () and partial () derivatives as well as grid sensitivities . Total derivatives of with respect to and spatial derivatives permute according to [14]
After a lengthy mathematical development, can be expressed as the sum of field and surface integrals that include variations in the state variables, and integrals depending on sensitivities of geometrical quantities with respect to . Setting the multipliers of variations in the state variables to zero gives rise to the field adjoint equations (FAE) along with the adjoint boundary conditions (ABC). In the next subsections, the four field integrals in Equation (9) are further developed in order to derive the FAE, the ABC, and the expressions of the sensitivity derivatives ().
3.1. Development of the Integral
Substituting the residuals of the MF equations in Equation (9), the first field integral of this equation takes the form
Using the divergence theorem, its inviscid counterpart becomes
where (in a 3D flow) are the conservative flow variables, E the total energy per unit mass, and the inviscid flux Jacobian matrix. An arrow (→) underneath any underbraced term indicates where this term contributes. For instance, field integrals including variations in contribute to the field adjoint mean-flow equations . Integrals which contain sensitivities of geometric quantities contribute to the . Finally, gathers all surface integrals. Using the divergence theorem
Substituting the expression of the viscous fluxes, applying the divergence theorem, and rearranging the indices, becomes
Note that, in integrals over and or their boundaries (, ), superscripts denoting the fluid (F) or solid (S) domains are omitted in quantities such as and T. Arrays V, are
The adjoint stresses and adjoint heat flux are defined as
Variations in are taken into account by differentiating the Sutherland law [11] with respect to the fluid’s temperature. comprises field integrals over which include variations in . Differentiating Equation (5) (first option), source terms to the adjoint Spalart–Allmaras equation arise, as follows
3.2. Development of the Integral
Substituting the transport equation of , the second field integral of Equation (9) becomes
where , and contain the convection, diffusion, and source terms of the Spalart–Allmaras model, namely
The first two integrals can be rewritten using the divergence theorem as
Integrals including variations in (where ) contribute to the field adjoint Spalart-A-llmaras equation . Those including variations in contribute to both and as . The above field integrals which contribute neither to , nor to the can further be analyzed using the divergence theorem, as
Since the production and destruction of are functions of , vorticity , distance d, and , takes the form
where and the field integral including variations in distance contributes to the field adjoint distance equation . The partial derivatives of the production and destruction of with regard to , , d, and can be found in [15]. The last integral is rewritten as
3.3. Development of the Integral
Substituting the residual of the Eikonal equation in Equation (9) and applying the divergence theorem, becomes
3.4. Development of the Integral
In , using the heat conduction equation and the divergence theorem, the corresponding integral in Equation (9) takes the form
where, by defining as the adjoint heat fluxes in the solid domain,
3.5. Field Adjoint Equations (FAEs) and Adjoint Boundary Conditions (ABCs)
The multipliers of variations in the state variables give rise to , , , and . These read
where , , stand for the multipliers of , , and , respectively. are source terms added to and result from the differentiation of the Spalart–Allmaras model. Similarly, and are sources to and , resulting from the differentiation of the mean-flow and turbulence model equations, respectively. It should be mentioned that , , and do not depend on the adjoint distance variable ; thus, is numerically solved after solving or and first and contributes to the computation of . is the contribution of F to , which is non-zero only for .
Gathering all surface integrals without variations in or d into a single integral gives
splits into integrals over (a) the inlet/outlet boundaries and (b) the solid wall boundaries of ; the latter include the FSI and adiabatic walls (hub and shroud). For the ,
where variations in viscous stresses and heat flux are ignored. Eliminating the terms including variations in the flow variables gives rise to the adjoint inlet/outlet conditions, namely
where denotes any flow quantity extrapolated to from the interior of . For the inlet, stands for the velocity magnitude, and for the outlet, are the outgoing Riemann variables. For the solid walls of , taking into account the no-slip condition, Equation (15) becomes
The adjoint no-slip condition () eliminates surface integrals with variations in and p. Terms with variations in heat flux and T are eliminated by satisfying the adjoint adiabatic and FSI conditions. The former read along the adiabatic walls of and . The adjoint FSI conditions are and . Finally, setting and to zero over the boundaries of eliminates the surface integrals which contain variations in and d.
3.6. Expression for
The remaining field and surface integrals comprise the formula for computing the gradient of F
where
Grid sensitivities along the parameterized surfaces (here, the FSI and the cooling channel boundaries) are computed directly by the differentiation of the parameterization tool. Then, the spring analogy method undertakes their propagation into and .
4. The PUMA Software
PUMA is a GPU-accelerated software which involves a RANS equations’ solver, a heat conduction equation’s solver, and their adjoint counterparts along with a set of shape parameterization and grid deformation tools. It runs on a GPU cluster using the shared on-board memory for data transfer between GPUs on the same computational node and the MPI protocol between GPUs on different nodes. Data communications overlap with computations.
The flow and their adjoint equations are discretized on unstructured grids following the vertex-centered finite-volume approach. A multi-stage Runge–Kutta scheme, applied in pseudo-time, with residual smoothing is used to solve the equations. A second-order accurate, central differences scheme with artificial dissipation discretizes the inviscid fluxes. Residual smoothing employs the first-order accurate Jacobian of the fluid’s residuals, which is computed in double-, though stored in single-precision arithmetic. The mixed-precision arithmetic minimizes GPU memory transactions without jeopardizing solution accuracy. The heat conduction equation is also discretized using vertex-centered finite volumes and solved using a Krylov-based solver.
The flow and heat conduction solvers are loosely coupled by means of Aitken’s dynamic relaxation formula. Figure 1 illustrates a schematic representation of the coupling between the flow and heat conduction solvers. Temperature fields computed by the heat conduction solver in after performing a number of internal iterations are scaled according to Aitken’s formula and imposed as boundary conditions to the flow solver. The flow solver preforms a number of pseudo-time steps, and the computed heat fluxes on the FSI are communicated back to the heat conduction solver. The flow solver computes heat fluxes along the FSI by integrating the energy equation over the finite volumes next to it; for instance, for an FSI node i,
where j are its neighbors and , the inviscid and viscous energy fluxes crossing the finite volume interfaces between i and j, respectively. The stability of the coupling scheme is enhanced by computing and communicating the Jacobians of the computed heat fluxes with respect to along the FSI to the heat conduction solver. Heat fluxes along with their Jacobians are computed and communicated at each pseudo-time iteration of the heat conduction solver. The CHT coupled adjoint equations are solved in a similar way.
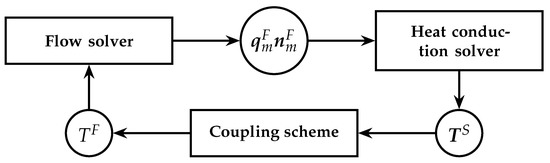
Figure 1.
Schematic representation of the coupling of the flow and heat conduction solvers. A similar coupling applies to the adjoint solver.
5. CHT Analysis of the C3X Turbine
The geometry of the C3X turbine linear cascade can be found in [3]. The blade, made of stainless steel with density and heat capacity , is cooled by 10 straight channels. Its thermal conductivity is a function of as . Its span is 7.62 cm long, with an axial chord of 7.816 cm. According to Case 158, for the hot gas, , , and (turbulence intensity) at the inlet, whereas at the outlet. For each cooling channel, experimental data for the average temperature and the coolant flow rate are available; to meet them, an iterative procedure for adjusting the total pressure and total temperature at the cooling channels’ inlets is applied.
An unstructured 3D grid with M nodes was generated with M for the hot gas, K for the coolant flow, and K for the solid domain. The grid has structured layers close to the pressure and suction sides and the cooling channels to account for the large spatial gradients of and in these regions. The rest of the fluid and solid domain is filled with prismatic elements. Both the Spalart–Allmaras and SST turbulence models were used in the analysis phase. The fields computed at the hub, shroud, and midspan of the solid blade are presented in Figure 2 (top left), illustrating the effect of the cooling fluid flow at the blade temperature. Pressure, temperature, and heat transfer coefficient distributions along the blade midspan are compared with measurements in the same figure. A good agreement is observed for both models, though the temperature along the suction side and close to the leading edge is overestimated due to the absence of a transition model.
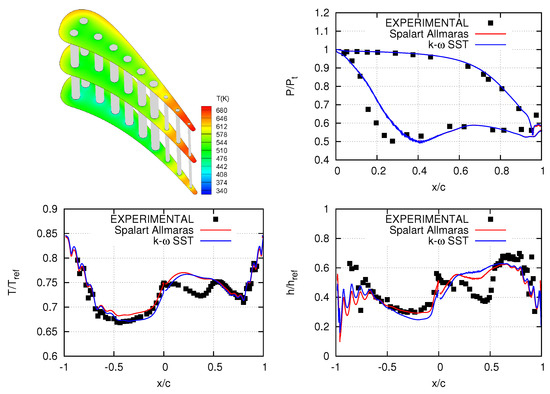
Figure 2.
Computed fields (top left) at the solid blade’s hub, midspan, and shroud. Computed pressure (top right), temperature (bottom left), and heat transfer coefficient (bottom right) distributions across the blade midspan compared with measurements. Pressure is non-dimensionalized by the inlet total pressure of 243,700 Pa, temperature by 811 , and the heat transfer coefficient by per-mode=symbol /.
The pressure, temperature, and heat transfer coefficient distributions at the blade midspan were also computed by a 2D CHT analysis, in which the average temperature and coolant flow rate per cooling channel were replaced by heat transfer coefficient values (since the 2D analysis refrains from computing the coolant flow). The heat transfer coefficients per cooling channel result from , where is the coolant thermal conductivity, D the channel diameter, and the Nusselt number. For turbulent flows in smooth pipes, the latter is given by , where the Reynolds number is determined by the channel’s diameter, the measured flow rate, and the coolant’s molecular viscosity. Cr is a correction for a fully developed thermal boundary layer to account for thermal entrance region effects and ranges from to for the 10 channels, [3].
An alternative computation is based on the post-processing of the heat flux and temperature fields at the blade midspan computed by the 3D CHT run. Figure 3 summarizes the heat transfer coefficients computed based on the two aforementioned approaches. The heat transfer coefficients based on the second approach, with both turbulence models, are slightly different, being lower than those based on the first approach. To measure the effectiveness of the computed heat transfer coefficients, 2D CHT analyses were performed based on them with the Spalart–Allmaras turbulence model. Figure 4 shows the computed temperature and heat transfer coefficient distributions at the blade midspan resulting from two 2D CHT analyses employing the heat transfer coefficients from the two approaches and also includes the 3D CHT analysis results as well as measurements. It can be seen that, using the heat transfer coefficients computed by the second approach, the 2D CHT analysis produces almost the same results with the 3D run. On the other hand, with the first approach, lower is computed. Though it is not shown here, both 2D runs obtain practically the same pressure field at the blade midspan with the 3D run. This was expected since the pressure field is mostly affected by the blade shape.
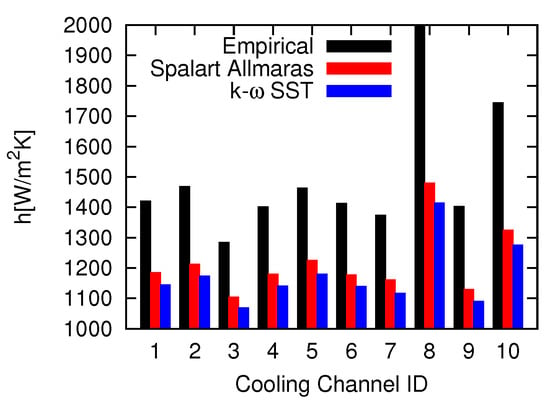
Figure 3.
Comparison of the heat transfer coefficients of the cooling channels computed by the two approaches.
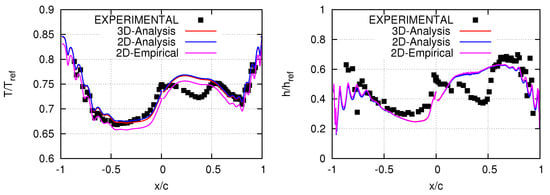
Figure 4.
Temperature (left) and heat transfer coefficient (right) distributions along the blade contour obtained by 3D and 2D CHT runs. The 2D runs use the channels’ heat transfer coefficients computed by the two approaches presented in the text.
6. Verification of the Adjoint Sensitivities
Prior to the optimization studies, the accuracy of the adjoint-based sensitivity derivatives is assessed. For this purpose, the sensitivity derivatives of the objective functions and flow constraints (, , and ) are computed by the developed continuous adjoint method and compared with finite differences (FDs). In this comparison, the 2D configuration with the heat transfer coefficients computed by the second approach and the Spalart–Allmaras turbulence model are used. The turbine blade shpae is parameterized using a 7 × 3 volumetric NURBS control grid. The control points at the leading and trailing edges are fixed while the rest are free to move in the axial and pitch-wise directions. In total, 38 design variables are used. The cooling holes, though potentially controlled by the same morphing box, are fixed without being affected by changes in the design variables. Figure 5 presents the computed adjoint and FD-based sensitivity derivatives which are in very good agreement. The influence of the frozen turbulence assumption (which is frequently made in the literature) is investigated. As shown in Figure 5, avoiding including the turbulence model equation into the adjoint formulation does not affect the gradients of the total pressure drop (), inlet capacity (), and exit flow angle (). However, this is not the case for the highest blade temperature (), where the frozen turbulence assumption significantly reduces the accuracy of the computed derivatives. For instance, for some design variables, this leads to derivatives that even have a wrong sign.
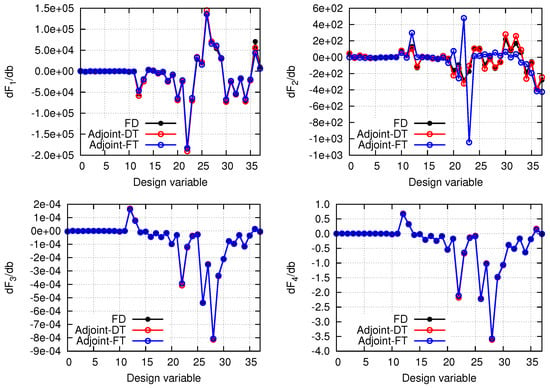
Figure 5.
Verification of the sensitivity derivatives computed by the adjoint method with the differentiated turbulence (DT) model and with the frozen turbulence (FT) assumption for (top left), (top right), (bottom left), and (bottom right). Finite differences are used as the reference values.
7. CHT Optimization of the C3X Turbine
The CHT optimization of the C3X turbine blade follows: The target was to minimize both the total pressure drop and the highest temperature of the blade while the inlet capacity and the hot gas exit flow angle were constrained to change up to % from their datum values. A first shape optimization was performed targeted at minimizing the total pressure drop under the above flow constraints. The 7 × 3 volumetric NURBS control grid of Figure 6a was used to control the blade shape. As in the verification study of the previous section, the control points at the leading and trailing edges remained constant, while the rest were free to move in the axial and pitch-wise directions. In this optimization run, in order to avoid the intersection of the cooling channels with the blade sides, the locations of their centers were controlled by the same control grid, while their radii were constant. In total, 38 design variables were used. To adapt the fluid domain grid to the changing boundaries, the spring analogy technique [16] was employed. The grid inside the blade was generated from scratch based on the new blade shape and cooling channel locations. Figure 6b shows the design variable bounds (used as extra geometric constraints). The method of moving asymptotes [17] was used, and its convergence is plotted in Figure 6b. The total pressure drop has decreased by ∼21% after 20 cycles by satisfying the flow constraints.
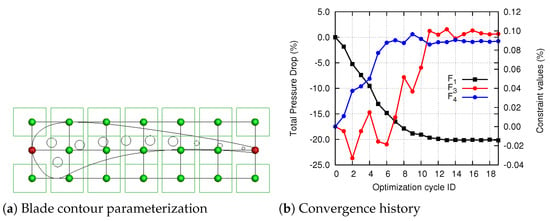
Figure 6.
First optimization run.
The best solution of the first optimization has almost the same highest blade temperature with the baseline, since this is mainly affected by the location of the cooling channels, which were only slightly changed by the control box of the first optimization. Thus, the outcome of the first optimization was further optimized for minimum highest temperature over the blade, aiming at refining the location of the channels. In this second optimization, the blade shape was not allowed to change, while the cooling channels were free to move leading to 20 design variables (2 per channel). Figure 7a shows the design variable bounds which were chosen so as to avoid channels overlapping with each other. To prevent the cooling channels from overlapping with the blade sides, the distance of each cooling channel from the airfoil sides was constrained to be higher than 30% of their radius. These 20 geometric constraints (2 per channel) ensured the generation of valid grids anew in each optimization cycle and kept the channels away from the blade sides, avoiding extremely high and high thermal stresses. After 45 optimization cycles, the blade’s highest was reduced by ∼30 K, still satisfying all geometric constraints. Figure 7b shows the convergence of the optimization algorithm, where the blade’s temperature is normalized with . For clarity, only the distance of the 10th cooling channel (the one closer to the leading edge) from the blade’s sides is plotted in Figure 7b, where distances are normalized with the channels’ radius. The best solution of the second optimization has a slightly increased (no more than ) total pressure drop compared to the best solution of the first run. This small increase was expected since reducing the highest on the blade results in a higher heat flux from the hot gas to the blade. At the same time, inlet capacity and hot gas exit angle differ no more than % from their datum values.
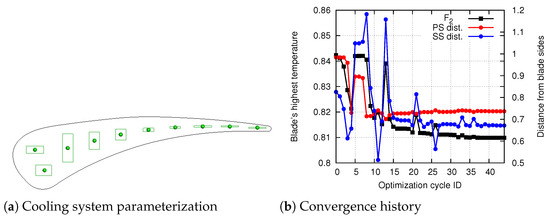
Figure 7.
Second optimization run.
Figure 8 presents the Mach number fields computed for the baseline and the optimized configuration (i.e., the outcome of the second optimization run). It is clear that the reduction in total pressure drop is mostly achieved by reducing the flow velocity in the passage throat region.
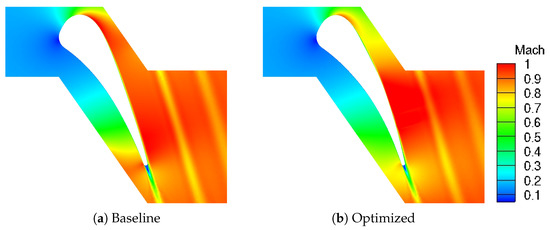
Figure 8.
Computed Mach number fields for the baseline and optimized configurations.
Figure 9 presents the computed and fields inside the blade for the baseline and the optimized configuration. In the latter, the first two cooling channels moved toward the leading edge where is high, while the remaining channels moved toward the trailing edge where the highest exists. Thanks to the geometric constraints, the cooling channels did not move too close to the blade sides, and the highest changed by less than ∼0.3% compared to the baseline. The optimized blade cooling system can also be seen in Figure 10.
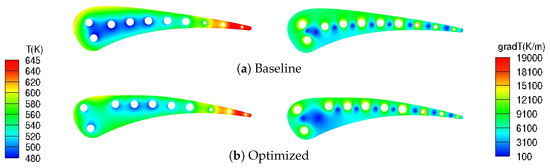
Figure 9.
Computed temperature (left) and temperature gradient magnitude (right) fields for the baseline and the optimized configurations.
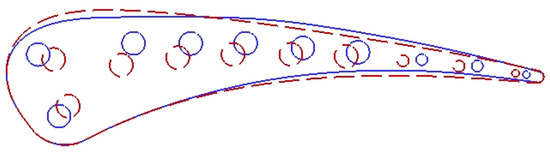
Figure 10.
Baseline (red) and optimized (blue) blade’s shape and cooling system.
8. Conclusions
The mathematical development of the continuous adjoint method for computing sensitivity derivatives in CHT problems involving turbulent compressible fluid flows was presented. The turbulence model equations are included in the adjoint formulation without making the frozen turbulence assumption, thus leading to an adjoint model that is consistent, in the continuous sense, to the one used in the CHT analysis. This was implemented in the in-house GPU accelerated software PUMA and used to optimize the internally cooled C3X turbine blade. Two optimization runs were performed. The first aims at reducing the total pressure drop while constraining the turbine inlet capacity and hot gas exit angle, allowing changes up to % compared to the baseline configuration. The second optimization started with the best solution of the first run, aiming at refining the cooling channel locations for minimum highest temperature over the blade. The optimized configuration has ∼20% less total pressure drop and ∼30 K lower highest blade temperature. The geometric constraints used in the second optimization run constrained the cooling channels from moving too close to the blade sides, increasing the highest temperature gradient magnitude inside the blade less than % of the baseline. The results show that the developed continuous adjoint CHT method, coupled with a gradient-based algorithm, provides a useful tool for the CHT optimization of internally cooled turbine blades. They also reveal possible losses in accuracy, regarding the gradient computation, from making the frozen turbulence assumption in the development of the adjoint method.
Author Contributions
Conceptualization, K.G.; software, X.T., K.T., V.A. and M.K.; validation, X.T. and M.K.; supervision, K.G. All authors contributed to writing and editing this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by European Union’s Horizon 2020 research and innovation program under Grant Agreement No 769025 (MADELEINE).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| CFD | Computational fluid dynamics |
| CHT | Conjugate heat transfer |
| FAE | Field adjoint equation |
| FDs | Finite differences |
| FSI | Fluid–solid interface |
| GPU | Graphics processing unit |
| NURBS | Non-uniform rational B-splines |
| RANS | Reynolds-averaged Navier–Stokes |
| SD | Sensitivity derivative |
References
- Moretti, R.; Errera, M.; Couaillier, V.; Feyel, F. Stability convergence and optimization of interface treatments in weak and strong thermal fluid-structure interaction. Int. J. Therm. Sci. 2017, 126, 23–37. [Google Scholar] [CrossRef]
- Gkaragkounis, K.; Papoutsis-Kiachagias, E.; Giannakoglou, K. The continuous adjoint method for shape optmization in Conjugate Heat Transfer problems with turbulent incompressible flows. Appl. Therm. Eng. 2018, 140, 351–362. [Google Scholar] [CrossRef]
- Hylton, L.; Mihelc, M.; Turner, E.; Nealy, D.; York, R. Analytical and Experimental Evaluation of the Heat Transfer Distribution over the Surfaces of Turbine Vanes. In NASA-CR-168015; Detroit Diesel Allison: Indianapolis, IN, USA, 1983. [Google Scholar]
- Andrei, L.; Andreini, A.; Facchini, B.; Winchler, L. A decoupled CHT procedure; application and validation on a gas turbine vane with different cooling configurations. Energy Procedia 2014, 45, 1087–1096. [Google Scholar] [CrossRef][Green Version]
- De Marinis, D.; de Tulio, M.; Napolitano, M.; Pascazio, G. A conjugate-heat-transfer immersed-boundary method for turbine cooling. Energy Procedia 2015, 82, 215–221. [Google Scholar] [CrossRef]
- Nowak, G.; Wroblewski, W. Optimization of blade cooling system with use of conjugate heat transfer approach. Int. J. Therm. Sci. 2011, 50, 1770–1781. [Google Scholar] [CrossRef]
- Mazaher, K.; Zeinalpout, M.; Bokaei, H. Turbine blade cooling passages optimization using reduced conjugate heat transfer methodology. Appl. Therm. Eng. 2016, 103, 1228–1236. [Google Scholar] [CrossRef]
- Wang, B.; Zhang, W.; Xie, G.; Xu, Y.; Xiao, M. Multiconfiguration Shape Optimization of Internal Cooling Systems of a Turbine Guide Vane Based on Thermomechanical and Conjugate Heat Transfer Analysis. J. Heat Transf. 2015, 136, 061004. [Google Scholar] [CrossRef]
- Trompoukis, X.; Tsiakas, K.; Asouti, V.; Kontou, M.; Giannakoglou, K. Continuous Adjoint Shape Optimization of Internally Cooled Turbine Blade. In Proceedings of the 14th European Turbomachinery Conference, Gdansk, Poland, 12–16 April 2021. [Google Scholar]
- Asouti, V.; Trompoukis, X.; Kampolis, I.; Giannakoglou, K. Unsteady CFD computations using vertex-centered finite volumes for unstructured grids on Graphics Processing Units. Int. J. Numer. Methods Fluids 2011, 67, 232–246. [Google Scholar] [CrossRef]
- Sutherland, W. The Viscosity of Gases and Molecular Force. Phil. Mag. 1893, 36, 507–531. [Google Scholar] [CrossRef]
- Spalart, P.; Allmaras, S. A one-equation turbulence model for aerodynamic flows. Rech. Aerosp. 1994, 1, 5–21. [Google Scholar]
- Menter, F.; Kuntz, M.; Langtry, R. Ten Years of Industrial Experience with SST Turbulence Model. Heat Mass Transf. 2003, 4, 625–632. [Google Scholar]
- Papadimitriou, D.; Giannakoglou, K. A continuous adjoint method with objective function derivatives based on boundary integrals, for inviscid and viscous flows. Comput. Fluids 2007, 36, 325–341. [Google Scholar] [CrossRef]
- Zymaris, A.; Papadimitriou, D.; Giannakoglou, K.; Othmer, C. Continuous adjoint approach to the Spalart-Allmaras turbulence model for incompressible flows. Comput. Fluids 2009, 38, 1528–1538. [Google Scholar] [CrossRef]
- Degand, C.; Farhat, C. A three-dimensional torsional spring analogy method for unstructured dynamic meshes. Comput. Struct. 2002, 80, 305–316. [Google Scholar] [CrossRef]
- Svanberg, K. A class of globally convergent optimization methods based on conservative convex separable approximations. SIAM J. Optim. 2002, 12, 555–573. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).