Fuzzy Controller Structures Investigation for Future Gas Turbine Aero-Engines
Abstract
1. Introduction
- Hydro-mechanical fuel control, which consists of a simple mechanical actuator controlled by the operator. In other words, in this embodiment, GTEs are manipulated by hydro-mechanical control systems.
- Hydro-mechanical/electronic fuel control, which is the former fuel flow controller with added an electronic control unit. This electronic unit performed the function of thrust setting, speed governing, and acceleration and deceleration in response to power lever inputs.
- Digital electronic engine control (DEEC), in this embodiment, functions carried out after input data from the airframe and engine were processed by the DEEC computer included setting the variable vanes, positioning compressor start bleeds, controlling gas-generator, adjusting the augmenter segment sequence valve, and controlling the exhaust nozzle position.
- Full authority digital engine (or electronic) control (FADEC), works by receiving multiple input variables of the current flight condition including air density, throttle lever position, engine temperatures, engine pressures, and many other parameters. The inputs are received by the electronic engine controller (EEC) and analyzed up to 70 times per second. Engine operating parameters such as fuel flow, stator vane position, air bleed valve position, and others are computed from this data and applied as appropriate. FADEC also controls engine starting and restarting procedures. The FADEC’s basic purpose is to provide optimum engine efficiency for a given flight condition [1].
- The first structure uses pure fuzzy control (PFC) strategy in which all control rules and loops are replaced by fuzzy rules.
- In the second structure, the controller keeps the industrial min–max structure in which the winner of different control loops will be selected by a pre-defined min–max strategy. However, control loops will be replaced by a fuzzy logic controller to result in a min–max fuzzy controller (MMFC).
2. PFC and MMFC Design
- Pure fuzzy controller (PFC)
- Min–max fuzzy controller (MMFC)
2.1. Pure Fuzzy Controller (PFC) Design
2.2. MIN–MAX Fuzzy Controller (MMFC) Design
- Steady-state control mode to meet pilot thrust level requirement.
- Transient control mode to reach the required thrust in a proper time.
- Physical limitations control mode to prevent the engine from damages and malfunctions (e.g., over-speed, over-temperature, surge, stall, etc.).
- PLA control loop: this loop has to supply the pilot desired thrust in each situation.
- Maximum speed limitation loop (MSLL): this loop is to prevent the engine from exceeding the rotor speed from the permissible amount. This control loop takes this responsibility to guarantee the integrity of the GTE.
- Maximum acceleration limitation loop (MALL): at the primary acceleration time abrupt fuel injection is the main cause of aerodynamic instability (surge and stall). MALL loop protects the engine against this fault.
- Maximum deceleration limitation loop (MDLL): at the primary sharp deceleration time control system must prevent fuel flow from abruptly reducing because the rotor inertia could lead to flame burnout. Therefore, the fuel flow reducing rate must be limited.
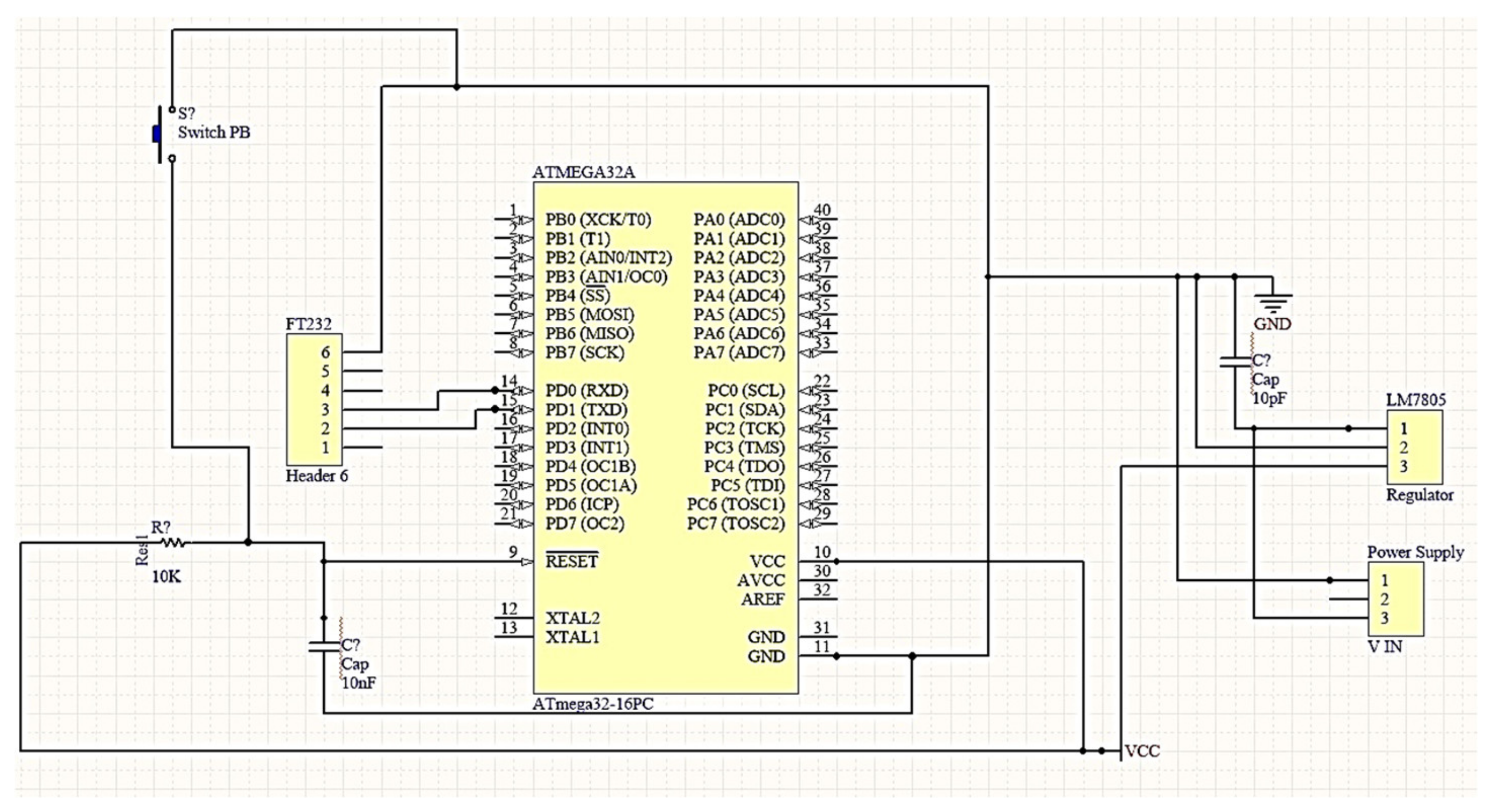
3. Hardware Implementation
3.1. Experimental Apparatus
3.2. Initial Preparation
3.2.1. PFC Controller Hardware Implementation
3.2.2. MMFC Hardware Implementation
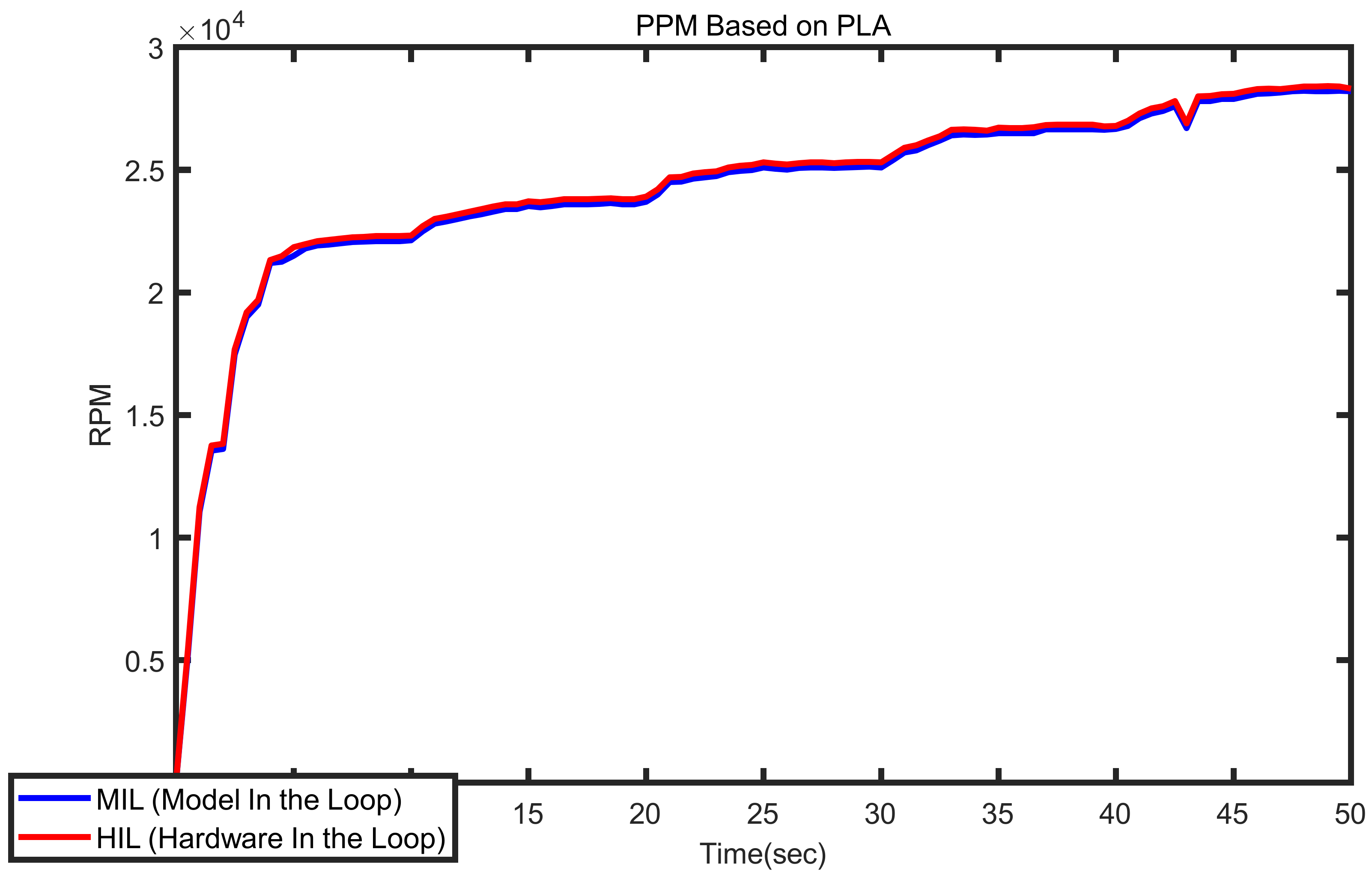
3.3. Hardware in the Loop Simulation
- The controller could be modeled in the software to be running on target computer hardware while it is connected to your physical plant or system. (The target computer hardware acts as the controller.).
- The other option is to implement the controller on the hardware, which can include production or embedded controls implementation, using a simulation of your plant or system. (Here, the target computer acts as a physical plant or system.).
- Simulation without time limitations;
- Real-time simulation;
- Simulation faster than real-time.
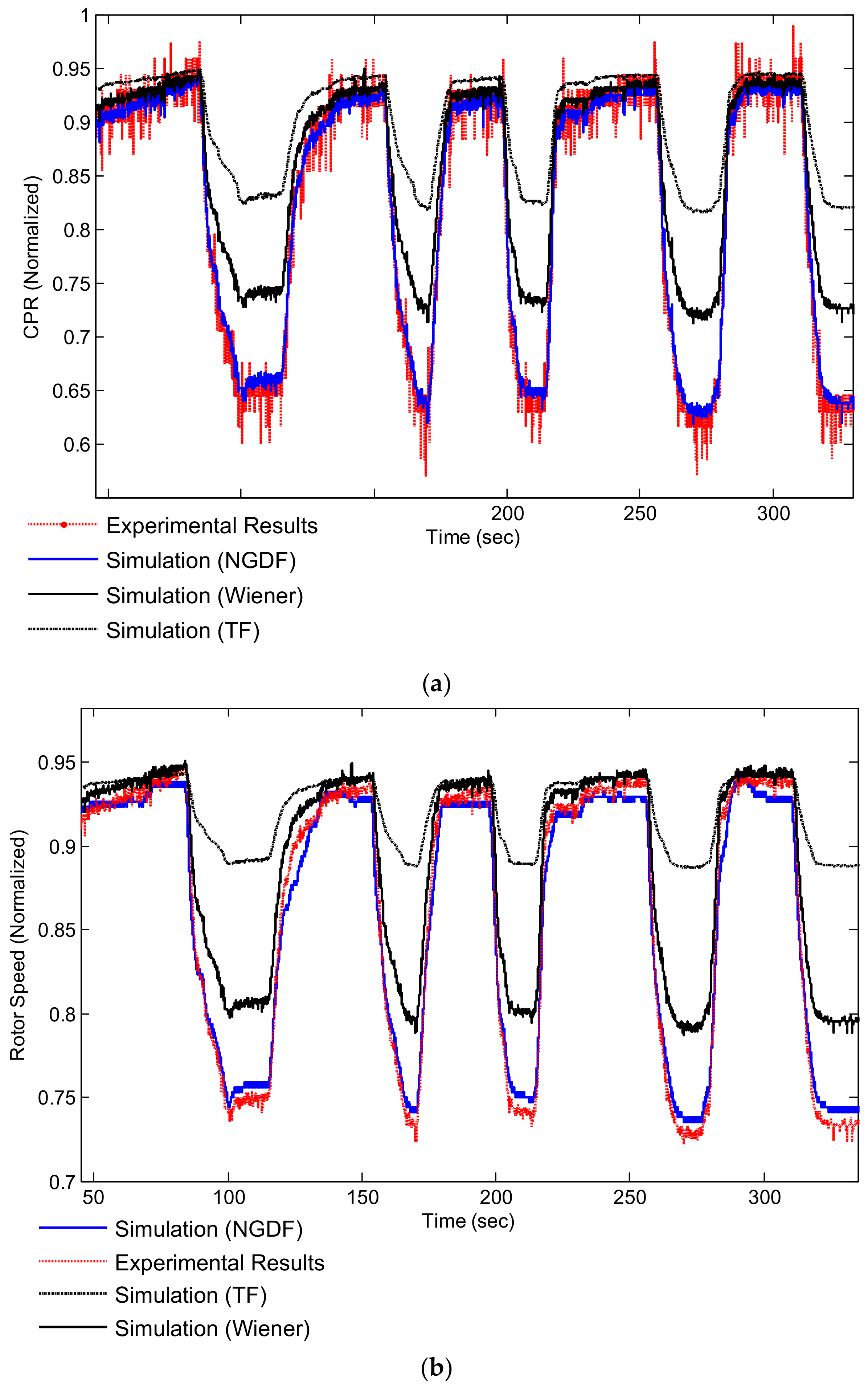
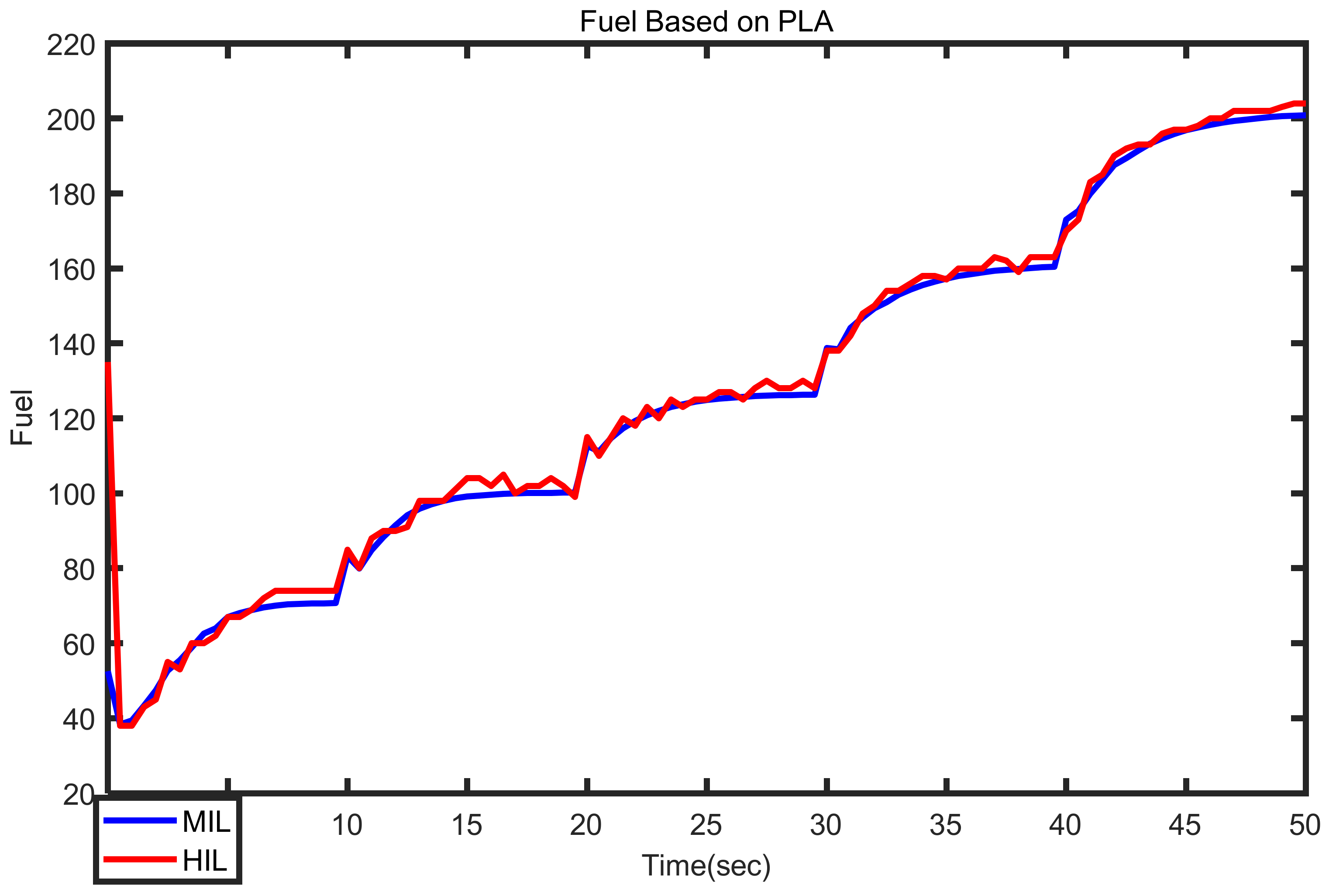
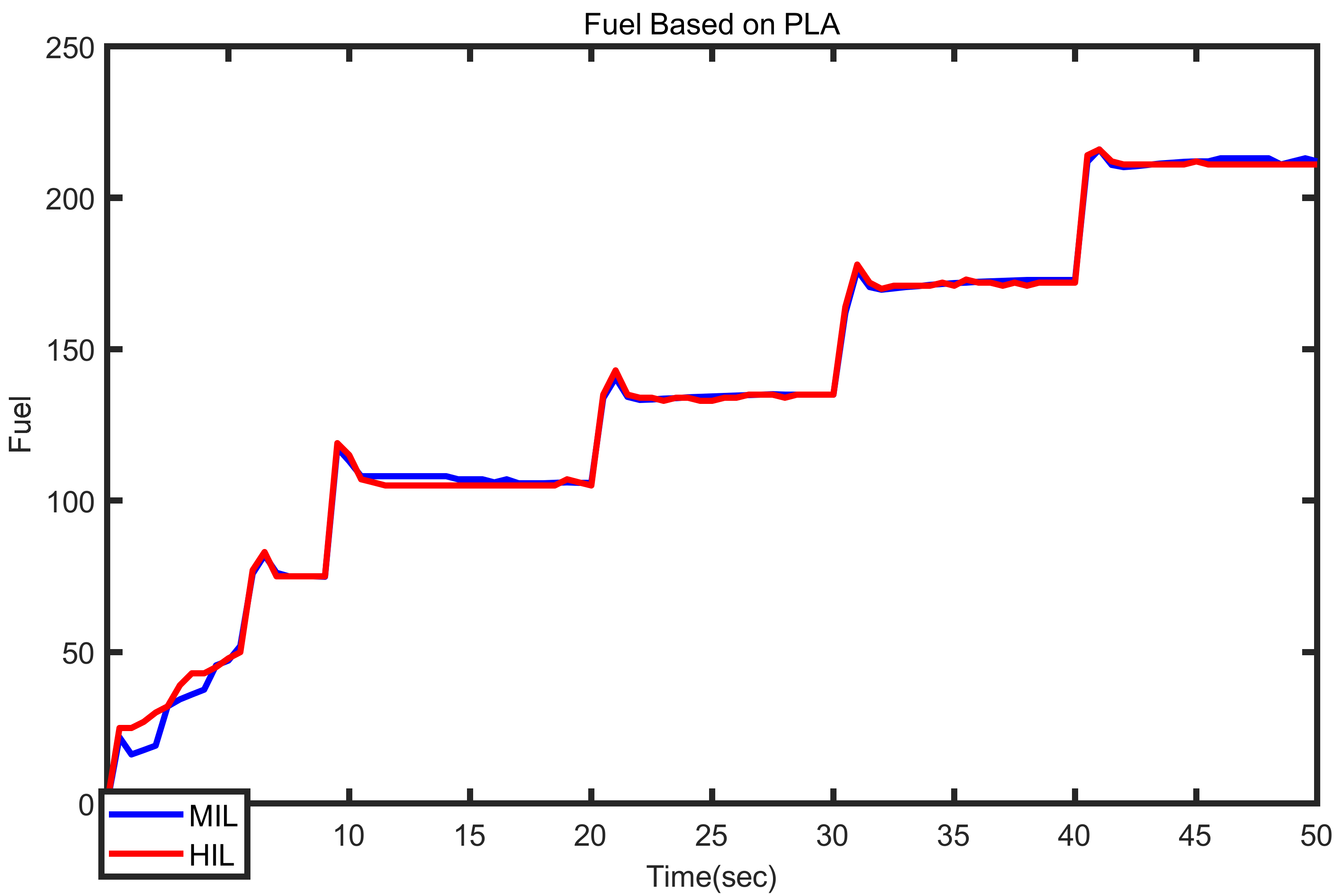
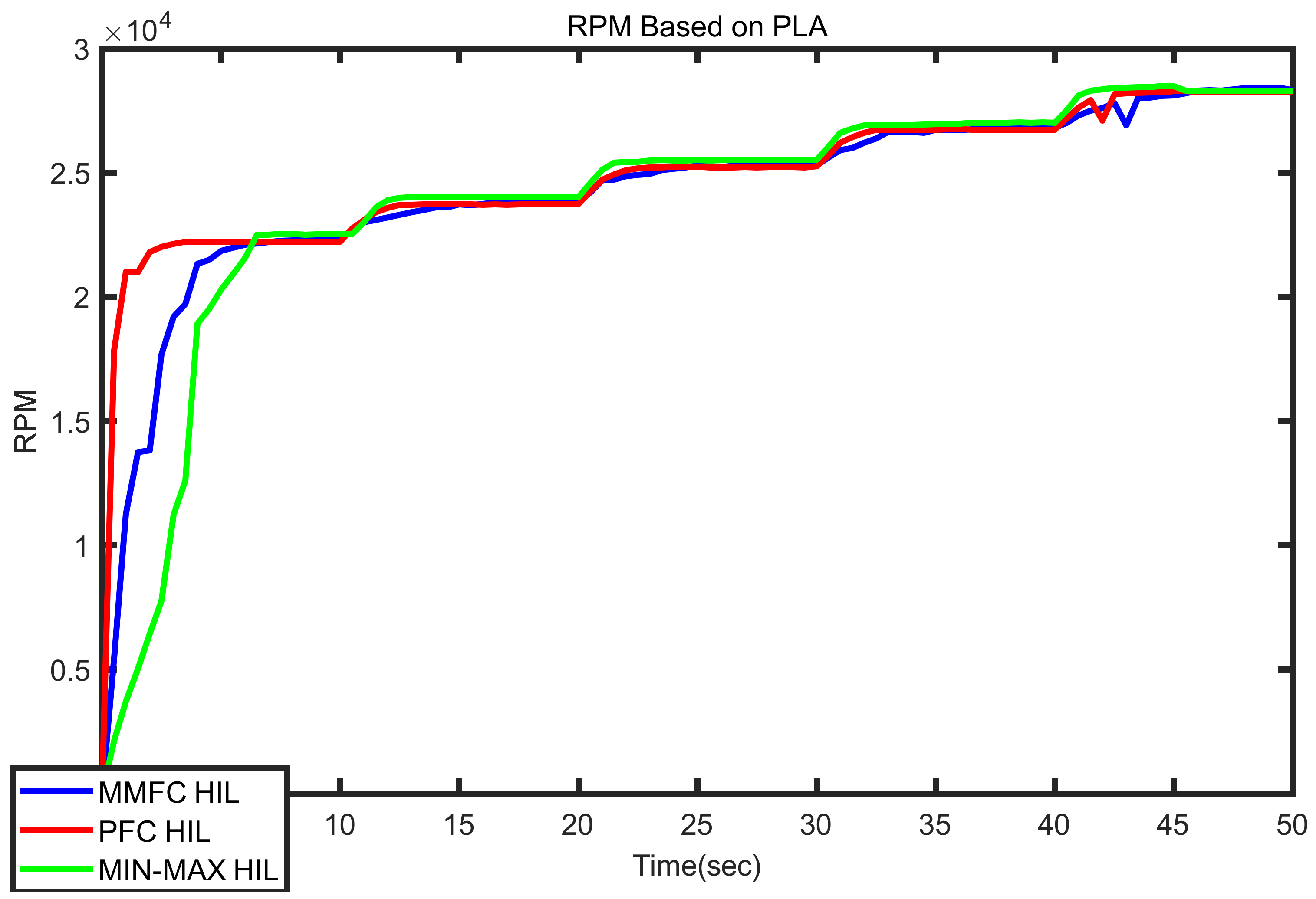
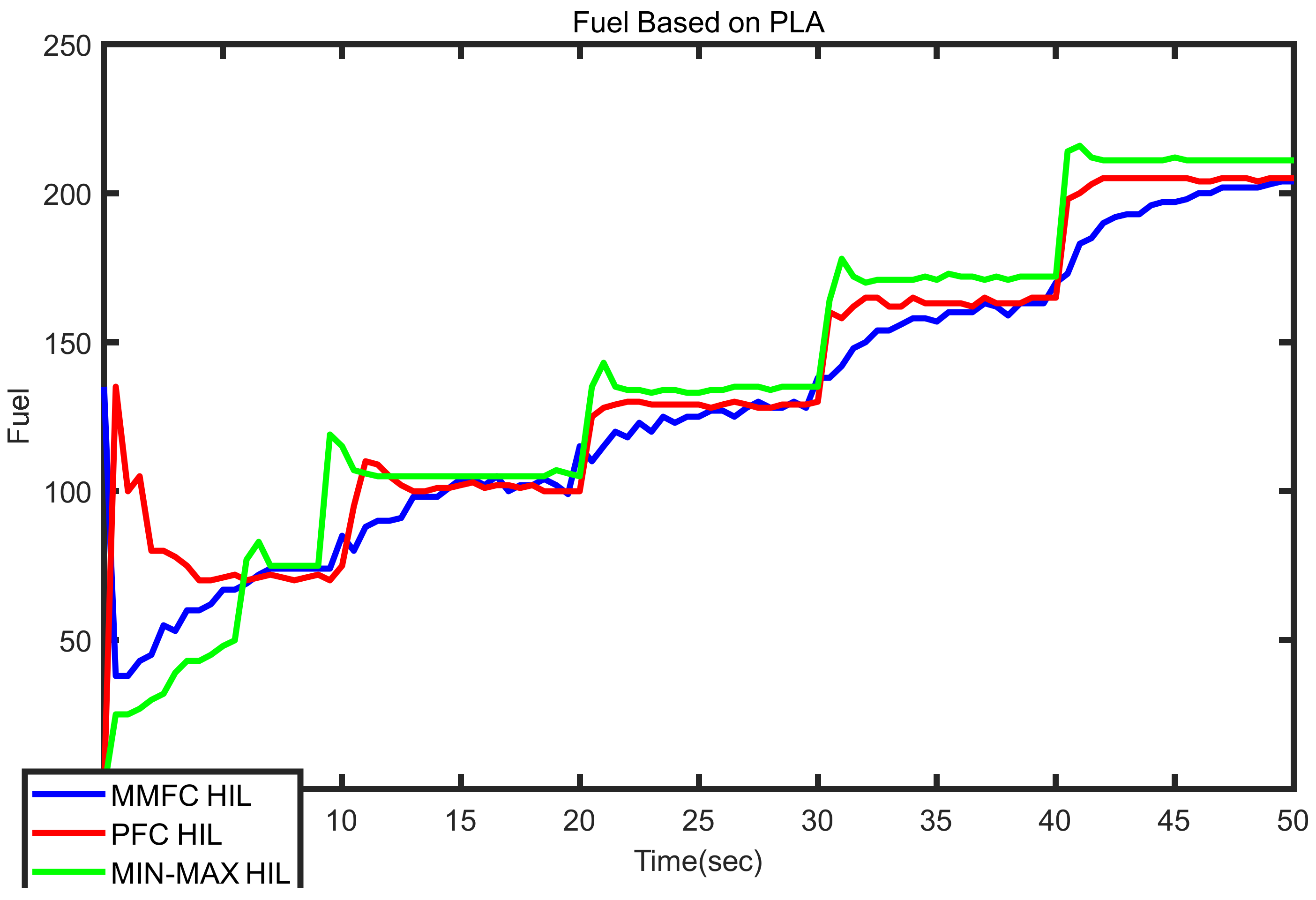
4. Results Analysis
5. Conclusions
- The pure fuzzy controller structure performs better in terms of pilot command tracking and, therefore, it is an appropriate candidate for control of the next generation of military aero-engines.
- The min–max Fuzzy controller structure performs better from fuel consumption and economic points of view that makes it a strong candidate for the next generation of civil aero-engines.
- Both fuzzy controller structures are feasible for real-world application and perform better than the conventional min–max controller in terms of fuel economy.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix A.1. Activating Codes for Calculating Time (Each Interrupt Overflow Led to Read Serial Port)
Appendix A.2. These Codes Activate Serial Port for Receive and Send Data to PC
Appendix A.3. Gaussian Input Membership Function
Appendix A.4. Defuzzification----Weighted Average Method
Appendix A.5. Sample PLA Membership Function
Appendix A.6. Input Membership Functions for Accdcc
References
- Lutambo, J.; Wang, J.; Yue, H.; Dimirovsky, G. Aircraft turbine engine control systems development: Historical Perspective. In Proceedings of the 34th Chinese Control Conference (CCC), Hangzhou, China, 28–30 July 2015. [Google Scholar]
- Jaw, L.C.; Mattingly, J.D. Aircraft Engine Controls; American Institute of Aeronautics and Astronautics: New York, NY, USA, 2009; ISBN 978-1-60086-705-7. [Google Scholar]
- Moir, I.; Seabridge, A. Engine Control Systems; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2008. [Google Scholar]
- Michels, K.; Klawonn, F.; Kruse, R.; Nürnberger, A. Fuzzy Control; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Silva, J.F.; Pinto, S.F. Power Electronics Handbook, 4th ed.; CRC Press: Boca Raton, FL, USA, 2018; pp. 1141–1220. [Google Scholar]
- Ghodekar, M.; Jadhav, S.P.; Jadhav, S.R. Design and simulation of Fuzzy and Fuzzy-PI controller for speed of Gas Turbine. In Proceedings of the International Conference on Automatic Control and Dynamic Optimization Techniques (ICACDOT), Pune, India, 9–10 September 2016. [Google Scholar]
- Mosaferin, R.; Fakharian, A. Fuzzy control for rotor speed of power plant gas turbine. In Proceedings of the 13th Iranian Conference on Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013. [Google Scholar]
- Karande, A.S.; Nigam, M.J.; Kadam, V. Design of a Fuzzy PID controller for a gas turbine power plant. In Proceedings of the Communication, Control and Intelligent Systems (CCIS), Mathura, India, 7–8 November 2015. [Google Scholar]
- Shete, S.A.; Jape, V.S. Design of a fuzzy modified model reference adaptive controller for a gas turbine rotor speed control using T-S fuzzy mechanism. In Proceedings of the International Conference on Technological Advancements in Power and Energy (TAP Energy), Kollam, India, 21–23 December 2017. [Google Scholar]
- Haijun, L.; Kai, Q. Design of master controller of 100kW micro gas turbine generator sets based on fuzzy-PID algorithm. In Proceedings of the 6th International Forum on Strategic Technology, Harbin, China, 22–24 August 2011. [Google Scholar]
- Bica, B.; Akat, G.; Chipperfield, A.J.; Fleming, P.J. Multiobjective design of a fuzzy controller for a gas turbine aero-engine. In Proceedings of the UKACC International Conference on Control 98 (Conf. Publ. No. 455), Swansea, UK, 1–4 September 1998. [Google Scholar]
- Balakrishnan, S.R.; Mishra, S.K.; Sundararajan, V.; Damodaran, K.A. Fuzzy Computing for Control of Aero Gas Turbine Engines. Def. Sci. J. 1994, 44, 295–304. [Google Scholar] [CrossRef][Green Version]
- Chipperfield, A.J.; Bica, B.; Fleming, P.J. Fuzzy scheduling control of a gas turbine aero-engine: A multiobjective approach. IEEE Trans. Ind. Electron. 2002, 49, 536–548. [Google Scholar] [CrossRef]
- Martucci, A.; Volponi, A.J. Fuzzy Fuel Flow Selection Logic for a Real Time Embedded Full Authority Digital Engine Control. ASME J. Eng. Gas Turbine Power 2003, 125, 909–917. [Google Scholar] [CrossRef]
- Richter, H. Advanced Control of Turbofan Engines; Springer: New York, NY, USA, 2012; ISBN 978-1-4614-1171-0. [Google Scholar] [CrossRef]
- Hadroug, N.; Hafaifa, A.; Guemana, M.; Kouzou, A.; Salam, A.; Chaibet, A. Heavy duty gas turbine monitoring based on adaptive neuro-fuzzy inference system: Speed and exhaust temperature control. Math. Ind. Case Stud. 2017, 8, 8. [Google Scholar] [CrossRef]
- Oglah, A.A.; Mohammed, A.J. Design of an Interval Fuzzy Type-2- PID Controller for a Gas Turbine Power Plant. Am. Sci. Res. J. Eng. Technol. Sci. (ASRJETS) 2018, 44, 155–169. [Google Scholar]
- Jafari, S.; Nikolaidis, T. Turbojet engine industrial min-max controller performance improvement using fuzzy norms. Electronics 2018, 7, 314. [Google Scholar] [CrossRef]
- Guolian, H.; Linjuan, G.; Congzhi, H.; Jianhua, Z. Fuzzy modeling and fast model predictive control of gas turbine system. Energy 2020, 200, 117465. [Google Scholar]
- Available online: http://www.aviationchief.com/turbine-engines.html (accessed on 13 February 2021).
- Bazazzadeh, M.; Badihi, H.; Shahriari, A. Gas Turbine Engine Control Design Using Fuzzy Logic and Neural Networks. Int. J. Aerosp. Eng. 2011, 2011, 156796. [Google Scholar] [CrossRef]
- Spang, H.A., III; Brown, H. Control of jet engines. Control Eng. Pract. 1999, 7, 1043–1059. [Google Scholar] [CrossRef]
- Kreiner, A.; Lietzau, K. The Use of Onboard Real-Time Models for Jet Engine Control; MTU Aero Engines: Munich, Germany, 2002. [Google Scholar]
- Monika, S.; Anuradha, T. Design and Implementation of Traffic Density Controller using Wireless Communications. Int. J. Innov. Technol. Explor. Eng. (IJITEE) 2019, 8. [Google Scholar]
- Altaf, K.; Akhtar, A.; Rehman, S.-U.; Iqbal, J. Design, implementation and real-time digital control of a cart-mounted inverted pendulum using Atmel AVR Microcontroller. In Proceedings of the 6th WSEAS International Conference on Signal Processing, Robotics and Automation, Corfu Island, Greece, 16–19 February 2007.
- Wang, W.; Xia, L. Design and implementation of a control system using AVR microcontroller. In Proceedings of the 2009 International Conference on Image Analysis and Signal Processing, Linhai, China, 11–12 April 2009. [Google Scholar]
- Nhivekar, G.S.; Nirmale, S.S.; Mudholker, R.R. Implementation of fuzzy logic control algorithm in embedded microcomputers for dedicated application. Int. J. Eng. Sci. Technol. 2011, 3, 276–283. [Google Scholar] [CrossRef]
- Banerji, S. Design and Implementation of an Unmanned Vehicle using a GSM Network with Microcontrollers. Int. J. Sci. Eng. Technol. Res. 2013, 2. [Google Scholar]
- Gupta, R. Body Control Unit Using the Implementation of AVR Microcontroller. Int. J. Eng. Res. Technol. (IJERT) 2013, 2. [Google Scholar]
- Shaikh Yusuf, H.; Khan, A.R.; Behere, S.H. AVR Microcontroller Based Data Acquisition System for Laboratory Experiments. Adv. Appl. Sci. Res. 2012, 3, 208–215. [Google Scholar]
- Duman, E.; Can, H.; Akin, E. Evaluating of a Fuzzy Chip by Hardware-in-the-Loop (HIL) Simulation. Int. Rev. Comput. Softw. 2008, 3. [Google Scholar]
- Valencia, A.; Linares, N.; Amaya, D. Control system using HIL, PID and Fuzzy Logic with Rapid Prototyping. Int. J. Appl. Eng. Res. 2016, 11, 5480–5487. [Google Scholar]
- Akbatı, O.; Üzgün, H.D.; Akkaya, S. Hardware-in-the-loop simulation and implementation of a fuzzy logic controller with FPGA: Case study of a magnetic levitation system. Trans. Inst. Meas. Control. 2019, 41, 2150–2159. [Google Scholar] [CrossRef]
- Amal, S.; Vishnu, V.; Chacko, R.V.; Ghugal, S.; Mengaji, P.; Karle, U. HIL simulation and controller prototyping of EV/HEV systems using multi-core xEV Real time Simulator. In Proceedings of the 2017 IEEE Transportation Electrification Conference (ITEC-India), Pune, India, 13–15 December 2017. [Google Scholar]
- Chu, L.; Chao, L. Hardware-in-the-loop Simulation of Traction Control Algorithm Based on Fuzzy PID. Energy Procedia 2012, 16, 1685–1692. [Google Scholar] [CrossRef]
- Kumar, R.S.; Ganapathy, V. Hardware in the Loop Simulation and Implementation of Fuzzy Sliding Mode Control of Induction Motor Based on FPGA. Int. J. Innov. Comput. Inf. Control ICIC 2015, 11, 2215–2228. [Google Scholar]
- Rasaienia, A. Hardware in the Loop (HIL) Analysis of Fuzzy Controller for Ball and Beam System. Majlesi J. Mechatron. Syst. 2016, 5, 29–34. [Google Scholar]
- Lichtsinder, M.; Levy, Y. Jet engine model for control and real-time simulation. J. Eng. Gas Turbine Power 2006, 128, 745–753. [Google Scholar] [CrossRef]
- Saravanamuttoo, H.I.H.; MacIsaac, M.S. An overview of engine dynamic response and mathematical modelling concepts. In Engine Handling, Proceedings of the 60th Symposium of the AGARD Propulsion and Energetics Panel, Golden Coast Motel, Marathon, Attika, Greece, 11–14 October 1982; AGARD: Neuilly-sur-Seine, France, 1983. [Google Scholar]
- Kulikov, G.G.; Thompson, H.A. Dynamic Modeling of Gas Turbines; Industrial Control Center: Glasgow, UK, 2003. [Google Scholar]
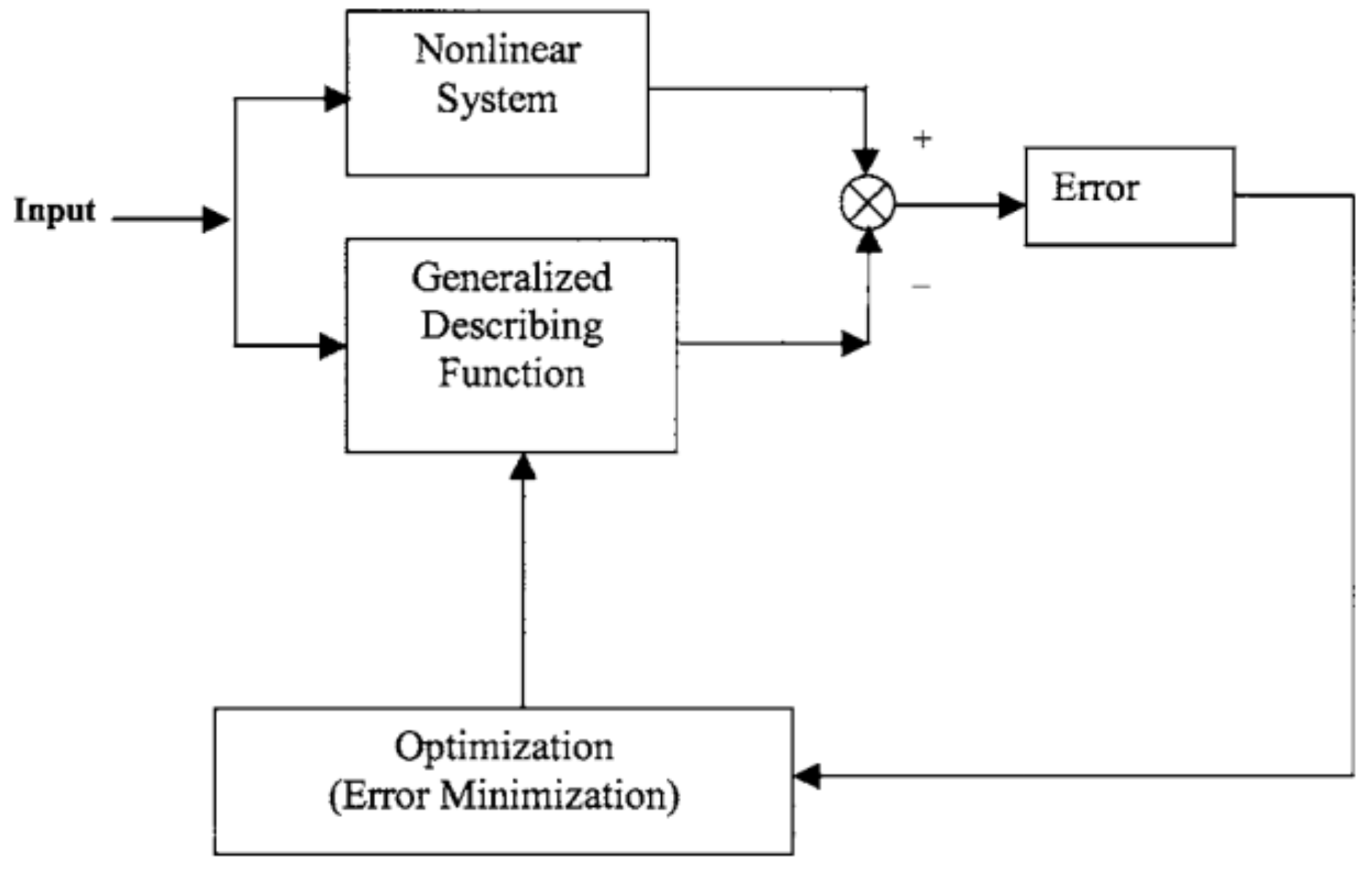
- Wills, A.; Ninness, B. Generalised Hammerstein-Wiener system estimation and a benchmark application. Control Eng. Pract. 2012, 20, 1097–1108. [Google Scholar] [CrossRef]
- Paduart, J.; Lauwers, L.; Pintelon, R.; Schoukens, J. Identification of a Wiener-Hammerstein system using the polynomial nonlinear state space approach. Control Eng. Pract. 2012, 20, 1133–1139. [Google Scholar] [CrossRef]
- Available online: http://www.leteckemotory.cz/motory/microturbo (accessed on 13 February 2021).
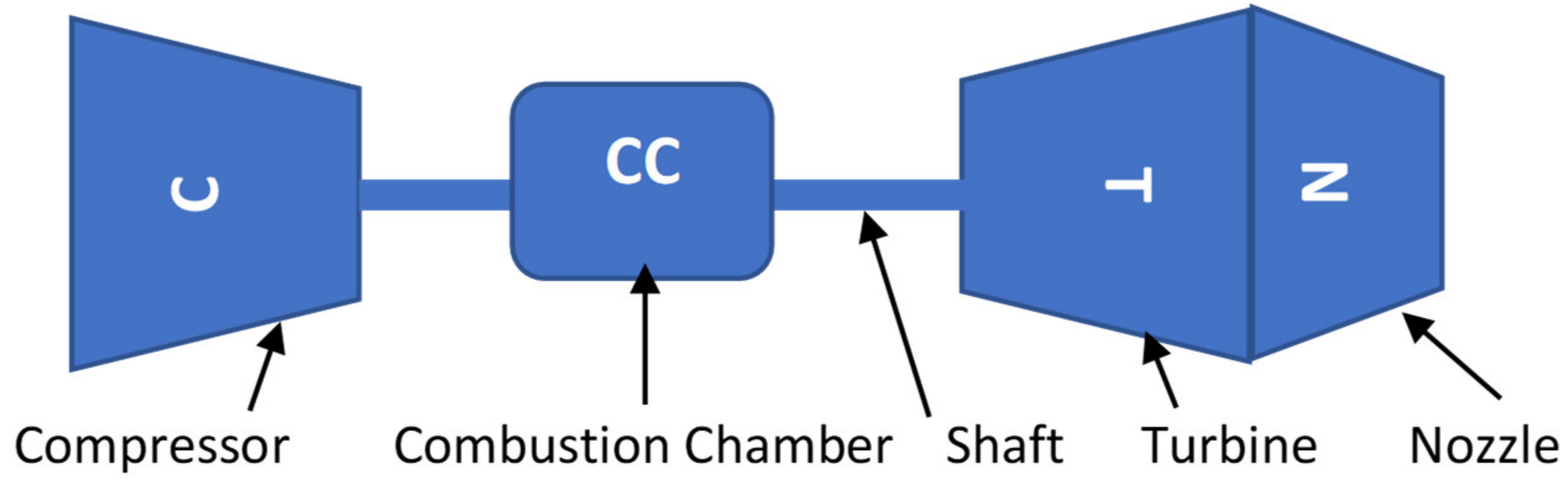





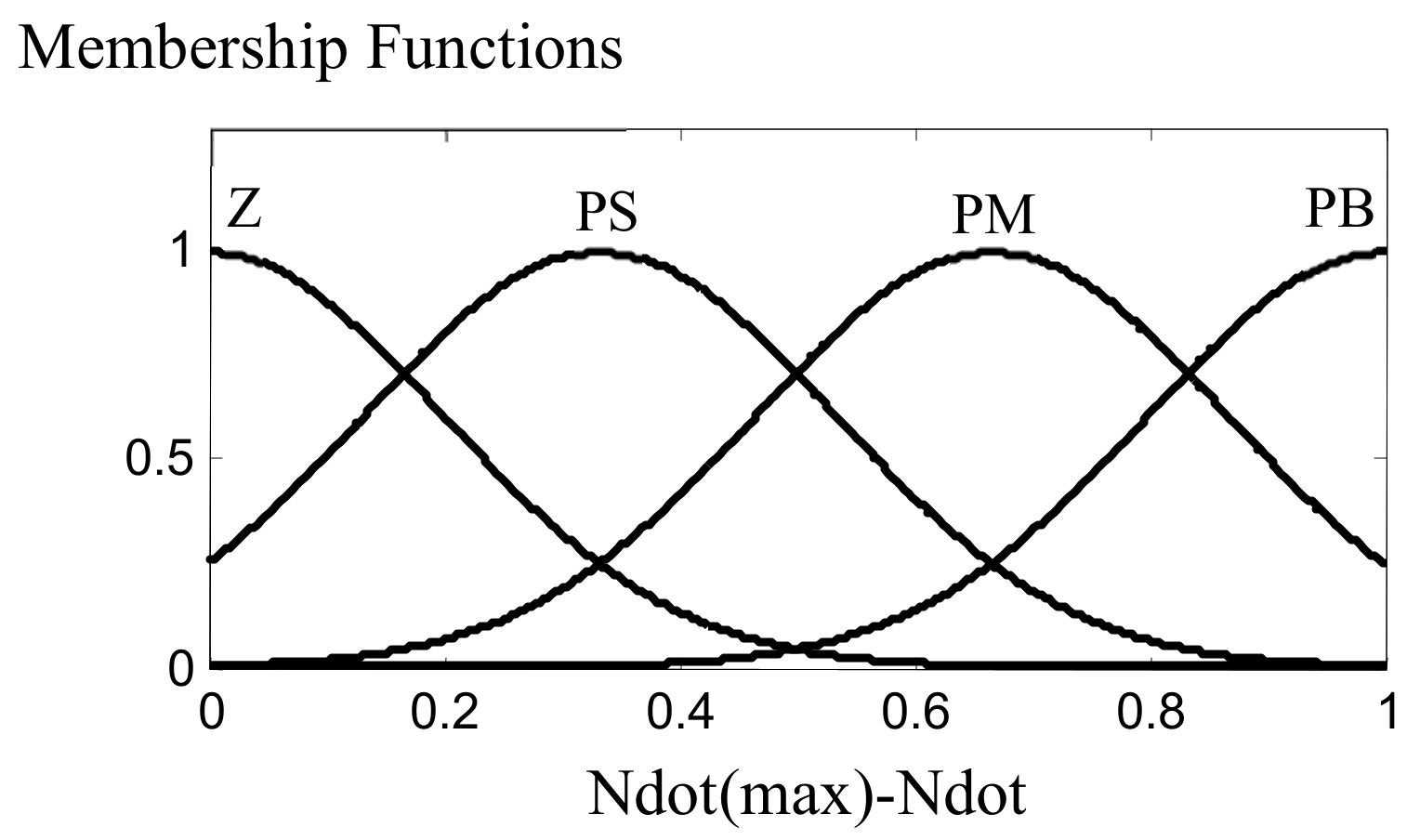
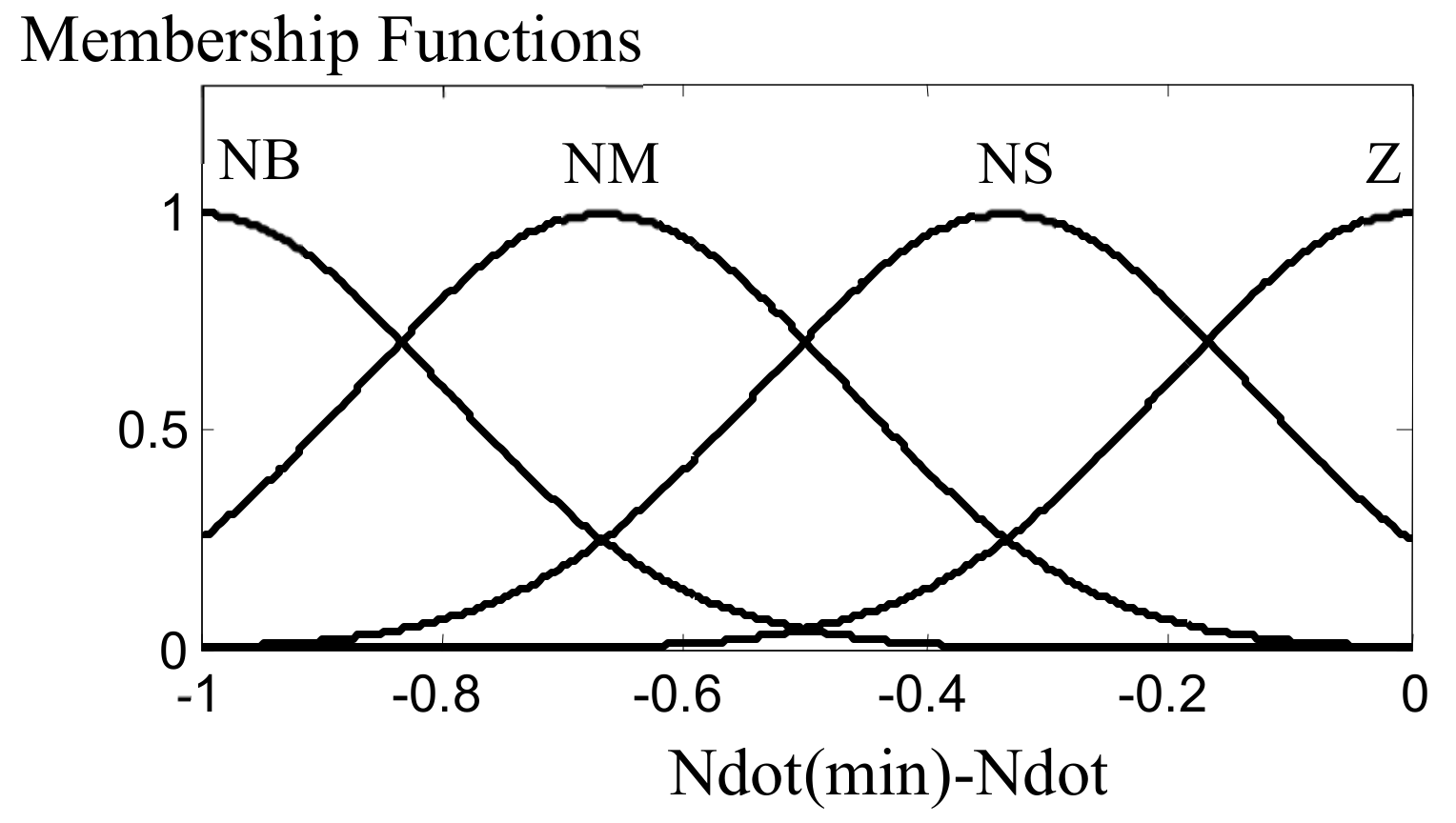






| Paper Title | Main Achievement | Publication Year |
|---|---|---|
| Fuzzy Computing for Control of Aero Gas Turbine Engines | Certain stipulations, rules, and fuzzy logic are suggested for the control of a single spool aero gas turbine (pure fuzzy) | 1994 [12] |
| Fuzzy Scheduling Control of a Gas Turbine Aero-Engine: A Multi-objective Approach | Combination of fuzzy logic and evolutionary algorithms (EA) to refine the control performance and to increase the flexibility of GTEs (pure fuzzy) | 2002 [13] |
| Fuzzy Fuel Flow Selection Logic for a Real-Time Embedded Full Authority Digital Engine Control | In order to achieve proper performance, Typical control loops chosen by min–max theory are replaced by fuzzy logic loops (min–max fuzzy) | 2003 [14] |
| Advanced Control of Turbofan Engines | Different control loops for turbofan engine control modes are designed and analyzed based on industrial min–max strategy and improved by fuzzy rules with respect to the implementation considerations (min–max fuzzy) | 2012 [15] |
| Heavy-duty gas turbine monitoring based on adaptive neuro-fuzzy inference system: speed and exhaust temperature control | Using an adaptive neuro-fuzzy inference system (ANFIS) to maintain turbine operation at optimum performance. The results obtained, based on the use of the Rowen model, show the effectiveness of the proposed system (pure fuzzy) | 2017 [16] |
| Design of an Interval Fuzzy Type-2 PID Controller for a Gas Turbine Power Plant | The selected model is Rowen’s model to present the mechanical behavior of the gas turbine, the main goal is aimed to improve the system dynamic performance, all gains for conventional PID and interval fuzzy type-2 PID are tuned using social spider optimization(SSO) technique, and showed the performance improvement for interval fuzzy type-2 PID controller in comparison with conventional PID via simulation (min–max fuzzy) | 2018 [17] |
| Turbojet engine industrial min–max controller performance improvement using fuzzy norms | The minimum and maximum functions in the industrial min–max strategy are replaced with the different fuzzy norms to improve the performance of the GTE FADEC (min–max fuzzy) | 2018 [18] |
| Fuzzy modeling and fast model predictive control of gas turbine system | For achieving high tracking performance and disturbance rejection ability within less settling time under various operating conditions, an improved fuzzy modeling approach and corresponding fast model predictive control algorithm were introduced and applied to a gas turbine system (pure fuzzy) | 2020 [19] |
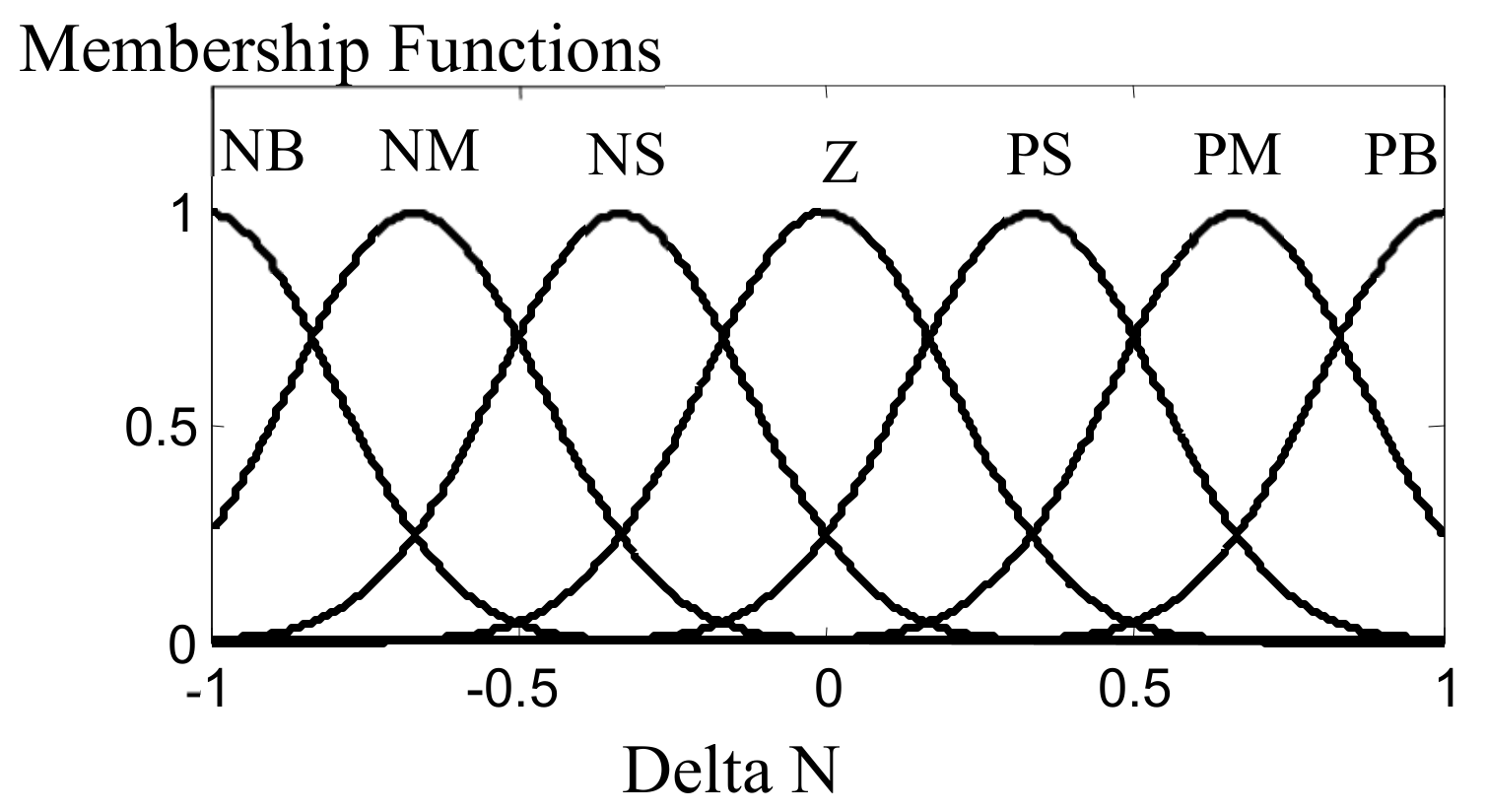
| Linguistic Variables | Symbol | Linguistic Variable | Symbol |
|---|---|---|---|
| Negative Big | NB | Positive Big | PB |
| Negative Medium | NM | Positive Medium | PM |
| Negative Small | NS | Positive Small | PS |
| Zero | Z |
| ΔNdot | Z | PS | PM | PB | NS | NM | NB | |
|---|---|---|---|---|---|---|---|---|
| ΔN | ||||||||
| Z | Z | PS | PS | PS | NS | NS | NS | |
| PS | NS | Z | PS | PS | NM | NM | NM | |
| PM | NM | NS | Z | PM | NM | NM | NB | |
| PB | NB | NM | NS | Z | NB | NB | NB | |
| NS | PS | PS | PM | PM | Z | NS | NS | |
| NM | PM | PM | PM | PB | PS | Z | NM | |
| NB | PB | PB | PB | PB | PM | PS | Z | |
| ΔN | NB | NM | NS | Z | PS | PM | PB |
| FMF (Transient Fuel Flow) | NB | NM | NS | Z | PS | PM | PB |
| ΔN = POS | ΔN = NEG | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Z | PS | PM | PB | Z | NS | NM | NB | ||
| FMF (Acc.) | Z | PS | PM | PB | FMF (Dec.) | Z | NS | NM | NB |
| Mean Response Time (s) | Fuel Consumption (kg/s) | |
|---|---|---|
| Pure Fuzzy Controller | 4.01 | 7.05 |
| Min–Max Fuzzy Controller | 4.18 | 6.76 |
| Min–Max Controller | 3.95 | 7.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY-NC-ND) license (http://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Mohammadi Doulabi Fard, S.J.; Jafari, S. Fuzzy Controller Structures Investigation for Future Gas Turbine Aero-Engines. Int. J. Turbomach. Propuls. Power 2021, 6, 2. https://doi.org/10.3390/ijtpp6010002
Mohammadi Doulabi Fard SJ, Jafari S. Fuzzy Controller Structures Investigation for Future Gas Turbine Aero-Engines. International Journal of Turbomachinery, Propulsion and Power. 2021; 6(1):2. https://doi.org/10.3390/ijtpp6010002
Chicago/Turabian StyleMohammadi Doulabi Fard, Seyed Jalal, and Soheil Jafari. 2021. "Fuzzy Controller Structures Investigation for Future Gas Turbine Aero-Engines" International Journal of Turbomachinery, Propulsion and Power 6, no. 1: 2. https://doi.org/10.3390/ijtpp6010002
APA StyleMohammadi Doulabi Fard, S. J., & Jafari, S. (2021). Fuzzy Controller Structures Investigation for Future Gas Turbine Aero-Engines. International Journal of Turbomachinery, Propulsion and Power, 6(1), 2. https://doi.org/10.3390/ijtpp6010002






