Thermal Performance Evaluation in Gas Turbine Aero Engines Accessory Gearbox

Abstract

This paper presents a methodological approach for mathematical modelling and physics-based analysis of accessory gearbox (AGB) thermal behavior in gas turbine aero engines. The AGB structure, as one of the main sources of heat in gas turbine aero engines, is firstly described and its power losses will be divided into load-dependent and no-load dependent parts. Different mechanisms of heat generation are then identified and formulated to develop a toolbox for calculation of the churning, sliding friction, and rolling friction losses between contact surfaces of the AGB. The developed tool is also capable of calculating the heat loss mechanisms in different elements of the AGB, such as gears, bearings, and seals. The generated model is used to simulate and analyze the AGB thermal performance in the different flight phases in a typical flight mission, where the obtained results are validated against publicly available data. The analysis of the results confirms the effectiveness of the proposed method to estimate the heat loss values in the AGBs of gas turbine aero engines and to predict the thermal loads of the AGB in different flight phases. The developed tool enables the gas turbine thermal management system designers to deal with the generated heats effectively and in an optimal way.

1. Introduction

Gas turbine engine (GTE) manufactures are facing huge challenges in developing the next generation of GTEs to meet all requirements, due to the increase of fuel price, power and efficiency demands, and limitations and restrictions set by governments and organizations (e.g., the Advisory Council for Aviation Research and Innovation in Europe has a target of a 75% reduction in CO₂ emissions and a 90% reduction of NOx emissions by 2050) [1,2]. One of these challenges is to deal with huge thermal loads generated by advanced GTEs components. The engine thermal management system (TMS) should be able to manage these heat loads in an optimal feature to get a safe and reliable operation for the engine. In other words, the main duty of the GTE TMS is to use engine heat sinks (oil, fuel, and air) to manage the thermal loads generated by engine heat sources (gearboxes, bearings, generators, pumps, etc.). There are a few studies in the literature focusing on the thermal management challenges and potential solutions for GTEs. An analytic review on this topic has recently been done by the authors [3], in which the different aspects, current challenges, and potential solutions for the TMS design procedure in new and next generation of GTEs were studied in detail. One of the main challenges in this field is the lack of physics-based models for thermal loads calculation in different TMS components to enable researchers and manufacturers to predict and analyze the thermal loads in each component at different flight phases, based on the geometry, mechanical loads, input and output powers, and other design parameters. This kind of model will enable TMS designers to do a precise sensitive analysis on design and operational parameters, as well as to get a reliable vision about the next generation of TMSs for GTEs [4].

The gearbox is one of the most important elements in gas turbine TMS as a noticeable amount of heat load is generated by this component [5]. So, it is significant to predict its power loss during the design phase to improve the mechanical system design through different perspectives. For instance, reducing gear operating temperature will contribute to better lubrication, less oil degradation, and improving the gear lifetime by improving the resistance to scuffing and micro-pitting [6].

Therefore, this paper will focus on developing a physics-based tool to calculate the thermal load generated by different elements of the accessory gearbox (AGB) in gas turbine aero engines.

2. Accessory Gearbox Heat Loss Mechanisms

The accessory gearbox drives the accessories of the engine like generator, fuel and oil pumps, hydraulic pumps, etc. So, it is an essential element for the operation of the engine or the aircraft on which it is mounted. The power loss mechanisms inside gearbox can be separated into two groups: no-load dependent losses and load-dependent losses. No-load dependent losses include churning losses caused by gears, seals, and bearings, and load-dependent losses are frictional losses caused by gears and bearings [7].

No-load dependent losses mainly consist of Windage and churning power losses, the churning losses are one of the main power losses especially at high oil fill level and rotational speeds [8]. This type of power loss occurs between gears even without torque transmission in the rotation of mechanical components and it is related to the density, viscosity, and immersion depth of the components on a sump lubricated gearbox, and it also depends on the internal design of gearbox casing and operating conditions. No-load losses of rolling bearings mainly depend on the size, type, and bearing arrangement, immersion depth, and lubricant viscosity [9].

Load-dependent power losses occur because of contacts between the gears’ teeth during power transmitting, which are mainly depends on friction coefficient, transmitted power, and sliding velocity in the contact area between teeth [9].

The dependence of no-load losses on the lubricant viscosity and the frictional losses is influenced by the oil characteristics and the ability to provide low friction coefficient and lubricant film. This is important to increase gearbox efficiency and to enhance gears and bearings life [10].

Most studies have focused on power loss, and gear efficiency is related to the planetary gear system, power gearbox (PGB). Some of these studies have focused on spin power losses, but most of the studies have investigated mechanical losses. These studies provide a significant database for predicting power loss in gears, but it considers only a single gear pair. The review of these studies discloses the need for a model can predict the power loss in the AGB for typical aero-engine.

The accessory gearbox consists of sets of spur gears connected to each other, each gear drives one element, such as the generator, or pump. The power losses can be divided into load-dependent and no-load dependent according to their mechanical component and their relation to transmitted torque that generates them [3]. In this way, the total power loss (PL) can be subdivided into no-load and load dependent related to gears ($P{L}_{G0}$ + $P{L}_G$), bearings ($P{L}_{B0}$ + $P{L}_B$), and no-load dependent for seals ($P{L}_{S0}$).

The total power losses in the accessory gearbox are the sum of all sources of losses in each contact pairs and single elements inside generated by load and no-load losses equal to the heat evacuation from AGB to the environment [9].

$$PL=P{L}_{G0}+P{L}_G+P{L}_{B0}+P{L}_B+P{L}_{S0}=Q_{AGB}$$

(1)

The share of power losses between different sources strongly depends on the gearbox design configuration.

3. Mathematical Modelling of Heat Losses

The physics-based model for heat loss calculation is described in this section.

3.1. No-Load Dependent Losses

Depending on the input speed and power, gearbox design and lubricant characteristics, the no-load dependent losses are a very important source of heat dissipation within an accessory gearbox. Due to the complicated design of the AGB, it is not straightforward to generate a model that consists of a general formulation to assess this mechanism of power loss. The main objective of this study is to accurately predict the power losses considering friction torque loss in the meshing gears.

3.1.1. Gears Churning Loss

In recent decades, many studies have investigated the influence of the energy loss mechanism and parameters on power loss in the gearbox. Boness (1989) [10] investigated the influence of diameter and oil fill level on a disk and drove an empirical formulation through experiments. Terekhov (1975) [11] studied single meshing gears rotating immersed in a fluid and developed an empirical equation using a dimensionless moment coefficient from several experiments. Höhn et al. [12] developed an empirical formation through experimental work, and concluded that reducing oil level can reduce the churning loss but not the gear temperature. Gear churning losses is the main source of power loss for splash lubricated gears, which is generated by rotating gears totally or partly immersed in fluid lubrication. Changenet et al. [13] developed a mathematical model for calculating the gear churning loss based on the series of experimental tests, and carried out a comprehensive dimensional analysis to tune the model. In this paper, this model is selected, since it overcomes some of the limitations of the previous research in gear churning losses from accuracy, validity range, and reliability points of view. The model proposed by Changenet et al. [13] depends on the regime of the flow and Reynolds number that defines the laminar-turbulent transition determined by experimental results. It is very difficult to determine the transition of the laminar-turbulent regime inside an oil sump, due to the infinite combination parameters and design features [14].

Gear churning power loss is mainly responsible for no-load dependent losses and depends on rotational speed, immersion area and depth, gear geometry, lubricant density, and viscosity, as shown in Equation (2):

$$P{L}_{G0}=\frac{1}{2} \rho {\mathsf{\Omega }}^{\mathbf{3}} A_i{R}^3{C}_m$$

(2)

where $\rho$ is the lubricant density,$\mathsf{\Omega }$ is the rotational speed in rad/s,$A_i$ is immersion surface area, $R=\frac{D}{2}$ is the pitch radius, and the $C_m$ expression has been determined depending on the flow regime:

For $Rec=\frac{\Omega .Rpb}{\upsilon }<6000$

$$C_m=1.36\left({\left(\frac{ h}{D}\right)}^{0.45}·{\left(\frac{V_{oil}}{D^3}\right)}^{0.1}· F{r}^{-0.21}·R{e}^{-0.21}\right)$$

(3)

For $Rec=\frac{\mathsf{\Omega }.rb}{\upsilon }>9000$

$$C_m=3.644·\left({\left(\frac{ h}{D}\right)}^{0.1}·{\left(\frac{b}{D}\right)}^{0.85}·{\left(\frac{V_{oil}}{D^3}\right)}^{-0.35}· F{r}^{-0.88}\right)$$

(4)

where $h$ is the immersion depth,$D$ is the gear pitch diameter,$V_{oil}$ is the oil volume,$\upsilon$ is the lubricant kinematic viscosity,$b$ is the tooth face width,$Fr=$ Froude number, depending on gear parameters $=\frac{{\mathsf{\Omega }}^{\mathbf{2}}R}{g}$, $Re=$ Reynolds number $=\frac{{\mathsf{\Omega }\mathrm{R}}^2}{\upsilon }$.

It should be mentioned that this formulation and corresponding flow regimes are valid for the steady-state operating condition.

3.1.2. Bearings Churning Loss

The bearing churning losses are mainly depending on the bearing geometry and type, speed and lubricant viscosity.

$$P{L}_{B0}=\mathsf{\Omega } .\left(f_0 \times {10}^{-7}·{\left(n ·{\mu }_{oil}\right)}^{2/3}·d_m{}^3\right)\times {10}^{-3}$$

(5)

where $f_0$ is bearing coefficients of loss,${\mu }_{oil}$ is the dynamic viscosity,$n$ is the rotation speed, and $d_m$ is the mean diameter.

3.1.3. Seals Churning Loss

The seal churning losses are mainly occurring between seal tip and shaft in the contact zone. However, many studies have been investigated on seals losses but this phenomenon still not well understood, due to small of the contact zone and difficult to parametrize. With regard to [15,16], the seal losses mainly depend on seal diameter and shaft speed. Equation (5) is used to predict the seal losses, but this formula does not consider the oil viscosity:

$$P_{Seal}=7.69 \times {10}^{-6} ·d_i{}^2 ·n$$

(6)

where $d_i$ is the shaft diameter.

3.2. Load Dependent Losses

Load dependent losses include gear mesh loss and power loss in bearings that could be calculated as follows:

3.2.1. Power Loss in Meshing Gears

Generally, the power loss due to gear mesh is determined by the normal load, relative rolling and sliding between lubricated meshing gears. Friction interaction between meshing gears must be considered as it is influenced by all characterized elements. The main contributors to power loss are the friction coefficient and load distribution along the line of contact of meshing gear [3]. This study will consider the friction coefficient and load distribution constant along the line of contact. Ohlendorf [17], has introduced the equation to calculate the load-dependent for spur gears.

$$P{L}_G=P_{in }·{\mathsf{\mu }}_m· H_v$$

(7)

where ${\mathsf{\mu }}_m$: mean friction coefficient along the path of the contact [18], $H_v$: is the gear loss factor. $P_{in }$: is the power input.

3.2.2. Power Loss in Bearings

According to Wimmer et al. [16], the bearings load dependent loss mainly depends on the load applied, mean diameter, and friction coefficient of the bearings:

$$P{L}_B=\frac{\pi }{30} ·n ·\left(\sqrt{F_R^2+F_A^2} · f_{1 } ·d_m\right)$$

(8)

where $F_R+F_A$ is the radial and axial load applied, $f_{1 }$ is the bearings friction coefficient, $d_m$ is the mean diameter.

Finally, by adding the values of Equations (2), (5)–(8) and putting them in Equation (1), the total heat loss in the accessory gearbox will be calculated.

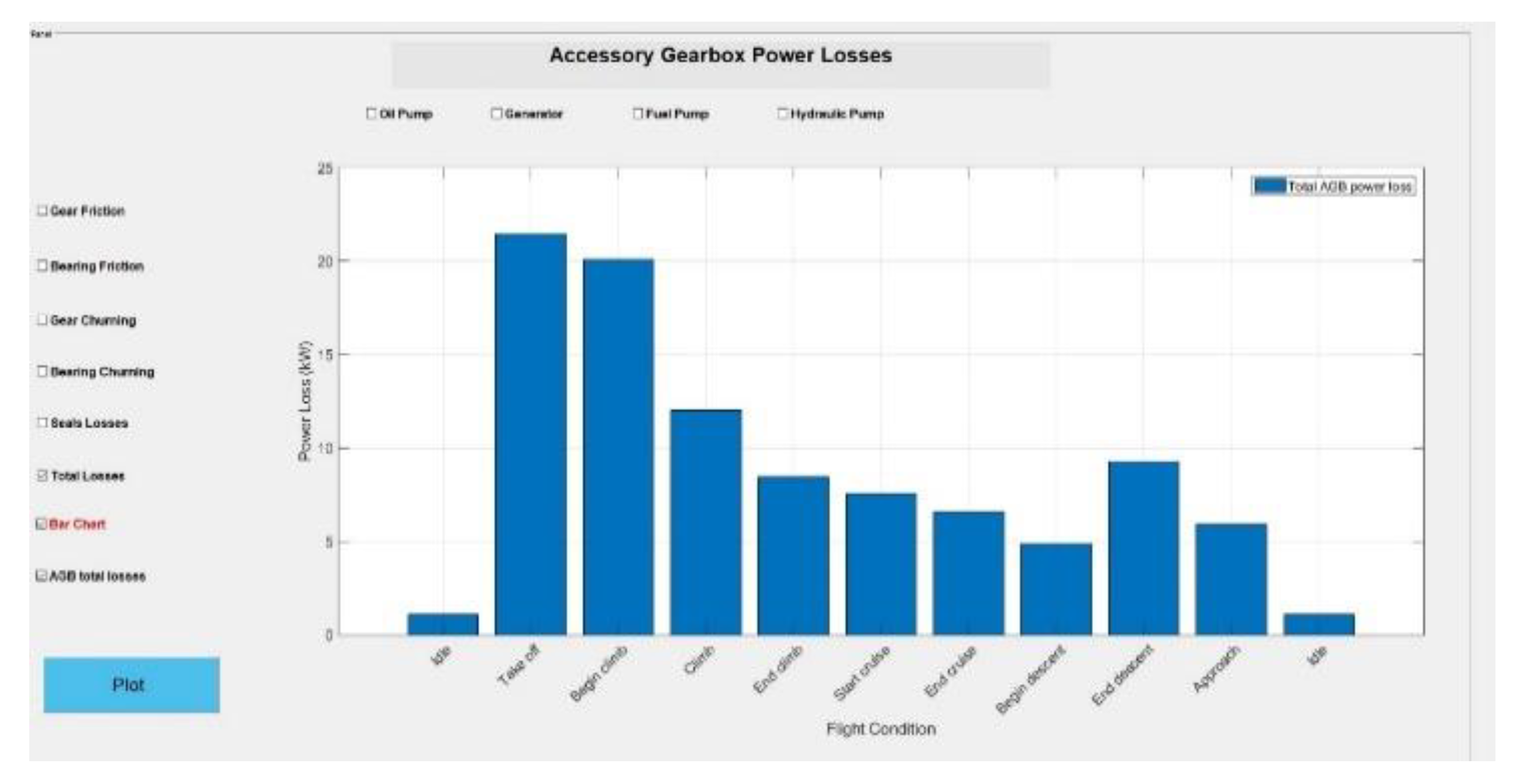
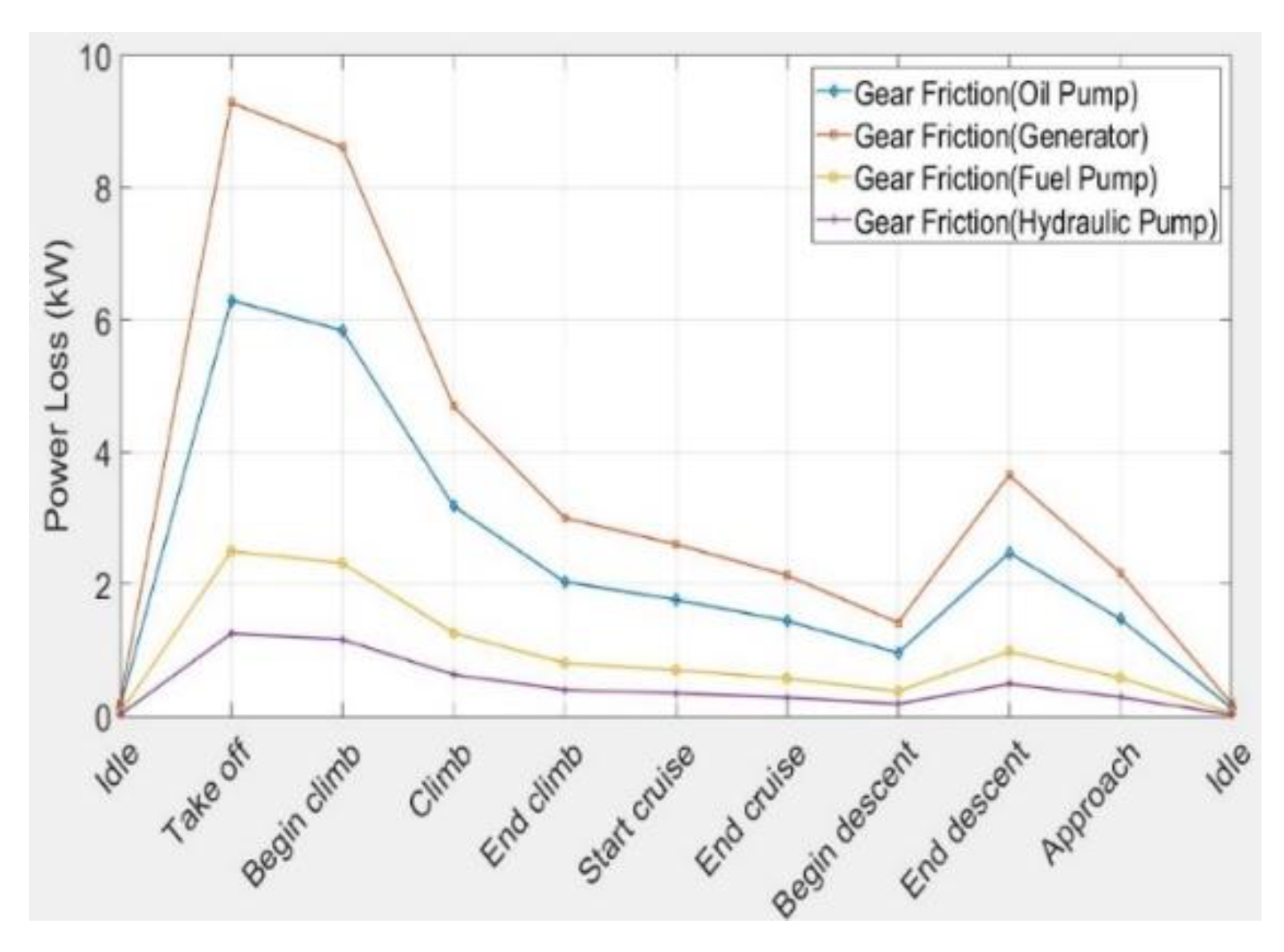
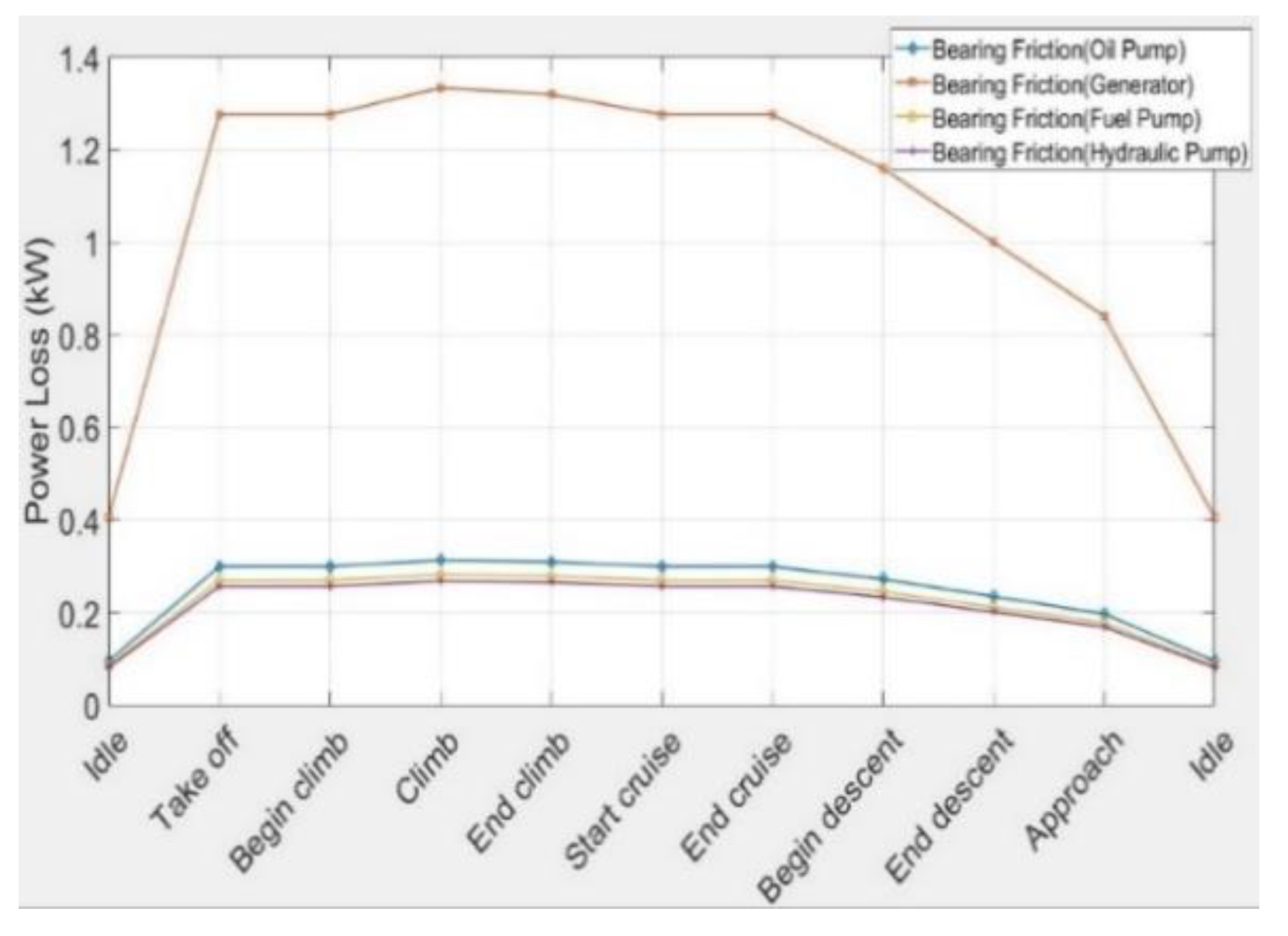
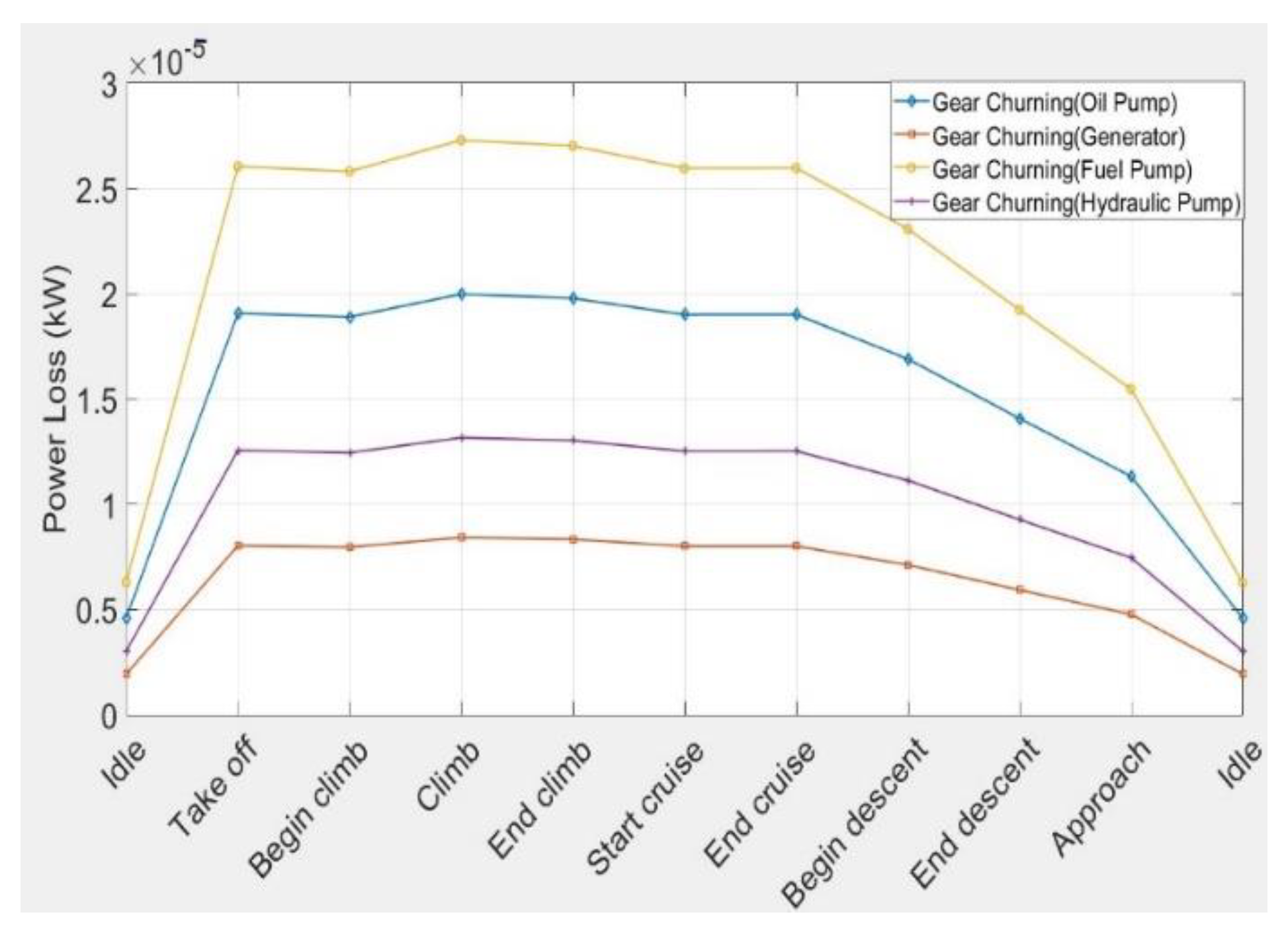
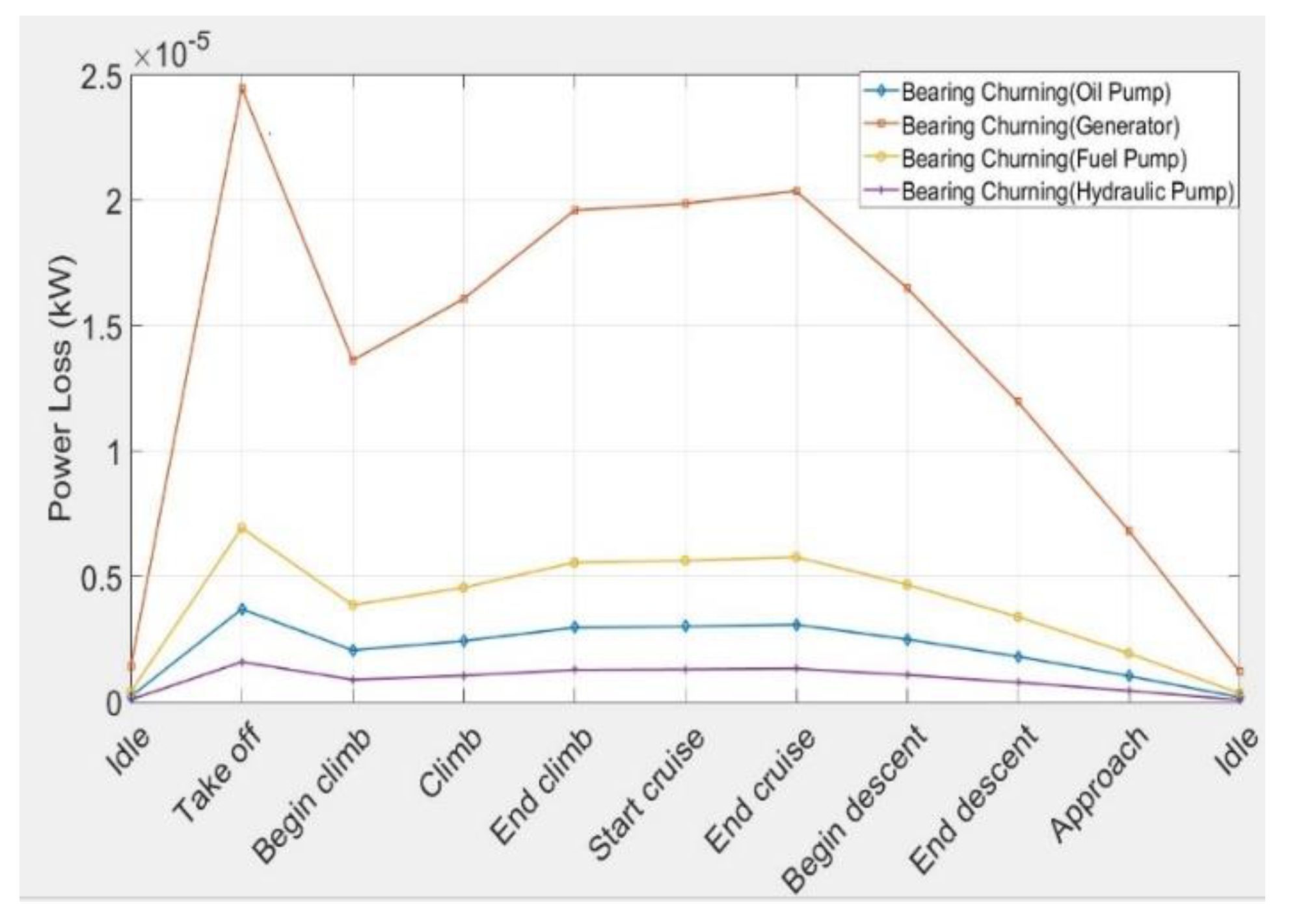
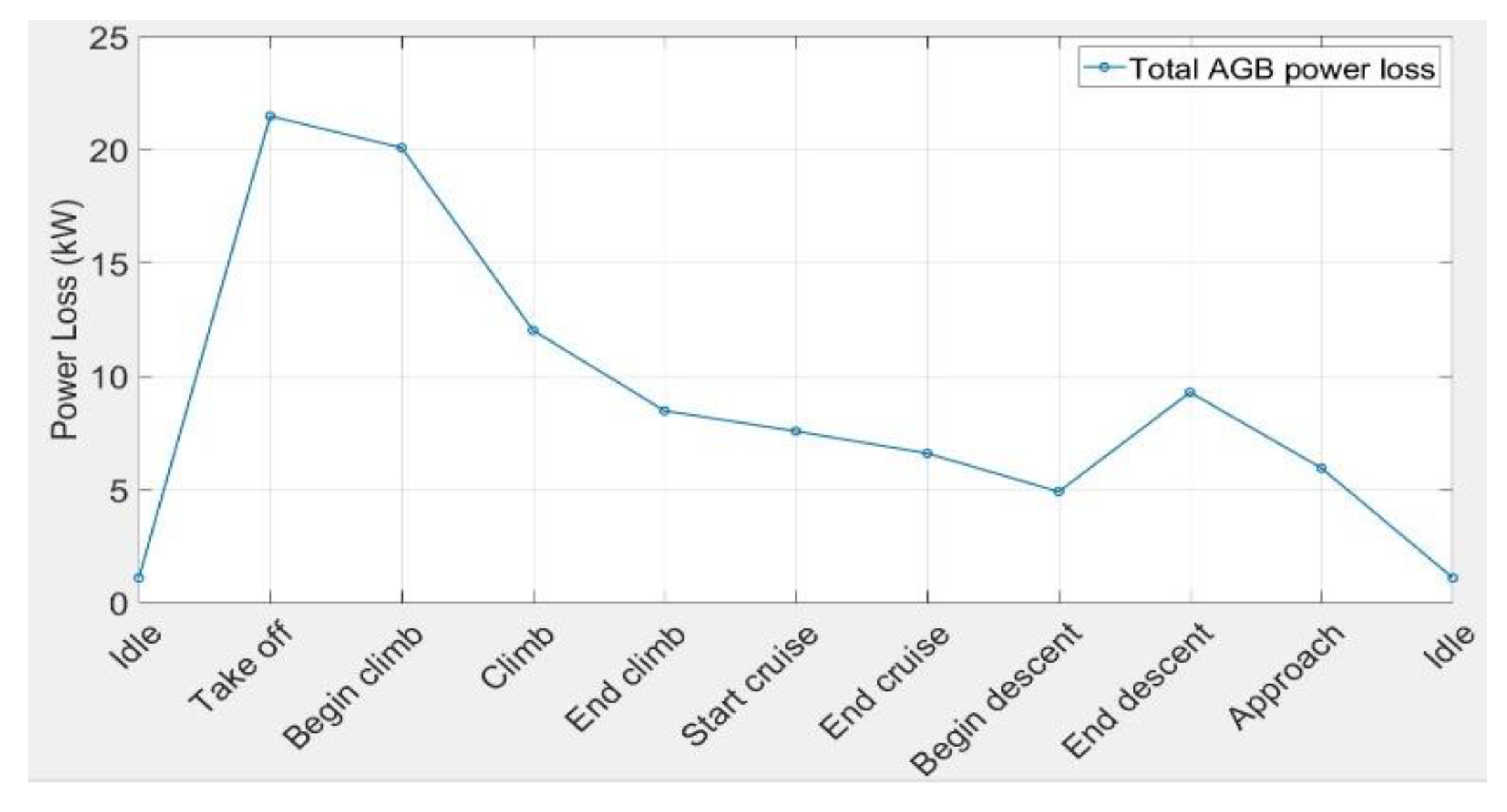
4. Results Analysis

The equations described in previous sections have been used to generate a simulation toolbox in MATLAB environment to calculate different power loss mechanisms in different elements of accessory gearbox for gas turbine engines. The toolbox is able to predict the heat load values in the AGB, due to friction and churning losses in gears and bearing and seals for each element.

It should be mentioned that in this study, the simulation model includes only the elements that have huge impacts on the total power losses while ignoring other elements (e.g., de-oiler). The schematic of accessory gearbox gear set configuration for an aero-engine is shown in Figure 1, it mainly consists of a set of spur gears connected to drive each element at different speed ratios and power, a ball bearing, and gear shaft, seals, a gearbox housing. According to [19], the typical speed of each element in the accessory gearbox at maximum power output, such as fuel pump, generator, and oil pump, are listed in

Table 1. Accessory gearbox drives speeds.

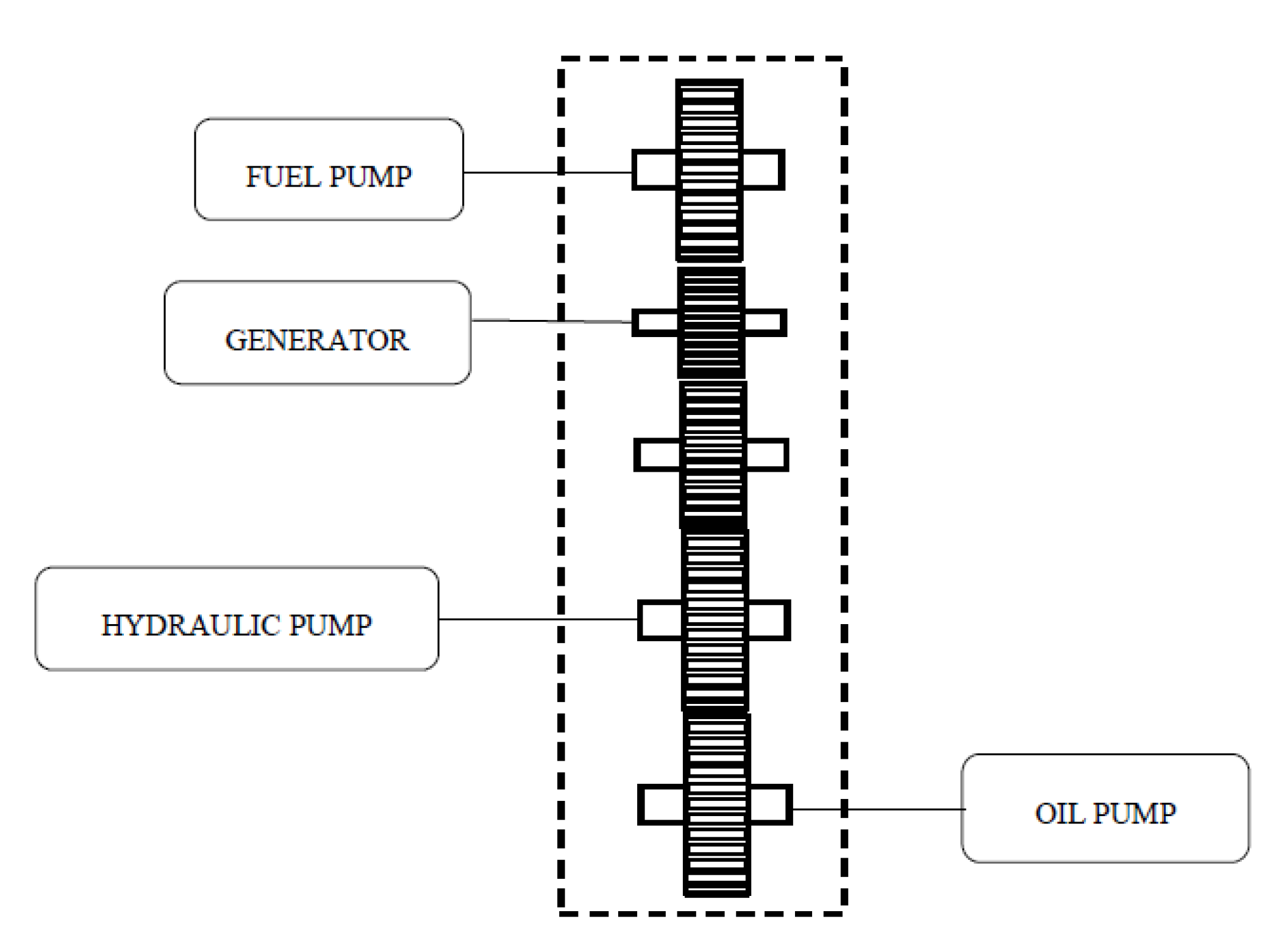
Component	Speed Ratio to HP Spool
Oil Pump	0.62
Generator	1.79
Fuel Pump	0.9
Hydraulic Pump	0.5

.

In this study, the power loss model of the accessory gearbox is simulated through operating in a different flight phase, wide range of operating conditions, with an input power and speed varied for each flight condition, according to engine manufacturer, the speed and power input data in the accessory gearbox are taken from real engine of CFM56 family through different flight phases. The first row of the

Table 2. Accessory gearbox speed and engine core power during flight phases.

Conditions	Idle	Take Off	Begin Climb	Climb	End Climb	Start Cruise	End Cruise	Begin Descent	End Descent	Approach
HP Power (kW)	825	24700	23200	14100	9700	8570	7260	5080	1090	6870
Speed (%)	0.28	0.88	0.88	0.92	0.91	0.88	0.88	0.80	0.69	058

presents the core engine power. A percentage of this power will be transmitted to the AGB at different flight phases. With regard to Rolls-Royce [20] and Pratt & Whitney [21], the AGB drives the accessories, fuel pumps, oil pumps, generators etc., by handling between 400–500 hp. The second raw presents the percentage of high-pressure rotational speed (from [19]), which is used as the input for the AGB physics-based model.

The simplified model of AGB internal structure of gears is shown in Figure 1. Reference [22] provides basic design parameters of the spur gear, which are also listed in

Table 3. Design parameters of AGB.

Parameter	Index	Unites	Value
Base helix angle	$\beta$	$°$	10
Bearing mean diameter	$d_m$	$m$	0.20
Pitch diameter	$d$	$m$	0.35
Immersed area	$A_i$	$m^2$	1.0996 × 10−6
Gear immersion depth	$h$	$m$	0.22
Shaft diameter	$d_i$	$m$	0.2
Oil volume	$V_{oil}$	$m^3$	0.0012
N of teeth (Oil Pump)	z	-	77
N of teeth (Fuel Pump)	z	-	75
N of teeth (Generator)	z	-	20
N of teeth (Hydraulic Pump)	z	-	67

.

Figure 2 shows the power loss toolbox generated with the graphical user interface (GUI) in MATLAB (R2019a) to enable the user to analyze different heat load mechanisms in different AGB elements separately and/or in total.

By applying the flight phases of Table 2 to the model generated in MATLAB, the results of the heat load in different elements of the AGB according to different heat loss mechanisms are generated, and will be analyzed here.

Figure 3 shows the friction loss in all AGB elements, where the gear connected to the generator has the highest friction loss in take-off condition compared to other elements, which mainly depends on the friction coefficient and the load applied to the meshing gears.

Figure 4 confirms that the bearings friction losses are influenced directly by the applied load and speed. This figure is also showing a direct relation between the power loss value and the increase of speed and power transmitted.

Figure 5 and Figure 6 show the losses due to gear and bearing churning in all AGB components, respectively. Regarding Section 3, the fluid viscosity and density index influence the churning losses where the oil properties change with oil temperature and operating conditions.

The fuel pump has a high loss compared to the generator due to the influence of gear diameter. It can be seen that the impact of the oil temperature on the churning power losses is mainly reflected in the density and dynamic viscosity of the oil. The churning losses at take-off condition seem to have a high value on all AGB components, due to change the viscosity of the oil. Additionally, the oil fill level influences the churning power loss, the losses increase with increasing the immersion level of the gear teeth.

Finally, Figure 7 shows the power loss produced by shaft seals which is considered as no-load dependent loss, and less important in the total losses. It can be seen that the seals losses varied with speed through all flight conditions. The results presented in Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7 confirms that the majority of the heat load in accessory gearbox is generated by gear and bearing friction mechanisms.

By adding the values of different heat loss mechanisms, Figure 8 shows the total power loss predicted in accessory gearbox components. It can be seen that:

• The gear set connected to the generator creates the highest value of loss in comparison with other elements due to the high power transmitted which causes high friction between the gears as the friction coefficient change with power transmitted.
• The oil and fuel pump gear sets have the next ranks in generating heat loads. The loss in hydraulic pump is less than 2 kW in all flight phases.
• The assumption of neglecting other elements (e.g., de-oiler and heat transfer from the engine components) is valid, as the generated heat loads would be very small (in the order of 1 kW and less).

By adding all values in Figure 8, Figure 9 shows the overall power loss occurs in accessory gearbox through all flight conditions. The model presented in this work seems to perform quite well in overall power loss prediction in AGB, given the proper geometry and operating conditions. The overall losses followed the trend of the friction losses because of the high heat generated between the friction surfaces compared to the heat produced by the gears and bearing digging in the oil.

A comparison of the results with the value reported in [23] shows that the total accessory gearbox power loss is quite close to the experimental value reported by manufacturers. In [23], the total heat load generated by the AGB for an 18 klbs engine at take-off condition is 17 kW. The case study of this paper is a CFM56-5 like with the thrust value of 25 klbs and the heat load calculated by the generated tool is 21.6 kW. The linear relationship works very well between these two values. However, more case studies and analyses are required to confirm and enhance the reliability and validity of the generated tool.

5. Conclusions

A MATLAB tool for predicting different heat loss mechanisms, as well as heat load values in accessory gearbox components of gas turbine aero engines, was developed based on the physics-based modelling approach. The tool is capable of calculating load-dependent and no-load dependent heat losses in AGB structure including churning loss in gears, bearings, and seals, as well as gear mesh loss and bearing friction loss at different flight phases. The heat losses could also be calculated in different gear sets in the AGB, including gear sets connected to the generator, oil pump, fuel pump, and hydraulic pump. The results of the simulation of a complete mission for a CFM56-5 AGB show that the friction losses in gears and bearing generate the majority of the heat load in the AGB. Moreover, between different elements of the AGB, the gear set connected to the generator creates the highest amount of heat loss in comparison with other elements. The heat load value is maximum at the take-off condition due to the high transmitted power and the highest rotational speed. This value for the case study is 21.6 kW, which is in good agreement with the reported experimental data in the literature. The tool could be used for thermal management system designers for different gas turbine aero-engines and different missions, because all design parameters (geometry, oil characteristics, load, and rotational speed) are considered in a physics-based feature in the tool, and could be tuned for other applications.