Characterization of Periodic Incoming Wakes in a Low-Pressure Turbine Cascade Test Section by Means of a Fast-Response Single Sensor Virtual Three-Hole Probe
Abstract
:1. Introduction
2. Experimental Setup
2.1. High-Speed Linear Cascade Facility
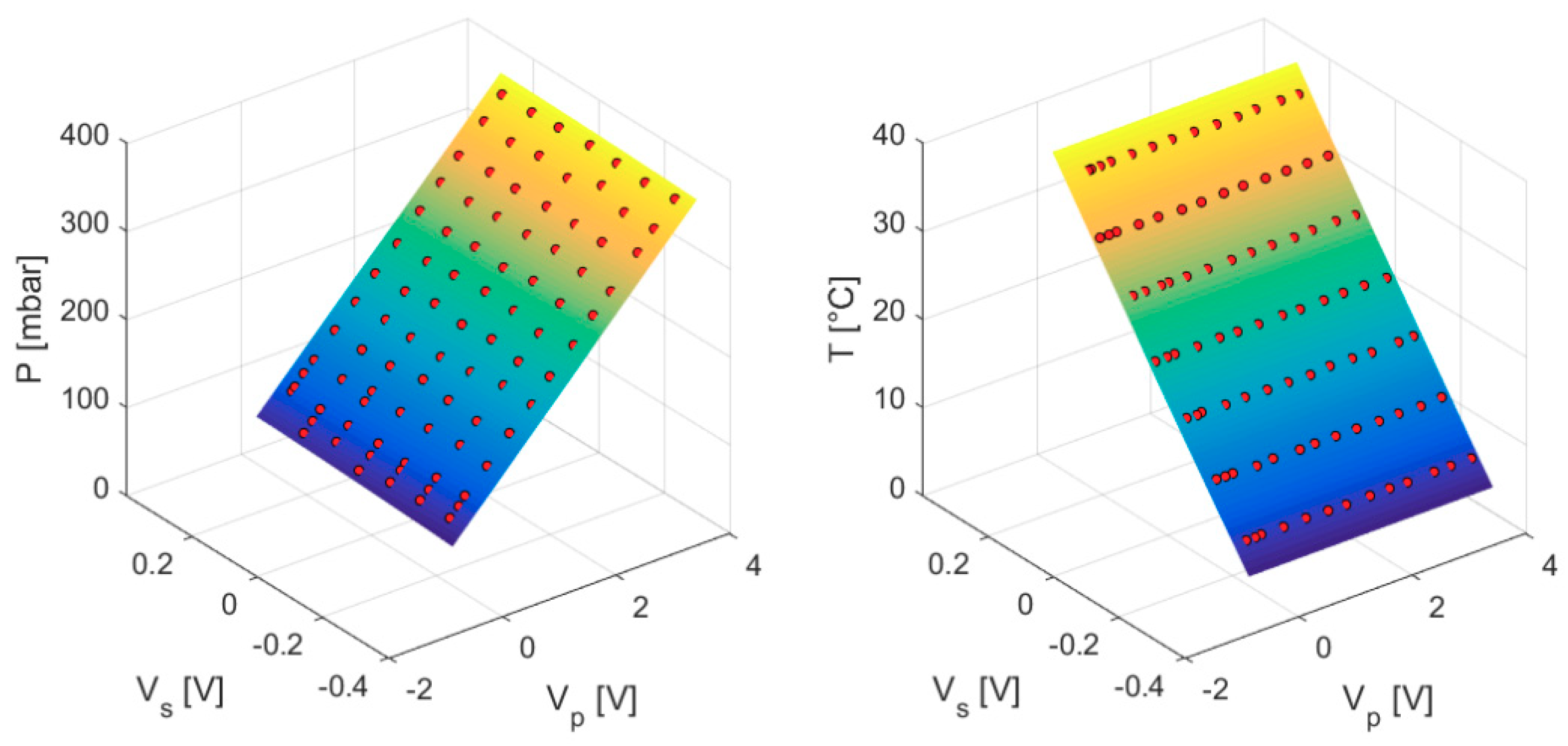
2.2. Instrumentation and Post-Processing
3. Results and Discussion
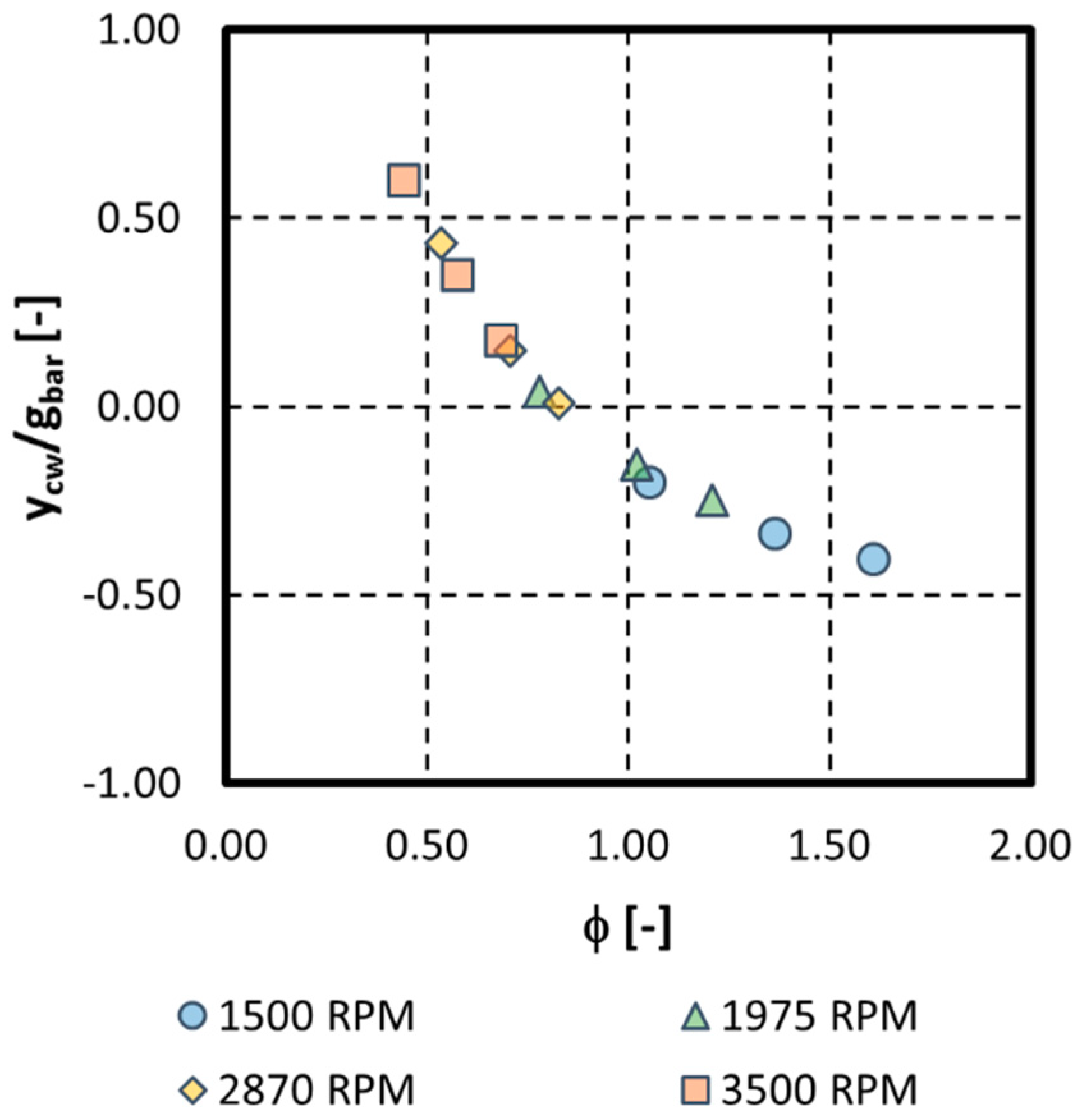
3.1. Matrix of Experiments
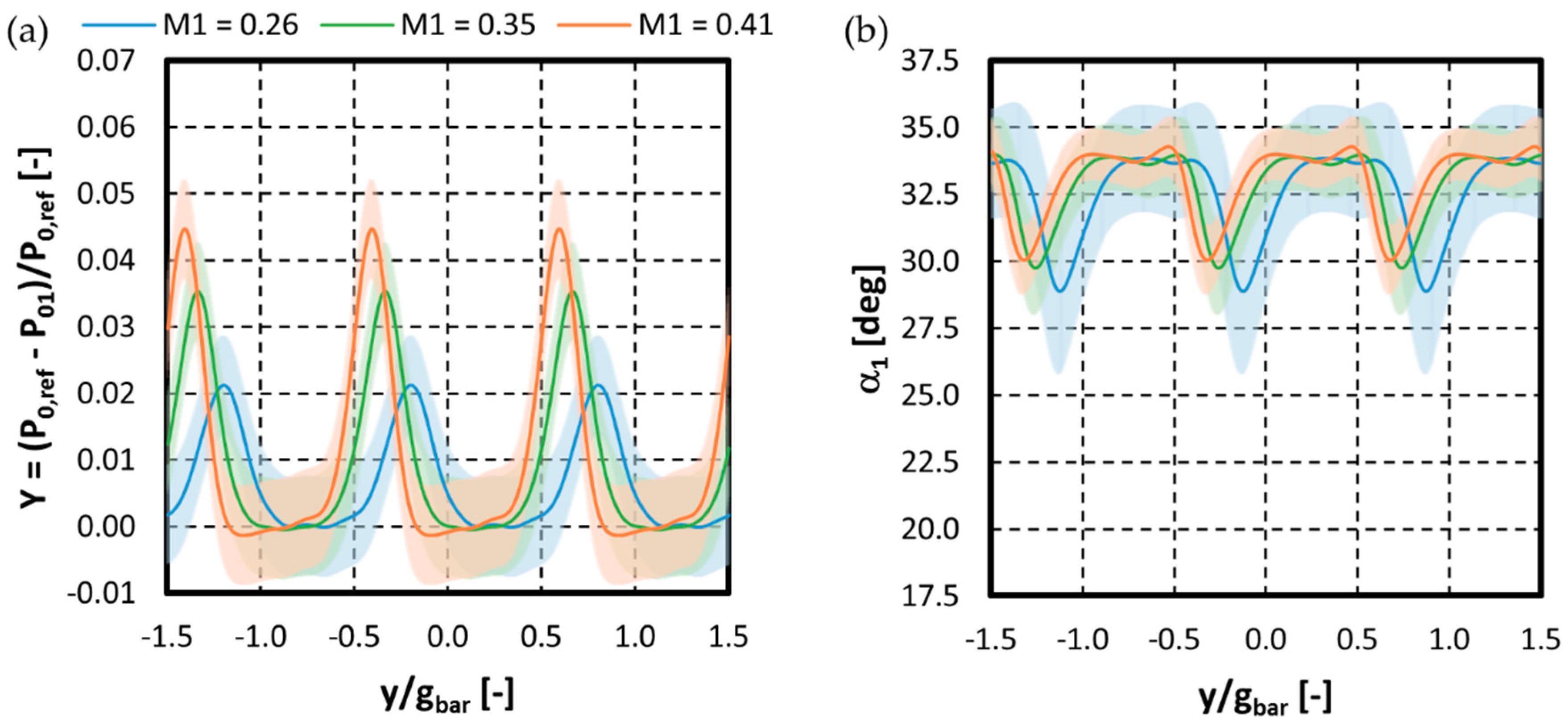
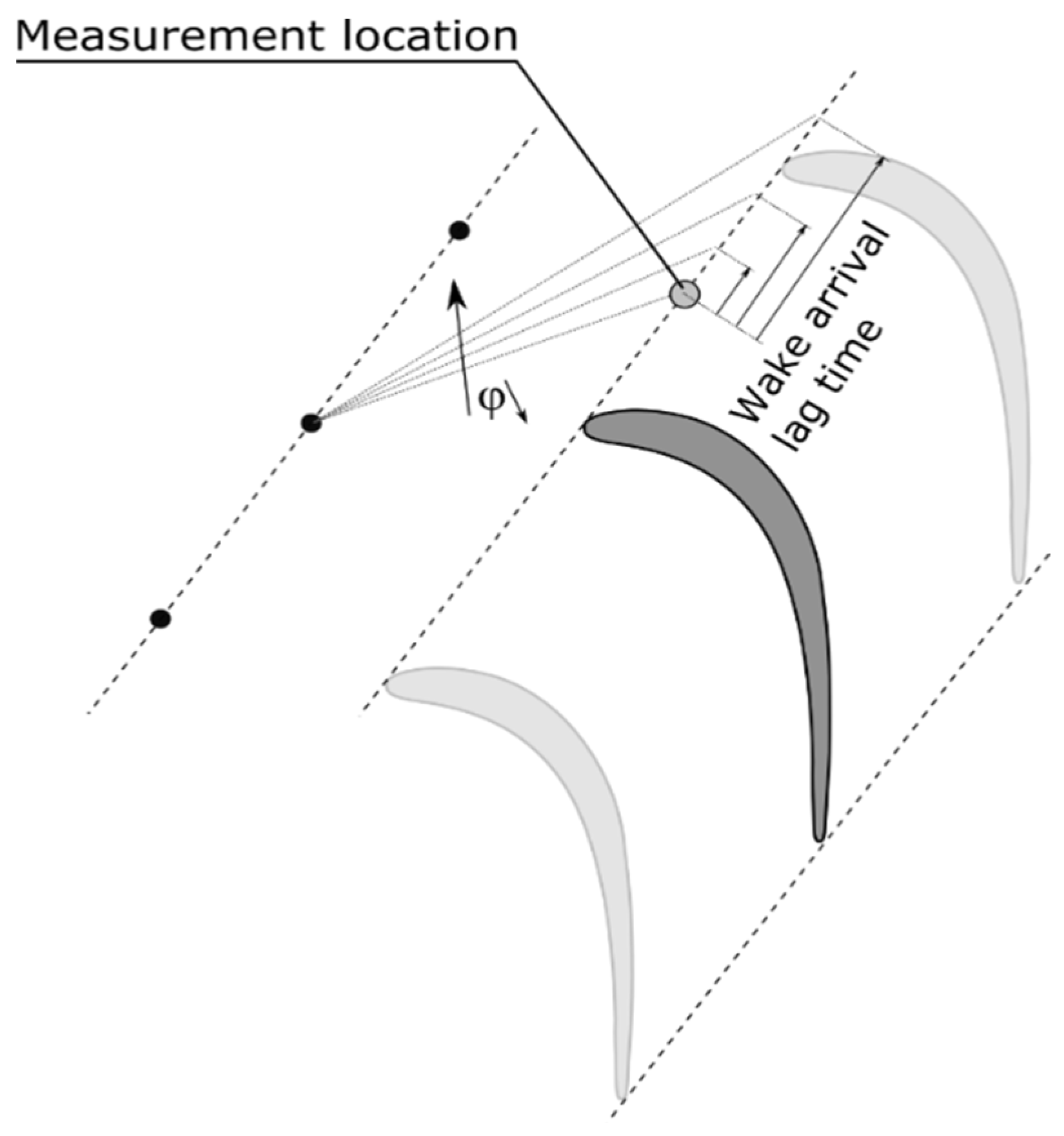
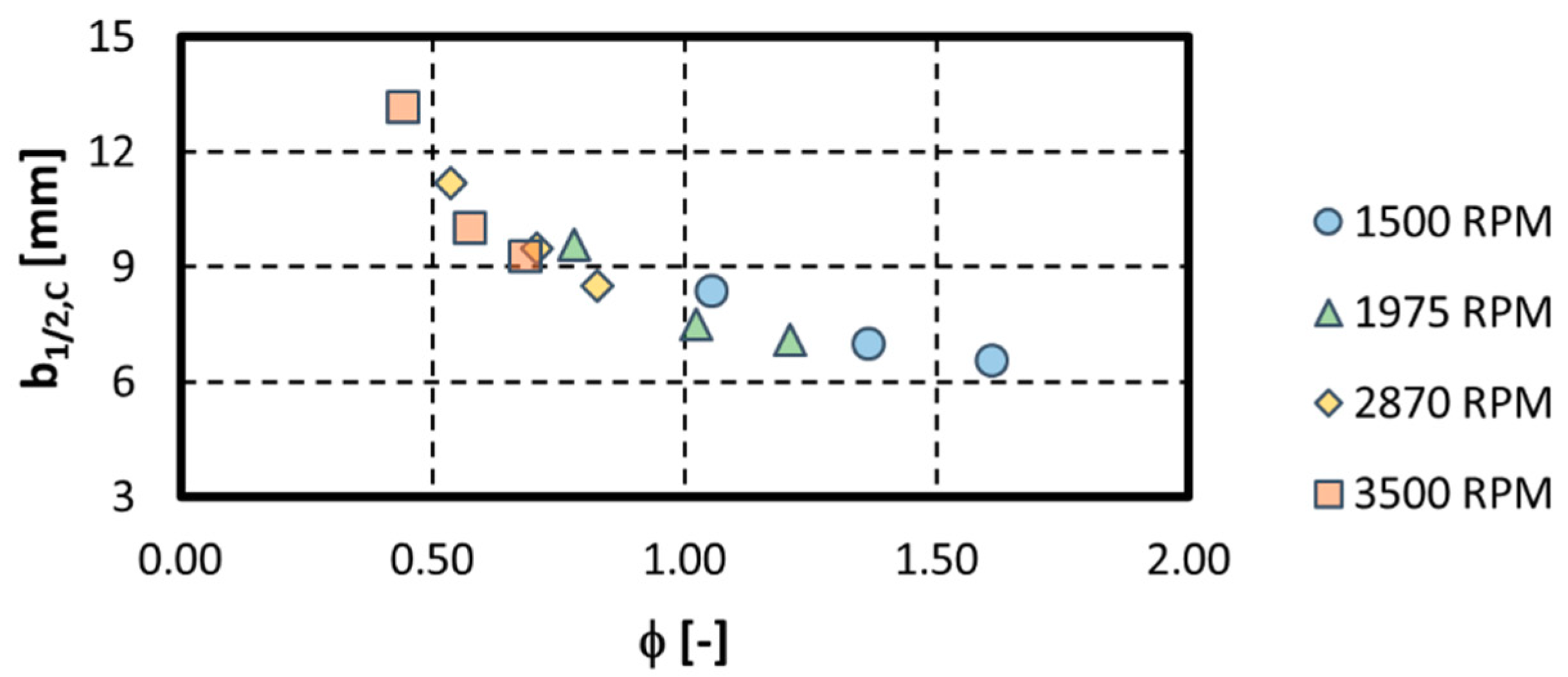
3.2. Characterization of the Incoming Wakes
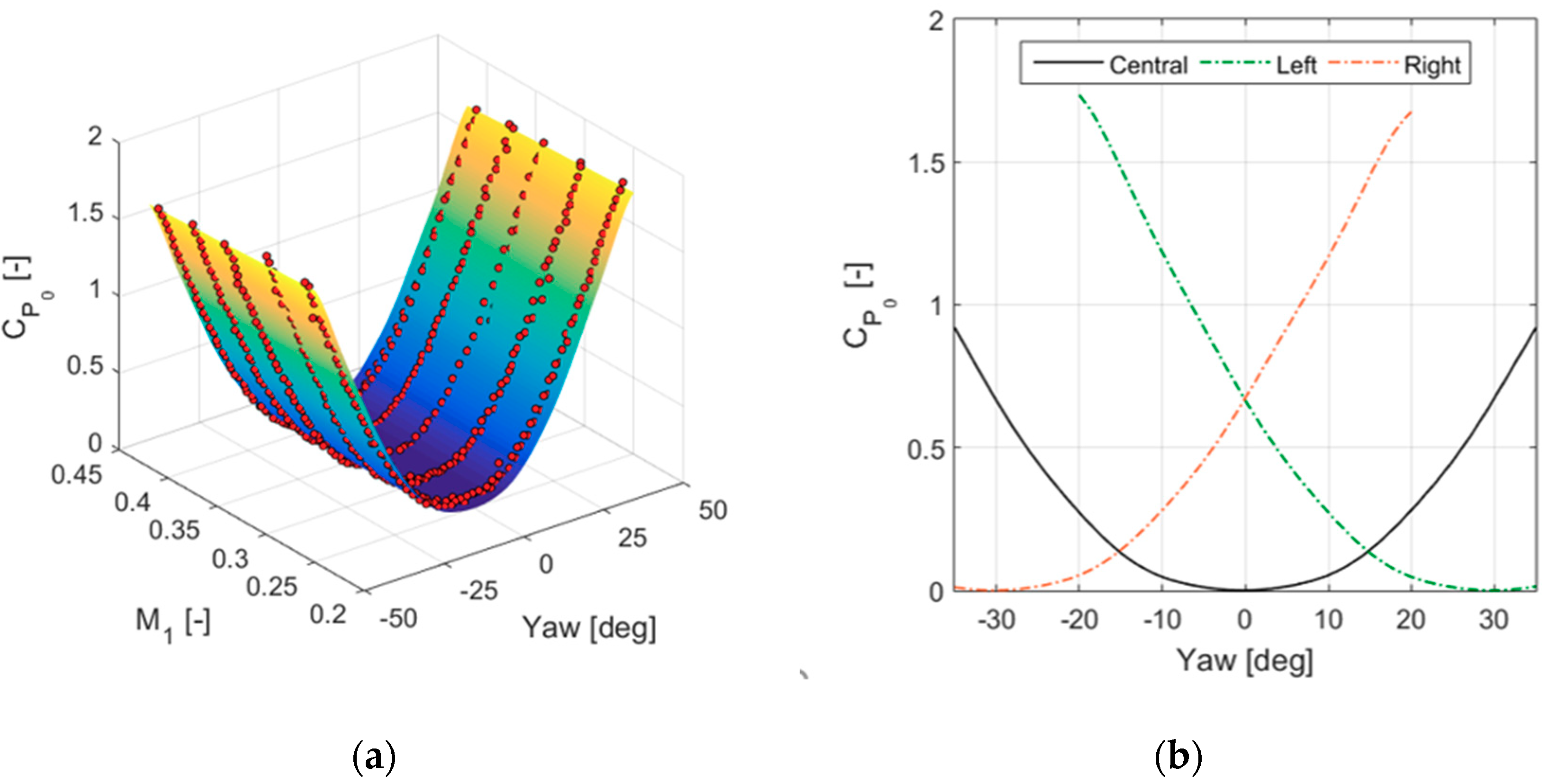
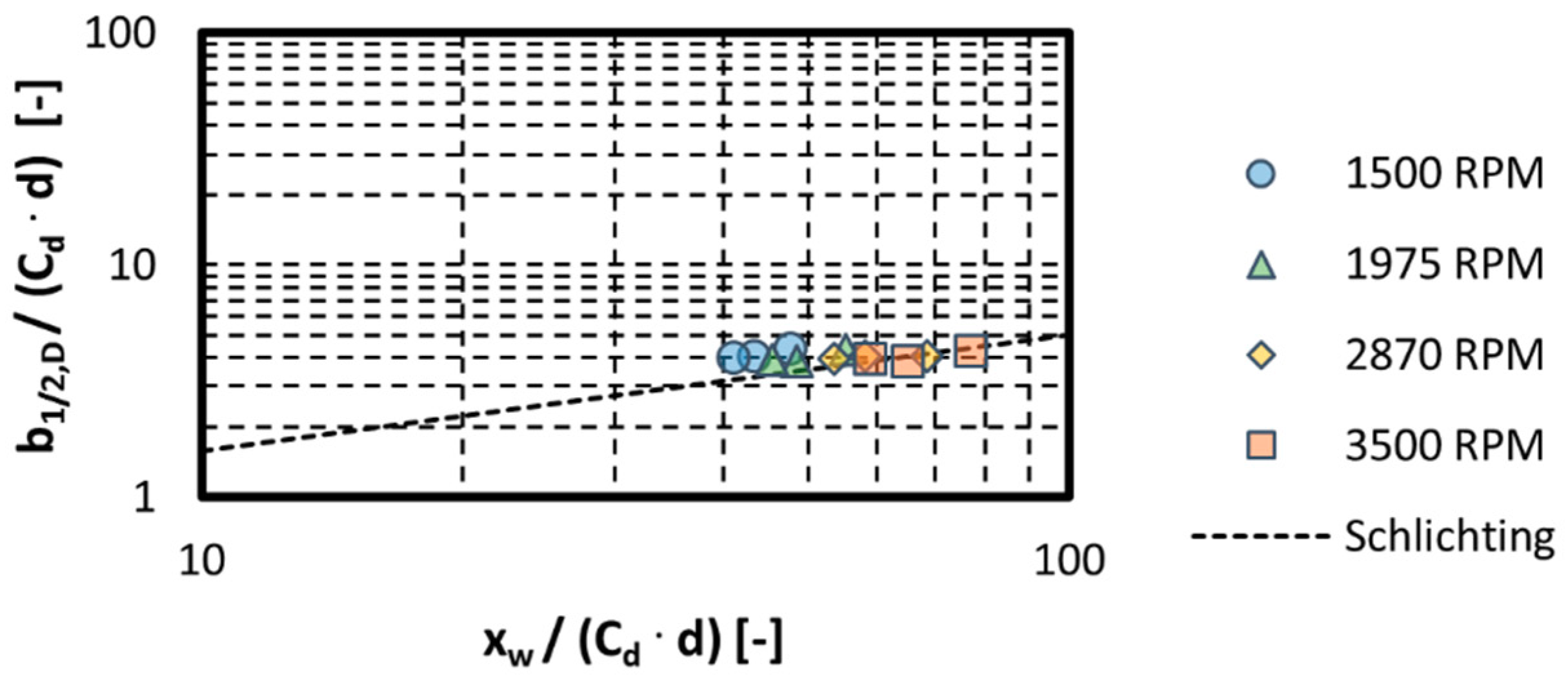
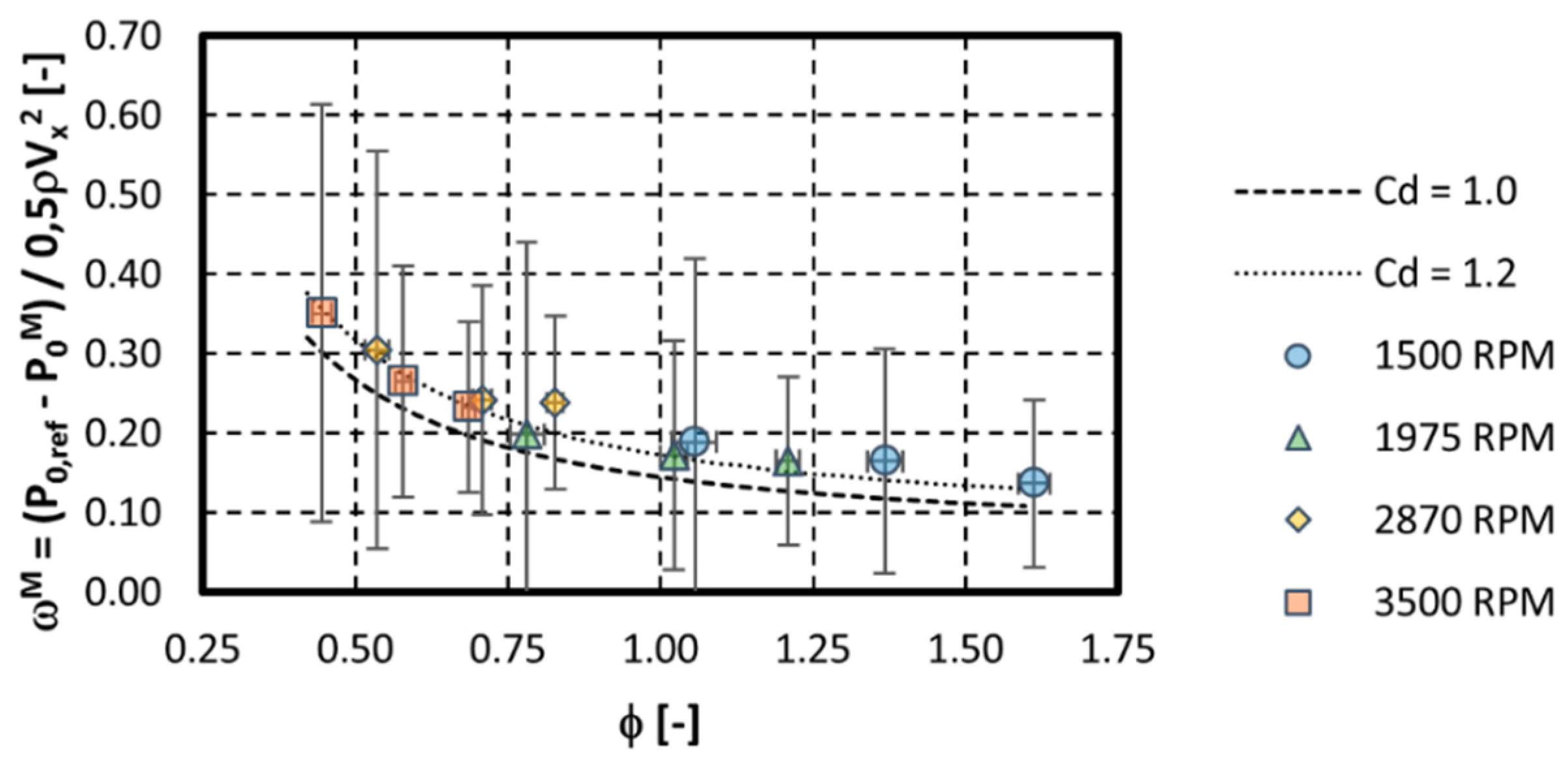
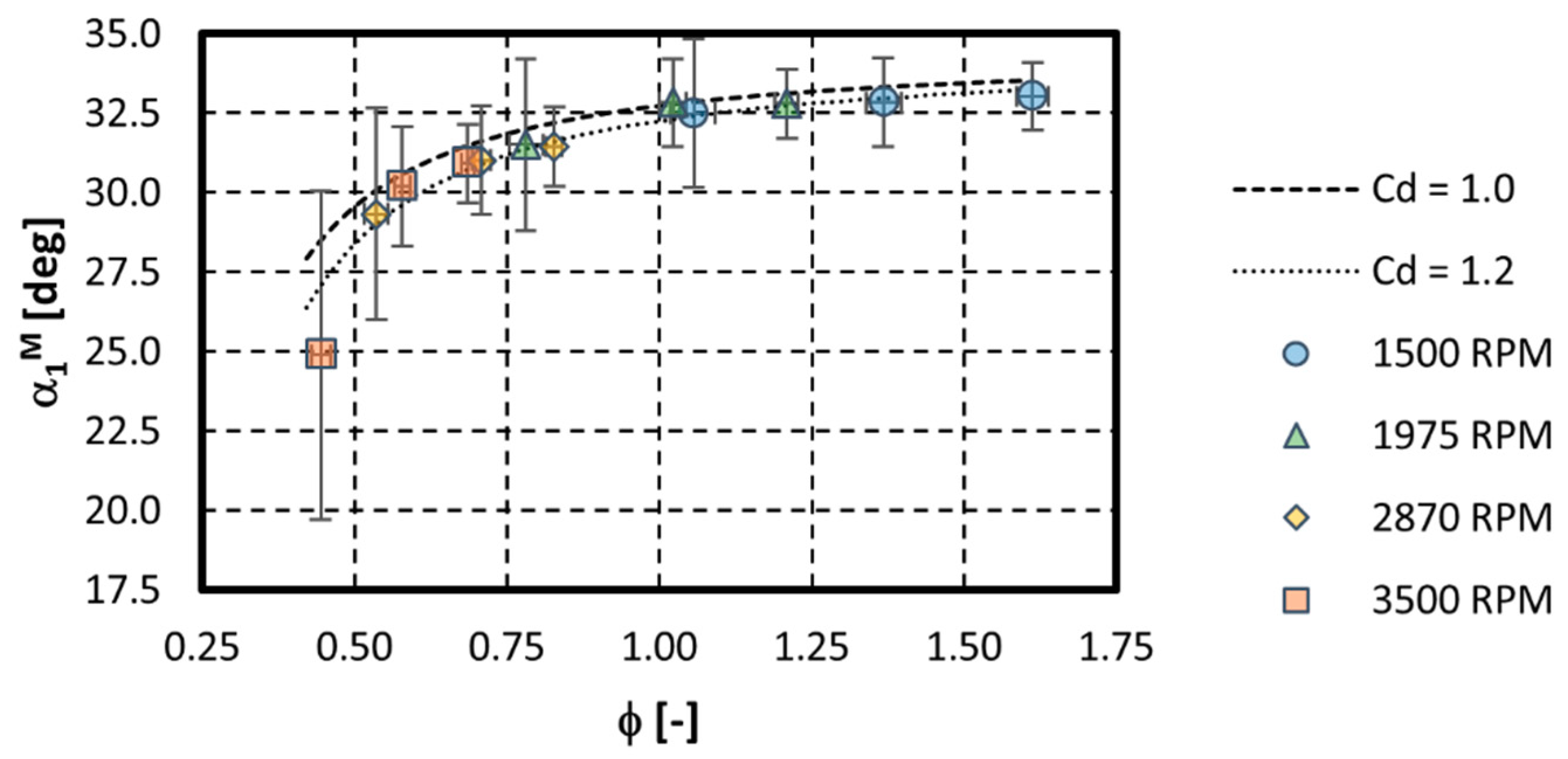
3.3. Comparison with Theory and Discussion
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| b1/2 | Wake half-width | Vp | Pressure voltage output | Superscripts | |
| C | Chord | Vs | Sense voltage output | M | Mass-averaged |
| Cax | Axial chord | V | Absolute velocity | ||
| Cd | Drag coefficient | Vdef | Velocity deficit ratio | Subscripts | |
| CP0 | Total pressure recovery | =∆Vmax/V | 0 | Total conditions | |
| d | Bar diameter | xw | Wake propagation length | 1 | Inlet conditions |
| fr | Reduced frequency | y | Tangential position | 2 | Outlet conditions |
| fbar | Bar passing frequency | ycw | Wake centre position | bar | Relative to the bar |
| g | Pitch | is | Isentropic | ||
| gbar | Bar pitch | Greek symbols | p | Related to the probe | |
| M | Mach number | α | Flow angle | s | Static conditions |
| P | Pressure | ϕ | Flow coefficient | x | Axial |
| Rm | Radius at mid-span | =V1,x/U | |||
| Re | Reynolds number | ρ | Density | ||
| T | Temperature | ω | Pressure loss coefficient | ||
| U | Peripheral speed | =∆P0/0,5ρ1V1,x | |||
| = (2π × (Ωrot/60)) × Rm | Ωrot | Rotational speed |
References
- Pfeil, H.; Eifler, J. Turbulenzverhaltnisse hinter rotierenden Zylindergittern. Forsch. Im Ing. 1976, 42, 27–32. [Google Scholar] [CrossRef]
- Schulte, V.; Hodson, H.P. Unsteady Wake-Induced Boundary Layer Transition in High Lift LP Turbines. J. Turbomach. 1998, 120, 28–35. [Google Scholar] [CrossRef]
- Funazaki, K.; Tetsuka, N.; Tanuma, T. Effects of Periodic Wake Passing upon Aerodynamic Loss of a Turbine Cascade Part I: Measurements of Wake-Affected Cascade Loss by Use of a Pneumatic Probe. In Proceedings of the International Gas Turbine & Aeroengine Congress & Exhibition, Indianapolis, IN, USA, 7–10 June 1999. [Google Scholar]
- Coton, T. Unsteady Wake-Boundary Layer Interaction on Advanced High Lift Low Pressure Turbine Airfoils. Ph.D. Thesis, Université de Liège, Liège, Belgium, 19 February 2004. [Google Scholar]
- Vera, M.; Hodson, H.P. Low speed vs. high speed testing of LP turbine blade-wake interaction. In Proceedings of the 16th Symposium on Measuring Techniques in Transonic and Supersonic Flow in Cascades and Turbomachines, Cambridge, UK, 23–24 September 2002. [Google Scholar]
- Schobeiri, M.T.; Öztürk, B. Experimental Study of the Effect of Periodic Unsteady Wake Flow on Boundary Layer Development, Separation, and Reattachment along the Surface of a Low Pressure Turbine Blade. J. Turbomach. 2004, 126, 663–676. [Google Scholar] [CrossRef]
- Berrino, M.; Simoni, D.; Ubaldi, M.; Zunino, P.; Bertini, F. Off-design performance of a highly loaded LP turbine cascade under steady and unsteady incoming flow conditions. In Proceedings of the ASME Turbo Expo 2014, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Mersinligil, M.; Brouckaert, J.F.; Desset, J. Unsteady Pressure Measurements with a Fast Response Cooled Probe in High Temperature Gas Turbine Environments. J. Turbomach. 2011, 133, 081603. [Google Scholar] [CrossRef]
- Dell’Era, G.; Mersinligil, M.; Brouckaert, J.F. Assessment of Unsteady Pressure Measurement Uncertainty—Part I: Single Sensor Probe. J. Turbomach. 2016, 138, 041601. [Google Scholar] [CrossRef]
- Dell’Era, G.; Mersinligil, M.; Brouckaert, J.F. Assessment of Unsteady Pressure Measurement Uncertainty—Part II: Virtual Three-Hole Probe. J. Turbomach. 2016, 138, 041602. [Google Scholar] [CrossRef]
- Michálek, J.; Monaldi, M.; Arts, T. Aerodynamic Performance of a Very High Lift Low Pressure Turbine Airfoil (T106C) at Low Reynolds and High Mach Number with Effect of Free Stream Turbulence Intensity. J. Turbomach. 2010, 134, 061009. [Google Scholar] [CrossRef]
- Dong, Y.; Cumptsy, N.A. Compressor Blade Boundary Layers: Part 2—Measurements with Incident Wakes. J. Turbomach. 1990, 112, 231–240. [Google Scholar] [CrossRef]
- Arts, T. Aerodynamic performance of two very high lift low pressure turbine airfoils (T106C—T2) at low Reynolds and high Mach numbers. In Proceedings of the 5th European Conference for Aerospace Sciences, Munich, Germany, 1 July 2013. [Google Scholar]
- Dullenkopf, K.; Schulz, A.; Wittig, S. The Effect of Incident Wake Conditions on the Mean Heat Transfer of an Airfoil. In Proceedings of the Gas Turbine and Aeroengine Congress and Exposition, Brussels, Belgium, 11–14 June 1990. [Google Scholar]
- Schlichting, H. Boundary Layer Theory, 6th ed.; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]


| Ωrot | M1,is = 0.26 | M1,is = 0.34 | M1,is = 0.41 |
|---|---|---|---|
| 1500 RPM | 1.05 | 1.35 | 1.60 |
| 1975 RPM | 0.78 | 1.02 | 1.21 |
| 2870 RPM | 0.54 | 0.70 | 0.83 |
| 3500 RPM | 0.44 | 0.58 | 0.69 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Clinckemaillie, J.; Arts, T. Characterization of Periodic Incoming Wakes in a Low-Pressure Turbine Cascade Test Section by Means of a Fast-Response Single Sensor Virtual Three-Hole Probe. Int. J. Turbomach. Propuls. Power 2019, 4, 26. https://doi.org/10.3390/ijtpp4030026
Clinckemaillie J, Arts T. Characterization of Periodic Incoming Wakes in a Low-Pressure Turbine Cascade Test Section by Means of a Fast-Response Single Sensor Virtual Three-Hole Probe. International Journal of Turbomachinery, Propulsion and Power. 2019; 4(3):26. https://doi.org/10.3390/ijtpp4030026
Chicago/Turabian StyleClinckemaillie, Julien, and Tony Arts. 2019. "Characterization of Periodic Incoming Wakes in a Low-Pressure Turbine Cascade Test Section by Means of a Fast-Response Single Sensor Virtual Three-Hole Probe" International Journal of Turbomachinery, Propulsion and Power 4, no. 3: 26. https://doi.org/10.3390/ijtpp4030026
APA StyleClinckemaillie, J., & Arts, T. (2019). Characterization of Periodic Incoming Wakes in a Low-Pressure Turbine Cascade Test Section by Means of a Fast-Response Single Sensor Virtual Three-Hole Probe. International Journal of Turbomachinery, Propulsion and Power, 4(3), 26. https://doi.org/10.3390/ijtpp4030026





