Heat Transfer in a Square Ribbed Channel: Evaluation of Turbulent Heat Transfer Models †
Abstract
1. Introduction
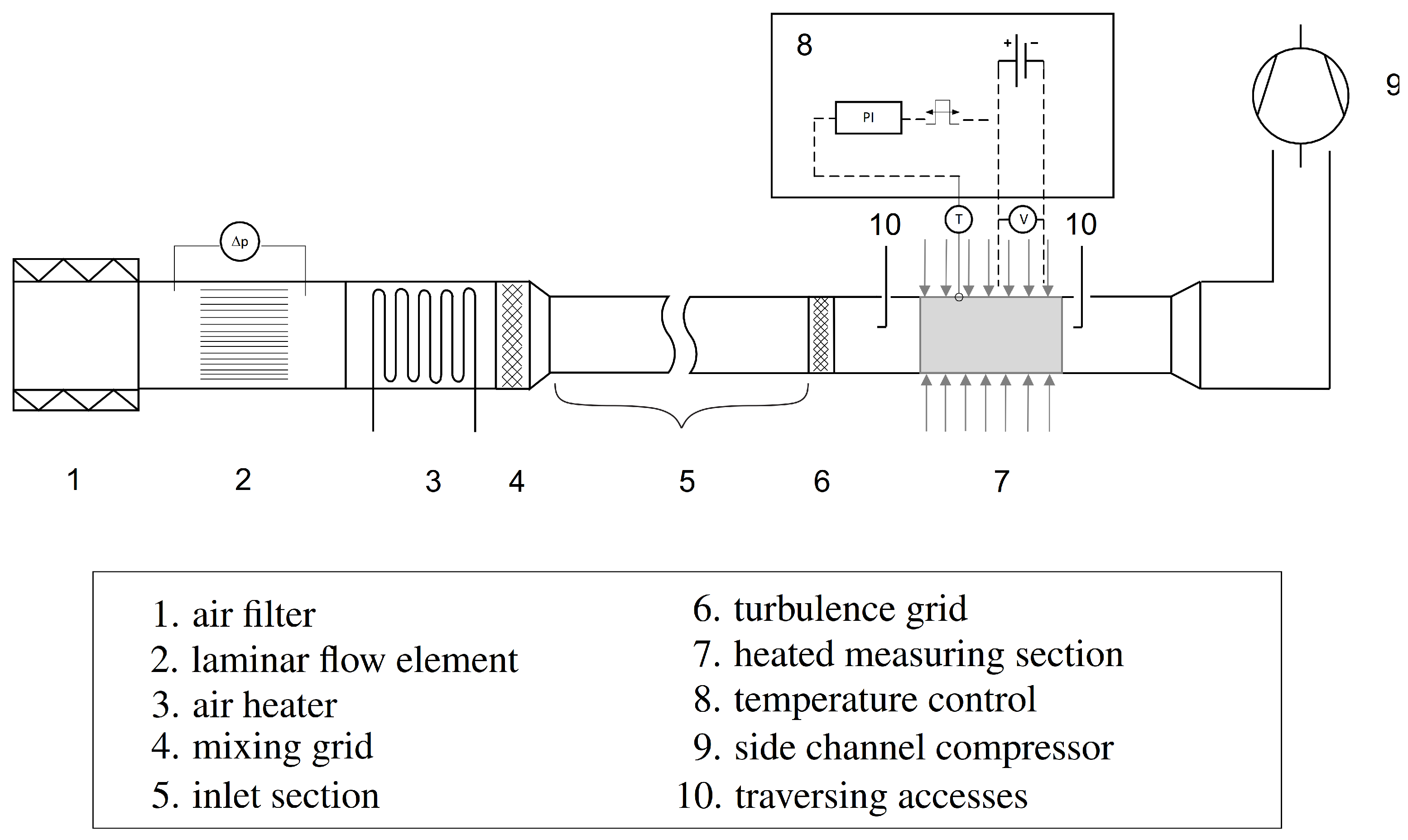
2. Experimental Setup
2.1. Overview of the Test Rig
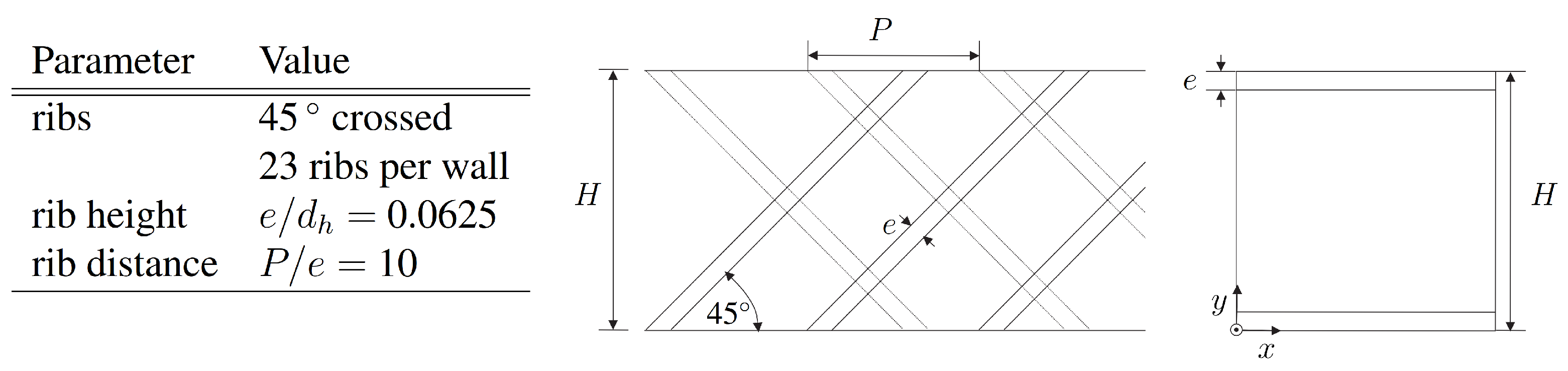
2.2. Description of the Configurations
2.3. Heat Transfer Measurements
3. Numerical Setup
3.1. Modelling
3.2. Meshing
3.3. Boundary Conditions
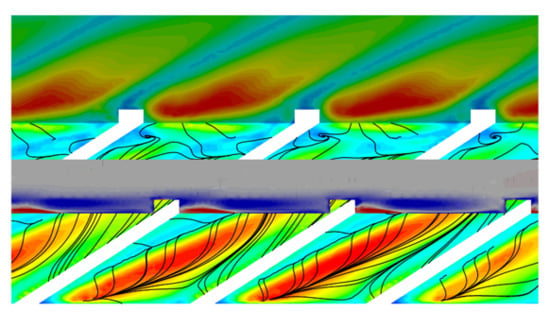
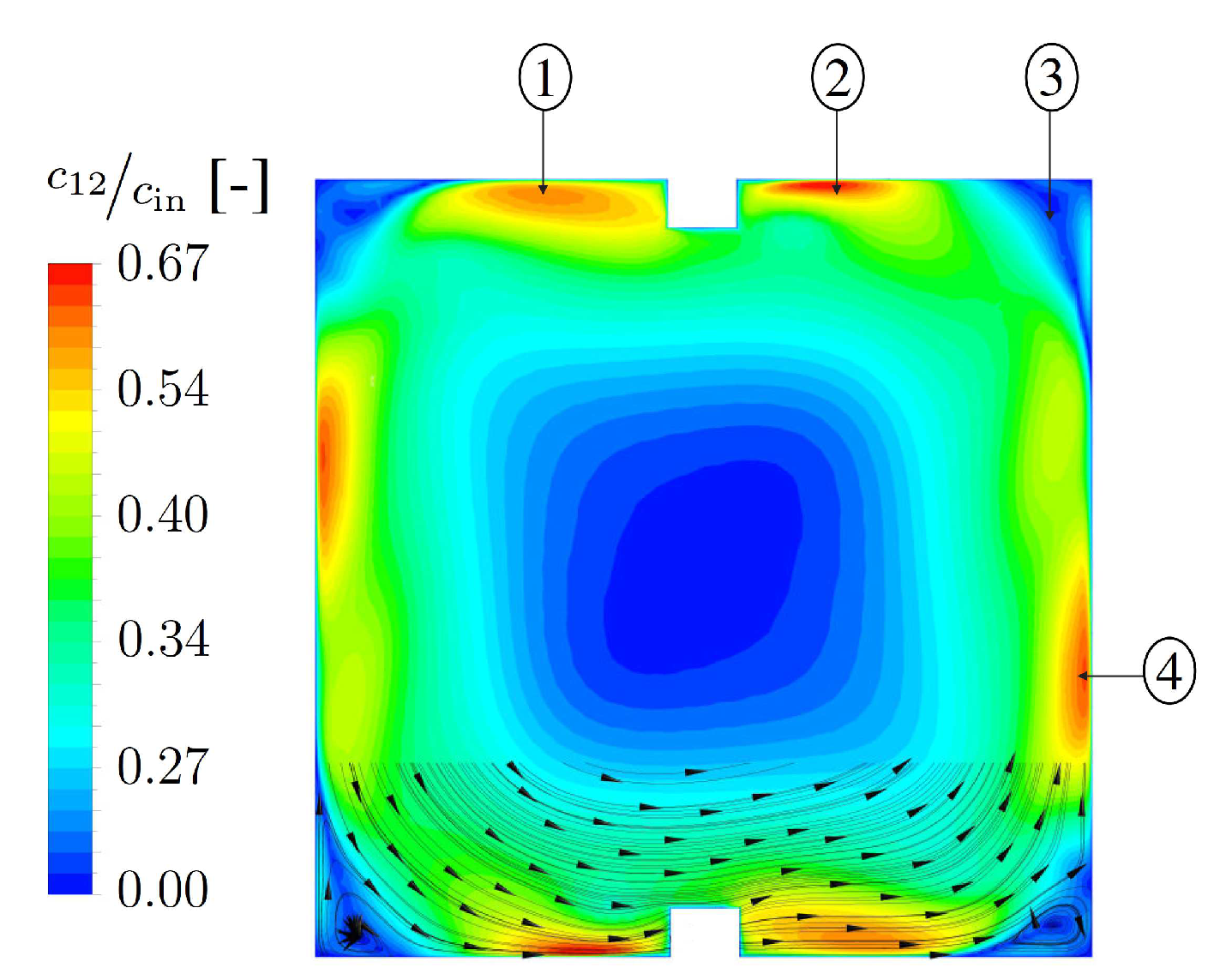
4. Results
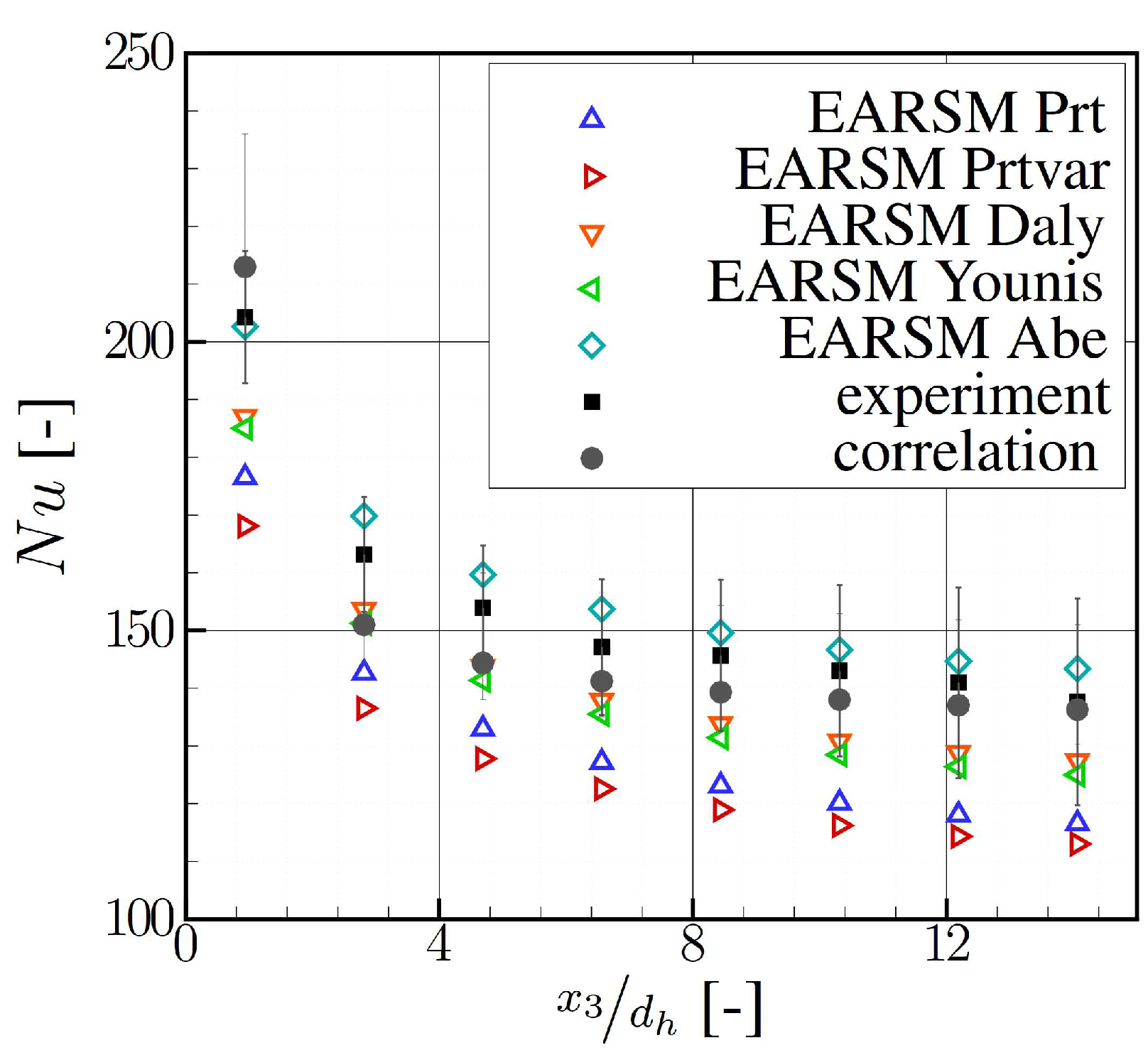
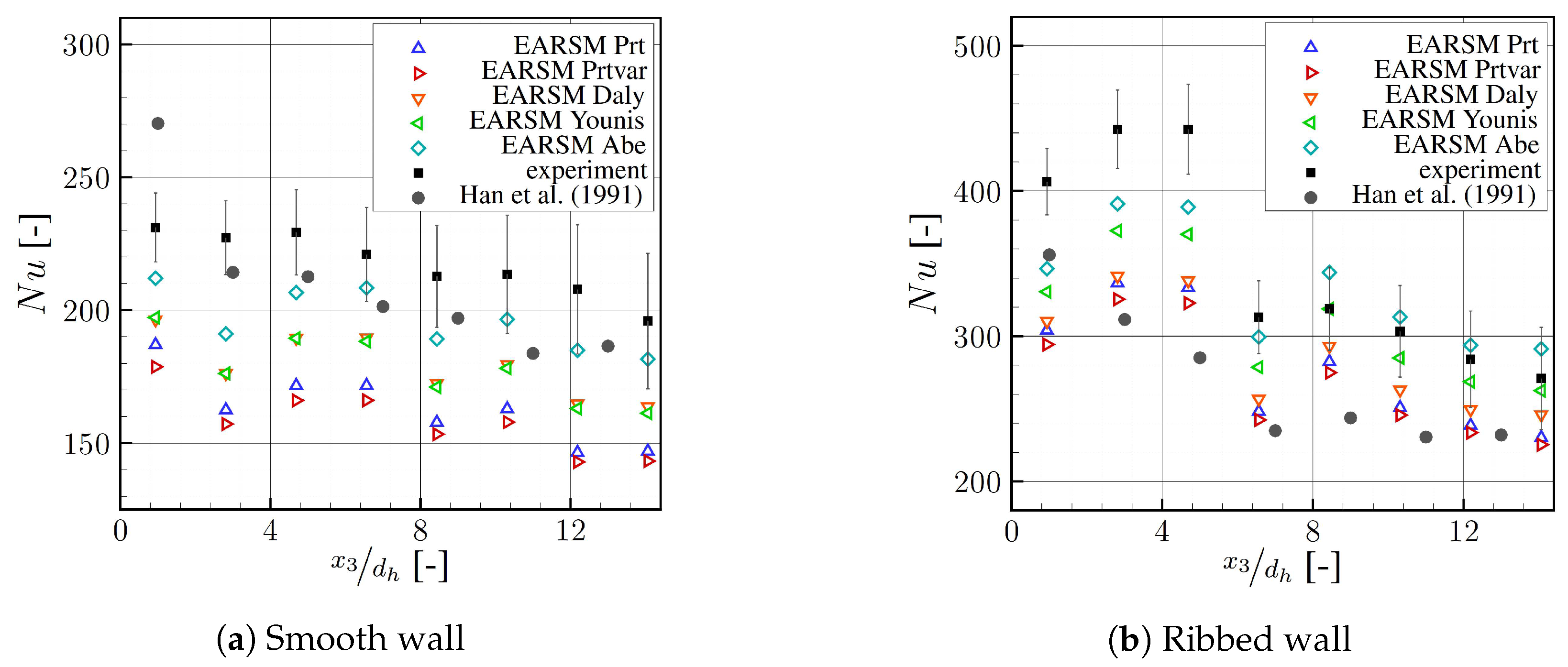
4.1. Smooth Configuration
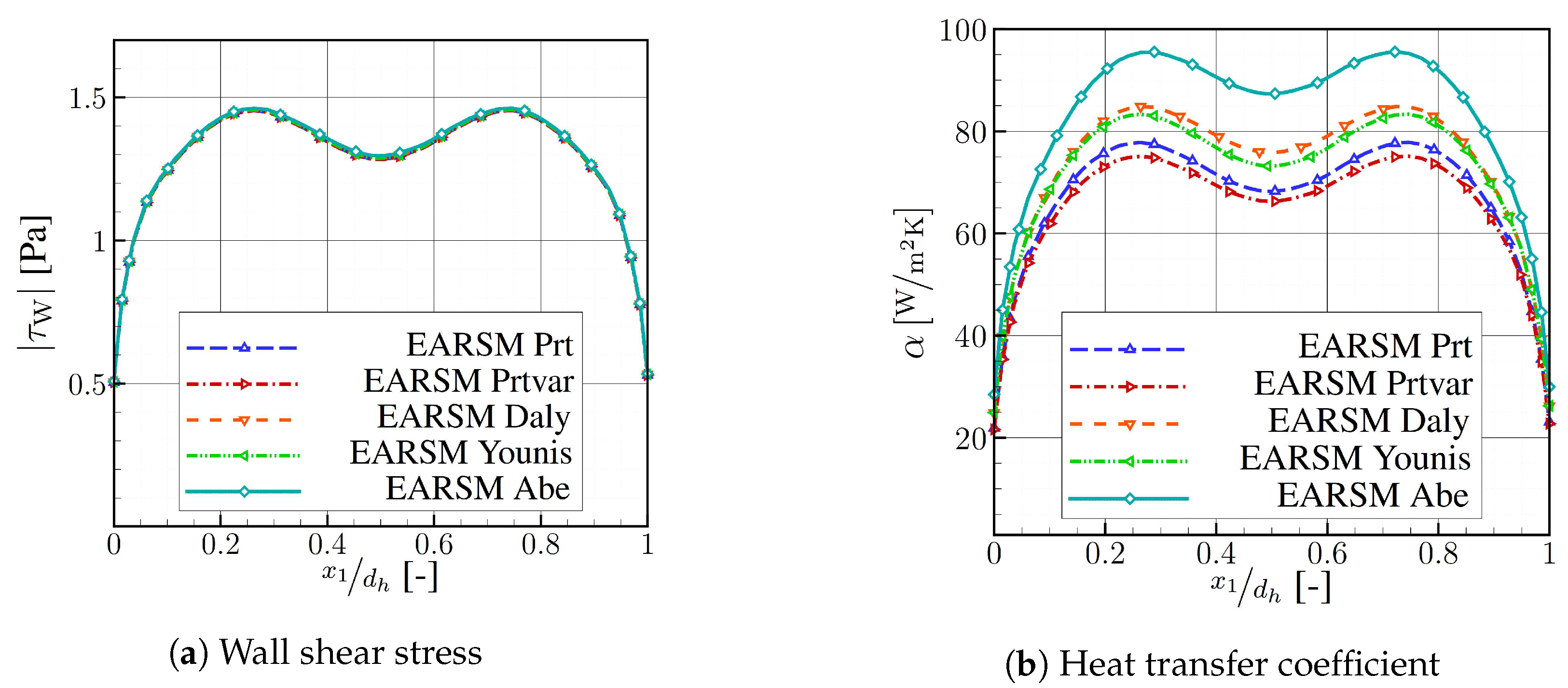
4.2. Ribbed Configuration
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| heat transfer coefficient | |
| heat flux | |
| T | temperature |
| dim.less wall distance | |
| hydraulic diameter | |
| density | |
| turb. dissipation rate | |
| dynamic viscosity | |
| shear stress | |
| Nusselt number | |
| Reynolds number | |
| Prandtl number | |
| e | rib height |
| h | specific enthalpy |
| C | constant |
| spec. heat capacity | |
| at const. pressure | |
| streamwise vorticity | |
| velocity | |
| coordinates | |
| pressure loss coeff. | |
| P | rib distance |
| k | turb. kinetic energy |
| thermal conductivity | |
| H | channel height |
| at const. pressure |
Sub-/Superscripts
| t | turbulent |
| fluctuation due to Favre averaging | |
| W | wall |
| Favre averaged | |
| i | index |
| Reynolds averaged |
References
- ERCOFTAC. Two-Dimensional Flow and Heat Transfer over a Smooth Wall with Square Sectioned Ribs. Available online: http://sgk.me.umist.ac.uk/workshop/ (accessed on 2 February 2013).
- Weihing, P.; Younis, B.A.; Weigand, B. Heat transfer enhancement in a ribbed channel: Development of turbulence closures. Int. J. Heat Mass Transf. 2014, 76, 509–522. [Google Scholar] [CrossRef][Green Version]
- Younis, B.A.; Weigand, B.; Spring, S. An Explicit Algebraic Model for Turbulent Heat Transfer in Wall-Bounded Flow With Streamline Curvature. J. Heat Transf. 2007, 129, 425–433. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Gibson, M.M.; Launder, B.E. Ground effects on pressure fluctuations in the atmospheric boundary layer. J. Fluid Mech. 1978, 86, 491–511. [Google Scholar] [CrossRef]
- Speziale, C.G.; Sarkar, S.; Gatski, T.B. Modelling the pressure-strain correlation of turbulence: an invariant dynamical systems approach. J. Fluid Mech. 1991, 227, 245–272. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Younis, B.A. Objective Model for the Fluctuating Pressure-Strain-Rate Correlations. J. Eng. Mech. 2009, 135, 1006–1014. [Google Scholar] [CrossRef]
- Rochhausen, S.; Krüppel, F.; Fiedler, J. Numerical Treatment of Turbulent Low-Mach-Flow for Turbine Cooling Applications. In Proceedings of the 11th World Congress on Computational Mechanics, Barcelona, Spain, 20–25 July 2014. [Google Scholar]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries, Inc.: Flintridge, CA, USA, 1993. [Google Scholar]
- Kays, W.M. Turbulent Prandtl Number—Where are we? ASME J. Heat Transf. 1994, 116, 195–284. [Google Scholar] [CrossRef]
- Nagano, Y.; Kim, C. A Two-Equation Model for Heat Transport in Wall Turbulent Shear Flows. J. Heat Transf. 1988, 110, 583–589. [Google Scholar] [CrossRef]
- Dietz, C.; Neumann, S.; Weigand, B. A comparative Study of the performance of explicit algebraic models for the turbulent heat flux. Numer. Heat Transf. 2007, 52(Part A), 101–126. [Google Scholar] [CrossRef]
- Vogel, J.C.; Eaton, J.K. Combined Heat Transfer and Fluid Dynamic Measurements Downstream of a Backward-Facing Step. J. Heat Transf. 1985, 107, 922–929. [Google Scholar] [CrossRef]
- Abe, K.; Suga, K. Towards the developement of a Reynolds-averaged algebraic turbulent scalar-flux model. Int. J. Heat Fluid Flow 2001, 22, 19–29. [Google Scholar] [CrossRef]
- Dietz, C. Computation of Heat Transfer in Internal Flows with Vortex-Generating Elements. Ph.D Thesis, Universität Stuttgart, Stuttgart, Germany, 2008. [Google Scholar]
- Kobiela, B. Wärmeübertragung in Einer Zyklonkühlkammer Einer Gastrubinenschaufel. Ph.D Thesis, Universität Stuttgart, Stuttgart, Germany, 2013. [Google Scholar]
- Wörz, B. Numerische Modellierung Turbulenter Strömung mit Wärmeübergang in Einer Konvektiv Gekühlten Turbinenschaufel. Ph.D Thesis, RWTH Aachen, Aachen, Germany, 2018. [Google Scholar]
- Han, J.C.; Zhang, Y.M.; Lee, C.P. Augmented Heat Transfer in Square Channels with Parallel, Crossed, and V-Shaped Angled Ribs. J. Heat Transf. 1991, 113, 590–596. [Google Scholar] [CrossRef]
- Grabe, M. Grundriss der Generalisierten Gauß’schen Fehlerrechnung; Springer: Berlin, Germany, 2011. [Google Scholar]
- Wieler, M. Experimentelle Untersuchung von Strömung und Wärmeübergang Konvektiver Kühlsysteme in Turbinenschaufeln. Ph.D Thesis, Universität Stuttgart, Stuttgart, Germany, 2007. [Google Scholar]
- Wallin, S.; Johannson, A.V. An explicit Algebraic Reynolds Stress Model for Incompressible and Compressible Turbulent Flows. J. Fluid Mech. 2000, 43, 89–132. [Google Scholar] [CrossRef]
- Daly, B.J.; Harlow, F.H. Transport Equations in Turbulence. Phys. Fluids 1970, 13, 2634–2649. [Google Scholar] [CrossRef]
- Roache, P.J. Quantivication of uncertainty in computational fluid dynamics. Ann. Rev. Fluid Mech. 1997, 29, 123–160. [Google Scholar] [CrossRef]
- Gnielinski, V. Ein neues Berechnungsverfahren für die Wärmeübertragung im Übergangsbereich zwischen laminarer und turbulenter Rohrströmung. Forsch. Ing. 1995, 61, 240–248. [Google Scholar] [CrossRef]


| Smooth | Ribbed | ||
|---|---|---|---|
| smooth | ribbed | ||
| wall | wall | ||
| 0.09 | 0.35 | 0.18 | |
| 0.075 | 0.1 | 0.1 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution NonCommercial NoDerivatives (CC BY-NC-ND) license (https://creativecommons.org/licenses/by-nc-nd/4.0/).
Share and Cite
Wörz, B.; Wieler, M.; Dehe, V.; Jeschke, P.; Rabs, M. Heat Transfer in a Square Ribbed Channel: Evaluation of Turbulent Heat Transfer Models. Int. J. Turbomach. Propuls. Power 2019, 4, 18. https://doi.org/10.3390/ijtpp4030018
Wörz B, Wieler M, Dehe V, Jeschke P, Rabs M. Heat Transfer in a Square Ribbed Channel: Evaluation of Turbulent Heat Transfer Models. International Journal of Turbomachinery, Propulsion and Power. 2019; 4(3):18. https://doi.org/10.3390/ijtpp4030018
Chicago/Turabian StyleWörz, Beate, Mark Wieler, Viola Dehe, Peter Jeschke, and Michael Rabs. 2019. "Heat Transfer in a Square Ribbed Channel: Evaluation of Turbulent Heat Transfer Models" International Journal of Turbomachinery, Propulsion and Power 4, no. 3: 18. https://doi.org/10.3390/ijtpp4030018
APA StyleWörz, B., Wieler, M., Dehe, V., Jeschke, P., & Rabs, M. (2019). Heat Transfer in a Square Ribbed Channel: Evaluation of Turbulent Heat Transfer Models. International Journal of Turbomachinery, Propulsion and Power, 4(3), 18. https://doi.org/10.3390/ijtpp4030018